УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
Е. М. Пантелова
В. А. Кисюк
О. С. Копылова
М. И. Кузин
ФГБОУ ВО Ставропольский государственный аграрный университет
Россия, г. Ставрополь
Аннотация: в данной статье мы рассмотрим применение уравнения Бернулли в гидродинамики, подробно рассмотрим вывод уравнения Бернулли для потока идеальной жидкости и для потока реальной жидкости.
Основным
уравнением гидродинамики считается полученное в 1738 году уравнение Даниила
Бернулли. Данное выражение демонстрирует закон сохранения энергии движущейся жидкости и создает
взаимосвязь между средней скоростью υ, давлением P, и пьезометрической
высотой z в разных сечениях потока.
Ключевые слова: уравнение Бернулли, жидкость, сечение, трубка Пито, энергия.
Рассмотрим трубопровод изменчивого диаметра, который расположен в пространстве под углом β (рис.1).
На данном участке трубопровода подберем произвольно два сечения: сечение 1-1 и сечение 2-2. От первого сечения ко второму ввысь по трубопроводу перемещается жидкость, расход которой равен Q.
Для того, что бы измерить давление жидкости применяются пьезометры – стеклянные трубки с тонкими стенками, в таких трубках жидкость поднимается на высоту .Уровень жидкости в пьезометрах, установленных в каждом из сечений, поднимается на разную высоту.
Рис.1 к выводу уравнения Бернулли для идеальной жидкости
Так же в сечениях 1-1 и 2-2 установлена трубка
с загнутым концом. Этот конец направлен навстречу потоку жидкости. Эти трубки
получили название трубки Пито. Если мы будем отсчитывать от пьезометрической
линии, то жидкость в таких трубках поднимется на разные уровни. Построим
пьезометрический отрезок следующим способом: если между заданными сечениями поставить
пару подобных пьезометров и провести в них кривую через показания уровней
жидкости, то мы получим зигзагообразную линию (рис.1).
Если мы будем отсчитывать от пьезометрической
линии, то жидкость в таких трубках поднимется на разные уровни. Построим
пьезометрический отрезок следующим способом: если между заданными сечениями поставить
пару подобных пьезометров и провести в них кривую через показания уровней
жидкости, то мы получим зигзагообразную линию (рис.1).
Относительно произвольной прямой 0-0, проходящей горизонтально, высота уровней в трубках Пито остается постоянной. Эту прямую назовем плоскостью сечения.
Уровень полной энергии трубопровода показывает горизонтальная линия, которая проведена, через показания уровней жидкости в трубках Пито.
Для сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли запишем в виде:
Так как два сечения подобранны произвольно, то полученное уравнение запишем иначе:
Данное уравнение можно прочесть следующим образом: сумма трех
членов уравнения Бернулли для любого сечения потока идеальной жидкости есть
величина постоянная.
z1 и z2 – удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;
и – удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
и – удельные кинетические энергии в тех же сечениях.
Таким образом, опираясь на уравнение Бернулли, мы получим, что в любом сечении полная удельная энергия идеальной жидкости остается постоянной.
Уравнение Бернулли можно объяснить геометрически. Дело в том, что
каждый член уравнения имеет линейную размерность. Смотря на рис.1 заметим, что
z
В данном случае уравнение Бернулли можно прочитать так: сумма
геометрической, пьезометрической и скоростной высоты для идеальной жидкости
есть величина постоянная.
Уравнение Бернулли для потока реальной жидкости и для потока идеальной жидкости немного различны, так как при движении реальной жидкости возникают силы трения, и что бы преодолеть эти силы жидкость тратит энергию. В результате полная удельная энергия жидкости в сечении 2-2 окажется меньше, чем в сечении 1-1, на величину потерянной энергии (рис.2)
Рис.2 к выводу уравнения Бернулли для реальной жидкости
Обозначим потерянную энергию (потерянный напор) за (имеет линейную размерность).
Запишем уравнение Бернулли для реальной жидкости в виде:
Из второго рисунка мы видим, что по мере того, как жидкость
движется от первого сечения ко второму потерянный напор (выделен штриховкой) во
время всего пути увеличивается. В итоге, уровень первоначальной энергии,
которой обладает жидкость в первом сечении, для второго сечения будет
складываться из четырех составляющих: геометрической высоты, пьезометрической
высоты, скоростной высоты и потерянного напора между двумя сечениями [7-10].
Коэффициенты и , которые зависят от режима течения жидкости, для ламинарного режима , а для турбулентного режима , называются коэффициентами Кориолиса. Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)
Рассмотрим пример решения задачи с помощью уравнения Бернулли.
В дождевальной установке вода подается сначала по трубе диаметром h2=40 мм, которая сужается до h1=24 мм. Статическое давление в широкой части трубы равно 250 кПа, скорость равна 14,4 м/с. Определить статическое давление в узкой части трубы. Плотность воды 103 кг/м3.
Решение.
Запишем уравнение неразрывности:
;
Получим, что скорость в узкой части трубки будет равна:
Уравнение Бернулли в данной задаче будет иметь вид:
Из этого уравнения выразим статическое давление в узкой части трубы:
Теперь найдем значение этого давления:
Мы получили, что статическое давление в узкой части дождевальной
установке равна .
Большая часть задач практической гидродинамики решается с помощью уравнения Бернулли. Для этого выбирают два сечения по длине потока жидкости, таким образом, чтобы для одного из них были известны величины: Р, ρ, g, а для другого сечения одна или две величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости, которое имеет вид: υ1ω 1 = υ2ω2.
1. Афанасьева В.С., Копылова О.С., Афанасьев М.А., Копылов В.Б. Проектирование урока физики в 8 классе по теме: «Изменение агрегатных состояний вещества» с учетом ФГОС // НаукаПарк. – 2014. – № 5 (25). – С. 2-9.
2.
Афанасьев М.А., Гуцевич А.А., Кисюк В.А., Хутов К.М.В., Якуба И.В.
Проектирование лабораторной работы по
гидростатическому давлению // В сборнике: Физико-технические проблемы создания новых технологий в агропромышленном
комплексе / Ставрополь.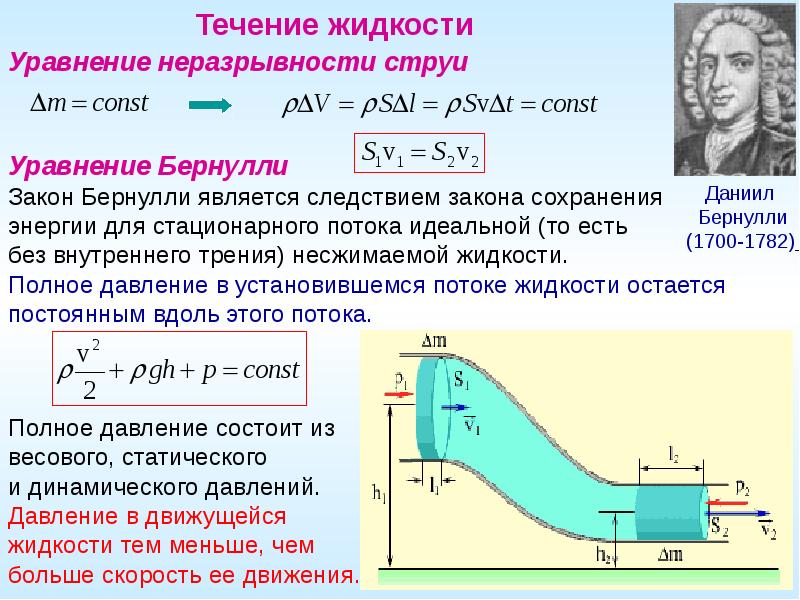 – 2015. – С. 11-15.
– 2015. – С. 11-15.
3. Вечер О.В., Хащенко А.А., Воробьев И.Н., Афанасьев М.А. Теоретический анализ скорости испарения жидкости с поверхности раздела двух жидких фаз // В сборнике: Применение современных ресурсосберегающих инновационных технологий в АПК III Международная научно-практическая конференция. / Ставрополь. – 2013. – С. 29-31.
4. Герасимов Е.В., Кисюк В.А., Овсянников С.А. Перспективы утилизации тепловых потерь двигателя // В сборнике: Актуальные проблемы научно-технического прогресса в АПК VII Международная научно-практическая конференция в рамках XIX Международной агропромышленной выставки “Агроуниверсал – 2013”. / Ставрополь. – 2013. – С. 69-73.
5.
Герасимов Е.В., Кисюк В.А., Алексеенко В.А., Сидельников Д.А. Определение режимных и конструктивных параметров работы обезвоживающего
устройства // В сборнике: Актуальные проблемы научно-технического прогресса в АПК Сборник научных статей XII Международной научно-практической
конференции, в рамках XVIII Международной агропромышленной выставки
“Агроуниверсал – 2016”.
6. Любая С.И., Стародубцева Г.П., Афанасьев М.А., Копылова О.С. Практикум для лабораторных работ по физике – Ставрополь, 2015.
7. Меньщиков А.В., Хащенко А.А., Афанасьев М.А. Общая характеристика процесса кипения жидкости и его применение в современной теплоэнергетике // В сборнике: Новые технологии в сельском хозяйстве и пищевой промышленности с использованием электрофизических факторов и озона VII Всероссийская научно-практическая конференция. / Ставрополь. – 2012. – С. 113-115.
8. Хайновский В.И., Горохов А.В., Афанасьев М.А. Методы и точность измерения коэффициента поверхностного натяжения жидкостей // В сборнике: Физико-технические проблемы создания новых технологий в агропромышленном комплексе III Российская научно-практическая конференция. / Ставрополь. – 2005. – С. 227-232.
9.
Хащенко А.А., Меньщиков А.В., Афанасьев М.А., Воробьев И.Н. Экспериментальное исследование величины перегретого слоя жидкости при
кипении // В сборнике: Новые технологии в сельском хозяйстве и пищевой промышленности с
использованием электрофизических факторов и озона VII Всероссийская научно-практическая конференция. /
Ставрополь. – 2012. – С. 111-112.
/
Ставрополь. – 2012. – С. 111-112.
10. Хащенко А.А., Меньщиков А.В., Афанасьев М.А., Пуля А.В., Коробов А.Ю. Экспериментальное исследование процессов испарения и кипения жидкостей // В сборнике: Новые технологии в сельском хозяйстве и пищевой промышленности с использованием электрофизических факторов и озона VII Всероссийская научно-практическая конференция. / Ставрополь. – 2012. – С. 108-111.
Сведения об авторе:
Пантелова Елизавета Михайловна – студентка 2 курса электроэнергетического факультета СтГАУ
Кисюк Василий Адамович – к. с. х. н., доцент кафедры физики СтГАУ
Копылова Оксана Сергеевна – к. ф. м. н., доцент кафедры физики СтГАУ
Кузин Михаил Игоревич – студент 4 курса электроэнергетического факультета СтГАУ
E. M. Pantelova
O. S. Kopylova
S. Kopylova
V. A. Kisuk
M. I. Kuzin
BERNOULLI’S EQUATION FOR IDEAL FLUID
Summary: in this article we will discuss the application of Bernoulli’s equation in fluid dynamics, a detailed look at the output of the Bernoulli’s equation for fluid flow and for the flow of a real fluid.
The basic equation of hydrodynamics is deemed to be received in 1738 Daniel Bernoulli equation. This expression demonstrates the law of conservation of energy of a moving fluid and creates a relationship between the average velocity υ, the pressure P, and the piezometric elevation z in the different sections of the stream. Many problems are solved using this equation.
Keywords: Bernoulli’s equation, liquid, section, Pitot’s tube, energy.
References:
1. Afanasyeva V. S., Kopylova O. S., Afanasiev M. A., Kopylov V.
B. Design of physics lessons in 8th grade on the topic: “Changing
aggregate States of substances” taking into account GEF // Naukar. – 2014.
– № 5 (25). – Pp. 2-9.
– 2014.
– № 5 (25). – Pp. 2-9.
2. Afanasyev M. A., Gutsevich, A., Kisuk V. A., Hytov, K.-M. V., Yakuba, I. V. Design of the laboratory work on hydrostatic pressure // In book: Physical-technical problems of creation of new technologies in agroindustrial complex / Stavropol. – 2015. – S. 11-15.
3. Vecher O. V., Khashchenko A. A., Vorob’ev I. N., Afanasyev M. A., Theoretical analysis of rate of evaporation of liquid from the surface of section of two liquid phases // In the book: the Use of modern resource-saving innovative technologies in agriculture III international scientific-practical conference. / Stavropol. – 2013. – P. 29-31.
4. Gerasimov E. V., Kisuk V. A., Ovsyannikov S. A. Prospects of
the use of thermal losses of the motor // In collection: Actual problems of
scientific-technical progress in agriculture VII international scientific-practical
conference in the framework of the XIX International agricultural exhibition
“Agrouniversal – 2013”. / Stavropol. – 2013. – P. 69-73.
– 2013. – P. 69-73.
5. Gerasimov E. V., Kisuk V. A., Alekseenko V. A., Sidelnikov D. A. Definition of operating and design parameters of the dewatering device // In collection: Actual problems of scientific-technical progress in agriculture the Collection of scientific articles of the XII International scientific-practical conference in the framework of the XVIII International agricultural exhibition “Agrouniversal – 2016”. / Stavropol. – 2016. – Pp. 273-277.
6. Lybaya S. I., Starodubtseva G. P., Afanasyev M. A., Kopylova O. S. Practicum for laboratory works on physics – Stavropol, 2015.
7. Menshikov V. A., Khashchenko A. A., Afanasyev M. A. General description of the process of boiling liquid and its application in modern power system // proceedings: New technologies in agriculture and food industry with the use of electro-physical factors and ozone VII all-Russian scientific-practical conference. / Stavropol. – 2012. – P. 113-115.
8. Khainovskii V. I., Gorokhov A. V., Afanasyev M. A. Methods and
accuracy of measurement of surface tension of liquids // In the book: Physical
and technical problems of creation of new technologies in agriculture III
Russian scientific-practical conference. / Stavropol. – 2005. – S. 227-232.
V., Afanasyev M. A. Methods and
accuracy of measurement of surface tension of liquids // In the book: Physical
and technical problems of creation of new technologies in agriculture III
Russian scientific-practical conference. / Stavropol. – 2005. – S. 227-232.
9. Khashchenko A. A., Menshikov A. V., Afanasyev M. A., Vorob’ev I. N. Experimental study of the value of a superheated layer of liquid at boiling // In the book: New technologies in agriculture and food industry with the use of electro-physical factors and ozone VII all-Russian scientific-practical conference. / Stavropol. – 2012. – S. 111-112.
10. Khashchenko A. A., Menshikov A. V., Afanasyev M. A., Pulia A. V., Korobov Y. A. Experimental study of the processes of evaporation and boiling of liquids // proceedings: New technologies in agriculture and food industry with the use of electro-physical factors and ozone VII all-Russian scientific-practical conference. / Stavropol. – 2012. – P. 108-111.
Уравнение Бернулли для потока реальной жидкости
В реальных потоках
жидкости присутствуют силы вязкого
трения. В результате слои жидкости
трутся друг об друга в процессе движения.
На это трение затрачивается часть
энергии потока. По этой причине в процессе
движения неизбежны потери энергии. Эта
энергия, как и при любом трении,
преобразуется в тепловую энергию. Из-за
этих потерь энергия потока жидкости по
длине потока, и в его направлении
постоянно уменьшается. Т.е. напор потока Hпотока в направлении движения потока становится
меньше. Если рассмотреть два соседних
сечения 1-1 и 2-2, то
потери гидродинамического напора Δh составят:
В результате слои жидкости
трутся друг об друга в процессе движения.
На это трение затрачивается часть
энергии потока. По этой причине в процессе
движения неизбежны потери энергии. Эта
энергия, как и при любом трении,
преобразуется в тепловую энергию. Из-за
этих потерь энергия потока жидкости по
длине потока, и в его направлении
постоянно уменьшается. Т.е. напор потока Hпотока в направлении движения потока становится
меньше. Если рассмотреть два соседних
сечения 1-1 и 2-2, то
потери гидродинамического напора Δh составят:
,
где H1-1– напор в первом сечении потока жидкости,
H2-2 – напор во втором сечении потока,
∆h – потерянный напор – энергия, потерянная
каждой единицей веса движущейся жидкости
на преодоление сопротивлений на пути
потока от сечения 1-1 до сечения 2-2.
С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть
Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.
Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём
.
Изменение энергии
по длине потока удобно проследить на
графиках.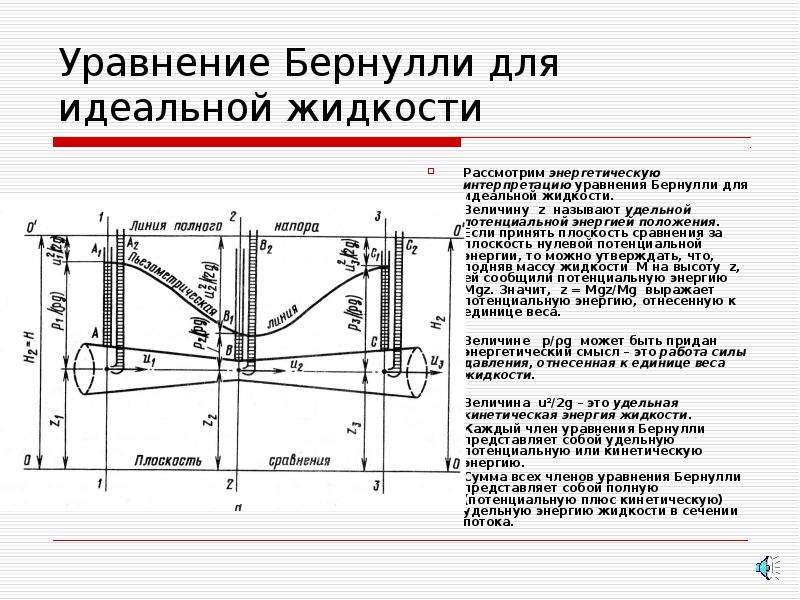 Из
уравнения Бернулли
для потока реальной жидкости (закона
сохранения энергии) видно, что
гидродинамическая линия для потока
реальной жидкости (с одним источником
энергии) всегда ниспадающая. То же
справедливо и для пьезометрической
линии, но только в случае равномерного
движения, когда скоростной напор а уменьшение напора происходит только
за счёт изменения потенциальной энергии
потока, главным образом за счёт уменьшения
давления P.
Из
уравнения Бернулли
для потока реальной жидкости (закона
сохранения энергии) видно, что
гидродинамическая линия для потока
реальной жидкости (с одним источником
энергии) всегда ниспадающая. То же
справедливо и для пьезометрической
линии, но только в случае равномерного
движения, когда скоростной напор а уменьшение напора происходит только
за счёт изменения потенциальной энергии
потока, главным образом за счёт уменьшения
давления P.
Пьезометрическим уклоном называют изменение удельной потенциальной энергии жидкости вдоль потока, приходящееся на единицу его длины.
Если
гидравлический уклон всегда положителен,
то пьезометрический может быть и
положительным, и отрицательным. При
равномерном движении жидкости, когда
скорость по длине потока не изменяется,
скоростной напор вдоль потока v2 / (2g) = const. Следовательно, пьезометрическая линия
параллельна энергетической, и
пьезометрический уклон равен
гидравлическому.
Следовательно, пьезометрическая линия
параллельна энергетической, и
пьезометрический уклон равен
гидравлическому.
Изменение удельной потенциальной энергии положения вдоль потока жидкости, приходящееся на единицу длины, называют геометрическим уклоном i и определяют по формуле
где l — расстояние между сечениями потока.
Сформулируем два условия применимости к потоку жидкости уравнения Бернулли: 1) движение жидкости должно быть установившимся; 2) движение жидкости в сечениях 1—2, 2—2 и 3—3,cоединяемых уравнением Бернулли, должно быть параллельно струйным или плавноизменяющимся, в промежутке же между сечениями 1—1, 2—2 и 3—3 движение жидкости может быть и резко меняющимся.
Hа
применении уравнения Бернулли основан
принцип действия приборов для измерения
скоростей и расходов жидкости. Одним
из таких приборов является расходомер
Вентури, состоящий
из двух
конических отрезков трубы, узкие концы
которых соединены
коротким цилиндрическим патрубком
длиной менее 10
диаметров
трубопровода (отношение диаметра
конфузора и диффузора соответственно d/D=:0,3. ..0,7). Принцип работы расходомера Вентури
базируется на уравнении Бернулли и
уравнении неразрывности потока, а также
на том, что перепад давлений на диафрагме,
измеряемый пьезометром либо дифманометром
пропорционален квадрату протекающего
через нее расхода
..0,7). Принцип работы расходомера Вентури
базируется на уравнении Бернулли и
уравнении неразрывности потока, а также
на том, что перепад давлений на диафрагме,
измеряемый пьезометром либо дифманометром
пропорционален квадрату протекающего
через нее расхода
Для определения местных скоростей при плавноизменяющемся безнапорном движении применяют метод Пито. Трубку, нижний конец которой изогнут под прямым углом, опускают навстречу потоку, и жидкость в трубке начинает подниматься над свободной поверхностью, где давление равно атмосферному, на высоту .
При определении местных скоростей в напорном потоке используют систему из двух трубок, одна из которых представляет собой обычный пьезометр, показывающий напор Р/, а другая,только что описанная, измеряет величину напора
Разность уровней в обеих трубках h представляет собой скоростной напор
Местные скорости находят с помощью трубки Пито по формуле
где k– поправочный коэффициент, определяемый для каждой трубки опытным путем
Уравнение Бернулли для потока и струйки жидкости
Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т. е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
Уравнение Бернулли выглядит так:
Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.
Содержание статьи
Смысл уравнения Бернулли
По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.
Отсюда вытекает, что поскольку член υ2/2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.
В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т. е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.
е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.
Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.
Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.
Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную
h = p/(ρ*g)
или
g*h = p/ρ
Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.
В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид
В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид
Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.
Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.
Отсюда следует, что между напором и удельной энергией существует очень простая зависимость
Н = э / g,
где э – удельная энергия
Уравнение Бернулли для элементарной струйки реальной жидкости
Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.
При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.
Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.
Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет
Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается
Величина Э1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.
Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде
Уравнение Бернулли для потока реальной жидкости
Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.
Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.
Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.
В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.
Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.
Слагаемое h1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
– hлп – линейные потери – сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
– hмп – местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости
Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет
h1-2 = hлп + hмп
Видео по теме
Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.
Вместе со статьей “Уравнение Бернулли для потока и струйки жидкости” читают:
Физические основы механики
При течении жидкости ее отдельные слои в общем случае текут с разными скоростями, скользят друг относительно друга, вследствие чего между ними возникают силы трения. Эти силы называют силами внутреннего трения. Они возникают не только в жидкостях, но и в газах.
Эти силы называют силами внутреннего трения. Они возникают не только в жидкостях, но и в газах.
Жидкость, в которой внутреннее трение (вязкость) полностью отсутствует, называется идеальной.
Выделим в стационарно текущей идеальной жидкости трубку тока, ограниченную сечениями и , по которой слева направо течет жидкость (рис. 9.12). Пусть в месте сечения заданы: скорость течения , давление и высота , на которой расположено это сечение. Аналогично, в месте сечения заданы скорость течения , давление и высота .
Рис. 9.12. К выводу уравнения Бернулли
За время объём жидкости переместится вдоль трубки тока, причем сечение переместится в положение , пройдя путь , сечение переместится в положение , пройдя путь . В силу уравнения непрерывности струи заштрихованные объёмы будут иметь одинаковую величину: .
Энергия каждой частицы жидкости слагается из её кинетической энергии и потенциальной энергии в поле сил тяжести. Полная энергия потока, протекающего за время через сечение , равна
Полная энергия потока, протекающего за время через сечение , равна
Аналогичное выражение для энергии потока имеем для сечения :
При стационарном течении между сечениями и энергия не накапливается. В идеальной жидкости силы трения отсутствуют, так что механическая энергия никуда не исчезает. Следовательно, изменение полной энергии жидкости равно работе, совершенной внешними силами
Силы давления на боковую поверхность трубки тока перпендикулярны в каждой точке к направлению перемещения частиц, вследствие чего работы не совершают. Отлична от нуля лишь работа сил давления, приложенных к сечениям и . Эта работа равна
Приравнивая изменение энергии потока работе сил давления , находим:
Сократив на и перенеся члены с одинаковыми индексами в одну часть равенства, получаем:
Сечения и были взяты совершенно произвольно. Поэтому можно утверждать, что
В стационарно текущей идеальной несжимаемой жидкости в любом сечении трубки тока величина
имеет одно и то же значение, другими словами, вдоль трубки тожа эта величина постоянна
Полученное нами соотношение называется уравнением Бернулли. Это уравнение выражает собой закон сохранения механической энергии при стационарном течении несжимаемой идеальной жидкости.
Это уравнение выражает собой закон сохранения механической энергии при стационарном течении несжимаемой идеальной жидкости.
В частном случае горизонтального течения жидкости уравнение Бернулли принимает вид
Из уравнения непрерывности
следует, что в месте сужения потока его скорость возрастает, а из уравнения Бернулли — что в этом месте падает давление.
Рис. 9.13. Скорости жидкости и давление в зависимости от сечения трубки
Когда идущие параллельными курсами корабли находятся слишком близко друг к другу, давление между ними падает и давление внешнего потока их сближает, и может привести к столкновению судов.
Пример. В сосуде проделано небольшое отверстие. Высота жидкости над отверстием равна . Найдем скорость вытекающей струи.
Применим уравнение Бернулли. В качестве сечения возьмем поверхность жидкости, а за сечение примем проделанное отверстие. Давления в обоих сечениях можно считать постоянными (и равными атмосферному). Скоростью жидкости в сечении можно пренебречь (если площадь сосуда много больше площади отверстия: >> ) Тогда имеем:
Скоростью жидкости в сечении можно пренебречь (если площадь сосуда много больше площади отверстия: >> ) Тогда имеем:
где — высота сечения над сечением (то есть уровень жидкости над отверстием), a — скорость истечения жидкости из отверстия. Получаем в итоге:
Указанное соотношение называется формулой Торричелли. Заметим, что скорость истечения струи равна скорости свободного падения тела с той же высоты. Это не удивительно, так как в основе обоих результатов лежит закон сохранения энергии при движении в однородном поле сил тяжести.
Рис. 9.14. Истечение жидкости из отверстия
Выводя уравнение Бернулли, мы пренебрегли сжимаемостью жидкости. Что касается газов, их сжимаемость намного больше, чем у жидкостей. Получим оценку применимости уравнения Бернулли к течению газов. Величина , называемая динамическим давлением, должна быть мала по сравнению со статическим давлением . Тогда колебания давления вследствие течения газа будут невелики и его сжимаемостью можно пренебречь. Следовательно, критерием применимости уравнения Бернулли к газам служит неравенство
Следовательно, критерием применимости уравнения Бернулли к газам служит неравенство
или
Приведем численную оценку. При нормальных условиях давление воздуха приблизительно равно 105 Па, а плотность воздуха 1,29 кг/м3. Отсюда
Это число близко к скорости звука и отличается от неё только коэффициентом 2 под знаком корня: в выражении для скорости звука под знаком корня стоит показатель адиабаты , равный для воздуха при комнатных температурах 1,4. Как будет видно позже, это не случайно, поэтому критерий применимости к газу приближения «несжимаемой жидкости», в котором он считается несжимаемым, можно сформулировать так. Можно пренебречь сжимаемостью газа при скоростях его течения много меньших скорости звука в этом газе:
При таких скоростях мы можем применять уравнение Бернулли к газам с тем же успехом, что и к жидкостям.
|
Уравнение Бернулли для потока реальной (вязкой) жидкости При переходе от элементарной струйки идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему конечные размеры и ограниченному стенками, необходимо учесть неравномерность распределения скоростей по сечению, а также потери энергии (напора). То и другое является следствием вязкости жидкости. При движении вязкой жидкости вдоль твердой стенки, например, в трубе, происходит торможение потока вследствие влияния вязкости, а также из-за действия сил молекулярного сцепления между жидкостью и стенкой. Поэтому наибольшего значения скорость достигает в центральной части потока, а по мере приближения к стенке она уменьшается практически до нуля. Получается распределение скоростей, подобное тому, которое показано на рис. 1.26. 2 + Р/(Рё) = const, т. е. предполагаем, что при движении жидкости отдельные струйки оказывают одна на другую в поперечном направлении такое же давление, как слои жидкости в неподвижном состоянии. Если умножить числитель и знаменатель выражения (1.54) на р/2, то нетрудно убедиться, что коэффициент а представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечении, но при равномерном распределении скоростей. * Это можно доказать, если в формуле (1.54) скорость v выразить в виде суммы v — i’cp + Ди, интеграл разбить на четыре интеграла и проанализировать численное значение каждого из них. Это и есть уравнение Бернулли для потока вязкой жидкости. От аналогичного уравнения для элементарной струйки идеальной жидкости полученное уравнение отличается членом, представляющим собой потерю полного напора, и коэффициентом, учитывающим неравномерность распределения скоростей. Кроме того, скорости, входящие в это уравнение, являются средними по сечениям. Если для струйки идеальной жидкости уравнение Бернулли представляет собой закон сохранения механической энергии, то для потока реальной жидкости оно является уравнением баланса энергии с учетом потерь. Энергия, теряемая жидкостью на рассматриваемом участке течения, разумеется, не исчезает бесследно, а лишь превращается в другую форму — тепловую. Так как удельная теплоемкость жидкостей обычно велика по сравнению с потерями удельной энергии, а также ввиду того, что тепловая энергия непрерывно рассеивается, повышение температуры часто бывает практически малозаметным. |
Уравнение Бернулли для потока реальной (вязкой) жидкости
Содержание:
Уравнение Бернулли для потока реальной (вязкой) жидкости
Уравнение Бернулли для потока реальной (вязкой) жидкости. Неоднородность следует учитывать при переходе от основного течения идеальной жидкости к действительному (вязкому) потоку жидкости, который имеет конечные размеры и ограничен величиной потока.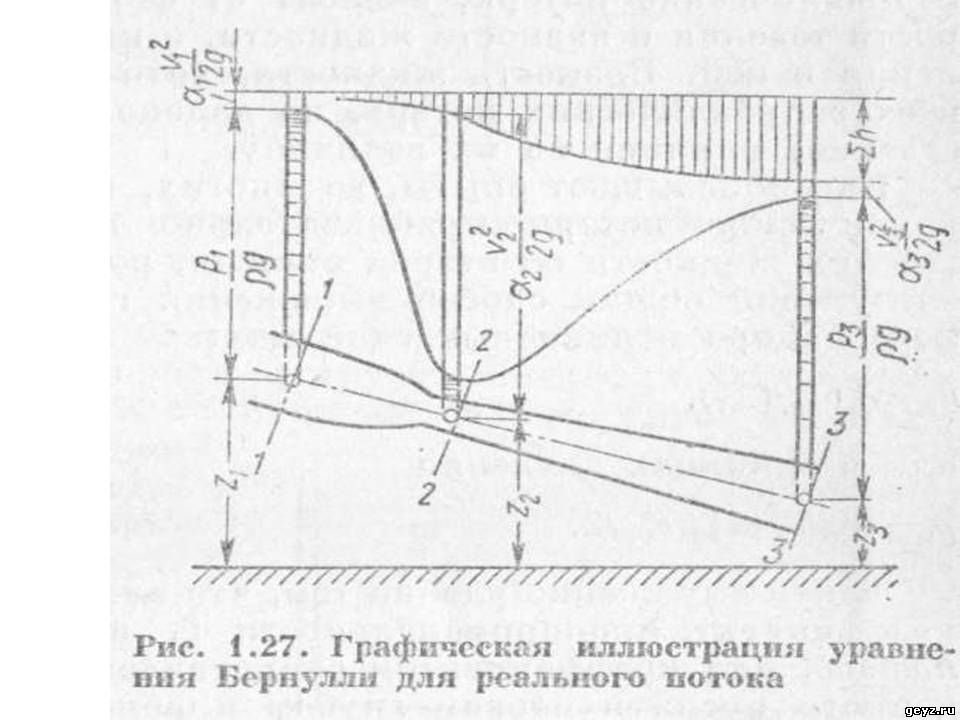 Сорок четыре Распределение скорости поперечного сечения и потери энергии (набор).DRU * oe с ним является результатом вязкости жидкости. Когда вязкая жидкость движется, например, вдоль твердой стенки в трубе, поток замедляется из-за эффектов вязкости и молекулярной агрегации между жидкостью и стенкой. Поэтому расход достигает максимального значения в центральной части потока, а по мере приближения к стенке он уменьшается почти до zero.
Сорок четыре Распределение скорости поперечного сечения и потери энергии (набор).DRU * oe с ним является результатом вязкости жидкости. Когда вязкая жидкость движется, например, вдоль твердой стенки в трубе, поток замедляется из-за эффектов вязкости и молекулярной агрегации между жидкостью и стенкой. Поэтому расход достигает максимального значения в центральной части потока, а по мере приближения к стенке он уменьшается почти до zero.
Поэтому то, что мы рассматриваем, является именно таким (или близким к ним) поперечным сечением. Вводим понятие мощности потока. Людмила Фирмаль
- As в результате получено распределение скоростей, показанное на рисунке. 1.26. Неравномерное распределение скорости означает, что некоторые слои или части жидкости скользят (сдвигаются) по другим слоям, что приводит к тангенциальным напряжениям (напряжениям трения).кроме того, движение вязких жидкостей часто сопровождается вращением частиц, образованием вихрей и перемешиванием.
 Все это требует энергозатрат. Таким образом, удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а равномерно рассеивается, преодолевая сопротивление, и поэтому уменьшается вдоль потока. Из-за неравномерного распределения скорости следует учитывать среднюю поперечную скорость gsr(см. 1.13) и среднее значение удельной энергии жидкости в этом сечении.
Все это требует энергозатрат. Таким образом, удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а равномерно рассеивается, преодолевая сопротивление, и поэтому уменьшается вдоль потока. Из-за неравномерного распределения скорости следует учитывать среднюю поперечную скорость gsr(см. 1.13) и среднее значение удельной энергии жидкости в этом сечении.
Прежде чем приступить к рассмотрению уравнения Бернулли для течения вязкой жидкости, сделайте следующие допущения: Основной закон гидростатического давления заключается в том, что в пределах рассматриваемого поперечного сечения потока, например、 (1.21), то есть гидростатическое давление в секции имеет одинаковое значение для всех точек в указанной секции: Р + Р1 (ФВ)= То есть, когда жидкость движется, мы предполагаем, что отдельные потоки оказывают такое давление друг на друга сбоку, когда слой жидкости находится в покое. Это факт, который теоретически может быть доказан, если поток этих поперечных сечений является арарелетом.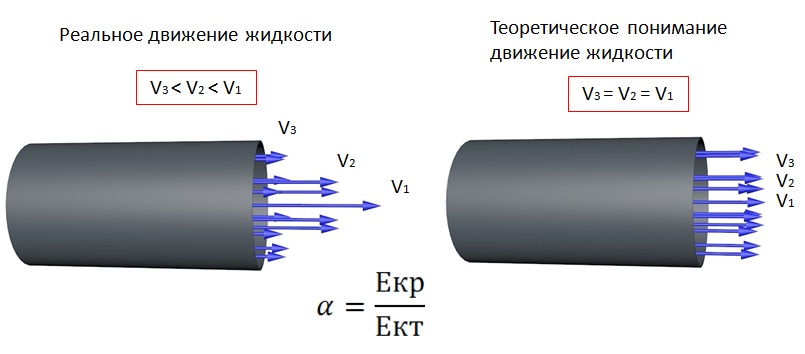 ср% 8 4-2 в、 (1.55) используя выражение # cf, вышеупомянутое выражение не может быть продублировано следующим образом: Это уравнение Бернулли*для течения вязкой жидкости. velocity. In кроме того, скорость, включенная в эту формулу, усредняется по всему участку. Умножьте уравнение (1.55) на форму уравнения Бернулли, соответствующую формуле (1.48).Где термин обозначает вид энергии на единицу массы, а термин № 2-С обозначает потерю удельной энергии жидкости. Умножение уравнения (-1.55) на p # дает 3-ю форму, описывающую уравнение Бернулли для течения вязкой жидкости, соответственно.
ср% 8 4-2 в、 (1.55) используя выражение # cf, вышеупомянутое выражение не может быть продублировано следующим образом: Это уравнение Бернулли*для течения вязкой жидкости. velocity. In кроме того, скорость, включенная в эту формулу, усредняется по всему участку. Умножьте уравнение (1.55) на форму уравнения Бернулли, соответствующую формуле (1.48).Где термин обозначает вид энергии на единицу массы, а термин № 2-С обозначает потерю удельной энергии жидкости. Умножение уравнения (-1.55) на p # дает 3-ю форму, описывающую уравнение Бернулли для течения вязкой жидкости, соответственно.
Смотрите также:
Методические указания по гидравлике
Возможно эти страницы вам будут полезны:
- Уравнение Бернулли для элементарной струйки идеальной жидкости.
- Вывод дифференциальных уравнений движения, идеальной жидкости и их интегрирование.
- Гидравлические потери (общие сведения).
- Уравнение Бернулли для относительного движения.

течение жидкостей. Режимы, смысл, решение
Как закон Всемирного Тяготения Ньютона действовал задолго до самого Ньютона, так и уравнение Бернулли существовало задолго до того, как родился сам Бернулли. Ему удалось лишь облечь это уравнение в наглядную форму, в чем его неоспоримая и огромная заслуга. Зачем мне уравнение Бернулли, спросите Вы, ведь я прекрасно жил и без него. Да, но оно может пригодиться Вам хотя бы на экзамене по гидравлике! Как говорится, «все не так уж плохо, если ты знаешь и можешь сформулировать уравнение Бернулли».
Кто такой Бернулли?
Даниил Бернулли – сын известного ученого Якоба Бернулли, швейцарский математик и физик. Жил с 1700 по 1782 годы, а с 1725 по 1733 трудился в Петербургской Академии наук. Помимо физики и математики Бернулли также изучал медицину наряду с Д’Аламбером и Эйлером считается отцом основателем математической физики. Успехи этого человека позволяют с уверенностью сказать, что это был настоящий «супермозг».
Успехи этого человека позволяют с уверенностью сказать, что это был настоящий «супермозг».
Д. Бернулли (1700-1782)
Идеальная жидкость и течение идеальной жидкости
Помимо известной нам материальной точки и идеального газа существует также идеальная жидкость. Какой-нибудь студент, конечно, может подумать, что эта жидкость – его любимое пиво или кофе, без которого невозможно жить. Но нет, идеальная жидкость – это жидкость, которая абсолютно несжимаема, лишена вязкости и теплопроводности. Тем не менее, такая идеализация дает вполне хорошее описание движения реальных жидкостей в гидродинамике.
Течением жидкости называется движение ее слоев относительно друг друга или относительно всей жидкости.
Помимо того есть разные режимы течения жидкости. Нас интересует тот случай, когда скорость потока в какой-то конкретной точке не меняется со временем. Такой поток называют стационарным. При этом скорость течения в различных точках стационарного потока может различаться.
При этом скорость течения в различных точках стационарного потока может различаться.
Поток жидкости– совокупность частиц движущейся жидкости.
Поток жидкости
Вывод уравнения Бернулли
Но как описать движение жидкости? Для этого нам нужно знать вектор скорости частиц, точнее зависимость его от времени. Совокупность скоростей в разных точках потока дает поле вектора скорости.
Рассмотрим стационарное течение жидкости по трубке. В одном месте сечение этой трубки равно S1, а в другой – S2. При стационарном потоке через оба сечения за одинаковый промежуток времени пройдет одинаковое количество жидкости.
Данное уравнение – уравнение неразрывности струи.
К выводу уравнения Бернулли
Узнав его, Бернулли решил установить связь между давлением и скоростью жидкости в разных сечениях. Полное давление – это сумма статистического (обусловлено потенциальной энергией жидкости) и динамического давлений (обусловлено кинетической энергией). Оказывается, сумма статического и динамического давлений в любом сечении трубы постоянна. Само же уравнение Бернулли имеет вид:
Оказывается, сумма статического и динамического давлений в любом сечении трубы постоянна. Само же уравнение Бернулли имеет вид:
Смысл уравнения Бернулли
Физический смысл уравнения Бернулли. Уравнение Бернулли является следствием закона сохранения энергии. Первый член уравнения Бернулли – это кинетическая энергия, второе слагаемое уравнения Бернулли – потенциальная энергия в поле силы тяжести, третье – работа силы давления при подъеме жидкости на высоту h.
Вот и все, друзья, не так уж и страшно. Совсем немного времени, а Вы уже знаете уравнение Бернулли. Даже если Вы не знаете больше ничего, с этими знаниями идти на экзамен или зачет гораздо лучше, чем просто так. А если Вам необходима помощь в том, как решать задачи на уравнение Бернулли – не стесняйтесь и оформляйте заявку. После того как наши авторы распишут решение уравнения Бернулли максимально подробно, у Вас не останется пробелов в знаниях.
Автор: Иван
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Динамика идеальных жидкостей
Динамика идеальных жидкостейДинамика идеальных жидкостей
Предположим, вы создали фонтанчик для воды в помещении. Вы соединили отрезки трубы разного диаметра в дорожку. по которому будет течь вода. Вы также вставили насос в цепь. Очень простая схема показана на рисунке на право.
Поработав насос на некоторое время, вода ускорится и начнет течь.
Насос создает градиент давления .Если мы
посмотрите на объем V воды на прямом участке трубы, пока вода
ускорения, то давление на стороне 1 этого объема отличается от давления
давление на стороне 2. Это приводит к действию чистой силы на объем воды в этом
раздел, и объем воды ускоряется.
Когда вода течет с выбранной скоростью, насос должен делать намного меньше работай. Если бы давление было одинаковым с обеих сторон объема V, то чистая сила будет равна нулю, и объем воды продолжит движение с постоянная скорость.Однако по-прежнему будет небольшой градиент давления из-за силам трения. Теперь насос должен работать только против трения. силы. Вода вязкая, между ее составляющими возникает трение. молекулы, скользящие друг мимо друга и мимо стенок контейнеров. В среде без трения насос больше не будет нужен, чтобы поддерживать поток воды. Такая среда без трения действительно может быть созданный. В то время как большинство жидкостей замерзают при почти нулевой абсолютной температуре, жидкость гелий становится сверхтекучей .Он течет без трения. Вам не нужна помпа для поддержания работы фонтана с сверхтекучим жидким гелием.
Ссылка: Сверхтекучий гелий (Youtube)
Уравнение неразрывности
Идеальные жидкости несжимаемы и текут стабильно без трения.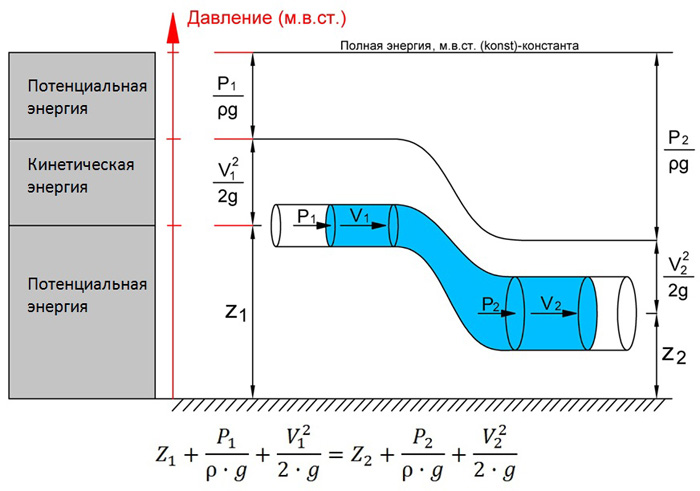 Поток ламинарный и может быть представлен графически как оптимизирует .
В прямом участке трубы с постоянной площадью поперечного сечения вся жидкость
частицы движутся с одинаковой скоростью.Различные линии тока не пересекаются.
Поток ламинарный и может быть представлен графически как оптимизирует .
В прямом участке трубы с постоянной площадью поперечного сечения вся жидкость
частицы движутся с одинаковой скоростью.Различные линии тока не пересекаются.
Для простоты предположим, что среда без трения Эта вода – идеальная жидкость, которая постоянно течет по контуру. Вода в секциях контур на разной высоте имеет разную гравитационную потенциальную энергию на единицу объема. На участках трубы с разной площадью поперечного сечения вода также должны иметь разную кинетическую энергию на единицу объема. В более узком в секциях трубы она должна течь быстрее, чем в более широких секциях, поскольку через каждое поперечное сечение должно проходить одинаковое количество воды. площадь за такое же количество времени.
Посмотрите на определенный объем воды. При движении граница 1 перемещает
расстояние l 1 , в то время как граница 2 перемещается на расстояние l 2 . Поскольку вода несжимаема, имеем
Поскольку вода несжимаема, имеем
Том 1 = Том 2,
(Том 1) / Δt = (Объем 2) / Δt,
Объемный расход ΔV // Δt везде одинаков. Теперь мы используем объем = площадь * длина. для баллона.
(Участок 1) * л 1 = (Участок 2) * л 2
(Площадь 1) * Δ л 1 / Δt = (Площадь 2) * Δl 2 / Δt
(Область 1) * v 1 = (Область 2) * v 2
Это уравнение неразрывности .Уравнение неразрывности является следствием сохранение массы воды .
Проблема:
Объемный расход воды по горизонтальной трубе 2 м. 3 / мин.
Определите скорость потока в точке, где диаметр трубы составляет
мм.
(а) 10 см,
(б) 5 см.
Решение:
- Рассуждение:
Уравнение неразрывности, A * v = ΔV / Δt = constant, объем расход везде одинаковый.
Площадь поперечного сечения трубы aA = πd 2 /4. - Детали расчета:
(πd 2 /4) v = (2 м 3 ) / (60 с). v = (0,042 / d 2 ) м / с с d, измеренным в м.
(а) d = 10 см: v = 4,24 м / с
(б) d = 5 см: v = 16,98 м / с.
Уравнение Бернулли
На разных участках трубопровода объем V воды может иметь разный потенциал. энергия и разная кинетическая энергия.Давление также разные на разных участках трубопровода
См. рисунок справа. Потенциальная энергия воды изменяется по мере ее движения. Пока вся вода движется, изменение потенциальной энергии такое же, как у объем V, который был перемещен из позиции 1 в позицию 2 на рисунке на право. Потенциал энергия воды в остальной части трубы такая же, как и потенциальная энергия воды, которая была в остальной части трубы до начала движения.У нас
изменение потенциальной энергии = (масса воды в В) * г * (изменение высоты)
= плотность * V * g * (h 2 – h 1 ) = ρVg (h 2 – h 1 ).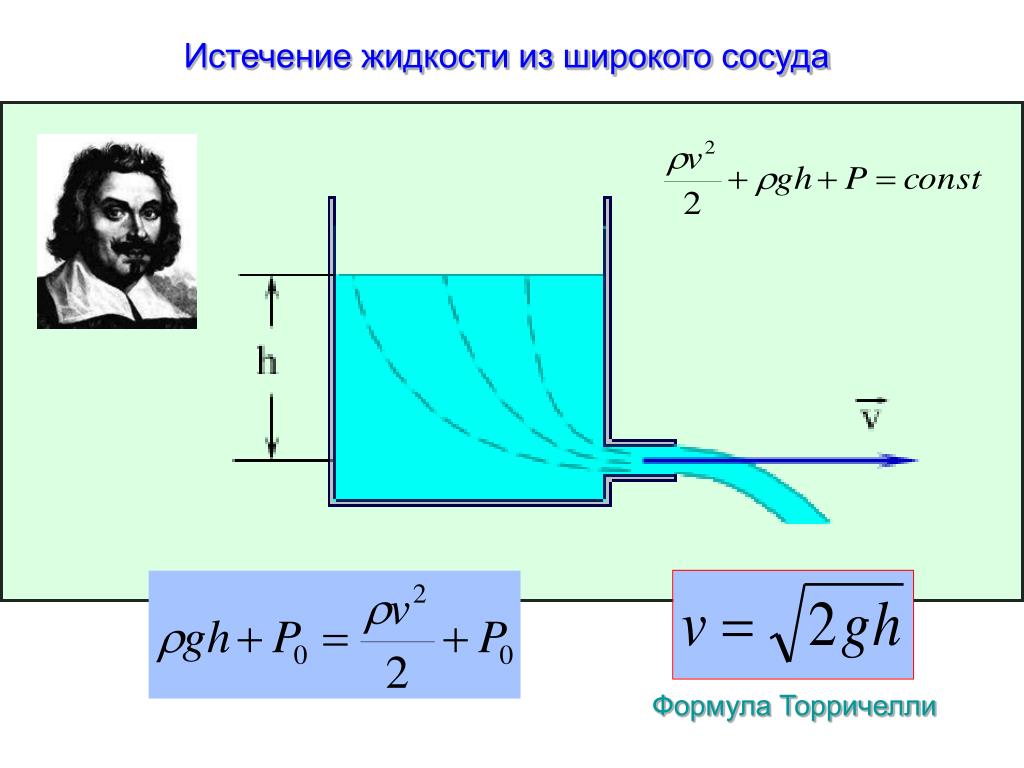
Кинетическая энергия воды также изменяется. Опять же, нам нужно только найти изменение кинетической энергии в малом объеме V, как если бы вода в положении 1 была заменена водой в позиции 2. Кинетическая энергия воды в остальной части трубы такая же, как кинетическая энергия воды, которая использовала быть в остальной части трубы до начала движения.У нас
изменение кинетической энергии = ½ мв 2 2 – ½ мв 1 2 = ½ρVv 2 2 – ½ρVv 1 2 .
Если сила, действующая на воду в положении 1, отличается от силы, действующей на
вода в положении 2, затем работа выполняется с водой по мере ее движения.
Пренебрежение
трение , объем выполненных работ W = F 1 л 1 –
F 2 л 2 .Но сила = давление, умноженное на площадь, поэтому
W = P 1 A 1 л 1 – P 2 A 2 л 2 = P 1 В – P 2 В.
Работа должна равняться изменению энергии. Таким образом, у нас есть
P 1 V – P 2 V = ρVg (h 2 -h 1 )
+ ½ρVv 2 2 – ½ρVv 1 2 ,
или
P 1 В + ρVgh 1 + ½ρVv 1 2 = P 2 В
+ ρVgh 2 + ½ρVv 2 2 .
Делим на V получаем
P 1 + ρgh 1 + ½ρv 1 2 = P 2 + ρgh 2 + ½ρv 2 2
или
P + ρgh + ½ρv 2 = постоянная.
Это уравнение Бернулли . Это следствие сохранение энергии воды .
Уравнение Бернулли | Безграничная физика
Применение уравнения Бернулли: давление и скорость
Для «идеального» потока вдоль линии тока без изменения высоты увеличение скорости происходит за счет уменьшения статического давления.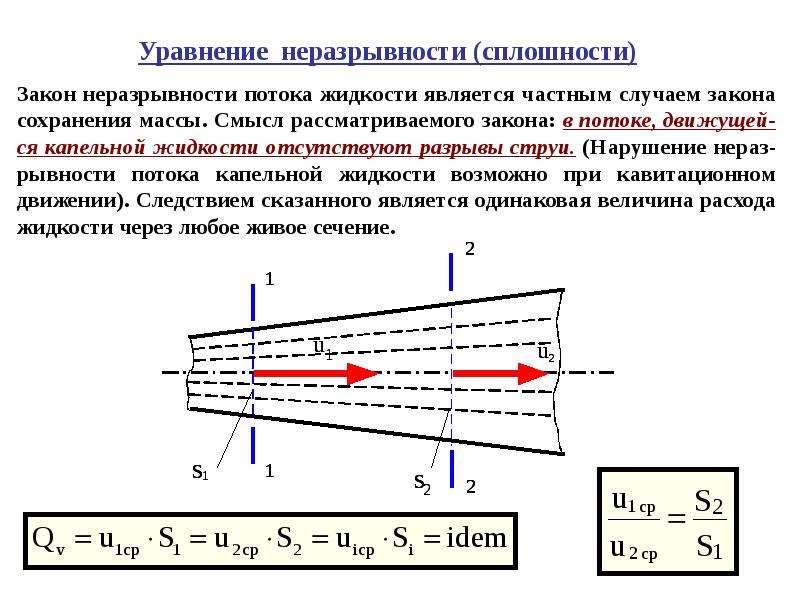
Цели обучения
Адаптировать уравнение Бернулли для нестационарных или сжимаемых потоков
Основные выводы
Ключевые моменты
- Простейшая форма уравнения Бернулли (стационарный и несжимаемый поток) утверждает, что сумма механической энергии, потенциальной энергии и кинетической энергии вдоль линии тока постоянна. Следовательно, любое увеличение одной формы приводит к уменьшению другой.
- Уравнение Бернулли учитывает только давление и гравитационные силы, действующие на частицы жидкости.Следовательно, если нет изменения высоты вдоль линии тока, уравнение Бернулли становится балансом между статическим давлением и скоростью.
- Установившееся уравнение Бернулли для несжимаемой жидкости может быть получено путем интегрирования 2-го закона Ньютона по линии тока.
Ключевые термины
- вязкость : Величина, выражающая величину внутреннего трения в жидкости, измеряемую силой на единицу площади, препятствующей равномерному потоку.

- Ideal Fluid : Невязкая и несжимаемая жидкость
- несжимаемый : Невозможно сжимать или конденсировать.
Применение уравнения Бернулли
Взаимосвязь между давлением и скоростью в идеальных жидкостях количественно описывается уравнением Бернулли, названным в честь его первооткрывателя, швейцарского ученого Даниэля Бернулли (1700–1782). Уравнение Бернулли утверждает, что для несжимаемой и невязкой жидкости полная механическая энергия жидкости постоянна. (Невязкая жидкость считается идеальной жидкостью без вязкости.)
Принцип Бернулли : Краткое введение в Принцип Бернулли для студентов, изучающих жидкости.2 [/ latex], где \ rho – плотность жидкости в (единица СИ: кг / м 3 ), а V – скорость жидкости (единица СИ: м / с). Единица измерения статического и динамического давления в системе СИ – паскаль.
Единица измерения статического и динамического давления в системе СИ – паскаль.
Syphoning : Сифонирование жидкости между двумя резервуарами. Расход на выходе можно определить, проведя линию тока от точки (A) к точке (C).
Статическое давление – это просто давление в данной точке жидкости, динамическое давление – это кинетическая энергия на единицу объема жидкой частицы.2 + \ rho \ text {g} \ Delta \ text {h} = \ text {constant} [/ latex].
Вывод уравнения Бернулли
Уравнение Бернулли может быть получено путем интегрирования 2-го закона Ньютона вдоль линии тока с силами гравитации и давления как единственными силами, действующими на элемент жидкости. Учитывая, что любой обмен энергией является результатом консервативных сил, полная энергия вдоль линии тока постоянна и просто переключается между потенциальной и кинетической.
Применение уравнения Бернулли
Уравнение Бернулли может применяться при сифонировании жидкости между двумя резервуарами. Еще одно полезное применение уравнения Бернулли – вывод закона Торричелли для потока из отверстия с острыми краями в резервуаре. Линию тока можно провести от верха пласта, где известна полная энергия, до точки выхода, где известны статическое давление и потенциальная энергия, а динамическое давление (скорость потока на выходе) – нет.
Еще одно полезное применение уравнения Бернулли – вывод закона Торричелли для потока из отверстия с острыми краями в резервуаре. Линию тока можно провести от верха пласта, где известна полная энергия, до точки выхода, где известны статическое давление и потенциальная энергия, а динамическое давление (скорость потока на выходе) – нет.
Адаптация уравнения Бернулли
Уравнение Бернулли может быть адаптировано к нестационарным и сжимаемым потокам.Однако предположение о невязком потоке остается как в нестационарной, так и в сжимаемой версиях уравнения. Эффекты сжимаемости зависят от скорости потока относительно скорости звука в жидкости. Это определяется безразмерной величиной, известной как число Маха. Число Маха представляет собой отношение скорости объекта, движущегося в среде, к скорости звука в среде.
Закон Торричелли
Закон Торричелли – это теорема о соотношении между скоростью выхода жидкости из отверстия в резервуаре и высотой жидкости над отверстием.
Цели обучения
Определите выходную скорость, изучив уравнение Бернулли.
Основные выводы
Ключевые моменты
- Закон Торричелли применим к невязкой несжимаемой жидкости («идеальной» жидкости).
- Вы можете получить результаты, применяя уравнение Бернулли между кровлей коллектора и выходным отверстием.
- Связь возникает из-за обмена потенциальной энергией в верхней части резервуара с кинетической энергией на выходе.
- Конечная кинетическая энергия эквивалентна тому, что твердое тело приобретет при падении с высоты h.
Ключевые термины
- inviscid : жидкость с нулевой вязкостью (внутреннее трение). На самом деле вязкость присутствует всегда. Однако она часто очень мала по сравнению с другими силами (например, гравитацией, давлением), и для обычных жидкостей (воды и воздуха) жидкость может быть приблизительно равна нулю вязкости.
Закон Торричелли – это теорема гидродинамики о соотношении между скоростью выхода жидкости из отверстия с острыми краями в резервуаре и высотой жидкости над этим выходным отверстием. 2 [/ латекс]
2 [/ латекс]
Это может быть решено для выходной скорости, в результате чего,
[латекс] \ text {v} _ \ text {e} = \ sqrt {2 \ text {gh} _ \ text {t}} [/ latex]
, где снова h t – разница высот между верхом резервуара и выходным отверстием. Из-за предположения об идеальной жидкости все силы, действующие на жидкость, являются консервативными, и, таким образом, существует обмен между потенциальной и кинетической энергией. В результате скорость, приобретаемая жидкостью, будет такой же, как у тела, если его просто сбросить с высоты h t .
Простой эксперимент по проверке закона Торричелли заключается в наполнении бутылки содовой водой и прокалывании на дне небольшого отверстия (около 1 см в диаметре). По мере того, как высота резервуара уменьшается, скорость на выходе также уменьшается. Скорость на выходе можно увеличить, закрыв верхнюю часть резервуара и создав в нем давление.
Закон Торичелли : Выходная скорость зависит от высоты жидкости над выходным отверстием.
Ideal Fluid : применяется к идеальной жидкости (невязкой, несжимаемой)
Поверхностное натяжение
Тенденция поверхности жидкости сопротивляться силе и вести себя как мембрана и является результатом сцепления между молекулами жидкости.
Цели обучения
Обобщите причину различного поверхностного натяжения на поверхности жидкости
Основные выводы
Ключевые моменты
- Поверхностное натяжение является результатом сцепления между молекулами жидкости. Молекулы на поверхности жидкости ощущают силу притяжения, притягивающую их к объему жидкости больше, чем твердое тело или жидкость на границе раздела.
- Когда встречается поверхность раздела жидкость-твердое тело-газ, контактный угол представляет собой меру относительной силы адгезионных и когезионных сил.
- Краевой угол смачивания определяет смачиваемость поверхности.
Ключевые термины
- когезия : Различные межмолекулярные силы, удерживающие твердые тела и жидкости вместе.

- смачиваемость : Способность твердой поверхности снижать поверхностное натяжение жидкости, контактирующей с ней, так что она растекается по поверхности и смачивает ее.
- адгезия : способность вещества прилипать к непохожему на него веществу.
Поверхностное натяжение – это способность поверхности жидкости сопротивляться приложенным к ней силам.Этот эффект является результатом сцепления молекул жидкости, заставляющих поверхность жидкости сокращаться до минимально возможной площади. Этот эффект наблюдается в природе у насекомых-водомётов, которые могут ходить по воде. Кроме того, скрепка или булавка могут поддерживаться поверхностным натяжением на границе раздела вода-воздух.
Поверхностное натяжение FBD : Диаграммы сил, показывающие направление сил для воды, поддерживающей ступню водомера (насекомого) и булавку. В обоих случаях вертикальной составляющей поверхностного натяжения достаточно, чтобы выдержать вес объекта.
В объеме жидкости молекулы тянутся одинаково во всех направлениях. Молекулы на поверхности ощущают большую силу притяжения по отношению к массивному материалу, чем материал границы раздела.
Поверхность жидкости – это граница раздела между другой жидкостью, твердым телом или и тем, и другим. Следовательно, поверхностное натяжение будет свойством поверхности раздела, а не просто жидкостью. Адгезия описывает силу притяжения между молекулами разных типов. Поверхность жидкости в контейнере – это поверхность раздела между жидкостью, воздухом и контейнером.Там, где встречаются поверхности, силы должны быть в равновесии. Это приводит к краевому углу на границе раздела. Краевой угол смачивания измеряется в жидкости и зависит от относительной силы сил сцепления в жидкости и сил сцепления между жидкостью и материалами поверхности раздела. Если молекулы жидкости сильно притягиваются к молекулам твердой поверхности (силы адгезии> силы сцепления), капля будет стремиться растекаться, и угол смачивания будет близок к нулю градусов. Если силы сцепления больше, чем силы сцепления, результирующие углы смачивания будут большими и образуют более круглую каплю.
Капля воды на листе : Когда капля воды образуется на листе, силы сцепления между молекулами воды превышают силы сцепления между водой и поверхностью листа. Лист представляет собой гидрофобную поверхность.
Контактный угол : Контактный угол – это угол, измеренный в жидкости, который получается, когда граница раздела жидкость-газ встречается с твердой поверхностью.
Когда жидкость представляет собой воду, поверхность с небольшим краевым углом смачивания называется гидрофильной.На гидрофобных поверхностях присутствуют большие углы смачивания. Угол смачивания определяет смачиваемость поверхности.
Объяснение уравнения Бернулли для идеального потока жидкости
Сначала мы обсудили уравнение Эйлера для потока жидкости, а затем мы интегрировали его для идеального потока жидкости вдоль линий тока, чтобы получить уравнение энергии для потока жидкости. Мы назвали это уравнением Бернулли. Это своего рода уравнение сохранения энергии, значение которого остается постоянным вдоль линии тока идеального потока жидкости.Каждый член уравнения имеет размерность энергии на единицу веса, то есть длину. Эти термины представляют различные типы энергии, связанные с жидкой частицей.
Возвращение к уравнению Бернулли
Уравнение Бернулли для идеального потока жидкости записывается как:
z + p / ρg + v2 / 2g = constant
Давайте сначала вспомним и проясним, при каких условиях применимо уравнение Бернулли. Это применимо для потока
- Вдоль линии потока
- Непрерывный
- Устойчивый
- Несжимаемый
- Невязкий, Invinsid, без трения
Что означают термины
Термин ‘z’ обозначает высоту рассматриваемая точка от опорного уровня, называемого датумом, где мы фиксируем потенциальную энергию равной нулю.«P» – давление жидкости в этой точке. «Ρ» – это плотность жидкости в точке, и для условий применимости уравнения Бернулли плотность жидкости постоянна. «G» – это ускорение свободного падения, и оно также принимается как постоянное, предполагая, что изменение высоты таково, что его значение можно считать постоянным. «V» – это средняя скорость жидкости в рассматриваемой точке.
Энергия, связанная с каждым термином
‘z’, высота жидкой частицы дает потенциальную энергию частицы в этой точке относительно нулевой точки.”Z”, умноженный на вес жидкой частицы, дает потенциальную энергию. Таким образом, «z» – это потенциальная энергия на единицу веса жидкой частицы. Если смотреть размерно, размер z равен м (метры), размер веса равен N (ньютонам), таким образом, размерность потенциальной энергии равна Нм, а размерность потенциальной энергии на единицу веса равна Нм / Н, т.е. есть, м. Это также называется потенциальным напором жидкости.
Второй член уравнения Бернулли, ‘p / ρg’, связан с энергией давления.Энергия давления – это работа, выполняемая давлением жидкости, как и pV-работа, выполняемая давлением в цилиндре для смещения поршня. «PV» – это проделанная работа, а «p / ρg» – это работа, выполненная на единицу веса жидкости. «V» – это объем вытесненной жидкости, который можно записать как W / ρg, где W – вес жидкой частицы. Таким образом, pV можно записать как pW / ρg, а работу, выполненную на единицу веса, как p / ρg. Это энергия давления жидкости на единицу веса или напор.
Член V2 / 2g имеет квадрат скорости в числителе, который указывает на кинетическую энергию.Но, как мы знаем, кинетическая энергия составляет ½ мВ2, поэтому третий член в уравнении Бернулли – это кинетическая энергия на единицу веса. Массу m можно записать как Вт / г, поэтому ½ мВ2 равно ½ WV2 / г или V2 / 2 г. Он имеет размеры Нм / Н или м, кинетическую энергию на единицу веса жидкой частицы, которую также называют скоростным напором.
Это то, что означает каждый термин в уравнении Бернулли и их интерпретации. В следующей статье мы обсудим некоторые применения уравнения Бернулли для гидравлики в гражданском строительстве.
Этот пост является частью серии: Анализ потока жидкости
Для эффективного проектирования гидравлических систем в гражданском строительстве очень важно сначала проанализировать поток жидкости через систему. В этой серии статей рассказывается, каковы концепции анализа потока жидкости и как эти концепции используются в контексте анализа потока жидкости?
- Кинематический анализ потока жидкости: описание положения и скорости
- Ускорения потока жидкости
- Динамика потока жидкости: уравнение энергии для идеального потока жидкости
- Объяснение уравнения Бернулли
- Применение уравнения Бернулли
Уравнение Бернулли –
Проверяемый товар
Требуется проверка этой статьи. Предлагаемый рецензент: Carmeljcaruana |
Уравнение Бернулли
Уравнение Бернулли показывает, как давление и скорость изменяются от одной точки к другой в текущей жидкости. В нем говорится, что полная механическая энергия жидкости сохраняется при ее перемещении из одной точки в другую, но часть этой энергии может быть преобразована из кинетической в потенциальную и наоборот по мере движения жидкости. В гидродинамике, которая изучает движение жидкости и связанные с ней внешние силы и внутренние сопротивления, уравнение Бернулли связывает давление с энергией.Уравнение Бернулли утверждает, что в идеальной жидкости, когда поток однороден и непрерывен, сумма давления, кинетической энергии и потенциальной энергии жидкости постоянна.
Как это работает?
Принцип Бернулли гласит, что сумма ДАВЛЕНИЯ, ПОТЕНЦИАЛЬНОЙ энергии и кинетической энергии жидкости НА ЕДИНИЦУ ОБЪЕМА, протекающей через трубку, является постоянной. Большая энергия, связанная с давлением в жидкости, соответствует более низкой КИНЕТИЧЕСКОЙ И ПОТЕНЦИАЛЬНОЙ энергии.Уменьшение давления при увеличении скорости жидкости (И ВИЦЕ ВЕРСА) называется эффектом Бернулли.
Итак, уравнение Бернулли гласит:
===== P₁ + ½𝜌v₁² + 𝜌gh₁ = P₂ + ½𝜌v₂² + 𝜌gh₂ =====
P₁ = давление в точке 1
½𝜌v₁² = кинетическая энергия НА ЕДИНИЦУ ОБЪЕМА в точке 1
𝜌gh₁ = потенциальная энергия НА ЕДИНИЦУ ОБЪЕМА в точке 1
P₂ = давление в точке 2
½𝜌v₂² = кинетическая энергия НА ЕДИНИЦУ ОБЪЕМА в точке 2
𝜌gh₂ = потенциальная энергия НА ЕДИНИЦУ ОБЪЕМА в точке 2
На этой диаграмме справа показан кровеносный сосуд, который сужается и возвращается к своему нормальному диаметру.В суженной области (препятствие потоку) по мере уменьшения диаметра скорость увеличивается (ПО УРАВНЕНИЮ НЕПРЕРЫВНОСТИ). Если диаметр уменьшается вдвое, скорость увеличивается на 4, соответственно увеличивается кинетическая энергия. Если предположить, что энергия сохраняется, увеличение кинетической энергии НА ЕДИНИЦУ ОБЪЕМА приводит к уменьшению ДАВЛЕНИЯ. Когда сосуд возвращается к своему первоначальному диаметру, кинетическая энергия также возвращается к своему первоначальному значению, И ТАК И ДАВЛЕНИЕ.
Одним из недостатков уравнения Бернулли является то, что оно может быть сложным для рутинного клинического использования, однако упрощенная версия (𝝙P = 4v²? ТРЕБУЕТСЯ ССЫЛКА
Эту статью проверил педагог
Статья была проверена педагогом, но впоследствии изменена. |
) говорит нам о разнице давления между правым желудочком и правым предсердием, при условии, что нет нарушения сердечного клапана.
Значение в клинической медицине
В эхокардиографии принцип Бернулли может применяться при интерпретации кровотока, который может описывать снижение локализованного давления, вызванное высокой скоростью потока вблизи закупорок, как упоминалось выше с иллюстрацией.В клинической медицине упрощенное уравнение позволяет легко оценить градиенты давления по скорости.
Еще одно использование уравнения Бернулли – маска Вентури. Маска Вентури – это медицинская кислородная маска, которая обеспечивает концентрацию кислорода пациентам, проходящим контролируемую кислородную терапию. От маски есть трубка, соединенная с соплом, которое подключается к источнику чистого кислорода (обычно от стены больницы). Трубка, которая напрямую соединена с маской, имеет небольшое окно, через которое воздух из помещения (с низким содержанием кислорода) может поступать в маску.Маска Вентури может контролировать количество поступающего воздуха с низким содержанием кислорода (воздуха, которым мы обычно дышим) вместе с чистым кислородом, поступающим из подсоединенного к ней сопла. Когда кислород поступает в трубку, он создает снижение давления из-за того, что кислород проходит через узкое отверстие трубки. Это падение давления позволяет воздуху течь в маску, смешиваясь с чистым кислородом из сопла, что является следствием принципа Бернулли.
Кто является отцом уравнения Бернулли?
Уравнение Бернулли было выведено Даниэлем Бернулли (1700-1783) в 1730-х годах.Даниэль Бернулли был швейцарским математиком и физиком, родившимся в семье математиков, в которую входили его отец Иоганн Бернулли и его дядя Якоб Бернулли.
Он опубликовал книгу под названием «Гидродинамика» (1738 г.), в которой он объяснил механику жидкости, имея в виду идею сохранения энергии, и гидродинамику. В книге описывается природа гидродинамического давления в потоке жидкости, которая впоследствии стала известна как принцип Бернулли.
Ему оказали большую честь при жизни, и он до сих пор пользуется большим уважением в области математической физики.[[Файл:]]
Ссылки:
Джордано Николас; Физика колледжа: рассуждения и отношения; 2-е изд .; 2013; 978-0-8400-5819-5
Rama, Durhaiah D .; Гидромеханика и машинное оборудование; 1-е изд .; 2002; 81-224-1386-2
Гриффин Брайан П .; Руководство по сердечно-сосудистой медицине; 4-е изд .; 2013; 978-1-4511-3160-4
Klabunde Richard E .; http://www.cvphysiology.com/Hemodynamics/H012.htm
Анестезия Великобритания; http://www.frca.co.uk/article.aspx?articleid=100482
Уравнение Бернулли – обзор
Интересное приложение уравнения Бернулли обнаруживается при опорожнении содовой соломки.Рассмотрим тонкую трубку, наполненную жидкостью посредством всасывания, а затем удерживаемую в вертикальном положении после герметизации верхнего конца, как показано на рис. 6.10.
Рисунок 6.10. Распределение давления в статическом водяном столбе
При условии, что длина трубы L не превышает максимальную высоту столба жидкости, который может выдерживать атмосферное давление, столб жидкости удерживается в положении против силы тяжести. В случае воды длина трубки должна быть меньше 10.33м. Ссылаясь на рис. 6.10, давление на верхнем конце трубы равно −γL. Давление атмосферное, т.е. нулевое манометрическое давление внизу, на открытом конце. Поскольку столб воды не движется, скорость по всей трубке равна нулю. Внезапно верхний уплотнитель снимается, и из трубки начинает стекать столб воды. Ускорение водяного столба настолько велико, что влиянием вязкости можно пренебречь, поэтому движение описывается нестационарной формой уравнения Бернулли, т.е.е. Уравнение (6.72), которое для настоящих целей может быть записано вдоль линии тока следующим образом:
(6.84) 1g∂V∂t + ∂∂s (pγ + ζ + V22g) = 0
или, используя определение полного напора H ,
(6,85) 1g∂V∂t = −∂H∂s
Таким образом, интегрируя по длине линии тока, получаем
(6,86) HL − H0 = −1g∫0L∂V∂ tds = −1gA∫0L∂Q∂tds
, где A – площадь поперечного сечения трубки, которая считается постоянной. Обратите внимание, что для обеспечения непрерывности Q не может быть функцией расстояния вдоль линии тока, и то же самое должно быть верно для ∂Q∂t.Следовательно, уравнение. (6.86) можно записать следующим образом:
(6.87) HL − H0 = −LgA∂Q∂t
Пусть h (t) будет высотой падающей свободной поверхности, когда жидкость стекает из трубы. Поскольку свободная поверхность представляет собой поверхность материала, она падает со скоростью, равной
(6,88) dhdt = −V
Обратите внимание, что после снятия верхнего уплотнения давление становится атмосферным и на верхнем конце. Если давление равно нулю на обоих концах колонки, оно должно быть равно нулю и внутри колонки.В противном случае колонка будет либо расширяться, либо сжиматься, что невозможно для несжимаемой жидкости. Кроме того, скорость должна быть равномерной по длине колонны, поскольку отсутствуют силы, которые могут вызвать конвективное ускорение. Поскольку длина дуги линии тока, s , направлена по вертикали, ζ , но в противоположном направлении, уравнение. (6,84) уменьшается до
(6,89) ∂v∂t = −g
Следовательно,
(6,90) d2hdt2 = −g
Таким образом, столб воды падает как твердое тело.
Даниэль Бернулли: принцип и уравнение Бернулли
Сегодня мы отмечаем вклад, который швейцарский математик и физик Даниэль Бернулли внес в мир науки и техники, представив принцип Бернулли для понимания механики жидкости.
Даниэль Бернулли, родившийся в Нидерландах 319 лет назад, изучал свое увлечение математикой и медициной под руководством своего отца Иоганна Бернулли, который слишком хорошо знал на собственном опыте о низкой заработной плате, которую может предложить карьера.
Принцип Бернулли
Принцип Бернулли гласит, что увеличение скорости жидкости происходит одновременно с уменьшением давления или уменьшением потенциальной энергии жидкости. Хотя Бернулли обнаружил, что давление уменьшается при увеличении скорости потока, на самом деле именно Леонард Эйлер создал уравнение Бернулли.
Принцип Бернулли можно вывести из принципа сохранения энергии. Это означает, что в установившемся потоке сумма всех форм энергии в жидкости будет одинаковой во всех точках этой линии тока.Хотя вся энергия остается постоянной, увеличение скорости жидкости будет означать увеличение динамического давления (кинетической энергии). Это происходит при одновременном уменьшении потенциальной энергии, включая статическое давление и внутреннюю энергию.
Уравнение Бернулли
Уравнение Бернулли может применяться к различным типам потоков жидкости, что приводит к различным формам уравнения.
Простейшая форма уравнения Бернулли – использование потока несжимаемой жидкости.Несжимаемые потоки – это жидкости и газы с низким числом Маха с постоянной плотностью жидкости независимо от давления потока.
Бернулли провел большую часть своих экспериментов с жидкостью и использовал уравнение:
Где:
v = Скорость потока жидкости в точке на линии тока g = ускорение под действием силы тяжести z = высота точки над базовой плоскостью p = Давление в выбранной точке ρ = Плотность жидкости во всех точках жидкости
Для применения уравнения Бернулли должны быть выполнены следующие допущения:
- Поток должен быть постоянным.(Скорость, давление и плотность не могут измениться в любой момент).
- Поток должен быть несжимаемым – даже при изменении давления плотность должна оставаться постоянной вдоль линии тока.
- Трение под действием сил вязкости должно быть минимальным.
Практическое применение для изучения принципов Бернулли
- Чтобы определить принцип Бернулли и провести прямые сравнения эксперимента и теории, воспользуйтесь экспериментальной теоремой Бернулли H5 компании TecQuipment.
- Эксперимент с уравнением Бернулли AF11 идеально подходит для исследования и подтверждения уравнения Бернулли для использования со стендом для измерения расхода воздуха AF10.
Дальнейшие эксперименты с принципами Бернулли
- Рассчитайте уравнение Бернулли с кавитацией в устройстве Вентури (h500).
- Продемонстрируйте дальнейшее применение уравнения Бернулли, экспериментируя с методами измерения расхода (h20).
Принцип Бернулли – Урок – Обучение инженерии
(3 Рейтинги)Быстрый просмотр
Уровень оценки: 11 (9–12)
Требуемое время: 30 минут
Зависимость урока: Нет
Тематические области: Физические науки, физика
Ожидаемые характеристики NGSS:
Резюме
Принцип Бернулли связывает давление жидкости с ее высотой и скоростью.Уравнение Бернулли можно использовать для аппроксимации этих параметров в воде, воздухе или любой жидкости с очень низкой вязкостью. Учащиеся используют соответствующее упражнение, чтобы узнать о взаимосвязях между компонентами уравнения Бернулли на реальных инженерных примерах и практических задачах. Эта инженерная программа соответствует научным стандартам нового поколения (NGSS).Инженерное соединение
Принцип Бернулли находит широкое применение в инженерной гидродинамике, от конструкции крыла в авиакосмической отрасли до проектирования труб для гидроэлектростанций.Например, в случае гидроэлектростанции, которая использует поток воды из горного водохранилища, знание перепада высот от водохранилища в горах до станции в городе помогает инженерам определить, с какой скоростью вода будет течь через генерирующие энергию турбины в растение.
Цели обучения
После этого урока учащиеся должны уметь:
- Вычислить неизвестное состояние жидкости (например, давление жидкости, скорость, плотность или высоту) в одной точке вдоль линии потока, если условия известны в другой точке на той же линии тока.
- Используйте уравнение Бернулли, чтобы объяснить, что более быстрый поток воздуха вызывает снижение давления, и приведите пример из реальной жизни.
Образовательные стандарты
Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными дисциплинами K-12, образовательные стандарты в области технологий, инженерии или математики (STEM).
Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты иерархически структурированы: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика; внутри типа по подтипу, затем по классу, и т. д. .
NGSS: научные стандарты нового поколения – наука| Ожидаемые характеристики NGSS | ||
|---|---|---|
HS-PS3-1.Создайте вычислительную модель для расчета изменения энергии одного компонента в системе, когда известно изменение энергии другого компонента (-ов) и потоки энергии в систему и из нее. (9–12 классы) Вы согласны с таким раскладом? Спасибо за ваш отзыв! | ||
| Нажмите, чтобы просмотреть другие учебные программы, соответствующие этим ожиданиям от результатов. | ||
| Этот урок посвящен следующим аспектам трехмерного обучения NGSS: | ||
| Наука и инженерная практика | Основные дисциплинарные идеи | Комплексные концепции |
| Создайте вычислительную модель или симуляцию явления, спроектированного устройства, процесса или системы. Соглашение о выравнивании: Спасибо за ваш отзыв! Используйте математические представления явлений для описания объяснений.Соглашение о выравнивании: Спасибо за ваш отзыв! | Энергия – это количественное свойство системы, которое зависит от движения и взаимодействия материи и излучения внутри этой системы. То, что существует единственная величина, называемая энергией, объясняется тем фактом, что общая энергия системы сохраняется, даже если внутри системы энергия непрерывно передается от одного объекта к другому и между его различными возможными формами. Соглашение о выравнивании: Спасибо за ваш отзыв! Сохранение энергии означает, что полное изменение энергии в любой системе всегда равно общей энергии, переданной в систему или из нее.Соглашение о выравнивании: Спасибо за ваш отзыв! Энергия не может быть создана или уничтожена, но ее можно переносить из одного места в другое и передавать между системами.Соглашение о выравнивании: Спасибо за ваш отзыв! Математические выражения, которые количественно определяют, как запасенная энергия в системе зависит от ее конфигурации (например, относительное положение заряженных частиц, сжатие пружины) и как кинетическая энергия зависит от массы и скорости, позволяют использовать концепцию сохранения энергии. для прогнозирования и описания поведения системы.Соглашение о выравнивании: Спасибо за ваш отзыв! Наличие энергетических ограничений, которые могут возникнуть в любой системе.Соглашение о выравнивании: Спасибо за ваш отзыв! | Модели можно использовать для прогнозирования поведения системы, но эти прогнозы имеют ограниченную точность и надежность из-за допущений и приближений, присущих моделям. Соглашение о выравнивании: Спасибо за ваш отзыв! Наука предполагает, что Вселенная представляет собой огромную единую систему, в которой согласованы основные законы.Соглашение о выравнивании: Спасибо за ваш отзыв! |
- Рассуждайте абстрактно и количественно.
(Оценки
К –
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Модель с математикой.(Оценки
К –
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Перегруппируйте формулы, чтобы выделить интересующее количество, используя те же рассуждения, что и при решении уравнений.(Оценки
9 –
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Решите линейные уравнения и неравенства с одной переменной, включая уравнения с коэффициентами, представленными буквами.(Оценки
9 –
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Какое альтернативное выравнивание вы предлагаете для этого контента?
Рабочие листы и приложения
Посетите [www.teachengineering.org/lessons/view/cub_bernoulli_lesson01], чтобы распечатать или загрузить.Больше подобной программы
Принцип Архимеда, Закон Паскаля и Принцип БернуллиСтуденты знакомятся с законом Паскаля, принципом Архимеда и принципом Бернулли. Поставляются основные определения, уравнения, практические задачи и инженерные приложения.
Вязкие жидкостистуденты знакомятся с сходствами и различиями в поведении упругих твердых тел и вязких жидкостей.Кроме того, вводятся свойства материала жидкости, такие как вязкость, а также методы, которые инженеры используют для определения этих физических свойств.
Повесть о тренииСтаршеклассники узнают, как инженеры математически проектируют дорожки для американских горок, используя подход, согласно которому криволинейная дорожка может быть аппроксимирована последовательностью множества коротких уклонов.Они применяют базовый расчет и теорему работы-энергии для неконсервативных сил для количественной оценки трения вдоль кривой …
Основы гидравлической энергииСтуденты узнают об основных концепциях, важных для гидравлической энергии, которая включает в себя как пневматические (газовые), так и гидравлические (жидкостные) системы.
Предварительные знания
законы алгебры и газа
Введение / Мотивация
(Обратите внимание, что рисунки 1 и 2 также доступны в виде слайдов PowerPoint в приложении Bernoulli Flow Graphics. Их также можно распечатать в виде прозрачных пленок или раздаточных материалов для учащихся.)
Вы когда-нибудь задумывались, как может летать самолет? Простой ответ заключается в том, что когда воздух обтекает крыло, самолет подталкивается воздухом с более высоким давлением под крылом по сравнению с более низким давлением над крылом. Но чтобы понять это явление более глубоко, мы должны взглянуть на раздел физики, известный как механика жидкости, и, в частности, на принцип, известный как уравнение Бернулли. Это уравнение может не только предсказать давление воздуха вокруг крыла самолета, но его также можно использовать для определения силы сильного ветра на небоскребе, давления в химическом реакторе или даже скорости воды, выходящей из шланга в свой задний двор.
Рис. 1. Простой пример потока в трубе: когда вода теряет высоту от верхнего конца трубы к нижнему, она набирает скорость. Чтобы найти точное значение любого параметра, мы применяем уравнение Бернулли к двум точкам в любом месте на одной и той же линии тока (представленной пунктирной линией). Copyright
Copyright © 2009 Karen King. Используется с разрешения. Все права защищены.
Уравнение Бернулли утверждает, что для идеальной жидкости (то есть с нулевой вязкостью, постоянной плотностью и установившимся потоком) сумма ее кинетической, потенциальной и тепловой энергии не должна изменяться.Это ограничение приводит к предсказуемой взаимосвязи между скоростью (скоростью) жидкости, ее давлением и ее возвышением (относительной высотой). В частности, учитывая две точки вдоль линии тока (воображаемая линия, касательная к направлению потока, как показано на рисунке 1), уравнение Бернулли утверждает, что:
, где v – скорость жидкости, ρ – плотность жидкости, z – относительная высота и P – давление. Применение этого уравнения к примеру поможет прояснить его.Рассмотрим водохранилище, расположенное в горах, с трубой, ведущей в город на более низкой высоте. По трубе вода поступает на гидроэлектростанцию, и мы хотим знать, с какой скоростью вода будет поступать в турбины станции. Рисунок 2 иллюстрирует эту ситуацию.
Рисунок 2. Пример резервуара. Решение справа от изображения демонстрирует, как использовать уравнение Бернулли для определения конечной скорости воды, когда она достигает города на более низкой высоте. Авторское право
Copyright © 2009 Карен Кинг, задача адаптирована из Knight, 2008.
А теперь вернемся к тому, как принцип Бернулли применим к крылу самолета. Когда воздушный поток разделяется вокруг крыла, воздух над крылом движется быстрее, чем воздух под ним, из-за формы крыла. Поскольку скорость верхнего воздуха увеличивается, его давление должно уменьшаться, чтобы поддерживать равновесие, как описано в уравнении Бернулли. Это приводит к большему давлению под крылом, чем над ним, что заставляет крыло подниматься вверх, обеспечивая полет!
Предпосылки и концепции урока для учителей
Уравнение Бернулли – важное выражение, связывающее давление, высоту и скорость жидкости в одной точке вдоль ее потока.Взаимосвязь между этими жидкостными условиями вдоль линии тока всегда равна одной и той же константе вдоль этой линии тока в идеализированной системе. Идеализированная система относится к жидкости с постоянной плотностью (несжимаемой) и невязкой.
Предположение, что жидкость невязкая, означает, что у нее нет вязкости. Поэтому определенные эффекты вязкости, такие как прилипание воды к стенкам трубы или емкости, не применяются.
Поскольку уравнение Бернулли равно константе во всех точках вдоль линии тока, мы можем приравнять две точки на линии тока.Используя информацию о системе в одной точке, мы можем найти информацию в другой.
Согласно эффекту Вентури, давление жидкости уменьшается с увеличением ее скорости. Уравнение Бернулли выражает это соотношение в математических терминах и включает термин, обозначающий высоту жидкости. Чтобы проиллюстрировать эту взаимосвязь, представьте, что вода движется по водной горке. В верхней части, где вы загружаете, вода движется медленно, ее толкает только вода позади нее. Когда горка опускается, вода быстро устремляется вниз, увеличивая скорость по мере падения.Таким образом, на скорость также влияет сила тяжести по высоте. Когда все эти члены связаны и масштабируются для плотности и силы тяжести, мы получаем уравнение Бернулли, где v – скорость жидкости, ρ – плотность жидкости, h – относительная высота, а P – давление. Обратите внимание, что у константы также есть единицы измерения давления.
Уравнение Бернулли также можно интерпретировать как выражение сохранения энергии, которое можно сформулировать как
, где KE – кинетическая энергия, PE – потенциальная энергия и Вт, – работа, выполняемая в системе.Представьте себе глыбу льда, скользящую по водной горке с некоторой скоростью. Кинетическая энергия блока равна половине его массы, умноженной на квадрат скорости, или
., где KE – кинетическая энергия, а м – масса. Блок также имеет определенную потенциальную энергию, описываемую
., где PE, – потенциальная энергия, а h – высота. Наконец, работа на блоке производится силой давления воды за ним (с силой F = PA , где P, – давление воды, а A, – площадь поверхности льда. это продвигается вперед).Когда блок перемещается на расстояние, эквивалентное его собственной ширине, Δx , то работа, выполняемая с блоком, составляет
., где V – объем. Уравнение сохранения энергии принимает вид
Разделив это уравнение на объем и вспомнив, что плотность, ρ Δ равно массе, деленной на объем, получится
, которое является уравнением Бернулли.
Инженеры могут установить уравнение Бернулли в одной точке, равное уравнению Бернулли в любой другой точке на линии тока, и решить для неизвестных свойств.Учащиеся могут проиллюстрировать эту взаимосвязь, выполнив упражнение «Выстрел под давлением», чтобы вычислить давление водяного пистолета! Например, инженер-строитель может захотеть узнать, насколько изменяется давление в трубе между верхом здания и землей.
Сопутствующие мероприятия
Закрытие урока
Уравнение Бернулли находит широкое применение, от конструкции крыла до потока в трубе.Согласно эффекту Вентури, когда скорость жидкости увеличивается, давление уменьшается, и наоборот. Уравнение Бернулли является математическим представлением этого. Уравнение Бернулли можно понять, управляя энергией текущей жидкости. Уравновешивая уравнение Бернулли в двух разных точках вдоль линии тока, можно рассчитать условия жидкости в одной точке, используя информацию из другой точки.
Словарь / Определения
Принцип Бернулли: В гидродинамике принцип Бернулли гласит, что для невязкого потока увеличение скорости жидкости происходит одновременно с уменьшением давления или уменьшением потенциальной энергии жидкости.Назван в честь голландско-швейцарского математика Даниэля Бернулли, который опубликовал свой принцип в своей книге «Гидродинамика» в 1738 году. Также называется эффектом Бернулли.
невязкий поток: поток, в котором можно игнорировать влияние вязкости жидкости.
линия тока: линия, касательная к потоку жидкости в любой момент времени.
Эффект Вентури: снижение давления жидкости, возникающее при протекании жидкости через суженный участок трубы.По мере увеличения скорости жидкости ее давление уменьшается, и наоборот. Назван в честь итальянского физика Джованни Баттиста Вентури (1746–1822).
Оценка
Оценка перед уроком
Matching: Чтобы помочь студентам с этим уроком и связанным с ним заданием, составьте список физических уравнений, которые они уже изучили, таких как кинетическая энергия, потенциальная энергия, работа, уравнения кинематики. Произвольно напишите термины физики на левой стороне доски и соответствующие половины уравнений (в произвольном порядке) на правой стороне доски.Попросите учащихся совместить правильные стороны вместе. Примеры:
Примеры соответствия для оценочного задания перед уроком.
Оценка после введения
Домашнее задание / Самостоятельная практика: Попросите учащихся заполнить Рабочий лист по уравнению Бернулли. Попросите всех учащихся решить первую задачу в классе и вместе обсудить ответ. Попросите учащихся выполнить вторую задачу в качестве домашнего задания.
Итоги урока Оценка
Вопрос для обсуждения: Во время следующего урока проведите пятиминутную дискуссию, спрашивая учащихся, что они узнали из домашнего задания.
Дополнительная поддержка мультимедиа
Вы можете использовать слайды PowerPoint на Рисунке 1. Простой поток в трубе и Рисунке 2. Пример коллектора с классом, как показано в прилагаемой Графике потока Бернулли.
См. Описания дополнительных реальных применений принципа Бернулли на веб-сайте Science Clarified: http://www.scienceclarified.com/everyday/Real-Life-Chemistry-Vol-3-Physics-Vol-1/Bernoulli-s- Принцип – Реальные приложения.html
Покажите учащимся интерактивную анимацию принципа Бернулли в виде разреза трубы с формой, которую вы можете изменить с помощью компьютерной мыши, что приведет к изменениям давления, площади поперечного сечения и скорости жидкости, протекающей через трубы, которые изображены ниже трубы. См. Марка. Веб-сайт Митчелла под названием «Анимированная демонстрация принципа Бернулли» http://home.earthlink.net/~mmc1919/venturi.html
использованная литература
Принцип Бернулли (определение).Последнее обновление 11 февраля 2010 г. Википедия, Бесплатная энциклопедия. По состоянию на 17 февраля 2010 г. http://en.wikipedia.org/w/index.php?title=Bernoulli%27s_principle&oldid=343435891
Рыцарь, Рэндалл. Физика для ученых и инженеров: стратегический подход . Второе издание. Сан-Франциско, Калифорния: Пирсон Эддисон-Уэсли, 2008.
Мансон, Б. Р., Янг, Д. Ф., Окииси, Т. Х. Основы механики жидкостей . Издание пятое. Нью-Йорк, штат Нью-Йорк: John Wiley & Sons, Inc., 2006.
Эффект Вентури (определение). Последнее обновление 12 февраля 2010 г. Википедия, Бесплатная энциклопедия. По состоянию на 17 февраля 2010 г. http://en.wikipedia.org/w/index.php?title=Venturi_effect&oldid=343508711
Другая сопутствующая информация
Просмотрите концентратор учебной программы по физике, согласованный с NGSS, чтобы найти дополнительные учебные программы по физике и физическим наукам, посвященные инженерным наукам.
авторское право
© 2009 Регенты Университета КолорадоАвторы
Джеймс Прагер; Карен Кинг; Дениз В.КарлсонПрограмма поддержки
Комплексная программа преподавания и обучения и лаборатория, Инженерный колледж, Университет Колорадо в БоулдереБлагодарности
Содержание этой учебной программы по цифровой библиотеке было разработано в рамках гранта Фонда улучшения послесреднего образования (FIPSE), Министерства образования США и Национального научного фонда GK-12, грант No.

 – 9 Июля 2014
– 9 Июля 2014 Кроме того, движение вязкой жидкости часто сопровождается вращением частиц, вихреобразованием и перемешиванием. Все это требует затраты энергии, поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений и, следовательно, уменьшается вдоль потока.
Кроме того, движение вязкой жидкости часто сопровождается вращением частиц, вихреобразованием и перемешиванием. Все это требует затраты энергии, поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений и, следовательно, уменьшается вдоль потока.  Это соответствует действительности и может быть доказано теоретически в том случае, когда течение в данных поперечных сечениях является параллельноструйным. Поэтому именно такие (или близкие к ним) поперечные сечения и будем рассматривать.
Это соответствует действительности и может быть доказано теоретически в том случае, когда течение в данных поперечных сечениях является параллельноструйным. Поэтому именно такие (или близкие к ним) поперечные сечения и будем рассматривать.  рис. 1.26) коэффициент а всегда больше единицы *, а при равномерном распределении скоростей равен единице.
рис. 1.26) коэффициент а всегда больше единицы *, а при равномерном распределении скоростей равен единице. 
 Этот процесс преобразования механической энергии
Этот процесс преобразования механической энергии  Все это требует энергозатрат. Таким образом, удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а равномерно рассеивается, преодолевая сопротивление, и поэтому уменьшается вдоль потока. Из-за неравномерного распределения скорости следует учитывать среднюю поперечную скорость gsr(см. 1.13) и среднее значение удельной энергии жидкости в этом сечении.
Все это требует энергозатрат. Таким образом, удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а равномерно рассеивается, преодолевая сопротивление, и поэтому уменьшается вдоль потока. Из-за неравномерного распределения скорости следует учитывать среднюю поперечную скорость gsr(см. 1.13) и среднее значение удельной энергии жидкости в этом сечении.


