Уравнение Бернулли
Дата добавления: 2014-07-19 | Просмотров: 1582
Для движущейся жидкости к потенциальной энергии (уравнение 3.3) необходимо прибавить кинетическую энергию
Ек=mw2/ 2.
С учетом этого
. (4.5)
Разделив левую и правую части уравнения (4.5) на единицу веса (mg), получим:
. (4.6)
Уравнение (4.6) получило название уравнения Бернулли для идеальной жидкости.
При движении реальной жидкости возникают силы трения жидкости о стенки трубопровода и между слоями (частицами) жидкости. При этом часть потенциальной энергии переходит в тепловую, так как возникают потери на трение (падение напора). Эти потери учитывают путем введения четвертого члена hп в уравнение (4.
. (4.7)
Все члены уравнения Бернулли имеют размерность в метрах движущейся жидкости. Поэтому левую часть уравнения обозначают Н и называют полным гидродинамическим напором, определяющим начальный запас энергии системы.
Геометрический напор – высота расположения (рис. 4.3) центра живого сечения потока над выбранной плоскостью (линией) сравнения. Пьезометрический напор в любом сечении потока может быть измерен с помощью пьезометра (манометра), скоростной напор измеряют с помощью скоростной трубки, потерянный напор определяется по разности между гидродинамическим напором и показанием скоростной трубки.
Для любого сечения при установившемся движении сумма геометрического Z, пьезометрического (р/ρg), скоростного (w2/2g) напоров и потерь (hn) является постоянной величиной, равной гидродинамическому напору (Н). Эта формулировка носит название геометрического смысла уравнения Бернулли.
Если единицы измерения членов уравнения Бернулли в метрах умножить и разделить на единицу веса в Н, то получим размерность удельной энергии:
Рис. 4.3. К определению членов уравнения Бернулли для реальной жидкости:
1 – напорный бак; 2 – трубопровод; 3 – пьезометр; 4 – скоростная трубка
Потерянный напор также может быть представлен в размерности удельной энергии. Удельная энергия потерь переходит в тепловую энергию и передается жидкости, стенкам трубопроводов и рассеивается в окружающую среду. Это приводит к потере давления в трубопроводе.
Энергетический смысл уравнения Бернулли:в соответствии с энергетическим смыслом его членов следует, что при установившемся движении реальной жидкости сумма удельных потенциальной энергии положения, потенциальной энергии давления, кинетической энергии и энергии потерь для любого поперечного сечения потока есть величина постоянная и равная удельной энергии гидродинамического напора.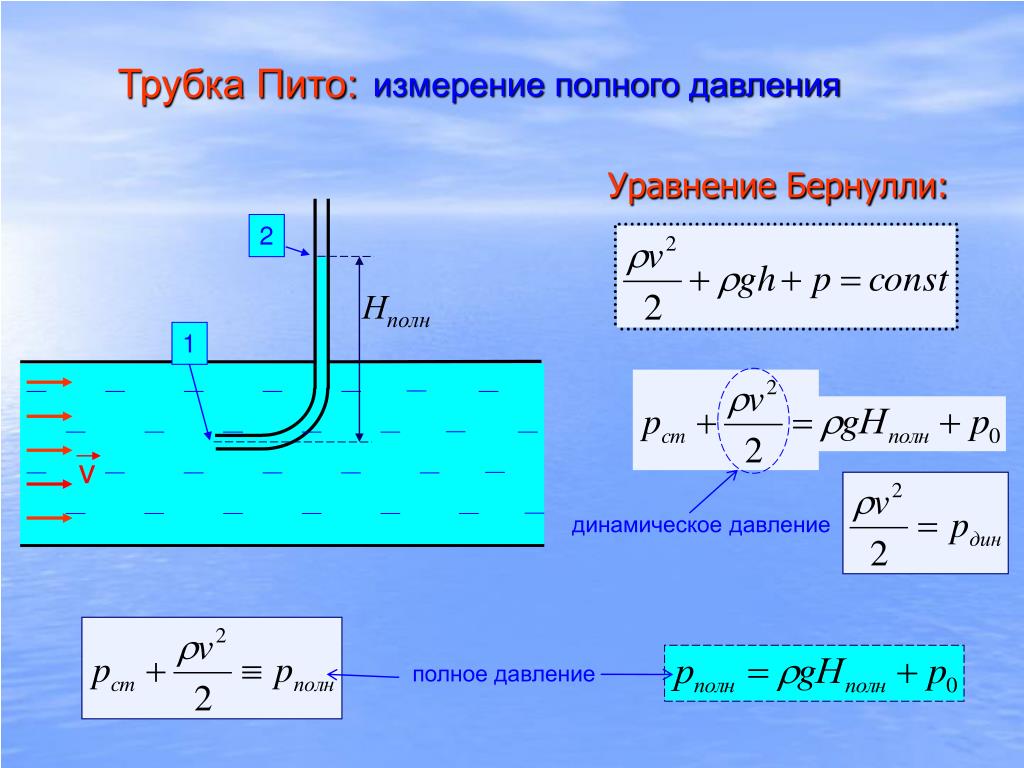
Уравнение Бернулли выражает частный случай закона сохранения энергии. При установившемся движении единицы веса несжимаемой жидкости, заключенной в объеме V, происходит непрерывный переход ее энергии из одной формы в другую, но полная энергия этой единицы объема остается неизменной по всей длине трубопровода.
35. Уравнение Бернулли для неустановившегося движения вязкой жидкости. Гидравлика
35. Уравнение Бернулли для неустановившегося движения вязкой жидкости. ГидравликаВикиЧтение
Гидравлика
Бабаев М А
Содержание
35. Уравнение Бернулли для неустановившегося движения вязкой жидкости
Уравнение Бернулли для неустановившегося движения вязкой жидкости
Для того, чтобы получить уравнение Бернулли, придется определить его для элементарной струйки при неустановившемся движении вязкой жидкости, а затем распространять его на весь поток
Прежде всего, вспомним основное отличие неустановившегося движения от установившегося. Если в первом случае в любой точке потока местные скорости изменяются по времени, то во втором случае таких изменений нет.
Приводим уравнение Бернулли для элементарной струйки без вывода:
здесь учтено, что ?? = Q; ?Q = m; m? = (КД)?.
Так же, как и в случае с удельной кинетической энергией, считать (КД)? не таккто просто. Чтобы считать, нужно связать его с (КД)?. Для этого служит коэффициент количества движения
Коэффициент a? принято называть еще и коэффициентом Бусинеска. С учетом a?, средний инерционный напор по живому сечению
Окончательно уравнение Бернулли для потока, получение которого и являлось задачей рассматриваемого вопроса имеет следующий вид:
Что касается (5), то оно получено из (4) с учетом того, что dQ = wdu; подставив dQ в (4) и сократив ?, приходим к (6).
Отличие hин от hпр прежде всего в том, что оно не является необратимым. Если движение жидкости с ускорением, что значит d?/t > 0, то hин > 0. Если движение замедленное, то есть du/t < 0, то hин < 0.
Уравнение (5) связывает параметры потока только в данный момент времени. Для другого момента оно может уже оказаться не достоверным.
Данный текст является ознакомительным фрагментом.
Административный регламент Министерства внутренних дел Российской Федерации исполнения государственной функции по контролю и надзору за соблюдением участниками дорожного движения требований в области обеспечения безопасности дорожного движения
Административный регламент Министерства внутренних дел Российской Федерации исполнения государственной функции по контролю и надзору за соблюдением участниками дорожного движения требований в области обеспечения безопасности дорожного движения Приложение к
14.
 Методы определения движения жидкости
Методы определения движения жидкости19. Уравнение неразрывности жидкости
19. Уравнение неразрывности жидкости Довольно часто при решении задач приходится определять неизвестные функции типа:1) р = р (х, у, z, t) – давление;2) nx(х, у, z, t), ny(х, у, z, t), nz(х, у, z, t) – проекции скорости на оси координат х, у, z;3) ? (х, у, z, t) – плотность жидкости.Эти неизвестные,
22. Дифференциальные уравнения движения невязкой жидкости
22. Дифференциальные уравнения движения невязкой жидкости
Уравнение Эйлера служит одним из фундаментальных в гидравлике, наряду с уравнением Бернулли и некоторыми другими. Изучение гидравлики как таковой практически начинается с уравнения Эйлера, которое служит
Изучение гидравлики как таковой практически начинается с уравнения Эйлера, которое служит
24. Форма Громеки уравнения движения невязкой жидкости
24. Форма Громеки уравнения движения невязкой жидкости Уравнения Громеки – попросту другая, несколько преобразованная форма записи уравнения Эйлера.Например, для координаты x Чтобы его преобразовать, используют уравнения компонентов угловой скорости для вихревого
25. Уравнение Бернулли
25. Уравнение Бернулли Уравнение Громеки подходит для описания движения жидкости, если компоненты функции движения содержат какуююто вихревую величину. Например, эта вихревая величина содержится в компонентах ?x, ?y,?z угловой скорости w.Условием того, что движение
26. Анализ уравнения Бернулли
26. Анализ уравнения Бернулли
это уравнение есть не что иное, как уравнение линии тока при установившемся движении.Отсюда следуют выводы:1) если движение установившееся, то первая и третья строки в уравнении Бернулли пропорциональны.2) пропорциональны строки 1 и 2,
Анализ уравнения Бернулли
это уравнение есть не что иное, как уравнение линии тока при установившемся движении.Отсюда следуют выводы:1) если движение установившееся, то первая и третья строки в уравнении Бернулли пропорциональны.2) пропорциональны строки 1 и 2,
27. Примеры прикладного применения уравнения Бернулли
27. Примеры прикладного применения уравнения Бернулли Во всех случаях требуется определить математическую формулу потенциальной функции, которая входит в уравнение Бернулли: но эта функция имеет разные формулы в разных ситуациях. Ее вид зависит от того, какие массовые
29. Энергетический смысл уравнения Бернулли
29. Энергетический смысл уравнения Бернулли Пусть теперь имеем установившееся движение жидкости, которая невязкая, несжимаемая.И пусть она находится под воздействием сил тяжести и давления, тогда уравнение Бернулли имеет вид: Теперь требуется идентифицировать каждое
30.
 Геометрический смысл уравнения Бернулли
Геометрический смысл уравнения Бернулли30. Геометрический смысл уравнения Бернулли Основу теоретической части такой интерпретации составляет гидравлическое понятие напор, которое принято обозначать буквой Н, где Гидродинамический напор Н состоит из следующих разновидностей напоров, которые входят в
31. Уравнения движения вязкой жидкости
31. Уравнения движения вязкой жидкости Для получения уравнения движения вязкой жидкости рассмотрим такой же объем жидкости dV = dxdydz, который принадлежит вязкой жидкости (рис. 1).Грани этого объема обозначим как 1, 2, 3, 4, 5, 6. Рис. 1. Силы, действующие на элементарный объем
32. Деформация в движущейся вязкой жидкости
32. Деформация в движущейся вязкой жидкости
В вязкой жидкости имеются силы трения, в силу этого при движении один слой тормозит другой. В итоге возникает сжатие, деформация жидкости. Из-за этого свойства жидкость и называют вязкой.Если вспомнить из механики закон Гука, то
В итоге возникает сжатие, деформация жидкости. Из-за этого свойства жидкость и называют вязкой.Если вспомнить из механики закон Гука, то
33. Уравнение Бернулли для движения вязкой жидкости
33. Уравнение Бернулли для движения вязкой жидкости Элементарная струйка при установившемся движении вязкой жидкостиУравнение для этого случая имеет вид (приводим его без вывода, поскольку его вывод сопряжен с применением некоторых операций, приведение которых
36. Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса
36. Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса Как нетрудно было убедиться в вышеприведенном опыте, если фиксировать две скорости в прямом и обратном переходах движения в режимы ламинарное ? турбулентное, то?1 ? ?2где ?1 – скорость, при которой
53.
 Дифференциальные уравнения неустановившегося движения
Дифференциальные уравнения неустановившегося движения53. Дифференциальные уравнения неустановившегося движения Для того, чтобы составить уравнение любого вида движения, нужно проецировать все действующие силы на систему и приравнивать их сумму к нулю. Так и поступим.Пусть имеем напорный трубопровод круглого сечения, в
48. Уравнение неразрывности
48. Уравнение неразрывности Согласно газовой теории потока течение газа в случае стационарности определяется с помощью специальной системы уравнений. В нее входят следующие соотношения:1) уравнение энергии для газового потока;2) уравнение состояния;3) уравнение для
Что означает уравнение Бернулли?
Что означает уравнение Бернулли?Уравнение Бернулли
P 1 + ρgh 1 + ½ρv 1 2 = P 2 + ρgh 2 + ½ρv 2 2
или
P + ρgh + ½ρv 2 = константа.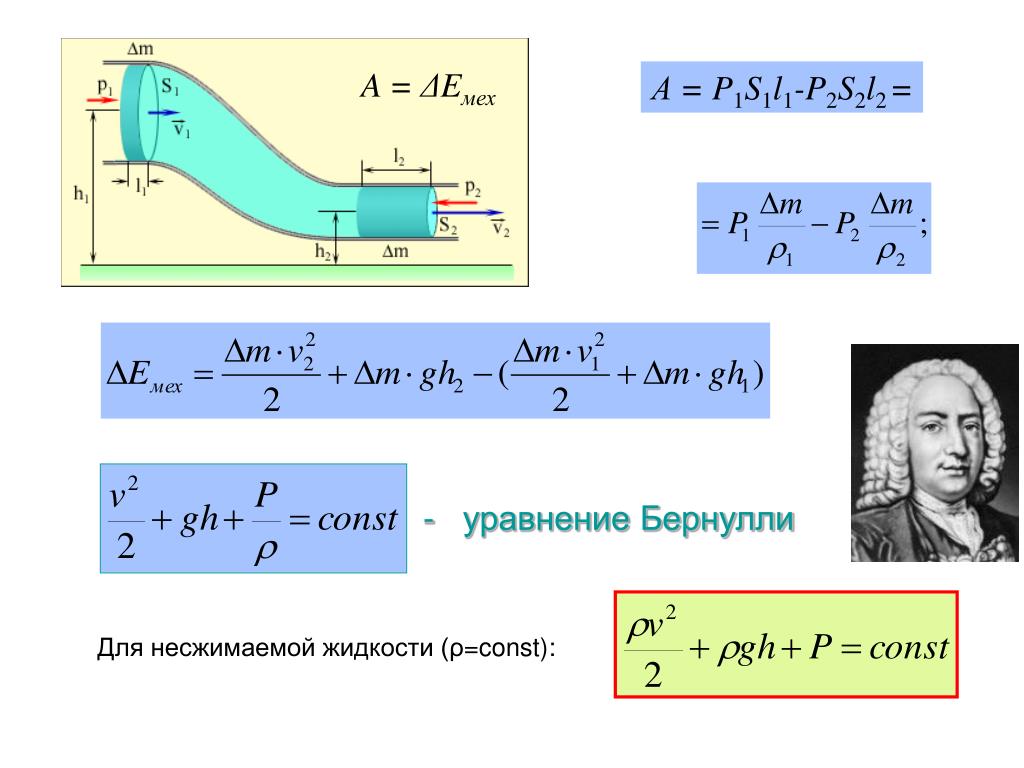
Жидкость в состоянии покоя (гидростатика)
Если жидкость покоится, то
С 1 + ргх 1 = P 2 + ρgh 2 ,
P низ + ρgh низ = P верх + ρgh верх ,
P низ = P верх + ρg(h верх – h низ ).
Давление в жидкости увеличивается линейно с глубиной.
Если жидкость покоится в горизонтальной трубе, P 1 = P 2 , давление везде одинаковое.
Жидкость, текущая по горизонтальной трубе
P 1 + ½ρv 1 2 = P 2 + ½ρv 2 2 .
Если жидкость (или несжимаемый газ)
течет без трения в установившемся режиме через горизонтальную
трубы с переменной площадью поперечного сечения, то давление зависит от скорости
жидкости.
Чем быстрее течет жидкость, тем меньше давление при том же высота.
Это может показаться вам нелогичным, но это следствие сохранения энергии. Молекулы жидкости в комнате температура всегда находится в движении, даже если вся жидкость в целом покоится. Это беспорядочное движение отвечает за давление, оказываемое жидкостью, даже в невесомом пространстве. В трубе это приводит к столкновениям с стены. Если жидкость течет по горизонтальной трубе с постоянной скорости, то и молекулы имеют упорядоченное движение. В узком отрезке по трубе жидкость течет быстрее, и больше ее энергии идет на упорядоченное движение. Это оставляет меньше энергии для случайного движения и поэтому приводит к более мягким столкновениям и более низкому давлению. Явления, которые можно понять с помощью уравнения Бернулли включают трубку Пито, эффект Вентури, распылители, ураганы, взмахи флаги и т.д.
Более быстрый поток –> больше кинетической энергии в упорядоченном движении –> меньше кинетической энергии при хаотичном движении –> меньшее давление
Проблема:
Трубку Вентури можно использовать в качестве расходомера жидкости. Если разница в
давление P 1 – P 2 = 21 кПа, найти расход жидкости в м 3 /с
учитывая, что радиус выпускной трубы равен 1 см, радиус входной трубы равен
2 см, а жидкость – бензин (ρ = 700 кг/м 3 ).
Если разница в
давление P 1 – P 2 = 21 кПа, найти расход жидкости в м 3 /с
учитывая, что радиус выпускной трубы равен 1 см, радиус входной трубы равен
2 см, а жидкость – бензин (ρ = 700 кг/м 3 ).
Решение:
- Обоснование:
Из уравнения Бернулли имеем P 1 + ρgh 1 + ½ρv 1 2 = Р 2 + ρgh 2 + ½ρv 2 2 ,.
ч является константой, поэтому P 1 + ½ρv 1 2 = P 2 + ½ρv 2 2 , или P 1 – P 2 = ½ρv 2 2 – ½ρv 1 2 .
Из уравнения неразрывности имеем
Область 1*v 1 = Область 2*v 2 . v 1 = (А 2 /А 1 )v 2 . - Детали расчета:
Используя P 1 – P 2 = ½ρv 2 2 – ½ρv 1 2 , у нас
21 кПа = 350 кг/м 3 (v 2 2 – v 1 2 ).
Вставка v 1 = (А 2 /А 1 )v 2 . в приведенное выше уравнение мы имеем
(1-(A 2 /A 1 ) 2 )v 2 2 ) = (21000/350)(м/с) 2 .
(А 2 /А 1 ) 2 = (1/4) 2 = 1/16. v 2 2 = (21000/350)(16/15)(м/с) 2 = 64(м/с) 2. .
против 2 = 8 м/с.
Объемный расход: A 2 v 2 = π(0,01 м) 2 *8 м/с = 0,0025 м 3 /с.
Реальные жидкости не идеальны. Но в достаточно коротком разделе ламинарное течение реальной жидкости можно приближенно считать идеальным, если потери энергии на этом участке очень малы по сравнению с упорядоченной кинетической энергией жидкости в разрезе. Тогда уравнение Бернулли приблизительно справедливо для этого сечения реальной жидкости.
Встроенный вопрос 1
Вы опускаете стекло в машине, когда едете по автостраде. Ан
пустой полиэтиленовый пакет на полу быстро вылетает в окно. Объяснять
Зачем.
Ан
пустой полиэтиленовый пакет на полу быстро вылетает в окно. Объяснять
Зачем.
Обсудите это со своими сокурсниками на форуме!
[Решено] Условия течения жидкости в уравнении Бернулли
- Стационарное, несжимаемое и идеальное
- Устойчивый, невращающийся и однородный
- Устойчивый, однородный и несжимаемый
- Ничего из вышеперечисленного
Вариант 1: Устойчивый, несжимаемый и идеальный 33,6 тыс. пользователей
20 вопросов
20 баллов
12 минут
Пояснение:
Принцип Бернулли в гидродинамике
Принцип Бернулли в гидродинамике гласит, что увеличение скорости жидкости происходит одновременно с уменьшением статического давления или уменьшением потенциальной энергии жидкости.
Следующие предположения сделаны при выводе уравнения Бернулли:
- Жидкость идеальна, т.
 е. вязкость равна нулю
е. вязкость равна нулю - Поток стабильный
- Поток несжимаемый
- Поток одномерный
- Течение идет вдоль линии тока
Важные моменты
Уравнение Бернулли:
Уравнение Бернулли утверждает, что при установившемся идеальном течении несжимаемой жидкости полная энергия в любой точке жидкости постоянна. Полная энергия состоит из энергии давления, кинетической энергии и потенциальной энергии или нулевой энергии. 92}}}{2} + gZ =Constant\)
- Уравнение Бернулли было получено в предположении, что жидкость невязкая и, следовательно, не имеет трения.
- Уравнение Бернулли можно рассматривать как формулировку принципа сохранения энергии, применимого к текущим жидкостям.
- В нем говорится, что в стационарном потоке сумма всех форм энергии в жидкости вдоль линии тока одинакова во всех точках на этой линии тока.
- Представлено в виде головы (общая энергия на единицу веса).

- Уравнение Бернулли можно получить, интегрируя уравнение движения Эйлера.
- Но вся реальная жидкость вязкая и, следовательно, создает сопротивление потоку.
- Таким образом, в потоке жидкости всегда есть некоторые потери и, следовательно, при применении уравнения Бернулли эти потери учитываются.
Таким образом, уравнение Бернулли для реальной жидкости между точкой 1 и точкой 2 в любом поле течения определяется как 2 + Кинетическая энергия в точке 2 + + Потенциальная энергия в точке 2 + Потеря энергии. 92\) = Кинетическая энергия в точке 2, 90 169
В то время как уравнение Бернулли сформулировано в терминах общепризнанных идей, таких как сохранение энергии и идеи давления, кинетической энергии и потенциальной энергии, его применение в приведенной выше форме ограничено случаями установившегося течения.
Поделиться в WhatsApp
Последние обновления SSC JE ME
Последнее обновление: 18 января 2023 г.
SSC JE ME Paper I 2022 Results & Cut-Off был опубликован. Экзамен SSC JE Paper II состоится 26 февраля 2023 г. Уведомление SSC JE ME 2023 будет выпущено 26 июля 2023 г. Экзамен запланирован на октябрь 2023 г. Комиссия (SSC) выпустила допуск для всех регионов для экзамена I экзамена SSC JE ME 2022 9 ноября 2022 года. Планируется, что экзамен I экзамена SSC JE ME будет проводиться с 14 ноября 2022 года по 16 ноября 2022 года. Кандидаты могут ознакомьтесь с пропускными картами SSC JE ME здесь. Кандидаты, успешно сдавшие экзамен, получат заработную плату в размере 1 000 000 рублей. 35 400 / – до рупий. 1 12 400 / – шкала заработной платы. Кандидаты могут подготовиться наилучшим образом, следуя лучшим книгам SSC JE ME, чтобы сдать экзамен.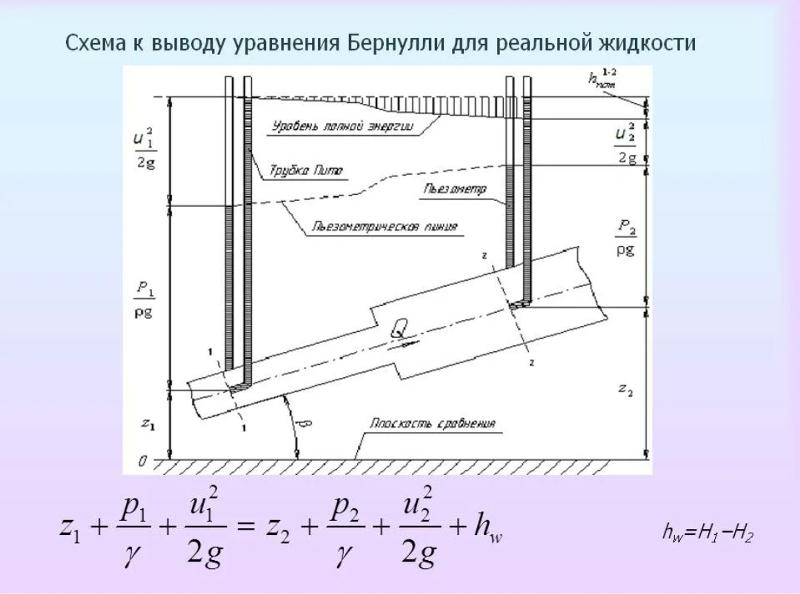


 е. вязкость равна нулю
е. вязкость равна нулю