Элементы гидро- и аэродинамики
Для того, чтобы описать такой сложный процесс, как движение жидкостей или газов, применяют разного рода упрощенные модели. Например, для упрощения используется предположение, что жидкость или даже газ несжимаемы и идеальны, не имеют внутреннее трение между слоями, которые движутся. Когда такая идеальная жидкость находится в движении, отсутствует переход механической энергии во внутреннюю, т.е. имеет место выполнение закона сохранения механической энергии. В свою очередь, из этого закона для стационарного потока идеальной и несжимаемой жидкости вытекает уравнение (принцип) Бернулли, которое было сформулировано в 1738 г.
Элементы гидродинамики. Уравнение Бернулли
Определение 1Стационарный поток жидкости – это поток без образования вихрей. В этом случае частицы жидкости осуществляют перемещение по постоянным во времени траекториям, называемым линиями тока.
В рамках имеющегося опыта можно утверждать, что возникновение стационарных потоков возможно лишь тогда, когда скорость движения жидкости достаточно мала.
Возьмем для рассмотрения стационарное течение идеальной несжимаемой жидкости по трубе переменного сечения (рис. 1.22.1). Различные части трубы располагаются на разных высотах.
Рис. 1.22.1. Поток идеальной жидкости в трубе переменного сечения.
Рассматриваемая труба имеет два сечения: S1и S2; Δt – это время прохождения жидкости в трубе. Так, за Δt через сечение S1 жидкость осуществит перемещение на l1=υ1Δt; через сечение S2 – на l2=υ2Δt (υ1 и υ2 – обозначение скоростей частиц жидкости в трубе соответствующих сечений). Условие несжимаемости будет иметь следующую запись: ΔV=l1S1=l2S2 или υ1S1=υ1S1, где ΔV является объемом жидкости, прошедшей через сечения S1 и S2.
С переходом жидкости из участка трубы большего сечения в участок меньшего сечения скорость движения потока увеличивается: жидкость перемещается с ускорением. Это означает, что жидкость испытывает воздействие силы. Если речь идет о движении потока в горизонтальной трубе, можно утверждать, что возникновение этой силы возможно только как следствие разности давления в широком и узком участках трубы (в широком участке давление должно быть больше, чем в узком).
Сила давления есть упругая сила сжатия жидкости.
Явление несжимаемости жидкости означает только то, что возникновение упругих сил имеет место при пренебрежимо малом изменении объема любой части жидкости.
Поскольку действует предположение, что жидкость идеальна, ее протекание по трубе происходит без трения, а значит к ее движению уместно применять закон сохранения механической энергии.
В процессе движения жидкости силы давления выполняют работу, которую запишем так:
ΔA=p1S1l1 – p2S2l2=p1S1υ1Δt – p2S2υ2Δt=(p1–p2)ΔV.
Определение 3Работа ΔA сил давления есть изменение потенциальной энергии упругой деформации жидкости, взятое с обратным знаком.
Те изменения, которые происходят за промежуток времени Δt в выделенной части жидкости, помещенной между участками трубы с сечениями S1 и S2 в начальный момент времени, в случае стационарного течения заключаются в перемещении массы жидкости Δm=ρΔV из участка с сечением S1 в участок сечением S2 (ρ – плотность жидкости). На рисунке 1.22.1 соответствующие объемы обозначены штриховкой. Закон сохранения механической энергии для этой массы будет иметь запись: E2–E1=ΔA=(p1–p2)ΔV. E1 и E2 здесь являются полными механическими энергиями массы Δm в поле тяготения и записываются так:
На рисунке 1.22.1 соответствующие объемы обозначены штриховкой. Закон сохранения механической энергии для этой массы будет иметь запись: E2–E1=ΔA=(p1–p2)ΔV. E1 и E2 здесь являются полными механическими энергиями массы Δm в поле тяготения и записываются так:
E1=∆mv122+∆mgh2; E2=∆mv222+∆mgh3.
Откуда можно вывести:
pv122+pgh2+p1=pv222+pgh3+p2.
Определение 4Выражение pv122+pgh2+p1=pv222+pgh3+p2 называется уравнением Бернулли.
Из уравнения Бернулли следует, что: pv22+pgh+p=const на всей протяженности рассматриваемой трубы. В частном случае, когда труба расположена горизонтально, уравнение Бернулли принимает вид: pv22+p=const.
Величина p обозначает статическое давление в жидкости, которое возможно измерить, используя манометр, двигающийся вместе с жидкостью. В практике давление в различных сечениях трубы определяют при помощи манометрических трубок, размещаемых через боковые стенки в поток жидкости таким образом, чтобы нижние концы трубок были параллельны скоростям частиц жидкости (рис.
Давление в жидкости, проходящей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в коих скорость больше.
Рис. 1.22.2. Использование манометров для определения давления в потоке.
В случае, когда сечение потока жидкости достаточно велико, уравнение Бернулли необходимо применять к линиям тока, т. е. линиям, вдоль которых происходит перемещение частиц жидкости при стационарном течении.
Пример 2Мы имеем широкий сосуд с отверстием в боковой стенке, в котором течет идеальная несжимаемая жидкость. При движении потока из отверстия линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие (рис. 1.22.3).
Рис. 1.22.3. Истечение жидкости из широкого сосуда.
Так как скорость жидкости вблизи поверхности в широком сосуде является пренебрежимо малой, уравнение Бернулли примет вид: pv22+p=const,
где p0 – атмосферное давление, h – перепад высоты вдоль линии тока.
v=2gh – это формула, выражающая скорость истечения потока и называемая формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости.
Элементы аэродинамики
Отличительной чертой газов от жидкостей является возможность значимо изменять свой объем. Расчеты позволяют утверждать, что сжимаемостью газов можно пренебречь, когда наибольшие скорости в потоке являются малыми по сравнению со скоростью звука в этом газе. Следовательно, уравнение Бернулли возможно использовать для достаточно широкого класса задач аэродинамики.
В числе подобных задач – исследование сил, осуществляющих воздействие на крыло самолета. Строго теоретически решить эту задачу достаточно затруднительно, и обычно для изучения сил используют экспериментальные методы. Уравнение Бернулли дает возможность только качественно объяснить появление подъемной силы крыла.
Рис. 1.22. 4 демонстрирует линии тока воздуха, обтекающего крыло самолета. Особый профиль крыла и наличие угла атаки (угла наклона крыла по отношению к набегающему потоку воздуха) определяют тот факт, что скорость течения воздуха над крылом становится больше, чем под крылом. В связи с этим на рис. 1.22.4 линии тока над крылом расположены ближе друг к другу, чем под крылом. Выводом из принципа Бернулли является то, что давление в нижней части крыла будет больше, чем в верхней, и в итоге мы имеем силу
4 демонстрирует линии тока воздуха, обтекающего крыло самолета. Особый профиль крыла и наличие угла атаки (угла наклона крыла по отношению к набегающему потоку воздуха) определяют тот факт, что скорость течения воздуха над крылом становится больше, чем под крылом. В связи с этим на рис. 1.22.4 линии тока над крылом расположены ближе друг к другу, чем под крылом. Выводом из принципа Бернулли является то, что давление в нижней части крыла будет больше, чем в верхней, и в итоге мы имеем силу
Fy→ – вертикальная составляющая силы F→, называемая подъемной силой.
Fx→ – горизонтальная составляющая силы F→, называемая силой сопротивления среды.
Подъемная сила дает возможность компенсации силы тяжести, осуществляющей действие на самолет, и этим она и определяет саму возможность движения тяжелых летательных аппаратов в воздушной среде.
Рис. 1.22. 4. Линии тока при обтекании крыла самолета и возникновение подъемной силы. α – угол атаки.
α – угол атаки.
Теорию подъемной силы крыла самолета сформулировал Н. Е. Жуковский в 1904 г., и она получила название теоремы Жуковского:
Подъёмная сила сегмента крыла бесконечного размаха равна произведению плотности газа (жидкости), скорости газа (жидкости), циркуляции скорости потока и длины выделенного отрезка крыла. Направление действия подъёмной силы получается поворотом вектора скорости набегающего потока на прямой угол против циркуляции.
Жуковский продемонстрировал, что при обтекании крыла значимое влияние оказывают силы вязкого трения в поверхностном слое. Итогом их воздействия является возникновение кругового движения или циркуляции воздуха вокруг крыла (обозначено стрелками зеленого цвета на рис. 1.22. 4). В верхней части крыла скорость циркулирующего воздуха соединяется со скоростью набегающего потока, в нижней же части эти скорости противоположно направлены. Подобный эффект и служит причиной появления разности давлений и образования подъемной силы.
Циркуляция воздуха, определяемая силами вязкого трения, появляется и вокруг тела, которое вращается. Практически значимым, к примеру, является вращение цилиндра.
При вращении цилиндра само тело влечет за собой примыкающие слои воздуха, создавая циркуляцию воздушного потока. Когда цилиндр установлен в набегающем потоке, возникает сила бокового давления, подобная подъемной силе крыла самолета. Такое явление носит название эффекта Магнуса.
На рис. 1.22.5 проиллюстрировано обтекание цилиндра, осуществляющего вращение, набегающим потоком. Примером эффекта Магнуса служит полет закрученного мяча при игре в теннис или футбол.
Рис. 1.22.5. Обтекание вращающегося цилиндра набегающим потоком воздуха.
Таким образом, на множество явлений аэродинамики оказывают значимое влияние силы вязкого трения. Они дают толчок к возникновению циркулирующих потоков воздуха вокруг крыла самолета или вокруг вращающегося тела, к появлению силы сопротивления среды и т. д. Уравнение Бернулли не берет в расчет силы трения. Вывод Бернулли опирается на закон сохранения механической энергии при течении жидкости или газа. Поэтому при помощи принципа Бернулли невозможно исчерпывающе объяснить явления, в которых имеется проявление сил трения. В подобных случаях возможно опираться лишь на качественные соображения – чем больше скорость, тем меньше давление в потоке газа.
д. Уравнение Бернулли не берет в расчет силы трения. Вывод Бернулли опирается на закон сохранения механической энергии при течении жидкости или газа. Поэтому при помощи принципа Бернулли невозможно исчерпывающе объяснить явления, в которых имеется проявление сил трения. В подобных случаях возможно опираться лишь на качественные соображения – чем больше скорость, тем меньше давление в потоке газа.
Особо заметное проявление имеют силы вязкого трения в потоке жидкостей. Некоторые жидкости обладают вязкостью такой значимой величины, что использование уравнения Бернулли может привести к качественно неверным результатам.
Пример 3К примеру, в случае истечения жидкости высокой вязкости через отверстие в стенке сосуда ее скорость может быть в десятки раз меньше той, что будет рассчитана по формуле Торричелли. Когда сферическое тело движется в идеальной жидкости, оно не должно встречать лобового сопротивления. Когда такое тело перемещается в вязкой жидкости, появляется сила сопротивления, и ее модуль будет пропорционален скорости υ и радиусу сферы r (закон Стокса) Fсопр ~υ·ċ·r.
Коэффициент пропорциональности в этом выражении имеет зависимость от свойств жидкости. Т.е., если шарик значимого веса бросить в высокий сосуд, содержащий вязкую жидкость (к примеру, глицерин), то спустя некоторое время скорость шарика установится на уровне определенного значения, не изменяющегося при последующем движении шарика. Когда движение будет происходить на некой установившейся скорости, силы, влияющие на шарик (сила тяжести mg→, выталкивающая сила FА→ и сила сопротивления средыFсопр), оказываются скомпенсированными, и их равнодействующая будет равна нулю.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.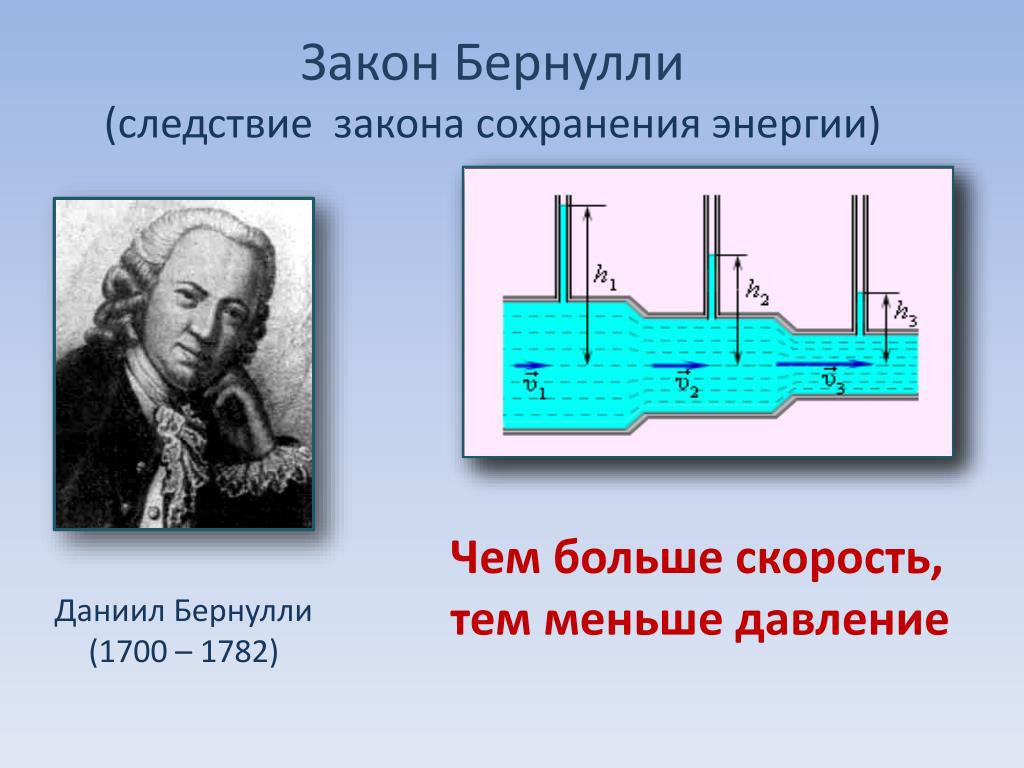 Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Уравнение Бернулли. Полная энергия потока. Скоростной напор. | Презентация к уроку:
Слайд 1
Модуль: Аэродинамика как наука ГБПОУ МГОК Автор курса: к.э.н. Шкромада Валентина Ивановна Код и наименование специальности: 25.02.08. Эксплуатация беспилотных авиационных систем УРАВНЕНИЕ БЕРНУЛЛИ. ПОЛНАЯ ЭНЕРГИЯ ПОТОКА. СКОРОСТНОЙ НАПОР ОП.07 основы аэродинамики, динамики полета и летно-технические характеристики беспилотных воздушных судов Наименование программы: Основы аэродинамики
Слайд 2
ОСНОВНЫЕ ЗАКОНЫ АЭРОДИНАМИКИ Используя аэродинамические законы, теоретическая аэродинамика позволяет сделать расчёты аэродинамических сил, действующих на летательный аппарат в полете Уравнение состояния идеального газа (уравнение Клапейрона или уравнение Менделеева- Клапейрона ) Объединенный газовый закон Уравнение постоянства расхода (уравнение неразрывности струи) – закон Эйлера Закон Бернулли
Слайд 3
УРАВНЕНИЕ БЕРНУЛЛИ Закон Бернулли – это следствие закона сохранения энергии для стационарного потока идеальной и несжимаемой жидкости В аэродинамике воздух рассматривается как несжимаемая жидкость , то есть, такая среда, плотность которой не меняется с изменением давления С тационарным считается поток, в котором частицы перемещаются по неизменным во времени траекториям, которые называют линиями тока. В таких потоках не образуются вихри
В таких потоках не образуются вихри
Слайд 4
УРАВНЕНИЕ БЕРНУЛЛИ Вернемся к примеру, рассмотренному на предыдущем занятии. Если жидкость течёт по трубе, имеющей разное поперечное сечение, то давление в разных местах трубы будет неодинаковое Мысленно выделим в трубе несколько сечений, обозначив их площади S 1 и S 2 . Соответственно, v 1 и v 2 – скорости течений несжимаемой жидкости через эти сечения
Слайд 5
УРАВНЕНИЕ БЕРНУЛЛИ С увеличением скорости потока жидкости уменьшается давление, и наоборот . Из уравнения неразрывности следует, что v 1 / v 2 = S 2 / S 1 Т.е ., скорости жидкостей обратно пропорциональны площадям сечений. И чем больше площадь сечения, тем меньше скорость жидкости , протекающей через него, и наоборот. При стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и наоборот
Слайд 6
УРАВНЕНИЕ БЕРНУЛЛИ Таким образом, уравнение Бернулли имеет вид: г де: ρ – плотность жидкости ν – скорость потока h – высота, на которой располагается элемент жидкости ɡ – ускорение свободного падения p – давление в точке пространства, в которой расположен центр массы элемента жидкости
Слайд 7
ПОЛНАЯ ЭНЕРГИЯ ПОТОКА. СКОРОСТНОЙ НАПОР Первое слагаемое уравнения Бернулли – кинетическая энергия потока, или динамическое давление. Его создаёт движение жидкости или газа В авиации его также называют скоростным напором
СКОРОСТНОЙ НАПОР Первое слагаемое уравнения Бернулли – кинетическая энергия потока, или динамическое давление. Его создаёт движение жидкости или газа В авиации его также называют скоростным напором
Слайд 8
ЗАКОН БЕРНУЛЛИ И АВИАЦИЯ С помощью этого закона можно просто объяснить, как возникает подъёмная сила для летательного аппарата тяжелее воздуха Во время полёта крыло самолёта как бы разрезает воздушный поток на две части. Одна часть обтекает верхнюю поверхность крыла, а другая нижнюю. Форма крыла такова, что верхний поток должен преодолеть больший путь для того, чтобы соединиться с нижним потоком в одной точке. Поэтому он двигается с большей скоростью. Так как скорость больше, то и давление над верхней поверхностью крыла меньше, чем под нижней. За счёт разности этих давлений и возникает подъёмная сила крыла
Слайд 9
ЗАКОН БЕРНУЛЛИ И АВИАЦИЯ Во процессе набора высоты воздушным судном возрастает разница давлений, следовательно, увеличивается и подъёмная сила, что позволяет аппарату подниматься вверх. Необходимо уточненить , что вышеописанные законы действуют, если скорость движения воздушного потока меньше скорости звука (до 340 м/с). На этих скоростях воздух можно рассматривать как несжимаемую жидкость. При скоростях выше скорости звука воздушный поток ведёт себя по-другому и его сжимаемостью пренебрегать уже нельзя. Воздух в этих условиях, как любой газ, старается расшириться и занять больший объём. Появляются значительные перепады давления или ударные волны. А сам воздушный поток не сужается, а, наоборот, расширяется. Решением задач о движении воздушных потоков со скоростями, близкими или превышающими скорость звука, занимается газовая динамика , возникшая как продолжение аэродинамики
Необходимо уточненить , что вышеописанные законы действуют, если скорость движения воздушного потока меньше скорости звука (до 340 м/с). На этих скоростях воздух можно рассматривать как несжимаемую жидкость. При скоростях выше скорости звука воздушный поток ведёт себя по-другому и его сжимаемостью пренебрегать уже нельзя. Воздух в этих условиях, как любой газ, старается расшириться и занять больший объём. Появляются значительные перепады давления или ударные волны. А сам воздушный поток не сужается, а, наоборот, расширяется. Решением задач о движении воздушных потоков со скоростями, близкими или превышающими скорость звука, занимается газовая динамика , возникшая как продолжение аэродинамики
Уравнение Бернулли
Загрузка
Даниэль Бернулли (Гронинген, 29 января 1700 — 27 июля 1782) был швейцарским математиком, который провел большую часть своей жизни в Базеле, где и умер. Член талантливой семьи математиков, физиков и философов, он особенно известен своими приложениями математики к механике, особенно гидромеханике, а также новаторскими работами в области вероятности и статистики. (Википедия)
Самые простые и популярные объяснения аэродинамической подъемной силы ссылаются на принцип Бернулли, который, в свою очередь, выводится из теоремы Бернулли. Его уравнение, исследованное в начале 1700-х годов Даниэлем Бернулли, определяет физические законы, на которых основано большинство аэродинамических правил. Это ныне известное уравнение является абсолютно фундаментальным для изучения воздушных потоков. Каждая попытка улучшить то, как машина Формулы-1 пробивает себе дорогу через молекулы воздуха, основывается на этой естественной взаимосвязи между скоростью жидкости (газа или жидкости) и давлением. Существует несколько форм уравнения Бернулли, три из которых обсуждаются в следующих параграфах: течение по одной линии тока, течение по многим линиям тока и течение по аэродинамическому профилю.
Существует несколько форм уравнения Бернулли, три из которых обсуждаются в следующих параграфах: течение по одной линии тока, течение по многим линиям тока и течение по аэродинамическому профилю.
Все три уравнения были получены с использованием нескольких предположений, возможно, наиболее важным из которых является то, что плотность воздуха не изменяется с давлением (т. е. воздух остается несжимаемым). Поэтому их можно применять только в дозвуковых ситуациях.
Так как автомобили F1 движутся намного медленнее, чем 1 Маха, эти уравнения могут быть использованы для получения очень точных результатов.
Низкоскоростное течение жидкости вдоль одной или нескольких линий тока интерпретируется на рисунке 1. На рисунке перечислены допущения относительно применения уравнения Бернулли к этому сценарию. В этой ситуации существует связь между скоростью, плотностью и давлением. Поскольку одиночный поток жидкости течет по трубе с изменяющейся площадью поперечного сечения (например, воздухозаборник F1), его скорость уменьшается от первой до второй станции, а его полное давление остается постоянным. При наличии нескольких линий тока общее давление равно одной и той же константе вдоль каждой линии тока. Однако это имеет место только в том случае, если перепады высот между линиями тока пренебрежимо малы. В противном случае каждая линия тока имеет уникальное полное давление.
При наличии нескольких линий тока общее давление равно одной и той же константе вдоль каждой линии тока. Однако это имеет место только в том случае, если перепады высот между линиями тока пренебрежимо малы. В противном случае каждая линия тока имеет уникальное полное давление.
Математическое и графическое объяснение уравнения Бернулли применительно к потоку жидкости через трубу с изменяющейся площадью поперечного сечения.
Применительно к низкоскоростным аэродинамическим профилям (например, крыльям прижимной силы F1) воздушный поток несжимаем, и его плотность остается постоянной. Тогда уравнение Бернулли сводится к простому соотношению между скоростью и статическим давлением.
(давление) + 0,5 (плотность) X (скорость)2 = константа
Из этого уравнения следует, что увеличение давления должно сопровождаться уменьшением скорости и наоборот. Интегрирование статического давления по всей поверхности аэродинамического профиля дает полную аэродинамическую силу, действующую на тело. Компоненты подъемной силы и сопротивления могут быть определены путем разложения этой силы.
Компоненты подъемной силы и сопротивления могут быть определены путем разложения этой силы.
Чтобы обсудить подъемную силу и прижимную силу, может оказаться полезным дать дополнительное объяснение связи, возникающей в приведенной выше форме уравнения Бернулли. Если жидкость обтекает объект с разными скоростями, более медленная жидкость будет оказывать большее давление на объект, чем более быстрая жидкость. Затем объект будет вынужден приближаться к более быстро движущейся жидкости. Результатом этого события является либо подъемная сила, либо прижимная сила, каждая из которых зависит от положения более длинной хорды крыла. Подъемная сила возникает, когда более длинная хорда направлена вверх, а прижимная сила возникает, когда она направлена вниз.
Подъемная сила в соответствии с применением уравнения Бернулли
Хотя принцип Бернулли является основным источником подъемной или прижимной силы в крыле самолета или гоночного автомобиля, эффект Коанда играет еще большую роль в создании подъемной силы.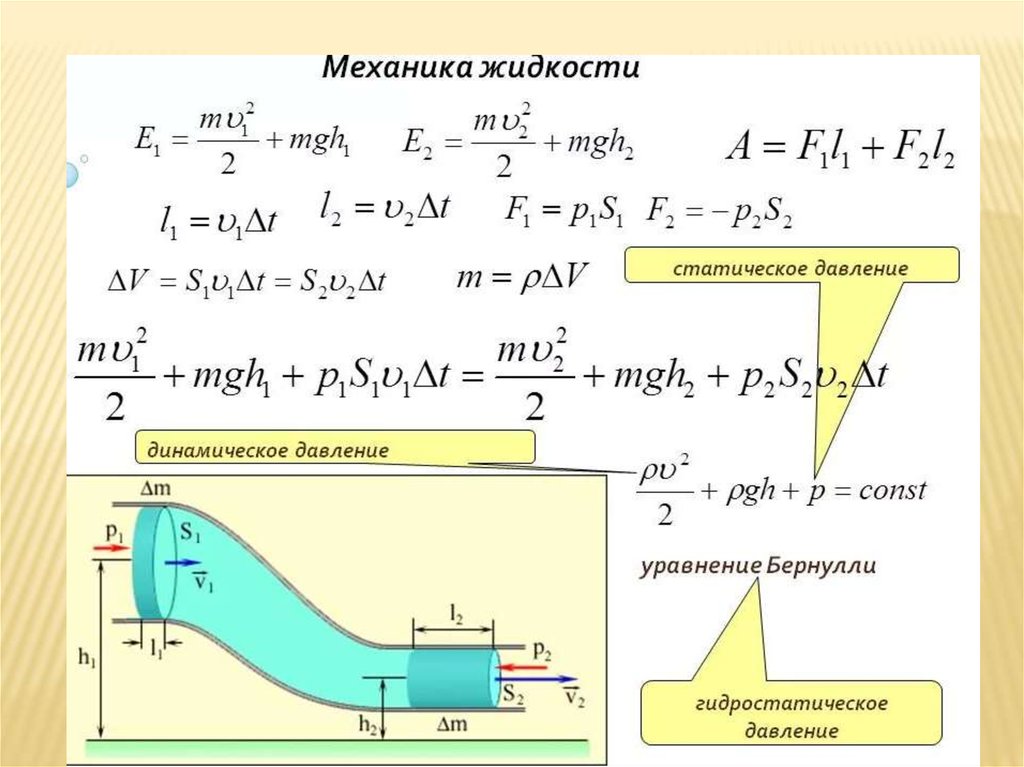 Чтобы узнать больше о взаимодействии принципа Бернулли и эффекта Коанда, ознакомьтесь с моей статьей здесь.
Чтобы узнать больше о взаимодействии принципа Бернулли и эффекта Коанда, ознакомьтесь с моей статьей здесь.
В то время как принцип Бернулли часто используется для объяснения явления аэродинамической подъемной силы, создаваемой воздушным потоком вокруг профиля крыла, существуют альтернативные объяснения, которые используют в той или иной комбинации: «эффект Коанды», понятие циркуляции и третий закон Ньютона. закон. Эти альтернативные объяснения, по крайней мере, столь же правомерны, как и объяснение, основанное на принципе Бернулли, и среди аэродинамиков считаются в некоторой степени превосходящими объяснение Бернулли. 901:35 Гордон Маккейб опубликовал отличную статью по этому аргументу «Объяснение и открытие в аэродинамике» от 2 февраля 2008 года. Вы можете скачать его работу здесь.
Из реферата:
“Цель этой статьи состоит в том, чтобы обсудить и прояснить объяснения, обычно приводимые для аэродинамической подъемной силы, создаваемой крылом, а затем проанализировать, как пример инженерного открытия, аэродинамические революции, которые произошли в Формуле 1 в за последние 40 лет.


 Так же и искусственный
самолеты полагаются на эти принципы для преодоления силы тяжести и достижения
полет.
Так же и искусственный
самолеты полагаются на эти принципы для преодоления силы тяжести и достижения
полет.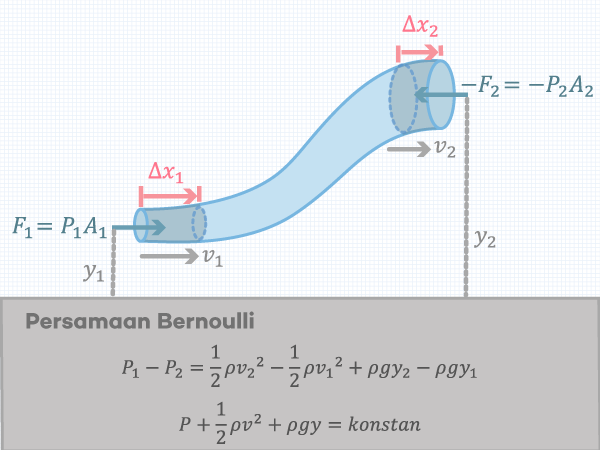 Самолет использует крылья для подъемной силы, а двигатели — для тяги. Перетащите
уменьшается за счет гладкой формы самолета, а его вес контролируется материалами, из которых он изготовлен.
построен из.
Самолет использует крылья для подъемной силы, а двигатели — для тяги. Перетащите
уменьшается за счет гладкой формы самолета, а его вес контролируется материалами, из которых он изготовлен.
построен из. Уравнение Бернулли записывается как:
Уравнение Бернулли записывается как:
 Результатом является чистая сила давления в восходящем (положительном) направлении.
направление. Эта сила давления является подъемной силой.
Результатом является чистая сила давления в восходящем (положительном) направлении.
направление. Эта сила давления является подъемной силой. Давление ветра в
перед вами больше, чем давление следа позади вас. Кожное трение, или вязкое
сопротивление, это то, с чем могут столкнуться пловцы. Поток воды вдоль тела пловца создает
сила трения, замедляющая пловца. Шероховатая поверхность вызовет большее сопротивление трения
чем гладкая поверхность. Чтобы уменьшить вязкостное сопротивление, пловцы пытаются создать контактные поверхности как
как можно более гладкими, надев шапочки для плавания и побрив ноги. Так же и крыло самолета
разработан, чтобы быть гладким, чтобы уменьшить сопротивление.
Давление ветра в
перед вами больше, чем давление следа позади вас. Кожное трение, или вязкое
сопротивление, это то, с чем могут столкнуться пловцы. Поток воды вдоль тела пловца создает
сила трения, замедляющая пловца. Шероховатая поверхность вызовет большее сопротивление трения
чем гладкая поверхность. Чтобы уменьшить вязкостное сопротивление, пловцы пытаются создать контактные поверхности как
как можно более гладкими, надев шапочки для плавания и побрив ноги. Так же и крыло самолета
разработан, чтобы быть гладким, чтобы уменьшить сопротивление.
 Ускорение
скорость изменения скорости во времени. Таким образом, тяга (T) создается за счет
ускорение массы воздуха.
Ускорение
скорость изменения скорости во времени. Таким образом, тяга (T) создается за счет
ускорение массы воздуха. Как каждый из них создает подъемную силу? Как быстро может двигаться каждый?
Каковы преимущества и недостатки каждого из них?
Как каждый из них создает подъемную силу? Как быстро может двигаться каждый?
Каковы преимущества и недостатки каждого из них?