Уравнение состояния идеального газа • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Термодинамические характеристики идеального газа описываются одним простым уравнением.
Математическая запись универсального газового закона проста:
pV = nRT *
Она содержит основные характеристики поведения газов: p, V и T — соответственно давление, объем и абсолютная температура газа (в градусах Кельвина), R — универсальная газовая постоянная, общая для всех газов, а n — число, пропорциональное числу молекул или атомов газа (так называемое число молей газа — см. Закон Авогадро).
Чтобы понять, как работает этот закон, давайте представим, что температура газа постоянна. В этом случае в правой части уравнения получается константа. Значит, произведение давления и объема при неизменной температуре оказывается неизменным. Повышение давления сопровождается уменьшением объема, и наоборот. Это не что иное, как закон Бойля—Мариотта — одна из первых экспериментально полученных формул, описывающих поведение газов. С другой стороны, при постоянном давлении (например, внутри воздушного шарика, где давление газа равно атмосферному) повышение температуры сопровождается увеличением объема. А это — закон Шарля, другая экспериментальная формула поведения газов. Закон Авогадро и закон Дальтона также являются следствиями универсального газового закона.
Этот закон представляет собой то, что в физике принято называть уравнением состояния вещества, поскольку он описывает характер изменения свойств вещества при изменении внешних условий. Строго говоря, этот закон в точности выполняется только для идеального газа. Идеальный газ представляет собой упрощенную математическую модель реального газа: молекулы считаются движущимися хаотически, а соударения между молекулами и удары молекул о стенки сосуда — упругими, то есть не приводящими к потерям энергии в системе. Такая упрощенная модель очень удобна, поскольку позволяет обойти очень неприятную трудность — необходимость учитывать силы взаимодействия между молекулами газа. И это себя оправдывает, поскольку в природных условиях поведение большинства реальных газов практически не отличается от поведения идеального газа — отклонения в поведении практически всех природных газов, например атмосферного азота и кислорода, от поведения идеального газа не превышают 1%. Это позволяет ученым спокойно включать уравнение состояния идеального газа даже в весьма сложные теоретические расчеты. Например, астрономы при моделировании горячих звезд обычно считают вещество звезды идеальным газом и весьма точно прогнозируют давления и температуры внутри них. (Заметьте, что вещество внутри звезды ведет себя как идеальный газ, хотя его плотность несопоставимо выше плотности любого вещества в земных условиях. А дело в том, что вещество звезды состоит из полностью ионизированных ядер водорода и гелия — то есть из частиц значительно меньшего диаметра, чем диаметр атомов земных газов.) В будущем, по мере совершенствования теоретических методов, возможно, будут выведены более точные уравнения для описания состояния реальных газов с учетом их характеристик на молекулярном уровне.
* Эта формула была получена в 1874 году Д. И. Менделеевым путем объединения закона Авогадро и общего газового закона (pV/T = const), сформулированного в 1834 году Б. П. Э. Клапейроном. Поэтому этот закон (в Европе, по крайней мере) принято называть законом Менделеева—Клапейрона. По существу, этот закон позволил ввести все ранее сделанные эмпирические заключения о характере поведения газов в рамки новой молекулярно-кинетической теории. (Примечание переводчика)
См. также:
elementy.ru
Формулу основного уравнения мкт идеального газа можно представить в виде
где – средняя кинетическая энергия поступательного движения молекул.
14. Абсолютная температура и её физический смысл
Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
Под понятием «температура» подразумевают степень нагретости тела.
Существует несколько температурных шкал. В абсолютной (термодинамической) шкале температура измеряется в кельвинах (К). Нуль в этой шкале называют абсолютным нулем температуры, приблизительно равен – 2730С. при абсолютном нуле прекращается поступательное движение молекул.
Термодинамическая температура Т связана с температурой по шкале Цельсия следующим соотношением:
Т = (t0 + 273)K
Для идеального газа существует пропорциональная зависимость между абсолютной температурой газа и средней кинетической энергией поступательного движения молекул:
,
где k – постоянная Больцмана, k = 1,38· 10 – 23 Дж/К
Таким образом, абсолютная температура является мерой средней кинетической энергии поступательного движения молекул. В этом заключается её физический смысл.
Подставляя в уравнение p = n выражение для средней кинетической энергии
= kT, получим
p = n ·kT = nkT
Из основного уравнения МКТ идеального газа p = nkT при подстановке
,
можно получить уравнение
, или A · kT
NA· k = R – универсальная газовая постоянная, R = 8,31
Уравнение называют уравнением состояния идеального газа (уравнением Менделеева-Клапейрона).
15. Газовые законы. Графики изопроцессов.
Изотермический процесс (Т = const) подчиняется закону Бойля – Мариотта: для данной массы газа при постоянной температуре произведение давления на объём есть величина постоянная.
, или , или
P 0 V | Изотерма идеального газа в координатных осях P,V представлена на графике. |
Изобарный процесс (р = const) подчиняется закону Гей-Люссака: для данной массы газа при постоянном давлении отношение объема газа к абсолютной температуре есть величина постоянная.
, или , или
V 0 T | Изобара идеального газа в координатных осях V, T представлена на графике. |
Изохорный процесс (V = const) подчиняется закону Шарля: для данной массы газа при постоянном объеме отношение давления газа к абсолютной температуре есть величина постоянная.
, или или
P 0 T |
Внутренняя энергия идеального газа. Способы изменения внутренней энергии.
Количество теплоты. Работа в термодинамике
Внутренней энергией называют сумму кинетической энергии хаотического движения молекул и потенциальной энергии их взаимодействия.
Так как молекулы идеального газа не взаимодействуют друг с другом, то внутренняя энергия U идеального газа равна сумме кинетических энергий хаотически движущихся молекул:
, где .
Таким образом,
,
где .
Для одноатомного газа i = 3, для двухатомного i = 5, для трех (и более)атомного i = 6.
Изменение внутренней энергии идеального газа
.
Внутренняя энергия идеального газа является функцией его состояния. Внутреннюю энергию можно изменить двумя способами:
Процесс изменения внутренней энергии системы без совершения механической работы называют теплообменом или теплопередачей. Существуют три вида теплопередачи: теплопроводность, конвекция и излучение.
Количеством теплоты называют величину, являющуюся количественной мерой изменения внутренней энергии тела в процессе теплопередачи.
Количество теплоты, необходимое для нагревания (или отдаваемое телом при охлаждении) определяется по формуле:
где с – удельная теплоемкость вещества
Работа в термодинамике
Элементарная работа d A = p dV. При p = const
studfiles.net
Калькулятор уравнения состояния идеального газа
Уравнение идеального газа — это простая формула, которая связывает основные параметры любого газообразного вещества. По сути, уравнение идеального газа представляет собой квинтэссенцию всех газовых законов.
Математические модели и идеальный газ
Простыми словами идеальный газ представляет собой математическую модель газообразного вещества, которая не учитывает взаимодействие между молекулами. В целом математические модели используются для построения рабочих научных теорий в области физики, химии или математики. К таким моделям относятся математический маятник, материальная точка, ньютоновская жидкость, и, естественно, идеальный газ. Такие модели не осуществимы на практике, но принятые допущения позволяют изучать реальные физические явления с математической точностью. К примеру, в материальной точке пренебрегают размером, но сохраняют ее массу. В идеальном газе пренебрегают силами сопротивления для изучения преобразования энергии из одного вида в другой.
На крайне малых расстояниях, когда молекулярные частицы практически сталкиваются, между ними возникают значительные силы отталкивания. Одновременно с этим на больших расстояниях наблюдаются слабые силы притяжения. В газах в нормальных условиях постоянно наблюдается явление, когда молекулы ударяются друг о друга. Идеальный же газ полностью игнорирует взаимодействие молекул, и так как частицы ведут себя как упругие шарики, в математической модели газа тепловая и кинетическая энергия эквиваленты благодаря отсутствию каких-либо потерь. Кроме того, в математической модели идеального газа размеры молекулярных частиц пренебрежительно малы по сравнению с расстоянием между ними. Для идеального газа справедливы следующие законы.
Основные газовые законы
Любой газ имеет 4 главных характеристики: объем V, давление P, температура T и количество вещества n. Эти параметры связаны между собой основными газовыми законами.
Закон Бойля-Мариотта утверждает, что при T = const произведение объема и давления не изменяется, следовательно, P×V = const. Из этого следует, что изменение одного параметра вызывает обратно пропорциональное изменение другого. Газовые реакции, протекающие при статической температуре, носят название изотермических.
Закон Шарля устанавливает, что при V = const отношение давления газа к его температуре не изменяется: P/T = const. Из формулы следует, что изменение одной характеристики сопровождается прямо пропорциональным изменением другой. Химические реакции с сохранением объемов носят название изохорических.
Закон Гей-Люссака гласит, что при P = const соотношение объема газообразного вещества к его температуре также постоянно: V/T = const. Это означает, что изменение одной величины вызывает прямо пропорциональное изменение другой. Тепловые процессы, которые протекают при статическом давлении, называются изобарическими.
Закон Авогадро утверждает, что в равных объемах газообразных веществ при одинаковых температуре и давлении содержится одинаковое число молекул n. Таким образом, при всех равных параметрах, количество моль двух газов также одинаково.
Закон идеального газа
Если взять все перечисленные законы и объединить их в одну элегантную формулу, то мы получим уравнение идеального газа, который связывает все параметры вещества и иллюстрирует относительное изменение этих величин. Математически закон идеального газа, который также носит название уравнения Менделеева-Клапейрона, записывается так:
Р × V = n × R × T,
где R — универсальная газовая постоянная, которая эквивалентна работе расширения/сжатия одного моля идеального газа в изобарическом процессе при изменении температуры на 1 кельвин.
В международной системе СИ газовая константа равна R = 8,3144 Дж/моль×К. В этом случае для правильных расчетов требуется давление выражать в паскалях, а объем — в кубических метрах. Для упрощения расчетов газовая константа выражается как R = 0,0821 л×атм/моль×К. В этом случае объем газа выражается в литрах, давление — в атмосферах, количество вещества — в моль, а температура — кельвинах.
Так как температура обычно выражается в градусах Цельсия, а все расчеты необходимо производить в кельвинах, мы напоминаем формулу для перевода значений из одной шкалы в другую:
T= t + T0,
где t — температура в градусах Цельсия, T0 — температура абсолютного нуля, равная -273 градуса.
Абсолютный нуль — это температура, при которой молекулы любого химического вещества теряют способность двигаться. Газообразные вещества при температуре -273 градуса теряют весь свой объем, однако в рамках термодинамики точка неподвижности молекул на практике недостижима.
Пример использования уравнения идеального газа
Вычисление молей
Пусть у нас есть баллон кислорода объемом V= 50 л, под давлением P = 1 атмосфера и при температуре 25 градусов Цельсия. Требуется узнать количество вещества, которое содержится в баллоне. Для этого воспользуемся уравнением Менделеева-Клапейрона и выразим из него количество вещества n:
n = P × V / R × T
Теперь необходимо перевести температуру по шкале Кельвина T = 25 + 273 = 298 К и подставить значения в формулу:
n = 1 × 50 / 0,0821 × 298 = 2,04
Таким образом, в баллоне объемом 50 л содержится 2,04 моль кислорода. Интересно, что справочное значение объема 1 моля идеального газа при нормальных условиях составляет 22,41 л, что приблизительно соответствует условию задачи, так как в нашем случае температура в баллоне несколько выше нормальной.
Наша программа позволяет вычислить любой неизвестный параметр из уравнения Менделеева-Клапейрона в случае, если заданы 3 любые величины. Для этого требуется ввести значения в соответствующие ячейки и кликнуть кнопку «Рассчитать», после чего в пустой ячейке отобразится искомое значение. Напоминаем, что указывать температуру следует в кельвинах для корректного расчета параметров при минусовой температуре.
Заключение
Изучение свойств идеального газа — неотъемлемая часть любого курса химии. Наш калькулятор пригодится школьникам и студентам начальных курсов для проверки заданий на тему «Идеальный газ».
bbf.ru
1.7 Уравнение состояния идеального газа.
Уравнение состояния идеального газа — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
, где:
p — давление,
Vμ — молярный объём,
T — абсолютная температура,
R — универсальная газовая постоянная.
Так как , где ν — количество вещества, а , где m — масса, μ — молярная масса, уравнение состояния можно записать:
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
Уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
— закон Бойля — Мариотта
— закон Гей-Люссака
— закон Шарля
1.8 Основное уравнение мкт
давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m0, концентрацией молекул n, средним значением квадрата скорости и средней кинетической энергией поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
2.1Молекулярно-кинетическое толкование параметров состояния.
Термодинамическая (абсолютная) температура с молекулярно-кинетической точки зрения — физическая величина, характеризующая интенсивность хаотического, теплового движения всей совокупности частиц системы и пропорциональная средней кинетической энергии поступательного движения одной частицы.
Связь между кинетической энергией, массой и скоростью выражаестя следующей формулой:
Ek = 1/2m • v 2
Таким образом частицы одинаковой массы и имеющие одинаковую скорость имеют и одинаковую температуру.
Средняя кинетическая энергия частицы связана с термодинамической температурой постоянной Больцмана:
Eср = 3/2kT
где:
k = 1.380 6505(24) × 10−23 Дж/K — постоянная Больцмана
T — термодинамическая температура, К
2.2Гипотеза о равном распределении энергии по степеням свободы
Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна
Из этой теоремы следует, что молярные теплоемкости газа Cp и CV и их отношение γ могут быть записаны в виде
где i – число степеней свободы газа.
Для газа, состоящего из одноатомных молекул (i = 3)
Для газа, состоящего из двухатомных молекул (i = 5)
Для газа, состоящего из многоатомных молекул (i = 6)
2.4Вывод уравнения состояния идеального газа.
Уравнение состояния идеального газа — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
, где:
p — давление,
Vμ — молярный объём,
T — абсолютная температура,
R — универсальная газовая постоянная.
Так как , где ν— количество вещества, а , где m — масса, μ — молярная масса, уравнение состояния можно записать:
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
Часто уравнение состояния можно представить вводя постоянную Больцмана
k=R/Na=1.38*10^-23 Дж/К
исходя из этого уравнение состояния можно переписать в виде
p=RT/Vm=kNaT/Vm=nkT
p= nkT
Давление идеального газа при данной температуре прямо пропорционально концентрации его молекул.
studfiles.net
3.Уравнение состояния идеального газа.
В любом из равновесных состояний параметры Р, Т и Vтермодинамической системы (т.е. газа, жидкости или твердого тела), как показывает опыт, закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение другого. Функциональная связь между давлением, объемом и температурой
f(P,V,N) = 0 (1)
называется уравнением состояния вещества. Если разрешить (1) относительно какого-либо из параметров, например, Р, то уравнение состояния примет вид
Р = Р(V, Т). (2)
Опыт показывает, что для жидкости и твердых тел характер зависимости Р = Р(V, Т) крайне индивидуален. Иначе обстоит дело в случае разреженных газов. Все достаточно разреженные газы подчиняются одному и тому же уравнению состояния –уравнению Клапейрона-Менделеева, которое может быть установлено, как на основе известных опытных газовых законов Бойля-Мариотта (РV = constдля данной массы газа), Гей-Люсака [Vt = V0 (1 + t)для постоянных массы и давлении газа] и Авогадро (при одинаковых Т и Р в равных объемах любого газа содержится одинаковое число молекул), так и на основе молекулярно-кинетической теории строения вещества. Это уравнение имеет вид
PV=MRT/(3)
или P=MRT/V=RT/,
где М – масса газа, - молярная масса,R– газовая постоянная,R=8,31 Дж/мольК,- плотность газа.
Отношение Z= М/- число молей газа. Тогда
PV=ZRT(4)
В случае газовой смеси величина Zв уравнении (4) равна полному числу молей всех газов, входящих в смесь
Z = Z1 + Z2 +….+ Zn= М1/1+ М2/2+ …+ Мn/n(5)
где М1, М2, …,Мn– массы отдельных газов, а1,2, …n– молярные массы этих газов.
Реальные газы подчиняются уравнению Клапейрона-Менделеева лишь приближенно – при достаточно низких давлениях и высоких температурах. При больших же Р и низких Т у всех газов наблюдаются отклонения от этого уравнения. Газ, который вполне точно подчиняется уравнению Клапейрона-Менделеева, в термодинамике называют идеальным газом. Такого газа в действительности нет, он является некоторой абстракцией, носвойства всех реальных газов приближаются к свойствам идеального газа при малых давлениях. Любой газ в пределе при Р0 неотличим от идеального. Большинство газов уже при атмосферном давлении и комнатной Т близки к идеальному.
Преобразуем (3). Обозначив массу одной молекулы через m, будем иметь М =mNи=mNА, гдеN– общее число молекул газа, аNА– число Авогадро. Тогда (3) можно записать в виде
PV = NRT/NA,
но отношение k=R/NA=1,3810-23Дж/К – постоянная Больцмана. Тогда
PV=NkT(6)
В виде (6) уравнение состояния справедливо независимо от того имеем мы дело с химически однородным газом или с произвольной смесью, т.к. оно совершенно не зависит от химической природы газа.
Выражая из (6) Р, получим
Р = NkT/V, ноN/V=n– число молекул в единице объема газа, тогда
P=nkT(7)
т.е. давление газа зависит только от его температуры и числа молекул в единице объема газа.
4. Барометрическая формула и распределение больцмана.
Если на молекулы газа не действуют никакие внешние силы, то вследствие теплового движения они равномерно распределяются по всему объему сосуда, так что в каждой единице объема содержится в среднем одинаковое число молекул. При одинаковой во всех частях объема температуре в газе устанавливается всюду одинаковое давление Р = nkT = const (в соответствии с законом Паскаля).
Иначе обстоит дело, когда газ находится в некотором силовом поле, в котором на каждую частицу газа действует внешняя сила, толкающая ее в определенном направлении. Под действием такой силы молекулы будут собираться преимущественно в тех областях пространства, куда их заталкивают внешние силы, и там концентрация частиц, а значит, и давление газа будут возрастать. Т.е. действие внешних сил на молекулы газа противоположно тому действию, которое оказывает на них беспорядочное тепловое движение.
В результате одновременного действия внешних сил и теплового движения молекул в газе при заданной температуре устанавливается некоторое неравномерное распределение молекул в пространстве, не изменяемое во времени. Это значит, что при действии внешних сил плотность идеального газа, находящегося в равновесных условиях, будет различной в различных местах пространства, т.е. она будет некоторой функцией координат
n= n(X,Y,Z).
Примером внешних сил является поле силы тяжести, а примером газа в таком силовом поле является земная атмосфера. Молекулы газов, составляющие атмосферный воздух, под влиянием теплового движения рассеялись бы в мировом пространстве, если бы отсутствовала сила тяжести. Напротив, если бы отсутствовало тепловое движение молекул, то под действием силы тяжести все молекулы воздуха упали бы на землю, и весь воздух собрался бы тончайшим слоем у поверхности Земли. Таким образом, само существование атмосферы является результатом одновременного действия силы притяжения молекул к Земле и их теплового движения. При этом в атмосфере устанавливается некоторое неравномерное распределение молекул воздуха по высоте. Соответственно этому распределению молекул устанавливается и определенный закон изменения давления с высотой.
Если бы земная атмосфера находилась в состоянии теплового равновесия, т.е. температура атмосферы была бы одинаковой на всех высотах, то в ней бы установилось так называемое барометрическое распределение плотности и давления с высотой.
Для определения барометрического закона изменения давления и плотности идеального газа с высотой рассмотрим вертикальный столб газа с площадью поперечного сечения S= 1, находящийся при постоянной температуре, рис.1.
Z
dZ P-dP
Z P
0 P0
Х
Рис.1.
Обозначим давление газа на некотором нулевом уровне Z= 0 (уровне моря, поверхности земли, дне сосуда и т.д.) через Р0, а давление на высотеZнад нулувым уровнем через Р. При увеличении высоты наdZдавление газа уменьшится на некоторую величинуdР. Это уменьшение давления равно весу столба газа высотойdZс площадью основанияS= 1
dP = – g dZ, (1)
где – - плотность газа. На основании уравнения состояния идеального газа, его плотностьравна
= P/RT(2)
Следовательно,
dP = – (P/RT)g dZ,
откуда
dP/P = – (/RT)g dZ.
Интегрируя это выражение, находим
р z
dP/P = – /R g dZ/Т
p0 0
или z
ln P/P0 = – /R g dZ/Т (3)
0
На небольших высотах над поверхностью земли ускорение силы тяжести gможно считать постоянным, не зависящим от высотыZ, и вынести его за знак интеграла. Кроме тего, если газ находится в тепловом равновесии при постоянной, не зависящей от высотыZтемпературе Т, то и Т можно вынести за знак интеграла. В этом случае получим
ln P/P0 = – gZ/RT,
откуда
Р/Р0=е – gZ/RT
или
Р = Р0 е – gZ/RT. (4)
Формула (4) характеризует изменение давления газа с высотой и называетсябарометрической формулой. Она показывает, что давление газа с высотой убывает по экспоненциальному закону. Характер этого убывания графически можно представить следующим образом, рис.2. Р
Р0
Z
Рис.2.
Прибор для определения высоты над земной поверхностью называется высотомером (илиальтиметром). Принцип его действия основан на использовании формулы (4). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.
Принимая во внимание, что =mNAиR=kNA, мы можем переписать барометрическую формулу в виде
Р = Р0 е – mgZ/ kT.
Так как P=nkT, то эта барометрическая формула выражает такжезакон убывания плотности газа с высотой
n = n0 е – mgZ/ kT (5)
где nиn0– числа молекул в единице объема газа в точках, разность высот между которыми равнаZ. Ввиду чрезвычайно малой массы газовых молекул убывание плотности газа и его давления заметно только при значительных изменениях высоты. В случае небольшого изменения высоты изменение давления и плотности газа оказываются весьма малыми. Поэтому в случае газа, заключенного в сосуд небольшой высоты, действием силы тяжести на молекулы газа можно пренебречь. Поскольку температура атмосферы Земли не постоянна и изменяется с высотой, то для более точного описания изменений ее давления и плотности с высотой в формулы (4) и (5) необходимо вводить соответствующие поправки на изменение температуры.
Поскольку входящая в формулу (5) величина mgZпредставляет собой потенциальную энергию молекул в поле тяготения, то эту формулу можно переписать в виде
n = n0 е – U(Z) /kT (6)
т.е. она выражает закон распределения молекул идеального газа по величине их потенциальной энергии в поле тяготения. Причем величина n0имеет смысл числа частиц с потенциальной энергией равной нулю(n = n0 при U = 0).
В середине 19 века Больцман показал, что для идеального газа, находящегося влюбом силовом поле, число частиц, обладающих заданной потенциальной энергиейU, определяется формулой, имеющей тот же вид, что и формула (6). Поскольку, в произвольном силовом поле потенциальная энергия частицы может зависеть от всех трех координат, характеризующих ее положение в пространстве, а не только от одной, как это имело место в частном случае поля тяготения, т.е.n=n(X,Y,Z) и соответственно этомуU=U(X,Y,Z). Таким образом, в любом силовом поле распределение частиц в пространстве выражается законом
n(X,Y,Z) = n0 е – U(X,Y,Z) / kT – закон Больцмана (7)
где U(X,Y,Z) – потенциальная энергия частиц во внешнем силовом поле, зависящая от координат той точки, в которой находится частица;n(X,Y,Z) – концентрация частиц в точке с координатамиX,Y,Z;n0– число частиц в единице объема (концентрация) в том месте пространства, где их потенциальная энергия равна 0.
Больцман показал, что при постоянной Т концентрация частиц убывает с ростом Uи возрастает с убываниемU, т.е.частицы концентрируются преимущественно в местах с меньшей потенциальной энергией.
Закон Больцмана (8) является весьма общим законом, применимым не только к идеальному газу, но и ко многим другим системам невзаимодействующих частиц.
studfiles.net
Давление газа.Ур-е состояния ид. газа.Изопроцессы
Давление газа возникает в результате столкновений молекул со стенками сосуда ( и на помещенное в газ тело ), в котором находится беспорядочно движущиеся молекулы газа. Чем чаше удары, тем они сильнее – тем выше давление. Если масса и объем газа неизменны, то его давление в закрытом сосуде всецело зависит от температуры. Давление зависит и от скорости поступательно движущихся газовых молекул. Единица измерения давления — паскаль p(Па). Измеряют давление газа манометром (жидкостным, металлическим и электрическим).
Идеальный газ – это модель реального газа. За идеальный газ принимают газ в сосуде, когда молекула, пролетая от стенки до стенки сосуда не испытывает столкновения с другими молекулами. Точнее, Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало ⇒ Eк >> Eр .
Основное уравнение МКТ связывает макроскопические параметры (давление p, объём V, температура T, масса m) газовой системы с микроскопическими параметрами (масса молекулы , средняя скорость их движения):
, где n— концентрация, 1/м3; m — масса молекулы, кг; — средняя квадратичная скорость молекул, м/с.
Уравнение состояния идеального газа — формула, устанавливающая зависимость между давлением, объёмом и абсолютной температурой идеального газа, характеризующее состояние данной системы газа. — уравнение Менделеева — Клапейрона (для произвольной массы газа). R = 8,31 Дж/моль·К — универсальная газовая постоянная. pV = RT – (для 1 моля).
Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества ν=const. Тогда:
Для постоянной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: — уравнение Клапейрона.
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры. Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака. Эти законы называют законами для изопроцессов:
Изопроцессы – это процессы, которые совершаются при одинаковом параметре или Т-температуре, или V-объеме, или р-давлении.
Изотермический процесс — — закон Бойля — Мариотта (при постоянной температуре и данной массы газа произведение давления на объем есть величина постоянная)
Изобарный процесс — — закон Гей-Люссака (при постоянном давлении для данной массы газа отношение объема к температуре есть величина постоянная)
Изохорный процесс — — закон Шарля (при постоянном объеме для данной массы газа отношение давления к температуре есть величина постоянная.
Вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
kaplio.ru
Уравнение Менделеева-Клапейрона, состояние идеального газа. Макропараметры: давление, объем, температура. Закон Дальтона о парциальных давлениях смеси
Тестирование онлайн
Уравнение состояния идеального газа
Взяли порцию газа некоторой массы и начали проводить над ней эксперименты. Например, изменяли некоторый параметр (например, температуру T) и наблюдали, как изменяются другие два параметра (объем V и давление p). При увеличении температуры, молекулы двигаются быстрее, соударения происходят чаще, значит, давление увеличивается и газ стремится занять больший объем. Или, если уменьшить объем, то частицам газа становится тесно, они чаще соударяются, увеличивается давление, а от большого числа соударений их скорость может увеличиваться, то есть может увеличиться температура.
Интуитивно пришли к зависимости трех макропараметров газа, которую вывел французский физик Б. Клапейрон
или
В любом состоянии одной и той же порции газа величина остается постоянной.
Д.И. Менделеев исследовал влияние изменения массы газы на макропараметры. Получил зависимость, которое носит название уравнение Менделеева-Клапейрона, оно же уравнение состояния идеального газа

Используя формулы химических характеристик вещества, основное уравнение возможно записать в ином эквивалентном виде.
Закон Дальтона
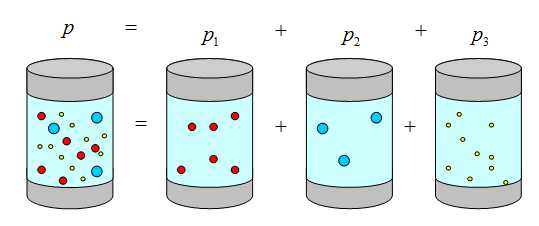
Давление смеси не взаимодействующих между собой газов равна сумме парциальных давлений каждого газа в отдельности
Парциальное давление – это давление компонента смеси, если бы он занимал весь предоставленный ему объем один.
fizmat.by
