2. Уравнение кинематики и динамики
2.1. На схеме рис. 1б изображён цилиндр в процессе движения вниз со скоростью и ускорением центра масс и ас и с угловыми скоростью и ускорением ω и ε . Изогнутая стрелка с обозначениями ω и ε показываетнаправление поворота цилиндра с увеличением угловой скорости. Векторыи при этом направлены вдоль оси Y перпендикулярно плоскости рисунка; проекции этих векторов на ось Y – отрицательные.
Примечание. Вектор угловой скорости всегда направлен вдоль оси вращения таким образом, что с его конца поворот тела виден против хода часовой стрелки. Вектор углового ускорения сонаправлен вектору , если угловая скорость увеличивается.
В т. Р, где нить касается поверхности цилиндра, находится
ц. с. и через эту точку проходит мгновенная
ось вращения, параллельная оси Y.К цилиндру приложены: сила тяжести G в точке С (центр масс) и силы натяжения S двух нитей в точках схода нитей с поверхности тела (на схеме рис. 1б эти точки объединены в т. Р).
Для теоретическою описания механического движения тела вначале надо установить, к какому типу относится исследуемое движение. В механике все движения твёрдых тел подразделяются на пять типов: поступательное, вращательное, плоское, сферическое и свободное. При исследовании каждого типа движения требуется соответствующая ему система уравнений кинематики и динамики.
2.2.
Качение тел при постоянной ориентации
оси мгновенного вращения является
частным случаем плоского движения.
Следовательно, скатывание тел по двум
отвесным нитям, стабилизирующим
ориентацию мгновенной оси, также
относится к типу плоского движения.
Примечание. Движение твёрдого тела называется плоским (или плоско-параллельным), если тело, перемещаясь в пространстве, совершает повороты, не имея закреплённых точек, и при этом каждая точка тела движется в одной и той же плоскости, параллельной некоторой неподвижной плоскости.
Плоское движение могут совершать тела любой формы (стержни, пластины, диски, пространственные фигуры). Это движение имеет ряд характерных особенностей, которые используются для проектирования машин и механизмов. Одной из таких особенностей является существование мгновенного центра скоростей (м. ц. с.) в плоскости движения каждой точки тела. Все м. ц. с. лежат на одной прямой, называемой мгновенной осью вращения. Относительно этой оси тело при плоском движении совершает повороты в пространстве. Положение мгновенной оси непрерывно изменяется, однако эта ось остается
Свойства плоского движения, в том числе методы определения положения м. ц. с., изучаются в курсе теоретической механики. В курсе общей физики обычно рассматривается только частный случай плоского движения – качение тел при постоянной ориентации оси мгновенного вращения.
В механике доказано,
что плоское движение можно исследовать
двумя способами. В первом
– плоское движение рассматривается
как совокупность двух движений:
поступательного движения вместе с
условной осью, проходящей через центр
масс тела, и вращательного движения
вокруг этой оси. 
При качении тел по поверхностям заданного профиля (например, в данной схеме по отвесным нитям) задача исследования упрощается, т. к. всегда известно расположение
2.3. Считаем, что при скатывании тела по отвесной нити в воздушной среде силами трения и сопротивления можно пренебречь. Силу натяжения нити S,силу тяжести G и радиус намотки нити принимаем постоянными.
При этих условиях уравнения, описывающие движение тела, имеют простой вид типа алгебраических выражений, которые формулируются на основе известных законов кинематики и динамики равнопеременного движения с постоянным ускорением центра масс и постоянным угловым ускорением.
В первом способе – динамика скатывания цилиндра, показанного на схеме рис. 1б, описывается уравнениями:
(1а)
(1б)
Здесь: т – масса
цилиндра; Jc – момент
инерции цилиндра относительно оси,
проходящей через центр масс; ас – линейное
ускорение центра масс, ε – угловое
ускорение цилиндра; r – радиус цилиндра.
Первое уравнение (1а) – это закон динамики движения центра масс тела под действием внешних сил: силы тяжести
Примечание. Уравнения (1) и следующие ниже уравнения (2) записаны в виде проекций на соответствующие оси координат: Z и Y.
В двух уравнениях (1) при известной массе
Р.Во втором способе применяются закон динамики для мгновенно-вращательного движения тела и формулы для расчёта ускорений и скоростей точек вращающегося тела:
(2б)
= (2в)
Здесь: Jp=Jc+r2· m – момент инерции относительно мгновенной оси в т. Р, который вычисляется по теореме Штейнера, если, например, известен .
Первое уравнение (2а) – это закон динамики мгновенно-вращательного движения тела вокруг мгновенной оси, проходящей через т. Р. Согласно уравнению (2а) вращение происходит под действием момента силы тяжести, т. к. момент сил натяжения нитей относительно точки Р
Уравнения
(2б) и (2в) получены из формулы Эйлера для
скоростей точек
при вращении тела вокруг оси в т.
Р, и в данной системе координат они
описывают условия кинематических
связей между проекциями линейных
и угловых скоростей и ускорений (с
учётом разных знаков проекций).
Однако системы уравнений (1)-(2) также недостаточно для расчёта параметров движущегося тела, т. к. количество неизвестных больше числа уравнений. Следовательно, невозможно сравнение теоретических результатов расчёта с данными опыта.
Систему (1)-(2) дополним уравнениями кинематики прямолинейного движения центра масс, учитывая, что т.
Длина
пути т. С равна высоте спуска h при
скатывании цилиндра из верхнего
положения в нижнее (см. рис. 1б). Время
спуска с высоты h измеряется
в опыте.
Если при скатывании по нити сама нить неподвижна, тогда центр масс тела движется прямолинейно по вертикали. Следует, однако, отметить, что приведённая здесь теория качения верна только для таких тел, у которых центр масс совпадает с центром симметрии. Если тело неоднородное, тогда центр масс и центр симметрии могут оказаться в разных точках, и расчёты движения усложняются
При
условии, что в верхнем положении тело
покоилось (т.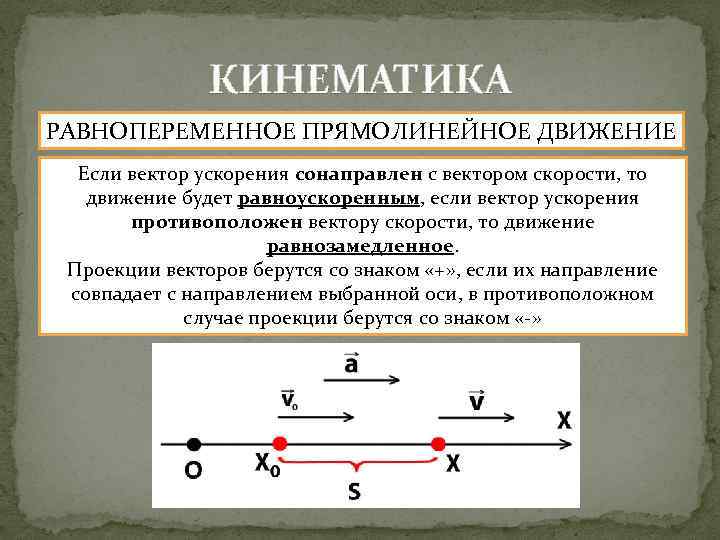
е.
=
0),
для длины пути центра масс получаем:
, (3)
где tK – время спуска, измеряемое в опыте.
Из (3) имеем:
(4)
При постоянном ускорении скорость центра масс в конце спуска равна:
(5)
С помощью уравнений (1)-(5) при известных (из опыта) h и tк полностью решается задача определения всех параметров при скатывании тела по отвесной нити.
Угловые скорость ω и ускорение ε вычисляются из (2б) и (2в). Неизвестный момент инерции Jp рассчитывается с помощью уравнения
(2а),
затем – с учётом теоремы Штейнера –
находим момент инерции Jс.
Силу натяжения нитей S можно найти из уравнений (1а), (1б) или почленным делением (1б) на (2а).
Примечание. В Приложении 1 дано дополнительное исследование некоторых свойств механического движения при скатывании тел по нитям, получен ряд формул, удобных для практических расчётов.
Значения ,ω , Jc, найденные с помощью уравнений (1)-(5), позволяют также исследовать энергетический баланс в проводимом опыте.
Основные понятия и уравнения кинематики
1. Тема урока: Основные понятия и уравнения кинематики.
Цель урока: повторить основныепонятия кинематики – траектория,
ускорение, скорость, пройденный путь и
перемещение.
2. План
1. Что изучает механика? Её основная задача.2. Кинематика. Основные понятия:
A.
B.
C.
D.
E.
F.
G.
тело отсчета, система координат, система отсчета
закон независимости движений
материальная точка и абсолютно твердое тело
поступательное и вращательное движение
траектория, путь, перемещение
скорость
ускорение
3.
Классификация механических движений.4. Основные уравнения.
5. Графики движений.
3. Что изучает механика? Её основная задача.
• Раздел физики – механика занимаетсяизучением механического движения тел.
Механическим движением называется
изменение
положения
тела
(в
пространстве) относительно других тел с
течением времени.
• Основная задача механики заключается в
определении положения тела в любой
момент времени.
4. Кинематика. Основные понятия:
• Механика состоит из двух основныхразделов: кинематики и динамики.
Раздел, который не рассматривает причин
возникновения механического движения и
описывает только его геометрические
свойства называется кинематикой. В
кинематике используются такие понятия
как траектория, путь и перемещение,
скорость и ускорение.
5. Относительность движения. Система отсчета.
ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ. СИСТЕМА ОТСЧЕТА.• Чтобы описать механическое движение тела (точки),
нужно знать его координаты в любой момент времени.
Для определения координат следует выбрать тело
отсчета и связать с ним систему координат. Часто
телом отсчета служит Земля, с которой связывается
прямоугольная декартова система координат. Для
определения положения точки в любой момент времени
необходимо также задать начало отсчета времени.
• Система координат, тело отсчета, с которым она связана,
и прибор для измерения времени образуют систему
отсчета, относительно которой рассматривается
движение тела
6. Закон независимости движений
• Движение реальных тел, как правило, сложное. Поэтомудля упрощения рассмотрения движений пользуются
законом независимости движений: всякое сложное
движение можно представить как сумму независимых
простейших движений.
• К простейшим движениям относятся поступательное и
вращательное. В физике широко пользуются моделями,
которые позволяют из всего многообразия физических
свойств выбрать главное, определяющее данное
физическое явление.
Одним из первых моделей реальныхтел являются материальная точка и абсолютно твердое
тело.
7. Материальная точка и абсолютно твердое тело.
МАТЕРИАЛЬНАЯ ТОЧКА И АБСОЛЮТНОТВЕРДОЕ ТЕЛО.
• Тело, размерами которого в данных условиях
движения
можно
пренебречь,
называют
материальной точкой. Тело можно рассматривать
как материальную точку, если его размеры малы по
сравнению с расстоянием, которое оно проходит, или
по сравнению с расстояниями от него до других тел.
• Абсолютно твердым телом называется тело,
расстояние между любыми двумя точками которого
остается постоянным при его движении. Эти модели
позволяют исключить деформацию тел при
движении.
8. Поступательное и вращательное движение.
• Поступательным называется движение, при котором отрезок,соединяющий любые две точки твердого тела, перемещается при
движении параллельно самому себе. Из этого следует, что все
точки тела при поступательном движении движутся одинаково,
т.
е. с одинаковыми скоростями и ускорениями.• Вращательным называется движение, при котором все точки
абсолютно твёрдого тела движутся по окружностям, центры
которых лежат на одной прямой, называемой осью вращения,
причем эти окружности лежат в плоскостях, перпендикулярных
оси вращения. Пользуясь законом независимости движений,
сложное движение твёрдого тела можно рассматривать как
сумму поступательного и вращательных движений.
9. Поступательное движение
Выберите верное утверждение о поступательномдвижении:
1. Поступательное движение – это движение тела, при
котором отрезок прямой, соединяющий две любые точки,
принадлежащие этому телу, перемещается, оставаясь
параллельным самому себе.
2. При поступательном движении все точки твердого тела
движутся одинаково, описывают одинаковые траектории
и в каждый момент времени имеют одинаковые скорости
и ускорения.
3. Движение парашютиста вниз
поступательного движения.
является
4. Луна вокруг Земли движется поступательно.
примером
10. Траектория, путь, перемещение
ТРАЕКТОРИЯ, ПУТЬ, ПЕРЕМЕЩЕНИЕ• Траекторией движения называется линия, вдоль которой
движется тело. Длина траектории называется пройденным
путем. Путь – скалярная физическая величина, сумма длин
отрезков траектории, может быть только положительным.
• Перемещением называется вектор, соединяющий начальную
и конечную точки траектории.
ПРИМЕРЫ:
пройденный путь –
вектор перемещения – S
a и b – начальная и конечная точки пути
при криволинейном движении тела.
S
С
D
Рис. 1
N
E
S
Рис. 2
ACDENB – траектория
вектор перемещения – S
11. Пример вектора перемещения
ПРИМЕР ВЕКТОРА ПЕРЕМЕЩЕНИЯА
В
К
С
+х(м)
-х(м)
-3 -2 -1
0
1
2 3
4
5
6
7
8
9 10 11 12 13 14 15
Перемещение – есть разность между конечным и начальным
положением и обозначается
x:
x x êîí õíà÷
Перемещение тела, находившегося в точке А :
Перемещение тела, находившегося в точке В :
Перемещение тела, находившегося в точке С :
Õ À 5 ( 3) 8 ì
Õ B 5 2 3ì
Õ C 5 13 8 ì
Разница между перемещением и путем состоит в том, что
путь не может быть равным нулю, тогда как перемещение может
равняться нулю.
12. Скорость
• Характер движения тела определяется его скоростью. Еслискорость постоянна, то движение называют равномерным
и уравнение движения выглядит следующим образом:
[м/с2]
s
t
x y
• Модуль скорости равен:
• Если скорость увеличивается на одинаковую величину за
одинаковые
промежутки времени, то движение
называется равноускоренным.
• Если скорость уменьшается на одинаковую величину за
одинаковые
промежутки времени, то движение
называется равнозамедленным. Такие виды движений
называют равнопеременным движением.
2
2
13. Средняя и мгновенная скорости
СРЕДНЯЯ И МГНОВЕННАЯ СКОРОСТИ• Быстрота изменения положения материальной точки в
пространстве с течением времени характеризуется
средней и мгновенной скоростями.
• Средняя скорость – векторная величина, равная
отношению перемещения к промежутку времени, за
которое это перемещение произошло:
Vср = s/ t.
• Мгновенной скоростью называется предел отношения
перемещения s к промежутку времени t, за которое это
перемещение произошло, при стремлении t к нулю:
Vмгн = lim t–>0 s/ t.
14. Сложение скоростей
СЛОЖЕНИЕ СКОРОСТЕЙ• Рассмотрим перемещение тела в подвижной системе координат.
Пусть S1 – перемещение тела в подвижной системе координат, S2–
перемещение подвижной системы координат относительно
неподвижной, тогда S – перемещение тела в неподвижной системе
координат равно:
s s1 s2
• Если перемещения S1 и S2 совершаются
одновременно, то:
s1 s2
s
t t t
v v1 v 2
• Таким образом
т.е скорость тела относительно неподвижной системы отсчета равна
сумме скорости тела в подвижной системе отсчета и скорости
подвижной системы отсчета относительно неподвижной. Это
утверждение называется классическим законом сложения
скоростей.
15. Ускорение
• Величина изменения скорости за единицу времени естьускорение:
a
t
2 1
t 2 t1
• В процессе движения скорость может измениться,
отсутствие изменения скорости приводит к отсутствию
ускорения.
• Неподвижное тело, либо тело движущее с постоянной
скоростью обладает нулевым ускорением.
• Ускорение определяет на сколько скорость увеличилась
при
равноускоренном
движении,
и
насколько
уменьшилась при равнозамедленном движении за 1
секунду.
16. Например:
• Велосипедист движется с ускорениема=5м/с2, тогда через каждую секунду его
скорость будет принимать значения:
a * t 5 *1 5 м / с
a * t 5 * 2 10 м / с
a * t 5 * 3 15 м / с
17. Среднее и мгновенное ускорение
• Величина,характеризующая
быстроту
изменения
скорости, называется ускорением.
• Среднее ускорение – величина, равная отношению
изменения скорости к промежутку времени, за которое
это изменение произошло:
аср = v/ t.
• Если v1 и v2 – мгновенные скорости в моменты времени
t1 и t2, то v=v2-v1, t=t2-t1.
• Мгновенное ускорение – ускорение тела в данный
момент времени. Это физическая величина, равная
пределу отношения изменения скорости к промежутку
времени, за которое это изменение произошло, при
стремлении промежутка времени к нулю:
aмгн = lim t–>0 v/ t.
18. Классификация механических движений
КриволинейноеПрямолинейное
(движение по окружности)
равномерное
равномерное
неравномерное
Равно
Равно
ускоренное
замедленное
неравномерное
19. Основные уравнения.
СКОРОСТЬРАВНОМЕРНОЕ
РАВНОЗАМЕДЛЕННОЕ
РАВНОУСКОРЕННОЕ
ДВИЖЕНИЕ
s
t
const
УСКОРЕНИЕ
a 0
0 at a 0
t
2 02 2aS
0 at
0
a
2
2
0 2aS
t
ПРОЙДЕННЫЙ
ПУТЬ
КООРДИНАТЫ
х х0 t
S t
2
at 2
at
S 0t
х х0 0t
2
2
S 0t
2
at
2
at 2
х х0 0t
2
20. Равномерное движение График зависимости х от t
• Уравнение прямой в координатах х, t в общем случае имеетвид:
у=b+kt
• b – это отрезок на оси OX, отсекаемой прямой;
• k – тангенс угла наклона прямой к оси Оt
X(м)
Пример:
По графику можно
записать уравнение
движения тела.
5
1
2
3
t (c)
-5
x0
21.
Равномерное движение График зависимости S от tПримерПо
графику
можно
определить:
1. Скорость движения,
которая определяется
тангенсом угла наклона
прямой к оси Оt –
S (м)
12
9
6
S
3ì / ñ
t
3
1 2 3 4
t (c)
2. Путь, пройденный телом за определенный интервал времени.
Например путь, пройденный велосипедистом за интервал времени от
t1=1с до t2=4с равен S=S2-S1=12-3=9м
22. График зависимости от t
Ра в н о м е р н о е д в и ж е н и еГрафик зависимости от t
(м)
const
S1 1 *t1
a 0
S2 2 *t2
1
t2 t1
2
t (c)
Пример:
По графику можно определить проекцию перемещения S1, S2. В 1м случае
проекция на ось положительна, во втором отрицательна. В обоих случаях
проекция перемещения численно равна площади прямоугольников.
23. Равноускоренное движение Скорость
0 at• График при a 0
• График при a 0
(м)
(м)
0
0
0
0
t (c)
t (c)
24.
Равноускоренное движение УскорениеРавноускоренное движение0
Ускорение a
• График при a 0
t
• График при a 0
а (м/с2)
а (м/с2)
0
0
t (c)
t (c)
25. Равноускоренное движение Перемещение
Равноускоренное движение2
at
Перемещение S 0t 2
• График при a 0
S (м)
• График при a 0
S (м)
0
0
t (c)
t (c)
26. Равноускоренное движение Координата
Равноускоренное движениеat
Координата х х t 2
2
• График при a 0
0
0
• График при a 0
х (м)
х(м)
х0
х0
0
0
t (c)
t (c)
27. Решение задач по теме: Основные понятия и уравнения кинематики.
Цель : закрепить путем решениязадач основные понятия кинематики
– траектория, ускорение, скорость,
пройденный путь и перемещение.
28. Задание №1 (уровни)
1. Двигаясь по шоссе, велосипедист проехал 900м соскоростью 15 м/с, а затем по плохой дороге 400м со
скорость10м/с.
С какой средней скоростью он проехалвесь путь?
2. На горизонтальном участке пути автомобиль ехал со
скоростью 72 км/ч в течении 10 мин, а затем проехал
подъем со скоростью 36 км/ч за 20 мин. Чему равна
средняя скорость на всем пути?
3. Первую половину пути автомобиль прошел со скоростью
20 км/ч, а вторую – 30 км/ч. Найти среднюю скорость на
всем участке.
29. Задание №2 (уровни)
1. Через 25 с после начала движения спидометравтомобиля показал скорость движения 36 км/с.
С каким ускорением двигался автомобиль?
2. При равнозамедленном движении автомобиля в
течении 5 с его скорость уменьшилась с 15 до 10
м/с. Чему равен модуль ускорения?
3. Скорость поезда, движущегося на подъеме с
ускорением 0,1 м/с 2 , уменьшается от 54 до 36
км/ч. Определите время подъема.
30. Задание №3
1. Расстояние между пунктами А и В по прямойлинии 5 км. Человек проходит это расстояние
туда и обратно за 2 ч. Чему будут равны путь и
перемещение человека за 1 ч, за 2ч?
2.
Ускорение автомобиля, начавшего движение 0,5м/с2 . Какой путь пройдет автомобиль за 4 с,
двигаясь с этим ускорением?
31. Задание №4
1. Автомобиль берет подъем длиной 1,95 км втечении 5 мин, и к концу подъема его скорость
равна 18 км/ч. Принимая, что ускорение с
которым движется автомобиль , постоянно,
определить его значение.
2. Автомобиль тормозит с ускорением, которое во
все время можно считать неизменным и равным
-4м/сек2. Какой путь пройдет он за это
времяторможения, если начнет тормозить при
скорости 16 м/с?
32. Задание №5
• Запишите уравнение координаты телаX(м)
6
1
2
3
t (c)
-6
33. Задание №6
S (м)По графику
определите:
1. Вид движения
2. Скорость
движения
16
12
8
4
1 2 3 4
t (c)
3. Путь, пройденный
велосипедистом за
интервал
времени
от t1=1с до t 2=3с
(м/с)
Задание №7
5
4
3
2
1
1 2 3 4 5 6
t (c)
Определите проекцию перемещения S1
за 6 с.
(м/с)
Задание №8
5
4
3
2
1
1 2 3 4 5 6
t (c)
Определите проекцию перемещения
(путь) S2, пройденный телом за 6 с.
36. Задание №9.
(м/с)1. Какой из графиков соответствует
равномерному движению?
0
2. Какой из графиков соответствует
равнопеременному движению,
при котором вектор ускорения
направлен
противоположно
вектору скорости?
0
3. Какой из графиков соответствует
t (c) равноускоренному движению,
при
котором
направление
вектора ускорения совпадает с
направлением
вектора
скорости?
37. Задание №10. Прочитайте график изображенный на рисунке
(м/с)1. Какой вид
движения?
2. Как
изменяется
скорость в
течении
каждой
секунды?
3
2
1
0
1
2
3
4
5
t (cек) 3. Чему равно
ускорение?
уравнений кинематики мобильного робота – MATLAB & Simulink
Узнайте подробности об уравнениях кинематики мобильного робота, включая одноколесный велосипед, велосипед, дифференциальный привод и модели Аккермана.
В этом разделе рассматриваются переменные и конкретные уравнения для каждой модели движения [1]. Для примера, который симулирует различных мобильных роботов, используя эти модели, см. Симуляцию различных кинематических моделей для мобильных роботов.
Обзор переменных
Состояние робота представлено в виде трехэлементного вектора: [xyθ].
Для заданного состояния робота:
x: Общее положение автомобиля по оси X в метрах
y: Общее положение автомобиля по оси Y в метрах
θ: Общее направление движения автомобиля в радианах
3
3 Кинематика Аккермана, состояние также включает угол поворота рулевого колеса:
Модели одноколесного велосипеда, велосипеда и дифференциального привода имеют общий управляющий вход, который принимает следующие значения:
Другие переменные, представленные в уравнениях кинематики:
R: радиус колеса в метрах
ϕ˙: скорость колеса в радианах/с
D: Ширина дорожки в метрах
L: Колесо база в метрах
ψ: автомобиль: колесо колеса в метрах
ψ: автомобиль: колесо колеса в метрах
ψ: автомобиль: колесо колеса в метрах
ψ: угол поворота в радианах
Кинематика одноколесного велосипеда
Уравнения кинематики одноколесного велосипеда моделируют одиночное катящееся колесо, которое вращается вокруг центральной оси, используя объект
unicycleKinematics.
Состояние модели одноколесного велосипеда — [xyθ].
переменные
x: глобальное транспортное средство x-положения в метрах
Y: Глобальное транспортное средство y-положения в метрах
θ: Глобальный заголовок в радианах
stragre: Уилья скорость в метрах/с
r: радиус колеса в метрах
v: скорость автомобиля в метрах/с
ω: угловая скорость автомобиля в радианах/с
В зависимости от аргумента “имя-значение”
VehicleInputsможно вводить только скорости колес или скорость транспортного средства и курсовую скорость. Это изменение ввода влияет на уравнения.Уравнение скорости колеса
[x˙y˙θ˙]=[rcos(θ)0rsin(θ)001][ϕ˙ω]Уравнение движения одноколесного велосипеда
Уравнение скорости транспортного средства и курсовой скорости (обобщенное)
Когда обобщенные входные данные задаются как скорость v=rϕ˙ и угловая скорость транспортного средства ω, уравнение упрощается до:
[x˙y˙θ˙]=[cos(θ)0sin(θ)001][vω]Уравнение движения одноколесного велосипеда
Кинематика велосипеда
Уравнения кинематики велосипеда моделируют транспортное средство, похожее на автомобиль, которое допускает переднее рулевое управление угол в качестве управляющего входа с использованием объекта
bikeKinematics.Модель велосипеда находится в состоянии [xyθ].
Переменные
x: Глобальное положение автомобиля по оси X в метрах
y: Общее положение автомобиля по оси Y в метрах
θ: Глобальный заголовок транспортных средств в Radians
L: Колесо, в метрах
ψ: угол рулевого управления в Radians
V: Скорость транспортного средства в метрах/с
ω:: Скорость транспортного средства в метрах/с
ω::: Скорость транспортного средства в метрах/с
ω::: Скорость транспортного средства в метрах/с
- 9001 °:. Угловая скорость движения транспортного средства в радианах/с
Кинематические уравнения
В зависимости от аргумента “имя-значение”
VehicleInputsможно ввести скорость транспортного средства как угол поворота рулевого колеса или скорость курса. Это изменение ввода влияет на уравнения.Уравнение угла поворота руля
[x˙y˙θ˙]=[vcos(θ)vsin(θ)vltan(ψ)][vω]
Уравнение скорости транспортного средства и курса (обобщенное)
3 В этом обобщенном формате курсовая скорость ω может быть связана с углом поворота ψ соотношением ω=vltanψ. Тогда ОДУ упрощается до:
[x˙y˙θ˙]=[cos(θ)0sin(θ)001][vω]Уравнение движения одноколесного велосипеда
Кинематика дифференциального привода
Уравнения кинематики дифференциального привода моделируют a транспортное средство, в котором колеса слева и справа могут вращаться независимо друг от друга с помощью
дифференциалDriveKinematicsобъект.Состояние модели дифференциального привода — [xyθ].
Переменные
X: Глобальное транспортное средство X-Position, в метрах
Y: Глобальное транспортное средство Y-Position, в метрах
θ: Глобальный заголовок транспортного средства, в Radians
θ: Глобальный автомобиль, Radians
θ: Глобальный автомобиль, Radians
θ: Глобальный автомобиль, Radians
θ: Глобальный автомобиль.
˙L: Скорость левого колеса в метрах/сϕ˙R: Скорость правого колеса в метрах/с
r: Радиус колеса в метрах
D: ширина дорожки в метрах
В: Скорость транспортного средства в метрах/с
ω: угловая скорость, направленная на автомобиль в радианах/с
Kinemance Agivation 9002
9002. VehicleInputs аргумент “имя-значение”, вы можете ввести скорость колеса либо как угол поворота руля, либо как курс. Это изменение ввода влияет на уравнения.Уравнение скорости колеса
[x˙y˙θ˙]=[r2cos(θ)r2cos(θ)r2sin(θ)r2sin(θ)-r/2dr/2d][ϕ˙Lϕ˙R]Уравнение движения дифференциального привода
Уравнение скорости транспортного средства и курса (обобщенное)
В обобщенном формате входные данные представлены как скорость v=r2(ϕ˙R+ϕ˙L) и угловая скорость транспортного средства ω=r2d(ϕ˙R-ϕ ˙Л). ОДУ упрощается до:
[x˙y˙θ˙]=[cos(θ)0sin(θ)001][vω]Уравнение движения одноколесного велосипеда
Кинематика Аккермана
Кинематические уравнения Аккермана моделируют автомобиль, похожий на автомобиль модель с рулевым механизмом Аккермана с использованием
ackermannKinematicsобъект. Уравнение регулирует положение шин осей в зависимости от ширины колеи, чтобы шины следовали по концентрическим окружностям. Математически это означает, что входными данными должна быть угловая скорость ψ˙ курса руления, и нет никакого обобщенного формата.Состояние модели дифференциального привода — [xyθψ].
Переменные
x: Глобальное положение автомобиля по оси X в метрах
y: Общее положение автомобиля по оси Y в метрах
θ: Глобальный заголовок транспортного средства в радианах
ψ: угол рулевого управления транспортного средства в Radians
L: Колесовое основание в метрах
V: скорость транспортного средства на метрах/с
9001- v: скорость автомобиля в метрах/с
- 111. Уравнения
Для кинематической модели Аккермана ОДУ:
[1] Линч, Кевин М. и Фрэнк С. Парк. Современная робототехника: механика, планирование и управление .
Cambridge University Press, 2017.Пример моделирования различных мобильных роботов с использованием этих моделей см. в разделе Моделирование различных кинематических моделей мобильных роботов.
Кинематика вращения
Кинематика вращенияДля движения с постоянным угловым ускорением α = ( ω f – ω i )/(t f – t i ) = Δ ω /Δt имеем
Δ ω = ω Δt, ω f = ω i + α Δt.
Это векторное уравнение. Это дает уравнение для каждой декартовой компоненты.
Для z-компоненты имеем
ω zf = ω zi + α z Δt.Если объект вращается вокруг оси Z и нет других компонентов ω и α , мы часто опускаем индекс z и просто напишите
ω f = ω я + αΔt.Угловое смещение θ относительно оси z определяется как
∆θ = ∫ ti тс (dθ/dt)dt = ∫ ti tf ωdt = ω i (t f – t i ) + ½ α (t f – t i ) 2 .Кинематические уравнения движения с постоянным угловым ускорением
Если объект вращается вокруг фиксированной оси Z с постоянным угловым ускорение α, имеем Δω = αΔt,
ω f = ω i + α(t f – t i ).
Угловое смещение θ относительно оси z определяется как
θ f = θ i + ω i (t f – t i ) + ½α(t f – t i ) 2 .
Комбинируя эти два уравнения, мы получаем
ω f 2 = ω i 2 + 2α(θ f – θ i ).
Эти уравнения имеют тот же вид, что и уравнения линейного движения с постоянным ускорением a.
Для движения по оси абсцисс имеемv f = v i + a(t f – t i ),
x f – x i = v x (t f – t i ) + ½a(t f – т и ) 2 .
v f 2 = v i 2 + 2а(х ф – х i ).Если мы заменим x на θ и a на α, то кинематическая уравнения линейного движения вдоль оси x преобразуются в кинематические уравнения для вращательного движения вокруг оси z.
С нашими определениями углового положения, скорости и ускорения мы имеем кинематические уравнения для вращательных движений, которые имеют тот же вид, что и кинематические уравнения поступательного движения. И те же уравнения имеют те же растворы. Решаем их точно так же. Но решения описывают различные физические ситуации. Например, пока θ ф может принимать любое значение, значение, которое не лежит между 0 и 2π радиан, просто говорит нам о том, что объект совершил более одного оборота.
Проблема:
Авиалайнер прибывает в терминал, двигатели выключены выключенный. Ротор одного из двигателей имеет начальный поворот по часовой стрелке угловая скорость 2000 рад/с.
Вращение двигателей замедляется с
угловое ускорение величиной 80 рад/с 2 .
(а) Определите угловую скорость через 10 с.
(b) Сколько времени требуется ротору, чтобы остановиться?Решение:
- Рассуждение:
В этой задаче начальная угловая скорость ω i и угловое ускорение α . Если выбираем направление начального углового ускорения быть направлением z, тогда
ω f = ω i – α(t f – t и ),
, так как α находится в отрицательном направлении z. - Подробности расчетов
(а) При t = 0 ω i = 2000/с.
При t = 10 с имеем ω f = 2000/с – (80/с 2 )(10 с) = 1200/с.
(б) Установка ω f = ω i – α(t f – t i ) = 0 мы можем найти время, за которое ротор придет отдыхать.
2000/с – (80/с 2 )t = 0, t = (2000/80) с = 25 с — это время, необходимое ротору для остановки.
Проблема:
Вращающемуся колесу требуется 3 с, чтобы сделать 37 оборотов. Его угловатый скорость в конце 3-секундного интервала 98 рад/с. Что постоянное угловое ускорение колеса?
Решение:
- Рассуждение:
Дано: Δθ = θ f – θ i = 37 оборотов, Δt = 3 с, ω f = 98 рад/с.
С использованием θ f – θ i = ω и (т ф – т и ) + ½α(t f – t i ) 2 и ω f = ω я + α(t f – t i ), у нас есть два уравнения, которые мы можем решить для двух неизвестных, ω i и α. - Детали расчета:
Использование θ f = θ i + ω i (t f – t i ) + ½α(t f – t i ) 2 с θ я = 0, имеем 37*2π = ω i *(3 с) + ½α(3 с) 2 .
Использование ω f = ω i + α(t f – t i ) имеем 98/s = ω i + α(3 с).
Решим это уравнение относительно ω i ω i = 98 с – α(3 с), и вставить его в первое уравнение.
37*2π = (98/с)(3 с) – α(3 с) 2 + ½α(3 с) 2 , 74π = 294 – α*(9с 2 ) + α*(4,5 с 2 ),
(4,5 с 2 )*α = 294 – 74π, α = 13,67/с 2 – постоянная ускорение колеса.
Модуль 8: Вопрос 1
Кинематические уравнения движения с постоянным линейным ускорением и движение с постоянным угловым ускорением имеют такой же вид. Сравнивать движение с постоянной скоростью с движением с постоянной угловой скоростью.
Обсудите это со своими однокурсниками на дискуссионном форуме!
Когда колесо вращается вокруг оси Z, каждая точка колеса имеет один и тот же угол скорость. Однако линейная скорость v точки P зависит от ее расстояния от оси вращения.
Когда точка P проходит угловое смещение 2π, тогда его пройденный путь равен s = 2πr.
Когда точка P проходит угловое смещение π, то его пройденный путь равен s = πr.
Когда точка P проходит угловое смещение θ, то его пройденное расстояние равно s = θr.
По угловой скорости ω скорость v точки P поэтомуv = ds/dt = rdθ/dt = rω,
, если r постоянно; v это тангенциальная скорость точки P.
Ссылка: Тангенциальная и угловая скорость (Youtube)
Тангенциальное ускорение a точки P, движущейся по круговой траектории, равно . углового ускорения на t = dv/dt = rdω/dt = rα.
радиальное или центростремительное ускорение равно r = v 2 /r = рω 2 .
Общее ускорение равно
a = (a t 2 + a r 2 ) ½ = (r 2 α 2 + r 2 ω 4 ) ½ = r(α 2 + ω 4 ) ½ .Проблема:
Если колеса автомобиля заменить на колеса большего диаметра, показания спидометра изменились? Объяснять!
Решение:
- Рассуждение:
Датчик спидометра определяет угловую скорость колеса. Используя v номинальное значение = r номинальное значение ω, спидометр отображает правильную скорость, если шины имеют номинальный радиус. Если вы положите больше шины на вашем автомобиле, то ваша фактическая скорость v фактический = r фактический ω больше отображаемой скорости v номинально = r номинально ω.
Проблема:
Автомобиль равномерно ускоряется из состояния покоя и достигает скорости 22 м/с в 9 с. Если диаметр шины равен 58 см, найдите
(а) число оборотов, которое шина делает во время этого движения, при условии, что нет проскальзывание и
(b) конечная скорость вращения шины в оборотах в секунду.Решение:
- Рассуждение:
Задано равномерное ускорение автомобиля a = Δv/Δt.
- Рассуждение:
Это изменение ввода влияет на уравнения.
˙L: Скорость левого колеса в метрах/с
Уравнение регулирует положение шин осей в зависимости от ширины колеи, чтобы шины следовали по концентрическим окружностям. Математически это означает, что входными данными должна быть угловая скорость ψ˙ курса руления, и нет никакого обобщенного формата.
Cambridge University Press, 2017.
Вращение двигателей замедляется с
угловое ускорение величиной 80 рад/с 2 . 
