Уравнения Максвелла в интегральной форме, с примерами
Система уравнений Максвелла является обобщением основных законов об электрических и электромагнитных явлениях. Она описывает абсолютно все электромагнитные явления. Являясь основой теории электромагнитного поля, эта система уравнений позволяет решать задачи, связанные с отысканием электрических и магнитных полей, создаваемых заданным распределением электрических зарядов и токов. Уравнения Максвелла были отправной точкой для создания общей теории относительности Эйнштейна. В теории Максвелла раскрывается электромагнитная природа света. Уравнения сформулированы Дж. Максвеллом в шестидесятых годах 19 века на основе обобщения эмпирических законов и развития идей ученых, исследовавших электромагнитные явления до него (Законы Кулона, Био – Савара, Ампера и, в особенности, исследования Фарадея). Сам Максвелл записал 20 уравнений с 20 неизвестными в дифференциальной форме, которые позднее были преобразованы.
Система уравнений Максвелла
В состав системы уравнений Максвелла входят четыре уравнения.
Первое уравнение:
Это Закон Фарадея (Закон электромагнитной индукции).
где -напряженность электрического поля, -вектор магнитной индукции, c – скорость света в вакууме.
Это уравнение говорит, о том, что ротор напряженности электрического поля равен потоку (т.е. скорости изменения во времени) вектора магнитной индукции сквозь этот контур.
Уравнение (1.1) представляет собой первое уравнение Максвелла в дифференциальной форме.
Это же уравнение можно записать в интегральной форме, тогда оно примет следующий вид:
или
где – проекция на нормаль к площадке dS вектора магнитной индукции,
– магнитный поток.
рис. 2.
Циркуляция вектора напряженности электрического поля вдоль замкнутого контура L (ЭДС индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность, ограниченную данным контуром. Знак минус по правилу Ленца означает направление индукционного тока.
Знак минус по правилу Ленца означает направление индукционного тока.
Согласно Максвеллу закон электромагнитной индукции (а это именно он), справедлив для любого замкнутого контура, произвольно выбранного в переменном магнитном поле.
Смысл этого уравнения: Переменное магнитное поле в любой точке пространства создает вихревое электрическое поле.
Второе уравнение Максвелла:
где -вектор магнитной напряженности, — плотность электрического тока, — вектор электрического смещения.
Данное уравнение Максвелла является обобщение эмпирического закона Био- Савара о том, что магнитные поля возбуждаются электрическими токами. Смысл второго уравнения в том, что источником возникновения вихревого магнитного поля является также переменное электрическое поле, магнитное действие которого характеризуется током смещения. ( -плотность тока смещения).
В интегральном виде второе уравнение Максвелла (Теорема о циркуляции магнитного поля) представлено следующим образом:
или
Циркуляция вектора напряжённости магнитного поля по произвольному контуру равна алгебраической сумме токов проводимости и тока смещения, сцепленных с контуром.
Когда Максвелл вводил уравнения (более ста лет тому назад!), природа электромагнитного поля была не понятна. В настоящее время природа поля выяснена, и стало ясно, что может быть названo «током» лишь формально. По pяду расчетных соображений такое название, не придавая ему прямого физического смысла, целесообразно сохранить, что в электротехнике и делается. По этой же причине вектор D, входящий в выражение для тока смещения, называют вектором электрического смещения.
Помимо первых двух уравнений в систему уравнений Максвелла входит теорема Гаусса-Остроградского для электрического и магнитного полей:
и
где —плотность электрического заряда.
Что в интегральном виде представляет собой следующее:
и
где -поток электрического смещения — поток магнитной индукции сквозь замкнутую поверхность, охватывающую свободный заряд q.
Смысл уравнения 3.2. Электрический заряд – источник электрической индукции.
Уравнение 4.2 выражает факт отсутствия свободных магнитных зарядов.
Полная система уравнений Максвелла в дифференциальном виде (характеризует поле в каждой точке пространства):
Полная система уравнений Максвелла в интегральном виде
Полная система уравнений Максвелла в интегральном виде (интегральная форма записи уравнений облегчает их физическую интерпретацию так ка делает их визуально ближе к известным эмпирическим законам):
Систему уравнений Максвелла дополняют «материальными уравнениями», связывающими векторы c величинами, описывающими электрические и магнитные свойства среды.
где – относительная диэлектрическая проницаемость, – относительная магнитная проницаемость, -удельная электропроводность, – электрическая постоянная, – магнитная постоянная. Среда предполагается изотропной, неферрромагнитной, несегнетоэлектрической.
На границе раздела двух сред выполняются граничные условия:
где — поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 2 в 1, единичный вектор, касательный к границе, — проекция вектора плотности поверхностных токов проводимости на единичный вектор.
Данные уравнения выражают непрерывность нормальных составляющих вектора магнитной индукции и скачок нормальных составляющих вектора смещения. Непрерывность касательных составляющих вектора напряженностей электрического поля на границе раздела и скачок этих составляющих для напряженности магнитного поля.
Примеры решения задач
Уравнения ⚠️ Максвелла в дифференциальной и интегральной форме: физический смысл
Уравнения Максвелла — основная идея и физическая суть
Закономерности, выведенные Максвеллом, в электродинамике имеют такое значение, как, к примеру, законы Ньютона для классической механики и постулаты Эйнштейна в теории относительности. Это фундаментальные уравнения, которые подтверждены экспериментальным путем.
Это фундаментальные уравнения, которые подтверждены экспериментальным путем.
Уравнения Максвелла являются системой уравнений в дифференциальном или интегральном виде, которые описывают любые электромагнитные поля, взаимосвязи токов и электрических зарядов в разных средах, включая вакуум.
Уравнения Максвелла подвергались критике со стороны современников ученого, так как не вписывались в установленные стандарты и представления того времени. Однако закономерности послужили началом активного развития науки и причиной переворота в восприятии картины мира. Постулаты предшествовали открытию радиоволн и продемонстрировали электромагнитную природу света. Формулы Максвелла справедливы для макромира и области квантовой механики.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Что описывают четыре уравнения
- Из первой закономерности рассматривается поток электрического поля Е сквозь какую-либо поверхность замкнутого типа.

- Второе уравнение Максвелла выражает закон Фарадея, на основе которого функционируют электрические моторы. В двигателях возникает ток в катушке в процессе вращения магнита.
- Третье уравнение Максвелла также представляет собой закон Гаусса, но в рамках электрического поля. В этом случае для потока магнитного поля будет характерно нулевое значение. Положительные и отрицательные заряды существуют отдельно друг от друга и порождают вблизи электрическое поле, а магнитные заряды — отсутствуют в природе.
- Четвертый постулат
 {}{\left(\frac{dpV}{dt} \right)}dV\Rightarrow div\vec{\delta }=-\left(\frac{dpV}{dt} \right)\)
{}{\left(\frac{dpV}{dt} \right)}dV\Rightarrow div\vec{\delta }=-\left(\frac{dpV}{dt} \right)\)Запись уравнения Максвелла в дифференциальной форме
\(roh\vec{H}=\sigma \vec{E}+\left(\frac{d\vec{D}}{dt} \right)\)
\(roh\vec{H}=\vec{\delta _{pr}+\vec{\delta _{sm}}}\)
\(rot\vec{E}=-\left(\frac{d\vec{B}}{dt} \right)\)
\(div\vec{D}=p\)
\(div\vec{B}=0\)
\(div\vec{\delta }=-\left(\frac{dpV}{dt} \right)\)
Уравнения Максвелла для электромагнитного поля
| на главную | доп. материалы | физика как наука и предмет | электричество и электромагнетизм |
Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.Введение Максвеллом понятия тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.

В основе теории Максвелла лежат рассмотренные выше четыре уравнения:
1. Электрическое поле может быть как потенциальным (ЕQ), так и вихревым (ЕB), поэтому напряженность суммарного поля Е = ЕQ + ЕB. Так как циркуляция вектора ЕQ равна нулю (см. (137.3)), а циркуляция вектора ЕB определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3.
 Теорема Гаусса для поля D (см.
(89.3)):
Теорема Гаусса для поля D (см.
(89.3)):(139.1)
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, то формула (139.1) запишется в виде
4. Теорема Гаусса для поля В (см. (120.3)):
Итак, полная система уравнений Максвелла в интегральной форме:
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):
где e0 и m0 — соответственно электрическая и магнитная постоянные, e и m — соответственно диэлектрическая и магнитная проницаемости, g — удельная проводимость вещества.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.
 Уравнения Максвелла не симметричны относительно электрического и
магнитного полей. Это связано с тем, что в природе существуют электрические
заряды, но нет зарядов магнитных.
Уравнения Максвелла не симметричны относительно электрического и
магнитного полей. Это связано с тем, что в природе существуют электрические
заряды, но нет зарядов магнитных.Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид
т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.
Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса
можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны.
 Однако если имеются поверхности разрыва – поверхности, на которых свойства среды
или полей меняются скачкообразно, то интегральная форма уравнений является более
общей.
Однако если имеются поверхности разрыва – поверхности, на которых свойства среды
или полей меняются скачкообразно, то интегральная форма уравнений является более
общей.Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше:
(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).
Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.
 е. электрическое и магнитное поля неразрывно
связаны друг с другом — они образуют единое электромагнитное поле.
е. электрическое и магнитное поля неразрывно
связаны друг с другом — они образуют единое электромагнитное поле.Теория Максвелла, являясь обобщением основных законов электрических и магнитных явлений, не только смогла объяснить уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения, что позволило Максвеллу предсказать существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 3×108 м/с. Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны.
 Электромагнитные волны на
опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что
законы их возбуждения и распространения полностью описываются уравнениями
Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена.
Электромагнитные волны на
опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что
законы их возбуждения и распространения полностью описываются уравнениями
Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена.К электромагнитному полю применим только принцип относительности Эйнштейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относительности Галилея.
Согласно принципу относительности Эйнштейна, механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них преобразуются по определенным правилам.
Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл.
 Taк, если электрическое поле создается системой неподвижных зарядов, то
эти заряды, являясь неподвижными относительно одной инерциальной системы
отсчета, движутся относительно другой и, следовательно, будут порождать не
только электрическое, но и магнитное поле. Аналогично, неподвижный относительно
одной инерциальной системы отсчета проводник с постоянным током, возбуждая в
каждой точке пространства постоянное магнитное поле, движется относительно
других инерциальных систем, и создаваемое им переменное магнитное поле
возбуждает вихревое электрическое поле.
Taк, если электрическое поле создается системой неподвижных зарядов, то
эти заряды, являясь неподвижными относительно одной инерциальной системы
отсчета, движутся относительно другой и, следовательно, будут порождать не
только электрическое, но и магнитное поле. Аналогично, неподвижный относительно
одной инерциальной системы отсчета проводник с постоянным током, возбуждая в
каждой точке пространства постоянное магнитное поле, движется относительно
других инерциальных систем, и создаваемое им переменное магнитное поле
возбуждает вихревое электрическое поле.Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, базирующейся на представлении об электромагнитном поле.
Уравнения Максвелла. Вихревое электрическое поле
1. УРАВНЕНИЯ МАКСВЕЛЛА
2. 1. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Если неподвижный проводящий контур
пронизывается переменным магнитным полем,
то в контуре появляется индукционный ток.
Возникновение индукционного тока говорит о
том, что изменение магнитного поля вызывает
появление в контуре сторонних сил F * qE * ,
действующих на носители тока (заряды).
Действие сторонней силы связано с появлением
вихревого электрического поля E * .
*
ЭДС индукции равна циркуляции E по контуру:
A* 1
i q q
1
*
F
dl
qE
dl
q
*
*
E
dl .3. 2. ПЕРВОЕ УРАВНЕНИЕ МАКСВЕЛЛА
По закону Фарадея
dФ
E dl dt ;
Ф BdS
*
d
L E dl dt
*
dФ
i dt
BdS .
S
Поскольку контур и поверхность S , для
которой вычисляется магнитный поток,
неподвижны, то операции дифференцирования по времени и интегрирования
по поверхности можно поменять местами:
d
B
BdS dS
dt S
t
S
B
L E dl S t dS .
*4. 3. ЗАКОН ФАРАДЕЯ В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
Первое уравнение Максвелла выражает закон
электромагнитной индукции Фарадея:
B
L E dl S t dS .
*
Преобразуем левую часть по теореме Стокса:
*
*
dS
E
dl
E
L
S
B
*
S E dS S t dS .
Ввиду произвольности выбора поверхности
интегрирования в каждой точке должно
выполняться равенство
B
*
E ,
t
выражающее закон электромагнитной индукции Фарадея в дифференциальной форме.5. 4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Вихревое электрическое поле E * , порождаемое
переменным магнитным полем существенно
отличается от порождаемого зарядами электростатического поля E0 .
Электростатическое поле потенциально E0 0 ,
его линии напряженности начинаются на положительных зарядах, заканчиваются на отрицательных.
Вихревое поле непотенциально
B
*
E ,
его линии напряженности
t
замкнуты сами на себя, для
создания поля требуются не электрические заряды,
а меняющееся во времени магнитное поле.
В общем случае E E0 E *
E E0 E *
B
E .
t6. 5. УРАВНЕНИЕ НЕПРЕРЫВНОСТИ
Рассмотрим воображаемую замкнутую поверхность S в некоторой среде с током.
Выражение
jdS определяет заряд, вышедший из объема
V,
S
ограниченного поверхностью S .
В силу закона сохранения заряда эта величина должна быть равна
скорости убывания заряда q , содержащегося в данном объеме:
S
dq
jdS ;
q dV
dt
V
d
dV
dV
dt V
t
V
По теореме Остроградского-Гаусса
j
dV
dV
j
V
V t
t
S
d
S jdS dt V dV ;
jdS
dV .
t
V
jdS j dV
S
V
– уравнение
непрерывности.
const j 0.7. 6. ТОК СМЕЩЕНИЯ
Теорема о циркуляции в виде H j
противоречит уравнению непрерывности:
H j ;
H 0
j 0,
но
j
.
t
Вывод: j 0 только для стационарных процессов, при нестационарных
процессах плотность зарядов может меняться со временем. В этом
В этом
случае в полном согласии с уравнением непрерывности j 0.
Чтобы согласовать теорему о циркуляции и уравнение непрерывности,
Максвелл ввел в правую часть теоремы о циркуляции дополнительное
слагаемое и назвал его плотностью тока смещения. Таким образом,
H j0 jc ;
j0 j ;
jп j jc . jc D H j D .
t
t
Сумму тока проводимости и тока смещения принято называть полным
током.8. 7. УРАВНЕНИЯ МАКСВЕЛЛА В ИНТЕГРАЛЬНОЙ ФОРМЕ
9. 8. УРАВНЕНИЯ МАКСВЕЛЛА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
Уравнения максвелла в интегральной форме. Максвелла уравнения
Значение уравнений Максвелла
Уравнения Дж. Максвелла создают основу для предложенной им теории электромагнитных явлений, которая объяснила все известные в то время эмпирические факты, некоторые эффекты предсказала. Главным выводом теории Максвелла стало положение о существовании электромагнитных волн, которые распространяются со скоростью света.
Замечание
Уравнения, предложенные Максвеллом, в электромагнетизме играют роль подобную роли законов Ньютона в классической механике.
 Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.
Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.Замечание 1
Сам Максвелл предложил двадцать уравнений в дифференциальной форме с двадцатью неизвестными величинами. В современном виде мы имеем систему уравнений Максвелла благодаря немецкому физику Г. Герцу и англичанину О. Хэвисайду . С помощью этих уравнений можно описать все электромагнитные явления.
Система уравнений Максвелла
Определение 1
Систему уравнений Максвелла составляют:
\ \ \ \
Выражения (1)-(4) называют полевыми уравнениями , они применимы для описания всех макроскопических электромагнитных явлений. Иногда уравнения системы Максвелла группируют в пары, первую пару составляют из второго и третьего уравнения, вторую пару — из первого и четвертого уравнений. При этом говорят, что в первую пару уравнений входят только основные характеристики поля ($\overrightarrow{E}\ и\ \overrightarrow{B}$), а во вторую пару – вспомогательные ($\overrightarrow{D}\ и\ \overrightarrow{H}$).

Каждое из векторных уравнений (1) и (2) эквивалентно трем скалярным уравнениям. Эти уравнения связывают компоненты векторов, которые находятся в левой и правой частях выражений. Так, в скалярном виде уравнение (1) представляется как:
В скалярном виде уравнение (2) запишем как:
Третье уравнение из системы Максвелла в скалярном виде:
Четвертое уравнение в скалярной форме примет следующий вид:
Для того чтобы рассмотреть конкретную ситуацию, систему уравнений (1)-(4) дополняют следующими материальными уравнениями, которые учитывают электромагнитные свойства среды:
Замечание 2
Необходимо отметить, что существует целый ряд явлений, в которых материальные уравнения существенно отличны от уравнений (5), например, если речь идет о нелинейных явлениях. В таких случаях получение материальных уравнений составляет отдельную научную задачу.
Физический смысл уравнений Максвелла
Уравнение (1) системы указывает на то, что двумя возможными источниками магнитного поля являются токи проводимости ($\overrightarrow{j}$) и токи смещения ($\frac{\partial \overrightarrow{D}}{\partial t}$).

Уравнение (2) является законом электромагнитной индукции и отображает тот факт, что переменное магнитное поле — один из источников возникновения электрического поля.
Следующим источником электрического поля служат электрические заряды, что и отображает уравнение (4), которое является, по сути, законом Кулона.
Уравнение (3) означает, что линии магнитной индукции не имеют источников (они либо замкнуты, либо уходят в бесконечность), что приводит к выводу об отсутствии магнитных зарядов, которые создают магнитное поле.
Материальные уравнения (5) — это соотношения между векторами поля и токами. Диэлектрические свойства среды заключены в диэлектрической проницаемости ($\varepsilon $). Магнитные свойства, которые описывает намагниченность, учтены в магнитной проницаемости ($\mu $). Проводящие свойства среды сосредоточены в удельной проводимости ($\sigma $).
Уравнения поля линейны и учитывают принцип суперпозиции.
Границы применимости уравнений Максвелла
Система уравнений Максвелла ограничена следующими условиями:
Материальные тела должны быть неподвижны в поле.

Постоянные $\varepsilon ,\ \mu ,\sigma $ могут зависеть от координат, но не должны зависеть от времени и векторов поля.
В поле не должно находиться постоянных магнитов и ферромагнитных тел.
Если существует необходимость учета движения среды, то уравнения системы Максвелла оставляют неизменными, а движение учитывается в материальных уравнениях, которые становятся зависимыми от скорости среды и существенно усложняются. Кроме прочего материальные уравнения перестают быть соотношениями между парами величин, как в (5). Например, плотность тока проводимости становится зависимой от индукции магнитного поля, а не только от напряженности электрического поля.
Замечание 3
Магнитное поле постоянных магнитов, например, можно описать, используя систему Максвелла, если известна намагниченность. Но, если заданы токи, то в присутствии ферромагнетиков описать поле при помощи данных уравнений не получится.
Пример 1
Задание: Докажите, что из уравнений Максвелла следует закон сохранения заряда.

Решение:
В качестве основания для решения задачи используем из системы Максвелла уравнение:
Проведем операцию дивергирования в обеих частях выражения (1.1):
Для выражения (1.2) в соответствии с теоремой равенстве нулю дивергенции ротора имеем:
Следовательно, получаем:
Рассмотрим второе слагаемое в правой части. Мы можем поменять порядок дифференцирования, так как время и пространственные координаты независимы, то есть записать:
В соответствии с системой Максвелла мы знаем, что источниками электрических полей служат заряды или:
Что позволяет нам записать уравнение (1.4) в виде:
Что дает нам закон сохранения заряда, который записан в виде:
Данное уравнение называют уравнением непрерывности тока, оно содержит в себе закон сохранения заряда, что совершенно очевидно, если выражение (1.8), записать в интегральной форме:
\[\oint\limits_S{\overrightarrow{j}}d\overrightarrow{S}=-\frac{\partial }{\partial t}\int{\rho dV}(1.
 9).\]
9).\]тогда если области замкнуты и изолированы получаем:
\[\oint\limits_S{\overrightarrow{j}}d\overrightarrow{S}=0\to \int{\rho dV}=const.\]
Что требовалось доказать.
Пример 2
Задание: Покажите, что уравнения $rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$ и $div\overrightarrow{B}=0$ , входящие в систему Максвелла не противоречат друг другу.
Решение:
За основу решения примем уравнение:
Возьмём дивергенцию от обеих частей уравнения:
В соответствии с теоремой равенстве нулю дивергенции ротора имеем:
Соответственно, получаем, что
Выражение $div\overrightarrow{B}=const$ не противоречит тому, что $div\overrightarrow{B}=0$.
Мы получили, что уравнения $rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$ и $div\overrightarrow{B}=0$ совместны, что требовалось показать.
Четыре уравнения, соответствующие нашим (модифицированным) утверждениям, называются уравнениями Максвелла в интегральной форме .

Выпишем их все рядом еще раз:
Чтобы получить уравнения Максвелла в среде, надо произвести замену:
то есть указать связь (так называемые «материальные» уравнения) между напряженностями и индукциями: и и дополнить систему уравнением закона Ома
Отметим, что приведенными выше простейшими соотношениями можно пользоваться не всегда. Ситуация заметно сложнее в присутствии таких веществ как сегнетоэлектрики, пьезоэлектрики, ферромагнетики, вещества анизотропные и тому подобное. Здесь наша цель показать, как формируется полная система уравнений, позволяющая (с учетом начальных и граничных условий, разумеется) рассчитать электромагнитное поле.
От уравнений в интегральной форме можно с помощью теорем векторного анализа перейти к уравнениям в дифференциальной форме, связывающим значения полей и и их пространственных и временных производных со значениями плотностей заряда и тока. Этими уравнениями мы пользоваться не будем, но все же приведем их хотя бы как часть шутки, опубликованной в одном из журналов в дни юбилея Максвелла:
«И сказал Бог:
И стал свет».

Непонятные значки div (читается «дивергенция ») и rot (читается «ротор ») – это особые операции дифференцирования, выполняемые над векторными полями. Дивергенция – по латыни «расхождение». Эта операция описывает конфигурацию силовых линий типа «ежа», расходящихся из точек, где имеются электрические заряды. Слово «ротор» в переводе не нуждается, оно явно ассоциируется с вращением. Эта операция описывает вихревые поля (кольцеобразные – замкнутые силовые линии) вокруг их источников – токов или других полей, меняющихся во времени.
Четыре интегральных уравнения и четыре дифференциальных эквивалентны. Максвелл показал, что все явления электромагнетизма можно полностью описать этими четырьмя уравнениями, являющимися обобщением экспериментальных фактов.
В приведенной шутке упоминался свет. Действительно, свет – это электромагнитное излучение определенного диапазона частот. Предсказание электромагнитных волн стало одним из величайших достижений теории Максвелла.
 Представим себе, что заряды и токи отсутствуют. Посмотрим на уравнения Максвелла в дифференциальной форме. Видно, что если поля не статические, но зависят от времени, то имеется вихревое электрическое и магнитные поля (соответствующие роторы отличны от нуля). Распространение полей без зарядов и токов – это и есть электромагнитные волны. И можно углядеть в уравнениях намек на скорость их распространения: туда входит комбинация e 0 m 0 , через которую может быть выражена скорость света в вакууме (см. (6.3))
Представим себе, что заряды и токи отсутствуют. Посмотрим на уравнения Максвелла в дифференциальной форме. Видно, что если поля не статические, но зависят от времени, то имеется вихревое электрическое и магнитные поля (соответствующие роторы отличны от нуля). Распространение полей без зарядов и токов – это и есть электромагнитные волны. И можно углядеть в уравнениях намек на скорость их распространения: туда входит комбинация e 0 m 0 , через которую может быть выражена скорость света в вакууме (см. (6.3))Но об этом – позже, в следующей части нашего курса.
В заключение же этой части процитируем слова Г. Герца об уравнениях Максвелла:
«Трудно избавиться от чувства, что эти математические формулы живут независимой жизнью и обладают своим собственным интеллектом, что они мудрее, чем мы сами, мудрее даже, чем их первооткрыватели, и что мы извлекаем из них больше, чем было заложено в них первоначально».
Пример использования уравнений Максвелла
Определить величину магнитного поля в зазоре конденсатора как функцию r расстояния от оси симметрии (рис.
 9.13)
9.13)Рис. 9.13. Конденсатор с круглыми пластинами в процессе зарядки
Решение
Запишем уравнение (9.13) для контура, показанного на Рис. 9.3 штрихованной линией. Интегрируя, получим
Очевидно, что магнитное поле не равно нулю только благодаря наличию меняющегося со временем электрического поля. В свою очередь, изменение электрического поля обусловлено увеличением заряда на обкладках конденсатора. Эту связь получим из соотношений
Окончательно находим
В основе теории Максвелла лежат рассмотренные выше четыре уравнения:
1. Электрическое поле может быть как потенциальным (Е Q ), так и вихревым (Е B ), поэтому напряженность суммарного поля Е =Е Q +Е B . Так как циркуляция вектора Е Q равна нулю (см. (137.3)), а циркуляция вектора Е B определяется выражением (137.
 2), то циркуляция вектора напряженности суммарного поля
2), то циркуляция вектора напряженности суммарного поляЭто уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля D (см. (89.3)):
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, то формула (139.1) запишется в виде
4. Теорема Гаусса для поля В (см. (120.3)):
Итак, полная система уравнений Максвелла в интегральной форме:
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):
где e 0 и m 0 – соответственно электрическая и магнитная постоянные, e и m – соответственно диэлектрическая и магнитная проницаемости, g – удельная проводимость вещества.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
Для стационарных полей (E= const и B= const) уравнения Максвелла примут вид
т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного – только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.
Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса
можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла – интегральная и дифференциальная – эквивалентны.
 Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше:
(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).
Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.
 е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле .
е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле .Ток смещения или абсорбционный ток – величина, прямо пропорциональная быстроте изменения электрической индукции. Это понятие используется вклассической электродинамике
Введено Дж. К. Максвеллом при построении теории электромагнитного поля.
Введение тока смещения позволило устранить противоречие в формуле Ампера для циркуляции магнитного поля, которая после добавления туда тока смещения стала непротиворечивой и составила последнее уравнение, позволившее корректно замкнуть систему уравнений (классической) электродинамики.
Строго говоря, ток смещения не является электрическим током, но измеряется в тех же единицах, что и электрический ток.
ного коэффициента) называется поток вектора быстроты изменения электрического поля через некоторую поверхность :
(СИ)
Введение Максвеллом понятия тока смещения, привело к завершению созданной им макроскопической теории электромагнитного поля, которая позволяет с единой точки зрения объяснить не только электрические и магнитные явления, но и предсказать новые, существования которых было впоследствии подтверждено.

В основе теории Максвелла лежат 4 уравнения:
1. Электрическое поле может быть как потенциальным, так и вихревым, поэтому напряженность результирующего поля равна:
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля :
Получаем
Итак, полная система уравнений Максвелла в интегральной форме:
1),
2),
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует связь.
Для изотропных, несегнетоэлектрических и неферромагнитных сред запишем формулы связи:
где – электрическая постоянная, – магнитная постоянная,
Диэлектрическая проницаемость среды, m – магнитная проницаемость среды,
r – удельное электрическое сопротивление, – удельная электрическая проводимость.

Из уравнений Максвелла вытекает, что:
источником электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, которые могут возбуждаться либо движущимися электрическими зарядами (токами), либо переменными электрическими полями.
Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе не существует магнитных зарядов.
Если и (стационарные поля), то уравнения Максвелла принимают следующий вид:
Источниками электрического стационарного поля являются только электрические заряды, источниками стационарного магнитного поля – только токи проводимости.
Электрическое и магнитное поле в данном случае независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.
Дифференциальная форма записи уравнений Максвелла:
3) ,
Интегральная форма записи уравнений Максвелла является более общей, если имеются поверхности разрыва.
 Дифференциальная форма записи уравнения Максвелла предполагает, что все величины в пространстве и времени изменяются непрерывно.
Дифференциальная форма записи уравнения Максвелла предполагает, что все величины в пространстве и времени изменяются непрерывно.Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же важную роль, как и законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с переменным электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным полем, т.е. электрическое и магнитное поле неразрывно связаны друг с другом – они образуют единое электромагнитное поле.
Свойства уравнений Максвелла
Уравнения Максвелла линейны. Они содержат только первые производные полей Е и В по времени и пространственным координатам и первые степени плотности электрических зарядов и токов j . Свойство линейности уравнений Максвелла связано с принципом суперпозиции, если два каких-нибудь поля удовлетворяют уравнениям Максвелла, то это относится и к сумме этих полей.

Уравнения Максвелла содержат уравнения непрерывности, выражающие закон сохранения электрического заряда. Чтобы получить уравнение непрерывности необходимо взять дивергенцию от обеих частей первого из уравнений Максвелла в дифференциальной форме записи:
Уравнения Максвелла выполняются во всех инерциальных системах отсчета. Они являются релятивистки инвариантными. Это есть следствие принципа относительности, согласно которому все инерциальные системы отсчета физически эквивалентны друг другу. Вид уравнений Максвелла при переходе от одной инерциальной системы отсчета к другой не меняется, однако входящие в них величины преобразуются по определенным правилам. Т.е. уравнения Максвелла являются правильными релятивистскими уравнениями в отличие, например, от уравнений механики Ньютона.
Уравнения Максвелла несимметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе электрические заряды существуют, а магнитные заряды нет.
Из уравнений Максвелла следует важный вывод о существовании принципиально нового явления: электромагнитное поле способно существовать самостоятельно – без электрических зарядов и токов. При этом изменение его имеет обязательно волновой характер. Поля такого рода называют электромагнитными волнами. В вакууме они всегда распространяются со скоростью равной скорости света. Теория Максвелла предсказала существование электромагнитных волн и позволила установить все их основные свойства.
В случае стационарных (то есть неменяющихся во времени) электрического и магнитного полей, происхождение которых связано с покоящимися зарядами для электрического поля и со стационарными токами для магнитного поля, эти поля являются независимыми друг от друга, что позволяет рассматривать их отдельно друг от друга.
Уравнения Максвелла – это система уравнений, описывающих природу происхождения и свойства электрического и магнитного полей.
Уравнения Максвелла для стационарных полей:
Таким образом, уравнения Максвелла для стационарных полей :
I.; II. ;
III.; IV. .
Векторные характеристики электростатического поля исвязаны между собой следующим соотношением:
,
где – электрическая постоянная, – диэлектрическая проницаемость среды.
Векторные характеристики магнитного поля и связаны между собой следующим соотношением:
,
где – магнитная постоянная, – магнитная проницаемость среды.
Тема 8. Уравнения Максвелла для электромагнитного поля
Согласно теории Максвелла для электромагнитного поля в случае нестационарных (то есть, изменяющихся во времени) электрического и магнитного полей, источниками электрического поля могут быть либо электрические заряды, либо изменяющееся во времени магнитное поле, а источниками магнитного поля могут быть либо движущиеся электрические заряды (электрические токи), либо переменное электрическое поле.
В отличие от стационарных полей переменные электрическое и магнитное поля не являются независимыми друг от друга и рассматриваются как электромагнитное поле.
Уравнения Максвелла, как система уравнений, описывающих природу происхождения и свойства электрического и магнитного полей в случае электромагнитного поля имеет вид:
I .
, то есть циркуляция вектора напряженности электрического поля определяется скоростью изменения вектора индукции магнитного поля ( скорость изменения вектора индукции ).Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
II .
, то есть поток вектора электрического смещения через произвольную замкнутую поверхностьS , равен алгебраической сумме зарядов, заключенных внутри объема V , ограниченного данной замкнутой поверхностью S ( объемная плотность заряда).III .
, то есть циркуляция вектора напряженности по произвольному замкнутому контуруL определяется полным током I полн. , пронизывающим поверхность S , ограниченную данным контуром L .полный ток I полн , складывающийся из тока проводимости I и тока смещения I см. , то есть I полн. = I + I см. .
Суммарный ток проводимости I определяется в общем случаечерез поверхностную плотность тока j (
)интегрированием, то есть.
Ток смещения I см ,пронизывающий поверхность S , определяется в общем
случаечерез поверхностную плотность тока смещения
(
) интегрированием, то есть:
.Введенное Максвеллом понятие «тока смещения», величина которого определяется скоростью изменения вектора электрического смещения , то есть величиной , показывает, что магнитные поля могут возбуждаться не только движущимися зарядами (электрическими токами проводимости), но и переменными электрическими полями.
IV .
, то есть поток вектора индукциимагнитного поля через произвольную замкнутую поверхность S равен нулю.уравнений Максвелла | Блестящая вики по математике и науке
Закон Лоренца, где qqq и v \ mathbf {v} v – электрический заряд и скорость частицы соответственно, определяет электрическое поле E \ mathbf {E} E и магнитное поле B \ mathbf {B} B, задавая общая электромагнитная сила F \ mathbf {F} F как
F = qE + qv × B. \ mathbf {F} = q \ mathbf {E} + q \ mathbf {v} \ times \ mathbf {B}. F = qE + qv × B.
По сути, часть электромагнитной силы, возникающей в результате взаимодействия с движущимся зарядом (qv q \ mathbf {v} qv), принимается за магнитное поле, а другая часть – за электрическое поле.
Закон Гаусса: Самым ранним из четырех уравнений Максвелла, которые были открыты (в эквивалентной форме закона Кулона), был закон Гаусса. В своей интегральной форме в единицах СИ он заявляет, что полный заряд, содержащийся внутри замкнутой поверхности, пропорционален общему электрическому потоку (сумме нормальной составляющей поля) через поверхность:
∫SE⋅da = 1ϵ0∫ρ dV, \ int_S \ mathbf {E} \ cdot d \ mathbf {a} = \ frac {1} {\ epsilon_0} \ int \ rho \, dV, ∫S E⋅da = ϵ0 1 ρdV,
, где коэффициент пропорциональности равен 1 / ϵ0, 1 / \ epsilon_0, 1 / ϵ0, обратной величине электрической постоянной.Полный заряд выражается как плотность заряда ρ \ rho ρ, проинтегрированная по области.
Закон Гаусса для магнетизма: Хотя магнитные диполи могут создавать аналогичный магнитный поток, который имеет аналогичную математическую форму, не существует эквивалентных магнитных монополей, и поэтому общий «магнитный заряд» во всем пространстве должен в сумме равняться нулю. Следовательно, закон Гаусса для магнетизма читается просто
.∫SB⋅da = 0. \ int_S \ mathbf {B} \ cdot d \ mathbf {a} = 0. ∫S B⋅da = 0.
Закон Фарадея: Электрическое и магнитное поля переплетаются, когда поля претерпевают временную эволюцию.В 1820-х годах Фарадей обнаружил, что изменение магнитного потока создает электрическое поле по замкнутому контуру. Это соотношение теперь называется законом Фарадея:
∫loopE⋅ds = −ddt∫SB⋅da. \ int_ \ text {loop} \ mathbf {E} \ cdot d \ mathbf {s} = – \ frac {d} {dt} \ int_S \ mathbf {B} \ cdot d \ mathbf {a}. ∫loop E⋅ds = −dtd ∫S B⋅da.
При ориентации петли, определенной в соответствии с правилом правой руки, отрицательный знак отражает закон Ленца.
Закон Ампера: Наконец, закон Ампера предполагает, что постоянный ток через поверхность приводит к возникновению магнитного поля (выраженного в единицах потока).Вдобавок Максвелл определил, что быстрые изменения электрического потока (d / dt) E⋅da (d / dt) \ mathbf {E} \ cdot d \ mathbf {a} (d / dt) E⋅da также могут приводить к к изменениям магнитного потока. В целом закон Ампера с поправкой Максвелла утверждает, что
∫loopB⋅ds = μ0∫SJ⋅da + μ0ϵ0ddt∫SE⋅da. \ int _ {\ text {loop}} \ mathbf {B} \ cdot d \ mathbf {s} = \ mu_0 \ int_S \ mathbf {J} \ cdot d \ mathbf {a} + \ mu_0 \ epsilon_0 \ frac {d} {dt} \ int_S \ mathbf {E} \ cdot d \ mathbf {a}. ∫loop B⋅ds = μ0 ∫S J⋅da + μ0 ϵ0 dtd ∫S E⋅da.
Таким образом,
- Закон Гаусса: ∫SE⋅da = 1ϵ0∫ρ dV \ int_S \ mathbf {E} \ cdot d \ mathbf {a} = \ frac {1} {\ epsilon_0} \ int \ rho \, dV ∫ S E⋅da = ϵ0 1 ρdV
- Закон Гаусса для магнетизма: SB⋅da = 0 \ int_S \ mathbf {B} \ cdot d \ mathbf {a} = 0 S B⋅da = 0
- Закон Фарадея: ∫loopE⋅ds = −ddt∫SB⋅da \ int_ \ text {loop} \ mathbf {E} \ cdot d \ mathbf {s} = – \ frac {d} {dt} \ int_S \ mathbf {B} \ cdot d \ mathbf {a} ∫loop E⋅ds = −dtd ∫S B⋅da
- Закон Ампера: ∫loopB⋅ds = μ0∫SJ⋅da + ϵ0μ0ddt∫SE⋅da.\ int _ {\ text {loop}} \ mathbf {B} \ cdot d \ mathbf {s} = \ mu_0 \ int_S \ mathbf {J} \ cdot d \ mathbf {a} + \ epsilon_0 \ mu_0 \ frac {d} {dt} \ int_S \ mathbf {E} \ cdot d \ mathbf {a}. ∫loop B⋅ds = μ0 ∫S J⋅da + ϵ0 μ0 dtd ∫S E⋅da.
В своей интегральной форме уравнения Максвелла могут использоваться для формулировки утверждений об области заряда или тока.
Уравнения Максвелла
Уравнения электромагнетизма Максвелла
Уравнения Максвелла представляют собой набор из четырех уравнений, которые описывают поведение электрического и магнитного полей и их взаимосвязь.В конечном итоге они демонстрируют, что электрическое и магнитное поля – это два проявления одного и того же явления.
В вакууме без заряда или тока уравнения Максвелла имеют дифференциальную форму:
· E = 0
· B = 0
∇ x E = – ( ∂ B / ∂ т)
∇ x B = µ 0 ε 0 ( ∂ E / ∂ т)
где E и B – электрическое поле и плотность магнитного потока, а ∇ · и ∇ × – операторы дивергенции и ротора соответственно.Переменные µ 0 и ε 0 являются фундаментальными универсальными константами, называемыми проницаемостью свободного пространства и диэлектрической проницаемостью свободного пространства, соответственно. В вакууме без электрических зарядов математические решения этих дифференциальных уравнений представляют собой плоские синусоидальные волны с электрическим полем и магнитными полями, перпендикулярными друг другу и направлению движения, имеющими скорость
, где распознается c как скорость света.
Уравнения Максвелла – это макроскопические выражения; они применяются к средним полям и не включают квантовые эффекты.
Уравнения Максвелла: общая форма
В самом общем виде уравнения Максвелла могут быть записаны как
· D = ρ (закон электричества Гаусса)
∇ · B = 0 (закон Гаусса) магнетизма)
∇ x E = – (∂ B / ∂t) (закон индукции Фарадея)
∇ x H = Дж + ∂ D / ∂t (закон Ампера)
В первом уравнении ρ – плотность свободного электрического заряда.В последнем уравнении Дж – это плотность свободного тока.
Для линейных материалов отношения между E , D , B и H равны
D = ε E
B = µ H
Здесь, ε – электрическая проницаемость, µ – магнитная проницаемость. Для нелинейных материалов e и µ зависят от напряженности поля. В изотропных средах e и µ не зависят от положения.В неизотропных средах e и µ можно описать как матрицы 3 × 3, которые представляют различные значения диэлектрической проницаемости и проницаемости вдоль различных пространственных осей среды. Во всех средах e и µ также меняются в зависимости от частоты излучения.
Чтобы соответствовать уравнениям Максвелла, величины векторов электрического и магнитного полей должны удовлетворять следующему соотношению:
Таким образом, в электромагнитном излучении вектор электрического поля имеет гораздо большую амплитуду, чем вектор магнитного поля.
Альтернативные формы уравнений Максвелла
Уравнения Максвелла обычно записываются несколькими способами. Форма, размещенная на передней панели этого веб-сайта, известна в виде точки:
Вышеупомянутые уравнения известны как «точечная форма», потому что каждое равенство истинно в каждой точке пространства. Однако, если мы проинтегрируем точечной формы над объемом получаем интегральную форму. Есть также форма гармонии времени и Уравнения Максвелла записаны только с E и H .А также в одной форме используется воображаемый магнитный заряд, который может быть полезен для решения некоторых проблем. Мы обсудим это ниже.
Интегральная форма уравнений Максвелла
Если точечная форма уравнений Максвелла верна в каждой точке, то мы можем интегрировать их по любому объему ( V ) или через любая поверхность и они по-прежнему будут правдой. Есть несколько приемов векторного исчисления, перечисленных в уравнении [1].
[Уравнение 1] Я не буду вдаваться в вывод, но вы используете теорему о расходимости первых двух уравнений Максвелла (законы Гаусса) и интегрируете через объем V с граничной поверхностью ( S ).Ты используешь Теорема Стокса о законе Фарадея и Ампера на открытой поверхности ( S ) с граничной линией ( L ). Результат ниже:
Уравнения Максвелла в интегральной форме.
Обратите внимание, что в первых двух уравнениях поверхность S является замкнутой поверхностью. (как поверхность сферы), что означает, что он охватывает трехмерный объем. В последних двух уравнениях поверхность S – открытая поверхность (в виде круга), имеющая граничную линию L (периметр открытой или незамкнутой поверхности).
Гармоническая по времени форма уравнений Максвелла
Мы знаем из теории преобразований Фурье что каждый сигнал во времени можно переписать как сумму синусоид (знак или косинус). Используя немного более сложная математика, и мы можем указать изменение времени в терминах суммы синусоид написано в сложной форме:
[Уравнение 2] В уравнении [2] f – это интересующая нас частота, которая равна равно .Следовательно, производная по времени функции в Уравнение [2] совпадает с исходной функцией, умноженной на. Это означает, что мы можем заменить производные по времени в точечной форме уравнений Максвелла [1] как в следующем:
Уравнения Максвелла в гармонической форме по времени.
Это известно как фазовая форма или гармоническая по времени форма уравнений Максвелла. Это совершенно законно, потому что эта форма сообщает нам, как ведут себя волны. если они колеблются на частоте f , и все волны могут быть разложены в сумму простые колеблющиеся волны.
Уравнения Максвелла, записанные только с помощью
E и HМы также можем переписать уравнения Максвелла, используя только E и H . Это означает, что мы собираемся избавиться от D , B и Плотность электрического тока Дж . Мы можем сделайте это, используя уравнения:
[Уравнение 3] Если мы подставим их в уравнение [1], мы можем получить уравнения Максвелла только с электричеством и Магнитные поля:
Уравнения Максвелла записаны с использованием только E и H .
Симметричная форма уравнений Максвелла – с магнитным зарядом
Что, если кто-то найдет магнитные монополи? Тогда нам придется изменить уравнения Максвелла. И тогда нам также пришлось бы изменить уравнения, чтобы учесть Магнитный ток (т.е. поток магнитного заряда).
Это не чисто абстрактное упражнение – некоторые инженерные проблемы можно решить. проще говоря, предположив, что данное распределение поля на самом деле является фиктивным магнитным заряд или магнитный ток – это упрощает решение.Так что ты тоже можешь прийти через следующую форму уравнений Максвелла, но вы должны знать, что некоторых терминов в действительности не существует:
Уравнения Максвелла, записанные с магнитным зарядом и магнитным током.
Как видите, мы ввели объемную плотность магнитного заряда во второе уравнение: и плотность магнитного тока к третьему уравнению.
Уравнения МаксвеллаЭта страница с формами уравнений Максвелла защищена авторским правом.Никакая часть не может быть воспроизведена кроме как с разрешения. Авторские права принадлежат Maxwells-Equations.com, 2012.
Уравнение электромагнитного поля Максвелла № 1
Уравнение электромагнитного поля Максвелла № 1Максвеллс Электромагнитный Полевое уравнение № 1
Автор Джордж Дж. Спикс
1.0 Формулировка уравнения
Следующее электростатическое поле уравнения будут разработаны в этом разделе:
Интегральная форма
Дифференциальные формы
Первое уравнение Максвелла основано на Гауссе закон электростатики, опубликованный в 1832 году, в котором Гаусс установил взаимосвязь между статическими электрическими зарядами и их сопутствующими статические поля.
Приведенное выше интегральное уравнение утверждает, что электрический поток через закрытая поверхность равна общему приложенному заряду.
Дифференциальная форма уравнения утверждает, что дивергенция или исходящий поток электрического потока из точки равен объемному заряду плотность в этой точке.
1.1. Уравнение Максвелла № 1; Площадь Интеграл
Выведем интеграл уравнение, рассматривая сумму плотности электрического потока на площадь поверхности, а затем как сумма объемов, содержащих электрические плата.Показано, что два интеграла равны, если они основаны на такое же обвинение. Два примера с использованием уравнений: показано.
1.1.1 Закон Гаусса
Закон электростатики Гаусса гласит, что линии электрического поток,
f E , исходит от положительного заряда, q , и прекращаются, если они прекращаются, на отрицательном заряде. Пространство внутри на которое оказывают свое влияние заряды, называется электростатическим полем.Схема на рис. 1.1 представляет заряды и три размерное поле. Поле визуализируется как состоящее из линий поток. Для изолированного заряда линии потока не оканчиваются и имеют вид считается продолжающимся до бесконечности.
Чтобы получить уравнение, связывающее электрическую заряда q и его потока
f E , предположим, что заряд центрирован в сфере радиус r метров. Плотность электрического потока D тогда равна электрический поток, исходящий от заряда, q , деленный на площадь сфера.кулонов на квадратный метр; где площадь перпендикулярно линиям потока. (Один кулон равен величина заряда 6,25
X 10 18 электронов.) Тогда заряд, заключенный в сфере, равен электрическому потоку плотность на его поверхности, умноженная на площадь, вмещающую заряд.q (кулоны включены) =
D x 4 r 2 .Линии потока, вносящие вклад в плотности потока те, которые оставляют сферу перпендикулярно поверхности сферы.Это приводит к интегральной формулировке этой части Закон Гаусса;
Знак интеграла указывает на суммирование бесконечно малые площади, d
a , чтобы получить всю площадь поверхности.Кружок на знаке интеграла означает, что интеграл или Суммирование площадей ведется по замкнутой сплошной поверхности.
Полужирные буквы обозначают, что буква представляет вектор, т. Е. эта величина имеет величину и направление.Расстояние, скорость, ускорение и сила – общие примеры векторов.
Д
– вектор плотности электрического потока в кулонах на квадратный метр.(указанная точка) следующий Д показывает, что при умножении двух векторы, D и d a .
Скалярное произведение (обсуждается ниже) указывает, что величины два вектора умножаются вместе, а затем этот продукт умножается косинусом угла между двумя векторами.Точечный продукт здесь позволяет определить эффективные линии потока, протекающего через поверхность.
1.1.2 Векторное произведение точек
Приложение векторного скалярного произведения может быть проиллюстрировано вычислением работать над следующей проблемой физики.
Напомним, что работа = сила, умноженная на расстояние. Работа равна продукту силы, то есть в направлении движения силы, умноженное на расстояние, на которое движется сила.
В следующем примере предположим, что человек толкает швабру по пол с ручкой швабры под углом 60 градусов к полу, как в Рисунок 1.2. На этих диаграммах стрелки используются для обозначения векторов.
Через ручка швабры. Как показано на диаграмме, только эта составляющая силы в направление параллельно полу используется при расчете работ. Мы видим, что сила параллельна полу;
20 фунтов x косинус 60 0 = 10 фунтов.
Какая работа выполняется при проталкивании швабры на 8 футов по полу?
10 фунтов x 8 футов = 80 футов.фунты
Используя скалярное произведение, уравнение работы выглядит так:
Работа = F orce d istance.
Скалярное произведение означает, что работа равна величине силы. умножить на величину пройденного расстояния, умножить на косинус угла между двумя векторами.
Или, работа = сила на ручке швабры, умноженная на расстояние, на которое сила перемещается, умноженное на косинус угла между силой и полом.
Работа = 20 фунтов умножить на 8 футов умножить на 1/2 = 80 фут-фунтов.
Только та составляющая полной силы в направлении, параллельном пол, полученный с помощью скалярного произведения, используется в расчет работы.
Это показывает, что скалярное произведение определяется как метод вектора умножение, в котором векторные величины умножаются вместе и затем этот продукт умножается на косинус включенных векторов угол.Всегда должен быть вектор на каждую сторону точки в скалярном произведении.
Следовательно, когда скалярное произведение используется в законе Гаусса, только то, что составляющая потока, параллельная вектору, представляющему площадь, будет вносят свой вклад в общую вложенную плату.
1.2 Закон Гаусса; Интегральная площадь Примеры
Способ определения заряда с помощью скалярного произведения аналогично нахождению Работы как скалярного произведения между приложенной Силой и Расстояние.С помощью этого метода только те компоненты векторных линий потока в том же направлении, что и вектор, представляющий площадь, будет суммируется в расчете начисления. Или, иначе говоря: только эти силовые линии, перпендикулярные поверхности, включены в результат скалярного произведения для получения прилагаемого заряда.
Скалярное значение всегда является результатом скалярного произведения. В этом случае, результат – количество кулонов. Примеры других скалярных величин температура, масса и мощность.Скалярная величина, в отличие от вектор, не имеет направления.
Дифференциальный элемент площади равен
d a . Вектор Представляющая область указывается перпендикулярно этой области. Использование скалярного произведения между вектором, представляющим площадь d a и плотность потока D , приводит к получению эффективного потока через площадь. Суммирование всей площади в квадратные метры.Предварительное уравнение (закон Гаусса) в нашей процедуре для получения Первое уравнение Максвелла теперь;
Это интегральное уравнение утверждает, что величина плотности электрического потока, нормального к поверхности, вызвана удельное количество заряда, q , заключенное в поверхность.
Рассмотрим следующие примеры определения плотности электрического потока на сферической поверхности и на цилиндрической поверхности.
1.2.1 Определение плотности потока на сфере
Предположим, что заряд в один кулон центрирован в сфере радиуса r. метров как на рисунке 1.3. Рассчитайте плотность электрического потока
D по поверхность на сфере. Интеграл или сумма площадей сфера 4 p r 2 кв.Вектор, представляющий область, направлен нормально к этой области. Вектор, представляющий небольшую область,
d a , тогда находится прямо на одной линии с линия электрического потока, выходящая из сферы. D представляет плотность линий электрического потока, выходящих из сфера. Угол между плотностью смещения, D , и стрелкой представляющий бесконечно малую область – ноль градусов. Косинус нуля градусов один.Переформулируя интегральное уравнение площадей закона Гаусса:
q (кулоны включены) =
один кулон = D x 4 p r 2 .
кулонов на квадратный метр на поверхности сфера.
1.2.2 Определение плотности потока на цилиндре
Предположим, что длинная линия стационарных зарядов составляет q кулонов на метр, как показано на рисунке 1.4. Имеется цилиндр длиной «L» и радиусом «r» с центром на зарядах. Какая плотность электрического потока на поверхность цилиндра?
Уравнение Гаусса:
Q T , полный прилагаемый заряд, = q кулонов на метр x L метров.
= Q T = D x 2pr x L.
D
в кулонах на квадратный метр =1,3 Уравнение Максвелла № 1; Объемный интеграл
Закон электростатики Гаусса также записано в виде интеграла по объему:
Это уравнение утверждает, что заряд заключенный в объем, равен объемной плотности заряда,
r , (rho) суммированы для весь том.q – заряд, заключенный в томе.
r
– объемная плотность заряда в кулонах на кубический метр.– бесконечно малый элемент объема.
Весь объем в кубических метрах.
Суммарный заряд, заключенный в объем, – это объем в кубических метрах. умноженное на плотность заряда в кулонах на кубический метр. Средняя громкость Плотность заряда, просуммированная для всего объема, является вложенным зарядом.А обсуждение r можно найти в разделе 1.5.3.
1,4 Уравнение Максвелла № 1; Заполненная интегральная форма
Для получения интегральной формы Уравнение Максвелла № 1, предположим, что эксперимент настроен так, что одинаковый заряд q кулонов содержится в каждом из уравнений закона Гаусса. Тогда интегралы от одного заряда должны быть равны.
Затем,
Таким образом, мы получили интегральный вид Уравнение Максвелла No.1. Это уравнение утверждает, что эффективная электрическая поле через поверхность, ограничивающую объем, равно полному заряду в объеме. Уравнение показывает что область, заключенная в левом интеграле, должна охватывать объем правого интеграла. Это похоже на утверждение, что площадь поверхности шара или коробки включает в себя объем мяча или коробки. Площадь и объем, указанный в уравнениях потребность не наблюдаемые физические поверхности, часто они будут математическими пределы.
Чтобы запомнить интегральную форму уравнения Максвелла № 1, рассмотрим что заряд q , заключенный в объем, должен быть равен объему плотность заряда,
r, умноженная на объем. Кроме того, тот же заряд q вызовет поток определенной площади. плотность, D , раз больше определенной площади. Площадь должна охватывать объем. В интегралы (суммы) должны быть равны, поскольку одинаковые количество кулонов должно быть получено с каждой стороны от знака равенства.1,5 Уравнение Максвелла № 1; Дифференциальная форма
Дифференциальная форма Уравнение Максвелла № 1:
это дифференциальный оператор читается как «del» (обсуждается ниже).
читается как «расхождение».
Д
– плотность электрического потока в кулонах на квадратный метр.г
(rho) – объемная плотность заряда в кулонов на кубический метр.1.5.1 Обсуждение (del)
– это математическое расширение обычного одномерного измерения. производная исчисления в трех измерениях.
Мы начнем обсуждение с обзора обычных производных.
В качестве примера для обозначения скорости используется производная. Скорость (v) – это увеличение расстояния, с , для увеличения время, т .
Скорость (v) =.
Поскольку изменение во времени очень мало, дифференциальное исчисление символ используется для скорости.
Теперь рассмотрим обычное одномерное измерение. производная для ускорения.
Вспомните уравнение для получения скорости объекта, когда он упал с высоты. Скорость, которой достигает объект, определяется;
Скорость, v, = ускорение свободного падения, g, умноженное на время в течение который объект падает.
Скорость = v = g t. Или
В интегральной форме закона Гаусса мы просуммировали бесконечно малые значения площади и объема, да и дв.Здесь мы используем дифференциала, ds, dv и dt, чтобы найти мгновенные скорости изменения расстояние и скорость относительно времени.
Существует правило дифференциального исчисления, на которое мы укажем здесь. так как мы будем использовать правило ниже.
Обратите внимание, что скорость равна ускорению (g), умноженному на время (t). Итак, мы можно взять производную от скорости следующим образом:
Правило исчисления состоит в том, что производная от умноженная на константу переменная – это константа.
Теперь мы расширим эту концепцию обычных производных до частичных производные, что позволит нам получить скорость изменения объема в трех измерениях, что, в свою очередь, приводит к определению
Ñ (дел). Чтобы проиллюстрировать скорость изменения трех измерений, предположим, что коробка расположена в начале прямоугольного систему координат, как показано на рисунке 1.5.Объем коробки, V, = длина x ширина x высота; знак равно Д x Ш x В.
Какова скорость изменения объема, когда только длина увеличивается на небольшое количество, но ширина и высота остаются неизменными?
Здесь используется символ частной производной. В символ для частных производных немного отличается от символа для обыкновенные (одномерные) производные. Символ указывает, что только один независимых переменных меняется на данный момент на рассмотрении. Зависимая переменная, объем,
v изменения, определяемые изменениями независимых переменных; L, W и H.Когда меняется только длина;Символ частной производной показывает, что изменение объема только из-за изменения длины. Ширина и высота удерживаются постоянный. Мы также видим, что производная переменной, умноженная на константу – постоянная, W умноженная на H. Из симметрии следует, что скорость изменение объема в зависимости от ширины или высоты выражается как частная производная.
Когда изменение объема происходит из-за одновременного изменения длины, ширины и высоты, изменения будут происходить в направлениях x, y и z и частные производные складываются, чтобы найти результирующую скорость изменения объем.Это достигается в векторной форме путем умножения каждого частичного производная по единичным векторам, указывающим в направлениях x, y и z. Ед. изм векторы указаны здесь и обсуждаются далее в разделе 1.5.2. С использованием единичные векторы и одновременные изменения в трех измерениях, общая изменение объема обозначено:
Для более общего случая тома
V изменение в направления x , y и z ;Это обсуждение обычных и частичных производных была направлена на получение группы трех частных производных термины в скобках выше.
означает градиент. В этой статье мы не будем использовать градиент.
Нам понадобится Ñ (del dot, обсуждается ниже) и Ñ 5 (дель-крест, обсуждается в Раздел 3).
1.5.2 Обсуждение компонентов вектора по отношению к
Прежде чем продолжить части дифференциальной формы уравнения Максвелла № 1, мы должны Рассмотрим компоненты x, y и z вектора в прямоугольные координаты.
В разделе 1.1.2 скалярное произведение двух векторов, силы и расстояния, использовался для расчета работы. Здесь мы рассчитаем ту же работу, используя компоненты вектора силы и расстояния и используют скалярное произведение.
Обратите внимание, что компоненты вектора силы в прямоугольном координаты размещаются либо на нуле, либо на 90 градусах от расстояния движение. Косинус нуля градусов равен единице, а косинус 90 градусов. равно нулю.
Из рисунка 1.3;
Компоненты вектора силы = 17,3 фунта. y + 10 фунтов. х .
Компоненты вектора расстояния = 0 футов y + 8 футов x .
Теперь процедура умножения векторов (точек) заключается в умножении величины компонент вектора и косинус угла между ними, посрочно.
Нулевое расстояние y, умноженное на две составляющие силы, равно нулю.
8 футов x расстояние, умноженное на 17.8 фунтов силы в направлении y раз косинус 90 градусов равен нулю. Направленное расстояние 8 футов x, умноженное на Сила 10 фунтов в направлении x, умноженная на косинус нуля градусов, составляет те же 80 фут-фунтов, которые мы нашли в предыдущем примере.
Следуют этой процедуре умножения компонент вектора x, y и z. при выполнении продукта ниже. Умножение компонентов вектора, которые всегда равны нулю или 90 градусов друг от друга, значительно упрощает векторную математику.
Мы определили компоненты в разделе 1.5.1. Выше мы обсуждали умножение скалярного произведения векторов, используя их компоненты. Эти две концепции сейчас используются для рассчитать
1.5.3 Вычислить
Компоненты вектора D являются его проекциями на x, y и z ось. Векторные направления D Компоненты обозначены единичные векторы x, y и z .На рисунке 1.6 вектор D начинается в начале координат, указывает вверх и вправо и является обозначен как выходящий из бумаги. Величины проекций Д по осям D x , Dy, и D z . На рисунке 1.7 показаны единичные векторы в направлениях x, y и z, которые дают компоненты D их векторные отношения. Одинаковый единичные векторы обозначены в
Уравнение для вектора
D в проекции на три оси координат: D = D x x + D y y + D z z. Теперь мы займемся указано скалярное произведение.Скалярное произведение означает, что мы должны умножить скобки, член по члену, умноженному на косинус включенного угла между каждой парой термины. Эта серия умножений может дать девять членов, но обратите внимание, что единичный вектор, помещенный в тот же единичный вектор:
Остальные шесть комбинаций единичного вектора Умножение скалярного произведения содержит косинус 90 градусов и следовательно, ноль.
Окончательный результат операция – это скаляр из трех членов:
Это уравнение указывает сумму изменения по плотности электрического потока,
D , в каждом из трех ортогональных направлений. В изменение происходит из-за небольшого, (приближающегося ноль), расстояние изменяется в тех же ортогональных направлениях.Изменение расстояния в трех ортогональных направлениях представляет собой объем измените, как показано в разделе 1.5.1. Следовательно, электрическая плотность ( D ) изменение в трех направлениях, что мы получили с использованием скалярного произведения с единичными векторами в del, на самом деле изменение объема блока. Поскольку заряд измеряется в кулонах, сумма заряд в кулонах. Результат сложения трех электрических плотностей изменения – кулоны на кубический метр. Это определяет
r , объемная плотность заряда, , как указано в разделе 1.3.1,6 Уравнение № 1, дифференциальное Форма заполнена
Выполняя указанные операция, которую мы получили
r , объемная плотность заряда. Это разница формулировка уравнения Максвелла №1.Уравнение утверждает, что дивергенция плотность электрического потока в точке равна заряду на единицу объем в этот момент. Скалярное произведение, как всегда, дает скаляр результат.В этом случае результат
р, количество кулонов расход за кубометр.1.7 Теорема о расходимости
Здесь поучительно продолжить использование только что разработанных интегральных и дифференциальных уравнений для уравнения Максвелла № 1, чтобы проиллюстрировать векторную идентичность называется “Теорема о расходимости Гаусса”. Этот тождество приравнивает векторный интеграл по поверхности к векторному интегралу по объему, и потребуется позже в Разделе 2.5.
Из раздела 1.4,
из раздела 1.5;
Путем замены на
r в интегральном уравнении получаем;Это типичная иллюстрация Гаусса. теорема о расходимости на примере вектора
D . В Дело в том, что каждый раз, когда у нас есть векторный поверхностный интеграл этого типа мы можем заменить интеграл объема. Если у нас есть векторный объем интеграл указанного выше типа можно заменить поверхностным интегралом.В интеграл расходимости вектора, просуммированный по объему, равен равный интегралу произведения вектора на его эффективную площадь суммирована по площади. Это аналогично заявлению о том, что объем шара содержится в пределах его площади поверхности. Круг на знак интеграла означает, что интеграл берется по непрерывной площадь.Если бы мы просто использовали теорему о расходимости Гаусса из списка учебников векторных тождеств, мы могли бы сразу записать дифференциальная форма уравнения Максвелла No.1 из интегральной формы. Этот более подробный способ получения личности будет полезно в более поздних выводах.
1,8 Связь
D , E и eПространство, в котором электрическая заряды оказывают свое влияние, называется полем электрического заряда. Электрический заряд q окружает электрическое поле поля Прочность
E . Напряженность электрического поля E вызывает величина плотности потока, D , в зависимости от диэлектрической проницаемости, e окружающая среда.D
находится в кулонов на квадратный метр.E
в ньютонах на кулон или в вольтах на метр.e
в кулонах 2 на ньютон-метр 2 .E
– это напряжение в пространстве, которое вызывает проявление D . В связи к этому уравнению и по причинам, обсуждаемым в разделе 3.7, D есть часто обозначается как плотность смещения электрического потока в дополнение к плотность электрического потока.Кроме того, в разделе 4 будет показано, что магнитно-индуцированное электрическое поле также обозначен E , с размером вольт на метр. Это индуцированное электрическое поле то же поле, что и напряженность статического поля, обсуждаемая здесь, но это генерируется изменяющимся магнитным полем.Диэлектрическая проницаемость
е – это степень, в которой окружающая среда позволяют плотности электрического потока, D , возникать из-за с учетом напряженности электрического поля, E .В воздухе или в свободном пространстве,е
= 8,85×10 -12 кулон 2 на ньютон-метр 2 .Эти понятия и определения будут использоваться в разделах 6 и 7.
1.9 Закон Кулона
В разделе 1.2.1 мы обнаружили, что плотность электрического потока D за счет заряда q, находящегося внутри сфера:
Затем, используя E и e, как определено в Разделе 1.8;
При следующем заряде q 2 , размещенный на расстоянии r метров от q 1 , сила испытывает q 2 . Сила равна
E умноженным на q 2 Ньютонов. Или,, где q 1 и q 2 обозначают физическое лицо обвинения. Это уравнение является законом Кулона. Напомним, что сила одного Ньютон разгонит массу в один килограмм на один метр в секунду 2 .
Закон Кулона гласит, что сила между двумя зарядами пропорционально произведению двух зарядов на расстояние между двумя зарядами в квадрате. Уравнение – это основа для экспериментального определения силы между двумя зарядами и диэлектрическая проницаемость различных сред. Этот важный электрический закон не включен в список Максвелла, поскольку считается производным от Гаусса закон, и не используется в этих уравнениях поля.
На этом обсуждение уравнения Максвелла завершено. Нет.1.
Физика для науки и техники II
из отдела академических технологий на Vimeo.
9.12 Дифференциальная форма уравнений Максвелла
Напомним уравнения Максвелла. В интегральной форме мы видели, что уравнения Максвелла были такими, что первым был закон Гаусса для электрического поля, а это электрическое поле, пунктирное с вектором приращения площади d A , интегрированное по замкнутой поверхности S , равно чистый заряд, заключенный в объеме, окруженном этой замкнутой поверхностью S , деленный на диэлектрическую проницаемость свободного пространства ε 0 .Следовательно, это был закон Гаусса для поля E .
Второе уравнение Максвелла было законом Гаусса для магнитного поля, и это было B dot d A , проинтегрированное по замкнутой поверхности, равное 0. Причина в том, что не может быть никаких магнитных монополей, поэтому у нас не может быть в качестве источника магнитного поля единственного северного полюса, изолированного северного полюса, магнитного северного полюса или магнитного южного полюса. Так было с законом Гаусса для поля B .
Третье уравнение Максвелла было законом индукции Фарадея, и оно было таким, что интеграл от E dot d l по замкнутому контуру C , замкнутый контур, равен отрицательному изменению магнитного потока, dΦ B сверх dt. И это был закон индукции Фарадея.
Последним уравнением Максвелла был закон Ампера-Максвелла, и он имел форму B точка d l , интегрированная по замкнутому контуру или замкнутому контуру, что равнялось μ 0 времени сетевой ток проходя через область, окруженную этим замкнутым контуром, плюс μ 0 ε 0 , изменение электрического поля во времени.Где ε 0 раз, это изменение электрического потока было током смещения, и оно просто указывало на то, что изменение электрического поля генерирует магнитное поле. В случае закона Фарадея изменение магнитного поля создает электрическое поле. Следовательно, это был закон Ампера-Максвелла.
Эти четыре уравнения представляют собой интегральную форму уравнений Максвелла. Как вы помните из математического анализа, брать производную всегда намного проще, чем интеграл.Итак, мы попытаемся выразить эти четыре уравнения в форме дифференциальных уравнений. Для этого мы сначала вспомним оператор, который мы ввели ранее, когда изучали электрическое поле и электрический потенциал. Мы обозначили этот оператор с помощью дельты, и в исчислении он известен как «оператор дель» ( ∇ ).
В прямоугольной системе координат, или в декартовой системе координат, явная форма этого оператора была ∂ над ∂x умножить на î единиц плюс ∂ над ∂ y умножить на ĵ единиц плюс ∂ над ∂ z раз k̂ единиц, где î , ĵ и k̂ были единичными векторами в прямоугольной системе координат вдоль направлений x , y и z .
Как мы видим из определения этого оператора, он просто берет частную производную функции, когда бы она ни действовала на нее, в этих конкретных направлениях. Как вы помните, мы видели это как физическое применение этого оператора, когда мы вычисляли электрическое поле из потенциала, и оно было равно – ∇ умноженной на потенциальную функцию. Мы назвали этот процесс «градиентом». Другими словами, всякий раз, когда оператор ∇ действовал на скалярную функцию, как в случае потенциала, он назывался градиентом потенциала.Итак, отрицательный градиент потенциала дал нам электрическое поле.
Интересный момент здесь с математической точки зрения заключается в том, что здесь оператор действует на скалярную функцию, оператор ∇ , и преобразует ее в вектор. Как вы помните, когда мы берем частную производную потенциальной функции по определенным направлениям, мы получаем компоненты электрического поля по этим направлениям.
Если мы посмотрим на этот оператор и возьмем его скалярное произведение с собой, то оно будет равно ∂ над ∂x î плюс ∂ над ∂ y ĵ плюс ∂ над ∂ z k̂ с точкой с тем же вектором, который равен ∂x î плюс ∂ над ∂ y ĵ и плюс ∂ над ∂ z k̂ .Опять же, как вы помните, частная производная состоит в том, что если функция, которую мы берем как производную, является функцией разных координат, тогда, когда мы берем частную производную по определенной координате, мы сохраняем другие постоянными. В этом смысле процесс получения производной ничем не отличается от получения полной производной этой функции.
Если мы посмотрим сюда и запишем это скалярное произведение в явной форме, у нас будет ∂ над ∂ x умноженное на ∂ над ∂ x даст нам вторую частную производную по отношению к x .То есть ∂2 над ∂ x 2, и у нас будет î точка î для векторной части, и у нас будет ∂2 над ∂ x ∂ y , î точка ĵ для второго члена, плюс ∂2 над ∂ x ∂ z , î точка k̂ . Затем перейдем к произведению второго члена плюс ∂2 над ∂ y ∂ x , ĵ точка î , плюс ∂2 над ∂ y 2, ĵ точка ĵ , плюс ∂2 по ∂ y ∂ z , ĵ точка k̂ .И умножение или взятие скалярного произведения всех этих трех членов здесь во второй скобке на ∂ над ∂ z , даст нам ∂2 над ∂ z ∂ x , k̂ dot î , плюс ∂2 над ∂ z ∂ y , k̂ dot ĵ , и последний член будет ∂2 над ∂ z 2, k̂ dot k̂ .
Здесь, если мы посмотрим на î точка î , ĵ точка ĵ и k̂ точка k̂ , эти векторы имеют величину 1 и угол между ними, поскольку они расположены вдоль в том же направлении, будет 0.Следовательно, если 1 умножить на 1, величина единичного вектора – умножить на косинус 0, то есть 1, это даст нам только 1. И затем аналогично, ĵ точка ĵ даст нам 1 и k̂ dot k даст нам всего 1.
Когда мы смотрим на эти перекрестные произведения, î точка , î точка k̂ , ĵ точка î , ĵ точка k̂ , величина первого вектора равна 1 , умноженное на величину второго вектора, равного 1, и умноженное на косинус угла между этими двумя векторами, который равен косинусу 90, потому что î перпендикулярно ĵ , которое также перпендикулярно k̂ , и аналогично ĵ перпендикулярно k̂ .Таким образом, все эти перекрестные члены, поскольку косинус 90 равен 0, дадут нам только 0. Следовательно, единственными оставшимися членами будут ∂2 над ∂ x 2, ∂2 над ∂ y 2 и ∂2 над ∂ y 2 ∂ z 2.
∇ точка ∇ представлена как ∇ 2, поэтому этот оператор будет равен ∂2 над ∂ x 2 плюс ∂2 над ∂ y 2 плюс ∂2 над ∂ x 2. Это еще один важный оператор в векторной алгебре. Он известен как «оператор Лапласа».Вы собираетесь подробно изучить эти операторы позже, когда будете изучать курс векторной алгебры. Итак, первый – оператор ∇, второй – оператор ∇ 2.
Здесь мы снова собираемся представить две важные теоремы в векторном исчислении, которые вы собираетесь подробно изучить позже в курсе векторной алгебры. Первая известна как теорема Стокса. Если мы говорим, что пусть β будет любым вектором, то теорема Стокса утверждает, что интеграл замкнутого контура от β dot d l , поэтому интеграл этого вектора смещения d l , проинтегрированный по замкнутому петля, равна ∇ cross β dot d A , интегрированная по поверхности S , и это поверхность, окруженная этим замкнутым контуром C .Итак, теорема Стокса просто утверждает, что если мы возьмем интеграл с обратной связью от вектора, β dot d l , он будет равен ∇ cross β dot d A .
Вторая важная теорема известна как теорема о расходимости. Опять же, для векторной величины β , эта теорема может быть выражена как интеграл от β точка d A над замкнутой поверхностью S равен ∇ dot β умножить на dV , проинтегрированный по объем, который окружен замкнутой поверхностью S .Таким образом, в теореме Стокса петлевой интеграл преобразуется в поверхностный интеграл или наоборот, а в случае теоремы о расходимости интеграл замкнутой поверхности преобразуется в объемный интеграл.
Вот несколько определений. Как я упоминал ранее, когда оператор действует на скалярную функцию, этот процесс называется градиентом U , а когда оператор ∇ действует на векторную величину посредством скалярного произведения, это называется дивергенцией β этого вектора.Если он действует на вектор через перекрестное произведение, это называется изгибом β . Если мы посмотрим, с чем связаны эти процессы, то изгиб вектора представляет собой направление вращения и дивергенцию вектора. Если он положительный, это указывает на вектор, созданный в этой точке, а если он отрицательный, то он представляет вектор, уничтоженный в этой точке. Это интересная терминология, связанная с векторным исчислением.
Хорошо. Теперь давайте рассмотрим каждое из уравнений Максвелла одно за другим, начиная с первого.Это был закон Гаусса для электрического поля: E dot d A , интегрированный по замкнутой поверхности, равен чистому заряду, заключенному в объеме, окруженном поверхностью, деленному на ε 0 диэлектрическая проницаемость свободных Космос. Чистый заряд, заключенный внутри объема, окруженного этой поверхностью, также может быть выражен в терминах плотности заряда как объемная плотность заряда ρ , умноженная на dV по ε 0 , интегрированная по объему, окруженному этой поверхностью. поверхность S .
Хорошо. Таким образом, у нас есть интеграл E точка d A над замкнутой поверхностью равен ρ умноженный на dV над ε 0 интегрированный по объему, который окружен этой замкнутой поверхностью S . Что ж, если мы вернемся к теореме о расходимости, здесь говорится, что β точка d A , интегрированная по замкнутой поверхности, равна расходимости β , интегрированной по объему, окруженному поверхностью.Если мы применим эту теорему для нашего случая, для нашего вектора у нас будет электрическое поле, вместо β у нас будет E , поэтому E dot d A над замкнутой поверхностью S будет равно а затем интеграл по объему расхождения E , умноженный на dV . То есть снова объем, окруженный S .
Итак, это прямо из теоремы о расходимости. Но правая часть также равна ρ , умноженному на dV на ε 0 , интегрированных по тому же объему, объем, окруженный S .Оба этих интеграла берутся по одному и тому же объему. Мы можем избавиться от интегралов. Тогда мы получаем расхождение E , равное ρ над ε 0 . Это дифференциальная форма закона Гаусса для поля E .
Когда мы смотрим на второе уравнение, которое было законом Гаусса для магнитного поля, B dot d A над замкнутой поверхностью S было равно 0, поэтому применяя теорему о расходимости и следуя аналогичному типу Процедура, которую мы завершаем здесь, дивергенция B равна 0 как второе уравнение Максвелла в дифференциальной форме, которое является законом Гаусса для поля B .
Теперь давайте рассмотрим третье уравнение Максвелла, которое является законом индукции Фарадея, и оно было задано как E точка d l по замкнутому контуру равно – dΦ B по сравнению с dt . Изменение потока во времени. Здесь поток, о котором мы говорим, – это чистый поток, текущий через поверхность, окруженную этим замкнутым контуром. Таким образом, правая часть в явном виде может быть выражена как минус d на dt of, и тогда поток в явном виде будет равен B dot d A , интегрированный по поверхности S , и это поверхность, окруженная петлей C .Поскольку интеграл берется по пространственным переменным, мы можем легко поместить оператор производной внутри интеграла. Таким образом, если мы сделаем это, мы получим минус-интеграл от d на dt от B dot d A , интегрированный по этой замкнутой поверхности S , которая окружена петлей C .
С другой стороны, левая часть закона Фарадея может быть выражена, опять же, в форме поверхностного интеграла, применяя теорему Стокса, которая просто гласит, что любой вектор, пунктирный с вектором смещения, проинтегрированным по замкнутому контуру равно curl этого вектора с пунктирной точкой d A вектор приращения площади поверхности, интегрированный по поверхности, заключенной в эту петлю C .Здесь вместо β в нашем случае имеется вектор электрического поля. Следовательно, этот интеграл может быть выражен как интеграл от ∇ cross E или curl от E , пунктирный с вектором приращения площади d A , интегрированным по поверхности S , которая представляет собой поверхность, окруженную замкнутым контуром С . Эти две поверхности являются одинаковыми поверхностями, поэтому мы можем избавиться от поверхностных интегралов.
Тогда это оставляет нас ∇ перекрестие E или curl E равно минус d B над dt .Теперь мы можем выразить это в наиболее общем виде как ∂ B по ∂ t , потому что магнитное поле может быть функцией не только времени, но и пространственных координат. Следовательно, отрицательная частная производная магнитного поля становится равной ∇ cross E . Из этого выражения, которое является дифференциальной формой закона Фарадея, мы легко можем увидеть, что изменение магнитного поля создает или генерирует электрическое поле. Это другой способ напомнить или выразить закон индукции Фарадея.Это также известно как изменение поля B создает поле E .
Хорошо. Теперь, если мы рассмотрим последнее уравнение Максвелла, которое является законом Ампера-Максвелла, и оно дается как B точка d l , интегрированная по замкнутому контуру, равна μ 0 умножить на i – плюс μ 0 раз больше тока смещения, что составляет ε 0 , изменение потока электрического поля во времени.Опять же, B точка d l , интегрированная по этому замкнутому контуру, может быть выражена как μ 0 раз, для закрытого i мы можем выразить это в терминах плотности тока, и это будет быть J точка dA , интегрированная по поверхности S , которая окружена этим замкнутым контуром C , плюс, для второго члена, мы имеем μ 0 ε 0 , снова , выразим поток в явном виде.Здесь мы говорим о потоке электрического поля через область, окруженную этой петлей C , так что d на dt из E dot d A , интегрированный по поверхности S , опять же, это это поверхность, окруженная петлей C .
Здесь μ 0 – постоянная величина, мы можем поместить ее внутрь этого интеграла, а также μ 0 ε 0 , а производная по времени может быть помещена внутри этого интеграла, поскольку интеграл берется по пространственным переменным.Мы можем выразить B точку d l , применив теорему Стокса, как мы сделали в предыдущем случае, в форме ∇ cross B dot d A , и это из теоремы Стокса, интегрировано по поверхности S , окруженное этой петлей C будет равно интегралу μ 0 J точка d A интегрировано по той же поверхности S плюс интеграл μ 0 ε 0 d более dt из E dot d A , опять же, интегрированный на той же поверхности S .
Итак, все эти интегралы взяты по одной и той же поверхности S , которая окружена замкнутым контуром C , и мы можем затем избавиться от интегралов, оставив нам дифференциальное уравнение в виде ротора магнитного поля B . равно μ 0 J плюс μ 0 ε 0 . Опять же, используя наиболее общую форму, учитывая, что электрическое поле может быть функцией как положения, так и времени, поэтому, используя здесь частную производную, ∂ E по ∂ t , мы получим дифференциальную форму Ампера. Закон Максвелла.Опять же, легко увидеть, что это выражение можно интерпретировать как изменение электрического поля, в данном случае создание магнитного поля. Итак, здесь мы можем сказать, что это закон Ампера-Максвелла, и он также известен как изменение поля E , генерирует поле B .
Итак, как только мы получим эти дифференциальные формы уравнений Максвелла, мы сможем выразить их здесь прямо напротив интегральных форм уравнений. Для закона Гаусса расходимость E равна ρ над ε 0 .Для закона Гаусса для магнитного поля дивергенция B равна 0. Для закона индукции Фарадея мы имеем поле создает электрическое поле.
Наконец, для закона Ампера-Максвелла крест B равен плюс μ 0 J плюс μ 0 ε 0 ∂ E over ∂ t , изменяющееся электрическое поле создает магнитное поле.Итак, это дифференциальные формы уравнений Максвелла. Эти четыре уравнения являются фундаментальными уравнениями электромагнитной теории, и с помощью этих четырех уравнений можно анализировать и объяснять каждое электромагнитное явление. Скажем, это дифференциальная форма, а это интегральные формы.
Уравнения Максвелла с дифференциальными формами
Сегодня я хочу взять уравнения Максвелла и написать их на языке дифференциальных форм. Полученные уравнения явно ковариантны (т.е. они выглядят так же после применения преобразования Лоренца) и выглядят намного проще, чем уравнения Максвелла в векторной записи. Это один из моих любимых примеров того, как дифференциальные формы могут облегчить жизнь.
Уравнения Максвелла
В единицах CGS уравнения Максвелла даются как- $ \ nabla \ cdot E = 4 \ pi \ rho $
- $ \ набла \ cdot B = 0 $
- $ \ nabla \ times E = – \ frac 1 c \ frac {\ partial B} {\ partial t} $
- $ \ nabla \ times B = \ frac {4 \ pi} c J + \ frac 1 c \ frac {\ partial E} {\ partial t} $
$ E $ – электрическое поле, $ B $ – магнитное поле, $ J $ – плотность электрического тока, $ \ rho $ – плотность электрического заряда.$ E, B $ и $ J $ – векторные поля, а $ \ rho $ – скалярное поле.
Если мы хотим написать уравнения Максвелла с дифференциальными формами, нам нужно решить, какой тип форм будет представлять $ E, B, J $ и $ \ rho $. Следуя Стерну и др., Мы решим это на основе того, как эти поля используются в различных уравнениях.
Сначала рассмотрим закон Фарадея. \ [\ oint_C E \ cdot d \ ell = – \ frac d {dt} \ int_S B \ cdot dA \]$ E $ интегрируется по кривой, поэтому $ E $ естественно соответствует 1-форме (поскольку единичные формы – это объекты, которые можно интегрировать по кривым).\плоский \ конец {выровнено} \] Мы можем использовать эти правила для записи уравнений Максвелла в терминах $ \ eta, \ beta, \ mathscr J, $ и $ \ rho $.
Начнем с первого уравнения. В левой части $ \ nabla \ cdot E $ преобразуется в $ \ star d \ star \ eta $, что является 0-формой. Мы хотим установить его равным 3-форме $ 4 \ pi \ rho $. Итак, мы используем звезду Ходжа, чтобы превратить $ \ star d \ star \ eta $ в форму 3 и найти, что $ \ star \ star d \ star \ eta = 4 \ pi \ rho $. В 3D $ \ star \ star = 1 $, поэтому наше уравнение составляет всего
1 ‘.$ d \ star \ eta = 4 \ pi \ rho $Теперь мы переходим ко второму уравнению. $ \ nabla \ cdot B $ становится $ \ star d \ star (\ star \ beta) $. Поскольку $ \ star \ star = 1 $, это просто становится $ \ star d \ beta $. Итак, наше уравнение $ \ star d \ beta = 0 $. Применение $ \ star $ к обеим сторонам дает $ d \ beta = 0 $.
2 ‘. $ d \ beta = 0 $Для третьего уравнения наши замены дают нам $ \ star d \ eta = – \ frac 1 c \ frac {\ partial \ star \ beta} {\ partial t} $. Применение $ \ star $ к обеим сторонам дает $ d \ eta = – \ frac 1 c \ star \ frac {\ partial \ star \ beta} {\ partial t} $.Но мы можем перетащить $ \ star $ внутрь производной, чтобы получить
3 ‘. $ d \ eta = – \ frac 1 c \ frac {\ partial \ beta} {\ partial t} $Наконец, мы переводим последнее уравнение. Наши правила замены дают нам
4 ‘. $ \ star d \ star \ beta = \ frac {4 \ pi} c \ star \ mathscr J + \ frac 1 c \ frac {\ partial \ eta} {\ partial t} $Собирая все уравнения вместе, мы имеют
1 ‘. $ d \ star \ eta = 4 \ pi \ rho $ 2 ‘. $ d \ beta = 0 $ 3 ‘. $ d \ eta = – \ frac 1 c \ frac {\ partial \ beta} {\ partial t} $ 4 ‘. $ \ star d \ star \ beta = \ frac {4 \ pi} {c} \ star \ mathscr J + \ frac 1 c \ frac {\ partial \ eta} {\ partial t} $ Сейчас , мы записали уравнения в дифференциальных формах. Но уравнения все еще не выглядят очень релятивистскими – у нас все еще есть большая разница между производными по пространству и времени. Для нашего следующего шага мы перестанем думать о формах в пространстве, которые меняются со временем, и вместо этого будем думать о формах в $ 3 + 1 $ -мерном пространстве-времени (т.е. пространство-время с 3-мя пространственными измерениями и 1-м измерением времени). В пространстве-времени у нас есть и пространственная внешняя производная, и пространственная звезда Ходжа, и внешняя производная пространства-времени, и пространственно-временная звезда Ходжа. Мы будем обозначать пространственные операторы $ d_s, \ star_s $ соответственно, и мы будем обозначать операторы пространства-времени $ d $ и $ \ star $.
Внешняя производная и звезда Ходжа в пространстве-времени
Прежде чем мы сможем написать уравнения Максвелла для пространства-времени, мы должны узнать, как наши пространственные операторы связаны с нашими операторами пространства-времени.0 \ wedge \ mathscr J = \ mathfrak J $ для четырехтока. Теперь наше уравнение имеет вид $ d \ star F = \ frac {4 \ pi} c \ mathfrak J $. Это позволяет нам, наконец, выразить уравнения Максвелла (в единицах cgs) как \ [\ begin {выровнено} dF = 0 \ quad \ text {и} \ quad d \ star F = \ frac {4 \ pi} c \ mathfrak J \ end {align} \]
Последние мысли
Я думаю, что эта форма уравнений Максвелла очень хороша. Поскольку $ F $ и $ \ mathfrak J $ являются координатно-независимыми объектами, вы можете сказать, что эти уравнения также должны быть лоренц-ковариантными.И уравнения не различают координаты пространства и времени.
Уравнения Максвелла в дифференциальной форме «Математик без извинений
Уравнения Максвелла в дифференциальной форме
До сих пор мы в основном следовали стандартному подходу к классическому электромагнетизму, и все, что я сказал, не должно быть чем-то новым для бывшего специалиста по физике, хотя в некоторых моментах мы добавили больше математической строгости, чем обычно.Но теперь я хочу пойти в другом направлении.
Начиная снова с уравнений Максвелла, мы видим все эти расхождения и завитки, которые, хотя и знакомы многим, на самом деле являются тяжелым оборудованием. В частности, они полагаются на риманову структуру. Мы хотим избавиться от этого, чтобы найти что-то, что работает без этого предположения, и в качестве первого шага перевернем все в дифференциальные формы.
Итак, предположим, что магнитное поле соответствует a-форме, а электрическое поле соответствует a-форме.Чтобы избежать путаницы между и электрической постоянной, давайте также заменим некоторые из наших постоянных скоростью света -. В то же время мы заменим -form. Теперь уравнения Максвелла выглядят так:
Теперь я хочу поиграть с некоторыми из этих звезд Ходжа:
Обратите внимание, что мы никогда не используем просто -форму, а используем -форму. Давайте вернемся назад и представим -форму, чтобы она соответствовала -form:
В статическом случае, когда производные по времени равны нулю, мы видим, насколько симметрична эта новая формулировка:
И для -формы, и для -формы внешняя производная обращается в нуль, и оператор связывает поля с источниками физического заряда и тока.


 {}{\left(\frac{dpV}{dt} \right)}dV\Rightarrow div\vec{\delta }=-\left(\frac{dpV}{dt} \right)\)
{}{\left(\frac{dpV}{dt} \right)}dV\Rightarrow div\vec{\delta }=-\left(\frac{dpV}{dt} \right)\)
 Теорема Гаусса для поля D (см.
(89.3)):
Теорема Гаусса для поля D (см.
(89.3)): Уравнения Максвелла не симметричны относительно электрического и
магнитного полей. Это связано с тем, что в природе существуют электрические
заряды, но нет зарядов магнитных.
Уравнения Максвелла не симметричны относительно электрического и
магнитного полей. Это связано с тем, что в природе существуют электрические
заряды, но нет зарядов магнитных. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды
или полей меняются скачкообразно, то интегральная форма уравнений является более
общей.
Однако если имеются поверхности разрыва – поверхности, на которых свойства среды
или полей меняются скачкообразно, то интегральная форма уравнений является более
общей. е. электрическое и магнитное поля неразрывно
связаны друг с другом — они образуют единое электромагнитное поле.
е. электрическое и магнитное поля неразрывно
связаны друг с другом — они образуют единое электромагнитное поле. Электромагнитные волны на
опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что
законы их возбуждения и распространения полностью описываются уравнениями
Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена.
Электромагнитные волны на
опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что
законы их возбуждения и распространения полностью описываются уравнениями
Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена. Taк, если электрическое поле создается системой неподвижных зарядов, то
эти заряды, являясь неподвижными относительно одной инерциальной системы
отсчета, движутся относительно другой и, следовательно, будут порождать не
только электрическое, но и магнитное поле. Аналогично, неподвижный относительно
одной инерциальной системы отсчета проводник с постоянным током, возбуждая в
каждой точке пространства постоянное магнитное поле, движется относительно
других инерциальных систем, и создаваемое им переменное магнитное поле
возбуждает вихревое электрическое поле.
Taк, если электрическое поле создается системой неподвижных зарядов, то
эти заряды, являясь неподвижными относительно одной инерциальной системы
отсчета, движутся относительно другой и, следовательно, будут порождать не
только электрическое, но и магнитное поле. Аналогично, неподвижный относительно
одной инерциальной системы отсчета проводник с постоянным током, возбуждая в
каждой точке пространства постоянное магнитное поле, движется относительно
других инерциальных систем, и создаваемое им переменное магнитное поле
возбуждает вихревое электрическое поле.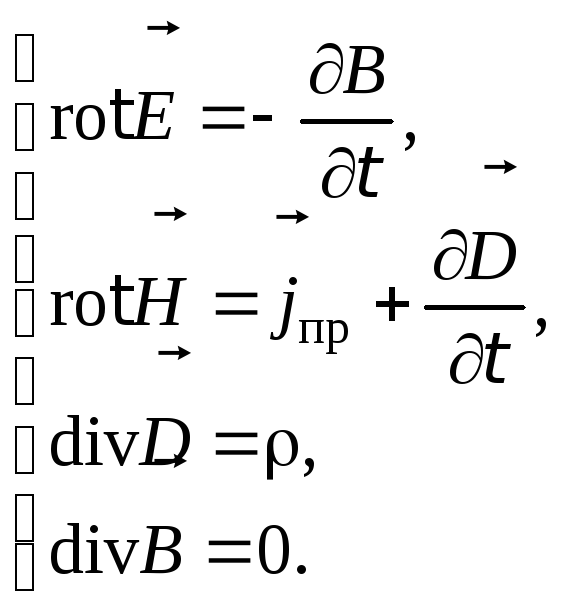


 В этом
В этом Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.
Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.



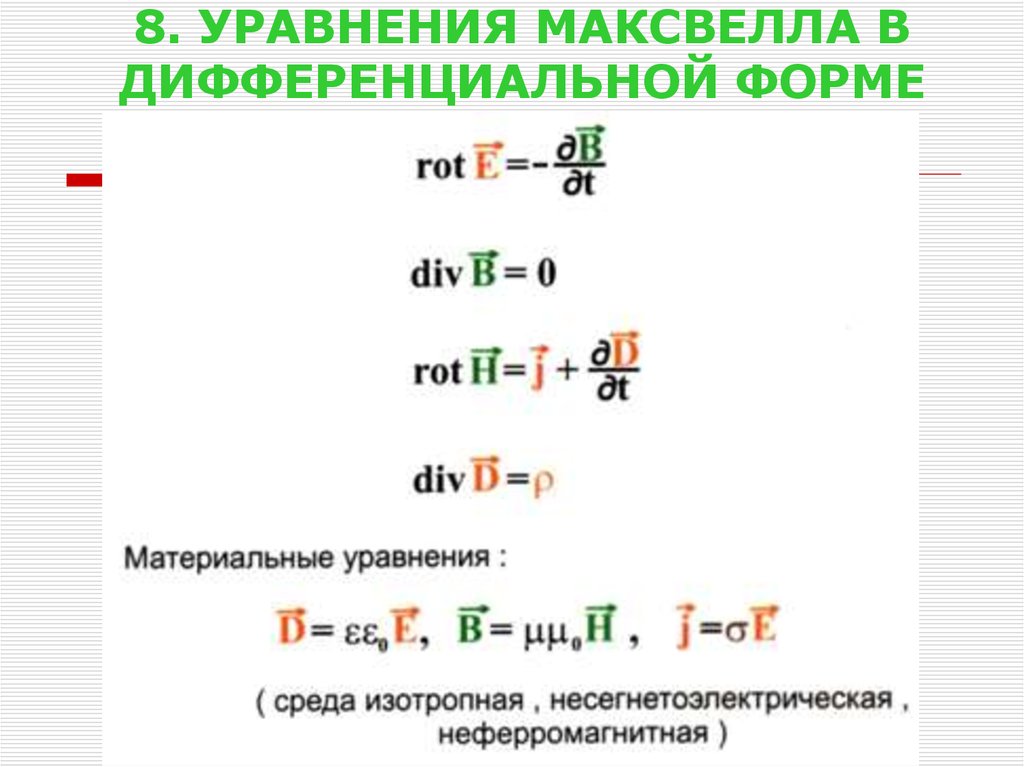 9).\]
9).\]

 Представим себе, что заряды и токи отсутствуют. Посмотрим на уравнения Максвелла в дифференциальной форме. Видно, что если поля не статические, но зависят от времени, то имеется вихревое электрическое и магнитные поля (соответствующие роторы отличны от нуля). Распространение полей без зарядов и токов – это и есть электромагнитные волны. И можно углядеть в уравнениях намек на скорость их распространения: туда входит комбинация e 0 m 0 , через которую может быть выражена скорость света в вакууме (см. (6.3))
Представим себе, что заряды и токи отсутствуют. Посмотрим на уравнения Максвелла в дифференциальной форме. Видно, что если поля не статические, но зависят от времени, то имеется вихревое электрическое и магнитные поля (соответствующие роторы отличны от нуля). Распространение полей без зарядов и токов – это и есть электромагнитные волны. И можно углядеть в уравнениях намек на скорость их распространения: туда входит комбинация e 0 m 0 , через которую может быть выражена скорость света в вакууме (см. (6.3)) 9.13)
9.13)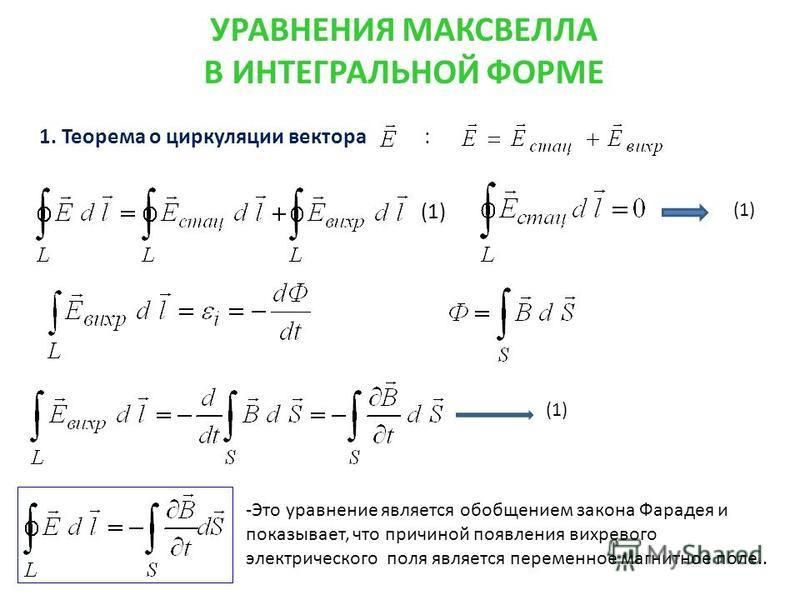 2), то циркуляция вектора напряженности суммарного поля
2), то циркуляция вектора напряженности суммарного поля
 Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей. е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле .
е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле .

 Дифференциальная форма записи уравнения Максвелла предполагает, что все величины в пространстве и времени изменяются непрерывно.
Дифференциальная форма записи уравнения Максвелла предполагает, что все величины в пространстве и времени изменяются непрерывно.