Уравнение радиус вектора для материальной точки: Turn cookies on or off – Computer

Векторный способ описания движения материальной точки – формулы с примерами, краткое определение

4.7

Средняя оценка: 4.7

Всего получено оценок: 143.

4.7

Средняя оценка: 4.7

Всего получено оценок: 143.

Кинематика описывает движение, не рассматривая его причины. Для такого описания может использоваться несколько способов. Кратко рассмотрим векторный способ описания движения материальной точки.

Описание движения

Описание движения — это ответ на вопрос, как менялось положение точки в пространстве со временем. Чтобы получить этот ответ, необходимо выбрать способ сопоставления моментов времени и положения в пространстве, способ измерения времени и способ определения положения точки.

Способом сопоставления может стать таблица или математическая функция. Таблица проще, однако она описывает только определенные моменты времени. Математическая функция описывает любой момент времени, поэтому используется чаще.

Для определения времени и положения в пространстве используется система отсчета.

Рис. 1. Система отсчета в физике.

Моменты времени отмечаются с использованием некоторого эталонного процесса. В прошлом таким процессом было суточное вращение Земли, в настоящее время используется частота излучения возбужденных атомов цезия.

Положение в пространстве может задаваться несколькими способами, одним из которых является векторный.

Радиус-вектор

Как известно из геометрии, вектор — это отрезок на плоскости или в пространстве, для которого можно указать начало и конец. При этом для вектора важны не абсолютные координаты начала и конца в пространстве, а их разница. Положение вектора можно менять, сохраняя ее (параллельный перенос), сам вектор при этом не изменится.

Последнее свойство векторов позволяет использовать их для однозначного задания положения точек в пространстве. Начало вектора помещается в начало координат, а конец вектора — в рассматриваемую точку. Вектор, построенный таким образом, называется радиус-вектором точки и обозначается $\overrightarrow r$.

Рис. 2. Радиус-вектор точки.

Векторная функция движения

При описании движения векторным способом задается соответствие между моментами времени и радиус-вектором:

$$\overrightarrow r=\overrightarrow r(t)$$

Данная формула — это уравнение движения точки, записанное в векторной форме. Функция $\overrightarrow r(t)$ — векторная функция, в которой используются правила действий с векторами.

Такая запись, как правило, заметно компактнее и проще, чем работа непосредственно с координатами точки. Однако математические действия с векторами требуют проецирования вектора на оси координат, алгебраического сложения длин, взятых с нужным знаком, и затем восстановления результата по проекциям. Поэтому векторный способ описания больше подходит тогда, когда требуется вывод законов и формул. В этом случае векторное уравнение позволяет выделить суть закона или формулы, не загромождая формулировки математическими выкладками.

Примером может служить векторная запись свободного падения тела с нулевой начальной скоростью и начальным положением $\overrightarrow {r_0}$:

$$\overrightarrow r=\overrightarrow {r_0}+{\overrightarrow { \mathrm{g}} t^2\over 2}$$

Такая запись одинаково пригодна для любого числа осей координат и любого их направления. Если же записать то же уравнение в координатной форме, то потребуется несколько уравнений (по числу координатных осей), при этом для каждой оси ускорение свободного падения $\mathrm{g}$ будет представлено соответствующей компонентой (проекцией). Можно задаться системой координат так, чтобы вектор $\mathrm{g}$ был параллелен одной из осей. В этом случае формулы заметно упрощаются, однако возможность задаться удобной системой координат имеется не всегда.

Поэтому для физических законов векторная форма находит самое широкое применение. Она имеет компактную однострочную форму, при этом описывая движение сразу по всем координатным осям.

Рис. 3. Векторный способ задания движения точки.

Что мы узнали?

В физике широкое применение находит векторный способ описания движения точки. Он имеет такую же точность, как координатный способ, но при этом учитывает сразу все координатные оси и записывается гораздо более компактно. Поэтому такой способ описания движения очень подходит для законов и формул: он позволяет выделить суть закона, не загромождая формулировку.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 143.

---

А какая ваша оценка?

Теоретическая механика (Голубева О.В.)

Теоретическая механика (Голубева О.В.)

Голубева О. В. Теоретическая механика. Изд-во «Высшая школа». Учебник составлен в соответствии с программой и содержит изложение теоретической механики и элементов специальной теории относительности. Первая часть — «Кинематика» посвящена изложению кинематики точки, произвольной системы и твердого тела. Вторая — центральная часть «Кинетика» включает в себя постулаты классической механики, динамику точки, вопросы приведения системы сил (элементы статики), основные теоремы и законы динамики систем, элементы динамики твердого тела, механики точки переменной массы и удара. В эту часть входит динамика голономных систем, основные принципы механики и теория малых колебаний системы. Последний раздел «Элементы специальной теории относительности» рассматривается как современное развитие и обобщение Ньютонианской механики. В учебнике даны элементы векторной алгебры, анализа и понятие многомерных векторов (тензора первого ранга). Рассмотренные примеры носят принципиальный характер и относятся к естественно научным вопросам (задача двух тел, маятник Фуко, закон Бера и т. д.) и вопросам теоретической физики (формула Резерфорда, теория осциллятора, двойной маятник и т. д.). Предназначается для студентов физико-математических факультетов педагогических институтов. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИЗА § 1. Векторные величины и некоторые операции над ними § 2. Вектор-функция Часть I. КИНЕМАТИКА § 1. Предмет теоретической механики и ее основные понятия § 2. Уравнение движения точки и ее траектория § 3. Скорость точки § 4. Ускорение точки § 5. Проекции ускорения на естественные оси § 6. Частные случаи движепия точки. Физический смысл тангенциального и нормального ускорения точки § 7. Уравнения движения точки в криволинейных координатах. Проекция скорости и ускорения на осн криволинейных координат ГЛАВА 2. КИНЕМАТИКА НЕСВОБОДНОЙ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК § 1. Механические системы и классификация связей § 2. Ограничения на скорость и ускорение, налагаемые геометрическими связями § 3. Число степеней свободы системы. Обобщенные координаты уравнения движения системы, обобщенные скорости ГЛАВА 3. КИНЕМАТИКА ТВЕРДОГО ТЕЛА ИЛИ НЕИЗМЕНЯЕМОЙ СРЕДЫ § 1. Уравнения движения абсолютно твердого тела § 2. Поступательное движение твердого тела § 3. Вращение твердого тела вокруг неподвижной оси § 4. Вращение тела около неподвижной точки. Теорема Даламбера § 5. Общий случай движения свободного твердого тела. Теорема Шаля Б. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ И ТВЕРДОГО ТЕЛА ГЛАВА 4 ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 2. Сложение скоростей § 3. Сложение ускорений ГЛАВА 5. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 2. Сложение вращений § 3. Плоскопараллельное движение твердого тела § 4. Кривошипно-шатупный механизм Часть II. КИНЕТИКА § 1. Вектор силы § 2. Тяжелая масса тел § 3. Закон инерции. Инерциальные системы координат § 1. Основной закон механики (второй закон Ньютона). Инертная масса. Принцип независимости действия сил § 5. Закон равенства действия и противодействия (третий закон Ньютона) Б. ДИНАМИКА ТОЧКИ § 1. Динамика точки и ее две основные задачи § 2. Характеристика сил § 3. Дифференциальные уравнения движения § 4. Определение уравнения движения точки по заданной силе § 5. Определение силы по заданному уравнению движения § 6. Интегрирование дифференциальных уравнений движения точки в случае сил частного вида ГЛАВА 8. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 1. 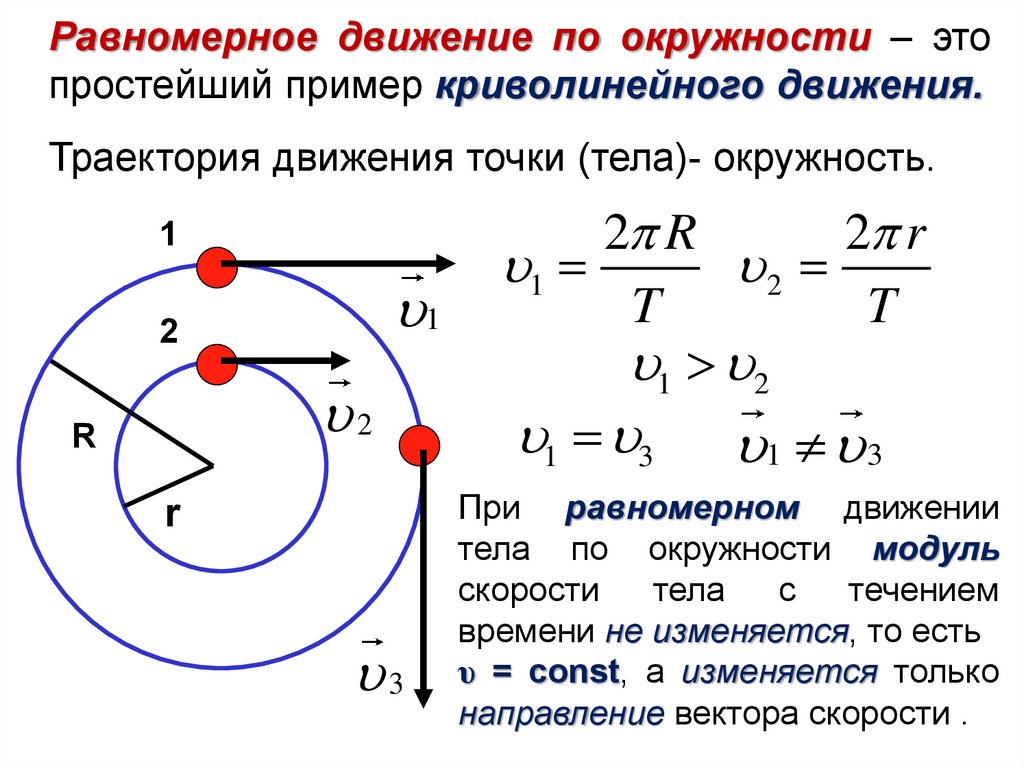Уравнение движелия материальной точки в неинерциальной системе координат § 2. Координатные системы, связанные с Землей § 3. Отклонение падающих тел от вертикали ГЛАВА 9. ДВИЖЕНИЕ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ § 1. Характерные особенности движения точки иод действием центральной силы § 2. Уравнения движения точки, находящейся под действием центральной силы § 3. Закон всемирного тяготения § 4. Задача двух тел § 5. Движение электрона в поле ионизированного атома (центральная отталкивающая сила) Б. СТАТИКА ГЛАВА 10. СТАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 2. Активные силы и силы реакции связей § 3. Система сходящихся сил § 4. Система параллельных сил § 5. Центр тяжести и центр масс § 6. Момент силы относительно точки и относительно оси § 7. Свойства пары сил § 8. Приведение произвольной системы сил § 9. Равновесие произвольной системы сил, действующих на твердое тело § 10. Раваовесне системы материальных точек Г. ДИНАМИКА СИСТЕМЫ ГЛАВА 11. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ В ИНЕРЦИАЛЬНОЙ СИСТЕМЕ КООРДИНАТ И ИХ ПЕРВЫЕ ИНТЕГРАЛЫ § 2. Принцип Даламбера. Основные уравнения диижения системы § 3. Теорема о количестве движения системы § 4. Теорема импульсов § 5. Теорема о количестве движения центра инерции системы и примеры ее применения § 6. Теорема о кинетическом моменте ГЛАВА 12. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ КООРДИНАТ § 1. Теорема о количестве движения в неинерциальной системе координат § 2. Теорема о кинетическом моменте в неинерциальной системе координат § 3. Законы сохранения § 4. Уравнения движения в расчетной системе координат Д. КОНСЕРВАТИВНЫЕ СИЛЫ ГЛАВА 13. РАБОТА СИЛЫ. ПОТЕНЦИАЛЬНОЕ ПОЛЕ § 2. Силовое поле и его частный случай — потенциальное поле § 3. Работа внутренних сил, действующих в системе ГЛАВА 14. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ § 1. Теорема о кинетической энергии и закон сохранения механической энергии точки § 2. 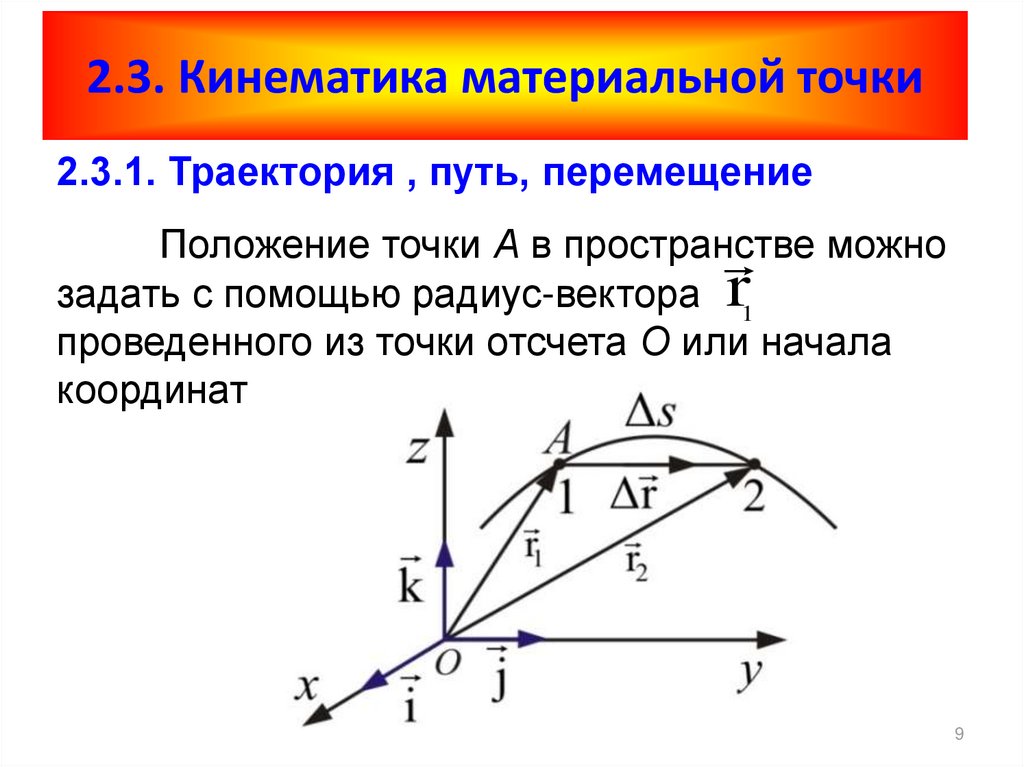Теорема о кинетической энергии системы § 3. Формула Кенига § 4. Закон сохранения механической энергии системы Е. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА § 1. Кинетический момент твердого тела в частных случаях его движения § 2. Вычисление моментов инерции относительно параллельных осей § 3. Эдлипсоид инерции ГЛАВА 16. ДИНАМИКА ПРОСТЕЙШИХ ВИДОВ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 2. Вращение твердого тела вокруг неподвижной оси § 3. Физический и математический маятники ГЛАВА 17. ДИНАМИКА ТЕЛА, ВРАЩАЮЩЕГОСЯ ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТЕЛА § 1. Кинематические уравнения Эйлера Углы Эйлера § 2. Динамические уравнения Эйлера § 3. Постановка задачи о движении твердого тела вокруг неподвижной точки § 4. Регулярная прецессия гироскопа § 5. Приближенная теория гироскопа § 6. Общий случай движения твердого тела Ж. ПРИМЕНЕНИЕ ОСНОВНЫХ УРАВНЕНИЙ ДИНАМИКИ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ВОПРОСАМ МЕХАНИКИ ГЛАВА 18. ДВИЖЕНИЕ ТОЧКИ ПЕРЕМЕННОЙ МАССЫ § 2. Примеры применения уравнения Мещерского. Задачи Циолковского ГЛАВА 19. УДАР § 1. Основное уравнение теории удара § 2. Гипотеза Ньютона § 3. Абсолютно упругий удар точки о сферу § 4. Прямое центральное соударение двух тел З. ДИНАМИКА СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ (АНАЛИТИЧЕСКАЯ МЕХАНИКА) ГЛАВА 20. ЗАДАЧА О ДВИЖЕНИИ СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ § 2. Перемещения и число степенен свободы системы § 3. Идеальные связи (основной постулат аналитической механики) § 4. Уравнения Лагранжа первого рода ГЛАВА 21. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА § 2. Уравнения Лагранжа второго рода § 3. Уравнения Лагранжа второго рода, как уравнения движения точки в 3n-мерном пространстве § 4. Уравнения Лагранжа второто рода для частных случаев сил, действующих на систему § 5. Первые интегралы уравнений движения ГЛАВА 22. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА § 2. Канонические уравнения Гамильтона 3. Первые интегралы канонических уравнений § 4. Скобки Пуассона § 5. Метод Рауса ГЛАВА 23. ОБЩИЕ ПРИНЦИПЫ МЕХАНИКИ § 2. Принцип Лагранжа — Даламбера и принцип виртуальных перемещений Лагранжа § 3. Вариационный интегральный принцип Гамильтона — Остроградского И. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ ГЛАВА 24. ПРЯМОЛИНЕЙНОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ § 2. Свободные колебания точки при наличии сопротивления среды § 3. Вынужденные колебания точки § 4. Резонанс ГЛАВА 25. ОБЩИЕ УРАВНЕНИЯ МАЛЫХ КОЛЕБАНИЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ § 2. Устойчивое равновесие консервативной системы § 3. Уравнения малых колебаний механических систем § 4. Малые колебания системы с одной степенью свободы ГЛАВА 26. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ § 2. Собственные колебания системы § 3. Главные координаты § 4. Вынужденные колебания системы с двумя степенями свободы § 5. Двойной математический маятник Часть III. УРАВНЕНИЯ МЕХАНИЧЕСКИХ ДВИЖЕНИИ ТОЧЕК СО СКОРОСТЯМИ, БЛИЗКИМИ К СКОРОСТИ СВЕТА (ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ) ГЛАВА 27. ВВЕДЕНИЕ В СПЕЦИАЛЬНУЮ ТЕОРИЮ ОТНОСИТЕЛЬНОСТИ § 2. Элементарные сведения об ортогональных преобразованиях ГЛАВА 28. СВОЙСТВА ПРОСТРАНСТВА И ВРЕМЕНИ ПРИ СКОРОСТЯХ ТОЧЕК, СРАВНИМЫХ СО СКОРОСТЬЮ СВЕТА (ПЕРВЫЙ ЗАКОН НЬЮТОНА В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ) § 1. Порвый закон Ньютона и свойства пространства и времени ньютонианской маханики § 2. Преобразования Лоренца § 3. Свойства пространства и времени при относительном движении координатных систем, сравнимых со скоростью света § 4. Преобразование скорости и ускорения (теорема сложения скоростей Эйнштейна) ГЛАВА 29. ВТОРОЙ ЗАКОН НЬЮТОНА В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 2. Второй закон Ньютона в специальной теории относительности § 3. Уравнение энергии в специальной теории относительности § 4. Закон взаимной связи массы и энергии ГЛАВА 30. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 2. Уравнения движения механических систем ГЛАВА 31. РЕЛЯТИВИСТСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ. 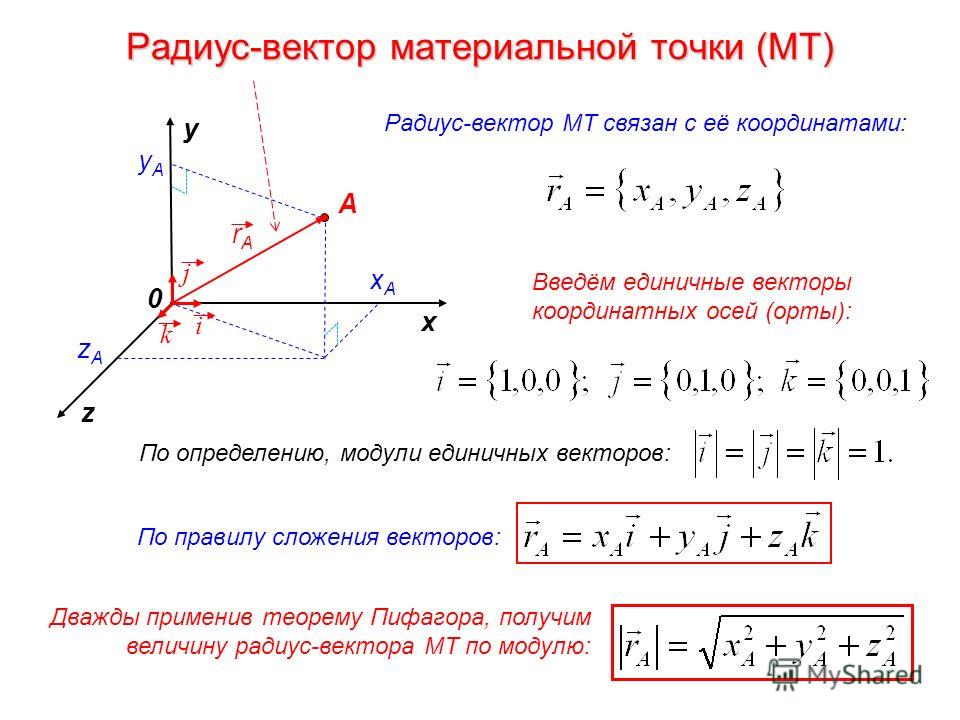РЕЛЯТИВИСТСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ § 1. Релятивистские уравнения движения точки в криволинейных координатах § 2. Релятивистские уравнения движения связных механических систем

(а) уравнение траектории точки y(x), график этой функции, (б) зависимость от времени векторов скорости v и ускорения w, а также модулей этих величин, (в) зависимость от времени угла α между векторами w и v, (d) вектор средней скорости, усредненный за первые t секунд движения, и модуль этого вектора.

И.Э. ​​ИРОДОВ, Л.А. СЕНА И С.С. КРОТОВ-ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ-Релятивистская механика

21 видео

РЕКЛАМА

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

Обновлено: 27 июня 2022 г.

Текстовое решение

Ответ

Правильный ответ: (a) y=−x2b/a2; б) v=ai−2btj, w=−2bj, v=√a2+4b2t2, w=2b; (в) tanα=a/2bt; (г) ⟨v⟩=ai−btj, |⟨v⟩|=√a2+b2t2.

Решение

As →r=at→l−bt2→j
Итак, x=at, y=−bt2
и, следовательно, y=−bx2a2
, что соответствует уравнению. параболы, график которой показан на рис.
(b) As vevr=at→l−bt2→j
→v=d→rdt=a→i−2bt→j (1)
Итак, v=√a2(−2bt)2=√a2+4b2t2
Дифф. уравнение (1) в.р.т. времени, мы получаем
→w=d→vdt=−2b→j
Итак, |→w|=w=2b
(c) cosα=→v⋅→wvw=(1→i−2bt→j)⋅( −2b→j)(√a2+4b2t2)2b
или, cosα=2bt√a2+4b2t2
, поэтому tanα=a2bt
или α=tan−1(a2bt)
(d) Вектор средней скорости
<→ v>=∫→vdt∫dt=t∫0(a→i−2bt→j)dtt=a→i−bt→j
Следовательно, |<→v>|=√a2+(−bt)2=√a2 +b2t2

Ответить

Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.

---

Похожие видео

Радиус-вектор точки A относительно начала координат изменяется со временем t как →r=atˆi−bt2ˆj, где a и b являются постоянными.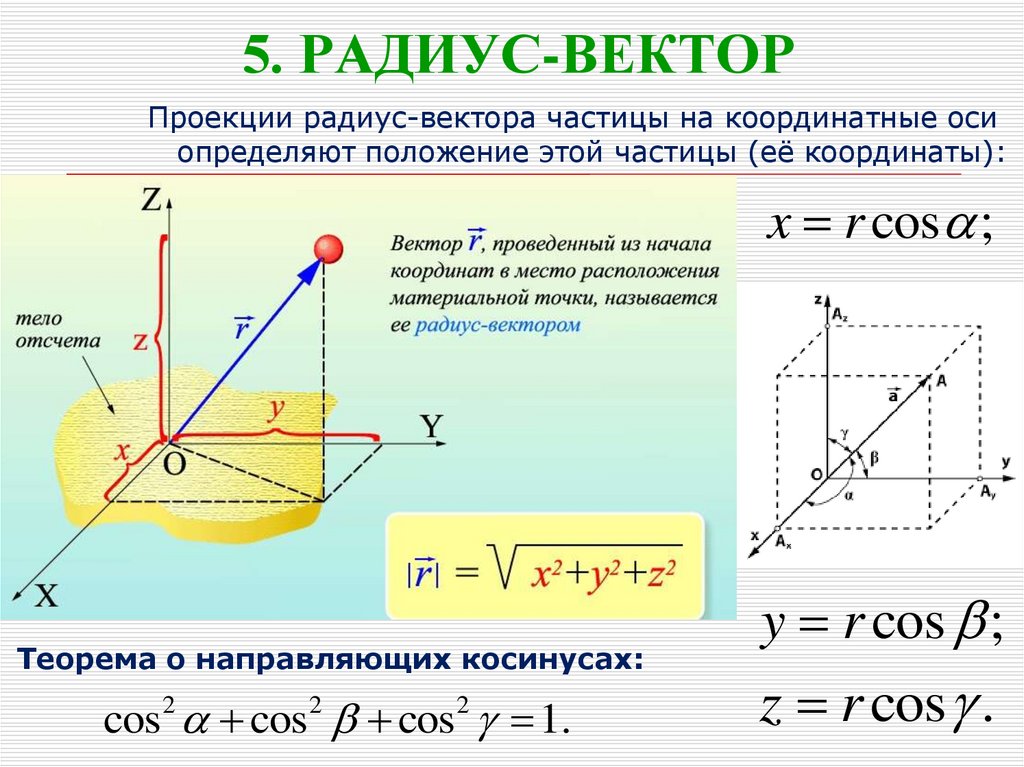 Уравнение траектории точки есть.

11745530

Радиус-вектор частицы изменяется со временем t как r=at(1−αt), где a — постоянный вектор, а α — положительный множитель. Найти:
(а) скорость v и ускорение w частиц как функции времени,
(б) интервал времени Δt, за который частица возвращается в исходные точки, и расстояние s, пройденное за это время.

12305798

Точка движется в плоскости xy по закону x=at, y=at(1−αt), где a и α — положительные постоянные, t — время. Найти:
(а) уравнение траектории точки y(x), построить эту функцию,
(б) скорость v и ускорение точки w как функции времени,
(в) момент t0, в который вектор скорости образует угол π/4 с вектором ускорения.

12305803

Частица движется в плоскости xy со скоростью v=ai+bxj , где i и j — орты осей x и y, a и b — константы. В начальный момент времени частица находилась в точке x=y=0 . Найти: а) уравнение траектории частицы у(х) , б) радиус кривизны траектории как функцию от х.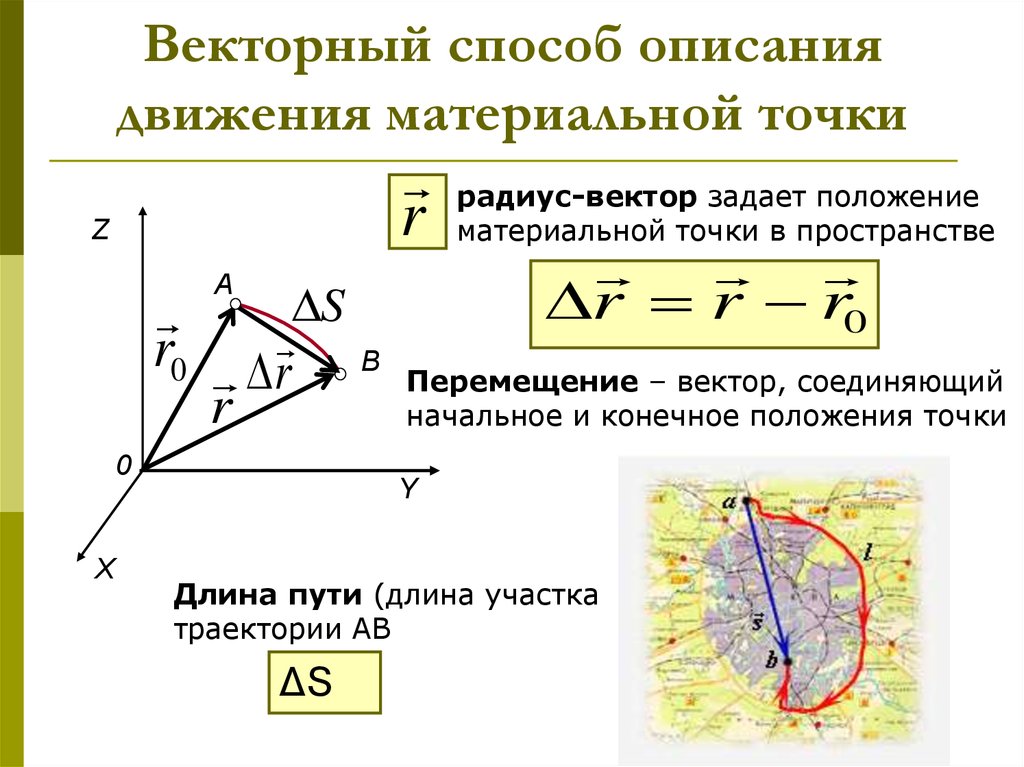 93, а i и j являются единичными векторами осей x и y. Найти: а) модули угловой скорости и углового ускорения в момент t=10,0 с, б) угол между векторами угловой скорости и углового ускорения в этот момент.

12305838

Вектор положения частицы определяется как vec(r ) = k cos omega hat(i) + k sin omega hat(j) = x hat(i) + yhat(j) , где k и omega константы и время t. Найдите угол между вектором положения и вектором скорости. Также определите траекторию частицы.

13025350

Вектор ardius точки A относительно начала координат изменяется со временем t как →r=atˆj−bt2ˆj, где a и b — константы. Найдите уравнение траектории точки.

15088846

Точка движется в плоскости xy в соответствии с уравнением x = at, y = at (l – bt), где a и b – положительные постоянные, а t – время. Момент, в который вектор скорости находится на уровне π/4 с вектором ускорения, определяется как:

16828149

Радиус-вектор точки зависит от времени t, как r = c t +(b t^(2))/(2) где c и b — постоянные векторы.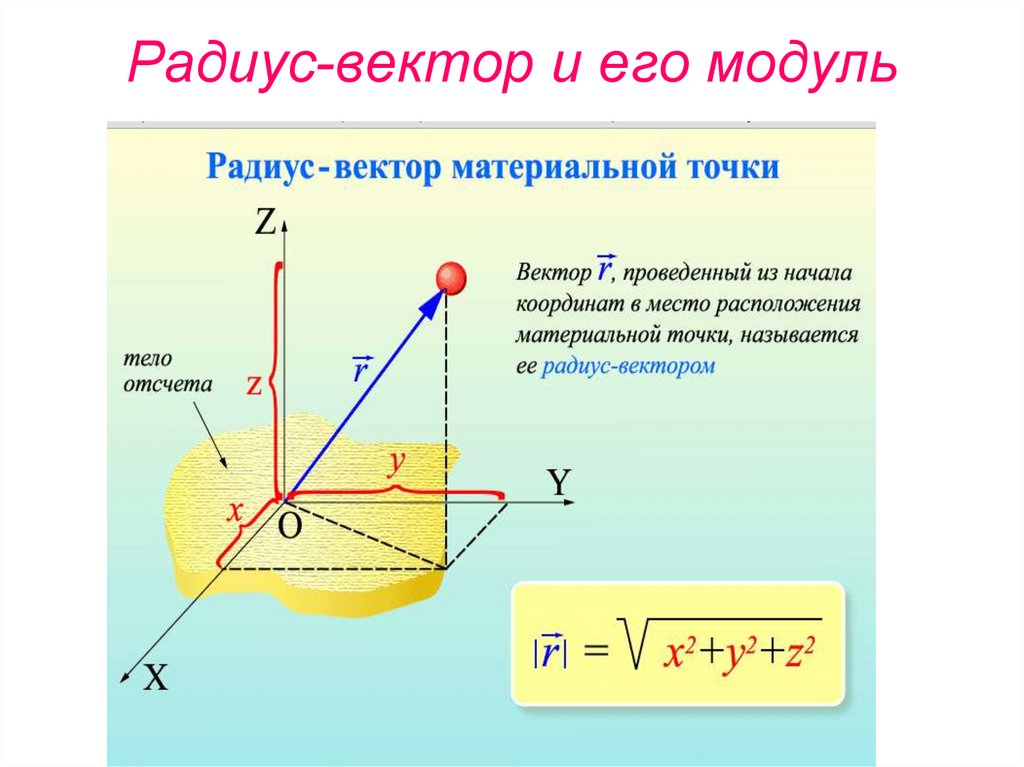 Найдите модуль скорости и ускорения в любой момент времени t. 9(2))/(2) где c и b — постоянные векторы. Найдите модуль скорости и ускорения в любой момент времени t.

643193044

Радиус-вектор точки A относительно начала координат изменяется со временем t как →r=atˆi−bt2ˆj, где a и b постоянны. Уравнение траектории точки есть.

644112405

Карта механики — анализ относительного движения (вектор)

В этом разделе представлено относительное движение с использованием векторной записи.

Анализ относительного движения — это один из методов, используемых для анализа тел, совершающих общее плоскостное движение . Общее плоское движение — это движение, при котором тела могут одновременно поступать и вращаться. Помимо анализа относительного движения, альтернативой является анализ абсолютного движения. Любой из этих методов можно использовать для решения любой общей задачи плоского движения, однако один метод может быть значительно проще в применении в определенных ситуациях.

Абсолютный анализ движения требует вычислений и, как правило, выполняется быстрее для простых задач и задач, где требуются только скорости (а не ускорения). Анализ относительного движения не требует исчисления, но требует использования нескольких систем координат и, как правило, его легче использовать для более сложных задач и задач, в которых анализируются скорости и ускорения.

Чтобы начать обсуждение анализа относительного движения, мы собираемся представить себе простую роботизированную руку, такую ​​как показанная ниже. В этой руке у нас есть две секции руки фиксированной длины с двигателями, вызывающими вращение в суставах A и B.

Этот робот-манипулятор имеет фиксированное основание в A и две секции руки фиксированной длины (AB и BC), которые управляются через моторы в суставах A и B. Конечный эффектор манипулятора находится в точке C.

Первым шагом в анализе относительного движения является разбиение движения на простые этапы и назначение поступательной системы координат (с направлениями x и y), прикрепленной к точек интереса вдоль твердых тел. Обратите внимание, что эта система координат будет перемещаться вместе с точкой интереса, но будет , а не вращаются вместе с объектом. (Мы будем использовать вращающиеся системы координат позже для более сложных задач в методе вращающихся реперов). Обычно мы начинаем с точки с известным движением (или с фиксированной точки) и продвигаемся оттуда шаг за шагом. В случае с нашей роботизированной рукой мы знаем, что сустав А не будет двигаться, поэтому мы начинаем с него. Определим скорость в точке В (относительно точки А), а затем в точке С (относительно точки В).

Ниже приведено изображение манипулятора с нарисованными системами координат.

В анализе относительного движения этого манипулятора используются две системы координат. Одна система координат в A является фиксированной системой (из которой рассматривается абсолютное движение), а одна поступательная система координат присоединена к B (точка как на AB, так и на BC). Эта трансляционная система координат перемещается с точкой на твердом теле, к которому они прикреплены, но не вращаются вместе с твердым телом.

Для анализа относительного движения мы можем определить скорость или ускорение конечной точки руки (C) относительно земли (A), найдя ускорение скорости B относительно A и добавив скорость или ускорение C по отношению к B, так же, как мы делали это с частицами. Обратите внимание, что скорости, которые относятся к фиксированной системе координат, часто обозначаются одним нижним индексом и считаются абсолютными скоростями и ускорениями.

Скорость:	\[\vec{v}_{C/A}=\vec{v}_{B/A}+\vec{v}_{C/B}\]
или	\[\vec{v}_{C}=\vec{v}_{B}+\vec{v}_{C/B}\]
Ускорение:	\[\vec{a}_{C/A}=\vec{a}_{B/A}+\vec{a}_{C/B}\]
или	\[\vec{a}_{C}=\vec{a}_{B}+\vec{a}_{C/B}\]

Уравнения анализа относительного движения, приведенные выше, предназначены для движения, состоящего из двух частей (в нашем примере рука состоит из двух частей), но мы можем легко расширить приведенное выше уравнение на три, четыре или даже больше частей для более сложных механизмов. добавление дополнительных шагов в левую часть нашего уравнения.

Чтобы использовать приведенные выше уравнения, нам нужно будет подставить известную нам информацию. Подстановка скоростей или ускорений, заданных как часть задачи для любых конкретных точек, — хорошее место для начала. Если бы, например, была задана скорость точек B или C, мы бы подставили ее для v _B или v _C соответственно. Помните, что точка A — это наша фиксированная точка на земле, поэтому v _C — это скорость точки C относительно земли, а v _C/B — это скорость точки C относительно точки B. Если какая-либо точка зафиксирована (кроме нашей исходной точки на земле, которая всегда будет фиксированной) мы также можем подставлять нули как для скорости, так и для ускорения этой точки. Помните, что приведенное выше уравнение является векторным уравнением, поэтому эти скорости имеют как величину, так и направление.

В некоторых случаях нам нужно проанализировать несколько точек на одном или нескольких твердых телах. Для этого используется другое обозначение:

Позиция:	\[\vec{r_B} = \vec{r_A} + \vec{r_{B/A}}\]
Скорость:	\[\vec{v_B} = \vec{v_A} + \vec{v_{B/A}} = \vec{v_A} + \vec{\omega} \times \vec{r_{B/A}} \]
Ускорение:	\[\vec{a_B} = \vec{a_A} + \vec{a_{B/A}} = \vec{a_A} + \vec{\alpha} \times \vec{r_{B/A}} + \vec{\omega} \times (\vec{\omega} \times \vec{r_{B/A}}) \]

В этом обозначении A и B являются двумя точками на одном твердом теле. Когда мы используем только один нижний индекс, он указывает положение/скорость/ускорение этой точки относительно фиксированной системы координат. Поскольку тело жесткое, расстояние между двумя точками не изменится, но вектор положения между ними может изменить ориентацию (отсюда и относительная скорость между двумя точками). Омега — это угловая скорость этого твердого тела (аналог тета-точки), а альфа — угловое ускорение этого твердого тела (аналог тета-двойной точки). 92 \vec{r_{B/A}} \] Как и ранее, этот манипулятор имеет фиксированное основание в точке A и две секции манипулятора фиксированной длины (AB и BC), которые управляются моторами в соединениях A и B. Концевой эффектор манипулятора находится в точке C.

Все векторы будут определены относительно координат x и y в показанной системе координат, а не радиального и тета-направлений, как указано выше.

Если мы хотим найти скорость и ускорение конечной точки С, зная угловые скорости и ускорения, мы найдем следующие соотношения:

Скорость в точке B:	\[\vec{v_B} = \vec{v_A} + \vec{\omega_{AB}} \times \vec{r_{B/A}}\]
Скорость в точке C:	\[\vec{v_C} = \vec{v_B} + \vec{\omega_{BC}} \times \vec{r_{C/B}}\] \[= \vec{v_A} + \vec{ \omega_{AB}} \times \vec{r_{B/A}} + \vec{\omega_{BC}} \times \vec{r_{C/B}}\]
Ускорение в точке B:	\[\vec{a_B} = \vec{a_A} + \vec{\alpha_{AB}} \times \vec{r_{B/A}} – \omega_{AB}^2 \vec{r_{B} /А}} \] 92 \vec{r_{C/B}} \]

Как только мы получим все в нашем векторном уравнении, мы разобьем векторное уравнение на компоненты x и y, чтобы найти любые неизвестные.