PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
 2 Термодинамика
2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
-
5.
 3 Фотометрия
3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
Физика Скорость равномерного прямолинейного движения. Уравнение равномерного прямолинейного движения
youtube.com/embed/lHkn_pE3M8g” frameborder=”0″ allowfullscreen=””>Материалы к уроку
3. Скорость равномерного прямолинейного движения. Уравнение равномерного прямолинейного движения.doc
64 KBСкачать3. Скорость равномерного прямолинейного движения. Уравнение равномерного прямолинейного движения.ppt
12.81 MBСкачать
Конспект урока
Наиболее простой вид движения – это прямолинейное равномерное движение.
Движение точки называется равномерным, если оно за любые равные промежутки времени проходит одинаковые пути.
Равномерное движение бывает двух видов: криволинейное и прямолинейное.
Прямолинейное движение.
Основной величиной, которая характеризует движение тела, является скорость его перемещения. Понятие скорость хорошо известно всем, даже тем, кто не изучал физику. Улитка движется со скоростью гораздо меньшей, чем человек, а гепард может перемещаться со скоростью значительно большей скорости человека. Однако научные достижения человека позволяют ему создавать технические средства, которые позволяют ему двигаться со скоростью гораздо большей, нежели скорость самых быстрых живых существ. Это и машины, и самолет, и ракеты с реактивным двигателем. Самой большой скорости относительно Земли человек достигает с помощью космических ракет.
Понятие скорость хорошо известно всем, даже тем, кто не изучал физику. Улитка движется со скоростью гораздо меньшей, чем человек, а гепард может перемещаться со скоростью значительно большей скорости человека. Однако научные достижения человека позволяют ему создавать технические средства, которые позволяют ему двигаться со скоростью гораздо большей, нежели скорость самых быстрых живых существ. Это и машины, и самолет, и ракеты с реактивным двигателем. Самой большой скорости относительно Земли человек достигает с помощью космических ракет.
В механике рассматривают скорость как векторную величину. А это означает лишь то, что скорость можно считать определенной только тогда, когда мы знаем ее модуль и направление.

Что же такое скорость равномерного прямолинейного движения точки? Допустим, что тело, двигаясь равномерно и прямолинейно в течение некоторого промежутка времени, передвигается из положения М1 в положение М2, совершив при этом перемещение ( .
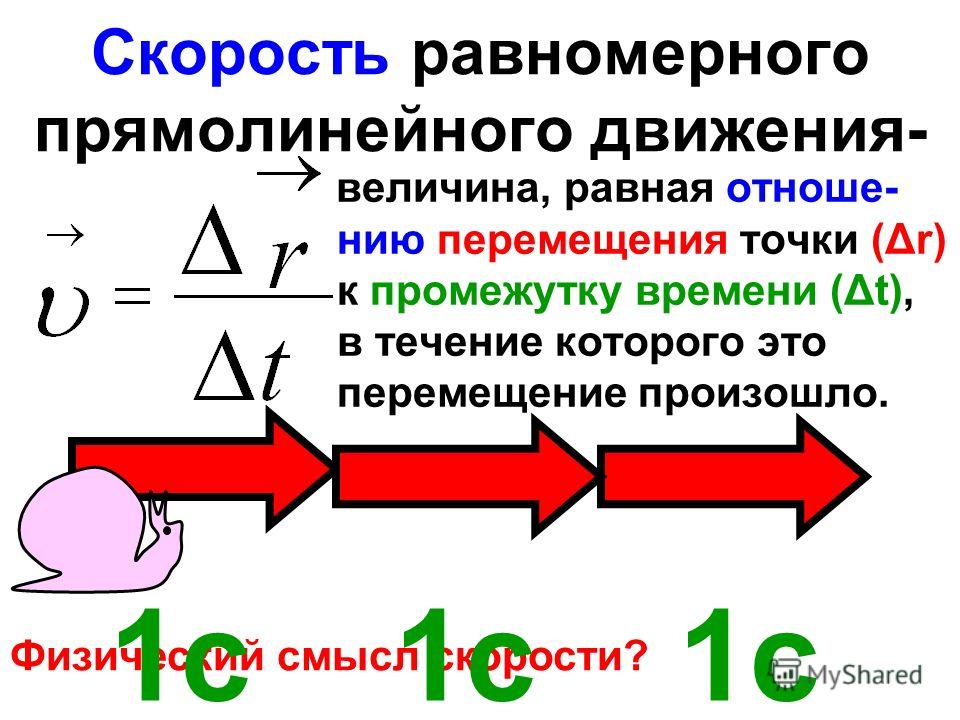
Вычислим отношение этого перемещения к промежутку времени, в течение которого это перемещение произошло. В результате будем иметь вектор, потому что если мы разделим вектор на скаляр, то результатом будет тоже вектор. Этот вектор получил название – скорость равномерного прямолинейного движения точки.
Скоростью равномерного прямолинейного движения точки называется величина, которая равна отношению перемещения к промежутку времени, в течение которого происходило это перемещение.
Скорость – это векторная величина, так как она равна отношению вектора к скаляру. Промежуток времени – величина положительная, поэтому направление вектора скорости будет таким же, как и направление вектора перемещения.

Модуль перемещения есть расстояние, пройденное телом за время. Так как тело движется равномерно, то модуль отношения перемещения ко времени, а значит, и модуль скорости, есть величина, численно равная расстоянию, пройденному телом за единицу времени.
Получим уравнение равномерного прямолинейного движения точки. Для этого воспользуемся определением скорости.

Если начальный момент времени t0 принять равным нулю, то вектор скорости равен отношению изменения радиус-вектора ко времени.
Из этого выражения мы можем выразить значение радиус-вектора в момент времени t.
Можно записать уравнение равномерного прямолинейного движения точки координатным способом. Для этого достаточно вместо векторного уравнения равномерного прямолинейного движения записать три соответствующих ему уравнения в проекциях на координатные оси. Радиус-вектор – это сумма двух векторов: радиус-вектора начального момента времени и произведения вектора скорости на время. Из этого можно сделать вывод, что проекции радиус-вектора на координатные оси должны быть равны сумме проекций этих векторов на те же самые координатные оси.

Выберем координатные оси таким образом, чтобы тело двигалось по одной из осей, к примеру, по оси ОХ. Тогда вектор r0 и вектор скорости составят с осями ОY и ОZ, угол равный 90 градусам. Из этого делаем вывод, что их проекции на эти оси равны нулю. Значит, равны нулю в любой момент времени и проекции радиус-вектора на оси ОY и ОZ.
Проекции радиус-вектора на координатные оси равны координатам его конца, поэтому в проекциях на ось ОХ уравнение равномерного прямолинейного движения можно записать в следующем виде: координата точки равна начальной координате плюс произведение проекции вектора скорости и времени. Это и есть уравнение равномерного прямолинейного движения точки, которое записано в координатной форме. Оно позволяет рассчитать координату х тела во время движения в любой момент времени, в том случае, если известны проекция его скорости на ось ОX и его начальная координата х0.
Подставляя это выражение в уравнение равномерного прямолинейного движения точки, записанное в координатной форме, получаем путь, пройденный телом, равен произведению вектора скорости на время.
Полученные результаты для наглядности изобразим на графике. Наиболее прост в понимании график, показывающий зависимость проекции скорости от времени. Эта прямая проходит параллельно оси времени. Площадь прямоугольника ОАВС, заштрихованная на рисунке, равна изменению координаты точки за время t. Ведь сторона ОА есть проекция вектора скорости, а сторона ОС – время движения t, поэтому путь, пройденный телом, равен произведению проекции вектора скорости на время.
Вы видите рисунок, на котором приведены примеры графиков зависимости координаты от времени для трех различных случаев равномерного прямолинейного движения.
Прямая 1 соответствует случаю, когда начальная координата точки равна нулю, проекция вектора скорости на ось ОХ больше нуля, то есть движение точки сонаправлено с осью ОХ.

Прямая 2 соответствует случаю, когда начальная координата точки меньше нуля, проекция вектора скорости на ось ОХ положительна. То есть точка движется вдоль прямой ОХ в сторону тела отсчета.
Прямая 3 соответствует случаю, когда начальная координата точки больше нуля, проекция вектора скорости отрицательна. Это означает, что точка движется вдоль оси ОХ в сторону, противоположную направлению оси.
Угол наклона α(альфа)2 прямой 2 больше, чем угол наклона α1 прямой 1. Значит, точка, график зависимости координаты от времени которой представлен прямой 1, за один и тот же промежуток времени пройдет расстояние меньшее, чем точка, представленная прямой 2. Поэтому можно сделать вывод, что точка 1 движется медленней, чем точка 2. Скорость точки 1 меньше, чем скорость точки 2.
Угол наклона α3 прямой 3 отрицательный. Это говорит о том, что движение происходит в сторону, противоположную оси ОХ.
Равномерного прямолинейного движения в природе не существует.
 Даже по самой гладкой автомагистрали автомобиль не сможет двигаться абсолютно прямо, в его движении всегда будут небольшие отклонения в какую-либо сторону. В этом случае направление вектора скорости автомобиля будет изменяться. Небольшая неровность асфальта, порыв ветра, чуть-чуть большее нажатие на педаль акселератора и другие, казалось бы, незначительные причины вызывают небольшие изменения модуля вектора скорости. Но если рассматривать движение автомобиля приближенно на протяжении небольшого промежутка времени, то движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений реальности, которое позволяет без больших усилий описывать многие движения.
Даже по самой гладкой автомагистрали автомобиль не сможет двигаться абсолютно прямо, в его движении всегда будут небольшие отклонения в какую-либо сторону. В этом случае направление вектора скорости автомобиля будет изменяться. Небольшая неровность асфальта, порыв ветра, чуть-чуть большее нажатие на педаль акселератора и другие, казалось бы, незначительные причины вызывают небольшие изменения модуля вектора скорости. Но если рассматривать движение автомобиля приближенно на протяжении небольшого промежутка времени, то движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений реальности, которое позволяет без больших усилий описывать многие движения.При неравномерном движении формула скорости является формулой средней скорости. При решении большинства задач описывать движение с помощью этой величины неудобно. Например, вычисленная по этой формуле средняя скорость современного военного самолета-истребителя оказывается равной нулю, потому что равно нулю его перемещение: самолет начинает и заканчивает свое движение в одной и той же точке на аэродроме.
 В то же время в полете приборы этого самолета фиксируют значения скорости, составляющие несколько тысяч километров в час.
В то же время в полете приборы этого самолета фиксируют значения скорости, составляющие несколько тысяч километров в час.В практических целях удобнее применять величину, называемую средней путевой скоростью или просто средней скоростью, которая равна отношению всего пройденного пути ко всему затраченному времени.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Вывод уравнений смещения и скорости гравитации Рона Куртуса
SfC Home > Physics > Gravity >
Рон Куртус
Вы можете вывести гравитационные уравнения для взаимосвязи между смещением и скоростью объекта, движущегося в вертикальном направлении, начиная с полученных уравнений скорость-время и смещение-время.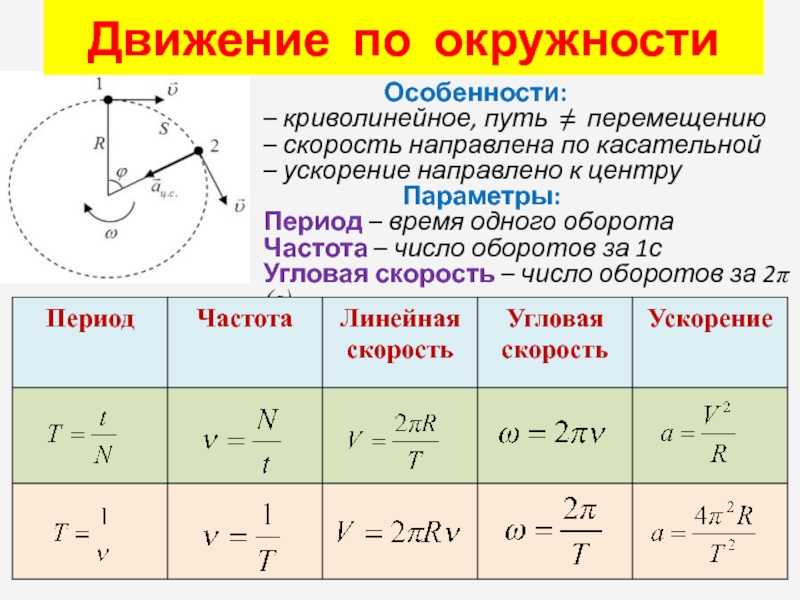
Примечание : Перемещение — векторная величина, обозначающая изменение положения в заданном направлении. Скорость — это вектор, указывающий скорость изменения положения в заданном направлении.
См. уроки “Вывод уравнений гравитации скорость-время” и “Вывод уравнений гравитации смещения-времени” .
Подставляя соотношение времени в уравнение перемещения, вы можете определить перемещение относительно скорости. Затем из полученного уравнения смещения вы можете определить уравнение для скорости, когда объект достигает заданного смещения от начальной точки.
На полученные уравнения влияет начальная скорость объекта. Это важно в последующих приложениях уравнений.
У вас могут возникнуть следующие вопросы:
- Что лежит в основе выводов?
- Что такое перемещение для данного уравнения скорости?
- Какова скорость для данного уравнения смещения?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц измерения
Полезный инструмент: Преобразование единиц измерения
Основа для расчета скорости перемещения
Чтобы определить перемещение от начальной точки при заданной скорости, начните с уравнений:
t = (v − v i )/г
(Получено из уравнения скорости гравитации во времени )
и
y = gt 2 /2 + v i t
( Получено из уравнения гравитации перемещения во времени )
где
- t – время в секундах (с)
- v вертикальная скорость в м/с или фут/с
- v i — начальная вертикальная скорость в м/с или футах/с
- g ускорение свободного падения (9,8 м/с 2 или 32 фут/с 2 )
- y — вертикальное смещение от начальной точки в м или футах
Примечание : Начальная скорость — это скорость, с которой объект освобождается после ускорения с нулевой скорости.
Начальная скорость не возникает мгновенно.
Подставив уравнение для t в уравнение для y , вы можете получить перемещение относительно скорости. Затем, решив это уравнение для v , вы получите скорость относительно уравнения смещения.
Зависимость смещения от скорости
Вывод смещения для заданной скорости
Чтобы вывести уравнение смещения, вы можете начать с уравнения времени:
t = (v − v i )/г
Возведение в квадрат обеих частей уравнения:
t 2 = (v − v i ) 2 /г 2
т 2 = (v 2 − 2vv i + v i 2 )/г 2
Рассмотрим уравнение смещения:
y = gt 2 /2 + v i t
Замените t 2 и t из приведенных выше уравнений:
y = g (v 2 − 2vv i + v i 2 )/2g 2 + v i (v − v i )/г
Умножьте v i (v − v i )/g на 2/2 и объедините одинаковые члены:
y = (v 2 − 2vv i + v i 2 )/2g + 2(vv i − v i 2 0 0 9 0 0 7 7 2
y = (v 2 − 2vv i + v i 2 + 2vv i − 2v i 2 )/2 г
Результирующее общее уравнение гравитации для смещения относительно скорости:
y = (v 2 − v i 2 )/2g
Получение скорости для заданного смещения
Чтобы получить скорость для заданного смещения, умножьте обе части числа
у = (v 2 – v i 2 )/2g на 2g и решить для v :
2gy = (v 2 − v i 2 )
v 2 = 2gy + v i 2
Возьмите квадратный корень из обеих частей уравнения, чтобы получить общее уравнение гравитации для скорости по отношению к перемещению:
v = ±√(2gy + v i 2 )
где
- ± означает плюс или минус
- √(2gy + v i 2 ) — квадратный корень из числа (2gy + v i 2 )
Резюме
Гравитационное уравнение для смещения объекта от начальной точки до достижения заданной скорости может быть получено из уравнений t = (v − v i )/g и y = gt 2 /2 + v i t . Это приводит к уравнению для скорости, когда объект достигает заданного смещения от начальной точки.
Это приводит к уравнению для скорости, когда объект достигает заданного смещения от начальной точки.
Производные уравнения:
y = (v 2 − v i 2 )/2g
v = ±√(2gy + v i 2 )
Будьте наблюдательны и любопытны
Ресурсы и ссылки
Рон Куртус «Условия
Веб -сайты
Гравитационные ресурсы
Падающие тела – Physics Hypertextbook
Уравнения для падения – Wikipedia
.(Примечание: Школа чемпионов может получать комиссионные за покупку книг)
Книги с самым высоким рейтингом по Simple Gravity Science
Книги с самым высоким рейтингом по продвинутой физике гравитации
Вопросы и комментарии
У вас есть вопросы, комментарии или мнения по этой теме? Если это так, отправьте электронное письмо с вашим отзывом. Я постараюсь вернуться к вам как можно скорее.
Я постараюсь вернуться к вам как можно скорее.
Поделиться этой страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_derivations_displacement_velocity.htm
Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.
Copyright © Ограничения
Где ты сейчас?
Школа Чемпионов
Гравитационные темы
Вывод уравнений перемещения-скорости гравитации
Перемещение, время и средняя скорость: значения и формулы
«Мы уже там?» Если вы когда-либо были пассажиром в ужасно долгом путешествии на летние каникулы или каникулы, вы знаете, насколько важны каждые миль. Возможно, вы попросили своего водителя немного ускориться, зная, что можете прибыть в пункт назначения немного раньше. И когда ответ на этот вопрос был ” Н о!” , возможно, вы изучали свой запланированный маршрут, ища более короткий путь, чтобы получить несколько дополнительных минут удовольствия.
Возможно, вы попросили своего водителя немного ускориться, зная, что можете прибыть в пункт назначения немного раньше. И когда ответ на этот вопрос был ” Н о!” , возможно, вы изучали свой запланированный маршрут, ища более короткий путь, чтобы получить несколько дополнительных минут удовольствия.
Даже самые, казалось бы, простые сценарии движения, такие как скучная поездка в гораздо менее скучный тематический парк, сводятся к набору фундаментальных величин кинематики. Ваше путешествие к пониманию того, как устроен мир, начинается с изучения того, как движутся самые основные системы: почему физическое положение в пространстве, направление движения, скорость движения и время имеют значение. В этой статье мы рассмотрим определения, а также соответствующие формулы и примеры смещения, расстояния, времени и средней скорости. Прежде чем вы это узнаете, вы гораздо лучше поймете все причины ответа, «Мы доберемся, когда доберемся!»
Определение смещения в физике
Возможно, наиболее легко наблюдаемым аспектом движения являются изменения положения во времени. Всякий раз, когда вы встаете со стула и идете на кухню, едете на автобусе из дома в школу или идете от входной двери к почтовому ящику, вы меняете физическое положение своего тела в пространстве. Мы понимаем эту концепцию позиционного изменения как смещение.
Всякий раз, когда вы встаете со стула и идете на кухню, едете на автобусе из дома в школу или идете от входной двери к почтовому ящику, вы меняете физическое положение своего тела в пространстве. Мы понимаем эту концепцию позиционного изменения как смещение.
Смещение — общее изменение положения объекта.
Перемещение является векторной величиной: оно имеет направление и величину.
Есть несколько способов измерить смещение. Мы можем использовать стандартную декартову координатную плоскость и вычислить разницу между различными точками. В качестве альтернативы мы можем рассчитать изменения положения различных зданий, городов, штатов или стран относительно друг друга на карте. Мы даже можем использовать координаты GPS. Независимо от того, как вы решите измерять, вам нужно помнить, чтобы сначала определить начало координат, положительное и отрицательное направления — не зная этих деталей, вы можете получить неверный расчет!
Расстояние по сравнению с перемещением
Вы должны быть хорошо знакомы с понятием расстояния от путешествий в повседневной жизни. Вы, наверное, знаете, сколько миль нужно, чтобы добраться до продуктового магазина от вашего дома, дома друга или члена большой семьи или другого места, которое вы часто посещаете. Теперь давайте определим, что мы подразумеваем под расстоянием в контексте физики.
Вы, наверное, знаете, сколько миль нужно, чтобы добраться до продуктового магазина от вашего дома, дома друга или члена большой семьи или другого места, которое вы часто посещаете. Теперь давайте определим, что мы подразумеваем под расстоянием в контексте физики.
Расстояние равно величине смещения.
Расстояние является скалярной величиной: оно имеет величину, но не имеет направления.
Теперь расстояние иногда путают с термином пройденного расстояния.
Пройденное расстояние — это длина пути от начала до конца.
Итак, в чем разница между всеми этими терминами? В отличие от смещения, которое может иметь отрицательное, положительное или нулевое значение, измерения расстояния всегда неотрицательны . Если это звучит немного запутанно, давайте проведем быстрый мысленный эксперимент. Представьте, что вы бегун, участвующий в гонке \(400\,\mathrm{m}\). Звучит пушка, и вы начинаете пробираться по трассе к финишу. Теперь длина вашего пути от начала до конца равна \(400\,\mathrm{m}, \), однако смещение от начала до конца равно \(0\,\mathrm{m} \) в каждом направлении.
Теперь длина вашего пути от начала до конца равна \(400\,\mathrm{m}, \), однако смещение от начала до конца равно \(0\,\mathrm{m} \) в каждом направлении.
Почему? Ну, ваша общая позиция не изменилась, так как вы закончили в той же позиции, что и начали. В результате расстояние между началом и концом также равно \(0\,\mathrm{m} \), поскольку расстояние является величиной смещения, а величина нуля равна нулю.
Рис. 1. Гонка на треке как пример зависимости пройденного расстояния от расстояния.
Формулы расстояния и смещения
Теперь, когда мы разобрались с различиями между расстоянием и перемещением, давайте посмотрим на формулы, которые нам нужно знать. Запишем формулу смещения математически как
\begin{align*} \text{смещение} &=\text{конечная позиция} – \text{начальная позиция} \\ \Delta x&=x_\text{f}-x_\text{i}, \ end{align*}
, где \(x_\text{i}\) — начальная позиция, а \(x_\text{f}\) — конечная позиция. Греческая буква \(\Дельта\), произносимая как «Дельта», указывает на изменение некоторой переменной .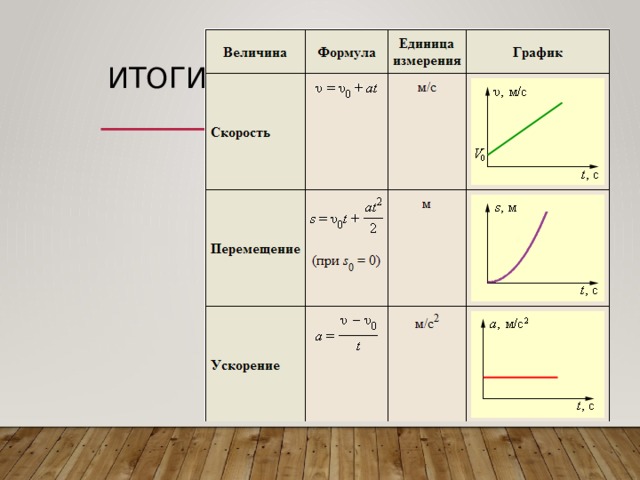 Таким образом, под \(\Delta x\) мы подразумеваем изменение положения или перемещение.
Таким образом, под \(\Delta x\) мы подразумеваем изменение положения или перемещение.
Если вы знаете длину каждого отрезка пути по прямой между несколькими парами точек, вы можете вычислить расстояние, просто найдя сумму всех отдельных длин. Мы также можем вычислить расстояние \(d\) между двумя точками на двумерной плоскости, используя формулу: 92.}} \end{align*}
Проще говоря, мы вычисляем величину вектора смещения , что приводит к скалярной величине. И расстояние, и перемещение измеряются в единицах длины с соответствующей базовой единицей СИ в метрах, представленной символом \(\mathrm{m}\).
Давайте рассмотрим пример сравнения формул смещения и расстояния, чтобы увидеть, как эти расчеты могут сильно отличаться на практике.
Предположим, вам нужно пойти в местный зоомагазин за припасами, расположенный в пяти милях от вашего дома. Вы начинаете свое путешествие дома, едете на машине в магазин и возвращаетесь домой. Какой у вас пройденный путь и перемещение в конце пути?
Какой у вас пройденный путь и перемещение в конце пути?
Рис. 2: График, демонстрирующий расчеты расстояния, пройденного расстояния и перемещения для одной поездки.
Начнем с расчета пройденного расстояния. В этом случае вы проехали пять миль дважды, поэтому пройденное расстояние равно
\begin{align*} s &=\mathrm{5\, mi+5\, mi=10\, mi}. \end{align*}
Расстояние, которое вы преодолели от начала до конца поездки, составляет десять миль. Далее посчитаем смещение,
\begin{align*} \Delta x &= x_\text{f} – x_\text{i}=0\,\mathrm{mi} \end{align*}
Итак, несмотря на то, что вы проехали десять миль, ваше перемещение, как и расстояние, равно нулю миль, потому что вы оказались в том же положении, что и начали.
В предыдущем примере ваше перемещение равно нулю миль, потому что ваше начальное и конечное положения не изменились. Другими словами, ваше положение не изменилось с тех пор, как вы начали и закончили дома. Давайте рассмотрим другой пример, на этот раз с поездкой, заканчивающейся в позиции, отличной от исходной.
Давайте рассмотрим другой пример, на этот раз с поездкой, заканчивающейся в позиции, отличной от исходной.
Вместо этого скажем, что после посещения того же зоомагазина, что и раньше, вы решили пойти в обход. На этот раз вы начинаете из дома, едете в зоомагазин, посещаете пекарню, а затем едете в школу. Пекарня находится в трех милях от зоомагазина, а школа — в десяти милях от пекарни. Найдите пройденное расстояние и свое перемещение в конце пути. Также рассчитайте расстояние до начальной точки.
Рис. 3: График, демонстрирующий расчеты расстояния, пройденного расстояния и перемещения для многоэтапной поездки.
Опять же, давайте просуммируем длину между каждой позицией для трех этапов пути, чтобы узнать пройденное расстояние:
\begin{align*} s&=\mathrm{5\, mi+3\, mi+ 10\, ми=18\, ми}. \end{align*}
Наконец, давайте найдем разницу в расположении между школой и домом, чтобы получить общее смещение:
\begin{align*} \Delta x &=\mathrm{-2\, mi-0\ , mi=-2\, mi}. \end{выравнивание*}
\end{выравнивание*}
У нас отрицательное значение смещения после этой поездки, потому что школа расположена слева от нашего дома, а мы выбрали положительное направление вправо. Теперь, чтобы вычислить расстояние, мы должны взять величину нашего смещения следующим образом:
$$\begin{align}\mathrm{distance}&=|-2\,\mathrm{mi}| =2\,\mathrm{mi}\end{align}.$$
Наше расстояние в конце этой поездки до исходной позиции равно \( 2\,\mathrm{mi} \).
Смещение в предыдущем примере равно \(\mathrm{-2\, mi}\), поскольку и зоомагазин, и пекарня расположены на положительной оси \(x\) справа от \(x=0 \,\mathrm{mi}\), а школа расположена на отрицательной оси \(x\). Школа находится в двух милях от вашего дома, но в противоположном направлении от зоомагазина и пекарни. Давайте рассмотрим еще один пример сравнения вычислений расстояния и смещения.
В предыдущих примерах исходной позицией был ваш дом. Если ваше начальное положение — школа, найдите расстояние и чистое перемещение для поездки, начинающейся в школе, посещающей пекарню и заканчивающейся в зоомагазине.
Опять же, начиная с расчета расстояния:
\begin{align*} d&=\mathrm{10\, mi+3\, mi=13\, mi}.\end{align*}
И, наконец, расчет смещения:
\begin{align*} \Delta x &=8\, \mathrm{mi}-(-2\,\mathrm{mi})=10\, \mathrm{mi}. \end{выравнивание*}
На этот раз наше смещение от начала координат положительное.
Давайте вспомним, что мы уже узнали о расстоянии и смещении.
- Расстояние представляет собой величину смещения и всегда неотрицательна.
- Пройденное расстояние — это длина пути от начала до конца.
- Расстояние не учитывает направление и является скалярной величиной.
- Смещение — это изменение положения между двумя точками, которое может быть нулевым, положительным или отрицательным.
- Перемещение зависит от направления и является векторной величиной.
Формула времени в физике
Понятие времени уже стало очень привычной частью повседневной жизни. У вас есть школьное расписание для смены занятий в определенные часы дня, будильник, установленный на определенный час, чтобы вставать по утрам, и представление о том, какую часть дня будут занимать определенные задачи. В физике время является важной переменной для понимания всех видов физических систем, и, в частности, его можно наблюдать по изменению некоторой величины.
У вас есть школьное расписание для смены занятий в определенные часы дня, будильник, установленный на определенный час, чтобы вставать по утрам, и представление о том, какую часть дня будут занимать определенные задачи. В физике время является важной переменной для понимания всех видов физических систем, и, в частности, его можно наблюдать по изменению некоторой величины.
Время — это измерение того, сколько времени требуется для события или наблюдаемого изменения.
Мы измеряем время в секундах, \(\mathrm{s}\), так как это основная единица времени в системе СИ. В практическом смысле, например, во время лаборатории, мы измеряем течение времени секундомером или обычными часами. Мы также можем определить время, пройденное движущимся объектом, используя формулу
\begin{align} \mathrm{time} &=\frac{\text{пройденное расстояние}}{\text{скорость}}, \\t& =\фрак{с} {v}. \end{выравнивание}
Конечно, время является скалярной величиной, математически определяемой с использованием других скалярных величин и измеряемой относительно предыдущей отметки времени, выбранной на часах. Мы понимаем, что время постоянно движется вперед, без отрицательного направления или эквивалента, и нет возможности отменить то, что уже было сделано в прошлом. Мы используем время как меру того, как долго длилось событие.
Мы понимаем, что время постоянно движется вперед, без отрицательного направления или эквивалента, и нет возможности отменить то, что уже было сделано в прошлом. Мы используем время как меру того, как долго длилось событие.
Определение средней скорости
Объект, положение которого изменяется, имеет измеримую скорость изменения, известную как скорость.
Скорость — скорость изменения положения.
Скорость — это еще один способ сказать: «Объект перемещается на это большое расстояние за каждую единицу времени». Средняя скорость — это просто средняя скорость изменения положения за весь период времени, в отличие от i мгновенной скорости , которая измеряется в определенный момент времени с использованием заданной функции скорости.
Скорость против скорости
Так же, как существует ключевое различие между расстоянием и перемещением, такое же различие существует для скорости и скорости.
Скорость — величина скорости.
Скорость описывает, насколько быстро объект перемещается в пространстве относительно времени или какое расстояние объект преодолевает за определенный период времени. В повседневном языке мы могли бы использовать термины «скорость» и «скорость» взаимозаменяемо, но в физике мы делаем важное различие между ними. Скорость — скалярная величина, числовое значение без направления, а скорость — векторная величина, имеющая как величину, так и направление.
Формулы скорости и средней скорости
В зависимости от имеющейся системы и заданных начальных условий существует несколько формул, которые мы можем использовать в физике для определения средней скорости и скорости. Простейшая формула для средней скорости:
\begin{align*} \text{средняя скорость} &= \frac{\text{смещение}}{\text{прошедшее время}}, \\ v_{\mathrm{avg }}&=\frac{\Delta x}{\Delta t}, \\ v_{\mathrm{avg}}&=\frac{x_\text{f} – x_\text{i}}{t_\text {f} – t_\text{i}}. \end{выравнивание*}
\end{выравнивание*}
Мы можем рассчитать среднюю скорость движущегося объекта, используя аналогичную формулу:
\begin{align*}\text{средняя скорость}&= \frac{\text{пройденное расстояние}}{\text{истекшее время} } =\frac{s}{t}.\end{align*}
И скорость, и скорость измеряются в единицах \(\mathrm{\frac{длина}{время}}\), наиболее распространенная единица измерения будучи \ (\ mathrm {\ frac {m} {s}} \). Давайте рассмотрим краткий пример расчета скорости движущегося автомобиля.
Обратите внимание, что пройденное расстояние обозначается \( с. \)
Допустим, вы ведете машину и проехали \( 10,2 \) миль за \( 25 \) минут. Какая у вас средняя скорость в милях в час?
Во-первых, мы хотим преобразовать \(\mathrm{25\, min}\) в \(\mathrm{h}\):
\begin{align*} \mathrm{\frac{1\, h} {60\, мин}\умножить на 25\, мин=0,42\, ч}. \end{align*}
Далее, мы хотим использовать формулу для средней скорости и решить:
\begin{align*} \text{средняя скорость}&=\frac{s}{t}, \\ & = \ mathrm {\ frac {10,2 \, mi} {0,42 \, h}}, \\ & = 24 \, \ mathrm {\ frac {mi} {h}}. \end{выравнивание*}
\end{выравнивание*}
Таким образом, ваша средняя скорость равна \(24\, \mathrm{ми}/ч\). Поскольку скорость является скалярной величиной, мы ожидали, что этот ответ будет неотрицательным, так что это хорошо.
Давайте рассмотрим пример расчета средней скорости с использованием уравнения для средней скорости.
Вы бежите \( 100.1\,\mathrm{m} \) к автобусной остановке, но бросаете блокнот на \( 72\,\mathrm{m}. \) Затем бежите обратно, чтобы забрать его в \ ( 23\,\mathrm{s}. \) Найдите свою среднюю скорость за 23-секундный интервал времени.
Рассчитаем скорость, используя \(x_\text{i}=0\, \mathrm{m}\) и \(x_\text{f}=72\, \mathrm{m}\):
\ begin{align*} v_\mathrm{avg}&=\frac{\Delta x}{\Delta t}, \\ v_\mathrm{avg}&=\mathrm{\frac{72\, m-0\, m}{23\, s}}, \\ v_\mathrm{avg}&=\mathrm{3.1\, \frac{m}{s}}. \end{align*}
Теперь, какой будет ваша средняя скорость, если вы также бросите перо в исходное положение и побежите за ним? Скажем, вам потребуется дополнительно \( 18\,\mathrm{s} \), чтобы вернуться в исходное положение.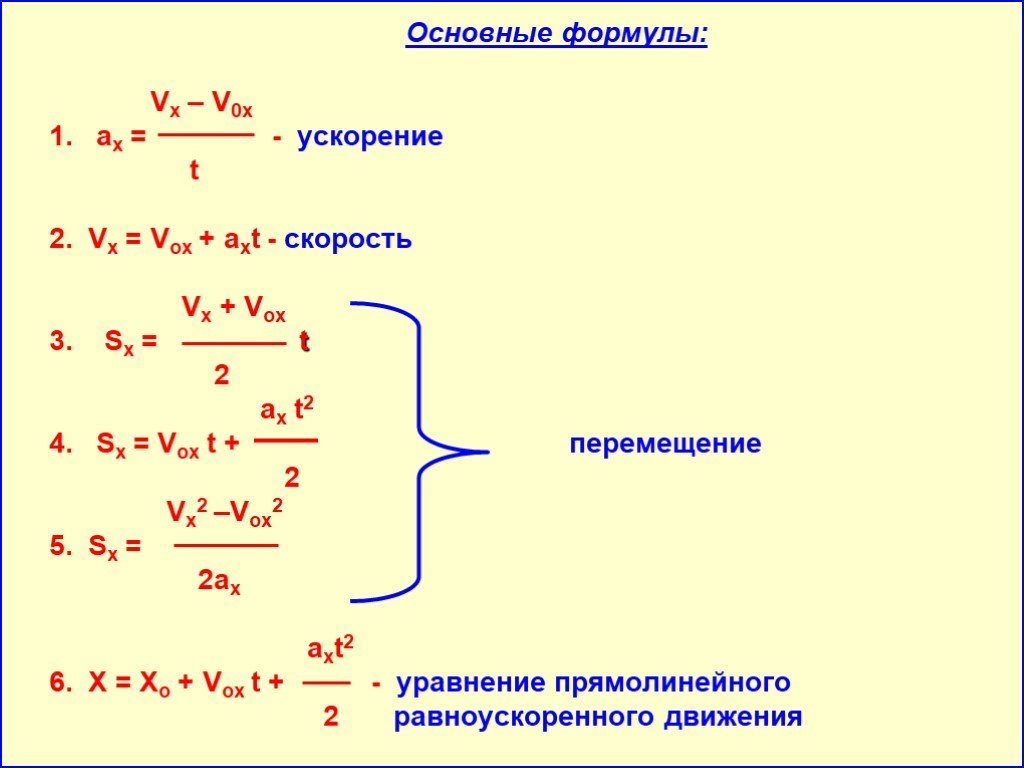 Давайте рассчитаем среднюю скорость вашего бега до автобусной остановки и обратно, чтобы забрать свой блокнот и ручку.
Давайте рассчитаем среднюю скорость вашего бега до автобусной остановки и обратно, чтобы забрать свой блокнот и ручку.
На этот раз общее истекшее время равно \(\mathrm{23\, с+18\, с=41\, с}\). Теперь найдем вашу среднюю скорость:
\begin{align*} v_\mathrm{avg}&=\mathrm{\frac{0\, m-0\, m}{41\, s}} \\ v_ \mathrm{avg}&=\mathrm{0\, \frac{m}{s}}. \end{align*}
Поскольку для этого расчета мы использовали только конечные точки, обе из которых равны нулю, средняя скорость также равна нулю. Какова средняя скорость? Используя формулу для средней скорости, при общем пройденном расстоянии \(\mathrm{200,2\, м}\) от бега туда и обратно между автобусной остановкой, мы получаем
\begin{align*} \text{средняя скорость}=\mathrm{\frac{200,2\, м}{41\, с}} =4,9\, \mathrm{\frac{м}{с}}. \end{align*}
Чтобы закончить наше обсуждение средней скорости, давайте кратко рассмотрим нахождение скоростей на графике.
График средней скорости
В дополнение к численному решению средней скорости также полезно графически отображать различные переменные движения, чтобы визуализировать проблему. Мы можем использовать позицию – временной график в качестве инструмента для изучения скорости объекта с учетом функции положения. Давайте используем следующий график, чтобы попрактиковаться в нахождении скорости между несколькими разными точками кривой.
Мы можем использовать позицию – временной график в качестве инструмента для изучения скорости объекта с учетом функции положения. Давайте используем следующий график, чтобы попрактиковаться в нахождении скорости между несколькими разными точками кривой.
Рис. 4: График положения в зависимости от времени, где наклон между любыми двумя точками равен средней скорости.
Мы можем найти среднюю скорость, рассчитав наклон между двумя точками на кривой. Рассчитаем среднюю скорость для трех разных отрезков графика по двум точкам с графика. Мы будем использовать нашу формулу \(v_{\mathrm{avg}}=\frac{\Delta x}{\Delta t}\) для каждого расчета.
Сначала найдем среднюю скорость между второй точкой \((4,8)\) и четвертой точкой \((12,2)\):
\begin{align*} v_{\mathrm{avg }} = \ mathrm {\ frac {2 \, m-8 \, m} {12 \, s-4 \, s} = -0,8 \, \ frac {m} {s}}. \end{align*}
Здесь средняя скорость отрицательна, и на графике мы видим нисходящий тренд. Далее найдем среднюю скорость между третьей точкой \((8,6)\) и пятой точкой \((18, 6)\):
Далее найдем среднюю скорость между третьей точкой \((8,6)\) и пятой точкой \((18, 6)\):
\begin{align*} v_{\mathrm{avg}} = \mathrm{\frac{6\, m-6\, m}{18\, s-8\, s}=0\, \frac{m}{s}}. \end{выравнивание*}
Средняя скорость равна нулю, поскольку положение не изменяется. Наконец, посчитаем среднюю скорость между точками один \((1, 3)\) и два \((4,8)\):
\begin{align*} v_{\mathrm{avg}}= \mathrm {\ гидроразрыва {8 \, м-3 \, м} {4 \, с-1 \, с} = 2 \, \ гидроразрыва {м} {с}}. \end{align*}
Между точками один и два наблюдается восходящий тренд, поэтому средняя скорость положительна.
Смещение, время и средняя скорость — основные выводы
Смещение — это общее изменение положения объекта.
Расстояние — это величина смещения.
Пройденное расстояние — это длина пути от начала до конца.
Время — это мера того, сколько времени занимает событие или наблюдаемое изменение.


 2 Термодинамика
2 Термодинамика
 3 Фотометрия
3 Фотометрия
 Начальная скорость не возникает мгновенно.
Начальная скорость не возникает мгновенно.