Уравнения движения тела формула: §6. Примеры движения тела. Методы решения задач. — ЗФТШ, МФТИ

§6. Примеры движения тела. Методы решения задач. — ЗФТШ, МФТИ

Рассмотрим некоторые характерные примеры движения тела, знание которых будет полезно при дальнейшем изучении физики.

1.Равномерное прямолинейное движение тела.

При равномерном прямолинейном движении тело совершает равные перемещения `Delta vecr`  за одинаковые промежутки времени  `Delta t`. Иными словами, скорость  `vec v` тела не зависит от времени и остаётся постоянной в процессе движения:

При этом зависимость `vec r(t)` имеет вид:

где  `vec r_0`  –  радиус-вектор тела в начальный момент времени  $$ t=0$$ . В этой связи вспомним замечание о начальных условиях, сделанное в §4.  Вектор  $$ {\overrightarrow{r}}_{0}$$  здесь является тем начальным условием, которое позволяет однозначно определить радиус-вектор $$ \overrightarrow{r}$$ тела в любой момент времени в процессе движения.

Векторное уравнение (7) равносильно системе двух скалярных уравнений, выражающих зависимость от времени $$ t $$ координат $$ x$$ и $$ y$$ движущегося тела:

где $$ {x}_{0}$$ и $$ {y}_{0}$$ – начальные координаты тела в момент времени $$ t=0$$, а $$ {v}_{x}$$ и $$ {v}_{y}$$ -проекции вектора скорости `vecv` на координатные оси $$ Ox$$ и $$ Oy$$ соответственно.  

Траектория равномерного прямолинейного движения тела графически представляет собой отрезок прямой линии (рис. 9), тангенс угла наклона которой к оси абсцисс равен отношению проекций скорости на оси координат: $$ \mathrm{tg}\alpha ={v}_{y}/{v}_{x}$$. Аналитическое уравнение траектории, т. е. зависимость $$ y\left(x\right)$$, легко получить, исключив параметр $$ t$$ из системы уравнений (8):

2. Неравномерное движение тела.

Для неравномерного движения характерно то, что с течением времени изменяется скорость движущегося тела, а в общем случае и его ускорение. В качестве примера может служить движение, при котором тело проходит различные участки своего пути с разной скоростью. Такое движение принято характеризовать, прежде всего, средней путевой скоростью. Причём прилагательное «путевая» в условиях задач часто опускается.

Другим характерным примером неравномерного движения служит так называемое равнопеременное движение, которое целесообразно рассмотреть подробно, не выходя при этом за рамки школьной программы.

3. Равнопеременное движение.

Равнопеременным называется такое неравномерное движение, при котором скорость `vec v` за любые равные промежутки   времени   `Delta t`  изменяется  на  одинаковую  величину   `Deltavecv`. В этом случае ускорение `veca` тела не зависит от времени и остаётся постоянным в процессе движения:

(при этом `vec v != “const”`, и траектория движения не обязательно прямолинейная).
При равнопеременном движении скорость $$ \overrightarrow{v}$$ тела изменяется с течением времени по закону

где `vecv_0` – скорость тела в начальный момент времени `t=0`.
В свою очередь, зависимость `vecr(t)` имеет вид:

где `vecr_0` – начальный радиус-вектор тела при `t=0`. Вновь заметим, что величины `vecv_0` и `vecr_0` представляют собой начальные условия, позволяющие в любой момент времени однозначно определить векторы `vecv` и `vecr`.

При координатном способе описания равнопеременного движения векторным уравнениям (11) и (12), равносильны следующие системы уравнений для проекций скорости и радиус-вектора тела на оси выбранной системы отсчёта.

2)/(2a_x)`.

Удобство этой формулы заключается в том, что она не содержит времени $$ t$$ в явном виде. Вместе с тем надо помнить, что формула получена в предположении о неизменности направления движения тела.

Одним из наиболее наглядных примеров равнопеременного движения является движение тела в поле тяжести Земли, которое мы имеем возможность наблюдать повседневно. Для решения задач в этом случае надо заменить в приведённых выше формулах вектор $$ \overrightarrow{a}$$ на ускорение свободного падения $$ \overrightarrow{g}$$, сообщаемое силой гравитационного притяжения всякому телу, движущемуся в поле тяжести Земли. Рассмотрим три конкретных случая такого движения.

Движение тела, брошенного вертикально.
Тело бросили с поверхности земли, сообщив ему начальную скорость $$ {\overrightarrow{v}}_{0}$$ направленную вертикально вверх. Пренебрегая сопротивлением воздуха, определите время $$ \tau $$ полёта тела до момента падения на землю; скорость тела в момент падения; максимальную высоту $$ H$$ подъёма тела над землёй; время $$ {\tau }_{1}$$ подъёма тела на максимальную высоту; путь `S`, пройденный телом за время полёта и перемещение тела. {2}+\mathrm{tg}\alpha x$$. 

График траектории тела представляетсобой участок параболы, ветви которой направлены вниз.

 

Движение тела под углом к горизонту, теория и онлайн калькуляторы

Движение тела под углом к горизонту, теория и онлайн калькуляторы

Начальные условия

Рассмотрим движение тела (материальной точки) брошенного под углом к горизонту с некоторой высоты $h_0$. Начальная скорость тела равна ${\overline{v}}_0$, вектор ${\overline{v}}_0$ составляет угол $\alpha $ с горизонтом (рис.1). Систему отсчета, в которой движется тело, свяжем с Землей. Ось X направим параллельно земле, ось Y вертикально вверх.

Движение тела под углом к горизонту происходит в поле тяжести Земли под воздействием силы тяжести. Силой сопротивления воздуха пренебрежём. В этом случае ускорение тела ($\overline{a}$) совпадает с ускорением свободного падения ($\overline{g}$):

\[\overline{a}=\overline{g}\left(1\right),\]

где $g=9,8\ \frac{м}{с^2}$.

2\left(5\right).\]

Уравнение $y(x)$ (функция (5)) показывает, что тело движется по параболе в плоскости, в которой лежат векторы $\overline{g}$ и ${\overline{v}}_0.$

Уравнение скорости движения тела брошенного под углом к горизонту

В векторном виде уравнение для скорости движения рассматриваемого нами тела в произвольный момент времени запишем:

\[\overline{v}(t)={\overline{v}}_0+\overline{g}t\left(6\right).\]

В скалярном виде уравнение (6) представим в виде системы уравнений:

\[\left\{ \begin{array}{c} v_x\left(t\right)=v_0{cos \alpha ,\ } \\ v_y\left(t\right)=v_0{sin \alpha \ }-gt \end{array} \right.\left(7\right).\]

В системе уравнений (7) мы еще раз видим, что движение тела под углом к горизонту по оси X равномерное, по оси Y равнопеременное. Причем, двигаясь вверх, тело уменьшает свою скорость от $v_{0y}$ до нуля, затем падая вниз скорость тела увеличивается.

Модуль вектора скорости в производный момент времени для рассматриваемого нами движения найдем как:

\[v=\sqrt{v^2_x{+v}^2_y\ \left(8\right). 2_0\frac{{{cos \alpha \ }sin \alpha \ }}{2g}\to {\sin \alpha \ }={cos \alpha \ }\to \alpha =\frac{\pi }{4}.\]

Ответ. $\alpha =\frac{\pi }{4}$

Пример 2

Задание. Какова скорость падения тела брошенного под углом горизонта $\alpha $ со скоростью $v_0$? Если тело бросили с земли. Сопротивление воздуха можно не учитывать.

Решение. За основу решения задачи примем кинематическое уравнение для скорости движения тела в поле тяжести Земли:

\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\left(2.1\right).\]

Начальные условия движения нашего тела:

\[\left\{ \begin{array}{c} {\overline{s}}_0=0 \\ v_{0x}=v_0{cos \alpha ,\ } \\ v_{0y}=v_0{sin \alpha \ } \end{array} \right.\ \left(2.2\right).\]

В проекциях на оси X и Y уравнение (2.1):

\[\left\{ \begin{array}{c} v_x\left(t\right)=v_0{cos \alpha ,\ } \\ v_y\left(t\right)=v_0{sin \alpha \ }-gt \end{array} \right. 2_y\ }=v_0.\]

Ответ. При заданных условиях величина скорости падения равна модулю скорости бросания.

Читать дальше: динамика прямолинейного движения связанных тел.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Уравнение движения тела с постоянным ускорением формула. Скорость при движении с постоянным ускорением

Изучением классического механического движения в физике занимается кинематика. В отличие от динамики, наука изучает, почему движутся тела. Она отвечает на вопрос, как они это делают. В данной статье рассмотрим, и движение с постоянным ускорением.

Понятие об ускорении

Когда тело движется в пространстве, за некоторое время оно преодолевает определенный путь, который является длиной траектории. Чтобы рассчитать этот путь, пользуются понятиями скорости и ускорения.

Скорость как физическая величина характеризует быстроту во времени изменения пройденного пути. Скорость направлена по касательной к траектории в сторону перемещения тела.

Ускорение — это несколько более сложная величина. Говоря кратко, она описывает изменение скорости в рассматриваемый момент времени. Математическое определение ускорения выглядит так:

Чтобы яснее понять эту формулу, приведем простой пример: предположим, что за 1 секунду движения скорость тела увеличилась на 1 м/с. Эти цифры, подставленные в выражение выше, приводят к результату: ускорение тела в течение этой секунды было равно 1 м/с 2 .

Направление ускорения совершенно не зависит от направления скорости. Его вектор совпадает с вектором результирующей силы, которая вызывает

Следует отметить важный момент в приведенном Эта величина характеризует не только изменение скорости по модулю, но и по направлению. Последний факт следует учитывать в случае криволинейного движения. Далее в статье будет рассматриваться только прямолинейное движение.

Скорость при движении с постоянным ускорением

Ускорение является постоянным, если оно в процессе движения сохраняет свой модуль и направление. Такое движение называют равноускоренным или равнозамедленным — все зависит от того, приводит ли ускорение к увеличению скорости или к ее уменьшению.

В случае движения тела с постоянным ускорением определить скорость можно по одной из следующих формул:

Первые два уравнения характеризуют равноускоренное перемещение. Отличие между ними заключается в том, что второе выражение применимо для случая ненулевой начальной скорости.

Третье уравнение — это выражение для скорости при равнозамедленном движении с постоянным ускорением. Ускорение при этом направлено против скорости.

Графиками всех трех функций v(t) являются прямые. В первых двух случаях прямые имеют положительный наклон относительно оси абсцисс, в третьем случае этот наклон является отрицательным.

Формулы пройденного пути

Для пути в случае движения с ускорением постоянным (ускорение a = const) получить формулы несложно, если вычислить интеграл от скорости по времени. Проделав эту математическую операцию для записанных выше трех уравнений, мы получим следующие выражения для пути L:

L = v 0 *t + a*t 2 /2;

L = v 0 *t – a*t 2 /2.

Графиками всех трех функций пути от времени являются параболы. В первых двух случаях правая ветвь параболы возрастает, а для третьей функции она постепенно выходит на некоторую константу, которая соответствует пройденному пути до полной остановки тела.

Решение задачи

Двигаясь со скоростью 30 км/ч, автомобиль начал ускоряться. За 30 секунд он прошел расстояние 600 метров. Чему было равно ускорение автомобиля?

В первую очередь переведем начальную скорость из км/ч в м/с:

v 0 = 30 км/ч = 30000/3600 = 8,333 м/с.

Теперь запишем уравнение движения:

L = v 0 *t + a*t 2 /2.

Из этого равенства выразим ускорение, получим:

a = 2*(L – v 0 *t)/t 2 .

Все физические величины в этом уравнении известны из условия задачи. Подставляем их в формулу и получаем ответ: a ≈ 0,78 м/с 2 . Таким образом, двигаясь с ускорением постоянным, автомобиль за каждую секунду увеличивал свою скорость на 0,78 м/с.

Рассчитаем также (для интереса), какую скорость он приобрел через 30 секунд ускоренного движения, получаем:

v = v 0 + a*t = 8,333 + 0,78*30 = 31,733 м/с.

Полученная скорость равна 114,2 км/ч.

Движение. Теплота Китайгородский Александр Исаакович

Прямолинейное движение с постоянным ускорением

Такое движение возникает, согласно закону Ньютона, тогда, когда в сумме на тело действует постоянная сила, подгоняющая или тормозящая тело.

Хотя и не вполне точно, такие условия возникают довольно часто: тормозится под действием примерно постоянной силы трения автомашина, идущая с выключенным мотором, падает с высоты под действием постоянной силы тяжести увесистый предмет.

Зная величину результирующей силы, а также массу тела, мы найдем по формуле a = F /m величину ускорения. Так как

где t – время движения, v – конечная, а v 0 – начальная скорость, то при помощи этой формулы можно ответить на ряд вопросов такого, например, характера: через сколько времени остановится поезд, если известна сила торможения, масса поезда и начальная скорость? До какой скорости разгонится автомашина, если известна сила мотора, сила сопротивления, масса машины и время разгона?

Часто нам бывает интересно знать длину пути, пройденного телом в равномерно-ускоренном движении. Если движение равномерное, то пройденный путь находится умножением скорости движения на время движения. Если движение равномерно-ускоренное, то подсчет величины пройденного пути производится так, как если бы тело двигалось то же время t равномерно со скоростью, равной полусумме начальной и конечной скоростей:

Итак, при равномерно-ускоренном (или замедленном) движении путь, пройденный телом, равен произведению полусуммы начальной и конечной скоростей на время движения. Такой же путь был бы пройден за то же время при равномерном движении со скоростью (1/2)(v 0 + v ). В этом смысле про (1/2)(v 0 + v ) можно сказать, что это средняя скорость равномерно-ускоренного движения.

Полезно составить формулу, которая показывала бы зависимость пройденного пути от ускорения. Подставляя v = v 0 + at в последнюю формулу, находим:

или, если движение происходит без начальной скорости,

Если за одну секунду тело прошло 5 м, то за две секунды оно пройдет (4?5) м, за три секунды – (9?5) м и т.д. Пройденный путь возрастает пропорционально квадрату времени.

По этому закону падает с высоты тяжелое тело. Ускорение при свободном падении равно g , и формула приобретает такой вид:

если t подставить в секундах.

Если бы тело могло падать без помех каких-нибудь 100 секунд, то оно прошло бы с начала падения громадный путь – около 50 км. При этом за первые 10 секунд будет пройдено всего лишь (1/2) км – вот что значит ускоренное движение.

Но какую же скорость разовьет тело при падении с заданной высоты? Для ответа на этот вопрос нам понадобятся формулы, связывающие пройденный путь с ускорением и скоростью. Подставляя в S = (1/2)(v 0 + v )t значение времени движения t = (v ? v 0)/a , получим:

или, если начальная скорость равна нулю,

Десять метров – это высота небольшого двух- или трехэтажного дома. Почему опасно прыгнуть на Землю с крыши такого дома? Простой расчет показывает, что скорость свободного падения достигнет значения v = sqrt(2·9,8·10) м/с = 14 м/с? 50 км/ч, а ведь это городская скорость автомашины.

Сопротивление воздуха не намного уменьшит эту скорость.

Выведенные нами формулы применяются для самых различных расчетов. Применим их, чтобы посмотреть, как происходит движение на Луне.

В романе Уэллса «Первые люди на Луне» рассказывается о неожиданностях, испытанных путешественниками в их фантастических прогулках. На Луне ускорение тяжести примерно в 6 раз меньше земного. Если на Земле падающее тело проходит за первую секунду 5 м, то на Луне оно «проплывет» вниз всего лишь 80 см (ускорение равно примерно 1,6 м/с 2).

Прыжок с высоты h длится время t = sqrt(2h /g ). Так как лунное ускорение в 6 раз меньше земного, то на Луне для прыжка понадобится в sqrt(6) ? 2,45 раз больше времени. Во сколько же раз уменьшается конечная скорость прыжка (v = sqrt(2gh ))?

На Луне можно безопасно прыгнуть с крыши трехэтажного дома. В шесть раз возрастает высота прыжка, cделанного с той же начальной скоростью (формула h = v 2 /(2g )). Прыжок, превышающий земной рекорд, будет под силу ребенку.

Из книги Физика: Парадоксальная механика в вопросах и ответах автора Гулиа Нурбей Владимирович

4. Движение и сила

Из книги Новейшая книга фактов. Том 3 [Физика, химия и техника. История и археология. Разное] автора Кондрашов Анатолий Павлович

Из книги Теория Вселенной автора Этэрнус

Из книги Занимательно об астрономии автора Томилин Анатолий Николаевич

9. Движение Луны Луна обращается вокруг Земли с периодом в 27 дней 7 часов 43 минуты и 11,5 секунды. Этот период называется звездным, или сидерическим, месяцем. Точно с таким же периодом обращается Луна и вокруг собственной оси. Поэтому понятно, что к нам постоянно обращена

Из книги Эволюция физики автора Эйнштейн Альберт

Эфир и движение Принцип относительности Галилея справедлив для механических явлений. Во всех инерциальных системах, движущихся относительно друг друга, применимы одни и те же законы механики. Справедлив ли этот принцип и для немеханических явлений, особенно тех, для

Из книги Физика на каждом шагу автора Перельман Яков Исидорович

Движение по кругу Раскройте зонтик, уприте его концом в пол, закружите и бросьте внутрь мячик, скомканную бумагу, носовой платок – вообще что-нибудь легкое и неломкое. Произойдет нечто для вас неожиданное. Зонтик словно не пожелает принять подарка: мяч или бумажный ком

Из книги Движение. Теплота автора Китайгородский Александр Исаакович

Движение относительно Закон инерции приводит нас к выводу о множественности инерциальных систем. Не одна, а множество систем отсчета исключают «беспричинные» движения.Если одна такая система найдена, то сразу же найдется и другая, движущаяся поступательно (без

Из книги Системы мира (от древних до Ньютона) автора Гурев Григорий Абрамович

Движение по окружности Если точка движется по окружности, то движение является ускоренным, уже хотя бы потому, что в каждый момент времени скорость меняет свое направление. По величине скорость может оставаться неизменной, и мы остановим внимание именно на подобном

Из книги 1. Современная наука о природе, законы механики автора Фейнман Ричард Филлипс

Реактивное движение Человек движется, отталкиваясь от земли; лодка плывет потому, что гребцы отталкиваются веслами от воды; теплоход также отталкивается от воды, только не веслами, а винтами. Также отталкиваются от земли и поезд, идущий по рельсам, и автомашина, –

Из книги Фарадей. Электромагнитная индукция [Наука высокого напряжения] автора Кастильо Сержио Рарра

VI. Движение твердых тел Момент силы Попробуйте рукой привести во вращение тяжелое маховое колесо. Тяните за спицу. Вам будет тяжело, если вы ухватитесь рукой слишком близко к оси. Переместите руку к ободу, и дело пойдет легче.Что же изменилось? Ведь сила в обоих случаях

Из книги автора

Как выглядит тепловое движение Взаимодействие между молекулами может иметь большее или меньшее значение в «жизни» молекул.Три состояния вещества – газообразное, жидкое и твердое – различаются одно от другого той ролью, которую в них играет взаимодействие

Из книги автора

ПРЕВРАТИТЬ ЭЛЕКТРИЧЕСТВО В ДВИЖЕНИЕ Фарадей заметил в опытах Эрстеда одну маленькую деталь, которая, как казалось, содержала ключ к пониманию проблемы.Он догадался, что магнетизм электрического тока всегда отклоняет стрелку компаса в одну сторону. Например, если

На данном уроке, тема которого: «Уравнение движения с постоянным ускорением. Поступательное движение», мы вспомним, что такое движение, каким оно бывает. Также вспомним, что такое ускорение, рассмотрим уравнение движения с постоянным ускорением и как им пользоваться для определения координаты движущегося тела. Рассмотрим пример задачи для закрепления материала.

Главная задача кинематики – определить положение тела в любой момент времени. Тело может покоиться, тогда его положение меняться не будет (см. рис. 1).

Рис. 1. Покоящееся тело

Тело может двигаться прямолинейно с постоянной скоростью. Тогда его перемещение будет изменяться равномерно, то есть одинаково за равные промежутки времени (см. рис. 2).

Рис. 2. Перемещение тела при движении с постоянной скоростью

Перемещение , скорость, умноженная на время, это мы давно умеем делать. Тело может двигаться с постоянным ускорением, рассмотрим такой случай (см. рис. 3).

Рис. 3. Движение тела с постоянным ускорением

Ускорение

Ускорение – это изменение скорости за единицу времени (см. рис. 4): Рис. 4. Ускорение Скорость – векторная величина, поэтому и изменение скорости, т. е. разность векторов конечной и начальной скорости, является вектором. Ускорение – тоже вектор, направленный туда же, куда и вектор разности скоростей (см. рис. 5). Мы рассматриваем прямолинейное движение, поэтому можно выбрать координатную ось вдоль прямой, вдоль которой происходит движение, и рассматривать проекции векторов скорости и ускорения на эту ось:

Тогда равномерно изменяется его скорость: (если его начальная скорость была равна нулю). Как теперь найти перемещение? Скорость умножить на время – нельзя : скорость постоянно менялась; какую брать? Как определить, где при таком движении будет находиться тело в любой момент времени – сегодня мы эту проблему решим.

Сразу определимся с моделью: мы рассматриваем прямолинейное поступательное движение тела. В таком случае можем применять модель материальной точки.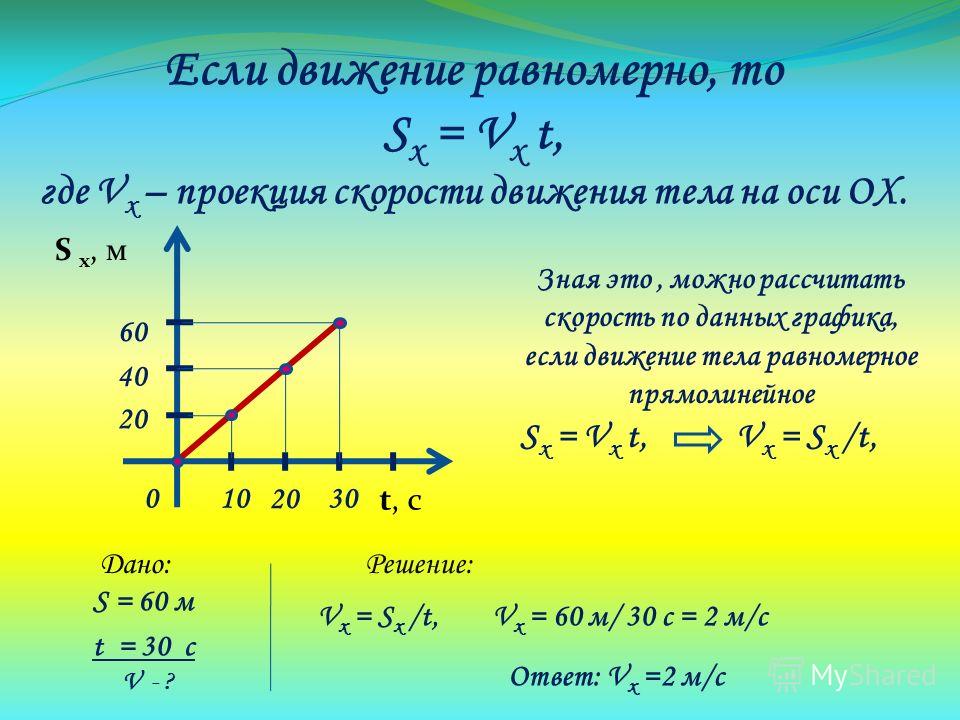 Ускорение направлено вдоль той же прямой, вдоль которой материальная точка движется (см. рис. 6).

Поступательное движение

Поступательное движение – это такое движение, при котором все точки тела движутся одинаково: с одинаковой скоростью, совершая одинаковое перемещение (см. рис. 7). Рис. 7. Поступательное движение А как еще может быть? Взмахните рукой и проследите: понятно, что ладонь и плечо двигались по-разному. Посмотрите на колесо обозрения: точки вблизи оси почти не движутся, а кабинки движутся с другой скоростью и по другим траекториям (см. рис. 8). Рис. 8. Движение выбранных точек на колесе обозрения Посмотрите на движущийся автомобиль: если не учитывать вращение колес и движение частей мотора, все точки автомобиля движутся одинаково, движение автомобиля считаем поступательным (см. рис. 9). Рис. 9. Движение автомобиля Тогда нет смысла описывать движение каждой точки, можно описать движение одной. Автомобиль считаем материальной точкой. Обратите внимание, что при поступательном движении линия, соединяющая любые две точки тела при движении, остается параллельной сама себе (см. рис. 10). Рис. 10. Положение линии, соединяющей две точки

Автомобиль ехал прямолинейно в течение часа. В начале часа его скорость была 10 км/ч, а в конце – 100 км/ч (см. рис. 11).

Рис. 11. Рисунок к задаче

Скорость изменялась равномерно. Сколько километров проехал автомобиль?

Проанализируем условие задачи.

Скорость автомобиля изменялась равномерно, то есть всё время пути его ускорение было постоянным. Ускорение по определению равно:

Автомобиль ехал прямолинейно, поэтому мы можем рассматривать его движение в проекции на одну ось координат:

Найдем перемещение.

Пример возрастающей скорости

На стол кладут орехи, по одному ореху в минуту. Понятно: сколько минут пройдет, столько орехов на столе окажется. А теперь представим, что скорость накладывания орехов равномерно возрастает с нуля: первую минуту орехов не кладут, во вторую кладут один орех, потом два, три и так далее. Сколько орехов окажется на столе через какое-то время? Понятно, что меньше, чем если бы максимальная скорость поддерживалась всегда. Причем хорошо видно, что меньше в 2 раза (см. рис. 12). Рис. 12. Количество орехов при разной их скорости выкладывании Так же и с равноускоренным движением: допустим, сначала скорость была равна нулю, в конце стала равна (см. рис. 13). Рис. 13. Изменение скорости Если бы тело постоянно двигалось с такой скоростью, его перемещение было бы равно , но поскольку скорость равномерно возрастала – то в 2 раза меньше.

Мы умеем находить перемещение при РАВНОМЕРНОМ движении: . Как обойти эту проблему? Если скорость изменяется не на много, то движение можно приближенно считать равномерным. Изменение скорости будет небольшим за небольшой интервал времени (см. рис. 14).

Рис. 14. Изменение скорости

Поэтому разобьем время в пути T на N небольших отрезков длительностью (см. рис. 15).

Рис. 15. Разбиение отрезка времени

Подсчитаем перемещение на каждом отрезке времени. Скорость прирастает на каждом интервале на:

На каждом отрезке мы будем считать движение равномерным и скорость приближенно равной начальной скорости на данном отрезке времени. Посмотрим, не приведет ли к ошибке наше приближение, если на небольшом промежутке движение будем считать равномерным. Максимальная ошибка будет равна:

и суммарная ошибка за всё время пути -> . При больших N принимаем ошибка близка к нулю. Это мы увидим и на графике (см. рис. 16): на каждом интервале будет ошибка, но суммарная ошибка при достаточно большом количестве интервалов будет пренебрежимо мала.

Рис. 16. Ошибка на интервалах

Итак, каждое следующее значение скорости на одну и ту же величину больше предыдущего. Из алгебры мы знаем, что это арифметическая прогрессия с разностью прогрессии :

Путь на участках (при равномерном прямолинейном движении (см. рис. 17) равен:

Рис. 17. Рассмотрение участков движения тела

На втором участке:

На n-м участке путь равен:

Арифметическая прогрессия

Арифметической прогрессией называется такая числовая последовательность, в которой каждое следующее число отличается от предыдущего на одну и ту же величину. Арифметическая прогрессия задается двумя параметрами: начальный член прогрессии и разность прогрессии . Тогда последовательность записывается так: Сумма первых членов арифметической прогрессии вычисляется по формуле:

Просуммируем все пути. Это будет сумма первых N членов арифметической прогрессии:

Т. к. мы разбили движение на много интервалов, то можно считать, что , тогда:

У нас было множество формул, и, чтобы не запутаться, мы не писали каждый раз индексы х, но рассматривали всё в проекции на координатную ось.

Итак, мы получили главную формулу равноускоренного движения: перемещение при равноускоренном движении за время T, которую мы наряду с определением ускорения (изменение скорости за единицу времени) будем использовать для решения задач:

Мы занимались решением задачи об автомобиле. Подставим в решение числа и получим ответ: автомобиль проехал 55,4 км.

Математическая часть решения задачи

С перемещением мы разобрались. А как определить координату тела в любой момент времени?

По определению перемещение тела за время – это вектор, начало которого находится в начальной точке движения, а конец – в конечной точке, в которой тело будет через время . Нам нужно найти координату тела, поэтому запишем выражение для проекции перемещения на ось координат (см. рис. 18):

Рис. 18. Проекция перемещения

Выразим координату :

То есть координата тела в момент времени равна начальной координате плюс проекция перемещения, которое совершило тело за время .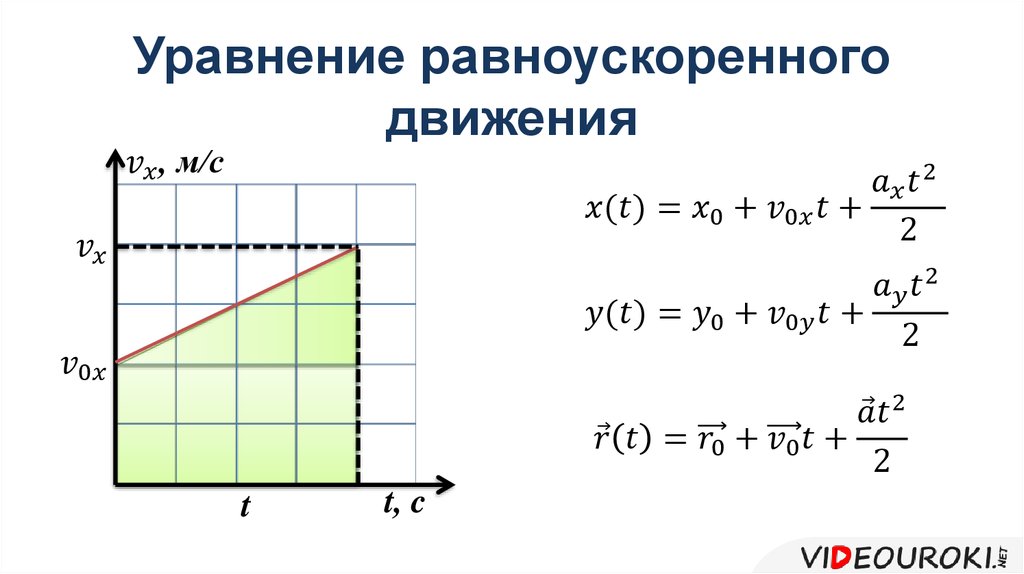 Проекцию перемещения при равноускоренном движении мы уже нашли, осталось подставить и записать:

Это и есть уравнение движения с постоянным ускорением. Оно позволяет узнать координату движущейся материальной точки в любой момент времени. Понятно, что момент времени мы выбираем в пределах промежутка, когда работает модель: ускорение постоянное, движение прямолинейное.

Почему уравнение движения нельзя применять для нахождения пути

В каких случаях мы можем считать перемещение по модулю равным пути? Когда тело движется вдоль прямой и не меняет направления. Например, при равномерном прямолинейном движении мы не всегда четко оговариваем, путь мы находим или перемещение, всё равно они совпадают. При равноускоренном движении скорость изменяется. Если скорость и ускорение направлены в противоположные стороны (см. рис. 19), то модуль скорости убывает, и в какой-то момент он станет равен нулю и скорость поменяет направление, то есть тело начнет двигаться в противоположную сторону. Рис. 19. Модуль скорости убывает И тогда, если в данный момент времени тело находится на расстоянии 3 м от начала наблюдения, то его перемещение равно 3 м, но если тело сначала прошло 5 м, затем развернулось и прошло еще 2 м, то путь будет равен 7 м. И как же его найти, если не знать этих чисел? Просто надо найти момент, когда скорость равна нулю, то есть когда тело развернется, и найти путь к этой точке и от нее (см. рис. 20). Рис. 20. Момент, когда скорость равна 0

Список литературы

1. Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
2. Ландсберг Г.С. Элементарный учебник физики; т.1. Механика. Теплота. Молекулярная физика – М.: Издательство «Наука», 1985.

1. Интернет портал «kaf-fiz-1586.narod.ru» ()
2. Интернет портал «Учеба – Легко» ()
3. Интернет портал «Гипермаркет знаний» ()

Домашнее задание

1. Что такое арифметическая прогрессия?
2. Какое движение называется поступательным?
3. Чем характеризуется векторная величина?
4. Запишите формулу для ускорения через изменение скорости.
5. Какой вид имеет уравнение движения с постоянным ускорением?
6. Вектор ускорения направлен в сторону движения тела. Как будет изменять свою скорость тело?

Ускорение. Прямолинейное движение с постоянным ускорением. Мгновеннная скорость.

Ускорение показывает, как быстро меняется скорость тела.

t 0 = 0c v 0 = 0 м/с Скорость изменилась на v = v 2 – v 1 в течение

t 1 = 5c v 1 = 2 м/ с промежутка времени = t 2 – t 1 . Значит за 1 с скорость

t 2 = 10c v 2 = 4 м/с тела увеличится на = .

t 3 = 15c v 3 = 6 м/с = или = . (1 м/с 2)

Ускорение – векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Физический смысл : а = 3 м/с 2 – это значит, что за 1 с модуль скорости меняется на 3 м/с.

Если тело разгоняется а>0, если тормозит а

Аt = ; = + аt мгновенная скорость тела в любой момент времени. (Функция v(t)).

Перемещение при равноускоренном движении. Уравнение движения

Д
ля равномерного движения S=v*t, где v и t являются сторонами прямоугольника под графиком скорости. Т.е. перемещение = площади фигуры под графиком скорости.

Аналогично можно найти перемещение при равноускоренном движении. Нужно всего лишь найти отдельно площадь прямоугольника, треугольника и сложить их. Площадь прямоугольника v 0 t, площадь треугольника (v-v 0)t/2, где мы делаем замену v – v 0 = аt . Получим s = v 0 t + аt 2 /2

s = v 0 t + аt 2 /2

Формула перемещения при равноускоренном движении

Учитывая, что вектор s = х-х 0 , получим х-х 0 = v 0 t + аt 2 /2 или вынесем начальную координату вправо х = х 0 + v 0 t + аt 2 /2

х = х 0 + v 0 t + аt 2 /2

По этой формуле можно найти координату ускоренно движущегося тела в любой момент времени

При равнозамедленном движении перед буквой «а» в формулах знак + можно заменить на –

Выясним, как зависит скорость от времени, если ускорение постоянно.
Пусть в начальный момент времени t0 = О скорость точки равнялась и0 (начальная скорость). Тогда, обозначив скорость в произвольный момент времени через v, получим в соответствии с формулой (1.16.1): V – Vr
(1.17.1) Отсюда (1.17.2)
v = v0 + at. Векторному уравнению (1.17.2) соответствуют три уравнения для проекций вектора скорости на оси координат. Ниже мы покажем, что движение с постоянным ускорением совершается в одной плоскости. Поэтому целесообразно совмещать систему координат XOY с этой плоскостью. Тогда формуле (1.17.2) будут соответствовать две формулы для проекций вектора скорости на координатные оси:
Vx = V0x + axf”
vy = % + V- (1.17.3)
При движении с постоянным ускорением скорость точ- icu и ее проекции изменяются со временем по линейному закону.
Для определения скорости в произвольный момент времени надо знать начальную скорость v0 и ускорение а.
Начальная скорость не зависит от того, какие тела действуют на данное тело в рассматриваемый момент времени. Она определяется тем, что происходило с телом в предшествующие моменты времени. Например, начальная скорость падающего камня зависит от того, просто ли мы выпустили его из рук или же он попал в данную точку, описав предварительно ту или иную траекторию. Ускорение же, наоборот, не зависит от того, что происходило с телом в предыдущее время, а лишь от действий на него других тел в данный момент. Подробно об этом будет рассказано в следующей главе.
Формулы (1.17.2) и (1.17.3) справедливы как для прямолинейного, так и для криволинейного движения.
Движение с постоянным ускорением
совершается в одной плоскости
Для доказательства данного утверждения воспользуемся формулой скорости v = v0 + at. Пусть ускорение а образует с начальной скоростью 50 некоторый угол а (рис. 1.49, а). Из кур-

Рис. 1.49
са математики известно, что два пересекающихся вектора лежат в одной плоскости. Вектор at имеет то же направление, что и а, так как t > 0. Поэтому векторы v и at расположены в той же плоскости, в которой лежат векторы а и v0. Сложив векторы 30 и at (рис. 1.49, б), получим вектор, который в любой момент времени t будет расположен в плоскости, в которой находятся векторы а и и0.
При движении с постоянным ускорением скорость точки и ее проекции меняются со временем по линейному закону.

Еще по теме § 1.17. СКОРОСТЬ ПРИ ДВИЖЕНИИ С ПОСТОЯННЫМ УСКОРЕНИЕМ:

1. Ситуация постоянного отношения. Употребление несов. вида при выражении ситуации постоянного отношения
2. 4. Факторы накопления капитала при данной норме накопления больше нуля и меньше 100%. Нестоимостные факторы накопления, или факторы накопления при данной величине капитала. Ускорение накопления при росте капитала (концентрация, централизация, кредит)
3. Структура дорожки Крамара из вихрей эфира, торсионные поля (СВИ, спайки и др.) зависят от радиуса крутящихся тел, от скорости вращения, движения и от других вполне конкретных физических параметров тел и среды, которые их порождают.
4. Теорема 35 Если тело В приводится в движение внешним толчком, то оно получает большую часть своего движения от постоянно окружающих его тел, а не от внешней силы.
5. §1.18. ГРАФИКИ ЗАВИСИМОСТИ МОДУЛЯ И ПРОЕКЦИИ УСКОРЕНИЯ И МОДУЛЯ И ПРОЕКЦИИ СКОРОСТИ ОТ ВРЕМЕНИ ПРИ ДВИЖЕНИИ С ПОСТОЯННЫМ УСКОРЕНИЕМ

Движение тела с переменной массой. Уравнение Мещерского. Формула Циолковского

Уравнение движения тела с переменной массой

Под переменной массой будем понимать массу тел, которая при медленном движении тел меняется за счет потери или приобретения вещества.

Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Принцип действия ракеты очень прост. Ракета с большой скоростью выбрасывает вещество (газы), воздействуя на него с большой силой. Выбрасываемое вещество с той же, но противоположно направленной силой в свою очередь действует на ракету и сообщает ей ускорение в противоположном направлении. На ракету действуют внешние силы: сила земной тяжести, гравитационное притяжение Солнца и планет, а также сила сопротивления среды, в которой движется ракета.

Рисунок 1.

Пусть $m(t)$- масса ракеты в произвольный момент времени $t$, а $v(t)$- ее скорость в тот же момент. Количество движения ракеты в этот момент времени будет $mv$. Спустя время $dt$ масса и скорость ракеты получат приращение $dm$ и $dv$ (величина $dm$ отрицательна). Количество движения ракеты станет равным $(m+dm)(v+dv)$. Сюда надо добавить количество движения газов, образовавшихся за время $dt$. Оно равно $dm_{газ} v_{газ} $, где $dm_{газ} $- масса газов, образовавшихся за время $dt$, а $v_{газ} $- их скорость. Вычитая из суммарного количества движения в момент $t+dt$ количество движения системы в момент времени $t$, найдем приращение этой величины за время $dt$. Это приращение равно $Fdt$, где $F$- геометрическая сумма всех внешних сил, действующих на ракету. Таким образом:

$(m+dm)(v+dv)+dm_{газ} v_{газ} -mv=Fdt$. (1)

Время $dt$ и приращения $dm$ и $dv$ устремим к нулю, т.к. нас интересуют предельные отношения или производные $dm/dt$ и $dv/dt$. Поэтому, раскрывая скобки, можно отбросить произведение $dm\cdot dv$, как бесконечно малую высшего порядка. Далее, ввиду сохранения массы, $dm+dm_{газ} =0$. Пользуясь этим, можно исключить массу газов $dm_{газ} $. А разность $v_{отн} =v_{газ} -v$ есть скорость истечения газов относительно ракеты — скорость газовой струи. С учетом этих замечаний уравнение (1) преобразуется к виду:

$mdv=v_{отн} dm+Fdt$. (2)

Разделив на $dt$, получаем:

$m\frac{dv}{dt} =v_{отн} \frac{dm}{dt} +F$. (3)

Уравнение Мещерского

По форме уравнение (3) совпадает с уравнением, выражающим второй закон Ньютона. Однако масса тела $m$здесь не постоянна, а меняется во времени из-за потери вещества. К внешней силе $F$ добавляется дополнительный член $v_{отн} \frac{dm}{dt} $, который может быть истолкован как реактивная сила, т.е. сила, с которой действуют на ракету вытекающие из нее газы. Уравнение (3) впервые было получено русским механиком И. В. Мещерским. Оно, так же как и эквивалентное ему уравнение (2), называется уравнением Мещерского или уравнением движения точки с переменной массой.

Формула Циолковского

Применим уравнение (2) к движению ракеты, на которую не действуют никакие внешние силы. Полагая $F=0$, получим:

Допустим, что ракета движется прямолинейно в направлении, противоположном скорости газовой струи $v_{отн} $. Если направление полета принять за положительное, то проекция вектора $v_{отн} $ на это направление будет отрицательной и равной $-v_{отн} $. Поэтому в скалярной форме предыдущее уравнение можно записать так $mdv=v_{отн} dm$. Тогда:

$\frac{dv}{dm} =-\frac{v_{отн} }{m} $ (4)

Скорость газовой струи $v_{отн} $ может меняться во время полета. Однако простейшим и наиболее важным является случай, когда она постоянна. Предположение о постоянстве сильно облегчает решение уравнения (4). В этом случае:

Значение постоянной интегрирования С определяется начальными условиями. {\frac{v}{v_{отн} } } $

Последнее соотношение называется формулой Циолковского.

• Формула Циолковского позволяет рассчитать запас топлива, необходимый, чтобы сообщить ракете скорость $\upsilon $.

• Величина достигаемой ракетой максимальной скорости не зависит от времени сгорания топлива.

• Оптимальным путем изменения достигаемой максимальной скорости является увеличение относительной скорости истечения газов.

• Для получения первой космической скорости при меньшем соотношении между массой ракеты и требуемой массы топлива целесообразно использование многоступенчатых ракет.

Примеры

Пример 1

Космический корабль двигался с постоянной по величине скоростью $v$. Для изменения направления его полета включается двигатель, выбрасывающий струю газа со скоростью $v_{отн} $ относительно корабля в направлении, перпендикулярном к его траектории. Определить угол $\alpha $, на который повернется вектор скорости корабля, если начальная масса его $m_{0} $, а конечная $m$. {2} r=\omega v$, причем $v=const$. Поэтому уравнение движения:

$m\frac{dv}{dt} =v_{отн} \frac{dm}{dt} $ переходит в: $mv\omega dt=-v_{отн} dm$.

Так как $d\alpha =\omega dt$ есть угол поворота за время $dt$, интегрируя наше уравнение, получим:

\[\alpha =\frac{v_{отн} }{v} \ln \frac{m_{0} }{m} .\]

Ответ: угол поворота вектора скорости равен: $\alpha =\frac{v_{отн} }{v} \ln \frac{m_{0} }{m} $

Пример 2

Ракета перед стартом имеет массу $m_{0} =250$кг. На какой высоте окажется ракета через $t=20$с после начала работы двигателей? Расход топлива равен $\mu =4$кг/с и скорость истечения газов относительно ракеты $v_{отн} $$=1500$м/с постоянны. Поле тяготения Земли считать однородным.

Дано: $m_{0} =250$кг, $t=20$с, $\mu =4$кг/с, $v_{отн}=1500$м/с.

Найти: $H$-?

Решение:

Рисунок 2.

Запишем уравнение Мещерского в однородном поле тяготения Земли в виде:

\[m\frac{\Delta v_{0} }{\Delta t} =\mu v_{отн} -mg,\]

где $m=m_{0} -\mu t$, а $v_{0} $- скорость ракеты в момент времени $t$. {2} }{2} +\frac{v_{отн} m_{0} }{\mu } (1-\frac{\mu t}{m_{0} } )\ln (1-\frac{\mu t}{m_{0} } )=3177,5$м

Ответ: через $20$с ракета окажется на высоте $H=3177,5$м.

Уравнение траектории тела – определение и формулы

Изучением движения тела в пространстве занимается большой раздел в физике — кинематика. Причём причины, заставляющие объект двигаться, исследует динамика. Путь, который проходит физическая точка, называют траекторией тела. Уравнение, описывающее этот процесс, зависит от направления, заданного действием, вызывающим изменение её положения. Форма же перемещения определяется выбранной системой координат и местом начального отсчёта.

Содержание

• Общие сведения
• Горизонтальное перемещение
• Движение тела под углом
• Решение задач

Общие сведения

Под движением тела понимают процесс его перемещения из одной точки пространства в другую. Произошедшее действие исследуют относительно другого объекта или выбранных начальных координат. При этом положение вовсе не обязательно может изменяться сразу ко всем окружающим его телам. Например, стоящий человек на Земле находится в состоянии покоя по отношению к планете, но движется относительно Солнца.

В физике принято любое изменение определять в системе пространственных координат. За оси принимают перпендикулярные линии x, y, z. Совокупность данных, используемых для изучения движения, называют системой отсчёта.

Существует несколько видов механического перемещения (во времени) физической точки:

• равномерное и равноускоренно прямолинейное;
• по дуге;
• гармоническое колебание.

При движении тело проходит определённый путь. Описать его можно виртуальной линией, при этом она может быть как прямой, так и кривой. Именно она и называется траекторией движения. По сути, эта линия соединяет последовательно все положения точки в пространстве — от начальной до конечной. Длина отрезка является пройденным путём и считается векторной величиной.

Изменение радиус-вектора r (значения, задающего положение точки в пространстве относительно другого тела) описывает кинематический закон: r = r (t). В трёхмерных декартовых координатах его можно записать так: r = xe + ye + ze = (x, y, z). Вектор, построенный из начальной точки движущегося тела в расположение её в данный момент времени, то есть приращение радиус-вектора за определённый промежуток t, как раз и называют перемещением.

Результирующее движение же равно векторной сумме последовательных изменений положения. При прямолинейном перемещении вектор пути совпадает с соответствующим участком траектории, а модуль перестановки равняется пройденному расстоянию.

Время, за которое тело пройдёт по установленной траектории пути, называют скоростью. Фактически это быстрота изменения координаты. Физики, исследуя передвижение, изучают не только положение материальной точки в начальный и конечный момент времени, но и закон, по которому происходит перемещение. Другими словами, они определяют зависимость радиус-вектора от времени.

Горизонтальное перемещение

Пусть имеется тело, брошенное горизонтально поверхности. Высота падения равняется h, а начальная скорость V0. Здесь систему отсчёта удобно связать с Землёй. Объект будет передвигаться под действием силы тяжести. Остальными силами, например, сопротивлением воздуха, можно пренебречь. Тело перемещается в плоскости, содержащей вектора ускорения и свободного падения (g).

Таким образом, система начальных условий будет выглядеть так: x (t = 0) = 0; y (t = 0) = 0; v0x = v0; voy = 0. Вектор ускорения постоянный, поэтому a = g. Если тело представить как совокупность материальных точек, движущихся по одинаковому пути, то путь можно определить как сумму перемещений по прямым. Уравнение скорости примет вид: v (t) = v0 + gt. Об изменении положения можно сказать, что оно выполняется с постоянной скоростью и ускорением в горизонтальной плоскости, являясь равномерным. Значит, проекцию на оси ординаты и абсциссы можно записать как vx = v0; vy = -gt.

Скорость перемещения рассчитывают по формуле: V = √‎(V ² x + V² y). После подстановки полученных ранее выражений равенство примет вид: V = √‎(V ² 0 + g ² t ²). Отсюда следует, что уравнение для вектора движения материальной точки будет: s (t) = s0 + V0t + (g t ²) / 2, где: s0 — смещение тела, соответствующее начальному моменту времени.

Так как s0 = y (t = 0) = h0, то скалярные выражения для координат изменяющей положение частицы можно представить в виде системы: x = V0t; y = h0 — (gt² / 2). Перемещение происходит по прямой как отдельное движение в двух плоскостях, при этом из формулы следует, что изменение положения будет соответствовать правой половине направленной вниз параболы. Учитывая то, что время можно определить из отношения икса к начальной скорости (t = x /V0), можно записать окончательную формулу для вычисления траектории движения тела: y = h0 — (gx²) / (2²V0) .

Можно сделать вывод, что уравнение траектории не записывается через время, поэтому частица будет и перемещаться обратно по той же самой траектории. Временные отрезки между точками пути будут одинаковы как при прямом, так и при обратном движении.

Каждому положению соответствует определённое значение скорости, которое не зависит от направления перемещения. Нужно отметить, что наибольшей величиной в горизонтальной траектории полёта будет начальная точка.

Движение тела под углом

Свободное падение является частным случаем равноускоренного, то есть на перемещаемый объект действует только сила притяжения. Если физическая точка перемещается, то кривая, которая описывается её радиус-вектором, обозначает пройденный путь. Эту траекторию можно описать некоторой математической функцией.

Итак, вектор скорости точки определяется как производная по времени: V = dr / dt = r. Ускорение же можно найти, продифференцировав скорость: a = dV / dt = d ² r / dt. Если обозначить производную времени точкой, то формулу можно переписать так: a = V = r.

Для того чтобы вывести формулу, нужно воспользоваться основными выражениями, определяющими проекции:

• ускорения: ax = 0, ay = — g, az = 0;
• радиус-вектора: rx (t) = V0 * cosat, ry (t) = v * sin (at — (g * t2)/2)), rz (t) = 0;
• скорости: vx (t) = V0 * cosa, vy (t) = V0 * sin (a — gt), vz (t) = 0.

Чтобы запись зависимости вертикальной оси от горизонтальной была как можно более компактной, соответствующие координаты rx и ry можно обозначить через икс и игрек. Из уравнения, связывающего координатную ось X и время, можно определить t как функцию ординаты. Линейное выражение будет иметь вид: t = x / (Vo * cosa).

Если полученную формулу для времени подставить в уравнение для игрек координаты, то вместо временного параметра появится икс. То есть можно будет вывести зависимость абсциссы от ординаты: y = V 0 * sinat — (g * t²) / 2 = (tga) * x — (g / 2 * V0 * cos²a) * x². Значение t нужно подставить в каждое слагаемое, но при этом учесть, что отношение синуса к косинусу называют тангенсом. Альфа в формуле — это угол между направлением начальной скорости и горизонтальным направлением (угол броска). После исключения времени из этих уравнений получим уравнение траектории.

В итоге останется два слагаемых. Первое будет линейно по иксу, а второе квадратично. Таким образом, зависимость игрека от икса в уравнении траектории — это парабола (справа стоит квадратичная функция). Она проходит через начало координат. Если верно равенство x = 0, то игрек тоже будет равняться нулю.

Следует обратить внимание на то, что в квадрате стоит отрицательный коэффициент. Известно, что если перед квадратичным слагаемым в уравнении параболы стоит отрицательное число, то концы кривой будут направлены вниз.

Решение задач

Решение практических заданий лучше всего помогает закрепить полученные знания. Существуют физические сборники, которые интересны тем, что включают в себя различные примеры, приближенные к реалистичным задачам. Прорешивая их самостоятельно, ученик не только лучше разберётся в теме, но и научится применять полученные знания на практике.

Вот два таких задания:

Пусть имеется тело, движение которого описывается равенствами: x = Vx * t; y = y0 + Vy * t. Нужно определить траекторию его перемещения, учитывая, что Vx = 20 см/с, Vy = 2 м/с, Yo = 0,2 м. Для решения задачи нужно записать систему, определяемую исходными данными. Затем из первого равенства выразить время: t = x / Vx. Полученную формулу можно подставить в выражение нахождения координат абсциссы: y = y0 + (Vy * x) / Vx. Если теперь использовать исходные данные, то уравнение, описывающее траекторию, примет вид: y = 0.2 + 4x. Равенство напоминает собой формулу прямой: y = k * x + b. Исходя из этого можно утверждать, что траектория пути также будет представлять собой прямую линию. Действительно, в этом можно убедиться, если построить график движения. Для этого нужно взять несколько произвольных значений для икса, подставить их в формулу и найти вторую координату.

Следующая задача довольно интересная. Нужно составить траекторию движения для тела, движущегося равномерно со скоростью два метра в секунду, при отклонении пути от оси икс на 60 градусов. За начало координат нужно принять точку (0, 0). Тогда начальный радиус-вектор тоже будет равен нулю: R = 0. Для успешного решения примера понадобится вспомнить скалярные уравнения для проекции при равномерном движении. Так как по условию вектор задан, то можно найти его проекцию на ось игрек: Vx = v * cos60 = 1; Vy = v * cos30 = √‎3. Отсюда: x = Vx * t = t; y = Vy * t = √‎3t.

Таким образом, чтобы успешно решать задачи, нужно знать несколько основных формул для определения местоположения тела, а также то, как выглядят уравнения параболы и прямой.

Стоит отметить, что существующие онлайн-калькуляторы не умеют вычислять формулы, описывающие траекторию пути. Но вместе с тем их можно использовать для выполнения расчётов или как справочники.

Предыдущая

ФизикаЗависимость силы тока от напряжения – формула, график и законы

Следующая

ФизикаФормула тонкой линзы – свойства, применение и расчеты

Движение материальной точки, брошенной под углом к горизонту.



Движение материальной точки, брошенной под углом к горизонту

Рассмотрим материальную точку М массой m, брошенную из точки О поверхности Земли с начальной скоростью v₀ под углом α к горизонту (см. рис. 1).

Определим движение точки М, считая, что на нее действует только сила тяжести G (сопротивлением воздуха пренебрегаем).

Возьмем начало координат в точке О, ось x направим по горизонтали вправо (в направлении траектории, по которой движется точка), а ось y – по вертикали вверх. Очевидно, что проекция ускорения на ось х будет равна нулю, поскольку единственная сила, действующая на точку – сила тяжести – направлена вертикально вниз (вдоль оси y), а согласно аксиоме Ньютона, без силы нет и ускорения.
Составим дифференциальные уравнения, описывающие движение точки:

m (d²x/dt²) = 0;     m(d²y/dt²) = – mg.

Сокращая равенства на m, получим:

d²x/dt² = 0;     (1)
  d²y/dt² = – g.     (2)

Интегрируя первое из этих уравнений (1), получим:

dx/dt = С₁, где С₁ – некоторая произвольная постоянная.

Следовательно, проекция скорости точки М на ось x все время остается величиной постоянной, равной
v_x = v₀ cosα или, на основании результата интегрирования уравнения (1), можно записать:

dx/dt = v₀ cosα.

Интегрируя это уравнение, получаем:

x = v₀t cosα + С₂.

По условию при t = 0    x = 0, следовательно, произвольная постоянная С₂ равна нулю.
Окончательно имеем:

x = v₀t cosα.

Интегрируем уравнение (2), находим:

v_y = dy/dt = – gt + C₃.

Подставив в это уравнение значение t = 0, найдем произвольную постоянную С₃:

С₃ = v_y = v₀ sinα, следовательно:

dy/dt = v₀ sinα – gt.

Интегрируя вторично, получаем:

y = v₀t sinα – gt²/2 + C₄.

Поскольку по условию t = 0     y = 0 , следовательно, произвольная постоянная С₄ равна нулю.
Окончательно получаем:

y = v₀t sinα – gt²/2.

Таким образом становится очевидным, что материальная точка М, брошенная с начальной скоростью v₀ под углом α к горизонту, движется согласно уравнениям:

x = v₀t cosα,     (3)
  y = v₀t sinα – gt²/2.     (4)

***



Определение траектории, высоты и дальности полета

Для определения траектории точки М исключаем из полученной системы уравнений движения время. Для этого из формулы (3) выражаем время: t = x/(v₀ cosα) и подставляем это значение в формулу (4).
Получим уравнение траектории:

y = x tgα – gx²/(2v₀² cos²α).

Траектория точки М представляет собой параболу с вертикальной осью симметрии.

Определим время полета точки М, для чего во второе уравнение движения (4) подставим значение y = 0.
Тогда уравнение движения примет вид:

v₀t sinα – gt²/2 = 0.

Отсюда находим два значения времени t, при которых ордината равна нулю (корни уравнения):

t₀ = 0;     t₂ = (2v₀ sinα)/g.

Первое значение времени соответствует началу полета, второе – конечной точке траектории полета.
Тогда общая продолжительность полета будет равна:

t₂ – t₀ = t₂ = (2v₀ sin α)/g.

Определим дальность полета по горизонтали, для чего в уравнение движения (3) подставим значение времени t₂:

x₂ = v₀t cosα = (v₀ cosα×2v₀ sinα)/g    или    x₂ = v₀t cosα = (v₀² sin 2α)/g.

Из полученного уравнения можно сделать вывод, что максимальная дальность полета x_max имеет место при sin2α = 1, т. е. при α = π/4 рад:

x_max = v₀²/g.

Определим наибольшую высоту подъема точки М, т. е. ее ординату в тот момент времени t₁, когда проекция скорости на ось y окажется равной нулю:

dy/dt = v_y = v₀ sinα – gt₁ = 0.

Из полученного равенства определим t₁:

t₁ = (v₀ sinα)/g = t²/2.

Следовательно, наибольший подъем точки имеет место в середине пути полета, при x₁ = x²/2.

Подставив значение t₁ в уравнение (4), получим:

y₁ = (v₀ sinα×v₀ sinα)/g – gv₀² sin 2α/(2g²).

Из полученного уравнения можно сделать вывод, что максимальной высоты точка достигает при sinα = 1 или при α = π/2 рад, т. е. когда точка брошена под углом 90˚ к горизонту (вертикально вверх).

Полученные формулы и зависимости позволяют решать различные задачи на движение тел и точек под действием силы тяжести в приближенной форме, поскольку они не учитывают силы сопротивления движению со стороны воздуха (аэродинамическое сопротивление).

***

Основы кинетостатики.
Принцип Даламбера (Д’Аламбера)



Главная страница

• Страничка абитуриента

Дистанционное образование

• Группа ТО-81
• Группа М-81
• Группа ТО-71
  

Специальности

• Ветеринария
• Механизация сельского хозяйства
• Коммерция
• Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

• Инженерная графика
• МДК.01.01. «Устройство автомобилей»
•    Карта раздела
•       Общее устройство автомобиля
•       Автомобильный двигатель
•       Трансмиссия автомобиля
•       Рулевое управление
•       Тормозная система
•       Подвеска
•       Колеса
•       Кузов
•       Электрооборудование автомобиля
•       Основы теории автомобиля
•       Основы технической диагностики
• Основы гидравлики и теплотехники
• Метрология и стандартизация
• Сельскохозяйственные машины
• Основы агрономии
• Перевозка опасных грузов
• Материаловедение
• Менеджмент
• Техническая механика
• Советы дипломнику

Олимпиады и тесты

• «Инженерная графика»
• «Техническая механика»
• «Двигатель и его системы»
• «Шасси автомобиля»
• «Электрооборудование автомобиля»

Уравнения движения твердого тела

Уравнения движения твердого тела

(Эйлеров законы)

 

Инерциальная система отсчета: Явный вид законы механики зависят от системы отсчета, используемой для обозначения движений. система отсчета часто является фоном события, а Земля является самая распространенная система отсчета. Например, второй закон Ньютона записывается как

 

 

когда ускорение рассчитывается относительно инерциальной системы отсчета. Точки инерциальной системы отсчета имеют без ускорения (чисто перевод с постоянной или нулевой скоростью, и без вращение). С другой стороны, этот же закон будет записан как

 

 

 

если ускорение рассчитывается с относительно кадра, который является чисто переводным с ускорением . Поэтому важно рассмотреть систему отсчета осторожно, прежде чем использовать какую-либо конкретную форму данного закона. Большую часть времени, законы движения записываются относительно инерциальной системы отсчета, то из этого формы можно вывести форму закона относительно других систем отсчета.

 

Законы Эйлера: Законы движения твердого тела известны как законы Эйлера. Эйлер вывел два закона движения жесткое тело. Два закона, записанные относительно инерциальной системы отсчета, таковы:

 

 

где O является фиксированной точкой на инерциальная система отсчета. Первый из двух законов Эйлера описывает как силы контролируют поступательное движение твердого тела (т. изменение скорости центра масс, ). Второй из двух законов Эйлера описывает, как изменяется угловой момент твердого тела определяется моментом сил и пары нанесены на тело. Законы Эйлера написаны для тела фиксированных материя (т. е. материя не может быть добавлена ​​к телу, материя не может быть вычтена из тела, и материя не может быть заменена другой материей).

 

Ан альтернативная форма этих законов, которая заменяет необходимость иметь фиксированную точку O на инерциальной системе отсчета, получается с помощью центра масс. Этот закон выводится ниже и определяется как

 

 

, где CM обозначает центр масс.

 

А третья альтернативная форма законов Эйлера может быть получена из второй альтернативной формы форма. Эта форма заменяет центр масс произвольным пункт P который может двигаться в в любом случае (это может быть ускорение). Эта форма законов Эйлера записывается как

 

 

, где это должность центр масс относительно выбранной точки P . Подробная информация о том, как получить эту форму, также приведена ниже. Четвертый форма законов Эйлера задается как

 

 

, где это должность пункт P относительно центра масса, и, как указано выше, P может быть выбран произвольно.

 

Это также будет показано, что линейный импульс твердого тела определяется выражением масса, умноженная на скорость центра масс тела, дает альтернативную форма первого закона Эйлера как

 

 

где м – полная масса твердого тела и это ускорение центра масс тела.

 

Линейный импульс частицы: Для одной частицы массой м его линейный импульс определяется его массой, умноженной на его скорость, так что импульс тела: Линейный импульс тела считается суммой линейных импульс его частиц. Например, если у человека есть тело, состоящее из несколько частиц, каждая из которых имеет массу и скорость , его линейный импульс равен

 

 

Это нетрудно видеть, что для сплошного тела суммирование можно заменить на и интегрирование для получения

 

 

 

 

 

положение центра масс тела можно найти из соотношения это отношение и взятие его производной по времени относительно инерциальной системы отсчета дает

 

 

где — скорость центр масс, измеренный относительно системы отсчета и м — полная масса тела. Таким образом, можно заключить, что линейный импульс тела определяется выражением Первый закон Эйлера: Используя приведенное выше соотношение для количества движения твердого тела, один можно заменить линейный импульс массой, умноженной на скорость центра массу, чтобы получить альтернативную форму первого закона Эйлера как

 

 

С масса постоянна в ньютоновской механике, приходим к соотношению центр масс и положение частицы совпадают, и каждый восстанавливается Второй закон Ньютона.

 

Угловой момент частицы: Символ H _O обозначает угловой импульса и для частицы с массой м определяется как момент количества движения вокруг точки O и определяется уравнением

 

 

Угловой момент для твердого тела: Угловой момент для твердого тела равен сумме углового импульс частиц в нем. Учитывая систему отсчета, точка O в этой системе отсчета, а жесткая тела, угловой момент твердого тела можно аппроксимировать как

где предполагается, что тело аппроксимируется суммой частей, каждая из которых имеет массу , положение и скорость .

 

 

Взятие предел по мере уменьшения частей приводит к следующему интегралу представление углового момента твердого тела

 

 

где м – полная масса тела и и соответственно, положение и скорость дм относительно выбранной системы отсчета и выбранной точки отсчета O на ней.

 

 

Отношение между моментами сил, когда момент взят относительно разных точек: Момент действия силы около O может быть связано с моментом той же силы, взятой около точки A по отношению между угловыми моментами, когда угловой момент берется примерно разным очки: угловой момент тела, взятый около O можно связать с угловым моментом того же тела, взятым около точки А по отношению

 

 

 

 

Альтернативные формы второго закона Эйлера: Полезную альтернативную форму второго закона Эйлера можно получить, используя вышеприведенные правила изменения точки отсчета записывают второй закон в виде преимущество первого закона Эйлера, и отмечая, что второй член на правая часть равна нулю, можно получить альтернативную форму второго закона Эйлера как

 

 

 

Важность этой формы состоит в том, что момент и угловой момент вычисляется относительно центра масс, который не обязательно должен находиться на инерционной Рамка. Таким образом, необходимость использования выбранной точки O на инерциальной системе отсчета была устранена в пользу центра масса, которая может ускоряться. Взяв момент первого закона Эйлера вокруг произвольная точка P и добавление ее к это уравнение дает

 

 

Один можно переписать в одной из двух других альтернативных форм

 

 

 

 

 

 

Мехрдад Негабан и Университет Небраски, 1999–2002 годы.

Все права защищены

Свободное копирование и распространение только для личного использования

 

Факультет инженерной механики, Университет Небраски, Lincoln, NE 68588-0526

 

 

Жесткие кузова

Жесткое тело представляет собой протяженную область материала, включает в себя все точки внутри него, и который движется так, что расстояния и углы между всеми его точками остаются постоянный. Положение твердого тела можно описать как положение одной точки $P$ внутри него вместе с угол поворота тела (один угол в 2D, три угла в 3Д).

	описание местоположения	описание скорости
Масса точек	вектор положения $\vec{r}_P$	вектор скорости $\vec{v}_P$
твердое тело в 2D	вектор положения $\vec{r}_P$ угол $\theta$	вектор скорости $\vec{v}_P$ угловая скорость $\omega$
твердое тело в 3D	вектор положения $\vec{r}_P$ угла $\theta,\phi,\psi$	вектор скорости $\vec{v}_P$ вектор угловой скорости $\vec{\omega}$

Ни точечные массы, ни твердые тела не могут физически существовать. поскольку никакое тело не может быть единственной точкой без протяженности, и никакое протяженное тело не может быть абсолютно жестким. Несмотря на это, эти очень полезные модели для механики и динамики.

Углы поворота твердых тел

Все точки твердого тела имеют одинаковый угловой поворот углы, как мы можем видеть на рисунке ниже. Поскольку угловая скорость – производная от углов поворота, это означает, что каждая точка твердого тела имеет одинаковую угловая скорость $\vec{\omega}$, а также тот же угловой ускорение $\vec{\alpha}$.

В 2D угол $\theta$ твердого тела угол вращение от фиксированной ссылки (обычно $\hat\imath$ направление), измеренное положительным против часовой стрелки. Угловой скорость равна $\omega = \dot\theta$, а угловой ускорение равно $\alpha = \dot\omega = \ddot\theta$. векторные версии этих $\vec\omega = \omega\,\hat{k}$ и $\vec\alpha = \alpha\,\hat{k}$, где $\hat{k}$ — внеплоскостное направление.

Показывать:

Все точки твердого тела вращаются с одинаковой скоростью. Тело $\mathcal{B}_1$ поворачивается на угол $\theta_1$, поэтому его угловая скорость равна $\omega_1 = \dot{\theta}_1$, а аналогично для второго тела.

Угловые величины ($\theta$, $\omega$, $\alpha$) для твердые тела не должны быть помечены точками. Если $P$ и $Q$ — точки на твердом теле, мы не пишем $\omega_P$ или $\omega_Q$ для угловой скорости около эти точки.

Вместо этого мы обозначаем угловые величины в соответствии с тело. Если у нас есть два твердых тела $\mathcal{B}_1$ и $\mathcal{B}_2$, то $\omega_1$ — угловая скорость первого тела (и всех точек на нем) и $\omega_2$ – угловая скорость второго тела.

Точки на твердых телах

Если мы знаем, как движется одна точка $P$ на твердом теле и мы также знаем, как вращается тело, то мы можем вычислить движение любой другой точки $Q$ на том же теле. формулы для этого приведены ниже.

\[\ начало {выровнено} \vec{r}_Q &= \vec{r}_P + \vec{r}_{PQ} \\ \vec{v}_Q &= \vec{v}_P + \vec{\omega} \times \vec{r}_{PQ} \\ \vec{a}_Q &= \vec{a}_P + \vec{\alpha} \times \vec{r}_{PQ} + \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PQ}) \конец{выровнено}\]

Точки $P$ и $Q$ — это две точки на жесткой тело. Векторы $\vec{\omega}$ и $\vec{\alpha}$ являются угловая скорость и угловое ускорение твердого тела тело.

Первое уравнение — это просто определение вектор смещения $\vec{r}_{PQ}$. Дифференциация первого уравнение дает \[\ начало {выровнено} \vec{r}_Q &= \vec{r}_P + \vec{r}_{PQ} \\ \dot{\vec{r}}_Q &= \dot{\vec{r}}_P + \dot{\vec{r}}_{PQ} \\ \vec{v}_Q &= \vec{v}_P + \vec{\omega} \times \vec{r}_{PQ}, \конец{выровнено}\] где производная от $\vec{r}_{PQ}$ получается из формулы вращения при условии, что этот вектор смещения просто вращается с жестким тело.

Если еще раз продифференцировать, то получим \[\ начало {выровнено} \vec{v}_Q &= \vec{v}_P + \vec{\omega} \times \vec{r}_{PQ} \\ \dot{\vec{v}}_Q &= \dot{\vec{v}}_P + \dot{\vec{\omega}} \times \vec{r}_{PQ} + \vec{\omega} \times \dot{\vec{r}}_{PQ} \\ \vec{a}_Q &= \vec{a}_P + \vec{\alpha} \times \vec{r}_{PQ} + \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PQ}), \конец{выровнено}\] где мы используем тот факт, что $\vec{\alpha} = \точка{\vec{\omega}}$.

Поскольку перекрестные произведения не являются ассоциативными, это очень важно вычислить член центростремительного ускорения со скобками, как показано. То есть мы не должны вычислить $(\vec{\omega} \times \vec{\omega}) \times \vec{r}_{PQ}$, так как это всегда ноль.

Терм $\vec{\omega} \times (\vec{\omega} \times \vec{r}_{PQ})$ в приведенном выше уравнении ускорения называется центростремительный (центростремительный) термин, как он есть всегда в направлении $-\vec{r}_{PQ}$ и поэтому действует из $Q$ к «центру» $P$.

Показывать: никто должность скорость ускорение

Две точки $P$ и $Q$ на движущемся и ускоряющемся твердом теле.

Прямоугольный брусок скользит по земле так, что точка контакта $P$ движется с постоянной скорость $3\rm\ м/с$ влево. 2$ по часовой стрелке. Какова скорость и ускорение $Q$ непосредственно перед ударом?

Используя обычный базис $\hat\imath,\hat\jmath$, известная информация непосредственно перед воздействием \[ \vec{r}_{PQ} = 2\,\шляпа\imath \qquad \vec{v}_P = -3\,\шляпа\imath \qquad \vec{a}_P = 0 \qquad \vec\omega = -2\,\шляпа{k} \qquad \vec\alpha = -3\,\шляпа{k}. \] Скорость и ускорение $Q$ определяются выражением \[\ начало {выровнено} \vec{v}_Q &= \vec{v}_P + \vec{\omega} \times \vec{r}_{PQ} \\ &= -3\,\шляпа\имат – 2\,\шляпа{к} \раз 2\,\шляпа\имат\\ &= -3\,\шляпа\имат – 4\,\шляпа\jmath\\ \vec{a}_Q &= \vec{a}_P + \vec{\alpha} \times \vec{r}_{PQ} + \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PQ}) \\ &= 0 – 3\,\шляпа{к} \умножить на 2\,\шляпа\imath – 2\,\шляпа{k} \times (-2\,\шляпа{k} \times 2\,\шляпа\imath) \\ &= -6\,\шляпа\jmath – 2\,\шляпа{k} \times (-4\,\шляпа\jmath) \\ &= -8\,\шляпа\imath – 6\,\шляпа\jmath. \конец{выровнено}\] 9\circ$, $\omega_1 = 4\rm\ рад/с$. Что такое $\omega_2$ и $\vec{v}_Q$ в это мгновение?

Взяв обычный базис $\hat\imath,\hat\jmath$ в $O$, мы можем использовать длины стержней и углы, чтобы найти векторы относительного положения: \[\ начало {выровнено} \vec{r}_{OP} &= 3\шляпа\imath + 3\шляпа\jmath\rm\ m \\ \vec{r}_{PQ} &= 4\hat\imath – 3\hat\jmath\rm\ m. \конец{выровнено}\] Используя векторные угловые скорости $\vec{\omega}_1 = \omega_1\,\hat{k}$ и $\vec{\omega}_2 = \omega_2\,\hat{k}$, теперь мы можем использовать #rkg-er, чтобы найти первый $\vec{v}_P$ а затем $\vec{v}_Q$ через неизвестный угловой скорость $\omega_2$: \[\ начало {выровнено} \vec{v}_{P} &= \vec{v}_O + \vec{\omega}_1 \times \vec{r}_{OP} \\ &= 4\шляпа{k} \times (3\шляпа\imath + 3\шляпа\jmath) \\ &= -12\шляпа\imath + 12\шляпа\jmath{\rm\ м/с} \\ \vec{v}_{Q} &= \vec{v}_P + \vec{\omega}_2 \times \vec{r}_{PQ} \\ &= (-12\шляпа\imath + 12\шляпа\jmath{\rm\ м/с}) + \omega_2\,\hat{k} \times (4\hat\imath – 3\hat\jmath) \\ &= (-12 + 3\omega_2)\,\шляпа\imath + (12 + 4\omega_2)\,\шляпа\jmath{\rm\ м/с}. \конец{выровнено}\] Последняя часть информации, которую нам нужно использовать, это ограничение на движение $\mathcal{B}_3$, а именно, что он может скользить только горизонтально. Это может можно выразить, сказав, что вертикальная составляющая $\vec{v}_Q$ равен нулю, или, в более общем смысле, что компонента в нормальном направлении $\hat{e}_n = \hat\jmath$ равно нулю. То есть: \[\ начало {выровнено} 0 &= \vec{v}_Q \cdot \шляпа{e}_n \\ &= \Big((-12 + 3\omega_2)\,\шляпа\imath + (12 + 4\omega_2)\,\шляпа\jmath\Большой) \cdot \шляпа\jmath \\ &= 12 + 4\omega_2 \\ \omega_2 &= -3{\rm\ рад/с}. \конец{выровнено}\] Подставляя это обратно в выражение выше для $\vec{v}_Q$ дает: \[\vec{v}_Q = -21\шляпа\imath{\rm\ м/с},\] который действительно не имеет вертикальной составляющей, так как ожидал.

Если $\vec{\alpha} = 0$ и $\vec{a}_P = 0$ для жесткого тела, то мы обычно говорили бы, что само тело не ускоряется. Это не означает, однако, что точки на телах не ускоряются. Если тело вращается (так что $\vec{\omega} \ne 0$), то центростремительное ускорение означает, что на самом деле большинство точек на теле ускоряются в любое время.

Твердые тела в 2D

Приведенные выше уравнения #rk-er действительны. как в 2D, так и в 3D. Если мы знаем, что находимся в 2D $\hat\imath,\hat\jmath$, то угловая скорость вектор ортогонален плоскости в направлении $\hat{k}$ и уравнения могут быть записаны в более простой форме с обозначение перпендикулярного вектора #rvv-en, как показано ниже.

\[\ начало {выровнено} \vec{r}_Q &= \vec{r}_P + \vec{r}_{PQ} \\ \vec{v}_Q &= \vec{v}_P + \omega \, \vec{r}_{PQ}^\perp \\ \vec{a}_Q &= \vec{a}_P + \alpha \, \vec{r}_{PQ}^\perp – \omega^2 \, \vec{r}_{PQ} \конец{выровнено}\]

Точки $P$ и $Q$ — это две точки на жесткой тело. Скаляры $\omega$ и $\alpha$ — это скаляры угловая скорость и угловое ускорение твердого тела тело (положительное против часовой стрелки).

Векторы положения $\vec{r}_P$ и $\vec{r}_Q$ лежат в плоскости $\hat\imath,\hat\jmath$, поэтому $\vec{v}_P$, $\vec{v}_Q$ и $\vec{r}_{PQ}$ также находятся в этом самолет. Угловая скорость и угловое ускорение векторы ортогональны и поэтому могут быть записаны: \[\ начало {выровнено} \vec{\omega} &= \omega\,\шляпа{k} \\ \vec{\alpha} &= \alpha\,\hat{k}. \конец{выровнено}\] Оценка #rkg-er и использование выражение перекрестного произведения #rvv-e9\перп, \конец{выровнено}\] и уравнение ускорения: \[\ начало {выровнено} \vec{a}_Q &= \vec{a}_P + \vec{\alpha} \times \vec{r}_{PQ} + \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PQ}) \\ &= \vec{a}_P + \alpha\,\hat{k} \times \vec{r}_{PQ} + \omega\,\hat{k} \times (\omega\,\hat{k} \times \vec{r}_{PQ}) \\ &= \vec{a}_P + \alpha\,\vec{r}_{PQ}^\perp + \omega\,\hat{k} \times (\omega\,\vec{r}_{PQ}^\perp) \\ &= \vec{a}_P + \alpha\,\vec{r}_{PQ}^\perp + \omega^2 (\vec{r}_{PQ}^\perp)^\perp \\ &= \vec{a}_P + \alpha\,\vec{r}_{PQ}^\perp – \omega^2 \vec{r}_{PQ}, \конец{выровнено}\] где мы использовали тот факт, что $\vec{r}^{\perp\perp} = -\vec{r}$ (два $9\circ$ вращение).

Если точка $M$ на твердом теле имеет нулевую скорость, то она называется мгновенным центром вращения , потому что скорость всех точек тела будет задана простым вращением вокруг $M$ с угловой скоростью $\vec{\omega}$ тела. В 2D мы всегда можем найти мгновенный центр со следующим уравнением, хотя это может быть вне физического тела. 9\перп \]

Точка $P$ имеет скорость $\vec{v}_P$ и прикреплена к твердое тело, вращающееся с угловой скоростью $\vec{\omega}$.

Мгновенный центр $M$ обладает тем свойством, что точка твердого тела в точке $M$ имеет нулевую скорость. Мы таким образом хочу: \[ 0 = \vec{v}_M = \vec{v}_P + \vec{\omega} \times \vec{r}_{PM}. \] Взятие другого векторного произведения на $\vec{\omega}$ дает: \[\ начало {выровнено} 0 &= \vec{\omega} \times \Big( \vec{v}_P + \vec{\omega} \times \vec{r}_{PM} \Big) \\ &= \vec{\omega} \times \vec{v}_P + \vec{\omega} \times (\vec{\omega} \times \vec{r}_{PM}) \\ &= \vec{\omega} \times \vec{v}_P – \omega^2 \, \vec{r}_{PM} \text{ (потому что $\vec\omega \perp \vec{r}_{PM}$)} \\ \vec{r}_{PM} &= \frac{1}{\omega^2} \vec{\omega} \times \vec{v}_P. \конец{выровнено}\] Здесь мы воспользовались тем, что если $\vec{r}_{PM}$ лежит в $\hat\imath,\hat\jmath$ плоскость и $\vec{\omega}$ находится в направление $\hat{k}$, затем от #rvv-e92\,\vec{r}_{PM}$, как при выводе #rkg-e2.

В 3D мгновенный центр будет только в том случае, если $\vec{v}_P$ ортогонален $\vec{\omega}$, и в этом случае будет много вариантов для мгновенного центра, все лежащих на прямой в направлении $\vec{\omega}$.

Если $M$ — мгновенный центр, значит, его скорость равна нулю, тогда скорость любой другой точки твердого тела равна определяется следующим уравнением.

\[ \vec{v}_{Q} = \vec{\omega} \times \vec{r}_{MQ} \]

Точка $M$ является мгновенным центром вращения твердое тело, вращающееся с угловой скоростью $\vec{\omega}$, а $Q$ — любая точка тела.

По определению мгновенный центр имеет $\vec{v}_M = 0$, поэтому формула скорости #rkg-er дает: \[\ начало {выровнено} \vec{v}_Q &= \vec{v}_M + \vec{\omega} \times \vec{r}_{MQ} \\ &= \vec{\omega} \times \vec{r}_{MQ}. \конец{выровнено}\]

Движение:	перевод	вар. перевод	вращение	вар. вращение	слайд
	петля	круг	спин	обратное вращение	колебания

Точка $P$	Корпус	$Q$ Скорость	$Q$ Ускорение
		нет	нет
		$\vec{v}_P$ (пер. )	$\vec{a}_P$ (пер.)
		$\vec{\omega} \times \vec{r}_{PQ}$ (вращ.)	$\vec{\alpha} \times \vec{r}_{PQ}$ (англ.)
			$\vec{\omega} \times (\vec{\omega} \times \vec{r}_{PQ})$ (цент)
		$\vec{v}_Q$ (всего)	$\vec{a}_Q$ (всего)

Скорость и ускорение точек твердого тела. совершающие различные движения.

Жидкости в движении твердого тела

Жидкости в движении твердого тела

Жидкости в движении твердого тела

Введение

• Напомним, для случая движения твердого тела уравнение движение потока жидкости (уравнение Навье-Стокса) сводится к
  
  Обратите внимание, что новый вектор “действующей гравитации”, Г , определяется как векторная сумма гравитации и отрицательного вектора ускорения. Этот новый эффективный вектор гравитации можно получить с помощью небольшой тригонометрии в качестве результирующего вектора добавления г и – .
  
  
• Рассмотрим два случая движения твердого тела: равномерное линейное ускорение твердого тела и жесткое вращение тела .

Равномерное линейное ускорение твердого тела

• Рассмотрим случай, когда жидкость равномерно ускоряется в каком-то направлении. Другими словами, каждая частица жидкости в контейнер чувствует точно такой же вектор ускорения, который постоянным во времени. В таком случае, поскольку и вектор гравитации и вектор ускорения постоянны, действующая сила тяжести вектор, G , также должен быть постоянным.
• Обратите внимание, что уравнение движения идентично уравнение гидростатики, за исключением того, что сила тяжести г заменен по эффективной гравитации G . Это делает проблемы этого типа не сложнее простой гидростатики. На самом деле для униформы линейное ускорение твердого тела, решение идентично гидростатики, но с заменой g на G , и с z (параллельно g , т.е. вниз) заменяется на s (параллельно Г ). Хороший способ запомнить это — представить себе, что ускоряющая жидкость вместо этого находится на планете, где гравитация действует в каком-то странном направлении (направление вектора G ) и с некоторой величины G. Одним из следствий этого является то, что изобары должны быть перпендикулярно G , т.е. перпендикулярно направлению с. На самом деле давление увеличивается линейно с расстоянием s, а не чем с з.
  
  
• В качестве примера рассмотрим стакан воды в лифте, который ускоряется:
  
  Здесь действующая сила тяжести все еще направлена ​​вниз, но больше величина, чем g. Изобары остаются горизонтальными поверхностями, т.к. в гидростатике. По сути все идентично гидростатике за исключением большей силы тяжести (представьте, например, что стакан сидит на планете Юпитер). Наше простое гидростатическое давление соотношение по-прежнему применяется, но с заменой g на G и z заменой по с, т.е.
  
  Также обратите внимание, что “ниже” и “выше” являются относительными также координировать s, а не z. При прочих равных, давление на дно ускорительного стакана будет больше чем на дне стационарного стакана (поскольку G больше, чем г).
  • Теперь рассмотрим стакан воды в лифте, который ускоряется равномерно вправо. Опять же, эффективный вектор силы тяжести может построить, как показано:
    
    Теперь, поскольку эффективная гравитация наклонена под некоторым углом к внизу слева изобары должны быть перпендикулярны этому направлению. Таким образом, изобары наклонены вниз и вправо, как показано на рисунке. Заметим, что поверхность остается изобарой постоянного давления p _и , и поэтому также наклонен, как нарисовано. В какой-то момент 1 в жидкости, давление можно найти из пересмотренного гидростатического зависимость давления следующая:
    
    

Вращение твердого тела

• Рассмотрим контейнер с некоторой жидкостью, который вращается вокруг вертикальная ось с некоторой постоянной угловой скоростью, как показано на эскиз:
• Для любого вида движения твердого тела уравнение движения для течения жидкости (уравнение Навье-Стокса) сводится к В твердом теле линейное ускорение, эффективный вектор силы тяжести, G , везде в жидкости было постоянным. Вот этого уже нет случае, поскольку ускорение вращающейся частицы жидкости относительно некоторой оси изменяется с расстоянием от оси. Фактически, для круговое движение, ускорение всегда направлено внутрь, к центр вращения (центростремительное ускорение). Это ускорение увеличивается линейно с радиусом (вывод см. в тексте): Таким образом, эффективный вектор силы тяжести G , непостоянная, но зависит от радиуса. На рисунке ниже эффективная гравитация вектор в точке A строится: Локально изобары вблизи точки A, конечно, по-прежнему перпендикулярны G , и они показано.
• Однако в других точках потока локальное эффективное вектор силы тяжести другой, так как местное ускорение другое. Например, в точке B (на большем радиусе, чем точка A) вектор ускорения внутрь больше, и G наклоняется дальше вправо, как показано ниже: Местные изобары вокруг точки B, перпендикулярные местной эффективный вектор гравитации, таким образом, наклонены вправо вверх даже сильнее, чем в точке A. На средней линии (точка C) местное ускорение равно нулю, а эффективная сила тяжести идентична к стандартной гравитации; изобары вблизи осевой линии вращающегося жидкости горизонтальны, как и в гидростатике:
• Если такой анализ проводить везде в потоке, изобары оказываются параболоидами, построенными путем вращения парабола вокруг своей оси для создания осесимметричной поверхности: Свободная поверхность, конечно, является изобарой, так как ее давление равно атмосферный. Давление увеличивается перпендикулярно изобарам.
• В тексте представлен более подробный математический вывод уравнений для давления и для изобар. Если происхождение определяется в самой нижней точке на свободной поверхности, как показано на эскиз выше, уравнения для давления и для изобар находятся:
• Когда p = p _a , второе приведенное выше уравнение принимает вид уравнение, описывающее свободную поверхность. Когда р больше стр. _a , это уравнение описывает изобары под поверхностью (при более высоком давлении). Теперь обозначим h как разницу между высота в центре свободной поверхности и на краю свободной поверхность. Получается, что по сравнению с исходной свободной поверхностью (контейнер вообще не вращается), поверхность опускается в центрировать на величину (h/2), равную величине подъема поверхности обод (также h/2). Это показано ниже:
• Рассмотрим числовой пример. Емкость с водой радиуса 4,0 дюйма вращается с фиксированной угловой скоростью 100 об/мин. Оценивать час: Простой эксперимент с вращающейся чашкой с водой может показать, что это предсказание довольно точное.
• Обратите внимание, что плотность не фигурирует в уравнении для изобар или в уравнении для h. Таким образом, вода может быть заменена с любой другой жидкостью, и результат будет идентичным. Давление будет расти быстрее с глубиной для более плотной жидкости, но форма свободной поверхности останется неизменной независимо от используемой жидкости. Кроме того, поскольку это вращение твердого тела, порции жидкости могут быть даже удалены или заменены твердый материал. Таким образом, любой вращающийся кусок жидкости, независимо от его формы, можно анализировать, как если бы он был частью большого контейнера вращение вокруг оси Z, как показано на рисунках выше.

Физика – Уравнения движения для задачи n тел

Задавать вопрос

Спросил 5 лет, 5 месяцев назад

Изменено 2 года, 4 месяца назад

Просмотрено 1к раз

$\begingroup$

Функция Лагранжа определяется как $\mathcal{L}(q,\dot{q}) = T(q,\dot{q}) – V(q,\dot{q})$, где $T$ определяет кинетическую энергию и $V$ потенциальную энергию. 93$ описывает положение $i$-й планеты в момент времени $t$.

Теперь мне нужно рассчитать уравнения движения.

Но теперь я не понимаю, как быть с $\frac{\partial \mathcal{L}}{\partial q_i}$. Первое, что меня смущает, это то, что $q_i$ — трехмерный вектор. Во-вторых, это производная от нормы, потому что в исчислении мы узнали, что норма не дифференцируема.

Может ли кто-нибудь объяснить мне эту проблему? Любая помощь очень ценится.

• обыкновенные дифференциальные уравнения
• физика
• математическая физика
• классическая механика
• уравнение Лагранжа Эйлера

$\endgroup$

0

$\begingroup$

$ \let\ss\стиль сценария \let\sss\scriptscriptstyle \пусть\дс\дисплейстайл \renewcommand{\+}{\hspace{1mu}} \renewcommand{\bs}[1]{\boldsymbol{#1}} \renewcommand{\dt}[1]{\overset{\sss \bullet}{#1}} \renewcommand{\ddt}[1]{\overset{\sss \bullet \bullet}{#1}} \renewcommand{\pow}[1]{\raise{.8ex}{\ss{#1}}} \renewcommand{\a}{\альфа} \renewcommand{\p}{\partial} \renewcommand{\r}{\bs{r}} \renewcommand{\rdot}{\dt{\r}} \renewcommand{\qdot}{\dt{q}} \renewcommand{\F}{\bs{F}} \renewcommand{\L}{\mathcal{L}} \renewcommand{\deriv}[3]{\frac{{#1}{#2}}{{#1}{#3}}} \renewcommand{\ddx}[2]{\deriv{d}}{#1}{#2}} \renewcommand{\pdx}[2]{\deriv{\partial}{#1}{#2}} \renewcommand{\lagrange}[1]{\ddx{}{t} \pdx{#1}{\qdot_\a} \+ – \+ \pdx{#1}{q_\a}} $

Позвольте мне немного изменить ваши обозначения. Пусть $q_\a$ будет набором координат, который мы используем для указания положения $\bs{r}_i = \boldsymbol{r}_i(q)$ планет. Начиная с закона Ньютона, если мы введем виртуальную работу и изменим нашу философию, мы придем к принципу Даламбера, для которого уравнения движения принимают вид \begin{уравнение} \sum_i (\F_i – m \,\bs{a}_i) \cdot \delta \r_i \; знак равно 0 \end{уравнение} где $\F_i$ — сила, а $\bs{a}_i$ — ускорение $i$-й планеты. Установка виртуальных перемещений в $\delta \r_i = \sum_\a (\p\r_i \+ / \+ \p q_\a) \; \delta q_\a $ приводит нас к системе из $3n$ уравнений Лагранжа (см. Гольдштейн § 1-4) \begin{уравнение} \L_\a[T] ​​= \; Ф_\а \end{уравнение} где обобщенная сила $F_\a = \sum_i \F_i \! \кдот\! \pdx{\r_i}{q_\a}$, кинетическая энергия $T = \sum_i \frac{1}{2} m_i \bs{v}_i \! \кдот\! \bs{v}_i$ и оператор Лагранжа $\L_\a = \lagrange{}$. Будем использовать не-скрипт $L$ для обозначения лагранжиана. При записи уравнений движения мы можем свободно переключаться между использованием сил \begin{уравнение} \F_i = \sum_{j \; : \; j \neq i} \frac{ G \, m_i m_j \, (\r_j – \r_i)}{|\r_j – \r_i|^3} \end{уравнение} и используя потенциал \begin{уравнение} V = \sum_{i,j \; : \; i Но ничто не мешает нам оставить соответствующие обобщенные силы на правой стороне. Теперь, если мы хотим получить более явное выражение для уравнений движения, нам нужно выбрать координаты. Для простоты воспользуемся декартовыми координатами и предположим, что на систему $\{q_1, q_2, q_3, q_4, \ldots, q_{3n}\} \equiv \{x_1, y_1, z_1, x_2, \ ldots, z_n \}$. Недекартовы координаты лучше всего обрабатываются с помощью тензорной нотации, которую я бы не стал представлять в сообщении Stack Exchange. Полезно видеть, как векторы расширяются. \begin{уравнение} \begin{массив}{rcl} \r_i &=& q_{3i-2} \+ \bs{i} + q_{3i-1} \+ \bs{j} + q_{3i} \+ \bs{k} \\ \bs{v}_i &=& \qdot_{3i-2} \+ \bs{i} + \qdot_{3i-1} \+ \bs{j} + \qdot_{3i} \+ \bs{k } \\ \F_i &=& F_{i1} \+ \bs{i} + F_{i2} \+ \bs{j} + F_{i3} \+ \bs{k} \\ \конец{массив} \end{уравнение} Позиции зависят только от трех координат, поэтому члены $\pdx{\r_i}{q_\a}$ отличны от нуля только для трех значений $\alpha$ (для которых они становятся $\bs{i}, \bs{j },$ или $\bs{k}$). Нетрудно видеть, что $\L_\a[T]$ — координатные ускорения, а $F_\a$ — компоненты силы. Таким образом, уравнения Лагранжа $\L_\a[T] ​​= F_\a$ отражают закон Ньютона \begin{уравнение} m_{i} \ddt{q}_{3i+j-3} = F_{ij} \end{уравнение} где мы определили $\a = 3i+j-3$ для удобства. Мы можем сжать эти $3n$ уравнений до $n$ векторных уравнений \begin{уравнение} m_{i} \bs{a}_i = \F_i \end{уравнение} Мы прошли полный круг. На самом деле нет никакой причины вводить лагранжиан, потому что: во-первых, ограничений нет, во-вторых, мы используем декартовы координаты, а в-третьих, у нас есть явные выражения для сил.

$\endgroup$

$\begingroup$

Давайте посмотрим на уравнения Эйлера-Лагранжа. Здесь нужно быть очень осторожным с индексами. $i$-частица в вашей системе представлена ​​ вектором $\vec{q}_{i}$. Условимся обозначать $a$-ю компоненту этого вектора через $q_{i,a}$. Таким образом, $i$ меняется от $1$ до $n$, а $a$ — от $1$ до $3$. {2 }. \end{уравнение} Аналогичную переписку необходимо сделать для $V$. Это может быть немного сложнее, но идея та же, так что, возможно, стоит попробовать, прежде чем я объясню больше.

Что касается вашего второго вопроса, вы правы в том, что норма недифференцируема при нуле . Обратите внимание, что в выражении для $T$ мы не говорим ни о каких нормах, вместо этого мы говорим о квадрате нормы, который совершенно дифференцируем. В выражении для $V$ ситуация совсем плачевная, речь идет не просто о норме, а даже о функции $1/\|\vec{q}_{i} – \vec{q}_{j }\|$, который ведет себя еще хуже. Я думаю, можно просто предположить, что $\vec{q}_{i} \neq \vec{q}_{j}$ для $i \neq j$…

$\endgroup$

6

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Динамика жесткого тела

Динамика двумерного твердого тела

В задачах динамики двумерного твердого тела тело движется в одной плоскости под действием сил, действующих в этой плоскости.

Ниже показано обычное твердое тело, на которое действуют произвольные силы в двух измерениях.

Полный набор скалярных уравнений, описывающих движение тела:

Где:

m масса тела

ΣF _x сумма сил в направлении х

ΣF _y сумма сил в направлении y

a _Gx — ускорение центра масс G в направлении x относительно инерциальной системы отсчета xyz, которая в данном случае является землей

a _Гр – ускорение центра масс G в направлении y относительно земли

α — угловое ускорение твердого тела относительно земли.

ΣM _G представляет собой сумму моментов относительно оси, проходящей через центр масс G (в направлении z, направленном за пределы страницы). Он определяется как сумма крутящего момента Στ из-за сил, действующих на тело (относительно оси, проходящей через центр масс G и направленной в направлении z). Использование ΣM _G — это просто другое соглашение об именах.

I _G – инерция вращения твердого тела вокруг оси, проходящей через центр масс G и направленной в направлении z (вне страницы)

Обратите внимание, что если бы твердое тело вращалось вокруг фиксированной точки O , уравнение конечного момента сохраняло бы тот же вид, если бы мы выбрали точку O вместо точки G . Таким образом, уравнение будет выглядеть так:

На рисунке ниже показана эта ситуация.

Где точка O является фиксированной точкой, прикрепленной к земле. Конкретным примером этого может быть маятник, качающийся вокруг фиксированной точки.

Вот несколько примеров задач, решаемых с помощью двумерных уравнений динамики твердого тела:

Физика игры в гольф
Требушет С физикой

Трехмерная динамика твердого тела

В трехмерных задачах динамики твердого тела тело испытывает движение во всех трех измерениях из-за сил, действующих во всех трех измерениях. Это наиболее общий случай для твердого тела.

Ниже показано обычное твердое тело, на которое действуют произвольные силы в трех измерениях.

Первые три из шести скалярных уравнений, описывающих движение тела, являются уравнениями силы. Они есть:

Где:

a _Gx ускорение центра масс G в направлении x относительно земли (инерциальная система отсчета)

а _Гр – ускорение центра масс G в направлении y относительно земли

a _Gz – ускорение центра масс G в направлении z относительно земли

Обратите внимание, что индексы x,y,z указывают на то, что величины разрешаются по осям xyz . Например, сила, действующая вдоль оси Z, разлагается на ее составляющие вдоль оси 9.0067 xyz осей в приведенных выше трех уравнениях. Обычно это можно сделать с помощью тригонометрии.

Однако нет необходимости разрешать величины по оси xyz . Для приведенных выше трех уравнений силы вместо этого можно решить величины по осям XYZ.

Для решения трехмерных задач динамики твердого тела необходимо вычислить шесть членов инерции твердого тела, соответствующих дополнительной сложности трехмерной системы. Для этого необходимо определить локальный xyz осей, которые лежат внутри твердого тела и прикреплены к нему (как показано на рисунке выше), так что он движется вместе с телом. Шесть членов инерции рассчитываются относительно xyz и зависят от ориентации xyz относительно твердого тела. Таким образом, разная ориентация xyz (относительно твердого тела) приведет к разным условиям инерции. Причина, по которой говорят, что xyz «движется вместе с телом», заключается в том, что условия инерции не будут меняться со временем по мере движения тела. Таким образом, вам нужно вычислить условия инерции только один раз, в начальном положении твердого тела, и все готово. Это имеет то преимущество, что математика остается максимально простой. Дополнительным преимуществом наличия xyz перемещение с твердым телом при моделировании движения тела во времени. Мы можем отслеживать ориентацию тела, отслеживая ориентацию xyz (поскольку они движутся вместе).

Для двумерных задач динамики твердого тела необходимо учитывать только один член инерции, и это I _G , как указано выше. Для этих задач I _G можно вычислить относительно любой ориентации твердого тела, и оно всегда будет одним и тем же, так как задача плоская. Поэтому нам не нужно определять оси xyz , который прикреплен к твердому телу и имеет определенную ориентацию относительно него (как мы это делаем в трехмерных задачах). Это связано с тем, что для плоских задач (где движение происходит в одной плоскости) I _G не зависит от ориентации xyz (относительно твердого тела).

Для общего случая (где мы имеем произвольную ориентацию xyz внутри твердого тела) последние три уравнения, описывающие движение твердого тела, являются уравнениями моментов (моментов). Они есть:

Где:

ΣM _Gx сумма моментов относительно оси x , проходящей через центр масс G

ΣM _Gy сумма моментов относительно оси y , проходящей через центр масс G

ΣM _Gz – сумма моментов относительно оси z , проходящей через центр масс G

w _x , w _y , w _z компоненты угловой скорости твердого тела относительно земли, разрешенные по локальным осям xyz. Для расчета этих составляющих необходимо сначала определить вектор угловой скорости твердого тела относительно глобальных осей XYZ, а затем разложить этот вектор по направлениям x , y , z , чтобы найти компоненты w _x , w _y , w _z . Это часто делается с помощью тригонометрии.

α _x , α _y , α _Z – это компоненты, а также в господстве, а также в господстве, а также в господном телу с расточкой. – Состояние. – Состояние. – Состояние. – Состояние. – Состояние. – Состояние. – Состояние. – Сознание. xyz осей. Для расчета этих составляющих необходимо сначала определить вектор углового ускорения твердого тела относительно глобальных осей XYZ, а затем разрешить этот вектор по x , Y , Z Найдите на поиск компонентов α _x , α _y , α 9008 9007 _Y , α 9008 9007 , α 9007 _{. Это часто делается с помощью тригонометрии.}

I _Gx – инерция вращения твердого тела вокруг оси x , проходящей через центр масс G

I _Гр – инерция вращения твердого тела вокруг y -ось, проходящая через центр масс G

I _Gz – инерция вращения твердого тела вокруг оси z , проходящей через центр масс G

I _Gxy является произведением инерции ( xy ) твердого тела относительно xyz

I _Gyz является произведением инерции ( yz ) твердого тела относительно хиз

I _Gzx является произведением инерции ( zx ) твердого тела относительно xyz

Шесть членов инерции оцениваются следующим образом с использованием интегрирования:

Ориентация xyz относительно твердого тела может быть выбрана так, что

Эта ориентация определяется как главное направление xyz .

При таком упрощении уравнения моментов принимают вид:

Они известны как уравнения движения Эйлера . Ясно, что лучше выбрать ориентацию xyz так, чтобы она лежала в главном направлении. Для каждого твердого тела существует главное направление. Если тело имеет две или три плоскости симметрии, главные направления будут совмещены с этими плоскостями. Для случая, когда в теле нет плоскостей симметрии, главное направление все же можно найти, но для этого нужно решить довольно сложное кубическое уравнение.

Обратите внимание, что для трех уравнений моментов и шести членов инерции их количества должны быть относительно осей xyz (это отличается от первых трех уравнений силы, где это необязательно). Для терминов инерции причина этого очевидна, поскольку именно так они определяются. Но на данный момент причины уравнений довольно сложны, но в основном они сводятся к тому, как они выводятся, что и обсуждается здесь.

Например, момент, действующий вокруг оси Y, должен быть разложен на его составляющие вдоль xyz осей, чтобы использовать приведенные выше уравнения моментов. Обычно это можно сделать с помощью тригонометрии.

Обратите внимание, что если бы твердое тело вращалось вокруг фиксированной точки O , приведенные выше уравнения моментов и шесть членов инерции сохраняли бы ту же форму, если бы мы выбрали точку O вместо точки G . Вы просто заменяете нижний индекс G на нижний индекс O , а все остальное остается прежним. Обратите внимание, что xyz осей будут иметь начало в точке O вместо точки G .

На рисунке ниже показана эта ситуация.

Где точка O является фиксированной точкой, прикрепленной к земле. Конкретным примером этого может быть волчок, прецессирующий вокруг фиксированной точки.

Для двумерных задач динамики твердого тела вектор углового ускорения всегда указывает в том же направлении, что и вектор угловой скорости. Однако для трехмерных задач динамики твердого тела эти векторы могут указывать в разных направлениях, как показано ниже.

Эти векторы могут быть выражены как:

В двух измерениях, чтобы найти угловое ускорение, вы просто дифференцируете величину угловой скорости по времени. В трех измерениях вы должны учитывать изменение величины и направления вектора угловой скорости (поскольку оба могут меняться со временем), так что это немного усложняет ситуацию. Это делается путем вычисления разности вектора угловой скорости за очень малый временной шаг Δt , где Δt →0. Для иллюстрации см. рисунок ниже.

Используя исчисление, угловое ускорение рассчитывается следующим образом (принимая предел как Δt →0):

Три уравнения силы и три уравнения момента, показанные здесь для трехмерных задач динамики твердого тела, «полностью описывают» все возможные движения твердого тела. Они включают полный набор уравнений, необходимых для решения наиболее общих задач динамики твердого тела. Все упрощения могут быть сделаны из этих шести уравнений. Например, если предположить плоское движение, шесть уравнений сводятся к уравнениям двумерной динамики, приведенным выше.

Обратите внимание, что положительные направления отдельных осей X, Y, Z соответствуют направлениям, показанным на первом рисунке. Точно так же положительные направления отдельных осей x , y , z также соответствуют направлениям, показанным на первом рисунке. Этот выбор соглашения о знаках важен при использовании приведенных здесь уравнений динамики твердого тела (особенно уравнений моментов). Это объясняется на странице уравнений движения.

Для получения дополнительной справочной информации см.:

Теорема о параллельных осях и параллельных плоскостях
Пристальный взгляд на скорость и ускорение

Вот несколько примеров задач, решаемых с использованием трехмерных уравнений динамики твердого тела:

Физика боулинга
Диск Эйлера Физика
Гироскоп Физика

Чтобы лучше понять динамику твердого тела, см. Механические волны.

Вернуться на страницу Полезные физические формулы

Вернуться к Задачи физики реального мира домашняя страница

сообщить об этом объявлении

Уравнения движения | Определение, формулы

Уравнения движения

Уравнения движения в физике — это основная концепция, которую мы все, возможно, изучали в средней школе. Важно понимать, что он означает и что мы с ним делаем с юных лет, чтобы в будущем стало легче понимать сложные понятия, связанные с ним.

Мы используем это понятие по-разному, например, занимаясь спортом или управляя автомобилем, даже не подозревая о том, что на самом деле его используем. В этой статье мы подробно обсудим уравнения движения в физике, а также рассмотрим другие подобные концепции.

Уравнения движения в физике – определение 

В кинематике уравнения движения определяются как основная концепция движения объекта, включая скорость, положение и ускорение, которые выполняются через различные интервалы времени. Эти три уравнения движения управляют движением объекта в 1, 2 и 3 измерениях.

Проще говоря, уравнения движения в физике — это набор уравнений, способных описать поведение физической системы в терминах ее движения как функции времени. Следовательно, уравнение движения есть отношение между этими величинами.

Уравнения движения для равномерного ускорения

Уравнения движения для равномерного ускорения включают три разных уравнения. Они называются законами постоянного ускорения. Следовательно, мы можем использовать эти уравнения для получения таких компонентов, как скорость (начальная и конечная), ускорение (а), перемещение (с) и время (t).

Следовательно, они применяются только при постоянном ускорении и прямолинейном движении. Ниже приведены три уравнения:

• Первое уравнение движения: v = u + at
• Второе уравнение движения: s = ut + 12 at ²
• Третье уравнение движения: v ² = u ² + 2as

где,

с = перемещение

u = начальная скорость

v = конечная скорость

a = ускорение

t = время движения

Мы можем назвать эти величины СУВАТ. Это перемещение, начальная скорость, конечная скорость, ускорение и время движения.

Уравнения движения – типы вывода

Следующие методы используются для вывода уравнений движения:

• Вывод уравнений движения с использованием простого алгебраического метода
• Вывод уравнений движения с использованием графического метода
• Вывод уравнений движения с использованием метода исчисления

Все они имеют три вывода уравнений движения. Давайте посмотрим на них ниже:

Первое уравнение движения – вывод

1. Простой алгебраический метод

Все мы знаем, что скорость изменения скорости зависит от ускорения тела.

Рассмотрим тело, имеющее массу m и начальную скорость u. Через некоторое время «t» он достигает своей конечной скорости «v». Эта конечная скорость обусловлена ​​ускорением «а». Следовательно,

Ускорение = Конечная скорость (или) Начальная скорость / Затраченное время

a = v – u/t или at = v – u

v = u + at

2. Графический метод

Взгляните на следующий график:

Отсюда

OD = u; OC = v и OE = DA = t

Равномерное ускорение = a

Начальная скорость = u

Конечная скорость = v

Пусть OE = t (время)

Из графика:

BE = AB + AE 

v = DC + OD (QAB = DC & AE = OD)

v = DC + u QOD = u

v = DC + u ……. (1)

Теперь,

a = v – u/t

a = OC – OD/t = DC/t

at = DC …….. (2)

Следовательно, подставив DC из (2) в ( 1) получим:

v = u + at

3. Метод исчисления

Мы знаем, что скорость изменения скорости описывает ускорение,

a = dv / dt

adt = dv

Проинтегрируем обе части: получится:

v = u + at 

Второе уравнение движения – вывод

1. Простой алгебраический метод

Рассмотрим расстояние «s». Мы все это знаем Также из v = u + at

s = u + u + at /2 × t

=2u + at / 2 × t

= 2UT + в ² /2

= 2UT / 2 + в ² /2

Следовательно, S = UT + 1 / 2AT ²

2. Графический метод
63
2. .

Посмотрим на приведенный ниже график:

OD = u, OC = v и OE = DA = t

Начальная скорость = u

Конечная скорость = v

Равномерное ускорение = a , мы видим, что расстояние, пройденное за заданное время t, образует площадь трапеции ABDOE.

За заданное время «t» пройденное расстояние равно «s».

Расстояние, с = площадь ∆ ABD + площадь ADOE.

s = 12 × AB × AD + (OD × OE)

= 12 × DC × AD + u × t [Поскольку AB = DC]

= 12 × at × t + ut [Поскольку DC = at]

= 12 × at × t + ut

Отсюда получаем:

s = ut + 1/2 at ²

3. Метод исчисления

Мы знаем, что скорость изменения смещения дает скорость.

Мы можем приравнять это как:

v = ds / dt 

ds = vdt 

При интегрировании уравнений вместе, UDT + ATDT)

Интеграция с обеих сторон:

Упрощение уравнения. Метод

Имеем v = u + at; следовательно, это можно записать как v – u / a

Кроме того, мы знаем, что

Расстояние = Средняя скорость × Время

Следовательно, мы можем записать постоянную скорость как:

Средняя скорость = Конечная скорость + Начальная скорость / 2 = v + u / 2

Следовательно, расстояние s = v + u / 2 × v – u / a

или s = v2 – u ² / 2a

или, мы можем записать это как:

v ²  = u ² + 2 ² /2as 

2. Графический метод

OD = u, OC = v и OE = DA = t

Начальная скорость = u

Конечная скорость = v

Равномерное ускорение = a На графике видно, что расстояние, пройденное за заданное время t, образует площадь трапеции ABDOE.

За заданное время «t» пройденное расстояние равно «s».

Следовательно, площадь трапеции ABDOE = 1 / 2 × (сумма параллельных салазок + расстояние между параллельными салазками)

Расстояние, s = 1 / 2 × DO + BE × OE = 12 u + v × t ……(3)

Из уравнения 2: a = v = ut,

t = v – ua …… ( 4)

Теперь подставим 4-е уравнение в 3-е. Получаем:

s = 12 u + v × (v – ua),

s = 12 × a × v + u (v – u)

2as = v + u (v – u)

2as = v ²  – u ²

Следовательно, мы можем записать это как:

v ²  = u ² + 2as

3. Расчетный метод

a = dv / dt 

Скорость изменения смещения дает скорость:

v = ds / dt 

Умножьте приведенные выше уравнения. Мы получаем:

A × DS / DT = V × DV / DT

Интеграция вышеуказанного уравнения,

AS = V ² – U ² / 2

v ²  = u ² + 2as 

Уравнения движения Приложения

Физические уравнения движения имеют многочисленные практические применения. Вот некоторые из них:

• Уравнения движения облегчают предсказание времени движения тела, просто сопоставляя его конечную и начальную скорости с его ускорением. Нет необходимости знать время движения тела.
• Это облегчает нам предсказание расстояния, пройденного телом, обеспечивая начальную и конечную скорости с ускорением. Нет необходимости знать время, затрачиваемое телом на путешествие.
• Уравнения движения очень помогут нам получить конечное значение скорости тела. Требуются значения ускорения и начальной скорости.
Заключение

В целом уравнениями движения в физике считаются соотношения, которые помогают нам связать физические величины, а именно расстояние, затрачиваемое время, ускорение, начальную и конечную скорость. Эти уравнения способны облегчить расчеты равномерно ускоренного движения по прямой.

В этом блоге мы поняли все понятия и производные, необходимые для этой темы.

Часто задаваемые вопросы 

1.