Уравнение движения тела в физике
В том случае, если мы имеем дело с твердым телом, которое в общем случае имеет 6 степеней свободы, то общая система уравнений движения должна содержать шесть независимых уравнений. Их можно представить в виде производных по времени от двух векторов: импульса и момента импульса тела.
Общие законы и уравнения движения системы тел
Произвольную систему тел всегда можно свести к системе материальных точек. Это видно из того, что отдельное тело конечных размеров всегда мысленно можно разбить на столь малые части (частицы), что каждую часть можно рассматривать как материальную точку. Таким образом, выясняя общие законы движения системы тел, можно исходить из представления о системе материальных точек. Соответственно, имеем первое уравнение:
где — полный импульс тела, – результирующая внешних сил, действующих на тело.
В случае поступательного движения твердого тела его скорость скорости центра масс этого тела: .
или
где — масса тела, — его ускорение.
Второе уравнение движения записывается для тела вращающегося относительно неподвижной точки (полюса), и имеет вид:
где — момент импульса, — момент внешних сил, приложенных к телу.
Уравнение движения твердого тела
Уравнение динамики твердого тела, вращающегося вокруг неподвижной точки О, в жестко связанной с телом подвижной системе координат (x’,y’,z’), начало которой находится в точке О, имеет вид:
где — угловая скорость вращения тела, а — относительная производная по времени от вектора — орты подвижной системы.
Если оси подвижной системы координат совпадают с главными осями инерции тела в точке О, то уравнения движения тела в проекциях на эти оси имеют вид:
где – главные моменты инерции тела в точке О, – проекции вектора угловой скорости тела на главные оси инерции, – моменты внешних сил относительно тех же осей. Эти уравнения называют динамическими уравнениями Эйлера.
Эти уравнения называют динамическими уравнениями Эйлера.
Уравнение движения тела, вращающегося вокруг неподвижной оси
Уравнение движения тела, вращающегося вокруг неподвижной оси (например, оси Оz):
или
где – момент инерции тела относительно оси Oz. Если тело не деформируется, то — постоянная, тогда уравнение движения:
где – угловое ускорение тела.
Свободное твердое тело в общем случае участвует одновременно в двух движениях- поступательном со скоростью центра масс и вращательном вокруг центра масс с угловой скоростью . Векторы и удовлетворяют двум дифференциальным уравнениям движения свободного тела (которые получают из 2 и 3), подстановкой соответствующих скоростей центра масс:
где m- масса тела, — скорость центра масс, — вектор результирующей внешней силы, — вектор результирующий моментов внешних сил относительно центра масс C, , где — радиус вектор и скорость малого элемента массой dm в поступательно движущейся системе координат с началом в точке C.
Примеры решения задач
Часть 15 — Движение несвободного твердого тела / Хабр
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений.
 Угловые скорость и ускорения в параметрах Родрига-Гамильтона
Угловые скорость и ускорения в параметрах Родрига-Гамильтона - Нестандартное введение в динамику твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
В прошлый раз мы рассмотрели один из способов получения дифференциальных уравнений движения твердого тела исходя из принципа Даламбера. Мы остановились на общей форме уравнений движения
Однако, внимательно взглянув на эти уравнения, меня следовало бы раскритиковать — дело в том, что в данных уравнениях число неизвестных слишком велико. К неизвестным следует отнести ускорение полюса
и угловое ускорение тела
, а также реакции связей
. И если движение тела ограничено хотя бы одной связью, число неизвестных величин в (1) и (2) превышает число уравнений.
Это происходит потому, что левая часть уравнений (1) и (2) содержит ускорения, вычисляемые для случая свободного движения тела, то есть в них имеются избыточные координаты. Поэтому, систему (1), (2) следует дополнить уравнениями связей, описывающими ограничения, налагаемые связями на координаты, скорости и ускорения точек тела.
Поэтому, систему (1), (2) следует дополнить уравнениями связей, описывающими ограничения, налагаемые связями на координаты, скорости и ускорения точек тела.
Этим мы сейчас и займемся — посмотрим, во что превращаются уравнения (1) и (2) при добавлении уравнений связей, и что дают нам полученные уравнения в практическом смысле.
Свободным называют такое тело, движение которого не ограничено связями. Соответственно в уравнениях (1) и (2) пропадают лишние неизвестные и они превращаются в
И для свободного тела нет смысла использовать произвольный полюс — лучше сменить центр приведения систем сил инерции на центр масс тела, записав уравнения движения в более простой форме
Уравнения (5) и (6) — дифференциальные уравнения свободного движения твердого тела. Они могут быть разрешены относительно ускорений и проинтегрированы численно, при заданных начальных условиях.
А теперь предположим, что движение тела ограничено сферическим шарниром, расположенным в точке
. Тогда, выбрав полюс в этой неподвижной точке, мы можем добавить уравнение связи
Тогда, выбрав полюс в этой неподвижной точке, мы можем добавить уравнение связи
Реакция сферического шарнира, выражается одной силой
, поэтому, с учетом (7) уравнения (1) и (2) можно переписать в виде
причем
, так как сила
приложена в точке
, значит, получаем окончательно
Уравнение (8) позволяет определить угловое ускорение тела, исходя из начальных условий задачи и известных активных сил, приложенных к телу, а уравнение (9) дает возможность, зная угловое ускорение, найти реакцию сферического шарнира. Таким образом мы получаем дифференциальные уравнения сферического движения.
Вращательным называется движение тела, когда две его точки остаются неподвижными в любой момент времени. Если выразить этот факт с помощью уравнений, то мы можем записать следующие уравнения связей
Условие (10) выражает неподвижность одной из точек тела, а условие (11) — неизменность направления оси вращения тела. Исходя из (11) можно выписать угловую скорость и угловое ускорение тела через параметры конечного поворота
Подставляем (12) и (10) в уравнение (2)
учитывая, что у нас две связи, и соответственно две реакции от подшипников, на которых происходит поворот тела. Причем сразу можно учесть, что
Причем сразу можно учесть, что
, так как первая реакция приложена в точке
. Кроме того выполним скалярное умножение последнего уравнения на орт оси вращения
Учтем, что момент второй реакции можно вычислить как
, при этом
, то есть получаем
Вторые слагаемые в обеих частях данного уравнения — смешанные произведения компланарных векторов и равны нулю, в итоге имеем
— дифференциальное уравнение вращения тела вокруг неподвижной оси, где
называют
моментом инерции твердого тела относительно оси вращения, а
— проекция векторного момента относительно неподвижной точки на ось проходящую через эту точку или —
момент силы относительно оси.
Выражение (14) крайне интересно. Если переписать его в тензорной форме, то мы получим формулу
позволяющую, по известному тензору инерции твердого тела определить его момент инерции относительно интересующей нас оси вращения, направление которой в пространстве задано ортом
. Момент инерции (16) является скалярной величиной, характеризующей распределение массы тела вокруг оси вращения. Эта величина, равно как и уравнение (13) хорошо известны из общего курса теоретической механики.
Момент инерции (16) является скалярной величиной, характеризующей распределение массы тела вокруг оси вращения. Эта величина, равно как и уравнение (13) хорошо известны из общего курса теоретической механики.
При поступательном движении, связи, наложенные на тело препятствуют его вращению. В этом случае мы можем записать очевидные равенства
Полагая идеальность связей, мы можем записать условие, накладываемое на их реакции
где
— вектор, касательный к траекториям точек тела. В случае поступательного движения, траектории всех его точек одинаковы, а значит и вектор касательной к траектории одинаков для всех точек. С учетом (17) и (18) можно переписать уравнение (1)
или
— дифференциальное уравнение поступательного движения тела в проекциях на касательную к траекториям его точек.
В данной статье мы рассмотрели, как преобразуются общие уравнения движения твердого тела (1) и (2) если дополнить их уравнениями связей. При этом, мы легко и непринужденно построили дифференциальные уравнения движения для всех частных случаев движения тела, изучаемых теоретической механикой.
при подготовке данной статьи использован метод, предложенный пользователем SeptiM. В связи с очевидным удобством работы, хочу выразить признательность автору, за проделанную им работу.
Продолжение следует…
Уравнения движения твердого тела
Страница 1 из 2
Поскольку твердое тело обладает в общем случае шестью степенями свободы, то общая система уравнений движения должна содержать шесть независимых уравнений. Их можно представить в виде, определяющем производные по времени от двух векторов: импульса и момента тела.
Первое из этих уравнений получается просто путем суммирования уравнений =f для каждой из составляющих тело частиц, где p — импульс частицы, а f — действующая на нее сила. Вводя полный импульс тела
P = p = μV
и полную действующую на него силу f=F, получим
= F. (34.1)
(34.1)
Хотя мы определили F как сумму всех сил f, действующих на каждую их частиц, в том числе со стороны других частиц тела, фактически в F входят лишь силы, действующие со стороны внешних источников. Все силы взаимодействия между частицами самого тела взаимно сокращаются; действительно, при отсутствии внешних сил импульс тела, как и всякой замкнутой системы, должен сохраняться, т.е. должно быть F=0.
Если U — потенциальная энергия твердого тела во внешнем поле, то сила F может быть определена путем дифференцирования ее по координатам центра инерции тела:
F = − . (34.2)
Действительно, при поступательном перемещении тела на δR настолько же меняются и радиус-векторы каждой точки тела, а потому изменение потенциальной энергии
δU = δ = δR = −δR f = −FδR .
Отметим в этой связи, что уравнение (34.1) может быть получено и как уравнение Лагранжа по отношению к координатам центра инерции
=
с функцией Лагранжа (32.4), для которой
= μV = P, = − = F.
Перейдем к выводу второго уравнения движения, определяющего производную по времени от момента импульса M. Для упрощения вывода удобно выбрать «неподвижную» (инерциальную) систему отсчета таким образом, чтобы в данный момент времени центр инерции тела покоился относительно нее.
Имеем
= [rp] = [p] + [r].
В силу сделанного нами выбора системы отсчета (в котором V=0) значение в данный момент времени совпадает со скоростью v=. Поскольку же векторы v и p = mv имеют одинаковое направление, то [p]=0. Заменив также на силу f, получим окончательно:
= K, (34. 3)
3)
где
K = [rf]. (34.4)
Поскольку момент М определен относительно центра инерции (см. здесь), он не меняется при переходе от одной инерциальной системы отсчета к другой. Это видно из формулы (9.5) с R=0. Отсюда следует, что зфавнение движения (34.3), полученное здесь при определенном выборе системы отсчета, тем самым, в силу галилеевского принципа относительности, справедливо в любой инерциальной системе.
Вектор [rf] называется моментом силы f, так что K есть сумма моментов всех сил, действующих на тело. Как и в полной силе F, в сумме (34.4) фактически должны учитываться лишь внешние силы; в соответствии с законом сохранения момента импульса сумма моментов всех сил, действующих внутри замкнутой системы, должна обращаться в нуль.
Движение тела переменной массы – Энциклопедия по машиностроению XXL
Движение тела переменной массы [c. 76]
76]Движение тела переменной массы. Железнодорожная платформа в момент / = 0 начинает двигаться под действием постоянной силы тяги F. Пренебрегая трением в осях, найти зависимость от времени скорости платформы v([c.82]
Особенно важным примером движения тела переменной массы является движение ракеты. Масса здесь изменяется из-за выбрасывания из ракеты газов и других продуктов сгорания топлива. [c.412]
ДВИЖЕНИЕ ТЕЛА ПЕРЕМЕННОЙ МАССЫ [c.123]
Получить уравнение движения тела переменной массы. Решение. Закон изменения импульса Р системы частиц [c.123]
Понятие о точке переменной массы. Обычно в теоретической механике масса движущегося тела рассматривается как величина постоянная. Между тем можно указать много примеров движения тел, когда масса их изменяется с течением времени. При этом изменение массы может происходить путем отделения от те за его частиц или присоединения к нему частиц извне. Примерами подобного изменения массы движущегося тела являются в первом случае — ракеты разных классов, реактивные снаряды, ракетные мины и торпеды, во втором— движение какой-нибудь планеты, масса которой возрастает от падающих на нее метеоритов. Обе причины переменности массы одновременно действуют, например, в реактивном самолете с прямоточным воздушно-реактивным двигателем, когда частицы воздуха засасываются в двигатель из атмосферы и затем выбрасываются из него вместе с продуктами горения топлива. Мы будем рассматривать только тот случай, когда процесс отделения от тела или присоединения к нему частиц происходит непрерывно. Тело, масса которого непрерывно изменяется с течением времени вследствие присоединения к нему или отделения от него материальных частиц, называют телом переменной массы. Если при движении тела переменной массы его размерами по сравне-
[c.593]
Примерами подобного изменения массы движущегося тела являются в первом случае — ракеты разных классов, реактивные снаряды, ракетные мины и торпеды, во втором— движение какой-нибудь планеты, масса которой возрастает от падающих на нее метеоритов. Обе причины переменности массы одновременно действуют, например, в реактивном самолете с прямоточным воздушно-реактивным двигателем, когда частицы воздуха засасываются в двигатель из атмосферы и затем выбрасываются из него вместе с продуктами горения топлива. Мы будем рассматривать только тот случай, когда процесс отделения от тела или присоединения к нему частиц происходит непрерывно. Тело, масса которого непрерывно изменяется с течением времени вследствие присоединения к нему или отделения от него материальных частиц, называют телом переменной массы. Если при движении тела переменной массы его размерами по сравне-
[c.593]
Как определяется реактивная сила при движении тела переменной массы Что означают величины, входящие в формулу
[c. 183]
183]
ДВИЖЕНИЕ ТЕЛ ПЕРЕМЕННОЙ МАССЫ И ЭЛЕМЕНТЫ КОСМОНАВТИКИ [c.107]
Уравнение движения тел переменной массы, связывающее силу с ускорением и учитывающее также изменение массы тел в процессе их движения, было получено И. В. Мещерским . [c.108]
Выведем основное уравнение движения тел переменной массы. При этом, пренебрегая размерами и формой тела, будем рассматривать его как материальную точку переменной массы. [c.108]
Реактивная сила при этом также равна нулю. Примером движения тела переменной массы с относительной скоростью, равной нулю, может служить нить, сматываемая с барабана. Скорость точки А барабана (рис. 85) будет Па = (о>С где со — угловая скорость вращения барабана, R — его радиус. Такой же скоростью обладает элемент Ат нити, отделяющейся от барабана, и поэтому относительная скорость этого элемента нити равна нулю. [c.110]
Пример 4. Рассмотрим движение тела переменной массы, в именно поступательное прямолинейное движение ракеты в свободном пространстве под действием только реактивной силы. Мае-
[c.181]
Мае-
[c.181]
Костицын В. Т. Об одном графическом решении задач движения тела переменной массы. Труды Института машиноведения. Семинар по теории машин и механизмов. Вып. 60. Изд. АН СССР, 1956. [c.234]
Важнейшим результатом исследования был вывод основной формулы ракетодинамики — движения тела переменной массы под действием реактивной силы в условиях отсутствия внешних сил (анализ движения тела переменной массы был также сделан в 1897 г. русским ученым И. В. Мещерским). Формула выражает зависимость между скоростью истечения продуктов сгорания (с), отношением массы топлива (М ) к массе конструкции ракеты (Mj) и конечной скоростью ракеты (v) [c.437]
Теорема количеств движения. Производная по времени от главного вектора количеств движения тела переменной массы, вычисленная в предположении постоянства масс, равна сумме главного вектора внешних сил и главного вектора реактивных сил
[c. 409]
409]
Задача о движении тела переменной массы, как видим, более сложная, чем задача о движении тела постоянной массы. Мы ею займемся на следующем занятии. [c.108]
Попытки теоретических исследований реактивного движения тел переменной массы были связаны с проблемами усиления судового движителя и с изобретением фабричного двигателя. [c.226]
Следующим крупным шагом в построении общей теории движения тел переменной массы была работа И. В. Мещерского (1904) в которой рассматривается самый общий случай одновременного присоединения и отделения частиц от основной точки. При таком процессе суммарная масса всего тела (основной точки) может быть неизменной, и тогда будет переменным лишь состав частиц. [c.232]
Из других работ по механике тел переменной массы Мещерского важное практическое значение имеет его исследование вращения твердого тела переменной массы вокруг неподвижной оси дополняющее ранние работы о поступательном движении тел переменной массы. [c.232]
[c.232]
Продолжением направления Мещерского можно считать существенные достижения ученых в построении общей теории движения тела переменной массы. [c.241]
В работе 1946 г. Космодемьянский выводит основные теоремы о движе- 241 НИИ центра масс системы, об изменении главного вектора количества движения, кинетического момента и кинетической энергии тела переменной массы. Однако уравнения движения тела переменной массы, выведенные этим путем, не описывали движения таких объектов, где необходимо было учитывать внутреннее относительное движение частиц, реактивное действие которых исключалось гипотезой удара или мгновенного контакта. [c.241]
В дальнейшем точечный метод вывода дифференциальных уравнений движения тела переменной массы использовали многие ученые В. ф. Котов, [c.242]
Наиболее важные достижения в деле построения общей теории реактивного движения тела переменной массы были сделаны в 40-х годах в трудах совет- 243 ских ученых (главные из них были коротко рассмотрены выше) на основе фундаментальной разработки богатейшего научного наследия Мещерского и Циолковского.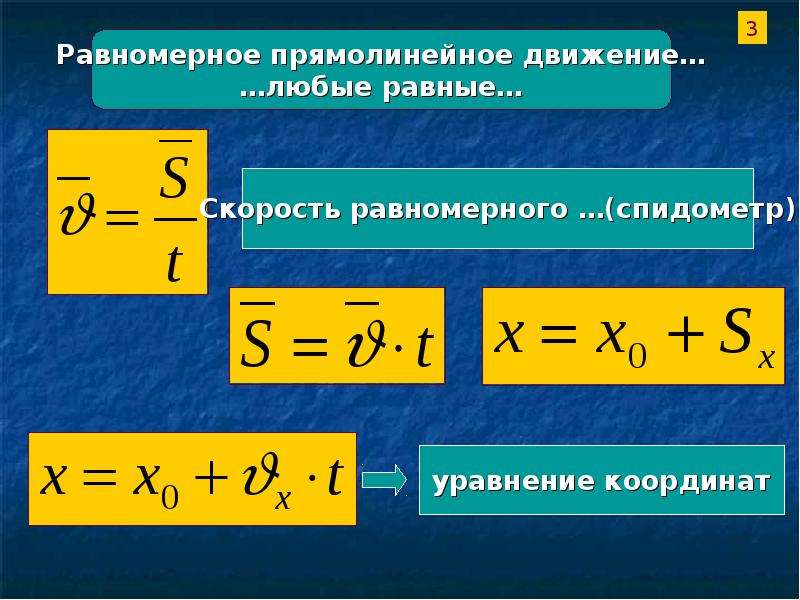 [c.243]
[c.243]
Во-вторых, задача о движении тел переменной массы также требует отыскания новых форм законов Ньютона. В самом деле, когда мы формулировали второй закон Ньютона в виде р—та, то предполагали, что масса т является постоянной и не меняется во время движения. Следовательно, необходимо специально проверить, можно ли применить этот закон в таком виде, если во время движения происходят какие-либо изменения массы т. [c.185]
Одно из важнейших практических применений закон сохранения количества движения нашел при решении задачи о движении тел переменной массы. Это решение становится особенно простым в том случае, когда присоединение (или отделение) частиц к движущемуся телу происходит так же, как при неупругом ударе,— силы [c.203]
Уравнения движения тел переменной массы и выражение для реактивной силы были впервые найдены петербургским профессором И. В. Мещерским в 1897 г. Уравнения Мещерского принадлежат к числу важнейших открытий в механике, сделанных на рубеже XIX и XX вв.
 С особой силой значение этих открытий выявилось в наши дни, когда уравнения Мещерского стали широко использоваться в ракетной технике. Формула для реактивной силы, с которой мы познакомились, сейчас является основной для расчета силы тяги ракетных и турбореактивных двигателей всех систем.
[c.205]
С особой силой значение этих открытий выявилось в наши дни, когда уравнения Мещерского стали широко использоваться в ракетной технике. Формула для реактивной силы, с которой мы познакомились, сейчас является основной для расчета силы тяги ракетных и турбореактивных двигателей всех систем.
[c.205]Применение второго закона Ньютону к движению тел переменной массы [c.209]
Книга является учебником для студентов высших технических учебных заведений представление о ее содержании дает оглавление, Материал в книге изложен так, что ею можно пользоваться при изучении курса как по кратким, так и по более полным программам. При этом та часть материала, которая может входить Б те или иные более полные программы, помещена в главы или параграфы, отмеченные зЬездочкой или набранные петитом. При чтении книги любая часть этого материала может опускаться без ущерба для понимания остального текста. Заметим однако, что ознакомиться с такими освещенными в учебнике весьма интересными вопросами, как движение в поле земного тяготения или движение тела переменной массы (ракеты), полезно студентам всех специальностей. [c.3]
[c.3]
Некоторые другие случаи движения тела переменной массы. Если рассмотреть движение тела, масса М которого с течением времени вследствие непрерывного присоединении к нему частиц возрастает (dAl/dOO), считая это тело тоже точкой переменной массы, а относительную скорость присоединяющихся частиц обозначить по-прежнему а, то нетрудно проверить, что для такого тела уравнение движения сохранит вид (25) или (26), только в уравнении (26), поскольку теперь AMldtXl, будет [c.288]
Именно в этой форме чаще всего второй закон Ньютона встречается в различных учебниках. Однако далеко не всегда можно полагать массу независи.мой от времени. Мы рассмотрим далее некоторые примеры движения тел переменной массы. Переменность массы [c.228]
Пример. В качестве прилоя1ения общей теоремы о движении центра масс материальной системы выведем уравнение движения тела переменной массы, которое называется уравнением Мещерского.
[c. 146]
146]
Другие задачи, решенные в трудах советских механиков, но постановке и методам решения в значительной мере тоже относятся к теории регулирования или оптимального управления. В них рассмотрено движение тела переменной массы в гравитационном поле с постоянной и убывающей мощностью, исследован вопрос о влияншг случайных отклонений от оптимальной (в том или другом отношении) программы движения, об учете ограниченности мощности тяги п т. д. [c.309]
Первые серьезные теоретические поиски в этих областях принадлежат Д. Бернулли и Л. Эйлеру (середина XVIII в.). Эйлер вывел уравнение поступательного движения объекта переменной массы (криволинейной трубки, по которой протекает несжимаемая жидкость движение считается одномерным) и уравнение вращательного движения тела переменного состава (турбины) около неподвижной оси. В течение полутораста лет специалисты по расчету действия гидравлических турбин и водометных движителей в десятках работ и исследований не смогли превзойти всеми забытые результаты Эйлера. Помимо того что он вывел названные типы уравнений движения тел переменной массы, он дал множество полезных рекомендаций для проектирования таких гидравлических двигателей и, самое главное, получил выра-
[c.226]
Помимо того что он вывел названные типы уравнений движения тел переменной массы, он дал множество полезных рекомендаций для проектирования таких гидравлических двигателей и, самое главное, получил выра-
[c.226]
В XVIII в. очень интересное исследование проблемы внутренней баллистики было проведено Ж. Лагранжем Он составил дифференциальные уравнения движения орудия, снаряда и пороховых газов внутри канала ствола. Откат орудия представлял собой пример реактивного движения тела переменной массы. [c.228]
Общетеоретические вопросы динамики реактивного движения тел переменной массы продолжали занимать большое место в литературе 30-х годов. Вертикальное движение ракеты рассматривал в своей работе В. П. Ветчин-вин учитывая силы тяжести и квадратичный закон сопротивления воздуха л считая плотность среды уменьшающейся экспоненциально с возрастанием высоты. Предполагалось, что масса ракеты изменяется по линейному закону в зависимости от времени. Актуальным для того времени теоретическим вопросам механики тел переменной массы были посвящены работы И. А. Меркулова В. С. Зуева , М. К. Тихонравова Несколько интересных книг.
[c.237]
Актуальным для того времени теоретическим вопросам механики тел переменной массы были посвящены работы И. А. Меркулова В. С. Зуева , М. К. Тихонравова Несколько интересных книг.
[c.237]
Следует напомнить, что механика тел переменной массы не сводится к одним только задачам о движении ракет и включает самые разнообразные случаи движения земных и небесных тел, масса (или состав частиц) которых изменяется, на что указывал И. В. Мещерский. Отправным пунктом работы Мещерского над проблемами движения тел переменной массы были преимущественно задачи астрономии. В этом направлении в 1920—1930 гг. была выполнена серия интересных работ. О работах Леви-Чивита уже говорилось выше, в работах его последователей Э. Альманзи, Э. Ферми, Р. Армел- [c.239]
Метод вывода уравнений движения системы точек Агостинелли по существу является точечным , т. е. уравнение Леви-Чивиты, записанное для одной точки переменной массы, суммируется по всем точкам системы. Как и в динамике системы постоянных масс, он приходит к общему уравнению динамики системы (к уравнению Даламбера — Лагранжа). Из этого уравнения при дополнительных частных предположениях получается ряд теорем и свойств движения тела переменной массы. Например, теорема о движе-
[c.240]
Как и в динамике системы постоянных масс, он приходит к общему уравнению динамики системы (к уравнению Даламбера — Лагранжа). Из этого уравнения при дополнительных частных предположениях получается ряд теорем и свойств движения тела переменной массы. Например, теорема о движе-
[c.240]
В 1951 г. А. А. Космодемьянский несколько видоизменил свой вывод основных теорем механики тела переменной массы по сравнению с 1946 г. Новые дифференциальные уравнения движения тела переменной массы были составлены для случаев, когда могло иметь место и относительное движение изменяющих масс по внутренним каналам тела. Кроме того, Космоде-242 мьянский вывел уравнения движения тела переменной массы в обобщенных координатах, которые по внешнему виду отличались от уравнений Лагранжа второго рода тем, что в правых частях к обычным обобщенным силам присоединялись реактивные силы. Там же он выводит канонические уравнения для тела переменной массы.
 [c.242]
[c.242]В 40 был огмечен один из важнейших результатов экспериментов было показано, что ускорения при движении тел зависят от состояния движения этих тел, от их скорости. Пользуясь тем, что эта зависимость слаба при малых скоростях, мы это явление не учитывали при формулировке законов. Вопрос о том, как учесть такую зависимость при больших скоростях, также непосредственно связан с рассмотрением движения тел переменной массы. [c.185]
Ускорение. Уравнение движения точки с постоянным ускорением
Мы с вами изучили равномерное прямолинейное движение, то есть
движение, при котором точка за любые равные промежутки времени совершает
одинаковые перемещения. Но, как мы уже отмечали, при реальном движении тел их
скорости обычно меняются или по модулю, или по направлению, или же одновременно
и по модулю, и по направлению. Например, когда автомобиль трогается с места,
его скорость постепенно возрастает. А при торможении на перекрёстке, наоборот, —
уменьшается.
А при торможении на перекрёстке, наоборот, —
уменьшается.
При вращательном движении скорость любой точки дисков электрофорной машины изменяется лишь по направлению (конечно же, при условии, что число оборотов в единицу времени не изменяется).
Наконец, при выстреле из пушки под некоторым углом к горизонту скорость ядра будет изменяться как по модулю, так и по направлению.
При этом очевидно, что в рассмотренных нами примерах изменение скорости может происходит как очень быстро, так и достаточно медленно.
Физическая векторная величина, характеризующая быстроту изменения скорости, называется ускорением.
Давайте вспомним, как определяется ускорение точки. Для этого
рассмотрим её неравномерное движение вдоль некоторой криволинейной траектории. Пусть
в некоторый момент времени t она
занимает положение М и имеет скорость υ. А спустя некоторый
промежуток времени Δt1 —
положение М1 и скорость υ1.
Найдём изменение скорости точки за это время как геометрическую разность векторов конечной и начальной скоростей и укажем эту разность на рисунке:
Если теперь мы с вами разделим вектор изменения скорости на промежуток времени, в течение которого это изменение произошло, то тем самым получим так называемый вектор среднего ускорения точки:
Он направлен точно так же, как и вектор изменения скорости.
Но как же нам определить ускорение точки в положении М?
Для этого будем уменьшать рассматриваемые промежутки времени и находить вектор
изменения скорости для каждого случая. Из полученного рисунка видим, что вектор
изменения скорости, а следовательно, и вектор среднего ускорения, уменьшается
по модулю и при этом меняется его направление. В конце концов промежуток времени
станет так мал, что можно будет пренебречь изменением скорости точки за это
время. Следовательно, при стремлении промежутка времени к нулю отношение будет
стремиться к своему некоторому предельному значению.
Физическая векторная величина, равная пределу отношения изменения скорости к промежутку времени, в течение которого это перемещение произошло, при стремлении промежутка времени к нулю, называется мгновенным ускорением (или просто ускорением):
Важно запомнить, что вектор ускорения направлен так же, как и вектор изменения скорости при стремлении промежутка времени к нулю. И в общем случае вектор ускорения не совпадает с направлением вектора скорости, а составляет с ним некоторый угол.
Как мы уже видели, при неравномерном движении по криволинейной траектории скорость точки непрерывно меняется по модулю и направлению. Поэтому вектор ускорения часто называют полным ускорением и представляют в виде суммы двух ускорений:
Первое ускорение называется тангенциальным (или касательным), так как направлено оно по касательной к траектории движения. Его модуль характеризует изменение модуля скорости:
Второе ускорение всегда направлено перпендикулярно вектору
мгновенной скорости и поэтому называется нормальным (нормаль — это
перпендикуляр) или центростремительным. Его модуль характеризует
изменение скорости по направлению:
Его модуль характеризует
изменение скорости по направлению:
А вектор центростремительного ускорения в любой момент времени направлен к центру кривизны траектории.
Конечно же движение точки может происходить как с постоянным, так и с переменным ускорением. Так, если отношение изменения скорости к промежутку времени в течение которого это изменение произошло одинаково для любого интервала времени, то говорят, что точка движется с постоянным ускорением. А движение точки называют равноускоренным движением:
Из формулы видно, что если скорость и промежуток времени выражены в единицах СИ, то единицей измерения ускорения является метр на секунду в квадрате (м/с2).
Также из формулы следует, что за единицу ускорения в СИ принимается ускорение такого равноускоренного движения, при котором за 1 с скорость точки изменяется на 1 м/с.
Теперь давайте выясним, как зависит скорость точки от времени
при её равноускоренном движении. Итак, пусть в начальный момент времени t0 скорость точки равнялась ,
а в момент времени t — .
Итак, пусть в начальный момент времени t0 скорость точки равнялась ,
а в момент времени t — .
Тогда ускорение точки равно изменению вектора скорости к промежутку времени, за который это изменение произошло:
Если начальный момент времени принять равным нулю, то из этого уравнения легко получить формулу для определения скорости точки в любой момент времени при её равноускоренном движении — уравнение скорости:
Таким образом, чтобы определить скорость точки в произвольный момент времени, необходимо знать её начальную скорость и ускорение.
На практике при вычислениях скорости мы будем пользоваться формулами, в которые входят не векторы, а их проекции на соответствующие координатные оси:
Из записанных формул видно, что при равноускоренном движении
скорость точки линейно зависит от времени. Значит, график скорости представляет
собой прямую линию, наклонённую к оси времени под некоторым углом. При этом чем
больше ускорение точки, тем больший угол с осью времени составляет график
проекции скорости.
При этом чем
больше ускорение точки, тем больший угол с осью времени составляет график
проекции скорости.
Теперь посмотрим на прямую 3. Что можно сказать о движении тела в этом случае?
Во-первых, очевидно, что за промежуток времени от нуля до t1 проекция скорости была положительна.
Во-вторых, скорость точки уменьшалась и в момент времени, равный t1 она стала равной нулю. Точка пересечения графика скорости с осью времени называется точкой поворота. В ней направление скорости меняется на противоположное, после чего тело начинает двигаться равноускоренно.
Теперь давайте вспомним, что основной задачей механики
является определение положения точки в любой момент времени. Получим уравнения,
которые позволяют это сделать для равноускоренного движения. Для примера
рассмотрим случай, когда проекция начальной скорости и ускорения положительны.
По аналогии со случаем равномерного прямолинейного движения логично
предположить, что проекция перемещения, совершённого телом за время t,
будет равна площади фигуры, ограниченной графиком, осью времени и
перпендикуляром, восставленным к графику из точки t. В данном случае эта
фигура — трапеция.
В данном случае эта
фигура — трапеция.
Для доказательства этого предположения рассмотрим очень малый промежуток времени Δt внутри выбранного интервала времени. По аналогии с мгновенной скоростью, если выбранный промежуток времени достаточно мал, то изменением скорости за это время можно пренебречь. То есть движение точки можно считать равномерным. Значит, проекция перемещения за это время будет равна площади этого маленького прямоугольника. При этом очевидно, что на такие узкие полоски мы можем разбить всю площадь фигуры под графиком скорости
Тогда, согласно рисунку, проекция перемещения при
равноускоренном движении определяется площадью трапеции. Площадь же трапеции,
как известно из геометрии, равна произведению полусуммы её оснований на высоту.
В нашем случае длина одного из оснований численно равна проекции начальной
скорости точки, второго — проекции скорости через время t.
Высота же трапеции численно равна времени.
Теперь вспомним, что по определению проекция перемещения численно равна разности конечной и начальной координат точки:
Тогда после небольших математических преобразований получим формулу для определения координаты точки при её равноускоренном движении:
Важно помнить, что в формулу входят проекции начальной скорости и ускорения точки. А они могут быть как положительными, так и отрицательными. Координата начального положения точки также может быть больше или меньше нуля,
Если движение точки происходит в пространстве, то для определения оставшихся двух координат используют уравнения, имеющие аналогичной вид:
Записанные нами формулы называются кинематическими уравнениями движения точки в координатной форме. Они применимы для описания как прямолинейного, так и криволинейного движения.
В общем виде кинематические уравнения движения можно записать с помощью одного векторного уравнения:
Теперь для закрепления материала решим с вами одну небольшую
задачку. Итак, на рисунке представлен график зависимости скорости точки от
времени. Определите, в какой момент времени координата точки станет равной 30
м, если в момент начала наблюдения её координата равнялась –6 м. Определите
скорость точки в этот момент времени.
Итак, на рисунке представлен график зависимости скорости точки от
времени. Определите, в какой момент времени координата точки станет равной 30
м, если в момент начала наблюдения её координата равнялась –6 м. Определите
скорость точки в этот момент времени.
Дифференциальные уравнения движения материальной точки. Две основные задачи динамики.
Динамика
Принцип независимости действия сил
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от действия каждой силы в отдельности.
Пусть к материальной точке А приложены силы F1 и F2 равнодействующая которых равна F на основании аксиомы параллелограмма запишем:
F1 + F2 = F.
Разделив обе части равенства на массу точки m, получим:
F1/m + F2/m = F/m, откуда имеем: а1 + а2 = а.
Применяя последовательно аксиому параллелограмма, можно показать, что при одновременном действии на материальную точку нескольких сил ее ускорение будет таким, как если бы действовала одна равнодействующая сила F = ΣFi.
Пользуясь изложенным выше принципом независимости действия сил, выведем уравнение движения материальной точки в дифференциальной форме.
***
Дифференциальные уравнения движения материальной точки
Пусть материальная точка А массой m движется в плоскости чертежа под действием равнодействующей силы F = ΣFi с ускорением а, тогда:
F = ma.
Спроецируем это векторной равенство на две взаимно-перпендикулярные оси координат x и y (оси и вектор силы F лежат в одной плоскости) и получим уравнение плоского движения материальной точки в координатной форме:
Fx = ΣX = max; Fy = ΣY = may.
Применяя теорему о проекции ускорения на координатную ось, эти уравнения можно записать в виде дифференциальных уравнений плоского движения точки:
ΣX = m(d2x/dt2); ΣY = m(d2y/dt2),
где ΣX и ΣY – алгебраические суммы проекций сил, действующих на точку, на соответствующие координатные оси; x и y – текущие координаты точки.
С помощью полученных дифференциальных зависимостей решаются две основные задачи динамики:
- по заданному движению точки определяют действующие на нее силы;
- зная действующие на точку силы, определяют ее движение.
В тех случаях, когда при решении задач имеем дело с несвободной материальной точкой, необходимо применять принцип освобождаемости, т. е. отбросить связи и заменить их реакциями, учитывая последние в уравнении движения наравне с действующими на точку активными силами.
***
Пример решения первой задачи динамики
Задача: движение тела массой m = 0,5 кг выражается уравнениями:
x = 2t; y = 3 + t – 5t2,
где x и y (в сантиметрах) – координаты точки в момент времени t (в секундах).
Определить силу, действующую на тело.
Решение.
Данный пример относится к первой задаче динамики. Прежде всего, пользуясь теоремой о проекции ускорения на координатную ось, определим проекции ускорения на оси x и y:
ax = d2x/dt2 = 0; ay = d2y/dt2 = – 10 см/с2 = – 0,1 м/с2.
Подставив эти значения в уравнение движения материальной точки, получим:
X = max = 0,5×0 = 0 Н; Y = may = 0,5×(- 0,1) = – 0,05 Н.
По полученным значениям проекций силы на координатные оси можно сделать вывод, что она параллельна оси ординат, направлена в сторону отрицательных ординат и по модулю равна:
F = √(X2 + Y2) = |Y| = 0,05 Н.
Задача решена.
***
Пример решения второй задачи динамики
Задача: на материальную точку массой m = 4 кг, лежащую на гладкой горизонтальной плоскости, действует горизонтальная сила F = 12 Н.
С какой скоростью будет двигаться материальная точка через время t = 10 с, если до приложения силы точка находилась в состоянии покоя?
Решение.
Данный пример относится ко второй задаче динамики.
Так как данная материальная точка лежит на гладкой горизонтальной плоскости, то под действием горизонтальной постоянной силы F точка будет двигаться прямолинейно равноускоренно. Направив координатную ось x вдоль траектории движения точки (вдоль вектора силы F), запишем уравнение ее движения:
Направив координатную ось x вдоль траектории движения точки (вдоль вектора силы F), запишем уравнение ее движения:
ΣX = max = ma.
Спроецировав на ось x действующие на точку силы, и подставив в это уравнение значение массы m, определим ускорение точки:
a = ΣX/m = F/m = 12/4 = 3 м/с2.
Применим формулу скорости равноускоренного движения и подставим в нее значения, получим:
v = v0 + at = at = 3×10 = 30 м/с.
Задача решена.
***
Движение материальной точки, брошенной под углом к горизонту
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Уравнения движения твердого тела
Уравнения движения твердого тела
(Эйлер законы)
Инерциальная система отсчета: Явная форма
законы механики зависят от системы отсчета, используемой для обозначения движений. То
система отсчета часто является фоном события, а Земля является
самая распространенная система отсчета. Например, второй закон Ньютона записывается как
То
система отсчета часто является фоном события, а Земля является
самая распространенная система отсчета. Например, второй закон Ньютона записывается как
когда ускорение рассчитывается относительно инерциальной системы отсчета.Точки инерциальной системы отсчета имеют без ускорения (чисто перевод с постоянной или нулевой скоростью, и без вращение). С другой стороны, этот же закон будет записан как
.
если
ускорение рассчитывается с
относительно кадра, который является чисто переводным с ускорением .Поэтому важно рассмотреть систему отсчета
осторожно, прежде чем использовать какую-либо конкретную форму данного закона. Большую часть времени,
законы движения записываются относительно инерциальной системы отсчета, то из этого
формы можно вывести форму закона относительно других систем отсчета.
Большую часть времени,
законы движения записываются относительно инерциальной системы отсчета, то из этого
формы можно вывести форму закона относительно других систем отсчета.
Законы Эйлера: Законы движения для твердого тела известны как законы Эйлера. Эйлер вывел два закона движения жесткое тело. Два закона, записанные относительно инерциальной системы отсчета, равны
.
где O является фиксированной точкой на
инерциальная система отсчета.Первый из двух законов Эйлера описывает
как силы контролируют поступательное движение твердого тела (т.
изменение скорости центра масс, ). Второй из двух законов Эйлера описывает, как изменяется
угловой момент твердого тела определяется моментом сил и
пары нанесены на тело. Законы Эйлера написаны для тела фиксированных
материя (т. е. материя не может быть добавлена к телу, материя не может быть вычтена
из тела, и материя не может быть заменена другой материей).
Ан альтернативная форма этих законов, которая заменяет необходимость иметь фиксированную точку O на инерциальной системе отсчета, получается с помощью центра масс. Этот закон получено ниже и указано
где CM обозначает центр масс.
А третья альтернативная форма законов Эйлера может быть получена из второй альтернативной формы форма.Эта форма заменяет центр масс произвольным точка P , которая может двигаться в в любом случае (это может быть ускорение). Эта форма законов Эйлера записывается как
.
где это позиция центр масс относительно выбранной точки P . Подробная информация о том, как получить эту форму, также приведена ниже. Четвертый форма законов Эйлера дается как
где это позиция
точка P относительно центра
масса, и, как указано выше, P может быть выбран
произвольно.
Это также будет показано, что линейный импульс твердого тела определяется выражением масса, умноженная на скорость центра масс тела, дает альтернативную форма первого закона Эйлера как
где м – полная масса твердого тела а это ускорение центра масс тела.
Линейный импульс частицы: Для одной частицы массой м его линейный импульс определяется произведением его массы на скорость, так что
Линейный импульс тела: Линейный импульс тела считается суммой линейных импульс его частиц.Например, если у человека есть тело, состоящее из несколько частиц, каждая из которых имеет массу и скорость , их линейный импульс равен
Это нетрудно видеть, что для сплошного тела суммирование можно заменить на и интеграция для получения
положение центра масс тела можно найти из соотношения
Перестановка это отношение и взятие его производной по времени относительно инерциальной системы отсчета дает
где скорость
центр масс, измеренный относительно системы отсчета, а м — полная масса тела. Следовательно, можно сделать вывод, что импульс тела равен
Следовательно, можно сделать вывод, что импульс тела равен
Альтернативная форма Первый закон Эйлера: Используя приведенное выше соотношение для количества движения твердого тела, один можно заменить линейный импульс массой, умноженной на скорость центра масса, чтобы получить альтернативную форму первого закона Эйлера как
С масса постоянна в ньютоновской механике, приходим к соотношению
Примечание: Для одной частицы центр масс и положение частицы совпадают, и каждый восстанавливается Второй закон Ньютона.
Угловой момент частицы: Символ H O обозначает угловой импульса и для частицы массой м определяется как момент количества движения вокруг точки O и определяется уравнением
Угловой момент
для твердого тела: Угловой момент для твердого тела равен сумме углового
импульс частиц в нем. Дана система отсчета, точка O в этой системе отсчета и жесткая
тела, можно аппроксимировать угловой момент твердого тела как
Дана система отсчета, точка O в этой системе отсчета и жесткая
тела, можно аппроксимировать угловой момент твердого тела как
где предполагается, что тело аппроксимируется суммой частей, каждая из которых имеет массу , положение и скорость .
Взятие предел по мере уменьшения частей приводит к следующему интегралу представление углового момента твердого тела
где м – полная масса тела и и соответственно, положение и скорость дм относительно выбранной системы отсчета и выбранной точки отсчета O на ней.
Отношение между моментами сил, когда момент взят относительно разных точек: Момент силы взят около O может быть связано с моментом той же силы, взятой около точки A по соотношению
Отношение между угловыми моментами, когда угловой момент берется примерно разным очки: угловой момент тела, взятый около O можно связать с угловым моментом того же тела, взятым относительно точки A , соотношением
Альтернативные формы второго закона Эйлера: Полезную альтернативную форму второго закона Эйлера можно получить, используя вышеупомянутые правила изменения точки отсчета, чтобы записать второй закон как
Взятие преимущество первого закона Эйлера, и отмечая, что второй член на правая часть равна нулю, можно получить альтернативную форму второго закона Эйлера как
Важность этой формы состоит в том, что момент и угловой момент
вычисляется относительно центра масс, который не обязательно должен находиться на инерционной
Рамка. Таким образом, необходимость использования выбранной точки O на инерциальной системе отсчета была устранена в пользу центра
масса, которая может ускоряться. Взяв момент первого закона Эйлера вокруг
произвольная точка P и добавление ее к
это уравнение дает
Таким образом, необходимость использования выбранной точки O на инерциальной системе отсчета была устранена в пользу центра
масса, которая может ускоряться. Взяв момент первого закона Эйлера вокруг
произвольная точка P и добавление ее к
это уравнение дает
Один можете переписать это в одной из двух других альтернативных форм
Мехрдад Негабан и Университет Небраски, 1999–2002 годы.
Все права защищены
Свободное копирование и распространение только для личного использования
Факультет инженерной механики, Университет Небраски, Линкольн, Небраска 68588-0526
Жесткие кузова
Твердые тела в 2D
Приведенные выше уравнения #rk-er действительны. как в 2D, так и в 3D. Если мы знаем, что находимся в 2D
$\hat\imath,\hat\jmath$, то угловая скорость
вектор ортогонален плоскости в направлении $\hat{k}$
и уравнения могут быть записаны в более простой форме с
обозначение перпендикулярного вектора #rvv-en, как показано ниже.2 \, \vec{r}_{PQ}
\конец{выровнено}\]
как в 2D, так и в 3D. Если мы знаем, что находимся в 2D
$\hat\imath,\hat\jmath$, то угловая скорость
вектор ортогонален плоскости в направлении $\hat{k}$
и уравнения могут быть записаны в более простой форме с
обозначение перпендикулярного вектора #rvv-en, как показано ниже.2 \, \vec{r}_{PQ}
\конец{выровнено}\]
Точки $P$ и $Q$ — это две точки на жесткой тело. Скаляры $\omega$ и $\alpha$ — это скаляры угловая скорость и угловое ускорение твердого тела тело (положительное против часовой стрелки).
Векторы положения $\vec{r}_P$ и $\vec{r}_Q$ лежат в
плоскости $\hat\imath,\hat\jmath$, поэтому $\vec{v}_P$,
$\vec{v}_Q$ и $\vec{r}_{PQ}$ также находятся в этом
самолет.Угловая скорость и угловое ускорение
векторы ортогональны и поэтому могут быть записаны: \[\ начало {выровнено}
\vec{\omega} &= \omega\,\шляпа{k} \\
\vec{\alpha} &= \alpha\,\hat{k}. \circ$
вращение).
\circ$
вращение).
Если точка $M$ на твердом теле имеет нулевую скорость, то она называется мгновенным центром вращения , потому что скорость всех точек тела будет задана простым вращением вокруг $M$ с угловой скоростью $\vec{\omega}$ тела. В 2D мы всегда можем найти мгновенный центр со следующим уравнением, хотя это может быть вне физического тела.\перп \]
Точка $P$ имеет скорость $\vec{v}_P$ и прикреплена к твердое тело, вращающееся с угловой скоростью $\vec{\omega}$.
Мгновенный центр $M$ обладает тем свойством, что
точка твердого тела в точке $M$ имеет нулевую скорость. Мы
таким образом хочу: \[
0 = \vec{v}_M =
\vec{v}_P + \vec{\omega} \times \vec{r}_{PM}. 2\,\vec{r}_{PM}$, как при выводе #rkg-e2.
2\,\vec{r}_{PM}$, как при выводе #rkg-e2.
В 3D мгновенный центр будет только в том случае, если $\vec{v}_P$ ортогонален $\vec{\omega}$, и в этом случае будет много вариантов для мгновенного центра, все лежащих на прямой в направлении $\vec{\omega}$.
Если $M$ — мгновенный центр, значит, его скорость равна нулю, тогда скорость любой другой точки твердого тела равна определяется следующим уравнением.
\[ \vec{v}_{Q} = \vec{\omega} \times \vec{r}_{MQ} \]
Точка $M$ является мгновенным центром вращения твердое тело, вращающееся с угловой скоростью $\vec{\omega}$, а $Q$ — любая точка тела.
По определению мгновенный центр имеет $\vec{v}_M =
0$, поэтому формула скорости #rkg-er дает: \[\ начало {выровнено}
\vec{v}_Q &= \vec{v}_M + \vec{\omega} \times \vec{r}_{MQ} \\
&= \vec{\omega} \times \vec{r}_{MQ}. \конец{выровнено}\]
\конец{выровнено}\]
анимация перезагрузить показать ярлыки
Скорость и ускорение точек твердого тела. совершающие различные движения.
13.17: уравнения движения Эйлера для вращения твердого тела
Вращение твердого тела может сбивать с толку тем, что задействованы две системы координат и, как правило, угловая скорость и угловой момент не совпадают.Движение твердого тела наблюдается в неподвижной инерциальной системе отсчета, тогда как проще вычислить уравнения движения в неподвижной системе с главной осью, для которой тензор инерции известен и постоянен. Твердое тело вращается с вектором угловой скорости \(\boldsymbol{\omega}\), который не совпадает с угловым моментом \(\mathbf{L}\). Для углового момента без крутящего момента \(\mathbf{L}\) сохраняется и имеет фиксированную ориентацию в фиксированной системе координат. Уравнения движения Эйлера, представленные ниже, даны в связанной с телом системе отсчета, для которой известен тензор инерции, поскольку это упрощает решение уравнений движения.Однако это решение должно быть повернуто обратно в фиксированную систему отсчета, чтобы описать вращательное движение, которое видит наблюдатель в инерциальной системе отсчета.
Уравнения движения Эйлера, представленные ниже, даны в связанной с телом системе отсчета, для которой известен тензор инерции, поскольку это упрощает решение уравнений движения.Однако это решение должно быть повернуто обратно в фиксированную систему отсчета, чтобы описать вращательное движение, которое видит наблюдатель в инерциальной системе отсчета.
В этой главе были представлены инерционные свойства твердого тела, а также углы Эйлера для преобразования между неподвижной и инерциальной системами отсчета. Это подготовило почву для решения уравнений движения твердого тела, а именно динамики вращательного движения вокруг неподвижной точки тела под действием внешних сил.Углы Эйлера используются для указания мгновенной ориентации твердого тела.
В ньютоновской механике вращательное движение подчиняется эквивалентному второму закону Ньютона, выраженному через внешний крутящий момент \(\mathbf{N}\) и угловой момент \(\mathbf{L}\)
\[\mathbf{N} = \left( \frac{d\mathbf{L}}{dt}\right)_{пробел} \]
Обратите внимание, что это отношение выражается в инерциальной системе отсчета, фиксированной в пространстве, а не в неинерциальной системе отсчета, фиксированной телом. Нижний индекс \(пробел\) добавлен, чтобы подчеркнуть, что это уравнение написано в инерциальной пространственно-фиксированной системе отсчета. Однако, как уже обсуждалось, от пространственно-закрепленной инерциальной системы отсчета гораздо удобнее перейти к закрепленной за телом системе отсчета, для которой известен тензор инерции твердого тела. Таким образом, следующим этапом является выражение вращательного движения в терминах фиксированной системы отсчета. Для простоты поступательное движение будем игнорировать.
Нижний индекс \(пробел\) добавлен, чтобы подчеркнуть, что это уравнение написано в инерциальной пространственно-фиксированной системе отсчета. Однако, как уже обсуждалось, от пространственно-закрепленной инерциальной системы отсчета гораздо удобнее перейти к закрепленной за телом системе отсчета, для которой известен тензор инерции твердого тела. Таким образом, следующим этапом является выражение вращательного движения в терминах фиксированной системы отсчета. Для простоты поступательное движение будем игнорировать.
Скорость изменения углового момента может быть записана в терминах фиксированного значения тела, используя преобразование из фиксированной в пространстве инерциальной системы отсчета \((\mathbf{\hat{x}}, \mathbf{\hat{y }},\mathbf{\hat{z}})\) во вращающуюся рамку \((\mathbf{\hat{e}}_1,\mathbf{\hat{e}}_2,\mathbf{\hat{ e}}_3)\), как указано в главе \(13.13\),
\[\mathbf{N} = \left( \frac{d\mathbf{L}}{dt}\right)_{space} = \left( \frac{d\mathbf{L}}{dt}\ right)_{тело} + \boldsymbol{\omega} \times \mathbf{L} \]
Однако ось тела \(\mathbf{\hat{e}}_i\) выбрана в качестве главной оси так, что
\[L_i = I_i \omega_i \]
, где главные моменты инерции записываются как \(I_i\). Таким образом, уравнение движения может быть записано с использованием фиксированной системы координат тела как
Таким образом, уравнение движения может быть записано с использованием фиксированной системы координат тела как
\[\begin{align} \mathbf{N} & = I_1 \dot{\omega}_1\mathbf{\шляпа{e}}_1 + I_2 \dot{\omega}_2\mathbf{\шляпа{e} }_2 + I_3 \dot{\omega}_3 \mathbf{\шляпа{e}}_3 + \begin{vmatrix} \mathbf{\шляпа{e}}_1 & \mathbf{\шляпа{e}}_2 & \ mathbf{\шляпа{е}}_3 \\ \omega_1 & \omega_2 & \omega_3 \\ I_1\omega_1 & I_2\omega_2 & I_3\omega_3 \end{vmatrix} \\ & = (I_1 \dot{\omega}_1 – (I_2 – I_3) \ omega_2 \ omega_3) \ mathbf {\ hat {e}} _1 + (I_2 \ dot {\ omega} _2 – (I_3 – I_1) \ omega_3 \ omega_1) \ mathbf {\ hat {e} }_2 + (I_3 \dot{\omega}_3 – (I_1 – I_2) \omega_1\omega_2)\mathbf{\hat{e}}_3 \end{align}\]
, где компоненты в осях, закрепленных на корпусе, указаны как
.\[\begin{align} N_1 = I_1 \dot{\omega}_1 – (I_2 – I_3) \omega_2\omega_3 \\ N_2 = I_2 \dot{\omega}_2 – (I_3 – I_1) \omega_3\omega_1 \notag \\ N_3 = I_3 \dot{\omega}_3 − (I_1 − I_2) \omega_1\omega_2 \notag \end{align}\]
Это уравнения Эйлера для твердого тела в силовом поле , выраженные в системе координат с фиксированными координатами .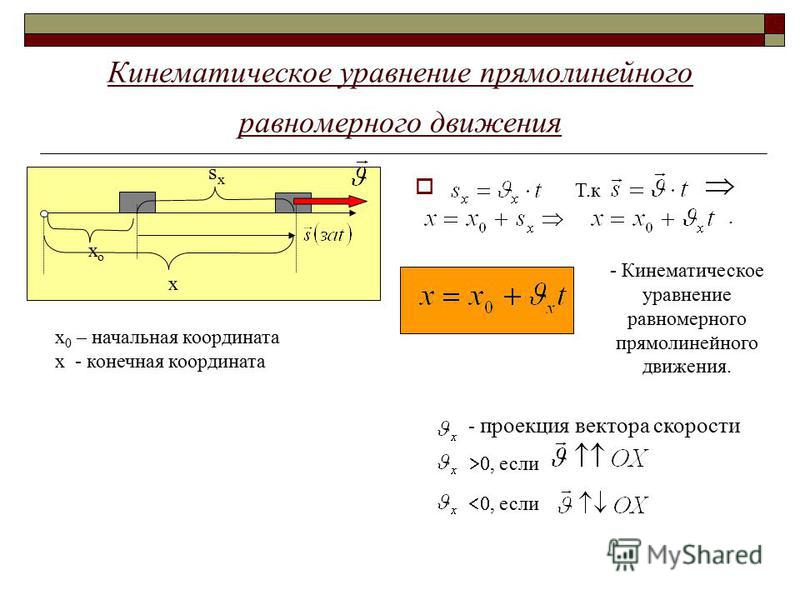 Они применимы для любого приложенного внешнего крутящего момента \(\mathbf{N}\).
Они применимы для любого приложенного внешнего крутящего момента \(\mathbf{N}\).
Движение твердого тела зависит от строения тела только через три главных момента инерции \(I_1\), \(I_2\) и \(I_3\). Таким образом, все тела, имеющие одинаковые главные моменты инерции, будут вести себя совершенно одинаково, даже если тела могут иметь очень разные формы. Как обсуждалось ранее, простейшей геометрической формой тела, имеющего три различных главных момента, является однородный эллипсоид.Таким образом, движение твердого тела часто описывается в терминах эквивалентного эллипсоида с теми же главными моментами.
Недостатком уравнений Эйлера является то, что решения дают изменение во времени \(\boldsymbol{\omega}\), как видно из осей фиксированной системы отсчета, а не в фиксированной инерциальной системе координат наблюдателя. Точно так же компоненты внешних крутящих моментов в уравнениях Эйлера задаются относительно системы фиксированных осей тела, что подразумевает, что ориентация тела уже известна. {доп}_i\). Однако эти трудности исчезают, когда внешние моменты равны нулю, или если известно движение тела и требуется вычислить приложенные моменты, необходимые для создания такого движения.
{доп}_i\). Однако эти трудности исчезают, когда внешние моменты равны нулю, или если известно движение тела и требуется вычислить приложенные моменты, необходимые для создания такого движения.
Жидкости в движении твердого тела
Жидкости в движении твердого тела Жидкости в движении твердого тела Введение
- Напомним, для случая движения твердого тела уравнение
движение потока жидкости (уравнение Навье-Стокса) сводится к
Обратите внимание, что новый вектор “действующей гравитации”, G , определяется как векторная сумма гравитации и отрицательного вектора ускорения.Этот новый эффективный вектор силы тяжести можно получить с помощью небольшой тригонометрии в качестве результирующего вектора добавления г и – .
- Рассмотрим два случая движения твердого тела: равномерное линейное ускорение твердого тела и жесткое
вращение тела .

Равномерное линейное ускорение твердого тела
- Рассмотрим случай, когда жидкость равномерно ускоряется в каком-то направлении.Другими словами, каждая частица жидкости в контейнер чувствует точно такой же вектор ускорения, который постоянным во времени. В таком случае, поскольку и вектор гравитации и вектор ускорения постоянны, действующая сила тяжести вектор, G , также должен быть постоянным.
- Обратите внимание, что уравнение движения идентично
уравнение гидростатики, за исключением того, что сила тяжести g заменена на по эффективной гравитации G . Это делает проблемы этого типа
не сложнее простой гидростатики.На самом деле для униформы
линейное ускорение твердого тела, решение идентично
гидростатики, но с заменой g на G , и с
z (параллельно g , т.е. вниз) заменяется на s (параллельно Г ). Хороший способ запомнить это — представить себе, что
ускоряющая жидкость вместо этого находится на планете, где гравитация
действует в каком-то странном направлении (направление вектора G ) и с
некоторой величины G.
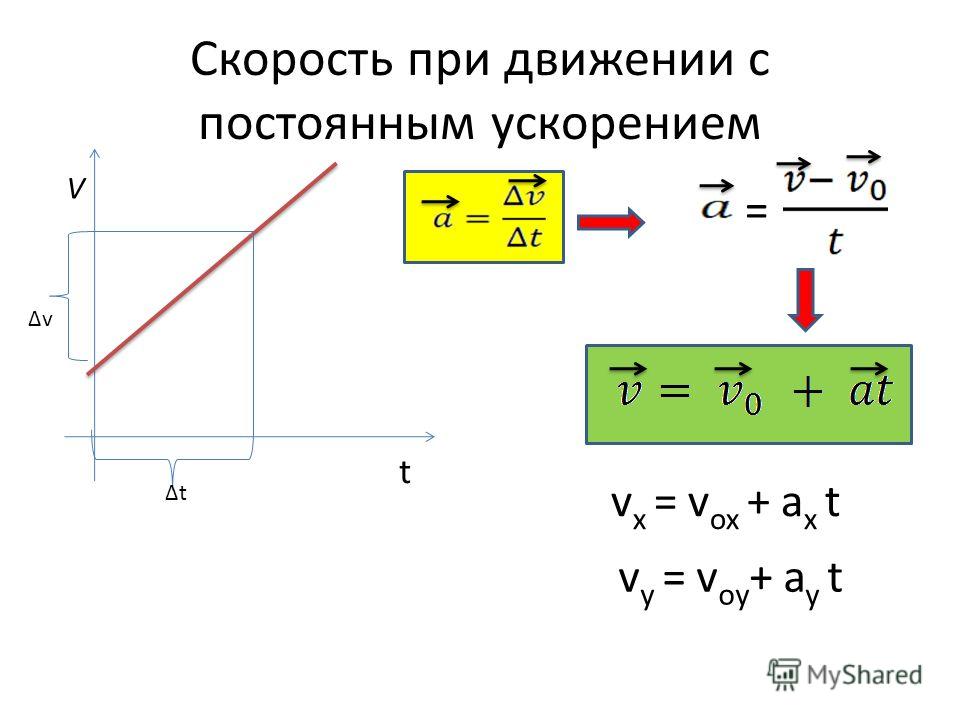 Одним из следствий этого является то, что изобары должны
быть перпендикулярно G , т.е.е. перпендикулярно направлению
с. На самом деле давление увеличивается линейно с расстоянием s, а не
чем с з.
Одним из следствий этого является то, что изобары должны
быть перпендикулярно G , т.е.е. перпендикулярно направлению
с. На самом деле давление увеличивается линейно с расстоянием s, а не
чем с з.
- В качестве примера рассмотрим стакан воды в лифте, который
ускоряется:
Здесь действующая сила тяжести все еще направлена вниз, но больше величина, чем g. Изобары остаются горизонтальными поверхностями, т.к. в гидростатике. По сути все идентично гидростатике за исключением большей силы тяжести (представьте, например, что стакан сидит на планете Юпитер).Наше простое гидростатическое давление соотношение по-прежнему применяется, но с заменой g на G и z заменой по с, т.е.
Также обратите внимание, что “ниже” и “выше” являются относительными также координировать s, а не z. При прочих равных, давление на дно ускорительного стакана будет больше чем на дне стационарного стакана (поскольку G больше, чем г).- Теперь рассмотрим стакан воды в лифте, который ускоряется
равномерно вправо.
 Опять же, эффективный вектор силы тяжести может
построить, как показано:
Опять же, эффективный вектор силы тяжести может
построить, как показано:
Теперь, поскольку эффективная гравитация наклонена под некоторым углом к внизу слева изобары должны быть перпендикулярны этому направлению.Таким образом, изобары наклонены вниз и вправо, как показано на рисунке. Обратите внимание, что поверхность остается изобарой постоянного давления p a , и поэтому также наклонен, как нарисовано. В какой-то момент 1 в жидкости, давление можно найти из пересмотренного гидростатического зависимость давления следующая:
- Теперь рассмотрим стакан воды в лифте, который ускоряется
равномерно вправо.
Вращение твердого тела
- Рассмотрим контейнер с некоторой жидкостью, который вращается вокруг вертикальная ось с некоторой постоянной угловой скоростью, как показано на эскиз:
- Для любого вида движения твердого тела уравнение движения
для течения жидкости (уравнение Навье-Стокса) сводится к В твердом теле линейное ускорение, эффективный вектор силы тяжести, G ,
везде в жидкости было постоянным.
 Вот этого уже нет
случае, поскольку ускорение вращающейся частицы жидкости
относительно некоторой оси изменяется с расстоянием от оси. Фактически, для
круговое движение, ускорение всегда направлено внутрь, к
центр вращения (центростремительное ускорение). Это ускорение
увеличивается линейно с радиусом (вывод см. в тексте): Таким образом, эффективный вектор силы тяжести, G , не является постоянным,
но зависит от радиуса. На рисунке ниже эффективная гравитация
вектор в точке A строится: Локально изобары вблизи точки
A, конечно, по-прежнему перпендикулярны G , и они
показано.
Вот этого уже нет
случае, поскольку ускорение вращающейся частицы жидкости
относительно некоторой оси изменяется с расстоянием от оси. Фактически, для
круговое движение, ускорение всегда направлено внутрь, к
центр вращения (центростремительное ускорение). Это ускорение
увеличивается линейно с радиусом (вывод см. в тексте): Таким образом, эффективный вектор силы тяжести, G , не является постоянным,
но зависит от радиуса. На рисунке ниже эффективная гравитация
вектор в точке A строится: Локально изобары вблизи точки
A, конечно, по-прежнему перпендикулярны G , и они
показано. - Однако в других точках потока локальное эффективное
вектор силы тяжести другой, так как местное ускорение другое.
Например, в точке B (на большем радиусе, чем точка A)
вектор ускорения внутрь больше, и G наклоняется дальше
вправо, как показано ниже: Местные изобары вокруг точки B, перпендикулярные местной
эффективный вектор гравитации, таким образом, наклонены вправо вверх даже
сильнее, чем в точке A.
 На средней линии (точка C)
местное ускорение равно нулю, а эффективная сила тяжести идентична
к стандартной гравитации; изобары вблизи осевой линии вращающегося
жидкости горизонтальны, как и в гидростатике:
На средней линии (точка C)
местное ускорение равно нулю, а эффективная сила тяжести идентична
к стандартной гравитации; изобары вблизи осевой линии вращающегося
жидкости горизонтальны, как и в гидростатике: - Если такой анализ проводить везде в потоке, изобары оказываются параболоидами, построенными путем вращения парабола вокруг своей оси для создания осесимметричной поверхности: Свободная поверхность, конечно, является изобарой, так как ее давление равно атмосферный.Давление увеличивается перпендикулярно изобарам.
- В тексте представлен более подробный математический вывод уравнений для давления и для изобар. Если происхождение определяется в самой нижней точке на свободной поверхности, как показано на эскиз выше, уравнения для давления и для изобар являются:
- Когда p = p a , второе приведенное выше уравнение принимает вид
уравнение, описывающее свободную поверхность. Когда р больше
p a , это уравнение описывает изобары под поверхностью
(при более высоком давлении).
 Теперь обозначим h как разницу между
высота в центре свободной поверхности и на краю свободной
поверхность. Получается, что по сравнению с исходной свободной поверхностью
(контейнер вообще не вращается), поверхность опускается в
центрировать на величину (h/2), равную величине подъема поверхности
обод (также h/2). Это показано ниже:
Теперь обозначим h как разницу между
высота в центре свободной поверхности и на краю свободной
поверхность. Получается, что по сравнению с исходной свободной поверхностью
(контейнер вообще не вращается), поверхность опускается в
центрировать на величину (h/2), равную величине подъема поверхности
обод (также h/2). Это показано ниже: - Рассмотрим числовой пример. Емкость с водой радиуса 4,0 дюйма вращается с фиксированной угловой скоростью 100 об/мин. Оценить час: Простой эксперимент с вращающейся чашкой с водой может показать, что это предсказание довольно точное.
- Обратите внимание, что плотность не фигурирует в уравнении для
изобар или в уравнении для h. Таким образом, вода может быть заменена
с любой другой жидкостью, и результат будет идентичным. Давление
будет расти быстрее с глубиной для более плотной жидкости, но
форма свободной поверхности останется неизменной независимо от
используемой жидкости. Кроме того, поскольку это вращение твердого тела,
порции жидкости могут быть даже удалены или заменены
твердый материал.
 Таким образом, любой вращающийся кусок жидкости, независимо от
его формы, можно анализировать, как если бы он был частью большого контейнера
вращение вокруг оси Z, как показано на рисунках выше.
Таким образом, любой вращающийся кусок жидкости, независимо от
его формы, можно анализировать, как если бы он был частью большого контейнера
вращение вокруг оси Z, как показано на рисунках выше.
Основные уравнения для N тел
Основные уравнения для N телNext: Якобиан N-M Up: Обзор астрофизического Предыдущий: Обзор астрофизического
Общая астрофизическая система N -тело состоит из частиц N двигаясь в соответствии с тремя законами движения Ньютона, со знакомым Ньютоном гравитационный закон является единственным источником силы.
Пусть – единичные векторы эталона Декартова ( x , y , z ) система.Пусть будет вектор положения частицы i . Пусть будет вектор, указывающий от частицы i к частице j , , т.е. положение частицы j относительно частицы i . Таким образом
Сила, с которой частица j действует на частицу i , равна
где G — гравитационная постоянная, — массы
частицы, является вектором, указывающим от частицы i к
частица j , является величиной этого вектора, и
является единичным вектором, указывающим в направлении . Пусть общая сила, действующая на частицу i , равна . Это сумма всех
сил от всех других частиц.
Таким образом, общая сила, действующая на частицу i , равна
Пусть общая сила, действующая на частицу i , равна . Это сумма всех
сил от всех других частиц.
Таким образом, общая сила, действующая на частицу i , равна
Для трехмерного пространства это набор 3 N второго порядка. обыкновенные дифференциальные уравнения (ОДУ), которые мы переводим в набор 6 N ОДУ первого порядка, полагая скорость а потом строить вектор фазового пространства всей системы как . Таким образом, система ОДУ первого порядка
где – вектор, представляющий ускорения всех частиц.
В любой момент времени положение и скорость каждой частицы известен. Таким образом, просто , и представляет собой набор производных по времени от скорости каждой частицы, где
Если используется смягчение силы, знаменатель вместо этого становится где – параметр смягчения.
Next: Якобиан N-M Up: Обзор астрофизического Предыдущий: Обзор астрофизического Wayne Hayes
Воскресенье, 29 декабря, 23:43:59 EST 1996
Об уравнениях движения упругих звеньев методом МКЭ
В статье представлено обсуждение уравнений движения плоских гибких механизмов. Метод конечных элементов (МКЭ) используется для получения вибрационного анализа звеньев. При выводе динамических уравнений обычно предполагается, что функция формы упругого движения может представлять движение твердого тела. В этой статье, в отличие от этого предположения, представлена модель функции формы, специально предназначенная для движения твердого тела, и ее влияние на упругое движение включено в уравнения движения; матрица инерции, связанная с вектором ускорения твердого тела, зависит как от функций формы упругих, так и от жестких элементов.Численные расчеты проведены с целью определения влияния принятой функции формы движения твердого тела на колебания звеньев в случае замкнутого и разомкнутого механизмов. Результаты численного моделирования показывают, что для анализа переходных процессов и для некоторых конкретных условий (например, пусковой диапазон, разомкнутые механизмы) влияние предполагаемых функций формы на вибрационный отклик может быть весьма значительным.
Метод конечных элементов (МКЭ) используется для получения вибрационного анализа звеньев. При выводе динамических уравнений обычно предполагается, что функция формы упругого движения может представлять движение твердого тела. В этой статье, в отличие от этого предположения, представлена модель функции формы, специально предназначенная для движения твердого тела, и ее влияние на упругое движение включено в уравнения движения; матрица инерции, связанная с вектором ускорения твердого тела, зависит как от функций формы упругих, так и от жестких элементов.Численные расчеты проведены с целью определения влияния принятой функции формы движения твердого тела на колебания звеньев в случае замкнутого и разомкнутого механизмов. Результаты численного моделирования показывают, что для анализа переходных процессов и для некоторых конкретных условий (например, пусковой диапазон, разомкнутые механизмы) влияние предполагаемых функций формы на вибрационный отклик может быть весьма значительным.
1.
 Введение
ВведениеВ последние годы значительное внимание уделяется анализу гибких механизмов.Необходимость учета гибкости звеньев обусловлена гораздо более высокой скоростью работы и большими ограничениями по весу и мощности элементов механизма. Следовательно, для высокоскоростной работы в процесс проектирования механизма должны быть включены как жесткое тело, так и упругие эффекты, чтобы уменьшить динамические реакции и позволить рычажному механизму выполнять заданные кинематические функции.
Многие работы, опубликованные в последние годы, связаны с приложениями специальных методов конечных элементов [1].В этих исследованиях реакцию механизма обычно получали с использованием так называемой «теории суперпозиции». В этом методе сначала определяется движение твердого тела, а затем решаются неизвестные упругие перемещения. При выводе уравнений движения делается предположение, что функция формы для твердотельного движения такая же, как и для упругого движения [2–6]. В результате матрица инерции системы для вектора упругих перемещений появляется также вместе с вектором ускорения твердого тела в правой части уравнений движения.
Использование ранее описанного метода, однако, не дает точных результатов при рассмотрении высокоскоростных систем, так как не обеспечивает взаимной динамической связи жесткого и упругого движений. Аналитическая процедура, разработанная Сонгом и Хаугом [7], представила метод «одного прохода», который одновременно моделирует как большие движения, так и малые упругие смещения звеньев. Однако взаимосвязи тел описываются большой системой уравнений связи, сформулированных для каждого типа соединений.Эта процедура значительно увеличивает размерность задачи и приводит к системе уравнений, состоящей как из дифференциальных, так и из алгебраических уравнений, решить которые непросто. Более поздние работы Нагараджана и Турчича [8, 9] и других [10, 11] допускали, что твердотельное и упругое движения влияют друг на друга, и как твердотельные, так и упругие степени свободы рассматриваются как обобщенные координаты в выводе.
Более поздние работы были направлены на разработку модели элементов более высокого порядка [12] или на учет влияния геометрических нелинейностей в высокоскоростных приложениях [13–15]. Статья Шейкера и Госала [14] посвящена нелинейному моделированию планарных манипуляторов; уравнения движения были получены в лагранжевой формулировке и обезразмерены с использованием двух характеристических скоростей. Эти значения позволили им предсказать, нужен ли нелинейный анализ или линейный случай дал удовлетворительные результаты. Кораем и др. [15] разработали подход Лагранжа к гибким мобильным манипуляторам для определения максимально допустимой динамической нагрузки.
Статья Шейкера и Госала [14] посвящена нелинейному моделированию планарных манипуляторов; уравнения движения были получены в лагранжевой формулировке и обезразмерены с использованием двух характеристических скоростей. Эти значения позволили им предсказать, нужен ли нелинейный анализ или линейный случай дал удовлетворительные результаты. Кораем и др. [15] разработали подход Лагранжа к гибким мобильным манипуляторам для определения максимально допустимой динамической нагрузки.
Наиболее часто для получения уравнений движения систем с гибкими телами используется подход Лагранжа [16].Однако по сравнению с уравнениями движения Лагранжа использование уравнений Гиббса-Аппеля [17, 18] упрощает вывод определяющих динамических уравнений. В этом втором методе сначала вычисляется вторая производная обобщенного вектора, а затем получается соответствующая вторая частная производная функции Гиббса. В уравнениях движения Лагранжа последовательность совершенно обратная, и когда общее перемещение точки представлено в векторной форме, уравнения Лагранжа не особенно подходят.
В настоящей статье обсуждается форма уравнений движения, используемая в теории суперпозиции упругих связей. Используется модель функции формы для плоского движения твердого тела, предложенная в [19, 20]. Таким образом, в отличие от многих других исследований [2–6], функция формы для упругого движения не используется для описания сколь угодно большого переноса твердого тела. Более того, как показано в Приложении, функция формы для плоских балочных элементов является лишь аппроксимацией распределения перемещений по жестким конечным элементам, и для точного описания жесткого движения следует использовать функцию формы, предложенную в этой статье.Использование различных функций формы для упругого и жесткого движений означает, что матрица инерции, стоящая за вектором ускорения твердого тела в уравнениях движения гибких механизмов, зависит как от функций формы упругих, так и жестких элементов. В статье обсуждается влияние принятых функций формы на колебательный отклик звеньев механизма.
2. Уравнения движения
Связь между нелинейными движениями твердого тела и линейной малой упругой деформацией является основной проблемой при решении динамики гибких механизмов.В теории суперпозиции упругие перемещения отделяются от перемещений твердого тела (которые вычисляются заранее) и решаются как неизвестные системы. Таким образом, на твердотельное движение не влияет упругое движение, а вибрация звеньев возникает за счет центробежных сил, возникающих при твердотельном движении механизма.
На рис. 1 представлен общий элемент плоской балки в трех системах отсчета. Рамка закреплена на земле и служит глобальной системой координат.Рамка, ориентированная на элемент, представляет собой вращающуюся систему отсчета, ось которой параллельна недеформированной центральной линии элемента. Начало репера находится в узловой точке конечного элемента и остается параллельным системе. Кадры и постоянно обновляются по мере перемещения элемента.
Предположим, что при движении механизма конечный элемент изменил свое положение, определяемое конечными точками 1 и 2, на точки 1′ и 2′ (пунктир) за счет твердотельного движения и на точки и из-за упругой деформации. Компоненты векторов узловых перемещений 11′ и 22′ могут быть выражены в относительной системе координат следующим вектором: или в местной системе координат по где – перемещения узлов 1 и 2 в направлении и соответственно, – перемещения узлов 1 и 2 в направлении и соответственно.
Компоненты векторов узловых перемещений 11′ и 22′ могут быть выражены в относительной системе координат следующим вектором: или в местной системе координат по где – перемещения узлов 1 и 2 в направлении и соответственно, – перемещения узлов 1 и 2 в направлении и соответственно.
Вектор смещения общей точки, принадлежащей конечному элементу, может быть выражен через перемещения концов элемента по формуле где – функция формы для движения твердого тела, которая может быть выражена как [6] где , и – следующая матрица преобразования: где угол между и глобальной системой координат.Поскольку продольные перемещения узлов в случае жесткого движения равны, функция формы для твердотельного движения (4) может быть представлена в другом виде, как показано в [22].
Положение общей точки в глобальной системе координат (см. рис. 1) обозначается и может быть записано как где – перемещение, связанное с движением твердого тела, – вектор упругой деформации в локальной системе координат . Вектор можно определить как сумму вектора начального положения и вектора смещения общей точки из-за движения твердого тела. Дифференцируя (6) по времени можно получить скорость и ускорение общей точки где – абсолютная угловая скорость системы отсчета, – матрица оператора булева типа, определяемая как При выводе (8) учтено постоянство вектора начального положения (см. рис. 1), откуда следуют следующие тождества: , .
Теперь рассмотрим упругое движение, описывающее колебания звеньев. Компоненты векторов узловых перемещений и за счет упругой деформации могут быть выражены в системах и через векторы и соответственно где: – перемещения узлов 1 и 2 в и направлении соответственно, – угловые деформации узлов 1 и 2, где – перемещения узлов 1 и 2 в и направлении соответственно.
Вектор преобразуется в где матрица преобразования Вводя матричные обозначения, необходимые в формулировке конечных элементов, вектор смещения может быть выражен через смещения конечных точек элемента: Функция формы для упругого смещения выглядит следующим образом:
где .
Уравнения движения получаются с использованием уравнений Гиббса-Аппеля [11]: где представляет собой обобщенную узловую степень свободы, – потенциальная энергия, – обобщенные силы, действующие на элемент, – функция Гиббса или «энергия ускорения». Энергия диссипации не участвует в сформулированных уравнениях движения; в случае структурного демпфирования матрицы демпфирования могут быть введены в систему уравнений движения как линейная комбинация матриц инерции и жесткости системы.
Функция Гиббса выражается следующим образом: где и – функция формы для движения твердого тела (4) и упругого движения (15) соответственно.
Энергия деформации элемента связана с вектором и определяется выражением где матрица жесткости элемента имеет тот же вид, что и для балочных элементов.
Подставляя выражения для функции Гиббса и энергии деформации элемента в уравнения Гиббса-Аппеля (16), получаем уравнения движения для одного элемента в следующем виде: где – матрица инерции элемента, – центробежная матрица, – гироскопическая матрица, – матрица коэффициентов, определяемая следующими обозначениями: и являются обобщенными силами, действующими на конечный элемент.
На уровне уравнений движения элементов существуют силы от соседних звеньев, которые на уровне размера системы являются внутренними силами и возникают в положительных и отрицательных парах, которые сокращаются. С учетом граничных условий и введения матрицы демпфирования уравнения движения системы записываются в виде [20] где матрицы коэффициентов являются глобальными матрицами, полученными из соответствующих матриц элементов, представляют обобщенные силы и , и представляют собой векторы ускорения, скорости и смещения (в узловых точках).Векторы и представляют собой собранные формы векторов элементов и с учетом граничных условий.
Пренебрегая членами связи твердого тела и упругого движения, уравнения движения (21) получаются в упрощенном виде как
В большинстве исследований гибкой многотельной формулировки [2–6] предполагается, что функция формы элемента, принятая для упругого движения, может быть использована для описания сколь угодно большого перемещения твердого тела. Таким образом, функцию формы для упругого смещения (15) можно использовать для определения смещения твердого тела, то есть где вектор подобен вектору (11), но смещения обусловлены движением твердого тела.
Таким образом, функцию формы для упругого смещения (15) можно использовать для определения смещения твердого тела, то есть где вектор подобен вектору (11), но смещения обусловлены движением твердого тела.
Из сравнения с (3) видно, что функция формы твердого тела, фигурирующая в функции Гиббса (17), теперь заменяется функцией формы упругого тела . Матрица коэффициентов, обозначаемая ранее (см. (20)) теперь равна , т.е. Допущение, сформулированное в (23), приводит к уравнениям движения, в которых матрица инерции, связанная с вектором ускорения твердого тела, совпадает с матрицей инерции системы. В упрощенном виде уравнения движения в глобальной системе координат имеют следующий вид [3]: Из сравнения (22) и (25) видно, что в предположении функции формы для движения твердого тела (4) матрицы инерции, связанные с вектором ускорения твердого тела в правой части уравнений движения, существенно различаются в двух рассмотренных случаях.
Решение матрицы (22) и (25) получено методом Ньюмарка для интегрирования уравнений. В численных примерах эффекты гравитации и демпфирования не учитываются.
В численных примерах эффекты гравитации и демпфирования не учитываются.
3. Иллюстративные примеры
Для определения влияния принятой формообразующей функции движения твердого тела на колебания звеньев рассмотрены два численных примера: первый – пример замкнуто-цепного механизма, четырех- стержневой, а второй представляет собой разомкнутый механизм двухзвенного планарного манипулятора.Также интересно сравнить предложенный метод с широко используемым предположением о применении функции формы элемента (в нашем случае конечного элемента балки) к движению твердого тела. Таким образом, расчеты ведутся для двух случаев.
Случай 1. Путем решения уравнений движения (22), которые были сформулированы для функции формы для движения твердого тела (4).
Случай 2. Путем решения часто используемых уравнений движения типа (25).
3.1. Четырехзвенный рычажный механизм
Предполагается, что все три подвижных элемента рычажного механизма являются деформируемыми. Всего использовалось шесть элементов — каждое звено представлено двумя конечными элементами. Соответствующее размещение узлов показано на рис. 2.
Всего использовалось шесть элементов — каждое звено представлено двумя конечными элементами. Соответствующее размещение узлов показано на рис. 2.
На вращательном соединении между кривошипом и муфтой, а также между муфтой и толкателем имеются узлы (номера 3 и 5), которые моделируются в предположении двух независимых вращательная степень свободы (слева и справа) в каждом из этих узлов.В узлах 1 и 7 ставились граничные условия нулевого поступательного перемещения.
В ходе численного моделирования решались уравнения движения (22) и (25). В обоих случаях вектор неизвестных функций (вектор узловых перемещений ) состоит из восемнадцати элементов: перемещений и в направлениях и соответственно подвижных узлов 2, 3, 4, 5 и 6 и углов узловых деформаций
Матрицы системы упругих колебаний , и имеют размерность .Порядок вектора узлового смещения для твердотельного движения различается в зависимости от рассматриваемого случая. В (22) он состоит из десяти элементов, т. е. перемещений подвижных узлов в направлении и соответственно за счет твердотельного движения (т. е. все перемещения с индексом 0): Таким образом, матрица в (22) имеет размерность из-за разного размера векторов и . В случае (25) вектор перемещения твердого тела состоит из 18 элементов, поскольку он стоит вблизи глобальной матрицы инерции, сформулированной для гибких элементов.Таким образом, вектор содержит элементы, входящие в балку конечными элементами: помимо перемещений имеются угловые деформации, которые в случае твердотельного движения положим равными 0. Вектор твердотельного перемещения в случае (25) как следует: Видно, что размерность вектора твердого тела в предлагаемом методе меньше (сравните (27) и (28)) и принятие функции формы для твердотельного движения в виде упругого движения приводит к искусственной замене этих угловые деформации при жестком движении равны 0.
е. перемещений подвижных узлов в направлении и соответственно за счет твердотельного движения (т. е. все перемещения с индексом 0): Таким образом, матрица в (22) имеет размерность из-за разного размера векторов и . В случае (25) вектор перемещения твердого тела состоит из 18 элементов, поскольку он стоит вблизи глобальной матрицы инерции, сформулированной для гибких элементов.Таким образом, вектор содержит элементы, входящие в балку конечными элементами: помимо перемещений имеются угловые деформации, которые в случае твердотельного движения положим равными 0. Вектор твердотельного перемещения в случае (25) как следует: Видно, что размерность вектора твердого тела в предлагаемом методе меньше (сравните (27) и (28)) и принятие функции формы для твердотельного движения в виде упругого движения приводит к искусственной замене этих угловые деформации при жестком движении равны 0.
Геометрические данные, взятые для численного моделирования, приведены в табл. 1 [3].
| ||||||||||||||||||||||||||||||||||||||||||
Входной крутящий момент, приложенный к кривошипу механизма, принимается следующим образом: где угол поворота коленвала.Данные для численного моделирования: Nm, Nm. Начальные условия (угол кривошипа и угловая скорость кривошипа) рад, рад/сек. Время моделирования составляет от 0 до 0,25 с и гарантирует выполнение кривошипом полного оборота.
Результаты компьютерного моделирования показывают, что в случае рассматриваемой четырехзвенной навески различия в уравнениях движения не оказывают существенного влияния на результаты. Деформации изгиба среднего пролета для стяжки (рис. 3) и толкателя (рис. 4) очень близки для двух рассмотренных случаев, а относительная разница в результатах не превышает 3 %.Таким образом, это вряд ли будет видно на рисунках, и для того, чтобы показать различия в деформациях в середине пролета, приведены дополнительные графики: на рисунке 5 для муфты и на рисунке 6 для толкателя.
Деформации изгиба среднего пролета для стяжки (рис. 3) и толкателя (рис. 4) очень близки для двух рассмотренных случаев, а относительная разница в результатах не превышает 3 %.Таким образом, это вряд ли будет видно на рисунках, и для того, чтобы показать различия в деформациях в середине пролета, приведены дополнительные графики: на рисунке 5 для муфты и на рисунке 6 для толкателя.
Отличие уравнений движения (22) и (25), соответствующих случаям 1 и 2, состоит только в векторе силы инерции в правых частях этих уравнений. Для (22) этот вектор равен , а для (25) . Было интересно исследовать, насколько близки друг к другу эти силы.На рисунке 7 представлена сила инерции как функция угла поворота кривошипа; в обоих случаях результаты очень близки и различия на рисунке не видны. Таким образом, на следующем рисунке 8 представлена разница между этими силами (т. е. ); его величина составляет примерно 1% от величины составляющих сил.
3.2. Двухзвенный планарный манипулятор
Второй пример касается разомкнутого механизма двухзвенного плоского манипулятора (рис. 9).Основные механические характеристики этого манипулятора такие же, как в [21] и приведены в табл. 2. Кроме того, следующие исходные характеристики: масса в узле 3 ( = 0,5 кг), момент инерции на ступице кг м 2 , и номинальная грузоподъемность кг.
| Ссылка I II | Link II | |
| момент инерции, м 4 | ||
| Модуль упругости, Н/м 2 | ||
| Массовая плотность, кг/м 3 | ||
Вибрация звеньев возникает за счет движения манипулятора, возбуждаемого внешними моментами, приложенными к звеньям манипулятора в шарнирах. Принималось, что значения крутящих моментов следующие: . Вибрационный анализ проводится путем решения уравнений движения (22) и (25), соответствующих двум рассмотренным случаям. Начальные условия: рад, рад, нулевые угловые скорости; время моделирования равно 0,25 сек.
Принималось, что значения крутящих моментов следующие: . Вибрационный анализ проводится путем решения уравнений движения (22) и (25), соответствующих двум рассмотренным случаям. Начальные условия: рад, рад, нулевые угловые скорости; время моделирования равно 0,25 сек.
С учетом упругих колебаний звеньев вектор узловых перемещений в (22) или (25) состоит из 12 элементов: перемещений и в направлениях и соответственно подвижных узлов 2, 3, 4 и 5 и узловых деформаций углы: По причине, описанной в разделе 3.1 вектор узловых перемещений для твердотельного движения в случае (22) равен а в случае (25) вида Матрицы системы , и в (22) и (25) имеют размерность , а матрица в (22) имеет размерность .
Горизонтальные и вертикальные перемещения наконечника манипулятора представлены на рисунках 10 и 11 соответственно. Теперь разница в результатах для двух рассмотренных случаев значительна и хорошо видна.В частности, смещения в направлении стартового диапазона значительно различаются. Следует, однако, отметить, что расчеты выполнены для нестационарного движения с внезапными моментами, приложенными к обоим звеньям манипулятора.
Следует, однако, отметить, что расчеты выполнены для нестационарного движения с внезапными моментами, приложенными к обоим звеньям манипулятора.
Для анализа влияния полезной нагрузки на перемещения наконечника манипулятора было проведено численное моделирование без полезной нагрузки. Результаты в вертикальном направлении представлены на рис. 12. Видно, что для приведенных данных из-за меньших сил инерции в случае отсутствия полезной нагрузки наблюдается увеличение виброотклика.
Предыдущие результаты были получены для линейной модели плоских балочных элементов, которая предполагает, что поперечные перемещения не зависят от осевых перемещений или сил. Если при выводе уравнений движения учитывать нелинейную зависимость деформации–перемещения [14, 20]; в динамических уравнениях появляется дополнительная геометрическая матрица жесткости, которую необходимо добавить к матрице жесткости элемента . Для балочного элемента эту матрицу можно представить в следующем виде [23]: где равно осевой силе в элементе.
Для оценки влияния нелинейных эффектов на динамическую характеристику рассматриваемого двухзвенного манипулятора было проведено дополнительное численное моделирование. Результаты деформации изгиба в середине пролета для звена I и II представлены на рисунках 13 и 14 соответственно для линейной (сплошная линия) и нелинейной (штриховая линия) моделей.
Результаты показывают, что в рассматриваемом случае геометрическая матрица жесткости оказывает очень малое влияние на решение уравнений движения.Однако в случае манипуляторов с низкой частотой рабочего момента [14] разница в результатах может быть значительной.
4. Выводы
В настоящей работе разработана конечно-элементная модель для анализа кинетоэластодинамических переходных характеристик гибкого механизма. В динамике многих тел существует прямая связь между выбором формы колебаний в предполагаемой системе координат и вибрационной реакцией деформируемых тел со связями. Приняв предложенную функцию формы для движения твердого тела, выводятся уравнения вибрации движения, и представлен сравнительный анализ с существующим широко используемым подходом. Разница в уравнениях движения между первым и предложенным подходами заключается в связи между упругими и твердотельными модами; а именно, вектор силы инерции, соответствующий ускорению твердого тела, различен для обоих подходов.
Разница в уравнениях движения между первым и предложенным подходами заключается в связи между упругими и твердотельными модами; а именно, вектор силы инерции, соответствующий ускорению твердого тела, различен для обоих подходов.
Представленный здесь метод проиллюстрирован для случаев плоских разомкнутых и замкнутых связей. Результаты численного моделирования показывают, что в случае рассматриваемого четырехзвенного механизма различия в уравнениях движения не оказывают существенного влияния на результаты.Противоположное наблюдение делается в случае разомкнутого механизма — двухзвенного планарного манипулятора — различия в результатах между двумя обсуждаемыми подходами значительны. Однако в этом случае предполагались жесткие условия возбуждения; переходная характеристика была исследована после ступенчатого крутящего момента, приложенного к звеньям. За исключением начального диапазона, решения очень близки друг к другу, что позволяет сделать вывод, что для стабильных условий работы (например, механизмы, циркулирующие с постоянной скоростью, анализируется установившийся отклик) два подхода, представленные в этой статье, должны дают вполне сходящиеся результаты.
Приложение
В этом приложении представлен вывод перемещений конечного элемента при движении твердого тела для двух различных функций формы, балочного конечного элемента (15) и жесткого элемента (4).
Рассмотрим жесткий конечный элемент длины в локальной системе координат, показанной на рис. 15.
Компоненты вектора узлового смещения выражаются в локальной системе координат по формуле (2). Вектор смещения общей точки, принадлежащей конечному элементу и определяемой координатой (см. рис. 15), может быть выражен через перемещения концов элемента по формуле (3) Для жестких элементов смещения в продольном направлении всех точек, принадлежащих элементу, равны; то есть отношение выполняется для любого .В поперечном направлении перемещение любой точки является линейной комбинацией поперечных перемещений концов элементов. Так, например, перемещения общей точки, определяемые координатами и, таковы (обратите внимание, что безразмерная координата, фигурирующая в формулировке функции формы, равна , поэтому расчеты предусмотрены для и ): Если предположить, что функция формы для упругого смещения (15) может быть использована для определения перемещений твердого тела, используется формула (23), а общие смещения точки формулируются как
Нетрудно показать, что при заданных значениях получаются следующие перемещения: Видно, что если формулировка для твердотельных перемещений верна, то результат для поперечных перемещений общей точки для неверен.
Используя функцию формы для движения твердого тела (4), общие смещения точек формулируются как (A.1) а продольные и поперечные перемещения при заданных значениях равны Видно, что для обоих значений полученные результаты теперь верны и фактически совпадают с ожидаемыми для движения твердого тела и показанными в (А.2). Разница лишь в формулировке, но ввиду того, что продольная деформация при жестком движении постоянна (т.е., ) полученные формулы дают одинаковые результаты.
Из этого краткого вывода можно заключить, что предположение о том, что функция формы для конечного элемента балки может также передавать движение твердого тела, является лишь приближением и что функция формы для движения твердого тела (4) должна использоваться для точного описания .
Это единственный способ решить задачу трех тел
Да, я пропустил все детали — но дело в том, что вы действительно можете решить эту задачу. Вот график для планеты, вращающейся вокруг звезды, показывающий общий эффективный потенциал в одном измерении.
Контент
Этот контент также можно просмотреть на сайте, откуда он взят.
С таким эффективным потенциалом в 1-D это как мячик на холме. Вы можете видеть, что в этом потенциале есть небольшой провал — это место, куда вы можете поместить объект, и он будет находиться на устойчивой круговой орбите. Вы также можете увидеть, сколько энергии вам нужно добавить, чтобы заставить его убежать или сделать все, что вам нравится.
Это задача двух тел. Это разрешимо.
Задача трех тел
Почему нас вообще волнует задача трех тел? Что, если вы хотите смоделировать движение Луны? Вы могли бы сказать, что Луна вращается вокруг Земли и что это проблема двух тел, но это явно не совсем так.Вместо этого движение Луны определяется ее гравитационным взаимодействием с Солнцем и Землей. Луна плюс Земля плюс Солнце равняются трем телам, задаче трех тел.
Но позвольте мне рассмотреть другую задачу трех тел. Предположим, что есть две звезды, вращающиеся вокруг друг друга (двойная звездная система) и планета.

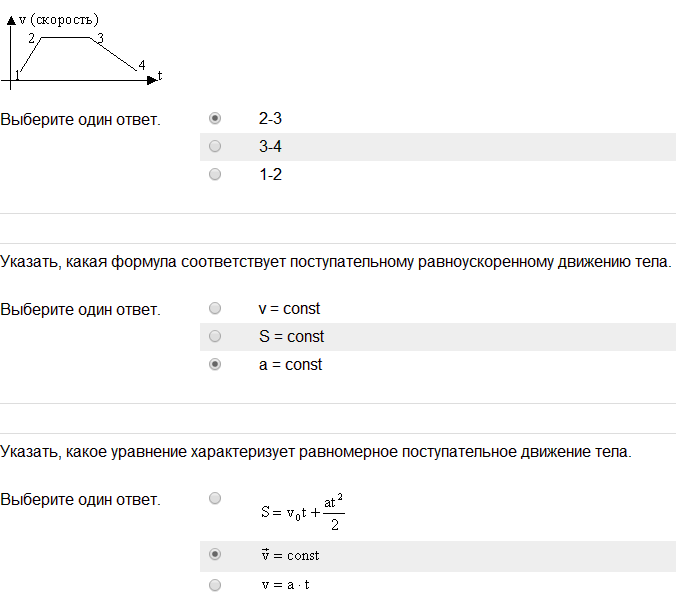 254 м.
254 м.