1,2,3,4 уравнения Максвелла для электромагнитного поля, смысл, суть, решение
Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.
Полезная и интересная информация по другим темам – у нас в телеграм.
Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.
Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.
Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.
Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
По порядку запишем и поясним все 4 уравнения. Сразу уточним, что записывать их будем в системе СИ.
Первое уравнение Максвелла
Современный вид первого уравнения Максвелла таков:
Тут нужно пояснить, что такое дивергенция. Дивергенция – это дифференциальный оператор, определяющий поток какого-то поля через определенную поверхность. Уместным будет сравнение с краном или с трубой. Например, чем больше диаметр носика крана и напор в трубе, тем большим будет поток воды через поверхность, которую представляет собой носик.
В первом уравнении Максвелла E – это векторное электрическое поле, а греческая буква «ро» – суммарный заряд, заключенный внутри замкнутой поверхности.
Так вот, поток электрического поля E через любую замкнутую поверхность зависит от суммарного заряда внутри этой поверхности. Данное уравнение представляет собой закон (теорему) Гаусса.
Третье уравнение Максвелла
Сейчас мы пропустим второе уравнение, так как третье уравнение Максвелла – это тоже закон Гаусса, только уже не для электрического поля, но для магнитного.
Оно имеет вид:
Что это значит? Поток магнитного поля через замкнутую поверхность равен нулю. Если электрические заряды (положительные и отрицательные) вполне могут существовать по отдельности, порождая вокруг себя электрическое поле, то магнитных зарядов в природе просто не существует.
Второе уравнение Максвелла
Второе уравнение Максвелла представляет собой ни что иное, как закон Фарадея. Его вид:
Ротор электрического поля (интеграл через замкнутую поверхность) равен скорости изменения магнитного потока, пронизывающего эту поверхность.
Чтобы лучше понять, возьмем воду в ванной, которая сливается через отверстие. Вокруг отверстия образуется воронка. Ротор – это сумма (интеграл) векторов скоростей частиц воды, которые вращаются вокруг отверстия.
Как Вы помните, на основе закона Фарадея работают электродвигатели: вращающийся магнит порождает ток в катушке.
Четвертое уравнение Максвелла
Четвертое – самое важное из всех уравнений Максвелла. Именно в нем ученый ввел понятие тока смещения.
Это уравнение еще называется теоремой о циркуляции вектора магнитной индукции. Оно говорит нам о том, что электрический ток и изменение электрического поля порождают вихревое магнитное поле.
Приведем теперь всю систему уравнений и кратко обозначим суть каждого из них:
Первое уравнение: электрический заряд порождает электрическое поле
Второе уравнение: изменяющееся магнитное поле порождает вихревое электрическое поле
Третье уравнение: магнитных зарядов не существует
Четвертое уравнение: электрический ток и изменение электрической индукции порождают вихревое магнитное поле
Решая уравнения Максвелла для свободной электромагнитной волны, мы получим следующую картину ее распространения в пространстве:
Надеемся, эта статья поможет систематизировать знания об уравнениях Максвелла.
А если понадобиться решить задачу по электродинамике с применением этих уравнений, можете смело обратиться за помощью в студенческий сервис. Подробное объяснение любого задания и отличная оценка гарантированы.
Почему теорию Максвелла так трудно понять? / Хабр
Скромность не всегда добродетель
В 1865 году Джеймс Клерк Максвелл опубликовал свою статью “Динамическая теория электромагнитного поля” в “Философских трудах Королевского общества”. Ему было тогда тридцать четыре года. Оглядываясь назад, мы можем заметить, что работа Максвелла была самым важным событием девятнадцатого века в истории физических наук. Если говорить в общем о естественных науках, то статья Максвелла была второй по значимости после “Происхождения видов” Дарвина. Но важность работ Максвелла не была очевидна для его современников. Более двадцати лет его теория электромагнетизма в основном игнорировалась. Физикам было трудно ее понять из-за обилия сложных уравнений. Математикам было трудно ее понять, потому что Максвелл использовал для объяснений физический язык.
Этот труд был расценен как неясное предположение без должного количества экспериментальных доказательств. Физик Михаил Пупин в своей автобиографии “От иммигранта к изобретателю” описывает, как он путешествовал из Америки в Европу в 1883 году в поисках того, кто понимал Максвелла. Он отправился изучать теорию Максвелла, как рыцарь в поисках Святого Грааля.
Пупин сначала поступил в Кембридж с твердым намерением изучить теорию у самого Максвелла. Он не знал, что Максвелл умер четыре года назад. Узнав, что Максвелл умер, он остался в Кембридже и был назначен преподавателем колледжа. Но его наставник знал о теории Максвелла меньше, чем он сам, и был заинтересован только в том, чтобы научить Михаила решать математические задачи трипоса. Михаил Пупин был поражен, обнаружив, как он говорит, “как мало было физиков, которые уловили смысл теории, даже через двадцать лет после того, как она была сформулирована Максвеллом в 1865 году”. В конце концов он бежал из Кембриджа в Берлин и поступил студентом к Герману фон Гельмгольцу.
Гельмгольц понимал теорию и учил Пупина тому, что знал сам. Пупин вернулся в Нью-Йорк, стал профессором Колумбийского университета и обучал последующие поколения студентов, которые впоследствии распространили Евангелие Максвелла по всей Америке.
Как случилось, что теория Максвелла была так широко проигнорирована? В конце концов, Максвелл не был похож на своего современника Грегора Менделя, монаха, работавшего в безвестном монастырском саду в Богемии. Максвелл был известным профессором, директором Кавендишской лаборатории в Кембридже, ведущей фигурой в британском научном сообществе. Свидетельством его высокого положения можно считать то, что он был президентом секции А (математические и физические науки) Британской ассоциации содействия развитию науки, когда ассоциация провела свое ежегодное собрание в Ливерпуле в 1870 году. Он выступил с президентской речью в Ливерпуле, которая была опубликована во втором томе недавно основанного журнала “Nature”.
Стиль его выступления показывает нам, почему его теорию не воспринимали всерьез. Можно было ожидать, что он воспользуется возможностью, предоставленной президентской платформой, чтобы объявить миру о важности открытий, которые он сделал пять лет назад. Он не сделал ничего подобного. Он был абсурдно и раздражающе скромен.
Максвелл в первую очередь объявил тему своего выступления – обзор последних достижений, которые были сделаны на границе между математикой и физикой. Затем он с большим энтузиазмом рассказал о вихревой теории молекул, недавно предложенной сэром Уильямом Томсоном (впоследствии ставшим лордом Кельвином).
Теория, которую сэр Уильям основал на великолепных гидродинамических теоремах Гельмгольца, ищет свойства молекул в кольцевых вихрях однородной несжимаемой жидкости без трения. Гельмгольц показал, что в идеальной жидкости такое кружащееся кольцо, если оно однажды возникло, будет продолжать кружиться вечно, всегда будет состоять из той же самой части жидкости, которая была сначала закручена, и никогда не может быть разрезана надвое какой-либо естественной причиной.
Эти кольцевые вихри способны к таким разнообразным связям и узловатым самоинволюциям, что свойства различных узловатых вихрей должны быть столь же различны, как и свойства различных видов молекул.
Эти кольцевые вихри способны к таким разнообразным связям и узловатым самоинволюциям, что свойства различных узловатых вихрей должны быть столь же различны, как и свойства различных видов молекул.И так далее. Максвелл объяснил, как древняя теория о том, что материя состоит из атомов, столкнулась с логическим парадоксом. С одной стороны, атомы должны были быть твердыми, непроницаемыми и неразрушимыми. С другой стороны, данные спектроскопии и химии показали, что атомы имеют внутреннюю структуру и находятся под влиянием внешних сил. Этот парадокс в течение многих лет блокировал прогресс в понимании природы материи. Теперь, наконец, вихревая теория молекул разрешила парадокс. Вихри в эфире мягкие и имеют внутреннюю структуру, и тем не менее, согласно Гельмгольцу, они индивидуальны и неразрушимы. Оставалось только вывести факты спектроскопии и химии из законов взаимодействия вихрей, предсказанных гидродинамикой идеальной жидкости. Максвелл считал эту вихревую теорию материи замечательным примером плодотворного взаимодействия математики и физики.
Неясно, верил ли Максвелл всерьез в то, что говорил о вихревой теории. Возможно, он хотел, чтобы его речь развлекала слушателей, а не просвещала их. У него было хитрое чувство юмора, и вполне возможно, что он хвалил теорию вихря, зная, что более проницательные члены аудитории поймут, что теория была шуткой. Только в конце своего выступления Максвелл кратко упомянул о своей теории электромагнетизма.
Другая теория электричества, которую я предпочитаю, отрицает действие на расстоянии и приписывает электрическое действие напряжениям и давлениям во всепроникающей среде, причем эти напряжения одинаковы по характеру с теми, которые известны инженерам, и среда идентична той, в которой предполагается распространение света.
Фраза “Другая теория электричества, которую я предпочитаю”, кажется, намеренно скрывает тот факт, что это была его собственная теория. Неудивительно, что вихри Кельвина произвели на его слушателей большее впечатление, чем уравнения Максвелла.
Мораль этой истории заключается в том, что скромность не всегда является добродетелью. Максвелл и Мендель оба были чрезмерно скромны. Скромность Менделя задержала прогресс биологии на пятьдесят лет. Скромность Максвелла замедлила прогресс физики на двадцать лет. Для прогресса науки будет лучше, если люди, делающие великие открытия, не будут слишком скромны, чтобы трубить в свои собственные трубы. Если бы у Максвелла было такое же эго, как у Галилея или Ньютона, он бы позаботился о том, чтобы его работы не игнорировались. Максвелл был таким же великим ученым, как Ньютон, и гораздо более приятным человеком. Но, к сожалению, он не начал президентскую речь в Ливерпуле словами, подобными тем, которые Ньютон использовал, чтобы представить третий том своей Principia Mathematica: “… исходя из тех же принципов, я теперь демонстрирую структуру системы мира”. Ньютон не называл свой закон всемирного тяготения “очередной теорией тяготения, которую я предпочитаю”.
Теория Максвелла и квантовая механика
Помимо скромности Максвелла, были и другие причины, по которым его теорию было трудно понять.
Он заменил ньютоновскую вселенную материальных объектов, взаимодействующих друг с другом на расстоянии, вселенной полей, простирающихся через пространство и взаимодействующих только локально с материальными объектами. Понятие поля было трудно понять, потому что поля неосязаемы. Ученые того времени, включая самого Максвелла, пытались представить поля как механические структуры, состоящие из множества маленьких колесиков и вихрей, простирающихся в пространстве. Эти структуры должны были переносить механические напряжения, которые электрические и магнитные поля передавали между электрическими зарядами и токами. Чтобы поля удовлетворяли уравнениям Максвелла, система колес и вихрей должна была быть чрезвычайно сложной.
Если попытаться визуализировать теорию Максвелла с помощью таких механических моделей, она выглядит как возврат к астрономии Птолемея с планетами, движущимися по циклам и эпициклам в небе. Это не похоже на изящную астрономию Ньютона. Уравнения Максвелла, записанные в неуклюжих обозначениях, которыми пользовался Максвелл, были пугающе сложными, а его механические модели – еще хуже.
Теория Максвелла становится простой и понятной только тогда, когда вы отказываетесь мыслить в терминах механических моделей. Вместо того чтобы думать о механических объектах как о первичных, а об электромагнитных напряжениях как о вторичных следствиях, вы должны думать об электромагнитном поле как о первичном, а о механических силах как о вторичном конструкте. Мысль о том, что первичными составляющими Вселенной являются поля, не сразу пришла в голову физикам поколения Максвелла. Поля – это абстрактное понятие, далекое от привычного мира вещей и сил. Уравнения поля Максвелла являются уравнениями в частных производных.
Чтобы вычислить энергии или напряжения, вы берете квадрат напряженности электрического поля или умножаете одну составляющую поля на другую. Двухслойная структура мира – основная причина, по которой теория Максвелла казалась загадочной и трудной. Объекты на первом уровне, объекты, которые действительно фундаментальны, являются абстракциями, не доступными непосредственно нашим чувствам. Объекты, которые мы можем чувствовать и осязать, находятся на втором слое, и их поведение лишь косвенно определяется уравнениями, действующими на первом слое. Двухслойная структура мира подразумевает, что основные процессы природы скрыты от нашего взгляда.Теперь мы считаем само собой разумеющимся, что электрические и магнитные поля являются абстракциями, не сводимыми к механическим моделям. Чтобы убедиться в этом, достаточно взглянуть на единицы измерения электрического и магнитного полей. Условная единица напряженности электрического поля – квадратный корень из джоуля на кубический метр. Джоуль – это единица энергии, а метр – единица длины, но квадратный корень из джоуля – это не единица чего-то осязаемого.
Через шестьдесят лет после того, как Максвелл опубликовал свою теорию, Шредингер, Гейзенберг и Дирак изобрели квантовую механику. Квантовая механика была принята гораздо быстрее, чем теория Максвелла, потому что она сделала множество определенных предсказаний об атомных процессах и эксперименты показали, что все предсказания были правильными.
Прошло около тридцати лет после Максвелла, прежде чем его уравнения стали понятны всем. Для достижения согласованного понимания квантовой механики потребуется по меньшей мере вдвое больше времени. Мы все еще ведем страстные споры между сторонниками различных интерпретаций квантовой механики, Копенгагенской интерпретации, многомировой интерпретации, декогерентной интерпретации, интерпретаций скрытых переменных и многих других. Причина этих споров заключается в том, что различные интерпретаторы пытаются описать квантовый мир словами повседневного языка, а язык не подходит для этой цели.
Для понимания квантовой механики может оказаться полезным подчеркнуть сходство между квантовой механикой и теорией Максвелла. В двух отношениях теория Максвелла может дать ключ к тайнам квантовой механики.
Во-первых, попытки понять квантовую механику в терминах языка, основанного на классических понятиях, аналогичны попыткам понять теорию Максвелла в терминах механических моделей. Теория Максвелла стала изящной и понятной только после того, как были оставлены попытки представить электромагнитные поля с помощью механических моделей.
Вторая связь между теорией Максвелла и квантовой механикой заключается в глубоком сходстве структуры. Подобно теории Максвелла, квантовая механика делит Вселенную на два слоя. Первый слой содержит волновые функции Шредингера, матрицы Гейзенберга и векторы состояний Дирака. Величины в первом слое подчиняются простым линейным уравнениям. Их поведение можно точно рассчитать. Но их нельзя наблюдать непосредственно. Второй слой содержит вероятности столкновений и превращений частиц, интенсивности и поляризации излучения, математические ожидания энергий и спинов частиц.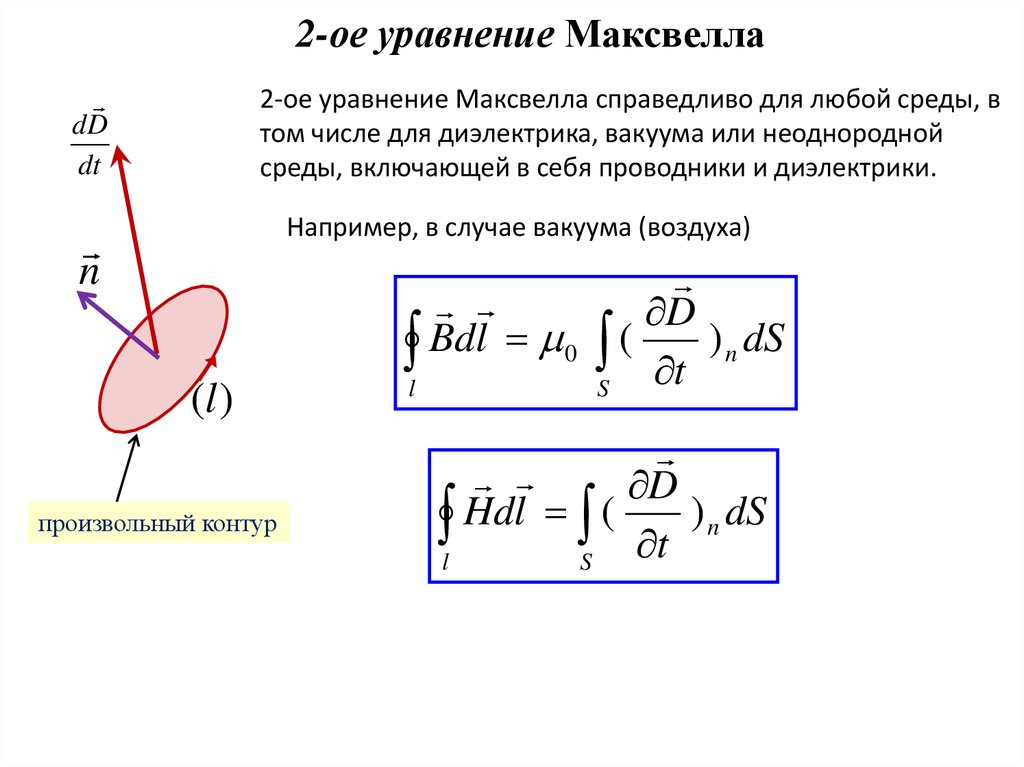
Величины во втором слое могут быть непосредственно наблюдаемы, но не могут быть непосредственно вычислены. Они не подчиняются простым уравнениям. Это либо квадраты величин первого слоя, либо произведения одной величины первого слоя на другую. В квантовой механике, как и в теории Максвелла, Природа живет в абстрактном математическом мире первого слоя, но мы, люди, живем в конкретном механическом мире второго слоя. Мы можем описать Природу только абстрактным математическим языком, потому что наш вербальный язык находится дома только во втором слое.
Как и в случае с теорией Максвелла, абстрактное качество величин первого слоя проявляется в единицах, в которых они выражаются. Например, волновая функция Шредингера выражается в единице, которая является квадратным корнем из обратного кубического метра. Уже один этот факт ясно показывает, что волновая функция – это абстракция, навсегда скрытая от нашего взгляда. Никто никогда не измерит напрямую квадратный корень из кубического метра. Конечная важность теории Максвелла гораздо больше, чем ее непосредственные достижения в объяснении и объединении явлений электричества и магнетизма.
Его конечная важность состоит в том, чтобы стать прототипом для всех великих триумфов физики двадцатого века. Это прототип теории относительности Эйнштейна, квантовой механики, теории обобщенной калибровочной инвариантности Янга-Миллса и единой теории полей и частиц.
Все эти теории основаны на концепции динамических полей, введенной Максвеллом в 1865 году. Все они имеют одинаковую двухслойную структуру, отделяющую мир простых динамических уравнений от мира человеческого наблюдения. Все они воплощают в себе то же качество математической абстракции, которое сделало теорию Максвелла трудной для понимания его современниками. Мы можем надеяться, что глубокое понимание теории Максвелла приведет к рассеиванию тумана непонимания, который все еще окружает интерпретацию квантовой механики. И мы можем надеяться, что глубокое понимание теории Максвелла поможет проложить путь к дальнейшим триумфам физики в XXI веке.
Познакомьтесь с уравнениями Максвелла — вы используете их прямо сейчас | WIRED
org/Person”> Ретт АлленНаука
Уравнения Джеймса Клерка Максвелла имеют большое значение в физике, объясняя основы электричества и магнетизма. Вот суть того, как они работают.
Поведение магнитов можно объяснить с помощью уравнений Максвелла, которые также описывают поведение легких и бытовых предметов, таких как электродвигатели. LAWRENCE LAWRY/Getty Images
Если вы достаточно долго общаетесь с физиками, кто-нибудь в конце концов расскажет об уравнениях Максвелла. Может быть, как часть шутки, или на футболке, или в татуировке. Но они будут где-то. Поэтому, даже если вы не являетесь специалистом в области физики, вам не помешает получить общее представление об этих культовых уравнениях.
Уравнения Максвелла имеют большое значение в физике. С их помощью мы можем моделировать электромагнитную волну, также известную как свет. О, так работает большинство электрических генераторов и даже электродвигателей.
По сути, вы используете уравнения Максвелла прямо сейчас, даже если вы этого не знаете. Почему они называются «уравнениями Максвелла»? Это после Джеймса Клерка Максвелла. Он был 19ученый 19-го века, который как бы собрал их воедино, хотя многие другие внесли свой вклад.
Этих уравнений четыре, и я пройдусь по каждому из них и дам концептуальное объяснение. Не волнуйтесь, вам не нужно будет освежать свои навыки исчисления. Если вы хотите следовать математике, позвольте мне указать, что есть два разных способа записи этих уравнений: либо в виде интегралов, либо в виде пространственных производных. Я приведу обе версии, но опять же, если математика выглядит непривлекательно, просто игнорируйте ее.
Закон Гаусса
Ретта Аллена
Краткая версия состоит в том, что закон Гаусса описывает структуру электрического поля из-за электрических зарядов. Что такое поле? Мне нравится это описание:
Это энергетическое поле, созданное всеми живыми существами.
Оно окружает нас, проникает в нас и связывает воедино галактику.Ой, подождите. Это было описание Силы Оби-Ваном в году Звездных войн, Эпизод IV . Но это не ужасное описание электрического поля. Вот еще одно определение (мное):
Самые популярные
Если взять два электрических заряда, между ними существует сила взаимодействия. Электрическое поле — это сила, приходящаяся на единицу заряда одного из этих зарядов. Итак, это что-то вроде области, описывающей, как электрический заряд ощущает силу. Но реально ли это? Что ж, поле может иметь как энергию, так и импульс, так что оно, по крайней мере, так же реально, как и эти вещи.
Не беспокойтесь об уравнении. Это довольно сложно, и я просто хочу добраться до идеи, стоящей за этим. (Если вы уже видели это уравнение физики, вы можете подумать, что я собираюсь ввести электрический поток, но давайте посмотрим, смогу ли я сделать это, «не зная потока».
) Итак, давайте просто скажем, что закон Гаусса утверждает, что электрические поля направлены от положительных зарядов к отрицательным зарядам. Мы можем назвать это кулоновским полем (по имени Шарля-Огюстена де Кулона).
Ретт Аллен
Всем известно, что положительные заряды — красные, а отрицательные — синие. На самом деле, я не знаю, почему я всегда делаю плюсы красными — их все равно не видно. Кроме того, вы можете заметить, что электрическое поле из-за отрицательных зарядов выглядит короче. Это потому, что эти стрелки начинаются дальше от заряда. Одна из ключевых идей кулоновского поля состоит в том, что напряженность поля уменьшается по мере удаления от одиночного точечного заряда.
Но подождите! Не все электрические поля выглядят так. Электрическое поле также подчиняется принципу суперпозиции. Это означает, что полное электрическое поле в любом месте представляет собой векторную сумму электрического поля из-за любых точечных зарядов, находящихся поблизости. Это означает, что вы можете создавать классные поля, подобные приведенному ниже, которые являются результатом двух равных и противоположных зарядов (называемых диполем).
А вот код Python, который я использовал для его создания.
Ретт Аллен
Самый популярный
Это дипольное поле будет важно для следующего уравнения.
Закон Гаусса для магнетизма
Ретт Аллен
Да, это очень похоже на другой закон Гаусса. Но почему предыдущее уравнение не называется «законом Гаусса для электрики»? Во-первых, это потому, что «электричество» — это ненастоящее слово (пока). Во-вторых, первым появился другой закон Гаусса, поэтому он получил простое название. Это как в третьем классе, когда в классе был ученик по имени Джон. Потом к классу присоединился еще один Джон, и все стали называть его Джон 2. Это несправедливо, но иногда так бывает.
Итак, первое, что нужно сделать в этом уравнении, это B . Мы используем это для представления магнитного поля. Но вы заметите, что другая сторона уравнения равна нулю. Причиной этого является отсутствие магнитных монополей.
Взгляните на это изображение железных опилок вокруг стержневого магнита (наверняка вы видели что-то подобное раньше).
Rhett Allain
Самый популярный
Это выглядит похоже, потому что это математически то же самое. Магнитное поле стержневого магнита похоже на электрическое поле диполя. Но могу ли я получить отдельный магнитный «заряд» сам по себе и получить что-то похожее на электрическое поле из-за точечного заряда? Неа.
Вот что произойдет, если сломать магнит пополам. Да, я обманул. На картинке выше показаны два стержневых магнита. Но поверьте мне, если вы разорвете магнит на две части, он будет выглядеть вот так.
Ретт Аллен
Это все еще диполь. Вы не можете заставить магнитное поле выглядеть как электрическое поле из-за точечного заряда, потому что нет отдельных магнитных зарядов (называемых магнитным монополем). Это в основном то, что говорит закон Гаусса для магнетизма — что не существует такой вещи, как магнитный монополь.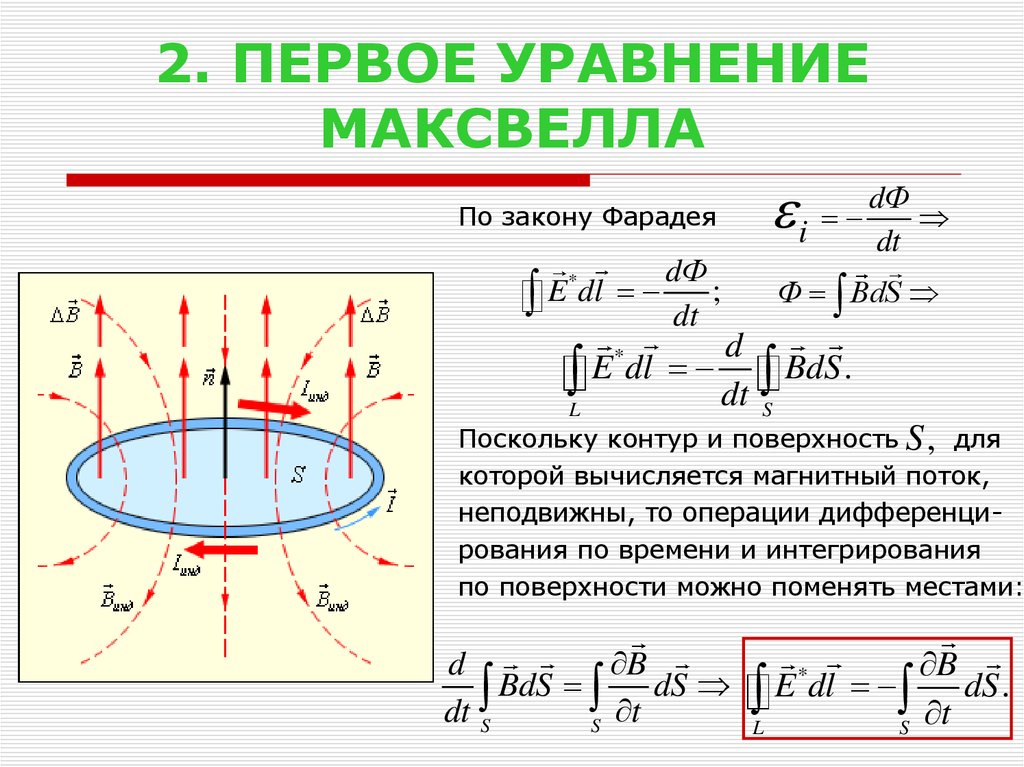
Хорошо, я должен быть ясным здесь. у нас никогда не было видел магнитный монополь. Они могут существовать.
Закон Фарадея
Ретт Аллейн
Суперкороткая версия этого уравнения состоит в том, что существует другой способ создания электрического поля. Не только электрические заряды создают электрические поля. На самом деле, вы также можете создать электрическое поле с изменяющимся магнитным полем. Это ОГРОМНАЯ идея, поскольку она устанавливает связь между электрическими и магнитными полями.
Самые популярные
Позвольте мне начать с классической демонстрации. Вот магнит, катушка с проволокой и гальванометр (он в основном измеряет крошечные электрические токи). Когда я перемещаю магнит в катушку или из нее, я получаю ток.
Ретт Аллен
Rhett Allain Если вы просто держите магнит в катушке, тока нет. Это должно быть изменяющееся магнитное поле. О, а где же электрическое поле? Что ж, способ получить электрический ток — создать электрическое поле в направлении провода.
Это электрическое поле внутри провода толкает электрические заряды, создавая ток.
Но в этом электрическом поле есть что-то другое. Вместо того, чтобы указывать от положительных зарядов и указывать на отрицательные заряды, картина поля просто рисует круги. В таком случае я буду использовать название «кудрявое электрическое поле» (термин я взял у авторов моих любимых учебников по физике). При этом мы можем назвать электрическое поле, состоящее из зарядов, «кулоновским полем» (из-за закона Кулона).
Вот грубая диаграмма, показывающая взаимосвязь между изменяющимся магнитным полем и индуцированным волнистым электрическим полем.
Rhett Allain
Самый популярный
Обратите внимание, что я показываю направление магнитного поля внутри этого круга, но это действительно направление . это важно.
Закон Ампера-Максвелла
Ретта Аллена
Вы видите сходство? Это уравнение похоже на закон Фарадея, верно? Ну и заменяет E на B и добавляет дополнительный термин.
Основная идея здесь в том, что это уравнение говорит нам о двух способах создания магнитного поля. Первый способ – с помощью электрического тока.
Вот супербыстрая демонстрация. У меня есть магнитный компас с проводом над ним. Когда течет электрический ток, он создает магнитное поле, которое перемещает стрелку компаса.
Ретт Аллен
Rhett AllainИз этой демонстрации трудно понять, но форма этого магнитного поля волнистая. Вы можете увидеть это, если я положу несколько железных опилок на бумагу, через которую будет проходить электрический ток.
Rhett Allain
Самый популярный
Может быть, вы можете немного лучше увидеть форму этого поля с помощью этого численного расчета. Это показывает небольшую часть провода с электрическим током и результирующим магнитным полем.
Rhett Allain
На самом деле, этот образ может показаться сложным в создании, но на самом деле это не так уж и сложно.
Вот учебник по использованию Python для расчета магнитного поля. Есть и другой способ создания фигурного магнитного поля — с помощью изменяющегося электрического поля. Да, точно так же изменяющееся магнитное поле создает искривленное электрическое поле. Вот как это будет выглядеть.
Rhett Allain
Самый популярный
Обратите внимание, что я даже изменил цвета вектора, чтобы они соответствовали предыдущему фигурному изображению, потому что меня волнуют детали предыдущего фигурного поля. Но позвольте мне просто резюмировать самую крутую часть. Изменяющиеся электрические поля создают волнистые магнитные поля. Изменяющиеся магнитные поля создают искривленные электрические поля. ПОТРЯСАЮЩИЕ.
Что насчет света?
Наиболее распространенной темой, связанной с уравнениями Максвелла, является электромагнитная волна. Как это работает? Предположим, у вас есть область пространства, в которой нет ничего, кроме электрического поля и магнитного поля. Нет электрических зарядов и нет электрического тока. Допустим, это выглядит так.
Ретт Аллен
Позвольте мне объяснить, что здесь происходит. Существует электрическое поле, направленное НА экран вашего компьютера (да, трудно работать с трехмерным изображением на 2D-экране), и магнитное поле, направленное вниз. Эта область с полем движется вправо с некоторой скоростью v. А что насчет ящика? Это просто очертание какого-то региона. Но вот в чем дело. По мере того, как электрическое поле перемещается в эту коробку, возникает изменяющееся поле, которое может создавать магнитное поле. Если вы нарисуете другой прямоугольник перпендикулярно этому, вы увидите, что будет меняющееся магнитное поле, которое может создать магнитное поле. В самом деле, если эта область пространства движется со скоростью света (3 х 10 8 м/с), то изменяющееся магнитное поле может вызвать изменяющееся электрическое поле. Эти поля могут поддерживать друг друга без каких-либо зарядов или токов.
Это электромагнитный импульс.
Электромагнитная волна представляет собой колеблющееся электрическое поле, которое создает колеблющееся магнитное поле, создающее колеблющееся электрическое поле. Большинству волн для движения требуется какой-либо тип среды. Звуковой волне нужен воздух (или какой-то другой материал), волне в океане нужна вода. ЭМ волна в этом не нуждается. Это его собственная среда. Он может путешествовать по пустому пространству — и это хорошо, так как мы можем получать свет от солнца здесь, на Земле.
Обновлено 19.12.2019, 16:30 по восточному времени: статья была обновлена, чтобы исправить написание второго имени Джеймса Клерка Максвелла.
Другие великие истории WIRED
- Как 6000-летний рак собаки распространился по всему миру
- Эти хаотичные игры – худший кошмар судьи
- Этот международный наркоторговец создал биткойн? Может быть!
- Как воздушные шары Loon доставляют интернет
- Социальные сети могут сделать невозможным взросление
- 💻 Обновите свою рабочую игру с любимыми ноутбуками нашей команды Gear, клавиатурами, вариантами набора текста и наушниками с шумоподавлением
- 📩 Хотите большего? Подпишитесь на нашу ежедневную рассылку новостей и никогда не пропустите наши самые свежие и интересные истории
Ретт Аллен — адъюнкт-профессор физики в Университете Юго-Восточной Луизианы.
Он любит преподавать и говорить о физике. Иногда он разбирает вещи и не может собрать их обратно.
ТемыТочечная физикаэлектрическое полемагнетизмсвет
Еще из WIREDУравнения Максвелла
Уравнения Максвелла представляют собой набор из 4 сложных уравнений, описывающих мир электромагнетизма. Эти уравнения описывают, как электрические и магнитные поля распространяются, взаимодействуют и как на них влияют. по объектам.
Джеймс Клерк Максвелл [1831–1879] был гением уровня Эйнштейна/Ньютона, который взял набор известных экспериментальных законов (Закон Фарадея, Закон Ампера) и объединил их в симметричную связную систему уравнений, известную как Уравнения Максвелла. Максвелл одним из первых определил скорость распространения электромагнитных волн. (ЭМ) волн была такой же, как скорость света, и, следовательно, сделать вывод, что электромагнитные волны и видимые свет был действительно то же самое.
Уравнения Максвелла имеют решающее значение для понимания Антенн и
Электромагнетизм.
На них страшно смотреть — они настолько сложны, что большинство инженеров-электриков и физиков
даже толком не знаю, что они означают. Окутан сложной математикой (вероятно, поэтому «интеллектуальные» люди могут чувствовать свое превосходство
при их обсуждении), трудно добиться истинного понимания этих уравнений.
Отсюда и причина создания этого веб-сайта — интуитивно понятный учебник по уравнениям Максвелла. Я буду избегать, если в
все возможные математические трудности, которые возникают, а вместо этого опишите, что означают уравнения. А также
не бойтесь – математика настолько сложна, что те, кто разбирается в сложном векторном исчислении, все равно не смогут
применять уравнения Максвелла во всем, кроме простейших сценариев. Поэтому интуитивное знание
Уравнения Максвелла намного превосходят знания, основанные на математических манипуляциях. Чтобы понять мир,
вы должны понимать, что означают уравнения, а не только знать математические конструкции. я считаю принятым
методы преподавания электромагнетизма и уравнения Максвелла не дают понимания.