Дифференциальные уравнения первого порядка – rajak.rs
Общий вид дифференциального уравнения первого порядка:
$F\left( {x,y,y’} \right) = 0$.
Его общее решение имеет вид:
$y = f\left( {x,c} \right)$.
Простейшие дифференциальные уравнения первого порядка.
- Дифференциальные уравнения с разделёнными перемеными: \[{f_1}\left( x \right)dx = {f_2}\left( y \right)dy,\] где множителем при $dx$ является функция, зависящая только от $x$, а множителем при $dy$ является функция, зависящая только от $y$. Решение находится методом интегрирования обеих частей.\[\int {{f_1}\left( x \right)dx} = \int {{f_2}\left( y \right)dy} + C\]
- Дифференциальные уравнения вида \[y’ = {f_1}\left( x \right){f_2}\left( y \right)dy,\] где правая часть представляет собой произведение двух функций, из которых одна не зависит от $x$, а вторая не зависит от $y$, называется уравнением с разделяющимися переменными. Метод решения:\[\int {\frac{{dy}}{{{f_2}\left( x \right)}}} = \int {{f_1}\left( x \right)dx} + C\]
- Дифференциальные уравнения с разделяющимися переменными, записанные в форме дифференциалов: \[{f_1}\left( x \right) \cdot {f_2}\left( y \right)dx + {f_3}\left( x \right) \cdot {f_4}\left( y \right)dy = 0\] для решения таких дифференциальных уравнений их надо привести к уравнениям с разделёнными переменными.
 n} \cdot \varphi \left( {\frac{y}{x}} \right)\]
n} \cdot \varphi \left( {\frac{y}{x}} \right)\]Однородная функция нулевой степени может быть записана в виде \[f\left( {x,y} \right) = \varphi \left( {\frac{y}{x}} \right)\]
Если функции $M\left( {x,y} \right)$ и $N\left( {x,y} \right)$ однородные одной и той же степени $n$, то дифференциальное уравнение \[M\left( {x,y} \right)dx + N\left( {x,y} \right)dy = 0\] называется
Уравнение $y’ = f\left( {x,y} \right)$ называется однородным, если оно имеет вид: \[y’ = \varphi \left( {\frac{y}{x}} \right)\]
Очевидно, что $f\left( {x,y} \right)$ однородная функция нулевого измерения.
Однородные уравнения приводятся к уравнению с разделяющимися перемеными при помощи подстановки.
$t = \frac{y}{x}$ т.е. $y = tx$ и $y’ = t’x + t$ или в дифференциалах $dy = tdx + xdt$.
Линейные уравнения первого порядка.
Линейным дифференциальным уравнением первого порядка называется такое дифференциальное уравнение, в которое неизвестные функции $y$ и ${y’}$ входят в первых степенях и не перемножаются между собой.

\frac{{z’}}{{\left( {1 – n} \right)}} + P\left( x \right)z\left( x \right) = Q\left( x \right) \hfill \\
\frac{{dz}}{{dx}} + \left( {1 – n} \right)P\left( x \right)z\left( x \right) = Q\left( x \right)\left( {1 – n} \right) \hfill \\
\end{gathered} \]Это линейное уравнение I-го порядка, для его решения применяем, например, подстановку Бернулли.Дифференциальные уравнения первого порядка
Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.
Дифференциальные уравнения первого порядка, разрешенные относительно производной
Как решать дифференциальные уравнения первого порядка
Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:
.
Разделив это уравнение на , при , мы получим уравнение вида:
,
где .
Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем и умножаем уравнение на . Получаем уравнение в форме дифференциалов:
.Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении – независимая переменная, а – это функция от . Разделим уравнение на :
.
Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что и поменялись местами.Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:
,
то замечаем, что . Тогда делаем подстановку . После этого уравнение примет более простой вид:
.Если и это не помогает, то пытаемся найти интегрирующий множитель ⇓.
Уравнения с разделяющимися переменными
;
.
Делим на и интегрируем. При получаем:
.
Подробнее >>>Уравнения, приводящиеся к уравнениям с разделяющимися переменными
Делаем подстановку . Тогда
;
.
Далее разделяем переменные и интегрируем.
Подробнее >>>Однородные уравнения
Решаем подстановкой:
,
где – функция от . Тогда
;
.
Разделяем переменные и интегрируем.
Подробнее >>>Уравнения, приводящиеся к однородным
Вводим переменные и :
;
.
Постоянные и выбираем так, чтобы свободные члены обратились в нуль:
;
.
В результате получаем однородное уравнение в переменных и .
Подробнее >>>Обобщенные однородные уравнения
Делаем подстановку . Получаем однородное уравнение в переменных и .
Подробнее >>>Линейные дифференциальные уравнения
Есть три метода решения линейных уравнений.1) Метод интегрирующего множителя.
Умножаем уравнение на интегрирующий множитель :
;
.
Далее интегрируем.
Подробнее >>>2) Метод Бернулли.
Ищем решение в виде произведения двух функций и от переменной :
.
;
.
Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>3) Метод вариации постоянной (Лагранжа).
Здесь мы сначала решаем однородное уравнение:
Общее решение однородного уравнения имеет вид:
,
где – постоянная. Далее мы заменяем постоянную на функцию , зависящую от переменной :
.
Подставляем в исходное уравнение. В результате получаем уравнение, из которого определяем .
Подробнее >>>Уравнения Бернулли
Подстановкой уравнение Бернулли приводится к линейному уравнению.Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной :
.
Подставляем в исходное уравнение:
;
.
В качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .Подробнее >>>
Уравнения Риккати
Оно не решается в общем виде. Подстановкой
уравнение Риккати приводится к виду:
,
где – постоянная; ; .
Далее, подстановкой:
оно приводится к виду:
,
где .Свойства уравнения Риккати и некоторые частные случаи его решения представлены на странице
Дифференциальное уравнение Риккати >>>Уравнения Якоби
Решается подстановкой:
.
Подробнее >>>Уравнения в полных дифференциалах
При условии
.
При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:
.
Тогда
.
Отсюда получаем интеграл дифференциального уравнения:
.Для нахождения функции , наиболее удобным способом является метод последовательного выделения дифференциала.
 Для этого используют формулы:
Для этого используют формулы:
;
;
;
.
Подробнее >>>Интегрирующий множитель
Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель . Интегрирующий множитель – это такая функция, при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.
Подробнее >>>Уравнения, не решенные относительно производной y’
Уравнения, допускающие решение относительно производной y’
Сначала нужно попытаться разрешить уравнение относительно производной . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.
Уравнения, допускающие разложение на множители
Если удастся уравнение разложить на множители:
,
то задача сводится к последовательному решению более простых уравнений:
;
;
;
Подробнее >>>Уравнения, не содержащие x и y
Здесь – постоянная:
,
где – корень уравнения
.
Подробнее >>>Уравнения, не содержащие x или y
или
Ищем решение в параметрическом виде. Вводим параметр . Полагаем . Тогда
или .
Далее интегрируем уравнение:
;
.
В результате получаем выражение второй переменной через параметр .Более общие уравнения:
или
также решаются в параметрическом виде. Для этого нужно подобрать такую функцию , чтобы из исходного уравнения можно было выразить или через параметр .
Чтобы выразить вторую переменную через параметр , интегрируем уравнение:
;
.
Подробнее >>>Уравнения, разрешенные относительно y
Уравнения Клеро
Такое уравнение имеет общее решение
Подробнее >>>Уравнения Лагранжа
Решение ищем в параметрическом виде. Полагаем , где – параметр.
Подробнее >>>Уравнения, приводящиеся к уравнению Бернулли
Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр и делая подстановку .
Подробнее >>>Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.Автор: Олег Одинцов. Опубликовано:
Дифференциальные уравнения, приводимые к уравнениям первого порядка
Дифференциальные уравнения второго порядка, в которых правая часть не зависит от неизвестной функции и её производной
Таким дифференциальным уравнением второго порядка является уравнение вида $y”=f\left(x\right)$. В нем правая часть не зависит от неизвестной функции $y$ и её производной $y’$, а зависит только от $x$. Решается это уравнение последовательным интегрированием.
Представим его в таком виде: $\frac{d}{dx} \left(y’\right)=f\left(x\right)$, откуда $d\left(y’\right)=f\left(x\right)\cdot dx$.
Интегрируем первый раз, используя то свойство, что неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: $\int d\left(y’\right) =\int f\left(x\right)\cdot dx $ или $y’=\int f\left(x\right)\cdot dx +C_{1} $, где $C_{1} $ — произвольная постоянная.

Таким образом, дифференциальное уравнение второго порядка сведено теперь к дифференциальному уравнению первого порядка, которое можно представить в таком виде: $dy=\left(\int f\left(x\right)\cdot dx +C_{1} \right)\cdot dx$.
Интегрируем полученное дифференциальное уравнение повторно: $y=\int \left(\int f\left(x\right)\cdot dx +C_{1} \right)\cdot dx =\int \left(\int f\left(x\right)\cdot dx \right)\cdot dx +\int C_{1} \cdot dx$. Окончательно получаем:$y=\int \left(\int f\left(x\right)\cdot dx \right)\cdot dx +C_{1} \cdot x+C_{2} $, где $C_{2} $ — произвольная постоянная.
Процесс интегрирования завершен. Получена неизвестная функция $y$, которая является общим решением данного дифференциального уравнения второго порядка.
Алгоритм решения дифференциального уравнения второго порядка $y”=f\left(x\right)$ может быть представлен в следующем виде:
- находим интеграл $I_{1} \left(x\right)=\int f\left(x\right)\cdot dx $ и записываем первую производную искомой функции в виде $y’\left(x,C_{1} \right)=I_{1} \left(x\right)+C_{1} $;
- находим интеграл $I_{2} \left(x\right)=\int I_{1} \left(x\right)\cdot dx $ и записываем окончательно общее решение данного дифференциального уравнения: $y=I_{2} \left(x\right)+C_{1} \cdot x+C_{2} $;
- для поиска частного решения начальные условия подставляем в выражение для первой производной $y’$, а также в общее решение; в результате находим значения произвольных постоянных $C_{1} $ и $C_{2} $.

Дифференциальные уравнения второго порядка, не содержащие неизвестной функции
Указанные дифференциальные уравнения второго порядка допускают понижение порядка посредством замены переменных. После этого к полученным дифференциальным уравнениям первого порядка могут быть применены известные методы решения.
Дифференциальное уравнение второго порядка, не содержащее неизвестной функции $y$, имеет вид $y”=f\left(x,y’\right)$.
Для его решения применяют замену $y’=z\left(x\right)$.
При этом $y”=z’\left(x\right)$. После подстановки данное дифференциальное уравнение приобретает вид дифференциального уравнения первого порядка относительно $z$, то есть $z’=f\left(x,z\right)$. Решая его, находим $z\left(x\right)=\phi \left(x,C_{1} \right)$.
В свою очередь, поскольку $y’=z\left(x\right)$, то $y’=\phi \left(x,C_{1} \right)$. Это также дифференциальное уравнение первого порядка, которое допускает непосредственное интегрирование.
 Следовательно, интегрируя еще раз, окончательно получаем общее решение $y=\int \phi \left(x,C_{1} \right)\cdot dx +C_{2} $.
Следовательно, интегрируя еще раз, окончательно получаем общее решение $y=\int \phi \left(x,C_{1} \right)\cdot dx +C_{2} $.Алгоритм решения дифференциального уравнения второго порядка $y”=f\left(x,y’\right)$ может быть представлен в следующем виде:
- переписываем данное дифференциальное уравнение в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y”$ на $z’$, а $y’$ — на $z$;
- полученное дифференциальное уравнение первого порядка решаем одним из подходящих известных методов;
- найденное решение $z=\phi \left(x,C_{1} \right)$ представляем в виде дифференциального уравнения первого порядка $y’=\phi \left(x,C_{1} \right)$, которое допускает непосредственное интегрирование;
- находим интеграл $I=\int \phi \left(x,C_{1} \right)\cdot dx $ и получаем общее решение в виде $y=I+C_{2} $.
Задача 2
Найти общее решение дифференциального уравнения$y”-\frac{y’}{x} =3\cdot x$.
Данное дифференциальное уравнение не содержит неизвестной функции $y$, поэтому переписываем его в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y”$ на $z’$, а $y’$ — на $z$.
 {2} +C_{2} $.
{2} +C_{2} $.Дифференциальные уравнения второго порядка, не содержащие независимой переменной
Указанные дифференциальные уравнения второго порядка также допускают понижение порядка посредством замены переменных. После этого к полученным дифференциальным уравнениям первого порядка могут быть применены известные методы решения.
Дифференциальное уравнение второго порядка, не содержащее независимой переменной $x$, имеет вид $y”=f\left(y,y’\right)$.
Для его решения применяют замену $y’=z\left(y\right)$.
Ищем вторую производную: $y”=\frac{d\left(y’\right)}{dx} =\frac{d\left(y’\right)}{dy} \cdot \frac{dy}{dx} =\frac{dz}{dy} \cdot \frac{dy}{dx} =\frac{dz}{dy} \cdot z\left(y\right)$.
Подставляем выражения для $y’$ и $y”$ в данное дифференциальное уравнение: $z\cdot \frac{dz}{dy} =f\left(y,z\right)$. Получили дифференциальное уравнение первого порядка относительно переменной $z$, которая является функцией $y$. Решая его, находим $z\left(y\right)=\phi \left(y,C_{1} \right)$.

В свою очередь, поскольку $\frac{dy}{dx} =z\left(y\right)$, то $\frac{dy}{dx} =\phi \left(y,C_{1} \right)$. Полученное дифференциальное уравнение представляет собой дифференциальное уравнение первого порядка с разделяющимися переменными, общее решение которого можно найти из выражения $\int \frac{dy}{\phi \left(y,C_{1} \right)} =x+C_{2} $.
Алгоритм решения дифференциального уравнения второго порядка $y”=f\left(y,y’\right)$ может быть представлен в следующем виде:
- переписываем данное дифференциальное уравнение в виде дифференциального уравнения первого порядка относительно переменной $z$, формально заменив $y”$ на $z\cdot z’$, а $y’$ — на $z$;
- полученное дифференциальное уравнение первого порядка решаем одним из подходящих известных методов;
- найденное решение $z=\phi \left(y,C_{1} \right)$ представляем в виде дифференциального уравнения первого порядка $\frac{dy}{dx} =\phi \left(y,C_{1} \right)$, которое является дифференциальным уравнением с разделяющимися переменными;
- находим интеграл $I=\int \frac{dy}{\phi \left(y,C_{1} \right)} $ и получаем общее решение в виде $I=x+C_{2} $.

Простейшие = решаемые аналитически обыкновенные дифференциальные уравнения первого порядка. Виды дифференциальных уравнений первого порядка.
Простейшие = решаемые аналитически обыкновенные дифференциальные уравнения первого порядка. Виды дифференциальных уравнений первого порядка.
Уравнения с разделяющимися переменными и сводящиеся к ним
Однородные уравнения и сводящиеся к ним
Линейные уравнения и сводящиеся к ним
Уравнение в полных дифференциалах . Интегрирующий множитель.
Уравнения не разрешенные относительно производной и сводящиеся к нимУравнения с разделяющимися переменными и сводящиеся к ним
1. y’=f(x)*g(y) – например: y’=x*y*(y+2), где f(x)=х; g(y)=y*(y+2)
или
m(x)*n(y)dy+p(x)*q(y)dx=0
(Примеры и методы решений)
2. Уравнение вида y’=f(ax+by) приводится к уравнению с разделяющимися переменными
(Примеры и методы решений)
Однородные уравнения
1.
 y’=f(y/x)
y’=f(y/x) или
M(x,y)dx+N(x,y)dy=0,
где M(x,y) и N(x,y) однородные функции одной и той же степени “n”.
(Примеры и методы решений)
2. сводится к однородному уравнению.
(Примеры и методы решений)
Линейные уравнения
1. y’+a(x)y=b(x)
(Примеры и методы решений)
2. Уравнение y’+a(x)y=b(x)yn (Бернулли) сводится к однородному
(Примеры и методы решений)
3. Уравнение y’+a(x)y+b(x)y2=c(x) (Риккати) в некоторых случаях сводится к уравнению Бернулли.
(Примеры и методы решений)
Уравнение в полных дифференциалах. Интегрирующий множитель.
1. M(x,y)dx+N(x,y)dy=0,
если выполняется условие
Интегрирующий множитель- множитель, умножив на который обе стороны уравнения, мы получим уравнение в полных дифференциалах (если оно таким и не было изначально).
(Примеры и методы решений)
Уравнения не разрешенные относительно производной
Общий вид : F(x,y,y’)=0,
1. Случай, когда из уравнения F(x,y,y’)=0 можно выразить y’ через x, y.
2. Случай, когда уравнение F(x,y,y’)=0 можно разрешить относительно у (простейший вариант метода введения параметра).
3. Случай, когда уравнение F(x,y,y’)=0 можно разрешить относительно х.
4. Уравнение Лагранжа y=xφ(y’)+ψ(y’). Уравнение Клеро y=xy’+ψ(y’)
5. Особые решения.
(Примеры и методы решений)1.3. Уравнения первого порядка и их геометрический смысл
Дифференциальное уравнение первого порядка может быть записано в общем виде, аналогичному уравнению -го порядка (1.3):
. (1.4)
Если это уравнение разрешить относительно производной, то
.
 (1.5)
(1.5)Простейший пример такого уравнения
, (1.6)
Из которого неизвестная функция находится интегрированием
,
Где слева стоит неопределенный интеграл. Если функция имеет первообразную , то .
В этом простейшем случае решение содержит произвольную постоянную , которая может быть определена, если задать Начальное условие
или , (1.7)
Где и – некоторые числа, то есть при некотором значении независимой переменной заранее задано значение искомой функции .
Геометрически начальное условие (1.7) означает, что на плоскости задана точка , через которую должна проходить искомая интегральная кривая. При таком начальном условии решение уравнения (1.6) можно представить в виде
.
Рассмотрим уравнение (1.5). Пусть – область определения функции на плоскости . Возьмём некоторую точку и вычислим значение функции в ней . В соответствии с исходным дифференциальным уравнением получим значение производной неизвестной функции в заданной точке, то есть .
 Поскольку производная функций определяет угловой коэффициент наклона касательной к графику функции, то тем самым определим угловой коэффициент касательной к той интегральной кривой уравнения, которая проходит через точку .
Поскольку производная функций определяет угловой коэффициент наклона касательной к графику функции, то тем самым определим угловой коэффициент касательной к той интегральной кривой уравнения, которая проходит через точку .Возьмем теперь другую точку и вычислим для нее величину . Это есть коэффициент наклона касательной к интегральной кривой, проходящей через эту новую точку. Точно так же, беря новые точки в области , получим множество элементарных «кусочков» интегральных кривых этого уравнения, проходящих через взятые точки.
Геометрический смысл дифференциального уравнения (1.5) заключается в том, что оно устанавливает зависимость между координатами точек интегральной кривой и значением производной , то есть в каждой точке определяется направление касательной к искомой интегральной кривой. Таким образом, уравнение (1.5) определяет поле направлений, и задача интегрирования дифференциального уравнения заключается в том, чтобы найти кривые, направления касательных к которым в каждой точке совпадают с направлением поля.
 Каждая из интегральных кривых представляет собой график решения исходного дифференциального уравнения. Найти решение уравнения с начальным условием (1.7) геометрически означает выделение из множества интегральных кривых той кривой, которая проходит через точку . Всё множество интегральных кривых представляет общее решение дифференциального уравнения. При графическом представлении решения дифференциального уравнения часто пользуются изоклинами.
Каждая из интегральных кривых представляет собой график решения исходного дифференциального уравнения. Найти решение уравнения с начальным условием (1.7) геометрически означает выделение из множества интегральных кривых той кривой, которая проходит через точку . Всё множество интегральных кривых представляет общее решение дифференциального уравнения. При графическом представлении решения дифференциального уравнения часто пользуются изоклинами.Изоклиной Называется геометрическое место точек, для которых производная некоторой функции имеет одно и то же значение. Уравнение изоклины имеет вид . Для дифференциального уравнения (1.5) изоклины представляются равенством . Графический метод решения дифференциального уравнения с помощью изоклин используется в том случае, когда аналитическое решение невозможно.
< Предыдущая Следующая > Дифференциальные уравнения первого порядка
Дифференциальные уравнения.

Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции (или нескольких неизвестных функций). Вместо производных могут содержаться дифференциалы.
Если неизвестные функции зависят от одного аргумента, то дифференциальное уравнение называется обыкновенным, если от нескольких, то уравнение называется дифференциальным уравнением с частными производными. Будем рассматривать только обыкновенные дифференциальные уравнения.
Общий вид дифференциального уравнения с одной неизвестной функцией таков:
F(х, у, у’, у”, …, у(n))=0.
Порядком дифференциального уравнения называется порядок наивысшей из производных, входящих в это уравнение.
Функция у=(х) называется решением дифференциального уравнения, если последнее обращается в тождество после подстановки у=(х).

Основной задачей теории дифференциальных уравнений является нахождение всех решений данного дифференциального уравнения. В простейших случаях эта задача сводится к вычислению интеграла. Поэтому решение дифференциального уравнения называют также его интегралом, а процесс нахождения всех решений — интегрированием дифференциального уравнения.
Вообще интегралом данного дифференциального уравнения называют всякое уравнение, не содержащее производных, из которого данное дифференциальное уравнение вытекает как следствие.
Уравнение вида F(x, y, y‘)=0, где х — независимая переменная; у — искомая функция; у’ — её производная, называется дифференциальным уравнением первого порядка.
Если уравнение можно разрешить относительно у’, то оно принимает вид: y‘=f(x, y) и называется уравнением первого порядка, разрешенным относительно производной.

Дифференциальное уравнение удобно записать в виде: , являющемся частным случаем более общего уравнения (в симметрической форме):P(x,y)dx+Q(x, y)dy =0, где Р(x, y) и Q (x, y) — известные функции.
Уравнение в симметричной форме удобно тем, что переменные х и у в нем равноправны, т.е. каждую из них можно рассматривать как функцию от другой.
Решением дифференциального уравнения первого прядка называется функция у=(х), которая при подстановке в уравнение обращает его в тождество.
График решения дифференциального уравнения называется интегральной кривой.
Ответ на вопрос о том, при каких условиях уравнение имеет решение, дает теорема Коши, которая называется теоремой о существовании и единственности решения дифференциального уравнения и является основной в теории дифференциальных уравнений.

Теорема (теорема Коши). Если функция f(x, у) и ее частная производная f‘y(x, у) определены и непрерывны в некоторой области G плоскости Оху, то какова бы ни была внутренняя точка (х0; у0) области G, в некоторой окрестности этой точки существует единственное решение уравнения y‘=f(x, у), удовлетворяющее условиям: у=уо при х=х0.
Теорема Коши дает возможность по виду дифференциального уравнения решать вопрос о существовании и единственности его решения. Это особенно важно в тех случаях, когда заранее неизвестно, имеет ли данное уравнение решение.
Геометрически теорема утверждает, что через каждую внутреннюю точку (x0; у0) области G проходит единственная интегральная кривая.
 Очевидно, что в области G уравнение
имеет бесконечное число различных
решений.
Очевидно, что в области G уравнение
имеет бесконечное число различных
решений.Условия, в силу которых функция у=(х) принимает заданное значение у0 в заданной точке х0, называют начальными условиями решения.
Отыскание решения уравнения, удовлетворяющего начальным условиям, — одна из важнейших задач теории дифференциальных уравнений. Эта задача называется задачей Коши.
С геометрической точки зрения решить задачу Коши — значит из множества интегральных кривых выделить ту, которая проходит через заданную точку (х0; у0) плоскости Оху.
Точки плоскости, через которые либо проходит более одной интегральной кривой, либо не проходит ни одной интегральной кривой, называются особыми точками данного уравнения.
Общим решением уравнения в некоторой области G плоскости Оху называется функция у=(х, С), зависящая от х и произвольной постоянной С, если она является решением уравнения при любом значении постоянной С, и если при любых начальных условиях таких, что (х0; у0)G, существует единственное значение постоянной С=С0 такое, что функция у=(х, С0) удовлетворяет данным начальным условиям (х0, С)=С0.

Частным решением уравнения в области G называется функция у=(х, С0), которая получается из общего решения у=(х, С) при определенном значении постоянной С=С0.
Геометрически общее решение представляет собой семейство интегральных кривых на плоскости Оху, зависящее от одной произвольной постоянной С, а частное решение — одну интегральную кривую этого семейства, проходящую через заданную точку (х0; у0).
Иногда начальные условия называют условиями Коши, а частным решением называют решение какой-нибудь задачи Коши.
Геометрический смысл уравнения. Пусть дано дифференциальное уравнение первого порядка y‘=f(x, у) и пусть функция у=(х) – его решение.
 График решения представляет
собой непрерывную интегральную кривую,
через каждую точку которой можно провести
касательную. Из уравнения следует, что
угловой коэффициент у’ касательной
к интегральной кривой в каждой ее точке
(х;
у) равен значению
в этой точке правой части уравнения f(x,
у). Таким образом,
уравнение y‘=f(x,
у) устанавливает
зависимость между координатами точки
(х;
у) и
угловым коэффициентом у’ касательной
к графику интегральной кривой в той же
точке. Зная х и у, можно указать
направление касательной к этой
интегральной кривой в точке (х;
у).
Сопоставим каждой точке (х;
у) интегральной
кривой направленный отрезок, угловой
коэффициент которого равен f(х,
у). Получим так
называемое поле
направлений данного
уравнения, раскрывающее геометрический
смысл дифференциального уравнения
первого порядка.
График решения представляет
собой непрерывную интегральную кривую,
через каждую точку которой можно провести
касательную. Из уравнения следует, что
угловой коэффициент у’ касательной
к интегральной кривой в каждой ее точке
(х;
у) равен значению
в этой точке правой части уравнения f(x,
у). Таким образом,
уравнение y‘=f(x,
у) устанавливает
зависимость между координатами точки
(х;
у) и
угловым коэффициентом у’ касательной
к графику интегральной кривой в той же
точке. Зная х и у, можно указать
направление касательной к этой
интегральной кривой в точке (х;
у).
Сопоставим каждой точке (х;
у) интегральной
кривой направленный отрезок, угловой
коэффициент которого равен f(х,
у). Получим так
называемое поле
направлений данного
уравнения, раскрывающее геометрический
смысл дифференциального уравнения
первого порядка.Итак, с геометрической точки зрения уравнение y‘=f(x, у) определяет на плоскости Оху поле направлений, а решение этого уравнения — интегральная кривая, направление касательной к которой в каждой точке совпадает с направлением поля в этой точке.

Построив на плоскости поле направлений данного дифференциального уравнения, можно приближенно построить интегральные кривые.
Линейные дифференциальные уравнения первого порядка. Метод Бернулли
Все кто ищет готовые ответы на линейные дифференциальные уравнения пришли по правильному адресу. У нас Вы сможете не только получить быстрый ответ, но и научиться методике решения уравнений. Будет ли сложной схема Бернулли для линейных уравнений зависит от Вашего уровня подготовки. Разберите внимательно приведенные ответы и сделайте выводы, что и как Вам нужно углубленно изучить.
Линейным дифференциальным уравнением первого порядканазывается уравнение вида y’+p(x)*y=g(x), где p(x) и g(x) – непрерывные на определенном промежутке функции.Алгоритм метода Бернулли
1. Решение линейного дифференциального уравнения необходимо представить в виде произведения двух неизвестных функций y=u*v от аргумента u=u(x),v=v(x).
 Одну из этих функций можно выбрать произвольно, а вторая определяется из дифференциального уравнения.
Одну из этих функций можно выбрать произвольно, а вторая определяется из дифференциального уравнения.
2. По правилу производная произведения равна y=u*v,то y’=u’v+uv’.
3. Подставим запись функции y=u*v и производной y’=u’v+uv’ в уравнение y’+p(x)*y=g(x) и получим u’v+uv’+p(x)*u*v= g(x). Сгруппируем второй и третий слагаемые, вынеся общий множитель (u) за скобки и придем к диф. уравнению u’v+u(v’+p(x)*v)=g(x).
4. Сперва определяем частное решение v=v(x), для этого решаем диф. уравнения v’+p(x)*v=0 и за произвольную постоянную интегрирования берем ноль (С=0). Данное уравнение является дифференциальным уравнением с разделяющимися переменными.
5. Далее подставим найденную функцию v=v(x) в исходное диф. уравнение u’v+uv’+p(x)*u*v= g(x), которое при этом упростится до вида u’v+u*0=g(x), то есть к дифференциальному уравнению с разделяющимися переменными u’v(х)=g(x) относительно u(x). Из этого уравнения находим u=u(x)+С.
6. Имея u=u(x) и v=v(x) находим общее решение ДУ через произведение y=u*v=( u(x)+С)* v(x).
7. Если задана задача Коши то с дополнительной условия на решение y(x0)=y0 определяем сталую С.Пример 1. Найти решение задачи Коши
Решение:Имеем неоднородное дифференциальное уравнение первого порядка. Запишем его в правильном виде, для этого перенесем в правую сторону функцию
Далее по схеме Бернулли делаем замену переменных y=u*v, y’=u’v+uv’, где u=u(x) і v=v(x).
Учитывая что множители в левой части уровне
и y2=u2v2
получим следующее уравнение
Согласно алгоритму Бернулли уравнение разделим на 2, для этого дужку слева (выделена черным) приравняем к нулю
Сводим к дифференциальному уравнению с разделенными переменными
и решаем интегрированием
В результате получили экспоненту с отрицательным показателем синуса. При этом исходное дифференциальное уравнение достаточно упростится для поиска второй неизвестной пока функции
Перенесем экспоненту с отрицательным показателем в правую сторону
и сведем к ДУ с разделенными переменными
Интегрированием уравнения в дифференциалах
находим решение дифференциального уравнения
Как описано в начале, общее решение дифференциального уравнения равно произведению функций
Но это еще не конечная ответ к задаче. Найдем частичное решение дифференциального уравнения (задача Коши), для этого определим постоянную с начального условия на функцию
Найдем частичное решение дифференциального уравнения (задача Коши), для этого определим постоянную с начального условия на функцию
Сталая равна нулю, это позволяет упростить формулу решения диф. уравнения, хотя мало кто из Вас увидит эту подсказку
Мы нашли частичный решение дифференциального уравнения и он равен экспоненте в степени “икс” y=ex.Пример 2. Решить дифференциальное уравнение та задачу Коши
Решение:Задано неоднородное дифференциальное уравнение первого порядка, которое перепишем в виде
Выполняем замену переменных в уравнении
, где “у” и “в” принимают функциональные зависимости
Находим выражения которые фигурируют в записи
и подставляем в исходное дифференциальное уравнение
Далее схема вычислений заключается в разделении переменных. По алгоритму Бернулли выражение, содержащее “v” приравняем к нулю
Записываем уравнение в дифференциалах
Видим что имеем уравнение с разделяющимися переменным, поетому целесообразно разделить переменные
Проинтегрировав обе части
получим логарифм и синус.
Далее экспонируем обе части и таким образом находим одну из неизвестных функций
Исходное дифференциальное уравнение при этом упростится к виду
Экспоненту в отрицательном показателе переносим вправо от знака равенства
Далее распишем уравнения через дифференциалы (/2)
и сведем к уравнению с разделенными переменными
Интеграл в правой части выглядит тяжелым для высчисления, но если внести дужку под дифференциал, то получим показатель экспоненты
Окончательно после интегрирования получим
Общий интеграл дифференциального уравнения записываем через произведение функций
Чтобы найти частичное решение дифференциального уравнения (задачи Коши) используем начальное условие
Из него определим постоянную и подставим в уравнение частного решения дифференциального уравнения
На этом и построен алгоритм Бернулли вычислений дифференциальных уравнений такого типа. Используйте алгоритм решения уравнения Бернулли ко всем подобным дифференциальным уравнениям.
Используйте алгоритм решения уравнения Бернулли ко всем подобным дифференциальным уравнениям.Линейные уравнения первого порядка
Линейные уравнения первого порядка
Дифференциальное уравнение первого порядка называется линейным , если его можно выразить в форме
, где P и Q являются функциями x . Метод решения таких уравнений аналогичен методу решения неточных уравнений. Там неточное уравнение было умножено на интегрирующий коэффициент, что затем упростило решение (поскольку уравнение стало точным).
Чтобы решить линейное уравнение первого порядка, сначала перепишите его (если необходимо) в приведенной выше стандартной форме; затем умножьте обе стороны на интегрирующий коэффициент
Полученное уравнение,
Тогдалегко решить не потому, что он точен, а потому, что левая часть схлопывается:
Следовательно, уравнение (*) становится
, что делает его восприимчивым к интеграции, что дает решение:
Не запоминайте это уравнение для решения; запомните шаги, необходимые для этого.

Пример 1: Решите дифференциальное уравнение
Уравнение уже выражено в стандартной форме: P (x) = 2 x и Q (x) = x . Умножение обеих сторон на
преобразует данное дифференциальное уравнение в
Обратите внимание, как левая часть сворачивается в ( мкг ) ′; как показано выше, это всегда будет происходить .Объединение обеих сторон дает решение:
Пример 2: Решить IVP
Обратите внимание, что дифференциальное уравнение уже имеет стандартную форму. Поскольку P (x) = 1/ x , интегрирующий коэффициент равен
.Умножение обеих сторон дифференциального уравнения стандартной формы на μ = x дает
Обратите внимание, как левая сторона автоматически сжимается до ( мкг ) ′.Интегрирование обеих сторон дает общее решение:
Применение начального условия y (π) = 1 определяет константу c :
Таким образом, желаемое частное решение –
.
или, поскольку x не может равняться нулю (обратите внимание на коэффициент P (x) = 1/ x в данном дифференциальном уравнении),
Пример 3: Решите линейное дифференциальное уравнение
Сначала перепишите уравнение в стандартной форме:
Поскольку интегрирующий коэффициент здесь равен
умножьте обе части уравнения стандартной формы (*) на μ = e −2 / x ,
свернуть левую часть,
и интегрировать:
Таким образом, общее решение дифференциального уравнения может быть явно выражено как
Пример 4: Найдите общее решение каждого из следующих уравнений:
а.
г.
Оба уравнения представляют собой линейные уравнения в стандартной форме с P (x) = –4 / x .
 С
Синтегрирующий коэффициент будет
для обоих уравнений. Умножение на μ = x −4 дает
Интегрирование каждого из этих результирующих уравнений дает общие решения:
Пример 5: Постройте интегральную кривую
., который проходит через происхождение.
Первый шаг – переписать дифференциальное уравнение в стандартной форме:
с
интегрирующий коэффициент
Умножение обеих частей уравнения стандартной формы (*) на μ = (1 + x 2 ) 1/2 дает
Как обычно, левая сторона сворачивается в (μ y )
и интеграция дает общее решение:
Чтобы найти конкретную кривую этого семейства, которая проходит через начало координат, подставьте ( x, y ) = (0,0) и оцените константу c :
Следовательно, искомая интегральная кривая равна
.
, который показан на Рисунке 1.
Рисунок 1
Пример 6: Объект движется вдоль оси x таким образом, что его положение в момент времени t > 0 определяется линейным дифференциальным уравнением
Если объект находился в позиции x = 2 в момент времени t = 1, где он будет в момент времени t = 3?
Вместо того, чтобы иметь x в качестве независимой переменной и y в качестве зависимой, в этой задаче t является независимой переменной, а x является зависимой.Таким образом, решение не будет иметь форму « y = некоторая функция от x », а вместо этого будет « x = некоторая функция от t ».
Уравнение имеет стандартную форму для линейного уравнения первого порядка с P = t – t −1 и Q = t 2 .
 С
Синтегрирующий коэффициент
Умножение обеих частей дифференциального уравнения на этот интегрирующий коэффициент преобразует его в
Как обычно, левая сторона автоматически сворачивается,
и интеграция дает общее решение:
Теперь, поскольку задано условие « x = 2 при t = 1», это фактически IVP, и константа c может быть оценена:
Таким образом, положение объекта x как функция времени t задается уравнением
и, следовательно, позиция в момент времени t = 3 равна
, что примерно равно 3.055.
Уравнение первого порядка – обзор
Чтобы выразить уравнения. (8.2.6) и (8.2.7) как систему уравнений первого порядка, определим новые переменные u ( x, η ) и υ ( x, η ) через
(8.2 .9a) f ′ = u
(8.
 2.9b) u ′ = υ
2.9b) u ′ = υи запишем их как
(8.2.9c) (bυ) ′ + m + 12fυ + m (1 − u2) = x (u ∂u∂x − υ∂f∂x)
(8.2.10) η = 0, u = 0, f = fw (x); η = ηe, u = 1
Обозначим точки сетки прямоугольник, показанный на рис.8.1 по
(8.2.11) x0 = 0, xn = xn − 1 + kn, n = 1,2,…, Nη0 = 0, ηj = ηj − 1 + hj, j = 1,2,…, J
и напишите разностные уравнения, которые аппроксимируют уравнения. (8.2.9), рассматривая один прямоугольник сетки, как на рис. 8.1. Начнем с написания конечно-разностных аппроксимаций обыкновенных дифференциальных уравнений (8.2.9a, b) для средней точки ( x n , η j –1/2 ) отрезка P 1 P 2 , используя производные с централизованной разностью,
(8.2.12a) fjn − fj − 1nhj = ujn + uj − 1n2≡uj − 1 / 2n
(8.2.12b) ujn − uj − 1nhj = υjn + υj − 1n2≡υj − 1 / 2n
. дифференциальное уравнение (8.2.9c) аппроксимируется центрированием вокруг средней точки ( x n –1/2 , η j –1/2 ) прямоугольника P 1 P 2 P 3 P 4 .
 Это можно сделать в два этапа. На первом этапе мы центрируем его примерно ( x n –1/2 , η ) без указания η .Если мы обозначим его левую часть как L , то конечно-разностное приближение к уравнению. (8.2.9c) равно
Это можно сделать в два этапа. На первом этапе мы центрируем его примерно ( x n –1/2 , η ) без указания η .Если мы обозначим его левую часть как L , то конечно-разностное приближение к уравнению. (8.2.9c) равно(8.2.13) 12 (Ln + Ln − 1) = xn − 1/2 [un − 1/2 (un − un − 1kn) −υn − 1/2 (fn − fn −1kn)]
(8.2.14a) αn = xn − 1 / 2kn, α1 = mn + 12 + αn, α2 = mn + αn
(8.2.14b) Rn − 1 = −Ln − 1 + αn [ (fυ) n − 1− (u2) n − 1] −mn
(8.2.14c) Ln − 1≡ [(bυ) ′ + m + 12fυ + m (1 − u2)] n − 1
Уравнение . (8.2.12) можно записать как
(8.2.15) [(bυ) ′] n + α1 (fυ) n − α2 (u2) n + αn (υn − 1fn − fn − 1υn) = Rn − 1
Знак идентификации вводит полезное сокращение: [] n –1 означает, что количество в квадратных скобках оценивается как x = x n –1 .
Далее мы центрируем уравнение. (8.2.15) о точке ( x n –1/2 , η j –1/2 ), то есть выбираем η = η j –1/2 и получаем
(8.
 2.16) hj − 1 (bjnυjn − bj − 1nυj − 1n) + α1 (fυ) j − 1 / 2n − α2 (u2) j − 1 / 2n + αn (υj − 1 / 2n − 1fj − 1 / 2n − fj − 1 / 2n − 1υj − 1 / 2n) = Rj − 1 / 2n − 1
2.16) hj − 1 (bjnυjn − bj − 1nυj − 1n) + α1 (fυ) j − 1 / 2n − α2 (u2) j − 1 / 2n + αn (υj − 1 / 2n − 1fj − 1 / 2n − fj − 1 / 2n − 1υj − 1 / 2n) = Rj − 1 / 2n − 1, где
(8.2.17a) Rj − 1 / 2n − 1 = −Lj − 1 / 2n − 1 + αn [(fυ) j − 1 / 2n − 1− (u2) j − 1 / 2n − 1] −mn
(8.2.17b) Lj − 1 / 2n − 1 = {hj − 1 (bjυj − bj − 1υj − 1) + m + 12 (fυ) j − 1/2 + m [1− (u2) j − 1/2]} n − 1
Ур.(8.2.12) и (8.2.16) накладываются для j = 1, 2,…, J – 1 при данном η , а преобразованная толщина пограничного слоя η e равна быть достаточно большим, чтобы асимптотически u → 1. Последнее обычно выполняется, когда υ ( η e ) меньше примерно 10 –3 .
Система линейных дифференциальных уравнений первого порядка
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.
 Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т.
 д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Дифференциальное уравнение первой степени первого порядка – исчисление
Содержание
- 1 Определение
- 1,1 В неявной форме
- 1.
 2 В явной форме
2 В явной форме - 1.3 Преобразование между формами
- 2 Существование и уникальность решений
- 2.1 Стратегии решения в частных случаях
Определение
В неявной форме
A Дифференциальное уравнение первой степени первого порядка – это дифференциальное уравнение, которое является как дифференциальным уравнением первого порядка, так и дифференциальным уравнением первой степени. В явном виде он имеет вид:
где – известные функции.Здесь – независимая переменная, а – зависимая переменная.
В явной форме
Любое дифференциальное уравнение первой степени первого порядка может быть преобразовано в (почти) эквивалентное явное дифференциальное уравнение первого порядка, т. Е. В дифференциальное уравнение вида:
Преобразование между формами
Дифференциальное уравнение первой степени первого порядка может быть преобразовано в явный вид следующим образом.
 Начнем с:
Начнем с:Теперь разделите обе стороны на и сложите, получив явную форму.
Обратите внимание, что процесс может повлечь за собой небольшое изменение набора решений. В частности, любое решение, которое идентично удовлетворяет обоим и может быть потеряно при разделении. В большинстве случаев таких решений нет, и их обычно не более конечного числа.
Наличие и уникальность решений
- Теорема существования Пеано гарантирует существование локального решения любой задачи с начальным значением для явного дифференциального уравнения первого порядка с точкой начального значения при условии, что оно является непрерывным.
- Теорема Пикара-Линделёфа устанавливает существование и единственность при несколько более сильных предположениях о непрерывности и дифференцируемости.
Стратегии решения в частных случаях
Ниже приведены некоторые форматы уравнений, для которых известны общие стратегии. Обратите внимание, что буква больше не используется для функции решения, но может использоваться для других функций:
Тип уравнения Краткое изложение стратегии решения линейное дифференциальное уравнение первого порядка, которое в упрощенном виде выглядит как Используйте интегрирующий коэффициент, где.  Общее решение – это
Общее решение – эторазделимое дифференциальное уравнение, которое имеет форму (любое автономное дифференциальное уравнение первой степени первого порядка является разделимым, хотя существуют разделимые дифференциальные уравнения, которые не являются автономными) Разделите и решите как. Также найдите решения, соответствующие где. точное дифференциальное уравнение первого порядка Попытайтесь найти такую связь, используя неявное дифференцирование. Найти, даже если он существует, может быть непросто. Дифференциальное уравнение Бернулли () Разделите обе части на (отложите возможное стационарное решение), затем замените, чтобы получить линейное дифференциальное уравнение первого порядка с зависимой переменной и независимой переменной. Линейные уравнения первого порядка
Линейные уравнения первого порядкаЗдесь мы узнаем, как решить линейный первый порядок уравнения; это дифференциальные уравнения, которые нелегко решить как разделяемые уравнения, но могут соответствовать форме:
Взглянув на это, мы имеем dy / dx само по себе, P (x) y – некоторая функция строго от x, умноженная на один y, и Q (x) – некоторая функция строго от x.
Чтобы решить эти проблемы, нам необходимо выполнить следующие шаги:
- Убедитесь, что уравнение соответствует форме линейного уравнения первого порядка.
- Найдите коэффициент интегрирования и умножьте его на все уравнение.
- Это заставляет правило продукта с одной стороны; узнайте, какие термины использовались в правиле продукта, и запишите их как производную.
- Объедините обе стороны.
- Решите относительно y, если оно легко решается.
Пример 1:
Найдите конкретное решение дифференциального уравнения:
Во-первых, нам нужно убедиться, что оно соответствует форме:
Мы видим, что оно соответствует; dy / dx сам по себе равен P (x) = -4, который умножается на один y, а Q (x) является функцией только от x.Теперь мы найдем интегрирующий коэффициент, который обозначается греческой буквой мю. Коэффициент интегрирования для одного из этих уравнений всегда будет возводиться к интегралу от P (x):
На данный момент мы можем опустить константу C; он будет внесен позже.
 Теперь, когда у нас есть интегрирующий коэффициент, мы умножаем его на исходное уравнение:
Теперь, когда у нас есть интегрирующий коэффициент, мы умножаем его на исходное уравнение:Итак, почему мы это сделали? Что ж, эта часть хороша интересно; мы только что установили правило продукта слева сторона уравнения.Давайте посмотрим на эту часть уравнения: после умножив интегрирующий коэффициент, мы должны увидеть правило продукта. Напомним, что правило произведения – f g ‘= g f’; глядя на уравнение, мы должны увидеть, какой член какой:
Зная это, мы можем переписать левую часть уравнения:
* Кроме того, это также может быть хорошей идеей, особенно с более сложными проблемами, чтобы различать ваши уравнение, чтобы убедиться, что оно совпадает:
Это совпадает, так что мы в порядке.Если это не так, это скорее всего означает, что где-то была ошибка, и нам придется вернитесь и попробуйте еще раз разобраться.
Вернемся туда, где мы были: теперь, когда у нас есть левая сторона, написанная как производная, мы можем интегрировать обе части.
 Левая сторона останется
то же самое, поскольку интеграл от производной сокращается:
Левая сторона останется
то же самое, поскольку интеграл от производной сокращается:Теперь мы можем решить относительно y. Обратите внимание, что C не сводит на нет все, что окружает его в этих задачах:
Теперь, когда у нас есть общее решение, мы можем подключить в наших начальных условиях и получите конкретное решение:
Пример 2:
Найдите частное решение дифференциального уравнения:
Во-первых, нам нужно убедиться, что это уравнение имеет правильную форму.Похоже, подходит; dy / dx сам по себе равен P (x) = 3x 2 , который умножается на один y, а Q (x) является функцией x, не умноженной ни на что другое. Таким образом, мы можем найти наш интегрирующий коэффициент:
Затем мы умножаем интегрирующий коэффициент на все уравнение:
Теперь мы можем взглянуть на левую часть уравнения и увидеть, какие члены представляют f, f ‘, g и g’. Это подскажет нам, какие термины использовать, когда мы переписываем левую часть как правило произведения:
Правило произведения говорит, что fg = fg ‘+ gf’, поэтому теперь мы можем переписать левую часть уравнения как производную.
 of fg, что равняется тому, что у нас есть сейчас:
of fg, что равняется тому, что у нас есть сейчас:Теперь мы можем интегрировать обе стороны:
Затем мы просто решаем для y, чтобы найти общее решение:
Наконец, мы можем использовать наши начальные условия для получения конкретного решения:
Пример 3:
Найдите частное решение дифференциального уравнения:
Первое, что мы должны заметить, это то, что это уравнение еще не в надлежащем виде.Проблема в том, что dy / dx не сам по себе; Давайте разделим каждый член на x, чтобы выделить его:
Теперь он в правильной форме: y ‘изолирован, P (x) умножается на один y, а Q (x) – само по себе. Поскольку у нас есть уравнение в правильной форме, мы можем найти наш коэффициент интегрирования:
После исключения e и ln и упрощения наш коэффициент интеграции равен x 3 . Затем мы можем умножить это на все уравнение, чтобы заставить правило произведения с левой стороны:
Установив правило продукта, мы можем идентифицировать какие члены взяты из исходного уравнения, а какие являются производными:
Теперь мы можем переписать левую часть как производную произведения f и g:
Затем мы берем интеграл от обеих частей:
Теперь достаточно решить для y, чтобы получить общее решение:
Теперь у нас есть общее решение; найти конкретное решение, нам нужно использовать начальные условия и решить для C:
Пример 4: Смешивание раствора в резервуаре
Резервуар изначально содержит 120 галлонов чистого воды.
 Рассол, содержащий 1 фунт соли на галлон, поступает в
резервуар со скоростью 3 галлона / мин, а хорошо перемешанный раствор покидает резервуар со скоростью 4
галлонов / мин, опорожнение резервуара через 120 минут или 2 часа. Оцените выражение для
количество соли в резервуаре через t минут, и найдите, сколько соли находится в резервуаре за t = 60 минут.
Рассол, содержащий 1 фунт соли на галлон, поступает в
резервуар со скоростью 3 галлона / мин, а хорошо перемешанный раствор покидает резервуар со скоростью 4
галлонов / мин, опорожнение резервуара через 120 минут или 2 часа. Оцените выражение для
количество соли в резервуаре через t минут, и найдите, сколько соли находится в резервуаре за t = 60 минут.Сначала давайте определим некоторые переменные. Для проблем с резервуаром Q (t) = количество раствора в резервуаре в любой момент времени t, а dQ / dt = скорость выхода решения.Изначально в баке чистая вода (без соли), поэтому Q (0) = 0.
Начнем с записи dQ / dt. Мы знаем скорость в; он указан в задаче и не меняется. Однако скорость меняется со временем, в зависимости от количества соли. в баке. Мы знаем, что в резервуаре будет некоторое количество Q, и что резервуар будет пуст через 120 минут; таким образом, время будет 120-t, оставляя нам оставшееся время до опустошения резервуара:
Теперь у нас есть функция, связанная с dQ / dt, которая представляет собой изменение количества соли во времени.
 Немного переписав это, мы получим:
Немного переписав это, мы получим:Это линейное уравнение первого порядка в терминах Q и t, и мы знаем, как их решить! Сначала найдите коэффициент интегрирования:
Затем умножьте коэффициент интегрирования на каждый член, чтобы принудительно применить правило произведения:
Теперь мы можем найти f и g в результате правила произведения и переписать левую часть уравнение как производная:
Теперь переписываем как производную от f и g:
Затем мы интегрируем обе стороны:
Теперь мы можем решить для Q, чтобы найти общее решение:
Наконец, мы можем использовать начальные условия, чтобы найти C для конкретного решения, которое является выражением для количество соли в баке через t минут:
Теперь у нас есть выражение для количества соли в резервуаре как функция времени.Сколько соли в баке после 60 минут (t = 60)?
4.5 Линейные уравнения первого порядка – Исчисление Том 2
Цели обучения
- 4.5.1 Напишите линейное дифференциальное уравнение первого порядка в стандартной форме.
- 4.5.2 Найдите интегрирующий коэффициент и используйте его для решения линейного дифференциального уравнения первого порядка.
- 4.5.3 Решение прикладных задач, связанных с линейными дифференциальными уравнениями первого порядка.
Ранее мы изучали приложение дифференциального уравнения первого порядка, которое включало решение относительно скорости объекта.В частности, если мяч подбрасывается вверх с начальной скоростью v0v0 футов / с, то задача с начальным значением, описывающая скорость мяча через tt секунд, задается формулой
. dvdt = −32, v (0) = v0. dvdt = −32, v (0) = v0.В этой модели предполагается, что единственная сила, действующая на мяч, – это сила тяжести. Теперь мы усугубим проблему, допустив возможность воздействия на мяч сопротивления воздуха.
Сопротивление воздуха всегда действует в направлении, противоположном движению. Следовательно, если объект поднимается, сопротивление воздуха действует в направлении вниз.Если объект падает, сопротивление воздуха действует в направлении вверх (рис. 4.24). Нет точной зависимости между скоростью объекта и действующим на него сопротивлением воздуха. Для очень маленьких объектов сопротивление воздуха пропорционально скорости; то есть сила, обусловленная сопротивлением воздуха, численно равна некоторой постоянной kk, умноженной на v.v. Для более крупных (например, размером с бейсбольный мяч) объектов, в зависимости от формы, сопротивление воздуха может быть приблизительно пропорционально квадрату скорости. Фактически, сопротивление воздуха может быть пропорционально v1.5, v1.5 или v0.9, v0.9, или некоторые другие возможности v.v.
Рис. 4.24. Силы, действующие на движущийся бейсбольный мяч: сила тяжести действует в направлении вниз, а сопротивление воздуха действует в направлении, противоположном направлению движения.
Мы будем работать с линейным приближением сопротивления воздуха. Если предположить, что k> 0, k> 0, то выражение для силы FAFA, обусловленной сопротивлением воздуха, будет FA = −kv.FA = −kv. Следовательно, сумма сил, действующих на объект, равна сумме силы тяжести и силы, обусловленной сопротивлением воздуха.Это, в свою очередь, равно массе объекта, умноженной на его ускорение в момент времени tt (второй закон Ньютона). Это дает нам дифференциальное уравнение
mdvdt = −kv − mg. mdvdt = −kv − mg.Наконец, мы накладываем начальное условие v (0) = v0, v (0) = v0, где v0v0 – начальная скорость, измеренная в метрах в секунду. Это составляет g = 9,8 м / с2. G = 9,8 м / с2. Задача начальной стоимости становится
. mdvdt = −kv − mg, v (0) = v0. mdvdt = −kv − mg, v (0) = v0.(4,13)
Дифференциальное уравнение в этой начальной задаче является примером линейного дифференциального уравнения первого порядка.(Напомним, что дифференциальное уравнение является первым порядком, если производная высшего порядка, которая появляется в уравнении, равна 1.) 1.) В этом разделе мы изучаем линейные уравнения первого порядка и исследуем метод нахождения общего решения этих уравнений. типы уравнений, а также решение начальных задач с их участием.
Определение
Дифференциальное уравнение первого порядка является линейным, если его можно записать в виде
a (x) y ′ + b (x) y = c (x), a (x) y ′ + b (x) y = c (x),(4.14)
, где a (x), b (x), a (x), b (x) и c (x) c (x) – произвольные функции от x.Икс.
Помните, что неизвестная функция yy зависит от переменной x; x; то есть xx – независимая переменная, а yy – зависимая переменная. Некоторые примеры линейных дифференциальных уравнений первого порядка:
(3×2−4) y ′ + (x − 3) y = sinx (sinx) y ′ – (cosx) y = cotx4xy ′ + (3lnx) y = x3−4x. (3×2−4) y ′ + (x− 3) y = sinx (sinx) y ′ – (cosx) y = cotx4xy ′ + (3lnx) y = x3−4x.Примеры нелинейных дифференциальных уравнений первого порядка включают
(y ′) 4− (y ′) 3 = (3x − 2) (y + 4) 4y ′ + 3y3 = 4x − 5 (y ′) 2 = siny + cosx. (y ′) 4− (y ′). 3 = (3x − 2) (y + 4) 4y ′ + 3y3 = 4x − 5 (y ′) 2 = sin + cosx.Эти уравнения нелинейны из-за таких членов, как (y ‘) 4, y3, (y’) 4, y3 и т. Д. Из-за этих членов невозможно привести эти уравнения в ту же форму, что и уравнение 4.14.
Стандартная форма
Рассмотрим дифференциальное уравнение
(3×2−4) y ′ + (x − 3) y = sinx. (3×2−4) y ′ + (x − 3) y = sinx.Наша основная цель в этом разделе – найти метод решения уравнений такого вида. Полезно, чтобы коэффициент при y′y ′ был равен 1,1. Чтобы это произошло, разделим обе части на 3×2−4.3×2−4.
y ′ + (x − 33×2−4) y = sinx3x2−4y ′ + (x − 33×2−4) y = sinx3x2−4Это называется стандартной формой дифференциального уравнения. Мы будем использовать его позже при нахождении решения общего линейного дифференциального уравнения первого порядка. Возвращаясь к уравнению 4.14, мы можем разделить обе части уравнения на a (x) .a (x). Это приводит к уравнению
y ′ + b (x) a (x) y = c (x) a (x). y ′ + b (x) a (x) y = c (x) a (x).(4,15)
Теперь определим p (x) = b (x) a (x) p (x) = b (x) a (x) и q (x) = c (x) a (x). Q (x) = c (х) а (х). Тогда уравнение 4.14 становится
y ′ + p (x) y = q (x). y ′ + p (x) y = q (x).(4,16)
Мы можем записать любое линейное дифференциальное уравнение первого порядка в этой форме, и это называется стандартной формой для линейного дифференциального уравнения первого порядка.
Пример 4.15
Написание линейных уравнений первого порядка в стандартной форме
Приведите каждое из следующих линейных дифференциальных уравнений первого порядка в стандартную форму. Определите p (x) p (x) и q (x) q (x) для каждого уравнения.
- y ′ = 3x − 4yy ′ = 3x − 4y
- 3xy′4y − 3 = 23xy′4y − 3 = 2 (здесь x ≠ 0) x ≠ 0)
- y = 3y′ − 4×2 + 5y = 3y′ − 4×2 + 5
Решение
- Добавьте 4y4y к обеим сторонам:
В этом уравнении p (x) = 4p (x) = 4 и q (x) = 3x.д (х) = 3х. - Умножьте обе стороны на 4y − 3,4y − 3, затем вычтите 8y8y из каждой стороны:
3xy′4y − 3 = 23xy ′ = 2 (4y − 3) 3xy ′ = 8y − 63xy′ − 8y = −6.3xy′4y − 3 = 23xy ′ = 2 (4y − 3) 3xy ′ = 8y − 63xy′− 8у = −6.
Наконец, разделите обе части на 3x3x, чтобы коэффициент y′y ′ был равен 1: 1:
. y′ − 83xy = −2x.y′ − 83xy = −2x.(4.17)
Это допустимо, поскольку в исходной постановке задачи мы предполагали, что x ≠ 0.x ≠ 0. (Если x = 0x = 0, тогда исходное уравнение становится 0 = 2,0 = 2, что явно является ложным утверждением.)
В этом уравнении p (x) = – 83xp (x) = – 83x и q (x) = – 23x.q (x) = – 23x. - Вычтите yy с каждой стороны и прибавьте 4×2−5: 4×2−5:
3y′ − y = 4×2−5.3y′ − y = 4×2−5.
Затем разделите обе стороны на 3: 3:
. y′ − 13y = 43×2−53. y′ − 13y = 43×2−53.
В этом уравнении p (x) = – 13p (x) = – 13 и q (x) = 43×2−53.q (x) = 43×2−53.
КПП 4.15
Приведите уравнение (x + 3) y′2x − 3y − 4 = 5 (x + 3) y′2x − 3y − 4 = 5 в стандартную форму и определите p (x) p (x) и q (x). .q (х).
Интегрирующие факторы
Теперь мы разработаем технику решения любого линейного дифференциального уравнения первого порядка.Начнем со стандартной формы линейного дифференциального уравнения первого порядка:
y ′ + p (x) y = q (x). y ′ + p (x) y = q (x).(4,18)
Первый член в левой части уравнения 4.15 – это производная неизвестной функции, а второй член – это произведение известной функции на неизвестную функцию. Это чем-то напоминает правило продукта из раздела «Правила дифференциации». Если мы умножим уравнение 4.16 на еще не определенную функцию μ (x), μ (x), то уравнение станет
μ (x) y ′ + μ (x) p (x) y = μ (x) q (x).μ (x) y ′ + μ (x) p (x) y = μ (x) q (x).(4,19)
Левая часть уравнения 4.18 может быть идеально согласована с правилом произведения:
ddx [f (x) g (x)] = f ′ (x) g (x) + f (x) g ′ (x). ddx [f (x) g (x)] = f ′ (x) g (x) + f (x) g ′ (x).Последовательное сопоставление дает y = f (x), g (x) = μ (x), y = f (x), g (x) = μ (x) и g ′ (x) = μ (x ) p (x) .g ′ (x) = μ (x) p (x). Взяв производную от g (x) = μ (x) g (x) = μ (x) и положив ее равной правой части g ′ (x) = μ (x) p (x) g ′ ( x) = μ (x) p (x) приводит к
μ ′ (x) = μ (x) p (x). μ ′ (x) = μ (x) p (x).Это разделимое дифференциальное уравнение первого порядка для μ (x).μ (х). Мы знаем p (x) p (x), потому что оно входит в решаемое нами дифференциальное уравнение. Разделение переменных и интегрирование дает
μ ′ (x) μ (x) = p (x) ∫μ ′ (x) μ (x) dx = ∫p (x) dxln | μ (x) | = ∫p (x) dx + Celn | μ ( x) | = e∫p (x) dx + C | μ (x) | = C1e∫p (x) dxμ (x) = C2e∫p (x) dx.μ ′ (x) μ (x) = p (x) ∫μ ′ (x) μ (x) dx = ∫p (x) dxln | μ (x) | = ∫p (x) dx + Celn | μ (x) | = e∫p (x) dx + C | μ (x) | = C1e∫p (x) dxμ (x) = C2e∫p (x) dx.Здесь C2C2 может быть произвольной (положительной или отрицательной) константой. Это приводит к общему методу решения линейного дифференциального уравнения первого порядка.Сначала умножим обе части уравнения 4.16 на интегрирующий множитель μ (x) .μ (x). Это дает
μ (x) y ′ + μ (x) p (x) y = μ (x) q (x). μ (x) y ′ + μ (x) p (x) y = μ (x) q (x) ).(4,20)
Левую часть уравнения 4.20 можно переписать как ddx (μ (x) y) .ddx (μ (x) y).
ddx (μ (x) y) = μ (x) q (x). ddx (μ (x) y) = μ (x) q (x).(4,21)
Затем проинтегрируйте обе части уравнения 4.21 относительно x.x.
∫ddx (μ (x) y) dx = ∫μ (x) q (x) dxμ (x) y = ∫μ (x) q (x) dx.ddx (μ (x) y) dx = ∫μ (x) q (x) dxμ (x) y = ∫μ (x) q (x) dx.(4.22)
Разделите обе части уравнения 4.22 на μ (x): μ (x):
y = 1μ (x) [∫μ (x) q (x) dx + C]. y = 1μ (x) [∫μ (x) q (x) dx + C].(4,23)
Поскольку µ (x) µ (x) вычислялась ранее, мы закончили. Важное замечание о константе интегрирования C: C: Может показаться, что мы непоследовательны в использовании константы интегрирования. Однако интеграл, включающий p (x) p (x), необходим для нахождения интегрирующего множителя для уравнения 4.15. Для решения уравнения необходим только один интегрирующий коэффициент; следовательно, можно безопасно присвоить значение CC для этого интеграла.Мы выбрали C = 0. C = 0. При вычислении интеграла в квадратных скобках в уравнении 4.21 необходимо оставить открытыми возможности выбора значения интегрирующей константы, потому что наша цель – найти общее семейство решений уравнения 4.15. Именно это и гарантирует этот интегрирующий фактор.
Стратегия решения проблем
Стратегия решения проблем: решение линейного дифференциального уравнения первого порядка
- Приведите уравнение в стандартную форму и определите p (x) p (x) и q (x).д (х).
- Вычислите интегрирующий коэффициент μ (x) = e∫p (x) dx.μ (x) = e∫p (x) dx.
- Умножаем обе части дифференциального уравнения на μ (x) .μ (x).
- Проинтегрируйте обе части уравнения, полученного на шаге 3,3, и разделите обе части на μ (x) .μ (x).
- Если есть начальное условие, определите значение C.C.
Пример 4.16
Решение линейного уравнения первого порядка
Найти общее решение дифференциального уравнения xy ′ + 3y = 4×2−3x.xy ′ + 3y = 4×2−3x. Предположим, что x> 0.x> 0.
Решение
- Чтобы преобразовать это дифференциальное уравнение в стандартную форму, разделите обе части на x: x:
y ′ + 3xy = 4x − 3.y ′ + 3xy = 4x − 3.
Следовательно, p (x) = 3xp (x) = 3x и q (x) = 4x − 3.q (x) = 4x − 3. - Интегрирующий коэффициент равен μ (x) = e∫ (3 / x) dx = e3lnx = x3.μ (x) = e∫ (3 / x) dx = e3lnx = x3.
- Умножение обеих частей дифференциального уравнения на μ (x) μ (x) дает
x3y ′ + x3 (3x) y = x3 (4x − 3) x3y ′ + 3x2y = 4×4−3x3ddx (x3y) = 4×4−3×3.x3y ′ + x3 (3x) y = x3 (4x − 3) x3y ′ + 3x2y = 4×4−3x3ddx (x3y) = 4×4−3×3. - Объедините обе части уравнения.
∫ddx (x3y) dx = ∫4×4−3x3dxx3y = 4×55−3×44 + Cy = 4×25−3×4 + Cx − 3. ddx (x3y) dx = ∫4×4−3x3dxx3y = 4×55−3×44 + Cy = 4×25−3×4 + Cx− 3. - Нет начального значения, значит, проблема устранена.
Анализ
Возможно, вы заметили условие, наложенное на дифференциальное уравнение; а именно, x> 0.x> 0. Для любого ненулевого значения C, C общее решение не определено при x = 0.х = 0. Кроме того, когда x <0, x <0, интегрирующий коэффициент изменяется. Коэффициент интегрирования задается уравнением 4.19 как f (x) = e∫p (x) dx.f (x) = e∫p (x) dx. Для этого p (x) p (x) получаем
e∫p (x) dx = e∫ (3 / x) dx = e3ln | x | = | x | 3, e∫p (x) dx = e∫ (3 / x) dx = e3ln | x | = | х | 3,, поскольку x <0.x <0. Поведение общего решения меняется при x = 0x = 0 в основном из-за того, что p (x) p (x) там не определено.
КПП 4.16
Найти общее решение дифференциального уравнения (x − 2) y ′ + y = 3×2 + 2x.(х – 2) у ‘+ у = 3х2 + 2х. Предположим, что x> 2.x> 2.
Теперь мы используем ту же стратегию, чтобы найти решение проблемы с начальным значением.
Пример 4.17
Линейная задача первого порядка с начальным значением
Решите задачу начального значения
y ′ + 3y = 2x − 1, y (0) = 3. y ′ + 3y = 2x − 1, y (0) = 3.Решение
- Это дифференциальное уравнение уже имеет стандартную форму с p (x) = 3p (x) = 3 и q (x) = 2x − 1.q (x) = 2x − 1.
- Коэффициент интегрирования равен μ (x) = e∫3dx = e3x.μ (x) = e∫3dx = e3x.
- Умножение обеих частей дифференциального уравнения на μ (x) μ (x) дает
e3xy ′ + 3e3xy = (2x − 1) e3xddx [ye3x] = (2x − 1) e3x.e3xy ′ + 3e3xy = (2x − 1) e3xddx [ye3x] = (2x − 1) e3x.
Интегрируйте обе части уравнения:
∫ddx [ye3x] dx = ∫ (2x − 1) e3xdxye3x = e3x3 (2x − 1) −∫23e3xdxye3x = e3x (2x − 1) 3−2e3x9 + Cy = 2x − 13−29 + Ce − 3xy = 2×3−59 + Ce − 3x.∫ddx [ye3x] dx = ∫ (2x − 1) e3xdxye3x = e3x3 (2x − 1) −∫23e3xdxye3x = e3x (2x − 1) 3−2e3x9 + Cy = 2x − 13−29 + Ce− 3xy = 2×3−59 + Ce − 3x. - Теперь подставьте x = 0x = 0 и y = 3y = 3 в общее решение и решите относительно C: C:
y = 23x − 59 + Ce − 3×3 = 23 (0) −59 + Ce − 3 (0) 3 = −59 + CC = 329.y = 23x − 59 + Ce − 3×3 = 23 (0) −59 + Ce − 3 (0) 3 = −59 + CC = 329.
Следовательно, решением начальной задачи является
y = 23x − 59 + 329e − 3x.y = 23x − 59 + 329e − 3x.
КПП 4.17
Решите начальную задачу y′ − 2y = 4x + 3y (0) = – 2.y′ − 2y = 4x + 3y (0) = – 2.
Приложения линейных дифференциальных уравнений первого порядка
Мы рассмотрим два различных приложения линейных дифференциальных уравнений первого порядка. Первый связан с сопротивлением воздуха по отношению к поднимающимся или падающим объектам; второй включает в себя электрическую схему.Другие приложения многочисленны, но большинство из них решаются аналогичным образом.
Свободное падение с сопротивлением воздуха
Мы обсуждали сопротивление воздуха в начале этого раздела. В следующем примере показано, как применить эту концепцию к мячу, движущемуся вертикально. На силу сопротивления воздуха могут влиять и другие факторы, например размер и форма объекта, но здесь мы их игнорируем.
Пример 4.18
Мяч с воздушным сопротивлением
Ракетбол бьет прямо вверх с начальной скоростью 22 м / с.Масса ракетки примерно 0,04270,0427 кг. Сопротивление воздуха действует на мяч с силой, численно равной 0,5v, 0,5v, где vv представляет собой скорость мяча в момент времени t.t.
- Найдите скорость мяча как функцию времени.
- Сколько времени нужно, чтобы мяч достиг максимальной высоты?
- Если мяч ударит с начальной высоты 11 метров, какой высоты он достигнет?
Решение
- Масса m = 0.0427 кг, k = 0,5, m = 0,0427 кг, k = 0,5 и g = 9,8 м / с2. G = 9,8 м / с2. Начальная скорость v0 = 2v0 = 2 м / с. Следовательно, начальная задача равна
0,0427dvdt = -0,5v-0,0427 (9,8), v0 = 2,0,0427dvdt = -0,5v-0,0427 (9,8), v0 = 2.
Разделив дифференциальное уравнение на 0,04270,0427, получим
dvdt = -11,7096v-9,8, v0 = 2. dvdt = -11,7096v-9,8, v0 = 2.
Дифференциальное уравнение линейное. Использование стратегии решения задач для линейных дифференциальных уравнений:
Шаг 1. Перепишем дифференциальное уравнение как dvdt + 11.7096v = -9,8.dvdt + 11,7096v = -9,8. Это дает p (t) = 11,7096 p (t) = 11,7096 и q (t) = – 9,8 q (t) = – 9,8
. Шаг 2. Коэффициент интегрирования равен μ (t) = e∫11.7096dt = e11.7096t.μ (t) = e∫11.7096dt = e11.7096t.
Шаг 3. Умножьте дифференциальное уравнение на μ (t): μ (t):
. e11.7096tdvdt + 11.7096ve11.7096t = −9.8e11.7096tddt [ve11.7096t] = – 9.8e11.7096t.e11.7096tdvdt + 11.7096ve11.7096t = -9.8e11.7096tddt [ve11.7096t] = – 9.8e11. 7096т.
Шаг 4. Объедините обе стороны:
∫ddt [ve11.7096t] dt = ∫ − 9.8e11.7096tdtve11.7096t = −9.811.7096e11.7096t + Cv (t) = – 0.8369 + Ce − 11.7096t.∫ddt [ve11.7096t] dt = ∫ − 9.8e11.7096tdtve11.7096t = −9.811.7096e11.7096t + Cv (t) = – 0.8369 + Ce − 11.7096t.
Шаг 5. Решите относительно CC, используя начальное условие v0 = v (0) = 2: v0 = v (0) = 2:
v (t) = – 0,8369 + Ce − 11,7096tv (0) = – 0,8369 + Ce − 11,7096 (0) 2 = −0,8369 + CC = 2,8369.v (t) = – 0,8369 + Ce − 11,7096tv (0) = -0,8369 + Ce-11,7096 (0) 2 = -0,8369 + CC = 2,8369.
Следовательно, решение задачи с начальным значением: v (t) = 2,8369e-11,7096t-0,8369.v (t) = 2,8369e-11,7096t-0,8369. - Мяч достигает максимальной высоты, когда скорость равна нулю.Причина в том, что при положительной скорости она увеличивается, а при отрицательной – падает. Следовательно, когда он равен нулю, он не поднимается и не падает и находится на максимальной высоте:
2,8369e-11,7096t-0,8369 = 02,8369e-11,7096t = 0,8369e-11,7096t = 0,83692,8369≈0,295lne-11,7096t = ln0,295≈ − 1,221−11,7096t = −1,221t≈0,104,2,8369e-11,7096 t − 0,8369 = 02,8369e − 11,7096t = 0,8369e − 11,7096t = 0,83692,8369≈0,295lne − 11,7096t = ln0,295≈ − 1,221−11,7096t = −1,221t≈0,104.
Следовательно, требуется примерно 0.1040,104 секунды для достижения максимальной высоты. - Чтобы найти высоту мяча как функцию времени, используйте тот факт, что производной положения является скорость, т. Е. Если h (t) h (t) представляет высоту в момент времени t, t, то h ′ (t ) = v (t). h ′ (t) = v (t). Поскольку мы знаем v (t) v (t) и начальную высоту, мы можем сформировать задачу с начальным значением:
h ′ (t) = 2,8369e − 11,7096t − 0,8369, h (0) = 1. h ′ (t) = 2,8369e − 11,7096t − 0,8369, h (0) = 1.
Интегрирование обеих частей дифференциального уравнения по tt дает
∫h ′ (t) dt = ∫2.8369e − 11.7096t − 0.8369dth (t) = – 2.836911.7096e − 11.7096t − 0.8369t + Ch (t) = – 0.2423e − 11.7096t − 0.8369t + C.∫h ′ (t) dt = ∫2.8369e −11.7096t − 0.8369dth (t) = – 2.836911.7096e − 11.7096t − 0.8369t + Ch (t) = – 0.2423e − 11.7096t − 0.8369t + C.
Решите для CC, используя начальное условие:
h (t) = – 0,2423e − 11,7096t − 0,8369t + Ch (0) = – 0,2423e − 11,7096 (0) −0,8369 (0) + C1 = −0,2423 + CC = 1,2423.h (t) = – 0,2423 e − 11,7096t − 0,8369t + Ch (0) = – 0,2423e − 11,7096 (0) −0,8369 (0) + C1 = −0,2423 + CC = 1,2423.
Следовательно,
h (t) = – 0,2423e − 11,7096t − 0,8369t + 1,2423.h (t) = – 0,2423e − 11,7096t − 0,8369t + 1,2423.
После 0,1040,104 секунды высота будет равна
. h (0,104) = – 0,2423e − 11,7096t − 0,8369t + 1,2423≈1,0836h (0,104) = – 0,2423e − 11,7096t − 0,8369t + 1,2423≈1,0836 метра.
КПП 4.18
Вес пенни составляет 2,52,5 грамма (Монетный двор США, «Спецификации монет», по состоянию на 9 апреля 2015 г., http://www.usmint.gov/about_the_mint/?action=coin_specifications), а верхняя смотровая площадка Эмпайр-стейт-билдинг находится на высоте 369369 метров над улицей.Поскольку копейка представляет собой небольшой и относительно гладкий объект, сопротивление воздуха, действующее на копейку, на самом деле довольно мало. Мы предполагаем, что сопротивление воздуха численно равно 0.0025v.0.0025v. Кроме того, пенни падает, и ему не сообщается начальная скорость.
- Задайте задачу начального значения, которая представляет падающий пенни.
- Решите задачу для v (t) .v (t).
- Какова конечная скорость пенни (т.е. вычислить предел скорости при приближении tt к бесконечности)?
Электрические схемы
Источник электродвижущей силы (эл.g., батарея или генератор) создает поток тока в замкнутой цепи, и этот ток вызывает падение напряжения на каждом резисторе, катушке индуктивности и конденсаторе в цепи. Правило петли Кирхгофа гласит, что сумма падений напряжения на резисторах, катушках индуктивности и конденсаторах равна общей электродвижущей силе в замкнутой цепи. У нас есть три результата:
- Падение напряжения на резисторе равно
где RR – коэффициент пропорциональности, называемый сопротивлением , и ii – ток. - Падение напряжения на катушке индуктивности определяется по формуле
.
где LL – константа пропорциональности, называемая индуктивностью , а ii снова обозначает ток. - Падение напряжения на конденсаторе равно
.
, где CC – постоянная пропорциональности, называемая емкостью , , а qq – мгновенный заряд конденсатора. Связь между ii и qq такова: i = q′.i = q ′.
Мы используем единицы вольт (В) (В) для измерения напряжения E, E, амперы (A) (A) для измерения тока i, i, кулоны (C) (C) для измерения заряда q, q, Ом (Ом ) (Ом) для измерения сопротивления R, R, Генриса (H) (H) для измерения индуктивности L, L и фарадов (F) (F) для измерения емкости C.C. Рассмотрим схему на рисунке 4.25.
Рисунок 4.25 Типовая электрическая цепь, содержащая генератор напряжения (VS), (VS), конденсатор (C), (C), индуктор (L), (L) и резистор (R). (R).Применяя к этой схеме правило петли Кирхгофа, мы позволяем EE обозначать электродвижущую силу, создаваемую генератором напряжения. Тогда
Подставляя выражения для EL, ER, EL, ER и ECEC в это уравнение, получаем
Li ′ + Ri + 1Cq = E.Li ′ + Ri + 1Cq = E.(4,24)
Если в цепи нет конденсатора, уравнение принимает вид
Li ′ + Ri = E.Li ′ + Ri = E.(4,25)
Это дифференциальное уравнение первого порядка в i.i. Схема называется схемой LRLR.
Затем предположим, что в цепи нет индуктора, но есть конденсатор и резистор, поэтому L = 0, R 0, L = 0, R ≠ 0 и C ≠ 0.C ≠ 0. Тогда уравнение 4.23 можно переписать как
Rq ′ + 1Cq = E, Rq ′ + 1Cq = E,(4,26)
, которое является линейным дифференциальным уравнением первого порядка. Это называется схемой RC . В любом случае мы можем установить и решить задачу с начальным значением.
Пример 4.19
Определение тока в электрической цепи
RLСхема имеет последовательно электродвижущую силу, равную E = 50sin20tV, E = 50sin20tV, резистор 5Ω, 5Ω и индуктор 0,4H.0.4H. Если начальный ток равен 0,0, найдите ток в момент времени t> 0. t> 0.
Решение
У нас есть резистор и катушка индуктивности в цепи, поэтому мы используем уравнение 4.24. Падение напряжения на резисторе равно ER = Ri = 5i.ER = Ri = 5i. Падение напряжения на катушке индуктивности определяется как EL = Li ′ = 0,4i′.EL = Li ′ = 0,4i ′. Электродвижущая сила становится правой частью уравнения 4.24. Следовательно, уравнение 4.24 превращается в
. 0,4i ′ + 5i = 50sin20t. 0,4i ′ + 5i = 50sin20t.Разделив обе части на 0,40,4, получим уравнение
i ′ + 12,5i = 125sin20t.i ′ + 12,5i = 125sin20t.Поскольку начальный ток равен 0, этот результат дает начальное условие i (0) = 0. i (0) = 0. Мы можем решить эту начальную задачу, используя пятиэтапную стратегию решения дифференциальных уравнений первого порядка.
Шаг 1. Перепишем дифференциальное уравнение в виде i ′ + 12,5i = 125sin20t.i ′ + 12,5i = 125sin20t. Это дает p (t) = 12,5p (t) = 12,5 и q (t) = 125sin20t.q (t) = 125sin20t.
Шаг 2. Коэффициент интегрирования равен μ (t) = e∫12,5dt = e12,5t.μ (t) = e∫12,5dt = e12,5t.
Шаг 3. Умножьте дифференциальное уравнение на μ (t): μ (t):
. e12.5ti ′ + 12.5e12.5ti = 125e12.5tsin20tddt [ie12.5t] = 125e12.5tsin20t.e12.5ti ′ + 12.5e12.5ti = 125e12.5tsin20tddt [ie12.5t] = 125e12.5tsin20t.Шаг 4. Объедините обе стороны:
∫ddt [ie12.5t] dt = ∫125e12.5tsin20tdtie12.5t = (250sin20t − 400cos20t89) e12.5t + Ci (t) = 250sin20t − 400cos20t89 + Ce − 12.5t.∫ddt [ie12.5t] dt = ∫125e12.5tsin20tdtie12.5t = (250sin20t − 400cos20t89) e12,5t + Ci (t) = 250sin20t − 400cos20t89 + Ce − 12,5t.Шаг 5. Решите относительно CC, используя начальное условие v (0) = 2: v (0) = 2:
i (t) = 250sin20t − 400cos20t89 + Ce − 12,5ti (0) = 250sin20 (0) −400cos20 (0) 89 + Ce − 12,5 (0) 0 = −40089 + CC = 40089.i (t) = 250sin20t− 400cos20t89 + Ce − 12,5ti (0) = 250sin20 (0) −400cos20 (0) 89 + Ce − 12,5 (0) 0 = −40089 + CC = 40089.Следовательно, решение задачи начального значения i (t) = 250sin20t − 400cos20t + 400e − 12.5t89 = 250sin20t − 400cos20t89 + 400e − 12,5t89.i (t) = 250sin20t − 400cos20t + 400e − 12,5t89 = 250sin20t − 400cos20t89 + 400e − 12,5t89.
Первый член можно переписать как одну функцию косинуса. Сначала умножьте и разделите на 2502 + 4002 = 5089: 2502 + 4002 = 5089:
. 250sin20t − 400cos20t89 = 508989 (250sin20t − 400cos20t5089) = – 508989 (8cos20t89−5sin20t89) .250sin20t − 400cos20t89 = 508989 (250sin20t − 400cos20t5089) = – 508989 (8cos20t89−5).Затем определим φφ как острый угол такой, что cosφ = 889.cosφ = 889. Тогда sinφ = 589sinφ = 589 и
−508989 (8cos20t89−5sin20t89) = – 508989 (cosφcos20t − sinφsin20t) = – 508989cos (20t + φ).−508989 (8cos20t89−5sin20t89) = – 508989 (cosφcos20t − sinφsin20t) = – 508989cos (20t + φ).Следовательно, решение можно записать как
i (t) = – 508989cos (20t + φ) + 400e − 12,5t89.i (t) = – 508989cos (20t + φ) + 400e − 12,5t89.Второй член называется членом затухания , потому что он быстро исчезает по мере увеличения t . Фазовый сдвиг задается формулами φ, φ, а амплитуда установившегося тока равна 508989.508989. График этого решения представлен на рис. 4.26:
.Рисунок 4.26
КПП 4.19
Схема имеет последовательно электродвижущую силу, равную E = 20sin5tE = 20sin5t V, конденсатор с емкостью 0,02F, 0,02F и резистор 8Ω.8Ω. Если начальный заряд 4C, 4C, найдите заряд в момент времени t> 0. t> 0.
Раздел 4.5 Упражнения
Являются ли следующие дифференциальные уравнения линейными? Объясните свои рассуждения.
208.dydx = x2y + sinxdydx = x2y + sinx
Напишите следующие дифференциальные уравнения первого порядка в стандартной форме.
213.y ′ = x3y + sinxy ′ = x3y + sinx
214.y ′ + 3y − lnx = 0y ′ + 3y − lnx = 0
215.−xy ′ = (3x + 2) y + xex − xy ′ = (3x + 2) y + xex
. 216.dydt = 4y + ty + tantdydt = 4y + ty + tant
Каковы интегрирующие коэффициенты для следующих дифференциальных уравнений?
219.y ′ + exy = sinxy ′ + exy = sinx
220.y ′ = xln (x) y + 3xy ′ = xln (x) y + 3x
221.dydx = tanh (x) y + 1dydx = tanh (x) y + 1
Решите следующие дифференциальные уравнения, используя интегрирующие множители.
225.xy ′ = 3y − 6x2xy ′ = 3y − 6×2
226.(х + 2) y ′ = 3x + y (x + 2) y ′ = 3x + y
229.sin (x) y ′ = y + 2xsin (x) y ′ = y + 2x
Решите следующие дифференциальные уравнения. Используйте свой калькулятор, чтобы нарисовать семейство решений. Существуют ли определенные начальные условия, которые изменяют поведение решения?
233.[T] (x + 2) y ′ = 2y − 1 (x + 2) y ′ = 2y − 1
234.[T] y ′ = 3et / 3−2yy ′ = 3et / 3−2y
235.[T] xy ′ + y2 = sin (3t) xy ′ + y2 = sin (3t)
236.[T] xy ′ = 2cosxx − 3yxy ′ = 2cosxx − 3y
237.[T] (x + 1) y ′ = 3y + x2 + 2x + 1 (x + 1) y ′ = 3y + x2 + 2x + 1
238.[T] sin (x) y ′ + cos (x) y = 2xsin (x) y ′ + cos (x) y = 2x
239.[T] x2 + 1y ′ = y + 2×2 + 1y ′ = y + 2
240.[T] x3y ′ + 2x2y = x + 1x3y ′ + 2x2y = x + 1
Решите следующие задачи с начальными значениями, используя интегрирующие коэффициенты.
241.y ′ + y = x, y (0) = 3y ′ + y = x, y (0) = 3
242.y ′ = y + 2×2, y (0) = 0y ′ = y + 2×2, y (0) = 0
243.xy ′ = y − 3×3, y (1) = 0xy ′ = y − 3×3, y (1) = 0
244.x2y ′ = xy − lnx, y (1) = 1x2y ′ = xy − lnx, y (1) = 1
245.(1 + x2) y ′ = y − 1, y (0) = 0 (1 + x2) y ′ = y − 1, y (0) = 0
246.xy ′ = y + 2xlnx, y (1) = 5xy ′ = y + 2xlnx, y (1) = 5
247.(2 + x) y ′ = y + 2 + x, y (0) = 0 (2 + x) y ′ = y + 2 + x, y (0) = 0
248.y ′ = xy + 2xex, y (0) = 2y ′ = xy + 2xex, y (0) = 2
249.xy ′ = y + 2x, y (0) = 1xy ′ = y + 2x, y (0) = 1
250.y ′ = 2y + xex, y (0) = – 1y ′ = 2y + xex, y (0) = – 1
251.Падающий объект массой мм может достичь конечной скорости, когда сила сопротивления пропорциональна его скорости с постоянной пропорциональностью k.k. Составьте дифференциальное уравнение и решите для скорости, заданной начальной скоростью 0,0.
252.Используя выражение из предыдущей задачи, какова конечная скорость? ( Подсказка: Изучите поведение ограничения; приближается ли скорость к значению?)
253.[T] Используя уравнение для конечной скорости, найдите упавшее расстояние. Сколько времени нужно, чтобы упасть на 5000–5000 метров, если масса 100–100 кг, ускорение свободного падения 9.89,8 м / с 2 , а константа пропорциональности равна 4? 4?
254.Более точный способ описания предельной скорости состоит в том, что сила сопротивления пропорциональна квадрату скорости с константой пропорциональности k.k. Составьте дифференциальное уравнение и решите скорость.
255.Используя выражение из предыдущей задачи, какова конечная скорость? ( Подсказка: Изучите ограничивающее поведение: приближается ли скорость к значению?)
256.[T] Используя уравнение для конечной скорости, найдите упавшее расстояние. Сколько времени нужно, чтобы упасть с высоты 50005000 метров, если масса равна 100100 кг, ускорение свободного падения составляет 9,8 м / с и 29,8 м / с2, а коэффициент пропорциональности равен 4 × 4? Это займет больше или меньше времени, чем вы изначально предполагали?
Для следующих проблем определите, как параметр aa влияет на решение.
257.Решите общее уравнение y ′ = ax + y.y ′ = ax + y. Как изменение аа меняет поведение?
258.Решите общее уравнение y ′ = ay + x.y ′ = ay + x. Как изменение аа меняет поведение?
259.Решите общее уравнение y ′ = ax + xy.y ′ = ax + xy. Как изменение аа меняет поведение?
260.Решите общее уравнение y ′ = x + axy.y ′ = x + axy. Как изменение аа меняет поведение?
261.Решите y′ − y = ekty′ − y = ekt с начальным условием y (0) = 0. y (0) = 0. Когда kk приближается к 1,1, что происходит с вашей формулой?
Дифференциальные уравнения первого порядка
Разделение переменных
Вопросы о дифференциальных уравнениях в STEP и других экзаменах по продвинутой математике бывают нескольких форм.В первую очередь, это могут быть дифференциальные уравнения первого порядка, т. Е. Наивысшая существующая производная является первым или более высоким порядком, т. Е. Существует производная, превышающая первую. Иногда вопрос подводит вас к конкретному способу решения дифференциального уравнения. Однако чаще вам потребуется применять стандартный метод решения, и в этой статье рассматриваются два основных метода для дифференциальных уравнений первого порядка. Тем не менее, стоит отметить, что, как и в случае с большинством экзаменов по STEP и другим экзаменам по продвинутой математике, вам следует убедиться, что вы очень хорошо знаете все дифференцирование и интеграцию на A-Level; что включает в себя важное неявное дифференциация.Помня об этом заключительном моменте, давайте перейдем к нашему первому методу – разделению переменных.
Первый метод, используемый для «разделимых» дифференциальных уравнений первого порядка, – это разделение переменных. Дифференциальное уравнение первого порядка \ (dy / dt \) называется сепарабельным, если его можно записать в виде:\ (\ hspace {3.25 in} \ frac {dy} {dt} = f (y) g ( t). \)
Тогда разделение переменных означает разделение на \ (f (y) \), а затем интегрирование по \ (t \), i.д .:
\ (\ hspace {3 in} \ int \ frac {1} {f (y)} dy = \ int g (t) dt. \)
На самом деле ничего больше, кроме этого! Хотя, конечно, интегралы в левой и правой частях могут быть не очень простыми; они часто требуют от вас замены. Это одна из причин, почему знание интеграции A-Level наизнанку имеет ключевое значение; и вам следует рассмотреть возможность прохождения модуля 10, чтобы получить там несколько советов и подсказок.
Метод интегрирующих множителей
Наш второй метод использует правило произведения для дифференцирования для решения дифференциальных уравнений первого порядка, которые могут быть записаны в форме:\ (\ hspace {3.{-3t}. \)
Итак, это два метода, с которыми вам нужно познакомиться, чтобы приступить к решению задач дифференциальных уравнений первого порядка STEP. Однако, чтобы по-настоящему все проверить, давайте перейдем к рассмотрению части прошлого вопроса STEP.
Пример
Этот отрывок взят из Вопроса 6 по STEP III 2008 и дает хорошее введение в дифференциальные уравнения первого порядка в STEP. Во-первых, нас сначала просят дифференцировать \ (y \) относительно \ (x \).2 + 2xp \ right) = 2p \ frac {dp} {dx} + 2x \ frac {dp} {dx} + 2p. \)
Тогда, реализуя LHS, \ (dy / dx \) можно заменить на \ (p \) и соответствующим образом переставив, находим:
\ (\ hspace {1,85 дюйма} \ frac {dp} {dx} = – \ frac {p} {2p + 2x} \ Rightarrow \ frac {dx} {dp} = – \ frac {(2p + 2x)} {p} = – 2-2 \ frac {x} {p}, \)
по мере необходимости.
Итак, теперь у нас есть дифференциальное уравнение для \ (x \), которое нам нужно решить. Сначала мы спрашиваем себя, разделим ли он, и мы надеемся, что ответ будет отрицательным.2. \)
Сводка
Вот и все! Мы рассмотрели два основных метода решения дифференциальных уравнений первого порядка в STEP и других экзаменах по продвинутой математике.

 n} \cdot \varphi \left( {\frac{y}{x}} \right)\]
n} \cdot \varphi \left( {\frac{y}{x}} \right)\]




 Для этого используют формулы:
Для этого используют формулы:



 Следовательно, интегрируя еще раз, окончательно получаем общее решение $y=\int \phi \left(x,C_{1} \right)\cdot dx +C_{2} $.
Следовательно, интегрируя еще раз, окончательно получаем общее решение $y=\int \phi \left(x,C_{1} \right)\cdot dx +C_{2} $. {2} +C_{2} $.
{2} +C_{2} $.

 y’=f(y/x)
y’=f(y/x) 
 (1.5)
(1.5) Поскольку производная функций определяет угловой коэффициент наклона касательной к графику функции, то тем самым определим угловой коэффициент касательной к той интегральной кривой уравнения, которая проходит через точку .
Поскольку производная функций определяет угловой коэффициент наклона касательной к графику функции, то тем самым определим угловой коэффициент касательной к той интегральной кривой уравнения, которая проходит через точку . Каждая из интегральных кривых представляет собой график решения исходного дифференциального уравнения. Найти решение уравнения с начальным условием (1.7) геометрически означает выделение из множества интегральных кривых той кривой, которая проходит через точку . Всё множество интегральных кривых представляет общее решение дифференциального уравнения. При графическом представлении решения дифференциального уравнения часто пользуются изоклинами.
Каждая из интегральных кривых представляет собой график решения исходного дифференциального уравнения. Найти решение уравнения с начальным условием (1.7) геометрически означает выделение из множества интегральных кривых той кривой, которая проходит через точку . Всё множество интегральных кривых представляет общее решение дифференциального уравнения. При графическом представлении решения дифференциального уравнения часто пользуются изоклинами.



 Очевидно, что в области G уравнение
имеет бесконечное число различных
решений.
Очевидно, что в области G уравнение
имеет бесконечное число различных
решений.
 График решения представляет
собой непрерывную интегральную кривую,
через каждую точку которой можно провести
касательную. Из уравнения следует, что
угловой коэффициент у’ касательной
к интегральной кривой в каждой ее точке
(х;
у) равен значению
в этой точке правой части уравнения f(x,
у). Таким образом,
уравнение y‘=f(x,
у) устанавливает
зависимость между координатами точки
(х;
у) и
угловым коэффициентом у’ касательной
к графику интегральной кривой в той же
точке. Зная х и у, можно указать
направление касательной к этой
интегральной кривой в точке (х;
у).
Сопоставим каждой точке (х;
у) интегральной
кривой направленный отрезок, угловой
коэффициент которого равен f(х,
у). Получим так
называемое поле
направлений данного
уравнения, раскрывающее геометрический
смысл дифференциального уравнения
первого порядка.
График решения представляет
собой непрерывную интегральную кривую,
через каждую точку которой можно провести
касательную. Из уравнения следует, что
угловой коэффициент у’ касательной
к интегральной кривой в каждой ее точке
(х;
у) равен значению
в этой точке правой части уравнения f(x,
у). Таким образом,
уравнение y‘=f(x,
у) устанавливает
зависимость между координатами точки
(х;
у) и
угловым коэффициентом у’ касательной
к графику интегральной кривой в той же
точке. Зная х и у, можно указать
направление касательной к этой
интегральной кривой в точке (х;
у).
Сопоставим каждой точке (х;
у) интегральной
кривой направленный отрезок, угловой
коэффициент которого равен f(х,
у). Получим так
называемое поле
направлений данного
уравнения, раскрывающее геометрический
смысл дифференциального уравнения
первого порядка.
 Одну из этих функций можно выбрать произвольно, а вторая определяется из дифференциального уравнения.
Одну из этих функций можно выбрать произвольно, а вторая определяется из дифференциального уравнения.
 Найдем частичное решение дифференциального уравнения (задача Коши), для этого определим постоянную с начального условия на функцию
Найдем частичное решение дифференциального уравнения (задача Коши), для этого определим постоянную с начального условия на функцию 
 Используйте алгоритм решения уравнения Бернулли ко всем подобным дифференциальным уравнениям.
Используйте алгоритм решения уравнения Бернулли ко всем подобным дифференциальным уравнениям.

 С
С
 С
С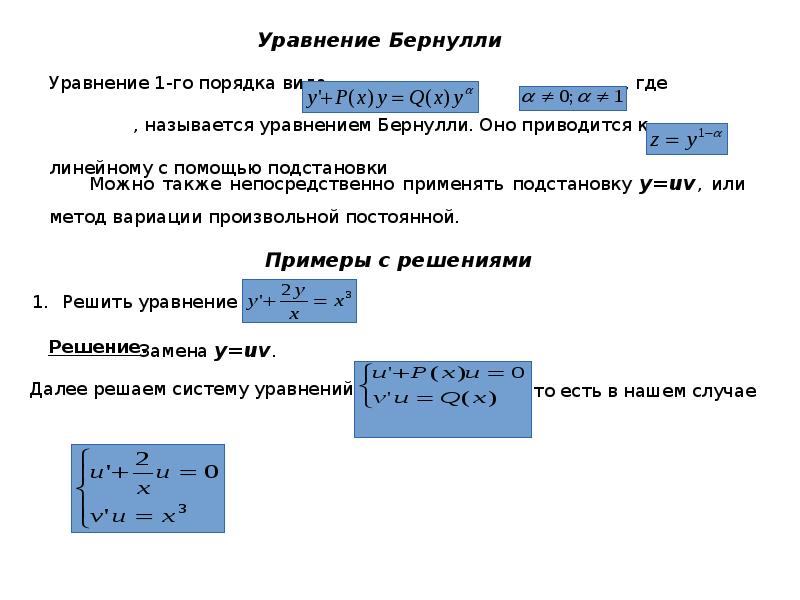 2.9b) u ′ = υ
2.9b) u ′ = υ Это можно сделать в два этапа. На первом этапе мы центрируем его примерно ( x n –1/2 , η ) без указания η .Если мы обозначим его левую часть как L , то конечно-разностное приближение к уравнению. (8.2.9c) равно
Это можно сделать в два этапа. На первом этапе мы центрируем его примерно ( x n –1/2 , η ) без указания η .Если мы обозначим его левую часть как L , то конечно-разностное приближение к уравнению. (8.2.9c) равно 2.16) hj − 1 (bjnυjn − bj − 1nυj − 1n) + α1 (fυ) j − 1 / 2n − α2 (u2) j − 1 / 2n + αn (υj − 1 / 2n − 1fj − 1 / 2n − fj − 1 / 2n − 1υj − 1 / 2n) = Rj − 1 / 2n − 1
2.16) hj − 1 (bjnυjn − bj − 1nυj − 1n) + α1 (fυ) j − 1 / 2n − α2 (u2) j − 1 / 2n + αn (υj − 1 / 2n − 1fj − 1 / 2n − fj − 1 / 2n − 1υj − 1 / 2n) = Rj − 1 / 2n − 1 Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. 2 В явной форме
2 В явной форме Начнем с:
Начнем с: Общее решение – это
Общее решение – это
 Теперь, когда у нас есть интегрирующий коэффициент, мы умножаем его на исходное уравнение:
Теперь, когда у нас есть интегрирующий коэффициент, мы умножаем его на исходное уравнение: Левая сторона останется
то же самое, поскольку интеграл от производной сокращается:
Левая сторона останется
то же самое, поскольку интеграл от производной сокращается: of fg, что равняется тому, что у нас есть сейчас:
of fg, что равняется тому, что у нас есть сейчас: Рассол, содержащий 1 фунт соли на галлон, поступает в
резервуар со скоростью 3 галлона / мин, а хорошо перемешанный раствор покидает резервуар со скоростью 4
галлонов / мин, опорожнение резервуара через 120 минут или 2 часа. Оцените выражение для
количество соли в резервуаре через t минут, и найдите, сколько соли находится в резервуаре за t = 60 минут.
Рассол, содержащий 1 фунт соли на галлон, поступает в
резервуар со скоростью 3 галлона / мин, а хорошо перемешанный раствор покидает резервуар со скоростью 4
галлонов / мин, опорожнение резервуара через 120 минут или 2 часа. Оцените выражение для
количество соли в резервуаре через t минут, и найдите, сколько соли находится в резервуаре за t = 60 минут. Немного переписав это, мы получим:
Немного переписав это, мы получим: