Производная функции заданной неявно – формулы и примеры с решением
Содержание:
- Нахождение производной функции
- Для нахождения производной функции, заданной неявно, нам понадобиться понятие частной производной
Неявное задание функции — это задание ее выражением вида . (12.1) Если соответствующее уравнение можно решить относительно или , то мы вернемся к обычному заданию функции. Однако иногда такое решение приводит к сложным формулам, а иногда его и вовсе нельзя найти. Так, например, уравнение окружности в форме (12.2) проще, чем следующее из него выражение . (12.3) Если в (12.1) левая часть — произвольный многочлен, содержащий и в степени выше четвертой, то в общем случае это уравнение нельзя разрешить соответственно относительно или . Также не разрешается, например, простое с виду уравнение . (12.4)
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Однако и в тех случаях, когда нет решения в виде формулы, прямо дающей способ вычисления для данного , все равно есть определенная функция , при каждом можно, решая уравнение численно, найти соответствующее , можно построить кривую в плоскости .
Возможно, что кривая будет существовать не при всех (в случае окружности, например, лишь при между и , где — радиус окружности), при данном может быть больше одного значения (в случае окружности, например, два значения, в соответствии со знаком у корня квадратного). Однако эти осложнения не отменяют основного факта: определяет как функцию .
Как найти производную ? Можно ли это сделать, не решив уравнение, т. е. не выразив явно?
Это было сделано еще Ньютоном. Пусть удовлетворяют уравнению: . (12.1) Возьмем соседние значения , также удовлетворяющие уравнению: . (12.5) Запишем, пользуясь (12.1): (12.6)
Разность представляет собой приращение функции , рассматриваемой как функция одной переменной при неизменном . Это приращение, как мы знаем, в пределе *) может быть выражено так:
.
Мы отмечаем здесь, что при вычислении производной по функции двух переменных и мы считаем постоянным. Вычисленную таким образом производную называют частной производной, и в ее обозначении вместо прямой буквы пишут круглую : Аналогично для первой разности в (12.
Условие (12.5) дает , или
Переходя к пределу при , получим слева производную, а справа при этом можно будет отбросить . Окончательно
. (12.7)
Обратите внимание на знак минус в (12.7) и на то, что в данном случае нельзя просто «сократить» в числителе и знаменателе. Покажем применение (12.7) на примере уравнения (12.2). Имеем ; (12.8) Легко убедиться, что этот результат совпадает с тем, что получится, если вычислить производную (12.3). Найдем производную в случае (12.4):
Возможно вам будут полезны данные страницы:
Что такое производная |
Определение производной |
Смешанная производная |
Производная экспоненты |
Таким образом, в выражение производной неявной функции входят обе величины, и . Чтобы найти ее численно, нужно при заданном найти численно .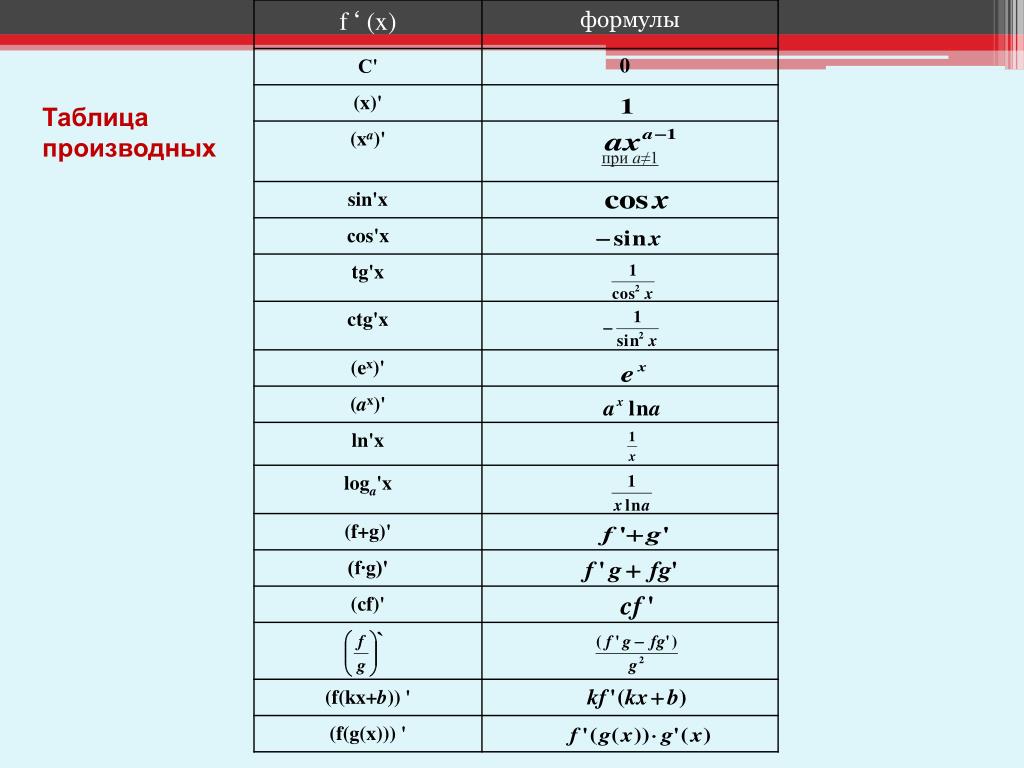
Но если бы мы не имели формулы (12.7), то для нахождения производной нам пришлось бы находить численно два значения и при двух соседних и и находить отношение . При этом чем ближе и , тем точнее пришлось бы вычислять и , а это часто затруднительно.
Заметим, наконец, что если приводит к неоднозначной кривой, т. е. при одном значении есть два или больше значений (несколько ветвей кривой), то выражение (12.7) при данном при подстановке разных дает значения производной в соответствующих точках.
Читателю предлагается проверить это на примере уравнения окружности (12.2), для которого производная дана формулой (12.8).
Нахождение производной функции
Для нахождения производной функции, заданной неявно, нам пришлось ввести новое понятие — понятие частной производной. Это понятие имеет большое значение и необходимо для функций нескольких переменных, которые мы в этой книге не изучаем. По существу, мы уже неявно пользовались понятием частной производной даже в таких элементарных вопросах, как производная произведения нескольких функций или, например, производная степени (см.
Покажем применение (7) на примере уравнения (2). Имеем ; тогда , (4.12.8) .
Легко убедиться, что этот результат совпадает с тем, что получится, если вычислить производную функции (3). Найдем производную в случае (4):
Таким образом, в выражение производной неявной функции входят обе величины и . Чтобы найти ее численно, нужно найти значение , отвечающее заданному . Но если бы мы не имели формулы (7), то для нахождения производной нам пришлось бы находить численно два значения и , отвечающие двум соседним значениям и , а затем искать отношение и предел этого отношения.
При этом чем ближе к тем точнее пришлось бы вычислять и а это часто вовсе не так просто. Использование же формулы (7) обычно не представляет труда.
Если приводит к неоднозначной функции , т.
Для нахождения производной функции, заданной неявно, нам понадобиться понятие частной производной
Оно имеет большое значение, так как необходимо для изучения функций нескольких переменных (которых, впрочем, мы в этой книге почти не касаемся). Неявно мы уже пользовались понятием частной производной: так, определенный интеграл есть функция двух переменных; выше мы находили частные производные по одному из пределов, считая второй предел интегрирования закрепленным (постоянным). Даже в таких элементарных вопросах, как производная произведения нескольких функций или, например, производная степени , по существу, у нас «работали» частные производные. В самом деле, когда мы говорили, что складывается из членов, получающихся при взятии производной по переменной , входящей в , и производной по , входящей в выражение , то мы имели в виду частные производные.
Соответствующее общее правило можно записать так: если ,
то
.
Решение квадратных уравнений через производные / Хабр
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант.
Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Где — время, — начальная скорость, — ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Разве формула перемещения для РУД не является следствием решения квадратного уравнения?
Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.
В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска :
[подставили в производную первого порядка ]
Корнем такого уравнения относительно будет:
А значением исходной функции при таком аргументе будет:
Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль».
Иными словами, нам от положения необходимо «дойти до нуля».
Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:
, также как и
Тогда, подставив все известные величины, получим:
Поделим все на :
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
Производные формулы и приложения для вырожденных стохастических дифференциальных уравнений с дробными шумами
“>Алос, Э., Мазе, О., Нуаларт, Д.: Стохастическое исчисление по отношению к гауссовым процессам. Анна. Вероятно. 29 , 766–801 (2001)
Статья MathSciNet МАТЕМАТИКА Google ученый
Арнодон, М., Талмайер, А., Ван, Ф.Ю.: Градиентные оценки и неравенства Харнака на некомпактных римановых многообразиях. стох. Процесс. заявл. 119 , 3653–3670 (2009)
Статья MathSciNet МАТЕМАТИКА Google ученый
Аяче, А., Ши, Н.Р., Сяо, Ю.М.: Многопараметрическое многофракционное броуновское движение: локальный недетерминизм и совместная непрерывность местного времени. Анна. Инст. А. Пуанкаре, вероятно. Стат. 47 , 1029–1054 (2011)
Статья MathSciNet МАТЕМАТИКА Google ученый
Бао, Дж., Ван, Ф.Ю., Юань, К.
: Формула производной и неравенство Харнака для вырожденных функциональных СДУ. стох. Дин. 13 , 1–22 (2013)
Статья MathSciNet МАТЕМАТИКА Google ученый
Бао, Дж., Ван, Ф.Ю., Юань, К.: Формулы висмута и приложения для функциональных SPDE. Бык. науч. Мат. 137 , 509–522 (2013)
Статья MathSciNet МАТЕМАТИКА Google ученый
Бодуэн, Ф., Оуян, К.: Ядерное разложение с малым временем для решений стохастических дифференциальных уравнений, управляемых дробными броуновскими движениями. стох. Процесс. заявл. 121 , 759–792 (2011)
Статья MathSciNet МАТЕМАТИКА Google ученый
Бодуэн, Ф., Оуян, К., Тиндел, С.: Верхние границы плотности решений стохастических дифференциальных уравнений, управляемых дробными броуновскими движениями.
Анна. Инст. А. Пуанкаре, вероятно. Стат. 50 , 111–135 (2014)
Статья MathSciNet МАТЕМАТИКА Google ученый
Биаджини Ф., Ху Ю., Оксендал Б., Чжан Т.: Стохастическое исчисление дробного броуновского движения и приложения. Спрингер, Лондон (2008)
Книга МАТЕМАТИКА Google ученый
Бисмут, Дж. М.: Большое отклонение и исчисление Маллявена. Биркхойзер, Бостон (1984)
МАТЕМАТИКА Google ученый
Кутин Л., Цянь З.: Стохастический анализ, анализ грубых траекторий и дробные броуновские движения. Вероятно. Теория отн. Поля 122 , 108–140 (2002)
Статья MathSciNet МАТЕМАТИКА Google ученый
Да Прато, Г., Рёкнер, М., Ван, Ф.
Ю.: Сингулярные стохастические уравнения в гильбертовом пространстве: неравенства Харнака для их полугрупп переходов. Дж. Функц. Анальный. 257 , 992–1017 (2009)
Статья MathSciNet МАТЕМАТИКА Google ученый
Decreusefond, L., Üstünel, A.S.: Стохастический анализ дробного броуновского движения. Потенциальный анал. 10 , 177–214 (1998)
Статья MathSciNet МАТЕМАТИКА Google ученый
Донг, З., Се, Ю.: Эргодичность линейного SPDE, управляемая шумом Леви. Дж. Сист. науч. Комплекс 23 , 137–152 (2010)
Статья MathSciNet МАТЕМАТИКА Google ученый
Драйвер, B.: Повторное рассмотрение интеграции по частям для измерения теплового ядра. Дж. Матем. Чистый Appl. 76 , 703–737 (1997)
Статья MathSciNet МАТЕМАТИКА Google ученый
“>Элворти, К.Д., Ли, X.М.: Формулы для производных тепловых полугрупп. Дж. Функц. Анальный. 125 , 252–286 (1994)
Статья MathSciNet МАТЕМАТИКА Google ученый
Fan, XL: Неравенство Харнака и формула производной для SDE, обусловленного дробным броуновским движением. науч. Китайская математика. 561 , 515–524 (2013)
Статья MathSciNet МАТЕМАТИКА Google ученый
Fan, XL: Формула интегрирования по частям и приложения для SDE, управляемых дробными броуновскими движениями. стох. Анальный. заявл. 33 , 199–212 (2015)
Статья MathSciNet МАТЕМАТИКА Google ученый
Fan, XL: Логарифмические неравенства Соболева для дробной диффузии. Статист. Вероятно. лат. 106 , 165–172 (2015)
Статья MathSciNet МАТЕМАТИКА Google ученый
“>Фан, С.Л., Рен, Ю.: Формулы Висмута и приложения для стохастических (функциональных) дифференциальных уравнений, управляемых дробными броуновскими движениями. стох. Дин. 7 , 19 (2017)
МАТЕМАТИКА Google ученый
Фанг, С., Ли, Х., Луо, Д.: Тепловые полугруппы и обобщенные потоки на полных римановых многообразиях. Бык. науч. Мат. 135 , 565–600 (2011)
Статья MathSciNet МАТЕМАТИКА Google ученый
Гуйлин, А., Ван, Ф.Ю.: Вырожденные уравнения Фоккера – Планка: формула Висмута, градиентная оценка и неравенство Харнака. Дж. Дифференц. Экв. 253 , 20–40 (2012)
Статья MathSciNet МАТЕМАТИКА Google ученый
Хайрер, М.: Эргодичность стохастических дифференциальных уравнений, управляемых дробным броуновским движением.
Анна. Вероятно. 33 , 703–758 (2005)
Статья MathSciNet МАТЕМАТИКА Google ученый
Хайрер, М., Пиллаи, Н.С.: Эргодичность гипоэллиптических СДУ, обусловленных дробным броуновским движением. Анна. Инст. А. Пуанкаре, вероятно. Стат. 47 , 601–628 (2011)
Статья MathSciNet МАТЕМАТИКА Google ученый
Харамильо, А., Нуаларт, Д.: Асимптотические свойства производной местного времени самопересечения дробного броуновского движения. стох. Процесс. заявл. 127 , 669–700 (2017)
Артикул MathSciNet МАТЕМАТИКА Google ученый
Никифоров А.Ф., Уваров В.Б. Специальные функции математической физики. Биркхойзер, Бостон (1988)
Книга МАТЕМАТИКА Google ученый
“>Нурдин И., Саймон Т.: Об абсолютной непрерывности одномерных СДУ, приводимых в движение дробным броуновским движением. Стат. Вероятно. лат. 76 , 907–912 (2006)
Статья MathSciNet МАТЕМАТИКА Google ученый
Нуаларт, Д.: Исчисление Маллявена и смежные темы, 2-е изд. Спрингер, Берлин (2006)
МАТЕМАТИКА Google ученый
Нуаларт, Д., Оукнин, Ю.: Регуляризация дифференциальных уравнений дробным шумом. стох. Процесс. заявл. 102 , 103–116 (2002)
Статья MathSciNet МАТЕМАТИКА Google ученый
Нуаларт, Д., Рэшкану, А.: Дифференциальные уравнения, основанные на дробном броуновском движении. Собирать. Мат. 53 , 55–81 (2002)
MathSciNet МАТЕМАТИКА Google ученый
“>Нуаларт, Д., Соссеро, Б.: Исчисление Маллявена для стохастических дифференциальных уравнений, управляемых дробным броуновским движением. стох. Процесс. заявл. 119 , 391–409 (2009)
Статья MathSciNet МАТЕМАТИКА Google ученый
Приола, Э.: Формулы для производных вырожденных диффузионных полугрупп. Дж. Эвол. Экв. 6 , 577–600 (2006)
Статья MathSciNet МАТЕМАТИКА Google ученый
Салофф-Кост, Л.: Сходимость к равновесию и логарифмическая постоянная Соболева на многообразиях с ограниченной снизу кривизной Риччи. Коллок. Мат. 67 , 109–121 (1994)
Статья MathSciNet МАТЕМАТИКА Google ученый
Самко С.Г., Килбас А.А., Маричев О.И. Дробные интегралы и производные, теория и приложения.
Издательство Gordon and Breach Science Publishers, Yvendon (1993)
МАТЕМАТИКА Google ученый
Соссеро, Б.: Транспортные неравенства для стохастических дифференциальных уравнений, управляемых дробным броуновским движением. Бернулли 18 , 1–23 (2012)
Статья MathSciNet МАТЕМАТИКА Google ученый
Ван, Ф.Ю.: Производная формула и неравенство Харнака для СДУ, управляемых процессами Леви. стох. Анальный. заявл. 32 , 30–49 (2014)
Статья MathSciNet МАТЕМАТИКА Google ученый
Ван, Ф.Ю.: Неравенства Харнака для стохастических дифференциальных уравнений в частных производных. Springer, Берлин (2013)
Книга МАТЕМАТИКА Google ученый
“>Ван, Ф.Ю., Сюй, Л.: Производные формулы и приложения для гипердиссипативных стохастических уравнений Навье – Стокса/Бюргерса. инф. Размеры. Анальный. Квантовая вероятность. Относ. Верхний. 15 , 1–19 (2012)
Статья Google ученый
Wang, FY, Zhang, XC: Формула производной и приложения для вырожденных диффузионных полугрупп. Дж. Матем. Чистый Appl. 99 , 726–740 (2013)
Статья MathSciNet МАТЕМАТИКА Google ученый
Ян, Л.Т.: Дробная производная для дробного броуновского местного времени. Мат. З. 283 , 437–468 (2016)
Статья MathSciNet МАТЕМАТИКА Google ученый
Янг, Л.К.: Неравенство типа Гельдера, связанное с интегрированием Стилтьеса. Акта Математика. 67 , 251–282 (1936)
Артикул MathSciNet МАТЕМАТИКА Google ученый
“>Цэле, М.: Интегрирование с учетом фрактальных функций и стохастического исчисления I. Вероятность. Теория отн. Поля 111 , 333–374 (1998)
Статья MathSciNet МАТЕМАТИКА Google ученый
Чжан, С.К.: Неравенство Харнака для полулинейных SPDE с мультипликативным шумом. Стат. Вероятно. лат. 83 , 1184–1192 (2013)
Статья MathSciNet МАТЕМАТИКА Google ученый
Чжан, XC: Стохастические потоки и формулы Бисмута для стохастических гамильтоновых систем. стох. Процесс. заявл. 120 , 1929–1949 (2010)
Статья MathSciNet МАТЕМАТИКА Google ученый
Производная формула: простое для понимания руководство
В этой статье
Что такое производная формула?
Что такое производная?
Элементы производной
Ключевые формулы производных
Решение производных шаг за шагом
Типы деривативов
Что такое производная формула?
Производные формулы — это уравнения, которые дают быстрые решения общих задач производных.
Мы называем их правилами, такими как правило мощности и правило цепочки, и это лишь некоторые из них.
Подробнее об этом позже.
Эти формулы взяты из предельного определения производной и упрощают процесс дифференцирования. Вот почему мы также можем называть их формулами дифференцирования.
Что такое производная?
Производная функции в точке xxx равна наклону касательной в xxx.
Это значение наклона представляет мгновенную скорость изменения в этой точке. Дифференцирование – это процесс нахождения производной функции.
Например, на приведенном ниже графике функция f(x)=ln(x)f(x) = \ln{(x)}f(x)=ln(x) выделена синим цветом. Красная линия — это f(x)=x−1f(x) = x-1f(x)=x−1, которая является касательной к fff в точке x=1x = 1x=1. Касательная линия к точке функции — это линия, которая едва касается функции в этой точке. Наклон этой касательной f(x)=x−1f(x) = x-1f(x)=x−1 равен 111, что означает, что производная f(x)=ln(x)f(x ) = \ln{(x)}f(x)=ln(x) равно 111 при x=1x = 1x=1.
Мы формально определяем производные, используя ограничения: Delta{x} \to 0} \frac{{f\left( {x + \Delta{x} } \right) – f\left( x\right)}}{\Delta{x} }=Lf'( x)=Δx→0limΔxf(x+Δx)−f(x)=L
Приведенное выше уравнение представляет собой предел средней скорости изменения fff в интервале [x,x+Δx][x, x +\Delta{x}][x,x+Δx] как Δx\Delta{x}Δx приближается к 0. Мы также знаем среднюю скорость изменения функции как наклон секущей.
В этом обозначении Δx\Delta{x}Δx представляет небольшое изменение xxx. Если этот предел существует, то LLL является производной.
Элементы производной
Обозначение f’(a)f’(a)f’(a) представляет производную функции fff в некоторой точке aaa. Вы можете услышать, как это обозначение читается вслух как «производная от fff, оцениваемая как aaa», или как «fff, простое число как aaa».
Выражения f’(x)f’(x)f’(x) и dydx\frac{dy}{dx}dxdy представляют общую производную функцию fff. Последняя запись называется записью Лейбница.
Подставляя любую точку aaa в результирующую функцию f’(x)f’(x)f’(x), мы можем определить наклон касательной к fff в любой точке кривой. 9{n-1}dxd(xn)=nxn−1
Особый случай степенного правила
В этом случае nnn=1
ddx(x)=1\frac d{dx}(x)=1dxd (x)=1
Постоянное множественное правило
ddx(c⋅f(x))=c⋅f′(x)\frac d{dx}(c\cdot f(x))=c\cdot f ‘(x)dxd(c⋅f(x))=c⋅f'(x)
Цепное правило
ddxf(g(x))=f'(g(x))g'(x)\ frac{d}{dx}f(g(x)) = f'(g(x))g'(x)dxdf(g(x))=f'(g(x))g'(x )
Правило продукта
ddx[f(x)⋅g(x)]=f'(x)⋅g(x)+f(x)⋅g'(x)\frac{d}{dx}[ f(x) \cdot g(x)] = f'(x) \cdot g(x) + f(x)\cdot g'(x)dxd[f(x)⋅g(x)]=f ‘(х)⋅г(х)+f(х)⋅г'(х) 9xdxd(ex)=ex
По словам доктора Тима Шартье, два производных правила, которые меняют правила игры, — это правило продукта и правило частного:
Он также объясняет другие формулы дифференцирования для поиска с примерами:
youtube.com/embed/-R5wh_BIGm4″ title=”YouTube video player” frameborder=”0″ allow=”accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””> Решение производных шаг за шагом
Теперь мы обсудим, как найти производные. Мы можем решить производную двумя способами:
Используя формальное предельное определение производной
Использование основных формул производных
Вот шаги для нахождения производных с использованием определения предела:
Шаг 1
Подставьте свою функцию в определение предела формулы производной:
f'(x)=limΔx→0f(x+Δx)−f(x)Δx=Lf'(x) = \mathop{\lim}\limits_{\Delta{x} \to 0} \ frac{{f\left( {x + \Delta{x} } \right) – f\left( x\right)}}{\Delta{x} }=Lf'(x)=Δx→0limΔxf( х+∆x)−f(x)=L 92}{\Delta{x}}=Δx→0limΔx6xΔx+3Δx2
=limΔx→06x+3Δx= \mathop {\lim }\limits_{\Delta{x} \to 0}6x + 3 \Delta{x}=Δx→0lim6x+3Δx
Шаг 3.
ОценитеТеперь проверьте предел, когда Δx\Delta{x}Δx приближается к 0. Многочлены всегда непрерывны. Чтобы оценить этот предел, мы можем подставить Δx=0\Delta{x} = 0Δx=0 непосредственно в функцию, с которой мы остались.
f'(x)=limΔx→06x+3Δxf'(x)= \mathop {\lim }\limits_{\Delta{x} \to 0}6x + 3\Delta{x}f'(x )=Δx→0lim6x+3Δx
92f(x)=3×2 равно f’(x)=6xf’(x) = 6xf’(x)=6x. Это общая формула производной для любой точки на кривой fff.Чтобы найти производную в одной точке, мы можем подставить x=ax = ax=a в f’(x)=6xf’(x) = 6xf’(x)=6x.
Например, мы можем сказать, что:
f'(1)=6(1)=6f'(1) = 6(1) = 6f'(1)=6(1)=6, что представляет собой наклон касательной в точке x= 1х = 1х=1.
f'(5)=6(5)=30f'(5) = 6(5) = 30f'(5)=6(5)=30, что представляет собой наклон касательной при x=5x = 5x= 5.
f'(-60)=6(-60)=-360f'(-60) = 6(-60) = -360f'(-60)=6(-60)=-360, что представляет собой наклон касательная в точке x=-60x = -60x=-60.
xf(x)=4×4+ex. 9x=16×3+exПрактический пример 3
Для более сложного примера найдем производную f(x)=sin(4x)cos(2x)f(x) = \sin{(4x)}\cos{(2x)}f(x )=sin(4x)cos(2x).
Во-первых, нам понадобится правило произведения. Это говорит о том, что производная произведения функций равна сумме первой функции, умноженной на производную от второй, и второй функции, умноженной на производную от первой.
f'(x)=sin(4x)⋅ddxcos(2x)+cos(2x)⋅ddxsin(4x)f'(x) = \sin{(4x)} \cdot \frac{d }{dx}\cos{(2x)} + \cos{(2x)} \cdot \frac{d}{dx}\sin{(4x)}f'(x)=sin(4x)⋅dxdcos (2x)+cos(2x)⋅dxdsin(4x)
Наряду с правилами производных синуса и косинуса нам также понадобится цепное правило, так как у нас есть композиция функций, использующая функции синуса и косинуса.
Цепное правило гласит, что производная композиции функций равна производной внешней функции, умноженной на производную внутренней функции.
Это означает, что производная sin(4x)\sin{(4x)}sin(4x) равна 4cos(4x)4\cos{(4x)}4cos(4x), а производная cos( 2x)\cos{(2x)}cos(2x) равно −2sin(2x)-2\sin{(2x)}−2sin(2x).
f'(x)=sin(4x)⋅ddxcos(2x)+cos(2x)⋅ddxsin(4x)f'(x) = \sin{(4x)} \cdot \frac{d }{dx}\cos{(2x)} + \cos{(2x)} \cdot \frac{d}{dx}\sin{(4x)}f'(x)=sin(4x)⋅dxdcos (2x)+cos(2x)⋅dxdsin(4x)
=sin(4x)⋅−2sin(2x)+cos(2x)⋅4cos(4x)= \sin{(4x)} \cdot -2\sin{(2x)} + \cos{(2x)} \cdot 4\cos{(4x)}=sin(4x)⋅−2sin(2x)+cos(2x)⋅4cos(4x)
= −2sin(4x)sin(2x)+4cos(2x)cos(4x)= -2\sin{(4x)}\sin{(2x)} + 4\cos{(2x) }\cos{(4x)}=−2sin(4x)sin(2x)+4cos(2x)cos(4x)
=4cos(2x)cos(4x)−2sin(4x)sin(2x )= 4\cos{(2x)}\cos{(4x)} – 2\sin{(4x)}\sin{(2x)}=4cos(2x)cos(4x)−2sin(4x)sin(2x )
Типы производных финансовых инструментов
Первая и вторая производные дают разную информацию о поведении функции.
Мы используем знак первой производной, чтобы определить, является ли функция возрастающей, убывающей или постоянной на интервале III:
Если f’(x)>0f’(x) > 0f’(x)>0 для каждого xxx на III, то fff увеличивается на III.
Если f'(x) для каждого x на I, то f убывает на I.
Если f’(x)=0f’(x) = 0f’(x)=0 для каждого xxx на III, то fff постоянна на III.
Мы находим вторые производные, просто взяв производную от первой производной. Вторые производные сообщают нам форму функции. Эта характеристика называется вогнутостью.
По знаку второй производной определяем интервалы вогнутости:
Если f’’(x)>0f’’(x) > 0f’’(x)>0 для каждого xxx на III, то fff вогнуто вверх на III.
Если f’’(x) для каждого x на I, то f вогнута вниз на III.
Если f’’(x)=0f’’(x) = 0f’’(x)=0 для каждого xxx на III, то fff не имеет вогнутости.
Доктор Ханна Фрай обсуждает тесты первой и второй производной:
Курс Outlier по исчислению производных поможет вам больше попрактиковаться в дифференцировании и других навыках вычисления производных.
Вот почему:Outlier предлагает доступные занятия в колледже за небольшую часть стоимости — на 80 % дешевле, чем в традиционном колледже.
Заработайте 3 кредита колледжа за каждый пройденный курс. Курс аккредитован Университетом Питтсбурга, который входит в число 60 лучших школ.
Курсы исчисления являются интерактивными и преподаются всемирно известными профессорами математики, в том числе Тимом Шартье из колледжа Дэвидсона, Ханной Фрай из Университетского колледжа Лондона и Джоном Уршелем из Массачусетского технологического института.
Ресурсы курса включают наборы вопросов, викторины и цифровой учебник, основанный на активном обучении. У вас также будет доступ к бесплатным репетиторам и учебной группе.
Перевести кредиты легко.
Если вы выполните работу и не пройдете, вы получите полный возврат средств.
Окна экзамена гибкие, а лекции можно просматривать по запросу в любом месте.
xf(x)=4×4+ex. 9x=16×3+ex
Вот почему: