Ускорение через радиус: Формула центростремительного ускорения в физике

Глава 7. Вращательное движение. Кинематика и динамика

Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел

(7.1)

В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан – безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.

1) к полному обороту тела (угол поворота – радиан), получим связь угловой скорости и периода вращения

(7.2)

Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.

Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим

(7.3)

Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.

Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна

(7.4)

Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах

(7.5)

Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине

(7.6)

Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.

Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.

Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»).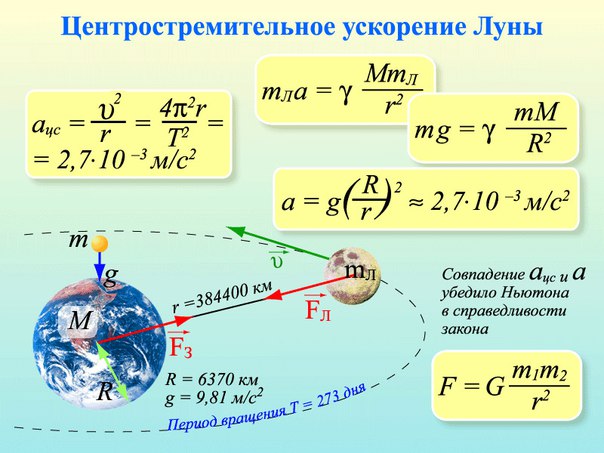 Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (

задача 7.1.1 – ответ 2).

Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем

(правильный ответ – 2).

Применяя определение угловой скорости к колесу (задача 7.1.3), получаем

(правильный ответ 1).

Из формулы (7.2) имеем

(задача 7.1.4 – правильный ответ

4).

Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска

А теперь по формуле (7. 5) для второй точки получаем

(ответ 2).

Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ –

3).

Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно

(ответ 4).

Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи –

1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).

Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).

Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с², получим для равнодействующей =2 Н (ответ 2).

Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1

(ответ 1).

Для сравнения центростремительных ускорений материальных точек в задаче 7. 2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем

(ответ 3).

Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим

(7.5)

Поэтому

(ответ 1).

Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)

где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем

(ответ 2).

Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения

Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства

(ответ 4).

В задаче 7. 2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем

(ответ 3).

В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает

(1)

На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем

Подставляя в эту формулу силу из формулы (1), находим (ответ 2).

В задаче 7. 2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем

где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим

(ответ 3).

Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):

где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно

(задача 7. 2.9 – ответ 1).

Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).

Физические основы механики

Представим себе материальную точку, движущуюся по некоторой криволинейной траектории . Запишем скорость в виде

и заметим, что вектор

— это единичный вектор, касательный к траектории и совпадающий по направлению с вектором скорости. Продифференцируем вектор скорости, записанный в данном представлении, и получим

Мы представили ускорение в виде двух слагаемых. Заметим прежде всего, что слагаемые ортогональны друг другу. Действительно, поскольку вектор — единичный, то

Дифференцируя это скалярное произведение, получаем

то есть

по свойству скалярного произведения.

Таким образом, мы разложили ускорение на сумму двух взаимно ортогональных составляющих, обозначем их и :

Обсудим физический смысл каждого слагаемого. Слагаемое

— это тангенциальное ускорение, которое характеризует быстроту изменения модуля скорости. Эта часть полного ускорения направлена либо по скорости, когда производная dv/dt > 0, то есть движение ускоренное, либо в сторону противоположную скорости, когда эта производная dv/dt < 0, то есть движение замедленное. Если движение равномерное dv/dt = 0, то есть скорость, если и меняется, то лишь по направлению, то тангенциальная часть ускорения равна нулю:

Слагаемое

направлено по нормали к траектории — перпендикулярно касательной к траектории и называется нормальным ускорением. Если тангенциальное ускорение определяет скорость, с которой меняется модуль вектора скорости, то нормальное ускорение определяет скорость, с которой меняется направление вектора скорости.

Рис. 2.10. К определению кривизны траектории

Рассмотрим «достаточно гладкую», в остальном произвольную плоскую криволинейную траекторию. Плоскую, то есть все точки траектории лежат в некоторой плоскости, — исключительно для упрощения выкладок, получаемый в рамках этого предположения, результат годится и для любой «достаточно гладкой» пространственной кривой, чьи точки уложить в одну плоскость невозможно. Последнее обстоятельство мы здесь рассматривать не будем, оно строго доказывается методами аналитической геометрии. Слова «достаточно гладкая» означают, что кривая описывается непрерывной функцией, имеющей непрерывные первую и вторую производные. С точки зрения физических приложений, требование существования непрерывных первых двух производных фактически не является ограничением на форму траектории, так как практически всегда выполнено. Проще говоря, на траектории не должно быть “углов” типа показанного на рисунке 2.11.

Рис. 2.11.

Такую «гладкую» кривую на любом её бесконечно малом участке можно заменить (рис. 2.12) участком окружности некоторого радиуса. Радиус этой окружности, аппроксимирующей траекторию на её бесконечно малом участке в окрестности некоторой точки, принято называть радиусом кривизны траектории в этой точке. Центр этой окружности принято называть центром кривизны траектории в данной точке. Кривизной траектории называется величина C = 1/R. Подчеркнем, что радиус кривизны, как и центр кривизны траектории — её локальные характеристика: каждой точке траектории соответствует свой радиус кривизны и свой центр кривизны. Исключениями являются: 1) окружность, её радиус кривизны во всех её точках один и тот же и равен радиусу окружности, центр кривизны «один на всех» и совпадает с центром окружности, и 2) прямая, для любой точки прямой радиус кривизны бесконечен, а центр кривизны находится в бесконечно удаленной от прямой точке. Это легко понять: давайте увеличивать радиус окружности, чем больше радиус окружности, тем ближе любой её конечный участок к участку прямой. На равнине, лучше всего на пляже, с высоты человеческого роста до горизонта не более пяти километров, — в этих пределах Земля плоская.

Рис. 2.12. К определению радиуса кривизны траектории

Вычислим модуль производной , входящей в выражение для нормального ускорения. Направлен вектор по нормали к траектории к центру к центру кривизны, что поясняет рис. 2.13.

Рис. 2.13. Графическое определение радиуса кривизны траектории

Для этого прежде всего перейдем от дифференцирования по времени к дифференцированию по «пути»: , имеем:

По определению производная кривизне кривой C, а величина ей обратная равна радиусу кривизны кривой R. Собирая всё вместе, для нормального ускорения окончательно получаем:

,

где нормаль перпендикулярна к касательной и всегда направлена к центру кривизны, см. рис. 11.

Приведем некоторое дополнительное пояснение к рисунку 11. Возьмем неподалеку от точки 1 точку 2. Построим в этих точках касательные единичные векторы ₁ и ₂. Перпендикуляры к этим касательным пересекутся в некоторой точке O₂. Заметим, что для кривой, не являющейся окружностью, расстояния R₁ и R₂ будут немного отличаться друг от друга. Если теперь точку 2 приближать к точке 1, пересечение перпендикуляров O₂ будет перемещаться вдоль прямой O₂1 и в пределе окажется в некоторой точке O₁. Расстояния R₁ и R₂ будут стремиться к общему пределу R, равному радиусу кривизны, а точка O₁ и будет центром кривизны для точки 1. Действительно, окружность радиусом R с центром в 0 проходит через точку 1 и касается траектории (так как радиус ортогонален орту ₁). Кроме того, по построению бесконечно близкая точка 2 также лежит на этой окружности. Таким образом, построенная окружность действительно «сливается» с траекторией в точке 1.

Итак, в общем случае ускорение имеет две составляющие — тангенциальную

направленную вдоль касательной и определяющую скорость изменения модуля вектора скорости нормальную

направленную перпендикулярно скорости к центру кривизны траектории и пропорциональную угловой скорости вращения вектора скорости при движении частицы вдоль криволинейной траектории (рис. 2.14).

Рис. 2.14. Тангенциальное и нормальное ускорения при ускоренном криволинейном движении.

Действительно , где и есть угловая скорость вращения вектора скорости .

Полное ускорение

определяется по правилу параллелограмма. Модуль полного ускорения в соответствии с теоремой Пифагора равен

Выпишем без вывода формулы, связывающие радиус кривизны плоской траектории с координатами траектории. Если известна зависимость y = y(x), то

Если же траектория задана в параметрическом виде, x = x(t), y = y(t), то

Пример криволинейного движения с постоянным ускорением (тело, брошенное под углом к горизонту) приведен на следующем рисунке:

Рис. 2.15. Движение тела, брошенного под углом к горизонту

Расчет скорости и ускорений точки в заданный момент времени

Пример решения задачи по определению в заданный момент времени скорости, полного, касательного, нормального ускорений, радиуса кривизны и вида траектории точки по известным уравнениям её движения в координатной форме.

Задача

Даны уравнения движения точки M:

x=(3cos2πt/3)+3 см;
y=(2sin2πt/3)-2 см.

Определить вид траектории и в момент времени t=1 c найти скорость точки, полное, касательное, нормальное ускорения и радиус кривизны траектории в данной точке.

Другие примеры решений >
Помощь с решением задач >

Решение

Координатный способ задания движения – это траектория движения точки в параметрической форме.

Исключим параметр t:

cos2πt/3=(x-3)/3,
sin2πt/3=(y+2)/2,
(cos2πt/3)²+(sin2πt/3)²=1=((x-3)²/3²)+((y+2)²/2²),
((x-3)²/3²)+((y+2)²/2²)=1

получили эллипс с полуосями 3 см и 2 см (рисунок 1.7).

Наш видеоурок по теме:

В момент времени t=1 c координаты точки:

x=(3cos2π∙1/3)+3=3cos120^o+3=3∙(-1/2)+3=1,5 см;
y=(2sin2π∙1/3)-2=2sin120^o-2=2∙(3^1/2/2)-2=-0,27 см.

Рисунок 1.7

Движение начинается из точки A:

x_t=0=(3cos2π∙0/3)+3=3+3=6 см;
y_t=0=(2sin2π∙0/3)-2=0-2=-2 см.

Учитывая графики изменения функций синуса и косинуса, можно утверждать, что точка M движется по эллипсу из точки A против хода часовой стрелки.

Скорость точки:

Vx=dx/dt=d((3cos2πt/3)+3)/dt=

=3∙(-sin2πt/3)∙2π/3+0=-2πsin2πt/3 см/с;
Vy=dy/dt=d((2sin2πt/3)-2)/dt=

=2∙(cos2πt/3)∙2π/3-0=(4/3)πcos2πt/3 см/с.

В момент времени t=1:

Направление вектора скорости определяется направляющими косинусами:

Таким образом, вектор скорости определен и по величине и по направлению (рисунок 1.8).

Ускорение точки:

Для t=1 c:

Полное ускорение:

Рисунок 1.8

Направление вектора ускорения:

Результаты расчетов показаны на рисунке 1.8.

Касательное ускорение определяется по формуле (1.11):

Нормальное ускорение можно определить либо из формулы (1.5), либо из формулы (1.12). По формуле (1.12) получим:

Результат может быть проверен (см. выше расчет):

Радиус кривизны траектории в точке M:

ρ=V²/a_n=5,83²/9,44=3,60 см.

Другие примеры решения задач >>

. Определите нормальное ускорение и радиус кривизны траектории тела, движущейся с ускорением

Номера 79 б и 89 б пожалуйста

Номера 59 б и 69 б пожалуйста

Помогите с физикойВелосипедист и автомобиль подъезжают по перпендикулярным дорогам к перекрёстку. Когда велосипедист проезжал перекрёсток, автомобиль … ещё не доехал до перекрёстка 100 м. Какое время после этого пройдёт до момента, когда велосипедист и автомобиль окажутся на минимальном расстоянии, если их скорости постоянны и равны V1=7 м/с у велосипедиста и V2=24 м/с у автомобиля? Ответ запишите в секундах, округлив до сотых.​

Два человека стоят на расстоянии h2 и h3 от стенки и l —друг от друга. Один из них сказал слово, другой услышал конец слова, совпавшее с началом эха э … того же слова. Скорость звука c. Определите длительность звучания слова.

При температуре 10 °С относительная влажность воздуха была равна 72 %. Используя данные таблицы, определи, на сколько уменьшилась или увеличилась отно … сительная влажность воздуха, если температуру повысили до 20 °С.Ответ (округли до десятых): относительная влажность воздуха на %.t, °С p, кПа ρ0, гм310 1,23 9,411 1,33 1012 1,4 10,713 1,49 11,414 1,6 12,115 1,71 12,816 1,81 13,617 1,93 14,518 2,07 15,419 2,2 16,320 2,33 17,3​

Определи массу паров воды в воздухе актового зала объёмом 52 м³ при температуре воздуха 24 °С и относительной влажности 62 %. Плотность насыщенного па … ра равна 17,3 гм3. Ответ (округли до десятых): г. ​

8 класс. почему в решении задачи два времени одинаковые?сайт: http://fizportal.ru/kinematics-problem-1-1-6задача: Спортсмены бегут колонной длины l со … скоростью v. Навстречу бежит тренер со скоростью uрешение:Мысленно остановим колону, тогда тренер кроме своей скорости будет иметь скорость колонны, направленную в противоположную сторону. С этой относительной скоростью v+u он в течение времениt=lv+u,пробежит вдоль колонны и сравняется с хвостом. Голова колоны, развернувшись, будет двигаться с относительной скоростью v−u и через времяt=l/v−uгде l/ – длина новой «колоны» после обгона. Тогдаl/v−u=lv+uи длина новой колонныl/=v−uv+ul.Ответ: когда все спортсмены развернуться длина новой колоны будет равна l/=v−uv+ul

Літак піднімається вгору з швидкістю v = 700 км/год і за t = 4 хв досягає висоти h = 4 км. З якою швидкістю рухається по поверхні Землі тінь від літ … ака, якщо Сонце в зеніті?

Помогите решить задачу по кинематике: Из города А выехали с одинаковыми скоростями два автомобиля, второй через 12 минут после первого. Они поочередно … , с интервалом в 14 минут, обогнали одного и того же велосипедиста. Во сколько раз скорость автомобилей больше скорости велосипедиста? (Кирик – с/р и к/р, 9 класс)

На гладкой горизонтальной поверхности покоится уголок массы M, который с помощью лёгкой нити и двух блоков соединён со стенкой и бруском массы m (см. … рисунок). Брусок касается внут- ренней поверхности уголка. Нити, перекинутые через блок, прикреп- лённый к стене, натянуты горизонтально. Вначале систему удерживают в состоянии покоя, а затем отпуска- ют. Найдите ускорение a уголка. Блоки лёгкие. Трение в системе отсутствует.

Радиус кривизны траектории

В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из  задач представляет собой целый набор, поэтому неясностей не должно остаться.

Задача 1. Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:

   

Откуда :

   

То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.

К задаче 1

Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому

   

Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и . Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:

   

Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:

   

   

   

Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :

   

Определим полную скорость тела в момент времени :

   

Угол наклона вектора скорости к горизонту в этот момент равен:

   

А можно было сразу и косинус найти:

   

Тогда искомый радиус кривизны траектории равен:

   

Ответ: м, м, м.

 

Задача 2. Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б).
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:

   

Определим теперь радиус кривизны в вершине:

   

По условию :

   

   

   

   

   

б) Мы уже определили , осталась максимальная высота подъема.

   

Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:

   

   

   

Приравниваем и :

   

Откуда .

   

   

   

Ответ: а) , б) .

Движение по окружности | LAMPA

Найдем угловую скорость. Известно, что ω=φt\omega=\frac{\varphi}{t}ω=tφ​. В качестве угла φ\varphiφ можно взять полный оборот, то есть угол 2π2\pi2π радиан, а в качестве времени — время одного полного оборота, то есть период TTT. Поэтому

ω=2πT,\omega=\frac{2\pi}{T}{,}ω=T2π​,ω=2πT=2π⋅1T=2πν.\omega=\frac{2\pi}{T}=2\pi\cdot\frac{1}{T}=2\pi\nu{.}ω=T2π​=2π⋅T1​=2πν.

Эти формулы мы тоже рекомендуем запомнить. Это будет полезно.

Единица измерения угловой скорости [ω]=радс[\omega]=\frac{\text{рад}}{\text{с}}[ω]=срад​.

Оказывается, что линейная скорость VVV и угловая скорость ω\omegaω связаны друг с другом. Рассмотрим пример из жизни. На детских площадках наверняка все видели карусель. Представьте, что карусель вращается. Вы сами сидите на сиденьи этой карусели, а ваш друг не стал сидеть на сиденьи, а “пролез” поближе к центру карусели.

Поскольку каждый из вас поворачивается вокруг карусели на один и тот же угол за то же время, то угловые скорости у вас равны: ωвы=ωдруг\omega_{вы}=\omega_{друг}ωвы​=ωдруг​. Но вот линейные скорости у вас не равны: Vвы≠VдругV_{вы}\neq V_{друг}Vвы​≠Vдруг​. Это нам подсказывает наш жизненный опыт. Тот, кто сидит поближе, двигается медленнее.

Чем ближе к центру находится тело — тем меньше его линейная скорость VVV. И наоборот: чем дальше от центра (чем больше расстояние от центра), тем больше скорость VVV.

Линейная скорость VVV также будет больше и в том случае, если будет больше быстрота поворота вокруг оси, то есть угловая скорость ω\omegaω.

По-простому: чем дальше сидишь от оси (чем больше RRR) и чем быстрее вращается тело (чем больше ω\omegaω), тем больше линейная скорость VVV.

Линейную скорость VVV можно пойти по формуле:

V=ω⋅R.V=\omega\cdot R{.}V=ω⋅R.

Эту формулу можно вывести строго. Возьмем уже известные нам формулы:

V=2πR⋅νV=2\pi R\cdot \nuV=2πR⋅ν и ω=2π⋅ν\omega=2\pi\cdot \nuω=2π⋅ν.

Из них видно, что в первой формуле вместо 2πν2\pi\nu2πν можно подставить ω\omegaω:

V=2πR⋅ν=2πνR=(2πν)⋅R=ω⋅RV=2\pi R\cdot \nu=2\pi\nu R=(2\pi\nu)\cdot R=\omega\cdot RV=2πR⋅ν=2πνR=(2πν)⋅R=ω⋅R.

Мы получили формулу V=ω⋅RV=\omega\cdot RV=ω⋅R.

Расчет RCF-RPM on-line

Расчет RCF-RPM on-line

Он-лайн калькулятор может быть использован для:

• расчета параметра RPM (обороты в минуту) при работе по протоколам к нашим наборам или методикам, приведенным в статьях;
• указания универсальной величины центрифугирования RCF (g) в своих публикациях.

Отличие

RCF от RPM

В статьях рекомендуется указывать универсальную величину – относительное ускорение центрифуги (RCF, Relative Centrifugal Force), которая измеряется в g. Это дает возможность воспроизвести методику в любой лаборатории. Если установить одно и то же значение RCF на разных центрифугах, они будут осаждать образец с одинаковой эффективностью.

Некоторые модели центрифуг не позволяют задать ускорение RCF, на них возможно установить только частоту вращения (RPM, Rotation Per Minute), которая измеряется в оборотах в минуту. RPM характеризует условия центрифугирования только на выбранной модели центрифуги: если установить одно и то же значение RPM на центрифугах с разными роторами, они будут осаждать образец с разной эффективностью.

RCF, RPM и радиус ротора центрифуги связаны формулой:

, где:

RPM – частота вращения в оборотах в минуту,
RCF – относительное ускорение центрифуги в g,
r – радиус ротора в сантиметрах.

Из этой формулы следует два вывода:

• Чем больше радиус ротора, тем меньше нужно оборотов в минуту, чтобы поддерживать то же относительное ускорение. Информацию о роторе указывают в руководстве по эксплуатации центрифуги.
• Любое изменение частоты вращения сильно влияет на эффективность центрифугирования, поскольку RCF прямо пропорционально квадрату RPM.

Перевести

g в об/мин или наоборот

Радиус ротора (см):

Введите радиус ротора центрифуги в сантиметрах.

RCF (g):

При заполнении поля RCF (g) или RPM (об/мин),
второе значение рассчитается автоматически.

Угловое ускорение | Физика

Цели обучения

К концу этого раздела вы сможете:

• Опишите равномерное круговое движение.
• Объясните неравномерное круговое движение.
• Вычислить угловое ускорение объекта.
• Обратите внимание на связь между линейным и угловым ускорением.

Равномерное круговое движение и гравитация обсуждаются только равномерное круговое движение, то есть движение по кругу с постоянной скоростью и, следовательно, с постоянной угловой скоростью.Напомним, угловая скорость ω определялась как скорость изменения угла θ во времени:

[латекс] \ omega = \ frac {\ Delta \ theta} {\ Delta t} \\ [/ latex]

, где θ – это угол поворота, как показано на Рисунке 1. Отношение между угловой скоростью ω и линейной скоростью v также было определено в Угол поворота и Угловая скорость как

v = rω

или

[латекс] \ omega = \ frac {v} {r} \\ [/ латекс]

, где r – радиус кривизны, также видно на рисунке 1.Согласно соглашению о знаках, направление против часовой стрелки считается положительным направлением, а направление по часовой стрелке – отрицательным

.

Рис. 1. На этом рисунке показано равномерное круговое движение и некоторые из его определенных величин.

Угловая скорость непостоянна, когда фигуристка тянет на руках, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается, когда он выключен. Во всех этих случаях имеется угловое ускорение , при котором изменяется ω .Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение α определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается следующим образом:

[латекс] \ alpha = \ frac {\ Delta \ omega} {\ Delta t} \\ [/ latex],

, где Δ ω – это изменение угловой скорости , а Δ t – изменение во времени. Единицы углового ускорения: (рад / с) / с, или рад / с ² . Если ω увеличивается, то α положительно.Если ω уменьшается, то α отрицательно.

Пример 1. Расчет углового ускорения и замедления велосипедного колеса

Предположим, что подросток кладет велосипед на спину и запускает вращение заднего колеса от состояния покоя до конечной угловой скорости 250 об / мин за 5,00 с. (а) Рассчитайте угловое ускорение в рад / с ² . (b) Если теперь она нажимает на тормоза, вызывая угловое ускорение -87,3 рад / с ² , сколько времени потребуется колесу, чтобы остановиться?

Стратегия для (а)

Угловое ускорение можно найти непосредственно из его определения в [latex] \ alpha = \ frac {\ Delta \ omega} {\ Delta t} \\ [/ latex], поскольку даны окончательная угловая скорость и время.Мы видим, что Δ ω составляет 250 об / мин, а Δ t составляет 5,00 с.

Решение для (а)

Вводя известную информацию в определение углового ускорения, получаем

[латекс] \ begin {array} {lll} \ alpha & = & \ frac {\ Delta \ omega} {\ Delta t} \\ & = & \ frac {\ text {250 об / мин}} {\ text {5.00 s}} \ text {.} \ end {array} \\ [/ latex]

Поскольку Δ ω выражается в оборотах в минуту (об / мин), и нам нужны стандартные единицы рад / с ² для углового ускорения, нам нужно преобразовать Δ ω из об / мин в рад / с:

[латекс] \ begin {array} {c} \ Delta {\ omega} & = & 250 \ frac {\ text {rev}} {\ text {min}} \ cdot \ frac {2 \ pi \ text {rad }} {\ text {rev}} \ cdot \ frac {1 \ text {min}} {60 \ text {sec}} \\ & = & 26.{2} \ text {.} \ End {array} \\ [/ latex]

Стратегия для (b)

В этой части мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение углового ускорения и решив для Δ t , что дает

[латекс] \ Delta t = \ frac {\ Delta \ omega} {\ alpha} \\ [/ latex].

Решение для (b)

Здесь угловая скорость уменьшается с 26,2 рад / с (250 об / мин) до нуля, так что Δ ω составляет –26.{2}} \\ & = & \ text {0,300 с.} \ End {array} \\ [/ latex]

Обсуждение

Обратите внимание, что угловое ускорение, когда девушка вращает колесо, небольшое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение велико и отрицательно. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит сильное замедление – изменение скорости велико за короткий промежуток времени.

Если бы велосипед в предыдущем примере был на колесах, а не перевернут, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорение. При круговом движении линейное ускорение составляет по касательной к окружности в интересующей точке, как показано на рисунке 2. Таким образом, линейное ускорение называется касательным ускорением a _t .

Рис. 2. При круговом движении линейное ускорение a возникает по мере изменения величины скорости: a касается движения. В контексте кругового движения линейное ускорение также называется тангенциальным ускорением a _t .

Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Из «Равномерного кругового движения и гравитации» мы знаем, что центростремительное ускорение при круговом движении, a _c , относится к изменениям направления скорости, но не ее величины.Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рисунке 3. Таким образом, a _t и a _c перпендикулярны и независимы друг от друга. Касательное ускорение a _t напрямую связано с угловым ускорением α и связано с увеличением или уменьшением скорости, но не с ее направлением.

Рис. 3. Центростремительное ускорение a _c возникает при изменении направления скорости; он перпендикулярен круговому движению.Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.

Теперь мы можем найти точное соотношение между линейным ускорением a _t и угловым ускорением α . Поскольку линейное ускорение пропорционально изменению величины скорости, оно определено (как это было в одномерной кинематике) равным

.

[латекс] {a} _ {\ text {t}} = \ frac {\ Delta v} {\ Delta t} \\ [/ latex].

Для кругового движения обратите внимание, что v = rω , так что

[латекс] {a} _ {\ text {t}} = \ frac {\ Delta \ left (\ mathrm {r \ omega} \ right)} {\ Delta t} \\ [/ latex].

Радиус r постоянен для кругового движения, поэтому Δ ( rω ) = r (Δ ω ). Таким образом,

[латекс] {a} _ {\ text {t}} = r \ frac {\ Delta \ omega} {\ Delta t} \\ [/ latex].

По определению, [латекс] \ alpha = \ frac {\ Delta \ omega} {\ Delta t} \\ [/ latex]. Таким образом,

a _t = rα ,

или

[латекс] \ alpha = \ frac {{a} _ {\ text {t}}} {r} \\ [/ latex]

Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны.Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес автомобиля, тем больше ускорение автомобиля. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение для данного углового ускорения α .

Пример 2. Расчет углового ускорения колеса мотоцикла

Мощный мотоцикл может разгоняться от 0 до 30.0 м / с (около 108 км / ч) за 4,20 с. Каково угловое ускорение его колес радиусом 0,320 м? (См. Рисунок 4.)

Рис. 4. Линейное ускорение мотоцикла сопровождается угловым ускорением его колес.

Стратегия

Нам дана информация о линейных скоростях мотоцикла. Таким образом, мы можем найти его линейное ускорение a _t . Затем выражение [latex] \ alpha = \ frac {{a} _ {\ text {t}}} {r} \\ [/ latex] может использоваться для определения углового ускорения.{2} \ end {array} \\ [/ latex].

Обсуждение

Радианы безразмерны и присутствуют в любом соотношении между угловыми и линейными величинами.

Итак, мы определили три вращательные величины – θ, ω и α . Эти величины аналогичны трансляционным величинам x, v и a . В таблице 1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.

Таблица 1. Вращательные и поступательные величины

ротационный	Трансляционный	Отношения
θ	x	[латекс] \ theta = \ frac {x} {r} \\ [/ latex]
ω	в	[латекс] \ omega = \ frac {v} {r} \\ [/ латекс]
α	а	[латекс] \ alpha = \ frac {{a} _ {t}} {r} \\ [/ latex]

Установление соединений: практический эксперимент

Сядьте, поставив ноги на землю, на вращающийся стул.Поднимите одну ногу так, чтобы она была разогнута (выпрямлена). Используя другую ногу, начните вращаться, отталкиваясь от земли. Прекратите толкать землю ногой, но позвольте стулу вращаться. От исходной точки, с которой вы начали, нарисуйте угол, угловую скорость и угловое ускорение вашей ноги как функцию времени в виде трех отдельных графиков. Оцените величину этих величин.

Проверьте свое понимание

Угловое ускорение – это вектор, имеющий как величину, так и направление.Как обозначить его величину и направление? Проиллюстрируйте на примере.

Решение

Величина углового ускорения составляет α , а ее наиболее распространенные единицы – рад / с ² . Направление углового ускорения вдоль фиксированной оси обозначается знаком + или a -, так же как направление линейного ускорения в одном измерении обозначается знаком + или a -. Например, представьте, что гимнастка делает сальто вперед. Ее угловой момент был бы параллелен ковру слева от нее.Величина ее углового ускорения будет пропорциональна ее угловой скорости (скорости вращения) и ее моменту инерции относительно оси вращения.

Исследования PhET: Ladybug Revolution

Присоединяйтесь к божьей коровке и исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с координатами x, y, скоростью и ускорением жука, используя векторы или графики.

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

• Равномерное круговое движение – это движение с постоянной угловой скоростью [latex] \ omega = \ frac {\ Delta \ theta} {\ Delta t} \\ [/ latex].
• При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т.е. угловое ускорение) равна [latex] \ alpha = \ frac {\ Delta \ omega} {\ Delta t} \\ [/ латекс].
• Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, заданному как [latex] {a} _ {\ text {t}} = \ frac {\ Delta v} {\ Delta t} \\ [ /латекс].
• Для кругового движения обратите внимание, что [latex] v = \ mathrm {r \ omega} [/ latex], так что

  [латекс] {a} _ {\ mathrm {\ text {t}}} = \ frac {\ Delta \ left (\ mathrm {r \ omega} \ right)} {\ Delta t} \\ [/ latex] .

• Радиус r постоянен для кругового движения, поэтому [latex] \ mathrm {\ Delta} \ left (\ mathrm {r \ omega} \ right) = r \ Delta \ omega \\ [/ latex]. Таким образом,

  [латекс] {a} _ {\ text {t}} = r \ frac {\ Delta \ omega} {\ Delta t} \\ [/ latex].

• По определению [латекс] \ Delta \ omega / \ Delta t = \ alpha \\ [/ latex].Таким образом,

  [латекс] {a} _ {\ text {t}} = \ mathrm {r \ alpha} \\ [/ latex]

  или

  [латекс] \ alpha = \ frac {{a} _ {\ text {t}}} {r} \\ [/ latex].

Концептуальные вопросы

1. Между вращательными и поступательными физическими величинами существуют аналогии. Определите вращательный член, аналогичный каждому из следующих: ускорение, сила, масса, работа, поступательная кинетическая энергия, линейный импульс, импульс.

2. Объясните, почему центростремительное ускорение меняет направление скорости при круговом движении, но не его величину.

3. При круговом движении тангенциальное ускорение может изменять величину скорости, но не ее направление. Поясните свой ответ.

4. Предположим, что блюдо стоит на краю вращающейся пластины микроволновой печи. Испытывает ли она ненулевое тангенциальное ускорение, центростремительное ускорение или и то, и другое, когда: а) пластина начинает вращаться? (б) Пластина вращается с постоянной угловой скоростью? (c) Пластина замедляется до остановки?

Задачи и упражнения

1.На пике торнадо имеет диаметр 60,0 м и скорость ветра 500 км / ч. Какова его угловая скорость в оборотах в секунду?

2. Integrated Concepts Ультрацентрифуга ускоряется от состояния покоя до 100 000 об / мин за 2,00 мин. а) Каково его угловое ускорение в рад / с ² ? б) Каково тангенциальное ускорение точки на расстоянии 9,50 см от оси вращения? (c) Каково радиальное ускорение в м / с ² и кратное g этой точки при полных оборотах в минуту?

3. Integrated Concepts У вас есть точильный камень (диск) весом 90,0 кг, радиусом 0,340 м и вращающимся со скоростью 90,0 об / мин, и вы прижимаете к нему стальной топор с радиальной силой 20,0 Н. (a) Предполагая, что кинетический коэффициент трения между сталью и камнем равен 0,20, рассчитайте угловое ускорение точильного камня. б) Сколько оборотов сделает камень, прежде чем остановится?

4. Необоснованные результаты Вам говорят, что баскетболист вращает мяч с угловым ускорением 100 рад / с ² .(а) Какова конечная угловая скорость мяча, если мяч стартует из состояния покоя и ускорение длится 2,00 с? б) Что неразумного в результате? (c) Какие посылки необоснованны или непоследовательны?

Глоссарий

угловое ускорение:

Скорость изменения угловой скорости во времени

изменение угловой скорости:

разница между конечным и начальным значениями угловой скорости

тангенциальное ускорение

ускорение в направлении, касательном к окружности в интересующей точке при круговом движении

Избранные решения проблем и упражнения

1. ω = 0,737 об / с

3. (а) −0.26 рад / с ² (б) 27 об

4.4 Равномерное круговое движение – Университетская физика, том 1

Цели обучения

К концу этого раздела вы сможете:

• Найдите центростремительное ускорение объекта, движущегося по круговой траектории.
• Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.
• Объясните разницу между центростремительным ускорением и тангенциальным ускорением, возникающим в результате неравномерного кругового движения.
• Оцените центростремительное и тангенциальное ускорение при неравномерном круговом движении и найдите вектор полного ускорения.

Равномерное круговое движение – это особый тип движения, при котором объект движется по кругу с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение.Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах действительно ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение в терминах векторов.

Центростремительное ускорение

В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность.В этом случае вектор скорости меняется, или

Это показано на (Рисунок). Поскольку частица движется против часовой стрелки во времени

по круговой траектории, его вектор положения перемещается из

С

по

Вектор скорости имеет постоянную величину и касается пути, поскольку он изменяется от

.

С

по

только меняет направление.Поскольку вектор скорости

перпендикулярно вектору положения

треугольников, образованных векторами положения и

и векторы скорости и

похожи. Кроме того, с

и

два равнобедренных треугольника. Из этих фактов мы можем сделать утверждение

или

Рисунок 4.18 (a) Частица движется по кругу с постоянной скоростью, временами имея векторы положения и скорости.

и

(b) Векторы скорости, образующие треугольник. Два треугольника на рисунке похожи. Вектор

указывает на центр круга в пределах

Мы можем найти величину ускорения от

Направление ускорения также можно найти, отметив, что как

и, следовательно,

приближаются к нулю, вектор

приближается к направлению, перпендикулярному

В пределе

перпендикулярно

с

касается окружности, ускорение

указывает на центр круга.Таким образом, частица, движущаяся по кругу с постоянной скоростью, имеет ускорение с величиной

.

Направление вектора ускорения – к центру круга ((Рисунок)). Это радиальное ускорение и называется центростремительным ускорением , поэтому мы даем ему индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (означает искать ») и, таким образом, принимает значение« поиск центра ».”

Рис. 4.19. Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении. Также показан вектор скорости, касающийся окружности.

Давайте рассмотрим несколько примеров, которые иллюстрируют относительные величины скорости, радиуса и центростремительного ускорения.

Пример

Создание ускорения 1

g

Самолет летит со скоростью 134,1 м / с по прямой и делает разворот по круговой траектории на уровне земли.Каким должен быть радиус окружности, чтобы вызвать центростремительное ускорение 1 g для пилота и самолета по направлению к центру круговой траектории?

Стратегия

Учитывая скорость струи, мы можем найти радиус окружности в выражении для центростремительного ускорения.

Решение

Установите центростремительное ускорение равным ускорению свободного падения:

Решая для радиуса, находим

Значение

Чтобы создать у пилота большее ускорение, чем g , струе придется либо уменьшить радиус своей круговой траектории, либо увеличить скорость на существующей траектории, либо и то, и другое.

Проверьте свое понимание

Радиус маховика 20,0 см. Какова скорость точки на краю маховика, если она испытывает центростремительное ускорение

?

[показывать-ответ q = ”fs-id116516

09 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id116516

09 ″]

134,0 см / с

[/ hidden-answer]

Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны круговой траектории.Типичные центростремительные ускорения приведены в следующей таблице.

Типичное центростремительное ускорение

Объект	Центростремительное ускорение (м / с 2 или коэффициент g )
Земля вокруг Солнца
Луна вокруг Земли
Спутник на геостационарной орбите	0.233
Внешний край компакт-диска при воспроизведении
Струя в бочке ролика	(2–3 г )
Американские горки	(5 г )
Электрон, вращающийся вокруг протона в простой модели атома Бора

Уравнения движения для равномерного кругового движения

Частица, совершающая круговое движение, может быть описана ее вектором положения

(рисунок) показывает частицу, совершающую круговое движение против часовой стрелки.Когда частица движется по окружности, ее вектор положения выметает угол

с осью x- . Вектор

образующий угол

с осью x- показан с его компонентами вдоль осей x и y . Величина вектора положения

.

и также является радиусом круга, так что с точки зрения его составляющих

Здесь,

– это константа, называемая угловой частотой частицы.Угловая частота измеряется в радианах (рад) в секунду и представляет собой просто количество радианов угловой меры, через которую проходит частица за секунду. Угол

, которое вектор положения имеет в любой конкретный момент времени, равен

.

.

Если T – это период движения или время для завершения одного оборота (

рад), затем

Рис. 4.20. Вектор положения частицы, движущейся по кругу, с ее компонентами по осям x и y.Частица движется против часовой стрелки. Угол

– угловая частота

в радианах в секунду, умноженное на t.

Скорость и ускорение можно получить из функции положения путем дифференцирования:

Из (Рисунок) можно показать, что вектор скорости тангенциальный к окружности в месте нахождения частицы с величиной

.

Аналогично, вектор ускорения находится путем дифференцирования скорости:

Из этого уравнения мы видим, что вектор ускорения имеет величину

.

и направлен против вектора положения, к началу координат, потому что

Пример

Круговое движение протона

Протон имеет скорость

и движется по окружности в плоскости xy радиуса r = 0.175 м. Каково его положение в плоскости xy в момент времени

?

При t = 0 положение протона

и вращается против часовой стрелки. Набросайте траекторию.

Решение

По приведенным данным протон имеет период и угловую частоту:

Положение частицы в

с A = 0.175 м –

Из этого результата мы видим, что протон расположен немного ниже оси x . Это показано на (Рисунок).

Рис. 4.21 Вектор положения протона на

Показана траектория протона. Угол, под которым протон движется по окружности, составляет 5,712 рад, что немного меньше одного полного оборота.

Значение

Мы выбрали начальное положение частицы на оси x –.Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас было бы другое конечное положение при t = 200 нс.

Неравномерное круговое движение

Круговое движение не обязательно должно иметь постоянную скорость. Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.

При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а круг имеет фиксированный радиус.Если скорость частицы тоже меняется, то мы вводим дополнительное ускорение в направлении, касательном к окружности. Такое ускорение происходит в точке на вершине, которая изменяет скорость вращения, или в любом ускоряющем роторе. В работе «Векторы смещения и скорости» мы показали, что центростремительное ускорение – это скорость изменения направления вектора скорости во времени. Если скорость частицы изменяется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:

Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения направлено радиально внутрь к центру окружности.Таким образом, частица, движущаяся по кругу с тангенциальным ускорением, имеет общее ускорение , которое является векторной суммой центростремительного и тангенциального ускорений:

Векторы ускорения показаны на (Рисунок). Обратите внимание, что два вектора ускорения

и

перпендикулярны друг другу, при этом

в радиальном направлении и

в тангенциальном направлении.Общее ускорение

точки под углом

и

Рис. 4.22. Центростремительное ускорение указывает на центр круга. Тангенциальное ускорение является касательным к окружности в месте расположения частицы. Общее ускорение – это векторная сумма тангенциального и центростремительного ускорений, которые перпендикулярны.

Пример

Полное ускорение при круговом движении

Частица движется по окружности радиуса r = 2.0 мес. В интервале времени от t = 1,5 с до t = 4,0 с его скорость изменяется со временем согласно

.

Каково полное ускорение частицы при t = 2,0 с?

Стратегия

Нам даны скорость частицы и радиус круга, поэтому мы можем легко вычислить центростремительное ускорение. Направление центростремительного ускорения – к центру круга. Мы находим величину тангенциального ускорения, взяв производную по времени

.

, используя (рисунок) и оценив его как t = 2.0 с. Мы используем это и величину центростремительного ускорения, чтобы найти полное ускорение.

Решение

Центростремительное ускорение

направлен к центру круга. Касательное ускорение

Суммарное ускорение

и

от касательной к окружности. См. (Рисунок).

Рис. 4.23 Векторы тангенциального и центростремительного ускорения.Чистое ускорение

– это векторная сумма двух ускорений.

Значение

Направления центростремительного и тангенциального ускорений можно описать более удобно в терминах полярной системы координат с единичными векторами в радиальном и тангенциальном направлениях. Эта система координат, которая используется для движения по криволинейным траекториям, подробно обсуждается далее в книге.

Сводка

• Равномерное круговое движение – это движение по окружности с постоянной скоростью.
• Центростремительное ускорение

  – это ускорение, которое должно иметь частица, чтобы двигаться по круговой траектории. Центростремительное ускорение всегда направлено к центру вращения и имеет величину

  .

• Неравномерное круговое движение возникает, когда существует тангенциальное ускорение объекта, выполняющего круговое движение, так что скорость объекта изменяется. Это ускорение называется тангенциальным ускорением.

  Величина тангенциального ускорения – это скорость изменения величины скорости во времени.Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Общее ускорение – это векторная сумма тангенциального и центростремительного ускорений.

• Объект, выполняющий равномерное круговое движение, можно описать уравнениями движения. Вектор положения объекта

  , где A – величина

  .

  , который также является радиусом круга, и

  – угловая частота.

Концептуальные вопросы

Может ли центростремительное ускорение изменить скорость частицы, совершающей круговое движение?

Может ли тангенциальное ускорение изменить скорость частицы, совершающей круговое движение?

[show-answer q = ”fs-id11651623 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id11651623 ″]

да

[/ hidden-answer]

Проблемы

Маховик вращается со скоростью 30 об / с.Каков полный угол в радианах, на который точка на маховике поворачивается за 40 с?

Частица движется по кругу радиусом 10 м с постоянной скоростью 20 м / с. Какая величина ускорения?

[показывать-ответ q = ”fs-id11651685 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id11651685 ″]

[/ hidden-answer]

Кэм Ньютон из Carolina Panthers бросает идеальную футбольную спираль на 8.0 об / с. Радиус профессионального футбола составляет 8,5 см по середине короткой стороны. Что такое центростремительное ускорение шнурков на футбольном мяче?

Аттракцион ярмарки вращает своих пассажиров внутри контейнера в форме летающей тарелки. Если горизонтальный круговой путь, по которому следуют гонщики, имеет радиус 8,00 м, при скольких оборотах в минуту гонщики подвергаются центростремительному ускорению, равному ускорению силы тяжести?

[показывать-ответ q = ”fs-id11651661 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id11651661 ″]

, что равно

[/ hidden-answer]

Бегун, участвующий в забеге на 200 м, должен обойти конец трассы, имеющей дугу окружности с радиусом кривизны 30.0 мес. Бегун начинает забег с постоянной скоростью. Если она преодолевает 200-метровый рывок за 23,2 с и бежит с постоянной скоростью на протяжении всей гонки, каково ее центростремительное ускорение при прохождении криволинейной части трассы?

Каково ускорение Венеры по направлению к Солнцу, если принять круговую орбиту?

[показывать-ответ q = ”fs-id116516

11 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id116516

11 ″]

Венера находится на расстоянии 108,2 миллиона км от Солнца и имеет период обращения 0.6152 г.

[/ hidden-answer]

Экспериментальная реактивная ракета движется вокруг Земли вдоль экватора прямо над ее поверхностью. С какой скоростью должна двигаться струя, если величина ее ускорения составляет g ?

Вентилятор вращается с постоянной скоростью 360,0 об / мин. Какова величина ускорения точки на одной из лопастей на расстоянии 10,0 см от оси вращения?

[показывать-ответ q = ”fs-id1165168934870 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165168934870 ″]

[/ hidden-answer]

Точка, расположенная на секундной стрелке больших часов, имеет радиальное ускорение

.

Как далеко находится точка от оси вращения секундной стрелки?

Глоссарий

угловая частота

скорость изменения угла, с которым объект движется по круговой траектории

центростремительное ускорение

Компонент ускорения объекта, движущегося по окружности, радиально направленной внутрь к центру окружности

тангенциальное ускорение

Величина

– это временная скорость изменения скорости.Его направление касается окружности.

общее ускорение

векторная сумма центростремительного и тангенциального ускорений

Центростремительная сила и ускорение – AP Physics 1

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Резюме уравнения для величины центростремительной силы

Фелиция Черри
Менеджер по продуктам в области физических наук, физики и наук о Земле

Практически каждый урок физики изучает круговое движение.Студенты тратят много времени на изучение основной формулы и решение задач. В этой статье описывается вывод уравнения для центростремительной силы на основе алгебры.

Вывод уравнения

Это первое уравнение должно быть вам знакомо. Это, вероятно, наиболее часто используемое уравнение в любом первом курсе физики и способ, которым большинство студентов-физиков учатся выражать Второй закон Ньютона:

Уравнение 1.

Чистая сила, действующая на объект, равна массе объекта, умноженной на ускорение объекта. Уравнение 2 применяет этот принцип к объектам, движущимся с равномерным круговым движением, когда объект движется с постоянной скоростью, но продолжает менять направление, так что он движется по круговой траектории. На объект, движущийся в равномерном круговом движении, действует сила, направленная в центр круговой траектории, называемая центростремительной силой . Уравнение 2 повторяет Уравнение 1 для объектов, движущихся с равномерным круговым движением. F _c обозначает центростремительную силу, а _c обозначает центростремительное ускорение.

Уравнение 2.

Уравнение для величины центростремительной силы имеет следующий вид:

Уравнение 3.

При описании линейного движения ускорение обычно описывается как изменение скорости, деленное на изменение во времени. Математически ускорение можно выразить так:

Уравнение 4.

Из Уравнение 2 и Уравнение 3 , центростремительное ускорение или _c , можно выразить как:

Уравнение 5.

В следующем разделе будет объяснено, почему центростремительное ускорение равно квадрату скорости, деленному на радиус, как записано в уравнении 5 .

В следующем списке определены символы, используемые в этом разделе:
F = величина силы (в ньютонах, Н)
F _c = центростремительная сила, направленная в центр круговой траектории (Н )
м = масса объекта, движущегося по круговой траектории (в килограммах, кг)
v = тангенциальная скорость объекта (метры в секунду, м / с)
v ₁ = начальная скорость (метры в секунду, м / с) (в некоторых текстах это vi или v ₀ )
v ₂ = конечная скорость (метры в секунду, м / с) (в некоторых текстах это v _f )
r = радиус круговой траектории (в метрах, м)
a = величина ускорения (в метрах в секунду в квадрате, м / с ² )
a _c = центростремительное ускорение, направленное в центр круговой траектории (м / с ² ) 9117 9 Δ обозначает изменение, например Δv = ( v ₂ – v ₁ )

Примечание: Этот вывод анализирует векторы, описывающие движение объекта, движущегося в равномерном круговом движении, и использует аналогичные треугольники, чтобы связать скорость объекта с радиусом круговой траектории.

Почему центростремительное ускорение равно квадрату скорости, разделенному на радиус

Рассмотрим объект, движущийся с постоянной скоростью по круговой траектории. Скорость объекта постоянна, но скорость меняется, потому что направление объекта постоянно меняется. Рассмотрим скорость в два момента на круговой траектории. На рис. 1 v ₁ представляет начальную скорость. На рис. 2 v ₂ представляет скорость через короткий промежуток времени.

Уравнение 1.

Рис. 1. Диаграммы 1 (слева) и 2 (справа) иллюстрируют изменение направления вектора скорости от времени 1 ко времени 2. На диаграмме 2 показано, что угол между векторами скорости равен углу между радиусами в момент времени 1 и момент времени 2.

Рис. 2. Диаграммы 3, 4 и 5.

Пока длина и направление векторов остаются неизменными, их можно рисовать любым удобным способом.На диаграмме 3 показано сложение и вычитание векторов v ₁ и v ₂ .

Векторы -v ₁ , v ₂ и Δv образуют треугольник, который похож на треугольник, образованный радиусами, нарисованными в момент времени 1 и момент времени 2, и хордой Δr .

Величина векторов v ₁ и v ₂ равна и имеет величину v.

│ v ₁ │ = │ v ₂ │ = v

Поскольку треугольники похожи, верно следующее:

Уравнение 6.

Δr = длина хорды между местоположением объекта в момент времени 1 и момент времени 2.
r = радиус окружности.

Круговой сегмент s представляет собой расстояние, пройденное объектом с момента 1 до момента 2.

Уравнение 7.

Если угол θ очень мал, можно сделать следующее приближение.

Уравнение 8.

Это позволяет сделать следующую замену:

Уравнение 9.

Подставляя v Δt вместо Δr в Уравнение 6 :

Уравнение 10.

Перестановка для Δ v / Δt дает Уравнение 11.

Уравнение 11.

Δv / Δt – это ускорение, указанное в уравнении 4 :

Умножение ускорения на массу объекта дает центростремительную силу, как показано в уравнении (Уравнение 3) .

Уравнение 3 и Уравнение 4 можно использовать для решения многих физических задач.

Ресурсы

К этим изделиям могут применяться уравнения центростремительной силы и центростремительного ускорения.

Центростремительная и центробежная сила – ускорение

Центростремительная и центробежная сила – это пара сил действия-противодействия, связанная с круговым движением.

Центростремительное ускорение

Скорость – это вектор, определяющий, насколько быстро (или медленно) пройдено расстояние и направление движения. Поскольку вектор скорости (направление) тела изменяется при движении по окружности – возникает ускорение.

Это ускорение называется центростремительным ускорением и может быть выражено как

a _c = v ² / r

= ω ² r

= (2 π n _{об / с} ) ² r

= (2 π n _{об / мин} /60) ² r

= (π n _{об / мин} /30) ^r (1)

где

a _c = центростремительное ускорение (м / с ² , фут / с ² )

v = тангенциальная скорость (м / с, фут / с)

r = радиус окружности (м, фут)

ω = угловая скорость (рад / с)

n _{об / с} = оборотов в секунду (об / с, 1 / с)

n _{об / мин} = оборотов в минуту (об / мин, 1 / мин)

Центростремительная сила

По секундам Ньютона По закону центростремительная сила может быть выражена как

F _c = ma _c

= mv ² / r

= m ω ² r 9144 = m (2 π n _s ) ² r

= m (2 π n _{об / мин} /60) ² r

= м (π n _{об / мин} /30) ² об (2)

где

F _c = центростремительная сила (Н, фунт _f )

m = масса (кг, пули )

Третий закон Ньютона Центростремительная сила, действующая на объект, имеет центробежную силу такой же величины, действующую в противоположном направлении.

Пример – центростремительное ускорение и сила, действующая на автомобиль по кривой

Метрические единицы

Автомобиль с массой 1000 кг проезжает по кривой радиусом 200 м со скоростью 50 км / ч . Центростремительное ускорение можно рассчитать как

a _c = ((50 км / ч) (1000 м / км) (1/3600 ч / с)) ² / (200 м)

= 0,965 м / с ²

= 0.1 g

, где

1 g = ускорение свободного падения (9,81 м / с ² )

Центростремительная сила может быть рассчитана как

F _c = (1000 кг) ( 0,965 м / с ² )

= 965 Н

= 0,97 кН

В зависимости от силы тяжести – вес:

F _г = (1000 кг) ( 9,81 м / с ² )

= 9810 N

= 9.8 кН

Имперские единицы

Автомобиль с массой (сила тяжести) 3000 фунтов движется по кривой радиусом 100 футов со скоростью 15 миль / ч .

Массу автомобиля можно рассчитать как

м = (3000 фунтов) / (32 фут / с ² )

= 94 пули

Центростремительное ускорение можно рассчитать как

a _c = ((15 миль / ч) (5280 футов / миля) / (3600 с / ч)) ² / (100 футов)

= 4.84 фут / с ²

Центростремительную силу можно рассчитать как

F _c = (94 пули) (4,84 фут / с ² )

= 455 фунтов _f

Центростремительный (центробежный) калькулятор – скорость

Этот калькулятор можно использовать, если известна скорость объекта – например, автомобиля на повороте.

Центростремительная (центробежная) сила – об / мин

Уравнение (2) можно изменить, чтобы выразить центростремительную или центробежную силу как функцию числа оборотов в минуту – об / мин – как

F _c = 0.01097 mrn _{об / мин} ² (3)

где

n _{об / мин} = число оборотов в минуту (об / мин)

Центростремительный (центробежный) Калькулятор – об / мин

можно использовать скорость вращения объекта известна – как токарный стакан в токарном станке.

Центробежная сила

Сила – это абстракция, представляющая толкающее и тянущее взаимодействие между объектами.Третий закон Ньютона гласит, что

• для каждой действующей силы существует равная и противоположная сила реакции.

Следовательно, должна быть равная и противоположная центростремительной силе сила реакции – центробежная сила .

Круговое движение

ФИЗИКА Автомобили и их способность преодолевать повороты

Термин “прохождение поворотов” описывает без номеров способность автомобиля двигаться быстро по кривой.В физику плоской кривой встроено ограничение прохождения поворотов. фактор. Этот фактор – центростремительное ускорение. Центростремительное ускорение можно найти по телефону

Где _с равно центростремительному ускорению, v равно скорости автомобиля вокруг кривая, а R представляет радиус кривой. Кривая, которая как Размещено ограничение скорости 25 ^м / с и имеет радиус 50 м, требует центростремительного ускорения 6.5 ^м / с ² . В пересчете на g это 0,66 g ( ^6,5 / 9,8 = 0,66).
Центростремительная сила, необходимая автомобилю, чтобы проехать по пологому углу. обеспечивается трением между шинами автомобиля и дорогой. Это значение описывается в таких журналах, как Car и Driver , как автомобиль боковое ускорение . Чтобы найти поперечное ускорение автомобиля, автомобиль поворачивает круг заданного радиуса. Затем он медленно ускоряется, пока не начинает соскальзывать за пределы круга.Это тот момент, когда трение между шинами и дорогой оказало максимальное воздействие трения. Максимальное поперечное ускорение автомобиля можно рассчитать по формуле формула для центростремительного ускорения, показанная выше.
Кривая определяет, какое центростремительное ускорение необходимо для безопасного перемещаться по кривой. Он определяет это по скорости движения кривой. пройденный путь и радиус кривой. Используйте уравнение: V ² / R.

В приведенном выше примере для кривой требуется 0,66 г без скольжение. Если поперечное ускорение автомобиля больше или равно расчетное центростремительное ускорение кривой, тогда она будет вращаться вокруг по кривой без проскальзывания. Если боковое ускорение автомобиля меньше центростремительного ускорения, тогда автомобиль выскользнет наружу кривой до тех пор, пока радиус не станет достаточно большим, чтобы позволить кривым центростремительным ускорение равняется боковому ускорению автомобиля.

ПРИМЕР № 1
1. На кривой указано ограничение скорости 25 миль в час, 11,16 ^м / с. Радиус кривых – 40 метров.
• С каким центростремительным ускорением автомобиль может двигаться по кривой без скольжения?

Это означает, что автомобиль может ехать по кривой без проскальзывания, если шины создают фрикционные усилие 3,11 м / с ² , 0,318 г. В машине и У водителя эта сила трения описывается как «боковое ускорение».” Ограничивающий фактор для этой кривой составляет 0,317 г.

ПРИМЕР № 2
При движении по дороге на высоте 25 ^м / с, автомобилю необходимо преодолеть поворот радиусом 19 м. Какая центростремительная сила необходимо сделать кривую и что будет, если трение между шины автомобиля и дороги не равны или не превышают центростремительная сила, необходимая для кривой.
РЕШЕНИЕ

3.36 г! Нет легковые автомобили, которые это делают. Автомобиль не сделает поворот. Водителю нужно будет повернуть колеса, но машина продолжит движение. Если бы поворот был наклонным, машина съехала бы за пределы поворота. до тех пор, пока центростремительное ускорение, необходимое для преодоления кривой, не станет равным центростремительное ускорение, которое может вызвать автомобиль. Предположим, машина может проявлять центростремительное ускорение 0,88 g. Потом;

Следовательно, R = 72.47м. В автомобиль будет скользить наружу по кривой с наклоном до радиуса поворот равен 72,47 метра. Или пока забор не остановит машину.

Нажмите здесь для некоторых физических проблем, связанных с автомобилями и их способностью проходить повороты. При нажатии на эту ссылку откроется новое окно. Закройте, чтобы вернуться на эту страницу.

Равномерное круговое движение

Равномерное круговое движение

Равномерное круговое движение

Объект, движущийся по окружности радиуса r с постоянной скоростью v ускоряется.В направление его вектора скорости все время меняется, но величина вектор скорости остается постоянным. Вектор ускорения не может иметь составляющей в направлении вектора скорости, так как такая составляющая будет вызвать изменение скорости. Следовательно, вектор ускорения должен быть перпендикулярно вектору скорости в любой точке окружности. Этот ускорение называется радиальное ускорение или центростремительного ускорения , и это указывает к центру круга.Величина центростремительного вектор ускорения равен _c = v ² / r. (Мы пропускаем вывод этого выражения.)

Ссылка: Равномерное круговое движение

Проблема:

Опишите, как водитель может управлять автомобилем, движущимся с постоянной скоростью, чтобы
(а) ускорение равно нулю, или
(б) величина ускорения остается постоянной.

Решение:

• Рассуждение:
  (a) Водитель должен заставить машину двигаться по прямой линия.
  (b) Водитель должен заставить машину двигаться по кругу. (или по прямой с a = 0).

Проблема:

Орбита Луны вокруг Земля приблизительно круглая со средним радиусом 3,85 * 10 ⁸ м. Луна совершает один оборот вокруг Луны за 27,3 дня. Земля. Найти
(а) средняя орбитальная скорость Луны и
(б) его центростремительное ускорение.

Решение:

• Рассуждение:
  Расстояние, которое луна проходит за один орбитальный период T, равно d = 2πr.
  Его скорость v = расстояние / время = d / T.
  Центростремительное ускорение Луны v ² / r.
• Детали расчета:
  (а) Расстояние, которое луна проходит за 27,3 дня, равно d = 2πr = 2,41 * 10 ^9. г.
  Его скорость v = d / (27,3 суток) = (d / (2,36 * 10 ⁶ с)) = 1023 м / с.
  (б) Центростремительное ускорение Луны v ² / r = 2,725 * 10 ^-3 м / с ² .

Проблема:

Если вращение Земли увеличилось так, что центростремительное ускорение было равно ускорению свободного падения на экваторе,
(а) какова будет тангенциальная скорость человека, стоящего на экваторе, и
б) как долго будет день?

Решение:

• Рассуждение:
  Если бы центростремительное ускорение было равно ускорению свободного падения на экваторе, то v ² / r = g.
• Детали расчета:
  (а) Радиус Земли составляет 6368 км. Хотим v ² / r = 9,8 м / с ² , или v ² = (9,8 м / с ² ) * 6,368 * 10 ⁶ м, или v = 7900 м / с.
  (b) Продолжительность дня будет t = 2πr / v = 5065 s = 84,4 мин.

---

Неравномерное круговое движение

Тележка американских горок, движущаяся по петле, меняет скорость, а также направление движения.Его ускорение имеет радиальную составляющую и тангенциальную составляющую. компонент, a = a _r + а _т . В тангенциальная составляющая вызывает изменение скорости, и ее величина определяется как _т. = dv / dt, а радиальная составляющая вызывает изменение направления и его величина определяется как _r = v ² / r, где r – радиус кривизна в рассматриваемой точке. Компоненты , , _, и a _t перпендикулярны друг другу и величина a равно a = (a _r ² + a _t ² ) ^½ .

Проблема:

Фигуристка выполняет восьмерку, состоящую из двух равных касательных. круговые дорожки. На протяжении первого круга она равномерно увеличивает скорость, а во втором круге она движется с постоянной скоростью. Сделайте набросок ее вектор ускорения в нескольких точках по пути движения.

Решение:

• Рассуждение:
  На протяжении первого контура величина тангенциального ускорения a _t постоянно.Величина радиального ускорения а _r увеличивается как v ² / r, когда скорость конькобежца увеличивается как v = a _t t = (2a _t d) ^½ , где d – пройденный путь. Когда фигурист трогается с места, вектор ускорения равен по касательной к петле. Но угол θ, который он составляет с касательной увеличивается как tanθ = a _r / a _t = v ² / (ra _t ) = 2d / r. Во втором цикле _t = 0 и _r равно константа, а вектор ускорения указывает на центр контура.

Проблема:

Автомобиль, скорость которого увеличивается со скоростью 0,6 м / с ² , едет по круговой дороге радиусом 20 м. Когда мгновенная скорость машина 4 м / с, найти
(а) компонент тангенциального ускорения и
(б) величина и направление общего ускорения.

Решение:

• Рассуждение:
  Тангенциальное ускорение автомобиля имеет заданную постоянную величину. Его направление касательно окружности.
  Радиальное ускорение имеет величину v ² / r. Его направление перпендикулярна касательному ускорению и указывает на центр круга.
• Детали расчета:
  (а) Тангенциальное ускорение автомобиля имеет постоянная величина 0,6 м / с ² .
  (b) Когда v = 4 м / с, радиальное ускорение имеет величину a _r = v ² / r = (16 м / с ² ) / (20 м) = 0.8 м / с ² , a = (a _r ² + a _t ² ) ^½ = 1 м / с ² .
  Пусть θ – угол, который вектор ускорения составляет с линией, направленной от положение автомобиля по направлению к центру круга. Тогда tanθ = a _t / a _r = 0,75, θ = 36,9 ^o .
  

Проблема:

Цифра справа представляет собой полное ускорение движущейся частицы. по часовой стрелке по кругу радиуса 2.5 м в данный момент времени. На это мгновенно, найди
а) центростремительное ускорение,
(б) скорость частицы, и
(c) его тангенциальное ускорение.

Решение:

• Рассуждение:
  Нам нужно найти компонент вектора a .
• Детали расчета
  (а) a _r = a cos (30 ^o ) = 12,99 м / с ² .
  (б) а _р = v ² / r, v ² = ra _r , v = 5.7 м / с.
  (c) a _t = a sin (30 ^o ) = 7,5 м / с ² .

---

Модуль 3: Вопрос 2

Может ли центростремительное ускорение изменить скорость кругового движения?

Обсудите это со своими однокурсниками на дискуссионном форуме!

---

Общие единицы измерения углов: градуса и радиана . Мы имеем 360 ^o = 2π радиан. Длина окружности радиуса r равна 2πr.Длина дуги окружности, составляющей 180 ^o , составляет πr. Длина дуги, содержащей 90 ^o , составляет (π / 2) r. Мы видим, что длина Дуга окружности, имеющая угол θ, равна θr, где θ измеряется в радианах.

Для малых углов θ, sinθ ~ θ, если θ измеряется в радианах. Вы можете убедиться в этом, посмотрев на таблицу или график.

угол (град.)	угол (рад)	sin (угол)
0	0	0
0. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: