различные варианты использования и проблемы с фактами –
Когда объект движется по кругу, сила будет стремиться притянуть объект к центру.
Сила, которая пытается притянуть объект в круговом движении к центру, известна как центростремительная сила, и, таким образом, центростремительное ускорение – это ускорение, действующее в нем.
Поскольку центростремительное ускорение состоит как из величины, так и из направления, оно является векторной величиной. В этой статье мы попытаемся выяснить, как найти центростремительное ускорение с помощью или без помощи некоторых величин. Формула для центростремительного ускорения дается как: ac = V2/r
Илиc = гω2
Где,
ac = центростремительное ускорение.
v = скорость объекта.
r = радиус траектории.
ω= угловая скорость.
Существуют различные способы найти центростремительное ускорение без полной информации, в зависимости от того, какой тип информации предоставлен. Одним из таких методов является определение центростремительной силы, хотя есть несколько значений, которые необходимо иметь заранее, чтобы найти какое-либо значение. Формула для центростремительная сила дается как: Fc = мв2/r
Одним из таких методов является определение центростремительной силы, хотя есть несколько значений, которые необходимо иметь заранее, чтобы найти какое-либо значение. Формула для центростремительная сила дается как: Fc = мв2/r
Где,
Fc= центростремительная сила.
m = масса объекта.
v = скорость объекта.
r = радиус орбиты объекта.
Как и в этом разделе, нужно найти центростремительное ускорение без скорости, предполагая, что скорость не указана в вопросе. Это означает, что в задаче должна быть указана другая информация, такая как центростремительная сила, масса объекта и радиус объекта, с помощью которых можно найти скорость объекта, а затем подставить ее в формулу для центростремительного ускорения. чтобы получить окончательный ответ.
Вопрос: Чему равно центростремительное ускорение автомобиля массой 200 кг, совершающего разворот по окружности диаметром 50 м? Сила, действующая на автомобиль, равна 500 Н.
Ответ: Радиус окружности можно найти, разделив диаметр на 2, так как радиус равен половине диаметра. Таким образом, радиус равен 25 м. Формула для центростремительной силы дается как: Fc = мв2/r
Таким образом, радиус равен 25 м. Формула для центростремительной силы дается как: Fc = мв2/r
Измените эту формулу, чтобы получить выражение для скорости. Следовательно, v2 = Фcг / м
Замените 500 Н на Fc, 25 м для r и 200 кг для m в формулу, чтобы найти скорость.
Формула для нахождения центростремительного ускорения имеет вид:c = V2/r
Замена 7.91 м/с2 для v и 25 м для r в формулу для расчета центростремительного ускорения.
Следовательно, центростремительное ускорение автомобиля равно 2.5 м / с2.
Как найти центростремительное ускорение с радиусом и скоростьюСамый простой способ вычислить центростремительное ускорение — это использовать скорость объекта, движущегося по круговому пути, и радиус его кругового пути. Здесь используется та же формула, что была показана ранее, т.c = V2/r
Вопрос: Предмет массой 3 кг привязан к концу веревки длиной 2 м и вращается вокруг, закрепив один конец веревки. Если она составляет 250 об/мин, то найти центростремительное ускорение этого тела.
Если она составляет 250 об/мин, то найти центростремительное ускорение этого тела.
Ответ: Чтобы найти центростремительное ускорение, нужно сначала найти скорость тела. Чтобы найти скорость объекта, используется формула угловой скорости ω, заданная как: ω = dθ/dt
Где,
θ = угловое вращение
t = время
Если тело вращается со скоростью «N» оборотов в минуту, то формула имеет вид: ω = 2πN/T.
Где,
T = период оборота
Здесь период считается оборотами в минуту. Поскольку 1 мин = 60 с, Т = 60 с. Единицей СИ для этой формулы является рад/с. Подставьте 250 вместо N в формулу для расчета угловой скорости.
Теперь есть два уравнения для нахождения центростремительного ускорения:c=v2/ г и аc=rω2. Приравняйте оба этих уравнения, чтобы найти скорость. Следовательно,
Подставьте 2 м вместо r и 26.16 рад/с вместо ω в формулу для расчета скорости.
Теперь подставьте 52. 32 м/с вместо v и 2 м вместо r в формулу для расчета центростремительного ускорения.
32 м/с вместо v и 2 м вместо r в формулу для расчета центростремительного ускорения.
Следовательно, центростремительное ускорение тела равно 1368.7 м / с2.
Читайте о различных типах ускорения на Центростремительное ускорение против ускорения
Как найти центростремительное ускорение по времени и радиусуИспользуется формула, включающая угловая скорость, чтобы найти центростремительное ускорение используя время и радиус. аc = гω2
А для нахождения угловой скорости используется формула ω = 2πN/T
Вопрос: Рассчитайте центростремительное ускорение мяча, привязанного к концу веревки с фиксированной осью на расстоянии 1.5 м от центра. Отжим 170 об/мин.
Ответ: 1 мин = 60 сек. Подставьте 170 вместо N и 60 вместо T в формулу для расчета угловой скорости.
Подставьте значение ω в формулу для центростремительного ускорения, включающую угловую скорость.
Следовательно, центростремительное ускорение мяча равно 474.72 м / с2.
Как найти центростремительное ускорение без массыСуществуют две основные формулы для нахождения центростремительное ускорение и, как отмечалось ранее, ни одна из формул центростремительного ускорения не включает массу в нем, поэтому легко найти центростремительное ускорение, если остальные значения заданы.
Задача: найти центростремительное ускорение автомобиля, движущегося по перекрестку со скоростью 50 км/ч. Длина круга около 40 м.
Ответ: Формула, используемая для этой задачи, будетc = V2/r
Длина раунда означает диаметр раунда. Поскольку диаметр равен 40 м, радиус окружности будет равен 20 м. Теперь нужно перевести скорость из км/ч в м/с. Чтобы преобразовать скорость, нужно умножить заданную скорость на 1000 м/3600 сек. Следовательно,
Подставьте 13.8 м/с вместо v и 20 м вместо r в формулу для расчета центростремительного ускорения.
Следовательно, центростремительное ускорение автомобиля равно 9.52 м / с2.
Как найти центростремительное ускорение с периодомВремя (T), необходимое объекту для совершения одного полного оборота, называется период. Если указан период, то с помощью периода можно найти скорость тела и подставить это значение скорости в формулу для центростремительного ускорения. Формула для нахождения скорости с помощью периода имеет вид: v = 2πN/T
Где,
N = обороты.
Т = период времени.
Вопрос: Если винт истребителя имеет диаметр 2.50 м и вращается со скоростью 1100 об/мин, то каково центростремительное ускорение кончика винта при этих обстоятельствах?
Ответ: Чтобы найти радиус гребного винта, диаметр необходимо разделить на 2. Следовательно, радиус гребного винта при заданном диаметре равен 1.25 м. Здесь пропеллер вращается со скоростью 1100 оборотов в минуту, что означает, что он вращается со скоростью 1100 оборотов за 60 секунд. Поэтому подставьте 1100 вместо N и 60 с вместо T в формулу для расчета скорости объекта.
Поэтому подставьте 1100 вместо N и 60 с вместо T в формулу для расчета скорости объекта.
Теперь формула для расчета центростремительного ускорения дается как:c = V2/r
Подставьте 115.13 м/с вместо v и 1.25 м вместо r в формулу, чтобы рассчитать центростремительное ускорение винта.
ac = V2/r
= (115.13 м/с)2/ 1.25m
= 10,603.9 м / с2
Следовательно, центростремительное ускорение воздушного винта равно 10,603.9 м / с2.
Как найти центростремительное ускорение из тангенциального ускоренияВеличина изменения скорости по отношению к изменению во времени известна как Тангенциальное ускорение. Формула для тангенциального ускорения задается как:T = дв/дт
Где,
aT = тангенциальное ускорение.
dv = изменение скорости.
dt = изменение во времени.
Направление тангенциального ускорения обозначается касательной к окружности, тогда как направление центростремительного ускорения направлено к центру окружности (радиально внутрь). Поэтому объект в круговое движение с тангенциальным ускорением испытает полное ускорение, которое является суммой тангенциального ускорения и центростремительного ускорения. Формула для полного ускорения задается как: a = aT +c
Поэтому объект в круговое движение с тангенциальным ускорением испытает полное ускорение, которое является суммой тангенциального ускорения и центростремительного ускорения. Формула для полного ускорения задается как: a = aT +c
Где,
а = полное ускорение.
aT = тангенциальное ускорение.
ac = центростремительное ускорение.Диаграмма, изображающая движение объекта под действием тангенциальное ускорение и центростремительное ускорение.
Итак, если дать полное ускорение и тангенциальное ускорение, легко найти центростремительное ускорение любого объекта.
Вопрос: каково центростремительное ускорение объекта, который имеет чистое ускорение (общее ускорение) 256.9 м/с?2 и тангенциальное ускорение 101.4 м/с2?
Ответ: Приведенная формула для соотношения центростремительного ускорения и тангенциального ускорения: a = aT +c
Переставить формула для расчета центростремительного ускорения.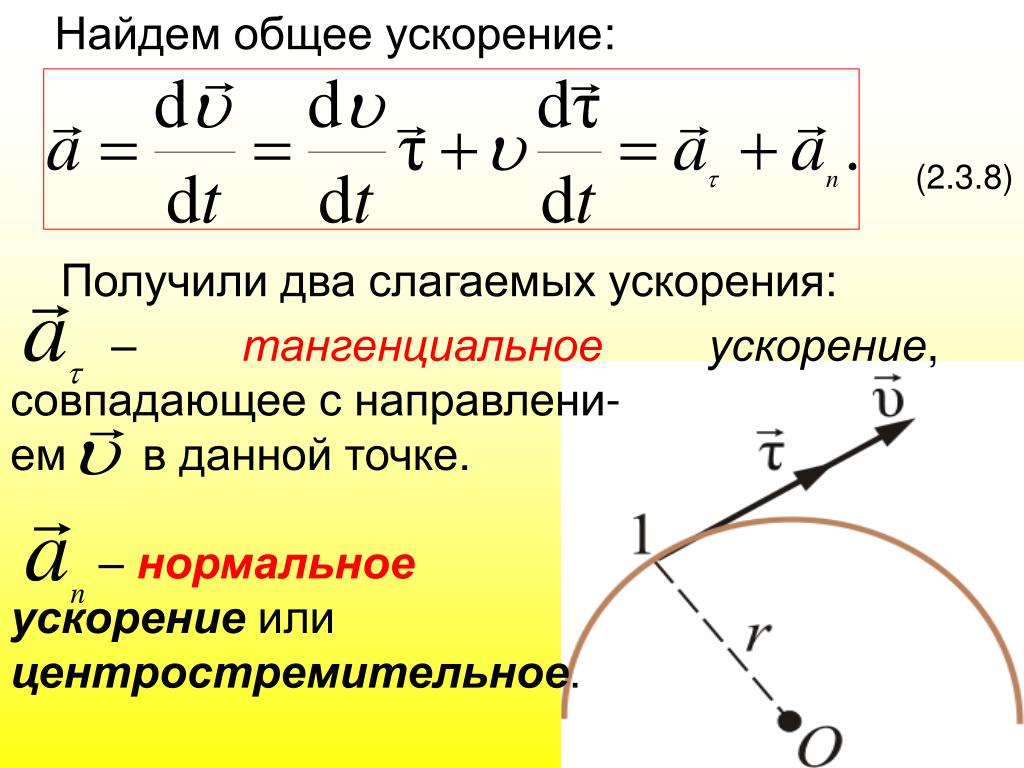
ac = а – аT
Замена 256.9 м/с2 для а и 101.4 м/с2 дляT в приведенную выше формулу для расчета центростремительного ускорения.
Следовательно центростремительное ускорение объекта 155.5 м / с2.
Еще один простой способ найти центростремительное ускорение по данной формуле, включающей угол, который задается как: tanθ = aT/ac
Вопрос: Найдите центростремительное ускорение объекта, который образует угол 1.6º по отношению к вектору центростремительного ускорения и имеет тангенциальное ускорение 6.5 м/с.2.
Ответ: Чтобы найти центростремительное ускорение, нужно модифицировать данное уравнение.
Замена 6.5 м/с2 дляT и 1.6º для θ в приведенное выше уравнение для расчета центростремительного ускорения.
Следовательно центростремительное ускорение объекта 232.7 м / с2.
Как найти центростремительное ускорение маятникаКогда маятник движется, центростремительное ускорение на него действует тангенциальное ускорение. Чистая сила отвечает за центростремительное ускорение в нижней части качелей.
Чистая сила отвечает за центростремительное ускорение в нижней части качелей.
Формула для того же дается как: Напряжение – Вес = mac
Где,
(Натяжение – Вес) = результирующая сила.
m = масса объекта (качка маятника).
Таким образом, эта формула далее записывается как: T – mgcosθ = mac
Где,
Т = напряжение
g = ускорение свободного падения.
Нужно просто изменить данное уравнение, чтобы найти центростремительное ускорение.
ac = Т/м – gcosθ
Вопрос: найти центростремительное ускорение маятника массой 0.250 кг, образующей угол с нормалью 27°. Натяжение боба 97 Н.
Ответ: Величина ускорения свободного падения для Земли равна 9.8 м/с.2. Замените 97 Н на T, 0.250 кг на m, 27° на θ и 9.8 м/с.2 для g в приведенную выше формулу для расчета центростремительного ускорения.
Следовательно центростремительное ускорение маятника 379.3 м / с2.
Центростремительное ускорение в физике
Оглавление
Время чтения: 5 минут
691
Что такое центростремительное ускорение
Центростремительное ускорение — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.
Центростремительное ускорение, которое также называют нормальным ускорением, всегда направлено к центру окружности, по которой движется точка. {2} / \mathrm{R}\right) * \mathbf{n}\]
{2} / \mathrm{R}\right) * \mathbf{n}\]
Где R – радиус окружности, n – единичный вектор нормали к траектории.
Тангенциальное ускорение
Это ускорение (dv/dt) * τ, оно характеризует изменение скорости по величине за единицу времени и является её производной. В системе СИ тангенциальное ускорение измеряется в м/c2. Оно может быть, как положительным, так и отрицательным. При положительных значениях тангенциального ускорения модуль скорости движущейся по окружности точки возрастает и движение именуют ускоренным. При отрицательных значениях величина скорости понижается и движение называют замедленным. Если тангенциальное ускорение постоянно, то к словам ускоренный и замедленный добавляется приставка «равно».
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нормальное или центростремительное ускорение
Это вторая составляющая разложенного нами движения (v2/R)*n. Обозначим её как an Поясним, откуда взялись квадрат скорости, радиус и n.
Обозначим её как an Поясним, откуда взялись квадрат скорости, радиус и n.
Одновременно умножаем и делим v * (dτ/dt) на стремящийся к нулю элемент длины траектории, т. е. v*(dτ/dl)(dl/dt). Последний множитель в этом выражении есть скорость, его можно записать как v *(dτ/dl)*v. Отсюда v2*(dτ/dl). dl допустимо представить как R*dϕ. dϕ здесь есть малый угол поворота вокруг центра окружности.
n = dϕ/dτ. Это ясно из геометрических соображений. Δτ = τ ′- τ есть разность единичных касательных векторов в рассматриваемой нами точке (τ) и бесконечно близкой к ней точке (τ ′). По величине она равна 2sin(dϕ/2). Здесь dϕ есть угол между τ и τ ′. Эта разность в рассматриваемой точке имеет направление к нормали n под углом dϕ/2. Из-за малости dϕ становится возможным совпадение его с вектором нормали n. Также из-за малости dϕ синус допустимо разложить в ряд Тейлора. В результате всего этого мы приходим к тому, что Δτ = Δϕ * n. Для бесконечно малых это выражение переходит в dτ = dϕ * n.
Для бесконечно малых это выражение переходит в dτ = dϕ * n.
Мгновенную скорость можно выразить соотношением v =ω*R. После этого формула центростремительного ускорения приобретает у нас вид an = (ω*R)2/R = ω2*R.
Теперь о том, в чем измеряется центростремительное ускорение в физике. Хотя некоторым может показаться странным, но меряется оно, также как и тангенциальное ускорение в метрах на секунду квадрат, т. е. м/c2.
Первым (или одним из первых), кто стал пользоваться понятием центростремительного ускорения, был по-видимому Христиан Гюйгенс. Именно с его времени понятие нормального ускорения в физике начали повсеместно применять при решении самых разных механических задач.
Примеры решения задач
Примеры
Задача №1.
Поезд движется со скоростью 54 километра в час по закруглению, радиус которого равен 1 километру.
Найти чему равно его центростремительное ускорение.
Дано:
Радиус R = 1 км = 1000 м. {2}\].
{2}\].
Оценить статью (78 оценок):
Поделиться
Радиальное ускорение — определение, единицы измерения и тангенциальное ускорение
Мы знаем, что когда на тело действует внешняя сила, оно начинает ускоряться, и это то, о чем говорит второй закон Ньютона. Ускорение есть не что иное, как изменение скорости объекта в единицу времени. Это векторная величина, которая имеет как величину, так и направление. Измеряется в мс-2, однако в физике есть еще один термин — радиальное ускорение.
Итак, вы знаете, что такое радиальное ускорение? Хорошо! Когда угловая скорость изменяется в единицу времени, это радиальное ускорение.
Мы знаем, что тело может совершать два типа движения: линейное и круговое. Когда это линейное движение, мы учитываем только ускорение; однако во время кругового движения, которое на самом деле является угловым ускорением.
Мы знаем, что при круговом движении направление угловой скорости постоянно меняется со временем, поэтому его угловое ускорение получает две следующие составляющие, а именно:
Итак, начнем с радиального ускорения:
Радиальное ускорение обозначается как «ar» и представляет собой скорость изменения угловой скорости, направление которой направлено к центру, по окружности которого движется тело.
Это происходит из-за центростремительной силы. Таким образом, центростремительная сила является причиной радиального ускорения.
Тело, масса которого равна ‘m’, а сила, действующая на него, равна ‘mar’…..(1)
Формула для центростремительной силы, действующей на камень, движущийся по кругу, такова: mv2 /r….(2)
Приравнивая (1) и (2):
mar = mv2 /r
Таким образом, получаем формулу радиального ускорения:
ar = v2/r….(3)
2 Уравнение (3) называется центростремительным ускорением.
Единицы радиального ускорения
Единицы измерения следующие:
Символически эти две единицы записываются как ωs-2 или ms-2 соответственно.
Радиальный компонент
Предположим, ваш ребенок катается на карусели. Направление вектора скорости, взятого из вашего положения, будет касательным круговой траектории, по которой вращается карусель. Однако центростремительное ускорение направлено радиально внутрь или к центру, что заставляет вас вращаться.
Направление вектора скорости, взятого из вашего положения, будет касательным круговой траектории, по которой вращается карусель. Однако центростремительное ускорение направлено радиально внутрь или к центру, что заставляет вас вращаться.
А из формулы в уравнении (3) видно, что чем больше радиус окружности вращения, тем меньше ее скорость изменения скорости или радиальное ускорение и наоборот. По этой причине мы видим, что маленькие карусели вращаются намного быстрее, чем большие.
Теперь совершенно ясно, что радиальная составляющая является основной причиной того, что любой объект продолжает совершать круговое движение.
У тела, ускорение которого всегда направлено по радиусу, как следует из его названия, существует еще одна составляющая ускорения всякий раз, когда объект движется с неравномерной скоростью, и это тангенциальное ускорение (at). Касательное ускорение действует по касательной к траектории, по которой движется объект при круговом движении.
На рисунках ниже показано изменение радиального ускорения в зависимости от тангенциального ускорения:
(изображение будет обновлено в ближайшее время)
Это для центростремительного или радиального ускорения.
(Изображение скоро будет обновлено)
Вы можете видеть касательные, проведенные к пути объекта с изменяющейся скоростью.
Мы должны иметь в виду, что результирующее ускорение является суммой этих двух типов ускорений, и формула вместе с требуемой цифрой приведена ниже:
Формула: a = ar + at….(4)
Уравнение (4) утверждает, что под радиальной составляющей ускорения понимается составляющая результирующего ускорения, перпендикулярная мгновенной скорости при движении по любой общей пути (не обязательно для кругового движения). Так как эта составляющая ускорения всегда направлена по радиусу кривизны траектории (движения снаряда), то этому виду ускорения присвоено название радиальное ускорение.
Так как эта составляющая ускорения всегда направлена по радиусу кривизны траектории (движения снаряда), то этому виду ускорения присвоено название радиальное ускорение.
(изображение скоро будет обновлено)
Радиальное и тангенциальное ускорение
Радиальное ускорение всегда соответствует нормали к мгновенной скорости, поэтому его также называют нормальным ускорением.
Радиальное ускорение всегда направлено к мгновенному центру кривизны траектории, поэтому его также называют центростремительным ускорением.
Радиальное или центростремительное ускорение никогда не определяется только для кругового движения, оно может быть определено для любого типа движения.
Величина радиального ускорения в любой момент равна v2/r, где v — скорость, а r — радиус кривизны в данный момент.
 В случае кругового движения r будет радиусом; также направление радиального ускорения идет по радиусу кривизны.
В случае кругового движения r будет радиусом; также направление радиального ускорения идет по радиусу кривизны.Величина тангенциального ускорения равна скорости изменения скорости частицы относительно время, и оно всегда касается пути.
Касательные и нормальные ускорения являются перпендикулярными компонентами результирующего ускорения, поэтому их векторная сумма возвращает результирующее ускорение.
В случае равномерного кругового движения или UCM тангенциальное ускорение всегда равно нулю, так как скорость не меняется. Другими словами, результирующий вектор ускорения в случае УВМ ортогонален мгновенной скорости.
Тело, движущееся с постоянной скоростью, никогда не испытывает тангенциального ускорения независимо от характера траектории.

При любом прямолинейном движении (равномерном/неравномерном) радиальное ускорение всегда равно нулю. Это потому, что радиус кривизны прямой линии бесконечен.
Тело, движущееся по криволинейной траектории, будет иметь некоторое ненулевое радиальное ускорение.
Все мы знаем, что согласно закону движения Ньютона любое конкретное тело или объект имеет тенденцию изменять скорость во время движения, и это зависит от силы и количества силы, приложенной к телу или объекту. Ускорение — это мера скорости изменения скорости и направления конкретного тела или объекта, при этом движение может быть либо линейным, либо круговым.
Линейное ускорение относится к типу ускорения, связанного с линейным движением, а тип ускорения, связанного с круговым движением, известен как угловое ускорение.
Ускорение, направленное к центру, известно как радиальное ускорение и измеряется в радианах на квадратную секунду, а причиной ускорения является центростремительная сила.
Когда объект или тело движется с неравномерной скоростью, это тангенциальное ускорение.
Особенности и характеристики радиального ускорения:
Угловое ускорение можно разделить на радиальное и тангенциальное ускорение
Радиальное ускорение определяется как ускорение объекта, направленное к центру.
Если радианы на секунду в квадрате, который представлен как ωs-2, то как измеряется радиальное ускорение.
Радиальное ускорение также известно как центростремительное ускорение.
Компонент углового ускорения, тангенциальный к круговой траектории, — это и есть Тангенциальное ускорение.
6.
 3 Центростремительная сила — University Physics Volume 1
3 Центростремительная сила — University Physics Volume 1Цели обучения
К концу этого раздела вы сможете:
- Объясните уравнение центростремительного ускорения
- Примените второй закон Ньютона, чтобы составить уравнение для центростремительной силы
- Использование концепции кругового движения при решении задач, связанных с законами движения Ньютона
В книге «Движение в двух и трех измерениях» мы рассмотрели основные понятия кругового движения. Объект, совершающий круговое движение, например один из гоночных автомобилей, показанных в начале этой главы, должен ускоряться, потому что он меняет направление своей скорости. Мы доказали, что это направленное по центру ускорение, называемое центростремительным ускорением, определяется формулой
ac=v2rac=v2r
, где v — скорость тела, направленная по касательной к кривой в любой момент времени. Если мы знаем угловую скорость ωω, то можем использовать
ac=rω2. ac=rω2.
ac=rω2.
Угловая скорость показывает скорость, с которой объект вращается по кривой, в рад/с. Это ускорение действует по радиусу криволинейной траектории и поэтому также называется радиальным ускорением.
Ускорение должно создаваться силой. Любая сила или комбинация сил может вызвать центростремительное или радиальное ускорение. Вот лишь несколько примеров: натяжение веревки на тросовом шаре, сила земного притяжения на Луне, трение между роликовыми коньками и полом катка, сила наклона проезжей части, действующая на автомобиль, и силы на трубе вращающейся центрифуги. . Любая результирующая сила, вызывающая равномерное круговое движение, называется центростремительной силой. Направление центростремительной силы совпадает с направлением центростремительного ускорения к центру кривизны. Согласно второму закону движения Ньютона, результирующая сила равна массе, умноженной на ускорение: Fnet=ma.Fnet=ma. Для равномерного кругового движения ускорение равно центростремительному ускорению:  а=а.с.а=а.с. Таким образом, величина центростремительной силы FcFc равна
а=а.с.а=а.с. Таким образом, величина центростремительной силы FcFc равна
Fc=mac.Fc=mac.
Подставляя выражения для центростремительного ускорения acac(ac=v2r;ac=rω2),(ac=v2r;ac=rω2), получаем два выражения для центростремительной силы FcFc через массу, скорость, угловую скорость и радиус кривизны:
Fc=mv2r;Fc=mrω2.Fc=mv2r;Fc=mrω2.
6,3
Вы можете использовать любое более удобное выражение для центростремительной силы. Центростремительная сила F→cF→c всегда перпендикулярно пути и указывает на центр кривизны, потому что a→ca→c перпендикулярно скорости и указывает на центр кривизны. Обратите внимание, что если вы решите первое выражение для r , вы получите
r=mv2Fc.r=mv2Fc.
Это означает, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть крутую кривую, как на рис. 6.20.
Рисунок
6.20
Сила трения дополняет центростремительную силу и численно равна ей.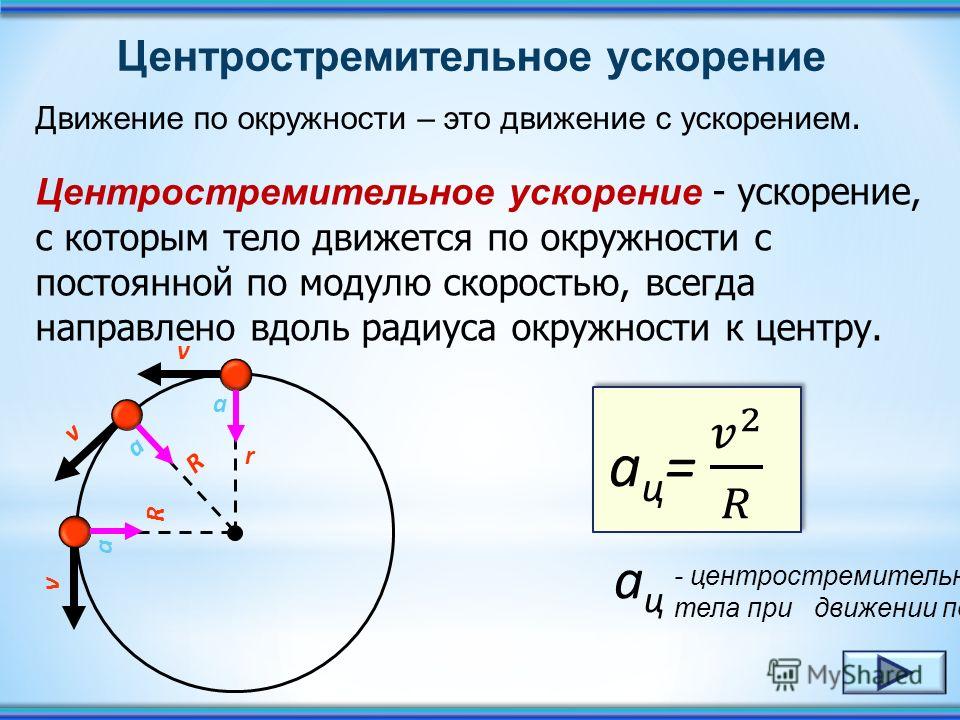 Центростремительная сила перпендикулярна скорости и вызывает равномерное круговое движение. Чем больше Fc,Fc, тем меньше радиус кривизны r и круче кривая. Вторая кривая имеет те же самые v , но больший FcFc дает меньшее r ‘.
Центростремительная сила перпендикулярна скорости и вызывает равномерное круговое движение. Чем больше Fc,Fc, тем меньше радиус кривизны r и круче кривая. Вторая кривая имеет те же самые v , но больший FcFc дает меньшее r ‘.
Пример 6.15
Какой коэффициент трения нужен автомобилям на плоской кривой?
(a) Рассчитайте центростремительную силу, действующую на автомобиль массой 900,0 кг, который движется по кривой радиусом 500,0 м со скоростью 25,00 м/с. (b) Предполагая, что кривая не имеет наклона, найдите минимальный статический коэффициент трения между шинами и дорогой, причем статическое трение является причиной, удерживающей автомобиль от проскальзывания (рис. 6.21).
Рисунок
6.21
Этот автомобиль на ровном месте удаляется и поворачивает влево. Центростремительная сила, заставляющая автомобиль поворачивать по круговой траектории, возникает из-за трения между шинами и дорогой.
Стратегия
- Мы знаем, что Fc=mv2r.Fc=mv2r. Таким образом,
Fc=mv2r=(900,0 кг)(25,00 м/с)2(500,0 м)=1125 Н.Fc=mv2r=(900,0 кг)(25,00 м/с)2(500,0 м)=1125 Н.
- На рис. 6.21 показаны силы, действующие на автомобиль на кривой без уклона (на ровной поверхности). Трение направлено влево, удерживая автомобиль от скольжения, и, поскольку это единственная горизонтальная сила, действующая на автомобиль, трение в данном случае является центростремительной силой. Мы знаем, что максимальное статическое трение (при котором шины катятся, но не скользят) равно µsN,µsN, где µsµs — статический коэффициент трения, а
Fc≡f=µsN=µsmg.
Теперь у нас есть связь между центростремительной силой и коэффициентом трения. Используя уравнение Fc≡f=µsN=µsmg.
Fc≡f=µsN=µsmg.Fc=mv2r,Fc=mv2r,
мы получаемmv2r=мксмг.mv2r=мксмг.
Мы решаем это для мкс, мкс, учитывая, что масса сокращается, и получаеммкс=v2rg.мкс=v2rg.
Подставляя известные,
Значение
Коэффициент трения, показанный на рис. 6.21(b), намного меньше, чем обычно наблюдается между шинами и дорогами. Автомобиль все еще преодолевает кривую, если коэффициент больше 0,13, потому что статическое трение является реактивной силой, которая может принимать значение меньше, но не больше, чем мксН.мксН. Более высокий коэффициент также позволит автомобилю проходить поворот на более высокой скорости, но если коэффициент трения меньше, безопасная скорость будет меньше 25 м/с.
Проверьте свое понимание 6,9
Автомобиль, движущийся со скоростью 96,8 км/ч, движется по кривой окружности радиусом 182,9 м по ровной проселочной дороге. Каким должен быть минимальный коэффициент трения покоя, чтобы автомобиль не скользил?
Кривые с наклоном
Давайте теперь рассмотрим кривую с наклоном s , где наклон дороги помогает вам преодолевать кривую (рис. 6.22). Чем больше угол θθ, тем быстрее вы сможете взять кривую. Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. В «идеально наклонной кривой» угол θθ таков, что вы можете преодолевать кривую на определенной скорости без помощи трения между шинами и дорогой.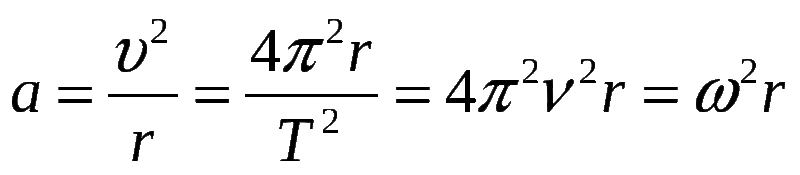 Мы выведем выражение для θθ для идеально изогнутой кривой и рассмотрим связанный с ним пример.
Мы выведем выражение для θθ для идеально изогнутой кривой и рассмотрим связанный с ним пример.
Рисунок 6.22 Автомобиль на этой кривой с уклоном удаляется и поворачивает влево.
Для идеального крена чистая внешняя сила равна горизонтальной центростремительной силе при отсутствии трения. Составляющие нормальной силы Н в горизонтальном и вертикальном направлениях должны быть равны центростремительной силе и весу автомобиля соответственно. В случаях, когда силы не параллельны, удобнее всего рассматривать составляющие вдоль перпендикулярных осей — в данном случае вертикального и горизонтального направлений.
На рис. 6.22 показана диаграмма свободного кузова автомобиля на кривой без трения. Если угол θθ идеален для скорости и радиуса, то чистая внешняя сила равна необходимой центростремительной силе. Единственными двумя внешними силами, действующими на автомобиль, являются его вес w→w→ и нормальная сила дороги N→.N→. (На поверхность без трения может воздействовать только сила, перпендикулярная поверхности, т.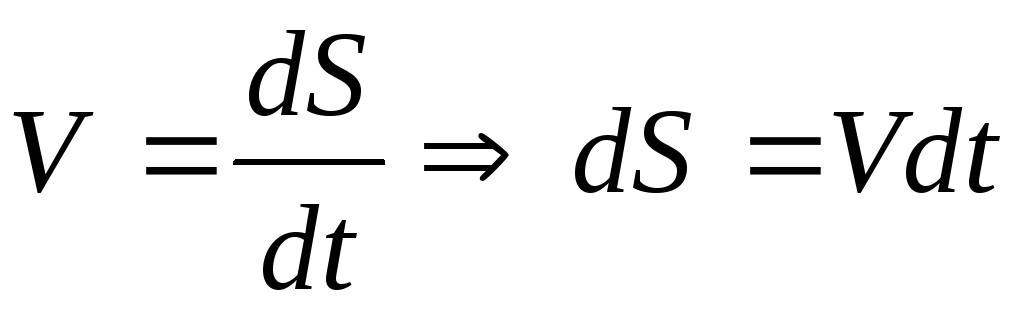
Nsinθ=mv2r.Nsinθ=mv2r.
Поскольку автомобиль не отрывается от поверхности дороги, результирующая вертикальная сила должна быть равна нулю, а это означает, что вертикальные составляющие двух внешних сил должны быть равны по величине и противоположны по направлению. Из рисунка 6.22 мы видим, что вертикальная составляющая нормальной силы равна Ncosθ,Ncosθ, а единственной другой вертикальной силой является вес автомобиля. Они должны быть равны по величине; таким образом,
Ncosθ=мг.Ncosθ=мг.
Теперь мы можем объединить эти два уравнения, чтобы исключить N и получить желаемое выражение для θθ. Решение второго уравнения относительно N=mg/(cosθ)N=mg/(cosθ) и подстановка его в первое дает
Решение второго уравнения относительно N=mg/(cosθ)N=mg/(cosθ) и подстановка его в первое дает
mgsinθcosθ=mv2rmgtanθ=mv2rtanθ=v2rg.mgsinθcosθ=mv2rmgtanθ=mv2rtanθ=v2rg.
Взятие арктангенса дает
θ=загар-1(v2rg).θ=загар-1(v2rg).
6,4
Это выражение можно понять, если рассмотреть зависимость θθ от v и r . Большое θθ получается при большом v и маленький р. То есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам проходить кривую с большей или меньшей скоростью, чем если бы кривая была без трения. Обратите внимание, что θθ не зависит от массы транспортного средства.
Пример 6.16
Какова идеальная скорость для крутого крутого поворота?
Кривые на некоторых тестовых трассах и гоночных трассах, таких как Daytona International Speedway во Флориде, очень крутые.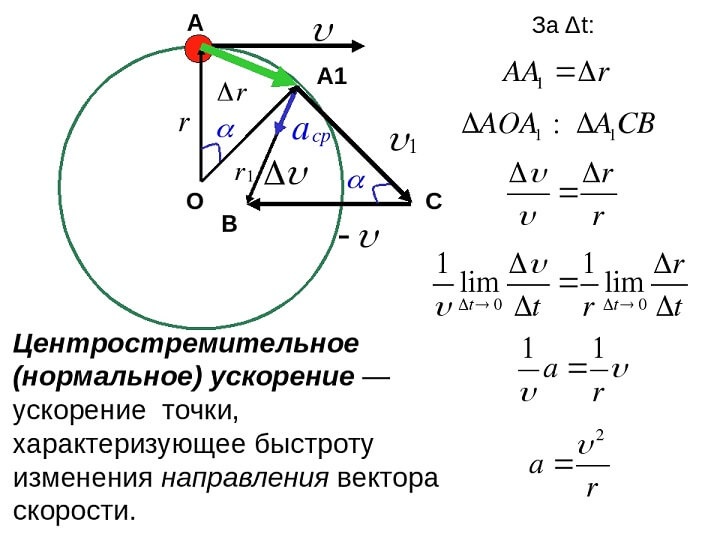 Этот крен с помощью трения шин и очень стабильной конфигурации автомобиля позволяет проходить повороты на очень высокой скорости. Чтобы проиллюстрировать это, рассчитайте скорость, с которой следует двигаться по кривой радиусом 100,0 м с наклоном 31,0°31,0°, если бы на дороге не было трения.
Этот крен с помощью трения шин и очень стабильной конфигурации автомобиля позволяет проходить повороты на очень высокой скорости. Чтобы проиллюстрировать это, рассчитайте скорость, с которой следует двигаться по кривой радиусом 100,0 м с наклоном 31,0°31,0°, если бы на дороге не было трения.
Стратегия
Прежде всего заметим, что все члены в выражении для идеального угла кривой с креном, кроме скорости, известны; таким образом, нам нужно только переставить его так, чтобы скорость появилась в левой части, а затем подставить известные величины.
Раствор
Начиная с
tanθ=v2rg,tanθ=v2rg,
получаем
v=rgtanθ.v=rgtanθ.
Учитывая, что tan31.0°=0.609,tan31.0°=0.609, получаем
v=(100.0м)(9.80м/с2)(0.609)=24,4 м/с.v=(100,0 м)(9,80 м/с2)(0,609)=24,4 м/с.
Значение
Это примерно 165 км/ч, что соответствует очень крутому виражу и довольно резкому повороту.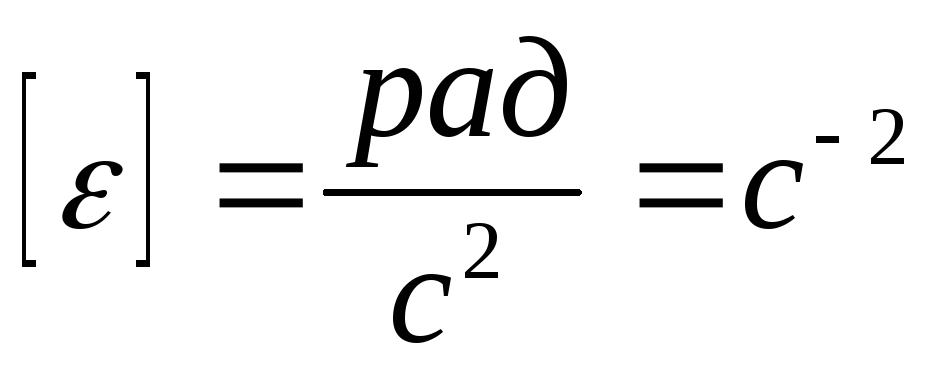 Трение в шинах позволяет автомобилю проходить поворот на значительно более высоких скоростях.
Трение в шинах позволяет автомобилю проходить поворот на значительно более высоких скоростях.
Самолеты также совершают повороты по крену. Подъемная сила из-за силы воздуха, действующей на крыло, действует под прямым углом к крылу. Когда самолет кренится, пилот получает большую подъемную силу, чем необходимо для горизонтального полета. Вертикальная составляющая подъемной силы уравновешивает вес самолета, а горизонтальная составляющая ускоряет его. Угол крена, показанный на рис. 6.23, определяется как θθ. Мы анализируем силы так же, как рассматривали случай, когда автомобиль огибает кривую с креном.
Рисунок 6.23 При вираже горизонтальная составляющая подъемной силы неуравновешена и ускоряет самолет. Нормальная составляющая подъемной силы уравновешивает вес самолета. Угол крена определяется как θθ. Сравните векторную диаграмму с диаграммой, показанной на рис. 6.22.
Интерактивный
Вместе с божьей коровкой исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол или выбрать постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой xy – положение, скорость и ускорение с использованием векторов или графиков.
Вращайте карусель, чтобы изменить ее угол или выбрать постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой xy – положение, скорость и ускорение с использованием векторов или графиков.
Интерактивный
Круговое движение требует силы, так называемой центростремительной силы, которая направлена к оси вращения. Эта упрощенная модель карусели демонстрирует эту силу.
Силы инерции и неинерциальные (ускоренные) системы отсчета: сила Кориолиса
Что общего между взлетом реактивного самолета, поворотом автомобиля, катанием на карусели и круговым движением тропического циклона? Каждая проявляет силы инерции — силы, которые просто кажутся возникающими из-за движения, потому что система отсчета наблюдателя ускоряется или вращается. Большинство людей согласятся, что при взлете в реактивном самолете вас как будто вдавливают обратно в сиденье, когда самолет ускоряется на взлетно-посадочной полосе. Однако физик сказал бы, что вы склонны оставаться неподвижными, в то время как сиденье толкает вас вперед. Еще более распространенный опыт возникает, когда вы делаете крутой поворот на своей машине, скажем, вправо (рис. 6.24). Вы чувствуете, как будто вас отбрасывает (то есть принудительно ) влево относительно автомобиля. Опять же, физик сказал бы, что вы едете по прямой (вспомните первый закон Ньютона), но машина движется вправо, а не то, что вы испытываете силу слева.
Однако физик сказал бы, что вы склонны оставаться неподвижными, в то время как сиденье толкает вас вперед. Еще более распространенный опыт возникает, когда вы делаете крутой поворот на своей машине, скажем, вправо (рис. 6.24). Вы чувствуете, как будто вас отбрасывает (то есть принудительно ) влево относительно автомобиля. Опять же, физик сказал бы, что вы едете по прямой (вспомните первый закон Ньютона), но машина движется вправо, а не то, что вы испытываете силу слева.
Рисунок
6.24
а) Водитель автомобиля чувствует себя вынужденным сместиться влево относительно автомобиля при повороте направо. Это сила инерции, возникающая из-за использования автомобиля в качестве системы отсчета. б) В земной системе отсчета водитель движется прямолинейно, подчиняясь первому закону Ньютона, а машина движется вправо. Слева на водителя относительно Земли силы нет. Вместо этого справа на автомобиль действует сила, заставляющая его поворачиваться.
Вместо этого справа на автомобиль действует сила, заставляющая его поворачиваться.
Мы можем согласовать эти точки зрения, изучив используемые системы отсчета. Давайте сосредоточимся на людях в машине. Пассажиры инстинктивно используют автомобиль в качестве системы отсчета, тогда как физик может использовать Землю. Физик может сделать такой выбор, потому что Земля представляет собой почти инерциальную систему отсчета, в которой все силы имеют идентифицируемое физическое происхождение. В такой системе отсчета законы движения Ньютона принимают форму, данную в законах движения Ньютона. Автомобиль является неинерциальной системой отсчета, потому что он ускоряется в сторону. Сила слева, ощущаемая пассажирами автомобиля, представляет собой инерционную силу, не имеющую физического происхождения (она возникает исключительно из-за инерции пассажира, а не из-за какой-либо физической причины, такой как напряжение, трение или гравитация). Автомобиль, как и водитель, фактически ускоряется вправо. Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, такого как гравитация.
Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, такого как гравитация.
Физик выберет любую систему отсчета, наиболее удобную для анализируемой ситуации. Для физика не проблема включить силы инерции и второй закон Ньютона, как обычно, если это удобнее, например, на карусели или на вращающейся планете. Неинерциальные (ускоренные) системы отсчета используются, когда это полезно. При обсуждении движения астронавта в космическом корабле, летящего со скоростями, близкими к скорости света, необходимо учитывать различные системы отсчета, как вы оцените при изучении специальной теории относительности.
Теперь давайте мысленно прокатимся на карусели, а именно на быстро вращающейся карусели для игровой площадки (рис. 6.25). Вы принимаете карусель за систему отсчета, потому что вращаетесь вместе. При вращении в этой неинерциальной системе отсчета вы чувствуете силу инерции, которая стремится сбить вас с толку; это часто называют центробежной силой (не путать с центростремительной силой). Центробежная сила является широко используемым термином, но на самом деле его не существует. Вы должны крепко держаться, чтобы противодействовать своей инерции (которую люди часто называют центробежной силой). В земной системе отсчета нет силы, пытающейся сбросить вас; подчеркнем, что центробежная сила — фикция. Вы должны цепляться за то, чтобы заставить себя двигаться по кругу, потому что иначе вы пойдете по прямой, сразу же с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прикладываете, действует по направлению к центру круга.
Центробежная сила является широко используемым термином, но на самом деле его не существует. Вы должны крепко держаться, чтобы противодействовать своей инерции (которую люди часто называют центробежной силой). В земной системе отсчета нет силы, пытающейся сбросить вас; подчеркнем, что центробежная сила — фикция. Вы должны цепляться за то, чтобы заставить себя двигаться по кругу, потому что иначе вы пойдете по прямой, сразу же с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прикладываете, действует по направлению к центру круга.
Рисунок
6,25
а) Всаднику на карусели кажется, что его сбрасывают. Эту силу инерции иногда ошибочно называют центробежной силой, пытаясь объяснить движение всадника во вращающейся системе отсчета. (b) В инерциальной системе отсчета и в соответствии с законами Ньютона его увлекает инерция (у незаштрихованного всадника Fnet=0Fnet=0 и он движется прямолинейно). Сила FцентростремительнаяFцентростремительная необходима, чтобы вызвать движение по окружности.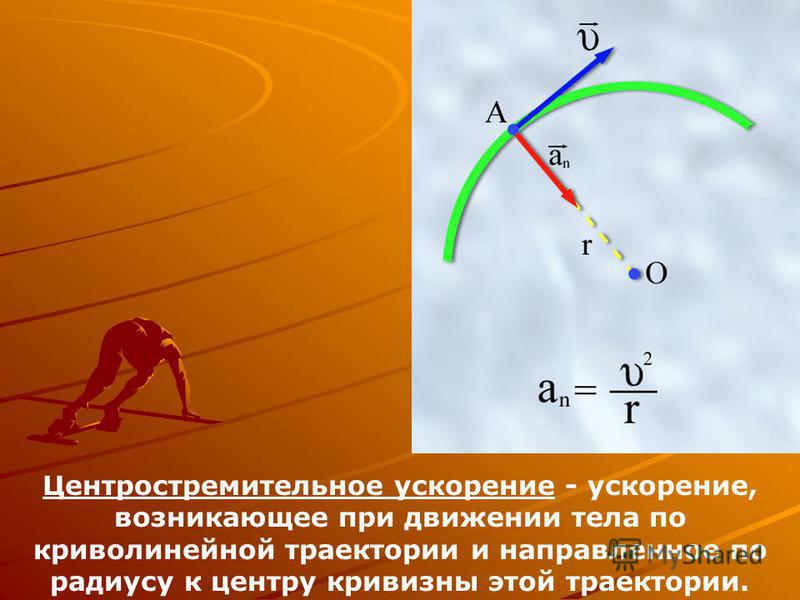
Этот инерционный эффект, уносящий вас от центра вращения, если нет центростремительной силы, вызывающей круговое движение, хорошо используется в центрифугах (рис. 6.26). Как упоминалось ранее в этой главе, центрифуга вращает образец очень быстро. Если смотреть со стороны вращающейся системы отсчета, сила инерции выбрасывает частицы наружу, ускоряя их осаждение. Чем больше угловая скорость, тем больше центробежная сила. Но на самом деле происходит то, что инерция частиц несет их вдоль линии, касательной к окружности, в то время как пробирка движется по круговой траектории под действием центростремительной силы.
Рисунок
6,26
Центрифуги используют инерцию для выполнения своей задачи. Частицы в жидком осадке оседают, потому что их инерция уносит их от центра вращения. Большая угловая скорость центрифуги ускоряет седиментацию. В конечном итоге частицы вступают в контакт со стенками пробирки, которые затем создают центростремительную силу, необходимую для того, чтобы заставить их двигаться по окружности постоянного радиуса.
Давайте теперь рассмотрим, что происходит, если что-то движется во вращающейся системе отсчета. Например, что, если вы сдвинете мяч прямо от центра карусели, как показано на рис. 6.27? Мяч движется по прямой относительно Земли (при условии пренебрежимо малого трения) и по кривой вправо на поверхности карусели. Человек, стоящий рядом с каруселью, видит, как мяч движется прямо, а карусель вращается под ним. В системе отсчета карусели мы объясняем кажущуюся кривую вправо с помощью силы инерции, называемой силой Кориолиса, которая заставляет мяч изгибаться вправо. Любой человек в этой системе отсчета может использовать силу Кориолиса, чтобы объяснить, почему объекты следуют кривым траекториям, и позволяет нам применять законы Ньютона в неинерциальных системах отсчета.
Рисунок
6,27
Глядя вниз на вращение карусели против часовой стрелки, мы видим, что шарик, скользящий прямо к краю, движется по кривой вправо. Человек двигает мяч к точке B , начиная с точки A . Обе точки поворачиваются в заштрихованные положения ( A ’ и B ’), показанные во времени, когда мяч движется по криволинейной траектории во вращающейся системе отсчета и по прямой траектории в системе отсчета Земли.
Обе точки поворачиваются в заштрихованные положения ( A ’ и B ’), показанные во времени, когда мяч движется по криволинейной траектории во вращающейся системе отсчета и по прямой траектории в системе отсчета Земли.
До сих пор мы считали Землю инерциальной системой отсчета, практически не беспокоясь о последствиях ее вращения. Тем не менее, такие эффекты существуют — например, в чередовании погодных систем. Большинство последствий вращения Земли можно качественно понять по аналогии с каруселью. Если смотреть сверху на Северный полюс, Земля вращается против часовой стрелки, как и карусель на рис. 6.27. Как и на карусели, любое движение в Северном полушарии Земли вызывает действие силы Кориолиса вправо. Как раз обратное происходит в Южном полушарии; там сила слева. Поскольку угловая скорость Земли невелика, сила Кориолиса обычно незначительна, но для крупномасштабных движений, таких как ветры, она оказывает существенное влияние.
Сила Кориолиса заставляет ураганы в северном полушарии вращаться против часовой стрелки, тогда как тропические циклоны в южном полушарии вращаются по часовой стрелке. (Термины ураган, тайфун и тропический шторм являются региональными названиями циклонов, представляющих собой штормовые системы, характеризующиеся центрами низкого давления, сильными ветрами и проливными дождями.) Рисунок 6.28 помогает показать, как происходит это вращение. Воздух течет к любой области низкого давления, а тропические циклоны содержат особенно низкое давление. Таким образом, ветры направляются к центру тропического циклона или к погодной системе низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с восходящим воздухом, что также приводит к охлаждению и образованию облаков, что делает модели низкого давления хорошо видимыми из космоса.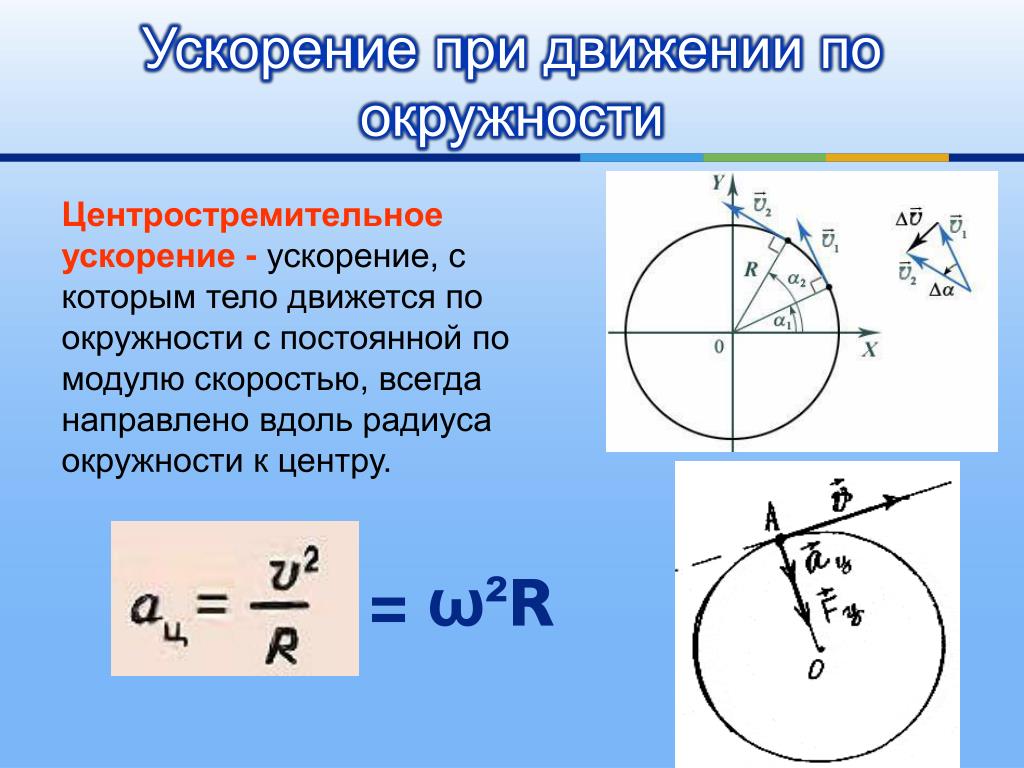 И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, поскольку высокое давление связано с опусканием воздуха, что приводит к чистому небу.
И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, поскольку высокое давление связано с опусканием воздуха, что приводит к чистому небу.
Рисунок 6,28 (a) Вращение этого урагана в Северном полушарии против часовой стрелки является основным следствием действия силы Кориолиса. (b) Без силы Кориолиса воздух попадал бы прямо в зону низкого давления, например, в тропических циклонах. (c) Сила Кориолиса отклоняет ветры вправо, вызывая вращение против часовой стрелки. (d) Ветер, идущий от зоны высокого давления, также отклоняется вправо, создавая вращение по часовой стрелке. (e) Противоположное направление вращения создается силой Кориолиса в Южном полушарии, что приводит к тропическим циклонам. (кредит a и кредит e: модификации работы НАСА)
Вращение тропических циклонов и траекторию шарика на карусели с таким же успехом можно объяснить инерцией и вращением системы под ними. Когда используются неинерциальные системы отсчета, необходимо изобрести силы инерции, такие как сила Кориолиса, чтобы объяснить кривую траекторию.

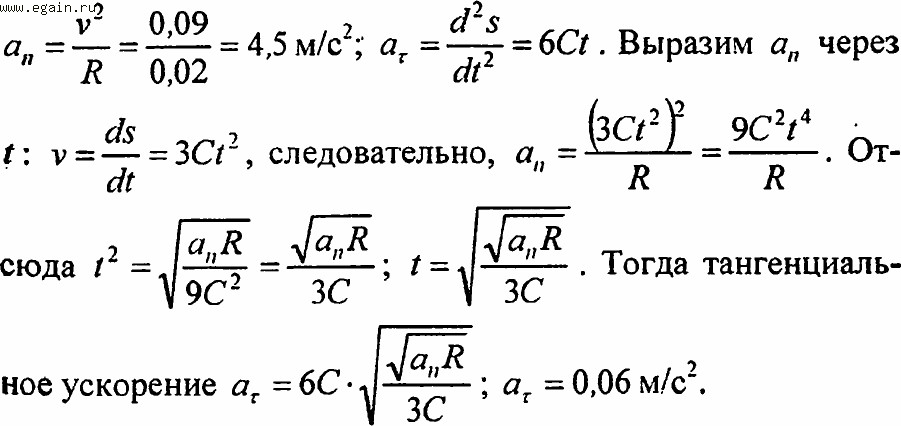 В случае кругового движения r будет радиусом; также направление радиального ускорения идет по радиусу кривизны.
В случае кругового движения r будет радиусом; также направление радиального ускорения идет по радиусу кривизны.
 Fc≡f=µsN=µsmg.
Fc≡f=µsN=µsmg.