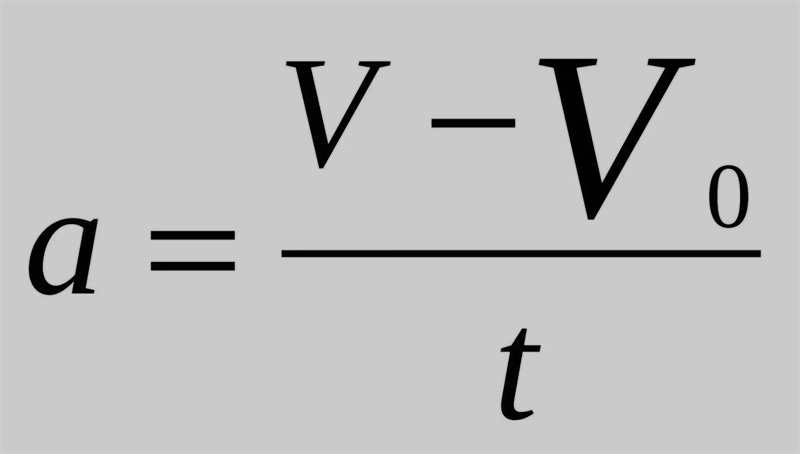Главная
Ускорение через скорость: Что такое ускорение? (статья) | Ускорение

Ускорение через скорость: Что такое ускорение? (статья) | Ускорение

Содержание

формулы и пример решения типовой задачи

Ускорение и скорость – это две важные кинематические характеристики любого типа движения. Знание зависимости этих величин от времени позволяет рассчитать пройденный телом путь. Данная статья содержит ответ на вопрос, как найти ускорение, зная скорость и время.

Понятие о скорости и ускорении

Прежде чем давать ответ на вопрос, как, зная скорость и время, найти ускорение, рассмотрим каждую из характеристик с точки зрения физики.

Скоростью называется величина, которая определяет быстроту изменения координат в пространстве при движении тела. Скорость вычисляется по формуле:

v = dl/dt.

Где dl – пройденный телом путь за время dt. Скорость всегда направлена вдоль касательной в траектории перемещения.

Движение может происходить либо с постоянной во времени скоростью, либо с переменной. В последнем случае говорят о наличие ускорения. В физике ускорение определяет быстроту изменения величины v, что в виде формулы записывается так:

a = dv/dt.

Это равенство является ответом на вопрос, как найти ускорение по скорости. Для этого достаточно лишь взять первую производную по времени от v.

Направление ускорения совпадает с направлением разницы векторов скорости. В случае прямолинейного ускоренного движения величины a и v направлены в одну сторону.

Как найти ускорение, зная скорость и время?

При изучении механики сначала рассматривают равномерное и равноускоренное типы движения по прямой траектории. В обоих случаях для определения ускорения следует выбрать промежуток времени Δt. Затем, необходимо определить значения скоростей v1 и v2 на концах этого промежутка. Среднее ускорение определится так:

a = (v2 – v1)/Δt.

В случае равномерного движения скорость остается постоянной (v2 = v1), поэтому величина a будет равна нулю. В случае же равноускоренного перемещения постоянной будет величина a, поэтому она не зависит от промежутка времени Δt в формуле.

Для более сложных случаев движения, когда скорость является некоторой функцией времени, следует пользоваться формулой для a через производную, которая была представлена в пункте выше.

Пример решения задачи

Разобравшись с вопросом, как найти ускорение, зная время и скорость, решим простую задачу. Предположим, что тело, двигаясь по некоторой траектории, изменяет свою скорость в соответствии с таким уравнением:

v = 3*t2 – t + 4.

Чему будет равно ускорение тела в момент времени t = 5 секунд?

Ускорение является первой производной величины v по переменной t, имеем:

a = dv/dt = 6*t – 1.

Чтобы ответить на вопрос задачи, следует подставить известное значение времени в полученное уравнение: a = 29 м/c2.

Ускорение. Движение. Теплота

Ускорение

Для того чтобы охарактеризовать непостоянство скорости, физика пользуется понятием ускорения.

Ускорением называют изменение скорости за единицу времени. Вместо того чтобы говорить: «скорость тела изменилась на величину a за 1 секунду», мы говорим короче: «ускорение тела равно a».

Если мы обозначим через v1 скорость прямолинейного движения в первый момент времени, а через v2 скорость в последующий, то правило расчета ускорения a выразится формулой

где t – время, в течение которого нарастала скорость.

Скорость измеряется в см/с (или м/с и т.д.), время – в секундах. Значит, ускорение измеряется в см/с за секунду. Число сантиметров в секунду делится на секунды. Таким образом, единица ускорения будет см/с2 (или м/с2 и т.д.).

Разумеется, ускорение может меняться во время движения. Однако мы не будем этим непринципиальным обстоятельством усложнять изложение. Будем молчаливо предполагать, что во время движения скорость набирается равномерно. Такое движение называется равномерно-ускоренным.

Что такое ускорение криволинейного движения?

Скорость есть вектор, изменение (разность) скоростей есть вектор, значит, и ускорение – тоже вектор. Для того чтобы найти вектор ускорения, надо разделить векторную разность скоростей на время. А как строить вектор изменения скорости, мы уже говорили.

Шоссе делает поворот. Отметим два близких положения автомашины и скорости ее представим векторами (рис. 14). Вычитая векторы, мы получим величину, вовсе не равную нулю; деля ее на промежуток времени, найдем величину ускорения. Ускорение имело место и тогда, когда величина скорости при повороте не менялась. Криволинейное движение всегда ускоренное. Неускоренное только равномерное прямолинейное движение.

Говоря о скорости движения тела, мы все время оговаривали точку зрения на движение. Скорость тела относительна. С точки зрения одной инерциальной системы она может быть большой, с точки зрения другой инерциальной системы – малой. Не нужно ли делать такие же оговорки, когда мы говорим об ускорении? Конечно, нет. Ускорение в противоположность скорости абсолютно. С точки зрения всех мыслимых инерциальных систем ускорение будет одним и тем же.

Действительно, ведь ускорение зависит от разности скоростей тела в первый и второй момент времени, а эта разность, как мы уже знаем, будет одинаковой со всех точек зрения, т.е. является абсолютной.

Ускорение операций управляемого диска – Azure Virtual Machines

  • Статья
  • Чтение занимает 10 мин
Были ли сведения на этой странице полезными?

Оцените свои впечатления

Да Нет

Хотите оставить дополнительный отзыв?

Отзывы будут отправляться в корпорацию Майкрософт. Нажав кнопку “Отправить”, вы разрешаете использовать свой отзыв для улучшения продуктов и служб Майкрософт. Политика конфиденциальности.

Отправить

В этой статье

Применимо к: ✔️ виртуальные машины Linux ✔️ виртуальные машины Windows ✔️ гибкие масштабируемые наборы ✔️ однородные масштабируемые наборы

Azure предлагает возможность увеличить производительность в виде операций ввода-вывода в секунду и скорости в МБ/с, это называется ускорение виртуальных машин и дисков. Вы можете эффективно использовать ускорение, чтобы повысить производительность как виртуальных машин, так и дисков.

Ускорение ресурсов виртуальных машин Azure и дисков не зависят друг от друга. Для подключения диска с поддержкой ускорения не требуется наличие виртуальной машины с поддержкой ускорения. Аналогичным образом, для виртуальной машины с поддержкой ускорения не требуется наличие диска с поддержкой ускорения.

Распространенные сценарии

В следующих сценариях ускорение дисков приносит существенную пользу.

  • Улучшение времени запуска. При ускорении дисков экземпляр будет запускаться быстрее. Например, диск ОС по умолчанию для виртуальных машин с поддержкой уровня “Премиум” — это диск P4 с производительностью до 120 операций ввода-вывода в секунду и 25 МБ/с. При ускорении диск P4 выдает 3500 операций ввода-вывода в секунду и 170 МБ/с, а значит время запуска сократится в шесть раз.
  • Обработка пакетных заданий — некоторые рабочие нагрузки приложений циклические по своей природе. Для них большую часть времени хватает базовой производительности, а более высокая производительность нужна в течение коротких отрезков. Примером этого является программа учета, которая обрабатывает ежедневные транзакции с небольшим объемом операций ввода-вывода на диске.
    В конце месяца эта программа завершает согласование отчетов, а вот для этого требуется значительно больший трафик на диске.
  • Пики трафика — веб-серверы и их приложения могут столкнуться со всплесками трафика в любое время. Если веб-сервер поддерживается виртуальными машинами или дисками, у которых есть ускорение, то с пиковыми нагрузками трафика будет проще справиться.

Ускорение на уровне дисков

В настоящее время существуют два типа управляемых дисков, поддерживающие ускорение: твердотельные накопители ценовой категории “Премиум” и твердотельные накопители ценовой категории “Стандартный”. Другие типы дисков сейчас невозможно ускорить. Существуют две модели ускорения дисков.

  • Модель ускорения по запросу, при которой диск будет изменяться при превышении его текущей емкости. В этой модели за каждое ускорение диска взимается дополнительная плата. Ускорение дисков по требованию доступно только для дисков SSD (цен. категория “Премиум”) емкостью более 512 ГиБ.
  • Модель на основе кредитов, в которой диск будет ускоряться только в том случае, если в его кредитном контейнере есть кредиты на ускорение. Эта модель не требует дополнительной оплаты при ускорении диска. Ускорение дисков за кредиты доступно только для дисков SSD (цен. категории “Стандартный” и “Премиум”) емкостью 512 ГиБ и меньше.

Твердотельные накопители Azure ценовой категории “Премиум” могут использовать любую модель ускорения, а твердотельные диски ценовой категории “Стандартный” на данный момент поддерживают только ускорение на основе кредитов.

Кроме того, можно изменить уровень производительности управляемых дисков, что будет идеальным вариантом, если нужно избежать постоянного использования ускорения при рабочей нагрузке.

Ускорение дисков за кредитыВключение ускорения по запросуИзменение уровня производительности
СценарииИдеально подходит для краткосрочного масштабирования (не более 30 минут).
Идеально подходит для краткосрочного масштабирования (без ограничения по времени).Идеальный вариант, если в противном случае рабочая нагрузка непрерывно использует ускорение.
СтоимостьБесплатныйТарификация может отличаться, дополнительные сведения см. в разделе Выставление счетов.Стоимость каждого уровня производительности фиксирована, дополнительные сведения см. в разделе Цены на управляемые диски.
ДоступностьДоступно только для дисков SSD (цен. категории “Стандартный” и “Премиум”) емкостью 512 ГиБ и меньше.Доступно только для дисков SSD уровня “Премиум” емкостью более 512 ГиБ.Доступно для дисков SSD уровня “Премиум” любых размеров.
ВключениеПо умолчанию включено на подходящих дисках.Включается пользователем.Пользователь должен вручную изменить свой уровень.

Включение ускорения по запросу

Диски SSD (цен. категория “Премиум”), использующие модель ускорения дисков по запросу, могут ускоряться сверх первоначально подготовленных целей и так часто, как это необходимо для рабочей нагрузки, вплоть до максимальной цели ускорения. Например, на диске P30 размером 1 ТиБ количество подготовленных операций ввода-вывода в секунду составляет 5000. Но если на этом диске включить функцию ускорения, то рабочие нагрузки могут выдавать для него операции ввода-вывода вплоть до максимальной производительности ускорения в 30 000 операций ввода-вывода в секунду и скоростью 1 000 Мбит/с. Дополнительные целевые показатели нагрузки на каждом поддерживаемом диске см. в статье целевые показатели масштабируемости и производительности для дисков виртуальных машин.

Если вы предполагаете, что ваши рабочие нагрузки будут часто выходить за пределы подготовленного целевого объекта производительности, ускорение дисков не будет целесообразным решением. В этом случае мы рекомендуем изменить уровень производительности диска на более высокий, чтобы повысить производительность базовых показателей. Просмотрите сведения о выставлении счетов и оцените их на соответствие шаблону трафика рабочих нагрузок.

Прежде чем включить ускорение по запросу, изучите следующую информацию:

  • На дисках SSD ценовой категории “Премиум”, объем которых менее 512 ГиБ, невозможно включить ускорение по запросу. На дисках SSD ценовой категории “Премиум” менее 512 ГиБ всегда будет использоваться ускорение на основе кредита.
  • Ускорение по запросу поддерживается только для дисков SSD ценовой категории “Премиум”. Если такой диск SSD с включенным режимом ускорения по запросу переключается на другой тип диска, то ускорение отключается.
  • Ускорение по запросу не отключается автоматически при изменении уровня производительности. Если вы хотите изменить уровень производительности, но не хотите использовать ускорение дисков, его необходимо отключить.
  • Ускорение по запросу можно включить только при отсоединении диска от виртуальной машины или при остановке виртуальной машины. Ускорение по запросу можно отключить через 12 часов после включения.
Доступность по регионам

Сейчас модель по запросу для ускорения дисков доступна во всех регионах Azure.

Выставление счетов

За диски SSD (цен. категория “Премиум”), использующие модель ускорения по запросу, взимается фиксированная плата за почасовое ускорение, а плата за транзакции применяется к любым транзакциям, связанным с ускорением за пределами подготовленного целевого объекта. Плата за транзакции взимается на основе модели оплаты по мере использования, принимая во внимание операции ввода-вывода диска без кэширования, в том числе операции чтения и записи, превышающие подготовленные целевые объекты. Ниже приведен пример шаблонов трафика диска на основе расчетного часа:

Конфигурация диска: SSD (цен. категория “Премиум”) — 1 Тиб (P30) с включенным ускорением дисков.

  • От 00:00:00 до 00:10:00 — количество операций ввода-вывода в секунду ниже подготовленного целевого объекта в 5 000 операций ввода-вывода в секунду
  • От 00:10:01 до 00:10:10 — приложение запустило пакетное задание, которое привело к ускорению операций ввода-вывода в секунду диска и 6 000 операций ввода-вывода в секунду в течение 10 секунд
  • От 00:10:11 до 00:59:00 — количество операций ввода-вывода в секунду ниже подготовленного целевого объекта в 5 000 операций ввода-вывода в секунду
  • От 00:59:01 до 01:00:00 — приложение запустило другое пакетное задание, которое привело к ускорению операций ввода-вывода в секунду диска и 7 000 операций ввода-вывода в секунду в течение 60 секунд

Плата за ускорение этого расчетного часа состоит из таких двух типов расходов:

Первый тип — фиксированная плата за использование ускорения в X долл.  США (определяется вашим регионом). Эта фиксированная плата взимается за диск всегда, независимо от статуса подключения, и действует до тех пор, пока диск не будет отключен.

Второй — это плата за транзакции, связанные с ускорением. Ускорение дисков выполнено в двух временных сегментах. От 00:10:01 до 00:10:10 — аккумулятивная транзакция, связанная с ускорением, составляет (6 000 – 5 000) X 10 = 10 000. От 00:59:01 до 01:00:00 — аккумулятивная транзакция, связанная с ускорением, составляет (7 000 – 5 000) X 60 = 120 000. Общее число транзакций ускорения — 10 000 + 120 000 = 130 000. Плата за транзакцию ускорения будет взиматься в размере Y долл. США из расчета 13 единиц из 10 000 транзакций (на основе региональных цен).

Таким образом, общие затраты на ускорение диска за этот расчетный час равны $X + $Y. Такое же вычисление применяется и для ускорения сверх подготовленного целевого объекта (Мбит/с). Мы преобразуем избыток МБ в транзакции с размером операций ввода-вывода 256 КБ. Если объем трафика на диске превышает подготовленные операции ввода-вывода в секунду и Мбит/с, для расчета количества транзакций ускорения можно использовать приведенный ниже пример.

Конфигурация диска: SSD (цен. категория “Премиум”) — 1 Тб (P30) с включенным ускорением дисков.

  • От 00:00:01 до 00:00:05 — приложение запустило пакетное задание, которое привело к ускорению операций ввода-вывода в секунду диска с результатом 10 000 операций ввода-вывода в секунду и скорости 300 Мбит/с в течение пяти секунд.
  • От 00:00:06 до 00:00:10 — приложение запустило задание восстановления, которое привело к ускорению операций ввода-вывода в секунду диска с результатом 6 000 операций ввода-вывода в секунду и скорости 600 Мбит/с в течение пяти секунд.

Транзакция ускорения учитывается как максимальное количество транзакций ускорения операций ввода-вывода в секунду или Мбит/с. От 00:00:01 до 00:00:05 — аккумулятивная транзакция, связанная с ускорением, с максимальным количеством в ((10 000 – 5 000), (300 – 200) * 1024/256)) * 5 = 25 000 транзакций. От 00:00:06 до 00:00:10 — аккумулятивная транзакция, связанная с ускорением, с максимальным количеством в ((6 000 – 5 000), (600 – 200) * 1024/256)) * 5 = 8 000 транзакций. Кроме того, чтобы узнать общую стоимость включения ускорения дисков по запросу, необходимо учитывать и фиксированную плату за включение ускорения.

Ознакомьтесь со сведениями на странице цен на Управляемые диски, чтобы узнать больше о ценах и использовании Калькулятора цен Azure для выполнения оценок для рабочей нагрузки.

Сведения о включении ускорения по запросу см. в разделе Включение ускорения по запросу.

Ускорение дисков за кредиты

Для дисков SSD (цен. категория “Премиум”) размером P20 и меньше можно использовать платное ускорение дисков. Для дисков SSD (цен. категория “Стандартный”) размером E30 и меньше можно использовать платное ускорение дисков. Для дисков SSD (цен. категория “Премиум” и “Стандартный”) платное ускорение дисков доступно во всех регионах общедоступных облаков, а также облаков для государственных организаций и Китая. По умолчанию функция ускорения включается для всех новых и имеющихся развертываний дисков поддерживаемых размеров. Для ускорения на уровне виртуальной машины можно использовать только платное ускорение дисков.

Ускорение операций на уровне виртуальной машины

для ускорения на уровне виртуальной машины используется только модель на основе кредита, которая по умолчанию включена для большинства Premium служба хранилища поддерживаемых виртуальных машин.

Поток ускорения

Система платного ускорения одинаково применяется как на уровне виртуальной машины, так и на уровне диска. Ваш ресурс (виртуальная машина или диск) будет запускаться с полным количеством кредитов в контейнере ускорения. Эти кредиты позволяют выполнять ускорение на максимальной скорости 30 минут. Вы накапливаете кредиты каждый раз, когда показатели использования операций ввода-вывода или МБ/с ресурса ниже целевого уровня производительности. Если вы накопили кредиты на ускорение для ресурса, а рабочая нагрузка нуждается в дополнительной производительности, ресурс может использовать эти кредиты, чтобы повысить лимиты производительности и тем самым увеличить свою производительность в соответствии с потребностями рабочей нагрузки.

Решение о том, как потратить имеющиеся кредиты, остается за вами. Вы можете использовать свои 30 минут кредитов ускорения на протяжении дня последовательно или в отдельных случаях. При развертывании ресурсы предоставляются с полным распределением кредитов. Если вы используете все кредиты, их пополнение будет длиться один день. Вы можете тратить кредиты по своему усмотрению, при этом для ускорения операций ресурсов не обязательно, чтобы контейнер был полон. Накопление кредитов на ускорение зависит от каждого ресурса, поскольку оно зависит от неиспользуемых операций ввода-вывода в секунду и МБ/с с использованием ниже целевого уровня производительности. Ресурсы с более высокой базовой производительностью могут накапливать кредиты на ускорение быстрее, чем ресурсы с более низкой базовой производительностью. Например, при простое диска P1 будет накапливаться 120 операций ввода-вывода в секунду, в то время как при простое диска P20 — 2 300.

Состояния ускорения

Если включить функцию ускорения, ресурсу может быть присвоено одно из трех указанных ниже состояний.

  • Накопление — трафик операций ввода-вывода используется меньше целевого уровня производительности. Накопление кредитов на ускорение для операций ввода-вывода в секунду и скорости (МБ/с) происходит отдельно друг от друга. Ваш ресурс может накапливать кредиты на операции ввода-вывода в секунду и использовать кредиты на скорость (МБ/с) или наоборот.
  • Ускорение — трафик операций ввода-вывода превышает целевой уровень производительности. Трафик ускорения будет независимо потреблять кредиты операций ввода-вывода или пропускной способности.
  • Константа — трафик операций ввода-вывода используется в соответствии с целевым уровнем производительности.

Примеры ускорения операций

В следующих примерах показано, как ускорение работает с различными сочетаниями виртуальных машин и дисков. Чтобы упростить примеры для дальнейшего использования, мы сосредоточимся на скорости (МБ/с), однако к операциям ввода-вывода применяется та же логика.

Виртуальная машина с увеличивающейся производительностью с дисками, не поддерживающими ускорение

Сочетание виртуальных машин и дисков:

  • Standard_L8s_v2
    • Операции МБ/с без кэширования: 160
    • Макс. ускорение МБ/с: 1 280
  • Диск ОС P50
    • Подготовленные МБ/с: 250
    • Разбивка по запросу: не включено
  • 2 диска данных P50
    • Подготовленные МБ/с: 250
    • Разбивка по запросу: не включено

После начальной загрузки на виртуальной машине запускается приложение с некритичной рабочей нагрузкой. Для этой рабочей нагрузки требуется скорость 30 МБ/с, которая равномерно распределяется по всем дискам.

Затем приложению необходимо обработать пакетное задание, для которого требуется скорость 600 МБ/с. Диск Standard_L8s_v2 ускоряет операции в соответствии с этим спросом, а затем запросы к дискам равномерно распределяются по дискам P50.

Виртуальная машина, поддерживающая ускорение, с дисками с увеличивающейся производительностью

Сочетание виртуальных машин и дисков:

  • Standard_L8s_v2
    • Операции МБ/с без кэширования: 160
    • Макс. ускорение МБ/с: 1 280
  • Диск ОС P4
    • Подготовленные МБ/с: 25
    • Макс. ускорение МБ/с: 170
  • 2 диска данных P4
    • Подготовленные МБ/с: 25
    • Макс. ускорение МБ/с: 170

При запуске виртуальная машина ускоряет операции, чтобы отправить диску ОС запрос на предельную скорость 1 280 МБ/с, а диск ОС в ответ предоставляет скорость 170 МБ/с.

После запуска вам нужно запустить приложение с некритической рабочей нагрузкой. Для этого приложения требуется скорость 15 МБ/с, которая равномерно распределяется по всем дискам.

Затем приложению необходимо обработать пакетное задание, для которого требуется скорость 360 МБ/с. Диск Standard_L8s_v2 ускоряется в соответствии с этим спросом, а затем отправляет запрос. Диску ОС требуется всего лишь скорость 20 МБ/с. Оставшиеся 340 МБ/с обрабатываются с помощью ускорения дисков данных P4.

Дальнейшие действия

Ускорение без новых людей и овертаймов – Digital Enterprise

На тренингах я рассказываю о том, что гибкие практики ориентированы на оптимизацию по скорости. Это очень легко понимается и принимается группой. Что тут сложного? Мы не за стопроцентную утилизацию, нам важно обеспечить максимальную скорость изменений. А дальше? Дальше я рассказываю о том, что целевая картинка – это не прирост скорости на 10-20-50 процентов, а кратное увеличение скорости поставки. Вот тут уже начинаются вопросы.

Люди, знающие разработку ПО не понаслышке, которые годами решают практические задачи в своем бизнесе, за редким исключением, не могут представить себе кратного ускорения без увеличения ресурсов. Для них рассказ о том, что возможно выпускать обновления кратно быстрее без переработок и увеличения количества людей, выглядит как попытка продать волшебную таблетку. Их сомнения явно читаются в задаваемых вопросах. Для того, чтобы двигаться дальше, нужно вернуть доверие.

В первую очередь, стоит еще раз напомнить, почему нам нужно кратное ускорение, а не прибавка в 10-50 процентов. Не секрет, что основная претензия бизнес-заказчиков в адрес команд разработки – это скорость. Бизнес работает в конкурентной среде с высокой неопределенностью, и быстрое получение новых возможностей от собственного ИТ является вопросом выживания. Гибкие практики призваны за счет культурных, структурных и инженерных преобразований увеличить скорость поставки. Но давайте смотреть правде в глаза. Эти преобразования на большом и сложном ИТ-ландшафте стоят дорого, очень-очень дорого. И без кратного ускорения эти затраты на такие преобразования никогда не окупятся.

Теперь поговорим о том, откуда можно взять это самое кратное ускорение. Давайте для начала представим жизненный путь задачи следующим образом:

Там, где находится желтый флажок, – возникла идея. Это еще не задача, которую разработка может начать решать. Это некоторое видение проблемы, решив которую, бизнес может получить преимущества или снизить свои риски. Идей у бизнеса всегда много. Гораздо больше, чем у разработки имеется фактических возможностей по их реализации. Часть этих идей погибнет в эволюционном отборе, про некоторые из них разработка даже никогда не узнает. Тем не менее, именно от момента возникновения идеи мы считаем время вывода на рынок, тот самый time-to-market, за который так переживает бизнес-заказчик. Итак, некоторое количество идей, преодолев естественный отбор, доходит до зеленого флажка. В этот момент происходит принятие решения о том, что мы точно будем делать эту штуку, и идея превращается в задачу (а скорее в набор задач) для разработки. Но мы помним, что задач у нас по-прежнему гораздо больше, чем возможностей. И очень редко у разработки есть возможность немедля начать работу над задачей, которую только что принесли. Особенно комичной в этом контексте выглядит попытка определить срок поставки задачи в точке принятия решения. Даже если мы сегодня можем точно оценить время, необходимое на производство этой задачи и тех задач, что стоят перед ней (а это уже неправда), все равно никто нам не сможет гарантировать, что завтра очередь будет такой же. Так что попытка угадать срок поставки в момент принятия решения о разработке – дело неблагодарное. Тем не менее, решение о производстве принято, и заказчик уже ожидает от разработки результат, несмотря на то, что разработка еще не начала работать над задачей. От зеленого флажка до поставки результата считается время ожидания (Customer Lead Time).

Что же дальше? Дальше команда разработки начинает работу по производству изменений. Именно за красным флажком, при переходе задачи через точку принятия обязательств, у разработки возникают обязательства доставить результат заказчику. Конечно, заказчик по-прежнему может отказаться от задачи. Это может произойти в любой момент, даже тогда, когда большая часть работы выполнена. Мы все читали «Манифест гибкой разработки» и знаем про постоянную готовность к изменениям. Но являясь ответственными, мотивированными профессионалами, (манифест писали именно для таких ребят) мы должны помнить о том, что чем ближе задача к стадии готовности, тем дороже обходятся связанные с ней изменения. Разработка должна помнить об этом и не давать забывать заказчику. От красного флажка (точки принятия обязательств) до момента поставки считается время в системе (System Lead Time). Это очень важный показатель. Время в системе – одна из ключевых характеристик, определяющих насколько эффективной является разработка. Анализируя статистику по этому показателю, можно с высокой вероятностью предсказывать сроки выпуска для новых задач, выявлять риски и классифицировать задачи. Но сейчас мы используем эту метрику для того, чтобы показать, каким образом можно добиться кратного ускорения поставки, не нанимая дополнительных людей и не работая шестнадцать часов в день вместо восьми.

Давайте пока рассмотрим только нашу производственную систему, не обращая внимания на то, что происходит перед ней. Итак, внутри нашей системы, как правило, много задач, очень много задач. Там присутствуют задачи разных типов, приоритетов и размеров. Этих задач гораздо больше, чем людей в команде. Я видел от нескольких десятков до нескольких сотен задач у команд из 7-9 человек. Эти задачи не возникли из ниоткуда и не собрались там по злому умыслу разработчиков. Все дело в том, что, разрываясь между срочным и важным, люди склонны отказываться от выбора и выбирать понятное. Зачем нам разбираться с текущей задачей, где ничего не понятно и нужно спросить человека, который вчера ушел в отпуск? Как раз для таких задач у нас есть статус «отложено». А вместо нее мы возьмем новую интересную задачку, мы же не бездельники… В итоге между точкой принятия обязательств и точкой поставки (исполнения обязательств) находятся десятки задач, в которые «вморожены» сотни человеко-часов. Очень недешевых человеко-часов! Мало того, что значительная часть этих трудозатрат станет безусловными потерями в чистом виде (задачи «протухают»), беда еще и в том, что наличие большого количества задач в системе затрудняет координацию и приоритизацию. Управлять этим застывшим потоком и поставлять хотя бы что-то оказывается непросто. Сомневаетесь? Это кажется незначительным? Давайте посмотрим на то, как выглядит обычная история жизни задачи в производственной системе. 

Для отдельной задачи из всего времени, которое она находится в системе, в среднем 90% составляет время ожидания! А для большого количества команд эта цифра еще выше – 95-97%. Не верите, что у вас так? Давайте попробуем измерить реальное время производства (Touch Time) для выпущенных вами задач и соотнести его с временем в системе. Только честно!

Отношение времени производства ко времени в системе, выраженное в процентах, называется эффективностью потока. Как было сказано выше, для обычных команд разработки этот показатель находится в диапазоне от 3% до 10%. А теперь представьте себе, что благодаря сокращению количества работы в системе мы можем сократить ожидание для отдельно взятой задачи, с 95% времени до 70%. Эффективность в 30% – нормальный показатель для команд, управляющих работой в потоке. При этом время производства у нас останется тем же. Не нужно делать работу быстрее, достаточно только перестать начинать «лишнюю» работу и фокусироваться на доведении дел до конца. А если при этом мы еще за счет автоматизации минимизируем время на этапах, не добавляющих ценность (например, при тестировании) и избавимся от лишней работы? Вот вам, как минимум, трехкратный прирост в скорости на одной только производственной системе. Разумеется, это все не бесплатно. Уменьшая количество элементов (задач) в системе мы, скорее всего, получим некоторое снижение количества элементов, поставляемых за интервал времени (Delivery Rate). Но при этом мы получим кратное уменьшение времени в системе для всех поставляемых элементов и существенное снижение времени ожидания каждой задачи для бизнес-заказчиков. Выбирая между количеством и скоростью, мы делаем выбор в пользу скорости потому, что именно скорость является основным требованием бизнеса.

О том, с чего начинается путь к скорости и что же происходит там, где «водятся драконы», читайте в следующей статье. А лучше приходите на наши курсы по гибким практикам, и там мы разберем историю с кратным ускорением поставки более подробно.

Скорость, скорость и ускорение

Скорость, скорость и ускорение

Скорость, скорость и ускорение

Время

Мы измеряем момент времени t с помощью часов. Единица времени СИ – это второй. Показание часов в секундах зависит от выбора источника. Часы в разных часовых поясах имеют разные показания и показания остановки. смотреть зависит от того, когда он был запущен. Временной интервал ∆t = t позже – t ранее определяется как разница между более поздним временем и более раннее время.Это всегда неотрицательное число (положительное или нулевое). Интервал ∆t – это скаляр, число с единицами измерения.

Скорость и скорость

Когда объект движется в пространстве, его положение меняется. Предположим, что в момент времени t 1 он находится в позиции P 1 , а в более позднее время t 2 он находится в позиция П 2 . Вектор смещения: d = P 2 – П 1 . На временном интервале ∆t = t 2 – t 1 объект сместился на d . Его средняя скорость дюйм этот временной интервал ∆t определяется как < v > = d / ∆t. Смещение d – вектор, временной интервал ∆t равен скаляр. Деление вектора на скаляр дает другой вектор. Среднее скорость < v > вектор. Средняя скорость – это расстояние, пройденное за время интервал ∆t, деленный на ∆t.Расстояние – это скаляр, т.е. число с единицами. Разделив расстояние на ∆t, получим другой номер с единицами. Таким образом, средняя скорость скаляр.

Проблема:

За 5 минут бегун один раз пробегает дистанцию ​​в одну милю. Какой его Средняя скорость? Какая у него средняя скорость?

Решение:

  • Обоснование:
    Через 5 минут бегун возвращается в исходное положение. P 2 – P 1 = 0. Смещение равно нулю. Пройденное расстояние составляет одну милю.
  • Детали расчета:
    Смещение равно нулю, поэтому его средняя скорость равна нулю.
    средняя скорость – это расстояние, пройденное за время интервал ∆t. Средняя скорость следовательно, (1 миля) / (5 минут) = (12 миль) / (60 минут) = 12 миль / ч.

    Примечание. Скорость – это скаляр, скорость – вектор. Средняя скорость в целом не равна к величине средней скорости.
Проблема:

Спринтер бежит на север по прямой и преодолевает расстояние 100 м за 12 с. Какая у нее средняя скорость? Какая у нее средняя скорость?

Решение:

Сводка

Средняя скорость – это расстояние, разделенное на время, которое потребовалось, чтобы преодолеть это расстояние. Если человек идет 1 км на запад, затем разворачивается и идет 1 км на восток, расстояние это человек преодолевает 2 км.Если преодолеть это расстояние за 20 минут, то средняя скорость 2 км / 20 минут = 2000 м / (20 * 60 с) = 1,67 м / с.

Средняя скорость – вектор. Это вектор смещения, указывающий от начального положения к конечному положению, делится на время. В приведенном выше примере начальная и конечная позиции совпадают. Вектор смещения равен нулю. Итак, средняя скорость равна нулю.

Ссылка: Скорость и скорость (пожалуйста, исследуйте!)

Поскольку величина и направление вектора смещения зависят от система отсчета, в которой система координат закреплена и в состоянии покоя, скорость объекта и зависит от системы отсчета, относительно которой он измеряется.

Проблема:

Автомобиль переместился вперед на расстояние 6 м, а ребенок переместился вперед от заднего сиденья до переднего на расстояние 1 м в интервале времени 2 с. Найдите среднюю скорость ребенка относительно машины и относительную скорость. к дороге.

Решение:

  • Рассуждение:
    Скорость объекта зависит от системы отсчета,
  • Детали расчета:
    Использование автомобиля в качестве системы отсчета и привязка системы координат к машина, водоизмещение ребенка d = (1 м) и .
    Его скорость < v > = (1 м) / (2 с) i = (0,5 м / с) i .
    Использование дороги в качестве системы отсчета и привязка системы координат к дорога, водоизмещение ребенка d = (6 м) i + (1 м) i = (7 м) i .
    Его скорость < v > = (7 м) / (2 с) i = (3,5 м / с) i .

Примечание: скорость объекта зависит от системы отсчета, она равна не количество, с которым согласны все наблюдатели.Объект может покоиться в одном система отсчета и имеющая ненулевую скорость в другой системе отсчета.
Когда родители говорят ребенку сидеть спокойно в движущейся машине, они имеют в виду сидеть спокойно. по отношению к машине, а не по отношению к дороге.

Остановлен, вы ждете, пока светофор не изменит цвет с красного на зеленый, когда внезапно у вас появляется ощущение, что вы двигаетесь, даже если вы нажимаете на педаль тормоза. Но потом вы замечаете, что большой грузовик или автобус в полоса рядом с вами – это транспортное средство, которое фактически движется относительно земля.Чтобы сделать вывод о том, что мы движемся относительно земли, мы в основном полагаются на визуальные подсказки. Когда мы видим, как движется наше окружение, мы делаем вывод, что мы переезжаем. Обычно мы можем быстро установить истинное ситуации, так как мы подсознательно понимаем, что есть несоответствие и быстро получить дополнительную информацию из нашего окружения.

Моделирование ниже исследует относительное движение. Вид всегда водитель в автомобиле или кто-то движется с той же скоростью, что и водитель смотрит прямо в картинку.Вы можете выбрать три разных ситуаций и масштабирования и поворота обзора, Пожалуйста, нажмите на изображение!

Разгон

Всякий раз, когда скорость объекта изменяется, объект ускоряется. Предположим, что в момент времени t 1 объект имеет скорость v 1 , и в более позднее время t 2 он имеет скорость v 2 . Изменение в скорость ∆ v = v 2 – v 1 в интервале времени ∆t = t 2 – t 1 . Среднее ускорение объекта за этот промежуток времени ∆t определяется как < a > = ∆ v / ∆t. Среднее ускорение < a > – вектор. Это вектор скорости в последний момент времени минус вектор скорости в начальное время, деленное на временной интервал.

Ссылка: Разгон

Примечание: когда ваша скорость МЕНЯЕТ , вы ускоряетесь. Вы ускоряетесь, когда вы ИЗМЕНИТЬ свою скорость, ИЗМЕНИТЬ направление движения или и то, и другое. Ключевое слово – ИЗМЕНИТЬ .

Если ваша скорость НЕ меняется, то, как бы быстро вы двигаетесь, вы НЕ ускоряетесь с .

постоянная скорость <--> нулевое ускорение

Проблема:

Вы едете с постоянной скоростью 20 миль / ч по кварталу, проверяя район.Вы ускоряетесь?

Решение:

  • Рассуждение:
    Да, направление вектора скорости все время меняется.
Проблема:

Вы едете на восток со скоростью 30 миль в час. Вы видите, как мяч катится по дорога и ты сильно ломаешься, потому что боишься, что прибежит ребенок после бала. Вы останавливаетесь через 0,8 секунды. Каково направление вашего средняя скорость за этот короткий промежуток времени? Какое у вас среднее ускорение?

Решение:

  • Рассуждение:
    Направление вашей средней скорости – восток.Вы путешествуете на восток с снижая скорость до полной остановки. Изменение вашей скорости составляет ∆ v = v 2 – v 1 = 0-30 миль / ч восток = -30 миль / ч восток = 30 миль в час на запад.
  • Детали расчета:
    Переведем в единицы СИ.
    30 миль в час, умноженные на 1609 м / милю, умноженные на 1 час / (3600 с) = 13,4 м / с.
    Ваше среднее ускорение составляет ∆ v / ∆t = (13,4 м / с) / (0,8 с) запад = 16.8 м / с 2 запад.

Ссылки: Ускорение, Равномерное круговое движение

Примечание: ускорение абсолютное. Ускорение объекта не зависит от системы отсчета, это количество, с которым согласны все наблюдатели. Даже без внешних ссылок вы можете определить, ускоряетесь ли вы.

Пример:

Поездка на лифте: Вы на мгновение чувствуете себя тяжелее, когда лифт ускоряется вверх, и становится легче когда он ускоряется вниз.

Модуль 1: Вопрос 2

Когда вы резко поворачиваете машину налево, незакрепленные предметы на приборной панели начинают скользить Направо. Эти объекты ускоряются вправо?

Обсудите это со своими однокурсниками в дискуссионный форум!

Ссылки: Ускорение, Равномерное круговое движение

Скорость, скорость и ускорение – Физика для детей

Посмотрите вокруг и наблюдайте за тем, что вы видите.Вы можете увидеть людей, цветы, птиц, автомобили, автобусы и многое другое. Можете ли вы сказать, что общего во всем, что вы видите вокруг? Это движение или движение. Все в этой Вселенной движется. Скорость движения каждого объекта вокруг вас разная. Некоторые могут двигаться очень быстро, в то время как другие могут двигаться очень медленно. Но во всем вокруг видно определенное движение. Вы можете сказать, что некоторые объекты в вашей комнате или зданиях, которые вы видите, не двигаются, или, если вы стоите на месте, вы не двигаетесь.Но заметьте, что вы живете на планете Земля, которая постоянно движется вокруг Солнца. Луна движется вокруг Земли, Солнце и планеты движутся по галактике. Свет перемещается из одного места в другое, и даже крошечная частица атома постоянно перемещается.

Разница между скоростью, скоростью и ускорением?

Это движение и скорость движения получили некоторые основные термины в физике. Он известен как физика движения и включает такие термины, как скорость, скорость и ускорение.Давайте посмотрим на них по очереди.

Что такое скорость?

Термины «Скорость» и «Скорость» часто используются в повседневной жизни для обозначения одного и того же, но оба они сильно отличаются друг от друга. Скорость – это мера того, насколько быстро или медленно движется объект. Скорость – это скалярная величина, потому что ее можно измерить числовым значением. Мы знаем, что:

Какова формула скорости?

Скорость = Расстояние / Время.

Что такое скорость?

Скорость – это направление, в котором движется объект.Это скорость, с которой объект меняет свое положение. Скорость – это векторная величина, то есть она состоит из двух основных характеристик. Его можно описать как числовым значением, так и направлением.

Какова формула скорости?

Скорость = (изменение расстояния) / (изменение во времени)

Рассмотрим пример: автомобиль едет по шоссе со скоростью 60 км / час. Возможно, в данный момент машина движется с этой скоростью, но она может изменить свою скорость позже.Но здесь мы не знаем, в каком направлении едет машина. Но если мы говорим, что машина движется со скоростью 60 км / час в северном направлении, то мы знаем, что скорость составляет 60 км / час на север.

Что такое ускорение?

А вот и поворот в истории – Ускорение. Ускорение – это измерение того, насколько скорость объекта изменяется в определенный момент времени, который обычно составляет 1 секунду. Таким образом, скорость движущегося объекта со временем может как увеличиваться, так и уменьшаться.

Итак, машина движется со скоростью 60 км / час на север. Водитель нажимает на педаль газа, и машина начинает двигаться все быстрее и быстрее. Это изменение скорости, известное как ускорение.

Какова формула ускорения?

Ускорение = (изменение скорости) / (изменение во времени)

Давайте посмотрим на другой пример. Предположим, вы едете на велосипеде. Вы начинаете с медленного нажатия на педали, а через некоторое время начинаете нажимать на педали очень быстро.Итак, вы ускоряетесь, чтобы увеличить свою скорость.

Ускорение измеряется в метрах / секунду в квадрате.

Итак, если у вас есть скорость в метрах в секунду и время в секундах, вы можете рассчитать ускорение, используя формулу. Ускорение, как и скорость, также является вектором, поскольку имеет числовую величину в метрах в секунду, а также направление.

Когда у нас есть объект, который изменяет скорость на постоянное время, это называется постоянным ускорением.Здесь движущийся объект продолжает набирать скорость или постоянно увеличивает свою скорость. Предположим, вы бросаете мяч на склон, он будет двигаться вниз все быстрее и быстрее с каждой секундой. В 1-ю секунду скорость равна 10 м / с, в 2-ю секунду – 15 м / с, а в 3-ю секунду – 20 м / с. Таким образом, имеется постоянное ускорение 5 м / с.

Когда у нас есть объект, который изменяет свою скорость, замедляясь или уменьшаясь, это называется отрицательным ускорением или замедлением.Предположим, вы едете на велосипеде и перестанете нажимать на педали, колеса начнут двигаться все медленнее и медленнее. Это отрицательное ускорение. Здесь скорость движущегося объекта продолжает уменьшаться.

5 интересных фактов о скорости, скорости и ускорении

  1. Сила тяжести – важная причина ускорения. Сила тяжести Земли, притягивающая падающий объект к себе, ускоряет его ускорение. Итак, если вы ныряете с доски для плавания, вы начнете с небольшой скорости, но скорость увеличивается каждую секунду из-за силы тяжести.
  2. Галилей был первым ученым, измерившим скорость.
  3. Самая высокая скорость во всей Вселенной – это скорость света. Скорость света 299 792 458 м / с.
  4. Ньютон обнаружил, что кинетическая энергия движущегося объекта линейна с его массой и квадратом его скорости. Масса объекта может изменить его скорость. Гравитация других планет отличается от силы тяжести Земли, потому что у них разные массы.
  5. Термин «убегающая скорость» используется для обозначения минимальной скорости, которую должно иметь тело, чтобы избежать гравитационного притяжения Земли.

с физикой (скорость спринта) –

Скорость – это изменение расстояния за время, необходимое для того, чтобы изменение расстояния произошло. Например, если бы я начал бег из неподвижного положения (начальное расстояние «Di») и пробежал 40 ярдов (конечное расстояние «Df») за 4,4 секунды, моя средняя скорость за весь забег была бы изменением расстояния (40 ярдов), деленным на время, необходимое для прохождения этого расстояния (4,4 секунды).

Средняя скорость = изменение расстояния (Df-Di) / время (t)

Средняя скорость = (40-0) / (4.4) = 9,09 ярдов в секунду

Средняя скорость на дистанции такой длины не может сказать тренеру целую группу. Да, он говорит нам, какую скорость мы должны иметь в среднем, чтобы пробежать 40 ярдов за 4,4 секунды, но спринт редко (обычно никогда) не происходит с постоянной скоростью. Обычно мы либо замедляемся, либо ускоряемся и редко сохраняем скорость.

Итак, чтобы сделать это более применимым, мы можем захотеть взглянуть на расщепление расстояний и соответствующие скорости.Мы можем сделать это так просто: мы можем взглянуть на тот же 40-ярдовый бег, но на этот раз с разбегом по 10 ярдов.

Почему это выгодно? Это может сказать тренеру, ускоряется ли спортсмен все 40 ярдов и никогда не достигает максимальной скорости (скорость продолжает расти), это может сказать тренеру, с какими разделами (фазами спринта) спортсмен борется больше всего ( низкая начальная скорость по сравнению с другими спортсменами), и это также может сообщить тренеру, может ли методика, которую они тестируют (сани или работа с превышением скорости), слишком тяжелая или слишком легкая.

После того, как мы нашли времена разделения скорости, мы можем использовать эти числа, чтобы помочь нам определить скорость ускорения спортсмена.

разделов времени лучших спринтов на 100 м (ускорение и скорость могут быть рассчитаны исходя из приведенного выше времени)

Ускорение = (Изменение скорости) / Время

Изменения ускорения на шпагате могут сказать тренеру, насколько быстро меняется скорость, но не дает тренеру обратной связи о достигнутой максимальной скорости.Важно отметить различия между ускорением и скоростью, потому что на ускорение влияют изменения скорости, но на скорости фактической скорости не обязательно влияют изменения ускорения.

Спортсмен A: Переходит с бега со 6 ярдов в секунду до 8 ярдов в секунду за 0,5 секунды

Ускорение = изменение скорости / время

Ускорение = (8 ярдов / сек – 6 ярдов / сек) / 0,5

Ускорение = (2 ярда / сек) / 0.5

Ускорение = 4 ярда в секунду в секунду

Спортсмен B : ускоряется с бега со 4 ярдов в секунду до 6 ярдов в секунду за 0,5 секунды

Ускорение = изменение скорости / время

Ускорение = (6 ярдов / сек – 4 ярдов / сек) / 0,5

Ускорение = (2 ярда / сек) / 0,5

Ускорение = 4 ярда в секунду в секунду

У обоих спортсменов одинаковое ускорение, но разные максимальные скорости!

Нравится:

Нравится Загрузка…

Связанные

% PDF-1.5 % 572 0 объект> эндобдж xref 572 106 0000000016 00000 н. 0000003781 00000 н. 0000002416 00000 н. 0000003955 00000 н. 0000004679 00000 п. 0000004719 00000 н. 0000004766 00000 н. 0000004831 00000 н. 0000005059 00000 н. 0000005165 00000 п. 0000005333 00000 п. 0000005632 00000 н. 0000005948 00000 н. 0000050513 00000 п. 0000050549 00000 п. 0000053206 00000 п. 0000053365 00000 п. 0000053521 00000 п. 0000053680 00000 п. 0000053840 00000 п. 0000054003 00000 п. 0000054171 00000 п. 0000054336 00000 п. 0000054537 00000 п. 0000054837 00000 п. 0000054928 00000 п. 0000056120 00000 п. 0000056281 00000 п. 0000056445 00000 п. 0000056770 00000 п. 0000057270 00000 п. 0000057645 00000 п. 0000058155 00000 п. 0000058533 00000 п. 0000059146 00000 п. 0000059730 00000 п. 0000060481 00000 п. 0000061043 00000 п. 0000061496 00000 п. 0000061561 00000 п. 0000061625 00000 п. 0000062234 00000 п. 0000062756 00000 п. 0000063520 00000 п. 0000064039 00000 п. 0000064566 00000 п. 0000064893 00000 п. 0000065419 00000 п. 0000066168 00000 п. 0000066924 00000 п. 0000069585 00000 п. 0000071728 00000 п. 0000074219 00000 п. 0000076626 00000 п. 0000079038 00000 п. 0000081444 00000 п. 0000082046 00000 п. 0000082672 00000 п. 0000083245 00000 п. 0000085668 00000 п. 0000087763 00000 п. 0000087935 00000 п. 0000087989 00000 п. 0000088202 00000 п. 0000088374 00000 п. 0000088443 00000 п. 0000088499 00000 н. 0000088555 00000 п. 0000088728 00000 п. 0000088809 00000 п. 0000093969 00000 п. 0000097545 00000 п. 0000101735 00000 н. 0000106405 00000 п. 0000112322 00000 н. 0000117347 00000 н. 0000122387 00000 н. 0000130454 00000 н. 0000135292 00000 н. 0000135448 00000 н. 0000135819 00000 н. 0000140363 00000 п. 0000140827 00000 н. 0000141134 00000 н. 0000141348 00000 н. 0000141508 00000 н. 0000141893 00000 н. 0000152231 00000 н. 0000152799 00000 н. 0000153705 00000 н. 0000203673 00000 н. 0000204542 00000 н. 0000215983 00000 н. 0000216481 00000 н. 0000222359 00000 п. 0000222947 00000 н. 0000223256 00000 н. 0000223364 00000 н. 0000223472 00000 н. 0000223640 00000 н. 0000224219 00000 п. 0000224539 00000 н. 0000224667 00000 н. 0000224780 00000 н. 0000225304 00000 н. 0000225412 00000 н. трейлер ] >> startxref 0 %% EOF 574 0 obj> поток x ڤ TyPSGy! D!) GE 摐 F% b = F

Скорость, ускорение и время | м / с до км / ч и т. д.

Введение

В этой статье мы узнаем о нескольких важных атрибутах, их единицах измерения и методах преобразования между различными единицами измерения.

  • Скорость
  • Скорость
  • Разгон
  • Время

Преобразование единиц скорости, ускорения и времени-PDF

Узнайте о преобразовании единиц скорости, ускорения и времени.м / с до км / ч, км / ч до миль / ч, м / с2 до км / с2, час до секунд и т. д. с примерами. Вот загружаемый PDF-файл, чтобы узнать больше.

📥 Преобразование единиц скорости, ускорения и времени-PDF

Загрузить

Читайте также,

Определение

Скорость

Скорость определяется как скорость, с которой объект движется (преодолевает определенное расстояние).Это скаляр , поскольку он определяет только величину , а не направление.

Производная единица измерения скорости в системе СИ – метр в секунду ( м / с).

Скорость

Скорость определяется как скорость изменения положения объекта относительно системы координат.

Скорость – это вектор , величина , поскольку она описывает как величину , величину и направление .

Производная единица измерения скорости в системе СИ составляет метра в секунду ( м / с).

Разгон

Ускорение также является величиной вектора и определяется как скорость изменения скорости с изменением во времени.

Производная единица измерения ускорения в системе СИ составляет метр в секунду в квадрате ( м / с 2 ).

Время

Измеряемый период, в течение которого происходит действие / событие, – это Время.

Производная единица измерения времени в системе СИ – секунды.

Международная система единиц (СИ)

Международная система единиц – это современная форма метрической системы. Единицы, перечисленные в этой системе, используются как стандартные единицы измерения почти во всех странах мира.

Преобразование единиц времени

В этом разделе мы рассмотрим различные единицы измерения времени и формулы преобразования, необходимые для преобразования значения из одной единицы в другую.

Преобразователь единиц

Часы в секунду (час в сек)

от минут до часа (от минут до часов)

Минут до дня (от мин до дней)

дней в минуту (дней в мин)

От часов до дней (от часов до дней)

Секунд до недели

Преобразование единиц скорости / скорости

В этом разделе мы увидим различные формулы для преобразования значений между различными представлениями единиц измерения скорости / скорости.

Как правило, метод, используемый для получения формулы, основан на использовании отдельных единиц в числителе и знаменателе.

Преобразователь единиц

Метр в секунду в километр в час (м / сек в км / ч)

Километр / час в метр / секунду (км / ч до м / с)

Километр / секунда до миль / час (км / с до миль / ч)

футов в секунду до метра в секунду (ft / s to m / s)

миль в час до метра в секунду (миль / ч до м / с)

Метр / сек до футов / сек (м / сек до фут / сек)

Километр в секунду до метра в секунду (км / с до м / с)

Сантиметр в секунду до метра в секунду (см / с до м / с)

фут в минуту до метра в секунду (фут в минуту до м / с)

миль в час до футов в секунду (миль / ч в фут / с)

Оборотов в минуту до метра в секунду

, где 2 × π × r = линейная скорость

Радиан в секунду до метра в секунду (рад / с до м / с)

Метр / сек до числа Маха (м / сек до числа Маха)

Мах – это отношение скорости движущегося объекта в жидкости к скорости звука в той же среде.Поскольку это соотношение, у него нет размеров.

Скорость звука непостоянна. Он меняется в зависимости от температуры и атмосферного давления.

Преобразование единиц ускорения

В этом разделе мы увидим различные формулы для преобразования между различными единицами измерения ускорения.

Как правило, метод, используемый для получения формулы, основан на использовании отдельных единиц в числителе и знаменателе.

Преобразователь единиц

футов / с 2 до метров / с 2 (фут / с 2 до м / с 2 )

Метр в секунду 2 в километр в секунду 2 (м / с 2 в км / с 2 )

Метр в секунду 2 в километр / час 2 (м / с 2 в км / ч 2 )

футов / с 2 до километров / с 2 (фут / с 2 до км / с 2 )

км / с 2 до футов / с 2 (км / с 2 до футов / с 2 )

Километров в час 2 до метров в секунду 2 (км / ч 2 до метров в секунду 2 )

Метр / сек 2 футов / сек 2 (м / с 2 футов / сек 2 )

миль / сек 2 до километров / час 2 (миль / с 2 до км / ч 2 )

км / ч 2 до миль / час 2 (км / ч 2 до миль / ч 2 )

галлона в километр / час 2 (1 галлон в км / ч 2 )

1 галлон = 1 сантиметр в секунду 2

Примеры

В этом разделе мы увидим несколько примеров преобразования единиц измерения.

Преобразование скорости 90 метров в секунду в километры в час

Чтобы преобразовать значение из м / с в км / ч, нам нужно умножить его на 3,6

Итак, 90 м / с = 90 × 3,6 = 324 км / час

Преобразование скорости 10 футов в секунду в метры в секунду

Чтобы преобразовать значение из фут / с в м / с, нам нужно умножить его на 0,3048

Итак, 10 фут / с = 10 × 0.3048 = 3,048 м / с

Преобразование скорости 25 миль / ч в футы в секунду

Чтобы преобразовать значение из миль / ч в фут / сек, нам нужно умножить его на 1,47

Итак, 25 миль / ч = 25 × 1,47 = 36,7 фут / с

Преобразование ускорения 120 метров в секунду в квадрате в километр в час в квадрате

Чтобы преобразовать значение из метров в секунду 2 в километры в час 2 , нам нужно умножить его на 12960

Итак, 120 м / с 2 = 120 × 12960 = 15,55 200 км / час 2

Перевести 58 галлонов в квадратный километр в час

Чтобы преобразовать значение из галлона в километр / час 2 , нам нужно умножить его на 129.6

Итак, 58 галлонов = 58 × 129,6 = 7516,8 км / ч 2

Сколько минут в 4 днях?

Часов в сутки = 24

часов за 4 дня = 24 × 4 = 96

Минут в 1 час = 60

Итак, минуты за 96 часов = 96 × 60 = 5760

Сколько секунд в неделе?

Количество дней в 1 неделе = 7

Количество часов в сутки = 24

Количество минут в 1 часе = 60

Количество секунд в 1 минуте = 60

Итак, количество секунд в 1 неделе = 60 × 60 × 24 × 7 = 604800

Сводка

В этой статье мы узнали о времени, скорости, скорости и ускорении.Мы узнали их определения, единицы измерения и правила / формулы преобразования между различными единицами измерения.

Это может служить кратким справочником по любой из концепций, упомянутых выше.

Написано Гаятри Сивасубраманян, учителем Cuemath

Часто задаваемые вопросы (FAQ)

Сколько недель в 6 месяцах?

Количество дней в году (12 месяцев) = 365 (366 раз в 4 года)

Количество дней в году (6 месяцев) = 365/2 = 182.5

Количество дней в неделе = 7

Итак, количество недель в 6 месяцах = 182,5 / 7 = 26,07 (примерно 26 недель)

В чем разница между скоростью и скоростью?

И скорость, и скорость – это отношение расстояния, пройденного объектом, ко времени, затраченному на движение.

But Speed ​​- это количество Scalar . Он учитывает только величину независимо от направления.

В то время как скорость – это величина Vector , которая представляет как величину, так и направление.

Какая связь между скоростью и ускорением?

Ускорение – это скорость изменения скорости. Он обозначает изменение скорости во времени.

Сколько секунд в часе?

Количество секунд в минуте = 60

Количество минут в часе = 60

Итак, количество секунд в часе = 60 × 60 = 3600

Сколько минут в день?

Количество минут в часе = 60

Количество часов в сутки = 24

Итак, количество минут в сутках = 60 × 24 = 1440

Определить: Расстояние VS.водоизмещение, скорость VS. скорость, ускорение, положение, скорость, ускорение – временные графики

Примечания:
На этом уроке мы узнаем:
  • Определение и разница между смещением и расстоянием
  • Определение и разница между скоростью и скоростью
  • Определение ускорения
  • Position Vs. График времени
  • Скорость Vs. График времени
  • Разгон против. График времени

Примечания:

Объем Vs.Расстояние

Смещение: определяется как изменение положения, ΔX = Xf − Xi \ Delta X = X_ {f} -X_ {i} ΔX = Xf −Xi.
Это векторная величина, она имеет как величину, так и направление.


Расстояние: длина пути, пройденного между двумя точками. Он также определяется как величина смещения между двумя положениями.
Это скалярная величина, она имеет только величину.

Пример:

Спортсмен бегает по прямоугольному полю, как показано ниже, длиной 240 см и шириной 120 см. {2} (AC) 2 = 57600cm2 + 14400cm2
(AC) (AC) (AC) = 268.33 см

ΔX = AC = 268,33 см \ Delta X = AC = 268,33 \, смΔX = AC = 268,33 см

  • A \, A \, A → B \, B \, B → C \, C \, C → D \, D D

    Расстояние (d): AB + BC + CDAB + BC + CDAB + BC + CD = 240 см + 120 см + 240 см = 600 см
    Смещение (ΔX): ΔX = Xf − Xi = XD − XA = AD (\ Delta X): \ Delta X = X_ {f} – X_ {i} = X_ {D} – X_ {A} = A_ {D } (ΔX): ΔX = Xf −Xi = XD −XA = AD = 120 см

  • A \, A \, A → B \, B \, B → C \, C \, C → D \, D \, D → A \, A A

    Расстояние (d): AB + BC + CD + ADAB + BC + CD + ADAB + BC + CD + AD = 240 см + 120 см + 240 см + 120 см = 720 см
    Смещение (ΔX): ΔX = Xf − Xi = XA − XA = (\ Delta X): \ Delta X = X_ {f} -X_ {i} = X_ {A} -X_ {A} = (ΔX): ΔX = Xf −Xi = XA −XA = 0

    • Скорость по сравнению сСкорость

    Средняя скорость: изменить положение, разделенное на затраченное время; Vavg = ΔXΔt = Xf − Xitf − ti \ large V_ {avg} = \ frac {\ Delta X} {\ Delta t} = \ frac {X_ {f} – X_ {i}} {t_ {f} – t_ { i}} Vavg = ΔtΔX = tf −ti Xf −Xi
    Это векторная величина, которая имеет как величину, так и направление.

    Средняя скорость: общее пройденное расстояние, разделенное на затраченное время; Savg = dt \ large S_ {avg} = \ frac {d} {t} Savg = td
    Это скалярная величина, имеющая только величину.

    Мгновенная скорость: скорость в момент времени.

    Мгновенная скорость: скорость в момент времени.

    Разгон

    Говорят, что объект, скорость которого изменяется, ускоряется, он определяет, насколько быстро изменяется скорость объекта.

    Среднее ускорение: определяется как изменение скорости, деленное на затраченное время.
    Это векторная величина, которая имеет как величину, так и направление.{2}} с2м

    Графический анализ

    Позиция Vs. График времени

    На следующем графике показано положение Vs. временной график для объекта, движущегося с постоянной скоростью.

    Использование позиции Vs. на временном графике можно найти следующие количественные показатели;


    1. Средняя скорость
      Чтобы найти VavgV_ {avg} Vavg, найдите наклон графика.

      Vavg = slope = RiseRun = V_ {avg} = slope = \ frac {Rise} {Run} = Vavg = slope = RunRise = x2 − x1t2 − t1 = ΔXΔt \ large \ frac {x_ {2} – x_ {1}} {t_ {2} – t_ {1}} = \ frac {\ Delta X} {\ Delta t} t2 −t1 Х2 – х1 = ΔtΔX

      Пример;

      Vavg = slope = RiseRun = V_ {avg} = slope = \ frac {Rise} {Run} = Vavg = slope = RunRise = 50−105−1 = 404 \ large \ frac {50-10} {5-1} = \ frac {40} {4} 5−150−10 = 440 = 10 м / с

    2. Мгновенная скорость
      3. Чтобы найти мгновенную скорость по графику, вычислите наклон графика в этот момент времени.

    Vinst V_ {inst} Vinst при t = 2 с, Vinst = slope = t = 2s, V_ {inst} = slope = t = 2s, Vinst = slope = 20−02−0 = \ large \ frac {20 – 0} {2- 0} = 2−020−0 = 10 м / с

    Примечание: для тел, движущихся с постоянной скоростью; Vinst = VavgV_ {inst} = V_ {avg} Vinst = Vavg

    На следующем графике показано положение по сравнению с положением. временной график для объекта, движущегося с переменной скоростью (скорость НЕ постоянна).

    1. Средняя скорость
      Чтобы найти VavgV_ {avg} Vavg, найдите наклон графика.

      Vavg = slope = RiseRun = V_ {avg} = slope = \ frac {Rise} {Run} = Vavg = slope = RunRise = x2 − x1t2 − t1 = ΔXΔt \ large \ frac {x_ {2} – x_ {1}} {t_ {2} – t_ {1}} = \ frac {\ Delta X} {\ Delta t} t2 −t1 Х2 – х1 = ΔtΔX

      VV V avg (2,8 с → 5,0 с) = slope = RiseRun = x2 − x1t2 − t1 = 25−7,55−2,8 \ large \ frac {Rise} {Run} = \ frac {x_ {2} – x_ { 1}} {t_ {2} – t_ {1}} = \ frac {25 – 7.5} {5-2.8} RunRise = t2 −t1 x2 −x1 = 5−2.825−7.5 = 7.95 РС

    2. Мгновенная скорость
      3. Чтобы найти мгновенную скорость по графику, вычислите наклон графика в этот момент времени.Для этого нарисуйте касательную в этот момент времени и вычислите наклон касательной.

      VinstV_ {inst} Vinst при t = 2st = 2s t = 2s

      VinstV_ {inst} Vinst = наклон касательной = RiseRun = x2 − x1t2 − t1 = 3,75−1,252−1 \ large \ frac {Rise} {Run} = \ frac {x_ {2} – x_ {1} } {t_ {2} – t_ {1}} = \ frac {3. {2}} s2m Переменное ускорение
      Среднее ускорение
      Чтобы найти среднее ускорение по графику, вычислите наклон графика в течение определенного интервала времени.aavg = \ large a_ {avg} = \, aavg = slope = RiseRun = V2 − V1t2 − t1 = 25−55−2 = 203 \ large \ frac {Rise} {Run} = \ frac {V_ {2} – V_ {1}} {t_ {2} – t_ {1}} = \ frac {25 – 5} {5-2} = \ frac {20} {3} RunRise = t2 −t1 V2 −V1 = 5−225−5 = 320 = 6,67 м / с 2

      Мгновенное ускорение
      Чтобы найти мгновенное ускорение по графику, вычислите наклон графика в этот момент времени. Для этого нарисуйте касательную в этот момент времени и вычислите наклон касательной.

      ainsta_ {inst} ainst при t = 2st = 2st = 2s;

      ainst = \ large a_ {inst} = \, ainst = наклон касательной = RiseRun = V2 − V1t2 − t1 = 3.75−1.252−1 = \ large \ frac {Rise} {Run} = \ frac {V_ {2} – V_ {1}} {t_ {2} – t_ {1}} = \ frac {3.75 – 1.25} {2-1} = RunRise = t2 −t1 V2 −V1 = 2 −13,75−1,25 = 2,5 м / с 2

      Примечание: для тел, движущихся с переменным ускорением; ainst ≠ aavg a_ {inst} \ neq a_ {avg} ainst  = aavg

      Смещение как площадь под графиком
      Использование Velocity Vs.График времени. Вы можете найти смещение, рассчитав площадь под графиком.

      Перемещение от 1 до 5 с;

      Площадь треугольника = 12 \ large \ frac {1} {2} 21 основание × высота = 12 \ large \ frac {1} {2} 21 × 40 × 4 = 80 м

      Примечание: поскольку движение происходит по прямой линии, смещение равно пройденному расстоянию.

      Давайте рассмотрим следующие значения скорости: График времени, на котором объект меняет направление при движении.

      Водоизмещение полное; область под графиком
      Площадь треугольника = 12 \ large \ frac {1} {2} 21 основание × высота = 12 \ large \ frac {1} {2} 21 × 10 × 50 = 250 м.

      Общее пройденное расстояние; пройденное расстояние от 0 до 5 секунд + пройденное расстояние от 5 до 10 секунд
      Общее расстояние = 50 м + 50 м = 100 м

      Примечание: Расстояние и Смещение отличаются, поскольку объект изменил направление.

      Разгон | Encyclopedia.com

      История

      Линейное ускорение

      Криволинейное ускорение

      Силы G

      Ресурсы

      Считается, что объект ускоряется, если его скорость изменяется по направлению или по величине. Ускорение – это векторная величина. Если, однако, известно, что ускорение происходит по прямой линии, его часто определяют как скалярную величину (чистое число). Поскольку единицей скорости является расстояние в единицу времени, единицей ускорения является скорость в единицу времени; в метрических единицах это (м / с) / с или м / с 2 .

      Материальный объект ускоряется только под действием ненулевой чистой силы. Сэр Исаак Ньютон (1642–1727) определил ускорение в своем втором законе движения как отношение силы, действующей на объект, к его массе: a = ф / м .

      Изучение движения Галилео Галилеем (1564–1642) в конце шестнадцатого и начале семнадцатого веков и сэром Исааком Ньютоном в середине семнадцатого века является краеугольным камнем современной западной экспериментальной науки.Около 20 лет Галилей кропотливо рассчитывал движения объектов, катящихся по плавным склонам. Он обнаружил, что расстояние, которое прошел объект, пропорционально квадрату времени, в течение которого он находился в движении. Из этих экспериментов возникла первая правильная концепция ускоренного движения.

      Ньютон хотел знать, каков характер ускорения и почему оно вообще происходит. Чтобы создать модель, которая поможет объяснить, как работала известная вселенная семнадцатого века, Ньютон дал науке и физике строго определенное понятие «силы».В своем втором законе движения он утверждал, что ускорение вызывается неуравновешенной силой (такой как толчок или притяжение), действующей на объект. Ньютон показал, что гравитацию можно рассматривать как особый тип ускорения. Ускорение массы под действием силы тяжести создает силу, которую мы называем весом. Общее определение массы состоит в том, что это количество вещества в теле; С другой стороны, вес – это сила, испытываемая неподвижным телом в заданном гравитационном поле. В ньютоновской (нерелятивистской) физике масса тела не меняется в зависимости от его местоположения или состояния движения; его вес делает.

      Объект, движущийся по прямой линии, ускоряется, если его скорость (обычно называемая скоростью) увеличивается или уменьшается. Прямолинейное ускорение ( a ) может быть как положительным, так и отрицательным, в зависимости от того, является ли его направление положительным ( a ) или отрицательным ( a ).

      Движение автомобиля может помочь объяснить линейное ускорение. Спидометр автомобиля измеряет величину скорости. Если автомобиль трогается с места и постоянно ускоряется в положительном направлении до 60 миль в час (миль / ч) за 10 секунд, каково его ускорение за эти 10 секунд? Скорость автомобиля изменяется на 60 миль в час за 10 секунд, поэтому его ускорение составляет 60 миль в час / 10 с = +6 миль / час / с.(Эти единицы могут быть преобразованы в м / с 2 , если необходимо.) Это означает, что его ускорение изменяется на шесть миль в час за каждую секунду, когда он ускоряется. Если автомобиль тронулся со скоростью 60 миль в час и остановился после 10 секунд устойчивого торможения, его среднее ускорение будет равно –6 миль / час / с.

      При криволинейном движении – движении по любой траектории, кроме прямой – величина скорости объекта может оставаться или не оставаться постоянной, но направление его движения постоянно меняется. Поэтому он ускоряется.Если наш автомобиль едет со скоростью 60 миль в час на повороте дороги, он испытывает ускорение, потому что его направление меняется, пока он движется по повороту. Американские горки и другие аттракционы заставляют своих гонщиков испытывать быстрые изменения в ускорении, заставляя их быстро двигаться по изогнутым дорожкам.

      Сила, испытываемая объектом из-за ускорения, иногда выражается как часть

      КЛЮЧЕВЫЕ УСЛОВИЯ

      Ускорение – Скорость, с которой скорость объекта изменяется во времени.

      Круговое ускорение – Ускорение, при котором меняется направление движения.

      Сила – Воздействие на объект внешнего агента, которое вызывает ускорение, изменяющее состояние движения объекта.

      Силы «G» – Явное увеличение веса тела из-за быстрого ускорения; сила в 2 G означает, что тело чувствует силу, в два раза превышающую его собственный вес.

      Gravity— Специальное ускорение 9.81 м / с 2 , создаваемое притяжением массы Земли к близлежащим объектам на поверхности Земли.

      Линейное ускорение – Ускорение, при котором изменяется величина (скорость) движения.

      Масса— Мера количества вещества в объекте.

      Вектор— Величина или термин, который может быть выражен как величиной (числом), так и направлением.

      Скорость— Скорость и направление движущегося объекта.

      Невесомость – Состояние, вызываемое свободным ускорением к Земле с той же скоростью, что и сила тяжести, и отсутствием обычных эффектов веса.

      сила, которую тот же объект испытал бы из-за собственного веса, если бы он был неподвижен на поверхности Земли, обозначается как 1 G. Ускорение, которое заставляет объект ощущать силу, равную удвоенному весу, например, подвергает его воздействию 2 G. Астронавты испытывают до 7 G во время старта космического корабля, но, оказавшись на орбите свободного падения, они не испытывают силы G.Понятие «невесомость» в космосе часто понимают неправильно. Это не вызвано тем фактом, что объекты на низкой околоземной орбите далеки от массы Земли; на самом деле они подвержены почти такой же гравитации, как и предметы на поверхности. Однако они свободно падают под действием силы тяжести, как люди в падающем лифте. Они остаются в воздухе из-за своего касательного или бокового движения. В некотором смысле они всегда свободно падают к Земле, но движутся вбок достаточно быстро, чтобы не заметить ее. Если боковая скорость движущегося по орбите объекта уменьшается, например, путем запуска ракеты против направления его движения, он падает к поверхности Земли.

      См. Также Ускорители; Гравитация и гравитация; Законы движения; Скорость.

      КНИГИ

      Бедфорд, Энтони М. и Уоллес Фаулер. Инженерная механика: статика и динамика . Река Аппер Сэдл, Нью-Джерси: Prentice Hall, 2004.

      Burnett, Betty. Законы движения: понимание равномерного и ускоренного движения . Нью-Йорк: Rosen Publishing Group, 2004.

      Милликен, Уильям Ф. Уравнения движения . Кембридж, Массачусетс: Bentley Publishers, 2006.

      Serway, Raymond A. и Jerry S. Faughn. College Physics Vol. Я .

    Оставить комментарий