формула через радиус и ускорение, угловую скорость
Содержание:
- Угловое ускорение – что это?
-
Угловая скорость
- Основные формулы для вычисления угловой скорости
- Связь между угловой скоростью и нормальным (центростремительным) ускорением
-
Основные формулы для расчета углового ускорения
- Угловое ускорение маховика
- Среднее угловое ускорение
- Тангенциальное ускорение
- Мгновенное угловое ускорение
Содержание
- Угловое ускорение – что это?
-
Угловая скорость
- Основные формулы для вычисления угловой скорости
- Связь между угловой скоростью и нормальным (центростремительным) ускорением
-
Основные формулы для расчета углового ускорения
- Угловое ускорение маховика
- Среднее угловое ускорение
- Тангенциальное ускорение
- Мгновенное угловое ускорение
Угловое ускорение – что это?
Угловое ускорение \(\varepsilon\) – физическая величина, характеризующая изменение угловой скорости при движении тела. {-2}\)
{-2}\)
Угловая скорость
Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Угловая скорость \(\omega\) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.
При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).
Вектор угловой скорости направлен вдоль оси вращения.
Основные формулы для вычисления угловой скорости
Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):
- \(\omega=\frac nt\), где \(n\) – количество оборотов за единицу времени \(t\).

Угловое ускорение маховика
\(\varepsilon=\frac\omega t=\frac{2\pi n}t\), где \(n\) – количество оборотов за единицу времени \(t\).
Среднее угловое ускорение
Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.
\(\left\langle\varepsilon\right\rangle=\frac{\triangle\omega}{\triangle t}\)
Тангенциальное ускорение
Тангенциальным (касательным) ускорением \(a_\tau\)
\(a_\tau=\varepsilon r\), где \(\varepsilon\) – угловое ускорение, \(r\) – радиус кривизны траектории в заданной точке.
Мгновенное угловое ускорение
Мгновенное угловое ускорение \(\alpha\) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.
 2}\)
2}\)Рейтинг: 2.19 (Голосов: 16)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Формула для расчета линейной скорости
Понятие скорости
Когда мы сравниваем движение каких-либо тел, то говорим, что одни тела двигаются быстрее, а другие – медленнее. Такую простую терминологию мы используем в повседневной жизни, говоря, например, о движении транспорта. В физике быстрота движения тел характеризуется определенной величиной. Эта величина называется скоростью. Общее определение скорости (в случае, если тело движется равномерно):
Определение 1
Скорость при равномерном движении тела – это физическая величина, показывающая, какой путь прошло тело за единицу времени.
Под равномерным движением тела подразумевается, что скорость тела постоянна. Формула нахождения скорости: $v=\frac{s}{t}$, $s$ – это пройденный телом путь (то есть длина линии), $t$ – время (то есть промежуток времени, за который пройден путь).

Согласно международной системе СИ, единица измерения линейной скорости является производной от двух основных единиц – метра и секунды, то есть измеряется в метрах в секунду (м/с). Это значит, что под единицей скорости понимается скорость такого равномерного движения, при котором путь в один метр тело проходит за одну секунду.
Также скорость часто измеряют в км/ч, км/с, см/с.
Рассмотрим простой пример задачи на вычисление скорости.
Пример 1
Задача. Двигаясь равномерно, поезд за 4 ч проходит 219 км. Найти его скорость движения.
Решение. $v=\frac{219 км}{4 ч}=54,75\frac{км}{ч}$. Переведём километры в метры и часы в секунды: $54,75\frac{км}{ч}=\frac{54750 м}{3600c}\approx 15,2\frac{м}{c}$.
Ответ. $54,75\frac{км}{ч}$ или $15,2\frac{м}{c}$.
Из примера мы видим, что числовое значение скорости отличается в зависимости от выбранной единицы измерения.
Кроме числового значения, скорость имеет направление. Числовое значение величины в физике называют модулем.
 Когда у физической величины есть и направление, то эту величину называют векторной. То есть скорость – это векторная физическая величина.
Когда у физической величины есть и направление, то эту величину называют векторной. То есть скорость – это векторная физическая величина.На письме модуль скорости обозначается $v$, а вектор скорости – $\vec v$.
В свою очередь, такие величины как путь, время, длина и другие характеризуются только числовым значением. Тогда говорят, что это скалярные физические величины.
В случае, когда движение является неравномерным, используют понятие средней скорости. Формула средней скорости: $v_{ср}=\frac{s}{t}$, где $s$ – это весь пройденный телом путь, $t$ – всё время движения. Рассмотрим пример задачи на среднюю скорость, чтобы понять разницу.
Пример 2
Задача. Некоторый транспорт за 2,5 часа преодолевает путь в 213 км. Найти его $v_{ср}$.
Решение. $v_{ср}=\frac{213 км}{2,5 ч}= 85,2 \frac{км}{ч}=\frac{213000 м}{9000 с}\approx 23,7\frac{м}{с} $.
Ответ. $85,2 \frac{км}{ч}$ или $23,7\frac{м}{с} $.
Линейная скорость
Определение линейной скорости относится к разделу физики о механике и подразделу о кинематике в рамках вопроса движения по окружности.
 В измерении скорости движения по окружности выделяют угловую скорость и линейную скорость.
В измерении скорости движения по окружности выделяют угловую скорость и линейную скорость.Дадим определение линейной скорости.
Определение 2
Линейная скорость $V$ – это физическая величина, показывающая путь, который прошло тело за единицу времени.
Формула линейной скорости:
$V=\frac{S}{t}$, где $S$ – путь, $t$ – время, за которое точка прошла путь $S$.
Также существует иной вариант этой формулы:
$V=\frac{l}{t}$, где $l$ – путь, $t$ – время, за которое точка прошла по дуге $l$.
В некоторых учебниках линейная скорость также обозначается маленькой буквой $v$.
Есть ещё одна формула, по которой можно найти линейную скорость:
$v=\frac{2\pi R}{T}$.
$2\pi$ соответствует полной окружности (360 угловым градусам).
$\vec V$ направленена по касательной к тракетории.
Связь между линейной и угловой скоростями
Чтобы проследить связь между линейной и угловой скоростями, нужно дать определение угловой скорости.
 2 R$.
2 R$.С помощью элементарных математических действий из этих двух формул выводится связь между $V$ и $\omega$.
Таким образом, в данной статье мы разобрали следующие понятия:
- скорость;
- линейная и угловая скорость;
- связь между линейной и угловой скоростями.
4. Кинематика движения по окружности: задачи с ответами
(Все задачи по кинематике и ответы к ним находятся также в zip-архиве (332 кб), который можно скачать и открыть на своем компьютере. Попробуйте решить все задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)
4.1. Радиус рукоятки колодезного ворота в 3 раза больше радиуса вала, на который наматывается трос. Какова линейная скорость конца рукоятки, если ведро с глубины 10 м поднимается за 20 с? [1,5 м/с]
4.2. С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом 40 м, чтобы центростремительное ускорение равнялось ускорению свободного падения? [20 м/с]
4.
 3. Маховик делает 3 оборота в минуту. Найти угловую скорость вращения маховика. [0,314 с−1]
3. Маховик делает 3 оборота в минуту. Найти угловую скорость вращения маховика. [0,314 с−1]4.4. Угловая скорость вращения лопастей колеса ветродвигателя 6 с−1. Найти центростремительное ускорение концов лопастей, если их линейная скорость равна 20 м/с. [120 м/с2]
4.5. Период вращения платформы карусельного станка 3,14 с. Найти центростремительное ускорение крайних точек платформы, если ее диаметр 5 м. [10 м/с2]
4.7. Минутная стрелка часов в 1,5 раза длиннее часовой. Во сколько раз линейная скорость конца минутной стрелки больше конца часовой? [в 18 раз]
4.8. Какова скорость поезда, если его колеса, имеющие диаметр 1,2 м, делают 160 оборотов в минуту? [10 м/с]
4.
 9. Определить скорость и ускорение точек поверхности Земли, находящихся на широте 30°. Радиус Земли равен 6400 км. [400 м/с; 2,5 см/с2]
9. Определить скорость и ускорение точек поверхности Земли, находящихся на широте 30°. Радиус Земли равен 6400 км. [400 м/с; 2,5 см/с2]4.11. Через блок радиусом R = 50 мм, вращающийся вокруг горизонтальной оси, перекинута нить. Грузы, привязанные к концам нити, движутся с постоянной скоростью v = 20 см/с друг относительно друга. Определить угловую скорость вращения блока. [2 Гц]
4.12. Горизонтальная платформа радиусом 2 м равномерно вращается вокруг вертикальной оси с угловой скоростью 2,5 об/мин. По краю платформы шагает человек со скоростью 1 м/с относительно платформы. Определить ускорение человека, если он шагает; а) в направлении вращения; б) в противоположном направлении. [ 1,15 м/с
4.
 13. Цилиндр радиусом R зажат между двумя параллельными рейками (рисунок слева). Рейки движутся параллельно самим себе с постоянными скоростями v1 и v2. Определить угловую скорость вращения цилиндра и линейную скорость его центра. Проскальзывания нет.
13. Цилиндр радиусом R зажат между двумя параллельными рейками (рисунок слева). Рейки движутся параллельно самим себе с постоянными скоростями v1 и v2. Определить угловую скорость вращения цилиндра и линейную скорость его центра. Проскальзывания нет.Ответ к задаче 4.13: w = v1 + v2 ; vo = . 2R 2 4.14. Пропеллер самолета радиусом 1,5 м вращается с частотой 2000 об/мин. Скорость самолета относительно земли 162 км/ч. Определить скорость точки на конце пропеллера. Что представляет собой траектория движения этой точки? [316 м/с]
4.15. Скорость точки A вращающегося диска равна 50 см/с, а скорость точки B, находящейся на 10 см ближе к оси диска, равна 40 см/с. Определить угловую скорость вращения диска.
 [1 с−1]
[1 с−1]4.16. По горизонтальной дороге без проскальзывания катится тонкий обруч радиуса R со скоростью vo (рисунок слева). Найти зависимость скорости точек обруча v от угла α. [ v(α) = 2vocos α ]
4.17. Диск катится без проскальзывания с постоянной скоростью v по горизонтальной дороге. Радиус диска равен R. Найти геометрическое место точек на диске, скорости которых в данный момент времени равны v. [окружность радиусом R с центром в точке касания]
4.18. Два диска связаны между собой шкивом. Левый диск крутится с угловой скоростью w. Определить линейную скорость точки A правого диска (рисунок слева). [ vA = wR1R2/R3 ]
4.19. Кривошип OA, вращаясь с угловой скоростью w = 2,5 с−1, приводит в движение колесо радиусом r = 5 см, катящееся по неподвижному колесу радиусом R = 15 см. Найти скорость точки B (рисунок слева).
 [ vB = 2w(R + r) = 100 см/с ]
[ vB = 2w(R + r) = 100 см/с ]4.20. Кривошип OA, вращаясь вокруг точки O, приводит в движение колесо 1 радиусом R = 20 см, катящееся по внутренней поверхности круга 2. Колесо 1, соприкасаясь с колесом 3, заставляет его вращаться вокруг точки O (рисунок слева). Во сколько раз угловая скорость колеса 3 больше угловой скорости кривошипа, если радиус колеса 3 равен r = 10 см? [ w3/w = 2(R + r)/r = 6 ]
4.21. Точка движется по окружности со скоростью v = at, где a = 0,5 м/с2. Найти ее полное ускорение в момент, когда она пройдет 0,1 длины окружности после начала движения. [ ap = a√(1 + 4π2)/5 = 0.8 м/с2 ]
4.22. Если колесо катится по горизонтальной дороге без проскальзывания, то траекторией любой точки обода колеса является линия, называемая циклоидой (рисунок слева). Определить радиус кривизны циклоиды в верхней точке, если радиус колеса R. [ 4R ]
4.
 23. Малый радиус несущей части трамвайного колеса равен r, а большой радиус — R. Определить радиус кривизны циклоиды в верхней точке (рисунок слева). [ (R + r)2/R ]
23. Малый радиус несущей части трамвайного колеса равен r, а большой радиус — R. Определить радиус кривизны циклоиды в верхней точке (рисунок слева). [ (R + r)2/R ]4.24. По вертикальной цилиндрической проволочной спирали с постоянной скоростью v соскальзывает бусинка (рисунок слева). Определить ускорение бусинки, если радиус витков спирали равен R, а шаг спирали — h. [ a = 4π2Rν2/(4π2R2 + h2) ]
4.25. Тело движется по окружности радиуса R со скоростью, которая зависит от времени по закону: v(t) = kt. Найти зависимость полного ускорения от времени. [ a(t) = k√(1 + k2t4)/R) ]
4.26. Через какое время встречаются минутная и часовая стрелки часов? [около 1,09 ч; около 65,5 мин]
4.27. Зависимость координат движущегося тела от времени имеют вид: x(t) = Rsin wt; y(t) = Rcos wt. Определить траекторию движения и ускорение тела.
 [окружность радиусом R; a = w2R ]
[окружность радиусом R; a = w2R ]4.28. Плоский обруч движется так, что в некоторый момент времени скорости концов диаметра AB лежат в плоскости обруча, перпендикулярны AB и равны vA и vB. Определить скорости точек C и D, если CD тоже диаметр перпендикулярный AB и эти скорости тоже лежат в плоскости обруча (рисунок слева). [ vС = vD = √((vA2 + vB2)/2) ]
4.29. Точка начинает двигаться по окружности радиуса R с тангенциальным ускорением a. Как зависит от времени угол между векторами скорости и полного ускорения? [ tg φ = at2/R ]
4.30. При движении точки по окружности радиуса R центростремительное ускорение зависит от пройденного пути по закону aц = aS, где a — известная постоянная. Определить зависимость скорости точки от времени (vo = 0). [ v(t) = aRt/2 ]
4.31. Тело брошено со скоростью vo под углом α к горизонту.
 Определить среднюю за время полета угловую скорость вращения вектора скорости тела. [ <w> = αg/(vosin α) ]
Определить среднюю за время полета угловую скорость вращения вектора скорости тела. [ <w> = αg/(vosin α) ]4.32. Направление вращения Земли вокруг своей оси совпадает с направлением ее вращения вокруг Солнца. Сколько суток было бы в году, если бы Земля вращалась вокруг своей оси в противоположную сторону? [367 суток]
4.33. Внешний радиус подшипника равен R, а радиус шариков — r. Подшипник катится по горизонтальной поверхности с постоянной скоростью v (рисунок слева). При этом внутренняя втулка не вращается. Определить угловую скорость вращения шариков. Проскальзывания нет. [ w = v/(2r) ]
4.34. Тело начинает двигаться по окружности из состояния покоя с равномерно возрастающей скоростью. Сколько оборотов сделает тело к моменту, когда центростремительное ускорение станет равно тангенциальному? [ n = π/4; примерно 0,8 оборота ] На правах рекламы: для специальной техники Volvo.
Далее: 40 задач по относительному движению и движению со связями.
 | Вернуться к списку разделов КИНЕМАТИКИ.
| Вернуться к списку разделов КИНЕМАТИКИ.Равномерное движение точки по окружности – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость.
При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть \(v = const,\) а изменяется только направление вектора скорости. Тангенциальное ускорение в этом случае отсутствует \( (a_r = 0),\) а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительным ускорением (нормальное ускорение) \(a_n\), или \(a_{цс}\).
 \circ18\)’ . Угловая скорость равномерного движения тела по окружности – это величина \(\omega\), равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершен этот поворот: \(ω = \frac φ t \). Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени \(t: υ= \frac l t \). Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина \(l\) дуги окружности, пройденной точкой, связана с углом поворота φ выражением \(l = Rφ\), где \(R\) – радиус окружности.
\circ18\)’ . Угловая скорость равномерного движения тела по окружности – это величина \(\omega\), равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершен этот поворот: \(ω = \frac φ t \). Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени \(t: υ= \frac l t \). Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина \(l\) дуги окружности, пройденной точкой, связана с углом поворота φ выражением \(l = Rφ\), где \(R\) – радиус окружности.Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:
\(υ = \frac l t =\frac{ Rφ} t = Rω\), или \(υ = Rω\).
Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.
 2\).
2\).Вопросы
Два велосипедиста совершают кольцевую гонку с одинаковой угловой скоростью. Положения и траектории движения велосипедистов показаны на рисунке. Чему равно отношение линейных скоростей велосипедистов \(\frac{v_1}{v_2}\)?
Самолет летит по окружности в горизонтальной плоскости с постоянной по модулю скоростью. Как направлен вектор ускорения самолета?
В центрифуге стиральной машины белье при отжиме движется по окружности с постоянной по модулю скоростью в горизонтальной плоскости. Как при этом направлен вектор его ускорения?
Материальная точка движется по окружности с постоянной по модулю скоростью по часовой стрелке.
 В какой точке траектории ускорение тела направлено по стрелке?
В какой точке траектории ускорение тела направлено по стрелке? Шарик движется по окружности с радиусом \(r\) со скоростью \(v\). Как изменится величина его центростремительного ускорения, если радиус окружности увеличить в 3 раза, оставив модуль скорости шарика прежним?
Круг радиусом 50 см вращается со скоростью 54 км/ч. Угловая скорость точек, наиболее удаленных от оси вращения, равна
Первая космическая скорость на некоторой планете равна \(υ\). Если спутник запускают с высоты, равной трем радиусам этой планеты, то его скорость должна быть
Первая космическая скорость для Земли – 8 км/с.
 Если известно, что радиус планеты равен \(\frac58\) от земного, а ускорение свободного падения \(\frac35\) от земного, то приближенное значение первой космической скорости для планеты
Если известно, что радиус планеты равен \(\frac58\) от земного, а ускорение свободного падения \(\frac35\) от земного, то приближенное значение первой космической скорости для планетыЛуна вращается вокруг Земли по круговой орбите радиусом 400 000 км с периодом примерно 27,3 суток. Каким будет перемещение Луны за 54,6 суток?
За 15 с точка прошла равномерно половину окружности, радиус которой равен 150 см. Ускорение точки равно
Если за 10 с точка прошла равномерно половину окружности, радиус которой 100 см, то ускорение точки равно
Тело движется равномерно по окружности.
 В этом случае будут справедливы следующие утверждения
В этом случае будут справедливы следующие утвержденияЧему равна линейная скорость точки, находящейся на расстоянии 20 см от оси вращения лопасти вентилятора, который делает 720 оборотов в минуту?
Мотоциклист двигается по окружности со скоростью 36 км/ч. При этом коэффициент трения шин о дорогу составляет 0,4. Каков радиус этой окружности?
Чему равно центростремительное ускорение велосипедиста, двигающегося со скоростью 18 км/ч по кривой дороге с радиусом кривизны 50 м?
Чему будет равно центростремительное ускорение шарика, если он движется по окружности с радиусом 50 см и со скоростью 0,25 м/с?
Чему равна угловая скорость вращения турбины, если она совершает 1800 оборотов в минуту?
Определите центростремительное ускорение спутника Юпитера Ганимеда, если он находится на расстоянии 1 070 400 км от планеты, а период обращения составляет 172 часа.

Чему равна скорость мотоцикла, если его колесо радиусом 25 см за 10 секунд совершает 50 оборотов?
Чему равна скорость шарика, вращающегося по окружности радиусом 250 см с ускорением 0,1 м/с²?
Какова должна быть скорость автомобиля при движении по выпуклому мосту радиусом 2,5 м, чтобы пассажир в верхней его точке находился в состоянии невесомости? ( g ≈ 10 м/с² )
С какой скоростью должен ехать водитель по средней части выпуклого моста с радиусом кривизны 1,6 м, чтобы не оказывать давление на этот мост? ( g ≈ 10 м/с²)
Сообщить об ошибке
Физика Скорость при движении с постоянным ускорением.
 Уравнение движения с постоянным ускорением
Уравнение движения с постоянным ускорениемМатериалы к уроку
Конспект урока
Выясним зависимости скорости точки от времени при ее движении с постоянным ускорением. Для этого воспользуемся формулой: вектор ускорения равен отношению вектора изменения скорости к промежутку времени, в течение которого оно произошло.
Вектор изменения скорости равен разнице двух векторов: вектора скорости точки в начальный момент времени и вектора скорости точки в конечный момент времени. Интервал времени можно вычислить как разность между конечным и начальным моментом времени.
Подставив эти выражения в формулу ускорения, получим, что ускорение равно отношению разности вектора скорости точки в начальный момент времени и вектора скорости точки в конечный момент времени к разности между конечным и начальным моментом времени.
Если начальный момент времени принять равным нулю, то получим, что вектор ускорения равен отношению разности вектора скорости точки в начальный момент времени и вектора скорости в конечный момент времени к значению времени. Из этой формулы мы можем выразить значение вектора скорости точки в любой момент времени.
Получаем, что вектор скорости точки равен сумме вектора начальной скорости точки и произведения вектора ускорения и времени.
Этому уравнению, записанному в векторной форме, на плоскости соответствуют два уравнения для проекций на координатные оси OX и OY:
– проекция вектора скорости на ось ОХ равна сумме проекции на эту ось вектора начальной скорости и произведения проекции вектора ускорения на ось ОХ и значения времени;
– проекция вектора скорости на ось ОY равна сумме проекции на эту ось вектора начальной скорости и произведения проекции вектора ускорения на ось ОY и значения времени.
По виду этих уравнений мы видим, что скорость при движении с постоянным ускорением меняется по линейному закону.
Для того чтобы определить скорость точки в любой момент времени надо знать его начальную скорость и ускорение, с которым оно движется. Начальную скорость можно измерить. Ускорение зависит от того, как действуют на данное тело другие тела.
Начальная скорость зависит не от того, как действуют на данное тело другие тела в рассматриваемый момент времени, а от того, что происходило с этим телом ранее. К примеру, начальная скорость тележки, которая катится под горку, зависит от того, просто ее отпустили или же толкнули, совершив некоторое усилие.
Совершенно противоположная ситуация с ускорением, оно не зависит от того, что происходило с телом в предыдущие моменты, а зависит только лишь от действия на него других тел в данный момент времени. Катящаяся под гору тележка затормозит или даже остановится, наехав на кочку. Ускорение, полученное тележкой, будет зависеть от того, какое воздействие окажет на нее кочка, то есть от величины кочки.
Зависимость проекции скорости от времени можно наглядно изобразить на графике. Горизонтальная ось – это ось времени, вертикальная – ось скорости. График имеет вид прямой выходящей из точки, определяемой значением начальной скорости в момент времени равный 0. Если тело не имеет начальной скорости, то график зависимости проекции скорости на ось ОX от времени представляет собой прямую, выходящую из начала координат. На рисунке этот график показан в виде прямой 1 (эл). По этому графику можно найти проекцию ускорения на ось X: так как в данном случае начальная скорость равна нулю, то проекция ускорения будет равна отношению проекции скорости в какой-то момент времени к значению времени. Для определения значения этих величин можно выбрать любую точку и восстановить из нее перпендикуляры к осям. В нашем примере значение времени – 5 секунд, значение скорости – 30 м/с, подставив в формулу полученные значения, получаем, что ускорение равно 6 м/с2.
Горизонтальная ось – это ось времени, вертикальная – ось скорости. График имеет вид прямой выходящей из точки, определяемой значением начальной скорости в момент времени равный 0. Если тело не имеет начальной скорости, то график зависимости проекции скорости на ось ОX от времени представляет собой прямую, выходящую из начала координат. На рисунке этот график показан в виде прямой 1 (эл). По этому графику можно найти проекцию ускорения на ось X: так как в данном случае начальная скорость равна нулю, то проекция ускорения будет равна отношению проекции скорости в какой-то момент времени к значению времени. Для определения значения этих величин можно выбрать любую точку и восстановить из нее перпендикуляры к осям. В нашем примере значение времени – 5 секунд, значение скорости – 30 м/с, подставив в формулу полученные значения, получаем, что ускорение равно 6 м/с2.
Графики 2 и 3 соответствуют движениям тел с начальной скоростью отличной от нуля. График 2 соответствует равноускоренному движению, так как с течением времени скорость данного тела увеличивается. График 3 направлен вниз, значит, значение скорости с течением времени уменьшается – это график равнозамедленного движения.
График 3 направлен вниз, значит, значение скорости с течением времени уменьшается – это график равнозамедленного движения.
Угол между графиком и осью времени зависит от модуля вектора ускорения. Чем больше угол, тем быстрее изменяется скорость, и больше модуль вектора ускорения. На графике видно, что угол между графиком и осью времени у графика 1 меньше, чем у графика 2. Это означает, модуль вектора ускорения 2 графика больше модуля вектора ускорения 1 графика, значит 2 тело быстрее изменяет свою скорость.
Тела 2 и 3 движутся с одинаковыми по модулю ускорениями, потому что графики их движения образуют с осью времени одинаковые углы.
Теперь выведем уравнения, позволяющие рассчитывать положение точки для этого движения в любой момент времени.
Предположим, что движение с постоянным ускорением совершается в одной плоскости, обозначим плоскость ХОY. В том случае если вектор начальной скорости и вектор ускорения не лежат на одной прямой, то точка будет двигаться по кривой линии. Поэтому в этом случае с течением времени будут изменяться и координата х, и координата у.
Поэтому в этом случае с течением времени будут изменяться и координата х, и координата у.
Обозначим через x0 и y0 координаты в начальный момент времени, а через х и у координаты в момент времени t. Тогда за время t изменение координаты x будет равно х-х0, а координаты y – y-y0.
Выразим значение координаты х в момент времени t: она равна сумме х0 и изменению координаты дельта х. Координата y в момент времени t: она равна сумме y0 и изменению координаты дельта y.
Значит, для нахождения положения точки в любой момент времени надо знать ее начальные координаты и уметь находить изменения координат за время движения.
Если движение происходит так, что проекция скорости изменяется со временем, величину дельта х, за время t можно найти следующим образом. Мы уже изучили, что при равномерном движении изменение координаты точки за время дельта t можно определить с помощью графика зависимости скорости от времени по площади прямоугольника. Такой график изображен на рисунке. Длина отрезка ОС соответствует времени движения. Разделив его на малые интервалы времени, в этих пределах проекцию скорости будем считать постоянной и равной ее среднему значению. Теперь рассмотрим интервал дельта t1. Тогда перемещение на этом участке, и соответственно площадь заштрихованного прямоугольника численно равна изменению координаты точки за время t1. Сумма всех этих площадей численно равна изменению координаты точки за все время t. Чем сильнее мы уменьшим интервал дельта t, тем точнее будет результат. Если дельта t устремить к нулю, то площадь фигуры АВСО будет стремиться к изменению координаты тела дельта х.
Длина отрезка ОС соответствует времени движения. Разделив его на малые интервалы времени, в этих пределах проекцию скорости будем считать постоянной и равной ее среднему значению. Теперь рассмотрим интервал дельта t1. Тогда перемещение на этом участке, и соответственно площадь заштрихованного прямоугольника численно равна изменению координаты точки за время t1. Сумма всех этих площадей численно равна изменению координаты точки за все время t. Чем сильнее мы уменьшим интервал дельта t, тем точнее будет результат. Если дельта t устремить к нулю, то площадь фигуры АВСО будет стремиться к изменению координаты тела дельта х.
Если мы имеем дело с равноускоренным движением, то изменение координаты тела численно равно площади трапеции АВСО. Длины оснований ОА и ВС этой трапеции численно равны проекциям начальной и конечной скоростей, а длина высоты ОС – времени движения.
По формуле для площади трапеции имеем: дельта х равно произведению полусуммы проекций начальной и конечной скорости на этом интервале времени и значения промежутка времени.
Учитывая, что проекция вектора конечной скорости равна сумме проекции начальной скорости и произведения проекции ускорения и времени, получаем что дельта х равно сумме произведения проекции начальной скорости и времени и полусуммы произведения проекции ускорения и квадрата времени.
Это пример, когда проекция вектора начальной скорости и проекция вектора ускорения положительны. Однако, она справедлива даже в том случае, если одна или обе величины отрицательны.
Изменение координаты дельта y можно найти таким же способом, и оно имеет аналогичный вид: дельта y равно сумме произведения проекции начальной скорости и времени и полусуммы произведения проекции ускорения и квадрата времени.
Подставив полученные значения изменения координат дельта x и дельта y в выведенные ранее формулы, получим выражения для координат при движении с постоянным ускорением как функции времени (их еще иногда называют кинематическими уравнениями движения).
Эти формулы часто применяют для описания как прямолинейного, так и криволинейного движения точки. Однако следует учитывать, что ускорение должно быть постоянным.
Однако следует учитывать, что ускорение должно быть постоянным.
При движении точки в плоскости ХОY двум уравнениям соответствует одно векторное уравнение: радиус-вектор точки равен начальному радиус-вектору плюс произведение вектора начальной скорости и промежутка времени плюс полусумма вектора ускорения и квадрата времени.
Следует обратить внимание на то, что при помощи этих формул можно найти только лишь положение движущейся точки в любой момент времени. Для нахождения пути нужно значительно более подробно исследовать траекторию, определить точки, в которых могло произойти изменение направления движения.
Полученные уравнения вместе с формулами для проекций скорости дают возможность решать любую задачу о движении с постоянным ускорением.Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.
 1 Кинематика
1 Кинематика - 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 2.
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.
 3 Магнетизм
3 Магнетизм - 4.4 Электромагнитные колебания и волны
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика.
 Квантовая теория
Квантовая теория - 6.2 Ядерная физика
- 6.1 Атомная физика.
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
Центростремительная сила – Резюме – Гиперучебник по физике
[закрыть]
Способы ускорения Сила, которая… создаст движущийся объект … или… параллельно
скоростиизменить скорость (ускорить) ускорить (в обычном смысле этого слова) антипараллельно
скоростиизменить скорость (замедлить) замедлить (это еще один способ ускориться) перпендикулярно
скоростиизменить направление (повернуть) ускорение центростремительно (что также является еще одним способом ускорения) - A центростремительное ускорение ( a c )
- возникает всякий раз, когда движущийся объект меняет направление
- не меняет скорость объекта
- действует под прямым углом к скорости в любой момент
- направлен к центру круга (поиск центра)
- также известен как радиальное ускорение .

- A центростремительная сила ( F c )
- это сила, которая заставляет движущийся объект менять направление
- — это не конкретная сила, а название, данное любой силе или комбинации сил, ответственных за центростремительное ускорение
- действует под прямым углом к скорости в любой момент
- направлен к центру круга (поиск центра)
- также известен как радиальная сила .
- Направления в круговом движении
- Скорость ( v ) является касательной (лежит по касательной к траектории).
- Центростремительное ускорение и центростремительная сила бывают центростремительными (направлены к центру окружности) или радиальными (находятся на радиусе окружности).
- Центростремительное ускорение перпендикулярно скорости.
- Центростремительная сила параллельна центростремительному ускорению.
- Уравнения [в единицах СИ]
- скорость и скорость
линейные количества v = 2π р Т где v = скорость [м/с] π = математическая константа r = радиус кругового пути [м] Т = период обращения [с] угловые величины v = ω × r где v = вектор поступательной скорости [м/с] r = радиус-вектор [м] ω = вектор угловой скорости [рад/с] - частота и период
линейные количества ƒ = 1 Т где f = частота вращения [Гц = 1/с = с −1 ] Т = период обращения [с] угловые величины ω = 2π = 2πƒ Т где ω = величина угловой скорости или угловой частоты [рад/с] π = математическая константа Т = период обращения [с] f = частота вращения [Гц = 1/с = с −1 ] - центростремительное ускорение
линейные количества а в = v 2 = 4π 2 р р Т 2 где а в = центростремительное ускорение [м/с 2 ] v = скорость [м/с] r = радиус кругового пути [м] π = математическая константа Т = период обращения [с] угловые величины A C = −ω 2 R = ω × V .
где а в = вектор центростремительного ускорения [м/с 2 ] ω = величина угловой скорости или угловой частоты [рад/с] r = радиус-вектор [м] ω = вектор угловой скорости [рад/с] v = вектор поступательной скорости [м/с]
- скорость и скорость
- А центробежная сила …
- это вымышленная сила (он же кажущаяся сила или псевдосила )
- не является результатом взаимодействия между объектами
- перестает существовать, когда объект перестает двигаться по кругу
- — иллюзия во вращающейся системе отсчета .
- кажется направленным от центра круга (центр убегает)
- Круговое движение, при котором скорость постоянна, называется равномерным круговым движением .

5.3: Скорость, ускорение и сила
- Последнее обновление
- Сохранить как PDF
- Код страницы
- 14461
- Безграничный
- Безграничный
- Выражают взаимосвязь между углом поворота и расстоянием
- Выразите центростремительное ускорение через скорость вращения
- Выразите уравнения для центростремительной силы и ускорения
- Когда объект вращается вокруг оси, точки на краях объекта перемещаются по дуге.
- Угол, огибаемый этими дугами, называется углом вращения и обычно обозначается символом тета .
- Мера того, насколько быстро объект вращается относительно времени, называется угловой скоростью. Обычно он представлен греческим символом омега . Как и его аналог линейной скорости, это вектор.

- Чтобы объект мог двигаться по кругу, он должен постоянно менять направление.
- Поскольку скорость является вектором, изменения направления вызывают изменения скорости.
- Изменение скорости называется ускорением. Изменение скорости из-за кругового движения известно как центростремительное ускорение.
- Центростремительное ускорение можно рассчитать, разделив квадрат линейной скорости на радиус окружности, по которой движется объект.
- Когда объект находится в равномерном круговом движении, он постоянно меняет направление и, следовательно, ускоряется. Это угловое ускорение.
- Сила, действующая на объект при равномерном круговом движении (называемая центростремительной силой), действует на объект из центра круга.
- радианы : Угол, образуемый в центре окружности дугой окружности той же длины, что и радиус окружности.
- ускорение : Величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).

- круговое движение : Движение таким образом, что выбранный путь является круговым.
- скорость : Векторная величина, обозначающая скорость изменения положения по отношению ко времени или скорость с компонентом направления.
- центростремительный : Направленный или движущийся к центру.
- угловая скорость : Векторная величина, описывающая круговое движение объекта; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
- Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
- OpenStax College, Угол вращения и угловая скорость.
 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/ . Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/ . Лицензия : CC BY: Attribution - радиана. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/radians . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, угол поворота и угловая скорость. 25 января 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution - Угловая скорость. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Angular_velocity . Лицензия : CC BY: Attribution
- Колледж OpenStax, Центростремительное ускорение. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42084/latest/ . Лицензия : CC BY: Attribution
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/circular-motion .
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - скорость. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/velocity . Лицензия : CC BY-SA: Attribution-ShareAlike
- ускорение. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/acceleration . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, угол поворота и угловая скорость.
 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution - Угловая скорость. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Angular_velocity . Лицензия : CC BY: Attribution
- Центростремительное ускорение. Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, Центростремительное ускорение. 25 января 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Атрибуция
Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Атрибуция - Колледж OpenStax, Центростремительная сила. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42086/latest/ . Лицензия : CC BY: Attribution
- центростремительный. Предоставлено : Викисловарь. Расположен по адресу : http://en.wiktionary.org/wiki/centripetal . Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/angular-velocity .
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, угол поворота и угловая скорость. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
- Угловая скорость. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Angular_velocity . Лицензия : CC BY: Attribution
- Центростремительное ускорение.
 Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, Центростремительное ускорение. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Attribution
- Колледж OpenStax, Центростремительная сила. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу 906:50 : http://cnx.org/content/m42086/latest/Figure_07_03_01a.jpg . Лицензия : CC BY: Attribution
- Обзор центростремительной силы.
 Расположен по адресу : http://www.youtube.com/watch?v=ldQWTNDBSSE . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Расположен по адресу : http://www.youtube.com/watch?v=ldQWTNDBSSE . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Безграничный
- Показать оглавление
- нет
- Теги
- ускорение
- угловая скорость
- центростремительный
- Круговое движение
- радиан
- скорость
- Определение кругового движения
- Что такое равномерное движение?
- Как рассчитать параметры кругового движения?
- Формулы кругового движения
- Часто задаваемые вопросы
- Гоночный автомобиль движется по круговой кривой;
- Искусственный спутник, вращающийся вокруг Земли;
- Наконечник минутной/секундной стрелки часов; и
- Вращение камня, привязанного к веревке.
- Используйте раскрывающееся меню . От до выберите набор параметров , которые вы хотите рассчитать. Мы выберем параметр радиус, скорость и ускорение, поскольку мы хотим рассчитать все параметры для этого примера.
- Введите период времени кругового движения, скажем,
4 секундыв строке 1. - Калькулятор отобразит частоту (
0,25 Гц) и угловую скорость (1,571 рад/с) кругового движения. - Введите радиус кругового пути, например
2 метра, в строке 2. Калькулятор покажет скорость (3,142 м/с) и центростремительное ускорение (4,935 м/с 2).
Угловое смещение (θ) — это угол
θ, образуемый в центре радиус-вектором за заданное время. Мы знаем, что:угол = дуга/радиус… следовательно, для цифры 1 мы можем написать:
θ = PQ/rЕдиницей углового смещения в системе СИ является радиан (
рад).Период времени (T) — это время, за которое объект совершает один оборот по круговой траектории.
 Единицей периода времени в системе СИ является секунда (
Единицей периода времени в системе СИ является секунда (с).Частота (ν) — количество оборотов, которое объект совершает за одну секунду. Единицей частоты в системе СИ является герц (
Гц).ν = 1/ТУгловая скорость (ω) — скорость изменения углового смещения во времени, т. е.
ω = Δθ / ΔtЕдиницей угловой скорости в системе СИ является радиан в секунду (
рад/с).Когда объект совершает один оборот (см. рис. 1), угол в центре составляет
2πрадиан. Это означает, что для периода кругового движенияt = T,θ = 2π. Следовательно, мы можем выразить угловую скорость как:ω = 2 * π/T…или:
ω = 2 * π * νУгловое ускорение (α) — скорость изменения угловой скорости во времени, т.
 е.
е.α = Δω / ΔtЕдиницей углового ускорения в системе СИ является
рад/с 2.Центростремительное ускорение (
α c) — это ускорение объекта, совершающего равномерное круговое движение. Он всегда действует на объект по радиусу и к центру круговой траектории.α с = v 2 / r- Возьмите квадрат линейной скорости .
- Разделите значение в шаге 1 на радиус кругового пути.
- Поздравляем! У вас вычислено центростремительное ускорение при круговом движении.
- Когда объект вращается вокруг оси, точки на краях объекта перемещаются по дуге.
- Угол, огибаемый этими дугами, называется углом вращения и обычно обозначается символом тета .
- Мера того, насколько быстро объект вращается относительно времени, называется угловой скоростью. Обычно он представлен греческим символом омега . Как и его аналог линейной скорости, это вектор.
- радианы : Угол, образуемый в центре окружности дугой окружности той же длины, что и радиус окружности.
- Чтобы объект мог двигаться по окружности, он должен постоянно менять направление.
- Поскольку скорость является вектором, изменения направления вызывают изменения скорости.
- Изменение скорости называется ускорением. Изменение скорости из-за кругового движения известно как центростремительное ускорение.

- Центростремительное ускорение можно рассчитать, разделив квадрат линейной скорости на радиус окружности, по которой движется объект.
- ускорение : Величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).
- круговое движение : Движение таким образом, что выбранный путь является круговым.
- скорость : Векторная величина, обозначающая скорость изменения положения по отношению ко времени или скорость с компонентом направления.
- Когда объект находится в равномерном круговом движении, он постоянно меняет направление и, следовательно, ускоряется. Это угловое ускорение.
- Сила, действующая на объект при равномерном круговом движении (называемая центростремительной силой), действует на объект из центра круга.

- центростремительный : направленный или движущийся к центру.
- угловая скорость : Векторная величина, описывающая круговое движение объекта; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
- Курирование и доработка.
 Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike - OpenStax College, Угол вращения и угловая скорость. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- радиан. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, угол вращения и угловая скорость. 25 января 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Угловая скорость.
 Предоставлено : Википедия. Лицензия : CC BY: Атрибуция
Предоставлено : Википедия. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Центростремительное ускорение. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Безгранично. Предоставлено 906:50: Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- скорость. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/velocity. Лицензия : CC BY-SA: Attribution-ShareAlike
- ускорение. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция - Колледж OpenStax, угол вращения и угловая скорость. 25 января 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Угловая скорость. Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Центростремительное ускорение. Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, Центростремительное ускорение. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/11e58ada3ac9ddc55f67ebca76ad3f26a96643fb/Figure_07_02_01a.jpg. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Центростремительная сила.
 17 сентября 2013 г. Предоставлено 906:50 : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено 906:50 : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - центростремительный. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено 906:50 : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, угол вращения и угловая скорость. 25 января 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Угловая скорость. Предоставлено : Википедия.
 Расположен по адресу : https://en.wikipedia.org/wiki/Angular_velocity. Лицензия : CC BY: Attribution
Расположен по адресу : https://en.wikipedia.org/wiki/Angular_velocity. Лицензия : CC BY: Attribution - Центростремительное ускорение. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, Центростремительное ускорение. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/11e58ada3ac9ddc55f67ebca76ad3f26a96643fb/Figure_07_02_01a.jpg. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Центростремительная сила. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/b0b6d1b912e067a3581bb36bbfc7e7d1dcd184fe/Figure_07_03_01a.jpg. Лицензия : CC BY: Attribution
- Обзор центростремительной силы.
 Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - Описать равномерное круговое движение
- Объясните неравномерное круговое движение
- Расчет углового ускорения объекта
- Соблюдать связь между линейным и угловым ускорением
Угол вращения и угловая скорость
Угол поворота является мерой того, насколько сильно вращается объект, а угловая скорость измеряет, насколько быстро он вращается.
цели обучения
Угол вращения и угловая скорость
Когда объект вращается вокруг оси, например, автомобильная шина или пластинка на проигрывателе, движение можно описать двумя способами. Точка на краю вращающегося объекта будет иметь некоторую скорость и будет перемещаться по дуге, перемещаясь на вращающемся объекте. Точка пройдет расстояние \(\mathrm{ΔS}\), но часто удобнее говорить о степени вращения объекта. Величина вращения объекта называется углом поворота и может измеряться в градусах или радианах. Поскольку угол поворота связан с расстоянием \(\mathrm{ΔS}\) и с радиусом \(\mathrm{r}\) уравнением \(\mathrm{Δθ=\frac{ΔS}{R}} \), обычно удобнее использовать радианы.
Точка пройдет расстояние \(\mathrm{ΔS}\), но часто удобнее говорить о степени вращения объекта. Величина вращения объекта называется углом поворота и может измеряться в градусах или радианах. Поскольку угол поворота связан с расстоянием \(\mathrm{ΔS}\) и с радиусом \(\mathrm{r}\) уравнением \(\mathrm{Δθ=\frac{ΔS}{R}} \), обычно удобнее использовать радианы.
Угол θ и длина дуги s : Радиус окружности поворачивается на угол \(\mathrm{Δθ}\). Длина дуги \(\mathrm{Δs}\) описана на окружности.
Скорость, с которой вращается объект, определяется угловой скоростью, которая представляет собой скорость изменения угла поворота во времени. Хотя угол сам по себе не является векторной величиной, угловая скорость является вектором. Направление вектора угловой скорости перпендикулярно плоскости вращения в направлении, которое обычно задается правилом правой руки. Угловое ускорение дает скорость изменения угловой скорости. Угол, угловая скорость и угловое ускорение очень полезны при описании вращательного движения объекта.
Направление угловой скорости : Угловая скорость описывает скорость вращения и ориентацию мгновенной оси, вокруг которой происходит вращение. Направление угловой скорости будет вдоль оси вращения. В этом случае (вращение против часовой стрелки) вектор направлен вверх.
Когда ось вращения перпендикулярна вектору положения, угловую скорость можно рассчитать, взяв линейную скорость \(\mathrm{v}\) точки на краю вращающегося объекта и разделив ее на радиус. Это даст угловую скорость, обычно обозначаемую \(\mathrm{ω}\), в радианах в секунду.
Угловая скорость : Муха на краю вращающегося объекта регистрирует постоянную скорость \(\mathrm{v}\). Объект вращается с угловой скоростью, равной \(\mathrm{\frac{v}{r}}\).
Центростремительное ускорение
Центростремительное ускорение — это постоянное изменение скорости, необходимое объекту для сохранения кругового пути.
цели обучения
Обзор
Как упоминалось в предыдущих разделах о кинематике, любое изменение скорости определяется ускорением. Часто изменения скорости являются изменениями величины. Когда объект ускоряется или замедляется, это изменение скорости объекта. Изменения величины скорости соответствуют нашему интуитивному и повседневному использованию термина ускорение. Однако, поскольку скорость является вектором, она также имеет направление. Следовательно, любое изменение направления движения объекта также должно сопровождаться ускорением.
Часто изменения скорости являются изменениями величины. Когда объект ускоряется или замедляется, это изменение скорости объекта. Изменения величины скорости соответствуют нашему интуитивному и повседневному использованию термина ускорение. Однако, поскольку скорость является вектором, она также имеет направление. Следовательно, любое изменение направления движения объекта также должно сопровождаться ускорением.
Равномерное круговое движение предполагает перемещение объекта по круговой траектории с постоянной скоростью. Поскольку скорость постоянна, обычно не думают, что объект ускоряется. Однако направление постоянно меняется по мере того, как объект пересекает круг. Таким образом, говорят, что он ускоряется. Это ускорение можно почувствовать, когда едешь на американских горках. Даже если скорость постоянна, быстрый поворот вызовет у гонщика ощущение силы. Это чувство — ускорение.
92r}\], где омега – скорость вращения, определяемая выражением \(\mathrm{\frac{v}{r}}\).
Центростремительное ускорение : Когда объект движется по окружности, направление вектора скорости постоянно меняется.
Центростремительная сила
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой (примером центростремительной силы является равномерное круговое движение).
цели обучения
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой. Равномерное круговое движение является примером действия центростремительной силы. Это можно увидеть в движении спутников вокруг Земли, в натяжении веревки при игре в мяч, в петле на американских горках или в ведре, раскачиваемом вокруг тела.
Обзор центростремительной силы : Краткий обзор центростремительной силы.
Ранее мы узнали, что любое изменение скорости является ускорением. Когда объект движется по круговой траектории, он постоянно меняет направление и, следовательно, ускоряется, в результате чего на объект действует постоянная сила. Эта центростремительная сила действует по направлению к центру кривизны, по направлению к оси вращения. Поскольку объект движется перпендикулярно силе, путь, по которому следует объект, является круговым. Именно эта сила удерживает мяч от выпадения из ведра, если вы непрерывно вращаете его по кругу. 92}\]
Ключевые точки
Ключевые термины
ЛИЦЕНЗИИ И АВТОРСТВО
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ПРЕДОСТАВЛЕННОЕ РАНЕЕ
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, КОНКРЕТНОЕ АВТОРСТВО
Эта страница под названием 5.3: Velocity, Acceleration, and Force распространяется по незаявленной лицензии и была создана, изменена и/или курирована Boundless.
Калькулятор кругового движения
Автор Purnima Singh, PhD
Отзыв Стивена Вудинга
Последнее обновление: 05 декабря 2021 г.
Калькулятор кругового движения Omni позволяет вычислить все параметры равномерного кругового движения . Если вы не знаете, что такое равномерное круговое движение, или чувствуете себя подавленным формулами кругового движения, не волнуйтесь! Наш калькулятор кругового движения поможет вам понять концепции равномерного кругового движения в физике.
Читайте дальше, чтобы узнать определение, примеры и формулы кругового движения. Вы также найдете примеры расчета параметров кругового движения (таких как период, частота, скорость и ускорение) с помощью нашего калькулятора равномерного кругового движения.
Определение кругового движения
Когда объект движется по круговой траектории , мы называем его движение круговым.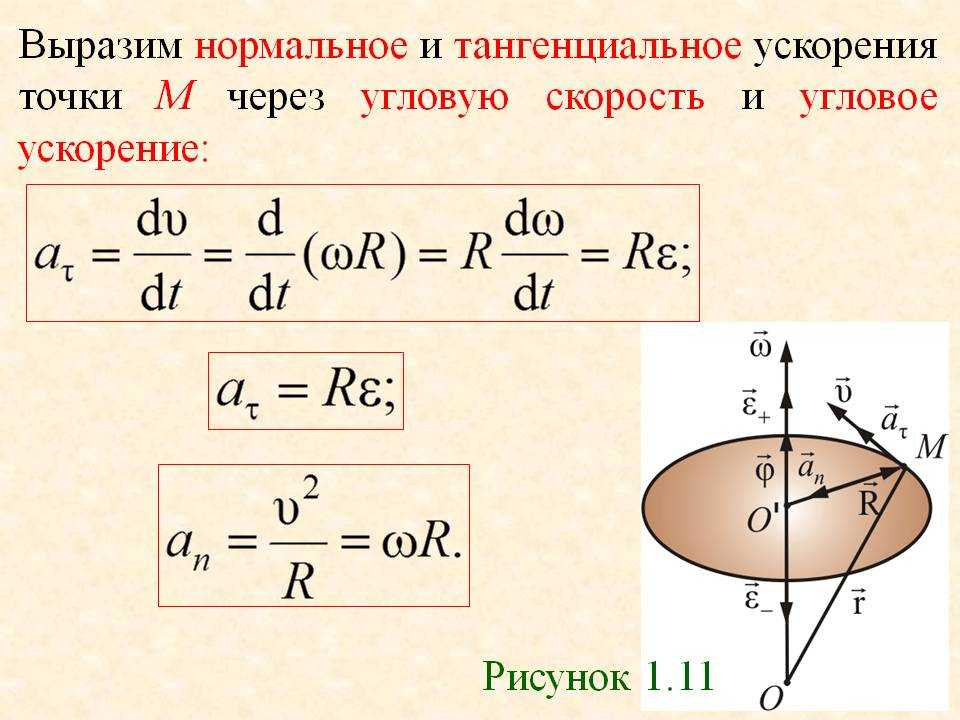 Некоторые распространенные примеры кругового движения:
Некоторые распространенные примеры кругового движения:
Круговое движение объекта может быть равномерным круговым движением или неравномерное круговое движение .
При круговом движении направление движения постоянно меняется . В любой момент направление движения тела, движущегося по окружности, лежит по касательной к окружности в этот момент.
Более простой способ визуализировать эту концепцию — представить себе вращающийся камень, привязанный к веревке; когда струна рвется, камень летит по касательной.
Что такое равномерное круговое движение?
При равномерном круговом движении объект движется по круговой траектории со скоростью постоянная скорость . Это означает, что объект будет проходить равные расстояния по окружности окружности за равные промежутки времени. В неравномерном круговом движении скорость объекта изменяется .
Это означает, что объект будет проходить равные расстояния по окружности окружности за равные промежутки времени. В неравномерном круговом движении скорость объекта изменяется .
Хотя при равномерном круговом движении скорость постоянна, направление движения постоянно меняется, как мы обсуждали в предыдущем разделе. Следовательно, скорость объекта, совершающего равномерное круговое движение, также непрерывно изменяется (см. рисунок 1).
Из-за изменения направления скорости объект испытывает ускорение, называемое центростремительным ускорением .
Из первого закона движения Ньютона мы знаем, что тело не может изменить направление своего движения само по себе. Для этого требуется внешняя сила. Это внешняя сила та удерживает объект, движущийся по круговой траектории , называется центростремительной силой .
Как рассчитать параметры кругового движения?
Давайте посмотрим, как использовать калькулятор равномерного кругового движения для расчета различных физических параметров кругового движения.
Мы также рекомендуем воспользоваться нашим калькулятором центробежной силы.
Формулы движения по окружности
Рассмотрим объект, движущийся по окружности окружности радиусом r (см. рис. 1) с центром в точке O . Пусть объект перемещается (против часовой стрелки) из P в Q за время t . Физические величины, описывающие это движение, и формулы кругового движения:0003
Часто задаваемые вопросы
Что является постоянным в равномерном круговом движении?
Скорость постоянна при равномерном круговом движении. Объект движется с постоянной скоростью по круговой траектории в равномерном круговом движении.
Какая центростремительная сила действует на объект, движущийся по окружности?
Центростремительная сила — это сила, которая действует на любой объект, движущийся по окружности . Величина центростремительной силы, действующей на объект, движущийся по окружности, равна произведению его массы на центростремительное ускорение.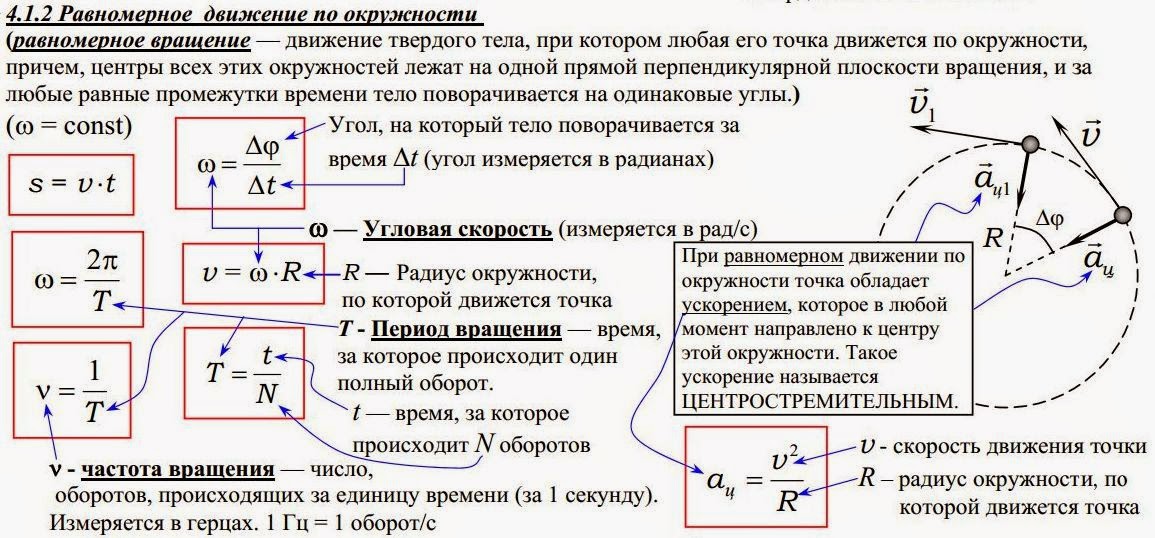 Центростремительная сила направлена к центру окружности.
Центростремительная сила направлена к центру окружности.
Какая связь между линейной скоростью и угловой скоростью?
Для объекта, совершающего равномерное круговое движение, линейная скорость v равна произведению угловой скорости ω и радиуса пути r .
Как найти ускорение при круговом движении?
Чтобы найти центростремительное ускорение при круговом движении, выполните следующие действия:
Purnima Singh, PhD
Я хочу вычислить
Период времени
Частота
Угловая скорость
Проверьте 19 похожих калькуляторов вращательного и периодического движения 🌎
Угловое ускорениеУгловое смещениеУгловая частота… Еще 16
Скорость, ускорение и сила | безграничная физика |
Угол вращения и угловая скорость
Угол поворота является мерой того, насколько сильно вращается объект, а угловая скорость измеряет, насколько быстро он вращается.
Цели обучения
Выразите взаимосвязь между углом поворота и расстоянием
Основные выводы
Ключевые моменты
Ключевые термины
Угол вращения и угловая скорость
Когда объект вращается вокруг оси, как, например, автомобильная шина или пластинка на проигрывателе, движение можно описать двумя способами. Точка на краю вращающегося объекта будет иметь некоторую скорость и будет перемещаться по дуге, перемещаясь на вращающемся объекте. точка пройдет расстояние
Точка на краю вращающегося объекта будет иметь некоторую скорость и будет перемещаться по дуге, перемещаясь на вращающемся объекте. точка пройдет расстояние
ΔS\Delta \text{S}ΔS
, но часто удобнее говорить о том, насколько объект повернулся. Величина вращения объекта называется углом поворота и может измеряться в градусах или радианах. Поскольку угол поворота связан с расстоянием
ΔS\Delta \text{S}ΔS
и с радиусом
r\text{r}r
уравнением
Δθ=ΔSR\Delta \theta = \frac{\Delta \text{S}}{\text{R}}Δθ=RΔS
, обычно удобнее использовать радианы.
Угол θ и длина дуги s : Радиус окружности поворачивается на угол
Δθ\Delta\thetaΔθ
. Длина дуги
Δs\Delta \text{s}Δs
описана на окружности.
Скорость, с которой вращается объект, определяется угловой скоростью, которая представляет собой скорость изменения угла поворота во времени. Хотя угол сам по себе не является векторной величиной, угловая скорость является вектором. Направление вектора угловой скорости перпендикулярно плоскости вращения в направлении, которое обычно задается правилом правой руки. Угловое ускорение дает скорость изменения угловой скорости. Угол, угловая скорость и угловое ускорение очень полезны при описании вращательного движения объекта.
Хотя угол сам по себе не является векторной величиной, угловая скорость является вектором. Направление вектора угловой скорости перпендикулярно плоскости вращения в направлении, которое обычно задается правилом правой руки. Угловое ускорение дает скорость изменения угловой скорости. Угол, угловая скорость и угловое ускорение очень полезны при описании вращательного движения объекта.
Направление угловой скорости : Угловая скорость описывает скорость вращения и ориентацию мгновенной оси, вокруг которой происходит вращение. Направление угловой скорости будет вдоль оси вращения. В этом случае (вращение против часовой стрелки) вектор направлен вверх.
Когда ось вращения перпендикулярна вектору положения, угловую скорость можно рассчитать, взяв линейную скорость
v\text{v}v
точки на краю вращающегося объекта и деления на радиус. Это даст угловую скорость, обычно обозначаемую как
ω\omegaω
, в радианах в секунду.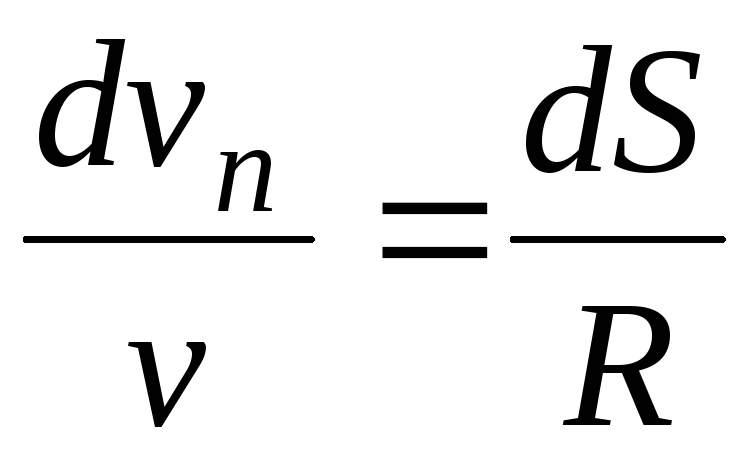
Угловая скорость : Муха на краю вращающегося объекта регистрирует постоянную скорость
v\text{v}v
. Объект вращается с угловой скоростью, равной
vr\frac{\text{v}}{\text{r}}rv
.
Центростремительное ускорение
Центростремительное ускорение — это постоянное изменение скорости, необходимое объекту для сохранения кругового пути.
Цели обучения
Выразите центростремительное ускорение через скорость вращения
Ключевые выводы
Ключевые моменты
Ключевые термины
Обзор
Как упоминалось в предыдущих разделах о кинематике, любое изменение скорости определяется ускорением. Часто изменения скорости являются изменениями величины. Когда объект ускоряется или замедляется, это изменение скорости объекта. Изменения величины скорости соответствуют нашему интуитивному и повседневному использованию термина ускорение. Однако, поскольку скорость является вектором, она также имеет направление. Следовательно, любое изменение направления движения объекта также должно сопровождаться ускорением.
Однако, поскольку скорость является вектором, она также имеет направление. Следовательно, любое изменение направления движения объекта также должно сопровождаться ускорением.
Равномерное круговое движение предполагает перемещение объекта по круговой траектории с постоянной скоростью. Поскольку скорость постоянна, обычно не думают, что объект ускоряется. Однако направление постоянно меняется по мере того, как объект пересекает круг. Таким образом, говорят, что он ускоряется. Это ускорение можно почувствовать, когда едешь на американских горках. Даже если скорость постоянна, быстрый поворот вызовет у гонщика ощущение силы. Это чувство — ускорение.
Центростремительное ускорение : Краткий обзор центростремительного ускорения для школьников-физиков.
Расчет центростремительного ускорения
Для вычисления центростремительного ускорения объекта, совершающего равномерное круговое движение, необходимо знать скорость, с которой движется объект, и радиус окружности, вокруг которой происходит движение.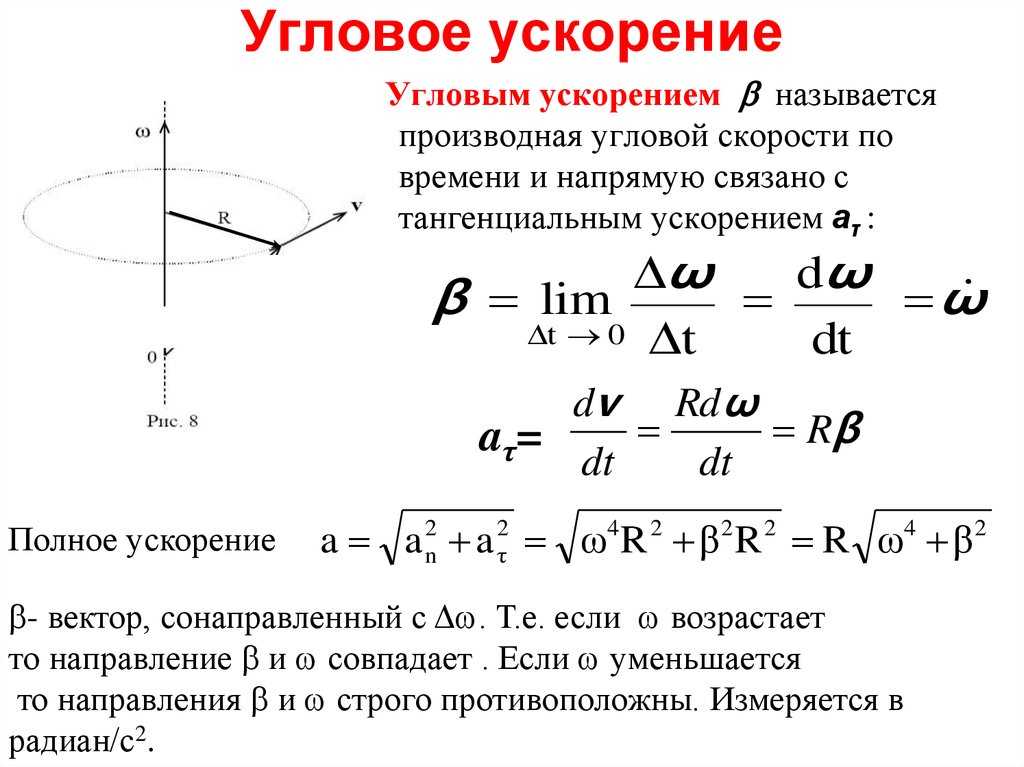 2}{\text{r}}ac=rv2 92 \text{r}ac=ω2r
2}{\text{r}}ac=rv2 92 \text{r}ac=ω2r
, где омега – это скорость вращения, определяемая выражением
vr\frac{\text{v}}{\text{r}}rv
.
Центростремительное ускорение : Когда объект движется по окружности, направление вектора скорости постоянно меняется.
Центростремительная сила
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой (примером центростремительной силы является равномерное круговое движение).
Цели обучения
Выразите уравнения для центростремительной силы и ускорения
Ключевые выводы
Ключевые моменты
Ключевые термины
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой. Равномерное круговое движение является примером действия центростремительной силы. Это можно увидеть в движении спутников вокруг Земли, в натяжении веревки при игре в мяч, в петле на американских горках или в ведре, раскачиваемом вокруг тела.
Обзор центростремительной силы : Краткий обзор центростремительной силы.
Ранее мы узнали, что любое изменение скорости есть ускорение. Когда объект движется по круговому пути, он постоянно меняет направление и, следовательно, ускоряется, в результате чего на объект действует постоянная сила. Эта центростремительная сила действует по направлению к центру кривизны, по направлению к оси вращения. Поскольку объект движется перпендикулярно силе, путь, по которому следует объект, является круговым. Именно эта сила удерживает мяч от выпадения из ведра, если вы непрерывно вращаете его по кругу. 92}{\text{r}}Fc=rmv2
Когда объект движется по круговому пути, он постоянно меняет направление и, следовательно, ускоряется, в результате чего на объект действует постоянная сила. Эта центростремительная сила действует по направлению к центру кривизны, по направлению к оси вращения. Поскольку объект движется перпендикулярно силе, путь, по которому следует объект, является круговым. Именно эта сила удерживает мяч от выпадения из ведра, если вы непрерывно вращаете его по кругу. 92}{\text{r}}Fc=rmv2
где:
Fc\text{F}_\text{c}Fc
– центростремительная сила,
м\text{m}m
— масса,
v\text{v}v
— скорость,
r\text{r}r
— радиус траектории движения.
Из второго закона Ньютона
F=m⋅a\text{F}= \text{m} \cdot \text{a}F=m⋅a
, мы видим, что центростремительное ускорение равно:
ac =v2r\displaystyle \text{a}_\text{c} = \frac{\text{v}^2}{\text{r}}ac=rv2 92Fc=mrω2
Лицензии и ссылки
Контент под лицензией CC, совместно используемый ранее
Лицензионный контент CC, конкретное указание авторства
10.1 Угловое ускорение | Texas Gateway
Цели обучения
К концу этого раздела вы сможете делать следующее:
Равномерное круговое движение и гравитация обсуждались только равномерное круговое движение, то есть движение по окружности с постоянной скоростью и, следовательно, с постоянной угловой скоростью. Напомним, что угловая скорость ωω размером 12{ω} {} определялась как скорость изменения во времени угла θθ размером 12{θ} {}
10,1 ω=ΔθΔt,ω=ΔθΔt, размер 12{ω= {{Δθ} над {Δt} } “,”} {}
, где θθ размер 12{θ} {} — это угол поворота, как показано на Рисунок 10. 3. Соотношение между угловой скоростью ωω размер 12{ω} {} и линейной скоростью vv размер 12{v} {} также было определено в Угле вращения и угловой скорости как
3. Соотношение между угловой скоростью ωω размер 12{ω} {} и линейной скоростью vv размер 12{v} {} также было определено в Угле вращения и угловой скорости как
10,2 v=rωv=rω размер 12{v=rω} { }
или
10,3 ω=vr,ω=vr, размер 12{ω= {{v} над {r} } } {}
, где rr размер 12{r} {} — радиус кривизны, а также показано на рисунке 10.3. Согласно соглашению о знаках, направление против часовой стрелки считается положительным направлением, а направление по часовой стрелке — отрицательным 9.0003
Рисунок 10.3 На этом рисунке показано равномерное круговое движение и некоторые из его определяемых величин.
Угловая скорость непостоянна, когда фигурист тянет руки, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается при выключении. Во всех этих случаях имеет место угловое ускорение, при котором изменяется величина ωω 12{ω} {}. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение αα величиной 12{α}{} определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается как
В форме уравнения угловое ускорение выражается как
10,4 α=ΔωΔt,α=ΔωΔt, размер 12{α= {{Δω} над {Δt} } «,»} {}
size 12{Δt} {} — изменение во времени. Единицы углового ускорения: рад/с/срад/с/с размер 12{ влево (“рад/с” вправо )”/с”} {} или рад/с2рад/с2 размер 12{“рад/с” rSup {размер 8{2} } } {}. Если размер ωω 12{ω} {} увеличивается, то размер αα 12{α} {} положителен. Если размер ωω 12{ω} {} уменьшается, то размер αα 12{α} {} отрицателен.
Пример 10.1 Расчет углового ускорения и замедления велосипедного колеса
Предположим, подросток кладет велосипед на спину и запускает вращение заднего колеса из состояния покоя до конечной угловой скорости 250 об/мин за 5 с. (a) Рассчитайте угловое ускорение в рад/с2рад/с2 size 12{“rad/s” rSup { size 8{2} } } {}. (b) Если теперь она ударит по тормозам, вызывая угловое ускорение –87,3 рад/с2–87,3 рад/с2 размера 12{“-87” “.” 3`”рад/с” rSup {размер 8{2} } } {}, сколько времени потребуется колесу, чтобы остановиться?
Стратегия для (а)
Угловое ускорение может быть найдено непосредственно из его определения в α=ΔωΔtα=ΔωΔt размер 12{α= { {Δω} над {Δt} } } {}, поскольку даны конечная угловая скорость и время. Мы видим, что ΔωΔω размера 12{Δω} {} составляет 250 об/мин, а ΔtΔt размера 12{Δt} {} составляет 5 с.
Мы видим, что ΔωΔω размера 12{Δω} {} составляет 250 об/мин, а ΔtΔt размера 12{Δt} {} составляет 5 с.
Решение для (а)
Вводя известную информацию в определение углового ускорения, получаем размер 12{α= {{Δω} над {Δt} } } {} # размер 12{ {}= {{“250″” об/мин”} свыше {5 “.” “00 с”} } “.”} {} } } {}
Поскольку ΔωΔω размер 12{Δω} {} выражается в оборотах в минуту (об/мин), а нам нужны стандартные единицы рад/с2рад/с2 размера 12{“рад/с” rSup { размер 8{2} } } {} для углового ускорения нам нужно преобразовать ΔωΔω размера 12{Δω} {} из об/мин в рад/с
10,6 Δω=250об/мин⋅2π рад⋅1 мин60 сек=26,2рад.Δω=250обмин⋅2π рад⋅1 мин60 сек=26,2рад.alignl { stack { размер 12{Δω=”250″ { {“об”} более {“мин”} } cdot { {2π” рад”} более {“60” “.” “0 с”} } } {} # размер 12{ {}=”26″ “.” 2 { {“рад”} над {“с”} } } {} } } {}
Подставив эту величину в выражение для размера αα 12{α} {}, получим
10,7 α=ΔωΔt=26,2 рад/с5,00 s=5,24 рад/с2.α=ΔωΔt=26,2 рад /s5.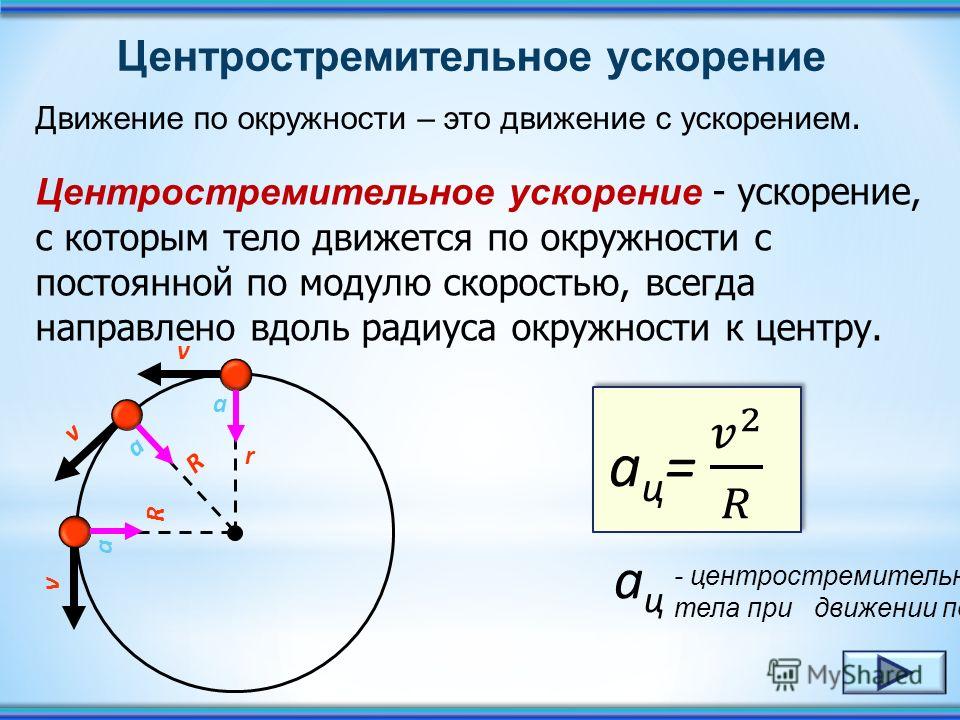 00 s=5,24 рад/с2.alignl { стек {
размер 12{α= {{Δω} над {Δt} } } {} #
размер 12{ {}= {{“26” “.” 2″ рад/с”} свыше {5 “.” “00”” с”} } “.” } {} #
размер 12{ {}=5 “.” “24”” рад/с” rSup {размер 8{2} } } {}
} } {}
00 s=5,24 рад/с2.alignl { стек {
размер 12{α= {{Δω} над {Δt} } } {} #
размер 12{ {}= {{“26” “.” 2″ рад/с”} свыше {5 “.” “00”” с”} } “.” } {} #
размер 12{ {}=5 “.” “24”” рад/с” rSup {размер 8{2} } } {}
} } {}
Стратегия для (б)
В этой части мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение углового ускорения и решая для ΔtΔt размер 12{Δt} {}, что дает
10,8 Δt=Δωα.Δt=Δωα. размер 12{Δt= {{Δω} над {α} } “.”} {}
Решение для (б)
Здесь угловая скорость уменьшается с 26,2 рад/с до 6,2 рад/с размером 12{“26” “.” 2`”рад/с”} {} (250 об/мин) до нуля, так что ΔωΔω размер 12{Δω} {} есть –26,2 рад/с – 26,2 рад/с, и αα размер 12{α} {} задан равным –87,3 рад/с2–87,3 рад/с2 размер 12{“-87” “.” 3`”рад/с” rSup {размер 8{2} } } {}. Таким образом,
10,9 Δt=–26,2 рад/с–87,3рад/с2=0,300 с.Δt=–26,2 рад/с–87,3рад/с2=0,300 с.alignl { stack {
размер 12{Δt= { { – “26” “. ” 2`”рад/с”} более { – “87” “.” 3`”рад/с” rSup {размер 8{2} } } } } {} #
=0 “.” “300”`”с” “.” {}
} } {}
” 2`”рад/с”} более { – “87” “.” 3`”рад/с” rSup {размер 8{2} } } } } {} #
=0 “.” “300”`”с” “.” {}
} } {}
Обсуждение
Обратите внимание, что угловое ускорение, когда девушка крутит колесо, небольшое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит большое замедление — изменение скорости сильно за короткий промежуток времени.
Если бы велосипед в предыдущем примере стоял на колесах, а не в перевернутом положении, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При круговом движении линейное ускорение равно по касательной к окружности в интересующей точке, как показано на рис. 10.4. Таким образом, линейное ускорение называется тангенциальным ускорением при размере 12{a rSub { size 8{t} } } {}.
10.4. Таким образом, линейное ускорение называется тангенциальным ускорением при размере 12{a rSub { size 8{t} } } {}.
Рис. 10.4 При движении по окружности линейное ускорение aa размера 12{a} {} возникает при изменении величины скорости: aa размера 12{a} {} касается движения. В контексте кругового движения линейное ускорение также называется тангенциальным ускорением при размере 12{a rSub {размер 8{t}}} {}.
Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Мы знаем из равномерного кругового движения и гравитации, что при круговом движении центростремительное ускорение,
acac size 12{a rSub { size 8{t} } } {} относится к изменениям направления скорости, но не к ее величине. Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рис. 10.5. Таким образом,
atat size 12{a rSub {size 8{t} } } {} и
acac size 12{a rSub { size 8{t} } } {} перпендикулярны и независимы друг от друга. Тангенциальное ускорение
atat size 12{a rSub { size 8{t} } } {} напрямую связан с угловым ускорением
αα размер 12{α} {} и связан с увеличением или уменьшением скорости, но не ее направления.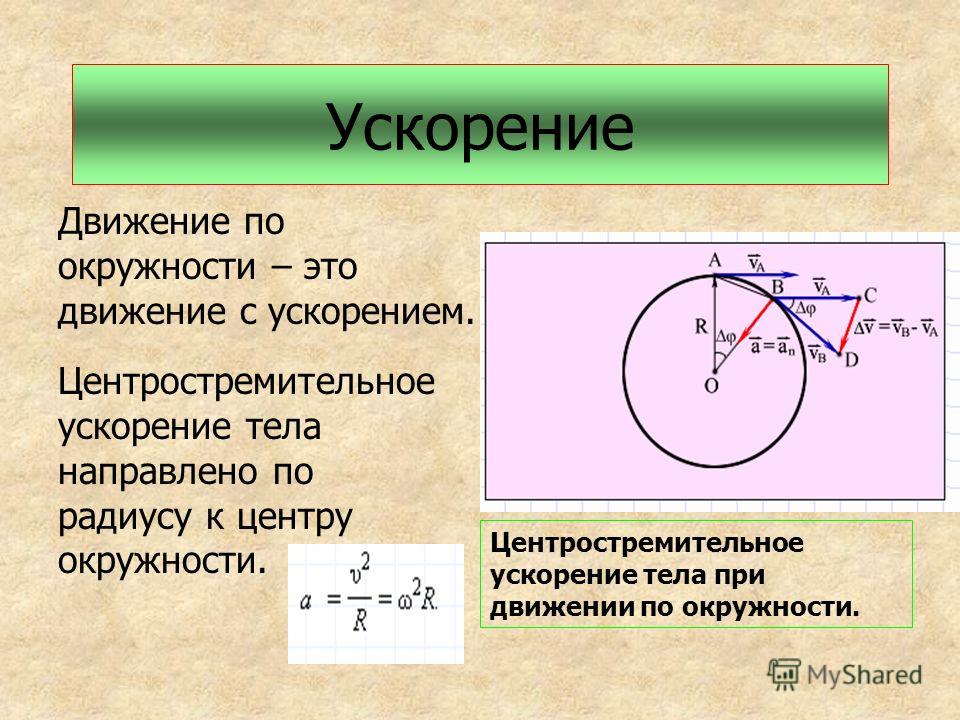
Рис. 10.5 Центростремительное ускорение acac size 12{a rSub { size 8{t} } } {} возникает при изменении направления скорости; оно перпендикулярно круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.
Теперь мы можем найти точное соотношение между линейным ускорением при размере 12{a rSub { размер 8{t} } } {} и угловым ускорением αα размером 12{α} {}. Поскольку линейное ускорение пропорционально изменению величины скорости, оно определяется так же, как и в одномерной кинематике, равным 9.0003
10.10 at=ΔvΔt.at=ΔvΔt. size 12{a rSub { size 8{t} } = {{Δv} over {Δt} } “.”} {}
Для кругового движения обратите внимание, что v=rωv=rω size 12{v=rω} {} , так что
10,11 at=ΔrωΔt.at=ΔrωΔt. size 12{a rSub { size 8{t} } = { {Δ left (rω right )} over {Δt} } “.”} {}
Радиус rr size 12{r} {} постоянен для кругового движения , и поэтому ∆(rω)=r(∆ω)∆(rω)=r(∆ω) size 12{∆ \( rω \) = r \( ∆ω \) } {}. Таким образом,
10,12 at=rΔωΔt. at=rΔωΔt. size 12{a rSub { size 8{t} } =r {{Δω} над {Δt} } “.”} {}
at=rΔωΔt. size 12{a rSub { size 8{t} } =r {{Δω} над {Δt} } “.”} {}
По определению, α=ΔωΔtα=ΔωΔt size 12{α= {{Δω} над {Δt} } } {}. Таким образом,
10,13 at=rα,at=rα, size 12{a rSub { size 8{t} } =rα} {}
или
10,14 α=atr.α=atr. size 12{α= { {a rSub { size 8{t} } } over {r} } } {}
Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное или тангенциальное ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес автомобиля, тем больше ускорение автомобиля. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении αα величиной 12{α}{}.
Пример 10.2 Расчет углового ускорения колеса мотоцикла
Мощный мотоцикл может разгоняться от 0 до 30 м/с (около 108 км/ч) за 4,20 с. Каково угловое ускорение его колес с радиусом 0,320 м? (См. рис. 10.6.)
Рис. 10.6 Линейное ускорение мотоцикла сопровождается угловым ускорением его колес.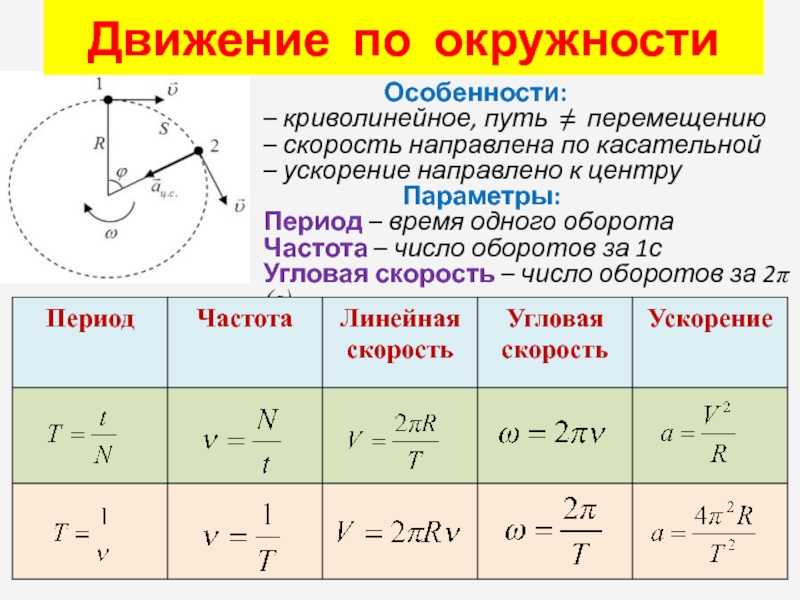
Стратегия
Нам дана информация о линейных скоростях мотоцикла. Таким образом, мы можем найти его линейное ускорение при размере 12{a rSub { size 8{t} } } {}. Тогда выражение α=atrα=atr size 12{a rSub { size 8{t} } =rα,““`α= { {a rSub { size 8{t} } } over {r} } } { } можно использовать для определения углового ускорения.
Решение
Линейное ускорение равно
10,15 at=ΔvΔt=30,0 м/с4,20 с=7,14 м/с2.at=ΔvΔt=30,0 м/с4,20 с=7,14 м/с2.alignl { stack { size 12{a rSub { size 8{t} } = {{Δv} over {Δt} } } {} # ““`= {{“30” “.” 0″ м/с”} более {4 “.” “20 с”} } {} # ““`=7 “.” “14”” м/с” rSup { размер 8{2} “.”} {} } } {}
Мы также знаем радиус колес. Ввод значений для atat size 12{a rSub { size 8{t} } } } {} и rr size 12{r} {} в α=atrα=atr size 12{a rSub { size 8{t} } =rα,““`α= {{a rSub { size 8{t} } } over {r} } } {}, мы получаем
10,16 α=atr=7,14 м/с20,320 м=22,3 рад/с2. α=atr=7,14 м/с20,320 м=22,3 рад/с2.alignl { stack {
size 12{α= { {a rSub { size 8{t} } } over {r} } } {} #
“`= {{7 “.” “14”” м/с” rSup {размер 8{2} } } свыше {0 “.” “320 м”} } {} #
” “=”22” “.” “3 рад/с” rSup {размер 8{2} } {}
} } {}
α=atr=7,14 м/с20,320 м=22,3 рад/с2.alignl { stack {
size 12{α= { {a rSub { size 8{t} } } over {r} } } {} #
“`= {{7 “.” “14”” м/с” rSup {размер 8{2} } } свыше {0 “.” “320 м”} } {} #
” “=”22” “.” “3 рад/с” rSup {размер 8{2} } {}
} } {}
Обсуждение
Единицы радианы безразмерны и появляются в любом соотношении между угловыми и линейными величинами.
До сих пор мы определили три величины вращения — θ, ωθ, ω размер 12{θ,ω} {} и αα размер 12{α} {}. Эти величины аналогичны поступательным величинам x, vx, v size 12{x,v} {} и aa size 12{a} {}. В таблице 10.1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.
| Вращательный | Трансляционное | Отношения |
|---|---|---|
| θθ размер 12{θ} {} | хх размер 12{х} {} | θ=xrθ=xr размер 12{θ= {{x} над {r} } } {} |
| ωω размер 12{ω} {} | вв размер 12{в} {} | ω=vrω=vr размер 12{ω= {{v} над {r} } } {} |
| αα размер 12{α} {} | размер аа 12 {а} {} | α=atrα=atr size 12{α= {{a rSub {size 8{t}} } over {r} } } {} |
Таблица 10. 1 Вращательные и поступательные величины
1 Вращательные и поступательные величины
Создание соединений: домашний эксперимент
Сядьте, поставив ноги на землю, на вращающийся стул. Поднимите одну ногу прямо перед собой. Используя другую ногу, начните вращать себя, отталкиваясь от земли. Прекратите использовать ногу, чтобы отталкиваться от земли, но позвольте стулу вращаться. От исходной точки, с которой вы начали, зарисуйте угол, угловую скорость и угловое ускорение вашей ноги как функцию времени в виде трех отдельных графиков. Оцените величины этих величин.
Проверьте свое понимание
Угловое ускорение представляет собой вектор, имеющий как величину, так и направление. Как мы обозначаем его величину и направление? Проиллюстрируйте примером.
Решение
Величина углового ускорения равна αα размеру 12{α} {}, а наиболее распространенными единицами измерения являются рад/с2рад/с2 размер 12{“рад/с” rSup {размер 8{2} } } {}. Направление углового ускорения вдоль фиксированной оси обозначается знаком + или -, так же как направление линейного ускорения в одном измерении обозначается знаком + или -.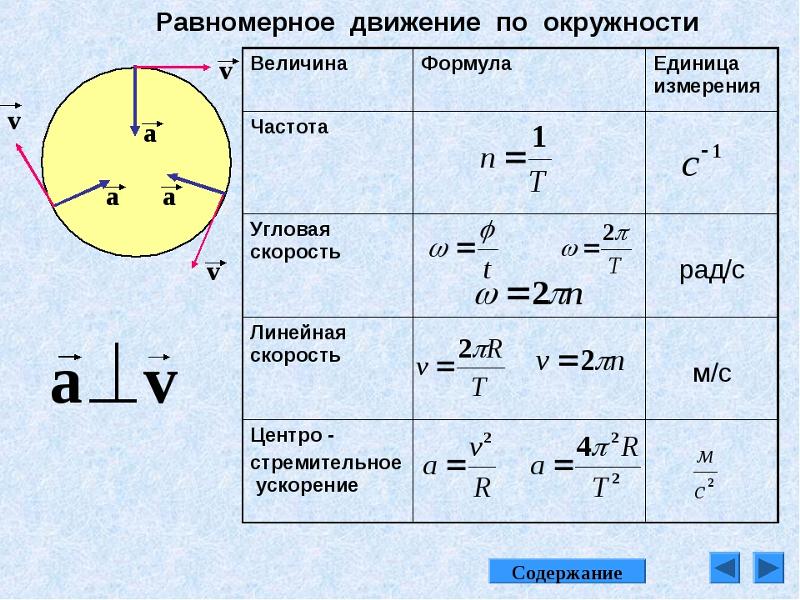 Например, рассмотрим гимнаста, выполняющего сальто вперед. Ее угловой момент был бы параллелен мату и слева от нее. Величина ее углового ускорения будет пропорциональна ее угловой скорости (скорости вращения) и ее моменту инерции относительно ее оси вращения.
Например, рассмотрим гимнаста, выполняющего сальто вперед. Ее угловой момент был бы параллелен мату и слева от нее. Величина ее углового ускорения будет пропорциональна ее угловой скорости (скорости вращения) и ее моменту инерции относительно ее оси вращения.
Исследования PhET: Революция божьей коровки
Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с положением, скоростью и ускорением жука x,y , используя векторы или графики.
Рис. 10.7 Революция божьей коровки
5 фактов, которые вы должны знать – Lambda Geeks
Центростремительная сила отвечает за центростремительное движение объекта, а действующая на него центробежная сила не позволяет объекту встретиться с центром круга.
Центростремительное ускорение и радиус, очевидно, связаны друг с другом, так как объект, движущийся по круговой траектории с приложением центростремительной силы, сохраняет ускорение объекта по радиусу окружности. Оба вектора остаются в уникальном направлении.
Оба вектора остаются в уникальном направлении.
Центростремительное ускорение проявляется, когда объект совершает круговое движение и проходит путь по окружности определенного радиуса.
Объект, движущийся по кругу, ускоряется, поддерживая постоянное расстояние от центра, равное радиусу кругового пути. Направление центростремительного ускорения объекта действует к центру кругового пути, прочерченного объектом по радиусу окружности.
Сила, удерживающая объект в круговом движении, называется центростремительной. Но это не только ответственность за движение объекта по круговой траектории. Сила действует против центростремительной силы и препятствует их падению внутрь. Сила, удерживающая их на месте при движении по круговой траектории, называется центробежной силой.
Найти центростремительное ускорение по радиусу На объект, ускоряющийся при круговом движении, действует центростремительная сила. Центростремительная сила, ускоряющая объект со скоростью v, определяется выражением:
Центростремительная сила, ускоряющая объект со скоростью v, определяется выражением:
F=mv 2 /r
Здесь m — масса объекта, а
r — радиус кругового пути.
Так как F=ma из второго закона Ньютона. Используя это в приведенном выше уравнении, мы получаем:
ma=mv 2 /r
Следовательно, формула для нахождения центростремительного ускорения тела при круговом движении имеет вид:
a=mv 2 /r
объекта составляет половину квадрата скорости объекта. Линейная скорость всегда перпендикулярна центростремительному ускорению, действующему внутрь.
Приведенное выше уравнение ясно показывает, что угловое ускорение обратно пропорционально радиусу кругового пути. Отсюда следует, что наибольшее центростремительное ускорение объекта мы будем иметь для объекта, распространяющегося по окружностям малого радиуса.
График центростремительного ускорения и радиуса Теперь давайте разберемся с обратной зависимостью между центростремительным ускорением и радиусом круговой траектории, работая на одном простом примере.
Предположим, что различные карусели с различными радиусами помещены в место для изучения влияния радиуса вращающегося колеса на центростремительное ускорение карусели. Крутящий момент прикладывается ко всем каруселям поочередно, поддерживая постоянную скорость 3 м/с.
Карусель; Изображение предоставлено: pixabayДля первой карусели радиус r = 1 м, следовательно, центростремительное ускорение для этого колеса составляет
a 1 = mv 2 /r
=
вторая карусель имеет радиус r=2 м, поэтому центростремительное ускорение этого колеса равно
a 2 =v 2 /r
. Третья карусель имеет радиус r= 3 м, следовательно, центростремительное ускорение этого колеса равно
a 3 =v 2 /r
Радиус четвертой карусели r=4 м, поэтому центростремительное ускорение этого колеса равно
a 4 =v 1 2 /r
Пятая карусель имеет радиус r=5 м, поэтому центростремительное ускорение этого колеса равно
a 5 =v 2 /r
Полученные данные записываются в Таблица ниже:
| № карусели | Radius (m) | Centripetal Acceleration (m/s 2 ) |
| 1 st | 1 | 3 |
| 2 nd | 2 | 1. 5 5 |
| 3 rd | 3 | 1 |
| 4 th | 4 | 0.75 |
| 5 th | 5 | 0.6 |
Построим график зависимости центростремительного ускорения от радиуса/с для приведенных выше данных.
Из приведенного выше графика можно сказать, что центростремительное ускорение объекта при круговом движении экспоненциально уменьшается с увеличением радиуса. Величина центростремительного ускорения уменьшается по радиусу.
Следовательно, чтобы сохранить центростремительное ускорение, скорость объекта должна увеличиваться по мере увеличения окружности пути, пройденного объектом.
Это связано с тем, что с увеличением радиуса центростремительная сила, действующая на объект, уменьшается. Мы можем связать это с кулоновской силой между двумя разноименными зарядами. По мере увеличения линейного расстояния между ними величина силы уменьшается.
Центростремительное ускорение объекта больше для малого радиуса окружности по сравнению с большими радиусами.
Если радиус кругового пути удвоить, сохраняя радиальную скорость объекта постоянной, то центростремительное ускорение объекта уменьшится вдвое.
Если объект движется со скоростью «u» по круговой траектории радиуса «r», и тот же объект движется по другой круговой траектории радиусом «2r» со скоростью «v», то изменение центростремительного ускорения равно,
Это уравнение дает изменение центростремительного ускорения объекта, движущегося с разными скоростями при движении по разным круговым путям разного радиуса.
Чему равно центростремительное ускорение автомобиля, движущегося по кольцевой дорожке стадиона со скоростью 20 км/ч? Диаметр стадиона составляет 70 метров.Дано: Скорость автомобиля
Диаметр стадиона d= 70 м.
Следовательно, радиус стадиона равен r= 35 м.
Формула для расчета центростремительного ускорения автомобиля вдоль стадиона:
a=v 2 /r
Подставляя значения в это уравнение, получаем
Следовательно, центростремительное ускорение автомобиля составляет 0,86 м/с 2 при движении по стадиону.
Что произойдет с центростремительным ускорением тела после уменьшения вдвое длины веревки, к которой он был привязан на длине 100 см, если скорость тела удвоится?Дано: Начальная длина каната, l 1 =100 см = 1 м
Конечная длина веревки равна l 2 =100/2 см = 50 см = 0,5 м
Пусть начальная скорость объекта равна «u», а конечная скорость равна «v». Конечная скорость в два раза больше начальной скорости, следовательно, v=2u.
Начальное центростремительное ускорение объекта равно
Конечное центростремительное ускорение объекта равно
Отсюда видно, что ускорение объекта увеличивается в 16 раз больше, чем начальное центростремительное ускорение объекта после уменьшения длину веревки наполовину.


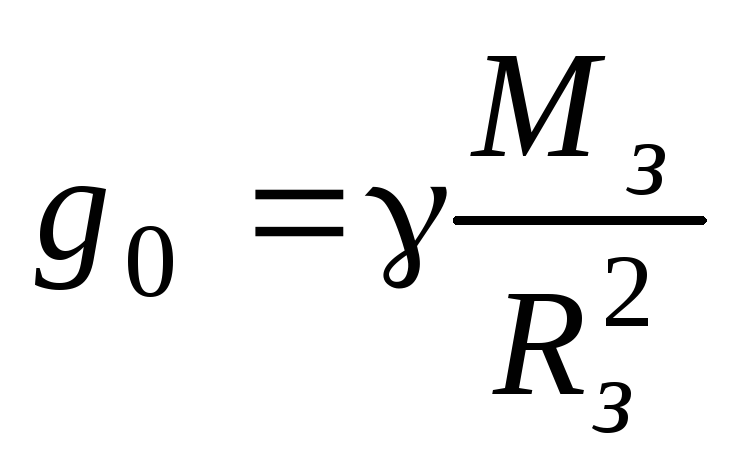 2}\)
2}\)
 Когда у физической величины есть и направление, то эту величину называют векторной. То есть скорость – это векторная физическая величина.
Когда у физической величины есть и направление, то эту величину называют векторной. То есть скорость – это векторная физическая величина. В измерении скорости движения по окружности выделяют угловую скорость и линейную скорость.
В измерении скорости движения по окружности выделяют угловую скорость и линейную скорость. 2 R$.
2 R$. 3. Маховик делает 3 оборота в минуту. Найти угловую скорость вращения маховика. [0,314 с−1]
3. Маховик делает 3 оборота в минуту. Найти угловую скорость вращения маховика. [0,314 с−1]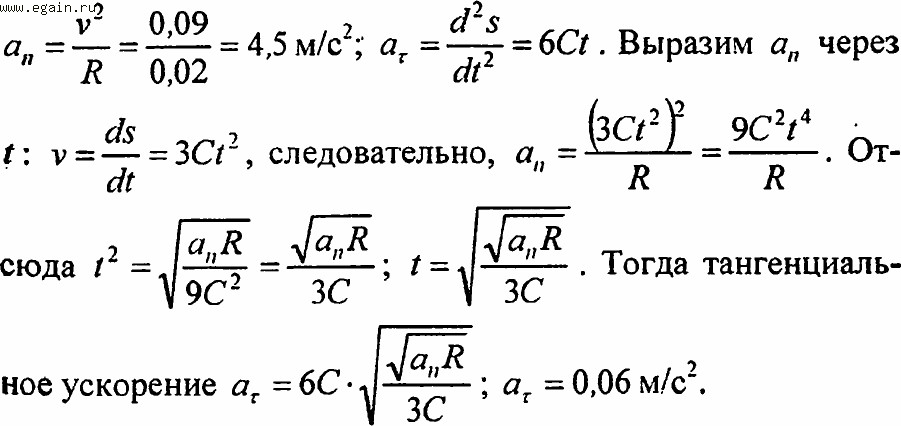 9. Определить скорость и ускорение точек поверхности Земли, находящихся на широте 30°. Радиус Земли равен 6400 км. [400 м/с; 2,5 см/с2]
9. Определить скорость и ускорение точек поверхности Земли, находящихся на широте 30°. Радиус Земли равен 6400 км. [400 м/с; 2,5 см/с2] 13. Цилиндр радиусом R зажат между двумя параллельными рейками (рисунок слева). Рейки движутся параллельно самим себе с постоянными скоростями v1 и v2. Определить угловую скорость вращения цилиндра и линейную скорость его центра. Проскальзывания нет.
13. Цилиндр радиусом R зажат между двумя параллельными рейками (рисунок слева). Рейки движутся параллельно самим себе с постоянными скоростями v1 и v2. Определить угловую скорость вращения цилиндра и линейную скорость его центра. Проскальзывания нет. [1 с−1]
[1 с−1] [ vB = 2w(R + r) = 100 см/с ]
[ vB = 2w(R + r) = 100 см/с ] 23. Малый радиус несущей части трамвайного колеса равен r, а большой радиус — R. Определить радиус кривизны циклоиды в верхней точке (рисунок слева). [ (R + r)2/R ]
23. Малый радиус несущей части трамвайного колеса равен r, а большой радиус — R. Определить радиус кривизны циклоиды в верхней точке (рисунок слева). [ (R + r)2/R ]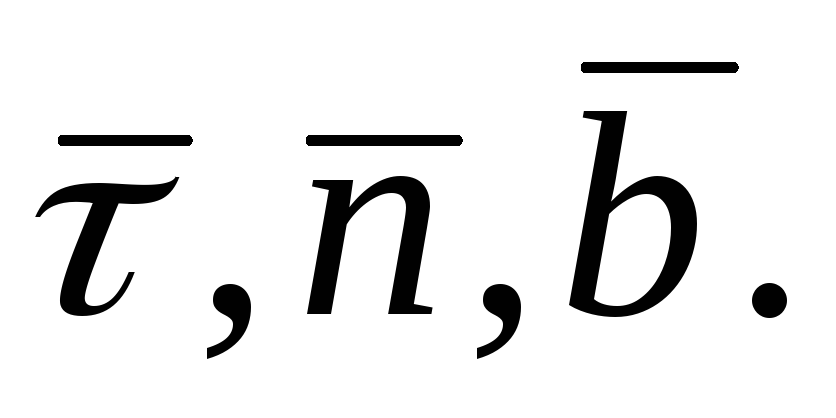 [окружность радиусом R; a = w2R ]
[окружность радиусом R; a = w2R ]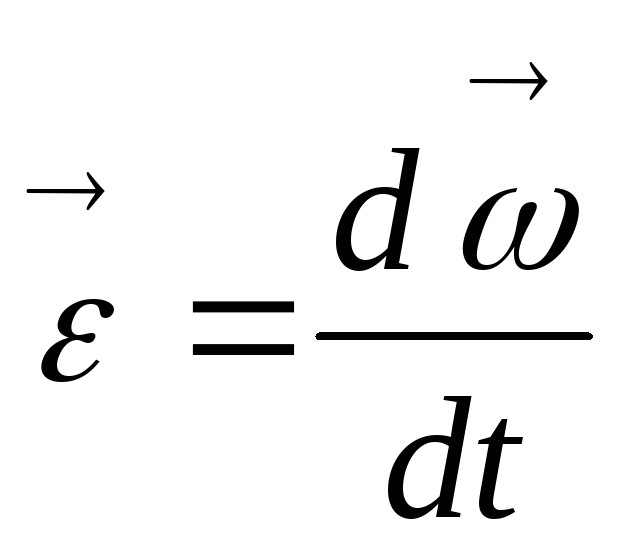 Определить среднюю за время полета угловую скорость вращения вектора скорости тела. [ <w> = αg/(vosin α) ]
Определить среднюю за время полета угловую скорость вращения вектора скорости тела. [ <w> = αg/(vosin α) ] | Вернуться к списку разделов КИНЕМАТИКИ.
| Вернуться к списку разделов КИНЕМАТИКИ. \circ18\)’ . Угловая скорость равномерного движения тела по окружности – это величина \(\omega\), равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершен этот поворот: \(ω = \frac φ t \). Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени \(t: υ= \frac l t \). Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина \(l\) дуги окружности, пройденной точкой, связана с углом поворота φ выражением \(l = Rφ\), где \(R\) – радиус окружности.
\circ18\)’ . Угловая скорость равномерного движения тела по окружности – это величина \(\omega\), равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершен этот поворот: \(ω = \frac φ t \). Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени \(t: υ= \frac l t \). Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина \(l\) дуги окружности, пройденной точкой, связана с углом поворота φ выражением \(l = Rφ\), где \(R\) – радиус окружности.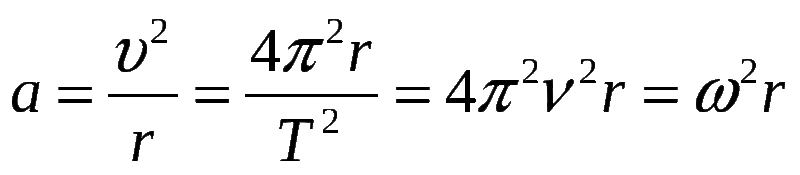 2\).
2\). В какой точке траектории ускорение тела направлено по стрелке?
В какой точке траектории ускорение тела направлено по стрелке?  Если известно, что радиус планеты равен \(\frac58\) от земного, а ускорение свободного падения \(\frac35\) от земного, то приближенное значение первой космической скорости для планеты
Если известно, что радиус планеты равен \(\frac58\) от земного, а ускорение свободного падения \(\frac35\) от земного, то приближенное значение первой космической скорости для планеты В этом случае будут справедливы следующие утверждения
В этом случае будут справедливы следующие утверждения
 Уравнение движения с постоянным ускорением
Уравнение движения с постоянным ускорением

 Горизонтальная ось – это ось времени, вертикальная – ось скорости. График имеет вид прямой выходящей из точки, определяемой значением начальной скорости в момент времени равный 0. Если тело не имеет начальной скорости, то график зависимости проекции скорости на ось ОX от времени представляет собой прямую, выходящую из начала координат. На рисунке этот график показан в виде прямой 1 (эл). По этому графику можно найти проекцию ускорения на ось X: так как в данном случае начальная скорость равна нулю, то проекция ускорения будет равна отношению проекции скорости в какой-то момент времени к значению времени. Для определения значения этих величин можно выбрать любую точку и восстановить из нее перпендикуляры к осям. В нашем примере значение времени – 5 секунд, значение скорости – 30 м/с, подставив в формулу полученные значения, получаем, что ускорение равно 6 м/с2.
Горизонтальная ось – это ось времени, вертикальная – ось скорости. График имеет вид прямой выходящей из точки, определяемой значением начальной скорости в момент времени равный 0. Если тело не имеет начальной скорости, то график зависимости проекции скорости на ось ОX от времени представляет собой прямую, выходящую из начала координат. На рисунке этот график показан в виде прямой 1 (эл). По этому графику можно найти проекцию ускорения на ось X: так как в данном случае начальная скорость равна нулю, то проекция ускорения будет равна отношению проекции скорости в какой-то момент времени к значению времени. Для определения значения этих величин можно выбрать любую точку и восстановить из нее перпендикуляры к осям. В нашем примере значение времени – 5 секунд, значение скорости – 30 м/с, подставив в формулу полученные значения, получаем, что ускорение равно 6 м/с2. 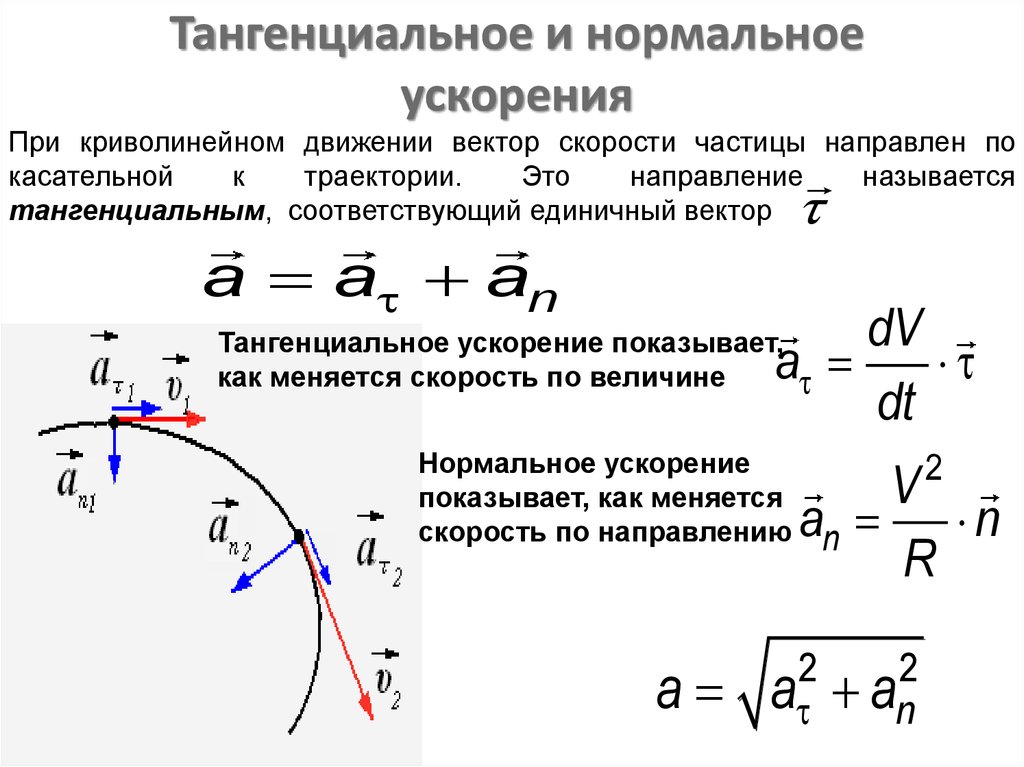 График 3 направлен вниз, значит, значение скорости с течением времени уменьшается – это график равнозамедленного движения.
График 3 направлен вниз, значит, значение скорости с течением времени уменьшается – это график равнозамедленного движения. Поэтому в этом случае с течением времени будут изменяться и координата х, и координата у.
Поэтому в этом случае с течением времени будут изменяться и координата х, и координата у.  Длина отрезка ОС соответствует времени движения. Разделив его на малые интервалы времени, в этих пределах проекцию скорости будем считать постоянной и равной ее среднему значению. Теперь рассмотрим интервал дельта t1. Тогда перемещение на этом участке, и соответственно площадь заштрихованного прямоугольника численно равна изменению координаты точки за время t1. Сумма всех этих площадей численно равна изменению координаты точки за все время t. Чем сильнее мы уменьшим интервал дельта t, тем точнее будет результат. Если дельта t устремить к нулю, то площадь фигуры АВСО будет стремиться к изменению координаты тела дельта х.
Длина отрезка ОС соответствует времени движения. Разделив его на малые интервалы времени, в этих пределах проекцию скорости будем считать постоянной и равной ее среднему значению. Теперь рассмотрим интервал дельта t1. Тогда перемещение на этом участке, и соответственно площадь заштрихованного прямоугольника численно равна изменению координаты точки за время t1. Сумма всех этих площадей численно равна изменению координаты точки за все время t. Чем сильнее мы уменьшим интервал дельта t, тем точнее будет результат. Если дельта t устремить к нулю, то площадь фигуры АВСО будет стремиться к изменению координаты тела дельта х.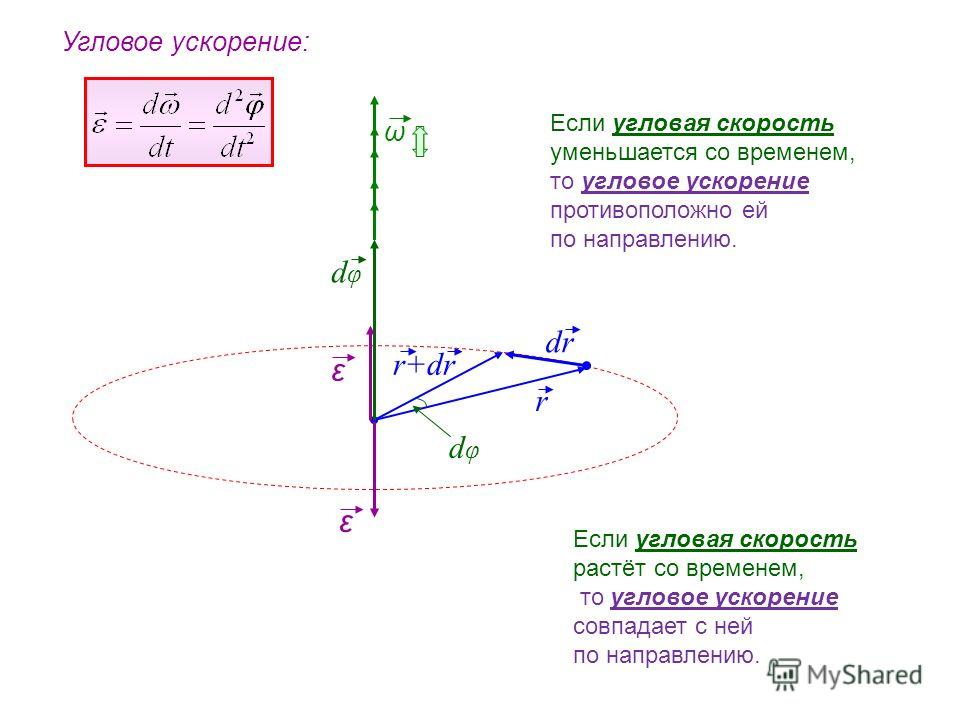
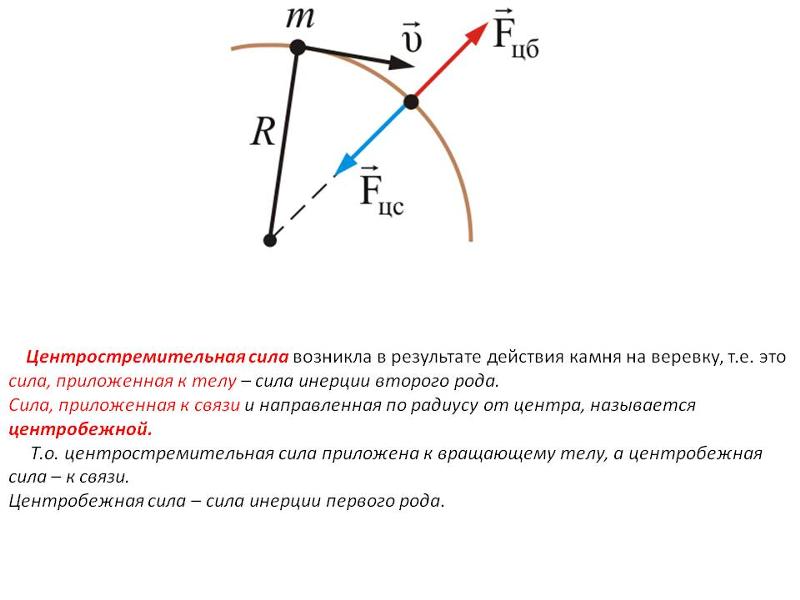 Однако следует учитывать, что ускорение должно быть постоянным.
Однако следует учитывать, что ускорение должно быть постоянным. 1 Кинематика
1 Кинематика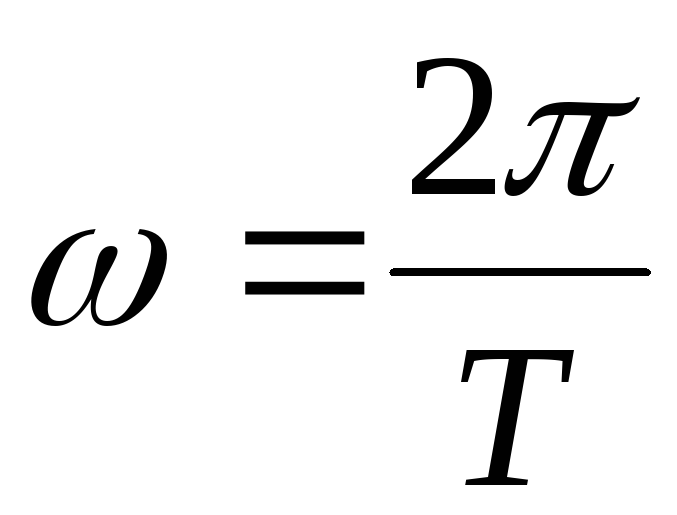 3 Магнетизм
3 Магнетизм Квантовая теория
Квантовая теория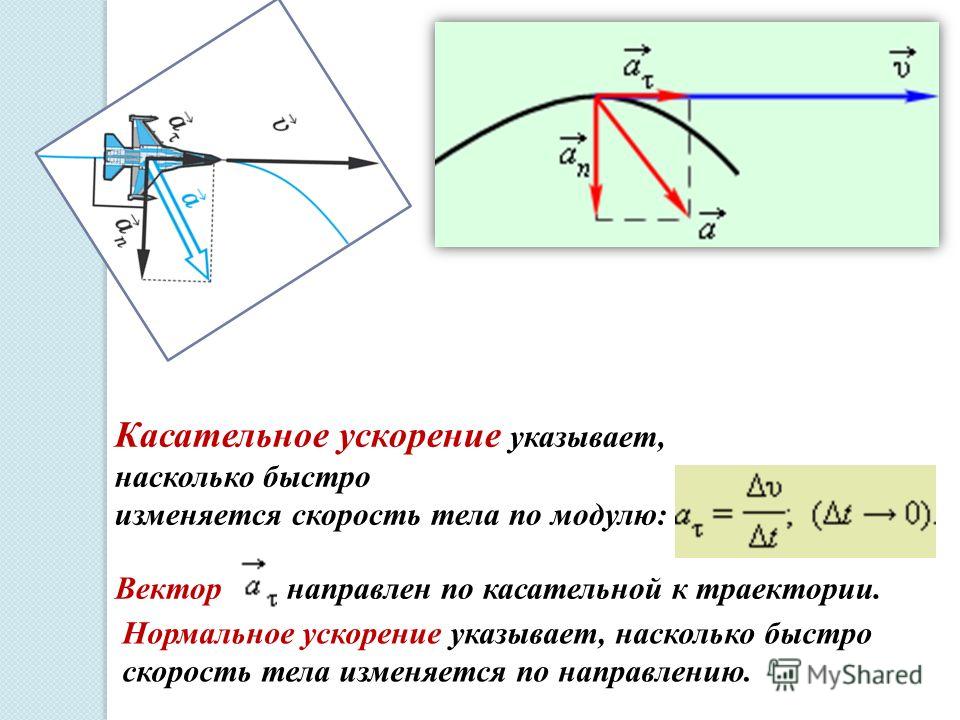 СТО
СТО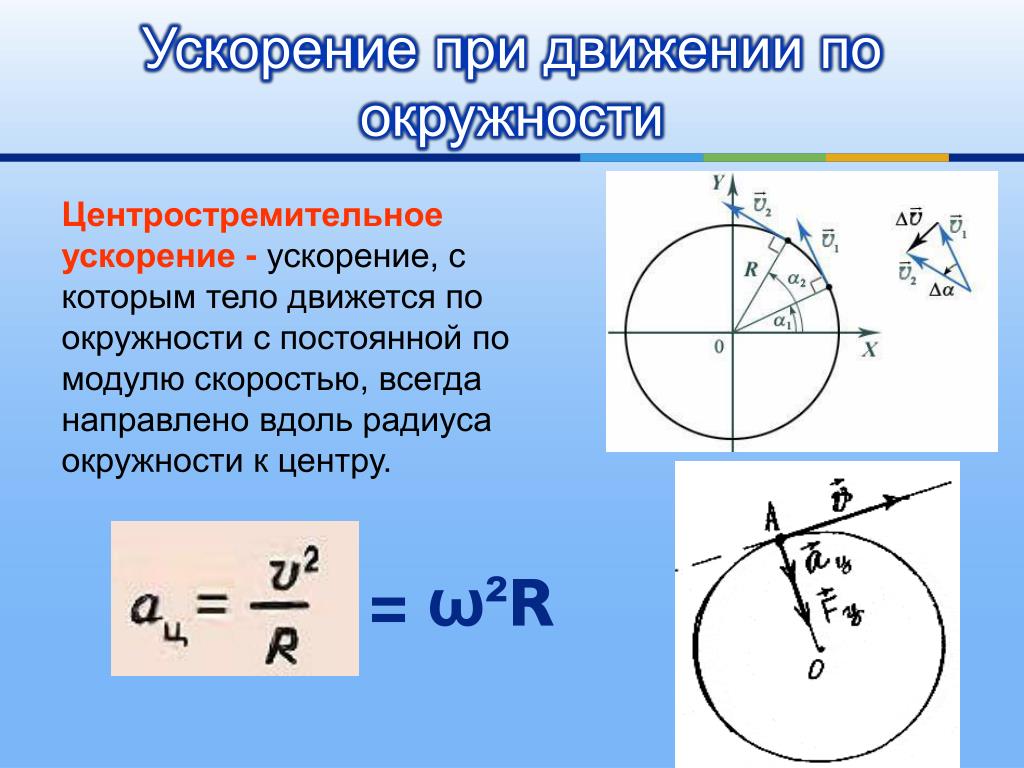
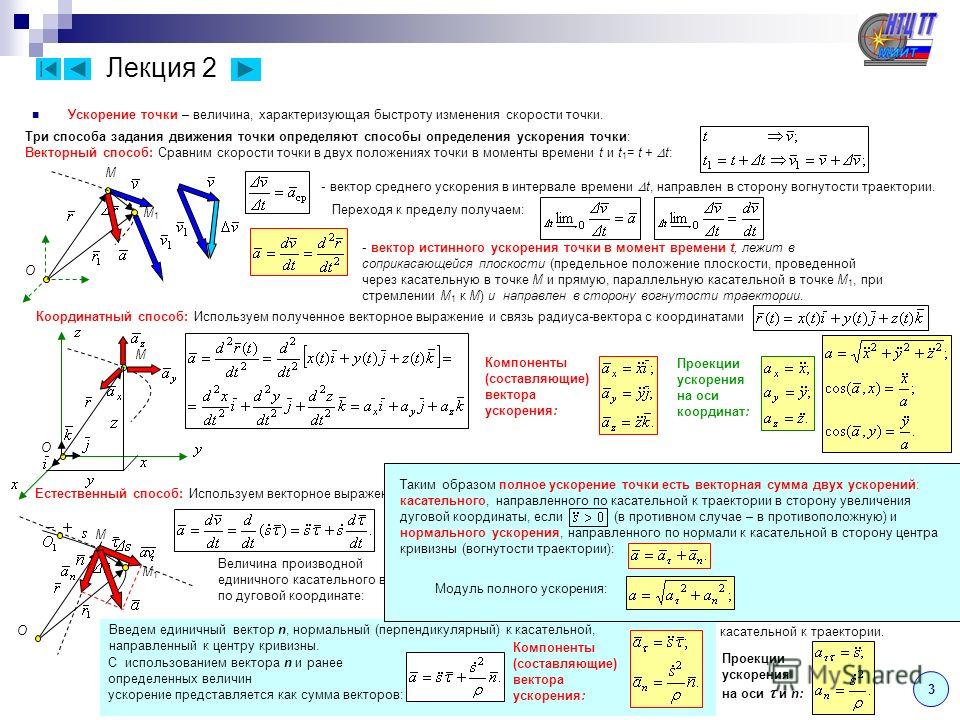



 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/ . Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/ . Лицензия : CC BY: Attribution  Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution  Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Атрибуция
Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Атрибуция  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube Расположен по адресу : http://www.youtube.com/watch?v=ldQWTNDBSSE . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Расположен по адресу : http://www.youtube.com/watch?v=ldQWTNDBSSE . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
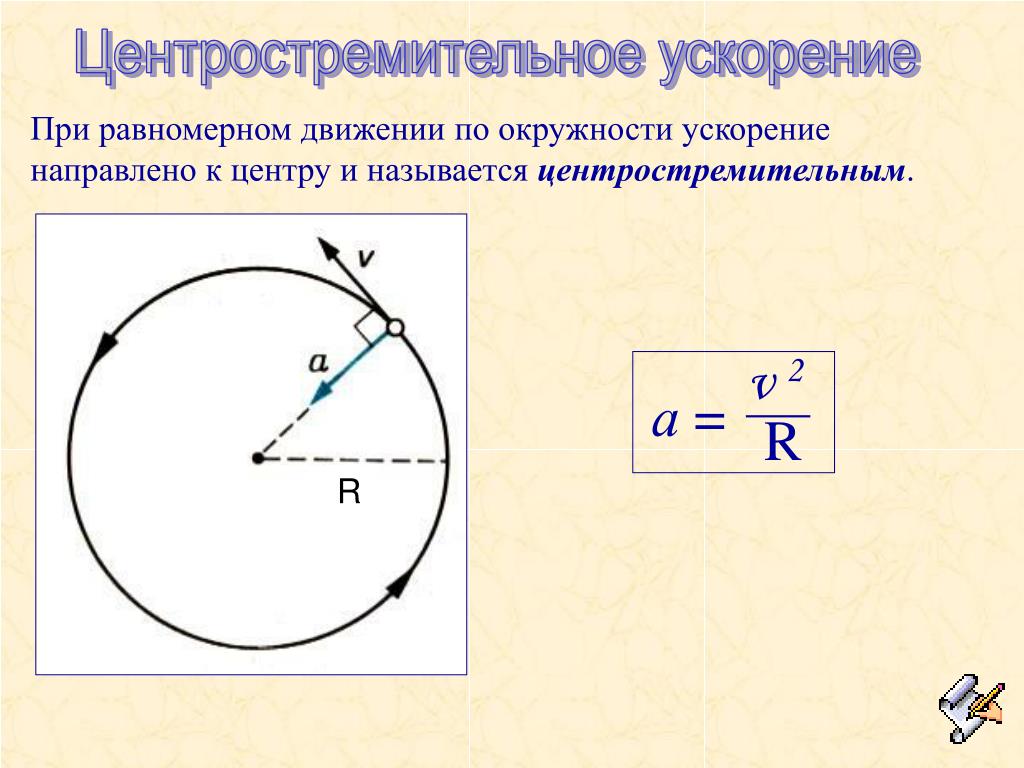 Единицей периода времени в системе СИ является секунда (
Единицей периода времени в системе СИ является секунда ( е.
е.

 Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Википедия. Лицензия : CC BY: Атрибуция
Предоставлено : Википедия. Лицензия : CC BY: Атрибуция  Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция  17 сентября 2013 г. Предоставлено 906:50 : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено 906:50 : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution  Расположен по адресу : https://en.wikipedia.org/wiki/Angular_velocity. Лицензия : CC BY: Attribution
Расположен по адресу : https://en.wikipedia.org/wiki/Angular_velocity. Лицензия : CC BY: Attribution  Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube