ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Прямолинейное равноускоренное движение. Ускорение. Перемещение при прямолинейном равноускоренном движении Номер 1460
- Учебники
- 7 класс
- Физика 👍
- Марон
- №1460
авторы: Марон, Позойский.
издательство: “Дрофа”
Раздел:
- Предыдущее
- Следующее
По данным, приведённым в таблице, составьте задачи и решите их.
| Время разгона, с | Скорость после разгона, км/ч | Пройденный путь, м | ||
|---|---|---|---|---|
| Автомобиль “Ока” | 30 | 100 | ? | ? |
| Гоночный автомобиль | 3,4 | 100 | ? | ? |
| Автомобиль ВАЗ | 19 | 100 | ? | ? |
| Гепард | 2 | 72 | ? | ? |
| Конькобежец − спринтер | 8,5 | ? | ? | 50 |
| Легкоатлет− спринтер | ? | 39,6 | ? | 40 |
| Велосипедист | 15 | ? | ? | 200 |
Во всех случаях движение во время разгона считать равноускоренным из состояния покоя. Проанализируйте полученные результаты.
reshalka.com
Решение 1
С каким ускорением движется Автомобиль “Ока”, если его скорость увеличивается от 0 до 100 км/ч за 30 с ? Какой путь пройдет автомобиль за время разгона?
Дано:
t = 30 c;
v0=0 м/с;
v = 100 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 27,8 м/с.
Решение:
Уравнение скорости:
v=v0+at;
a=v–v0t;
a=27,8−030=0,93м/с2;
S=at22;
S=0,93∗3022=418,5 м.
Ответ: 0,93 м/с2; 418,5 м.
Решение 2
Гоночный автомобиль движется 3,4 с равноускоренно из состояния покоя. Скорость после разгона составила 100 км/ч. Найдите ускорение и пройденный путь.
Дано:
t = 3,4 c;
v0=0 м/с;
v = 100 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 27,8 м/с.
Решение:
Уравнение скорости:
v=v0+at;
a=v–v0t;
a=27,8−03,4=8,2м/с2;
S=at22;
S=8,2∗3,422=47,4 м.
Ответ: 8,2 м/с2; 47,4 м.
Решение 3
С каким ускорением движется Автомобиль ВАЗ, если его скорость увеличивается от 0 до 100 км/ч за 19 с ? Какой путь пройдет автомобиль за время разгона?
Дано:
t = 19 c;
v0=0 м/с;
v = 100 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 27,8 м/с.
Решение:
Уравнение скорости:
v=v0+at;
a=v–v0t;
a=27,8−019=1,46м/с2;
S=at22;
S=1,46∗1922=269 м.
Ответ: 1,46 м/с2; 269 м.
Решение 4
Гепард за 2 с развивает скорость до 72 км/ч. Найдите ускорение и пройденный за это время путь.
Дано:
t = 2 c;
v0=0 м/с;
v = 72 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 20 м/с.
Решение:
Уравнение скорости:
v=v0+at;
a=v–v0t;
a=20−02=10м/с2;
S=at22;
S=10∗222=20 м.
Ответ: 10 м/с2; 20 м.
Решение 5
Конькобежец − спринтер дистанцию 50 м пробегает за 8,5 с. С каким ускорением двигался спортсмен? Какая установилась скорость после разгона?
Дано:
t = 8,5 c;
S = 50 м;
v0=0 м/с.
Найти:
a − ?
v − ?
Решение:
Уравнение движения:
S=v0t+at22;
Так как спорстмен начинает движение, то v0=0 м/с.
S=at22;
2S=at2;
a=2St2;
a=2∗508,52=1,38м/с2;
v = at;
v = 1,38 * 8,5 = 11,73 м/с.
Ответ: 1,38 м/с2; 11,73 м/с.
Решение 6
Легкоатлет− спринтер на дистанции 40 м разогнался до 39,6 км/ч. Найдите время его разгона и ускорение.
Дано:
S = 40 м.
v = 39,6 км/ч;
v0=0 м/с.
Найти:
a − ?
t − ?
СИ:
v = 11 м/с.
Решение:
S=v0+v2∗t;
2S=(v0+v)∗t;
t=2Sv0+v;
t=2∗400+11=7,3 с;
v=v0+at;
Так как v0=0 м/с, то v = at;
a=vt;
a=117,3=1,5м/с2.
Ответ: 1,5 м/с2; 7,3 с.
Решение 7
Велосипедист за 15 с проехал путь 200 м. Найдите ускорение и скорость после разгона.
Дано:
t = 15 c;
S = 200 м;
v0=0 м/с.
Найти:
a − ?
v − ?
Решение:
Уравнение движения:
S=v0t+at22;
Так как велосипедист начинает движение, то v0=0 м/с.
S=at22;
2S=at2;
a=2St2;
a=2∗200152=1,78м/с2;
v = at;
v = 1,78 * 15 = 26,7 м/с.
Ответ: 1,78 м/с2; 26,7 м/с.
Решение анализ
Среди 3−х автомобилей с наибольшим ускорением двигался гоночный автомобиль, затем автомобиль Ваз. Наименьшее ускорение имеет автомобиль “Ока”, т.к. ему нужно больше времени для разгона до 100 км/ч.
Среди 3−х спортсменом с наибольшим ускорением двигался велосипедист, затем легкоатлет−спринтер. Наименьшее ускорение имеет конькобежец − спринтер.
Ускорение гепарда выше ускорения автомобилей и спортсменов.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Ускорение. Равноускоренное прямолинейное движение. Школьный курс физики
Главная | Физика 10 класс | Ускорение. Равноускоренное прямолинейное движение
Среднее ускорение.
Введём ещё одну физическую величину, описывающую механическое движение, — ускорение. Оно характеризует быстроту изменения скорости движения тела. Ускорение является важнейшей физической величиной, так как действия одних тел на другие определяют не скорости тел, а быстроту изменения скоростей.
Пусть тело движется по криволинейной траектории (рис. 2.26, а). За промежуток времени Δt = t2 – t1 оно перейдёт из положения A1 в положение A2. При этом его скорость изменится. Обозначим начальную и конечную скорости движения тела через υ1 и υ2. Изменение скорости за время Δt равно Δ = 2 – 1. На рисунке 2.26, б проведено геометрическое вычитание векторов скоростей и построен вектор Δ.
Рис. 2.26
Среднее ускорение cp за промежуток времени Δt равно:
Средним ускорением называют физическую величину, равную отношению изменения скорости тела Δυ к интервалу времени Δt, в течение которого это изменение скорости произошло.
Направление вектора cp совпадает с направлением вектора Δ.
Если ускорение постоянно, то его можно вычислять как изменение скорости в единицу времени. Это позволяет установить единицу ускорения в СИ — метр на секунду в квадрате (м/с2).
На практике нужно уметь определять ускорение в каждой точке траектории. Это ускорение называют мгновенным. На разных участках траектории за одинаковые промежутки времени Δt изменение скорости Δ может быть различным как по модулю, так и по направлению. При уменьшении интервала времени Δt изменения скорости Δ уменьшаются по модулю и меняются по направлению (рис. 2.27).
Рис. 2.27
Соответственно, средние ускорения также меняются по модулю и по направлению. Но по мере приближения интервала Δt к нулю отношение Δ / Δt стремится к определённому предельному значению. Это предельное значение и есть мгновенное ускорение, или просто ускорение.
В то время как мгновенная скорость тела направлена по касательной к траектории, направление ускорения совпадает с направлением изменения скорости Δ за малый промежуток времени. Изменение же скорости только при прямолинейном движении совпадает с направлением самой скорости или противоположно ему. Поэтому ускорение может быть направлено под различными углами по отношению к траектории.
Равноускоренное прямолинейное движение.
Пусть за каждую секунду скорость тела возрастает на 1 м/с, а направление вектора изменения скорости остаётся постоянным. В этом случае среднее ускорение тела будет равно 1 м/с Такое движение называют равноускоренным.
Такое движение называют равноускоренным.
Движение тела называют равноускоренным, если его ускорение остаётся постоянным, т. е. не изменяется с течением времени (как по модулю, так и по направлению).
Равноускоренное движение может быть как прямолинейным, так и криволинейным. Далее мы рассмотрим равноускоренное прямолинейное движение.
Пусть в начальный момент времени t0 = 0 скорость движения тела равна 0. Тогда, обозначив скорость в произвольный момент времени через , получим в соответствии с формулой:
= 0 – / t.
Отсюда
= + t. (1)
Для равноускоренного движения в одной плоскости уравнению (1) будут соответствовать две формулы для проекций вектора скорости на оси
Графическое представление равноускоренного прямолинейного движения.
Если тело движется равноускоренно, то графиками модуля и проекции ускорения будут прямые, параллельные оси времени. Важно понимать, что модуль — неотрицательная величина, поэтому график модуля ускорения не может быть расположен ниже оси времени (рис. 2.28).
Рис. 2.28
В то же время проекции ускорения могут иметь как положительные (рис. 2.29, а), так и отрицательные значения (рис. 2.29, б).
Рис. 2.29
Из рисунка 2.29, б следует, что ускорение направлено противоположно оси X. По графику проекции ускорения можно найти, кроме αх, изменение проекции скорости Δυx. Оно численно равно площади прямоугольника OABC или OKMN, так как Δυx = αхt, а произведение axt численно равно площади прямоугольника OABC или OKMN.
Значение площади берётся со знаком «минус», если она расположена ниже оси времени, что соответствует рисунку 2.
На рисунке 2.30 изображены графики 1 и 2 проекций скорости двух тел при равноускоренном прямолинейном движении.
Рис. 2.30
Оба тела имеют начальную скорость, равную нулю. Первое тело движется в положительном направлении оси X и так как Δυx > 0, то α1х > 0. Второе тело движется противоположно оси X и так как Δυx
На рисунке 2.31 также изображены графики 1 и 2 проекций скорости двух тел.
Рис. 2.31
Оба тела имеют одно и то же значение проекции начальной скорости, соответствующее отрезку OA. Согласно графику 1 тело движется в положительном направлении оси X, причём модуль и проекция скорости равномерно возрастают.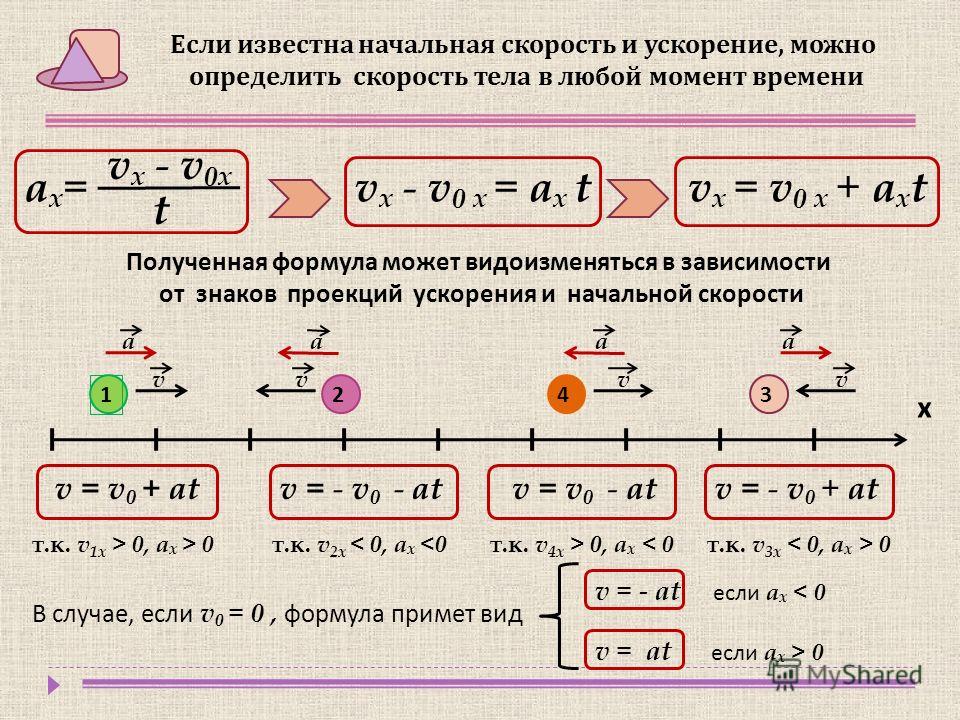 Согласно графику 2, тело в течение некоторого промежутка времени (отрезок OB) движется в положительном направлении оси X (υx > 0) с равномерно уменьшающимся до нуля (остановка) значением проекции скорости. После этого проекция скорости становится отрицательной. Это означает, что тело стало двигаться в направлении, противоположном положительному направлению оси X. Проекция ускорения тела отрицательна. Так как проекция скорости точки равномерно убывает, то проекция ускорения остаётся постоянной. Следовательно, тело движется равноускоренно.
Согласно графику 2, тело в течение некоторого промежутка времени (отрезок OB) движется в положительном направлении оси X (υx > 0) с равномерно уменьшающимся до нуля (остановка) значением проекции скорости. После этого проекция скорости становится отрицательной. Это означает, что тело стало двигаться в направлении, противоположном положительному направлению оси X. Проекция ускорения тела отрицательна. Так как проекция скорости точки равномерно убывает, то проекция ускорения остаётся постоянной. Следовательно, тело движется равноускоренно.
Координата и радиус-вектор при равноускоренном движении
Запишем уравнение для одной из координат движущегося тела:
х = x0 + Δx.
В случае равноускоренного движения изменение координаты можно определить с помощью графика зависимости проекции скорости от времени. Ранее мы показали, что изменение координаты Δx при равномерном прямолинейном движении можно найти по площади прямоугольника под графиком проекции скорости:
Δx = υxt.
Задача упрощалась тем, что υx = const.
При движении с постоянным ускорением проекция скорости тела изменяется в зависимости от времени по линейному закону. В курсе физики 9 класса было получено выражение для изменения координаты тела:
Подставляя значения изменения координат в кинематические уравнения: х = x0 + Δx, y = y0 + Δy, получим выражения для координат при движении тела с постоянным ускорением как функции времени:
(2)
Формулы (2) применимы для описания как прямолинейного движения (в этом случае целесообразно ось X направить по прямой, вдоль которой движется тело), так и криволинейного движения. Важно лишь, чтобы оно было равноускоренным.
Двум уравнениям (2) соответствует одно векторное уравнение:
(3)
Отметим, что при помощи уравнений (2) или (3) можно найти только положение движущегося тела в любой момент времени, но не пройденный путь. При равноускоренном прямолинейном движении возможно изменение направления скорости на противоположное (например, при движении брошенного вверх тела). В таком случае нужно определить, в какой точке траектории произошло изменение направления скорости. Путь находится в результате суммирования длин отрезков траектории, пройденных телом за указанное время.
При равноускоренном прямолинейном движении возможно изменение направления скорости на противоположное (например, при движении брошенного вверх тела). В таком случае нужно определить, в какой точке траектории произошло изменение направления скорости. Путь находится в результате суммирования длин отрезков траектории, пройденных телом за указанное время.
Вопросы:
1. Как можно определить среднее ускорение?
2. Какое движение тела называют равноускоренным прямолинейным?
3. Запишите выражение для скорости движения тела при равноускоренном прямолинейном движении.
4. Как можно определить координаты тела, совершающего равноускоренное движение?
5. Какую информацию можно получить, анализируя графики равноускоренного прямолинейного движения?
Вопросы для обсуждения:
1. Используя рисунок 2.32, докажите, что . При доказательстве воспользуйтесь методом разбиения площади трапеции на можество прямоугольников.
Рис. 2.32
2. На рисунке 2.33 приведены графики зависимости проекции скорости υx от времени t для тел 1 и 2. Как изменяются модули скоростей тел? Чему соответствуют отрезки ОС и OD?
Рис. 2.33
3. В трактате «Беседы и математические доказательства, касающиеся двух новых отраслей науки» (1638) Галилей приводит определения двух видов движения тел:
а) «…движением я называю такое, при котором расстояния, проходимые движущимся телом в любые равные промежутки времени, равны между собою»;
б) «…движением называется такое, при котором после выхода из состояния покоя в равные промежутки времени прибавляются и равные приращения скорости».
О каких видах движения идёт речь в первом и во втором случаях?
Пример решения задачи
Ружейная пуля движется равноускоренно внутри ствола длиной 0,6 м в течение 0,004 с. Найдите модуль скорости пули при вылете из ствола ружья и модуль ускорения её движения внутри ствола. Модуль начальной скорости движения пули считайте равным нулю.
Модуль начальной скорости движения пули считайте равным нулю.
Запишем кинематическое уравнение для пули: x(t) = αt2 / 2 (так как υ0 = 0 по условию задачи).
В момент вылета пули из ствола ружья (рис. 2.34) t = τ x(τ) = l. C учётом этого получим:
Подставим числовые данные:
α = 2 • 0,6 / 0,004 2 м/с2 = 75000 м/с2 = 75 км/с2
Найдём модуль скорости вылета υп пули:
υп = ατ; υп = 75000 • 0,004 м/с = 300 м/с.
Ответ: υп = 300 м/с, α = 75 км/с2
Упражнения:
1. Какой должна быть длина взлётной полосы, если самолёт для взлёта должен приобрести скорость, равную 240 км/ч, за 30 с?
2. Автомобиль, двигаясь равноускоренно и прямолинейно, через 10 с после начала движения достиг скорости, модуль которой равен 36 км/ч. Определите модуль ускорения, с которым двигался автомобиль.
Определите модуль ускорения, с которым двигался автомобиль.
Какой путь он прошёл:
а) за 10 с;
б) за последнюю секунду движения?
3. Склон горы длиной 100 м лыжник прошёл за 20 с, двигаясь с ускорением, равным 0,3 м/с2. Определите модуль скорости лыжника в начале и в конце склона.
4. Космическая ракета разгоняется из состояния покоя и, пройдя путь 200 км, достигает скорости, модуль которой равен 11 км/с. C каким по модулю ускорением она двигалась? Чему равно время разгона ракеты?
5. Покажите, что при равноускоренном движении по заданным значениям υ0x, υx и αx можно определить проекцию перемещения sx по
6. Какой путь пройдёт моторная лодка, если она движется прямолинейно 5 с с постоянной скоростью 1 м/с, а затем 5 с — равноускоренно с ускорением, равным 1 м/с2? Определите среднюю путевую скорость лодки за 10 с. Постройте график зависимости скорости и ускорения моторной лодки от времени.
Постройте график зависимости скорости и ускорения моторной лодки от времени.
Предыдущая страницаСледующая страница
Урок 7: Мгновенная скорость и ускорение
Урок 7: Мгновенная Скорость и ускорениеСКМ 541. Описание физического мира
Урок 7: Мгновенная скорость и ускорение
В уроке 6 было объяснено понятие средней скорости и ее вычисление основывалось только на расстояние между начальной и конечной точкой и время, затраченное на преодоление это расстояние. Результат не дает вам информации о фактическом пути вы прошли или какие изменения произошли в вашей скорости на этом пути. в пример, когда вы вернулись в исходную точку, и оба смещения а средняя скорость была равна 0 (в футах и футах в секунду соответственно), у вас абсолютно нет информации о том, как далеко вы на самом деле прошли или как быстро вы прошли прогулку.
Тем не менее,
когда вы разбиваете свою экскурсию на две составляющие (отъезд и приезд), возникает
было водоизмещение (+10 футов и -10 футов) и средняя скорость (+2 фута/с и -1
фут/с), связанный с каждым компонентом. Если вы еще сломали одну ногу
поездки… т. е. пробежать 8 футов за 3 секунды, проползти 2 фута за 1 секунду, с
остановка между в течение 1 секунды … у вас будет три дополнительных набора смещения
и векторы скорости, более полно описывающие поездку.
Если вы еще сломали одну ногу
поездки… т. е. пробежать 8 футов за 3 секунды, проползти 2 фута за 1 секунду, с
остановка между в течение 1 секунды … у вас будет три дополнительных набора смещения
и векторы скорости, более полно описывающие поездку.
Что произошло бы, если бы вы разбили каждый из этих новых сегментов на очень короткие интервалы времени? Вы бы улучшили полноту описания и смогли бы построить график величин векторов смещения и скорости как функции времени за каждый короткий промежуток времени на пути. В пределе бесконечно мало небольшие интервалы времени , каждый вектор скорости становится мгновенным скорость .
Поскольку мгновенная скорость может меняться со временем, вы
потребуется количество, которое описывает это изменение. Это количество, время
скорость изменения скорости во времени, называется ускорением, и оно тоже
является вектором. Как и временная скорость изменения смещения (т.е. скорости),
математическое определение – это разница между начальным вектором скорости
и конечный вектор скорости, деленный на интервал времени, в течение которого изменение
произошло. :
:
a = ( v 2 – v 1 ) / (t 2 -t 1 )
Как и в случае определения скорости, это среднее ускорение за период времени t 2 -t 1 . Ускорение могло изменяться вверх и вниз в течение периода времени, но вы нет информации об этом. Аналогично зависимости между средним и мгновенная скорость, вы можете попробовать ускорение на пути в меньшие промежутки времени, пока не достигнете бесконечно малого предела. В этом предел, каждый вектор ускорения становится мгновенным ускорением.
Что мы называем временной скоростью изменения ускорения? Давай не пойдем туда (Фу!). Приложения общей физики обычно ограничиваются постоянным ускорением, в котором среднее ускорение равно мгновенному ускорению. Так что вы нужно только заботиться о постоянном среднем ускорении.
элементы этого урока содержатся в следующих ссылках. Продолжать
каждый элемент ниже в указанном порядке. Вы можете добавить эту страницу в закладки, чтобы
вы сможете быстро найти эти элементы в будущем.
Вы можете добавить эту страницу в закладки, чтобы
вы сможете быстро найти эти элементы в будущем.
Принципы от Discovery
  Принципы по анализу
Открытие Пересмотрено
А Проблема для обсуждения
Домашнее задание
Когда вы закончили элементы этого урока, переходите к “Заданиям” раздел курса для заданий к Уроку 2.
2002 Барри Л. Лутц
Как найти постоянное ускорение в зависимости от расстояния и времени: задачи и примеры
Ускорение движущейся частицы можно описать производной второго порядка расстояния по времени. Эта связь расстояния и времени заставляет нас задуматься о том, как найти постоянное ускорение с расстоянием и временем.
Постоянное ускорение относится к постоянному изменению движения частицы. Поскольку мы обсудили постоянное ускорение на графике положение-время, мы знаем, что параболический путь, пройденный частицей во времени, дает постоянное ускорение. В этом посте мы узнаем, как найти постоянное ускорение с расстоянием и временем.
В этом посте мы узнаем, как найти постоянное ускорение с расстоянием и временем.
Положение частицы, в котором она находится до того, как она начнет прослеживать путь, и через определенное время положение того же объекта дает расстояние, пройденное частицей. Это расстояние, пройденное частицей с течением времени, дает скорость. Следовательно, мы должны выбрать точный способ нахождения постоянного ускорения. Если мы возьмем линейное расстояние, мы получим постоянную скорость; таким образом, ускорение будет равно нулю.
Изображение предоставлено: Изображение Михала Ярмолука из Pixabay Как найти постоянное ускорение в зависимости от расстояния и времени?Вывод постоянного ускорения в зависимости от расстояния и времени включает кинематические уравнения. Поскольку производная второго порядка расстояния по времени дает ускорение, расстояние должно быть функцией квадратичной формы.
Расстояние, пройденное частицей, составляет уравнение как для постоянного, так и для переменного ускорения в кинематическом уравнении движения. Следовательно, при нахождении постоянного ускорения нам нужно предположить, что путь, пройденный частицей, представляет собой параболическую кривую. Как найти постоянное ускорение со скоростью и временем
Следовательно, при нахождении постоянного ускорения нам нужно предположить, что путь, пройденный частицей, представляет собой параболическую кривую. Как найти постоянное ускорение со скоростью и временем
Чтобы найти постоянное ускорение, рассмотрим первое уравнение движения,
v=v 0 +at
Где v – конечная скорость, а v 0 — начальная скорость.
Теперь добавьте v 0 к обеим сторонам уравнения и разделите оба уравнения на 2; отсюда получаем
v+ v 0 /2 =(v+ v 0 + at )
v+ v 0 / 2=v 0 +1/2 at
Из общего выражения скорости
v=∆x/ ∆t
∆x изменение положения; его можно записать как ∆x=x-x 0
∆t — изменение времени t.
Изменение положения дает уравнение средней скорости, таким образом, мы можем переписать это уравнение как 0 +v а t
Но v + v0/2 = va; средняя скорость
v a = v 0 +1/2
Подставляя значение va в уравнение расстояния,
Приведенное выше выражение имеет квадратичную форму, мы можем дифференцировать приведенное выше уравнение относительно t как Снова дифференцируя приведенное выше уравнение,
D 2 X /DT 2 = D 2 x 0 /DT 2 + D 2 V 0 /DT 2 4. Получить постоянное ускорение
Получить постоянное ускорение
D 2 x /dt 2 = Константа
D 2 x 0 /DT 2 = Константа
D 2 V 4 9. 9. 9. 9. 9. 9. . 9. . 9. . 9. . 0
Как найти постоянное ускорение с учетом скорости и расстояния?Связь между расстоянием, пройденным телом, и скоростью может помочь нам найти постоянное ускорение. Криволинейное движение тела в 2-мерной плоскости дает установившееся изменение скорости, что дает постоянное ускорение.
Для постоянного ускорения изменение скорости должно быть равномерным. Кинематическое уравнение может дать равномерное изменение скорости с расстоянием. Скорость тела на криволинейном пути определяется следующим образом. Как найти постоянное ускорение с расстоянием и временем вместе со скоростью
Из первого кинетического уравнения движения мы можем решить независимое от времени уравнение скорости и расстояния.
Уравнение имеет вид v=v 0 +at
t=v – v 0 / a
Средняя скорость тела, начальная скорость которого равна v0, а конечная скорость равна v, может быть выражена формулой уравнение как
va=v + v 0 /2
Расстояние определяется как
x = x 0 +v a t
Подставляя значение времени и средней скорости в приведенное выше уравнение, мы получаем
x=x0+ (v + v 0 / 2 )/(v – v 0 / a)
Уравнение для расстояния можно составить, решив и переставив члены. Таким образом, искомое уравнение будет иметь вид0025 + V 2 -V 0 2
V 2 = V 0 2 + 2A (X -X 0 )
+ 2A (X -X 0 ). dv 0 / dt +2a dx/dt -dx 0 /dt
Поскольку dv/dt не что иное, как ускорение,
Коэффициент dx/dt -dx 0 /dt должен быть ненулевой функцией .
dv/dt и dv 0 / dt должны быть линейной функцией времени, чтобы получить постоянное ускорение.
Другой способ найти постоянное ускорение с учетом скорости и расстояния приведен ниже.
Из кинематического уравнения движения ускорение частицы можно записать как
a=v – v 0 /t
Из уравнения положения-времени для скорости имеем x 0 /t
Мы должны учитывать среднюю скорость, так как существует постоянное изменение скорости частицы в зависимости от времени прохождения расстояния x, и, следовательно, среднюю скорость можно записать как
v a = v+ v 0 / 2
Таким образом, время, затрачиваемое на преодоление расстояния, равно
t=x-x 0 / (v+ v 0 / 83) 90 из t в уравнении ускорения получаем
a=v- v0/ [2x-x 0 / (v+ v 0 )]
Переставляя слагаемые, получаем
a=v+v 0 / v – v 0 (2x-x 0 )
Решая приведенное выше уравнение, мы получаем
a=v 2 – v 0 2 / 2(x/x 0 )
Это дает уравнение для постоянного ускорения со скоростью и расстоянием.
Концепции, рассмотренные в предыдущих разделах, можно легко понять, решив примеры задач, приведенные в этом разделе.
Задача 1) Автомобиль движется с определенной скоростью, которая определяется расстоянием как функцией времени. Проверьте, является ли ускорение постоянным или нет, и найдите скорость автомобиля в момент времени t=9.секунды. Функция задается как X(t)=4t 2 -7t+12.Решение:
Путь, пройденный телом, определяется как функция времени как
X(t)=4t 2 -7t+12
/dt =4(2t)-7+0
Снова дифференцируя по t, получаем
d 2 x/dt 2 =8-0
Так как производная второго порядка расстояния по времени — ускорение, а полученное значение — постоянное число, ускорение постоянно на пути, пройденном автомобилем. А его ускорение 8 м/с 2 .
Чтобы найти скорость, мы знаем, что
dx/dt = v
v = 8t-7
В момент времени t=9 секунд скорость автомобиля определяется выражением
v = 8(9)- 7
v = 65 м/с.
Задача 2) Мяч первоначально движется со скоростью 4 м/с, измеренной на расстоянии 6 метров от начала координат. То же сейчас движется со скоростью 7 м/с, а его положение составляет 15 метров. Как найти постоянное ускорение с расстоянием и временем вместе со скоростью мяча.Решение:
Данные для расчета – начальная скорость мяча v 0 = 4м/с.
Конечная скорость мяча v = 7 м/с.
Положение мяча при измерении его начальной скорости x 0 = 6м.
Положение мяча при измерении его конечной скорости x = 15м.
Постоянное ускорение мяча равно
a=v 2 – v 0 2 / 2 ( x-x 0 )
а = 33/18
а = 1,83 м/с 2 .
Решение:
Данные, необходимые для расчета – Начальная скорость автомобиля v 0 = 33 м/с.
Расстояние, пройденное автомобилем x = 99м.
Время, затраченное автомобилем на преодоление заданного расстояния t = 22 с.
Кинематическое уравнение для данных данных: и, следовательно, мы предполагаем, что начальное положение автомобиля равно нулю. Следовательно, уравнение можно изменить следующим образом:
x=v 0 + 1/2 at 2
99-33=242(а)
а = 0,27 м/с 2 .
Задача 4) измеренная скорость частицы 7 м/с на расстоянии 12 метров. Скорость той же частицы измеряется на расстоянии 39 метров как 11 м/с. Найдите ускорение.Решение:
Скорость частицы v 1 = 7 м/с.
Скорость той же частицы v 2 = 11 м/с.
Положение частицы при скорости v 1 равно х 1 = 12 м.
Положение частицы со скоростью v 2 равно x 2 = 39м.
Ускорение частицы равно
a=v 2 – v 0 / (2(x-x 0 ))
a=11 2 -7 2 4( -12)
а = 1,333 м/с 2 .
Задача 5) Как найти постоянное ускорение с расстоянием и временем, если заданная функция имеет вид x(t)= 8t 2 +12t+4 и, следовательно, найти начальное расстояние t=0 и конечное расстояние в t=4 секунды и, следовательно, найти скорость.Решение:
Данное уравнение является функцией, зависящей от времени, чтобы найти постоянное ускорение, дифференцированное по времени t
dx/dt =8(2t)+12+0
dx/dt =16t+ 12
При повторном дифференцировании по t
d 2 x/dt 2 =16+0 = 16
Из приведенного выше уравнения ускорение постоянно, а ускорение равно 16 м/с 2 .
Расстояние при t=0 равно x(t)= 8t 2 +12t+4
X(0)=8(0)+12(0)+4
X(0)=4
Исходное положение 4 метра.
Расстояние t=4 равно
X(4)= 8(4)+12(4)+4
X(4)=84
Скорость определяется выражением
v=x – x 0 / t- t 0
v=84-4/ 4-0
v = 20 м/с.
Задача 6) Найти постоянное ускорение функции x(t)=3t 3 +9т 2 +3т+6.Решение:
Функция задается как
x (t) = 3T 3 +9T 2 +3T +6
Дифференцированный W.R.T до T
DX/DT = 8 (3T 33333333333333333333333333333333333333333333333333333333333333333333333. 2 ) +9 (2T)+3+0
DX/ DT T = 24T 2 +18T+3
Differing снова
D 2 X/ DT 2 T = 48T+18
8 а = 48t+18 м/с 2 .
Ускорение в данном уравнении непостоянно. Путь, описываемый данной функцией, не является криволинейным, и имеет место флуктуация скорости.
