Формула ускорения – Помощник для школьников Спринт-Олимпик.ру
Суммарный результат всех сил, действующих на объект, как гласит второй закон Ньютона, называется ускорением. Формула его будет изменяться в зависимости от скорости и направления движения предмета. В повседневной жизни этот термин употребляется довольно редко, услышать его можно чаще всего в рекламе автомобилей. Но в физике его значение гораздо шире, чем просто время, за которое машина разгоняется.
Содержание
- Определение и свойства
- Другие формы
- Особые случаи
- Единица измерения
- Действие на людей
Определение и свойства
Любое изменение скорости тела приводит к ускорению (ᾱ) как в сторону увеличения, что обычно подразумевается, так и снижения, то есть замедления. Также этот термин может означать смену направления (центростремительность). Это связано с прямой зависимостью сил, которые действуют на объект, от изменения скорости (v), являющейся величиной векторной и имеющей направление. Так ускоряться будут:
Так ускоряться будут:
- падающее яблоко;
- автомобиль, останавливающийся на светофоре;
- вращающаяся планета и т. п.
Например, транспортное средство начинает движение с места и продолжает ехать, увеличивая v, — это ᾱ линейное (или тангенциальное). Пассажиры внутри машины будут ощущать его как силу, которая прижимает их к спинкам сидений. Если автомобиль поворачивает, то есть меняет направление, то это уже ᾱ радиальное. Люди в салоне будут наклоняться в сторону, противоположную движению.
Когда водитель решит остановиться, это тоже будет ускорением, но только в противоположном направлении v движения авто. В космосе такое ᾱ называют ретроградным горением или замедлением. Пассажиры будут чувствовать, будто что-то их толкает вперёд. Принято различать два вида ᾱ:

Например, мотоцикл набирает скорость 50 м/с за 10 с, его среднее ᾱ = 50 / 10 = 5 м/с².
Другие формы
Можно взять материальный предмет, например, спутник, который вращается вокруг Земли. Он двигается по окружности и ускоряется, причина этого — изменение направления траектории движения. При этом его скоростной режим может не изменяться. В этом случае речь идёт о центростремительном (направленном к центру) ᾱ.
Ускорение тела относительно состояния свободного падения (ᾱ правильное) измеряется акселерометром. В механике для предмета с постоянной массой (m) ᾱ центра m тела пропорционально действующему на него вектору силы (суммы всех сил). Здесь действует второй закон Ньютона: F = m * ᾱ → ᾱ = F / m.
Скорость частицы, которая движется по криволинейной траектории, можно записать как функцию времени v(t) = v(t) * v(t) / v(t) = v(t) * ut(t), где единичный вектор касательной (ut) к траектории равен v(t) / v(t) и указывает направление движения в конкретный момент времени. Это и есть формула центростремительного ускорения, которое создаётся при круговом движении. Можно использовать цепное правило дифференцирования, чтобы записать формулу для произведения двух функций, если принять во внимание, что ᾱ частицы происходит по некой кривой проекции. Последовательность действий уравнения следующая:
В уравнении un — единичный вектор нормали, r — мгновенный радиус кривизны, который основывается на колеблющемся круге в момент времени t. Все эти компоненты являются тангенциальным, радиальным или нормальным ускорением, формула которого может быть представлена в виде функции.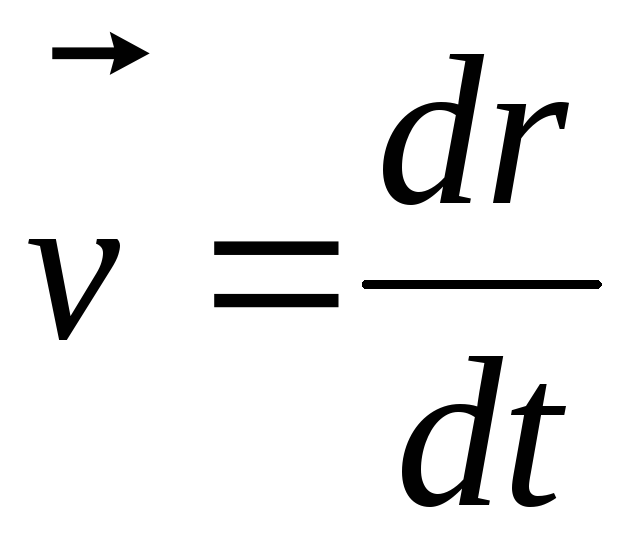
Особые случаи
Если при движении v изменяется на равную величину, то есть объект равноускоренный в каждый одинаковый период времени, то это можно охарактеризовать как равномерное или постоянное ускорение. Пример этого в физике — формула ускорения свободного падения тела, вид которой при отсутствии сопротивления будет зависеть от гравитационного поля и силы стандартной гравитации (g).
Чтобы составить уравнение, придётся проделать небольшой путь от самых основ. Второй закон Ньютона гласит, что Fg = mg. В кинематике есть формулы, которые связывают смещение (sₒ), начальную (vₒ) и зависящую от времени v(t) скорость и ускорение с прошедшим временем (t):
- s(t) = sₒ + vₒt + 1/2ᾱt² = sₒ + (vₒ + v(t)/2 * t;
- v(t) = vₒ² + ᾱt;
- v²(t) = vₒ² + 2ᾱ * [s(t) — sₒ].
Наглядно расчёт разности можно увидеть, если начертить график.
Частица будет испытывать ускорение, которое возникает в результате изменения направления вектора скорости, тогда как её величина остаётся постоянной при равномерном круговом движении. Производная от расположения точки на кривой по времени, то есть её v, оказывается всегда точно касательной к линии, соответствующей ортогональному радиусу в этой точке.
Это ускорение постоянно меняет направление скорости, которая будет касаться соседней точки, тем самым заставляя вектор скорости совершать вращательные движения по кругу. Формула будет выглядеть следующим образом: ᾱс = v² / r. Надо помнить, что v здесь — произведение угловой скорости ω на r.
Единица измерения
Ускорение рассчитывается путём деления метров в секунду (м/с) на секунды (с). Деление расстояния по времени вдвое равно делению расстояния на квадрат времени. Таким образом, единицей ускорения СИ является метр в секунду в квадрате (м/с²). Чтобы было весело изучать физику, можно рассмотреть несколько интересных примеров в таблице.
Чтобы было весело изучать физику, можно рассмотреть несколько интересных примеров в таблице.
| ᾱ ( м/с²) | Событие |
| 0,5 | гидравлический лифт |
| 0,63 | ускорение свободного падения (УСП) на Плутоне |
| 1 | лифт на кабеле |
| 1,6 | ускорение свободного падения на Луне |
| 8,8 | Международная космическая станция |
| 10—40 | механический прямолинейный старт пилотируемой ракеты |
| 20 | космический челнок |
| 9,8 | УСП на Земле |
| 20—50 | американские горки |
| 80 | предел устойчивой человеческой терпимости |
| 0—150 | тренировочная центрифуга |
| 600 | автоматические подушки безопасности |
| 1 млн | пуля в стволе пистолета |
| 24,8 | УСП на Юпитере |
Другая часто используемая единица — ускорение силы тяжести g. Поскольку все знакомы с влиянием гравитации на физические объекты, это делает их удобным стандартом для сравнения ускорений. Все чувствуют себя нормально при 1 g, вдвое тяжелее при 2 g и невесомо при 0 g. Эта единица измерения имеет значение 9,80665 м/с², но для повседневного использования достаточно 9,8 м/с², а 10 м/с² удобно для быстрых подсчётов.
Поскольку все знакомы с влиянием гравитации на физические объекты, это делает их удобным стандартом для сравнения ускорений. Все чувствуют себя нормально при 1 g, вдвое тяжелее при 2 g и невесомо при 0 g. Эта единица измерения имеет значение 9,80665 м/с², но для повседневного использования достаточно 9,8 м/с², а 10 м/с² удобно для быстрых подсчётов.
Действие на людей
Хотя термин «сила g» часто используется, g — мера ускорения, а не силы. Особую обеспокоенность у людей вызывают физиологические эффекты этого явления. Чтобы понять смысл, лучше обратиться к примерам:
 Вопреки распространённому мнению, именно ускорение делает поездку интересной. Тщательно разработанные горки позволят пассажирам на короткое время максимально ускориться (как равноускориться, так и равнозамедлиться) от 3 до 4 g — это то, что даёт поездке ощущение опасности.
Вопреки распространённому мнению, именно ускорение делает поездку интересной. Тщательно разработанные горки позволят пассажирам на короткое время максимально ускориться (как равноускориться, так и равнозамедлиться) от 3 до 4 g — это то, что даёт поездке ощущение опасности.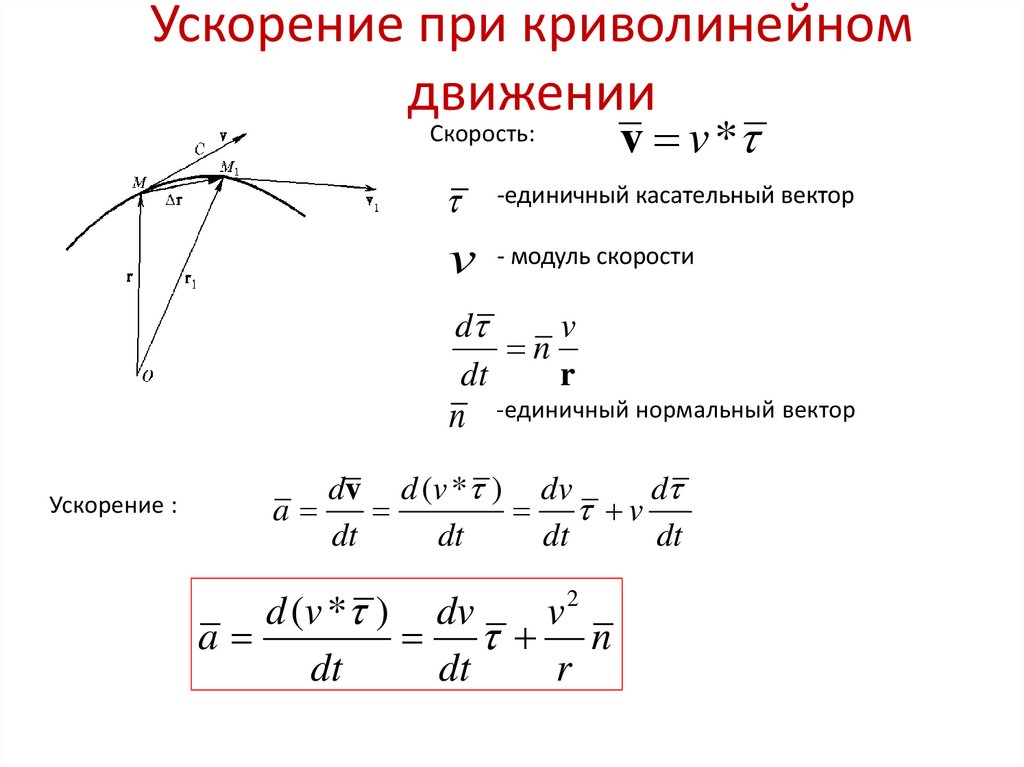
По оценкам экспертов, ускорение во время аварии, в которой погибла принцесса Диана, составляло порядка 70—100 g.
Этого было достаточно, чтобы оторвать лёгочную артерию от её сердца и спровоцировать травму, которую практически невозможно пережить. Если бы Диана была пристёгнута ремнём безопасности, ускорение составило бы примерно 30 или 35 g. Это грозило несколькими переломами, но все остались бы живы.
Предыдущая
ФизикаЭлектрический ток в электролитах – механизм возникновения, законы и применение
Следующая
ФизикаНаправление электрического тока – условия и причины возникновения
Как рассчитать ускорение с помощью силы и массы: исчерпывающие подходы и факты
Как рассчитать ускорение с помощью силы и массы – это известный вопрос, на который нужно ответить. Мы знаем ускорение, которое действует на тело, где сила и масса существенно влияют на него.
Мы знаем ускорение, которое действует на тело, где сила и масса существенно влияют на него.
Ускорение измеряет, насколько скорость изменяется в данный момент времени. Скорость – это фактическая скорость, с которой объект изменяется в соответствии с системой отсчета. Скорость зависит от того, какая сила перемещает объект вперед или назад.
Ускорение, действующее на тело, в основном зависит от силы и массы, и как рассчитать ускорение с помощью силы и массы – это то, что мы обсудим далее. Когда неуравновешенная сила не равна нулю, действие на тело будет иметь большее ускорение, когда чистая сила не равна нулю.
Когда равнодействующая сила действующее на тело больше, ускорение, действующее на тело, также будет больше. Еще один момент, который следует помнить, это то, что масса также влияет на ускорение. Чем меньше масса, тем больше ускорение.
Как мы все знаем, законы Ньютона были применены к нескольким открытиям, а для ускорения мы используем Второй закон Ньютона. Это удобно, когда мы используем его для расчета ускорения любого движущегося тела.
Это удобно, когда мы используем его для расчета ускорения любого движущегося тела.
Согласно второму закону Ньютона сила, действующая на тело, пропорциональна массе, постоянной во всем и изменяющейся скорости. Формула имеет вид F = ма. Мы получаем ускорение как а = Ф / м.
В этом контексте мы рассматриваем заставить быть сетью сила. Потому что на тело действует несколько сил, поддерживающих его движение, например, нормальная сила, сила трения и так далее. Следовательно, мы считаем, что полная сила, действующая на тело, является равнодействующей силой.
Как найти ускорение по чистой силе и массеВо-первых, нам нужно понять, как сила и масса влияют на ускорение движущегося тела. Масса – это вес движущегося тела, а сила – это не что иное, как чистая сила, действующая на тело, которая запускает его движение.
Все это возможно только благодаря одной формуле, которая подчиняется Второму закону Ньютона и выводится из него. Формула выглядит так: а = Ф / м.
Формула выглядит так: а = Ф / м.
Здесь сила имеет разные случаи; сила может быть нормальной, силой трения, силой натяжения, силой тяжести, Равнодействующая сила, и чистая сила. Здесь, в этом случае, мы рассматриваем силу как результирующую силу. И эта конкретная сила случается с неуравновешенной силой.
При воздействии на тело эта неуравновешенная сила заставляет тело менять свое положение покоя, из которого оно начинает двигаться. Тогда у тела не будет другого выбора, кроме как совершить движение.
Простые примеры, иллюстрирующие, как найти ускорение с помощью силы и массыКогда прикладываемая масса меньше, ускорение больше и наоборот. Возьмем небольшой пример мяча массой 10 кг, катящегося под гору с силой 40 Н. Поэтому мы также должны учитывать направление, в котором движется мяч. Пусть она будет перпендикулярна зоне, по которой движется.
Согласно уравнению Второго закона Ньютона, f = mxa
Итак, a = F / m
а = 40/10
a = 4 мс-2
Давайте также проиллюстрируем другой пример для лучшего понимания. В деревне был холм, на котором мало кто пользовался, потому что на нем было слишком много камней и мелких камней, которые могли скатиться и поранить пешеходов.
В деревне был холм, на котором мало кто пользовался, потому что на нем было слишком много камней и мелких камней, которые могли скатиться и поранить пешеходов.
Однажды из-за проливных дождей скала и камни больше не оставались неподвижными и начали быстро катиться с холма. Теперь давайте посчитаем ускорение большого камня массой 500 кг, который скатывается с силой 1500 Н.
По формуле a = F / m
а = 15000/500
a = 30 мс-2
Помимо ускорения с силой и массой, есть еще один решающий фактор: сила тяжести. Кроме того, в этом разделе мы подробно рассмотрим реальный пример того, как вычислить ускорение с помощью силы и массы.
Группа мальчиков приехала в деревню на летние каникулы. Один из мальчишек из деревни очаровал своего друга рекой, имеющей прыгающий конец. Следовательно, все мальчики захотели попробовать. Один за другим прыгали в реку с прыжковой точки.
Теперь посчитайте ускорение мальчика весом 30 кг, который прыгает в реку с силой 120 Н. Мы знаем формулу, а = Ф / м. Следовательно, a = 120/30, a = 3 мс-2.
Мы знаем формулу, а = Ф / м. Следовательно, a = 120/30, a = 3 мс-2.
Всегда есть любопытство по поводу того, как все работает и воплощается в реальность. Точно так же мы обычно видим движение транспортного средства, но задумывались ли мы, как физики, о физике, лежащей в основе этой причины?
Каждый день то, что мы видим, воспринимаем физику, но не осознаем ее. Как было сказано ранее, мы видим машину, движущуюся или даже едущую в ней; мы никогда не замечаем науки, стоящей за этим процессом. Поэтому главное, что нужно делать, – это замечать и признавать их в нашей повседневной жизни.
Ускорение движения тела и выводы – это то, что мы рассмотрим в этом разделе. Итак, с этого момента, где бы и когда бы мы ни увидели движущийся автомобиль или автобус, мы немедленно должны знать, что ускорение способствует такому процессу.
Во-первых, нам нужно увидеть, какое отношение масса имеет к ускорению. Масса – это вес того конкретного тела, который связан с ускорением. Когда масса мала, ускорение больше. Следовательно, вот как рассчитать ускорение с силой и массой.
Масса – это вес того конкретного тела, который связан с ускорением. Когда масса мала, ускорение больше. Следовательно, вот как рассчитать ускорение с силой и массой.
Это просто здравый смысл; когда предмет тяжелый, его сложно переместить с одного места на другое. Когда масса легкая, ее можно быстро мобилизовать. Следовательно, масса имеет прямую связь с ускорением.
«Автомобиль N Motion» by TheBusyBrain под лицензией CC BY 2.0Задачи о том, как рассчитать ускорение с помощью силы и массы1 задачи:
Кафе находится на углу города. Каждое утро несколько велосипедистов проезжают по городу и пересекают кафе. Скамейки кафе вынесены на улицу, поэтому вид улучшается, так как это пляжное кафе.
Однажды один из велосипедистов ехал слишком быстро, двинулся и слегка задел гигантскую статую, расположенную рядом. Эта статуя из-за своего тяжелого веса медленно упала на землю. Теперь посчитайте, с каким ускорением статуя весом 800 кг обладает силой тяжести 1100 Н.
Решение:
а = Ф / м
а = 1100/800
a = 1.375 мс-2
2 задачи:
В данный момент объект неподвижен. Когда чистая сила 175 Н действует на этот объект весом 50 кг, какое ускорение он будет использовать, чтобы выйти из своего исходного положения?
Решение:
а = Ф / м
а = 175/50
a = 3.5 мс-2
Часто задаваемый вопросКакие несколько примеров ускорения в повседневной деятельности?Ускорение – это скорость, с которой объект движется в данный момент времени. Это зависит от изменения скорости с заданным временем.
- Когда объект движется на юг на 10N м / с с постоянной скоростью, он остается в том же темпе до тех пор, пока не будет приложена сила. Таким образом, при приложении силы он будет двигаться со скоростью 2 мс-15. Теперь объект называется ускоряющимся.
- Девушка идет на север со скоростью 10 мс-2.
 Говорят, что у девушки постоянная скорость, а значит, и ускорение равно нулю.
Говорят, что у девушки постоянная скорость, а значит, и ускорение равно нулю. - Когда мяч катится с холма, он ускоряется при приложении силы. Если мяч весит меньше, ускорение больше, а если мяч весит больше, ускорение со временем становится меньше.
- Когда мальчик прыгает со скалы с приложенной к нему силой, он будет ускоряться еще больше, а затем, наконец, остановится под действием силы тяжести. Но величина необходимого ускорения будет зависеть от прилагаемой силы: если сила увеличивается, то ускорение увеличивается; если сила уменьшается, ускорение уменьшается.
- Мальчик движется на север с ускорением 9 мс.-2. Постепенно на мальчика действует другая сила, и теперь размер меняется на 15 мс.-2. Теперь говорят, что мальчика ускоряют за счет действующей на него чистой силы.
Что такое ускорение? Виды ускорения. Формулы. Пример решения задачи
org/Person”> От Masterweb
11.12.2018 15:00
Раздел физики, ответственный за изучение особенностей движения в пространстве тел, называется кинематикой. В данной статье рассмотрим, какие физические величины в кинематике используются для описания перемещений объектов, а также раскроем, что такое ускорение.
Физические величины в кинематике
Когда тело движется в пространстве, то нам важно знать, какое расстояние оно проходит за указанный промежуток времени и вдоль какой траектории движется.
Для описания пройденных расстояний в физике используют понятие пути – L. В случае движения по окружности вместо пути пользуются понятием угла поворота – θ. Величину L в СИ измеряют в метрах (м), а величину θ – в радианах (рад.).
Помимо пути важно знать также скорость движения тел. Под ней понимают быстроту прохождения расстояний. Математическое выражение для линейной скорости принимает вид:
v¯ = d L / d t
Для описания движения по окружности применяют угловую скорость ω, которая рассчитывается так:
ω¯ = d θ / d t
Третьей важной величиной кинематики является ускорение.
Что такое ускорение? Это величина в физике, которая показывает, как быстро меняется скорость во времени. Математически это можно записать так:
a¯ = d v¯ / d t
Если подставить в эту формулу ускорения выражение для скорости, получим:
a¯ = d2 L / d t2
Ускорение – это первая производная скорости по времени или вторая производная по времени пройденного пути.
Тангенциальное и нормальное ускорение
Выше было дано определение, что такое ускорение. Оно называется полным. В общем случае направление полного ускорения не совпадает с направлением вектора скорости. Последний является касательной к траектории движения в любой ее точке.
Поскольку скорость – это величина векторная, то ее изменение предполагает возможность менять модуль и направление. В первом случае говорят о наличии у тела тангенциального ускорения, во втором – нормального.
Формула тангенциального ускорения at не отличается от таковой для ускорения полного a.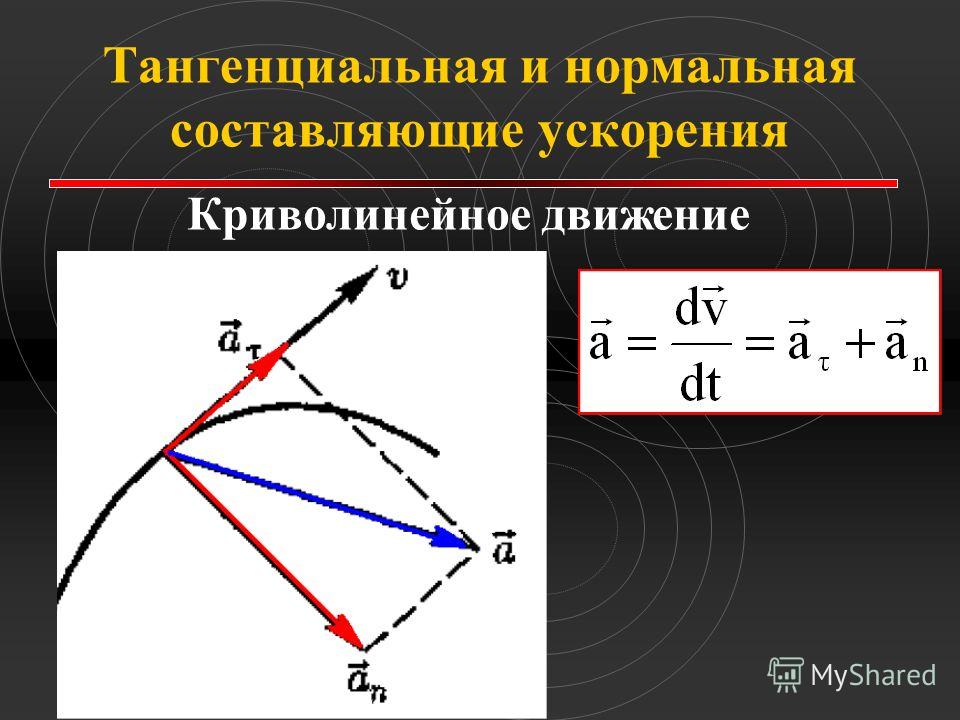 Формула имеет вид:
Формула имеет вид:
at = d v / d t
То есть тангенциальное, или касательное, как его еще называют, ускорение является производной от модуля скорости по времени. Вектор at¯ совпадает с вектором v¯ при ускоренном движении и противоположен ему при замедленном движении.
Нормальное ускорение – это физическая величина, которая приводит к искривлению прямолинейной траектории перемещения тел. Направлено оно вдоль радиуса кривизны траектории, то есть нормально по отношению к ней. Формула для его определения имеет вид:
ac = v2 / r
Нормальное ускорение ac зависит от модуля скорости v и радиуса кривизны траектории r. Очевидно, что в случае движения по прямой радиус r можно считать равным бесконечности. Последнее означает, что нормальное ускорение равно нулю для прямолинейного движения.
Для движения по окружности вектор ac¯ направлен к ее центру вдоль радиуса. По этой причине величину ac также называют центростремительным ускорением.
Полное ускорение
Вектор полного ускорения – это всегда сумма тангенциальной и нормальной компонент. Поскольку они перпендикулярны друг другу, то для вычисления модуля полного ускорения можно воспользоваться теоремой Пифагора. Искомая формула ускорения полного примет вид:
a = √(at2 + ac2)
Чтобы определить, куда направлен вектор a¯, достаточно вычислить угол между ним и какой-либо компонентой. Например, угол φ между векторами a¯ и at¯ равен:
φ = arctg(ac / at)
Напомним, что центростремительное ускорение отлично от нуля только тогда, когда кривизна траектории движения отлична от бесконечности. В случае же прямолинейного движения полное ускорение по величине и направлению равно тангенциальной компоненте.
Угловое ускорение
Рассматривая, что такое ускорение, следует остановиться на соответствующей угловой характеристике.
Выше было введено понятие угловой скорости, которая измеряется в радианах в секунду (рад/с). Если найти производную этой скорости по времени, то мы получим величину углового ускорения:
Если найти производную этой скорости по времени, то мы получим величину углового ускорения:
α¯ = ω¯ / d t
Несложно показать, что угловая величина связана с тангенциальной компонентой полного ускорения следующим соотношением:
at = α × r
При постоянном угловом ускорении касательная компонента at будет больше для точек, которые находятся дальше от оси вращения.
К нормальной компоненте угловое ускорение не имеет никакого отношения.
Решение задачи на определение ускорения
Предположим, что, двигаясь с ускорением постоянным вдоль прямой линии, тело прошло расстояние 100 метров. Известно, что начальная скорость тела была равна 1 м/с. Отмеченное расстояние тело преодолело за 5,5 секунды. С каким ускорением происходило движение?
Согласно условию задачи, речь идет о равноускоренном движении вдоль прямой траектории. Пройденный путь в этом случае может быть вычислен по формуле:
L = v0 × t + a × t2 / 2
Выражаем из равенства величину a, имеем:
a = 2 × (L – v0 × t) / t2
Все величины в правой части равенства известны из условия. Подставляем их и записываем ответ: a = 6,25 м/с2. То есть в течение каждой из 5,5 секунд скорость тела возрастает на 6,25 м/с. Найденное значение полного ускорения совпадает с тангенциальной компонентой.
Подставляем их и записываем ответ: a = 6,25 м/с2. То есть в течение каждой из 5,5 секунд скорость тела возрастает на 6,25 м/с. Найденное значение полного ускорения совпадает с тангенциальной компонентой.
Формула пересчета ускорения из движущейся s – со в «неподвижную» s
СЕМИНАР 1 Кинематика точки Вектор скорости, модуль вектора скорости, вектор ускорения, модуль вектора ускорения.
Тангенциальное ускорение.
– тангенциальное ускорение – производная от модуля скорости по времени. Для нахождения тангенциального ускорения сначала находим модуль скорости как функцию времени и затем дифференцируем эту функцию по времени.
Нормальное ускорение.
Вектору скорости присущи два
атрибута: модуль и направление в
пространстве. Производная вектора
скорости по времени, может быть
представлена в виде суммы двух слагаемых.
Одно из этих слагаемых – это тангенциальное
(касательное) ускорение.
В соответствии с теоремой Пифагора, получаем полезную формулу .
Радиус кривизны траектории.
Можно показать, что нормальное ускорение, характеризующее быстроту изменения направления скорости, связано с величиной скорости формулой . Здесь ρ – радиус кривизны траектории. Отсюда получаем . Именно такой формулой будем пользоваться для нахождения радиуса кривизны траектории в этом разделе.
Вращательное движение твердого тела вокруг постоянной оси
Угловая скорость, угловое ускорение.
При описании вращательного
движения твердого тела, наряду с векторами
перемещения любых точек твердого тела,
вводят единый для всех точек вектор
элементарного угла поворота
.
Кроме линейных скоростей точек твердого
тела, вводят единую для всех точек
угловую скорость
. Угловое ускорение
.
Формула, связывающая величину угловой
скорости и частоты вращения.
Угловое ускорение
.
Формула, связывающая величину угловой
скорости и частоты вращения.
Связь угловых характеристик движения с линейными.
,; , ; , . Здесь – радиус – вектор, рассматриваемой точки твердого тела, начинающийся в любой точке оси вращения; R – расстояние от рассматриваемой точки твердого тела до оси вращения.
Кинематика относительного движения (Галилей, Кориолис)
, – скорость и ускорение материальной точки относительно S – СО; , – скорость и ускорение материальной точки относительно S – СО; – радиус-вектор материальной точки относительно S – СО; , – скорость и ускорение S

тоже утверждает, что ускорение материальной точки относительно “неподвижной” S – СО складывается из ускорения материальной точки относительно движущейся S – СО и ускорения точки S – СО, через которую проходит (в этот момент) материальная точка, относительно S – СО. Кориолисово ускорение . Оно связано, во-первых, с тем, что вектор поворачивается вместе с S – СО и, во-вторых, с тем, что из-за перемещения материальной точки относительно S – СО, изменяется радиус-вектор , а значит и скорость .
СЕМИНАР 2 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНО ДВИЖУЩЕГОСЯ ТВЕРДОГО ТЕЛА
Инерциальные системы отсчета
Важная роль выбора системы отсчета
впервые продемонстрирована Коперником
(около 1500г.). В системе отсчета введенной
Коперником, связанной с Солнцем и
звездами, настолько упростился характер
движения планет, что трудолюбивый Кеплер
(в 1609-1619гг. ) сумел сформулировать три
знаменитых закона, описывающих движение
планет. Следуя Копернику, Ньютон навсегда
в качестве тел отсчета выбрал Солнце и
звезды. Опираясь на законы Кеплера,
Ньютон установил закон всемирного
тяготения, а затем и три закона движения
(около 1666г.). Все это было сделано
применительно к коперниковой
(гелиоцентрической), инерциальной
системе отсчета.
) сумел сформулировать три
знаменитых закона, описывающих движение
планет. Следуя Копернику, Ньютон навсегда
в качестве тел отсчета выбрал Солнце и
звезды. Опираясь на законы Кеплера,
Ньютон установил закон всемирного
тяготения, а затем и три закона движения
(около 1666г.). Все это было сделано
применительно к коперниковой
(гелиоцентрической), инерциальной
системе отсчета.
Первый закон Ньютона содержит не только закон инерции Галилея, но и определение инерциальной системы отсчета:
Существуют такие системы отсчета, назовем их инерциальными (ИСО), в которых тело, изолированное от других тел, сохраняет свою скорость постоянной.
Нахождение силы из закона движения.
Импульсом материальной точки
называется величина, равная произведению
массы точки на ее скорость
.
По определению, сила – это величина,
показывающая, как быстро изменяется
импульс материальной точки со временем,
то есть
,
причем последние два равенства
справедливы, если масса тела постоянна.
Интегрирование уравнения движения. Сила линейно зависит от времени.
– уравнение движения материальной точки в векторной форме. В проекции на оси прямоугольной системы координат уравнения движения принимают вид ; ;
Интегрируем соответствующее дифференциальное уравнение методом разделения переменных.
Интегрирование уравнения движения. Сила зависит от координаты.
В уравнении движения делаем замену. Тогда уравнение принимает вид , то есть переменные разделились и можно выполнить интегрирование.
Неинерциальные системы отсчета
Система отсчета, относительно которой материальная точка движется с ускорением, при условии, что на эту точку не действуют другие тела, называется неинерциальной (НСО).
Можно сказать иначе. Система отсчета,
которая движется поступательно с
ускорением и/или вращается относительно
инерциальной системы отсчета (ИСО),
называется неинерциальной (НСО).
Введем следующие обозначения:
, – скорость и ускорение материальной точки относительно неинерциальной S – СО;
– радиус-вектор материальной точки относительно неинерциальной S – СО;
– ускорение неинерциальной S – СО относительно инерциальной S – СО в поступательном движении;
, – угловая скорость и угловое ускорение неинерциальной S – СО относительно инерциальной S – СО во вращательном движении.
В этих обозначениях уравнение движения материальной точки в неинерциальной системе отсчета имеет вид: .
В правой части уравнения:
– сумма всех сил, действующих на материальную точку со стороны других тел, то есть тех сил, которые определены в рамках системы законов Ньютона;
– сила инерции, действующая в НСО, движущейся поступательно с ускорением ;
– сила инерции, действующая в НСО, вращающейся с угловым ускорением;
– центробежная сила инерции, действующая в НСО, вращающейся с угловой скоростью ;
– сила инерции Кориолиса,
действующая в НСО, вращающейся с угловой
скоростью
,
если материальная точка движется
относительно НСО со скоростью
и при условии, что векторы
и составляют угол, не равный 0
СЕМИНАР 3 ИМПУЛЬС, МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И МОМЕНТ ИМПУЛЬСА (ЗАКОНЫ ИЗМЕНЕНИЯ И СОХРАНЕНИЯ)
Закон изменения импульса для одной материальной точки.
Второй закон Ньютона для материальной точки, когда на нее действует постоянная сила, может быть переписан в виде закона изменения импульса – приращение импульса материальной точки равно импульсу силы (произведению силы на время, за которое импульс точки изменился на), действующей на материальную точку.
Система материальных точек.
Импульс системы материальных точек – это сумма (конечно векторная) импульсов материальных точек: . Производная импульса системы материальных точек по времени равна сумме всех сил, действующих на систему, и, с учетом третьего закона Ньютона, равна сумме внешних сил, действующих на систему материальных точек: .
Сохранение импульса системы
взаимодействующих тел.
Из закона изменения импульса следует, что если , то. Для проекций на выделенное направление X можно утверждать, что из следует , если .
Уравнение движения тела с изменяющееся массой – уравнение Мещерского Здесь m – масса, – ускорение тела в рассматриваемый момент времени, – сумма всех внешних сил, – реактивная сила.
Центр масс. Система отсчета центра масс.
Центром масс системы материальных точек называется точка пространства, радиус-вектор которой находится по формуле . Соответственно скорость центра масс равна . Системой отсчета центра масс (Ц-системой) называется такая система отсчета, относительно которой покоится центр масс рассматриваемой системы частиц, и, которая движется поступательно относительно инерциальной системы отсчета.
Работа постоянной силы.
– работа постоянной силы,
приложенной к телу, определяется как
скалярное произведение вектора силы
на вектор перемещения тела.
Работа переменной силы.
Разделяем конечное перемещение на такие элементарные перемещения, чтобы на любом из них можно было считать силу постоянной по величине и по направлению. Тогда можно ввести понятие элементарной работы . Затем учитываем замечательное свойство работы – аддитивность (свойство складываться): .
Мощность силы .
Теорема о приращении кинетической энергии. – приращение кинетической энергии материальной точки или поступательно движущегося твердого тела равно работе всех сил, приложенных к материальной точке или к телу.
Потенциальная энергия взаимодействия системы материальных точек.
Для того, чтобы работа силы,
приложенной к телу, при переносе тела
из позиции 1 в позицию 2 не зависела от формы траектории,
необходимо, чтобы сумма
была полным дифференциалом. В свою
очередь, для того, чтобы указанная сумма
была полным дифференциалом, должны
выполняться равенства
;
;
. Только при выполнении этих условий
можно сопоставить точкам пространства некоторую функцию координат и назвать ее потенциальной энергией, а
силу потенциальной или консервативной.
Определение формулируется не для
потенциальной энергии, а для ее приращения
,
или ее убыли
.
Только при выполнении этих условий
можно сопоставить точкам пространства некоторую функцию координат и назвать ее потенциальной энергией, а
силу потенциальной или консервативной.
Определение формулируется не для
потенциальной энергии, а для ее приращения
,
или ее убыли
.
Таким образом, потенциальная энергия неопределенна с точностью до постоянной – уровня отсчета потенциальной энергии. Определение приращения потенциальной энергии в дифференциальной форме имеет вид . Отсюда .
Физика от чего зависит ускорение
Содержание
- 1 Основные формулы для равноускоренного движения
- 2 Сила тяжести и ускорение свободного падения
- 3 Закон всемирного тяготения
- 4 Как определяют ускорение силы тяжести
- 5 Что мы узнали?
- 6 История открытия
- 7 Физическая сущность
- 8 Формулы для расчёта
- 9 Ускорение на других планетах
- 10 Воздействие перегрузок на человека
Основные формулы для равноускоренного движения
Равноускоренное движение — самый простой вид неравномерного движения. Равноускоренным называется движение с ускорением, постоянным по модулю и направлению:
Равноускоренным называется движение с ускорением, постоянным по модулю и направлению:
Δv — изменение скорости (“дельта v “), м/с;
Δt — промежуток времени, (“дельта t “)за которое произошло изменение скорости, с.
Из формулы (1) следует, что размерность ускорения будет выражаться в метрах на секунду в квадрате:
Второй закон Ньютона гласит:
F — сила, действующая на тело, Н;
m — масса тела, кг;
a — ускорение, м/с 2 .
Сила тяжести и ускорение свободного падения
При свободном падении на Землю все тела, независимо от их массы, движутся одинаково. Свободное движение является равноускоренным движением. Ускорение, с которым падают на Землю тела в пустоте, называется ускорением свободного падения (или ускорением силы тяжести). Условие пустоты или, что тоже самое, вакуума, требуется для исключения влияния сопротивления атмосферного воздуха. Сила притяжения Fт со стороны Земли на тело массой m, называется силой тяжести:
Определением ускорения силы тяжести впервые систематически занимался Галилео Галилей — итальянский математик, физик, астроном. 2>$ .
2>$ .
И хотя это открытие датировано 1589г., современное, общепринятое среднее значение g практически не отличается от этого значения. Когда от расчетов не требуется высокой точности, то принимают, что модуль g равен 10 м/с 2 .
Последовавшие за Галилеем более точные измерения показали, что значение g не является абсолютной константой, а зависит от местоположения измерений в разных точках Земли. Ответ на этот вопрос нашел английский ученый Исаак Ньютон.
Закон всемирного тяготения
В 1682 г. Ньютон открыл закон всемирного тяготения, из которого следует:
- все тела притягиваются друг к другу;
- сила тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними;
- векторы сил тяготения направлены вдоль прямой, соединяющей тела.
Этот закон универсален, и для случая пары тел, одно из которых является произвольным телом массой m, а второй — Земля, в виде формулы выглядит так:
Mз — масса Земли, кг;
Rз — радиус Земли, м;
h — высота, на которой находится тело, относительно поверхности Земли, м;
G — гравитационная постоянная, равная 6,6720 * 10 -11 Н*м 2 * кг -2 .
Из формул (4) и (5) следует, что:
Из (6) следует, что ускорение силы тяжести будет зависеть от высоты h и величины радиуса Земли, который для обычных расчетов принимается равным примерно 6400 км. Но поскольку форма Земли не является идеальным шаром, а сплюснута к полюсам, то точные значения g будут отличаться от среднего значения в 9,81 м/с 2 :
- максимальное значение gмакс = 9,83 м/с 2 — на полюсах Земли, где Rз меньше;
- минимальное значение gмин = 9,79 м/с 2 — на экваторе Земли, где Rз больше.
Рис. 2. Зависимость ускорения свободного падения на полюсах, экваторе и от вращения Земли.
Из формулы (6) также следует, что ускорение силы тяжести на других планетах, имеющих массу, отличающуюся от массы Земли, будет для космонавтов значительно отличаться от привычных земных условий. Так, например:
- На Марсе — gМарса = 3,86 м/с 2 ;
- На Меркурии — gМеркурия = 3,7 м/с 2 ;
- На Луне — gЛуны = 1,62 м/с 2 ;
- На Нептуне — gНептуна = 11,0 м/с 2 .

Как определяют ускорение силы тяжести
Для точного измерения силы тяжести, а значит, и ускорения, используется прибор, называемый гравиметром. Прибор применяется при поиске полезных ископаемых и для сбора информации археологами, палеонтологами, гидрологами и представителями других профессий, изучающих поверхность Земли.
Рис. 3. Гравиметры:.
Следует упомянуть еще два фактора, влияющих на значение ускорения свободного падения:
- Известно, что Земля вращается вокруг своей оси, имея при этом так называемое центростремительное ускорение, которое влияет на величину ускорения свободного падения;
- Масса Земли распределена неравномерно, например, в местах расположения больших месторождений металлических руд ускорение силы тяжести будет больше, а там, где есть пустоты (газовые месторождения) ускорение будет несколько меньше.
Эти факторы дают очень малые отклонения от средних значений g , но зато их регистрация позволяет, например, геологам находить новые месторождения полезных ископаемых.
Что мы узнали?
Итак, мы узнали, что такое ускорение силы тяжести. Сила тяжести возникает вследствие действия силы гравитации, подчиняющейся закону Ньютона (формула (5)). На Земле среднее значение ускорения силы тяжести gЗемли равно 9,81 м/с 2 . Для точного определения ускорения силы тяжести требуется использование современных приборов, называемых гравиметрами.
ФИЗИКА
Вопрос 1. Кинематика материальной точки (частицы). Скорость и ускорение при одномерном движении точки. Выражение для перемещения ΔX через скорость Vx. Выражение для ΔVx через ускорение .
Механика – часть науки о природе. Одним из разделов механики является кинематика. Кинематика – это раздел механики, посвященный изучению геометрических свойств движений без учета их масс и действующих на них сил. Основная задача механики – определить положение тела в любой момент времени. Время – непрерывно и неоднородно меняющаяся переменная. Положение тела – положение тела относительно других тел. Тело, размерами которого можно пренебречь в условиях данной задачи, называется материальной точкой. Совокупность тел, выделенная для рассмотрения, называется механической системой. Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов образуют систему отсчета. Для того чтобы получить возможность описывать движение количественно, приходится связывать с телами, образующими систему отсчета, какую-либо систему координат, например, декартову.
Положение тела – положение тела относительно других тел. Тело, размерами которого можно пренебречь в условиях данной задачи, называется материальной точкой. Совокупность тел, выделенная для рассмотрения, называется механической системой. Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов образуют систему отсчета. Для того чтобы получить возможность описывать движение количественно, приходится связывать с телами, образующими систему отсчета, какую-либо систему координат, например, декартову.
Абсолютно твердое тело – тело, деформациями которого в условиях данной задачи можно пренебречь.
Движение твердого тела:
1) поступательное –это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе.
2) вращательное – это такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Ось вращения может находиться вне тела.
Ось вращения может находиться вне тела.
Одномерным называется движение тела, при котором его положение в пространстве может быть полностью охарактеризовано при помощи одной координаты (например, положение поезда можно задать, указав расстояние вдоль железнодорожного полотна до станции отправления). Прямолинейное движение является важнейшим частным случаем одномерного. При движении тела его координата изменяется во времени, на языке математики это означает, что координата является функцией аргумента t.
Эту функцию можно задать при помощи таблицы, графика, аналитического выражения.
Для одномерного равноускоренного движения (скорость и ускорение):
ΔVx= Δt
Вопрос 2. Средняя скорость и среднее ускорение при прямолинейном движении частицы. Путь в случае изменения направления движения.
Средней скоростью называют отношение Δ к Δt.
= Δ / Δt
Δ — перемещение тела
сонаправлена с Δ .
Среднее ускорение — физическая величина, численно равная отношению изменения скорости ко времени, за которое оно произошло:
Криволинейное равноускоренное (равнопеременное) движение также можно рассматривать как одномерное. В этом случае используется обобщенная координата S, часто называемая путем. Эта координата соответствует длине пройденной траектории (длине дуги кривой). Таким образом, формула приобретает вид:
Вопрос 3. Равнопеременное прямолинейное движение. Выражения для ΔVx и Δx для равноускоренного движения.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
ΔVx= Δt
Вопрос 4*. Равнопеременное прямолинейное движение ( = const). Выражения для Vx(t) и x(t). Графики этих функций при различных знаках vx(t) и . Графический смысл перемещения Δx и ускорения на графике vx(t).
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.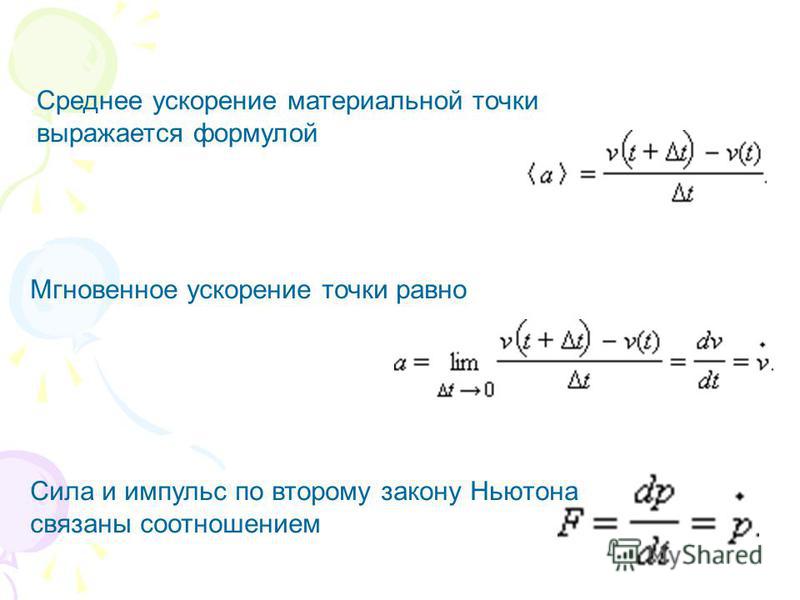
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Формула скорости равнопеременного движения в любой момент времени:
= + t
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени).
Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия.
График зависимости скорости от времени показывает, что
При этом перемещение численно равно площади фигуры 0abc.
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
Основания трапеции 0abc численно равны:
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
Дата добавления: 2018-04-15 ; просмотров: 734 ; ЗАКАЗАТЬ РАБОТУ
История открытия
Учёные Древней Греции разделяли любое движение на два типа: естественное и принудительное. Перемещение тела под воздействием гравитации считалось естественным, так как не имело видимой причины и происходило само собой.
Аристотель считал, что скорость падения напрямую зависит от массы. Это ошибочное утверждение родилось в результате примитивных наблюдений. Философ приводил в пример движение к земле яблок и листьев. Очевидно, что последние летели гораздо медленнее. Исследователи тех времён ещё очень мало понимали в физике. Такие понятия, как сопротивление воздуха и ускорение были неизвестны.
Такие понятия, как сопротивление воздуха и ускорение были неизвестны.
Утверждения Аристотеля считались неоспоримым постулатом вплоть до начала XVII века. Галилео Галлилей решительно отверг древнюю классификацию движения. В результате проведения нескольких опытов с движением тела по наклонной плоскости, учёный ввёл понятие ускорения.
Определение ускорения свободного падения в физике
Основное внимание Галлилей уделял изучению процесса свободного падения. Самым знаменитым стал эксперимент, проведённый на Пизанской башне.
С сооружения высотой 60-м были одновременно сброшены два предмета:
- маленький металлический шарик весом в пол фунта;
- большая круглая бомба, весившая 100 фунтов.
Результат был просто ошеломляющим. Оба тела достигли земли практически одновременно, а небольшая разница была объяснена силой сопротивления воздушной среды. Надо заметить, что наука тех лет существенно отличалась от сегодняшней. Считалось, что воздух не мешает падению, а, напротив, увеличивает его скорость.
Считалось, что воздух не мешает падению, а, напротив, увеличивает его скорость.
Ещё одним заблуждением того времени было утверждение о том, что любое движение со временем прекращается, даже если на его пути нет преград. Галлилей опроверг и этот ошибочный закон физики, введя определение инерции.
В XVI веке ещё не существовало точных хронометров. Из-за этого ускорение падения тел с Пизанской башни было рассчитано довольно грубо. Для более точного измерения учёный изучал равноускоренное движение шарика по наклонной плоскости. А более или менее правильное значение ускорения сумел вычислить Гюйгенс в 1660 г.
Физическая сущность
Свободным падением может называться равноускоренное движение тела в результате действующей на него силы тяжести, происходящее в вакууме. Атмосфера Земли способна тормозить ускорение и замедлять падающие предметы. Однако, если величина сопротивления воздуха небольшая, ей можно пренебречь. 2. Из-за воздействия центробежных сил на экваторе его значение немного меньше, а на полюсах, соответственно, больше.
2. Из-за воздействия центробежных сил на экваторе его значение немного меньше, а на полюсах, соответственно, больше.
Величина ускорения свободного падения зависит от нескольких факторов:
- географических координат, точнее, широты;
- расстояния до поверхности планеты;
- времени суток;
- геомагнитных аномалий.
Вектор свободного падения всегда направлен вниз. Это можно наглядно увидеть, подбросив какой-либо предмет. Благодаря воздействию ускорения, его движение будет постепенно замедляться. Затем оно полностью остановится и направится в обратную сторону.
Формулы для расчёта
Галилей понимал, что исследование падения тел с Пизанской башни является несовершенным. Был поставлен новый эксперимент, в котором учёному удалось увеличить время движения и уменьшить сопротивление воздуха. Отполированные латунные шарики скатывались по желобам, расположенным под определённым углом наклона. 2), где:
2), где:
- G — гравитационная постоянная;
- M — масса планеты;
- R — радиус планеты.
При помощи этой зависимости можно рассчитать значение g на поверхности любой планеты во вселенной.
Существуют задачи, для решения которых необходим более точный расчёт. В таком случае используется другая, расширенная формула: g=G (M/(R2+h)), где h — это высота над поверхностью планеты.
Стоит помнить, что для максимальной точности расчётов придётся учитывать большое количество факторов. Ускорение может измеряться при помощи специального прибора — гравиметра.
Ускорение на других планетах
Как видно из формулы, гравитационное ускорение напрямую зависит от массы и радиуса планеты. Из этого следует, что значение g на других планетах будет отличаться от земного.
Таблица показателя ускорения g для основных объектов Солнечной системы.
| Наименование | Ускорение, м/с. 11м/с. 2 11м/с. 2Воздействие перегрузок на человекаБлагодаря научно-техническому прогрессу и стремительному развитию технологий, современный человек имеет возможность пользоваться довольно быстрыми средствами передвижения. Чтобы попасть в любую точку планеты на самолёте, потребуется не более суток. Быстрая скорость передвижения неминуемо связана с таким понятием, как перегрузка. Любая перегрузка являет собой отношение двух ускорений:
За единицу измерения принято брать гравитационное ускорение на Земле — 9,80665 м/с². Таким образом, нулевую перегрузку можно ощутить на себе лишь в невесомости. Перегрузка является векторной величиной. Для людей и других живых организмов огромное значение имеет её направление. Это связано с тем, что организм приспособлен к постоянному воздействию гравитационного ускорения. Характер положительной перегрузки заключается в том, что её вектор направлен вниз — от головы к ногам. Показатель перегрузки для различных ситуаций:
Военным и спортивным лётчикам приходится постоянно испытывать большие перегрузки. Для уменьшения вредного воздействия на организм существуют специальные защитные костюмы.
Что такое ускорение? Виды ускорения. Формулы. Пример решения задачи :: SYL.ruРаздел физики, ответственный за изучение особенностей движения в пространстве тел, называется кинематикой. В данной статье рассмотрим, какие физические величины в кинематике используются для описания перемещений объектов, а также раскроем, что такое ускорение. Физические величины в кинематикеКогда тело движется в пространстве, то нам важно знать, какое расстояние оно проходит за указанный промежуток времени и вдоль какой траектории движется. Для описания пройденных расстояний в физике используют понятие пути – L. Помимо пути важно знать также скорость движения тел. Под ней понимают быстроту прохождения расстояний. Математическое выражение для линейной скорости принимает вид:
Для описания движения по окружности применяют угловую скорость ω, которая рассчитывается так:
Третьей важной величиной кинематики является ускорение. Что такое ускорение? Это величина в физике, которая показывает, как быстро меняется скорость во времени. Математически это можно записать так:
Если подставить в эту формулу ускорения выражение для скорости, получим:
Ускорение – это первая производная скорости по времени или вторая производная по времени пройденного пути. Тангенциальное и нормальное ускорениеВыше было дано определение, что такое ускорение. Оно называется полным. В общем случае направление полного ускорения не совпадает с направлением вектора скорости. Последний является касательной к траектории движения в любой ее точке. Поскольку скорость – это величина векторная, то ее изменение предполагает возможность менять модуль и направление. В первом случае говорят о наличии у тела тангенциального ускорения, во втором – нормального. Формула тангенциального ускорения at не отличается от таковой для ускорения полного a. Формула имеет вид:
То есть тангенциальное, или касательное, как его еще называют, ускорение является производной от модуля скорости по времени. Вектор at¯ совпадает с вектором v¯ при ускоренном движении и противоположен ему при замедленном движении. Нормальное ускорение – это физическая величина, которая приводит к искривлению прямолинейной траектории перемещения тел.
Нормальное ускорение ac зависит от модуля скорости v и радиуса кривизны траектории r. Очевидно, что в случае движения по прямой радиус r можно считать равным бесконечности. Последнее означает, что нормальное ускорение равно нулю для прямолинейного движения. Для движения по окружности вектор ac¯ направлен к ее центру вдоль радиуса. По этой причине величину ac также называют центростремительным ускорением. Полное ускорениеВектор полного ускорения – это всегда сумма тангенциальной и нормальной компонент. Поскольку они перпендикулярны друг другу, то для вычисления модуля полного ускорения можно воспользоваться теоремой Пифагора. Искомая формула ускорения полного примет вид:
Чтобы определить, куда направлен вектор a¯, достаточно вычислить угол между ним и какой-либо компонентой.
Напомним, что центростремительное ускорение отлично от нуля только тогда, когда кривизна траектории движения отлична от бесконечности. В случае же прямолинейного движения полное ускорение по величине и направлению равно тангенциальной компоненте. Угловое ускорениеРассматривая, что такое ускорение, следует остановиться на соответствующей угловой характеристике. Выше было введено понятие угловой скорости, которая измеряется в радианах в секунду (рад/с). Если найти производную этой скорости по времени, то мы получим величину углового ускорения:
Несложно показать, что угловая величина связана с тангенциальной компонентой полного ускорения следующим соотношением:
При постоянном угловом ускорении касательная компонента at будет больше для точек, которые находятся дальше от оси вращения. К нормальной компоненте угловое ускорение не имеет никакого отношения. Решение задачи на определение ускоренияПредположим, что, двигаясь с ускорением постоянным вдоль прямой линии, тело прошло расстояние 100 метров. Известно, что начальная скорость тела была равна 1 м/с. Отмеченное расстояние тело преодолело за 5,5 секунды. С каким ускорением происходило движение? Согласно условию задачи, речь идет о равноускоренном движении вдоль прямой траектории. Пройденный путь в этом случае может быть вычислен по формуле:
Выражаем из равенства величину a, имеем:
Все величины в правой части равенства известны из условия. Подставляем их и записываем ответ: a = 6,25 м/с2. То есть в течение каждой из 5,5 секунд скорость тела возрастает на 6,25 м/с. Найденное значение полного ускорения совпадает с тангенциальной компонентой. Объяснение урока: ускорение в зависимости от расстояния и времениВ этом пояснении мы научимся рассчитывать ускорение используя начальную скорость объекта, его перемещение и его ускорение время по формуле 𝑠=𝑢𝑡+12𝑎𝑡. Представьте себе объект, движущийся по прямой линии со скоростью 𝑢. Предположим, что этот объект постоянно ускоряется так, что через некоторое время 𝑡, он движется с новой скоростью 𝑣. Если мы выберем начальный момент времени равным 0, то мы можем нанести точки для этого объекта на графике скорость-время следующим образом. Мы видим, что со временем скорость нашего объекта увеличивается. И нам это говорят увеличение происходит с постоянной скоростью. Следовательно, объект постоянно ускоряется, а так как ускорение вообще равно изменению скорости, деленному на соответствующее изменение во времени, мы можем написать 𝑎=𝑣−𝑢𝑡. Графически ускорение равно наклону прямой линии
соединяя точки (0,𝑢) и
(𝑡,𝑣). По этому графику мы можем определить полное перемещение нашего объекта, поскольку оно Ускоряться. Это смещение равно площади под кривой. Используя данную информацию о нашем объекте, мы можем вычислить его перемещение за этот промежуток времени. Чтобы вычислить площадь под нашей кривой, мы можем разделить это площадь на прямоугольную часть и треугольную часть следующим образом. Пусть переменная 𝑠 представляет смещение, мы пишем 𝑠=+.areaarea Поскольку площадь имеет форму треугольника, она будет равна половина произведения основания треугольника на его высоту. Треугольник основание — это время 𝑡, а его высота — это скорость 𝑣−𝑢: площадь=12×𝑡×(𝑣−𝑢). Площадь, будучи прямоугольником, будет равна основанию прямоугольника (𝑡) умножить на его высоту (𝑢): площадь=𝑡×𝑢. Таким образом, 𝑠=12×𝑡×(𝑣−𝑢)+𝑡×𝑢. Напоминая, что
𝑎=𝑣−𝑢𝑡,
мы можем умножить обе части этого уравнения, чтобы получить
𝑎×𝑡=𝑣−𝑢. Следовательно, мы можем заменить 𝑣−𝑢 в нашем уравнении для смещение с 𝑎×𝑡 следующим образом: 𝑠=12×𝑡×(𝑎×𝑡)+𝑡×𝑢. Немного переставляя, получаем следующий результат. Формула: перемещение в терминах начальной скорости, прошедшего времени, и постоянное ускорениерассмотреть 𝑠=𝑢×𝑡+12×𝑎×𝑡. Этот результат представляет собой уравнение движения, описывающее смещение равномерно ускоряющийся объект с точки зрения его начальной скорости 𝑢, ускорение 𝑎 и ускорение время 𝑡. Обратите внимание, что это векторное уравнение. Это означает направления смещения, необходимо учитывать начальную скорость и ускорение. Эта формула применяется, даже если начальная скорость 𝑢 равно нулю. В этом случае график зависимости скорости от время появляется, как показано ниже, и соотношение для смещения 𝑠 упрощает до 𝑠=12×𝑎×𝑡(𝑢=0). Давайте потренируемся работать с общим уравнением движения, используя несколько
Примеры. Пример 1: Анализ графика зависимости скорости от времениГрафик показывает изменение скорости объекта во времени.
ОтветЧасть 1 По горизонтальной оси времени линия 𝑡=0 перекрывает вертикальную ось (скорость). Показано, что скорость в это время 20 м/с. Часть 2 Учитывая, как долго объект ускоряется, мы знаем, что это равно отрезок времени, в течение которого скорость объекта изменяется. На графике показано изменение скорости от 0 до 15 секунд, поэтому наш ответ состоит в том, что объект ускоряется за 15 секунд. Часть 3 В конце этих
15 секунд,
новая скорость объекта задается соответствующим
значение вертикальной оси. Часть 4 Чтобы найти ускорение объекта, мы можем вспомнить, что в общем случае 𝑎=Δ𝑣Δ𝑡, где Δ𝑣 — изменение скорости и Δ𝑡 – соответствующее изменение во времени. Для рассматриваемого объекта, Δ𝑣=50/−20/=30/мсмсм а также Δ𝑡=15.с Следовательно, ускорение 𝑎=30/15=2/.mssms Часть 5 Мы можем найти смещение объекта двумя разными способами. Во-первых, мы можем использовать алгебраический метод. Вспоминая уравнение движения 𝑠=𝑢×𝑡+12×𝑎×𝑡, где 𝑠 — перемещение объекта, 𝑢 — его начальная скорость, 𝑎 — его ускорение, а 𝑡 — время ускорения можно подставить в известные значения 𝑢, 𝑡 и 𝑎 следующим образом: 𝑠=(20/)×(15)+12×2/×(15)=300+225=525.mssmssmmm Другой способ определить это смещение — определить его графически. Смещение 𝑠 нашего объекта равно площади под
кривая на нашем графике. На этом рисунке мы разделяем область под кривой на треугольную область (𝐴) и прямоугольная область (𝐴). Общая площадь (и, следовательно, смещение нашего объекта) определяется суммой 𝐴 и 𝐴: 𝑠=𝐴+𝐴. Поскольку фигура, соответствующая 𝐴, является треугольником, его площадь равна половине основания треугольника, умноженной на его высоту. Глядя на рисунок выше, мы видим, что база – это время 15 с а высота это скорость 50/−20/мс, или 30 м/с. Следовательно, 𝐴=12×(15)×(30/)=225.smsm Поскольку 𝐴 — прямоугольник, его площадь равна основанию (также 15 с) умножить на его высоту 20 м/с: 𝐴=(15)×(20/)=300.smsm Следовательно, 𝑠=225+300=525.ммм Перемещение объекта за этот интервал времени равно 525 м. Можно рассматривать ускорение на расстоянии, на котором начальная скорость
и конечная скорость объекта известны, а также время, за которое объект
ускоряется. Теперь рассмотрим пример с использованием этого метода. Пример 2. Определение смещения объекта, ускоряющегося в направлении начальной скоростиОбъект имеет начальную скорость 12 м/с. Объект ускоряется с 2,5 м/с 2 в том же направлении его скорости для время 1,5 с. Каково перемещение тела за это время? Отвечать до одного десятичного знака. Ответ Поскольку этот объект ускоряется с постоянной скоростью, мы можем описать его движение
используя уравнения движения. В частности, мы будем использовать соотношение
𝑠=𝑢×𝑡+12×𝑎×𝑡,
где 𝑠 — перемещение объекта,
𝑢 — его начальная скорость,
𝑎 — его ускорение, а
𝑡 — время его ускорения. Обратите внимание, что перемещение,
скорость и ускорение являются векторами, указывая на то, что относительное
важно направление этих величин. Наша постановка задачи говорит нам, что в данном случае все эти векторные величины имеют одинаковое направление. Моделирование объекта в виде точки, мы можем выбрать эти векторы с положительными величинами, чтобы указать на Правильно. Обратите внимание, что относительные длины трех стрелок нельзя сравнивать, так как они обозначают разные физические величины. На диаграмме выше показано, что перемещение объекта одинаково направление как его ускорение и начальная скорость. Поскольку эти значения положительным, то перемещение также будет положительным. Зная, что 𝑢=12/мс, 𝑎=2,5/мс, и 𝑡=1,5 с, 𝑠=(12/)×(1,5)+12×2,5/×(1,5)=18+2,8125=20,8125.mssmssmmm Округляя этот результат до одного десятичного знака, находим, что смещение объект 20,8 м. Пример 3. Определение расстояния, пройденного равномерно замедляющимся автомобилем Автомобиль движется на восток и проходит точку 𝑃
это 45 м
к востоку от транспортной развязки. ОтветЭскиз автомобиля при прохождении точки 𝑃 может выглядеть как следует. В указанный момент водитель автомобиля нажимает на тормоз, давая автомобилю постоянное замедление 2,5 м/с 2 на запад, заставляя машину замедляться. После 10 секунд этого замедление, мы хотим найти общее расстояние автомобиля к востоку от пересекающиеся дороги. Поскольку замедление автомобиля постоянно во времени, мы можем описать
движения автомобиля из точки 𝑃 по уравнению
движение
𝑠=𝑢×𝑡+12×𝑎×𝑡,
где 𝑠 — смещение автомобиля от точки
𝑃, 𝑢 — его начальная скорость,
𝑎 — его ускорение, а
𝑡 — прошедшее время. Это уравнение включает векторные величины, поэтому определяет положительное направление и отрицательное направление в нашем сценарии будут полезный. Мы выбираем положительное направление на восток, т. е. любое вектор, указывающий на запад, считается отрицательным. Следовательно начальная скорость автомобиля 𝑢 положителен, а его ускорение 𝑎 отрицательный. Решение смещения автомобиля от точки 𝑃 согласно приведенному выше уравнению движения имеем 𝑠=(30/)×(10)+12×−2,5/×(10)=300+(−125)=175.mssmssmmm Здесь нужно вспомнить, что машина стартовала 45 м к востоку от с. пересекающиеся дороги. Таким образом, общее расстояние автомобиля к востоку от Перекресток десять секунд после прохождения точки 𝑃 175+45=220.mmm Теперь рассмотрим ситуацию, в которой движущийся объект ускоряется в
направление, противоположное его начальному движению, заканчивающееся конечной скоростью и
смещение также противоположно направлению начальной скорости. Пример 4: Расчет смещения объекта в направлении движения объекта Начальная скоростьОбъект имеет начальную скорость 32 м/с. Объект ускоряется с 12 м/с 2 в направлении, противоположном его скорости, за время 5,5 с. Каково чистое смещение объекта в направлении его первоначального скорость за это время? ОтветВ этом примере используются векторные величины, поэтому важно соблюдать осторожность. отслеживать положительные и отрицательные знаки. Мы можем произвольно выбрать начальная скорость объекта должна быть направлена вправо, а это означает, что его ускорение направлено влево следующим образом. На этой диаграмме мы не можем сравнивать относительную длину стрелок
потому что они соответствуют разным физическим величинам. мы знаем
однако чистое смещение объекта будет положительным, если оно
указывает вправо относительно начальной точки и отрицательный, если он указывает
Слева. Поскольку наш объект ускоряется с постоянной скоростью, мы можем использовать следующее уравнение движения для описания его движения: 𝑠=𝑢×𝑡+12×𝑎×𝑡, где 𝑠 — перемещение объекта, 𝑢 — его начальная скорость, 𝑎 — его ускорение, а 𝑡 — время, за которое объект ускоряется. Мы определили начальную скорость 𝑢 быть позитивным (+32/) мс, поэтому ускорение 𝑎 должно быть отрицательным (−12 м/с). Подставляем эти значения в наше уравнение вместе со временем 𝑡=5,5 с, получаем 𝑠=(32/)×(5,5)+12×−12/×(5,5)=176+(−181,5)=−5,5.mssmssmmm Чистое смещение объекта в направлении его начального скорость −5,5 м, сообщая нам, что стрелка чистого смещения на рисунке выше должна указывать на слева. Наконец, мы рассмотрим пример, в котором мы находим скорость объекта. Пример 5: Расчет начальной скорости в направлении ускоренияАвтомобиль, который первоначально двигался с постоянной скоростью, имеет чистое перемещение 45 м после ускорение по прямой на 1,5 м/с 2 в течение 15 секунд. Какова была начальная скорость автомобиля в направлении ускорение? ОтветПоскольку перемещение, ускорение и скорость являются векторными величинами, мы должны быть осторожны, чтобы понять относительные направления, в которых они действуют. Обратите внимание, что данный рабочий объем (45 м) и ускорение (1,5 м/с 2 ) оба положительны, что говорит нам о том, что эти векторы указывают в одном направлении. Мы хотим найти начальную скорость автомобиля относительно знака принято считать, что движение в направлении ускорения автомобиля положительный. Так как автомобиль ускоряется с постоянной скоростью в течение
временной интервал 15 с,
мы можем использовать следующее уравнение движения, чтобы описать его движение:
𝑠=𝑢×𝑡+12×𝑎×𝑡,
где 𝑠 – водоизмещение автомобиля,
𝑢 — его начальная скорость,
𝑎 — его ускорение, а
𝑡 – время ускорения. Мы можем изменить это уравнение, чтобы найти начальную скорость 𝑢. Вычитание 12×𝑎×𝑡 с обеих сторон дает 𝑠−12×𝑎×𝑡=𝑢×𝑡. Деление обеих частей уравнения на 𝑡 дает 𝑠−×𝑎×𝑡𝑡=𝑢 чтобы 𝑢=𝑠−×𝑎×𝑡𝑡. Подставляя известные значения для 𝑠 (45 м), 𝑎 (1,5 м/с 2 ), и 𝑡 (15 с), имеем 𝑢=(45)−×1,5/×(15)15=−8,25/.mmsssms Тот факт, что 𝑢 отрицательно, означает, что он действует в направлении против ускорения автомобиля. Относительно этого положительного направления тогда начальная скорость автомобиля −8,25 м/с. Ключевые моменты
5 фактов, которые вы должны знать — Lambda GeeksУскорение — это скорость изменения скорости. Поскольку скорость является векторной величиной, ускорение также является векторной величиной. В результате она требует как величины, так и направления. Итак, в этой статье мы рассмотрим, как найти величину ускорения. Мы используем формулы и соотношения для расчета величины. Мы можем представить величину в терминах единиц. Поскольку ускорение определяется как изменение скорости во времени, единицей СИ для него является 9.0219 ㎨ . На ускорение влияют различные факторы, такие как скорость, время, сила и так далее. Мы рассмотрим несколько различных методов оценки величины ускорения. Давайте читать дальше. 1. Как найти величину ускорения Из определения ускорения: Как мы все знаем, ускорение относится к скорости изменения скорости. (Здесь векторная величина выделена жирным шрифтом, а вертикальные линии обозначают величину вектора или мы можем сказать абсолютное значение вектора, которое всегда положительно.) Используя скорость и время, приведенное выше уравнение может быть использовано для определения величины ускорения. 2. Как найти величину ускорения Из второго закона Ньютона:Второй закон Ньютона гласит, что сила получается путем умножения ускорения на массу тела. Так как же определить величину ускорения? Итак, согласно второму закону Ньютона сила, действующая на тело, пропорциональна его ускорению, тогда как масса обратно пропорциональна ускорению . Переведем эти утверждения в формулу величины ускорения: и Таким образом, 3. Как найти величину ускорения Из векторных составляющих ускорения: Как найти величину ускорения Из векторных составляющих ускорения: Ускорение является векторной величиной, как мы все знаем. Чтобы получить эту величину, сложите вместе компоненты ускорения. Здесь можно использовать простое правило сложения векторов. Если задействованы две компоненты вектора, мы можем написать: В декартовой плоскости мы можем использовать координаты X и Y. Как в этом случае определить величину ускорения? В декартовой системе координат компоненты X и Y перпендикулярны друг другу. Величину ускорения можно рассчитать, возведя значения в квадрат, а затем вычислив квадратный корень из суммы. В результате получается следующее уравнение: Формула величины ускорения в трехмерном пространстве: 4. Как найти величину центростремительного ускорения: Из-за постоянного изменения направления при круговом движении скорость меняется, что приводит к ускорению. Ускорение направлено в направлении центра круга. Уравнения движения — это, по сути, уравнения, которые объясняют движение любой физической системы и демонстрируют взаимосвязь между перемещением объекта, скоростью, ускорением и временем. Когда величина ускорения постоянна, кинематическое уравнение движения в одном измерении также используется для расчета величины ускорения. Ниже приведены уравнения движения: Когда мы делаем ускорение предметом уравнения, мы получаем следующее:
Вот как мы можем найти величина ускорения. Решенные примеры Нахождение величины ускорения: Задача 1: Автомобиль трогается с места и достигает скорости 54 км/ч за 3 секунды. Найдите его ускорение? Найдите его ускорение? Решение: Автомобиль трогается с места. Таким образом, начальная скорость автомобиля VI = 0 м/с VF = 54 км/ч = (54 ✕ 1000)/3600 = 15 м/с ΔT = 3 с Таким Ускорение : A = (VF – VI) / ΔT = (15 – 0) / 3 = Задача 2: Определить удручение применяется к объекту массой 3 кг, а затем к объекту массой 6 кг.Решение: Применяемая сила F = 12 N Массы объекта M1 = 3 кг M2 = 6 кг Ускорение объекта с массой 3 кг a1 = F / M1 = 12 = 12 кг a1 = F / M1 = 12 = 12 = 12. / 3 = Ускорение объекта с массой 6 кг A2 = F / M2 = 12/6 = Потому что масса и аккурация. Задача 3: Тело движется вдоль оси x согласно соотношению , где x выражено в метрах, а t – в секундах. Найдите ускорение тела в момент времени t = 3 с.Solution: Here : t = 3s Velocity v = dX/dt = d/dt () = -2 + 6t Acceleration : a = dv/dt = d/dt (-2 + 6t) = Как мы видим, для этого движения ускорение не зависит от времени; ускорение будет постоянным на протяжении всего движения, а величина ускорения составит . Задача 4: Вычислите центростремительное ускорение точки на расстоянии 7,50 см от оси ультрацентрифуги, вращающейся со скоростью об/мин. Решение: Здесь мы даем: Расстояние от центра R = 7,5 см = 0,0750 м Англосная скорость Сейчас = 589 м/с Таким образом, Centripetal Acceler AcceLater Acceleratore Acceleratore AcceLatorpatore AcceLatorptatore AcceLatoreTATATATTAL ACCELATTAL ACCELATTAL ACCELATTAL ACCELATTAL ACCELATTAL ACCELATTAL ACCELATTAL ACCELARETAL ACCELATTO = = В этой статье вы узнаете, что мы подразумеваем под мгновенным ускорением или проще ускорением при описании движения частицы. Мы рассмотрим определение и формулу мгновенного ускорения на примере, который демонстрирует, как использовать формулу на практике. Мы также рассмотрим другие важные вещи, которые вам следует знать, например, как представлено мгновенное ускорение на графике скорость-время . Ускорение a, которое имеет частица в момент t, равно значению, к которому среднее ускорение, рассчитанное для интервала времени Δt, включающего момент t, приближается как интервал времени Δt становится все меньше и меньше, т. Мы знаем, что среднее ускорение a за интервал времени Δt выражается как: где Δv — изменение скорости, происходящее в течение Δt. Формула для мгновенного ускорения a почти такая же, за исключением того, что нам нужно указать, что нас интересует, к чему приближается отношение Δv к Δt, когда Δt приближается к нулю. Мы можем указать это, используя обозначение предела. Итак, формула мгновенного ускорения:
Чтобы продемонстрировать, как использовать эту формулу на практике, рассмотрим простой пример. Рассмотрим частицу, скорость которой (в метрах в секунду) в момент времени t (в секундах) равна 2t 2 : v = 2t 2 Итак, в 1 с скорость равна 2 м /с, через 2 с скорость 8 м/с, через 3 с скорость 18 м/с и т. Допустим, мы хотим найти ускорение частицы в момент времени t = 3 с. Первое, что нам нужно сделать, это выбрать интервал времени Δt, который включает момент 3 с. Этот интервал времени Δt начинается в некоторый момент t 1 и заканчивается в некоторый момент t 2 так, что t 1 ≤ 3 с ≤ t 2 1 = 3 с так, чтобы t 1 было как можно ближе к 3 с, а Δt можно было уменьшить, выбрав значения t 2 , которые ближе к 3 с. t 1 = 3 с t 2 > 3 с Начнем с выбора t 2 равным 3,1 с. T 1 = 3 S T 2 = 3,1 S ΔT = T 2 – T 1 = 3,1 S – 3 с = 0,1 с . :
Let’s find the velocity v 1 at instant t 1 : v 1 = 2t 1 2 V 1 = 2 (3) 2 м/с V 1 = 18 м/с и скорость v 2 на мгновенном T 2 : V 0 2. v 2 = 2 (3,1) 2 м/с V 2 = 19,22 м/с Теперь мы можем рассчитать среднее ускорение:
|


 Кровь оттекает от мозга и при показателе более 10 g человек может потерять сознание за считаные секунды. При отрицательном значении кровь, напротив, бьёт в голову. Это переносится гораздо хуже и может привести к кровоизлиянию и смерти.
Кровь оттекает от мозга и при показателе более 10 g человек может потерять сознание за считаные секунды. При отрицательном значении кровь, напротив, бьёт в голову. Это переносится гораздо хуже и может привести к кровоизлиянию и смерти.
 В случае движения по окружности вместо пути пользуются понятием угла поворота – θ. Величину L в СИ измеряют в метрах (м), а величину θ – в радианах (рад.).
В случае движения по окружности вместо пути пользуются понятием угла поворота – θ. Величину L в СИ измеряют в метрах (м), а величину θ – в радианах (рад.).
 Направлено оно вдоль радиуса кривизны траектории, то есть нормально по отношению к ней. Формула для его определения имеет вид:
Направлено оно вдоль радиуса кривизны траектории, то есть нормально по отношению к ней. Формула для его определения имеет вид: Например, угол φ между векторами a¯ и at¯ равен:
Например, угол φ между векторами a¯ и at¯ равен:

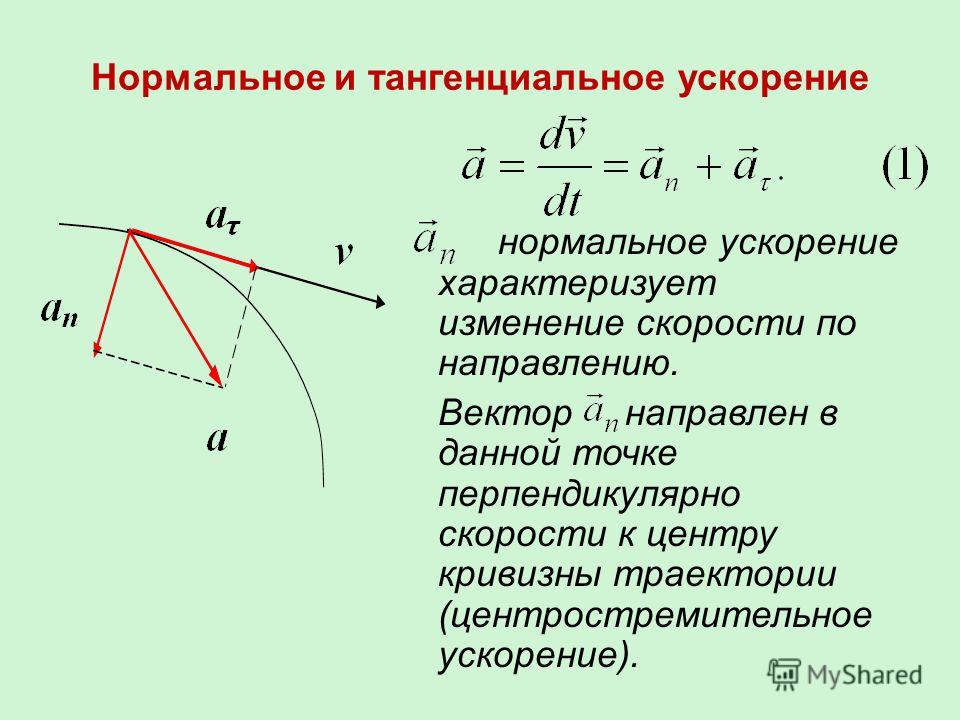


 Это значение
50 м/с.
Это значение
50 м/с.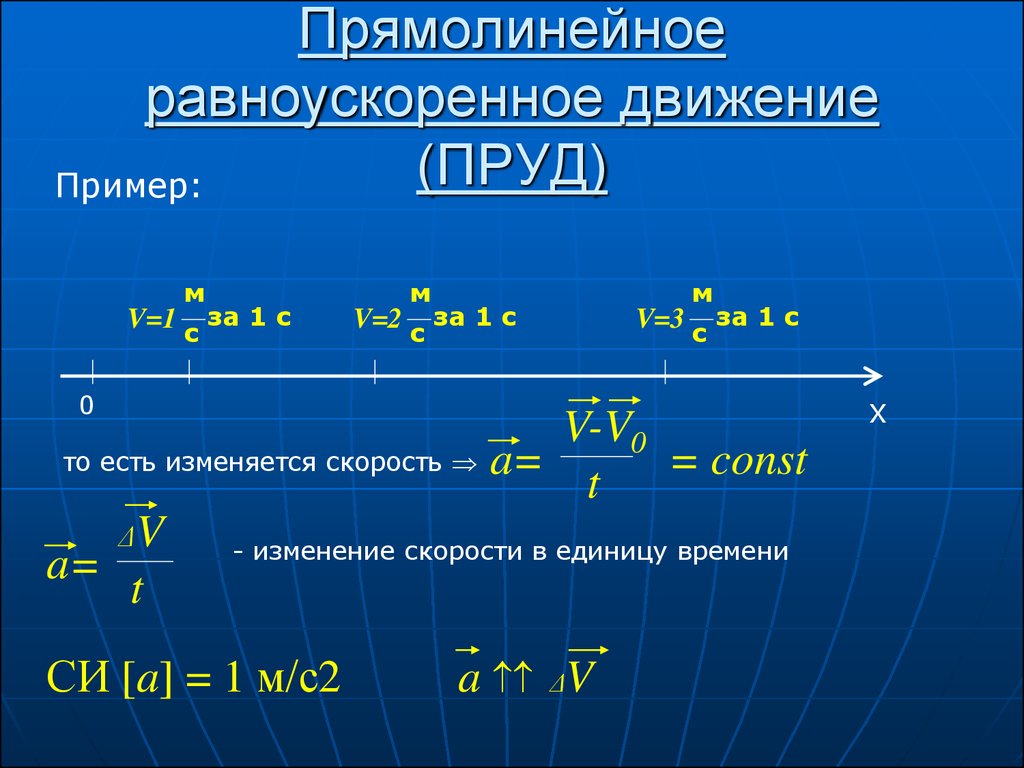


 Когда автомобиль проходит точку 𝑃,
его скорость 30 м/с
и водитель притормаживает, ускоряясь на запад в
2,5 м/с 2 . какая
расстояние к востоку от перекрестка находится автомобиль
через 10 с после срабатывания тормозов
применяемый?
Когда автомобиль проходит точку 𝑃,
его скорость 30 м/с
и водитель притормаживает, ускоряясь на запад в
2,5 м/с 2 . какая
расстояние к востоку от перекрестка находится автомобиль
через 10 с после срабатывания тормозов
применяемый?

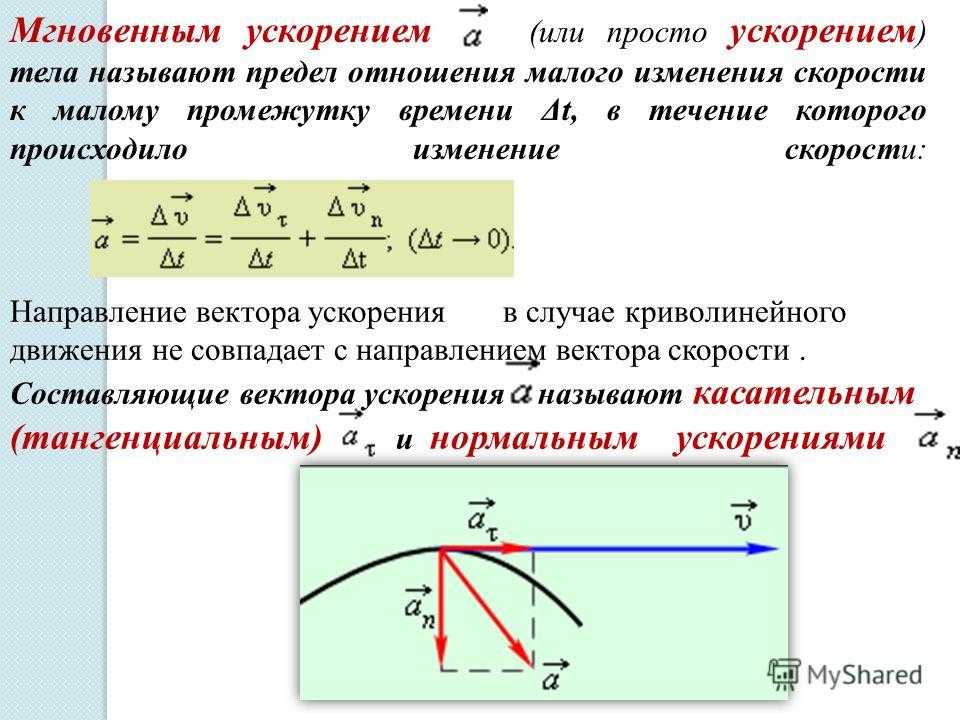



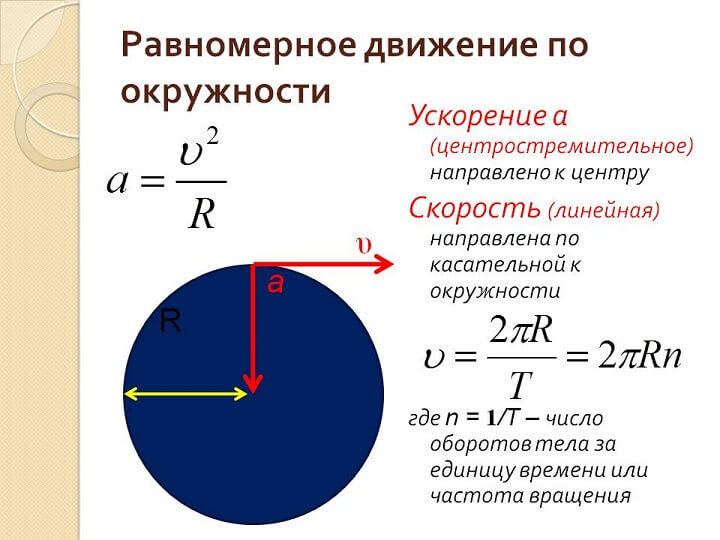 Если начальная скорость тела равна vi, а его конечная скорость равна vf, ускорение можно рассчитать, разделив изменение скорости на интервал времени Δt:
Если начальная скорость тела равна vi, а его конечная скорость равна vf, ускорение можно рассчитать, разделив изменение скорости на интервал времени Δt:  Возведение скорости тела v в квадрат и деление ее на расстояние тела от центра окружности дает величину центростремительного ускорения. Таким образом, центростремительное ускорение:
Возведение скорости тела v в квадрат и деление ее на расстояние тела от центра окружности дает величину центростремительного ускорения. Таким образом, центростремительное ускорение: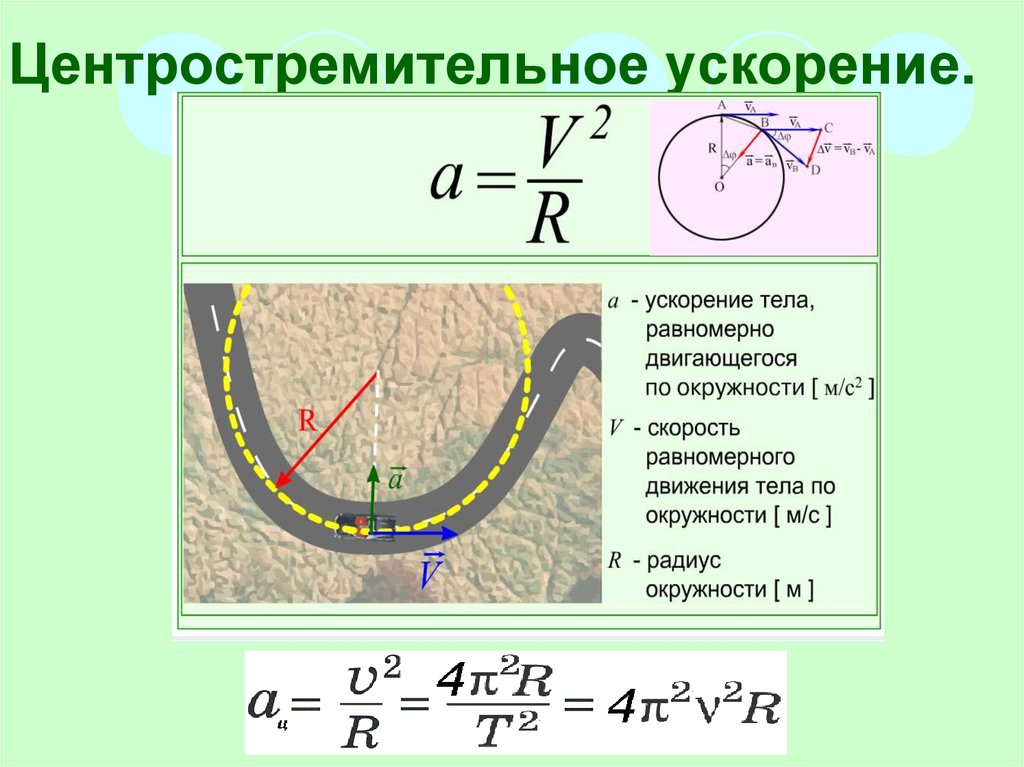 что по мере увеличения массы ускорение уменьшается.
что по мере увеличения массы ускорение уменьшается. 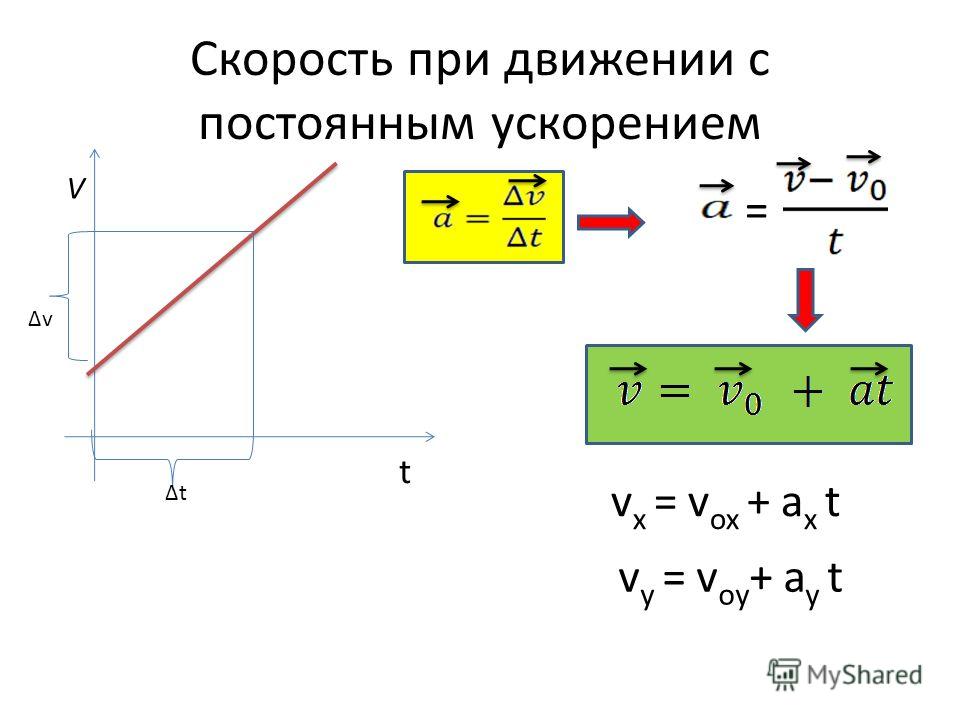 е. по мере приближения Δt к 0.
е. по мере приближения Δt к 0. д.
д. = 2t 2 2
= 2t 2 2 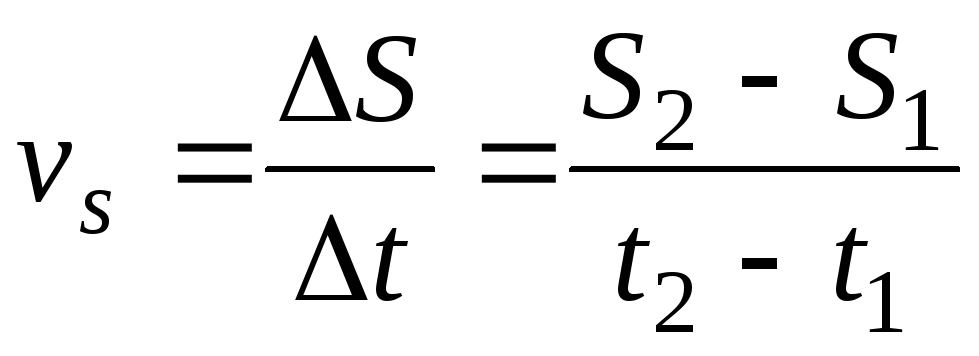
 1202 m/s
1202 m/s
 − т
− т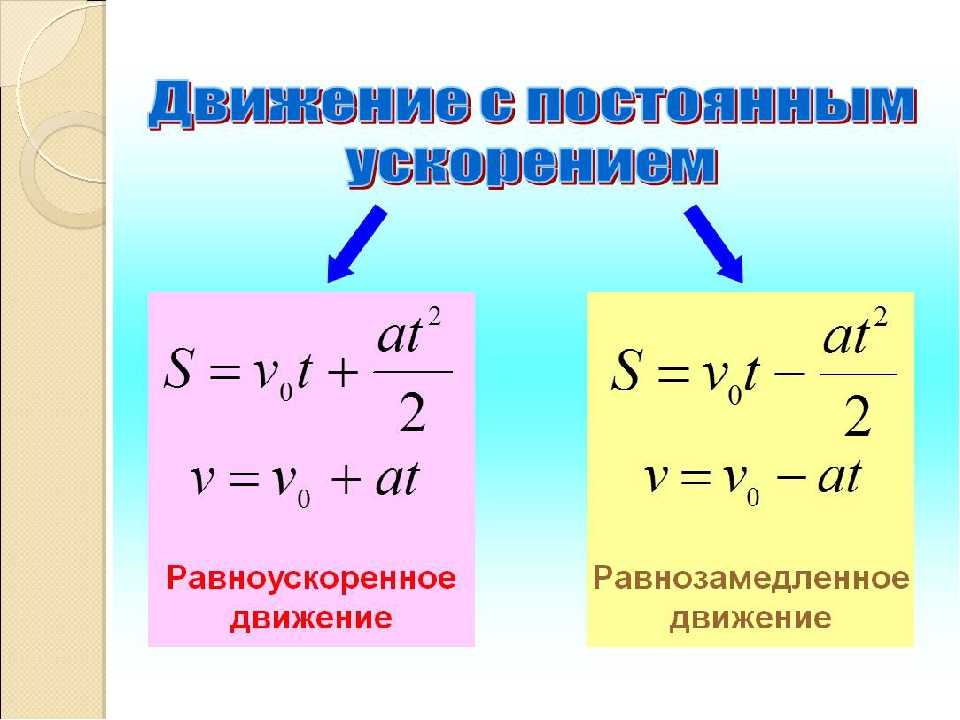 SO,
SO,
 a210864t(s)321O2)(m/s
a210864t(s)321O2)(m/s

 vtOttvθ
vtOttvθ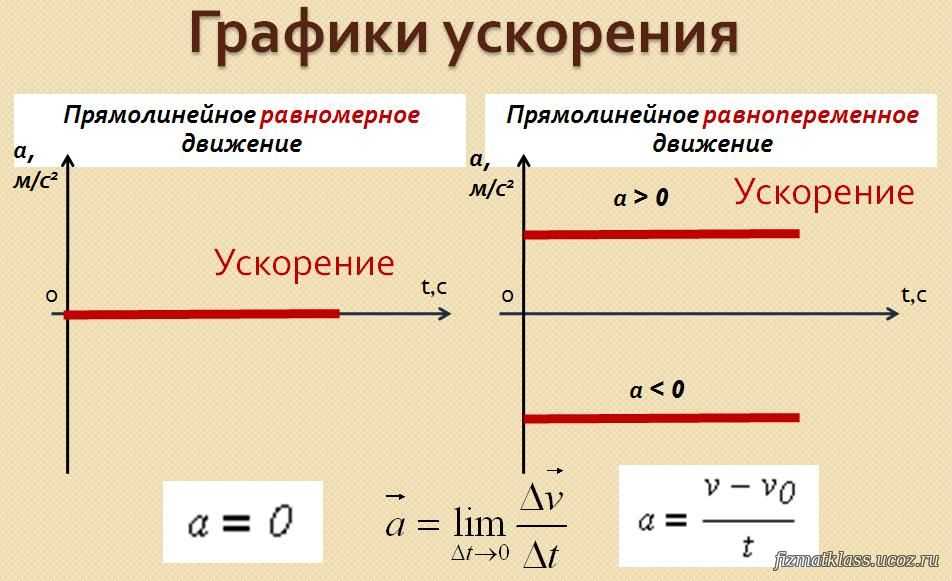
 1 Равномерное и неравномерное ускорение:
1 Равномерное и неравномерное ускорение: Мгновенное ускорение, известное как точное движение и местоположение, определяется предельным отношением изменения скорости в течение заданного интервала времени к интервалу времени, если интервал времени стремится к нулю.
Мгновенное ускорение, известное как точное движение и местоположение, определяется предельным отношением изменения скорости в течение заданного интервала времени к интервалу времени, если интервал времени стремится к нулю.

 Для данного интервала времени его можно обозначить как . математически,
Для данного интервала времени его можно обозначить как . математически, м/с 2
м/с 2  Какова была величина среднего ускорения тигровой акулы?
Какова была величина среднего ускорения тигровой акулы?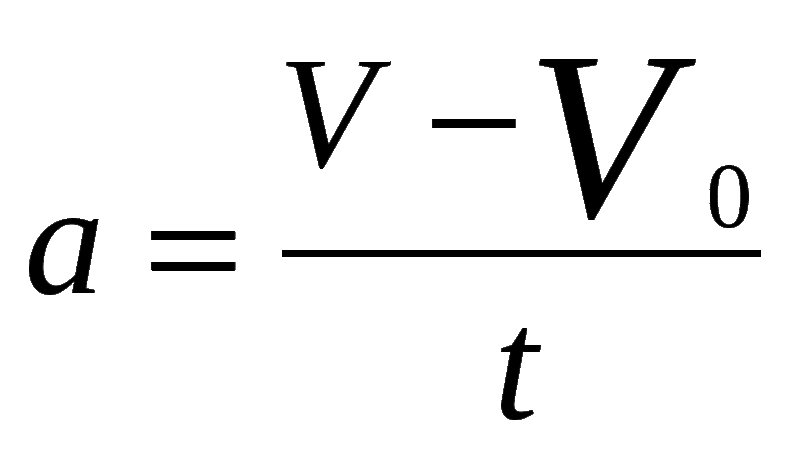 8 • Рейтинг +11k
8 • Рейтинг +11k


 точка.
точка.

 Как мы уже говорили, объект, падающий с высоты, падает практически с постоянным ускорением. Если мы пренебрежем эффектами сопротивления воздуха и почти ничтожным гравитационным притяжением других объектов, это будет совершенно постоянное ускорение. Ускорение свободного падения также не зависит от массы объекта.
Как мы уже говорили, объект, падающий с высоты, падает практически с постоянным ускорением. Если мы пренебрежем эффектами сопротивления воздуха и почти ничтожным гравитационным притяжением других объектов, это будет совершенно постоянное ускорение. Ускорение свободного падения также не зависит от массы объекта.


 Какое уравнение следует использовать?
Какое уравнение следует использовать? Какое уравнение следует использовать?
Какое уравнение следует использовать?

 Если скорость изменения скорости тела остается постоянной во времени, то говорят о постоянном ускорении.
Если скорость изменения скорости тела остается постоянной во времени, то говорят о постоянном ускорении. Каково ускорение?
Каково ускорение? Какое уравнение следует использовать?
Какое уравнение следует использовать? Кто упадет на землю раньше? (Игнорируйте влияние сопротивления воздуха.)
Кто упадет на землю раньше? (Игнорируйте влияние сопротивления воздуха.) Какие из следующих кривых отображают это на графике смещения во времени?
Какие из следующих кривых отображают это на графике смещения во времени?