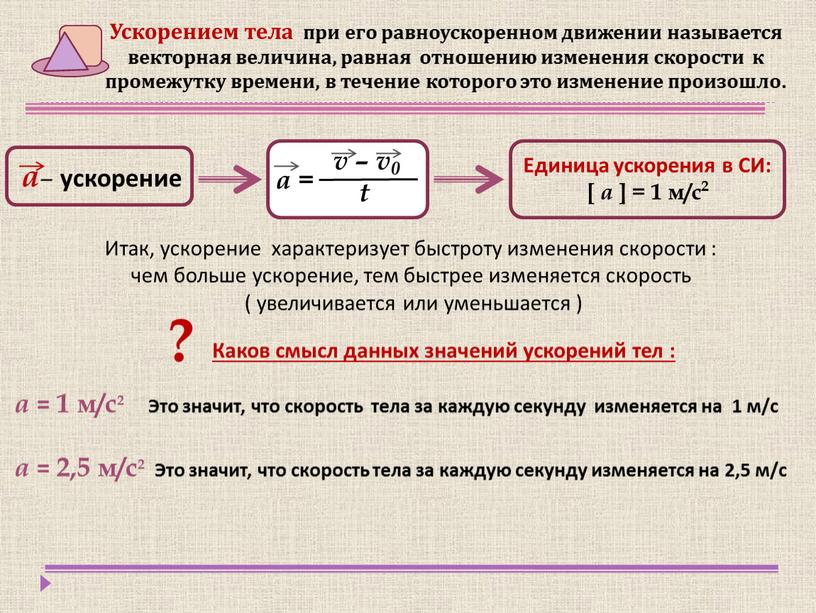
где $\bar{r}$ – радиус – вектор, который определяет положение материальной точки в пространстве.
Вектор ускорения располагается в плоскости соприкосновения, в которой находится главная нормаль и касательная к траектории, при этом он имеет направление в сторону вогнутости траектории.
Единицы измерения ускорения
Основными единицами измерения ускорения в системе СИ является: [a]=м/с2
в СГС: [a]=см/с2
Виды ускорения
Если построить соприкасающуюся плоскость, в любой точке траектории, то вектор $\bar{a}$ разложим на две взаимно перпендикулярные составляющие:
$$\bar{a}=\bar{a}_{n}+\bar{a}_{\tau}(3)$$где $\bar{a}_n$ – вектор, направленный по главной нормали к центру кривизны траектории материальной точки – это нормальное ускорение; $\bar{a}_{\tau}$ – вектор, направленный по касательной к траектории – это касательное ускорение. При этом выполняются равенства:
$$a_{n}=\frac{v^{2}}{R}(4)$$ $$a_{\tau}=\frac{d}{d t}|\bar{v}|(5)$$ $$|\bar{a}|=a=\sqrt{a_{\tau}^{2}+a_{n}^{2}}=\sqrt{\left(\frac{v^{2}}{R}\right)^{2}+\dot{v}^{2}}(6)$$где $|\bar{v}|=v$ – модуль вектора скорости, R – радиус кривизны траектории,
an – проекция вектора
$\bar{a}_n$ на направление единичного вектора главной нормали
$(\bar{n})$, aт – проекция вектора
$\bar{a}_{\tau}$ на направление единичного вектора касательной
$\left(\bar{\tau}=\frac{\bar{v}}{v}\right)$. Величина an определяет быстроту изменения направления скорости, а величина
aт – быстроту изменения модуля скорости.
Величина an определяет быстроту изменения направления скорости, а величина
aт – быстроту изменения модуля скорости.
Если $a_{\tau}=0$, то такое движение называют равномерным. При $a_{\tau}=$ const движение является равнопеременным (при $a_{\tau} < 0$ равнозамедленным, при $a_{\tau} > 0$ равноускоренным).
Средним ускорением материальной точки $\langle\bar{a}\rangle$ на отрезке времени от $t$ до $t+\Delta t$ называется векторная величина, равная отношению:
$$\langle\bar{a}\rangle(t, \Delta t)=\frac{\Delta \bar{v}}{\Delta t}=\frac{\bar{v}(t+\Delta t)-\bar{v}(t)}{\Delta t}(7)$$Формула ускорения в разных системах координат
В декартовых координатах проекции ускорения (ax,ay,az) на оси (X,Y,Z)можно представить как:
$$a_{x}=\dot{v}_{x}=\ddot{x}, \quad a_{y}=\dot{v}_{y}=\ddot{y}, a_{z}=\dot{v}_{z}=\ddot{z}(9)$$Соответственно, имеем:
$$\bar{a}=\ddot{x i}+\ddot{y} \bar{j}+\ddot{z} \bar{k}(10)$$где $\bar{i}, \bar{j}, \bar{k}$ – единичные орты по осям X,Y.
Ответ. $a=\approx 13,5$ м/с2
Слишком сложно?
Формула ускорения не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова зависимость ускорения материальной точки от времени (a(t)), если частица перемещается по оси X и ее скорость изменяется в соответствии с уравнением: $v=\alpha \sqrt{x}$, где $\alpha$ – постоянная большая нуля? В начальный момент времени (при t=0 с) материальная точка находилась в начале координат (x=0 м). Нарисуйте график a(t).
Решение. Из условий задачи можно записать, что:
Используя формулу (2.1) найдем зависимость координаты xот времени (x(t) ):
$$\int \alpha d t=\int \frac{d x}{\sqrt{x}} \rightarrow \alpha t=2 \sqrt{x}+C(2.2)$$где постоянную интегрирования найдем из начального условия задачи. Мы знаем, что x(0)=0, значит C=0. {2}}{2}$ ускорение от времени не зависит, значит, график a(t) принимает вид (рис.2).
{2}}{2}$ ускорение от времени не зависит, значит, график a(t) принимает вид (рис.2).
Читать дальше: Формула давления.
Урок 4. равномерное движение точки по окружности – Физика – 10 класс
Законы Кеплера
Орбиты небесных тел – траектории, по которым движутся в космическом пространстве Солнце, звёзды, планеты, кометы, а также искусственные космические аппараты (искусственные спутники Земли, Луны и других планет, межпланетные станции и т. п.). Формы орбит и скорости, с которыми движутся по ним небесные тела, определяются главным образом силой всемирного тяготения. При исследовании движения небесных тел в большинстве случаев допустимо считать их материальными точками.
Указанные упрощения приводят к так называемой задаче двух тел. Одно из решений этой задачи было дано И. Кеплером, полное решение задачи было получено И. Ньютоном.
Заслуга открытия законов движения планет принадлежит выдающемуся немецкому учёному
 В начале XVII в. Кеплер, изучая обращение Марса вокруг Солнца, установил три закона движения планет.
В начале XVII в. Кеплер, изучая обращение Марса вокруг Солнца, установил три закона движения планет.Первый закон Кеплера. Каждая планета обращается по эллипсу, в одном из фокусов которого находится Солнце.
Второй закон Кеплера(закон площадей). Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади.
Третий закон Кеплера. Квадраты звёздных периодов обращения планет относятся как кубы больших полуосей их орбит.
Ньютон доказал, что одна из притягивающихся материальных точек обращается вокруг другой по орбите, имеющей форму эллипса (или окружности, которая является частным случаем эллипса), параболы или гиперболы. В фокусе этой кривой находится вторая точка. Форма орбиты зависит: от масс рассматриваемых тел; от расстояния между ними; от скорости, с которой одно тело движется относительно другого.
Движение небесных тел
Чтобы начав движение вблизи поверхности Земли, тело преодолело земное притяжение и навсегда покинуло Землю по параболической орбите, необходимо сообщить ему начальную скорость не меньше 11,2 км/с. Эта скорость называется второй космической скоростью. Наименьшая начальная скорость, которую нужно сообщить телу, чтобы оно стало искусственным спутником Земли, называется первой космической скоростью. Она равна 7,91 км/с. Большинство тел Солнечной системы движется по эллиптическим орбитам. Только некоторые малые тела Солнечной системы – кометы, возможно, движутся по параболическим или гиперболическим орбитам. В задачах космического полёта наиболее часто встречаются эллиптические и гиперболические орбиты. Так, межпланетные станции отправляются в полет, имея гиперболическую орбиту относительно Земли; затем они движутся по эллиптическим орбитам относительно Солнца по направлению к планете назначения.
Эта скорость называется второй космической скоростью. Наименьшая начальная скорость, которую нужно сообщить телу, чтобы оно стало искусственным спутником Земли, называется первой космической скоростью. Она равна 7,91 км/с. Большинство тел Солнечной системы движется по эллиптическим орбитам. Только некоторые малые тела Солнечной системы – кометы, возможно, движутся по параболическим или гиперболическим орбитам. В задачах космического полёта наиболее часто встречаются эллиптические и гиперболические орбиты. Так, межпланетные станции отправляются в полет, имея гиперболическую орбиту относительно Земли; затем они движутся по эллиптическим орбитам относительно Солнца по направлению к планете назначения.
Ориентация орбиты в пространстве, её размеры и форма, а также положение небесного тела на орбите определяются шестью величинами, называемыми элементами орбиты. Орбиты небесных светил имеют некоторые характерные точки, которые получили собственные названия. Так, ближайшая к Солнцу точка орбиты небесного тела, движущегося вокруг Солнца, называется перигелием, а наиболее удалённая от него точка эллиптической орбиты – афелием.
Методы, разработанные в небесной механике, позволяют очень точно на много лет вперёд определить положение любых тел Солнечной системы.
Формулы кинематики с пояснениями по физике / Блог / Справочник :: Бингоскул
Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.
Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.
Путь, время, скорость
S=v *t
- S – путь
- v – скорость
- t – время
Равномерное движение
x=x_0 + v*t
- x – координата
- x0 – начальная координата
- v – скорость
- t – время
Равномерно ускоренное движение:
ускорениеa=\frac { v – v_0 } { t }
- a – ускорение
- v – скорость
- v0 – начальная скорость
- t – время
Равномерно ускоренное движение:
скоростьv=v_0 + at
- v – скорость
- v0 – начальная скорость
- a – ускорение
- t – время
Равномерно ускоренное движение:
путьS=vt + \frac { at^2 } { 2 }
- s – путь
- v – скорость
- t – время
- a – ускорение
Равномерно ускоренное движение:
координатаx=x_0 + vt + \frac { at^2 } { 2 }
- x – координата
- x0 – начальная координата
- v – скорость
- t – время
- a – ускорение
Высота тела, брошенного вертикально вверх (вниз)
h=h_0 + v_ { 0 } t – \frac { gt^2 } { 2 }
- h – высота
- h0 – начальная высота
- v0 – начальная скорость
- t – время
- g – ускорение свободного падения
Скорость тела, брошенного вертикально вверх (вниз)
v=v_0 – gt
- v – скорость
- v0 – начальная скорость
- g – ускорение свободного падения
- t – время
Скорость, ускорение, время
v=at
- v – скорость
- a – ускорение
- t – время
Скорость свободно падающего тела
v=gt
- v – скорость
- g – ускорение свободного падения
- t – время
Центростремительное ускорение
a=\frac { v^2 } { R }
- a – центростремительное ускорение
- v – скорость
- R – радиус
Угловая скорость
\omega=\frac { \phi } { t }
- ω – угловая скорость
- φ – угол
- t – время
Равномерное круговое движение
l=R\phi
- l – длина дуги окружности
- R – радиус
- φ – угол
Равномерное круговое движение: линейная скорость
v=R \omega
- v – линейная скорость
- R – радиус
- ω – угловая скорость
Период вращения
T=\frac { t } { N }
- T – период
- t – время
- N – число вращений
T=\frac { 2 \pi R } { v }
- T – период
- R – радиус
- v – линейная скорость
T=\frac { 2 \pi } { \omega }
- T – период
- ω – угловая скорость
Центростремительное ускорение
a=\frac { 4 \pi^ { 2 } R } { T^2 }
- a – центростремительное ускорение
- R – радиус
- T – период вращения
a=4 \pi^ { 2 } Rn^2
- a – центростремительное ускорение
- R – радиус
- n – частота вращения
Частота вращения
n=\frac { 1 } { T }
- n – частота вращения
- T – период вращения
Центростремительное ускорение
a=\omega ^ { 2 } R
- a – центростремительное ускорение
- ω – угловая скорость
- R – радиус
Дальность броска тела, брошенного под углом к горизонту
x=v_0t \cos(\alpha)
- x – координата (дальность)
- v0 – начальная скорость
- t – время
- α – угол
Высота подъема тела, брошенного под углом к горизонту
y=v_0t \sin (\alpha) – \frac { gt^2 } { 2 }
- y – координата (высота подъема )
- v0 – начальная скорость
- t – время
- g – ускорение свободного падения
- α – угол
Вертикальная скорость тела, брошенного под углом к горизонту
v_y=v_0* \sin (\alpha) – gt
- vy – вертикальная скорость
- v0 – начальная скорость
- α – угол
- g – ускорение свободного падения
- t – время
Максимальная высота подъема тела, брошенного под углом к горизонту
h_max =\frac { v_0^2* \sin (\alpha)^ { 2 } } { 2g }
- hмакс – максимальная высота
- v0 – начальная скорость
- α – угол
- g – ускорение свободного падения
Общее время движения тела, брошенного под углом к горизонту
t=\frac { 2v_0 * \sin (\alpha) } { g }
- t – время
- v0 – начальная скорость
- α – угол
- g – ускорение свободного падения
Дальность броска тела, брошенного горизонтально
x=x_0 + vt
- x – координата (дальность)
- x0 – начальная координата
- v – скорость
- t – время
Высота подъема тела, брошенного горизонтально
y=y_0 – \frac { gt^2 } { 2 }
- y – координата (высота подъема)
- y0 – начальная координата (высота)
- g – ускорение свободного падения
- t – время
Общее время движения тела, брошенного горизонтально
t_max=\sqrt { \frac { 2h } { g } }
- tмакс – максимальное время
- h – высота
- g – ускорение свободного падения
Смотри также:
Как найти ускорение и скорость,если известно только время и путь
задача по физике масса 25т путь 1200 км\ч высота 9 км найти энергию кинетическую энергию потенциальную и просто энергию
Угол силовых линий магнитного поля силой 3 Н на длине 20 см при пропускании тока 4 А по прямой в однородном магнитном поле с индукцией 7,5 Тл.
помогите пожалуйста
l1=l2=0,28 N=1 U=6 B t=2 саат 7200секунд P? A?
Знайдіть теплоту, яку виділяє спіраль електрочайника за 4 хвилини, якщо через нього тече струм 8 А Напруга – 220В. Відповідь надайте у джоулях. 25 б! … !!
даю 25 балов
помогите пожалуйста
1. Електролічильник показує 536 кВт/год. Яку величину показує лічильник? Подайте значення цієї величини в СІ.
2. Дов
… жину провідника збільшили в 2 рази, а площу поперечного перерізу зменшили в 4 рази. Як зміниться кількість теплоти, що виділятиметься при проходженні струму в провіднику? Відповідь поясніть.
3. Яку роботу виконує двигун за 6 хв роботи, якщо напруга на двигуні 12 В, а сила струму дорівнює 600 мА.
4. Резистори з опором 7 і 12 Ом з’єднані послідовно. Напруга на ділянці кола рівна 36 В. Скільки теплоти виділиться на обох резисторах за 12 с?
5. В електричному чайнику налито 1 л води. Початкова температура води 18 °С. Скільки часу необхідно зачекати, щоб закипіла вода, якщо сила струму в нагрівальному елементі 8 А, а напруга 220 В.
На рисунке изображены два тела и силы, действующие на них (2 клетки — 25 H). Для каждого случая определите модуль равнодействующей и изобразите ее.
8.Автомобіль має повну механічну енергію 15 МДж з’їхав з гори його енергія стала 3 МДж. Якою він енергією володіє? Яка енергія змінилася і як?
ПОМОГИТЕ ПРОШУ!!!!!! 50 БАЛЛОВ!!!!!!СПАМ, НЕПРАВИЛЬНЫЕ ОТВЕТЫ-БАН!!!!!!!!!!!!!!!!!!! Если угол преломления равен 30 °, под каким углом свет падал на … поверхность воды?
.Гвинтокрил має кінетичну енергію 4 МДж і потенціальну енергію 9 МДж. Чому дорівнює повна енергія? очень срочно
что это такое⚠️, в чем измеряется, как найти через скорость и время, формулы
Что такое ускорение
Ускорение \(\overrightarrow а\) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени. 2}{2S}\)
2}{2S}\)
Где \(a\) — достигнутое ускорение тела, \(S\) — пройденный путь (расстояние), \(t\) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: \(a\;=\;\frac{V-V_0}t\), где \(V_0\) и \(V\) начальная и конечная скорости соответственно, \(a\) — достигнутое ускорение тела, \(t\) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: \(a\;=-\;\frac{V-V_0}t\), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
\(\overrightarrow a=\frac{\overrightarrow F}m\)
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
\( \overrightarrow a=\lim_{t\rightarrow0}\frac{\triangle\overrightarrow V}{\triangle t}\)
Максимальное ускорение
\(a_{max}=\omega v_{max},\) где \(a_{max}\) — максимальное ускорение, \(\omega\) — круговая (угловая, циклическая) частота, \(v_{max}\) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
\(\overrightarrow{a_{ср}}=\frac{\triangle\overrightarrow V}{\triangle t}\), где \(\overrightarrow{a_{ср}}\) — среднее ускорение, \(\triangle\overrightarrow V\) — изменение скорости, \( \triangle t\) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось \(х\):
\(a_x=\frac{V_x-V_{0x}}t\), где где \(a_x\) — проекция ускорения на ось \(х\), \(V_x\) — проекция текущей скорости на ось \(х\), \(V_{0x}\) — проекция начальной скорости на ось \(х\), \(t\) или \(\triangle t\) — промежуток времени, за который произошло изменение проекции скорости.
Центрифугирование: как определить ускорение (число g) в зависимости от скорости вращения и диаметра ротора
Центрифугирование – способ разделения неоднородных, дисперсных жидких систем на фракции по плотности под действием центробежных сил. Центрифугирование осуществляют в центрифугах, принцип работы которых основан на создании центробежной силы, увеличивающей скорость разделения компонентов смеси по сравнению со скоростью их разделения только под влиянием силы тяжести. Разделение веществ с помощью центрифугирования основано на разном поведении частиц в центробежном поле. В центробежном поле частицы, имеющие разную плотность, форму или размеры, осаждаются с разной скоростью.
Скорость осаждения, или седиментации, зависит от центробежного ускорения (g), прямо пропорционального угловой скорости ротора (w, рад/с) и расстоянию между частицей и осью вращения (r, см): g = v2x r. Поскольку один оборот ротора составляет 2π радиан, то угловую скорость можно записать так: v = p x n/60, где n – скорость в оборотах в минуту, π – константа, выражающая отношение длины окружности к длине её диаметра. Угловая скорость – характеристика скорости вращения тела, измеряется обычно в радианах в секунду, полный оборот (360°) составляет 2π радиан.
Поскольку один оборот ротора составляет 2π радиан, то угловую скорость можно записать так: v = p x n/60, где n – скорость в оборотах в минуту, π – константа, выражающая отношение длины окружности к длине её диаметра. Угловая скорость – характеристика скорости вращения тела, измеряется обычно в радианах в секунду, полный оборот (360°) составляет 2π радиан.
Центробежное ускорение тогда будет равно: g =p2x r x n2/900.
Центробежное ускорение обычно выражается в единицах g (ускорение свободного падения, равное 980 м/с2) и называется относительным центробежным ускорением (ОЦУ), т. е. ОЦУ=g/980 или ОЦУ = 1,11 x 10-5 x r x n2 .
е. ОЦУ=g/980 или ОЦУ = 1,11 x 10-5 x r x n2 .
Относительное ускорение центрифуги (rcf) задается, как кратное от ускорения свободного падения (g). Оно является безразмерной величиной и служит для сравнения производительности разделения и осаждения. Относительное ускорение центрифуги (rcf) зависит от частоты вращения и радиуса центрифугирования.
Существует номограмма, выражающая зависимость относительного ускорения центрифуги (rcf) от скорости вращения ротора (n) и радиуса (r) – среднего радиуса вращения столбика жидкости в центрифужной пробирке (т.е. расстояния от оси вращения до середины столбика жидкости). Радиус измеряется (см) от оси вращения ротора до середины столбика жидкости в пробирке, когда держатель находится в положении центрифугирования.
Номограмма для определения относительного ускорения центрифуги (rcf) в зависимости от скорости вращения и диаметра ротора
r – радиус ротора, см
n – скорость вращения ротора, оборотов в минуту
rcf (relative centrifuge force) – относительное ускорение центрифуги
Радиус центрифугирования rmax– это расстояние от оси вращения ротора до дна гнезда ротора.
Для определения ускорения с помощью линейки совмещаем значения радиуса и числа оборотов на и на шкале rcf определяем его величину.
Пример: на шкале А отмечаем значение rрадиуса для ротора – 7,2 см, на шкале С отмечаем значение скорости ротора –14,000 об/мин, соединяем эти две точки. Точка пересечения образованного отрезка со шкалой В показывает значение ускорения для данного ротора. В данном случае ускорение равно 15’000.
Конвертер ускорения • Механика • Компактный калькулятор • Онлайн-конвертеры единиц измерения
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления. Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Боинг 737-7h5 N776WN Американской авиакомпании Southwest Airlines, разгоняющийся во время взлета. Аэропорт Форт-Лодердейл/Холливуд (FLL) в штате Флорида, США. 9 августа, 2010.
Общие сведения
Ускорение — это изменение скорости тела за определенный отрезок времени. В системе СИ ускорение измеряется в метрах в секунду за секунду. Также часто используются другие единицы. Ускорение может быть постоянным, например ускорение тела в свободном падении, а может изменяться, например ускорение двигающегося автомобиля.
Инженеры и дизайнеры учитывают ускорение при проектировании и изготовлении автомобилей. Водители используют знания о том как быстро ускоряет или замедляет скорость их автомобиль во время вождения. Также знания об ускорении помогают строителям и инженерам предотвратить или свести к минимуму повреждения, вызванные резким ускорением или замедлением, связанным с ударами или толчками, например, при столкновениях автомобилей или во время землетрясений.
Пирамида «Трансамерика» в Сан-Франциско, США. Это здание устойчиво к силам кручения, которые действуют на него во время сейсмических явлений.
Защита от ускорений с помощью амортизирующих и демпфирующих конструкций
Если строители учитывают возможные ускорения, здание становится более устойчиво к толчкам, что помогает спасти жизнь людей во время землетрясений. В местах с высокой сейсмичностью, например в Японии, здания строят на специальных платформах, которые уменьшают ускорение и смягчают толчки. Конструкция этих платформ похожа на подвеску в автомобилях. Упрощенная подвеска также используется в велосипедах. Ее чаще устанавливают на горных велосипедах, чтобы уменьшить неприятные ощущения, травмы, а также повреждение велосипеда из-за резких ударных ускорений при движении по неровным поверхностям. Мосты также устанавливают на подвесках, чтобы уменьшить ускорение, которое придают мосту движущиеся по нему автомобили. Ускорения, вызванные движением внутри и снаружи зданий, мешают музыкантам в музыкальных студиях. Для его уменьшения всю студию звукозаписи подвешивают на демпфирующих устройствах. Если музыкант устраивает домашнюю студию звукозаписи в помещении без достаточной звукоизоляции, то подвесить ее в уже построенном здании очень сложно и дорого. В домашних условиях устанавливают на подвески только пол. Поскольку влияние ускорения уменьшается с увеличением массы, на которую оно воздействует, вместо использования подвесок иногда утяжеляют стены, пол и потолок. Потолки тоже иногда устраивают подвесными, так как это не так сложно и дорого сделать, но помогает уменьшить проникновение в помещение внешних шумов.
Упрощенная подвеска также используется в велосипедах. Ее чаще устанавливают на горных велосипедах, чтобы уменьшить неприятные ощущения, травмы, а также повреждение велосипеда из-за резких ударных ускорений при движении по неровным поверхностям. Мосты также устанавливают на подвесках, чтобы уменьшить ускорение, которое придают мосту движущиеся по нему автомобили. Ускорения, вызванные движением внутри и снаружи зданий, мешают музыкантам в музыкальных студиях. Для его уменьшения всю студию звукозаписи подвешивают на демпфирующих устройствах. Если музыкант устраивает домашнюю студию звукозаписи в помещении без достаточной звукоизоляции, то подвесить ее в уже построенном здании очень сложно и дорого. В домашних условиях устанавливают на подвески только пол. Поскольку влияние ускорения уменьшается с увеличением массы, на которую оно воздействует, вместо использования подвесок иногда утяжеляют стены, пол и потолок. Потолки тоже иногда устраивают подвесными, так как это не так сложно и дорого сделать, но помогает уменьшить проникновение в помещение внешних шумов.
Ускорение в физике
Второй закон Ньютона
Второй закон Ньютона
Согласно второму закону Ньютона сила, действующая на тело, равна произведению массы тела и ускорения. Силу можно вычислить с помощью формулы F = ma, где F — сила, m — масса, и a — ускорение. Так сила, действующая на тело, изменяет его скорость, то есть придает ему ускорение. Согласно этому закону ускорение зависит не только от величины силы, которая толкает тело, но и пропорционально зависит от массы тела. То есть, если сила действует на два тела, А и B, и B — тяжелее, тогда B будет двигаться с меньшим ускорением. Эта склонность тел противостоять изменению в ускорении называется инерцией.
Мотоцикл, двигающийся с ускорением. Тур де Бос 2010, город Квебек (Канада).
Инерцию легко увидеть в повседневной жизни. Например, автомобилисты не носят шлем, а мотоциклисты обычно путешествуют в шлеме, и часто — в другой защитной одежде, например кожаных куртках с утолщениями. Одна из причин — при столкновении с автомобилем более легкий мотоцикл и мотоциклист быстрее изменят свою скорость, то есть начнут двигаться с большим ускорением, чем автомобиль.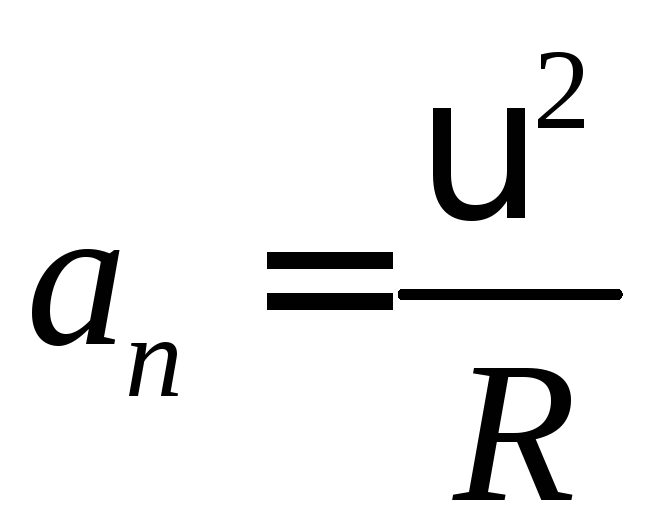 Если его не накроет мотоциклом, то мотоциклист, вероятно, вылетит из сидения мотоцикла, так как он еще легче, чем мотоцикл. В любом случае мотоциклист получит серьезные травмы, в то время как водитель — гораздо меньшие, так как автомобиль и водитель получат при столкновении намного меньшее ускорение. В этом примере не учитывается сила всемирного тяготения; предполагается, что она пренебрежимо мала по сравнению с другими силами.
Если его не накроет мотоциклом, то мотоциклист, вероятно, вылетит из сидения мотоцикла, так как он еще легче, чем мотоцикл. В любом случае мотоциклист получит серьезные травмы, в то время как водитель — гораздо меньшие, так как автомобиль и водитель получат при столкновении намного меньшее ускорение. В этом примере не учитывается сила всемирного тяготения; предполагается, что она пренебрежимо мала по сравнению с другими силами.
Ускорение и движение по кругу
Велосипедисты испытывают центростремительное ускорение на поворотах. Тур де Бос 2010, город Квебек (Канада).
У тела, которое движется по кругу со скоростью одинаковой величины — переменная векторная скорость, так как его направление постоянно изменяется. То есть, это тело движется с ускорением. Ускорение направлено в сторону оси вращения. В этом случае она в центре окружности, которая является траекторией движения тела. Это ускорение, а также вызывающая его сила, называются центростремительными. Согласно третьему закону Ньютона, у каждой силы есть противодействующая ей сила, действующая в противоположном направлении. В нашем примере эта сила называется центробежной. Именно она удерживает вагонетки на американских горках, даже когда те двигаются в перевернутом состоянии по вертикальным круговым рельсам. Центробежная сила толкает вагонетки от центра окружности, созданной рельсами, так что они прижимаются к рельсам.
В нашем примере эта сила называется центробежной. Именно она удерживает вагонетки на американских горках, даже когда те двигаются в перевернутом состоянии по вертикальным круговым рельсам. Центробежная сила толкает вагонетки от центра окружности, созданной рельсами, так что они прижимаются к рельсам.
Ускорение и сила притяжения
Гравитационное притяжение планет — одна из основных сил, которая действует на тела и придает им ускорение. Например, эта сила притягивает к поверхности Земли тела, находящиеся рядом с Землей. Благодаря этой силе тело, которое отпустили рядом с поверхностью Земли, и на которое не действуют никакие другие силы, находится в свободном падении, пока не столкнется с поверхностью Земли. Ускорение этого тела, называемое ускорением свободного падения, равно 9,80665 метров в секунду за секунду. Эта постоянная величина обозначается g и ее часто используют, чтобы определить вес тела. Так как согласно второму закону Ньютона F = ma, то вес, то есть сила, которая действует на тело — это произведение массы и ускорения свободного падения g. Массу тела легко вычислить, поэтому вес тоже легко найти. Стоит заметить, что слово «вес» в обиходе часто обозначает свойство тела, массу, а не силу.
Массу тела легко вычислить, поэтому вес тоже легко найти. Стоит заметить, что слово «вес» в обиходе часто обозначает свойство тела, массу, а не силу.
Ускорение свободного падения — разное для разных планет и астрономических объектов, так как оно зависит от их массы. Ускорение свободного падения вблизи от Солнца в 28 раз больше чем земное, вблизи Юпитера больше в 2,6 раза, а возле Нептуна — в 1,1 раза. Ускорение рядом с другими планетами меньше земного. Например, ускорение у поверхности Луны равно 0,17 ускорения у поверхности Земли.
Ускорение и транспортные средства
Тесты на ускорение для автомобилей
Существует ряд тестов для измерения характеристик автомобилей. Один из них направлен на то, чтобы проверить их ускорение. Для этого измеряют время, за которое автомобиль разгоняется с 0 до 100 километров (62 мили) в час. В странах, где не используют метрическую систему, проверяют разгон с нуля до 60 миль (97 километров) в час. Машины с самым быстрым разгоном доходят до этой скорости примерно за 2,3 секунды, что меньше, чем время, за которое тело достигнет такой скорости в свободном падении. Существуют даже программы для мобильных телефонов, которые помогают вычислить это время разгона, используя встроенные акселерометры телефона. Впрочем, трудно сказать насколько точны такие вычисления.
Существуют даже программы для мобильных телефонов, которые помогают вычислить это время разгона, используя встроенные акселерометры телефона. Впрочем, трудно сказать насколько точны такие вычисления.
Влияние ускорения на людей
Ускорение
При движении автомобиля с ускорением пассажиров тянет в сторону, противоположную движению и ускорению. То есть, назад — при ускорении, и вперед — при торможении. При резких остановках, например во время столкновения, пассажиров так резко дергает вперед, что они могут вылететь из сидений и удариться об обшивку автомобиля или окна. Вероятно даже, что они разобьют своим весом стекло и вылетят из машины. Именно из-за этой опасности во многих странах были приняты законы о том, чтобы во всех новых автомобилях должны быть установлены ремни безопасности. Во многих странах также было законодательно закреплено требование о том, что водитель, все дети, и, по крайней мере, пассажир на переднем сидении обязаны пристегиваться ремнями безопасности во время движения.
Космические аппараты во время выхода на орбиту Земли двигаются с большим ускорением. Возвращение на Землю, наоборот, сопровождается резким замедлением. Это не только вызывает у космонавтов дискомфорт, но и опасно, поэтому они проходят интенсивный курс тренировок перед тем, как отправляться в космос. Такие тренировки помогают космонавтам легче переносить перегрузки связанные с высоким ускорением. Пилоты скоростных самолетов также проходят эту тренировку, так как эти самолеты достигают высокого ускорения. Без тренировки резкое ускорение вызывает отток крови от мозга и потерю цветного зрения, потом — бокового, затем — зрения вообще, а дальше — потерю сознания. Это опасно, так как пилоты и космонавты не могут в таком состоянии управлять самолетом или космическим аппаратом. Пока тренировки на перегрузки не стали обязательным требованием в подготовке пилотов и космонавтов, перегрузки с высоким ускорением иногда заканчивались авариями и смертью пилотов. Тренировки помогают предотвратить потерю сознания и позволяют пилотам и космонавтам переносить большое ускорение в течение более продолжительного времени.
Внутри кабины космического аппарата «Аполлон» CM-011A на борту авианосца «Хорнет» (USS Hornet CV-12)
Кроме тренировок в центрифуге, описанных ниже, космонавтов и пилотов обучают специальному приему сокращения мышц живота. При этом кровеносные сосуды сужаются и меньше крови попадает в нижнюю часть тела. Предотвратить отток крови из мозга во время ускорения помогают также противоперегрузочные костюмы, так как встроенные в них специальные подушки наполнены воздухом или водой и давят на живот и ноги. Эти приемы предотвращают отток крови механически, в то время как тренировки в центрифуге помогают человеку повысить выносливость и привыкание к высокому ускорению. Сама центрифуга представляет собой горизонтальную трубу с кабиной на одном конце трубы. Она вращается в горизонтальной плоскости и создает условия с большим ускорением. Кабина снабжена карданным подвесом и может вращаться в разных направлениях, обеспечивая дополнительную нагрузку. Во время тренировок на космонавтах или пилотах надеты датчики и врачи следят за их показателями, например за пульсом. Это необходимо для обеспечения безопасности, а также помогает следить за адаптацией людей. В центрифуге можно имитировать как ускорение в нормальных условиях, так и баллистическое вхождение в атмосферу при авариях. Космонавты, которые проходят подготовку на центрифуге, говорят, что испытывают при этом сильный дискомфорт в груди и в горле.
Это необходимо для обеспечения безопасности, а также помогает следить за адаптацией людей. В центрифуге можно имитировать как ускорение в нормальных условиях, так и баллистическое вхождение в атмосферу при авариях. Космонавты, которые проходят подготовку на центрифуге, говорят, что испытывают при этом сильный дискомфорт в груди и в горле.
Литература
Автор статьи: Kateryna Yuri
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
В поисках ускорения
Как было показано ранее в Уроке 3 (а также в Уроке 2), результирующая сила – это векторная сумма всех индивидуальных сил. В Уроке 2 мы узнали, как определить чистую силу, если известны величины всех отдельных сил. В этом уроке мы узнаем, как определить ускорение объекта, если известны величины всех индивидуальных сил. Три основных уравнения, которые будут полезны: уравнение для чистой силы (F net = m • a), уравнение для гравитационной силы (F grav = m • g) и уравнение для силы трения (F frict = μ • F norm ).
Процесс определения ускорения объекта требует, чтобы известны масса и чистая сила. Если масса (м) и полезная сила (F net ) известны, то ускорение определяется с помощью уравнения.
a = F нетто / м Ваша очередь практиковатьсяТаким образом, задача включает использование приведенных выше уравнений, данной информации и вашего понимания законов Ньютона для определения ускорения.Чтобы понять, как применяется этот метод, попробуйте выполнить следующие практические задачи. Решив проблемы, нажмите кнопку, чтобы проверить свои ответы.
Практика № 1Приложенная сила 50 Н используется для ускорения объекта вправо по фрикционной поверхности. Объект встречает трение 10 Н. Используйте диаграмму, чтобы определить нормальную силу, чистую силу, массу и ускорение объекта.(Пренебрегая сопротивлением воздуха.)
Практика № 2
Приложенная сила 20 Н используется для ускорения объекта вправо по фрикционной поверхности. Объект встречает трение 10 Н. Используйте диаграмму, чтобы определить нормальную силу, чистую силу, коэффициент трения (μ) между объектом и поверхностью, массу и ускорение объекта.(Пренебрегая сопротивлением воздуха.)
Объект встречает трение 10 Н. Используйте диаграмму, чтобы определить нормальную силу, чистую силу, коэффициент трения (μ) между объектом и поверхностью, массу и ускорение объекта.(Пренебрегая сопротивлением воздуха.)
Практика № 3
Объект весом 5 кг скользит вправо и сталкивается с силой трения, которая его замедляет. Коэффициент трения (μ) между объектом и поверхностью составляет 0,1. Определите силу тяжести, нормальную силу, силу трения, чистую силу и ускорение.(Пренебрегая сопротивлением воздуха.)
Еще пара практических задач представлена ниже. Вы должны постараться решить как можно больше проблем без помощи заметок, решений, учителей и других учеников. Примите решение индивидуально решать проблемы. А пока стоит упомянуть важное предостережение:
Не допускайте, чтобы код заставил проблему в форме ранее решенной проблемы.Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom.Проблемы в физике редко выглядят одинаково. Вместо того, чтобы решать проблемы наизусть или путем имитации ранее решенной проблемы, используйте свое концептуальное понимание законов Ньютона для поиска решений проблем. Используйте свои знания о весе и массе, чтобы найти m или Fgrav в проблеме. Используйте свое концептуальное понимание чистой силы (векторная сумма всех сил ), чтобы найти значение Fnet или значение отдельной силы.Не отделяйте решение физических задач от вашего понимания концепций физики. Если вы не можете решать физические задачи, подобные приведенным выше, это не обязательно означает, что у вас есть математические трудности. Вполне вероятно, что у вас проблемы с физическими концепциями.
 Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащемуся исследовать влияние изменений прилагаемой силы, чистой силы, массы и трения на ускорение объекта. Проверьте свое понимание
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащемуся исследовать влияние изменений прилагаемой силы, чистой силы, массы и трения на ускорение объекта. Проверьте свое понимание 1. Эдвардо применяет силу в 4,25 Н, направленную вправо, к 0.Книга массой 765 кг для ускорения движения по столешнице. Коэффициент трения между книгой и столешницей 0,410. Определите ускорение книги.
2. В физической лаборатории Кейт и Роб используют подвесную массу и систему шкивов для приложения силы 2,45 Н, направленной вправо, на тележку массой 0,500 кг, чтобы разогнать ее по гусенице с низким коэффициентом трения. Если общая сила сопротивления движению тележки равна 0.72 Н, тогда какое ускорение тележки?
3,3 Среднее и мгновенное ускорение
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте среднее ускорение между двумя точками времени.

- Рассчитайте мгновенное ускорение с учетом функциональной формы скорости.
- Объясните векторную природу мгновенного ускорения и скорости.
- Объясните разницу между средним ускорением и мгновенным ускорением.
- Найдите мгновенное ускорение в заданное время на графике зависимости скорости от времени.
Важность понимания ускорения распространяется на наш повседневный опыт, а также на огромные просторы космического пространства и крошечный мир субатомной физики. В повседневном разговоре разогнать означает разогнаться; нажатие педали тормоза приводит к замедлению движения автомобиля.Мы, например, знакомы с ускорением нашей машины. Чем больше ускорение, тем больше изменение скорости за заданный промежуток времени. Ускорение широко наблюдается в экспериментальной физике. Например, в экспериментах с линейным ускорителем частиц субатомные частицы ускоряются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной. В космосе космические лучи – это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывающихся массивных звездах) и активных ядрах галактик.Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат очень проникающее излучение, которое может, например, повредить электронику, установленную на космических кораблях.
В космосе космические лучи – это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывающихся массивных звездах) и активных ядрах галактик.Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат очень проникающее излучение, которое может, например, повредить электронику, установленную на космических кораблях.
Среднее ускорение
Формальное определение ускорения согласуется с этими только что описанными понятиями, но является более всеобъемлющим.
Среднее ускорение
Среднее ускорение – скорость изменения скорости:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {{v} _ {\ text {f}} – {v} _ {0}} {{t} _ {\ text {f}} – {t} _ {0}}, [/ latex]
, где [latex] \ overset {\ text {-}} {a} [/ latex] – среднее ускорение, v – скорость, а t – время.(Полоса над и означает среднее ускорение ).
Поскольку ускорение – это скорость в метрах, разделенная на время в секундах, единицы измерения ускорения в системе СИ часто обозначают сокращенно м / с 2 , то есть метры в секунду в квадрате или метры в секунду в секунду. Это буквально означает, на сколько метров в секунду изменяется скорость каждую секунду. Напомним, что скорость – это вектор, он имеет как величину, так и направление, что означает, что изменение скорости может быть изменением величины (или скорости), но также может быть изменением направления.Например, если бегун, движущийся со скоростью 10 км / ч на восток, замедляется до остановки, меняет направление, продолжает свой бег со скоростью 10 км / ч на запад, его скорость изменилась в результате изменения направления, хотя величина скорости одинаковы в обоих направлениях. Таким образом, ускорение происходит, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по обоим направлениям.
Ускорение как вектор
Ускорение – это вектор в том же направлении, что и изменение в скорости, [latex] \ text {Δ} v [/ latex]. Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Следовательно, ускорение – это изменение скорости или направления, или и того, и другого.
Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Следовательно, ускорение – это изменение скорости или направления, или и того, и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда в направлении движения. Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называется замедлением (рисунок), мы говорим, что поезд ускоряется в направлении, противоположном его направлению движения.
Рисунок 3.10 Поезд метро в Сан-Паулу, Бразилия, замедляется при входе на станцию. Он ускоряется в направлении, противоположном направлению его движения. (Источник: Юсуке Кавасаки)
Термин замедление может вызвать путаницу в нашем анализе, потому что он не является вектором и не указывает на конкретное направление относительно системы координат, поэтому мы не используем его. Ускорение – это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат. В случае поезда на (Рисунок) ускорение составляет в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.
В случае поезда на (Рисунок) ускорение составляет в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.
Если движущийся объект имеет скорость в положительном направлении по отношению к выбранной исходной точке и приобретает постоянное отрицательное ускорение, объект в конечном итоге останавливается и меняет направление. Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это проиллюстрировано на (Рисунок).
Рисунок 3.11 Объект, движущийся с вектором скорости на восток при отрицательном ускорении, останавливается и меняет направление на противоположное. Через достаточно долгое время он проходит исходную точку в обратном направлении.
Пример
Расчет среднего ускорения: скакун покидает ворота
Скаковая лошадь, выходящая из ворот, ускоряется из состояния покоя до 15,0 м / с на запад за 1,80 с. Какое у него среднее ускорение?
Какое у него среднее ускорение?
Рисунок 3.12 Скаковые лошади ускоряются из-за ворот. (кредит: Джон Салливан)
Стратегия
Сначала мы рисуем эскиз и назначаем систему координат задаче (рисунок). Это простая проблема, но всегда помогает ее визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Рисунок 3.13 Определите систему координат, данную информацию и то, что вы хотите определить.
Мы можем решить эту проблему, определив [latex] \ text {Δ} v \, \ text {and} \, \ text {Δ} t [/ latex] из заданной информации, а затем вычислив среднее ускорение непосредственно из уравнение [латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {{v} _ {\ text {f}} – {v} _ {0}} {{t} _ {\ text {f}} – {t} _ {0}} [/ latex].
Решение
Сначала определите известные: [latex] {v} _ {0} = 0, {v} _ {\ text {f}} = – 15. 0 \, \ text {m / s} [/ latex] (отрицательный знак указывает направление на запад), Δ t = 1.80 с.
0 \, \ text {m / s} [/ latex] (отрицательный знак указывает направление на запад), Δ t = 1.80 с.
Во-вторых, найдите изменение скорости. Поскольку лошадь движется с нуля до –15,0 м / с, ее изменение скорости равно ее конечной скорости:
[латекс] \ text {Δ} v = {v} _ {\ text {f}} – {v} _ {0} = {v} _ {\ text {f}} = – 15.0 \, \ text { РС}. [/ латекс]
Наконец, подставьте известные значения ([latex] \ text {Δ} v \, \ text {and} \, \ text {Δ} t [/ latex]) и решите для неизвестного [latex] \ overset {\ text {-}} {a} [/ latex]:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {-15.{2}. [/ латекс]
Значение
Отрицательный знак ускорения указывает на то, что ускорение направлено на запад. Ускорение 8,33 м / с 2 на западе означает, что лошадь увеличивает свою скорость на 8,33 м / с на западе каждую секунду; то есть 8,33 метра в секунду в секунду, что мы записываем как 8,33 м / с 2 .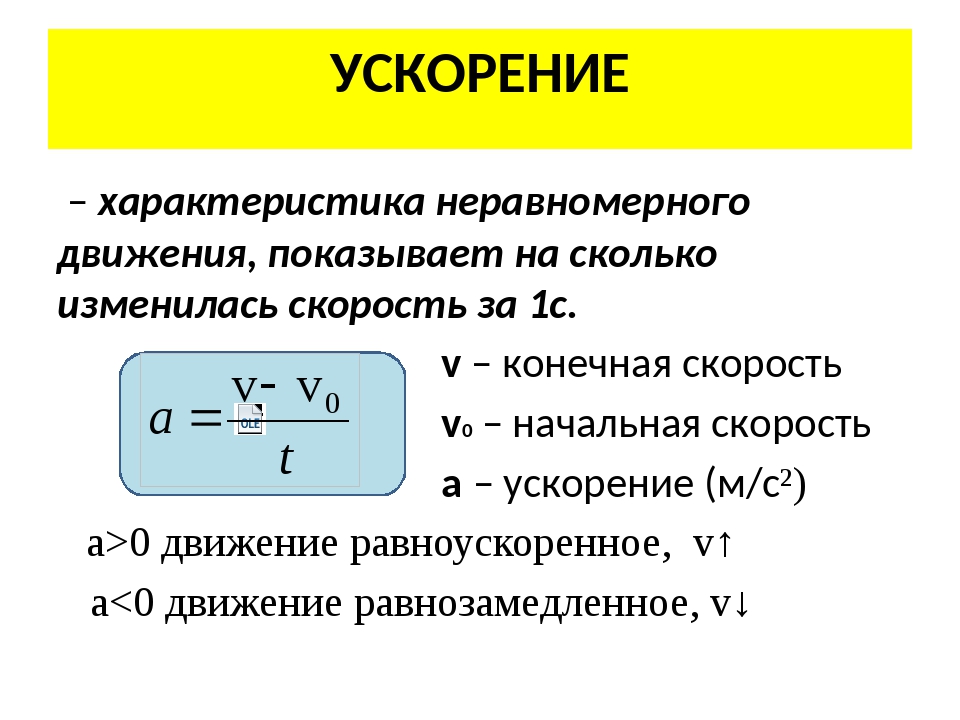 Это действительно среднее ускорение, потому что поездка не гладкая. Позже мы увидим, что ускорение такой величины потребовало бы от всадника держаться с силой, почти равной его весу.{2}. [/ латекс]
Это действительно среднее ускорение, потому что поездка не гладкая. Позже мы увидим, что ускорение такой величины потребовало бы от всадника держаться с силой, почти равной его весу.{2}. [/ латекс]
Мгновенное ускорение
Мгновенное ускорение a или ускорение в определенный момент времени получается с использованием того же процесса, что и для мгновенной скорости. То есть мы вычисляем среднюю скорость между двумя точками времени, разделенными [латексом] \ text {Δ} t [/ latex], и позволяем [latex] \ text {Δ} t [/ latex] приближаться к нулю. Результатом является производная функции скорости v ( t ), которая равна мгновенному ускорению и математически выражается как
[латекс] a (t) = \ frac {d} {dt} v (t).[/ латекс]
Таким образом, аналогично скорости, являющейся производной функции положения, мгновенное ускорение является производной функции скорости. Мы можем показать это графически так же, как мгновенную скорость. На (Рисунок) мгновенное ускорение в момент времени t 0 – это наклон касательной к графику зависимости скорости от времени в момент времени t 0 . Мы видим, что среднее ускорение [латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} [/ latex] приближается к мгновенному ускорению, как [латекс] \ text {Δ} t [/ latex] стремится к нулю.Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, поскольку наклон кривой там тоже равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
На (Рисунок) мгновенное ускорение в момент времени t 0 – это наклон касательной к графику зависимости скорости от времени в момент времени t 0 . Мы видим, что среднее ускорение [латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} [/ latex] приближается к мгновенному ускорению, как [латекс] \ text {Δ} t [/ latex] стремится к нулю.Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, поскольку наклон кривой там тоже равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
Рис. 3.14 На графике зависимости скорости от времени мгновенное ускорение представляет собой наклон касательной.(a) Показано среднее ускорение [латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {{v} _ { \ text {f}} – {v} _ {i}} {{t} _ {\ text {f}} – {t} _ {i}} [/ latex] между временами [латекс] \ text {Δ} t = {t} _ {6} – {t} _ {1}, \ text {Δ} t = {t} _ {5} – {t} _ {2} [/ латекс] и [латекс] \ текст {Δ} t = {t} _ {4} – {t} _ {3} [/ latex]. Когда [latex] \ text {Δ} t \ to 0 [/ latex], среднее ускорение приближается к мгновенному ускорению в момент времени t0. В виде (а) мгновенное ускорение показано для точки на кривой скорости при максимальной скорости.В этой точке мгновенное ускорение – это наклон касательной, равный нулю. В любое другое время наклон касательной – и, следовательно, мгновенное ускорение – не будет нулевым. (b) То же, что (a), но показано для мгновенного ускорения при минимальной скорости.
Когда [latex] \ text {Δ} t \ to 0 [/ latex], среднее ускорение приближается к мгновенному ускорению в момент времени t0. В виде (а) мгновенное ускорение показано для точки на кривой скорости при максимальной скорости.В этой точке мгновенное ускорение – это наклон касательной, равный нулю. В любое другое время наклон касательной – и, следовательно, мгновенное ускорение – не будет нулевым. (b) То же, что (a), но показано для мгновенного ускорения при минимальной скорости.
Чтобы проиллюстрировать эту концепцию, давайте рассмотрим два примера. Во-первых, простой пример показан с использованием (Рисунок) (b), графика зависимости скорости от времени (Рисунок), для графического определения ускорения. Этот график изображен на (Рисунок) (а), который представляет собой прямую линию.Соответствующий график ускорения в зависимости от времени находится по наклону скорости и показан на (Рисунок) (b). В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным.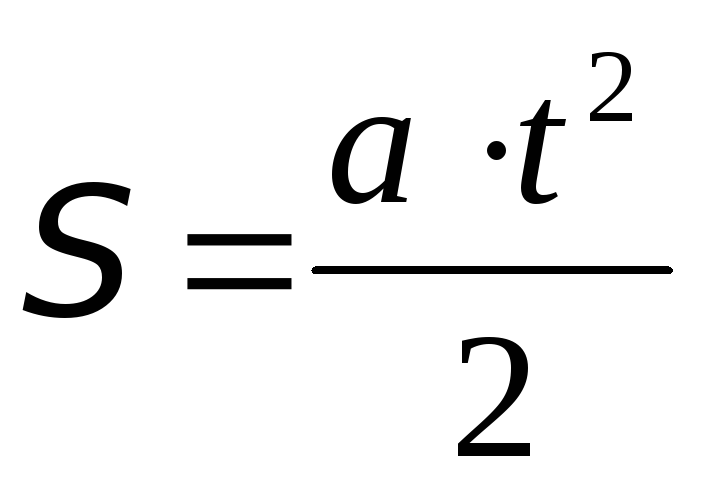 В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.
В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.
Рис. 3.15 (a, b) График зависимости скорости от времени является линейным и имеет постоянный отрицательный наклон (a), который равен ускорению, показанному на (b).
Если мы знаем функциональную форму скорости, v ( t ), мы можем вычислить мгновенное ускорение a ( t ) в любой момент времени в движении, используя (рисунок).{2} \, \ text {m / s} [/ латекс].
- Найдите функциональную форму ускорения.
- Найдите мгновенную скорость при t = 1, 2, 3 и 5 с.
- Найдите мгновенное ускорение при t = 1, 2, 3 и 5 с.
- Интерпретируйте результаты (c) в терминах направлений векторов ускорения и скорости.
Стратегия
Функциональную форму ускорения находим, взяв производную от функции скорости.{2} [/ латекс]
 Частица движется быстрее.
Частица движется быстрее.При t = 2 с, скорость увеличилась до [latex] v (2 \, \ text {s)} = 20 \, \ text {m / s} [/ latex], где она максимальна, что соответствует моменту, когда ускорение равно нулю. Мы видим, что максимальная скорость возникает, когда наклон функции скорости равен нулю, что является просто нулем функции ускорения.
При t = 3 с, скорость равна [latex] v (3 \, \ text {s)} = 15 \, \ text {m / s} [/ latex], а ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицательный. Частица замедляется.
При t = 5 с, скорость равна [latex] v (5 \, \ text {s)} = – 25 \, \ text {m / s} [/ latex], а ускорение становится все более отрицательным. Между моментами времени t = 3 с и t = 5 с частица уменьшила свою скорость до нуля, а затем стала отрицательной, таким образом изменив свое направление.Теперь частица снова ускоряется, но в противоположном направлении.
Мы можем увидеть эти результаты графически на (Рисунок).
Рис. 3.16 (а) Скорость в зависимости от времени. Касательные линии указаны в моменты времени 1, 2 и 3 с. Наклоны касательных – это ускорения. При t = 3 с скорость положительная. При t = 5 с скорость отрицательна, что указывает на то, что частица изменила направление на противоположное. (б) Ускорение против времени. Сравнивая значения ускорений, представленные черными точками, с соответствующими наклонами касательных линий (наклон линий через черные точки) на (а), мы видим, что они идентичны.
Значение
Выполняя численный и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении. Численный анализ дополняет графический анализ, давая полное представление о движении. Нуль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительное и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю и в конечном итоге становится отрицательным, скорость достигает максимума, после чего начинает уменьшаться. Если мы подождем достаточно долго, скорость также станет отрицательной, что указывает на изменение направления. Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление движения.
Если мы подождем достаточно долго, скорость также станет отрицательной, что указывает на изменение направления. Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление движения.
Проверьте свое понимание
Самолет приземляется на взлетно-посадочной полосе, летящей на восток. Опишите его ускорение.
Показать решениеЕсли принять восток за положительное значение, то самолет имеет отрицательное ускорение, потому что он ускоряется в сторону запада.Он также замедляется; его ускорение противоположно направлению его скорости.
Ощущение ускорения
Вы, вероятно, привыкли испытывать ускорение, когда заходите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит со многими другими объектами в нашей Вселенной, с которыми мы не имеем прямого контакта. (Рисунок) представлено ускорение различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.
| Разгон | Значение (м / с 2 ) |
|---|---|
| Скоростной поезд | 0,25 |
| Лифт | 2 |
| Гепард | 5 |
| Объект в свободном падении без сопротивления воздуха у поверхности Земли | 9,8 |
| Максимум космического челнока во время запуска | 29 |
| Пик парашютиста при нормальном раскрытии парашюта | 59 |
| Самолет F16 выходит из пикирования | 79 |
| Взрывной выброс сиденья с самолета | 147 |
| Ракета Спринт | 982 |
| Максимальное пиковое ускорение ракетных салазок | 1540 |
| Прыгающая блоха | 3200 |
| Бейсбольный удар битой | 30 000 |
| Смыкание губок муравья-ловушки | 1 000 000 |
| Протон в большом адронном коллайдере | [латекс] 1.{9} [/ латекс] |
В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют никакого отношения к размеру объекта или его массивности. Ускорение также может сильно меняться со временем во время движения объекта. У дрэг-рейсинга сразу после старта наблюдается большое ускорение, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения.(Рисунок) графически сравнивает среднее ускорение с мгновенным ускорением для двух очень разных движений.
Рис. 3.17 Графики мгновенного ускорения в зависимости от времени для двух различных одномерных движений. (а) Ускорение меняется незначительно и всегда в одном и том же направлении, поскольку оно положительное. Среднее значение за интервал почти такое же, как и ускорение в любой момент времени. (b) Ускорение сильно различается, возможно, представляя пакет на конвейерной ленте почтового отделения, который ускоряется вперед и назад, когда он натыкается.В такой ситуации необходимо учитывать небольшие интервалы времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.
Сводка
- Ускорение – это скорость изменения скорости. Ускорение – это вектор; он имеет как величину, так и направление. Единица измерения ускорения в системе СИ – метр на секунду в квадрате.
- Ускорение может быть вызвано изменением величины или направления скорости, либо и тем, и другим.
- Мгновенное ускорение a ( t ) является непрерывной функцией времени и дает ускорение в любой конкретный момент во время движения.Он рассчитывается по производной функции скорости. Мгновенное ускорение – это наклон графика зависимости скорости от времени.
- Отрицательное ускорение (иногда называемое замедлением) – это ускорение в отрицательном направлении в выбранной системе координат.
Концептуальные вопросы
Может ли скорость быть постоянной при ненулевом ускорении?
Показать решениеНет, в одном измерении для постоянной скорости требуется нулевое ускорение.
Может ли скорость быть постоянной, если ускорение не равно нулю? Объяснять.
Приведите пример, в котором скорость равна нулю, а ускорение – нет.
Показать решениеМяч подбрасывается в воздух, и его скорость равна нулю на вершине броска, но ускорение не равно нулю.
Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, в каком направлении он ускоряется? Ускорение положительное или отрицательное?
Знаки плюс и минус используются в одномерном движении для обозначения направления.{2} [/ латекс]
Доктор Джон Пол Стапп был офицером ВВС США, изучавшим влияние экстремального ускорения на человеческое тело. 10 декабря 1954 года Стапп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м / с (1015 км / ч) за 5,00 с и резко остановившись всего за 1,40 с. Вычислите его (а) ускорение в направлении его движения и (б) ускорение, противоположное его направлению движения. Выразите каждое значение кратным г (9,80 м / с 2 ), взяв его отношение к ускорению свободного падения.
Нарисуйте график зависимости ускорения от времени из следующего графика зависимости скорости от времени.
Покажи ответПассажир выезжает на машине из гаража с ускорением 1,40 м / с 2 . а) Сколько времени ей нужно, чтобы набрать скорость 2,00 м / с? (b) Если она затем тормозит до остановки за 0,800 с, каково ее ускорение?
Предположим, что межконтинентальная баллистическая ракета переходит из состояния покоя в суборбитальную скорость 6,50 км / с за 60,0 с (фактическая скорость и время засекречены).Каково его среднее ускорение в метрах в секунду и кратное g (9,80 м / с 2 )?
Самолет, взлетая с места, движется по взлетно-посадочной полосе с постоянным ускорением в течение 18 с, а затем взлетает со скоростью 60 м / с. Какое среднее ускорение самолета?
Глоссарий
- среднее ускорение
- скорость изменения скорости; изменение скорости с течением времени
- мгновенное ускорение
- ускорение в определенный момент времени
3.4 Движение с постоянным ускорением – Университетская физика, том 1
Задачи обучения
К концу этого раздела вы сможете:
- Определите, какие уравнения движения следует использовать для решения неизвестных.
- Используйте соответствующие уравнения движения, чтобы решить задачу о преследовании двух тел.
Вы можете догадаться, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени.Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.
Обозначение
Во-первых, сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением.Поскольку прошедшее время равно Δt = tf − t0Δt = tf − t0, принятие t0 = 0t0 = 0 означает, что Δt = tfΔt = tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x0x0 – это начальная позиция , а v0v0 – начальная скорость . Мы не ставим нижние индексы на окончательные значения. То есть t – это последнее время , x – это конечное положение , а v – это конечная скорость . Это дает более простое выражение для затраченного времени: Δt = tΔt = t.Это также упрощает выражение для смещения x , которое теперь равно Δx = x − x0Δx = x − x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv = v − v0Δv = v − v0. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
Δt = tΔx = x − x0Δv = v − v0, Δt = tΔx = x − x0Δv = v − v0,, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь мы делаем важное предположение, что ускорение постоянно .Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
a– = a = постоянная. a– = a = постоянная.Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения. Во-первых, ускорение равно постоянным в большом количестве ситуаций.Более того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
Замена упрощенных обозначений для ΔxΔx и ΔtΔt дает
v– = x − x0t.v– = x − x0t.Решение относительно x дает нам
x = x0 + v – t, x = x0 + v – t,3,10
, где средняя скорость
v– = v0 + v2.v– = v0 + v2.3,11
Уравнение v– = v0 + v2v– = v0 + v2 отражает тот факт, что при постоянном ускорении v – v– представляет собой простое среднее значение начальной и конечной скоростей. Рисунок 3.18 графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость в течение 1-часового интервала от 40 км / ч до 80 км / ч составляет 60 км / ч:
v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.В части (b) ускорение не является постоянным. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рисунок 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0andvv0andv. Средняя скорость равна 12 (v0 + v) = 60 км / ч22 (v0 + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не равна 12 (v0 + v) 12 (v0 + v), но превышает 60 км / ч.Решение для окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
Подстановка упрощенных обозначений для ΔvΔv и ΔtΔt дает
а = v − v0t (константа). a = v − v0t (константа).Решение для v дает
v = v0 + at (constanta). v = v0 + at (constanta).3,12
Пример 3,7
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70.0 м / с, а затем ускоряется против движения со скоростью 1,50 м / с 2 за 40,0 с. Какова его конечная скорость?Стратегия
Сначала мы идентифицируем известные: v0 = 70 м / с, a = -1,50 м / с2, t = 40sv0 = 70 м / с, a = -1,50 м / с2, t = 40 с.Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы рассчитываем окончательную скорость, используя уравнение 3.12, v = v0 + atv = v0 + at.
Решение
Подставьте известные значения и решите: v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с.Рисунок 3.19 представляет собой эскиз, показывающий векторы ускорения и скорости.
Рис. 3.19. Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы самолет остановился и начал движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.Помимо полезности при решении задач, уравнение v = v0 + atv = v0 + at дает нам представление о взаимосвязях между скоростью, ускорением и временем.Мы видим, например, что
- Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
- Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v 0 ), как и ожидалось (другими словами, скорость постоянна)
- Если a отрицательно, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Решение для конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с
Добавление v0v0 к каждой стороне этого уравнения и деление на 2 дает
v0 + v2 = v0 + 12at. v0 + v2 = v0 + 12at.Так как v0 + v2 = v – v0 + v2 = v– для постоянного ускорения, имеем
v– = v0 + 12at.v– = v0 + 12at.Теперь мы подставляем это выражение для v – v– в уравнение для смещения, x = x0 + v – tx = x0 + v – t, что дает
х = х0 + v0t + 12at2 (константа).х = х0 + v0t + 12at2 (константа).3,13
Пример 3.8
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м / с 2 . Предположим, драгстер ускоряется из состояния покоя с этой скоростью в течение 5,56 с. Рис. 3.20. Как далеко он пролетит за это время?Рис. 3.20. Пилот Top Fuel в армии США Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фото любезно предоставлено США.Армия.)
Стратегия
Сначала нарисуем набросок Рис. 3.21. Нас просят найти смещение, которое составляет x , если мы примем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулевой и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 когда мы идентифицируем v0v0, aa и t из постановки задачи.Рис. 3.21. Эскиз разгоняющегося драгстера.
Решение
Во-первых, нам нужно определить известные.Запуск из состояния покоя означает, что v0 = 0v0 = 0, a задается как 26,0 м / с 2 и t задается как 5,56 с.Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:
x = x0 + v0t + 12at2.x = x0 + v0t + 12at2.Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до
Подстановка идентифицированных значений a и t дает
x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м. x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м.Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут преодолеть четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.Что еще мы можем узнать, исследуя уравнение x = x0 + v0t + 12at2? X = x0 + v0t + 12at2? Мы видим следующие отношения:
- Смещение зависит от квадрата прошедшего времени, когда ускорение не равно нулю. В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
- Если ускорение равно нулю, то начальная скорость равна средней скорости (v0 = v -) (v0 = v–), и x = x0 + v0t + 12at2becomesx = x0 + v0t.x = x0 + v0t + 12at2becomesx = x0 + v0t.
Расчет конечной скорости по расстоянию и ускорению
Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим v = v0 + atv = v0 + at для t , мы получим
Подставляя это и v– = v0 + v2v– = v0 + v2 в x = x0 + v – tx = x0 + v – t, получаем
v2 = v02 + 2a (x − x0) (constanta). v2 = v02 + 2a (x − x0) (constanta).3,14
Пример 3.9
Расчет конечной скорости
Рассчитайте конечную скорость драгстера в Примере 3.8 без использования информации о времени.Стратегия
Уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.Решение
Сначала мы идентифицируем известные значения. Мы знаем, что v 0 = 0, поскольку драгстер запускается из состояния покоя. Мы также знаем, что x – x 0 = 402 м (это был ответ в примере 3.8). Среднее ускорение составило , а = 26.0 м / с 2 .Во-вторых, мы подставляем известные в уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) и решаем относительно v :
v2 = 0 + 2 (26,0 м / с2) (402 м). v2 = 0 + 2 (26,0 м / с2) (402 м).Таким образом,
v2 = 2,09 × 104 м2 / с2 v = 2,09 × 104 м2 / с2 = 145 м / с. v2 = 2,09 × 104 м2 / с2v = 2,09 × 104 м2 / с2 = 145 м / с.Значение
Скорость 145 м / с составляет около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость не достигает рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.Изучение уравнения v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) может дать дополнительное понимание общих соотношений между физическими величинами:
- Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
- При фиксированном ускорении машина, едущая вдвое быстрее, не просто останавливается на вдвое большем расстоянии. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Объединение уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных. Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.
Сводка кинематических уравнений (константа
a ) х = х0 + v0t + 12at2x = x0 + v0t + 12at2 v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях.Переставляя уравнение 3.12, получаем
Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико, приближаясь к нулю в том пределе, когда начальная и конечная скорости равны. Напротив, в пределе t → 0t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.
Аналогичным образом, переставляя уравнение 3.14, мы можем выразить ускорение в терминах скоростей и смещения:
а = v2-v022 (х-х0).а = v2-v022 (х-х0).Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример 3.10
Как далеко уезжает машина?
На сухом бетоне автомобиль может ускоряться противоположно движению со скоростью 7,00 м / с 2 , тогда как на мокром бетоне он может ускоряться противоположно движению со скоростью всего 5 м / с.00 м / с 2 . Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы нажать ногой на тормоз.Стратегия
Для начала нам нужно нарисовать набросок Рис. 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.Рис. 3.22. Пример эскиза для визуализации ускорения, противоположного движению и тормозному пути автомобиля.
Решение
- Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v 0 = 30,0 м / с, v = 0 и a = −7,00 м / с 2 ( a отрицательно, потому что оно находится в направлении, противоположном скорости) . Возьмем x 0 равным нулю. Ищем смещение ΔxΔx, или x – x 0 .
Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования – v2 = v02 + 2a (x − x0). v2 = v02 + 2a (x − x0). Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Мы знаем значения всех других переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы их использовать, но это потребовало бы дополнительных вычислений.)
В-третьих, мы изменим уравнение, чтобы найти x : x − x0 = v2 − v022ax − x0 = v2 − v022a и подставляем известные значения: х − 0 = 02− (30.0 м / с) 22 (-7,00 м / с2). X-0 = 02- (30,0 м / с) 22 (-7,00 м / с2). Таким образом, x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне. - Эта часть может быть решена точно так же, как (а). Единственное отличие состоит в том, что ускорение составляет −5,00 м / с 2 . Результат xwet = 90,0 м по мокрому бетону. xwet = 90,0 м по мокрому бетону.
- Когда водитель реагирует, тормозной путь такой же, как в пунктах (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время ко времени остановки.Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
Для этого мы, опять же, определяем известные и то, что мы хотим решить. Мы знаем, что v– = 30,0 м / sv– = 30,0 м / с, treaction = 0,500streaction = 0,500s и areaction = 0areaction = 0. Примем x0-реакцию x0-реакцию равной нулю. Ищем xreactionxreaction.
Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x0 + v – tx = x0 + v – t работает хорошо, потому что единственное неизвестное значение – x , что мы и хотим найти.
В-третьих, мы подставляем известные для решения уравнения: x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем при мгновенной реакции.
Наконец, мы добавляем смещение во время реакции к смещению при торможении (рис. 3.23), xbraking + xreaction = xtotal, xbraking + xreaction = xtotal, и найдите (a) равным 64,3 м + 15,0 м = 79.3 м в сухом виде и (b) должно составлять 90,0 м + 15,0 м = 105 м во влажном состоянии.
Рис. 3.23. Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, движущегося со скоростью 30,0 м / с. Также показаны общие расстояния, пройденные от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.
Значение
Смещения, обнаруженные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важен общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.Пример 3.11
Расчет времени
Предположим, автомобиль въезжает в движение по автостраде на съезде длиной 200 м. Если его начальная скорость равна 10,0 м / с, а он ускоряется со скоростью 2,00 м / с 2 , сколько времени потребуется машине, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)Стратегия
Сначала мы рисуем набросок Рис. 3.24. Нам предлагается решить за время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одной неизвестной, t .)Рис. 3.24. Эскиз автомобиля, ускоряющегося на съезде с автострады.
Решение
Опять же, мы определяем известные и то, что мы хотим решить. Мы знаем, что x0 = 0, x0 = 0,v0 = 10 м / с, a = 2,00 м / с2v0 = 10 м / с, a = 2,00 м / с2 и x = 200 м.
Нам нужно решить для т . Уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 работает лучше всего, потому что единственной неизвестной в уравнении является переменная t , которую нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.
Нам нужно изменить уравнение, чтобы найти t , затем подставив известные значения в уравнение:
200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2. 200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2.Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t s, где t – величина времени, а s – единица измерения. Остается
Затем мы используем формулу корней квадратного уравнения, чтобы найти t ,
t2 + 10t − 200 = 0t = −b ± b2−4ac2a, t2 + 10t − 200 = 0t = −b ± b2−4ac2a,, что дает два решения: t = 10.0 и t = −20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.Проверьте свое понимание 3.5
Ракета ускоряется со скоростью 20 м / с 2 во время пуска.Сколько времени нужно, чтобы ракета достигла скорости 400 м / с?
Пример 3.12
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с 2 за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа.Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.Решение
Сначала мы решаем для v0v0, используя x = x0 + v0t + 12at2: x = x0 + v0t + 12at2: x − x0 = v0t + 12at2x − x0 = v0t + 12at21.0 × 106m = v0 (120.0s) +12 (20,0 м / с2) (120,0 с) 21,0 × 106 м = v0 (120,0 с) +12 (20,0 м / с2) (120,0 с) 2v0 = 7133,3 м / с. V0 = 7133,3 м / с.Затем мы подставляем v0v0 в v = v0 + atv = v0 + at, чтобы найти окончательную скорость:
v = v0 + at = 7133.3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с. V = v0 + at = 7133,3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с.Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть не такими простыми, как простая подстановка в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также увидели общий подход к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности в наших задачах кинематики связан с движением двух взаимосвязанных тел, который называется задачами преследования двух тел .
Задачи преследования двух тел
До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть неизвестное, которое мы ищем, зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на рисунке 3.25.
Рис. 3.25. Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 идет сзади с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже.
Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависит от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример 3.13
Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с.В момент, когда газель проходит мимо гепарда, гепард из состояния покоя ускоряется со скоростью 4 м / с 2 , чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, – это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно рассмотрим проблему, становится ясно, что общим параметром для каждого животного является их положение x , позднее t . Поскольку оба они начинаются с x0 = 0x0 = 0, их смещения будут такими же в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое решает проблему смещения для каждого животного, мы сможем приравнять уравнения друг к другу и решить неизвестное, то есть время.Решение
- Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется.Поэтому мы используем уравнение 3.10 с x0 = 0x0 = 0: x = x0 + v – t = v – t. x = x0 + v – t = v – t. Уравнение для гепарда: гепард ускоряется из состояния покоя, поэтому мы используем уравнение 3.13 с x0 = 0x0 = 0 и v0 = 0v0 = 0: x = x0 + v0t + 12at2 = 12at2.x = x0 + v0t + 12at2 = 12at2. Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае мы решаем для t : x = v – t = 12at2t = 2v – a.x = v – t = 12at2t = 2v – a. Газель имеет постоянную скорость 10 м / с, что составляет ее среднюю скорость.Ускорение гепарда составляет 4 м / с 2 . Оценив t , время, за которое гепард достигнет газели, имеем t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.
- Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны дать одинаковый ответ.
Смещение гепарда: x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. Водоизмещение газели: x = v – t = 10 м / с (5) = 50 м. x = v – t = 10 м / с (5) = 50 м.Мы видим, что оба смещения равны, как и ожидалось.
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.Проверьте свое понимание 3,6
Велосипед имеет постоянную скорость 10 м / с. Человек начинает с отдыха и начинает бежать, чтобы догнать велосипед через 30 секунд, когда велосипед находится в том же положении, что и человек.Какое ускорение у человека?
Формула ускорения
Ускорение – это мера того, насколько быстро изменяется скорость объекта. Итак, ускорение – это изменение скорости, деленное на время. У ускорения есть величина (значение) и направление. Направление ускорения не обязательно должно совпадать с направлением скорости. Единицы измерения ускорения – метр на секунду в квадрате (м / с 2 ).
a = ускорение (м / с 2 )
v f = конечная скорость (м / с)
v i = начальная скорость (м / с)
t = время, в которое происходит изменение (с)
Δ v = краткая форма для «изменения» скорости (м / с)
Вопросы по формуле ускорения:1) Спортивный автомобиль движется с постоянной скоростью v = 5.00 м / с . Водитель нажимает на педаль газа, и машина ускоряется вперед. Через 10,0 секунд водитель прекращает ускорение и поддерживает постоянную скорость v = 25,0 м / с . Какое ускорение было у машины?
Ответ: Начальная скорость v i = 5,00 м / с в прямом направлении. Конечная скорость v f = 25,0 м / с в прямом направлении. Время, в которое произошло это изменение, – 10,0 с . Ускорение в прямом направлении со значением:
Ускорение автомобиля равно 2.00 м / с 2 , вперед.
2) Ребенок роняет камень со скалы. Камень падает на 15,0 с перед тем, как удариться о землю. Ускорение свободного падения g = 9,80 м / с 2 . Какая скорость была у камня за мгновение до того, как он упал на землю?
Ответ: Скала вышла из состояния покоя, поэтому начальная скорость равна v i = 0,00 м / с . Время, в которое произошло изменение: 15,0 с .Ускорение составляет 9,80 м / с 2 . Необходимо определить конечную скорость, поэтому измените уравнение:
v f = v i + at
v f = 0,00 м / с + (9,80 м / с 2 ) (15,0 с)
v f = 147 м / с
Камень падает, поэтому направление скорости вниз.
3.3 Среднее и мгновенное ускорение – University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте среднее ускорение между двумя точками времени.
- Рассчитайте мгновенное ускорение с учетом функциональной формы скорости.
- Объясните векторную природу мгновенного ускорения и скорости.
- Объясните разницу между средним ускорением и мгновенным ускорением.
- Найдите мгновенное ускорение в заданное время на графике зависимости скорости от времени.
Важность понимания ускорения распространяется на наш повседневный опыт, а также на огромные просторы космического пространства и крошечный мир субатомной физики.В повседневном разговоре разогнать означает разогнаться; нажатие педали тормоза приводит к замедлению движения автомобиля. Мы, например, знакомы с ускорением нашей машины. Чем больше ускорение, тем больше изменение скорости за заданный промежуток времени. Ускорение широко наблюдается в экспериментальной физике. Например, в экспериментах с линейным ускорителем частиц субатомные частицы ускоряются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной.В космосе космические лучи – это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывающихся массивных звездах) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат очень проникающее излучение, которое может, например, повредить электронику, установленную на космических кораблях.
Среднее ускорение
Формальное определение ускорения согласуется с этими только что описанными понятиями, но является более всеобъемлющим.
Среднее ускорение
Среднее ускорение – скорость изменения скорости:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {\ text {f}} – {v} _ { 0}} {{t} _ {\ text {f}} – {t} _ {0}}, [/ latex]
, где [latex] \ overset {\ text {-}} {a} [/ latex] – среднее ускорение, v – скорость, а t – время. (Полоса над и означает среднее ускорение ).
Поскольку ускорение – это скорость в метрах, разделенная на время в секундах, единицы измерения ускорения в системе СИ часто обозначают сокращенно м / с 2 , то есть метры в секунду в квадрате или метры в секунду в секунду.Это буквально означает, на сколько метров в секунду изменяется скорость каждую секунду. Напомним, что скорость – это вектор, он имеет как величину, так и направление, что означает, что изменение скорости может быть изменением величины (или скорости), но также может быть изменением направления. Например, если бегун, движущийся со скоростью 10 км / ч на восток, замедляется до остановки, меняет направление, продолжает свой бег со скоростью 10 км / ч на запад, его скорость изменилась в результате изменения направления, хотя величина скорости одинаковы в обоих направлениях.Таким образом, ускорение происходит, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по обоим направлениям.
Ускорение как вектор
Ускорение – это вектор в том же направлении, что и изменение в скорости, [latex] \ Delta v [/ latex]. Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Следовательно, ускорение – это изменение скорости или направления, или и того, и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда в направлении движения.Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называется замедлением Рисунок , мы говорим, что поезд ускоряется в направлении, противоположном его направлению движения.
Рисунок 3.10. Поезд метро в Сан-Паулу, Бразилия, замедляет ход при входе на станцию. Он ускоряется в направлении, противоположном направлению его движения. (Источник: Юсуке Кавасаки)Термин замедление может вызвать путаницу в нашем анализе, потому что он не является вектором и не указывает на конкретное направление относительно системы координат, поэтому мы не используем его.Ускорение – это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат. В случае поезда на рисунке ускорение составляет в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.
Если движущийся объект имеет скорость в положительном направлении по отношению к выбранной исходной точке и приобретает постоянное отрицательное ускорение, объект в конечном итоге останавливается и меняет направление.Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это показано на рисунке.
Рисунок 3.11 Объект, движущийся с вектором скорости на восток при отрицательном ускорении, останавливается и меняет направление на противоположное. Через достаточно долгое время он проходит исходную точку в обратном направлении.Пример
Расчет среднего ускорения: скакун покидает ворота
Скаковая лошадь, выходящая из ворот, набирает скорость от состояния покоя до 15.0 м / с на запад за 1.80 с. Какое у него среднее ускорение?
Рисунок 3.12. Скачки ускоряются из-за ворот. (кредит: Джон Салливан)Стратегия
Сначала мы рисуем эскиз и назначаем систему координат проблемному рисунку. Это простая проблема, но всегда помогает ее визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Рисунок 3.13 Определите систему координат, данную информацию и то, что вы хотите определить.Мы можем решить эту проблему, определив [latex] \ Delta v \, \ text {and} \, \ Delta t [/ latex] из заданной информации, а затем вычислив среднее ускорение непосредственно из уравнения [latex] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {\ text {f}} – {v} _ {0}} {{t } _ {\ text {f}} – {t} _ {0}} [/ latex].
Решение
Сначала определите известные: [latex] {v} _ {0} = 0, {v} _ {\ text {f}} = – 15.0 \, \ text {m / s} [/ latex] (отрицательный указывает направление на запад), Δ t = 1.80 с.
Во-вторых, найдите изменение скорости. Поскольку лошадь движется с нуля до –15,0 м / с, ее изменение скорости равно ее конечной скорости:
[латекс] \ Delta v = {v} _ {\ text {f}} – {v} _ {0} = {v} _ {\ text {f}} = – 15,0 \, \ text {м / с }. [/ latex]
Наконец, подставьте известные значения ([latex] \ Delta v \, \ text {and} \, \ Delta t [/ latex]) и найдите неизвестное [latex] \ overset {\ text {-}} {a } [/ latex]:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {-15.0 \, \ text {m / s}} {1.{2}. [/ Латекс]
Значение
Отрицательный знак ускорения указывает на то, что ускорение направлено на запад. Ускорение 8,33 м / с 2 на западе означает, что лошадь увеличивает свою скорость на 8,33 м / с на западе каждую секунду; то есть 8,33 метра в секунду в секунду, что мы записываем как 8,33 м / с 2 . Это действительно среднее ускорение, потому что поездка не гладкая. Позже мы увидим, что ускорение такой величины потребовало бы от всадника держаться с силой, почти равной его весу.{2}. [/ Латекс]
Мгновенное ускорение
Мгновенное ускорение a или ускорение в определенный момент времени получается с использованием того же процесса, что и для мгновенной скорости. То есть мы вычисляем среднюю скорость между двумя моментами времени, разделенными [латекс] \ Delta t [/ latex], и позволяем [latex] \ Delta t [/ latex] приближаться к нулю. Результатом является производная функции скорости v ( t ), которая равна мгновенному ускорению и математически выражается как
[латекс] a (t) = \ frac {d} {dt} v (t).[/ латекс]
Таким образом, аналогично скорости, являющейся производной функции положения, мгновенное ускорение является производной функции скорости. Мы можем показать это графически так же, как мгновенную скорость. На рисунке мгновенное ускорение в момент времени t 0 – это наклон касательной к графику зависимости скорости от времени в момент времени t 0 . Мы видим, что среднее ускорение [latex] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} [/ latex] приближается к мгновенному ускорению, как [latex] \ Delta t [/ latex ] стремится к нулю.Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, поскольку наклон кривой там тоже равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
Рис. 3.14. На графике зависимости скорости от времени мгновенное ускорение представляет собой наклон касательной.(a) Показано среднее ускорение [латекс] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {\ text {f}} – {v} _ {i}} {{t} _ {\ text {f}} – {t} _ {i}} [/ latex] между временами [латекс] \ Delta t = {t} _ {6} – {t} _ {1}, \ Delta t = {t} _ {5} – {t} _ {2} [/ latex] и [latex] \ Delta t = {t} _ {4} – { t} _ {3} [/ latex]. Когда [latex] \ Delta t \ равняется 0 [/ latex], среднее ускорение приближается к мгновенному ускорению в момент времени t0. В виде (а) мгновенное ускорение показано для точки на кривой скорости при максимальной скорости. В этой точке мгновенное ускорение – это наклон касательной, равный нулю.В любое другое время наклон касательной – и, следовательно, мгновенное ускорение – не будет нулевым. (b) То же, что (a), но показано для мгновенного ускорения при минимальной скорости.Чтобы проиллюстрировать эту концепцию, давайте рассмотрим два примера. Во-первых, простой пример показан с использованием рисунка (b), графика зависимости скорости от времени на рисунке, чтобы найти ускорение графически. Этот график изображен на рисунке (а), который представляет собой прямую линию. Соответствующий график ускорения в зависимости от времени находится по наклону скорости и показан на рисунке (b).В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным. В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.
Рис. 3.15. (a, b) График зависимости скорости от времени является линейным и имеет постоянный отрицательный наклон (a), который равен ускорению, показанному на (b).Если мы знаем функциональную форму скорости, v ( t ), мы можем вычислить мгновенное ускорение a ( t ) в любой момент времени в движении, используя рисунок.{2} \, \ text {m / s} [/ латекс].
- Найдите функциональную форму ускорения.
- Найдите мгновенную скорость при t = 1, 2, 3 и 5 с.
- Найдите мгновенное ускорение при t = 1, 2, 3 и 5 с.
- Интерпретируйте результаты (c) в терминах направлений векторов ускорения и скорости.
Стратегия
Функциональную форму ускорения находим, взяв производную от функции скорости.{2} [/ латекс]
При t = 2 с, скорость увеличилась до [latex] v (2 \, \ text {s)} = 20 \, \ text {m / s} [/ latex], где она максимальна, что соответствует моменту, когда ускорение равно нулю. Мы видим, что максимальная скорость возникает, когда наклон функции скорости равен нулю, что является просто нулем функции ускорения.
При t = 3 с, скорость равна [latex] v (3 \, \ text {s)} = 15 \, \ text {m / s} [/ latex], а ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицательный. Частица замедляется.
При t = 5 с, скорость равна [latex] v (5 \, \ text {s)} = – 25 \, \ text {m / s} [/ latex], а ускорение становится все более отрицательным. Между моментами времени t = 3 с и t = 5 с частица уменьшила свою скорость до нуля, а затем стала отрицательной, таким образом изменив свое направление.Теперь частица снова ускоряется, но в противоположном направлении.
Мы можем видеть эти результаты графически на рисунке.
Рис. 3.16. (а) Скорость в зависимости от времени. Касательные линии указаны в моменты времени 1, 2 и 3 с. Наклоны касательных – это ускорения. При t = 3 с скорость положительная. При t = 5 с скорость отрицательна, что указывает на то, что частица изменила направление на противоположное. (б) Ускорение против времени. Сравнивая значения ускорений, представленные черными точками, с соответствующими наклонами касательных линий (наклон линий через черные точки) на (а), мы видим, что они идентичны.Значение
Выполняя численный и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении. Численный анализ дополняет графический анализ, давая полное представление о движении. Нуль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительное и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю и в конечном итоге становится отрицательным, скорость достигает максимума, после чего начинает уменьшаться.Если мы подождем достаточно долго, скорость также станет отрицательной, что указывает на изменение направления. Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление движения.
Проверьте свое понимание
Самолет приземляется на взлетно-посадочной полосе, летящей на восток. Опишите его ускорение.
Показать решениеЕсли мы возьмем восток за положительное значение, тогда самолет будет иметь отрицательное ускорение, потому что он ускоряется на запад.Он также замедляется; его ускорение противоположно направлению его скорости.
Ощущение ускорения
Вы, вероятно, привыкли испытывать ускорение, когда заходите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит со многими другими объектами в нашей Вселенной, с которыми мы не имеем прямого контакта. На рисунке представлены ускорения различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.
| Разгон | Значение (м / с 2 ) |
|---|---|
| Скоростной поезд | 0,25 |
| Лифт | 2 |
| Гепард | 5 |
| Объект в свободном падении без сопротивления воздуха у поверхности Земли | 9,8 |
| Максимум космического челнока во время запуска | 29 |
| Пик парашютиста при нормальном раскрытии парашюта | 59 |
| Самолет F16 выходит из пикирования | 79 |
| Взрывной выброс сиденья с самолета | 147 |
| Ракета Спринт | 982 |
| Максимальное пиковое ускорение ракетных салазок | 1540 |
| Прыгающая блоха | 3200 |
| Бейсбольный удар битой | 30 000 |
| Смыкание губок муравья-ловушки | 1 000 000 |
| Протон в большом адронном коллайдере | [латекс] 1.{9} [/ латекс] |
В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют никакого отношения к размеру объекта или его массивности. Ускорение также может сильно меняться со временем во время движения объекта. У дрэг-рейсинга сразу после старта наблюдается большое ускорение, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения.На рисунке показано графическое сравнение среднего ускорения с мгновенным ускорением для двух очень разных движений.
Рис. 3.17. Графики мгновенного ускорения в зависимости от времени для двух различных одномерных движений. (а) Ускорение меняется незначительно и всегда в одном и том же направлении, поскольку оно положительное. Среднее значение за интервал почти такое же, как и ускорение в любой момент времени. (b) Ускорение сильно различается, возможно, представляя пакет на конвейерной ленте почтового отделения, который ускоряется вперед и назад, когда он натыкается.В такой ситуации необходимо учитывать небольшие интервалы времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.Сводка
- Ускорение – это скорость изменения скорости. Ускорение – это вектор; он имеет как величину, так и направление. Единица измерения ускорения в системе СИ – метр на секунду в квадрате.
- Ускорение может быть вызвано изменением величины или направления скорости, либо и тем, и другим.
- Мгновенное ускорение a ( t ) является непрерывной функцией времени и дает ускорение в любой конкретный момент во время движения.Он рассчитывается по производной функции скорости. Мгновенное ускорение – это наклон графика зависимости скорости от времени.
- Отрицательное ускорение (иногда называемое замедлением) – это ускорение в отрицательном направлении в выбранной системе координат.
Концептуальные вопросы
Может ли скорость быть постоянной при ненулевом ускорении?
Показать решениеНет, в одном измерении постоянная скорость требует нулевого ускорения.
Может ли скорость быть постоянной, если ускорение не равно нулю? Объяснять.
Приведите пример, в котором скорость равна нулю, а ускорение – нет.
Показать решениеМяч подбрасывается в воздух, и его скорость равна нулю на вершине броска, но ускорение не равно нулю.
Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, в каком направлении он ускоряется? Ускорение положительное или отрицательное?
Знаки плюс и минус используются в одномерном движении для обозначения направления.{2} [/ латекс]
Доктор Джон Пол Стапп был офицером ВВС США, изучавшим влияние экстремального ускорения на человеческое тело. 10 декабря 1954 года Стапп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м / с (1015 км / ч) за 5,00 с и резко остановившись всего за 1,40 с. Вычислите его (а) ускорение в направлении его движения и (б) ускорение, противоположное его направлению движения. Выразите каждое значение кратным г (9,80 м / с 2 ), взяв его отношение к ускорению свободного падения.
Нарисуйте график зависимости ускорения от времени из следующего графика зависимости скорости от времени.
Показать ответПассажир выезжает на машине из гаража с ускорением 1,40 м / с 2 . а) Сколько времени ей нужно, чтобы набрать скорость 2,00 м / с? (b) Если она затем тормозит до остановки за 0,800 с, каково ее ускорение?
Предположим, что межконтинентальная баллистическая ракета выходит из состояния покоя на суборбитальную скорость 6,50 км / с за 60 секунд.0 с (фактическая скорость и время классифицируются). Каково его среднее ускорение в метрах в секунду и кратное g (9,80 м / с 2 )?
Показать решение[латекс] a = 11,1 г [/ латекс]
Самолет, взлетая с места, движется по взлетно-посадочной полосе с постоянным ускорением в течение 18 с, а затем взлетает со скоростью 60 м / с. Какое среднее ускорение самолета?
Глоссарий
- среднее ускорение
- скорость изменения скорости; изменение скорости с течением времени
- мгновенное ускорение
- ускорение в определенный момент времени
Кинематика – Ускорение
Кинематика – Ускорение[Глава 2 цели]
BHS -> МистерСтэнбро -> Физика -> Механика -> Кинематика -> эта страница
Что такое ускорение:
Ускорение – это скорость, с которой изменения скорости. Другими словами, зная ускорение объекта показывает, насколько быстро движется объект меняется.
Так как скорость – это скорость, с которой изменяется положение, и ускорение – это скорость изменения скорости, ускорение – это «ставка ставки».
Когда происходит ускорение:
Очень важно отметить, что ускорение определяется в с точки зрения изменения скорости – не скорости . Это может показаться вроде мелочь, но это не так. Поскольку ускорение – это скорость изменения скорости,
Вы ускоряетесь всякий раз, когда вы:
- ускориться – Это несложно понять, так как это общепринятая концепция ускорения.
- замедлить – люди обычно называют это замедление, как если бы оно физически отличалось от случай “ускорения” – а для физика все равно – если ваша скорость меняется, вы ускоряетесь.
- изменить направление – Это может быть сложно понять. Поскольку скорость – это ваша скорость и направление, ваша скорость изменяется, если ваше направление меняется (даже если ваша скорость остается одно и тоже).Поскольку вы ускоряетесь, если ваша скорость меняется, Вы ускоряетесь, когда меняете направление – даже если ваша скорость останется прежней . Большинство людей ссылаются ускорение с изменением скорости (и увеличением скорости), поэтому они думают: “Хорошо, на тесте я должен сказать, что объект ускоряется, если он меняет направление, но это действительно «фальшивый» вид ускорения в отличие от «настоящего» ускорения ускорение “Нет.Это ускорение так же реально, как и «ускорение» (и «замедление») вида ускорения.
Что не является ускорением:
Поскольку ускорение связано с изменениями скорости – когда ваша скорость меняется, вы ускоряетесь, студенты часто получают заблуждение, что «ускорение – это изменение скорости». НЕТ !! Ускорение – это скорость, с которой скорость изменения – есть важное отличие!
Сказать, что «ускорение – это изменение скорости», все равно что сказать “скорость – это изменение положения” (это звучит глупо, но не Это?).Скорость показывает, насколько быстро меняется позиция. Acceleration показывает, насколько велика скорость меняется.
Ускорение – это , а не изменение скорости!
Расчет ускорения:
Предположим, что скорость спринтера изменяется от 0 м / с до 10 м / с за 2 секунды. секунд на старте гонки. Какое у нее ускорение?
Обратите внимание на нечетные единицы ускорения – расстояние (длину), разделенное в 2 раза.Единица времени определяется скоростью в числителе дробь, а другая – из знаменателя. Количество например, 4 мили / час / сек – это ускорения (4 мили / час / сек означает, что скорость меняется на 4 мили / час каждую секунду.).
Работа с ускорениями:
Пример:
Автомобиль трогается с места и разгоняется со скоростью 2 м / с / с в течение 5 секунд. Как быстро это будет происходить?
Решение:
Фраза «автомобиль заводится с покоя» означает, что автомобиль заводится. скорость 0 м / с.Ускорение 2 м / с / с означает, что автомобиль скорость меняется на 2 м / с каждую секунду. Если скорость машины начинается при 0 м / с и изменяется на 2 м / с в первую секунду, это будет 2 м / с по истечении 1 секунды. В течение второй секунды (?!) Его скорость увеличивается на 2 м / с – с 2 м / с до 4 м / с. Его скорость будет составлять 6 м / с через 3 секунды, 8 м / с через 4 секунды и 10 м / с через 5 секунд. секунд.
В качестве альтернативы, если хотите, есть более алгебраический подход.Если тогда , так . Если скорость начинается с 0 м / с и изменяется на 10 м / с, она заканчивается на 10 РС.
Указание направления ускорения:
Как и скорость, ускорения в одномерных движениях положительный, если они действуют в положительном направлении, и отрицательный, если они действовать в отрицательном направлении. Определить направление немного однако более абстрактно для ускорений, чем для скоростей – по крайней мере пока вы к этому не привыкнете.
Следует запомнить 3 вещи:
- Ускорение объекта – это изменение его скорости. делится на время.
- Если объект движется в положительном направлении, его скорость положительный. Если он движется в отрицательном направлении, его скорость отрицательная.
- Изменение скорости – это конечная скорость минус начальная скорость.
Пример:
Скорость автомобиля изменяется с +2 м / с до +10 м / с за 4 секунды.Какие это его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость
= 10 м / с – 2 м / с = 8 м / с. Его ускорение = его изменение скорости
деленное на затраченное время = (8 м / с) / (4 с) = 2 м / с / с.
Пример:
Скорость автомобиля изменяется с +10 м / с до +2 м / с за 4 секунды. Какие это его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость
= 2 м / с – 10 м / с = -8 м / с.Его ускорение = его изменение скорости
деленное на затраченное время = (-8 м / с) / (4 с) = -2 м / с / с.
Пример:
Скорость автомобиля изменяется с -2 м / с до -10 м / с за 4 секунды. Какие это его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость
= -10 м / с – (-2 м / с) = -10 м / с + 2 м / с = -8 м / с. Его ускорение =
его изменение скорости, деленное на затраченное время = (-8 м / с) / (4 с) =
-2 м / с / с.
Пример:
Скорость автомобиля изменяется с -10 м / с до -2 м / с за 4 секунды. Какие это его ускорение?
Решение:
Изменение скорости автомобиля = конечная скорость – начальная скорость
= -2 м / с – (-10 м / с) = -2 м / с + 10 м / с = 8 м / с. Его ускорение =
его изменение скорости, деленное на затраченное время = (8 м / с) / (4 с) = 2
м / сек / сек.
Из этих примеров обратите внимание, что вы просто следуете (простому) правил – особенно помня, что изменение скорости – это конечная скорость минус начальная скорость – НЕ большое число минус маленькое число!
Расчет ускорения при изменении только направления:
В приведенных выше примерах вы видели, что это довольно просто для расчета ускорения объекта при изменении его скорости используя алгебру.Объект также ускоряется при изменении его направления, но “нормальной” алгебры недостаточно для вычисления ускорения в в этом случае – вам нужно использовать векторную алгебру , и мы не будем потрудитесь с расчетом этих ускорений в этом курсе.
Тест на ускорение: Чтобы пройти практическую викторину по Первому закону Ньютона, вам понадобится браузер с поддержкой Java.
[Глава 2 цели] BHS -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница
последнее обновление 22 ноября 2005 г., автор: JL Stanbrough
| | Скорость измеряется в метрах в секунду (м / с),
Отрабатываем ускорение используя
Сила и разгон: Если силы на объект находится в равновесии, то его скорость будет постоянной (см. Стр. Сил) Если силы не сбалансированы, тогда объект будет ускоряться – что может означать ускорение, замедление или изменение направления.
Надо выяснить как сильно он разгоняется? См. Внизу страницы Продвинутый:
|

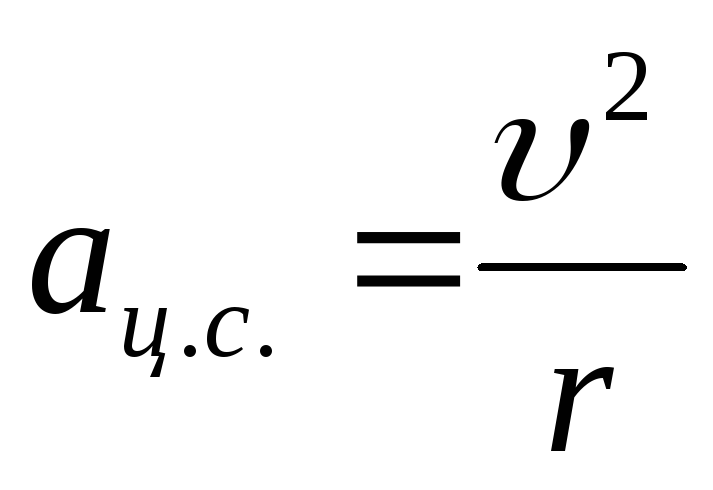 Проблемы в физике редко выглядят одинаково. Вместо того, чтобы решать проблемы наизусть или путем имитации ранее решенной проблемы, используйте свое концептуальное понимание законов Ньютона для поиска решений проблем. Используйте свои знания о весе и массе, чтобы найти m или Fgrav в проблеме. Используйте свое концептуальное понимание чистой силы (векторная сумма всех сил ), чтобы найти значение Fnet или значение отдельной силы.Не отделяйте решение физических задач от вашего понимания концепций физики. Если вы не можете решать физические задачи, подобные приведенным выше, это не обязательно означает, что у вас есть математические трудности. Вполне вероятно, что у вас проблемы с физическими концепциями.
Проблемы в физике редко выглядят одинаково. Вместо того, чтобы решать проблемы наизусть или путем имитации ранее решенной проблемы, используйте свое концептуальное понимание законов Ньютона для поиска решений проблем. Используйте свои знания о весе и массе, чтобы найти m или Fgrav в проблеме. Используйте свое концептуальное понимание чистой силы (векторная сумма всех сил ), чтобы найти значение Fnet или значение отдельной силы.Не отделяйте решение физических задач от вашего понимания концепций физики. Если вы не можете решать физические задачи, подобные приведенным выше, это не обязательно означает, что у вас есть математические трудности. Вполне вероятно, что у вас проблемы с физическими концепциями.