Ускорение формула через путь: Скорость и путь при равноускоренном движении — урок. Физика, 9 класс.

Как найти путь формула?

Как найти путь формула?

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось. S=V*t.

Как найти весь путь в физике?

Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t). где ˉr – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.

Как найти длину пути физика?

S = v ⋅ ( t 2 − t 1 ) = v ⋅ Δ t , где – скорость тела, — момент времени окончания движения, — момент времени начала движения, – время движения. График зависимости пути от времени на координатной плоскости в случае такого, называемого равномерным, движения является прямой линией.

Как найти путь в физике с ускорением?

Формула выглядит следующим образом:

1. s = v 0 t + a t 2 2 , где а — это ускорение. …
2. Зависимость ускорения от времени. …
3. Зависимость скорости от времени. …
4. Правило определения пути по графику v(t): численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.
5. Зависимость пути от времени.

Как найти путь через скорость?

1) Формула пути:

1. Чтобы найти расстояние, нужно скорость умножить на время.
2. Чтобы найти время, надо расстояние разделить на скорость.
3. Чтобы найти скорость, надо расстояние разделить на время.

Как найти скорость с ускорением?

V = V0 + а*t Итак, чтобы найти скорость, к начальной скорости прибавляем произведение ускорения на время. Если V0 = 0, то V = а*t. Чтобы найти время, нужно вначале найти разность между скоростью в данный момент и начальной скоростью, затем полученный результат разделить на ускорение.

Как найти скорость при равноускоренном движении?

Формулы для равноускоренного движения Формула для скорости при равноускоренном движении: v=v0+at v = v 0 + a t . Здесь v0 – начальная скорость тела, a=const a = c o n s t – ускорение. Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии.

Чему равно ускорение через скорость и время?

Ускорение – это физическая величина, равная отношению изменения скорости тела ко времени, за которое это изменение произошло (рис. 3).

Чему равно ускорение при равноускоренном движении?

Ускорение тела при его равноускоренном движении — это величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло: a → = v → − v 0 → t .

Как называется ускорение?

Ускорением называется физическая величина, характеризующая быстроту изменения скорости по модулю и направлению. … Это ускорение называется тангенциальной (касательной) составляющей ускорения и обозначается – at. Если V¢>0, то ускорение .

Что называют ускорением в каких единицах оно измеряется?

acceleratio ), характеризующая быстроту изменения скорости тела. Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2, м/с2). Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с.

Какая физическая величина называется ускорением?

Ускорение – это физическая величина, численно равная изменению скорости за единицу времени. Равноускоренное движение – движение тела, при котором скорость тела за равные промежутки времени изменяется одинаково, то есть движется с постоянным ускорением.

Вопрос №1. Перемещение, скорость, путь, ускорение. Вычисление пройденного пути при равномерном и равноускоренном прямолинейном движении.

Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением.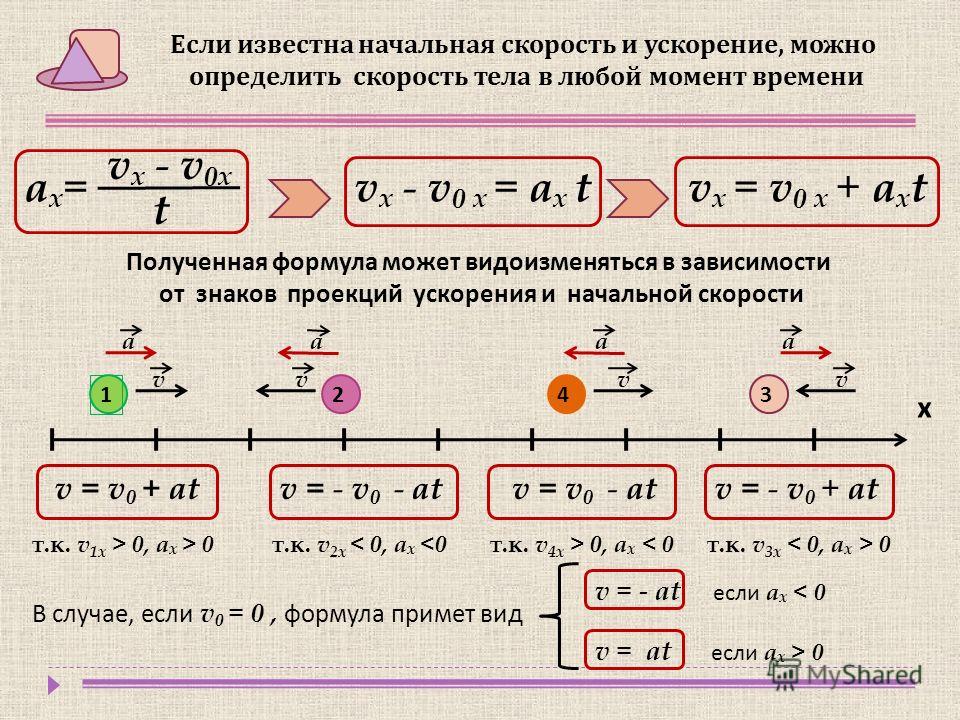 Перемещение есть векторная величина. ( )

Пройденный путь S равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.Ускорение – это величина, которая характеризует быстроту изменения скорости. Скорость — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.Прямолинейным равномерным движением называется механическое движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. ( ) Равноускоренным движением

называется такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. ( )

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии.

Нормальное ускорение, составляющая ускорения точки при криволинейном движении, направленная по главной нормали к траектории в сторону центра кривизны; Нормальное ускорение называется также центростремительным ускорением.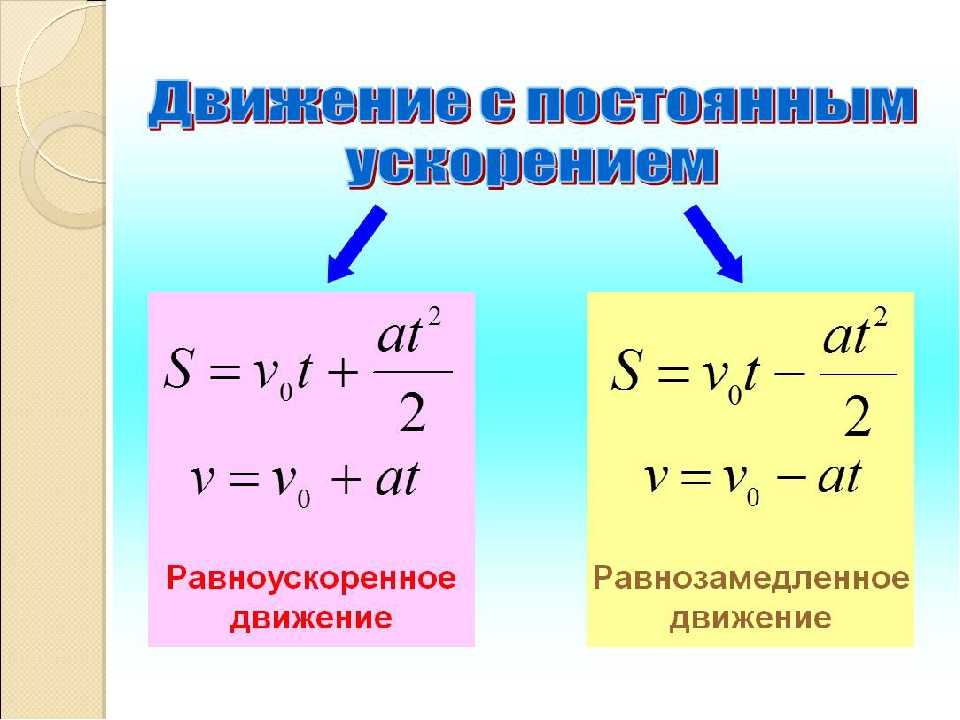 Численно Нормальное ускорение равно v2/r, где v — скорость точки, r — радиус кривизны траектории. При движении по окружности Нормальное ускорение может вычисляться по формуле rw2, где r — радиус окружности, w— угловая скорость вращения этого радиуса. В случае прямолинейного движения Нормальное ускорение равно нулю.

Тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения. Совпадает с направлением вектора скорости при ускоренном движении и противоположно направлено при замедленном. Характеризует изменение модуля скорости.

Принято описывать траекторию материальной точки при помощи радиус-вектора, направление, длина и начальная точка которого зависят от времени. При этом кривая, описываемая концом радиус-вектора в пространстве может быть представлена в виде сопряжённых дуг различной кривизны, находящихся в общем случае в пересекающихся плоскостях. При этом кривизна каждой дуги определяется её радиусом кривизны, направленном к дуге из мгновенного центра поворота, находящегося в той же плоскости, что и сама дуга.

При том прямая линия рассматривается как предельный случай кривой, радиус кривизны которой может считаться равным бесконечности.И потому траектория в общем случае может быть представлена как совокупность сопряжённых дуг.

Вопрос №3. Угловые скорость и ускорение. Вычисление угла поворота тела при равномерном и равноускоренном вращении. Связь линейных и угловых характеристик.

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени, а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно

Вопрос №4.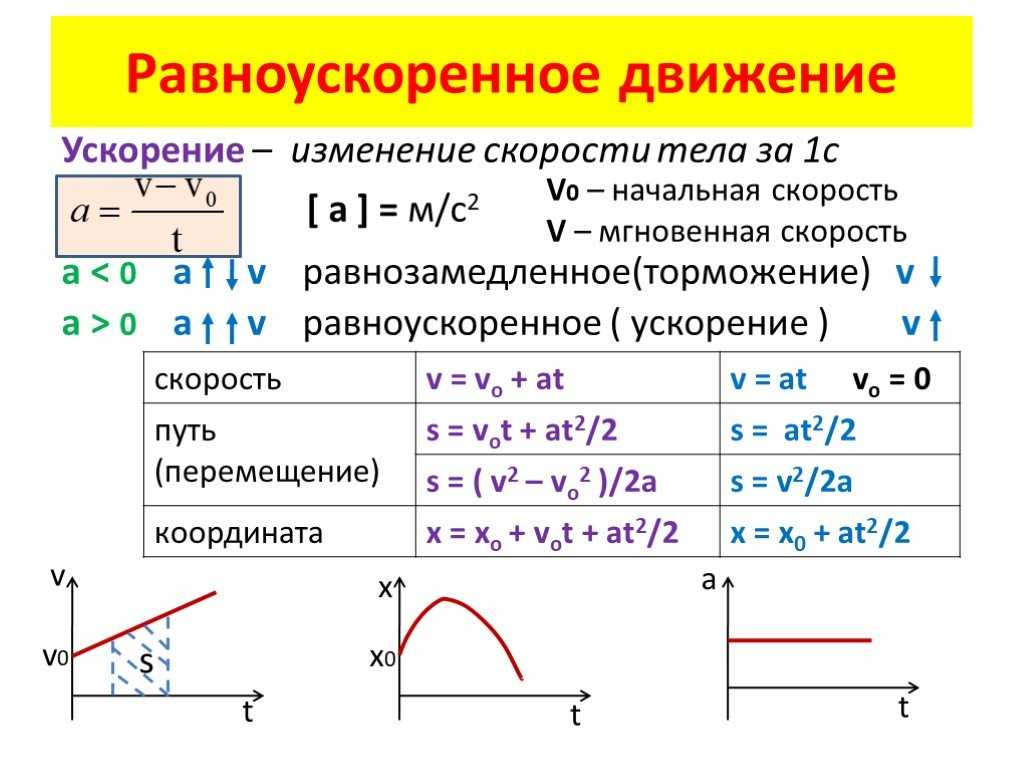

1-ый закон Ньютона. Инерциальные системы отсчета. Преобразования координат и скоростей Галилея. Импульс. Сила. 2-ой и 3-й законы Ньютона

Первый закон Ньютона: всякая мате­риальная точка (тело) сохраняет состоя­ние покоя или равномерного прямолиней­ного движения до тех пор, пока воздейст­вие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. По­этому первый закон Ньютона называют также законом инерции. Сила — это векторная величина, являюща­яся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и раз­меры.

Импульс— векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости. Второй закон Ньютона: В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. Третий закон Ньютона

: Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Вопрос №5. Закон сохранения импульса. Центр масс тела.

Центром масс системы материальных точек называется воображаемая точка С, положение которой характеризует распре­деление массы этой системы Зако́н сохране́ния и́мпульса утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.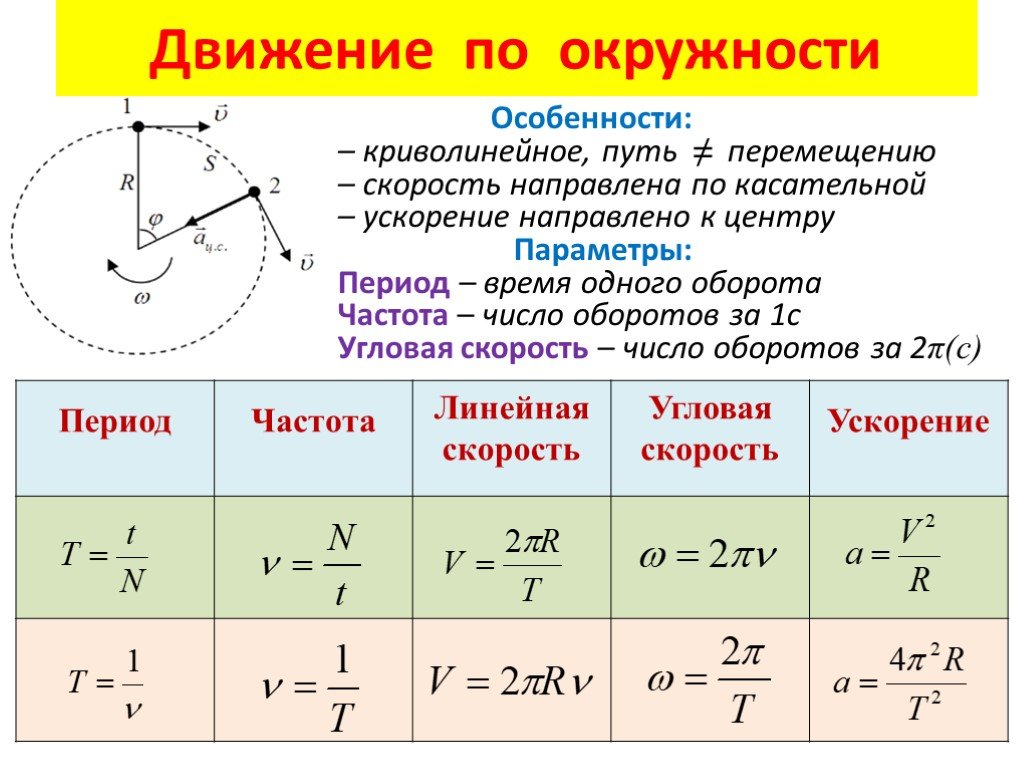

Вопрос №6. Принцип реактивного движения. Движение тел с переменной массой. Формула Мещерского. Формула Циолковского

Под реактивным понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела. При этом возникает т.н. реактивная сила, сообщающая телу ускорение.

Уравнение Мещерского — основное уравнение в механике тел переменной массы:

Формула Циолковского определяет скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической:

13.4 Движение по кривой

Мы уже видели, что если $t$ — это время, а местоположение объекта ${\bf r}(t)$, то производная ${\bf r}'(t)$ есть вектор скорости ${\bf v}(t)$. Поскольку ${\bf v}(t)$ — вектор, описывающий изменение ${\bf r}(t)$, так что ${\bf v}'(t)$ вектор, описывающий, как изменяется ${\bf v}(t)$, а именно, ${\bf a}(t)={\bf v}'(t)={\bf r}”(t)$ вектор ускорения .

Пример 13.4.1 Предположим, что ${\bf r}(t)=\langle \cos t,\sin t,1\rangle$. затем ${\bf v}(t)=\langle -\sin t,\cos t,0\rangle$ и ${\bf a}(t)=\langle -\cos t,-\sin t,0\rangle$. Это описывает движение объекта, движущегося по окружности радиуса 1, с постоянной Координата $z$ 1. Вектор скорости, разумеется, касается изгиб; обратите внимание, что ${\bf a}\cdot{\bf v}=0$, поэтому ${\bf v}$ и ${\bf a}$ перпендикулярны. На самом деле нетрудно видеть, что ${\bf a}$ указывает от местоположения объекта к центру окружности путь в $(0,0,1)$. $\квадрат$

Напомним, что единичный касательный вектор определяется выражением ${\bf T}(t)= {\bf v}(t)/|{\bf v}(t)|$, поэтому ${\bf v}=|{\bf v}|{\bf T}$. Если мы возьмем производная от обеих частей этого уравнения, мы получаем $$\eqalignno{{\bf a}&=|{\bf v}|'{\bf T}+|{\bf v}|{\bf T}’.& (13.4.1)\кр }$$ Также напомним определение кривизны, $\kappa=|{\bf T}’|/|{\bf v}|$ или $|{\bf T}’|=\kappa|{\bf v}|$. Окончательно, напомним, что мы определили единичный вектор нормали как ${\bf N}={\bf T}’/|{\bf T}’|$, поэтому ${\bf T}’=|{\bf T}’|{\bf N}= \каппа|{\bf v}|{\bf N}$.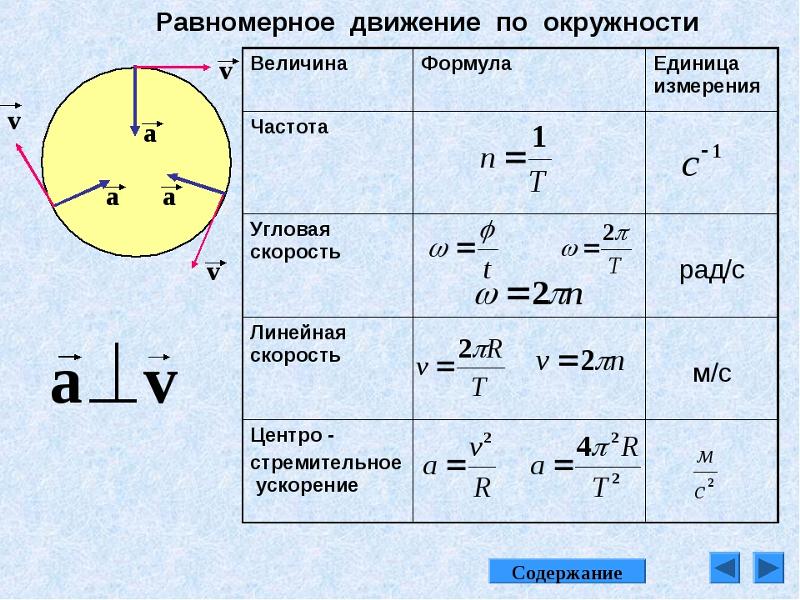

2$, обратите внимание, что эффект скорости увеличивается; удвоение скорости вокруг кривой учетверяет значение $a_N$. Вы чувствуете эффект от это как сила, толкающая вас к внешней стороне кривой, “центробежная сила.” 9т\угол$. Вычислить ${\bf v}$, ${\bf a}$, $a_T$ и $a_N$. (отвечать)

Пример 13.4.6 Предположим, что объект движется так, что его ускорение определяется выражением ${\bf a}=\langle -3\cos t,-2\sin t,0\rangle$. В момент времени $t=0$ объект находится в точке $(3,0,0)$, а вектор его скорости равен $\langle 0,2,0\угол$. Найдите ${\bf v}(t)$ и ${\bf r}(t)$ для объекта. (отвечать)

Пример 13.4.7 Предположим, что объект движется так, что его ускорение определяется выражением ${\bf a}=\langle -3\cos t,-2\sin t,0\rangle$. В момент времени $t=0$ объект находится в точке $(3,0,0)$, а вектор его скорости равен $\langle 0,2.1,0\угол$. Найдите ${\bf v}(t)$ и ${\bf r}(t)$ для объекта. (отвечать)

Пример 13.4.8 Предположим, что объект движется так, что его ускорение определяется выражением ${\bf a}=\langle -3\cos t,-2\sin t,0\rangle$. В момент времени $t=0$ объект находится в точке $(3,0,0)$, а вектор его скорости равен $\langle 0,2,1\угол$. Найдите ${\bf v}(t)$ и ${\bf r}(t)$ для объекта. (отвечать)

Пример 13.4.9 Предположим, что объект движется так, что его ускорение определяется выражением ${\bf a}=\langle -3\cos t,-2\sin t,0\rangle$. В момент времени $t=0$ объект находится в точке $(3,0,0)$, а вектор его скорости равен $\langle 0,2.1,1\угол$. Найдите ${\bf v}(t)$ и ${\bf r}(t)$ для объекта. (отвечать)

Пример 13.4.10 Опишите ситуацию, в которой нормальная составляющая ускорение равно 0, а тангенциальная составляющая ускорения равна ненулевой. Возможна ли тангенциальная составляющая ускорения быть равным 0, в то время как нормальная составляющая ускорения отлична от нуля? Объяснять. Наконец, возможно ли, чтобы объект двигался (не был неподвижным)? так что и тангенциальная, и нормальная составляющие ускорения равны 0? Объяснять.

Ускорение во время полета с двигателем

Ускорение во время полета с двигателем

Силы на модели ракеты меняются резко как по величине, так и по направлению на протяжении типичного полет. На этом рисунке показаны ускорения ракеты во время работы двигателя. часть полета после взлета. Ускорение возникает в ответ на действие Ньютона. первый закон движения. чистая внешняя сила применяется к ракете. Во время активной части полета ракета подвергается силы веса, тяги, и перетащите.

Ускорение модели ракеты с двигателем описывается выражением Второй закон Ньютона. В общем случае закон Ньютона предписывает, что сила, действующая на объект (F), равна равно изменению количества движения (масса, умноженная на скорость) в единицу времени. Если предположить, что масса постоянна, уравнение становится более знакомым сила равна массе (m), умноженной на ускорение (a). (F = м * а) Сила и ускорение являются векторными величинами, имеющими как модуль, так и направление, в то время как масса является скаляром и имеет только величину. (Математики будет часто обозначать вектор маленькой стрелкой над символом). Для модель ракеты, тяга (Т) силы сопротивления (D) изменяются со временем (t). Для обозначения что тяга, сопротивление и, следовательно, ускорение, все функции времени мы включаем символ «(t)» рядом с этими переменными. Тогда второй закон Ньютона записывается как [F(t) = m * a(t)]. Мы можем использовать алгебра для решения ускорений: [ a (t) = F (t) / m ].

Под В идеальных условиях траектория полета модели ракеты была бы идеально вертикально. На практике траектория полета наклонен из-за действие ветра. Угол, под которым траектория полета совершает с горизонталью называется углом наклона (б). Если мы рассмотрим силы в вертикальном (v) и горизонтальном (h) направлениях, получаем два уравнения для ускорения; один для вертикали и один для горизонтальный. «cos b» и «sin b» — тригонометрические функции. косинус и синус угла наклона. Вертикальное ускорение определяется следующим уравнением: ( av(t) = ([T(t) – D(t)] * sin b – W ) / m ). Горизонтальное ускорение определяется выражением: (ah(t) = ([T(t) – D(t)] * cos b)/m). Если бы траектория полета была совершенно вертикально, угол наклона будет 90 градусов.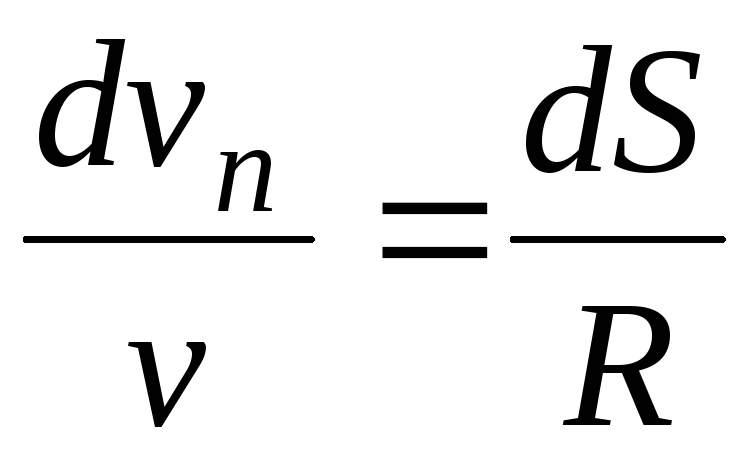 косинус 90 градусов равен нулю, поэтому горизонтальное ускорение будет нуль. Синус 90 градусов равен 1,0, поэтому вертикальное ускорение будет равно тяге минус сопротивление минус вес, деленный на массу.

Чтобы ракета летела как можно выше, нам нужна вертикальная ускорение должно быть максимально высоким. Учитывая ускорение уравнений, это говорит нам о том, что мы хотим, чтобы угол наклона был 90 градусов, тяга должна быть высокой, лобовое сопротивление низким, а вес низким. Все, что мы можем сделать с моделью ракеты, чтобы выполнить эти четыре цели улучшат характеристики ракеты.

Обратите внимание, что для модельной ракеты вес топлива относительно небольшой. к массе всего автомобиля. Итак, при определении ускорения мы можно предположить, что вес (или масса) остается почти постоянным. Это другое от полномасштабной ракеты, в которой топливо составляет большую часть от веса транспортного средства. Изменения веса (массы) пороха должны быть включены в любое определение скорости или ускорения во время полет.