Ускорение формула движения: Ускорение (видео) | Прямолинейное движение

{2}}\]. Иными словами, это звучит так: изменение расстояния в секунду, при изменении скорости движения в секунду (единицу времени).

Из формулы ускорения,  можно выразить и определить конечную скорость движения.

\[V=V_{n}+\alpha \Delta t\]

Однако, следует учесть следующее: что при вычислении по данной формуле, обязательно условие: ускорение, должно иметь постоянное значение.

Виды и характеристики ускорения:

В физике, также существует термин, как среднее ускорение.

Среднее ускорение — это изменение величины скорости к промежутку времени, при котором произошло данное изменение.

Данный вид ускорения, определяется по формуле, схожей с  определением равноускоренного ускорения.

\[\bar{\alpha}=\frac{\bar{V}_{1}-\bar{V}_{0}}{t}=\frac{\Delta \bar{V}}{t}\]

Ускорение может быть выражено, также отрицательном знаком. Это происходит, если начальная скорость имеет значение большее, чем конечная, Таким образом происходит процесс замедления.

{2}}\]

F — сила тяжести, Н;

M — масса первого тела (часто планеты), кг;

m — масса второго тела, кг;

R — расстояние между телами, м;

G — гравитационная постоянная;

G = 6,67 × 10^-11м³·кг^-1·с^-2.

Принцип вычисления ускорения при движении по окружности

При движении не прямолинейной поверхности, величина его будет изменяться.

Даже при условии, что модуль скорости остается величиной неизменной. В таких случаях ускорение вычисляется по следующему принципу:

• разность начальной и конечной скоростей;
• применение правил векторной математики;
• учитывается изменение направления.

Для определения результата ускорения при, таких условиях. Нужно применить и знать два определения.

1. Тангенциальное ускорение. Обозначается буквой α_t, направление движения по касательной к траектории направления. Тангенциальное значение может быть равно нулю в случае, если движение по заданной окружности, является равномерным. {2}}}\]

   Рассмотрим и закрепим данную тему на примере решения задачи.

   Необходимо найти и определить значение ускорение тела, при его движении за 20 секунд от 10 до 100 км/час.

   В начальной точке, тело движется со  следующей скоростью:

   \[V_{0}=\frac{10000}{3600}=2.77_{\text {м/сек }}\]

   Определяем скорость в конце движения:

   \[V_{K}=\frac{10000}{3600}=27.77_{\text {м/сек }}\]

   Полученные значения, подставляем в формулу и вычисляем значение ускорения:

   \[\alpha=\frac{V_{1}-V_{0}}{t}\]

   \[\alpha=\frac{27,77-2,77}{20}=1,25 \mathrm{м} / \text { сек. }\]

   Ответ: ускорение равняется 1,25 м/сек.

   Вывод:

   Как видно из решенного примера, тема ускорения не является слишком сложной. Однако, как и любой технической науке, никогда нельзя расслабляться. Нужно быть внимательным и сосредоточенным. На этом и построена вся система изучения физики и других технических предметов.

   Содержание

   Ускорение – формула, определение, закон кратко (физика 9 класс)

   4. 3

   Средняя оценка: 4.3

   Всего получено оценок: 298.

   Обновлено 6 Августа, 2021

   4.3

   Средняя оценка: 4.3

   Всего получено оценок: 298.

   Обновлено 6 Августа, 2021

   Из курса физики 9 класса известно, что движение бывает равномерным и неравномерным. При неравномерном движении за равные промежутки времени материальная точка проходит разные расстояния, мгновенная скорость её движения также изменяется. Мера быстроты изменения скорости называется ускорением. Поговорим на эту тему, дадим определение ускорения, приведём его формулу.

   Ускорение движения

   Большинство движений в природе неравномерны. Если рассмотреть такое движение, то расстояния, проходимые за одинаковые промежутки времени будут разными. Следовательно, и скорость (она равна отношению пройденного расстояния ко времени прохождения) тоже будет разной.

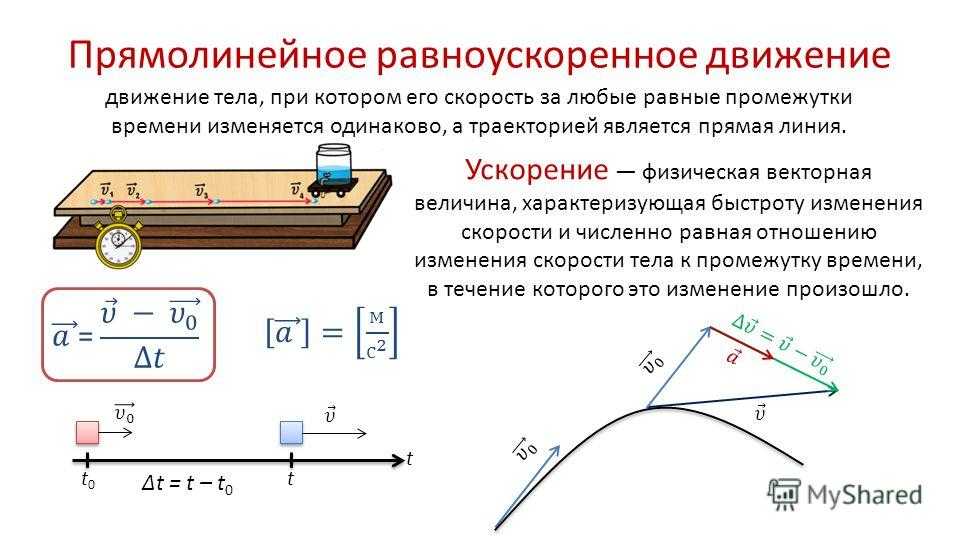
   Рис. 1. Пример неравномерного движения.

   Более того, для разных движений изменение скорости за одинаковые промежутки времени также будет неодинаково. К примеру, рассмотрим разгон мяча и автомобиля. К концу разгона и тот и другой могут достичь мгновенной скорости 50 метров в секунду. Однако автомобиль достигает такой скорости за десять секунд, а мяч — в сто раз быстрее, за одну десятую секунды. Как охарактеризовать такое различие?

   Физическая величина, характеризующая быстроту изменения скорости, называется ускорением.

   Формулу ускорения легко получить, если учесть, что скорость — это быстрота изменения координаты, а ускорение — это быстрота изменения скорости:

   $$\overrightarrow a={\overrightarrow v – \overrightarrow {v_0} \over t}$$

   где:

   • $\overrightarrow a$ — вектор ускорения;
   • $\overrightarrow {v_0}$ — вектор начальной скорости;
   • $\overrightarrow v$ — вектор скорости в момент времени $t$;
   • $t$ — время изменения скорости от $\overrightarrow {v_0}$ до $\overrightarrow v$.

   Фактически ускорение — это «скорость изменения скорости». Поэтому формула ускорения аналогична формуле скорости, только в числителе вместо координаты стоит скорость.

   Из приведённой формулы можно получить единицу измерения ускорения. Поскольку скорость в системе СИ измеряется в метрах в секунду, а время — в секундах, то ускорение получается в метрах в секунду в квадрате (иногда говорят метр в секунду за секунду).

   Рис. 2. Ускорение в физике.

   Равноускоренное движение

   По аналогии со скоростью ускорение может быть средним и мгновенным. Мгновенное ускорение — это ускорение, для которого промежуток времени измерения стремится к нулю:

   $$\overrightarrow a_{мгн}={\overrightarrow v – \overrightarrow {v_0} \over t},t\rightarrow 0$$

   В противном случае ускорение получается средним за время $t$.

   Движение, при котором мгновенное ускорение в любой момент времени остаётся постоянным и равным среднему ускорению за любой промежуток времени, называется равноускоренным. При равноускоренном движении скорость изменяется по линейному закону.

   Примером равноускоренного движения является свободное падение тела в первые секунды, когда сопротивление воздуха ещё пренебрежительно мало.

   Рис. 3. Свободное падение тела.

   Что мы узнали?

   Быстроту изменения скорости характеризует такая физическая величина, как ускорение. Единица измерения ускорения — метр в секунду за секунду. Движение, при котором мгновенное ускорение постоянно в любой момент времени, называется равноускоренным.

   Тест по теме

   Доска почёта

   Чтобы попасть сюда – пройдите тест.

   • Лиза Глазунова

     5/5

   Оценка доклада

   4.3

   Средняя оценка: 4.3

   Всего получено оценок: 298.

   ---

   А какая ваша оценка?

   Уравнения движения с постоянным ускорением

   Прямолинейное движение с равномерным ускорением (u.a.r.m.) , также известное как движение с постоянным ускорением , представляет собой прямолинейное движение с постоянным ускорением, отличным от нуля. В этом разделе мы будем изучать:

   • Понятие и свойства движения с постоянным ускорением
   • Уравнения движения с постоянным ускорением
   • Как вывести уравнения
   • Теорема Мертона

   Концепция движения с постоянным ускорением

   Движение с постоянным ускорением довольно часто встречается в вашей повседневной жизни.

   Объект, которому разрешено падать и который не встречает препятствий на своем пути (свободное падение), или лыжник, который спускается со склона непосредственно перед тем, как прибыть в зону прыжка, являются хорошими примерами этого. Движение с постоянным ускорением или равноускоренное прямолинейное движение (u.a.r.m.) имеет следующие свойства :
   • Траектория представляет собой прямую линию, поэтому нормальное или центростремительное ускорение равно нулю
   • Мгновенная скорость изменяет свою величину (скорость) равномерно: она увеличивается или уменьшается на одну и ту же величину в каждую единицу времени. Это подразумевает следующий пункт
   • Тангенциальное ускорение постоянно. Следовательно, среднее ускорение равно мгновенному ускорению для любого изучаемого периода (a=am)

   Тело движется с движение с постоянным ускорением или равномерно ускоренное прямолинейное движение (u.a. r.m.) , когда его траектория представляет собой прямую линию и его ускорение постоянно и отличается от 0 . Это означает, что скорость увеличивает или уменьшает свою величину равномерно .

   Равноускоренное прямолинейное движение

   В нашем примере автомобиль описывает н.а.м., поскольку он движется прямолинейно с постоянным ускорением, эквивалентным 2 м/с ² . [Обратите внимание, что в каждую секунду скорость и расстояние, пройденное телом, увеличиваются в зависимости от значения ускорения в предыдущую секунду.]

   Обратите внимание, что хотя в разговорной речи мы проводим различие между ускоряющимся и тормозящим телом, от с точки зрения физики, оба являются равноускоренными прямолинейными движениями . Разница в том, что в то время как один имеет положительное ускорение, другой имеет отрицательное ускорение.

   Уравнения движения с постоянным ускорением

   The equations of the constant acceleration motion or uniformly accelerated rectilinear motion (u.a.r.m.) are:

   v=v0+a⋅t

   x=x0+v0t+12at2

   Where:

   • x , x ₀ : Положение тела в данный момент времени ( x ) и в начальный момент времени ( x ₀ ). Его единицей в Международной системе (СИ) является метр (м)
   .
   • v , v ₀ : Скорость тела в данный момент времени ( v ) и в начальный момент времени ( v ₀ ). Его единицей в Международной системе является метр в секунду (м/с)
   .
   • : Ускорение кузова. Остается постоянным со значением, отличным от 0. Его единицей измерения в Международной системе является метр в секунду (м/с ² )
   • t : Время изучается. Его единицей в Международной системе является секунда ( с )

   Хотя первые являются основными уравнениями u.a.r.m. и единственные необходимые для решения упражнений, иногда полезно знать следующее выражение:

   v2=v02+2·a·∆x

   Приведенная выше формула позволяет связать скорость и пройденный путь, если известно ускорение, и может быть выведен из предыдущих, как вы можете видеть ниже.

   v=v0+a·tx=x0+v0·t+12·a·t2⇒t=v-v0a∆x=v0·t+12·a·t2⇒∆x=v0v-v0a+12·a ·в-в0а2;

   2·a·∆x=v2-v02

   Вывод уравнений движения с постоянным ускорением

   Чтобы вывести уравнений движения с постоянным ускорением или равноускоренного прямолинейного движения (u.a.r.m.) , необходимо принять во внимание, что:

   • Значение нормального или центростремительного ускорения равно ноль: an=0
   • Среднее ускорение, мгновенное ускорение и тангенциальное ускорение имеют одно и то же значение: a=aa=at=cst

   С учетом этих ограничений получаем:

   aa=aaa=ΔvΔt=v-v0t-t0=⏟t0=0x-x0t→v-v0=a⋅t→v=v0+a⋅t

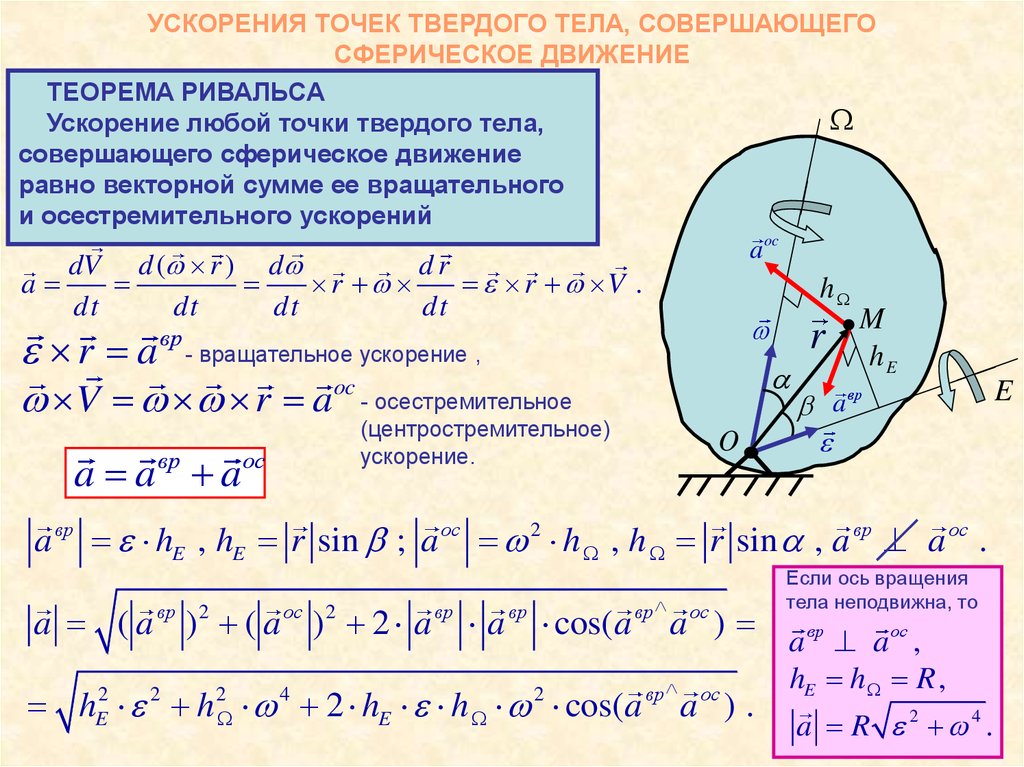
   Это первое уравнение связывает скорость тела с его ускорением при в любой момент времени и представляет собой прямую линию ( v ), наклон которой равен величине ускорения, а его координата y в начале координат является начальной скоростью ( v ₀ ). Нам нужно получить уравнение, которое позволит нам получить позицию. Существуют разные методы его вывода. Мы будем использовать теорема о средней скорости или правило равномерного ускорения Мертона :

   «Тело, движущееся с равноускоренным ускорением, за любой момент времени проходит такое же расстояние, какое прошло бы тело, движущееся с постоянной скоростью, равной средней скорости первого тела».

   Это означает, что

   ∆x=va⋅t

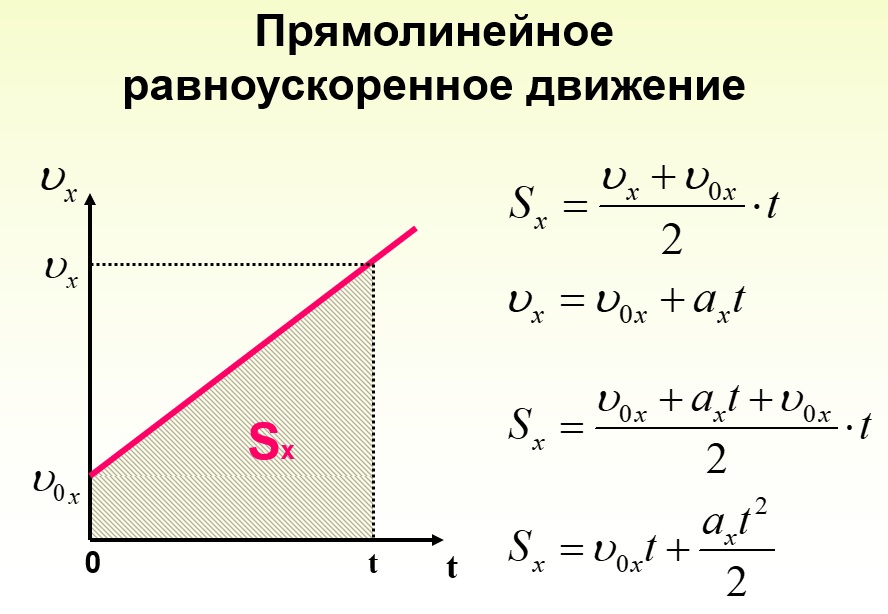
   Значение средней скорости при постоянном ускорении можно ясно увидеть на следующем рисунке:

   va=v+v02

   Если мы разовьем уравнения, которые мы видели до сих пор, мы получим уравнение положения в равноускоренном прямолинейном движении (u.a.r.m.) :

   ∆x=x-x0=va ⋅t=⏞1v+v02t=⏞2v0+at+v02t=2v0+at2t=22v0t+at22⇒x=x0+v0t+12at2

   Куда мы обращались:

   1. va=v+v02

   2. v=v0+a⋅t

   Наконец, обратите внимание, что в предыдущих уравнениях движение рассматривалось в ось х . Если мы перемещаемся по оси Y , например, в свободном падении или вертикальном старте, просто замените x на y для положения, в результате чего получится следующее уравнение:

   y=y0+v0t+12at2

   Пример

   Велосипедист начал утреннюю поездку и через 10 секунд его скорость составила 7,2 км/ч. В этот момент он видит приближающуюся собаку и тормозит на 6 секунд, пока велосипед не остановится. Рассчитайте:

   а) Ускорение до тех пор, пока он не начнет замедляться.
   b) Тормозное ускорение велосипеда.
   в) Общее пройденное расстояние.

   Решение

   21.7 Уравнения движения | Движение в одном измерении

   21.7 Уравнения движения (ESAHG)

   В этом разделе мы рассмотрим третий способ описания движения. Мы рассмотрели описание движения в терминах слова и графики. В этом разделе мы исследуем уравнения, которые можно использовать для описания движения.

   Этот раздел посвящен решению задач, связанных с равноускоренным движением. Другими словами, движение в постоянное ускорение. 9{-1}$} \text{ во время } t \\ \vec{s} & = \text{смещение} \text{(м)} \end{align*}

   Галилео Галилей из Пизы, Италия, первым определил правильный математический закон ускорения: общее пройденное расстояние, начиная с состояния покоя, пропорционально квадрату времени. Он также пришел к выводу, что объекты сохраняют свою скорость, если на них не действует сила — часто трение, принял аристотелевскую гипотезу о том, что объекты «естественно» замедляются и останавливаются, если не действует сила на них. Этот принцип был включен в законы движения Ньютона (1-й закон). 9{2} + 2\vec{a}\Delta \vec{x} \qquad (4) \конец{выравнивание*}

   Вопросы могут быть самые разные, но всегда будет работать следующий метод ответа на них. Используйте это, когда пытаясь ответить на вопрос, связанный с движением с постоянным ускорением. Вам нужны любые три известные величины (\({\vec{v}}_{i}\), \({\vec{v}}_{f}\), \(\Delta \vec{x}\), \(t\) или \(\vec{a}\)) чтобы вычислить четвертый.

   Стратегия решения проблем:

   1. Внимательно прочитайте вопрос, чтобы определить приведенные количества. Запишите их.

   2. Определите используемое уравнение. Запишите!!!

   3. Убедитесь, что все значения указаны в правильных единицах, и заполните их в своем уравнении.

   4. Подсчитайте ответ и проверьте единицы измерения.

   Рабочий пример 7: Уравнения движения 9{-1}$} \\ \Дельта\vec{x} & = \text{725}\text{м} \\ т & = \текст{10}\текст{с} \\ \vec{a} & = ? \конец{выравнивание*}

   Найдите уравнение движения, связывающее заданную информацию с ускорением

   Если вам трудно найти правильное уравнение, найдите неданную величину, а затем найдите уравнение, в котором есть эта величина.

   Мы можем использовать

   \[\ Delta \ vec {x} = {\ vec {v}} _ {i} t + \ frac {1} {2} \ vec {a} {t} ^ {2} \] 9{-1}$} \text{ (поскольку объект начинается с состояния покоя)} \\ \Delta \vec{x} & = \text{64}\text{m} \\ т & = \текст{4}\текст{с} \\ \vec{a} & = ? \\ \vec{v}_{f} & = ? \\ т & = ? \text{ на половине расстояния } \Delta \vec{x} = \text{32}\text{ м} \\ \Дельта\vec{x} & = ? \text{ в два раза быстрее } t \text{2}\text{ s} \конец{выравнивание*}

   Все величины указаны в единицах СИ. {-1}$} \text{ Восток} \end{выравнивание*} 9{-1}$}\) в \(\text{8}\) \(\text{s}\). Рассчитайте требуемое ускорение и общее расстояние, пройденное за это время.

   Решение еще не доступно

   Расширение: Нахождение уравнений движения (ESAHH)

   Следующее не является частью учебного плана и может рассматриваться как дополнительная информация.

   Вывод уравнения 1

   По определению ускорения:

   \[\vec{a}=\frac{\Delta \vec{v}}{t}\]

   , где \(\Delta \vec{v}\) – изменение скорости, т.е. \(\Delta v={\vec{v}}_{f} – {\vec{v}}_{i}\ ). Таким образом, мы есть

   \начать{выравнивать*} \vec{a} & = \frac{{\vec{v}}_{f} – {\vec{v}}_{i}}{t} \\ {\ vec {v}} _ {f} & = {\ vec {v}} _ {i} + \ vec {a} t \конец{выравнивание*}

   Вывод уравнения 2

   Мы видели, что смещение можно рассчитать по площади под графиком зависимости скорости от времени. Для равноускоренное движение самая сложная диаграмма зависимости скорости от времени, которую мы можем иметь, это прямая линия. Посмотрите на график ниже — он представляет собой объект с начальной скоростью \({\vec{v}}_{i}\) , разогнавшись до конечной скорости \({\vec{v}}_{f}\) за общее время т .

   Чтобы рассчитать конечное перемещение, мы должны вычислить площадь под графиком – это как раз площадь прямоугольник, добавленный к площади треугольника. Эта часть графика заштрихована для ясности.

   \начать{выравнивать*} {\ text {Площадь}} _ {△} & = \ frac {1} {2} b \ times h \\ & = \frac{1}{2} t \times \left({v}_{f} – {v}_{i}\right) \\ & = \frac{1}{2}{v}_{f}t – \frac{1}{2}{v}_{i}t \end{выравнивание*}\begin{выравнивание*} {\ text {Площадь}} _ {\ квадрат} & = l \ раз b \\ & = t\times {v}_{i} \\ & = {v}_{i}t \end{выравнивание*}\begin{выравнивание*} \text{Перемещение} & = {\text{Площадь}}_{\квадрат} + {\text{Площадь}}_{△} \\ \Delta \vec{x} & = {v}_{i}t + \frac{1}{2}{v}_{f}t – \frac{1}{2}{v}_{i} т\\ \ Delta \ vec {x} & = \ frac {\ left ({v} _ {i} + {v} _ {f} \ right)} {2} t \конец{выравнивание*} 9{2} \конец{выравнивание*}

   Вывод уравнения 4

   Это уравнение получено путем исключения переменной времени в приведенном выше уравнении. {2} + 2 \ vec {a} \ Delta \ vec {x} \конец{выравнивание*}

   Это дает нам конечную скорость с точки зрения начальной скорости, ускорения и смещения и составляет не зависит от переменной времени.

   Реальные приложения (ESAHI)

   То, что мы узнали в этой главе, можно непосредственно применить к безопасности дорожного движения. Мы можем проанализировать отношения между скоростью и тормозным путем. Следующий рабочий пример иллюстрирует это приложение.

   Рабочий пример 9: Тормозной путь 9{-2}$}\). Время его реакции на удар тормоза составляет \(\text{0,5}\) секунд. Врежется ли грузовик в ребенка?

   Проанализируйте проблему и определите, какая информация предоставляется

   Полезно нарисовать временную шкалу, подобную этой:

   Нам нужно знать следующее:

   • Какое расстояние преодолевает водитель, прежде чем нажать на тормоз.

   • Через сколько времени грузовик остановится после нажатия на тормоз.