Главная
Ускорение формула точки: Скорость и ускорение точки

Ускорение формула точки: Скорость и ускорение точки

Содержание

1.1.8 Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки

Видеоурок: Движение по окружности

Лекция: Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки

Движение по окружности

Траектория движения – окружность.

Так как скорость – векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться.


Любое криволинейное движение можно свести к нескольким движениям по окружности. Примером данного движения является бег по стадиону, ход стрелки часов, прогулка на корде лошади и другое.Основные характеристики движения

1. Линейная скорость


Мгновенная скорость (линейная) – на протяжении всего движения меняет свое направление вдоль касательной к траектории.
Так как траектория движения точки – окружность, то в качестве пути в числителе находится формула длины перемещения.

Поэтому формула мгновенной скорости приобретает следующий вид, где Т – период:

2. Центростремительное ускорение


Направлено перпендикулярно к линейной скорости на протяжении всего движения.

Центростремительное ускорение определяется по формуле:

3. Период вращения


Период вращения – это величина, определяющая время, за которое тело делает одно полное вращение.

Период – это скалярная величина. Основной единицей периода является [Т]=1с.  

Период определяется по формуле:

где N – количество оборотов, t – время, за которое они были совершены.


4. Частота вращения


Определяет, насколько часто совершаются обороты в единицу времени.

Частота – скалярная величина. Измеряется в [n] = 1с-1.

Частота определяется по формуле:

5. Угловое перемещение


Угловое перемещение – величина, которая определяется углом поворота радиуса, соединяющего центр описываемой окружности, с точкой, где находится тело, относительно начального его положения.


Данная величина может измеряться в градусной или радианной мере углов.

6. Угловая скорость


Это значение, которое определяет, насколько изменяется угловое перемещение со временем.

Измеряется в 1 рад/с.Определяется по формуле:
где
– угловая скорость материальной точки, 1/с
– угол поворота радиус – вектора, рад- промежуток времени, с

Угловое перемещение связано с линейной скоростью и центростремительным ускорением следующей формулой:



Ускорение точки равно нулю если. Ускорение точки. Физический смысл вектора ω

Пусть теперь известна функция .

На рис. 5.10
и
 векторы скорости движущейся точки в моменты t и t . Чтобы получить приращение вектора скорости
перенесем параллельно вектор
в точкуМ :

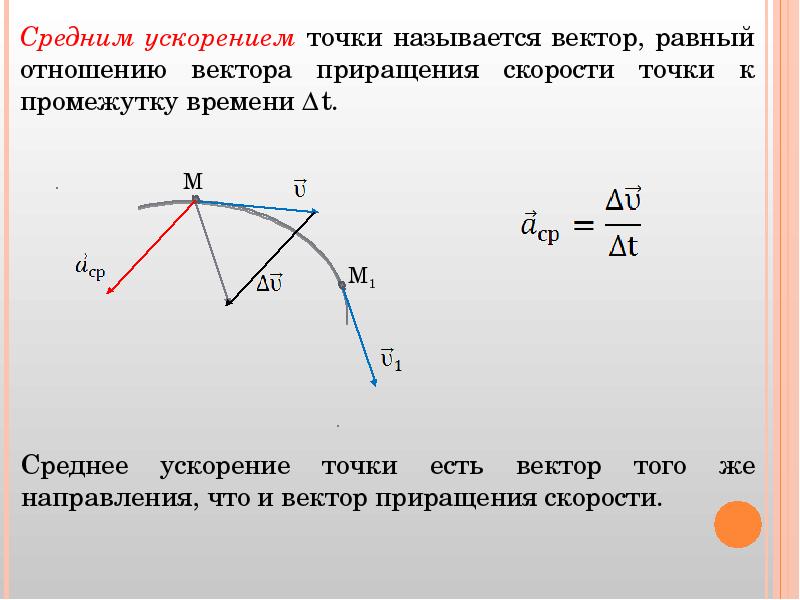
Средним ускорением точки за промежуток времени t называется отношение приращения вектора скорости
к промежутку времениt :

Следовательно, ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной радиус-вектора по времени

. (5.11)

Ускорение точки это векторная величина, характеризующая быстроту изменения вектора скорости по времени.

Построим годограф скорости (рис.5.11). Годографом скорости по определению является кривая, которую вычерчивает конец вектора скорости при движении точки, если вектор скорости откладывается из одной и той же точки.

Определение скорости точки при координатном способе задания её движения

Пусть движение точки задано координатным способом в декартовой системе координат

х = x (t ), y = y (t ), z = z (t )

Радиусвектор точки равен

.

Так как единичные векторы
постоянны, то по определению

. (5.12)

Обозначим проекции вектора скорости на оси

Ох , Оу и Oz через V x , V y , V z

(5.13)

Сравнивая равенства (5.12) и (5.13) получим


(5.14)

В дальнейшем производную по времени будем обозначать точкой сверху, т.е.

.

Модуль скорости точки определяется формулой

. (5.15)

Направление вектора скорости определяется направляющими косинусами:

Определение ускорения точки при координатном способе задания её движения

Вектор скорости в декартовой системе координат равен

.

По определению

Обозначим проекции вектора ускорения на оси Ох , Оу и Oz через а x , а y , а z соответственно и разложим вектор скорости по осям:

. (5.17)

Сравнивая равенства (5.16) и (5.17) получим

Модуль вектора ускорения точки вычисляется аналогично модулю вектора скорости точки:

, (5. 19)

а направление вектора ускорения  направляющими косинусами:

Определение скорости и ускорения точки при естественном способе задания её движения

Орты илежат всоприкасающейся плоскости , орты ивнормальной плоскости , орты и в спрямляющей плоскости .

Полученный трехгранник называется естественным.

Пусть задан закон движения точки s = s (t ).

Радиус вектор точкиМ относительно какойлибо фиксированной точки будет сложной функцией времени

.

Из дифференциальной геометрии известны формулы СерреФрене, устанавливающие связи между единичными векторами естественных осей и векторфункцией кривой

где   радиус кривизны траектории.

Используя определение скорости и формулы СерреФрене, получим:

. (5.20)

Обозначая проекцию скорости на касательную и учитывая, что вектор скорости направлен по касательной, имеем

. (5.21)

Сравнивая равенства (5.20) и (5.21), получим формулы для определения вектора скорости по величине и направлению

Величина положительна, если точкаМ движется в положительном направлении отсчета дуги s и отрицательна в противоположном случае.

Используя определение ускорения и формулы СерреФрене, получим:

Обозначим проекцию ускорения точки на касательную, главную нормаль и бинормаль
соответственно.

Тогда ускорение равно

Из формул (5.23) и (5.24) следует, что вектор ускорения всегда лежит в соприкасающейся плоскости и раскладывается по направлениям и:

(5.25)

Проекция ускорения на касательную
называетсякасательным или тангенциальным ускорением . Оно характеризует изменение величины скорости.

Проекция ускорения на главную нормаль
называется

нормальным ускорением . Оно характеризует изменение вектора скорости по направлению.

Модуль вектора ускорения равен
.

Если иодного знака, то движение точки будет ускоренным.

Если иразных знаков, то движение точки будет замедленным.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора — вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами — единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? «Наверное какой-то жуткий», подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y , чтобы вместо синуса подставить в нее формулу изменения x :

В итоге жуткий закон движения точки оказался обычной параболой , ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу:

как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки — это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам . В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора — это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике . А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Механическим движением называют изменение с течением вре­мени положения в пространстве точек и тел относительно какого-либо основного тела, с которым скреплена система отсчета. Кинема­тика изучает механическое движение точек и тел независимо от сил, вызывающих эти движения. Всякое движение, как и покой, относи­тельно и зависит от выбора системы отсчета.

Траекторией точки называют непрерывную линию, описывае мую движущейся точкой. Если траектория – прямая линия, то движе­ние точки называют прямолинейным, а если – кривая, то – криволиней­ным. Если траектория – плоская, то движение точки называют плоским.

Движение точки или тела, считается заданным или известным, если для каждого момента времени (t) можно указать положение точ­ки или тела относительно выбранной системы координат.

Положение точки в пространстве определяется заданием:

а) траектории точки;

б) начала О 1 отсчета расстояния по траектории (Рису­нок 11): s = О 1 М – криволиней­ная координата точки М;

в) направления положи­ тельного отсчета расстояний s;

г) уравнения или закона движения точки по траектории: S = s(t)

Скорость точки. Если точ­ка за равные промежутки време­ни проходит равные отрезки пути, то ее движение называют равномерным. Скорость равно­мерного движения измеряется отношением пути з, пройденно­го точкой за некоторый проме­жуток времени, к величине это­го промежутка времени: v = s/1. Если точка за равные промежут­ки времени проходит неравные пути, то ее движение называют неравномерным. Скорость в этом случае также переменна и являет­ся функцией времени: v = v(t). Рассмотрим точку А, которая перемещается по заданной тра­ектории по некоторому закону s = s(t) (Рисунок 12):

За промежуток времени t т. А переместилась в положение А 1 по дуге АА. Если промежуток времени Δt мал, то дугу АА 1 можно заменить хордой и найти в первом приближении величину средней скорости движения точки v cp = Ds/Dt. Средняя скорость направлена по хорде от т. А к т. А 1 .

Истинная скорость точки направлена по касательной к траекто­рии, а ее алгебраическая величина определяется первой производной пути по времени:

v = limΔs/Δt = ds/dt

Размерность скорости точки: (v) = длима/время, например, м/с. Если точка движется в сторону увеличения криволинейной координаты s, то ds > 0, и следовательно, v > 0, а в противном случае ds

Ускорение точки. Изменение скорости в единицу времени опреде­ляется ускорением. Рассмотрим движение точки А по криволинейной траектории за время Δt из положения A в положение A 1 . В положении A точка имела скорость v , а в положении A 1 – скорость v 1 (Рисунок 13). т.е. скорость точки изменилась по величине и направлению. Геометрическую разность, скоростей Δv найдем, построив из точки A вектор v 1.

Ускорением точки называют вектора “, равный первой производной от вектора скорости точки по времени:

Найденный вектор ускорения а может быть разложен на две взаимно-перпендикулярные составляющие но касательной и нормали к траек­тории движения . Касательное ускорение а 1 совпадает по на­правлению со скоростью при ускоренном движении или противополож­но ей при замененном движении. Оно характеризует изменение величи-ны скорости и равно производной от величины скорости по времени

Вектор нормального ускорения а направлен по нормали (пер­пендикуляру) к кривой в сторону вогнутости траектории, а модуль его равен отношению квадрата величины скорости точки к радиусу кри­визны траектории в рассматриваемой точке.

Нормальное ускорение характеризует изменение скорости по
направлению.

Величина полного ускорения: , м/с 2

Виды движения точки в зависимости от ускорения.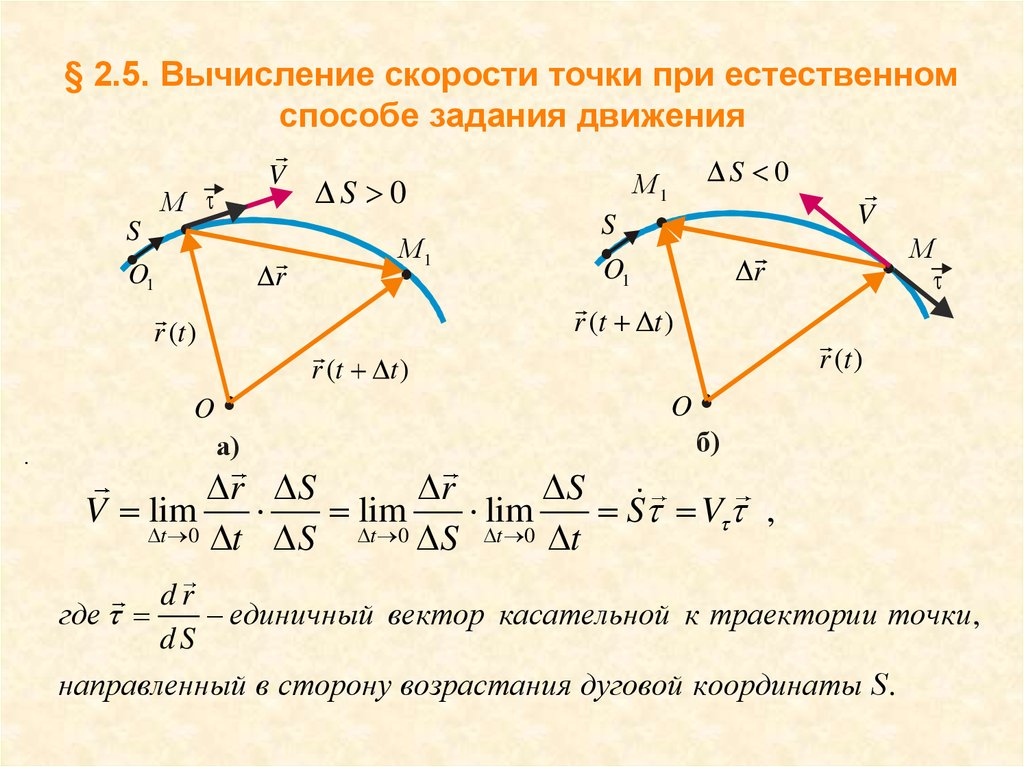

Равномерное прямолинейное движение (движение по инерции) характеризуется тем, что скорость движения постоянна, а радиус кри­визны траектории равен бесконечности.

То есть, r = ¥, v = const, тогда ; и поэтому . Итак, при движении точки по инерции ее ускорение равно нулю.

Прямолинейное неравномерное движение. Радиус кривизны траектории r = ¥, а n = 0, поэтому и а = а t и а = а t = dv/dt.

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

Рис. 1.8. Среднее ускорение. В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с 2 , то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

V 2 > v 1

а направление вектора ускорения совпадает с вектором скорости

Если скорость тела по модулю уменьшается, то есть

V 2

то направление вектора ускорения противоположно направлению вектора скорости Иначе говоря, в данном случае происходит замедление движения , при этом ускорение будет отрицательным (а

Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Введем единичный вектор τ, связанный с движущейся точкой A и направленный по касательной к траектории в сторону возрастания дуговой координаты (рис. 1.6). Очевидно, что τ – переменный вектор: он зависит от l. Вектор скорости v точки A направлен по касательной к траектории, поэтому его можно представить так

где v τ =dl/dt – проекция вектора v на направление вектора τ, причем v τ – величина алгебраическая. Кроме того, |v τ |=|v|=v.

Продифференцируем (1.22) по времени

(1.23)

Преобразуем последний член этого выражения

(1.24)

Определим приращение вектора τ на dl (рис. 1.7).


Как видно из рис. 1.7, угол , откуда , причем при .

Введя единичный вектор n нормали к траектории в точке 1, направленный к центру кривизны, запишем последнее равенство в векторном виде

Подставим (1.23) в (1.24) и полученное выражение в (1.22). В результате найдем

(1.26)

Здесь первое слагаемое называют тангенциальным a τ , второе – нормальным a n .

Таким образом, полное ускорение a точки может быть представлено как геометрическая сумма тангенциального и нормального ускорений.

Модуль полного ускорения точки

(1.27)

Направлено оно в сторону вогнутости траектории под углом α к вектору скорости, причем .

Если угол α острый, то tgα>0, следовательно, dv/dt>0, так как v 2 /R>0 всегда.

В данном случае величина скорости возрастает с течением времени – движение называют ускоренным (рис. 1.8).

В том случае, когда скорость с течением времени уменьшается по величине, движение называется замедленным (рис. 1.9).

Если же угол α=90°, tgα=∞, то есть dv/dt=0. В этом случае скорость с течением времени по величине не изменяется, а полное ускорение будет равно центростремительному

(1.28)

В частности, полное ускорение равномерного вращательного движения (R=const, v=const) есть центростремительное ускорение, по величине равное a n =v 2 /R и направленное все время к центру.

При прямолинейном движении, наоборот, полное ускорение тела равно тангенциальному. В данном случае a n =0, так как прямолинейную траекторию можно считать окружностью бесконечно большого радиуса, а при R→∞; v 2 /R=0; a n =0; a=a τ .

Ускорение точки при ее движении по окружности в физике

Ускорение точки при ее движении по окружности:

При равномерном прямолинейном движении ускорение равно нулю. А почему ускорение возникает при движении по окружности? Как оно направлено? Чему равен его модуль?

Пусть тело (рассматриваемое как материальная точка) движется по окружности радиусом R со скоростью, модуль которой не изменяется

Найдем ускорение тела в точке А. Перенесем вектор в эту точку и построим вектор Получились подобные равнобедренные треугольники ACD и ОАВ. Из их подобия следует:

где — модуль изменения скорости, — модуль перемещения. Разделим обе части равенства (2) на

При малых отношение практически равно модулю скорости тела а отношение — модулю его ускорения а в той же точке. В результате равенство (3) примет вид  откуда


Формула (4) определяет модуль ускорения в случае движения тела по окружности при

А каково направление ускорения Оно совпадает с направлением вектора при малых Из рисунка 92 видно, что чем меньше и вместе с ним угол тем направление вектора  ближе к направлению на центр окружности.

Значит, ускорение направлено по радиусу к центру окружности. Поэтому его называют центростремительным. В то же время вектор перпендикулярен скорости (т. е. направлен по нормали к ней). Поэтому ускорение называют также и нормальным ускорением.

А как связано центростремительное ускорение с угловой скоростью? Подставляя в формулу (4) выражение находим:

Отсюда, учитывая, что получим еще две полезные формулы:

Выведите самостоятельно выражение для центростремительного ускорения через угловую и линейную скорости:

Для любознательных:

А как направлено ускорение тела, движущегося по окружности, если модуль его скорости

На рисунке 93, а (вид сверху) мчащийся по кольцевой трассе автомобиль набирает скорость. Ускорение автомобиля равно сумме двух составляющих: Центростремительное ускорение обусловлено изменением направления скорости. А касательное к траектории ускорение возникает из-за изменения модуля скорости. При наборе скорости вектор направлен так же, как а вектор составляет с острый угол.

На рисунке 93, б автомобиль тормозит. Модуль скорости уменьшается, составляющая направлена противоположно вектору а угол между ускорением и скоростью  — тупой. В обоих случаях модуль ускорения
 

Главные выводы:

  1. Тело, движущееся по окружности со скоростью, модуль которой обладает центростремительным ускорением.
  2. Центростремительное ускорение перпендикулярно скорости и направлено к центру окружности.
  3. Модуль центростремительного ускорения

Пример решения задачи:

Период вращения первого колеса в 4 раза больше периода вращения второго колеса, а его радиус в 2 раза меньше радиуса второго колеса. У какого колеса больше центростремительное ускорение точек на его ободе? Во сколько раз?

Решение

Согласно формуле (6) отношение модулей центростремительных ускорений точек на ободе второго и первого колеса:

По условию задачи:


Тогда

Ответ:

Основные кинематические величины и их графики:

Центростремительное ускорение

Центростремительное ускорение ЦЕНТРОБЕЖНОЕ УСКОРЕНИЕ
(Редакция от 4 июля 2007 г.)

I. Введение

Цель этого упражнения – проверить уравнение центростремительного ускорения,

а = v 2 / г,

для объекта, движущегося с постоянной скоростью v по окружности радиуса r. Мы также проверим, что вектор ускорения направлен к центру круга.Воспользуемся графическим методом векторной арифметики.

I. Введение

Предположим, что объект изначально имеет вектор скорости v A , а через время Dt он имеет вектор скорости v B . Тогда его среднее ускорение за этот период равно

a avg = ( v B – v A ) / Dt.

Направление a avg совпадает с направлением v B – v A .Мы также будем называть эту разницу скоростей Dv .

a ср. = Dv / Dt.

Чтобы найти мгновенное ускорение объекта в одной точке P, мы хотели бы взять две точки, очень близкие по времени. Dt будет очень маленьким, и разница векторов Dv также будет очень маленькой. Однако нецелесообразно вычислять разность векторов таким способом, потому что небольшие ошибки при рисовании векторов приведут к большим ошибкам в разности векторов.Следовательно, в этой лабораторной работе мы возьмем довольно большие разницы во времени, и мы все равно увидим, что направление и величина среднего ускорения оказываются достаточно близкими к ожидаемым значениям.

II. Разделение работы

Студенты будут работать в группах по два , но каждый студент будет строить свои собственные конструкции. Вы будете использовать циркуль, чтобы нарисовать дугу окружности на миллиметровой бумаге. Нам нужно найти ускорение объекта, когда он движется под углом q в центре круга.Построим будем для q равным 30, 40, 50, 60, 70, 80, 90, 100, 110 и 120 градусов. Каждая группа будет делать только два из этих углов. Инструктор попросит некоторые группы выполнить 30 и 80 градусов, другие группы – 40 и 90 градусов и т. Д., Чтобы у нас была работа для всех этих углов. Позже вы разместите свои результаты на доске и вместе посмотрите рассчитанные средние ускорения.

В группе из двух учеников оба ученика должны выполнить построение для обоих углов.Когда у вас есть результаты, вы можете их сравнить. Если кажется, что разница есть, попробуйте выяснить, почему, а если нет, спросите инструктора.

III. Строительство

Установите циркуль на радиус ровно 10 см. Держите миллиметровку вертикально, поместите центр круга с левой стороны и нарисуйте дугу, начинающуюся прямо под центром и выходящую несколько дальше вашего значения q.

Мы будем думать об этой дуге как об чертеже части круга в масштабе 1 см, равном 1 м в реальном движении.

1 см на пространственной диаграмме = 1 м в реальном пространстве.

Запишите радиус вашего круга в метрах.

Точка A, начальная позиция движения, должна находиться прямо под центром, так чтобы радиус-вектор от центра к A был вертикальным. Вектор скорости, v A , составляет касательную к кривой в точке A, и поэтому должен быть проведен горизонтально. (Важная теорема плоской геометрии состоит в том, что касательная к окружности перпендикулярна радиусу в точке контакта.) Нарисуйте вектор скорости длиной 10 см. На диаграмме скоростей примем 1 см равным 1 м / с.

1 см на диаграмме скоростей = 1 м / с в реальной скорости.

Запишите скорость вашего движения в м / с.

Теперь найдите точку B, конечную позицию движения, используя транспортир. Это угол q вокруг дуги от A. Нарисуйте радиус-вектор от центра к B и проведите касательную к окружности в точке B.

Примечание. Чтобы провести касательную, не , а попытайтесь нарисовать линию, пересекающую окружность только в одной точке.Лучше использовать транспортир, чтобы нарисовать перпендикуляр к радиусу.

Нарисуйте вектор скорости v B по этой касательной длиной 10 см. (Помните, что мы рассматриваем однородное круговое движение , поэтому скорость постоянна.) Теперь нарисуйте вектор -v ​​ A с хвостом на голове v B . Вектор -v ​​ A по определению противоположен направлению v A , поэтому он горизонтален на бумаге и имеет длину 10 см.Теперь используйте определение векторного суммирования, чтобы построить v B + (-v A ) , что, в свою очередь, равно v B – v A или Dv .

IV. Направление разгона

Направление Dv – это направление ускорения. Ваш вектор указывает на центр круга?

Помните, что вектор скорости не имеет положения в пространстве.У него есть только длина и направление. (50 миль в час к северу в Чикаго – это та же скорость, что и 50 миль в час к северу в Нью-Йорке.) Найденное вами ускорение – это среднее ускорение объекта при его движении из точки A в точку B. Следовательно, на этот вектор можно смотреть так: на переместите в точку где-нибудь между A и B. Выберите точку на полпути по окружности от A до B и переместите Dv так, чтобы его хвост оказался в этой точке. Чтобы переместить его, используйте технику, описанную в части VII этой статьи.Теперь он указывает на центр круга?

V. Величина ускорения

Используя две шкалы (для расстояния и для скорости), вы можете рассчитать величину ускорения:

  1. Сначала вспомните свои значения r (в метрах) и v (в м / с).
  2. Затем найдите на диаграмме звездную величину Dv : Измерьте длину вектора линейкой в ​​см и преобразуйте в м / с. Теперь вам нужно найти временной интервал Dt.
  3. Сначала найдите период T для одного полного круга, учитывая, что длина окружности равна 2pr, а ваша скорость равна v. Это время будет в секундах.
  4. Затем найдите время, Dt, чтобы перейти от A к B для вашего строительства. Для этого используйте тот факт, что длина дуги от A до B составляет долю q / 360 от полной окружности (с q в градусах). Следовательно, Dt – это та же часть периода. Найдите дробь.
  5. Найдите Dt.
  6. Рассчитайте величину ускорения,
    a avg = Dv / Dt, Это будет в м / с 2 .

То, что вы нашли, используя определение ускорения как скорость изменения скорости , представляет собой среднее ускорение от точки A до точки B. Формула для мгновенного ускорения равна v 2 / r. Рассчитайте также это значение.

VI.Сбор результатов

Чтобы уменьшить объем рассматриваемых данных, два студента в группе должны усреднить два своих результата для каждого угла. Затем разместите на доске их значения q и avg . Затем все студенты в лаборатории должны скопировать таблицу и построить график зависимости avg от q, используя все точки. (Всего будет около 20 точек.) Нарисуйте плавную кривую как можно ближе ко всем точкам (не обязательно прямую, если она действительно не выглядит как прямая).Затем экстраполируйте кривую на q = 0. Этот предел, поскольку расстояние (и время) от точки A до точки B становится очень малым, является мгновенным ускорением. Отметьте теоретическое значение v 2 / r на вертикальной оси. Какая разница в процентах между вашим значением и этим теоретическим значением?

VII. Обратите внимание на перемещение вектора:

Важным свойством вектора является то, что он не имеет положения в пространстве. Если у вас есть вектор в точке P (как показано ниже), вы можете перерисовать его в точке Q с тем же величина и направление, и это один и тот же вектор.

На практике вы можете измерить угол b между вектором и горизонтальной линией в точке P. Затем вы используете транспортир, чтобы построить такой же угол в точке Q; затем нарисуйте вектор в точке Q, сделав его той же длины, что и на P.

Расстояние, скорость и ускорение

Расстояние, скорость и ускорение

Как упоминалось ранее, производная функции, представляющей положение частицы вдоль линии в момент времени t , является мгновенной скоростью в этот момент.Производная скорости, которая является второй производной функции положения, представляет мгновенное ускорение частицы в момент времени t .

Если y = с (t ) представляет функцию положения, то v = s ′ (t) представляет мгновенную скорость, а a = v ‘(t) = с ″ (t) представляет собой мгновенное ускорение частицы в момент времени t .

Положительная скорость указывает, что позиция увеличивается с увеличением времени, а отрицательная скорость указывает, что позиция уменьшается по времени. Если расстояние остается постоянным, то в такой промежуток времени скорость будет равна нулю. Точно так же положительное ускорение означает, что скорость увеличивается во времени, а отрицательное ускорение означает, что скорость уменьшается во времени. Если скорость остается постоянной в течение некоторого промежутка времени, тогда ускорение будет нулевым на этом интервале.

Пример 1: Положение частицы на линии определяется как s (t) = t 3 – 3 t 2 – 6 t + 5, где t измеряется в секундах, а с измеряется в футах. Находить

а. Скорость частицы в конце 2 секунды.

г. Ускорение частицы в конце 2 секунд.

Часть (а): скорость частицы

Часть (b): Ускорение частицы

Пример 2: Формула s (t) = −4.9 t 2 + 49 t + 15 дает высоту объекта в метрах после того, как он был брошен вертикально вверх из точки на высоте 15 метров над землей со скоростью 49 м / сек. Насколько высоко над землей поднимется объект?

Скорость объекта будет равна нулю в его наивысшей точке над землей. То есть v = s ′ (t) = 0, где

Высота над землей в 5 секундах

, следовательно, объект достигнет своей наивысшей точки на 137.5 м над землей.

Расчет ускорения для линейного движения

Внедрение второго закона Ньютона в мир управления движением.

Для любого приложения управления линейным перемещением решение проблемы требует как минимум трех точек данных:

  • Как далеко мне нужно переехать?
  • Насколько тяжелый груз?
  • Как быстро мне нужно туда добраться?

Эти три точки данных могут быть введены во второй закон движения Ньютона, согласно которому величина ускорения зависит от силы, действующей на него, и массы объекта.

$$ ускорение = \ frac {force} {масса} $$

Приведенное выше уравнение является основным строительным блоком всех расчетов ускорения профиля движения. Вы можете использовать это уравнение для определения максимальных теоретических ускорений, возможных для любого двигателя или исполнительного механизма, если вы знаете массу движущегося объекта и величину силы, создаваемой двигателем. Есть несколько противоположных сил, которые влияют на максимальное ускорение, например трение, сопротивление и гистерезис. С учетом потерь максимальное непрерывное ускорение, которое может быть достигнуто за счет линейного движения с прямым приводом, составляет от 5 до 10 G для приложений управления положением с обратной связью и от 10 до 20 G для приложений с синусоидальными колебаниями без обратной связи.

Несмотря на то, что существует бесконечное количество профилей движения, есть три профиля, которые лучше всего определяют ускорение для большинства приложений линейного движения.

  • треугольная
  • синусоидальный
  • трапециевидный

Треугольный профиль движения , также известный как профиль зуба пилы, является самым простым, поскольку он предполагает постоянное ускорение и замедление в профиле движения. Эта модель лучше всего подходит для понимания основных требований к вашему профилю движения.2}} $$

Профиль трапециевидного движения получен из треугольного профиля, поскольку он предполагает постоянное ускорение до тех пор, пока не будет достигнута желаемая скорость, а затем поддерживает постоянную скорость в течение некоторого времени. В этом случае вам необходимо знать две из трех переменных: время для достижения целевой постоянной скорости, заданной постоянной скорости или расстояние, доступное для достижения заданной постоянной скорости. Базовый трапециевидный профиль можно увидеть ниже.

  • Если две известные переменные время и расстояние для достижения постоянной скорости:
  • , то расчет ускорения, необходимого для ускорения до постоянной скорости, можно определить по следующей формуле:

$$ ускорение \: in \: G’s = \ frac {2 \ расстояние раз \: доступно \: до \: достичь \: \: target \: constant \: скорость \:} {(время \: до \: достичь \: цели \: постоянной \: скорости) ^ 2 \ раз ускорения \: из-за \: до \: гравитации} $$

пример

Чтобы получить ускорение, необходимо перейти на постоянную скорость после одного дюйма в 0.2}} $$

  • Если две известные переменные: скорость и время для достижения постоянной скорости:
  • , то расчет ускорения, необходимого для ускорения до постоянной скорости, можно определить по следующей формуле:

$$ ускорение \: in \: G’s = \ frac {2 \ times target \: constant \: velocity} {время \: до \: достижения \: \: target \: constant \: скорость \ раз ускорение \: due \: to \: gravity} $

пример

Чтобы получить ускорение, необходимо двигаться с постоянной скоростью 50 дюймов в секунду в 0.2}} $$

Этот тип профиля обычно используется в приложениях с большим перемещением, когда деталь должна достигать постоянной скорости. После определения ускорения в любом из этих приложений вы также можете вычислить недостающую переменную, будь то расстояние, время или скорость.

Третий общий профиль движения обычно используется в колебательных системах, это профиль синусоидального движения . 2 \ times displacement} {ускорение \: due \: to \: gravity} $$

пример

Чтобы получить ускорение, необходимое для колебания одного дюйма при частоте 20 Гц, вы подставляете это в уравнение выше, чтобы получить следующее:

$$ 20.2}} $$

  • Если две известные переменные максимальная скорость и частота колебаний в колебательной системе:
  • , то расчет ускорения, необходимого для колебания, можно определить по следующей формуле:

$$ ускорение \: in \: G’s = \ frac {2 \ times \ pi \ times frquency \: of \: осцилляция \ максимальное время \: скорость} {ускорение \: из-за \: к \: гравитации} $$

пример

Чтобы получить ускорение, необходимое для колебания на частоте 20 Гц с максимальной скоростью 50 дюймов в секунду, вы подставляете это в уравнение выше, чтобы получить следующее:

$$ 16.2}} $$

Независимо от профиля движения, основные решения для расчета ускорения дадут понимание ускорения, которое вы пытаетесь получить от системы. Понимая это, любой пользователь может проверить, какая технология лучше всего подходит для его желаемого приложения управления движением.

Угловое смещение, скорость, ускорение

Мы живем в мире, который определяется тремя пространственными измерениями и одним измерение времени.Объекты перемещаются в этом домене двумя способами. Объект переводит, или меняет адрес , с одного указать на другое. И объект вращается , или меняет ориентацию на . В общем, движение объекта включает в себя как поступательное движение во всех трех направлениях, так и вращение на ° 18 вокруг три основных оси.

На этой странице мы будем рассматривать только вращение твердого объекта вокруг одна ось.Вращение объекта аналогично перемещению в номере переменных, которые мы должны учитывать, но обозначения очень сбивают с толку, потому что он традиционно описывался с использованием греческих символов. На слайде в вверху страницы мы использовали традиционные греческие обозначения. Чтобы упростить соблюдение статьи 508, мы просто укажем названия переменных. здесь в тексте, а не использовать символьный шрифт. Theta – это символ, который выглядит как 0 с горизонтальной линией, проходящей через него. Phi – это символ, который выглядит как 0 с вертикальной линией, проходящей через него. Омега – это символ, который выглядит как фигурный w . Альфа – это символ, похожий на перекрещенную ленту.

Поскольку объект вращается вокруг оси вращения самым простым способом для описания движения использовать полярные координаты. Мы можем указать угловую ориентацию объекта на в любое время t , указав угол theta , на который объект повернулся от некоторой опорной линии.Изначально наш объект находится в ориентации «0», заданной углом тета 0 в момент времени t0 . Мы нарисовали красную линию на диске с указанием исходной ориентации. Объект вращается до тех пор, пока time t1 , а красная линия поворачивается на угол theta 1 . Мы можем определить угловое смещение – фи как разница угла между условием «0» и условием «1».

фи = тета 1 – тета 0

Угловое смещение – это векторная величина, означающая, что угловое смещение имеет размер и направление, связанные с ним.Направление важно для более поздних математических процессов, но определение немного сбивает с толку. Как объект вращается из точки «0» в точку «1», вращается вокруг оси, поэтому направление угловое смещение измеряется по оси. Положительное значение направления оси определяется правилом правой руки . Вытяните правую руку, как если бы пожать кому-нибудь руку. Согните пальцы с основанием в точке «0» и наконечниками, идущими в точку «1».Ваш большой палец указывает перпендикулярно плоскости вращения в положительном направлении вдоль оси вращения.

Угловое смещение измеряется в единицах радиан . Два радиана пи равны 360 градусов. Угловое перемещение не является длиной (не измеряется в метрах или футах), поэтому угловое смещение отличается чем линейное перемещение. Поскольку твердый объект вращается вокруг оси вращения, все точек объекта испытывают такое же угловое смещение, но точки дальше от оси перемещаются дальше, чем точки ближе к оси.На слайде рассматриваем два очка; один расположен на радиусе ra на краю диска, и другой расположен на радиусе rb , что меньше ra . Как объект вращается за счет углового смещения phi , точка на краю диска перемещает расстояние на по круговой траектории. Точка руб. также перемещается в круговой путь, но расстояние сбн короче, чем расстояние сбн .В основном, длина кругового пути с равна радиус r в раз больше углового смещения phi , выраженного в радианах.

для углового перемещения phi ,

s = phi * r

ra> rb

sa> sb

Угловая скорость – омега объекта изменение угла во времени.Средняя угловая скорость – это угловое смещение, разделенное по временному интервалу:

омега = (тета 1 – тета 0) / (t1 – t0)

Это средняя угловая скорость за промежуток времени от t0 до t1 , но объект может ускоряться и замедляться в течение определенного промежутка времени. В любой момент объект может иметь угловую скорость, отличную от средней.Если мы сократим разница во времени вплоть до очень маленького (дифференциального) размера, мы можем определить мгновенная угловая скорость – это дифференциальное изменение угла, деленное на дифференциальное изменение во времени;

омега = д тета / дт

где символ d / dt – это дифференциал от исчисления. Угловая скорость равна векторная величина и имеет как величину, так и направление. Направление совпадает с направлением углового смещения, от которого мы определили угловая скорость.

Угловая скорость измеряется в радиан в секунду , или оборотов в секунду или оборотов в минуту (об / мин). Угловая скорость разная чем линейная скорость, которая измеряется длиной в единицу времени (футы в секунду или метры в секунду). Все точки объекта вращаются с одинаковой угловой скоростью, но находятся дальше от ось вращения движется с тангенциальной скоростью , отличной от , чем точки ближе к оси вращения.Тангенциальная скорость измеряется по круговой траектории. s , которые мы рассматривали ранее. Касательная скорость V равна угловой скорость омега в раз больше радиуса r :

для углового перемещения phi ,

V = омега * г

ra> rb

Va> Vb

Когда мы изначально укажите вращение нашего объекта с theta 0, и т0 , мы также должны указать начальную мгновенную угловую скорость omega 0 .Аналогично в конечной позиции theta 1, и t1 , угловая скорость меняется на угловую скорость omega 1 .

Среднее угловое ускорение – альфа объекта – это изменение угловой скорости во времени.

альфа = (омега 1 – омега 0) / (t1 – t0)

Как и угловая скорость, это только средняя угловая скорость. ускорение.В любой момент объект может иметь угловое ускорение, отличное от среднего. Если мы сократим разница во времени вплоть до очень маленького (дифференциального) размера, мы можем определить мгновенное угловое ускорение быть разницей в изменении угловая скорость, деленная на дифференциальное изменение во времени:

альфа = d омега / dt

Точно так же, как силы производят линейные ускорения, a крутящий момент производит угловые ускорения.Если мы можем определить крутящие моменты на объекте и то, как крутящие моменты меняются со временем, мы можем использовать уравнения, представленные на этом слайде, для определения углового ускорения, угловая скорость и угловое смещение объекта как функция времени. Авиационные инженеры используют эту информацию для прогнозирования вращения самолета в полете, которые становятся важными для устойчивости и управление самолетом.

Действия:
Экскурсии с гидом

Навигация..


Руководство для начинающих Домашняя страница

Анализ ускорения полюсов в пространственных движениях путем обобщения скорости смены полюсов

Качение конуса

Рассмотрим конус качения, изображенный на рис. 9.

Рис. 9

Иллюстрация числового примера: качение конуса конус на горизонтальной поверхности

Пусть радиус основания, высота и наклонная высота конуса равны \ (r = 0.2 \).

Угол \ (\ varphi \) можно определить как

$$ \ begin {выровненный} \ sin (\ varphi) = \ frac {r} {R} = 0,28, \ quad \ cos (\ varphi) = \ frac {h} {R} = 0,96. \ end {align} $$

(24)

Вектор положения точки B равен

$$ \ begin {align} {\ mathbf {r}} _ {OB} = \ begin {bmatrix} 0 \\ -h \ cos (\ varphi) \\ h \ sin (\ varphi) \ end {bmatrix} \ Equiv \ begin {bmatrix} 0 \\ -b \\ c \ end {bmatrix}. \ end {align} $$

(25)

Подвижная осода просто совпадает с поверхностью конуса, а неподвижная осода – это плоскость xy .Мгновенная ось вращения и угловая скорость параллельны оси y , а касательная плоскость осей сама по себе является плоскостью xy . Используя этот \ (\ mathbf {v} _B = \ varvec {\ omega} \ times \ mathbf {r} _ {OB} \), можно получить

$$ \ begin {align} \ varvec {\ omega} = \ begin {bmatrix} 0 \\ \ omega _ {y} \\ 0 \ end {bmatrix} = \ begin {bmatrix} 0 \\ 14.2857 \\ 0 \ end {bmatrix} {\ frac {{\ hbox {rad}} } {{\ hbox {s}}}}. \ end {align} $$

(26)

Этот вектор угловой скорости можно разложить на две составляющие: угловую скорость транспортировки \ (\ varvec {\ omega} _t \) и относительную угловую скорость \ (\ varvec {\ omega} _r \): \ (\ varvec {\ omega} = \ varvec {\ omega} _t + \ varvec {\ omega} _ {r} \) [26].Относительная угловая скорость описывает вращение конуса вокруг его оси симметрии OB , в то время как угловая скорость транспортировки характеризует вращение оси симметрии вокруг оси z . Используя указанные данные,

$$ \ begin {выровнено} \ varvec {\ omega} _t = \ begin {bmatrix} 0 \\ 0 \\ \ frac {v_ {Bx}} {b} \ end {bmatrix} = \ begin {bmatrix} 0 \\ 0 \\ 4.1 \ dot {6} \ end {bmatrix} \, {{\ frac {{\ hbox {rad}}} {{\ hbox {s}}}}} \ quad \ text {and} \ quad \ varvec {\ omega} _ {r} = \ begin {bmatrix} 0 \\ 14.2857 \\ 4.1 \ dot {6} \ end {bmatrix} \, {\ frac {\ mathrm {rad}} {\ mathrm {s}}}. \ end {align} $$

(27)

Обратите внимание, что из-за ограничения качения отношение величин этих векторов равно \ (| \ varvec {\ omega} _t | / | \ varvec {\ omega} _r | = \ sin (\ varphi) = r /Р\).

Скорости точек C и D могут быть определены по формуле Эйлера, исходя из того, что скорость точек вдоль оси y равна нулю:

$$ \ begin {align} \ mathbf {v } _C = \ mathbf {v} _A + \ varvec {\ omega} _ {} \ times \ mathbf {r} _ {AC} = \ varvec {\ omega} _ {} \ times \ mathbf {r} _ {AC } = \ begin {bmatrix} 2r \ cos (\ varphi) \ omega _ {y} \\ 0 \\ 0 \ end {bmatrix} = 2 \ mathbf {v} _B = \ begin {bmatrix} 3.84 \\ 0 \\ 0 \ end {bmatrix} \, {\ frac {\ mathrm {m}} {\ mathrm {s}}}, \ end {align} $$

(28)

$$ \ begin {align} \ mathbf {v} _D = \ varvec {\ omega} _ {} \ times \ mathbf {r} _ {AD} = \ begin {bmatrix} 0 \\\ omega _ {y } \\ 0 \ end {bmatrix} \ times \ begin {bmatrix} -r \\ \ mathbf {r} \ sin (\ varphi) \\ \ mathbf {r} \ cos (\ varphi) \ end {bmatrix} = \ begin {bmatrix} r \ cos (\ varphi) \ omega _ {y} \\ 0 \\ \ mathbf {r} \ omega _ {y} \ end {bmatrix} = \ begin {bmatrix} 1,92 \\ 0 \ \ 2 \ end {bmatrix} \, {\ frac {\ mathrm {m}} {\ mathrm {s}}}.2} = \ begin {bmatrix} r \\ 0 \\ -r \ cos (\ varphi) \ end {bmatrix} = \ begin {bmatrix} 0,14 \\ 0 \\ -0,1344 \ end {bmatrix} \, \ mathrm {м}. \ end {align} $$

(31)

Кроме того, точка A совпадает с геометрическим полюсом, который обозначим \ (A_g \) следующим образом. Точки \ (A_g \), \ (P_ {g1} \) и \ (P_ {g2} \) очевидно движутся по круговым траекториям с угловой скоростью \ (\ varvec {\ omega} _t \). Радиусы этих кругов равны \ (R_ {A_g} = R = 0,5 \, \ mathrm {m} \), \ (R_ {P_ {g1}} = 0.4216 \, \ mathrm {m} \) и \ (R_ {P_ {g2}} = b = h \ cos (\ varphi) = 0.4216 \, \ mathrm {m} \) соответственно. Все соответствующие скорости смены полюсов параллельны оси x и указывают в положительном направлении. Их величину можно определить, умножив радиусы окружностей на величину \ (\ varvec {\ omega} _t \): \ (| \ varvec {\ omega} _t | = 4.1 \ dot {6} \, {{ {\ mathrm {rad}} / {\ mathrm {s}}}} \). Таким образом,

$$ \ begin {align} \ mathbf {u} _ {A_g} = \ begin {bmatrix} 2.08 \ dot {3} \\ 0 \\ 0 \ end {bmatrix} \, {\ frac {\ mathrm {m}} {\ mathrm {s}}}, \ quad \ mathbf {u} _ {P_ {1g}} = \ begin {bmatrix} 1.75 \ dot {6} \\ 0 \\ 0 \ end {bmatrix} \, {\ frac {\ mathrm {m}} {\ mathrm {s}}}, \ quad \ mathbf {u} _ {P_ {2g }} = \ begin {bmatrix} 1.92 \\ 0 \\ 0 \ end {bmatrix} \, {\ frac {\ mathrm {m}} {\ mathrm {s}}}. \ end {align} $$

(32)

Теперь, используя (17), можно определить ускорения соответствующих материальных точек A, , \ (P_1 \) и \ (P_2 \): \ (\ mathbf {a} _ {A} = \ mathbf { u} _ {A_g} \ times \ varvec {\ omega} \), \ (\ mathbf {a} _ {P_ {1}} = \ mathbf {u} _ {P_ {g1}} \ times \ varvec {\ омега} \) и \ (\ mathbf {a} _ {P_ {2}} = \ mathbf {u} _ {P_ {g2}} \ times \ varvec {\ omega} \); таким образом,

$$ \ begin {align} \ mathbf {a} _ {A} = \ begin {bmatrix} 0 \\ 0 \\ 29.2}}. \ end {align} $$

(36)

Чтобы определить \ (\ alpha _ {y} \) и \ (\ alpha _ {z} \), у нас осталось только одно уравнение: \ (c \ alpha _ {y} + b \ alpha _ {z } = a_ {Bx} \). Итак, необходимо дополнительное уравнение. Мы можем использовать это – как это было получено в Разд. 5 – в случае сферических движений \ (\ varvec {\ alpha} \) должен быть параллелен касательной плоскости аксодов, т.е. \ (\ alpha _z = 0 \). Следовательно,

$$ \ begin {align} \ alpha _ {y} = \ frac {a_ {Bx}} {c} = 7.2}}. \ end {align} $$

(37)

В качестве альтернативы можно использовать то, что \ (\ mathbf {a} _A \) перпендикулярно касательной плоскости (на самом деле, достаточно использовать \ (a_ {Ax} = 0 \)), и

$$ \ begin {align} \ mathbf {a} _B = \ mathbf {a} _A + \ varvec {\ alpha} \ times \ mathbf {r} _ {AB} + \ varvec {\ omega} _ {} \ times (\ varvec {\ omega} _ {} \ times \ mathbf {r} _ {AB}). \ end {align} $$

(38)

При таком подходе можно определить как угловое ускорение \ (\ varvec {\ alpha} \), так и ускорение точки A :

$$ \ begin {align} \ mathbf {a} _ {A} = \ begin {bmatrix} 0 \\ 0 \\ 29.2}}, \ end {align} $$

(39)

, что соответствует (33). Аналогичным образом можно получить ускорения \ (P_ {g1} \) и \ (P_ {g2} \). Как только полюсные ускорения известны, скорости изменения полюсов могут быть определены с помощью (13), что приведет к тем же результатам, что и в (32).

Обратите внимание, что, используя формулу (10), получаем

$$ \ begin {align} {\ tilde {\ mathbf {u}}} _ {P_ {g2}} = \ begin {bmatrix} 1,92 \\ 0,58 \ точка {3} \\ 0 \ end {bmatrix} \, {\ frac {\ mathrm {m}} {\ mathrm {s}}}, \ end {align} $$

(40)

из-за движения проекции точки D параллельно оси y .

Мы можем сделать вывод, что ускорения точек вдоль мгновенной оси вращения можно было бы определить несколько легче, используя полюсные скорости, чем формулу Эйлера. Кроме того, требовалась некоторая информация об ускорении точки контакта (например, \ (\ mathbf {a} _A \)) или угловом ускорении \ (\ varvec {\ alpha} \) для решения задачи по формуле Эйлера – это было мотивацией настоящего исследования.

Еще одним преимуществом предложенного решения является то, что, хотя видимое движение геометрического полюса можно описать наглядно, создание мысленного представления о векторах ускорения является более трудным.

Вращение с проскальзыванием

Прежде чем ослабить ограничение качения, мы проанализируем, как это ограничение влияет на угловую скорость и угловое ускорение. Как было указано в предыдущем разделе, величины угловой скорости транспортировки и относительной угловой скорости не являются независимыми во время прокатки:

$$ \ begin {align} | \ varvec {\ omega} _t | = | \ varvec {\ omega} _r | \ frac {r} {R}. \ end {align} $$

(41)

Угловое ускорение можно разложить аналогично, как показано на рис.9:

$$ \ begin {align} \ varvec {\ alpha} = \ varvec {\ alpha} _t + \ varvec {\ alpha} _r + \ varvec {\ omega} _t \ times \ varvec {\ omega}, \ end {align} $$

(42)

где \ (\ varvec {\ alpha} _t \) – угловое ускорение транспортировки, \ (\ varvec {\ alpha} _r \) – относительное угловое ускорение, а член \ (\ varvec {\ omega} _t \ times \ varvec {\ omega} \) в [26] называется угловым ускорением вращения. \ (\ varvec {\ alpha} _r \) и \ (\ varvec {\ alpha} _t \) характеризуют изменение величины \ (\ varvec {\ omega} _r \) и \ (\ varvec {\ omega} _t \) соответственно.Следовательно, из (41) следует, что такое же соотношение должно выполняться между соответствующими компонентами углового ускорения:

$$ \ begin {align} | \ varvec {\ alpha} _t | = | \ varvec {\ alpha} _r | \ frac {r} {R}. \ end {align} $$

(43)

Если это условие выполняется, результат \ (\ varvec {\ alpha} _ \ parallel \ Equiv \ varvec {\ alpha} _t + \ varvec {\ alpha} _r = \ varvec {\ alpha} – \ varvec {\ omega} _t \ times \ varvec {\ omega} \) всегда параллельна угловой скорости \ (\ varvec {\ omega} \), а изменение направления \ (\ varvec {\ omega} \) характеризуется термин \ (\ varvec {\ alpha} _ \ perp \ Equiv \ varvec {\ omega} _t \ times \ varvec {\ omega} \).Как показано на рис. 9, векторы \ (\ varvec {\ omega} \) и \ (\ varvec {\ alpha} _ \ perp \) охватывают касательную плоскость аксод.

Если соотношение \ (| \ varvec {\ alpha} _t | \) и \ (| \ varvec {\ alpha} _r | \) не соответствует ограничению качения, соотношение компонентов угловой скорости изменится и конус начинает скользить.

Рис. 10

Иллюстрация числового примера: скользящее движение конуса по горизонтальной поверхности. Подвижная аксода – это еще один конус, не совпадающий с контуром тела.IAR находится как раз на линии соприкосновения движущейся оси и фиксированной оси – последняя не изображена на рисунке

Рисунок 10 иллюстрирует ситуацию, когда

$$ \ begin {align} \ frac {| \ varvec {\ alpha} _t |} {| \ varvec {\ alpha} _r |} = \ frac {| \ varvec {\ omega} _t |} {| \ varvec {\ omega} _r |} = 2 \ frac {r} {R }. \ end {align} $$

(44)

Теперь эти отношения определяют геометрию другого конуса – подвижной оси – с вдвое большим углом на вершине, чем угол «материального» конуса.2}} \) и

$$ \ begin {align} \ frac {| \ varvec {\ alpha} _t |} {| \ varvec {\ alpha} _r |} = 2 \ frac {r} {R}, \ quad \ text {but} \ quad \ frac {| \ varvec {\ omega} _t |} {| \ varvec {\ omega} _r |} = \ frac {r} {R}. \ end {align} $$

(45)

Поскольку эти отношения различны, компоненты \ (\ varvec {\ alpha} \) могут быть определены на основе векторного треугольника на рис. 10, в то время как компоненты \ (\ varvec {\ omega} \) связаны друг к другу, как показано на рис.9. Сначала пусть угловая скорость равна

$$ \ begin {align} \ varvec {\ omega} = \ begin {bmatrix} 0 \\\ omega _ {y} \\ 0 \ end {bmatrix} = \ begin {bmatrix} 0 \\ 14.2857 \\ 0 \ end {bmatrix} {\ frac {\ mathrm {rad}} {\ mathrm {s}}}, \ end {align} $$

(46)

как в разд. 6.1. Предположим, что в этот начальный момент точка A находится как раз на IAR, как показано на рис. 9.

Согласно векторному треугольнику на рис. 10, компоненты углового ускорения равны

$$ \ begin { выровнено} \ varvec {\ alpha} = \ begin {bmatrix} – | \ varvec {\ omega} _t \ times \ varvec {\ omega} | \\ | \ varvec {\ alpha} – \ varvec {\ omega} _t \ раз \ varvec {\ omega} | \ cos (\ varphi) \\ 2 | \ varvec {\ alpha} – \ varvec {\ omega} _t \ times \ varvec {\ omega} | \ sin (\ varphi) \\ \ end {bmatrix} = \ begin {bmatrix} -59.2}}. \ end {align} $$

(47)

Поскольку соотношение составляющих углового ускорения не соответствует качению, направление угловой скорости и IAR начинает изменяться. За конечное время исходный конус движущейся аксоды (меньший конус на рис. 10) преобразуется в больший конус. Представить себе, как подвижная и неподвижная аксоды трансформируются в процессе движения, довольно сложно, даже положение общей касательной плоскости аксод трудно увидеть.

Чтобы определить касательную плоскость, можно использовать, что скорость изменения полюса и угловая скорость охватывают эту плоскость. Для расчета \ (\ mathbf {u} \) уравнение. (13) можно использовать.

Используя формулу Эйлера, можно определить ускорение точки A :

$$ \ begin {align} \ mathbf {a} _A = \ varvec {\ alpha} \ times \ mathbf {r} _ {OA} + \ varvec {\ omega} \ times (\ varvec {\ omega} \ times \ mathbf {r} _ {OA}) = \ begin {bmatrix} 2.9 \\ 0 \\ 29.7619 \ end {bmatrix} \, {\ гидроразрыв {\ mathrm {m}} {\ mathrm {s} ^ 2}}.2} = \ begin {bmatrix} 2.08 \ dot {3} \\ 0 \\ -0.203 \ end {bmatrix} \, {\ frac {\ mathrm {m}} {\ mathrm {s}}}. \ end {align} $$

(49)

Компоненты этого вектора можно определить и другим способом. Компонент x скорости изменения полюса может быть вычислен с учетом транспортной составляющей \ (\ varvec {\ omega} _t \) угловой скорости:

$$ \ begin {align} u_x = R \ varvec {\ omega} _t = 2.08 \ dot {3} \, \ mathrm {m / s}.2}} \ end {align} $$

(51)

перпендикулярно \ (\ varvec {\ omega} \) и параллельно касательной плоскости – точно так же, как \ (\ mathbf {u} \). Таким образом, \ (\ varvec {\ alpha} _ \ perp \) параллельно \ (\ mathbf {u} \), что означает, что

$$ \ begin {align} u_z = \ frac {u_x} {\ alpha _x} \ alpha _z = -0,035 \ cdot 5,8 = -0,203. \ end {align} $$

(52)

Таким образом,

$$ \ begin {align} \ mathbf {u} = \ begin {bmatrix} 2.2}}. \ end {align} $$

(54)

В этой задаче направление касательной плоскости аксодов не может быть определено без выполнения вычислений. Тем не менее, если угловое ускорение известно, величина и направление \ (\ mathbf {u} \) могут быть выражены, а полюсное ускорение может быть довольно легко вычислено.

Центростремительное ускорение | Блестящая вики по математике и науке

Центростремительное ускорение определяется как ac = ω2r.2 r.ac = ω2r.

Чтобы вычислить ускорение байкера, найдите изменение вектора скорости Δv⃗ = v⃗ (θ + Δθ) −v⃗ (θ) \ Delta \ vec {v} = \ vec {v} (\ theta + \ Delta \ theta) – \ vec {v} (\ theta) Δv = v (θ + Δθ) −v (θ), когда велосипед движется на угол Δθ. \ Delta \ theta.Δθ.

Увеличивая небольшой участок траектории, проверьте векторы, используемые для вычисления:

Чтобы найти разницу, выровняйте v⃗ (θ + Δθ) \ vec {v} (\ theta + \ Delta \ theta) v (θ + Δθ) и −v⃗ (θ) – \ vec {v} (\ theta) −v (θ) кончик к хвосту:

Сначала заметьте, что разность Δv⃗ \ Delta \ vec {v} Δv указывает прямо к центру круга.

Далее, очевидно, что угол между двумя векторами равен Δθ \ Delta \ thetaΔθ.

Длина разности Δv⃗ \ Delta \ vec {v} Δv определяется (приблизительно) длиной дуги, проходящей через v⃗ \ vec {v} v при ее повороте на Δθ \ Delta \ thetaΔθ. Используя s = θr, s = \ theta r, s = θr,

Δv⃗≈Δθ∣v∣. \ Delta \ vec {v} \ приблизительно \ Delta \ theta \ lvert v \ rvert.Δv≈Δθ∣v∣.

Деление обеих сторон на Δt, \ Delta t, Δt,

Δv⃗Δt≈ΔθΔt = ωv. \ Frac {\ Delta \ vec {v}} {\ Delta t} \ приблизительно \ frac {\ Delta \ theta} {\ Delta t} = \ omega v.2} {R}} ac = Rv2 и указывает прямо на центр круговой траектории. □ _ \ квадрат □

Хотя эта демонстрация показательна, она была несколько надуманной. Многие ограничения сохраняются на движение: радиус остается постоянным, скорость изменения радиуса остается постоянной, угловое ускорение отсутствует.

На самом деле существует гораздо более простой метод вычисления всех четырех ускорений, которые могут возникнуть во вращающихся системах отсчета, который включает использование теоремы Де Муавра.

Ускорение частицы

Ускорение движущейся частицы Справочная рамка

Система XYZ , показанная на Рисунке 1 является инерциальной системой отсчета, в то время как рамка X’Y’Z ‘ является движущейся (перевод + вращение) система отсчета. Положение точки P на рисунке можно выразить в рамках этих двух систем отсчета:

Рисунок 1

[1]

, где r o = положение начало вращающейся рамки, и r ‘= положение P относительно начала движущегося кадра.

Из [1] и [6] вращающейся системы отсчета, смещение точки P тогда можно выразить как

[2]

, где d r o = смещение из-за смещения начала отсчета вращающейся рамы, d r ‘ = смещение точки P относительно начала вращающейся рамки, d q x r ‘= смещение из-за вращения подвижной рамы, и ( d r ‘) rot = смещение точки P наблюдается во вращающейся рамке (или смещение P относительно подвижной рамы ).

Из [2], скорость точки P можно выразить как

[3]

, где v ‘ r = скорость точка P относительно подвижной системы отсчета. Таким образом, скорость точки P относительно начала движущейся системы отсчета можно разделить на скорость из-за к вращению рамы и скорости , наблюдаемой во вращающейся раме .

Ускорение точки P можно получить аналогично:

[4]

, где a = ускорение точки P , a o = ускорение начала координат подвижной рамы, и a ‘ r = ускорение точки P относительно движущейся рамки. Обратите внимание, что все векторы, входящие в уравнение скорости, показанное в [3], равны подлежит выведению и [9] вращающегося Система отсчета применялась ко всем случаям.[14] вращающейся системы отсчета показывает, что производная по времени от вектор угловой скорости не зависит от вращения подвижной системы отсчета. Как результат, ускорение точки P показывает 5 различных членов.

Верх

Центростремительное ускорение

1-й и 2-й члены в [4] результаты поступательного и вращательного ускорения движущегося эталона кадр соответственно.Третий член, w x ( w x r ‘), происходит из-за вращения подвижной рамы, и, как показано на рисунке 2, этот вектор направлен к центру вращения (точка C ). Это ускорение называется центростремительным ускорением . 4-й член из-за движения точки в движущейся рамке и называется кориолисовым датчиком ускорение . Последний член связан с ускорением точки в пределах движущаяся система отсчета.

Рисунок 2

Если движущаяся рамка не перемещается, а вращается с постоянной угловая скорость и точка P не перемещается внутри движущейся рамки, [4] можно упростить до

[ 5]

с

[6]

Другими словами, центростремительное ускорение – это основное требование для постоянного кругового движения тела вокруг оси вращения.Согласно 2-му закону движения Ньютона сила, действующая на частицу, равна ее силе. масса, умноженная на ускорение. Следовательно, из [6]:

[7]

Эта сила является центростремительной силой, которая вызывает постоянное круговое движение. движение тела. Обратите внимание, что эта сила действует в направлении центра вращения, точка C показана на рисунке 2.

Если угловая скорость вращающейся системы отсчета не равна константа, [4] уменьшается до

[8]

с

[9]

В случае плоского вращения, когда направление углового скорость не меняется, 1-й член [8] можно обозначить как тангенциальное ускорение , поскольку оно находится в направлении w x r ‘показано на рисунке 2.

Оставить комментарий