Ускорение мгновенная скорость: Мгновенная скорость и ускорение это - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Мгновенная скорость против ускорения: сравнительный анализ

Мы уже знакомы с терминами скорость и ускорение. В этом посте мы узнаем факты о мгновенной скорости и ускорении.

Скорость и ускорение взаимосвязаны друг с другом. Мгновенная скорость – это расчет скорости в любой конкретный период, а ускорение определяется как скорость изменения скорости (V) с учетом периода. Если взять производную от V_инст при t мы получаем ускорение.

В этой статье мы более подробно сконцентрируемся на мгновенной скорости и ускорении.

Мгновенная скорость: определение и факты

Термин скорость используется для обозначения или измерения скорости частицы за период.

Мы знаем, что значение скорости и что она обозначает. Теперь, переходя к слову мгновенная скорость, оно обозначает увеличение или уменьшение скорости частицы в определенный период, то есть показывает скорость в требуемый момент времени.
Он измеряется вдоль пути, по которому движется рассматриваемая частица.
График, используемый для построения мгновенной скорости (V_инст) показывает изменение скорости, т. е. увеличение или уменьшение тела.

Теперь дайте нам знать о другой необходимой величине, которую мы сосредоточим на мгновенной скорости и ускорении.

Ускорение: определение и факты

Ускорение – еще один важный термин, используемый в повседневной физике.

Ускорение в физических науках – одна из важнейших величин, без которой невозможно выполнение основных расчетов в механике.
Как правило, это вычисление или производная от изменения скорости движущегося объекта / тела по прошествии времени.
Если рассматривать ускорение от начала до конца движения, то оно называется средним ускорением.
Если мы рассмотрим расчет ускорения (а) в конкретный момент времени или период или в качестве предельного значения_{средний}, то оно называется мгновенным ускорением (a_инст).

Теперь давайте сконцентрируемся на главном фокусе статьи, мгновенной скорости в зависимости от ускорения.

Мгновенная скорость против ускорения

Здесь мы подробнее изучим идеи и факты о мгновенной скорости против ускорения.

Параметры сравнения	Мгновенная скорость	Ускорение
Определение	Он помогает измерить скорость тела по заданному маршруту в любой конкретный период t.	Термин «ускорение» определяет изменение скорости или скорости частицы в направлении траектории в интервале времени.
Термины, использованные при расчете	Смещение / Положение / Расстояние и время.	Скорость / Скорость и время.
Природа количества	Это физическая векторная величина.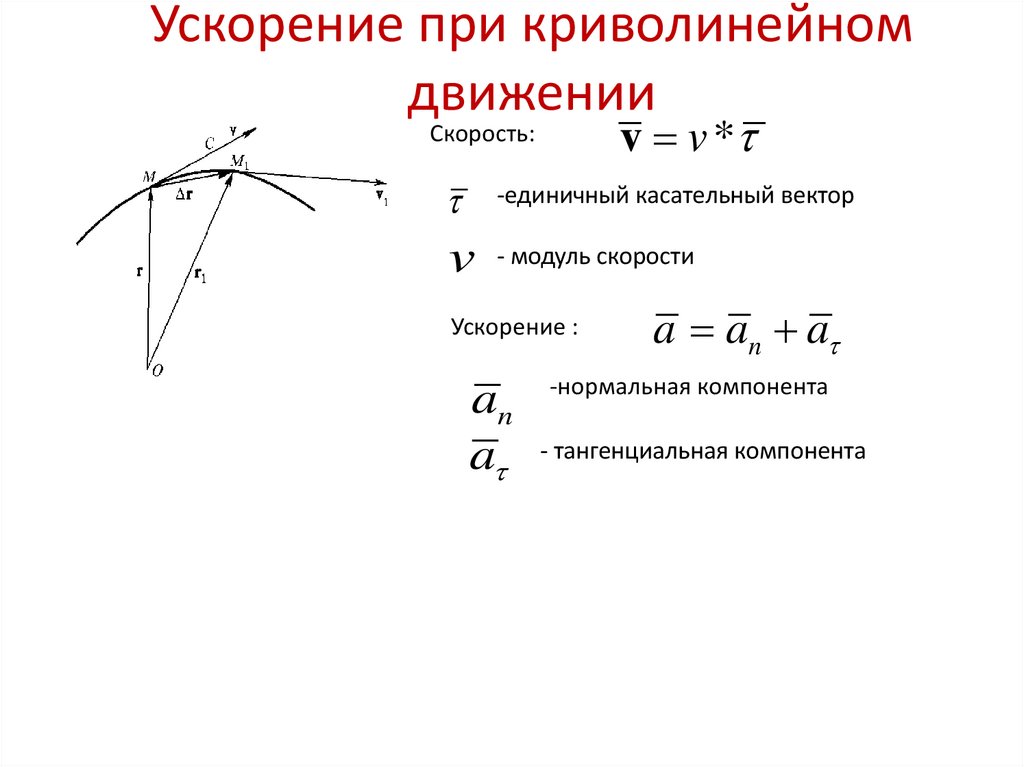	Это физическая векторная величина.
Производная от условий	Это производная от смещения / положения с учетом времени.	Это производная обоих изменений скорости / скорости частицы / объекта с учетом времени.
Формула	Смещение / время (д / т) = дс / дт	Скорость / Время (v / t) = dv / dt
Ед. изм	Измеряется в м / с	Измеряется в м / с²
Особенности	Он указывает скорость тела с указанием времени и направления маршрута.	Он указывает на изменение скорости для определенных интервалов.
Пример	Собака гоняется за костью.	Мужчина участвует в беге с препятствиями.

Итак, вот некоторые заметные отличия мгновенной скорости от ускорения.

Мгновенная скорость – это вектор или скалярная физическая величина?

Мы уже знаем, что мгновенная скорость или V является первичным вектором физических величин.

В общем, это термин, используемый для измерения изменения положения или смещения движущегося тела во времени. Из его определения мы можем отметить, что он состоит из обоих направлений, а также дает значение величины, которые являются существенными характеристиками вектора.

Теперь давайте сосредоточимся на следующих аспектах расчета этой мгновенной скорости в зависимости от ускорения в деталях.

Как найти мгновенную скорость на графике?

Мы можем найти мгновенную скорость различными методами; мы узнаем об одном здесь.

Мы можем измерить V_инст частицы или тела при движении в заданный период с помощью PT-графика. Мы должны выполнить только основные этапы построения значений, обозначения осей, определения наклона и рисования касательной; после этого получаем искомую V_инст тела.

Пора узнать о природе ускорения.

Чтобы узнать больше о проверке мгновенной скорости ниже,
Как рассчитать мгновенную скорость

Ускорение – это скалярная или векторная физическая величина?

Ускорение – это физический вектор, но иногда он может быть скаляром.

Поскольку ускорение означает как величину, так и направление, оно называется физической векторной величиной. Ускорение зависит от характера измерения, в котором оно происходит. Например, на числовой прямой ускорение является скалярным, тогда как координаты на плоскости или пространство считаются физической векторной величиной.

Теперь дайте нам знать, как найти это ускорение на графике.

Ускорение: шаги по поиску График скорости-времени

Один из способов найти значение ускорения движущегося тела – по графику скорость-время.

После указания осей и нанесения требуемых значений на график скорость-время, мы должны взять наклон для конкретных измерений. Здесь наклон равен необходимому ускорению объекта. Иногда вы даже можете использовать формулу для вычисления этого уклона.

Теперь сконцентрируйтесь на основных характеристиках мгновенной скорости.

Чтобы узнать больше о том, как разгоняться на графике, вы можете увидеть ниже
Как построить график постоянного ускорения

Примеры мгновенной скорости и ускорения в повседневной жизни

Для каждого движения объекта мы можем вычислить мгновенную скорость и ускорение. Таким образом, мы получаем множество повседневных примеров зависимости мгновенной скорости от ускорения.

Ребенку, бегающему марафон, требуется определенное время отдыха для каждого пункта назначения. Здесь, чтобы узнать изменение положения для каждой ступени, мы можем использовать мгновенную скорость, и если мы рассмотрим ее скорость / скорость, это будет ускорение.

Изображение Фото: Бесплатные изображения Pixabay

В теннисе положение мяча меняется при каждом ударе. Мы можем рассчитать изменение положения для каждого интервала, используя мгновенную скорость, и если это изменение скорости, то это ускорение шаров.

Изображение Фото: Бесплатные изображения Pixabay

При перемещении материалов из-за тяжелого багажа мы можем иногда менять позу или положение перемещаемых предметов. Здесь мы можем записать изменение положения с помощью мгновенной скорости, и если это изменение скорости, то это ускорение материалов.

Изображение Фото: Бесплатные изображения Pixabay

Таким образом, это некоторые примеры повседневной жизни В.

Часто задаваемые вопросы | FAQs

Можем ли мы рассматривать мгновенную скорость как ускорение?

И мгновенная скорость, и ускорение – разные величины по сравнению друг с другом.

Скорость изменения количества, если она рассчитывается со временем, принимается как производная от соответствующих величин. Здесь V принимается как мера положения во времени, а ускорение – это производная от изменения скорости после времени. Исходя из этого чутья, мы можем сказать, что и то, и другое являются производными и интегральными.

Каково определение мгновенной скорости?

Определение скорости почти аналогично мгновенная скорость с некоторой критической изменений.

Он принимается за предел V, так как период интервала почти стремится к нулю. Он даже известен как производная от расстояния / смещения с моментом t, который обозначает время. Единица измерения – длина и время. Это могут быть метры, километры, минуты или секунды и т. Д.

Что такое ускорение?

Ускорение измеряется как двойная производная перемещения и времени.

Смысл ускорения состоит в том, чтобы определить изменение скорости, которое увеличивается, уменьшается или постоянное изменение скорости с учетом соответствующего временного интервала и пути.
Это физическая векторная величина, которая играет важную роль при измерении изменений скорости.
Его также можно измерить на графике VT, потому что на этом графике наклон равен необходимому ускорению тела в движении.

Как найти мгновенную скорость с помощью ускорения?

И мгновенная скорость, и ускорение так или иначе связаны друг с другом.

Мы уже знали в наших предыдущих статьях о мгновенной скорости. Это первая производная смещения или положения по времени. Если рассматривать только производную скорости по времени, то это будет вторая производная положения и время. Следовательно, если мы рассматриваем Vinst в конкретный момент времени, то, взяв его производную, мы можем измерить a=d→vdt.

Средняя и мгновенная скорость | Кинематика

В этой статье мы поговорим о двух видах скорости перемещения: средней и мгновенной.

Рассмотрим следующий пример.

Небольшой грузовик, движущийся по маршруту Москва – Петушки, за тридцать минут проехал тридцать километров на восток. Ось x, вдоль которой двигался этот транспорт, направлена туда же. Вопрос: чему равна скорость перемещения грузовика в рассматриваемый промежуток времени?

Дать ответ к поставленной задаче нетрудно:

\vec{v}=\dfrac{\vec{s}}{\varDelta{t}}=\dfrac{+\thickspace30\thickspaceкм}{0,5\thickspaceч}=+\thickspace60\thickspaceкм/ч⠀

Отметим, что знак плюс писать необязательно.

Та скорость, которую мы сейчас нашли, – это средняя скорость. Я буду обозначать ее так: \vec{v}_{ср}. Средняя скорость является векторной величиной и равна отношению перемещения тела к промежутку времени, за которое это перемещение было совершено:

\vec{v}_{ср}=\dfrac{\vec{s}}{\varDelta{t}}

При этом наш грузовик мог ехать с непостоянной скоростью. Где-то он мог двигаться быстрее, где-то медленнее.

Представьте, что во время поездки вы находились рядом с водителем и в какой-то момент посмотрели на спидометр, где увидели скорость – пятьдесят пять километров в час. Если добавить направление, в котором двигался транспорт в это же самое мгновение, получится мгновенная скорость. Это скорость, которую имел грузовик в определенный момент времени. Мы будем обозначать ее так: \vec{v}(t).

Если вы попросите вашего учителя по физике дать вам формулу для вычисления мгновенной скорости, скорее всего, он или она покажет вам что-то в этом роде:

v(t)=\lim\limits_{\varDelta{t}\rarr0}\dfrac{\varDelta{x}}{\varDelta{t}}

v(t)=\dfrac{dx}{dt}

Чтобы найти мгновенную скорость, в общем случае требуется знать основы дифференциального исчисления. Но нам повезло, есть случаи, когда мы можем найти мгновенную скорость, не используя математический анализ.

Во-первых, если тело двигается равномерно, то есть с постоянной скоростью, его мгновенная скорость будет равна его средней скорости:⠀⠀ ⠀⠀⠀

\vec{v}(t)=\vec{v}_{ср}

Во-вторых, если дан график зависимости координаты тела от времени, угловой коэффициент касательной, проведенной к этому графику, будет равен мгновенной скорости:

\vec{v}(t)=k=\dfrac{\textcolor{#219653}{x_2-x_1}}{\textcolor{#F2994A}{t_2-t_1}}

В-третьих, если тело движется с постоянным ускорением, то есть его скорость со временем меняется на одну и ту же величину, мы можем найти значение мгновенной скорости, используя вот такую формулу:

v(t)=v_0+at

Здесь под буквами, обозначающими векторные величины, подразумеваются их абсолютные значения, их модули. Впрочем, чуть позже мы подробно поговорим с вами об этом уравнении.

Кратко повторим все.

Средняя скорость показывает, насколько быстро совершается то или иное перемещение.

Мгновенная скорость – это скорость тела в произвольный момент времени.

Зная среднюю скорость объекта, мы получаем лишь приближенное понятие о том, как именно он перемещался. Если же мы знаем скорость тела в любой момент времени, мы имеем очень точную картину его движения.

Сравнительный анализ – Lambda Geeks

Скорость и ускорение взаимосвязаны друг с другом. Мгновенная скорость — это расчет скорости в любой конкретный период, а ускорение определяется как скорость изменения скорости (V) с учетом периода. Если взять производную от V _инст с t, то получаем ускорение.

В этой статье мы сосредоточимся на подробностях сравнения мгновенной скорости и ускорения.

Мгновенная скорость: определение и факты

Термин скорость используется для обозначения или измерения скорости частицы за период.

Мы знаем значение скорости и то, что она обозначает. Теперь переходя к слову мгновенная скорость, оно обозначает увеличение или уменьшение скорости частицы в определенный период, т. е. показывает скорость в требуемый момент времени.
Измеряется вдоль пути, по которому движется рассматриваемая частица.
График, используемый для построения мгновенной скорости (V _inst ), показывает изменение скорости, т. е. увеличение или уменьшение тела.

Теперь дайте нам знать о другой необходимой величине, которую мы сосредоточим на мгновенной скорости по сравнению с ускорением.

Ускорение: определение и факты

Ускорение — еще один важный термин, используемый в повседневной физике.

Ускорение в физических науках является одной из важнейших величин, без которой невозможны базовые расчеты механики.
Это, как правило, дается как вычисление или производная изменения скорости объекта/тела в движении в зависимости от его времени.
Если рассматривать ускорение от начала до конца движения, то оно называется средним ускорением.
Если мы рассматриваем расчет ускорения(а) в определенное время или период или принимаем в качестве предельного значения _avg , тогда это называется мгновенным ускорением (a _inst ).

Теперь давайте сконцентрируемся на основной теме статьи, мгновенной скорости и ускорении.

Мгновенная скорость и ускорение

Здесь мы узнаем больше об идеях и фактах о мгновенной скорости и ускорении.

11111111111111999999999999999999999999999999999999999999999999999999999999999999989999999999999999999999999999999999999999999999999999999999999999999999999999999900se

Параметры сравнения	Мгновенная скорость	Ускорение
Определение	Помогает измерить скорость конкретного тела на любом заданном маршруте в любой момент времени.	Термин ускорение определяет изменение скорости или скорости частицы вдоль направления пути в интервале времени.
Термины, использованные при расчете	Перемещение/Положение/Расстояние и время.	Скорость/скорость и время.
Характер величины	Это физическая векторная величина.	Это физическая векторная величина.
Производная от условий	Это производная от смещения/положения с учетом времени.	Это производная обоих изменений скорости/скорости частицы/объекта с учетом времени.
Формула	Смещение/Время (D/T) = DS/DT	Selocity/Time (V/T) = DV/DT	Измеряется в м/с	Измеряется в м/с ²
Особенности	Указывает направление движения и скорость тела.	Указывает изменение скорости для определенных интервалов.
Пример	Собака гоняется за костью.	Мужчина участвует в беге с препятствиями.

Итак, вот некоторые заметные отличия мгновенной скорости от ускорения.

Является ли мгновенная скорость векторной или скалярной физической величиной ?
Мы уже знаем, что мгновенная скорость или V является первичным вектором физических величин.
В общем, это термин, используемый для измерения изменения положения или смещения движущегося тела во времени. Из его определения мы можем отметить, что он состоит из обоих направлений, а также дает значение величины, которая является существенными характеристиками вектора.
Теперь давайте сосредоточимся на следующих аспектах подробного расчета зависимости мгновенной скорости от ускорения.
Как найти мгновенную скорость на графике ?
Мы можем найти мгновенную скорость различными способами; мы узнаем об одном здесь.
Мы можем измерить V _момент частицы или тела при движении в определенный период с помощью P-T графика. Мы должны следовать только основным шагам построения графика значений, указания осей, определения наклона и рисования касательной; после этого получаем искомый V _инст кузова.
Пришло время узнать о природе ускорения.
Чтобы узнать больше о проверке мгновенной скорости ниже,
Как рассчитать мгновенную скорость
Является ли ускорение скалярной или векторной физической величиной ?
Ускорение — это физический вектор, но иногда он может быть скаляром.
Поскольку ускорение означает как величину, так и направление, оно называется физической векторной величиной. Ускорение зависит от природы измерения, в котором оно происходит. Например, на числовой прямой ускорение является скалярным, тогда как координаты в плоскости или пространство считаются физической векторной величиной.
Теперь дайте нам знать, как найти это ускорение на графике.
Ускорение: Шаги по нахождению с использованием графика зависимости скорости от времени
Один из способов определения значения ускорения движущегося тела — это построение графика зависимости скорости от времени.
После указания осей и нанесения необходимых значений на график скорость-время мы должны взять наклон для конкретных измерений. Здесь наклон равен требуемому ускорению объекта. Иногда можно даже использовать формулу для расчета этого наклона.
Теперь сосредоточьтесь на основных характеристиках мгновенной скорости.
Чтобы узнать больше о том, как ускорение на графике, вы можете увидеть ниже
Как построить график постоянного ускорения
Примеры зависимости мгновенной скорости от ускорения в повседневной жизни скорость и ускорение. Таким образом, мы получаем множество повседневных примеров зависимости мгновенной скорости от ускорения.
Ребенку, бегущему марафон, требуется определенное время для отдыха для каждого пункта назначения. Здесь, чтобы узнать изменение положения для каждой ступени, мы можем использовать мгновенную скорость, а если рассматривать его скорость/скорость, то это ускорение.

Изображение предоставлено: Pixabay free images
В теннисе положение мяча меняется при каждом ударе. Мы можем рассчитать изменение положения для каждого интервала, используя мгновенную скорость, и если это изменение скорости, то это ускорение шаров.

Изображение предоставлено: Pixabay free images
При перемещении материалов из-за тяжелого багажа мы можем иногда менять позу или положение при перемещении вещей. Здесь мы можем записать изменение положения с помощью мгновенной скорости, а если это изменение скорости, то это ускорение материала.
Изображение предоставлено: Pixabay бесплатные изображения
Таким образом, это некоторые примеры повседневной жизни V.
Часто задаваемые вопросы | Часто задаваемые вопросы
Можем ли мы рассматривать мгновенную скорость как ускорение?
И мгновенная скорость, и ускорение являются разными величинами по сравнению друг с другом.
Скорость изменения величины, если ее рассчитать во времени, то принимают как производную от соответствующих величин. Здесь V берется как мера положения во времени, а ускорение есть производная изменения скорости с течением времени. Из этого инстинкта мы можем сказать, что оба являются производными и неотъемлемыми.
Что такое определение мгновенной скорости?
Определение скорости почти аналогично определению мгновенной скорости с некоторыми критическими изменениями.
Принимается за предел V, так как период интервала почти стремится к нулю. Он даже известен как производная от расстояния/перемещения с моментом t, обозначающим время. За единицу измерения взяты длина и время. Оно может быть в метрах, километрах, минутах или секундах и т. д.
Что такое ускорение?
Ускорение измеряется как двойная производная смещения и времени.
Значение ускорения состоит в том, чтобы найти изменение скорости, которое увеличивается, уменьшается или постоянно изменяется в зависимости от соответствующего интервала времени и пути.
Это физическая векторная величина, которая является важным фактором при измерении изменений скорости.
Его также можно измерить на графике V-T, поскольку на этом графике наклон равен необходимому ускорению тела при движении.
Как найти мгновенную скорость с помощью ускорения?
Обе величины, мгновенная скорость и ускорение, так или иначе связаны друг с другом.
Мы уже знали в наших предыдущих статьях о мгновенной скорости. Это первая производная смещения или положения по времени. Если рассматривать только производную скорости по времени, то это будет вторая производная по положению и времени. Следовательно, если мы рассматриваем Vinst в конкретный момент времени, то, взяв его производную, мы можем измерить a=d→vdt.
Скорость, скорость и ускорение
Скорость, скорость и ускорение
Время
Мы измеряем момент времени t с помощью часов. Единицей времени в СИ является второй. Показания часов в секундах зависят от выбора источника. Часы в разных часовых поясах имеют разные показания и показания остановки часы зависят от того, когда они были запущены. Интервал времени ∆t = t _позже – t _ранее определяется как разница между более поздним временем и более раннее время. Это всегда неотрицательное число (положительное или нулевое). Интервал ∆t является скаляром, числом с единицами.
Скорость и Скорость
Когда объект перемещается в пространстве, его положение меняется. Предположим, что в момент времени t ₁ он находится в позиции P ₁ и позже t ₂ он находится в позиция P ₂ . Вектор смещения
д = Р ₂ – P ₁ . В интервале времени ∆t = t ₂ – t ₁ объект был вытеснен d . Его средняя скорость дюймов этот временной интервал ∆t определяется как < v > = д /∆t. Перемещение d является вектором, интервал времени ∆t равен скаляр. Деление вектора на скаляр дает другой вектор. Среднее скорость < v > является вектором. Средняя скорость – это расстояние, пройденное за время интервал ∆t, деленный на ∆t. Расстояние является скаляром, т. е. числом с единицами. Разделив расстояние на ∆t, получим другое число с единицами.

Следовательно, средняя скорость скаляр.
Проблема:
За 5 минут бегун пробегает один раз дистанцию длиной в одну милю. Какой его Средняя скорость? Какова его средняя скорость?
Решение:
Обоснование:
Через 5 минут бегун возвращается в исходное положение. P ₂ – P ₁ = 0. Смещение равно нулю. Это пройденное расстояние составляет одну милю.
Детали расчета:
Перемещение равно нулю, поэтому его средняя скорость равна нулю.
средняя скорость это расстояние, пройденное за время интервал ∆t. Средняя скорость поэтому (1 миля)/(5 минут) = (12 миль)/(60 минут) = 12 миль/ч.

Примечание. Скорость — это скаляр, а скорость — это вектор. Средняя скорость вообще не равна величине средней скорости.
Проблема:
Спринтер бежит на север по прямой и преодолевает расстояние 100 м за 12 с. Какова ее средняя скорость? Какова ее средняя скорость?
Решение:
Сводка
Средняя скорость это пройденное расстояние, деленное на время, необходимое для преодоления этого расстояния. Если человек проходит 1 км на запад, затем разворачивается и идет 1 км на восток, расстояние это человек покрывает 2 км. Если это расстояние преодолевается за 20 минут, то средняя скорость 2 км/20 минут = 2000 м/(20*60 с) = 1,67 м/с.

Средняя скорость является вектором. Это вектор смещения, указывающий из начального положения в конечное положение, разделить на время. В приведенном выше примере начальная и конечная позиция совпадают. Вектор смещения равен нулю. Значит, средняя скорость равна нулю.
Ссылка: Скорость и скорость (Пожалуйста, изучите!)
Поскольку величина и направление вектора смещения зависят от система отсчета, в которой система координат закреплена и находится в состоянии покоя, скорость объекта зависит от системы отсчета, относительно которой он измеряется.

Проблема:
Автомобиль продвинулся вперед на расстояние 6 м, при этом ребенок продвинулся вперед от заднего сиденья до переднего сиденья на расстоянии 1 м за промежуток времени 2 с. Найдите среднюю скорость ребенка относительно автомобиля и относительную к дороге.
Решение:
Обоснование:
Скорость объекта зависит от системы отсчета,
Детали расчета:
Использование автомобиля в качестве системы отсчета и привязка системы координат к автомобиль, водоизмещение ребенка д = (1 м) i .
Его скорость < v > = (1 м)/(2 с) i = (0,5 м/с) i .
Использование дороги в качестве системы отсчета и привязка системы координат к дорога, смещение ребенка d = (6 м) i + (1 м) i = (7 м) и .
Его скорость < v > = (7 м)/(2 с) i = (3,5 м/с) i .
Примечание. Скорость объекта зависит от системы отсчета. не та величина, с которой согласны все наблюдатели. Объект может находиться в состоянии покоя в течение одного системе отсчета и имеющей ненулевую скорость в другой системе отсчета.
Когда родитель говорит ребенку сидеть спокойно в движущейся машине, он имеет в виду сидеть спокойно по отношению к машине, а не по дороге.

Остановился, вы ждете смены сигнала светофора с красного на зеленый, когда вдруг у вас появляется ощущение, что вы двигаетесь, хотя и нажимаете на педали тормоза. Но затем вы замечаете, что большой грузовик или автобус в полоса рядом с вами – это транспортное средство, которое фактически движется относительно земля. Чтобы сделать вывод, что мы движемся относительно земли, мы в основном полагаются на визуальные подсказки. Когда мы видим, что наше окружение движется, мы сделать вывод, что мы движемся. Обычно мы можем быстро установить истинное ситуацию, так как мы подсознательно понимаем, что есть несоответствие и быстро получить дополнительную информацию из нашего окружения.

Симуляция ниже исследует относительное движение. Вид всегда у водителя автомобиля или у кого-то, движущегося с той же скоростью, что и водитель смотрит прямо в картину. Вы можете выбрать три разных ситуации и масштабировать и вращать вид, Пожалуйста, нажмите на изображение!
Часто средняя скорость не очень полезная величина. Мы хотим знать скорость тела в момент времени. Мы хотим знать мгновенное скорость. Чем больше мы уменьшаем временной интервал между двумя последовательными позициями измерений, тем ближе средняя скорость, измеренная за этот интервал времени к мгновенной скорости. Мы определяем
мгновенная скорость как
v = lim _∆t–>0 ∆ r /∆t = d r /dt,
где ∆ r – перемещение на интервале времени ∆t. Мгновенная скорость – это величина мгновенной скорости. С этого момента будем считать, что слова скорость и скорость обозначают мгновенную скорость и мгновенную скорости, если явно не указано иное.
Краткий обзор деривативов (пожалуйста, пересмотрите, если вы одновременно занимаетесь исчислением.)
Пример:
Предположим, что автомобиль движется по круговой дорожке с окружностью 1000 м. Он движется с постоянной скоростью v = 10 м/с. В t = 0 он находится в точке P
1 и движется на восток.
В t = 100 с снова в точке P ₁, двигаясь на восток. Его скорость, усредненная по 100 с равно 0.
В момент времени t = 50 с автомобиль находится в точке P ₂ и движется на запад. Его вектор смещения для первые 50 секунд d ₅₀ = 1000 м/π юж. = 318 м юж. Его скорость усредненное значение за первые 50 секунд равно v = d ₅₀ /(50 с) юг = 6,36 м/с юг.
В момент времени t = 25 с автомобиль находится в точке P ₃ . Вектор его смещения за первые 25 с d ₂₅ = 318 м/√2 юго-восток = 225 м юго-восток. Его скорость, усредненная по первые 25 с v = d ₂₅ /(25 с) юго-восток = 9 м/с юго-восток.
Чем короче временной интервал между последовательными измерениями положения, тем ближе средняя скорость к мгновенной скорости, которая равна 10 м/с касательной к окружности.
Ссылка: Средняя и мгновенная скорость
Проблема:
Может ли модуль средней скорости быть больше, чем средняя скорость?
Решение:
Обоснование:
Нет, для объектов, движущихся по прямой без изменения направления, средняя скорость есть величина средней скорости.

Если объект поворачивается вокруг или если он движется не по прямой, то средняя скорость больше, чем модуль средней скорости.
Поскольку величина и направление вектора смещения зависят от система отсчета, в которой система координат закреплена и находится в состоянии покоя, скорость объекта зависит от системы отсчета, относительно которой он измеряется.
Ускорение
Всякий раз, когда скорость объекта изменяется, объект ускорение. Предположим, что в момент времени t ₁ объект имеет скорость в ₁ , и в более позднее время t
2 он имеет скорость v ₂ . Изменение в скорость равна ∆ v = v ₂ – v ₁ на интервале времени ∆t = t ₂ – t ₁ . Среднее ускорение объекта за этот промежуток времени ∆t определяется как < a > = ∆ v /∆t. Среднее ускорение < a > является вектором. Это вектор скорости в последний момент времени минус вектор скорости в момент времени. начальное время, деленное на временной интервал.
Мы определяем мгновенное ускорение как
a = lim _∆t–>0 ∆ v /∆t = d v /dt,
, где ∆ v — изменение скорости в интервале времени ∆t. В дальнейшем будем считать, что слово ускорение обозначают мгновенное ускорение, если явно не указано иное.
Ссылка: Ускорение
Примечание: Всякий раз, когда ваша скорость ИЗМЕНЕНИЕ , вы ускоряетесь. Вы ускоряетесь, когда ИЗМЕНИТЬ скорость, ИЗМЕНИТЬ направление движения или и то, и другое. Ключевое слово ИЗМЕНИТЬ .
Если ваша скорость НЕ меняется, то как бы быстро вы движетесь, вы НЕ ускоряетесь.
постоянная скорость <--> нулевое ускорение
Проблема:
Вы едете с постоянной скоростью 20 миль/ч вокруг городского квартала, проверяя район. Вы ускоряетесь?
Решение:
Обоснование:
Да, направление вектора скорости меняется.
Проблема:
Вы движетесь на восток со скоростью 30 миль в час. Вы видите, как мяч катится по дорогу и сильно ломаешься, потому что боишься, что прибежит ребенок после бала. Вы останавливаетесь за 0,8 секунды. Каково направление вашего средняя скорость за этот короткий промежуток времени? Какое у вас среднее ускорение?
Решение:
Обоснование:
Направление вашей средней скорости — восток. Вы путешествуете на восток с снижая скорость до полной остановки. Изменение вашей скорости равно ∆ v = v ₂ – v ₁ = 0 – 30 миль в час на восток = -30 миль в час на восток = 30 миль в час на запад.
Детали расчета:
Переведем в единицы СИ.
30 миль в час умножить на 1609 м/милю умножить на 1 ч/(3600 с) = 13,4 м/с.
Ваше среднее ускорение равно ∆ v / ∆t = (13,4 м/с)/(0,8 с) запад = 16,8 м/с ² запад.