Узнаем что называют ускорением в физике: основные формулы
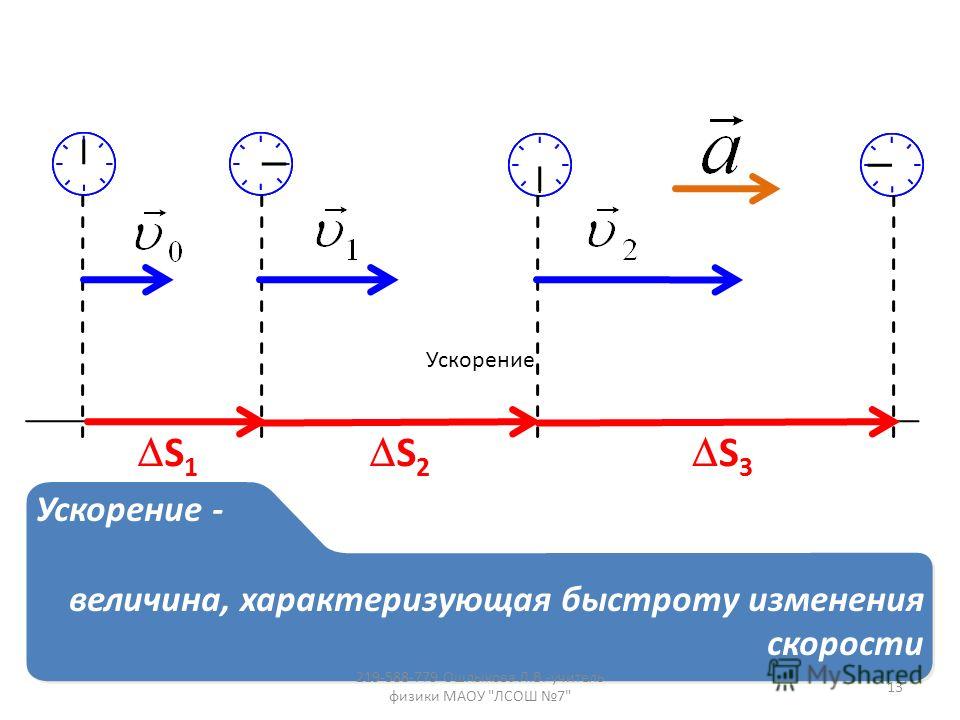
Отвечая на вопрос о том, что называют ускорением в физике, следует сказать, что это векторная величина, которая показывает, как изменяется скорость за единицу времени. В ньютоновской векторной механике ускорение обычно обозначают a→ и измеряют в системе международных единиц в м/с2.
Что называют ускорением?
Согласно постулатам механики Ньютона, частица (тело) не может двигаться по искривленной траектории, если на нее не действует никаких внешних сил, то есть такая частица будет прямолинейно двигаться. В то же время, движущаяся по прямой траектории частица, может увеличить свою скорость или уменьшить ее, если вектор силы, действующей на нее, параллельно вектору ее скорости.
В классической механике ответом на вопрос, что называют ускорением, является изменение скорости за данный промежуток времени, то есть a = dv/dt, что математически интерпретируется, как производная скорости по времени.
Ускорение и второй закон Ньютона
Ускорение тела a массой m, в соответствии со вторым закон Ньютона, пропорционально результирующей F силе, которая действует на это тело, то есть F = ma. Данное выражение действительно для любой инерциальной системе отсчета, то есть такой системе, которая находится в состоянии покоя, либо прямолинейно движется и равномерно.
Приведем следующие примеры использования этой формулы нахождения ускорения или действующей на тело силы.
- Ускорение при свободном падении на нашей планете своим существованием обязано силе тяжести, действующей на все без исключения объекты, имеющие какую-либо отличную от нуля массу. Оно обозначается g и равно 9,8 м/с2 недалеко от поверхности земли. Это означает, что если в гравитационном поле Земли какое-либо тело в состоянии свободного падения находится, то оно будет увеличивать свою скорость за каждую секунду полета на 9,8 м/с. После начала такого падения скорость в каждый момент времени для тела определяется по формуле: v = at = gt = 9,8t.
 При этом сила тяжести, действующая на данное тело, равна F = mg. Отметим, что в действительности при свободном падении на тело действует еще и сопротивление воздуха, сила которая зависит от скорости, а при ее определенном значении становится равной по модулю силе тяжести. В таком случае движение тела происходит с постоянной скоростью.
При этом сила тяжести, действующая на данное тело, равна F = mg. Отметим, что в действительности при свободном падении на тело действует еще и сопротивление воздуха, сила которая зависит от скорости, а при ее определенном значении становится равной по модулю силе тяжести. В таком случае движение тела происходит с постоянной скоростью. - Другой пример, когда можно пользоваться вторым законом Ньютона, это процесс торможения или ускорения автомобиля.
Среднее и мгновенное ускорение
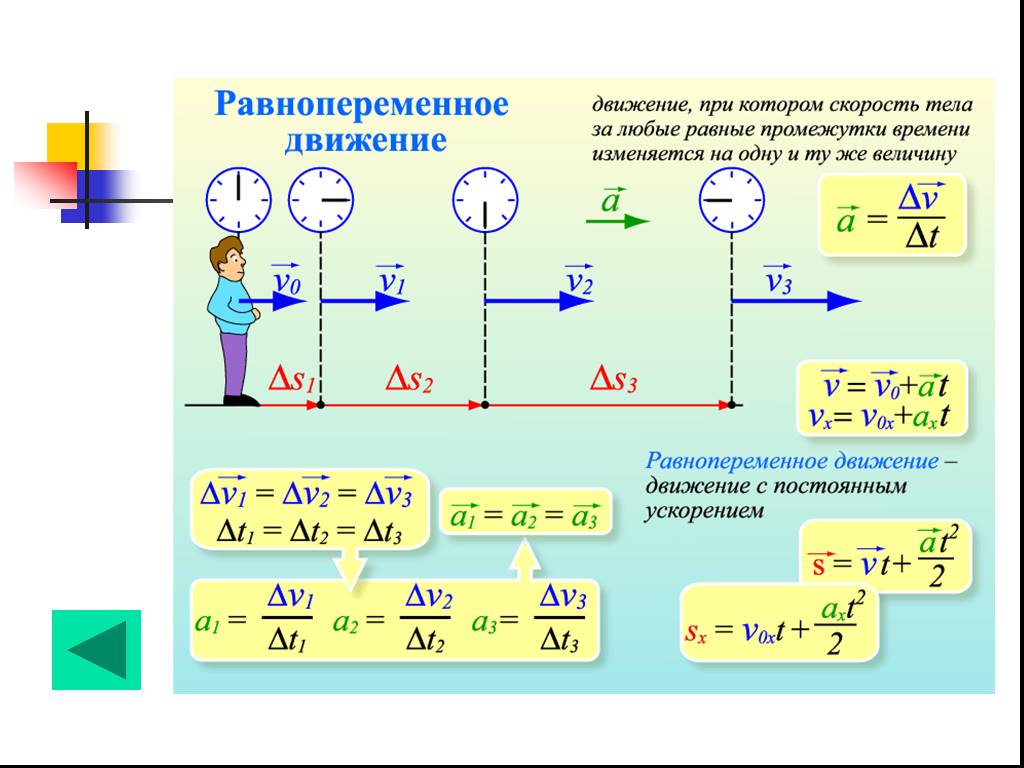
Когда тело движется, то вектор скорости и его модуль в общем случае меняются со временем, но вектор скорости направлен к траектории по касательной всегда. Например, пусть в t1 момент времени тело двигалось с v1→ скоростью, а в t2 момент времени со скоростью v2→. Отвечая на вопрос, что называют ускорением средним, скажем, что эта физическая величина определяется по формуле: a→ = Δv→/Δt, в которой Δt = t2 – t1 и Δv→ = v2→-v1→. Заметим, что вектор ускорения направлен так же, как и вектор изменения скорости Δv→.
Заметим, что вектор ускорения направлен так же, как и вектор изменения скорости Δv→.
Мгновенное ускорение в физике определяется как по времени производная скорости для конкретного момента времени, то есть a→ = dv→/dt. Учитывая, что скорость является производной по времени координаты тела, можно получить ускорение, если взять от координаты тела второй раз производную по времени, то есть a = d2r/dt2, где r – координата тела в t момент времени.
Круговое равномерное движение
Равномерное и круговое представляет собой такое движение, тело или частица при котором движется по окружности некоторого постоянного радиуса R с постоянным модулем скорости V, то есть это тело или частица проходит одинаковый путь за одинаковые промежутки времени. Так как тело движется по траектории окружности, то оно постоянно изменяет направление скорости.
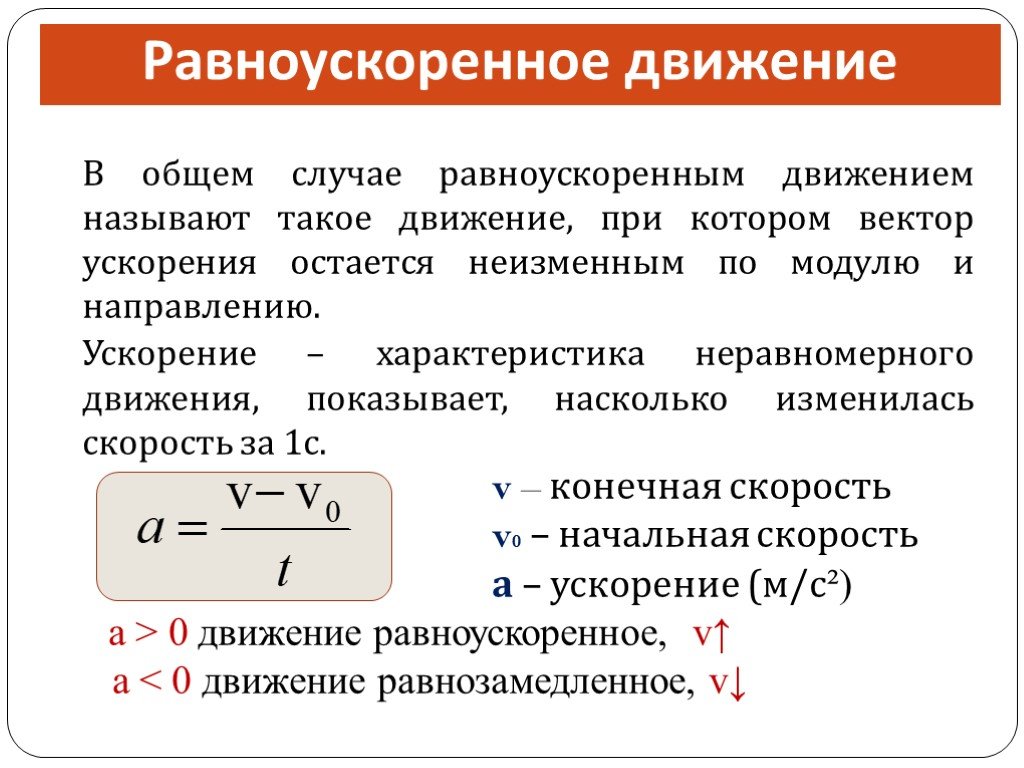
Если вектор ускорения разложить на пару компонентов так, что один из них будет направлен к траектории движения по касательной, а второй к центру окружности вдоль радиуса R, тогда первый компонент называется тангенциальным, а второй нормальным. Учитывая, что движение является равномерным, тангенциальный компонент ускорения равен нулю, а нормальный – постоянная величина, которая является ответом на вопрос, что называют центростремительным ускорением. Это ускорение направлено на изменение траектории движения объекта и не изменяет само значение скорости. Центростремительное ускорение в физике вычисляется по формуле a = v2/R.
Учитывая, что движение является равномерным, тангенциальный компонент ускорения равен нулю, а нормальный – постоянная величина, которая является ответом на вопрос, что называют центростремительным ускорением. Это ускорение направлено на изменение траектории движения объекта и не изменяет само значение скорости. Центростремительное ускорение в физике вычисляется по формуле a = v2/R.
Прямолинейное равномерно ускоренное движение
Если рассмотреть прямолинейное движение тела, то есть при этом движении вектор скорости не изменяет своего направления, а меняется лишь ее модуль, тогда формулу в любой момент t времени для скорости можно записать так: v = v0+∫t0a(t)dt, где v0 – начальная ненулевая скорость. В данном выражении присутствует зависимость ускорения от времени. Если действующая на тело сила является постоянной, тогда и ускорение не будет меняться с течением времени, в этом случае мы получаем простое выражение в t момент времени для скорости: v = v0+at.
Интегральное выражение для скорости можно проинтегрировать еще раз, тогда мы получим выражение для пути, который проходит данное тело за время t. Учитывая, что ускорение является постоянным, получаем формулу: x – x0 = v0t+at2/2, в которой x – x0 – разница конечной и начальной координат тела, которая показывает пройденный им путь.
Центростремительное ускорение. Равнопеременное движение по окружности.
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Центростремительное ускорение. Равнопеременное…
| Центростремительное ускорение. | ||
Вычислим величину ускорения при равномерном движении точки по окружности и найдем его направление. Пусть за некоторый промежуток времени t тело переместилось из точки А в точку А1 с постоянной по модулю скоростью. Рассмотрим треугольники АА1О и А1СВ. Эти треугольники равнобедренные и углы при их вершинах равны, т.к. АО┴СВ и А1О┴А1С (углы со взаимно перпендикулярными сторонами). Следовательно, эти треугольники подобны. Из подобия треугольников следует пропорция: или, переходя к физическим обозначениям . Разделим правую и левую части равенства на промежуток времени, за которое совершено перемещение, и учтем, что и . Тогда: . | Примеры: – Земля при вращении вокруг оси ацс=0,03 м/с2, – Земля при вращении вокруг Солнца ацс=0,006 м/с2, – Солнечная система при вращении вокруг центра Галактики ацс=3.10-10 м/с2.
| |
Теперь определим направление ускорения. Т.к. мы должны для определения ускорения брать предел при Δt→0, то из рисунка видно, что угол φ будет уменьшаться (→0), а b→900. Это значит, что прямая А1В (вектор ) будет стремиться наложиться на АО. Но вектор ускорения сонаправлен с вектором изменения скорости. Следовательно, вектор ускорения при равномерном движении по окружности направлен к центру окружности (центру вращения). Поэтому ускорение наз. центростремительным ускорением. | ||
Центростремительное ускорение меняет скорость только по направлению, но не меняет по величине. Вектор центростремительного ускорения перпендикулярен вектору скорости. Используя связь между угловой и линейной скоростями, получим: . | ||
Равнопеременное движение по окружности. Все уравнения для этого движения получим по аналогии с равнопеременным прямолинейным движением. | ||
Равнопеременное прямолинейноедвижение. | Равнопеременное движение по окружности. – угловое ускорение (рад/с2) | |
2.4: Ускорение – Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1485
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Определять и различать мгновенное ускорение, среднее ускорение и замедление.

- Рассчитать ускорение, зная начальное время, начальную скорость, конечное время и конечную скорость.
В повседневном разговоре ускорить означает ускорить. Ускоритель в автомобиле фактически может заставить его ускориться. Чем больше ускорение , тем больше изменение скорости за заданное время. Формальное определение ускорения соответствует этим понятиям, но более широкое.
Рисунок \(\PageIndex{1}\): Самолет снижает скорость или замедляется перед посадкой на Сен-Мартене. Его ускорение противоположно направлению его скорости. (кредит: Стив Конри, Flickr)Среднее ускорение — это скорость изменения скорости,
\[\bar{a}=\frac{Δv}{Δt}=\frac{ v_f−v_0}{t_f−t_0}\]
где \(\bar{a}\) — среднее ускорение, \(v\) — скорость, а \( t\) — время. (Черта над \(a\) означает 92\), метры в секунду в квадрате или метры в секунду в секунду, что буквально означает, на сколько метров в секунду скорость изменяется каждую секунду.
Вспомните, что скорость — это вектор: она имеет как величину, так и направление. Это означает, что изменение скорости может быть изменением величины (или скорости), но оно также может быть изменением направления. Например, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение происходит, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по тому и другому.
УСКОРЕНИЕ КАК ВЕКТОР
Ускорение представляет собой вектор, направленный в том же направлении, что и изменение скорости, \(Δv\). Поскольку скорость является вектором, она может изменяться как по величине, так и по направлению. Таким образом, ускорение — это изменение либо скорости, либо направления, либо того и другого.
Имейте в виду, что хотя ускорение происходит в направлении 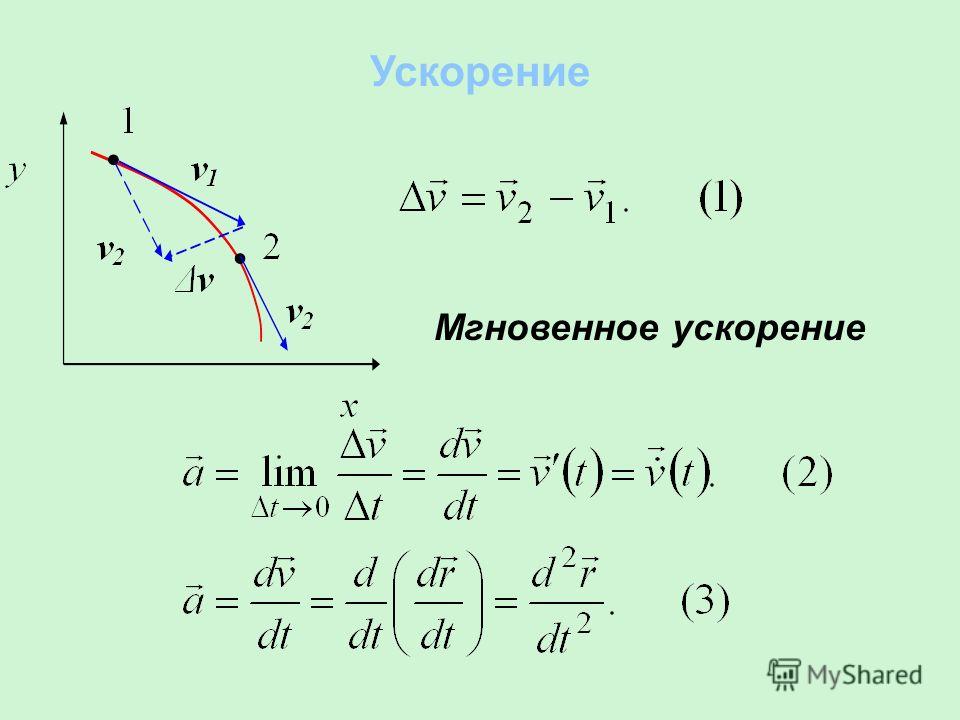 Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление.
Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление.
ПРЕДУПРЕЖДЕНИЕ О НЕПРАВИЛЬНОМ КОНЦЕПЦИИ: ЗАМЕДЛЕНИЕ VS. ОТРИЦАТЕЛЬНОЕ УСКОРЕНИЕ
Под замедлением всегда подразумевается ускорение в направлении, противоположном направлению скорости. Замедление всегда снижает скорость. Отрицательное ускорение, однако, является ускорением в отрицательном направлении в выбранной системе координат. Отрицательное ускорение может быть, а может и не быть замедлением, а замедление может считаться или не считаться отрицательным ускорением. Если ускорение имеет тот же знак, что и скорость, то тело ускоряется. Если ускорение имеет противоположный знак скорости, то объект замедляется. Например, рассмотрим рисунок \(\PageIndex{2}\).
Скаковая лошадь, выходящая из ворот, разгоняется из состояния покоя до скорости 15,0 м/с строго на запад за 1,80 с.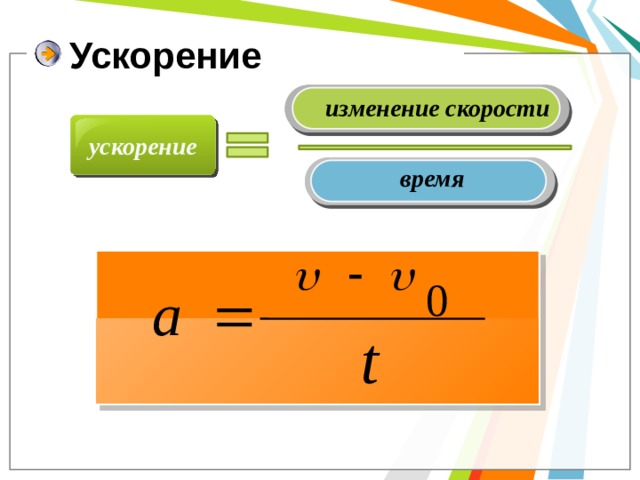 Каково его среднее ускорение?
Каково его среднее ускорение?
Стратегия
Сначала мы рисуем эскиз и назначаем проблеме систему координат. Это простая задача, но ее всегда полезно визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Мы можем решить эту проблему, определив \(Δv\) и \(Δt\) из данной информации, а затем рассчитав среднее ускорение непосредственно из уравнения \ref{averagea}:
\[\bar{a}=\ dfrac{Δv}{Δt}=\dfrac{v_f−v_0}{t_f−t_0}. \номер\]
Решение
- Определите известные. \(v_0=0 , v_f=−15,0 м/с\) (знак минус указывает направление на запад), \( Δt=1,80 с\).
- Найдите изменение скорости. Поскольку лошадь движется от нуля до \(−15,0 м/с\), изменение ее скорости равно ее конечной скорости: \[Δv=v_f=−15,0\, м/с .

Мгновенное ускорение
Мгновенное ускорение \(a\) или ускорение в конкретный момент времени получается тем же процессом, который обсуждался для мгновенной скорости во времени, скорости и скорости, т. е. путем рассмотрения бесконечно малого интервал времени. Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рисунке \(\PageIndex{6}\) показаны графики зависимости мгновенного ускорения от времени для двух очень разных движений. На рисунке \(\PageIndex{6a}\) ускорение незначительно меняется, а среднее значение по всему интервалу почти совпадает с мгновенным ускорением в любой момент времени. В этом случае мы должны относиться к этому движению так, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около \(1,8 м/с^2\)).
Рисунок \(\PageIndex{6}\): Графики зависимости мгновенного ускорения от времени для двух различных одномерных движений. а) Здесь ускорение меняется незначительно и всегда в одном и том же направлении, так как оно положительно. Среднее значение по интервалу почти такое же, как ускорение в любой момент времени. (b) Здесь ускорение сильно различается, возможно, представляя посылку на ленточном конвейере почтового отделения, которая ускоряется вперед и назад, когда она толкается. В такой ситуации необходимо рассматривать небольшие промежутки времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением. 2\) соответственно.
2\) соответственно.Следующие несколько примеров рассматривают движение поезда метро, показанное на рисунке \(\PageIndex{7}\). На рисунке \(\PageIndex{7a}\) челнок движется вправо, а на рисунке \(\PageIndex{7b}\) — влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые рассуждения, которые используются при решении задач.
Рисунок \(\PageIndex{7}\): Одномерное движение поезда метро, рассмотренное в примерах \(\PageIndex{2}\) – \(\PageIndex{5}\). Здесь мы выбрали ось x так, что + означает вправо, а – означает влево для перемещений, скоростей и ускорений. (a) Поезд метро движется вправо из \(x_0\) в \(x_f\). Его перемещение \(Δx\) равно +2,0 км. (b) Поезд движется влево из \(x_0\) в \(x_f\). Его перемещение \(Δx\) равно \(−1,5 км\). (Обратите внимание, что штриховой символ (′) используется просто для того, чтобы различить перемещение в двух разных ситуациях. Для того, чтобы все отображалось на диаграмме, расстояния и размеры автомобилей представлены в разных масштабах.)
Пример \(\PageIndex{2}\): Расчет перемещения поезда метро
Каковы величина и знак перемещений поезда метро, показанного в частях (a) и (b) рисунка \(\ Индекс страницы{7}\)?
Стратегия
Чертеж с системой координат уже предоставлен, поэтому нам не нужно делать эскиз, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает.
 Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение \( Δx=x_f−x_0\). Это просто, поскольку заданы начальная и конечная позиции.
Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение \( Δx=x_f−x_0\). Это просто, поскольку заданы начальная и конечная позиции.Решение
- Определите известное. На рисунке мы видим, что \(x_f=6,70\, км\) и \(x_0=4,70\, км\) для участка (а), а \(x’_f=3,75\, км\) и \(x ‘_0=5,25\, км\) для участка (б).
- Решите для смещения в части (a).\[\begin{align*} Δx &=x_f−x_0 \\[5pt] &=6,70\, км−4,70\, км \\[5pt] &=+2,00 \ , км \end{align*}\]
- Решите для перемещения в части (b).\[\begin{align*} Δx’ &=x’_f−x’_0 \\[5pt] &=3,75\, км−5,25\, км \\[5pt] &=−1,50\, км \end{align*}\]
Обсуждение
Направление движения в (а) вправо и, следовательно, его перемещение имеет положительный знак, тогда как движение в (б) влево и, следовательно, имеет отрицательный знак.
Пример \(\PageIndex{3}\): сравнение пройденного расстояния с перемещением — поезд метро
Каковы расстояния, пройденные для движений, показанных в частях (a) и (b) поезда метро на рисунке \(\PageIndex{7}\)?
Стратегия
Чтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны со смещением.
 Расстояние между двумя позициями определяется как величина смещения, найденная в примере \(\PageIndex{2}\). Пройденное расстояние — это общая длина пути, пройденного между двумя положениями (см. раздел о перемещении). В случае поезда метро, показанного на рисунке \(\PageIndex{7}\), пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.
Расстояние между двумя позициями определяется как величина смещения, найденная в примере \(\PageIndex{2}\). Пройденное расстояние — это общая длина пути, пройденного между двумя положениями (см. раздел о перемещении). В случае поезда метро, показанного на рисунке \(\PageIndex{7}\), пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.Решение
1. Перемещение по части (а) составило +2,00 км. Следовательно, расстояние между начальным и конечным положениями составило 2,00 км, а пройденное расстояние составило 2,00 км.
2. Перемещение для участка (b) составило \( −1,5 км\). Следовательно, расстояние между начальным и конечным положениями составило 1,50 км, а пройденное расстояние — 1,50 км.
Обсуждение
Расстояние является скаляром. У него есть величина, но нет знака, указывающего направление.
Пример \(\PageIndex{4}\): расчет ускорения: ускорение поезда метро
Предположим, поезд на рисунке \(\PageIndex{7a}\) разгоняется из состояния покоя до 30,0 км/ч за первые 20,0 с своего движения.
 Каково его среднее ускорение за этот промежуток времени?
Каково его среднее ускорение за этот промежуток времени?Стратегия
Сейчас стоит сделать простой набросок:
Рисунок \(\PageIndex{8}\): Эта задача состоит из трех шагов. Сначала мы должны определить изменение скорости, затем мы должны определить изменение времени и, наконец, мы используем эти значения для расчета ускорения.Решение
- Определите известное. \( v_0=0\) (поезда стартуют из состояния покоя), \( v_f=30,0 км/ч \) и \(Δt=20,0 с \).
- Вычислить \(Δv\). Так как поезд трогается с места, то изменение его скорости равно \(Δv=+30,0 км/ч \), где плюс означает скорость вправо.
- Подставьте известные значения и найдите неизвестное \(\bar{a}\). \[\bar{a}=\dfrac{Δv}{Δt}=\dfrac{+30,0 км/ч}{20,0 с}\nonumber\]
- Поскольку единицы смешаны (у нас есть и часы, и секунды для времени), нам нужно перевести все в единицы СИ метры и секунды. (Подробнее см. в разделе Физические величины и единицы.
 2 \номер\]
2 \номер\]
Обсуждение
Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд стартует из состояния покоя и заканчивается со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и изменение скорости, как это всегда и бывает. в конце пути поезд на рисунке \(\PageIndex{7a}\) замедляется до полной остановки со скорости 30,0 км/ч за 8,00 с. Каково его среднее ускорение при остановке?
Стратегия
Рисунок \(\PageIndex{9}\):.В этом случае поезд замедляется, и его ускорение отрицательно, потому что он движется влево. Как и в предыдущем примере, мы должны найти изменение скорости и изменение времени, а затем найти ускорение.
Решение
- Определите известные. \(v_0=30,0 км/ч, v_f=0 км/ч\) (поезд стоит, поэтому его скорость равна 0) и \(Δt=8,00 с \).
- Найдите изменение скорости \(Δv\). \[Δv=v_f−v_0=0−30,0 км/ч=−30,0 км/ч \номер\] 92.
 \номер\]
\номер\]
Обсуждение
Знак минус указывает на то, что ускорение направлено влево. Этот знак разумен, поскольку в этой задаче поезд изначально имеет положительную скорость, а отрицательное ускорение будет препятствовать движению. Опять же, ускорение имеет то же направление, что и изменение скорости, которое здесь отрицательно. Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости.
Графики зависимости положения, скорости и ускорения от времени для поездов в примере \(\PageIndex{4}\) и \(\PageIndex{5}\) показаны на рисунке \(\PageIndex{10}\ ). (Мы приняли, что скорость остается постоянной от 20 до 40 с, после чего поезд замедляется.)
Рисунок \(\PageIndex{10}\): (a) Положение поезда во времени. Обратите внимание, что положение поезда меняется медленно в начале пути, а затем все быстрее и быстрее по мере того, как он набирает скорость. Затем его положение меняется медленнее, так как он замедляется в конце пути. В середине пути, пока скорость остается постоянной, положение изменяется с постоянной скоростью. (b) Скорость поезда во времени. Скорость поезда увеличивается по мере того, как он ускоряется в начале пути. Он остается таким же в середине пути (где нет ускорения). Она уменьшается по мере торможения поезда в конце пути. в) ускорение поезда во времени. Поезд имеет положительное ускорение, так как в начале пути он ускоряется. Он не имеет ускорения, так как в середине пути движется с постоянной скоростью. Его ускорение отрицательно, так как в конце пути оно замедляется.
В середине пути, пока скорость остается постоянной, положение изменяется с постоянной скоростью. (b) Скорость поезда во времени. Скорость поезда увеличивается по мере того, как он ускоряется в начале пути. Он остается таким же в середине пути (где нет ускорения). Она уменьшается по мере торможения поезда в конце пути. в) ускорение поезда во времени. Поезд имеет положительное ускорение, так как в начале пути он ускоряется. Он не имеет ускорения, так как в середине пути движется с постоянной скоростью. Его ускорение отрицательно, так как в конце пути оно замедляется.Пример \(\PageIndex{6}\): Расчет средней скорости поезда метро
Какова средняя скорость поезда в части b примера \(\PageIndex{2}\), показанном еще раз ниже, если чтобы совершить поездку, требуется 5,00 мин.?
Рисунок \(\PageIndex{11}\)Стратегия
Средняя скорость равна смещению, деленному на время. Здесь оно будет отрицательным, так как поезд движется влево и имеет отрицательное смещение.

Раствор
- Определить известные. \[ x’_f=3,75 км,\, x’_0=5,25 км,\, Δt=5,00 мин. \номер\]
- Определить смещение, \(Δx’\). Мы обнаружили, что \( Δx’\) равно \(−1,5 км\) в примере \(\PageIndex{7}\).
- Найдите среднюю скорость. \[\bar{v}=\dfrac{Δx’}{Δt}=\dfrac{−1,50 км}{5,00 мин} \nonumber\]
- Преобразование единиц. \[\bar{v}=\dfrac{Δx’}{Δt}=(\dfrac{−1,50 км}{5,00 мин})(\dfrac{60 мин}{1}ч)=-18,0 км/ч \ не число\]
Обсуждение
Отрицательная скорость указывает на движение влево.
Пример \(\PageIndex{7}\): расчет замедления: поезд метро
Наконец, предположим, что поезд на рисунке \(\PageIndex{7}\) замедляется до остановки со скорости 20,0 км/ч за 10,0 с. Каково его среднее ускорение?
Стратегия
Еще раз нарисуем набросок:
Рисунок \(\PageIndex{12}\): Как и прежде, мы должны найти изменение скорости и изменение времени, чтобы рассчитать среднее ускорение. 9s2 \номер\]
9s2 \номер\]
Обсуждение
Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд изначально имеет отрицательную скорость (влево) в этой задаче, а положительное ускорение противодействует движению (и, следовательно, вправо). Опять же, ускорение имеет то же направление, что и изменение скорости, которое здесь положительно. Как и в примере \(\PageIndex{5}\), это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости.
Знак и направление
Пожалуй, самое важное, что следует отметить в этих примерах, — это знаки ответов. В выбранной нами системе координат плюс означает, что величина находится справа, а минус означает, что она находится слева. Это легко представить для смещения и скорости. Но это немного менее очевидно для ускорения. Большинство людей интерпретируют отрицательное ускорение как замедление объекта. Этого не было в примере \(\PageIndex{5}\), где положительное ускорение замедляло отрицательную скорость. Решающим отличием было то, что ускорение было в направлении, противоположном скорости. На самом деле отрицательное ускорение увеличивает отрицательную скорость. Например, поезд, движущийся влево на рисунке \(\PageIndex{11}\), ускоряется за счет ускорения влево. В этом случае и v, и a отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и скорость, то тело ускоряется. Если ускорение имеет противоположный знак скорости, то объект замедляется.
Решающим отличием было то, что ускорение было в направлении, противоположном скорости. На самом деле отрицательное ускорение увеличивает отрицательную скорость. Например, поезд, движущийся влево на рисунке \(\PageIndex{11}\), ускоряется за счет ускорения влево. В этом случае и v, и a отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и скорость, то тело ускоряется. Если ускорение имеет противоположный знак скорости, то объект замедляется.
Упражнение \(\PageIndex{1}\)
Самолет приземляется на взлетно-посадочной полосе, направляясь на восток. Опишите его ускорение.
- Ответить
Если мы возьмем восток за положительное значение, то ускорение самолета будет отрицательным, так как он движется на запад. Он также замедляется: его ускорение противоположно направлению его скорости.
ИССЛЕДОВАНИЯ PHET: МОДЕЛИРОВАНИЕ ДВИЖУЩЕГОСЯ ЧЕЛОВЕКА
Узнайте о графиках положения, скорости и ускорения с помощью моделирования PhET Moving Man. Перемещайте человечка вперед-назад с помощью мыши и зарисовывайте его движение. Установите положение, скорость или ускорение, и пусть симуляция переместит человека за вас.
Перемещайте человечка вперед-назад с помощью мыши и зарисовывайте его движение. Установите положение, скорость или ускорение, и пусть симуляция переместит человека за вас.
Резюме
- Ускорение — это скорость изменения скорости. В символах среднее ускорение \(\bar{a}\) равно \(\bar{a}=\dfrac{Δv}{Δt}=\dfrac{v_f−v_0}{t_f−t_0}\).
- Единицей ускорения в системе СИ является 2 .
- Ускорение является вектором и поэтому имеет как величину, так и направление.
- Ускорение может быть вызвано изменением величины или направления скорости.
- Мгновенное ускорение — это ускорение в определенный момент времени.
- Замедление — это ускорение с направлением, противоположным направлению скорости.
Глоссарий
- ускорение
- скорость изменения скорости; изменение скорости во времени
- среднее ускорение
- изменение скорости, деленное на время, за которое она изменяется
- мгновенное ускорение
- ускорение в конкретный момент времени
- замедление
- ускорение в направлении, противоположном скорости; ускорение, приводящее к уменьшению скорости
Эта страница под названием 2. 4: Acceleration распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
4: Acceleration распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- ускорение
- среднее ускорение
- замедление
- мгновенное ускорение
- источник@https://openstax.
 org/details/books/college-physics
org/details/books/college-physics
2.4 Ускорение – Колледж Физика главы 1-17
2 Кинематика
СводкаОпределите и различайте мгновенное ускорение, среднее ускорение и замедление.
Вычислите ускорение, зная начальное время, начальную скорость и конечную скорость. Рисунок 1. Самолет снижает скорость или замедляется перед посадкой на Сен-Мартене. Его ускорение противоположно направлению его скорости. (кредит: Стив Конри, Flickr).
В повседневном разговоре ускорить означает ускорить. Ускоритель в автомобиле фактически может заставить его ускориться. Чем больше ускорение , тем больше изменение скорости за заданное время. Формальное определение ускорения соответствует этим понятиям, но более широкое.
СРЕДНЕЕ УСКОРЕНИЕ
Среднее ускорение равно степени изменения скорости ,
v}}{\Delta{t}}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{v_f-v_0}{t_f-t_0}}[/latex] , 92},[/latex]метры в секунду в квадрате или метры в секунду в секунду, что буквально означает, на сколько метров в секунду скорость изменяется каждую секунду.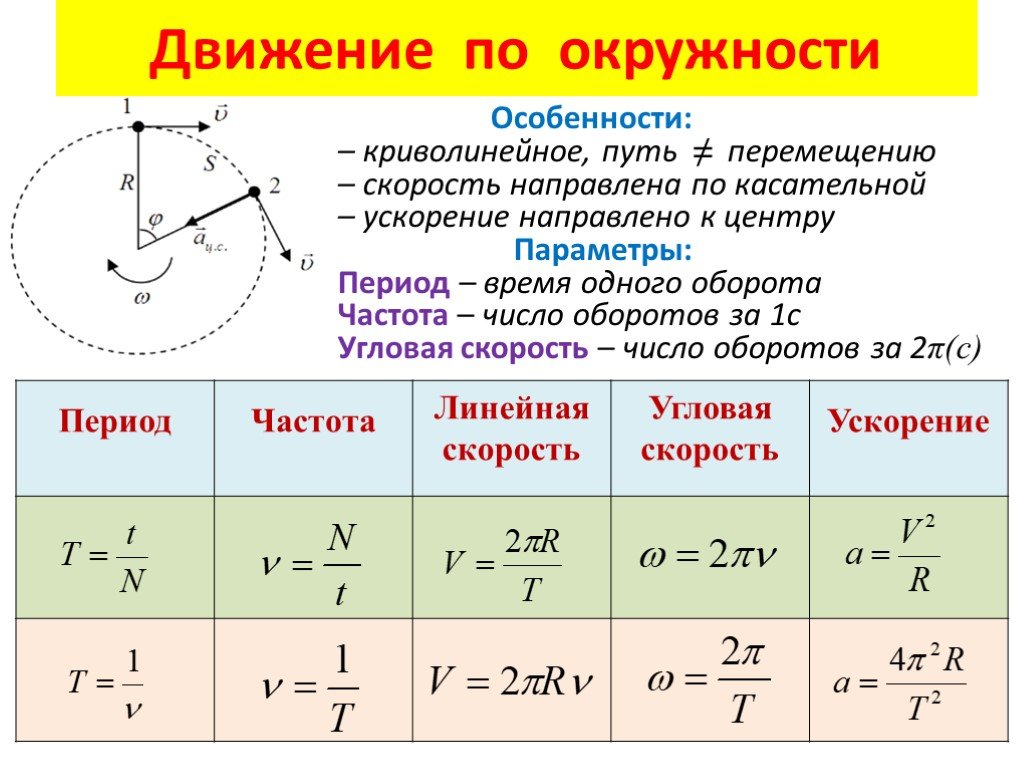
Напомним, что скорость — это вектор, у нее есть и величина, и направление. Это означает, что изменение скорости может быть изменением величины (или скорости), но оно также может быть изменением направления . Например, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение происходит, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по тому и другому.
УСКОРЕНИЕ КАК ВЕКТОР
Ускорение представляет собой вектор, направленный в том же направлении, что и изменение скорости, [латекс]\boldsymbol{\Delta{v}}[/латекс]. Поскольку скорость является вектором, она может изменяться как по величине, так и по направлению. Таким образом, ускорение — это изменение либо скорости, либо направления, либо того и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда совпадает с направлением движения .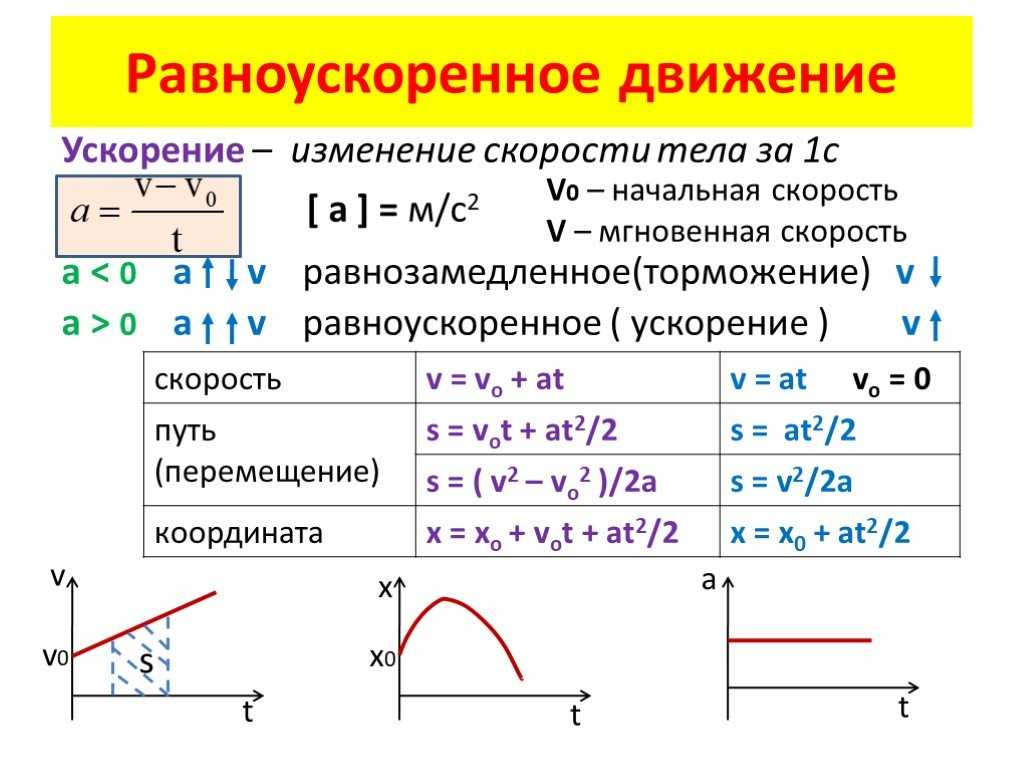 Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление .
Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление .
ПРЕДУПРЕЖДЕНИЕ О НЕПРАВИЛЬНОМ КОНЦЕПЦИИ: ЗАМЕДЛЕНИЕ VS. ОТРИЦАТЕЛЬНОЕ УСКОРЕНИЕ
Под замедлением всегда подразумевается ускорение в направлении, противоположном направлению скорости. Замедление всегда снижает скорость. Однако отрицательное ускорение равно ускорению в отрицательном направлении в выбранной системе координат . Отрицательное ускорение может быть, а может и не быть замедлением, а замедление может считаться или не считаться отрицательным ускорением. Например, рассмотрим рисунок 3.
Рисунок 3. (a) Этот автомобиль ускоряется, двигаясь вправо. Поэтому он имеет положительное ускорение в нашей системе координат. (b) Этот автомобиль замедляется, когда он движется вправо. Следовательно, в нашей системе координат он имеет отрицательное ускорение, потому что его ускорение направлено влево. Автомобиль тоже тормозит: направление его ускорения противоположно направлению его движения. (c) Этот автомобиль движется влево, но со временем замедляется. Следовательно, его ускорение положительно в нашей системе координат, потому что оно направлено вправо. Однако автомобиль замедляется, потому что его ускорение противоположно его движению. (d) Этот автомобиль ускоряется, когда он движется влево. Он имеет отрицательное ускорение, потому что он ускоряется влево. Однако, поскольку его ускорение направлено в том же направлении, что и его движение, оно ускоряется (а не замедляется).
Поэтому он имеет положительное ускорение в нашей системе координат. (b) Этот автомобиль замедляется, когда он движется вправо. Следовательно, в нашей системе координат он имеет отрицательное ускорение, потому что его ускорение направлено влево. Автомобиль тоже тормозит: направление его ускорения противоположно направлению его движения. (c) Этот автомобиль движется влево, но со временем замедляется. Следовательно, его ускорение положительно в нашей системе координат, потому что оно направлено вправо. Однако автомобиль замедляется, потому что его ускорение противоположно его движению. (d) Этот автомобиль ускоряется, когда он движется влево. Он имеет отрицательное ускорение, потому что он ускоряется влево. Однако, поскольку его ускорение направлено в том же направлении, что и его движение, оно ускоряется (а не замедляется).
Пример 1. Расчет ускорения: скаковая лошадь покидает ворота
Скаковая лошадь, выходящая из ворот, разгоняется из состояния покоя до скорости 15,0 м/с строго на запад за 1,80 с. Каково его среднее ускорение?
Каково его среднее ускорение?
Стратегия
Сначала мы рисуем эскиз и назначаем проблеме систему координат. Это простая задача, но ее всегда полезно визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Рисунок 5.
Мы можем решить эту проблему, идентифицируя [латекс]\жирныйсимвол{\Delta{v}}[/латекс]и[латекс]\жирныйсимвол{\Delta{t}}[/латекс ] исходя из предоставленной информации, а затем рассчитывая среднее ускорение непосредственно из уравнения {t}}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{v_f-v_0}{t_f-t_0}}[/latex].
Решение
1. Определите известные значения.[latex]\boldsymbol{v_0=0}[/latex],[latex]\boldsymbol{v_f=-15.0\textbf{ м/с}}[/latex] (знак минус указывает направление на запад),[latex]\boldsymbol{\Delta{t}=1,80\textbf{s}}[/latex]. 2}[/латекс]. 92}[/латекс]. Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы, чтобы всадник удерживался с силой, почти равной его весу.
2}[/латекс]. 92}[/латекс]. Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы, чтобы всадник удерживался с силой, почти равной его весу.
Мгновенное ускорение а или ускорение в конкретный момент времени получается с помощью того же процесса, который обсуждался для мгновенной скорости в главе 2.3 «Время, скорость и скорость», то есть путем рассмотрения бесконечно малого интервала время. Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рис. 6 показаны графики зависимости мгновенного ускорения от времени для двух очень разных движений. На рис. 6(а) ускорение немного меняется, и среднее значение по всему интервалу почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около[латекс]\boldsymbol{1. 2}[/латекс] соответственно.
2}[/латекс] соответственно.
В следующих нескольких примерах рассматривается движение поезда метро, показанного на рисунке 7. В (а) шаттл движется вправо, а в (б) он движется влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые рассуждения, которые используются при решении задач.
Рис. 7. Одномерное движение поезда метро, рассмотренное в Примере 2, Примере 3, Примере 4, Примере 5, Примере 6 и Примере 7. Здесь мы выбрали ось x так, что + означает вправо и − означает влево для перемещений, скоростей и ускорений. а) Поезд метро движется вправо с x 0 до x f . Его водоизмещение Δ x составляет +2,0 км. (b) Поезд движется влево от x’ o до x’ f . Его водоизмещение Δ x’ составляет -1,5 км . (Обратите внимание, что штриховой символ (′) используется просто для того, чтобы различать перемещение в двух разных ситуациях. Расстояние пути и размер автомобилей указаны в разных масштабах, чтобы все уместить на диаграмме.).
Здесь мы выбрали ось x так, что + означает вправо и − означает влево для перемещений, скоростей и ускорений. а) Поезд метро движется вправо с x 0 до x f . Его водоизмещение Δ x составляет +2,0 км. (b) Поезд движется влево от x’ o до x’ f . Его водоизмещение Δ x’ составляет -1,5 км . (Обратите внимание, что штриховой символ (′) используется просто для того, чтобы различать перемещение в двух разных ситуациях. Расстояние пути и размер автомобилей указаны в разных масштабах, чтобы все уместить на диаграмме.).
Пример 2. Расчет перемещения: поезд метро
Каковы величина и знак перемещений поезда метро, показанного в частях (a) и (b) на рис. 7?
Стратегия
Чертеж с системой координат уже предоставлен, поэтому нам не нужно делать эскиз, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает.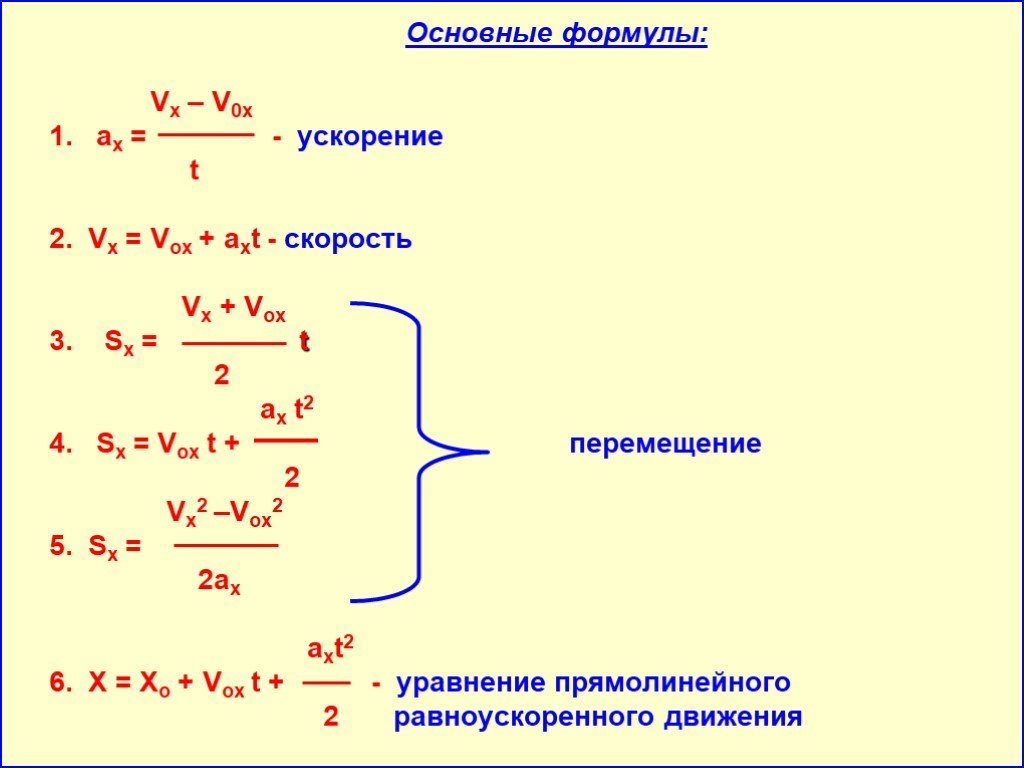 Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение [латекс]\жирныйсимвол{\Delta{x}=x_f-x_0}[/латекс]. Это просто, поскольку заданы начальная и конечная позиции.
Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение [латекс]\жирныйсимвол{\Delta{x}=x_f-x_0}[/латекс]. Это просто, поскольку заданы начальная и конечная позиции.
Решение
1. Найдите известные. На рисунке мы видим, что [латекс]\boldsymbol{x_f=6,70\textbf{ км}}[/латекс] и [латекс]\boldsymbol{x_0=4,70\textbf{ км}}[/латекс] для части (а) , и[латекс]\boldsymbol{x\prime_f=3,75\textbf{км}}[/латекс]и[латекс]\boldsymbol{x\prime_0=5,25\textbf{км}}[/латекс]для части (b) .
2. Найдите смещение в части (a).
[латекс]\boldsymbol{\Delta{x}=x_f-x_0=6,70\textbf{км}-4,70\textbf{км}=+2,00\textbf{км}}[/латекс]
3. Найдите смещение в части (b).
[латекс]\boldsymbol{\Delta{x}\prime=x\prime_f-x\prime_0=3,75\textbf{км}-5,25\textbf{км}=-1,50\textbf{км}}[/латекс]
Обсуждение
Направление движения в (а) право и, следовательно, его перемещение имеет положительный знак, тогда как движение в (б) влево и, следовательно, имеет отрицательный знак.
Пример 3. Расчет расстояния, пройденного с учетом смещения: поезд метро
Каковы расстояния, пройденные для движений, показанных в частях (a) и (b) поезда метро на рисунке 7?
Стратегия
Чтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны с перемещением. Расстояние между двумя положениями определяется как величина смещения, которое было найдено в примере 2. Пройденное расстояние — это общая длина пути, пройденного между двумя положениями. (См. Главу 2.1 Перемещение.) В случае поезда метро, показанного на рисунке 7, пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.
Решение
1. Перемещение по части (а) составило +2,00 км. Следовательно, расстояние между начальным и конечным положениями составило 2,00 км, а пройденное расстояние составило 2,00 км.
2. Перемещение для части (b) было [латекс]\boldsymbol{-1,5\textbf{км}}[/латекс]. Следовательно, расстояние между начальным и конечным положениями составило 1,50 км, а пройденное расстояние — 1,50 км.
Следовательно, расстояние между начальным и конечным положениями составило 1,50 км, а пройденное расстояние — 1,50 км.
Обсуждение
Расстояние является скаляром. У него есть величина, но нет знака, указывающего направление.
Пример 4: Расчет ускорения: поезд метро разгоняется
Предположим, что поезд на рис. 7(а) разгоняется из состояния покоя до 30,0 км/ч за первые 20,0 с своего движения. Каково его среднее ускорение за этот промежуток времени?
Стратегия
Сейчас стоит сделать простой набросок:
Рисунок 8.Эта задача состоит из трех шагов. Сначала мы должны определить изменение скорости, затем мы должны определить изменение времени и, наконец, мы используем эти значения для расчета ускорения.
Решение
1. Найдите известные.[latex]\boldsymbol{v_0=0}[/latex](поезда отправляются в состоянии покоя),[latex]\boldsymbol{v_f=30.0\textbf{ км/ч }}[/латекс] и [латекс]\boldsymbol{\Delta{t}=20,0\textbf{s}}[/латекс]. 2}[/латекс]
2}[/латекс]
Обсуждение
Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд стартует из состояния покоя и заканчивается со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и изменение скорости, как это всегда и бывает.
Пример 5: Расчет ускорения: поезд метро замедляется
Теперь предположим, что в конце пути поезд на рис. 7(а) замедляется до полной остановки со скорости 30,0 км/ч за 8,00 с. Каково его среднее ускорение при остановке?
Стратегия
Рис. 9.В этом случае поезд замедляется, и его ускорение отрицательно, потому что он движется влево. Как и в предыдущем примере, мы должны найти изменение скорости и изменение времени, а затем найти ускорение.
Решение
1. Найдите известные. [latex]\boldsymbol{v_0=30.0\textbf{ км/ч}}[/latex],[latex]\boldsymbol{v_f=0\textbf{ км/ч}}[/latex](поезд остановлен, поэтому его скорость равна 0) и[латекс]\жирныйсимвол{\Delta{t}=8,00\textbf{с}}[/латекс].
2. Найдите изменение скорости, [латекс]\жирныйсимвол{\Delta{v}}[/латекс].
[латекс]\boldsymbol{\Delta{v}=v_f-v_0=0-30,0\textbf{ км/ч}=-30,0\textbf{ км/ч}}[/латекс]
3. Подключите известные, [латекс]\boldsymbol{\Delta{v}}[/latex] и [латекс]\boldsymbol{\Delta{t}}[/latex], и найдите [латекс]\boldsymbol{\bar{a} }[/латекс].
[латекс]\boldsymbol{\bar{a}=}[/латекс][латекс]\boldsymbol{\frac{\Delta{v}}{\Delta{t}}}[/latex][латекс]\ boldsymbol{=}[/latex][латекс]\boldsymbol{\frac{-30,0\textbf{км/ч}}{8,00\textbf{с}}}[/latex] 92}[/латекс].
Знак минус указывает на то, что ускорение направлено влево. Этот знак разумен, поскольку в этой задаче поезд изначально имеет положительную скорость, а отрицательное ускорение будет препятствовать движению. Опять же, ускорение происходит в том же направлении, что и изменение скорости, которая здесь отрицательная. Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости.
Графики зависимости положения, скорости и ускорения от времени для поездов в Примере 4 и Примере 5 показаны на Рисунке 10 . (Мы приняли, что скорость остается постоянной от 20 до 40 с, после чего поезд замедляется.)
Рисунок 10. (а) Положение поезда во времени. Обратите внимание, что положение поезда меняется медленно в начале пути, а затем все быстрее и быстрее по мере того, как он набирает скорость. Затем его положение меняется медленнее, так как он замедляется в конце пути. В середине пути, пока скорость остается постоянной, положение изменяется с постоянной скоростью. (b) Скорость поезда во времени. Скорость поезда увеличивается по мере того, как он ускоряется в начале пути. Он остается таким же в середине пути (где нет ускорения). Она уменьшается по мере торможения поезда в конце пути. в) ускорение поезда во времени. Поезд имеет положительное ускорение, так как в начале пути он ускоряется. Он не имеет ускорения, так как в середине пути движется с постоянной скоростью. {\prime}_0=5,25\textbf{км}}[/latex ],[латекс]\жирныйсимвол{\Delta{t}=5,00\textbf{мин}}[/латекс]. 9{\prime}}{\Delta{t}}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{(\frac{-1,50\textbf{км}}{5,00\ textbf{ мин}})(\frac{60\textbf{ мин}}{1\textbf{ ч}})}[/latex][латекс]\boldsymbol{=-18,0\textbf{ км/ч}}[/ латекс]
{\prime}_0=5,25\textbf{км}}[/latex ],[латекс]\жирныйсимвол{\Delta{t}=5,00\textbf{мин}}[/латекс]. 9{\prime}}{\Delta{t}}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{(\frac{-1,50\textbf{км}}{5,00\ textbf{ мин}})(\frac{60\textbf{ мин}}{1\textbf{ ч}})}[/latex][латекс]\boldsymbol{=-18,0\textbf{ км/ч}}[/ латекс]Обсуждение
Отрицательная скорость указывает на движение влево.
Пример 7. Расчет замедления: поезд метро
Наконец, предположим, что поезд на рис. 11 замедляется до полной остановки со скорости 20,0 км/ч за 10,0 с. Каково его среднее ускорение?
Стратегия
Еще раз нарисуем набросок:
Рис. 12.
Как и прежде, мы должны найти изменение скорости и изменение времени для расчета среднего ускорения.
Решение
1. Определите известные значения.[latex]\boldsymbol{v_0=-20\textbf{ км/ч}}[/latex],[latex]\boldsymbol{v_f=0\textbf{ km/ h}}[/latex],[latex]\boldsymbol{\Delta{t}=10,0\textbf{s}}[/latex]. 2}[/латекс]
2}[/латекс]
Обсуждение
Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд изначально имеет отрицательную скорость (влево) в этой задаче, а положительное ускорение противодействует движению (и, следовательно, вправо). Опять же, ускорение происходит в том же направлении, что и изменение скорости, которая здесь положительна. Как и в примере 5, это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости.
Пожалуй, самое важное, что следует отметить в этих примерах, — это знаки ответов. В выбранной нами системе координат плюс означает, что величина находится справа, а минус означает, что она находится слева. Это легко представить для смещения и скорости. Но это немного менее очевидно для ускорения. Большинство людей интерпретируют отрицательное ускорение как замедление объекта. Этого не было в примере 7, где положительное ускорение замедляло отрицательную скорость. Решающим отличием было то, что ускорение было в направлении, противоположном скорости. В самом деле, отрицательное ускорение будет увеличить отрицательную скорость. Например, поезд, движущийся влево на рисунке 11, ускоряется за счет ускорения влево. В этом случае как [латекс]\boldsymbol{v}[/latex], так и [латекс]\boldsymbol{a}[/latex]отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и скорость, то тело ускоряется. Если ускорение имеет противоположный знак скорости, то объект замедляется.
Решающим отличием было то, что ускорение было в направлении, противоположном скорости. В самом деле, отрицательное ускорение будет увеличить отрицательную скорость. Например, поезд, движущийся влево на рисунке 11, ускоряется за счет ускорения влево. В этом случае как [латекс]\boldsymbol{v}[/latex], так и [латекс]\boldsymbol{a}[/latex]отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и скорость, то тело ускоряется. Если ускорение имеет противоположный знак скорости, то объект замедляется.
ИССЛЕДОВАНИЯ PHET: МОДЕЛИРОВАНИЕ ДВИЖУЩЕГОСЯ ЧЕЛОВЕКА
Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка вперед-назад с помощью мыши и зарисовывайте его движение. Установите положение, скорость или ускорение, и пусть симуляция переместит человека за вас.
Рис. 13. Движущийся человек.- Ускорение — скорость изменения скорости. В символах среднее ускорение [латекс]\boldsymbol{\bar{a}}[/латекс] равно
[латекс]\boldsymbol{\bar{a}=}[/латекс][латекс]\boldsymbol{\frac{\Delta{v}}{\Delta{t}}}[/latex][латекс]\boldsymbol {=}[/латекс][латекс]\boldsymbol{\frac{v_f-v_0}{t_f-t_0}}[/латекс].


 При этом сила тяжести, действующая на данное тело, равна F = mg. Отметим, что в действительности при свободном падении на тело действует еще и сопротивление воздуха, сила которая зависит от скорости, а при ее определенном значении становится равной по модулю силе тяжести. В таком случае движение тела происходит с постоянной скоростью.
При этом сила тяжести, действующая на данное тело, равна F = mg. Отметим, что в действительности при свободном падении на тело действует еще и сопротивление воздуха, сила которая зависит от скорости, а при ее определенном значении становится равной по модулю силе тяжести. В таком случае движение тела происходит с постоянной скоростью. Изобразим вектора скорости в этих точках и найдем вектор изменения скорости .
Изобразим вектора скорости в этих точках и найдем вектор изменения скорости .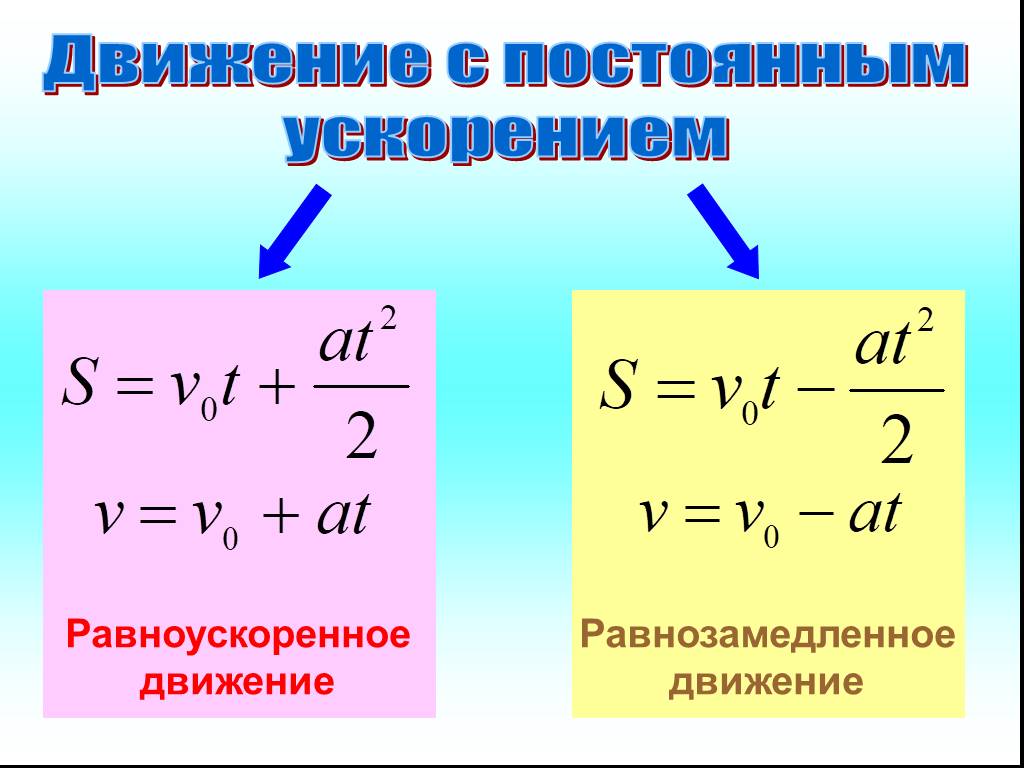


 2\) соответственно.
2\) соответственно.
 Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение \( Δx=x_f−x_0\). Это просто, поскольку заданы начальная и конечная позиции.
Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение \( Δx=x_f−x_0\). Это просто, поскольку заданы начальная и конечная позиции. Расстояние между двумя позициями определяется как величина смещения, найденная в примере \(\PageIndex{2}\). Пройденное расстояние — это общая длина пути, пройденного между двумя положениями (см. раздел о перемещении). В случае поезда метро, показанного на рисунке \(\PageIndex{7}\), пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.
Расстояние между двумя позициями определяется как величина смещения, найденная в примере \(\PageIndex{2}\). Пройденное расстояние — это общая длина пути, пройденного между двумя положениями (см. раздел о перемещении). В случае поезда метро, показанного на рисунке \(\PageIndex{7}\), пройденное расстояние равно расстоянию между начальным и конечным положениями поезда. Каково его среднее ускорение за этот промежуток времени?
Каково его среднее ускорение за этот промежуток времени? 2 \номер\]
2 \номер\] \номер\]
\номер\] В середине пути, пока скорость остается постоянной, положение изменяется с постоянной скоростью. (b) Скорость поезда во времени. Скорость поезда увеличивается по мере того, как он ускоряется в начале пути. Он остается таким же в середине пути (где нет ускорения). Она уменьшается по мере торможения поезда в конце пути. в) ускорение поезда во времени. Поезд имеет положительное ускорение, так как в начале пути он ускоряется. Он не имеет ускорения, так как в середине пути движется с постоянной скоростью. Его ускорение отрицательно, так как в конце пути оно замедляется.
В середине пути, пока скорость остается постоянной, положение изменяется с постоянной скоростью. (b) Скорость поезда во времени. Скорость поезда увеличивается по мере того, как он ускоряется в начале пути. Он остается таким же в середине пути (где нет ускорения). Она уменьшается по мере торможения поезда в конце пути. в) ускорение поезда во времени. Поезд имеет положительное ускорение, так как в начале пути он ускоряется. Он не имеет ускорения, так как в середине пути движется с постоянной скоростью. Его ускорение отрицательно, так как в конце пути оно замедляется.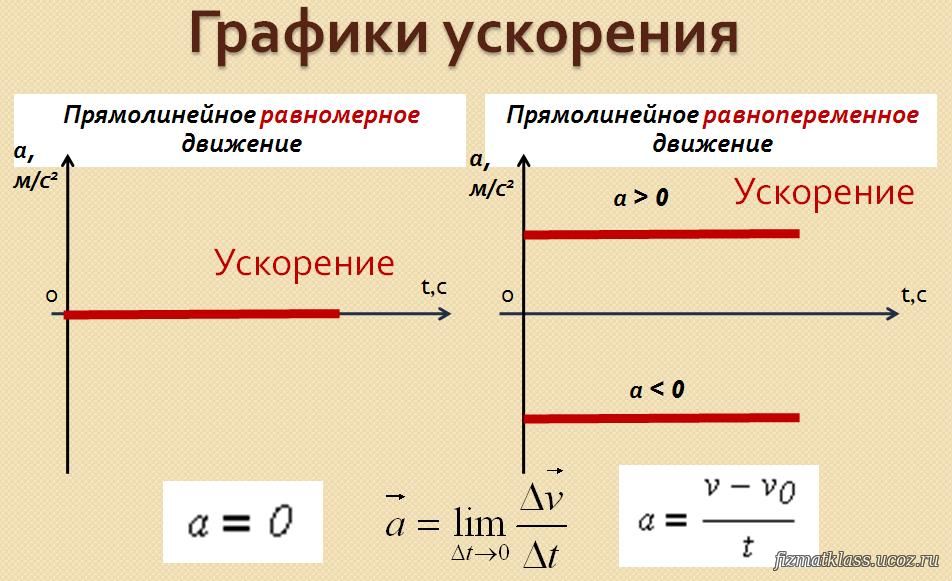
 9s2 \номер\]
9s2 \номер\] org/details/books/college-physics
org/details/books/college-physics