Ускорение. Равноускоренное прямолинейное движение
Неравномерное движение — это такое движение, при котором тело, за любые равные промежутки времени совершает разные перемещения, или, говорят, меняется проекция вектора скорости.
Для описания быстроты изменения положения тела с течением времени при неравномерном движении, вводится понятие средней скорости. Она показывает, какое перемещение в среднем совершало тело за единицу времени:
Но пользоваться этой формулой для определения модуля средней скорости можно лишь в том случае, если тело движется вдоль прямой в одну сторону. Во всех остальных случаях эта формула не работает.
Поэтому на практике пользуются понятием средней путевой скорости, с которым вы знакомы ещё с седьмого класса. Напомним, что средняя путевая скорость определяется отношением пути к промежутку времени, за который этот путь пройден. Она показывает, какой путь в среднем проходило тело за единицу времени:
Однако
следует помнить, что средняя скорость характеризует движение за весь промежуток
времени в целом.
Поэтому для описания такого движения вводится понятие мгновенной скорости, то есть скорости движения в данный момент времени или в данной точке траектории.
Теперь
вспомним, как определить мгновенную скорость тела. Для этого предположим, что у
нас есть шарик, который скатывается по наклонному жёлобу. Нас интересует
мгновенная скорость шарика, например, в точке А его траектории. Выделим небольшой
участок траектории, включающий в себя точку А. Разделив перемещение
шарика на этом участке траектории, на соответствующий промежуток времени найдём
среднюю скорость перемещения на этом участке. Это именно средняя скорость,
потому что скорость непрерывно изменяется, и в разных местах участка она
разная.
Разделив перемещение
шарика на этом участке траектории, на соответствующий промежуток времени найдём
среднюю скорость перемещения на этом участке. Это именно средняя скорость,
потому что скорость непрерывно изменяется, и в разных местах участка она
разная.
Рассмотрим меньшее перемещение — участок 2. Очевидно, что оно произойдёт за меньший промежуток времени. А средняя скорость шарика на этом участке хотя и не равна скорости в точке
При дальнейшем уменьшении перемещений и промежутков времени мы будем получать средние скорости, которые все меньше и меньше отличаются друг от друга и от мгновенной скорости шарика в точке А. В конце концов промежуток времени станет так мал, что можно будет пренебречь изменением скорости за это время (движение станет как бы равномерным). Тогда средняя скорость на этом участке и будет являться мгновенной скоростью шарика в точке А.
Таким образом, мгновенная скорость
Как
следует из формулы, направление мгновенной скорости совпадает с направлением
движения тела.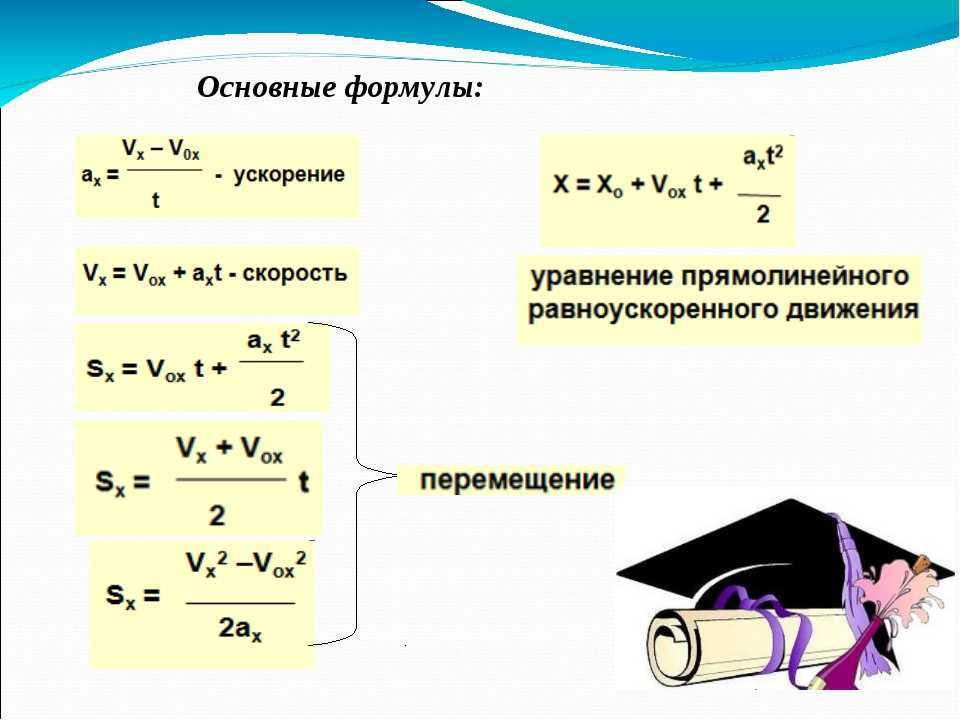
В дальнейшем мгновенную скорость мы будем называть просто скоростью.
Из всех видов неравномерного движения в школе изучают самое простое — прямолинейное равноускоренное движение. Так называют движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и туже величину, а траекторией движения тела является прямая линия.
Для того, чтобы описать насколько быстро меняется скорость тела, в физике ввели величину, которую назвали ускорением тела.
Ускорение — это физическая величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло:
Разумеется, ускорение, как и скорость, является векторной величиной. При этом направление вектора ускорения совпадает с направлением вектора изменения скорости тела.
Единицей
измерения ускорения в системе СИ является
На
прошлых уроках мы с вами, что основная задача кинематики сводится к нахождению положения
тела в любой момент времени.
Это есть уравнение скорости для равноускоренного движения.
Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя, поэтому перепишем уравнение в проекции на ось Ох:
Таким образом, зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени.
Как и в случае равномерного прямолинейного движения тела, зависимости кинематических величин от времени при равноускоренном движении можно изобразить графически.
Итак,
на графике представлены графики зависимости ускорений для трёх тел от времени.
Как видим, эти графики являются прямыми линиями, параллельными оси времени. И это не удивительно, ведь при равноускоренном движении модуль и направление вектора ускорения не меняется. При этом обратите внимание на то, что график располагается над осью времени, если тело движется равноускорено. Под осью времени в случае равнозамедленного движения (то есть когда проекция ускорения на координатную ось меньше нуля). И будет совпадать с осью времени, если тело движется прямолинейно и равномерно.
Теперь изобразим графики зависимости скорости от времени.
Как мы знаем при равноускоренном движении скорость с течением времени изменяется со временем. При этом, как видно из уравнения, зависимость скорости от времени является линейной функцией и поэтому график скорости имеет вид прямой, наклоненной к оси времени. Причём, чем больше угол наклона, тем большее ускорение имеет тело.
А теперь подумайте, какие изменения движения тела в ней происходят?
Всё
верно, в этой особой точке скорость тела меняет своё направление на
противоположное.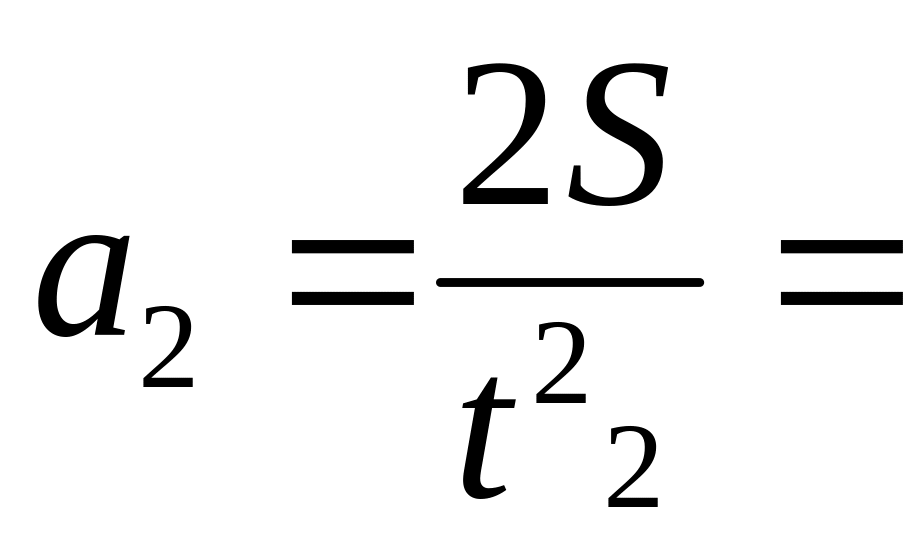 Такая точка называется точкой поворота.
Такая точка называется точкой поворота.
Теперь настало время вспомнить, как определить местоположение тела при равноускоренном движении. Для этого воспользуемся графиком зависимости скорости тела от времени. Давай разобьём график скорости на такие бесконечно малые прямоугольные участки, чтобы на них скорость тела можно было считать постоянной.
Тогда перемещение за бесконечно малый промежуток времени будет равно площади закрашенной полоски. А найдя суммарную площадь всех малых фигур на выбранном интервале времени, а она будет равна площади трапеции, мы определим перемещение тела.
Теперь подставим в записанную формулу уравнение скорости при равноускоренном движении.
Раскрыв скобки и приведя подобные, получим уравнение перемещения при равноускоренном движении в проекциях на координатную ось:
Так
как мы с вами рассматриваем прямолинейное движение, то в случае, когда скорость
и ускорение направлены в одну сторону, модуль перемещения равен пройденному
пути, поэтому, когда мы определяем модуль перемещения — мы определяем и
пройденный путь.
Заменив проекции соответствующими векторами, получим уравнение перемещения в векторном виде:
Учитывая, что Δs𝑥 = 𝑥 − 𝑥0, преобразуем уравнение перемещения в проекциях на координатную ось:
Полученное равенство называется основным кинематическим уравнением равноускоренного движения.
Теперь давайте рассмотрим некоторые важные зависимости между величинами равноускоренного прямолинейного движения.
И так, для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени. Следовательно, пути, пройденные телом за одну, две, три, четыре и так далее секунды будут относиться как квадраты последовательных натуральных чисел:
s1 : s2 : s3 = 12 : 22 : 32
И ещё одна важная зависимость: для любого равноускоренного движения, пути, пройденные телом за любые равные промежутки времени, будут относиться как последовательный ряд нечётных чисел:
s1-ю : s2-ю : s3-ю = 1 : 3 : 5
Так
как проекция перемещения квадратично зависит от времени, то графиком
перемещения для равноускоренного движения является парабола, положение вершины
которой зависит от направлений начальной скорости и ускорения тела.
Здесь стоит обратить внимание на то, что для равноускоренного движения графиком движения (то есть графиком зависимости координаты тела от времени), тоже является парабола, положение вершины которой, как и в случае с перемещением, так же зависит от направлений начальной скорости и ускорения тела.
Вопрос №1. Перемещение, скорость, путь, ускорение. Вычисление пройденного пути при равномерном и равноускоренном прямолинейном движении.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина. ( )
Пройденный
путь S
равен длине дуги траектории, пройденной
телом за некоторое время t.
Путь – скалярная величина.Ускорение – это величина, которая характеризует
быстроту изменения скорости. Скорость — векторная
физическая величина, характеризующая
быстроту перемещения и направление
движения материальной точки в пространстве
относительно выбранной системы
отсчёта. Прямолинейным
равномерным движением называется механическое движение, при
котором тело за любые равные промежутки
времени совершает одинаковые перемещения.
(
) Равноускоренным
движением называется такое движение, при котором
вектор ускорения
остается неизменным по модулю и
направлению. (
)
Прямолинейным
равномерным движением называется механическое движение, при
котором тело за любые равные промежутки
времени совершает одинаковые перемещения.
(
) Равноускоренным
движением называется такое движение, при котором
вектор ускорения
остается неизменным по модулю и
направлению. (
)
Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии.
Нормальное
ускорение,
составляющая ускорения точки при
криволинейном движении, направленная
по главной нормали к траектории в
сторону центра кривизны; Нормальное
ускорение называется также
центростремительным ускорением.
Численно Нормальное ускорение равно
v2/r, где v — скорость точки, r — радиус
кривизны траектории. При движении по
окружности Нормальное ускорение может
вычисляться по формуле rw2, где r — радиус
окружности, w— угловая скорость вращения
этого радиуса. В случае прямолинейного
движения Нормальное ускорение равно
нулю.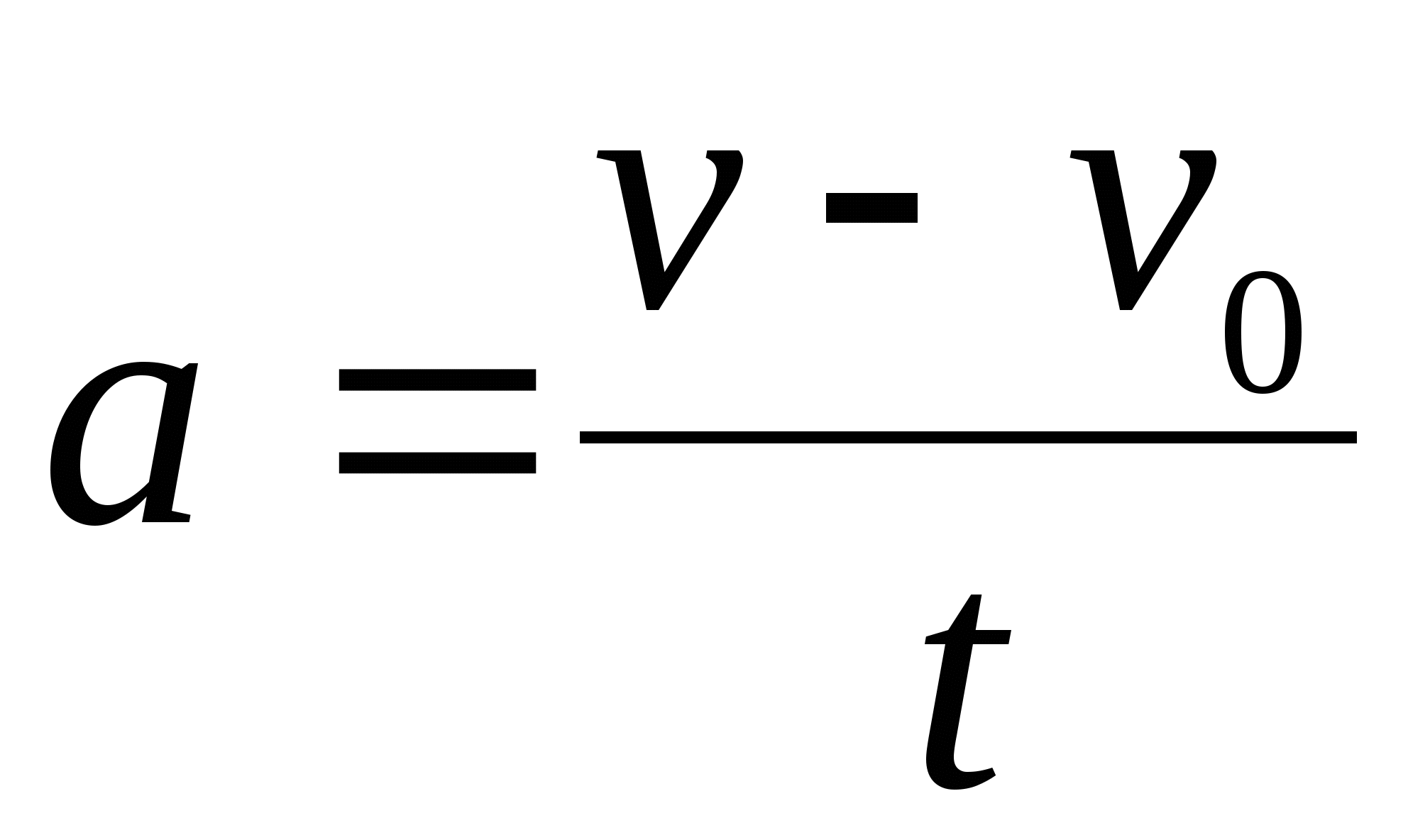
Тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения. Совпадает с направлением вектора скорости при ускоренном движении и противоположно направлено при замедленном. Характеризует изменение модуля скорости.
Принято
описывать траекторию материальной
точки при помощи радиус-вектора,
направление, длина и начальная точка
которого зависят от времени. При этом
кривая, описываемая концом радиус-вектора
в пространстве может быть представлена
в виде сопряжённых дуг различной
кривизны, находящихся в общем случае
в пересекающихся плоскостях. При этом
кривизна каждой дуги определяется её
радиусом кривизны, направленном к дуге
из мгновенного центра поворота,
находящегося в той же плоскости, что и
сама дуга. При том прямая линия
рассматривается как предельный случай
кривой, радиус кривизны которой может
считаться равным бесконечности.И потому
траектория в общем случае может быть
представлена как совокупность сопряжённых
дуг.
Вопрос №3. Угловые скорость и ускорение. Вычисление угла поворота тела при равномерном и равноускоренном вращении. Связь линейных и угловых характеристик.
Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени, а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно
Вопрос №4. 1-ый закон Ньютона. Инерциальные системы отсчета. Преобразования координат и скоростей Галилея. Импульс. Сила. 2-ой и 3-й законы Ньютона
Первый
закон Ньютона:
всякая материальная точка (тело)
сохраняет состояние покоя или
равномерного прямолинейного движения
до тех пор, пока воздействие со
стороны других тел не заставит ее
изменить это состояние. Стремление
тела сохранять состояние покоя или
равномерного прямолинейного движения
называется инертностью. Поэтому
первый закон Ньютона называют также
законом инерции. Сила —
это векторная величина, являющаяся
мерой механического воздействия на
тело со стороны других тел или полей,
в результате которого тело приобретает
ускорение или изменяет свою форму и
размеры. Импульс—
векторная физическая величина,
характеризующая меру механического
движения тела. В классической механике
импульс тела равен произведению массы
m этой точки на её скорость v, направление
импульса совпадает с направлением
вектора скорости. Второй
закон Ньютона:
В инерциальной системе отсчёта ускорение,
которое получает материальная точка,
прямо пропорционально равнодействующей
всех приложенных к ней сил и обратно
пропорционально её массе. Третий закон Ньютона:
Материальные
точки попарно действуют друг на друга
с силами, имеющими одинаковую природу,
направленными вдоль прямой, соединяющей
эти точки, равными по модулю и
противоположными по направлению:
Стремление
тела сохранять состояние покоя или
равномерного прямолинейного движения
называется инертностью. Поэтому
первый закон Ньютона называют также
законом инерции. Сила —
это векторная величина, являющаяся
мерой механического воздействия на
тело со стороны других тел или полей,
в результате которого тело приобретает
ускорение или изменяет свою форму и
размеры. Импульс—
векторная физическая величина,
характеризующая меру механического
движения тела. В классической механике
импульс тела равен произведению массы
m этой точки на её скорость v, направление
импульса совпадает с направлением
вектора скорости. Второй
закон Ньютона:
В инерциальной системе отсчёта ускорение,
которое получает материальная точка,
прямо пропорционально равнодействующей
всех приложенных к ней сил и обратно
пропорционально её массе. Третий закон Ньютона:
Материальные
точки попарно действуют друг на друга
с силами, имеющими одинаковую природу,
направленными вдоль прямой, соединяющей
эти точки, равными по модулю и
противоположными по направлению:
Вопрос
№5. Закон сохранения импульса. Центр
масс тела.
Закон сохранения импульса. Центр
масс тела.
Центром масс системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы Зако́н сохране́ния и́мпульса утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
Вопрос №6. Принцип реактивного движения. Движение тел с переменной массой. Формула Мещерского. Формула Циолковского
Под реактивным понимают движение тела, возникающее
при отделении некоторой его части с
определенной скоростью относительно
тела. При этом возникает т.н. реактивная
сила, сообщающая телу ускорение.
реактивная
сила, сообщающая телу ускорение.
Уравнение Мещерского — основное уравнение в механике тел переменной массы:
Формула Циолковского определяет скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической:
Центростремительная сила
Центростремительная силаЛюбое движение по криволинейной траектории представляет собой ускоренное движение и требует приложения силы, направленной к центру кривизны траектории. Эта сила называется центростремительной силой, что означает «сила поиска центра». Сила имеет величину Для раскачивания груза на струне требуется натяжение струны, и в случае разрыва струны груз будет перемещаться по касательной. Центростремительное ускорение
можно вывести для случая
круговое движение с момента
криволинейный путь в любой точке может
быть расширена до круга.
| Индекс Пример с массой на струне | |||
| Назад |
| Индекс | ||
| Назад |
Выражение центростремительного ускорения получено из анализа кругового движения с постоянной скоростью с использованием подобных треугольников. Обратите внимание, что если скорость удваивается до м/с на том же радиусе, ускорение равно учетверенное в м/с 2 . | Индекс | ||
| Назад |
Формула вывода Определение Концепция » ExamLimiT
Центростремительное ускорение является произведением квадрата угловой скорости и радиуса окружности. Вывод формулы, определение, единица измерения, размерность, понятие.
Определение: Частица, движущаяся по круговой траектории с постоянной скоростью, всегда имеет ускорение по направлению к центру окружности, которое называется радиальным ускорением, нормальным ускорением или центростремительным ускорением.
Если частица с угловой скоростью ω вращается по окружности радиуса r, то ее центростремительное ускорение равно
a c = ω 2 r = v 2 /r 9000 6
Обратите внимание, что скорость частицы всегда направлена по касательной к окружности, но центростремительное ускорение всегда направлено к центру этой окружности . Таким образом, при равномерном круговом движении скорость и центростремительное ускорение перпендикулярны друг другу .
Таким образом, при равномерном круговом движении скорость и центростремительное ускорение перпендикулярны друг другу .
- Расчет центростремительного ускорения
- Центростремительное ускорение: единица измерения и размерность
- Центростремительное ускорение: векторная форма:
- Центростремительное ускорение: решения проблем
- Несколько вопросов Ответы
- Оглянитесь на свои знания
Вывод центростремительного ускорения
Когда объект движется по круговой траектории, его направление постоянно меняется, и поэтому его линейная скорость не остается неизменной. Это изменение скорости при круговом движении создает ускорение, которое всегда направлено к центру окружности. Это известно как центростремительное ускорение. Здесь математически мы выведем формулу центростремительного ускорения простым способом.
Рассмотрим частицу массой м вращается по круговой траектории радиусом r с равномерной линейной скоростью v . За очень короткое время t ( t → 0) частица перемещается из точки A в точку B. В результате она образует угол θ (= ∠AOB) в центре окружности. Итак, угловая скорость частицы равна ω = θ/t .
За очень короткое время t ( t → 0) частица перемещается из точки A в точку B. В результате она образует угол θ (= ∠AOB) в центре окружности. Итак, угловая скорость частицы равна ω = θ/t .
В точке A линейная скорость частицы равна v по касательной AP. Составляющая этой скорости по радиусу АО равна нулю, так как АО и АР взаимно перпендикулярны.
В точке B скорость частицы v вместе с BQ. В этот момент v можно разделить на две перпендикулярные составляющие. Один v.cosθ параллельно Ap и вдоль BR, а другой v.sinθ параллельно AO и вдоль направления BS.
Если θ очень мало, так что θ → 0 , то мы можем рассматривать sinθ = θ и cosθ = 1 . Опять же, если угол ∠AOB очень мал, то можно считать, что BR и BS также перекрываются с AP и AO соответственно.
Итак, вдоль AB начальная скорость частицы = v , а конечная скорость равна vcosθ = v . Это означает, что изменение скорости ( v − v ) = 0
Это означает, что изменение скорости ( v − v ) = 0
или ускорение a t = изменение скорости/времени = 0/t = 0.
То есть вдоль направления AP или вдоль касательной окружности ускорение частицы равно нулю.
Теперь по направлению АО начальная скорость частицы = 0, а конечная скорость = vsinθ = vθ.
или изменение скорости = ( vθ − 0) = vθ .
или ускорение вдоль AP равно a c = vθ/t
или a c = vω [как ω 901 98 = θ/t ]
или a c = ( ωr ) r
или, a c = ω 2 r = ( v /r) 2 r = v 2 /r .
Таким образом, существует ускорение вдоль центра окружности. Это ускорение называется центростремительным ускорением. 9{2}r$$
- Где a c = центростремительное ускорение
- v = линейная скорость
- r = радиус окружности
- ω = угловая скорость.

Подумайте об этом : Может ли частица иметь ускорение при движении с постоянной скоростью?
Центростремительное ускорение: единица и размер
Единица центростремительного ускорения = (единица скорости) 2 / (единица радиуса)
= (м/с) 2 / м
= м/с 2
Размер центростремительного ускорения = [размер скорости] 2 / [размер радиуса)]
= [LT −1 9 0128 ] 2 / [L]
= [LT −2 ]
| Единица центростремительного ускорения в СИ | м/с 2 | 90 027
| СГС единица центростремительного ускорения | см/с 2 |
| FPS единица измерения центростремительного ускорения | фут/с 2 |
| Величина центростремительного ускорения | [LT −2 ] |
Центростремительное ускорение: векторная форма:
Центростремительное ускорение является векторной величиной . Она имеет как величину, так и направление. Его направление всегда направлено к центру круга.
Она имеет как величину, так и направление. Его направление всегда направлено к центру круга.
Соотношение между линейной и угловой скоростью в векторной форме определяется формулой –
$$\overrightarrow{v} = \overrightarrow{\omega} \times \overrightarrow{r}$$
Дифференцируя по времени t, получаем-
$$\frac{d\overrightarrow{v}}{dt} = \omega \times \frac{d\overrightarrow{r}}{dt} + \overrightarrow{ r} \times \frac{d\overrightarrow{\omega} }{dt}\\ \overrightarrow{a} = \overrightarrow{\omega} \times \overrightarrow{v} + \overrightarrow{r} \times \overrightarrow{\alpha} \\ \overrightarrow{a} = \overrightarrow{a_{c}}+\overrightarrow{a_{t}}$$
Где α – угловое ускорение. Таким образом, мы можем видеть, что когда объект вращается по круговой траектории, она состоит из двух видов ускорений, 9{2}}$$
Обратите внимание, что-
$$\overrightarrow{a_{c}} = \overrightarrow{\omega} \times \overrightarrow{v} \\ или, \overrightarrow{a_{c}} = \overrightarrow{\omega} \times (\overrightarrow{\omega} \times \overrightarrow{r})$$
– это векторная форма центростремительного ускорения.
Подумайте о : Какая физическая величина остается неизменной при равномерном круговом движении?
Центростремительное ускорение: решения проблем
Человек вращает стержень длиной 10 м. Вычислите угловую скорость, необходимую для создания центростремительного ускорения, в 5 раз превышающего ускорение свободного падения.
Ответ:
Здесь в этой задаче даны данные – r = 10м,
центростремительное ускорение a c = 5g, где g = 10 м/с 2 = ускорение свободного падения.
Мы знаем, a c = ω 2 r
или, ω 2 = a c / r = 3g / r
или ω 2 9012 8 = (5 × 10) / 10
или, ω 2 = 5
или, ω = √5
∴ ω = 2,236 рад/сек
Таким образом, требуемая угловая скорость составляет 2,236 рад/сек.
Найти радиальное ускорение часовой стрелки настенных часов длиной 0,2 м.
Ответ:
Для часовой стрелки период времени T = 12 часов, а r = 0,2 м.
Таким образом, его угловая скорость ω = 2π / T = 2π/12 = 2π / (12×3600) = 1,454 × 10–4 рад/сек.
Его линейная скорость v = ωr = 1,454 × 10–4 × 0,2 = 2,9 × 10–5 м/с
Его радиальное ускорение ac = v2/r = (2,92)р.
От чего зависит центростремительное ускорение?
Радиальное ускорение зависит от двух факторов: один из них — угловая скорость (или линейная скорость), а другой — радиус кругового пути. В принципе, центростремительное ускорение пропорционально квадрату угловой скорости.
Каковы единица и размерность центростремительного ускорения?
Единицей центростремительного ускорения является метр в секунду в квадрате в системе СИ.
Его размерность [LT -2 ]
Оглянитесь на свои знания
Какая формула для центростремительного ускорения является правильной?
v 2 /r
v/r
v 2 r
vr
[v2/r]
Длинный стержень длиной 2 м вращается вокруг центр с угловой скоростью 2 рад/с.

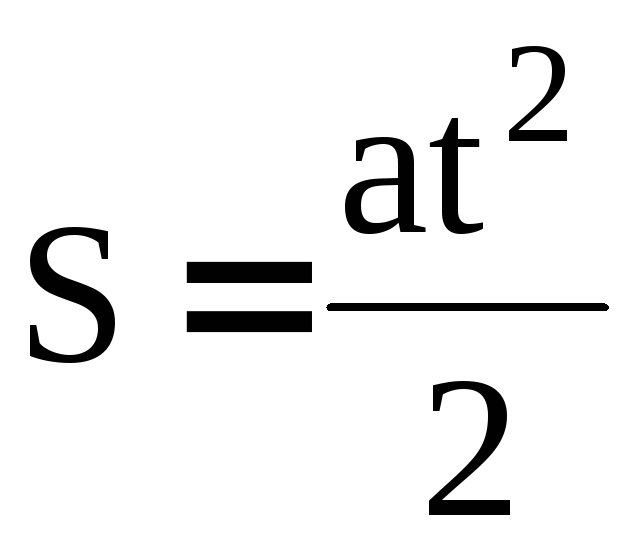
 Для вертикального круга скорость и натяжение должны различаться.
Для вертикального круга скорость и натяжение должны различаться. От отношения сторон треугольников:
От отношения сторон треугольников: