Равноускоренное движение: определение и формулы
Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.
Примеры равноускоренного движения:
- разгон самолета перед взлетом;
- падающая с крыши сосулька;
- торможение лыжника на горном склоне;
- разгоняющийся на склоне сноубордист;
- свободное падение в результате прыжка с парашютом;
- камень брошенный под углом к горизонту;
Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Равноускоренное движение: формулы
Формула для
скорости при равноускоренном движении:| Vк=Vн+at |
где: Vк — конечная скорость тела,
Vн — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.
Формула для
ускорения при равноускоренном движении:| a=(Vк-Vн)/t |
Во время движения тела ускорение остается постоянным.
Задача 1Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.
Формула
расстояния при равноускоренном движении- Если известны время, скорость начальная и скорость конечная
| S = t*(Vн+ Vк)/2 |
- Если известны время, скорость начальная и ускорение
| S = Vнt + at2/2 = t*(Vн + at/2) |
где: S — путь, пройденный за время t,
Vк — конечная скорость,
a — ускорение тела,
t — время.
 2 =1125 м.
2 =1125 м.Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
- Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
- Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.
Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.
Равноускоренное движение: графическиГрафик зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.
Взаимосвязь скорости, времени и расстояния:
На рисунке показан график, в котором скорость равномерно увеличивается.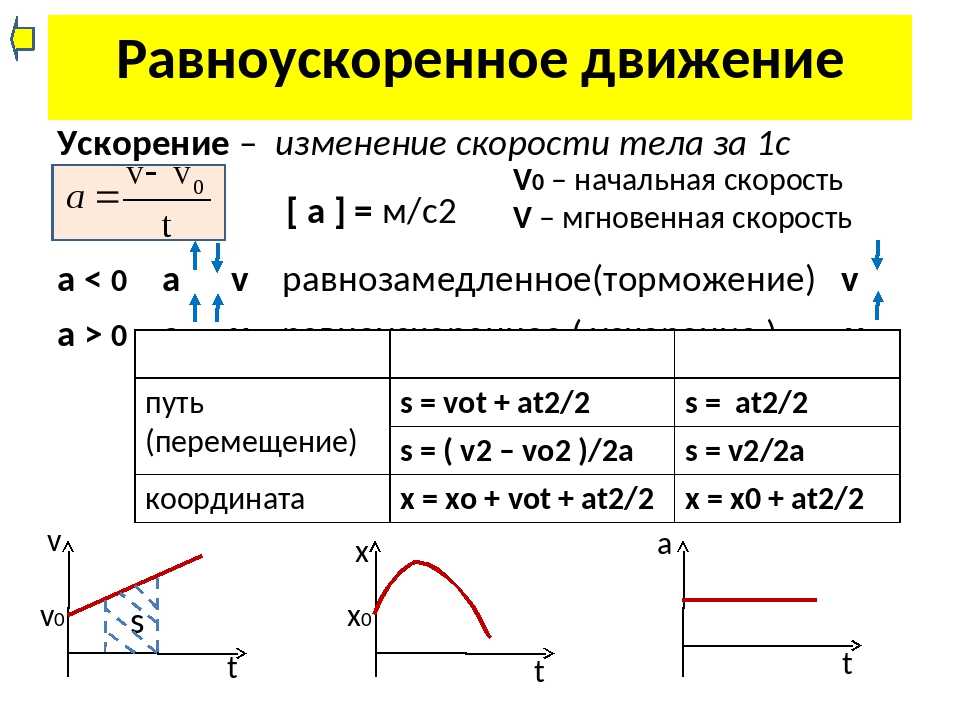
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника Vнt и треугольника at2/2. Получим: S = Vнt + at2/2.
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Задача 3Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.
Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
t — 2с.

Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = Vк2−Vн2
Получим: а = (Vк2−Vн2 )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = Vнt + at2/2.
Получаем: x(t) = 3t + 1,5t2
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*2
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.
Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:
- Конвертер единиц измерения расстояния (длины)
- Конвертер единиц измерения скорости
- Конвертер единиц измерения времени
Уравнение движения с постоянным ускорением.
 Поступательное движение 10 класс онлайн-подготовка на Ростелеком Лицей |
Поступательное движение 10 класс онлайн-подготовка на Ростелеком Лицей |Введение
Главная задача кинематики – определить положение тела в любой момент времени. Тело может покоиться, тогда его положение меняться не будет (см. рис. 1).
Рис. 1. Покоящееся тело
Тело может двигаться прямолинейно с постоянной скоростью. Тогда его перемещение будет изменяться равномерно, то есть одинаково за равные промежутки времени (см. рис. 2).
Рис. 2. Перемещение тела при движении с постоянной скоростью
Перемещение , скорость, умноженная на время, это мы давно умеем делать. Тело может двигаться с постоянным ускорением, рассмотрим такой случай (см. рис. 3).
Рис. 3. Движение тела с постоянным ускорением
Ускорение
|
Ускорение – это изменение скорости за единицу времени
Рис. Скорость – векторная величина, поэтому и изменение скорости, т. е. разность векторов конечной и начальной скорости, является вектором. Ускорение – тоже вектор, направленный туда же, куда и вектор разности скоростей (см. рис. 5). Рис. 5. Направление вектора ускорения Мы рассматриваем прямолинейное движение, поэтому можно выбрать координатную ось вдоль прямой, вдоль которой происходит движение, и рассматривать проекции векторов скорости и ускорения на эту ось: |
Тогда равномерно изменяется его скорость: (если его начальная скорость была равна нулю). Как теперь найти перемещение? Скорость умножить на время – нельзя : скорость постоянно менялась; какую брать? Как определить, где при таком движении будет находиться тело в любой момент времени – сегодня мы эту проблему решим.
Сразу определимся с моделью: мы рассматриваем прямолинейное поступательное движение тела. В таком случае можем применять модель материальной точки. Ускорение направлено вдоль той же прямой, вдоль которой материальная точка движется (см. рис. 6).
В таком случае можем применять модель материальной точки. Ускорение направлено вдоль той же прямой, вдоль которой материальная точка движется (см. рис. 6).
Рис. 6. Направление ускорения
Поступательное движение
|
Поступательное движение – это такое движение, при котором все точки тела движутся одинаково: с одинаковой скоростью, совершая одинаковое перемещение (см. рис. 7). Рис. 7. Поступательное движение А как еще может быть? Взмахните рукой и проследите: понятно, что ладонь и плечо двигались по-разному. Посмотрите на колесо обозрения: точки вблизи оси почти не движутся, а кабинки движутся с другой скоростью и по другим траекториям (см. рис. 8). Рис. 8. Движение выбранных точек на колесе обозрения Посмотрите на движущийся автомобиль: если не учитывать вращение колес и движение частей мотора, все точки автомобиля движутся одинаково, движение автомобиля считаем поступательным (см. Рис. 9. Движение автомобиля Тогда нет смысла описывать движение каждой точки, можно описать движение одной. Автомобиль считаем материальной точкой. Обратите внимание, что при поступательном движении линия, соединяющая любые две точки тела при движении, остается параллельной сама себе (см. рис. 10). Рис. 10. Положение линии, соединяющей две точки |
Задача
Автомобиль ехал прямолинейно в течение часа. В начале часа его скорость была 10 км/ч, а в конце – 100 км/ч (см. рис. 11).
Рис. 11. Рисунок к задаче
Скорость изменялась равномерно. Сколько километров проехал автомобиль?
Проанализируем условие задачи.
Скорость автомобиля изменялась равномерно, то есть всё время пути его ускорение было постоянным. Ускорение по определению равно:
Автомобиль ехал прямолинейно, поэтому мы можем рассматривать его движение в проекции на одну ось координат:
Найдем перемещение.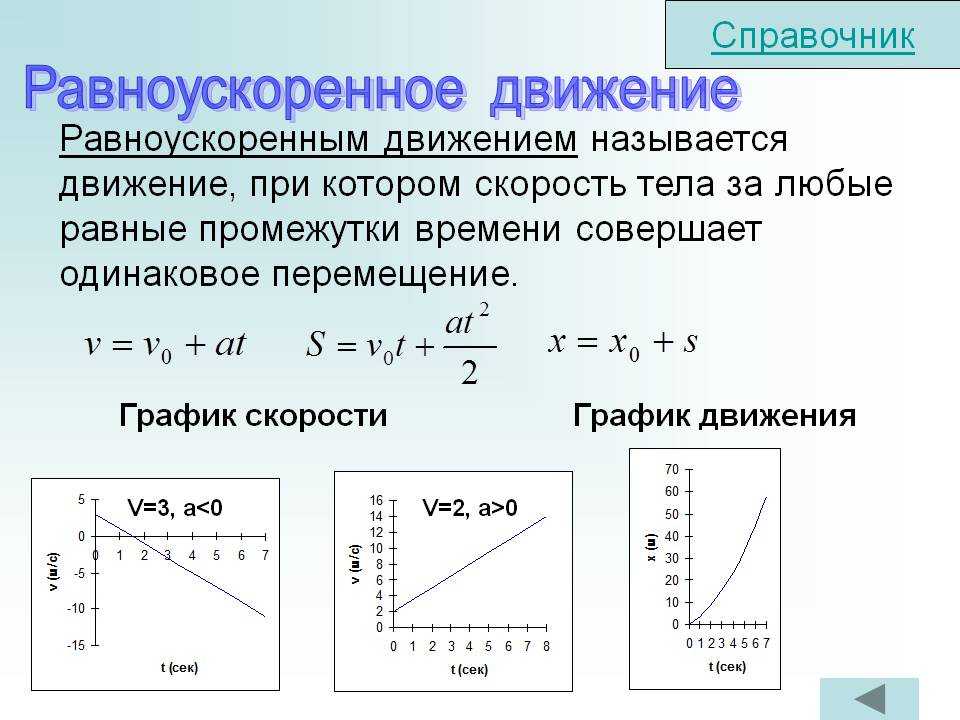
Пример возрастающей скорости
|
На стол кладут орехи, по одному ореху в минуту. Понятно: сколько минут пройдет, столько орехов на столе окажется. А теперь представим, что скорость накладывания орехов равномерно возрастает с нуля: первую минуту орехов не кладут, во вторую кладут один орех, потом два, три и так далее. Сколько орехов окажется на столе через какое-то время? Понятно, что меньше, чем если бы максимальная скорость поддерживалась всегда. Причем хорошо видно, что меньше в 2 раза (см. рис. 12). Рис. 12. Количество орехов при разной их скорости выкладывании Так же и с равноускоренным движением: допустим, сначала скорость была равна нулю, в конце стала равна (см. рис. 13). Рис. 13. Изменение скорости Если бы тело постоянно двигалось с такой скоростью, его перемещение было бы равно , но поскольку скорость равномерно возрастала – то в 2 раза меньше. |
Мы умеем находить перемещение при РАВНОМЕРНОМ движении: . Как обойти эту проблему? Если скорость изменяется не на много, то движение можно приближенно считать равномерным. Изменение скорости будет небольшим за небольшой интервал времени (см. рис. 14).
Рис. 14. Изменение скорости
Поэтому разобьем время в пути T на N небольших отрезков длительностью (см. рис. 15).
Рис. 15. Разбиение отрезка времени
Подсчитаем перемещение на каждом отрезке времени. Скорость прирастает на каждом интервале на:
На каждом отрезке мы будем считать движение равномерным и скорость приближенно равной начальной скорости на данном отрезке времени. Посмотрим, не приведет ли к ошибке наше приближение, если на небольшом промежутке движение будем считать равномерным. Максимальная ошибка будет равна:
и суммарная ошибка за всё время пути -> . При больших N принимаем ошибка близка к нулю. Это мы увидим и на графике (см. рис. 16): на каждом интервале будет ошибка, но суммарная ошибка при достаточно большом количестве интервалов будет пренебрежимо мала.
рис. 16): на каждом интервале будет ошибка, но суммарная ошибка при достаточно большом количестве интервалов будет пренебрежимо мала.
Рис. 16. Ошибка на интервалах
Итак, каждое следующее значение скорости на одну и ту же величину больше предыдущего. Из алгебры мы знаем, что это арифметическая прогрессия с разностью прогрессии :
Путь на участках (при равномерном прямолинейном движении (см. рис. 17) равен:
Рис. 17. Рассмотрение участков движения тела
На втором участке:
На n-м участке путь равен:
Арифметическая прогрессия
|
Арифметической прогрессией называется такая числовая последовательность, в которой каждое следующее число отличается от предыдущего на одну и ту же величину. Арифметическая прогрессия задается двумя параметрами: начальный член прогрессии и разность прогрессии . Сумма первых членов арифметической прогрессии вычисляется по формуле: |
Просуммируем все пути. Это будет сумма первых N членов арифметической прогрессии:
Т. к. мы разбили движение на много интервалов, то можно считать, что , тогда:
У нас было множество формул, и, чтобы не запутаться, мы не писали каждый раз индексы х, но рассматривали всё в проекции на координатную ось.
Итак, мы получили главную формулу равноускоренного движения: перемещение при равноускоренном движении за время T, которую мы наряду с определением ускорения (изменение скорости за единицу времени) будем использовать для решения задач:
Мы занимались решением задачи об автомобиле. Подставим в решение числа и получим ответ: автомобиль проехал 55,4 км.
Математическая часть решения задачи
|
Вычислим ускорение: Перемещение равно: Подставим числа и получим ответ: |
Определение координаты тела
С перемещением мы разобрались.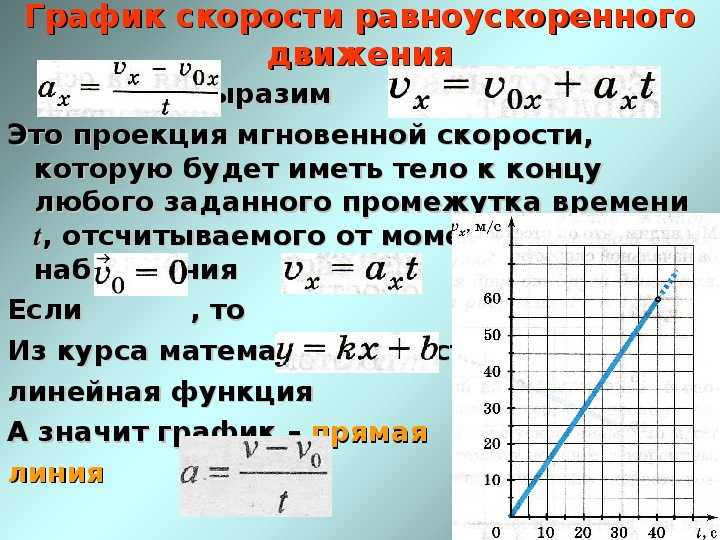 А как определить координату тела в любой момент времени?
А как определить координату тела в любой момент времени?
По определению перемещение тела за время – это вектор, начало которого находится в начальной точке движения, а конец – в конечной точке, в которой тело будет через время . Нам нужно найти координату тела, поэтому запишем выражение для проекции перемещения на ось координат (см. рис. 18):
Рис. 18. Проекция перемещения
Выразим координату :
То есть координата тела в момент времени равна начальной координате плюс проекция перемещения, которое совершило тело за время . Проекцию перемещения при равноускоренном движении мы уже нашли, осталось подставить и записать:
Это и есть уравнение движения с постоянным ускорением. Оно позволяет узнать координату движущейся материальной точки в любой момент времени. Понятно, что момент времени мы выбираем в пределах промежутка, когда работает модель: ускорение постоянное, движение прямолинейное.
Почему уравнение движения нельзя применять для нахождения пути
|
В каких случаях мы можем считать перемещение по модулю равным пути? Когда тело движется вдоль прямой и не меняет направления. При равноускоренном движении скорость изменяется. Если скорость и ускорение направлены в противоположные стороны (см. рис. 19), то модуль скорости убывает, и в какой-то момент он станет равен нулю и скорость поменяет направление, то есть тело начнет двигаться в противоположную сторону. Рис. 19. Модуль скорости убывает И тогда, если в данный момент времени тело находится на расстоянии 3 м от начала наблюдения, то его перемещение равно 3 м, но если тело сначала прошло 5 м, затем развернулось и прошло еще 2 м, то путь будет равен 7 м. И как же его найти, если не знать этих чисел? Просто надо найти момент, когда скорость равна нулю, то есть когда тело развернется, и найти путь к этой точке и от нее (см. рис. 20). Рис. 20. Момент, когда скорость равна 0 |
Список литературы
- Соколович Ю.
 А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с. - Ландсберг Г.С. Элементарный учебник физики; т.1. Механика. Теплота. Молекулярная физика – М.: Издательство «Наука», 1985.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет портал «kaf-fiz-1586.narod.ru» (Источник)
- Интернет портал «Учеба – Легко» (Источник)
- Интернет портал «Гипермаркет знаний» (Источник)
Домашнее задание
- Что такое арифметическая прогрессия?
- Какое движение называется поступательным?
- Чем характеризуется векторная величина?
- Запишите формулу для ускорения через изменение скорости.
- Какой вид имеет уравнение движения с постоянным ускорением?
- Вектор ускорения направлен в сторону движения тела.
 Как будет изменять свою скорость тело?
Как будет изменять свою скорость тело?
Полосы разгона и торможения – Исследование транспортной политики
Введение
Полосы разгона/торможения (также известные как полосы для смены скорости или вспомогательные полосы) позволяют водителям ускоряться или замедляться в пространстве, не используемом для высокоскоростного сквозного движения. На автострадах и некоторых крупных улицах изменение скорости может быть значительным и вызывать пробки и столкновения. Включение полос разгона/торможения в конструкцию проезжей части может уменьшить эти проблемы.
Выделенные полосы разгона позволяют автомобилям, выезжающим на главную дорогу, ускоряться, чтобы соответствовать потоку транспорта. Полосы замедления позволяют выезжающим автомобилям снижать скорость до более безопасной скорости перед поворотом на перекрестке, не влияя на основной поток движения.
Другая конфигурация может соединять полосу разгона с полосой торможения. После въезда на автостраду полоса разгона становится дополнительной полосой автомагистрали. Затем эта полоса становится полосой только для выезда на следующем выезде (полосой замедления). Полосы ускорения/торможения снижают влияние выезда и въезда на основные полосы движения.
Затем эта полоса становится полосой только для выезда на следующем выезде (полосой замедления). Полосы ускорения/торможения снижают влияние выезда и въезда на основные полосы движения.
Правильное использование полос разгона/торможения:
- Увеличивает среднюю скорость на автомагистралях и главных улицах.
- Уменьшает задержки на рампах.
- Повышает безопасность за счет уменьшения количества конфликтов между тихоходными и высокоскоростными транспортными средствами.
Резюме
Целевой рынок
Съезды на развязке автомагистралей
Полосы ускорения/торможения на съездах на развязках автомагистралей могут уменьшить заторы, создав определенные зоны для замедления движения и съезда с него. Эти полосы уменьшают эффект остановки и движения и столкновения, вызванные более медленным движением на развязках.
Участки между въездом на автостраду и съездом с нее
Полосы ускорения/торможения, используемые между последовательными съездами и въездом, позволяют ускорять и замедлять движение, не влияя на движение на автостраде. Эти полосы лучше всего работают на коротких въездных и выездных пандусах, требующих быстрого слияния въезжающих транспортных средств и замедления выезжающих транспортных средств, прежде чем покинуть основную полосу движения.
Эти полосы лучше всего работают на коротких въездных и выездных пандусах, требующих быстрого слияния въезжающих транспортных средств и замедления выезжающих транспортных средств, прежде чем покинуть основную полосу движения.
Главные улицы с высокими скоростями и поворотами
На основных улицах и подъездных путях без полос для разгона/торможения или поворотных площадок возникают заторы из-за замедления движения перед поворотом или ускорения после поворота. Различия в скорости сквозного трафика и входящего/выходящего трафика могут значительно замедлить движение, вызвать остановки и движения и увеличить количество столкновений.
Как это поможет?
- Способствует плавному увеличению транспортного потока, скорости и объема , позволяя транспортным средствам достигать надлежащей скорости в специально отведенном месте, а не на основных полосах движения. Например, выезжающий транспорт перемещается в указанную область, чтобы замедлиться.

- Увеличивает пропускную способность и эффективность перекрестка . Полосы ускорения/торможения позволяют транспортным средствам на основных улицах выезжать за пределы проезжей части или выезжать на нее, не прерывая поток и не тратя время сигнала.
- Повышает безопасность рамп , позволяя транспортным средствам набирать нужную скорость перед тем, как влиться в поток. Уменьшение помех снижает вероятность перегрузок и столкновений.
Примеры реализации
Lorem ipsum
Проблемы
Пространство полосы движения и полоса отчуждения являются основными проблемами проектирования при добавлении полос ускорения/торможения. Замена существующих обочин на пригодные для использования полосы движения может потребовать укрепления и расширения дорожного покрытия. Если обочину нельзя использовать, дорогу необходимо будет расширить. Это может потребовать большей полосы отвода и привести к более высоким затратам на строительство. Сложные, устаревшие или приподнятые конструкции делают проект еще более сложным и дорогостоящим. Ограничения полосы отвода на перекрестках могут потребовать полной реконструкции или изменения конструкции.
Сложные, устаревшие или приподнятые конструкции делают проект еще более сложным и дорогостоящим. Ограничения полосы отвода на перекрестках могут потребовать полной реконструкции или изменения конструкции.
Самым большим препятствием для проекта может быть установление институциональной ответственности. Немногие транспортные департаменты имеют сотрудников, которым поручено искать места, где можно установить недорогое лечение. Вклад, который могут внести полосы ускорения/замедления, упускается из виду в пользу более крупных или сложных программ.
Временные рамки проекта
Временная шкала для добавления полос ускорения/замедления зависит от:
- Использованного метода.
- Текущая геометрия дороги.
- Класс дорожного полотна.
Типичная главная улица может быть изменена за короткий промежуток времени (возможно, от одного до двух месяцев), чем эстакада автомагистрали (до года). При добавлении полос ускорения/торможения на проезжую часть следует учитывать стоимость, сложность, дизайн и выгоду.
Кто несет ответственность?
Местный офис TxDOT и города несут основную ответственность за установку и обслуживание полос ускорения/торможения. TxDOT может взять на себя ответственность за государственные дороги. Однако на городских дорогах местные органы власти контролируют строительство и управление поворотными полосами и полосами ускорения/торможения. В любом случае улучшения следует согласовывать с местными жителями и предприятиями, чтобы дорога обслуживала близлежащие земли.
Стоимость
Стоимость добавления полос разгона/торможения зависит от многих факторов. Затраты могут варьироваться от 50 000 до 100 000 долларов за простую замену плеча до 1 миллиона долларов и более за более сложные изменения. Замена обочин на полосы разгона/торможения стоит меньше, чем расширение проезжей части, что может потребовать увеличения полосы отвода. Кроме того, любое строительство на ровной улице стоит меньше, чем на эстакаде, из-за проектирования, времени строительства и стоимости материалов.
Потребность в данных
Полезные данные для добавления полос разгона/торможения включают изменения скорости на основных полосах движения, вызванные замедлением, выездом транспортных средств. Подсчет трафика на съездах с автомагистралей и въездах может помочь определить, где происходит большое количество въездов и выездов. Подсчет поворотов на крупных перекрестках улиц может помочь определить количество транспортных средств, замедляющих или ускоряющих движение. Измерение задержек в пути до и после начала использования этого метода может помочь оценить его эффективность. Кроме того, потребуются данные о текущей длине, ширине и наличии полос движения, а также въездных и выездных пандусов.
Передовой опыт полосы разгона/торможения
Тип местоположения: Автострады.
Практика Агентства: Координация планирования, проектирования, безопасности и эксплуатации.
Частота повторного анализа: После существенных изменений в землепользовании или застройки; по мере увеличения поездок или изменения поездок в этом районе; при расширении или реконструкции проезжей части.
Необходимые вспомогательные политики или действия: Способность финансировать улучшения, заключать межведомственные соглашения и вводить в действие политики там, где дороги пересекают границы юрисдикции.
Дополнительные стратегии: Управляемые полосы движения, переменные ограничения скорости, временное использование обочины и предупреждение об очереди.
Для получения дополнительной информации
Американская ассоциация государственных служащих автомобильных дорог и транспорта. Политика геометрического проектирования автомагистралей и улиц. Washington, D.C., 2011.
Crawford, J.A., T.B. Carlson, W.L. Eisele, and B.T. Kuhn. Набор инструментов штата Мичиган для уменьшения заторов на дорогах . Техасский институт транспорта A&M, Колледж-Стейшн, Техас, сентябрь 2011 г.
Департамент транспорта штата Мичиган. Руководство по проектированию дорог MDOT . Лансинг, Мичиган, 2011 г.
MnDOT 2007 Процесс сокращения узких мест.
Торбик, Д. Дж., Дж. М. Хаттон, К. Д. Бокенкрогер, Д. В. Харвуд, Д. К. Гилмор, М. М. Кношауг, Дж. Дж. Ронкетто, М. Брюэр, К. Фитцпатрик, С. Т. Крайслер и Дж. Стэнли. Отчет NCHRP 730: Руководство по проектированию терминалов въезда на магистральную автомагистраль.
Венглар С. и Дж. Викандер. «Улучшение работы автострады TxDOT в Остине после исследований: технический меморандум». Техасский институт транспорта A&M, Сан-Антонио, Техас, август 2001 г.
Скорость, скорость, ускорение и замедление
Скорость, скорость, ускорение и замедление1 Скорость, скорость, ускорение и замедление
Сегодняшняя цель – лучше понять, что мы подразумеваем под такими терминами, как как скорость, скорость, ускорение и замедление. Давайте начнем с пример, а именно движение мяча, брошенного вверх, а затем действовавшего под действием силы тяжести.
Основной источник путаницы в задачах такого рода связан с
стирание различия между скорость и скорость . скорость s по определению является величиной вектора скорости: s
:= |v|. Обратите внимание на контраст: Когда мы бросаем мяч вверх:
скорость s по определению является величиной вектора скорости: s
:= |v|. Обратите внимание на контраст: Когда мы бросаем мяч вверх:
| – скорость – | – скорость – |
| Изменение скорости происходит равномерно вниз. скорость становится меньше вверх и/или больше вниз, что является то же самое. | скорость снижается во время подъема траектории, и увеличиваясь во время последующей нисходящей траектории. |
На данный момент у нас есть проблема, потому что скорость изменения
скорость называется ускорение … но скорость изменения
скорость также называют ускорением! Очевидно, это создает огромные
возможность путаницы. Мы можем начать распутывать вещи следующим образом:
Мы можем начать распутывать вещи следующим образом:
| Скорость изменения скорости равна вектор ускорение . | Скорость изменения скорости – это скаляр . ускорение . |
| Законы физики проще всего записать в терминах скорость, а не скорость. В контексте физики неприукрашенное слово «ускорение», вероятно, относится к векторному ускорению, но это не гарантируется на 100%. |
Специального слова для противоположного вектору нет.
ускорение. Противоположное ускорению в направлении +X
также является ускорением, а именно ускорением в −X
направление. | Скалярное ускорение означает ускорение. Противоположное называется замедлением, что означает замедление. |
Не путайте векторное ускорение со скалярным ускорение. Скалярное ускорение можно рассматривать как одну составляющую вектора ускорения, а именно проекции в направлении «вперед» направление (хотя это не определено, если объект находится в состоянии покоя).
Повторяю: вектор ускорения определяется как изменение по скорости в единицу времени. Как следует из названия, это вектор. Этот термин применяется независимо от того, как ускорение ориентировано относительно к начальной скорости. Возможны несколько направлений. В следующей таблице показано, как преобразовать векторный язык в скалярный. язык в каждом случае:
| – Векторный язык – | – Соответствующий скалярный язык – |
Ускорение в том же направлении, что и скорость. | Ускорение. |
| Ускорение прямо противоположно скорости. | Замедление. |
| Ускорение под прямым углом к скорости. | Постоянная скорость. |
Примечание: Боковое ускорение соответствует повороту. В
случае равномерного движения по окружности величина
ускорение остается постоянным, а направление
ускорение остается перпендикулярным скорости. Это
классический пример ситуации, когда скалярное ускорение
равно нулю, даже если ускорение вектора не равно нулю. |
| Ускорение под некоторым нечетным углом относительно скорости. | Нет хороший способ описать это с точки зрения скаляров. |
| Ускорение объекта в момент когда его скорость равна нулю. | Невозможно описать это в терминах скаляров; формула скалярного ускорения дает фиктивные выражения вида 0/0. |
2 Примечания
2.1 Шаг назад: скалярная физика
Независимо от того, какую терминологию вы используете, это почти всегда плохая идея
формулировать задачи по физике с точки зрения скорости, поэтому следует придерживаться
к описанию движения в терминах векторов: положения, скорости и
ускорение (а именно векторное ускорение).
В частности, в случае движения мяча под действием гравитации, было бы неразумно и бесполезно (хотя и возможно) сформулируйте задачу в терминах скалярной скорости и скалярной ускорение. Используя эти идеи, вы могли бы сказать, что мяч «тормозится» на подъеме и «ускоряется» на спуске. Это буквально верно, но бесполезно предполагает, что физика разные на пути вверх и на пути вниз. (Подробнее о физика веса и гравитации, см. ссылку 1.) Было бы гораздо лучше анализировать проблему с точки зрения скорости (не скорости) плюс векторное ускорение. вектор ускорения тот же на протяжении всего полета, т. е. имеет постоянную величину и постоянную направление. Он всегда направлен вниз.
2.2 Шаг вперед: ускорение в пространстве-времени
Более подробное техническое обсуждение ускорения, включая обсуждение того, как вещи ускоряются, когда они уже движутся в почти скорость света, см. ссылку 2.
3 Ссылки
1.
Джон Денкер, «Вес, гравитационная сила и так далее» www.

 4. Ускорение
4. Ускорение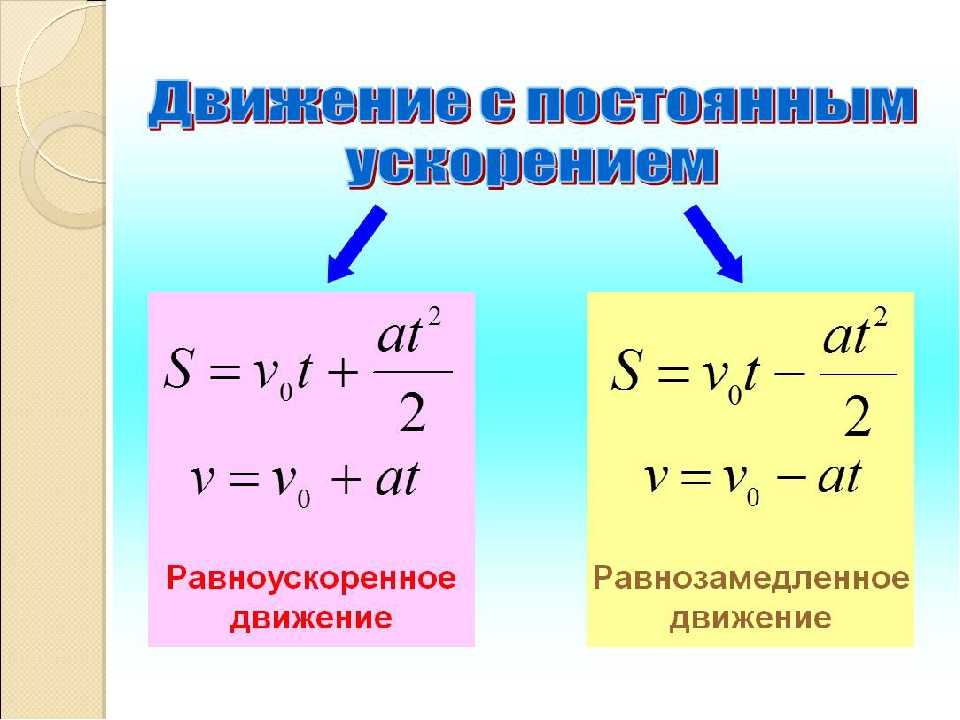 рис. 9).
рис. 9).
 Тогда последовательность записывается так:
Тогда последовательность записывается так: Например, при равномерном прямолинейном движении мы не всегда четко оговариваем, путь мы находим или перемещение, всё равно они совпадают.
Например, при равномерном прямолинейном движении мы не всегда четко оговариваем, путь мы находим или перемещение, всё равно они совпадают. А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с. Как будет изменять свою скорость тело?
Как будет изменять свою скорость тело?
