Ускорение точки это: Ускорение точки

1.3 Ускорение точки

Среднее ускорение  

характеризует изменение вектора скорости за малый промежуток времени  Δt . Ускорение точки в данный момент времени

Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.

15. Определение скорости и ускорения при координатном способе задания движения точки.

Связь векторного способа задания движения и координатного дается соотношением

Из определения скорости

Проекции скорости на оси координат равны производным соответствующих координат по времени:

Модуль и направление скорости определяются выражениями

Из определения ускорения

Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени

Модуль и направление ускорения определяются выражениями

16.

Тангенциальное и нормальное ускорение точки.

Нормальное и тангенциальное ускорение
При криволинейном движении скорость направлена по касательной к траектории. Поскольку направление скорости постоянно изменяется, то криволинейное движение – всегда движение с ускорением, в том числе, когда модуль скорости остается неизменным

В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением . Она характеризует изменение скорости по модулю.

Составляющая ускорения, направленная к центру кривизны траектории, т. е. перпендикулярно (нормально) скорости, называется нормальным ускорением . Она характеризует изменение скорости по направлению.

Здесь R – радиус кривизны траектории в данной точке. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения

17. Относительное, переносное и абсолютное движения. Теорема о сложении скоростей.

    Согласно теореме Кориолиса, абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений (рис. 3) 

                                        a_a = a_r  ⊕   a_e 

 ⊕  a_C   .

Рис. 3

    Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение a_r  направлено вдоль этой прямой и определяется выражением

    Переносным ускорением точки M является ускорение точки M диска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением

  a_e = a_e^вр  ⊕ 

 a_e^цс            ,

где  a_e^вр= ε⋅ OM  – вращательное ускорение точки M, направленное перпендикулярно отрезку OM ;

       a_e^цс= ω²⋅ OM – центростремительное ускорение точки M, направленное к центру диска.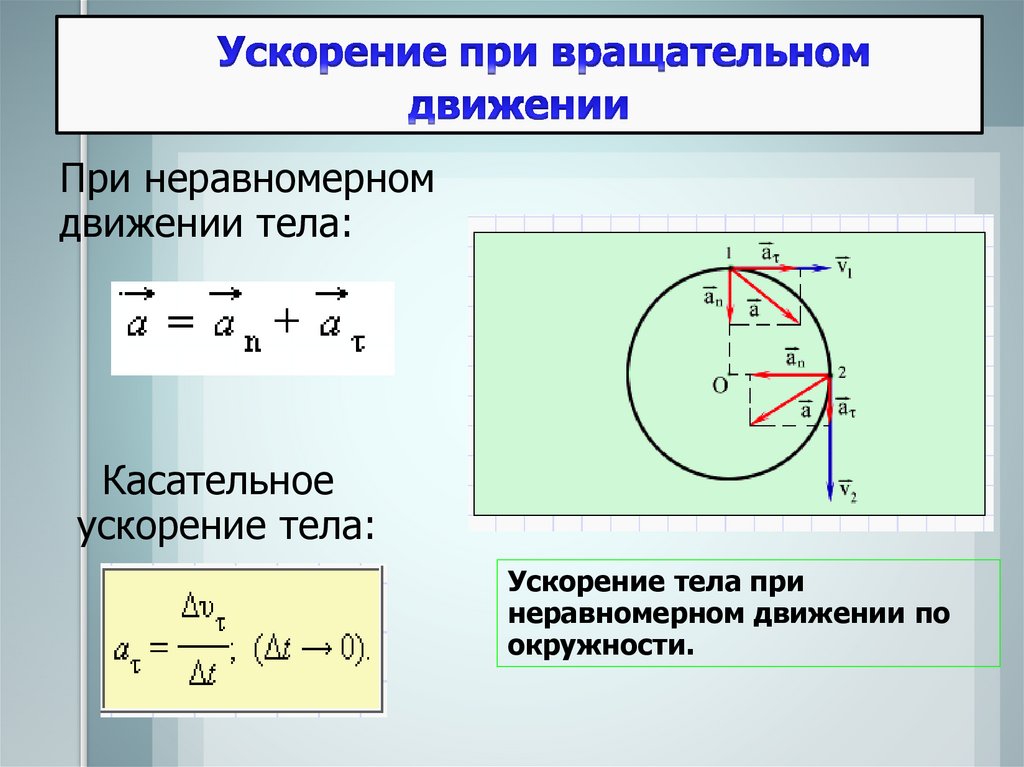

    Ускорение Кориолиса или поворотное ускорение определяется по формуле

a_C = 2 ω_e  ⊗  ν_r          , где  ω_e – переносная угловая скорость,  ν_r  – относительная скорость точки.

    Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.

    Величина ускорения Кориолиса определяется выражением

         a_C = 2

 ω_e  ν_r  sinα      ,

где  α  – угол между векторами ω_e  и ν_r  .

    Рассмотрим, какой физический смысл заложен в ускорение Кориолиса. Для простоты будем считать, что диск вращается с постоянной угловой скоростью, а точка M движется относительно диска с постоянной относительной скоростью (рис.4).

Рис. 4

    Пусть в момент времени t₁ точка M занимала положение M₁ и имела относительную скорость ν_{r 1} . За промежуток времени Δt точка M переместится в положение M₂ , при этом направление скорости ν_r изменится вследствие вращения диска. Вектор ν_r получит приращение Δν_r . Отношение  Δν_r /

 Δt определяет среднее ускорение точки за промежуток времени Δt . Предел отношения  Δν_r / Δt при  Δt→ 0 есть производная  dν_r /dt , как производная от вектора постоянного по величине.

    Рассмотрим, как изменяется переносная скорость в зависимости от относительного движения. В моменты времени t₁ и t₂ переносная скорость определяется выражениями ν

_e1= ω ⊗ OM₁  и  ν_e2= ω ⊗ OM₂ . Тогда приращение вектора  ν_e за счет относительного движения будет равно 

 Δν_e = ω  ⊗ OM₂ – ω ⊗  OM₁ = ω  ⊗ (OM₂ – OM₁) = ω ⊗  ν

_r⋅ Δt 

    Отношение Δν_e / Δt в пределе при  Δt→ 0 дает производную dν_e / d t = ω ⊗  ν_r  . Таким образом, ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.

Рис. 5

    Абсолютное ускорение точки в сложном движении в общем случае определяется геометрической суммой пяти слагаемых

    Для определения величины абсолютного ускорения удобнее пользоваться аналитическим методом сложения векторов:

Сложное движение точки Теорема Кориолиса

Здесь мы покажем, что при сложном движении, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где     – кориолисово ускорение.

Пример применения изложенной ниже теории приводится на странице “Сложное движение точки. Пример решения задачи”.

Сложное (составное) движение точки

Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат. Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы. Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.

Такое движение точки называется сложным или составным.

Сложное или составное движение точки

– это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.

Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).

Относительное движение точки при сложном движении

– это движение точки относительно тела (подвижной системы координат) считая, что тело покоится.

Переносное движение точки при сложном движении

– это движение точки, жестко связанной телом, вызванное движением тела.

Абсолютное движение точки при сложном движении

– это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.

Сложное движение. Точка M движется относительно движущегося тела.

Пусть Oxyz – неподвижная система координат, O_n x_o y_o z_o – подвижная система координат, жестко связанная с телом. Пусть   – единичные векторы (орты), направленные вдоль осей  x_o , y_o , z_o   подвижной системы координат. Тогда радиус-вектор     точки M  в неподвижной системе определяется по формуле:
(1)   ,
где     – радиус-вектор точки O_n   – начала подвижной системы координат, связанной с телом.

Относительная скорость и ускорение

При относительном движении изменяются координаты   x_o , y_o , z_o   точки относительно тела. А векторы     являются постоянными, не зависящими от времени. Дифференцируя (1) по времени, считая     постоянными, получаем формулы для относительной скорости и ускорения:
(2)   ;
(3)   .

Относительная скорость точки при сложном движении

– это скорость точки при неподвижном положении тела (подвижной системы координат), вызванная движением точки относительно тела.

Относительное ускорение точки при сложном движении

– это ускорение точки при неподвижном положении тела, вызванное движением точки относительно тела.

Переносная скорость и ускорение

При переносном движении изменяются векторы   , определяющие положение тела. Относительные координаты точки x_o , y_o , z_o   являются постоянными. Дифференцируя (1) по времени, считая x_o , y_o , z_o постоянными, получаем формулы для переносной скорости и ускорения:
(4)   ;
(5)   .

Переносная скорость точки при сложном движении

– это скорость точки, жестко связанной с телом, вызванная движением тела.

Переносное ускорение точки при сложном движении

– это ускорение точки, жестко связанной с телом, вызванное движением тела.

Производные по времени от     – это скорость и ускорение начала подвижной системы координат O_n :   ;   .

Найдем формулы для производных по времени от векторов   . Для этого возьмем две произвольные точки твердого тела A и B. Их скорости связаны соотношением:

(см. страницу “Скорость и ускорение точек твердого тела”). Рассмотрим вектор   , проведенный из точки A в точку B. Тогда
.
Дифференцируем по времени и применяем предыдущую формулу:
.
Итак, мы нашли формулу для производной по времени от вектора, соединяющего две точки тела:
.
Поскольку векторы     жестко связаны с телом, то их производные по времени определяются по этой формуле:
(6)   ,   ,   .

Подставляем в (4):

.
Таким образом, выражение (4) приводит к формуле для скорости точек твердого тела.

Выполняя подобные преобразования над формулой (5), получим формулу для ускорения точек твердого тела:
,
где     – угловое ускорение тела.

Абсолютная скорость и ускорение

При абсолютном движении изменяются как векторы   , определяющие положение тела, так и относительные координаты точки   x_o , y_o , z_o .

Абсолютная скорость точки при сложном движении

– это скорость точки в неподвижной системе координат.

Абсолютное ускорение точки при сложном движении

– это ускорение точки в неподвижной системе координат.

Теорема о сложении скоростей

При составном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.

Доказательство

Дифференцируем (1) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (2) и (4).
(1)   ;
(7)  
.

Теорема Кориолиса о сложении ускорений

При составном движении абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где
  – кориолисово ускорение.

Доказательство

Дифференцируем (7) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (3) и (5).
(7)   .

.

В последнем члене применим (6) и (2).

.
Тогда
.

Ньютоновская механика – Направление ускорения в наивысшей точке

спросил 7 лет, 8 месяцев назад

Изменено 3 года, 7 месяцев назад

Просмотрено 20 тысяч раз

$\begingroup$

Когда мяч брошен вертикально вверх, каково будет направление ускорения в высшей точке (где скорость равна нулю)? Вверх, вниз или произвольно?

• ньютоновская механика
• силы
• ускорение
• диаграмма свободного тела

$\endgroup$

6

$\begingroup$

Во время броска, пока мяч еще находится в вашей руке, он ускоряется вверх.

Как только мяч покидает вашу руку, он начинает замедляться. Здесь научное и обычное использование расходятся. Технически мяч испытывает направленную вниз силу, и его скорость со временем уменьшается, поэтому можно сказать, что он обладает отрицательным (направленным вниз) ускорением. Однако в обычном использовании, когда ускорение снижает скорость (величину скорости), это называется замедлением. Как только мяч достигнет своей вершины, он начнет падать вниз, и в этот момент и техническое, и обычное использование сходятся во мнении — он ускоряется вниз.

Итак, возникает вопрос, что именно вы имели в виду под своим вопросом? Технически мяч испытывает постоянное отрицательное (нисходящее) ускорение. В обычном использовании мяч замедляется до своего пика, а затем ускоряется вниз. В этом смысле на максимальной высоте мяч ускоряется вниз. В противном случае он остался бы на этой высоте навсегда, поскольку его вертикальная скорость была бы равна нулю, и эта скорость не претерпела бы никаких изменений. Тот факт, что только на мгновение мяч имеет нулевую скорость, не означает, что мяч не ускоряется — это просто означает, что скорость равна нулю.

$\endgroup$

$\begingroup$

Ускорение только из-за гравитации, то есть вниз. Таким образом, когда мяч достигает вершины своей траектории и его скорость становится равной нулю, его ускорение также направлено вниз.

После этого мяч ускоряется до тех пор, пока не достигнет земли (если бы не было земли, он бы колебался вокруг точки 0, откуда запрашивается гравитационное ускорение.)

Надеюсь, это поможет. 92}$ (в этот момент ускорение силы тяжести направлено против движения) мы видим, что значение $v$ медленно уменьшается со временем. В какой-то момент он становится $0$. Мяч находится со скоростью $0$ в этот момент (момент очень важен). После этого скорость становится недостаточно большой, чтобы идти против гравитации и двигаться вверх, и поэтому она проигрывает перед гравитацией и начинает подчиняться ее словам и опускаться вместе с ней.

Помните, что направление ускорения свободного падения всегда равно $9.2}$ к центру земли , как указано в теореме Ньютона о раковине (пожалуйста, прочтите ее, чтобы лучше понять).

$\endgroup$

$\begingroup$

Вопрос некорректен. Даже если вы бросите мяч по линии, проходящей через центр Земли («совершенно вертикально»), из-за вращения Земли и вас будет существовать поперечная скорость. Мяч будет иметь поперечную скорость в своей вершине, которая покажется вам, наблюдателю, как будто мяч движется на запад. Это связано с тем, что он имеет больший радиус, чем на земле, поэтому его поперечная скорость недостаточна для прохождения того же углового расстояния, что и вы.

Конечно, вы, вероятно, имели в виду “идеальную” ситуацию с однородным, плоским миром без движения, но имейте в виду, что эксперимент в реальном мире будет работать иначе.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Ньютоновская механика – Угол между скоростью и ускорением для движения снаряда

Задавать вопрос

спросил 1 год, 5 месяцев назад

Изменено 1 год, 5 месяцев назад

Просмотрено 805 раз

$\begingroup$

Предположим, у меня есть снаряд, и я запускаю его с наклонной скоростью, то есть у него есть как горизонтальная, так и вертикальная составляющие скорости. Если пренебречь сопротивлением воздуха и тому подобным, его траектория должна выглядеть так, как я нарисовал.

Здесь красная стрелка — постоянное ускорение вниз, зеленая стрелка — чистая скорость (векторная сумма ее компонентов) и угол между ускорением и скоростью, отмеченный желтым.

Я заполнил угол в областях, где, по моему мнению, угол между скоростью и ускорением был бы острым, что, как я думаю, представляет собой полное движение снаряда после того, как он пересечет свою максимальную высоту, пока он снова не достигнет земли.

Однако при поиске в сети, а также в вопроснике, который я видел, в нем говорится, что угол между скоростью и ускорением составляет минимум и острый в только одну точку.

Почему только одна точка? Имеет ли к этому какое-либо отношение слово «минимум»? Я думал, что угол будет острым в нескольких точках во второй половине движения снаряда.

• ньютоновская механика
• ньютоновская гравитация
• снаряд

$\endgroup$

$\begingroup$

Угол будет острый для всей второй половины движения снаряда, но будет минимальным и острым (оба момента времени) в точке, где мяч только что коснулся земли.