Ускорение точки формула: Ускорение точки

Ускорение материальной точки – определение направления

3.9

Средняя оценка: 3.9

Всего получено оценок: 264.

3.9

Средняя оценка: 3.9

Всего получено оценок: 264.

Большинство движений в Природе являются неравномерными, они происходят с ускорением или замедлением. Рассмотрим понятие «ускорение материальной точки» более подробно.

Неравномерное движение

При равномерном движении материальная точка проходит за одинаковые промежутки времени одинаковые расстояния, и измерение скорости на любом участке дает одно и то же значение.

При неравномерном движении ситуация иная. Измерение скорости в различные моменты времени дает различные результаты. Нередок случай, когда мгновенная скорость в любой точке пути отличается от мгновенной скорости в любой другой точке. Возникает вопрос определения не только координаты, но и скорости в каждый момент времени и в каждой точке пути для неравномерного движения.

Рис. 1. Примеры неравномерного движения.

Типичным примером неравномерного движения является свободное падение тел. За первые 0.1с падения тело проходит только 5см пути, и мгновенная скорость в конце этого промежутка составит 0,98 м/с. А в конце первой секунды тело пройдет 5м пути, и мгновенная скорость в этот момент будет равна 9,8 м/с. Как получить значение имеющейся мгновенной скорости в любой момент времени ?

Ускорение

Для исследования свободного падения можно измерять мгновенную скорость через равный промежуток времени (например, через 0.1с), и результаты представить в виде таблицы. В первом столбце будет момент времени, во втором – мгновенная скорость. В третьем столбце вычислим разницу мгновенной скорости между текущим и предыдущим моментом времени.

Получим :

t(сек)	v(м/с)	Δv(м/с)
0.0	0.00	–
0. 1	0.98	0.98
0.2	1.96	0.98
0.3	2.94	0.98
0.4	3.92	0.98
0.5	4.91	0.98

Сразу бросается в глаза, что цифры в последнем столбце таблицы одинаковы. Это означает, что, хотя скорость постоянно меняется, разница скорости за одинаковый промежуток времени составляет одинаковую величину. Следовательно, для вычисления скорости в любой момент времени можно ввести специальную меру – ускорение.

Ускорение материальной точки равно отношению изменения скорости материальной точки к промежутку времени, за который это изменение произошло.

$$\overrightarrow a= {\overrightarrow v – \overrightarrow v_0\over t}$$

Из представленной формулы можно получить единицу измерения ускорения.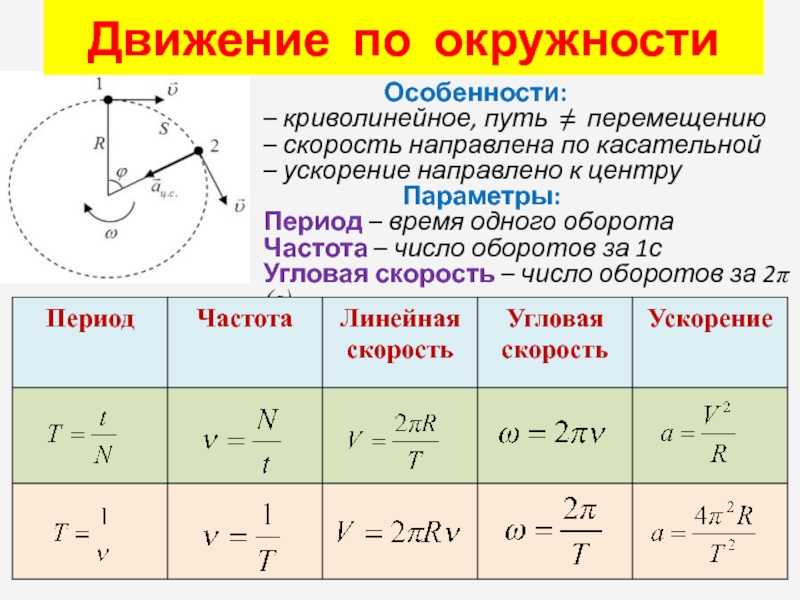

2$.

Рис. 2. Ускорение в физике.

Также из этой формулы видно, что ускорение – это векторная величина, и направление ускорения материальной точки совпадает с направлением изменения скорости. При этом и величину, и направление этого изменения необходимо получать с помощью правил сложения векторов. В частности, если конечная скорость больше начальной, и направлена в том же направлении, то и ускорение будет направлено туда же. Если конечная скорость меньше начальной, то ускорение будет направлено в противоположную сторону. В случае, если вектора начальной и конечной скоростей не параллельны, для определения результата следует либо пользоваться правилом параллелограмма, либо проецировать вектора на оси координат, и складывать или вычитать проекции в зависимости от их направления, а потом по проекциям получать результат.

Рис. 3. Сложение векторов.

Что мы узнали?

При неравномерном движении скорость тела изменяется. Для характеристики быстроты этого изменения вводится специальная величина – ускорение. Ускорение равно отношению изменения скорости за некоторый промежуток времени к величине этого промежутка.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

• Лза Якимова

  5/5

• Ярослав Никульшин

  4/5

Оценка доклада

3.9

Средняя оценка: 3.9

Всего получено оценок: 264.

---

А какая ваша оценка?

2.4. Ускорение точки при задании ее движения координатным способом

Определим модуль и направление ускорения точки по уравнениям ее движения в декартовых координатах. Пусть заданы уравнения движения точки (рис. 2.14)

Рис. 2.14

Проекции ускорения на оси координат определяются по формулам:

.

Так как первые производные от координат точки по времени равны проекциям скорости на соответствующие оси, т.

е.

то проекции ускорения точки можно представить в другом виде:

Следовательно, проекции ускорения точки на неподвижные оси декартовых координат равны вторым производным от соответствую­щих координат точки по времени или первым производным по времени от проекций скорости на соответствующие оси.

После вычисления проекций ускорения на координатные оси можно опре­делить модуль и направление ускорения точки:

Движение точки в плос­кости хОу задается двумя уравнениями движения:

Рис. 2.15

Модуль и направление ускорения точки в этом случае (рис. 2.15) опреде­ляются так:

Прямолинейное движение точки задается одним уравнением x=f(t). В этом случае модуль ускорения равен абсолютному значению его проекции на ось х, т. е.

Ускорение направлено в сторону оси х, если , и противоположно оси х, если .

2.5. Определение радиуса кривизны траектории при координатном способе задания движения

Касательное ускорение точки возможно лишь при неравномерном движении точки и характеризует изменение модуля скорости.

В том случае, если требуется определить касательное и нормаль­ное ускорения движения точки, которое задано уравнениями движения , то сначала определяют модули скорости и ускорения точки:

Согласно формуле

или

где знак плюс, полученный в ответе после вычисления дроби соответствует ускоренному движению точки, а знак минус – замедленному.

С другой стороны, модуль ускорения точки равен

,

тогда

Зная, что ,

находим радиус кривизны кривой по формуле

2.

6. Классификация движения точки по ускорениям ее движения

Равномерное движение.

Выясним зависимость характера движения точки от значений ее нормального и касательного ускорений.

С л у ч а й I: Если в течение некоторого промежутка времени нормальное и касательное ускорения точки равны нулю, то в течение этого промежутка не изменяются ни направление, ни модуль скорости, т.е. точка движется равномерно-прямолинейно и ее уско­рение равно нулю.

С л у ч а й II: . Если в течение некоторого проме­жутка времени не равно нулю нормальное ускорение и равно нулю касательное ускорение, то происходит изменение направления скорости без изменения ее модуля, т. е. точка движется равномерно-криволинейно и модуль ее ускорения (рис. 2.16)

.

Рис. 2.16

Если в некоторый момент времени, то точка не движется равномерно, а в этот момент времени модуль ее скорости имеет максимум, или минимум.

Уравнение равномерного движения точки имеет вид

.

Постоянную скорость равномерного движения точки можно определить из уравнения движения

.

Графики равномерного движения и его скорости представлены на рис. 2.17.

Рис. 2.17

Равнопеременное движение. При равнопеременном движении алгебраическое значение касательного ускорения остается во все время движения неизменным .

С л у ч а й III: . Если в течение некоторого проме­жутка времени равно нулю нормальное ускорение точки и не равно нулю касательное, то направление скорости не изменяется, а изменя­ется ее модуль, т.е. точка движется по прямой неравномерно. Модуль ускорения точки в этом случае (рис. 2.18)

а) Ускоренное движение б) Замедленное движение

Рис. 2.18

С л у ч а й IV: . Если в течение некоторого проме­жутка времени ни нормальное, ни касательное ускорения точки не равны нулю, то изменяется как направление, так и модуль ее ско­рости, т. е. точка совершает неравномерно-криволинейное движение. Модуль ускорения точки

Рис. 2.19

Графическое изображение ускорения точки при равнопеременном криволинейном движении представлено на рисунке 2.19, а ускоренного движения, рис. 2.19, б – замедленного движения.

Уравнение равнопеременного движения точки имеет вид

Если , то при ускоренном движении , а при замедленном движении . Формула скорости равнопеременного движения точки имеет вид

.

– ускоренное движение

Рис. 2.20

Графики замедленного движения, скорости и касательного ускорения представлены на рис. 2.21.

–– замедленное движение

Рис. 2.21

Задача 2.2. Определить траекторию, скорость и ускорение точки М шатуна кривошипно-ползунного механизма (рис. 2.22), если ОА=АВ=2b, а угол при вращении кривошипа растет пропорционально времени .

Рис. 2.22

Решение. Начинаем с определения уравнений движения точки М. Проводя оси и обозначая координаты точки М в произвольном положении через х и у, находим:

.

Заменяя его значением, получаем уравнения движения точки М:

.

Для определения траектории точки М представим уравнения движения в виде:

.

Возводя эти равенства в квадрат и складывая, получим

.

Итак, траектория точки М — эллипс с полуосями 3b и b.

Теперь находим скорость точки М:

.

Скорость оказывается величиной переменной, изменяющейся с течением времени в пределах от до .

Определяем проекции ускорения точки М:

отсюда

,

где r — длина радиуса-вектора, проведенного из центра О до точки М. Следо­вательно, модуль ускорения точки меняется пропорционально ее расстоянию от центра эллипса.

Направление ускорения определяем по направляющим косинусам:

.

Ускорение точки М все время направлено вдоль МО к центру эллипса.

Задача 2.3. Локомотив движется равномерно по закруглению радиусом R = 600 м, причем ускорение его центра тяжести равно а = 0,26 м/с².

Определить скорость центра тяжести локомотива.

Решение. По условию задачи необходимо определить скорость центра тяжести локомотива, т.е. задача сводится к кинематике точки. Движение точки задано естественным способом, так как известна траектория движения. Покажем на рис. 2.23 траекторию – дугу радиусом R, на ней выберем начало и положительное направление отсчета дуговой координаты s.

Рис. 2.23

При естественном способе задания движения ускорение точки равно

.

В случае равномерного движения . Тогда , но

,

где – радиус кривизны траектории в данной ее точке. В нашем случае = 600 м в любой точке траектории.

Окончательно имеем

м/с.

На рис. 2.23 в произвольном положении точки изображены ее вектор скорости, направленный в сторону возрастания дуговой координаты, и ускорение, равное нормальному ускорению и направленному к центру кривизны траектории.

Задача 2.4. По заданным уравнениям движения точки М установить вид ее траектории и для момента времени , найти положение точки на траектории, ее скорость, касательное, нормальное и полное ускорения, а также радиус кривизны траектории (рис. 2.24):

Рис. 2.24

, (2.5)

где х и у в сантиметрах, t – в секундах.

Решение. Параметрическим представлением траектории является сам закон движения. Уравнение траектории в координатной форме получаем, исключая из закона движения время:

.

Получили , то есть траекторией точки является парабола. Для построения траектории рассчитаем по уравнениям координаты точек параболы, отвечающие нескольким моментам времени. Результаты расчетов приведены в табл. 2.1.

Таблица 2. 1

t, с	0	0,5	1
х, cм	0	2	4
у, см	– 1	1	7

Траектория построена на рис. 2.24, на ней стрелкой показано направление движения точки из начального положения при с координатами .

Дифференцируя (2.5) по времени, находим проекции скорости точки на оси координат х, у:

. (2.6)

При .

По найденным проекциям определяем модуль скорости

.

Дифференцируя (2.6), находим проекции вектора ускорения

.

При .

По найденным проекциям определяем модуль ускорения

.

Определение касательного ускорения при

.

Определение нормального ускорения при

.

Определение радиуса кривизны при

.

Результаты вычислений для заданного момента времени приведены в табл. 2.2.

Таблица 2.2

Координаты, см		С к о р о с т ь, см/с			Ус к о р е н и е, см/с2					Радиус кривизны, см
х	у	vx	vy	v	ax	ay	a	a	an	
2	1	4	8	8,9	0	16	16	14,4	6,9	11,6

На рис. 2.24 показано положение точки М в заданный момент времени.

Векторы скорости и ускорения точки М построены в масштабе по их проекциям на оси координат: , там же показаны касательное и нормальное ускорения. Совпадение величин и , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.

Радиус кривизны проведен в сторону вогнутости траектории перпендикулярно к вектору скорости – по направлению .

Таблица 2.3

Видеоурок по физике – Ускорение

В видеоруководстве по ускорению обсуждается, что означает ускорение, как определить значение и направление ускорения, а также как различать ускоряющиеся и неускоряющиеся объекты на основе таблиц данных и точечных диаграмм. Многочисленные примеры, иллюстрации, анимация и примеры задач помогают в объяснениях. Видео урок отвечает на следующие вопросы:

1. Что такое ускоряющийся объект?
2. Что такое ускорение и как определить его величину и направление?
3. ​Чем равномерное и неравномерное ускорение отличаются друг от друга?

Чтобы повысить эффективность обучения, The Physics Classroom предоставляет следующие инструменты:

Заметки к уроку

Заметки к уроку предназначены для печати и использования при просмотре видео. Они организованы таким образом, чтобы учащиеся могли следить за видео, записывать некоторые заметки и оставлять видео с документом, на который можно ссылаться по мере продолжения обучения. Заметки к уроку доступны в формате PDF. Разрешается печатать заметки или включать ссылку на них из системы управления обучением.

Просмотр примечаний к уроку

Дополнительные средства обучения

Обучение требует усилий. Просмотр видео является относительно пассивным занятием. Одно дело слушать видео, представленное человеком, который понимает материал. Но совсем другое дело применить информацию из видео в стремлении лично разобраться в материале. На этой странице перечислены различные инструменты, которые можно использовать для применения нового обучения. Инструменты включают те, которые могут использоваться учащимися, и те, которые могут использоваться учителями со своими учениками в классе. Связанные ресурсы также включены в число этих инструментов.

Просмотр дополнительных средств обучения

Ресурсы для учителей

Так ты этому учишь? Может быть, мы сможем помочь. Мы занимаемся этим некоторое время, и у нас есть несколько ресурсов, которые могут оказаться вам полезными. Посетите страницу ресурсов для учителей и узнайте о некоторых инструментах, которые помогут вам преподавать и разрабатывать уроки.

Просмотреть ресурсы для учителей

Слайды из видеоурока

Некоторым учащимся полезно просматривать слайды презентации. Мы предоставляем их здесь, на нашем сайте. Анимации, присутствующие в видео, трансформируются в единую статичную картинку экрана в слайдах.

Просмотр слайдов

Вы можете просмотреть это видео на YouTube или здесь на нашем сайте:

Посмотреть видеоинструкцию

Помогите нам помочь вам

Это видео является частью нашей серии видеоуроков по кинематике. Другие видеоуроки вы можете найти здесь, на нашем сайте. Чтобы получать последние материалы из нашей серии видеоуроков по физике, мы предлагаем пользователям подписаться на канал The Physics Classroom на YouTube. Каждые Нравится и каждый Подписка помогает продвигать наше видео … так что спасибо за любую помощь, которую вы можете нам оказать. Когда вы помогаете нам, мы можем помочь вам больше.

Как рассчитать ускорение – манекены

С точки зрения физики, ускорение, a , это величина, на которую ваша скорость изменяется за заданный промежуток времени. Учитывая начальную и конечную скорости, v _i и v _F и начальное и последнее время, в течение которого изменяется ваша скорость, T _I и T _F , вы можете написать это.

В единицах измерения уравнение выглядит так:

Расстояние за время в квадрате? Не позволяйте этому сбить вас с толку. Вы получаете время в квадрате в знаменателе, потому что вы делите скорость на время. Другими словами, ускорение – это скорость, с которой изменяется ваша скорость, потому что в знаменателе скорости указано время. Для ускорения вы видите единицы измерения: метры в секунду ² , сантиметры в секунду ² , мили в секунду ² , футы в секунду ² или даже километры в час ² .

Возможно, для данной задачи проще использовать такие единицы измерения, как mph/s (мили в час в секунду). Это было бы полезно, если бы рассматриваемая скорость имела величину порядка нескольких миль в час, которая обычно изменялась в течение нескольких секунд.

Скажем, вы стали гонщиком, чтобы проанализировать свое ускорение на драгвее. После пробного забега вы знаете пройденное расстояние — 402 метра, или примерно 0,25 мили (величина вашего смещения) — и знаете время, которое на это ушло — 5,5 секунды. Итак, каково было ваше ускорение, когда вы мчались по трассе?

Ну, вы можете связать перемещение, ускорение и время следующим образом:

и это то, что вы хотите — вы всегда работаете с алгеброй, так что в конечном итоге вы связываете все известные вам величины с одной величиной, которую вы не знаю . В этом случае у вас есть

(Имейте в виду, что в этом случае ваша начальная скорость равна 0 — вам не разрешается разбегаться в дрэг-рейсинге!) Вы можете изменить это уравнение с помощью небольшой алгебры, чтобы решить для ускорения; просто разделите обе части на t ² и умножьте на 2, чтобы получить

Отлично. Подставив числа, вы получите следующее:

Ладно, ускорение примерно 27 метров в секунду ² . Что это более понятным языком? Ускорение свободного падения, г , равно 9,8 метра в секунду ² , так что это примерно 2,7 г — вы почувствуете, что вас толкнули обратно на сиденье с силой, примерно в 2,7 раза превышающей ваш собственный вес.

Эта статья из книги:

• Физика I Для чайников,

Об авторе книги:

Доктор Стивен Хольцнер написал более 40 книг по физике и программированию.