Ускорение в физике: Что такое ускорение? (статья) | Ускорение

Ускорение – формула, определение, закон кратко (физика 9 класс)

4.3

Средняя оценка: 4.3

Всего получено оценок: 223.

Обновлено 6 Августа, 2021

4.3

Средняя оценка: 4.3

Всего получено оценок: 223.

Обновлено 6 Августа, 2021

Из курса физики 9 класса известно, что движение бывает равномерным и неравномерным. При неравномерном движении за равные промежутки времени материальная точка проходит разные расстояния, мгновенная скорость её движения также изменяется. Мера быстроты изменения скорости называется ускорением. Поговорим на эту тему, дадим определение ускорения, приведём его формулу.

Ускорение движения

Большинство движений в природе неравномерны. Если рассмотреть такое движение, то расстояния, проходимые за одинаковые промежутки времени будут разными. Следовательно, и скорость (она равна отношению пройденного расстояния ко времени прохождения) тоже будет разной.

Рис. 1. Пример неравномерного движения.

Более того, для разных движений изменение скорости за одинаковые промежутки времени также будет неодинаково. К примеру, рассмотрим разгон мяча и автомобиля. К концу разгона и тот и другой могут достичь мгновенной скорости 50 метров в секунду. Однако автомобиль достигает такой скорости за десять секунд, а мяч — в сто раз быстрее, за одну десятую секунды. Как охарактеризовать такое различие?

Физическая величина, характеризующая быстроту изменения скорости, называется ускорением.

Формулу ускорения легко получить, если учесть, что скорость — это быстрота изменения координаты, а ускорение — это быстрота изменения скорости:

$$\overrightarrow a={\overrightarrow v – \overrightarrow {v_0} \over t}$$

где:

• $\overrightarrow a$ — вектор ускорения;
• $\overrightarrow {v_0}$ — вектор начальной скорости;
• $\overrightarrow v$ — вектор скорости в момент времени $t$;
• $t$ — время изменения скорости от $\overrightarrow {v_0}$ до $\overrightarrow v$.

Фактически ускорение — это «скорость изменения скорости». Поэтому формула ускорения аналогична формуле скорости, только в числителе вместо координаты стоит скорость.

Из приведённой формулы можно получить единицу измерения ускорения. Поскольку скорость в системе СИ измеряется в метрах в секунду, а время — в секундах, то ускорение получается в метрах в секунду в квадрате (иногда говорят метр в секунду за секунду).

Рис. 2. Ускорение в физике.

Равноускоренное движение

По аналогии со скоростью ускорение может быть средним и мгновенным. Мгновенное ускорение — это ускорение, для которого промежуток времени измерения стремится к нулю:

$$\overrightarrow a_{мгн}={\overrightarrow v – \overrightarrow {v_0} \over t},t\rightarrow 0$$

В противном случае ускорение получается средним за время $t$.

Движение, при котором мгновенное ускорение в любой момент времени остаётся постоянным и равным среднему ускорению за любой промежуток времени, называется равноускоренным.

При равноускоренном движении скорость изменяется по линейному закону.

Примером равноускоренного движения является свободное падение тела в первые секунды, когда сопротивление воздуха ещё пренебрежительно мало.

Рис. 3. Свободное падение тела.

Что мы узнали?

Быстроту изменения скорости характеризует такая физическая величина, как ускорение. Единица измерения ускорения — метр в секунду за секунду. Движение, при котором мгновенное ускорение постоянно в любой момент времени, называется равноускоренным.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.3

Средняя оценка: 4.3

Всего получено оценок: 223.

---

А какая ваша оценка?

Ускорение тела в физике, теория и онлайн калькуляторы

Ускорение тела в физике, теория и онлайн калькуляторы

Определение

Ускорением тела называют векторную величину показывающую быстроту изменения скорости движения тела. Обозначают ускорение как $\overline{a}$.

Среднее ускорение тела

Допустим, что в моменты времени $t$ и $t+\Delta t$ скорости равны $\overline{v}(t)$ и $\overline{v}(t+\Delta t)$. Получается, что за время $\Delta t$ скорость изменяется на величину:

\[\Delta \overline{v}=\overline{v}\left(t+\Delta t\right)-\overline{v}\left(t\right)\left(1\right),\]

тогда среднее ускорение тела равно:

\[\left\langle \overline{a}\right\rangle \left(t,\ t+\Delta t\right)=\frac{\Delta \overline{v}}{\Delta t}\left(2\right).\]

Мгновенное ускорение тела

Устремим промежуток времени $\Delta t$ к нулю, тогда из уравнения (2) получим:

\[\overline{a}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \overline{v}}{\Delta t}=\frac{d\overline{v}}{dt}\left(3\right).\ }\]

Формула (3) является определением мгновенного ускорения. Принимая во внимание, что в декартовой системе координат:

\[\overline{r}=x\left(t\right)\overline{i}+y\left(t\right)\overline{j}+z\left(t\right)\overline{k}\left(4\right),\ а\ \overline{v}=\frac{d\overline{r}}{dt}(5)\]

получаем:

\[\overline{a}=\overline{i}\frac{d^2x}{dt^2}+\overline{j}\frac{d^2y}{dt^2}+\overline{k}\frac{d^2z}{dt^2}=\frac{d^2\overline{r}}{dt^2}\left(6\right). 2_z}.\]

Для выяснения вопроса о направлении ускорения движения тела Вектор скорости представим как:

\[\overline{v}=v\overline{\tau }\left(8\right),\]

где $v$ – модуль скорости тела; $\overline{\tau }$ – единичный вектор касательный к траектории движения материальной точки. Подставим выражение (8) в определение мгновенной скорости, получим:

\[\overline{a}={\frac{d\overline{v}}{dt} =\frac{d}{dt}\left(v\overline{\tau }\right)=\overline{\tau }\frac{dv}{dt}+v\frac{d\overline{\tau }}{dt}\left(9\right).\ }\]

Единичный касательный вектор $\overline{\tau }$ определяется точкой траектории, которая в свою очередь характеризуется расстоянием ($s$) от начальной точки. Значит вектор $\overline{\tau }$ – это функция от $s$:

\[\overline{\tau }=\overline{\tau }\left(s\right)\left(10\right).\]

Параметр $s$ – функция от времени. Получаем:

\[\frac{d\overline{\tau }}{dt}=\frac{d\overline{\tau }}{ds}\frac{ds}{dt}\left(11\right),\]

где вектор $\overline{\tau }$ по модулю не изменяется. 2}.\]

Прямолинейное движение тела

Если траекторией движения материальной точки является прямая, то вектор ускорения направлен вдоль той же прямой, что и вектор скорости. Изменяется только величина скорости.

Переменное движение называют ускоренным, если скорость материальной точки постоянно увеличивается по модулю. При этом $a>0$, векторы ускорения и скорости сонаправлены.

Если скорость по модулю убывает, то движение называют замедленным ($a

Движение материальной точки называют равнопеременным и прямолинейным, если движение происходит с постоянным ускорением ($\overline{a}=const$). При равнопеременном движении мгновенная скорость ($\overline{v}$) и ускорение материальной точки связаны выражением:

\[\overline{v}={\overline{v}}_0+\overline{a}t\ \left(3\right),\]

где ${\overline{v}}_0$ – скорость тела в начальный момент времени.

Примеры задач с решением

Пример 1

Задание: Движения двух материальных точек заданы следующими кинематическими уравнениями: $x_1=A+Bt-Ct^2$ и $x_2=D+Et+Ft^2,$ чему равны ускорения этих двух точек в момент времени, когда равны их скорости, если $A$, B,C,D,E. 2}$

   

Пример 2

Задание: Движение материальной точки задано уравнением: $\overline{r}\left(t\right)=A\left(\overline{i}{\cos \left(\omega t\right)+\overline{j}{\sin \left(\omega t\right)\ }\ }\right),$ где $A$ и $\omega $ – постоянные величины. Начертите траекторию движения точки, изобразите на ней вектор ускорения этой точки. Каков модуль центростремительного ускорения ($a_n$) точки в этом случае?

Решение: Рассмотрим уравнение движения нашей точки:

\[\overline{r}\left(t\right)=A\left(\overline{i}{\cos \left(\omega t\right)+\overline{j}{\sin \left(\omega t\right)\ }\ }\right)\ \left(2.1\right).\]

В координатной записи уравнению (2.1) соответствует система уравнений:

\[\left\{ \begin{array}{c} x\left(t\right)=A{\rm cos}\left(\omega t\right), \\ y(t)=A{\sin \left(\omega t\right)\ } \end{array} \left(2. 2$

   

Читать дальше: условие равновесия тела.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Ускорение | Физика

Цели обучения

К концу этого раздела вы сможете:

• Определять и различать мгновенное ускорение, среднее ускорение и замедление.
• Вычислить ускорение, зная начальное время, начальную скорость, конечное время и конечную скорость.

 

Рис. 1. Самолет снижает скорость или замедляется перед посадкой на Сен-Мартене. Его ускорение противоположно направлению его скорости. (кредит: Стив Конри, Flickr)

В повседневном разговоре ускорить означает ускорить. Ускоритель в автомобиле фактически может заставить его ускориться. Чем больше ускорение , тем больше изменение скорости за заданное время. Формальное определение ускорения соответствует этим понятиям, но более широкое.

Среднее ускорение

Среднее ускорение равно скорости изменения скорости ,

[латекс]\bar{a}=\frac{\Delta v}{\Delta t}=\frac{{ v}_{f}-{v}_{0}}{{t}_{f}-{t}_{0}}\\[/латекс]

, где [латекс]\бар{а}\\[/латекс] — среднее ускорение, v — скорость, а t — время. (Полоса над и означает среднее ускорение .)

Поскольку ускорение представляет собой скорость в м/с, деленную на время в с, единицами СИ для ускорения являются м/с ² , метры в секунду в квадрате или метры в секунду в секунду, что буквально означает, на сколько метров в секунду скорость изменяется каждую секунду.

Вспомните, что скорость — это вектор, у него есть и величина, и направление. Это означает, что изменение скорости может быть изменением величины (или скорости), но оно также может быть изменением направления . Например, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение происходит, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по тому и другому.

Ускорение как вектор

Ускорение является вектором в том же направлении, что и изменение скорости, Δ v . Поскольку скорость является вектором, она может изменяться как по величине, так и по направлению. Таким образом, ускорение — это изменение либо скорости, либо направления, либо того и другого.

Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда совпадает с направлением движения . Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление .

Рис. 2. Поезд метро в Сан-Паулу, Бразилия, замедляет скорость перед въездом на станцию.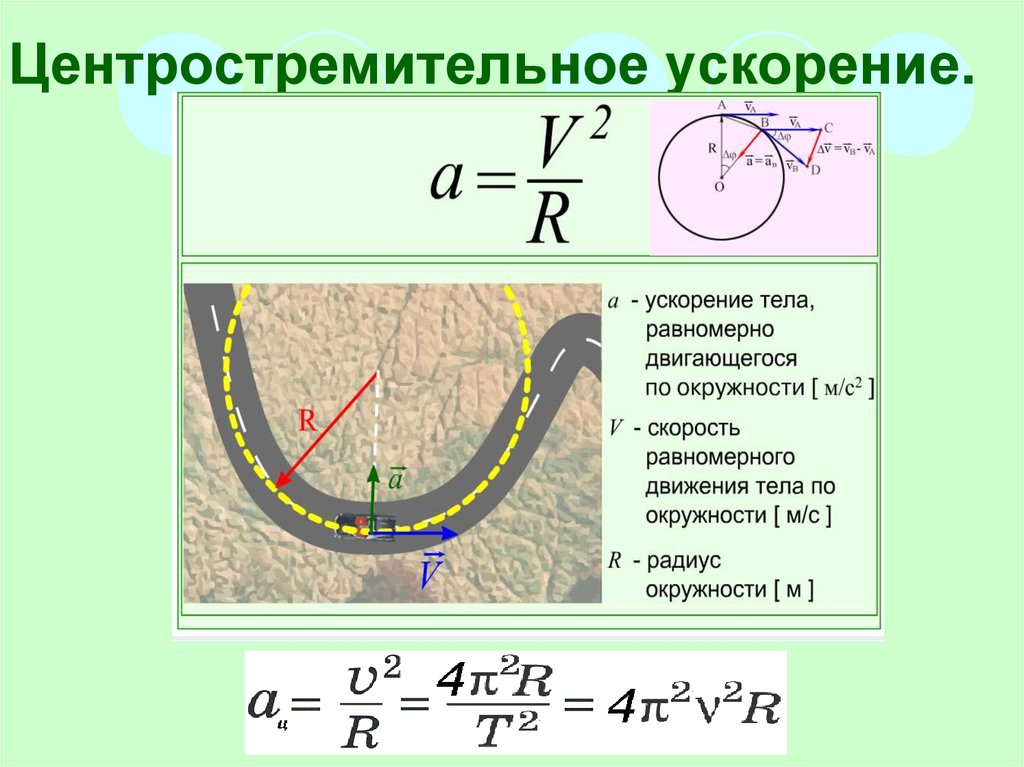 Он ускоряется в направлении, противоположном направлению его движения. (кредит: Юсуке Кавасаки, Flickr)

Предупреждение о неправильном понимании: замедление против отрицательного ускорения

Замедление всегда относится к ускорению в направлении, противоположном направлению скорости. Замедление всегда снижает скорость. Однако отрицательное ускорение равно ускорению в отрицательном направлении в выбранной системе координат . Отрицательное ускорение может быть, а может и не быть замедлением, а замедление может считаться или не считаться отрицательным ускорением. Например, рассмотрим рисунок 3.

Рисунок 3. (a) Этот автомобиль ускоряется, двигаясь вправо. Поэтому он имеет положительное ускорение в нашей системе координат. (b) Этот автомобиль замедляется, когда он движется вправо. Следовательно, в нашей системе координат он имеет отрицательное ускорение, потому что его ускорение направлено влево. Автомобиль тоже тормозит: направление его ускорения противоположно направлению его движения. (c) Этот автомобиль движется влево, но со временем замедляется. Следовательно, его ускорение положительно в нашей системе координат, потому что оно направлено вправо. Однако автомобиль замедляется, потому что его ускорение противоположно его движению. (d) Этот автомобиль ускоряется, когда он движется влево. Он имеет отрицательное ускорение, потому что он ускоряется влево. Однако, поскольку его ускорение направлено в том же направлении, что и его движение, оно ускоряется (а не замедляется).

Пример 1. Расчет ускорения: скаковая лошадь выезжает из ворот

Рис. 4. (кредит: Джон Салливан, PD Photo.org)

 

Скаковая лошадь, выйдя из ворот, разгоняется из состояния покоя до скорости 15,0 м/ с на запад через 1,80 с. Каково его среднее ускорение?

Стратегия

Сначала мы рисуем эскиз и назначаем проблеме систему координат. Это простая задача, но ее всегда полезно визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.

Рисунок 5.

Мы можем решить эту задачу, определив Δ v и Δ t по имеющейся информации, а затем рассчитав среднее ускорение непосредственно из уравнения [латекс]\bar{a}=\frac{\ Дельта v}{\Delta t}=\frac{{v}_{f}-{v}_{0}}{{t}_{f}-{t}_{0}}\\[/latex ].

Решение

1. Определите известные. v ₀ = 0, v _f = −15,0 м/с (знак минус указывает направление на запад), Δ 9{2}\\[/latex]

Обсуждение

Отрицательный знак ускорения означает, что ускорение направлено на запад. Ускорение 8,33 м/с ² строго на запад означает, что лошадь увеличивает свою скорость на 8,33 м/с строго на запад каждую секунду, то есть на 8,33 метра в секунду в секунду, что мы записываем как 8,33 м/с ² . . Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы, чтобы всадник удерживался с силой, почти равной его весу.

Мгновенное ускорение

Мгновенное ускорение a , или ускорение в определенный момент времени , получается тем же процессом, который обсуждался для мгновенной скорости во времени, скорости и скорости, т. е. рассматривая бесконечно малый отрезок времени. Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рис. 6 показаны графики зависимости мгновенного ускорения от времени для двух очень разных движений. На рис. 6(а) ускорение немного меняется, и среднее значение по всему интервалу почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение так, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около 1,8 м/с ² ). На рис. 6(b) ускорение резко меняется со временем. В таких ситуациях лучше рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, движение на интервалах времени от 0 до 1,0 с и от 1,0 до 3,0 с можно рассматривать как отдельные движения с ускорениями +3,0 м/с ² и –2,0 м/с ² соответственно.

Рис. 6. Графики зависимости мгновенного ускорения от времени для двух различных одномерных движений. а) Здесь ускорение меняется незначительно и всегда в одном и том же направлении, так как оно положительно. Среднее значение по интервалу почти такое же, как ускорение в любой момент времени. (b) Здесь ускорение сильно различается, возможно, представляя посылку на ленточном конвейере почтового отделения, которая ускоряется вперед и назад, когда она толкается. В такой ситуации необходимо рассматривать небольшие промежутки времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.

В следующих нескольких примерах рассматривается движение поезда метро, ​​показанного на рис. 7. В (а) шаттл движется вправо, а в (б) — влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые рассуждения, которые используются при решении задач.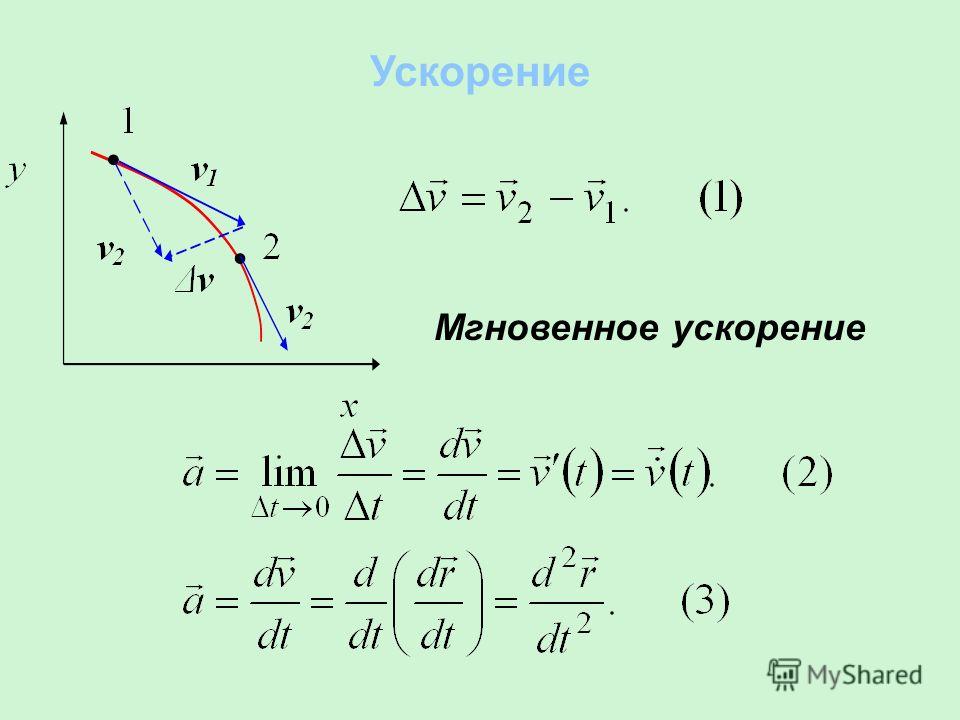

Рис. 7. Одномерное движение поезда метро, ​​рассмотренное в примере 2, примере 3, примере 4, примере 5, примере 6 и примере 7. Здесь мы выбрали ось x так, что + означает вправо, а − означает влево для перемещений, скоростей и ускорений. (a) Поезд метро движется вправо из x0 в xf. Его водоизмещение Δx равно +2,0 км. (b) Поезд движется влево от x′0 до x′f. Его смещение Δx′ равно −1,5 км. (Обратите внимание, что штриховой символ (′) используется просто для того, чтобы отличить перемещение в двух разных ситуациях. Расстояние пути и размер автомобилей представлены в разных масштабах, чтобы все уместить на диаграмме.)

Пример 2. Расчет перемещения: поезд метро

Каковы величина и знак перемещений поезда метро, ​​показанного в частях (а) и (б) на рис. 7?

Стратегия

Чертеж с системой координат уже предоставлен, поэтому нам не нужно делать эскиз, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает. Обратите особое внимание на систему координат. Для нахождения перемещения воспользуемся уравнением ∆ x = x _f − x ₀ . Это просто, поскольку заданы начальная и конечная позиции.

Решение

1. Определите известные. In the figure we see that x _f  = 6.70 km and x ₀  = 4.70 km for part (a), and x ′ _f  = 3.75 km and x ′ ₀  = 5,25 км для участка (b).

2. Найдите смещение в части (a).

[латекс]\Delta x={x}_{f}-{x}_{0}=6,70\text{км}-4,70\text{км} = \text{+}2,00\text{км} \\[/latex]

3. Найдите смещение в части (b).

[латекс]\Дельта x′ ={x′}_{f}-{x′}_{0}=\text{3,75 км}-\text{5,25 км} = -\text{1,50 км}\ \[/latex]

Обсуждение

Направление движения в (a) — вправо, и поэтому его смещение имеет положительный знак, тогда как движение в (b) — влево и, следовательно, имеет отрицательный знак .

Пример 3. Сравнение пройденного расстояния с перемещением: поезд метро

Какое расстояние пройдено при движениях, показанных в частях (а) и (б) поезда метро на рисунке 7?

Стратегия

Чтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны с перемещением. Расстояние между двумя положениями определяется как величина смещения, которое было найдено в примере 1. Пройденное расстояние — это общая длина пути, пройденного между двумя положениями. (См. Перемещение.) В случае поезда метро, ​​показанного на рисунке 7, пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.

Решение

1. Перемещение по части (а) составило +2,00 км. Следовательно, расстояние между начальным и конечным положениями составило 2,00 км, а пройденное расстояние составило 2,00 км.

2. Перемещение по части (b) составило −1,5 км. Следовательно, расстояние между начальным и конечным положениями составило 1,50 км, а пройденное расстояние — 1,50 км.

Обсуждение

Расстояние является скаляром. У него есть величина, но нет знака, указывающего направление.

Пример 4. Расчет ускорения: поезд метро разгоняется

Предположим, что поезд на рис. 7(а) разгоняется из состояния покоя до 30,0 км/ч за первые 20,0 с своего движения. Каково его среднее ускорение за этот промежуток времени?

Стратегия

Сейчас стоит сделать простой набросок:

Рисунок 8. Эта задача состоит из трех шагов. Сначала мы должны определить изменение скорости, затем мы должны определить изменение времени и, наконец, мы используем эти значения для расчета ускорения.

Решение

1. Найдите известные. v ₀  = 0 (поезда отправляются из состояния покоя), v _f   = 30,0 км/ч, Δ t  = 20,0 с.

2. Вычислить Δ v . Поскольку поезд стартует из состояния покоя, его скорость изменится на [латекс]\Дельта v\текст{=}\текст{+}\текст{30,0 км/ч}\\[/латекс], где плюс означает скорость до право.

3. Подставьте известные значения и найдите неизвестное, [латекс]\бар{а}\\[/латекс]. 9{2}\\[/latex]

Обсуждение

Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд стартует из состояния покоя и заканчивается со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и изменение скорости, как это всегда и бывает.

Пример 5. Расчет ускорения: поезд метро замедляется

Теперь предположим, что в конце пути поезд на рис. 7(а) замедляется до полной остановки со скорости 30,0 км/ч за 8,00 с. Каково его среднее ускорение при остановке?

Стратегия

Рис. 9. В этом случае поезд замедляется, и его ускорение отрицательно, потому что он движется влево. Как и в предыдущем примере, мы должны найти изменение скорости и изменение времени, а затем найти ускорение.

Решение

1. Определите известные. v ₀  = 30,0 км/ч, v _f  = 0 км/ч (поезд стоит, поэтому его скорость равна 0), а Δ t  = 8,00 с.

2. Решите изменение скорости, Δ v .

Δ V = V _F – V ₀ = 0 – 30,0 км/ч = – 30,0 км/ч

3. Подключа и найдите [латекс]\бар{а}\\[/латекс].

[латекс]\bar{a}=\frac{\Delta v}{\Delta t}=\frac{-\text{30}\text{.}\text{0 км/ч}}{8\ text{.}\text{00 s}}\\[/latex]

4. Преобразуйте единицы измерения в метры и секунды. 9{2}\text{.}\\[/latex]

Обсуждение

Знак минус указывает, что ускорение направлено влево. Этот знак разумен, поскольку в этой задаче поезд изначально имеет положительную скорость, а отрицательное ускорение противодействовало бы движению. Опять же, ускорение происходит в том же направлении, что и изменение скорости, которая здесь отрицательная. Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости.

Графики зависимости положения, скорости и ускорения от времени для поездов в Примере 4 и Примере 5 показаны на рисунке 10. (Мы приняли, что скорость остается постоянной от 20 до 40 с, после чего поезд замедляется. )

Рис. 10. (а) Положение поезда во времени. Обратите внимание, что положение поезда меняется медленно в начале пути, а затем все быстрее и быстрее по мере того, как он набирает скорость. Затем его положение меняется медленнее, так как он замедляется в конце пути. В середине пути, пока скорость остается постоянной, положение изменяется с постоянной скоростью. (b) Скорость поезда во времени. Скорость поезда увеличивается по мере того, как он ускоряется в начале пути. Он остается таким же в середине пути (где нет ускорения). Она уменьшается по мере торможения поезда в конце пути. в) ускорение поезда во времени. Поезд имеет положительное ускорение, так как в начале пути он ускоряется. Он не имеет ускорения, так как в середине пути движется с постоянной скоростью. Его ускорение отрицательно, так как в конце пути оно замедляется.

Пример 6. Вычисление средней скорости поезда метро

Какова средняя скорость поезда в части b примера 2, показанном еще раз ниже, если путь до места занимает 5,00 мин?

Рисунок 11.

Стратегия

Средняя скорость равна смещению, деленному на время. Здесь оно будет отрицательным, так как поезд движется влево и имеет отрицательное смещение.

Решение

1. Определите известные. x ′ _f = 3,75 км, x ′ ₀ = 5,25 км, Δ t = 5,00 мин.

2. Определить перемещение, Δ x ′. В Примере 2 мы нашли, что Δ x ′ равно −1,5 км.

3. Найдите среднюю скорость.

[латекс]\bar{v}=\frac{\Delta x′}{\Delta t}=\frac{-\text{1,50 км}}{\text{5,00 мин}}\\[/latex]

4. Преобразование единиц.

[латекс]\bar{v}=\frac{\Delta x′}{\Delta t}=\left(\frac{-1\text{. }\text{50 км}}{5\text{ .}\text{00 мин}}\right)\left(\frac{\text{60 мин}}{1 ч}\right)=-\text{18}\text{0,0 км/ч}\\ [/латекс]

Обсуждение

Отрицательная скорость указывает на движение влево.

Пример 7. Расчет замедления: поезд метро

Наконец, предположим, что поезд на рисунке 2 замедляется до полной остановки со скорости 20,0 км/ч за 10,0 с. Каково его среднее ускорение?

Стратегия

Еще раз нарисуем набросок:

Рис. 12.

Как и прежде, мы должны найти изменение скорости и изменение времени для расчета среднего ускорения.

Решение

1. Найдите известные. v ₀ = −20 км/ч, v _f = 0 км/ч, Δ t = 10,0 с.

2. Вычислить Δ v . Изменение скорости здесь действительно положительное, так как

[латекс]\Delta v={v}_{f}-{v}_{0}=0-\left(-\text{20 км/ч}\ right)\text{=}\phantom{\rule{0. 25}{0ex}}\text{+}\text{20 км/ч}\\[/latex]

3. Найдите [латекс]\bar{ а}\\[/латекс].

[латекс]\bar{a}=\frac{\Delta v}{\Delta t}=\frac{+\text{20}\text{0,0 км/ч}}{\text{10}\ текст{.}0 с}\\[/латекс] 9{2}\\[/latex]

Обсуждение

Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд изначально имеет отрицательную скорость (влево) в этой задаче, а положительное ускорение противодействует движению (и, следовательно, вправо). Опять же, ускорение происходит в том же направлении, что и изменение скорости, которая здесь положительна. Как и в примере 5, это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости.

Знак и направление

Пожалуй, самое важное, что следует отметить в этих примерах, — это знаки ответов. В выбранной нами системе координат плюс означает, что величина находится справа, а минус означает, что она находится слева. Это легко представить для смещения и скорости.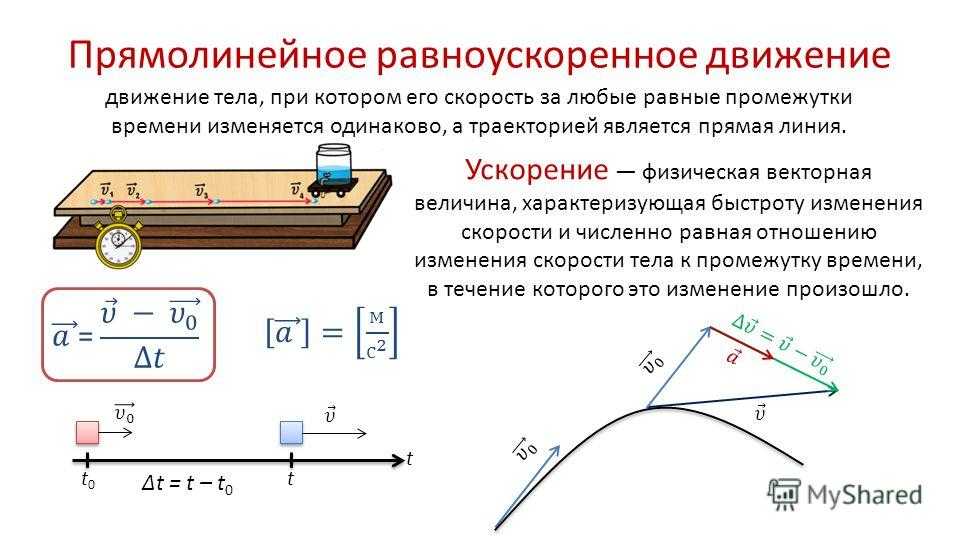 Но это немного менее очевидно для ускорения. Большинство людей интерпретируют отрицательное ускорение как замедление объекта. Этого не было в примере 2, где положительное ускорение замедляло отрицательную скорость. Решающим отличием было то, что ускорение было в направлении, противоположном скорости. В самом деле, отрицательное ускорение будет увеличить отрицательную скорость. Например, поезд, движущийся влево на рисунке 11, ускоряется за счет ускорения влево. В этом случае как v , так и a отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и изменение скорости, то тело ускоряется. Если ускорение имеет знак, противоположный изменению скорости, то тело замедляется.

Проверьте свое понимание

Самолет приземляется на взлетно-посадочную полосу, летящую на восток. Опишите его ускорение.

Решение

Если мы возьмем восток за положительное значение, то ускорение самолета будет отрицательным, так как он движется на запад. Он также замедляется: его ускорение противоположно направлению его скорости.

Исследования PhET: Моделирование движущегося человека

Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка вперед-назад с помощью мыши и зарисовывайте его движение. Установите положение, скорость или ускорение, и пусть симуляция переместит человека за вас.

Нажмите, чтобы загрузить симуляцию. Запуск с использованием Java.

Резюме раздела

Концептуальные вопросы

1. Возможно ли, чтобы скорость была постоянной, а ускорение не равно нулю? Приведите пример такой ситуации.

2. Может ли скорость быть постоянной, а ускорение не равным нулю? Объяснять.

3. Приведите пример, в котором скорость равна нулю, а ускорение – нет.

4. Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, то как направлено его ускорение? Ускорение положительное или отрицательное?

5. Знаки плюс и минус используются в одномерном движении для указания направления. Каков знак ускорения, уменьшающего модуль отрицательной скорости? положительной скорости?

Задачи и упражнения

1. Гепард может разогнаться из состояния покоя до скорости 30,0 м/с за 7,00 с. Каково его ускорение?

2. Профессиональное приложение. Доктор Джон Пол Стэпп был офицером ВВС США, изучавшим влияние экстремального замедления на организм человека. 10 декабря 1954, Стапп ехал на ракетных салазках, разгоняясь из состояния покоя до максимальной скорости 282 м/с (1015 км/ч) за 5,00 с, и резко возвращался в состояние покоя всего за 1,40 с! Вычислите его ускорение (а) и замедление (б). Выразите каждое число кратным г (9,80 м/с ² ), взяв его отношение к ускорению свободного падения.

3. Пассажирка выезжает из гаража задним ходом с ускорением 1,40 м/с ² .(a) Сколько времени потребуется ей, чтобы достичь скорости 2,00 м/с? (b) Если она затем затормозится до полной остановки через 0,800 с, каково ее замедление?

4. Предположим, что межконтинентальная баллистическая ракета выходит из состояния покоя до суборбитальной скорости 6,50 км/с за 60,0 с (фактическая скорость и время засекречены). Каково его среднее ускорение в м/с ² и в кратных g (9,80 м/с ² ).

Глоссарий

ускорение:

скорость изменения скорости; изменение скорости во времени

среднее ускорение:

изменение скорости, деленное на время, за которое она изменяется

мгновенное ускорение:

ускорение в определенный момент времени

замедление:

ускорение в направлении, противоположном скорости; ускорение, приводящее к уменьшению скорости

Выбранные решения проблем и упражнений

1. 4,29 м/с ²

3. (a) 1,43 S (B) -2,50 м/с ²

2.3: Аккетирование – Физико0001

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

14440

• Безграничный
• Безграничный

Графическая интерпретация

Графическое представление ускорения во времени может быть получено с помощью графика положения объекта во времени. 2}}\)

Ускорение — это вектор, указывающий в том же направлении, что и изменение скорости, хотя и не всегда в направлении движения. Например, когда объект замедляется или замедляется, его ускорение происходит в направлении, противоположном его движению.

Движение объекта можно изобразить графически, отобразив положение объекта во времени. Этот график зависимости расстояния от времени можно использовать для создания другого графика, показывающего изменения скорости во времени. Поскольку ускорение — это скорость в \(\mathrm{\frac{m}{s}}\), деленная на время в s, мы можем дополнительно вывести график ускорения из графика скорости или положения объекта.

— это график положения объекта во времени. Этот график подобен движению автомобиля. В начале положение объекта меняется медленно по мере того, как он набирает скорость. В середине скорость постоянна, а положение изменяется с постоянной скоростью. По мере замедления к концу позиция меняется медленнее. Из этого графика мы можем вывести график зависимости скорости от времени.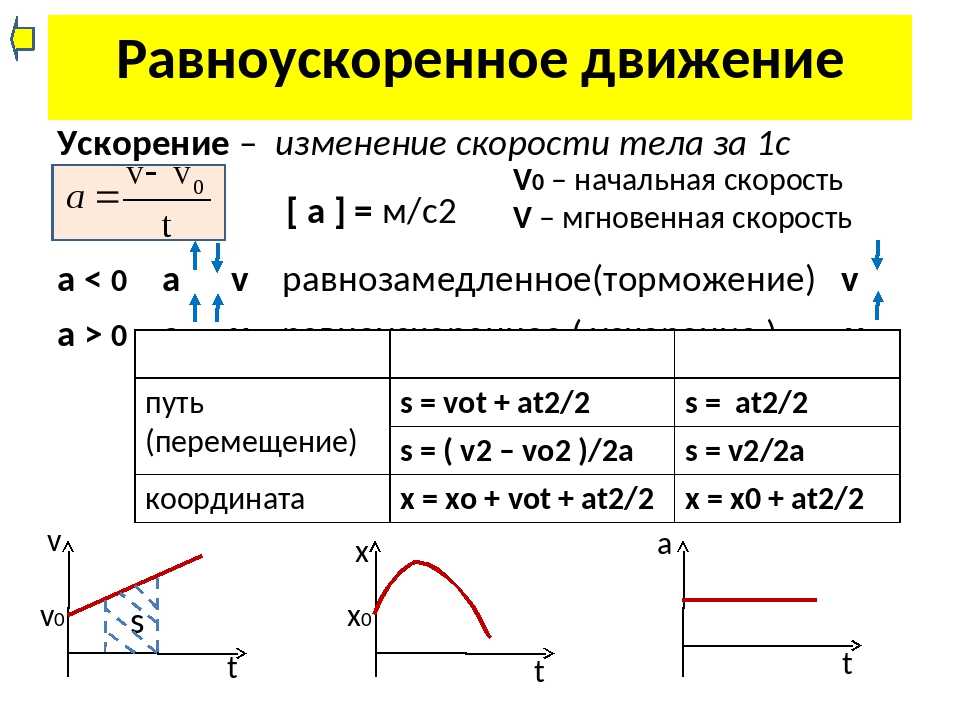

График зависимости положения от времени : Обратите внимание, что положение объекта меняется медленно в начале пути, а затем все быстрее и быстрее по мере того, как он набирает скорость. Затем его положение меняется медленнее, так как он замедляется в конце пути. В середине пути, пока скорость остается постоянной, положение изменяется с постоянной скоростью.

Показывает скорость объекта во времени. Скорость объекта увеличивается в начале по мере того, как он ускоряется в начале, затем остается постоянной в середине, а затем замедляется к концу. Обратите внимание, что этот график представляет собой график зависимости наклона предыдущей позиции от времени. Из этого графика мы можем дополнительно вывести график зависимости ускорения от времени.

Скорость в зависимости от времени : Скорость объекта увеличивается по мере его ускорения в начале пути. Он остается таким же в середине пути (где нет ускорения). Оно уменьшается по мере того, как объект замедляется в конце пути.

Для этого мы также построили бы наклон графика зависимости скорости от времени. На этом графике ускорение постоянно на трех разных стадиях движения. Как мы отмечали ранее, объект вначале увеличивает скорость и медленно меняет положение. График ускорения показывает, что в это время объект увеличивался с положительным постоянным ускорением. В середине, когда объект менял положение с постоянной скоростью, ускорение было равно 0. Это потому, что объект больше не меняет свою скорость и движется с постоянной скоростью. К концу движения объект замедляется. Это отображается как отрицательное значение на графике ускорения. Обратите внимание, что в этом примере движение объекта все еще вперед (положительное), но поскольку оно замедляется, ускорение отрицательное.

График зависимости ускорения от времени : Объект имеет положительное ускорение, так как он ускоряется в начале пути. Он не имеет ускорения, так как в середине пути движется с постоянной скоростью. Его ускорение отрицательно, так как в конце пути оно замедляется.

График движения : Краткое введение в диаграммы частиц и графики движения.

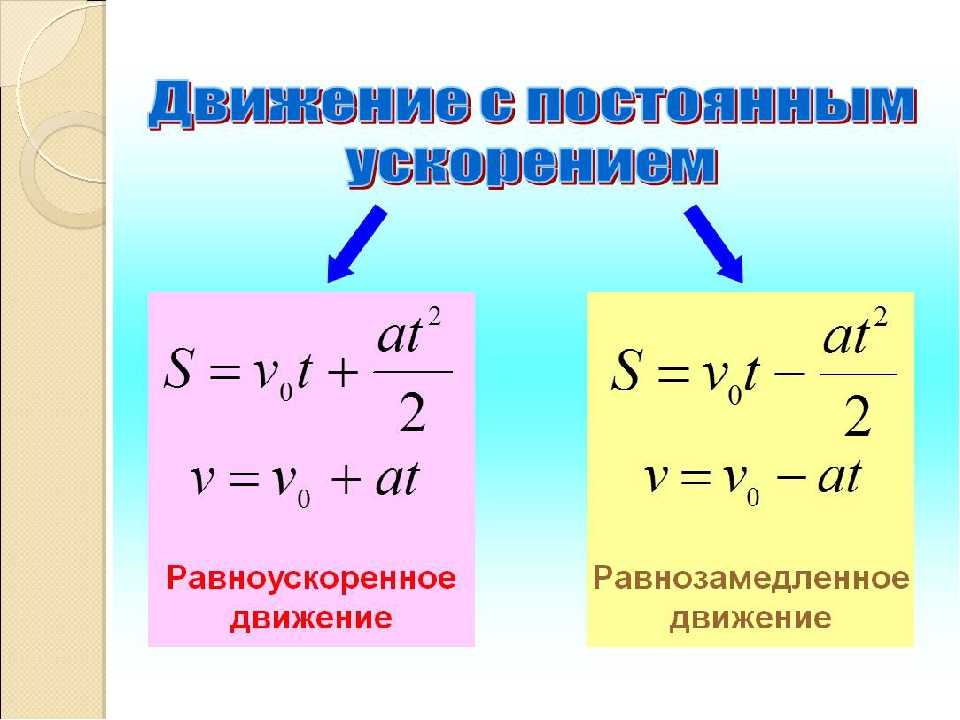
Движение с постоянным ускорением

Постоянное ускорение возникает, когда скорость объекта изменяется на одинаковую величину в каждый равный период времени.

цели обучения

• Описать, как постоянное ускорение влияет на движение объекта

Одномерное движение : Когда вы бросаете объект, он падает вертикально к центру Земли из-за постоянного ускорения силы тяжести.

Объект, испытывающий постоянное ускорение, имеет скорость, которая увеличивается или уменьшается на одинаковую величину в течение любого постоянного периода времени. Ускорение может быть легко получено из основных кинематических принципов. Он определяется как первая производная скорости по времени (то есть вторая производная положения по времени): 92}}\]

Предположение, что ускорение постоянно, серьезно не ограничивает количество ситуаций, которые мы можем изучать, и не снижает точность нашего рассмотрения, поскольку в большом количестве ситуаций ускорение является постоянным . Когда это не так, мы можем либо рассматривать его в отдельных частях постоянного ускорения, либо использовать среднее ускорение за период времени.

Движение падающих предметов представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. Например, если вы поднимете камень и бросите его, он упадет только вертикально вниз к земле. Если бы вы бросали камень, а не просто бросали его, он двигался бы по траектории, более похожей на снаряд, подобный тому, по которому следует удар по мячу.

Снарядное движение — это движение объекта, брошенного или спроецированного в воздух, и подвержено только ускорению свободного падения. Брошенный объект называется снарядом, а путь объекта называется его траекторией. В двумерном движении снаряда есть как вертикальная, так и горизонтальная составляющая.

Из-за алгебраических свойств постоянного ускорения существуют кинематические уравнения, связывающие перемещение, начальную скорость, конечную скорость, ускорение и время. Краткое изложение этих уравнений приведено ниже. 92_0+2a(x−x_0)}\end{align}\]

Постоянное ускорение с помощью векторов и алгебры : Это видео отвечает на вопрос «что такое ускорение? “.

Ключевые моменты

• Ускорение — это скорость, с которой скорость тела изменяется со временем.
• Ускорение — это вектор, указывающий в том же направлении, что и изменение скорости, но не всегда в направлении движения.
• Поскольку ускорение — это скорость в м/с, деленная на время в с, мы можем построить график ускорения на основе графика скорости или положения объекта.
• Предположение, что ускорение постоянно, серьезно не ограничивает количество ситуаций, которые мы можем изучать, и не снижает точность нашего лечения.
• Из-за алгебраических свойств постоянного ускорения существуют кинематические уравнения, которые можно использовать для расчета смещения, скорости, ускорения и времени.
• Расчеты с постоянным ускорением могут выполняться как для одномерного, так и для двумерного движения.

Ключевые термины

• ускорение : Величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).
• скорость : Векторная величина, обозначающая скорость изменения положения во времени или скорость с компонентом направления.
• позиция : Место или местоположение.
• кинематика : относящаяся к движению или кинематике

ЛИЦЕНЗИИ И ОТНОШЕНИЯ

CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ​​ПРЕДОСТАВЛЯЕМОЕ РАНЕЕ

• Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike

CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ​​СПЕЦИАЛЬНОЕ АВТОРСТВО

• Ускорение. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Acceleration . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42100/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
• позиция. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/position . Лицензия : CC BY-SA: Attribution-ShareAlike
• скорость. Предоставлено : Викисловарь. Расположен по адресу : en. wiktionary.org/wiki/velocity . Лицензия : CC BY-SA: Attribution-ShareAlike
• ускорение. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/acceleration . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42100/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
• Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42100/latest/?collection=col11406/1. 7 . Лицензия : CC BY: Attribution
• Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42100/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
• График движения. Расположен по адресу : http://www.youtube.com/watch?v=vYXf7Q9j9qA . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
• Ускорение. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Acceleration . Лицензия : CC BY-SA: Attribution-ShareAlike
• кинематич. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/kinematic . Лицензия : CC BY-SA: Attribution-ShareAlike
• ускорение. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/acceleration . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42100/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
• Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx. org/content/m42100/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
• Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42100/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
• График движения. Расположен по адресу : http://www.youtube.com/watch?v=vYXf7Q9j9qA . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
• Постоянное ускорение с помощью векторов и алгебры. Расположен по адресу : http://www.youtube.com/watch?v=-4pV1HibhlU .