Найти вектор скорости и ускорения точки, примеры решений
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно.
Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется
до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора,
то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость
его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно,
пока совсем не остановится.
Среднее ускорение
Среднее ускорение
где – вектор ускорения.
Направление вектора ускорения совпадает с направлением изменения скорости Δ = – 0 (здесь 0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).
В момент времени t1 (см. рис 1.8) тело имеет скорость 0. В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = – 0. Тогда определить ускорение можно так:
Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки,
при котором за одну секунду скорость этой точки увеличивается на 1 м/с.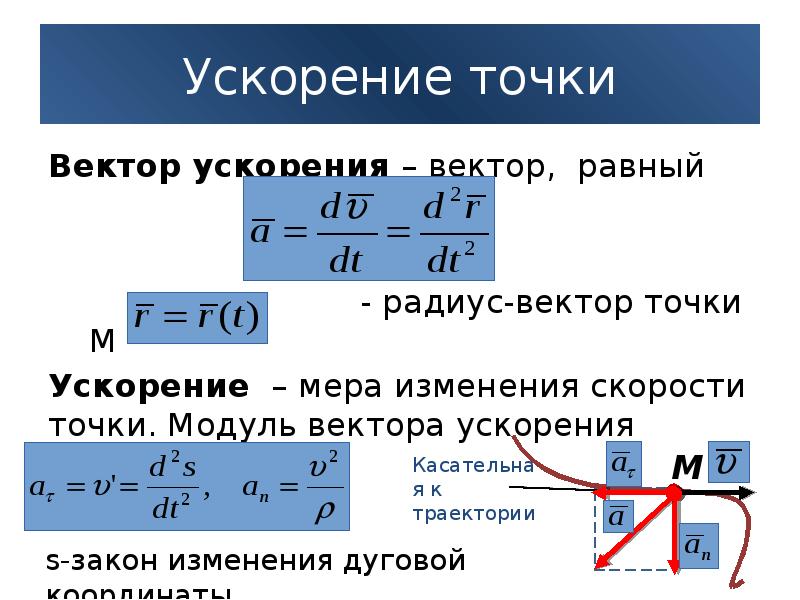 Иными словами,
ускорение определяет, насколько изменяется скорость тела за одну секунду. Например,
если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду
увеличивается на 5 м/с.
Иными словами,
ускорение определяет, насколько изменяется скорость тела за одну секунду. Например,
если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду
увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки)
Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями аХ, aY, aZ).
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > vа направление вектора ускорения совпадает с вектором скорости 2.1

Если скорость тела по модулю уменьшается, то есть
v21то направление вектора ускорения противоположно направлению вектора скорости 2. Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения τ (см.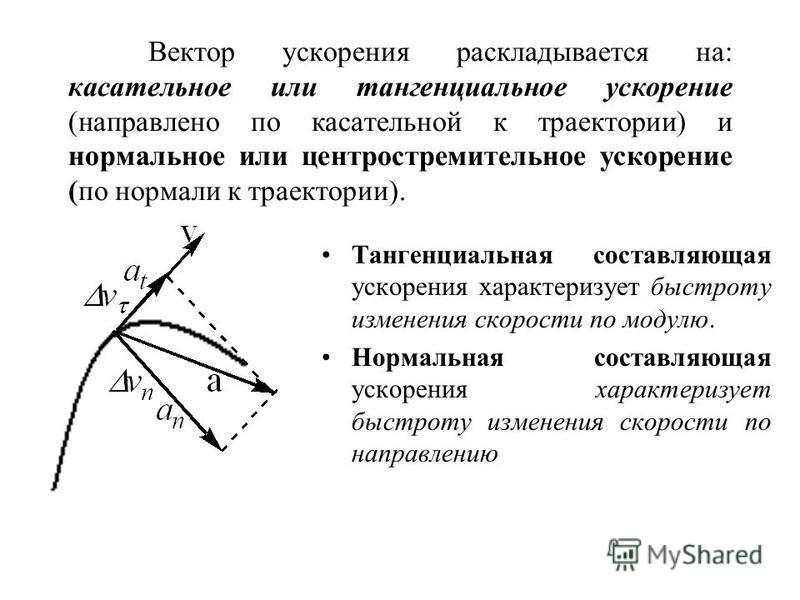 рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
= τ + n
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings. REQUIRED_FIELD}})
REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. LANGUAGE}}
{{$select.selected.display}}
LANGUAGE}}
{{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Векторный способ задания движения точки
Введение
Положение точки однозначно определяется заданием ее радиус-вектора , который изменяется со временем при движении точки. При векторном способе задания движения считается, что задан закон изменения радиус-вектора от времени . Векторный способ задания движения применяется для описания движения в общем виде, используя векторные формулы.
При векторном способе задания движения считается, что задан закон изменения радиус-вектора от времени . Векторный способ задания движения применяется для описания движения в общем виде, используя векторные формулы.
Например, для точки, движущейся с постоянным ускорением , радиус-вектор определяется одной векторной формулой:
,
где – постоянные векторы, не зависящие от времени. Применяя формулы, мы можем найти кинематические величины в векторном виде, не зависимо от выбранной системы координат.
При координатном способе задания движения, мы выбираем систему координат, и в ней задаем зависимости координат точки от времени . Таким образом, координатный способ привязан к выбранной системе координат, а векторный способ не зависит от системы координат.
Связь векторного способа задания движения с координатным осуществляется по формуле:
,
где – единичные векторы (орты) в направлении осей выбранной системы координат.
Основные формулы при векторном способе задания движения
Скорость точки
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы приводим основные результаты этой теории в векторном виде.
Здесь мы приводим основные результаты этой теории в векторном виде.
Итак, нам задана зависимость радиус-вектора материальной точки M от времени :
.
Дифференцируя радиус-вектор по времени, мы находим вектор скорости точки:
.
Модуль вектора скорости:
,
где в круглых скобках обозначено скалярное произведение векторов.
Скорость точки направлена по касательной к траектории. Пусть – единичный вектор в направлении касательной. Тогда скорость может быть направленной либо вдоль вектора :
,
либо в противоположную сторону:
.
Чтобы охватить эти два случая, вводят алгебраическую величину скорости :
.
Это скалярная величина, равная по абсолютной величине модулю скорости, но она может принимать как положительные, так и отрицательные значения:
.
При , вектор скорости сонаправлен с . При он направлен в противоположную сторону. Величина является проекцией вектора скорости на направление . Поскольку – это единичный вектор, то
.
Единичный вектор в направлении касательной к траектории:
.
Ускорение точки
Дифференцируя вектор скорости по времени, находим вектор ускорения точки:
.
Модуль вектора ускорения:
.
Разложим вектор ускорения на две взаимно перпендикулярные компоненты: – параллельную касательной к траектории; и – перпендикулярную к ней.
.
Компонента называется касательным, или тангенциальным ускорением, а компонента – нормальным ускорением.
Тангенциальное ускорение
Алгебраическая величина тангенциального ускорения – это скалярная величина, равная проекции полного ускорения на направление единичного вектора , касательного к траектории:
.
Тогда вектор тангенциального ускорения можно записать в следующем виде:
.
Величина может быть как положительной, так и отрицательной. При положительном , вектор касательного ускорения сонаправлен с единичным вектором . При отрицательном – вектор касательного ускорения направлен в противоположную сторону. Модуль равен модулю касательного ускорения:
Модуль равен модулю касательного ускорения:
.
Алгебраическая величина тангенциального ускорения равна производной по времени от алгебраической величины скорости:
.
Производная по времени модуля скорости:
.
Если между векторами скорости и ускорения острый угол, то движение ускоренное. Если между ними тупой угол, то движение замедленное.
Нормальное ускорение
Вектор нормального ускорения:
.
; .
Единичный вектор в направлении главной нормали траектории:
.
Вектор перпендикулярен вектору и направлен к центру кривизны траектории. Нормальное ускорение всегда направлено к центу кривизны траектории. Поэтому, если выразить его через единичный вектор главной нормали:
,
то . Поэтому .
Модуль нормального ускорения равен проекции полного ускорения на направление главной нормали:
.
Имеют место следующие формулы:
.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов. Опубликовано: Изменено:
Угловая скорость и ускорение как векторные величины
УГЛОВАЯ СКОРОСТЬ И УСКОРЕНИЕ КАК ВЕКТОРНЫЕ ВЕЛИЧИНЫ [c.35]В дальнейшем при рассмотрении общих случаев движения твердых тел придется иметь дело с вращениями вокруг подвижных осей, меняющих свое направление в пространстве, В этих случаях уже нельзя довольствоваться рассмотрением угловой скорости и углового ускорения как алгебраических величин, а становится необходимым связывать их с ориентацией в пространстве. Это достигается, если ввести угловые скорости и ускорения как векторы и в связи с этим для векторов линейных скоростей и ускорений установить векторные формулы, представляющие эти величины как по величине, так и по направлению. [c.222]
Так как движение тела, имеющего одну неподвижную точку, в каждый момент времени можно считать вращением вокруг мгновенной оси, то в качестве величин, характеризующих это движение, можно ввести мгновенную угловую скорость и мгновенное угловое ускорение вращения твердого тела вокруг неподвижной точки.
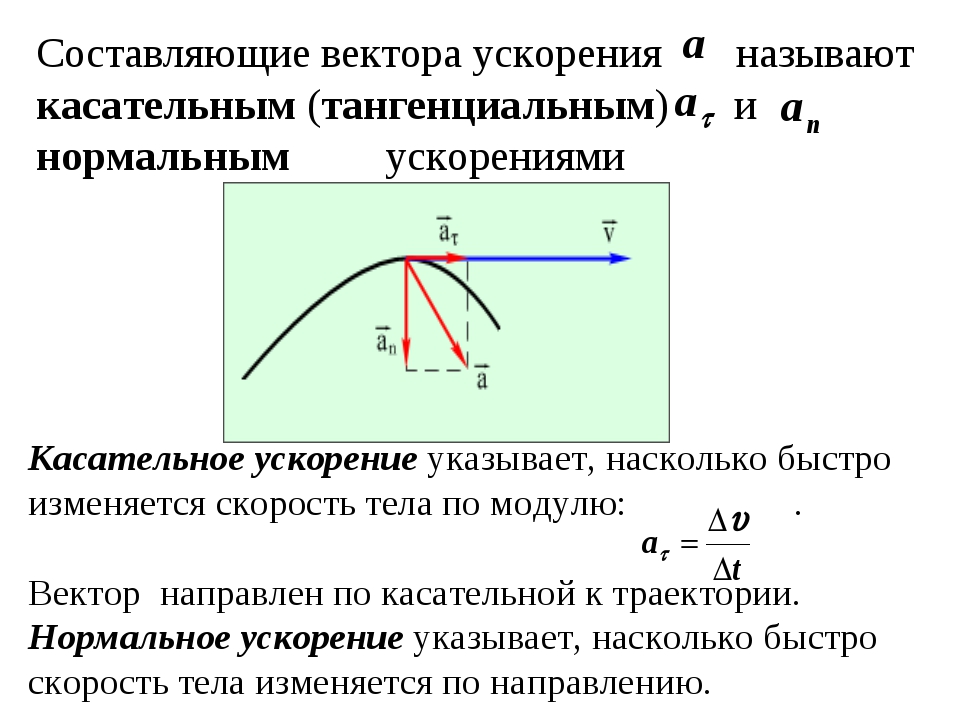 Очевидно, вводимая угловая скорость является векторной величиной, направленной в каждый момент времени по соответствующей мгновенной осп, и при
[c.171]
Очевидно, вводимая угловая скорость является векторной величиной, направленной в каждый момент времени по соответствующей мгновенной осп, и при
[c.171]Запись в виде векторного произведения особенно удобна для выражения угловой скорости и углового ускорения вращающегося тела. Мы видели, что повороты на конечный угол не являются векторами, потому что два таких поворота не подчиняются закону сложения векторов. Но угловая скорость, по определению, представляет собой предел отношения бесконечно малого угла поворота к бесконечно малому интервалу времени, за который происходит этот поворот. Порядок, в котором совершаются два бесконечно малых поворота, не влияет на окончательное положение предмета, если исключить слагаемые такого же порядка малости, как квадрат величины бесконечно малых поворотов, а эти слагаемые исчезают при соответствующем переходе к пределу. В одной из последующих глав мы докажем это и рассмотрим элементарную динамику вращающихся тел.
[c. 62]
62]
Угловая скорость и угловое ускорение твердого тела, вращающегося вокруг неподвижной оси, как векторы. Чтобы получить векторные формулы, определяющие векторы скорости и ускорения точек вращающегося вокруг неподвижной оси твердого тела, условились изображать угловую скорость этого тела вектором. Модуль вектора ш, изображающего угловую скорость тела, считают равным абсолютной величине угловой скорости тела, т. е. (о = 9 . При этом вектор ш откладывают по оси вращения так, чтобы наблюдатель, смотрящий с конца этого вектора в сторону его начала, видел вращение тела совершающимся против движения часовой стрелки (правило правого винта). Что касается начала вектора со, то оно может быть помещено в любой [c.298]
Это уравнение записано нами в скалярной форме. Однако для рассмотренного частного случая легко восстановить его векторный характер, рассматривая угловую скорость и угловое ускорение как векторы. Так как ось вращения постоянна, то вектор угловой скорости изменяется только по величине и, следовательно, вектор углового ускорения направлен по оси вращения. Вектор момента силы также направлен по оси вращения эти векторы совпадают по направлению, и мы можем написать уравнение моментов в следующем виде
[c.302]
Вектор момента силы также направлен по оси вращения эти векторы совпадают по направлению, и мы можем написать уравнение моментов в следующем виде
[c.302]
Линейная скорость и линейное ускорение являются векторными величинами. При вращательном движении угловая скорость и угловое ускорение однозначно определяются лишь тогда, когда известно положение оси вращения в пространстве и указано направление вращения вокруг нее. Поэтому угловую скорость и угловое перемещение определяют как векторы, направление которых связывается с направлением вращения. [c.24]
Поскольку угловая скорость — векторная величина, вектором должно быть и угловое ускорение. Но при вращении тела вокруг неподвижной оси мы обычно рассматриваем угловую скорость как [c.167]
Поскольку угловая скорость — векторная величина, вектором должно быть и угловое ускорение. Но при вращении тела вокруг неподвижной оси обычно рассматривают угловую скорость как скаляр и потому здесь нас могут интересовать только величина и знак углового ускорения. [c.57]
[c.57]
Так как движение тела, имеющего одну неподвижную точку, в каждый момент времени можно считать вращением вокруг мгновенной осп, то в качестве величин, характеризующих это движение, можно ввести Х гиовеииую угловую скорость и мгновенное угловое ускорение враще-JH H твердого тела вокруг неподвижной точки. Очевидно, вводимая угловая скорость является векторной величиной, направленной в каждый момент времени по соответствующей мгновенной оси, и при использовании правой системы координат вектор угловой скорости w направлен по мгновенной оси так, что с направления этого вектора видно вращение тела вокруг мгновенной оси, проис.ходящим против движения часовой стрелки. Величину вектора угловой скорости можно вырази гь через элементарный угол поворота Аф вокруг мгновенной оси за время ДЕ [c.168]
Формулы (8.6) и (8.10) определяют алгебраические величины угловой скорости и углового ускорения. Можно доказать, что угловая скорость и- угловое ускорение являются величинами векторными (рис. 1.104). Вращательное движение твердого тела в данный момент времени определяется вектором угловой скорости (й и вектором углового ускорения е. Вектор о направлен по оси вращения таким обррзом, что с его конца направление вращения наблюдается против движения часовой стрелки. Модуль этого вектора равен модулю производной угла поворота по времени 1 фМ I. Вектор углового ускорения е, так же как и ш, направлен по оси вращения. Если вращение ускоренное, то направления 0) и е совпадают, если замедленное — противоположны. Модуль вектора е равен модулю производной от угловой скорости по времени или модулю второй производной от угла поворота
[c.112]
1.104). Вращательное движение твердого тела в данный момент времени определяется вектором угловой скорости (й и вектором углового ускорения е. Вектор о направлен по оси вращения таким обррзом, что с его конца направление вращения наблюдается против движения часовой стрелки. Модуль этого вектора равен модулю производной угла поворота по времени 1 фМ I. Вектор углового ускорения е, так же как и ш, направлен по оси вращения. Если вращение ускоренное, то направления 0) и е совпадают, если замедленное — противоположны. Модуль вектора е равен модулю производной от угловой скорости по времени или модулю второй производной от угла поворота
[c.112]
Датчики кинематических величин. Датчиком называют измерительный пгеобра-зователь, переводящий измеряемую физическую величину в величину другого физического характера, чаще всего — электрическую. Датчики кинематических величин инерционного действия наиболее широко применяют для измерения кинематических величин точки и твердого тела — абсолютных перемещений, скоростей, ускорений и т. п. (см. гл. I, разделы 4 и 5). Как правило, датчики выполняют в виде отдельного конструктивного узла. Рассматриваемые датчики являются датчиками векторных величин и подразделяются на прямолинейные и угловые [18]. Прямолинейными называют датчики для измерения Ш1нематических величин, характеризующих движение точки тела (или всего тела при его поступательном движении) вдоль заданной датчиком прямой линии.
[c.135]
п. (см. гл. I, разделы 4 и 5). Как правило, датчики выполняют в виде отдельного конструктивного узла. Рассматриваемые датчики являются датчиками векторных величин и подразделяются на прямолинейные и угловые [18]. Прямолинейными называют датчики для измерения Ш1нематических величин, характеризующих движение точки тела (или всего тела при его поступательном движении) вдоль заданной датчиком прямой линии.
[c.135]
Система аэродинамических сил, действующих на ракету, характеризуется результирующей силой и результирующим моментом Мл относительно точк G. Для заданной геометрической конфигурации и при данных плотности и температуре воздуха в классической механике полета величины и являются вектор-функциями скорости V, угловой скорости вращения Q и абсолютного ускорения (dV/dOae . без существенной ошибки можно пренебречь влиянием ускорения, однако тогда необходимо интерпретировать вектор-функции переменных V и Q как сечения векторного пространства при равном нулю абсолютном ускорении (dV/d/)a6 , но не как сечения при равном нулю относительном ускорении Проекции (X, Y, Z) вектора R и (L, М, N)
[c. 127]
127]
Проанализируем, можно ли решить это векторное уравнение. Так как необходимые линейные и угловые скорости определены, то абсолютные величины нормальных ускорений, а также ускорение Кариолиса определяются. Направления всех ускорений известны (для ускорения Кариолиса см. рис. 19, в). [c.43]
УСКОРЕНИЕ – это… Что такое УСКОРЕНИЕ?
УСКОРЕНИЕ — (1) материальной точки векторная величина а, характеризующая быстроту изменения с течением времени вектора скорости v (см. (1)) точки: Согласно второму закону Ньютона (см.), ускорение прямо пропорционально результирующей механической силе F,… … Большая политехническая энциклопедия
УСКОРЕНИЕ — УСКОРЕНИЕ, величина, характеризующая быстроту изменения вектора скорости точки по его численному значению и направлению. При прямолинейном движении среднее ускорение равно отношению приращения скорости Dv к промежутку времени Dt, за который это… … Современная энциклопедия
УСКОРЕНИЕ — величина, характеризующая быстроту изменения вектора скорости точки по его численному значению и направлению. При прямолинейном движении среднее ускорение равно отношению приращения скорости ?v к промежутку времени ?t, за который это приращение… … Большой Энциклопедический словарь
При прямолинейном движении среднее ускорение равно отношению приращения скорости ?v к промежутку времени ?t, за который это приращение… … Большой Энциклопедический словарь
УСКОРЕНИЕ — УСКОРЕНИЕ, величина, на которую увеличивается СКОРОСТЬ предмета за определенный отрезок времени. Например, скорость камня, сброшенного со скалы, увеличивается от нуля с ускорением 9,81 м в секунду за секунду за счет действия силы земного… … Научно-технический энциклопедический словарь
УСКОРЕНИЕ — УСКОРЕНИЕ, ускорения, мн. нет, ср. 1. Действие по гл. ускорить ускорять. Ускорение темпа развития строительства. Необходимо ускорение доставки телеграмм. 2. Действие по гл. ускориться ускоряться. Ускорение хода поезда. 3. Величина изменения… … Толковый словарь Ушакова
Ускорение — термин, введенный в теорию русского стихосложения А. Белым («Символизм», М., 1910) для обозначения пропуска в стихе одного из предусмотренных данным размером ударений, т. е. ипостасы (см.), пиррихием в двусложных размерах и трибрахием в… … Литературная энциклопедия
е. ипостасы (см.), пиррихием в двусложных размерах и трибрахием в… … Литературная энциклопедия
ускорение — убыстрение, форсирование, учащение, увеличение быстродействия; стретто, акцелерация, приближение, катализация, форсировка, спурт, педалирование. Ant. торможение, остановка Словарь русских синонимов. ускорение / движения, темпа: убыстрение (разг.) … Словарь синонимов
УСКОРЕНИЕ — УСКОРЕНИЕ, я, ср. 1. см. ускорить, ся. 2. В физике: величина возрастания скорости движения в единицу времени. Единица ускорения. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
УСКОРЕНИЕ — «УСКОРЕНИЕ», СССР, киностудия ИМ. А.ДОВЖЕНКО, 1984, цв. Кинороман. По мотивам романа Павло Загребельного «Разгон». Герой фильма директор НИИ, ученый кибернетик Петро Карналь. Картина построена как ретроспектива воспоминаний героя о военной юности … Энциклопедия кино
Ускорение — (Acceleration, Beschleanigung) У. есть величина, котораявыражает быстроту изменения скорости, как по величине, так и понаправлению. Изменение скорости движения точки в течение промежуткавремени от момента t до момента t1, есть геометрическая… … Энциклопедия Брокгауза и Ефрона
есть величина, котораявыражает быстроту изменения скорости, как по величине, так и понаправлению. Изменение скорости движения точки в течение промежуткавремени от момента t до момента t1, есть геометрическая… … Энциклопедия Брокгауза и Ефрона
Ускорение создания профилей для трехмерного векторного видео с помощью GPGPU | Цыганов
1. Thorsten Scheuermann, Justin Hensley. Efficient histogram Generation Using Scattering on GPUs. Proceedings of the 2007 symposium on Interactive 3D graphics and games, ACM New York, NY, USA, 2007, pp. 33-37. doi: 10.1145/1230100.1230105
2. N. Cornelis, L. Van Gool. Fast Scale Invariant Feature Detection and Matching on Programmable Graphics Hardware. IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, 2008, pp. 1-8. doi: 10.1109/CVPRW.2008. 4563087
4563087
3. N. K. Govindaraju, E. S. Larsen, J. Gray, D. Manocha. A memory model for scientific algorithms on graphics processors. Proceedings of the ACM/IEEE Conference on Supercomputing (SC’06), NY, USA: ACM Press, 2006, no. 89, pp. 6-15. doi: 10.1109/SC.2006.2
4. V. Podlozhnyuk. Histogram calculation in CUDA. Technical report. NVIDIA, 2007, http://developer.download.nvidia.com/compute/cuda/1.1-Beta/x86_website/projects/histogram64/doc/histogram.pdf
5. Ramtin Shams, R. A. Kennedy. Efficient Histogram Algorithms for NVIDIA CUDA Compatible Devices. Australia, Gold Coast, ICSPCS, 2007. pp. 418-422.
6. Cedric Nugteren, Gert-Jan van den Braak, Henk Corporaal, Bart Mesman. High Performance Predictable Histogramming on GPUs: Exploring and Evaluating Algorithm Trade-offs. Proceedings of the Fourth Workshop on General Purpose Processing on Graphics Processing Units, NY, USA: ACM New York, 2011. pp. 1-9. doi: 10.1145/1964179.1964181
Proceedings of the Fourth Workshop on General Purpose Processing on Graphics Processing Units, NY, USA: ACM New York, 2011. pp. 1-9. doi: 10.1145/1964179.1964181
7. O. Fluck, S. Aharon, D. Cremers, M. Rousson. GPU histogram computation. ACM SIGGRAPH 2006 Research posters, SIGGRAPH ’06. ACM, 2006, p. 53. doi: 10.1145/1179622.1179683
8. Adityo Mahardito, Adang Suhendra, Deni Tri Hasta. Optimizing Parallel Reduction In Cuda To Reach GPU Peak Performance. Proceedings of The Second International Workshop on Open source and Open Content WOSOC 2010, Indonesia, Depok.: Gunadarma University, 2010, pp. 48-57.
9. Herbert Bay, Andreas Ess, Tinne Tuytelaars, Luc Van Gool. Speeded-Up Robust Features (SURF). Computer Vision and Image Understanding, New York, USA, 2008, vol. 110, no. 3, pp. 346-359. doi: 10.1016/j.cviu.2007.09.014
110, no. 3, pp. 346-359. doi: 10.1016/j.cviu.2007.09.014
10. Timothy B. Terriberry, Lindley M. French, John Helmsen. GPU Accelerating Speeded-Up Robust Features. Proceedings of the Fourth International Symposium on 3D Data Processing, Visualization and Transmission, Georgia Institute of Technology, Atlanta, GA, USA, 2008. pp. 355-362.
Разгон
Последняя математическая величина, обсуждаемая в Уроке 1, – это ускорение. Часто путают, что ускорение имеет значение, сильно отличающееся от значения, которое ассоциируется с ним спортивными комментаторами и другими людьми. Определение ускорения:
- Ускорение – это векторная величина, которая определяется как скорость, с которой объект изменяет свою скорость. Объект ускоряется, если он меняет свою скорость.
Спортивные комментаторы иногда говорят, что человек ускоряется, если он / она быстро движется. Однако ускорение не имеет ничего общего с быстрым движением. Человек может двигаться очень быстро, но при этом не ускоряться. Ускорение связано с изменением скорости движения объекта. Если объект не меняет свою скорость, значит, объект не ускоряется. Данные справа представляют движущийся на север ускоряющийся объект. Скорость меняется с течением времени. Фактически, скорость изменяется на постоянную величину – 10 м / с – каждую секунду. Каждый раз, когда скорость объекта изменяется, объект считается ускоряющимся; у него есть ускорение.
Однако ускорение не имеет ничего общего с быстрым движением. Человек может двигаться очень быстро, но при этом не ускоряться. Ускорение связано с изменением скорости движения объекта. Если объект не меняет свою скорость, значит, объект не ускоряется. Данные справа представляют движущийся на север ускоряющийся объект. Скорость меняется с течением времени. Фактически, скорость изменяется на постоянную величину – 10 м / с – каждую секунду. Каждый раз, когда скорость объекта изменяется, объект считается ускоряющимся; у него есть ускорение.
Значение постоянного ускорения
Иногда ускоряющийся объект меняет свою скорость на одну и ту же величину каждую секунду. Как упоминалось в предыдущем абзаце, приведенная выше таблица данных показывает, что объект меняет свою скорость на 10 м / с каждую последующую секунду. Это называется постоянным ускорением, поскольку скорость изменяется на постоянную величину каждую секунду. Не следует путать объект с постоянным ускорением с объектом с постоянной скоростью. Не дайте себя обмануть! Если объект меняет свою скорость – на постоянную или переменную величину – то это ускоряющийся объект. И объект с постоянной скоростью не ускоряется. Приведенные ниже таблицы данных отображают движения объектов с постоянным ускорением и изменяющимся ускорением. Обратите внимание, что каждый объект имеет изменяющуюся скорость.
Не дайте себя обмануть! Если объект меняет свою скорость – на постоянную или переменную величину – то это ускоряющийся объект. И объект с постоянной скоростью не ускоряется. Приведенные ниже таблицы данных отображают движения объектов с постоянным ускорением и изменяющимся ускорением. Обратите внимание, что каждый объект имеет изменяющуюся скорость.
Поскольку ускоряющиеся объекты постоянно меняют свою скорость, можно сказать, что пройденное расстояние / время не является постоянной величиной.Например, падающий объект обычно ускоряется при падении. Если бы мы наблюдали движение свободно падающего объекта (движение свободного падения будет подробно обсуждено позже), мы бы заметили, что объект имеет среднюю скорость примерно 5 м / с в первую секунду, примерно 15 м / с. во второй секунде примерно 25 м / с в третью секунду, примерно 35 м / с в четвертую секунду и т. д. Наш свободно падающий объект будет постоянно ускоряться. Учитывая эти средние значения скорости в течение каждого последовательного временного интервала в 1 секунду, мы могли бы сказать, что объект упадет на 5 метров в первую секунду, 15 метров во вторую секунду (для общего расстояния 20 метров), 25 метров в третью. второй (для общей дистанции 45 метров), 35 метров в четвертой секунде (для общей дистанции 80 метров через четыре секунды).Эти числа приведены в таблице ниже.
второй (для общей дистанции 45 метров), 35 метров в четвертой секунде (для общей дистанции 80 метров через четыре секунды).Эти числа приведены в таблице ниже.
| Время Интервал | Изменение скорости В течение интервала | пр. Скорость В течение интервала | Пройденное расстояние В течение интервала | Общее пройденное расстояние с От 0 с до конца интервала |
| 0 – 1.0 с | от 0 до ~ 10 м / с | ~ 5 м / с | ~ 5 м | ~ 5 м |
| 1,0 – 2,0 с | ~ 10-20 м / с | ~ 15 м / с | ~ 15 м | ~ 20 м |
| 2,0 – 3,0 с | ~ от 20 до 30 м / с | ~ 25 м / с | ~ 25 м | ~ 45 м |
3,0 – 4. 0 с 0 с | ~ 30-40 м / с | ~ 35 м / с | ~ 35 м | ~ 80 м |
Примечание. Используемый здесь символ ~ означает приблизительно.
Это обсуждение показывает, что свободно падающий объект, который ускоряется с постоянной скоростью, будет преодолевать разные расстояния за каждую последующую секунду. Дальнейший анализ первого и последнего столбцов приведенных выше данных показывает, что существует квадратная зависимость между общим пройденным расстоянием и временем путешествия для объекта, начинающегося из состояния покоя и движущегося с постоянным ускорением.2) расстояние; расстояние, пройденное за четыре секунды, в 16 раз превышает расстояние, пройденное за одну секунду. Для объектов с постоянным ускорением расстояние перемещения прямо пропорционально квадрату времени перемещения.
Расчет среднего ускорения
Среднее ускорение (a) любого объекта за заданный интервал времени (t) может быть вычислено с помощью уравнения
Это уравнение можно использовать для расчета ускорения объекта, движение которого отражено приведенной выше таблицей данных скорость-время. Данные скорости-времени в таблице показывают, что объект имеет ускорение 10 м / с / с. Расчет показан ниже.
Данные скорости-времени в таблице показывают, что объект имеет ускорение 10 м / с / с. Расчет показан ниже.
Значения ускорения выражаются в единицах скорости / времени. Типичные устройства ускорения включают следующее:
м / с / с
миль / час / с
км / час / с
м / с 2
Эти устройства могут показаться немного неудобными для начинающего студента-физика. Тем не менее, это очень разумные единицы, когда вы начинаете рассматривать определение и уравнение для ускорения.Причина появления единиц становится очевидной после изучения уравнения ускорения.
Поскольку ускорение – это изменение скорости во времени, единицы измерения ускорения – это единицы скорости, деленные на единицы времени, т.е. (м / с) / с или (миль / час) / с. Единицу измерения (м / с) / с можно математически упростить до м / с 2 .
Направление вектора ускорения
Поскольку ускорение является векторной величиной, с ним связано направление. Направление вектора ускорения зависит от двух вещей:
Направление вектора ускорения зависит от двух вещей:
- , ускоряется или замедляется объект
- , движется ли объект в + или – направлении
Общий принцип определения ускорения:
Если объект замедляется, то его ускорение происходит в направлении, противоположном его движению.
Этот общий принцип может применяться для определения того, является ли знак ускорения объекта положительным или отрицательным, вправо или влево, вверх или вниз и т. Д.Рассмотрим две таблицы данных ниже. В каждом случае ускорение объекта происходит в положительном направлении . В примере A объект движется в положительном направлении (то есть имеет положительную скорость ) и ускоряется. Когда объект ускоряется, ускорение совпадает с направлением скорости. Таким образом, этот объект имеет положительное ускорение. В примере B объект движется в отрицательном направлении (т. Е. Имеет отрицательную скорость) и замедляется. Согласно нашему общему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект также имеет положительное ускорение.
Согласно нашему общему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект также имеет положительное ускорение.
Тот же самый общий принцип может быть применен к движению объектов, представленных в двух таблицах данных ниже. В каждом случае ускорение объекта происходит в отрицательном направлении . В примере C объект движется в положительном направлении (т.е.е., имеет положительную скорость ) и замедляется. Согласно нашему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект имеет отрицательное ускорение. В Примере D объект движется в отрицательном направлении (т. Е. Имеет отрицательную скорость ) и ускоряется. Когда объект ускоряется, ускорение совпадает с направлением скорости. Таким образом, этот объект также имеет отрицательное ускорение.
Обратите внимание на использование положительных и отрицательных слов в приведенном выше обсуждении (Примеры A – D). В физике использование положительного и отрицательного всегда имеет физический смысл. Это больше, чем просто математический символ. Положительное и отрицательное, используемые здесь для описания скорости и ускорения движущегося объекта, описывают направление. И скорость, и ускорение являются векторными величинами, и полное описание величины требует использования прилагательного направленного действия.Север, юг, восток, запад, вправо, влево, вверх и вниз – все прилагательные направленного действия. Физика часто заимствует из математики и использует символы + и – как направленные прилагательные. В соответствии с математическим соглашением, используемым в числовых линиях и графиках, положительное значение часто означает вправо или вверх, а отрицательное – влево или вниз. Таким образом, сказать, что объект имеет отрицательное ускорение, как в примерах C и D, означает просто сказать, что его ускорение идет влево или вниз (или в любом направлении, которое было определено как отрицательное).Отрицательные ускорения не относятся к значениям ускорения, которые меньше 0.
В физике использование положительного и отрицательного всегда имеет физический смысл. Это больше, чем просто математический символ. Положительное и отрицательное, используемые здесь для описания скорости и ускорения движущегося объекта, описывают направление. И скорость, и ускорение являются векторными величинами, и полное описание величины требует использования прилагательного направленного действия.Север, юг, восток, запад, вправо, влево, вверх и вниз – все прилагательные направленного действия. Физика часто заимствует из математики и использует символы + и – как направленные прилагательные. В соответствии с математическим соглашением, используемым в числовых линиях и графиках, положительное значение часто означает вправо или вверх, а отрицательное – влево или вниз. Таким образом, сказать, что объект имеет отрицательное ускорение, как в примерах C и D, означает просто сказать, что его ускорение идет влево или вниз (или в любом направлении, которое было определено как отрицательное).Отрицательные ускорения не относятся к значениям ускорения, которые меньше 0. Ускорение -2 м / с / с – это ускорение с величиной 2 м / с / с, которое направлено в отрицательном направлении.
Ускорение -2 м / с / с – это ускорение с величиной 2 м / с / с, которое направлено в отрицательном направлении.
Чтобы проверить свое понимание концепции ускорения, рассмотрите следующие проблемы и соответствующие решения. Используйте уравнение ускорения, чтобы определить ускорение для следующих двух движений.
4.)РС.
(a) Каковы составляющие x- и y положения и скорости лыжника как функции времени? (b) Каковы ее положение и скорость при t = 10,0 с?
Фигура 4. 10
Лыжник имеет ускорение 2,1 м / с22,1 м / с2 на спуске 15 ° 0,15 °. Начало системы координат находится в лыжной базе.
10
Лыжник имеет ускорение 2,1 м / с22,1 м / с2 на спуске 15 ° 0,15 °. Начало системы координат находится в лыжной базе.Стратегия
Поскольку мы оцениваем компоненты уравнений движения в направлениях x и y , нам нужно найти компоненты ускорения и поместить их в кинематические уравнения.Компоненты ускорения находятся в системе координат на рисунке 4.10. Затем, вставив компоненты начального положения и скорости в уравнения движения, мы можем найти ее положение и скорость в более позднее время t .Решение
(a) Начало системы координат находится на вершине холма с осью y- вертикально вверх и осью x- горизонтально. Глядя на траекторию лыжника, можно увидеть, что составляющая ускорения x- положительна, а составляющая y- отрицательна.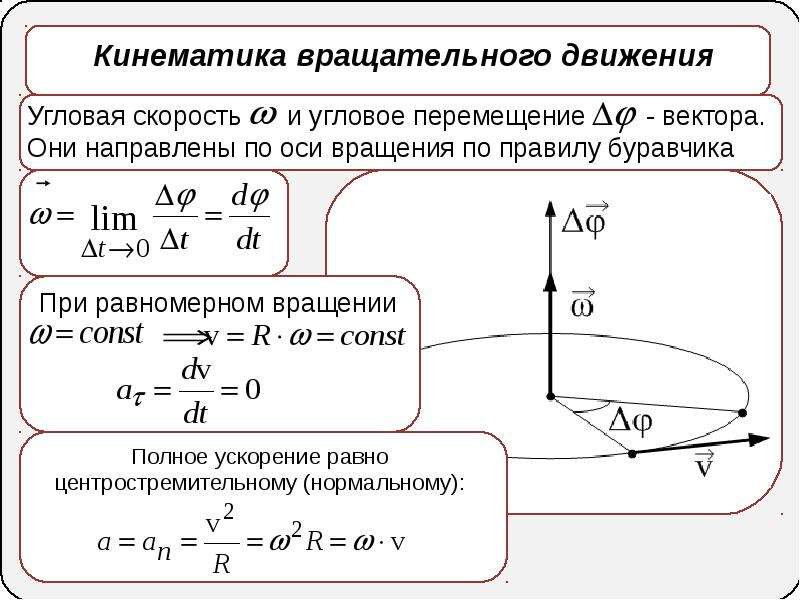 Поскольку угол составляет 15 ° 15 ° вниз по склону, находим ax = (2,1 м / с2) cos (15 °) = 2,0 м / с2ax = (2,1 м / с2) cos (15 °) = 2,0 м / с2 ay = (- 2,1 м / с2) sin15 ° = −0,54 м / с2.ay = (- 2,1 м / с2) sin15 ° = −0,54 м / с2.
Поскольку угол составляет 15 ° 15 ° вниз по склону, находим ax = (2,1 м / с2) cos (15 °) = 2,0 м / с2ax = (2,1 м / с2) cos (15 °) = 2,0 м / с2 ay = (- 2,1 м / с2) sin15 ° = −0,54 м / с2.ay = (- 2,1 м / с2) sin15 ° = −0,54 м / с2.Подставляя начальное положение и скорость в уравнение 4.12 и уравнение 4.13 для x , получаем
x (t) = 75,0 м + (4,1 м / с) t + 12 (2,0 м / с2) t2x (t) = 75,0 м + (4,1 м / с) t + 12 (2,0 м / с2) t2 vx (t) = 4,1 м / с + (2,0 м / с2) t.vx (t) = 4,1 м / с + (2,0 м / с2) t.Для у имеем
y (t) = – 50,0 м + (- 1,1 м / с) t + 12 (-0,54 м / с2) t2y (t) = – 50.0m + (- 1,1 м / с) t + 12 (-0,54 м / с2) t2 vy (t) = – 1,1 м / с + (- 0,54 м / с2) t.vy (t) = – 1,1 м / с + (- 0,54 м / с2) t.(b) Теперь, когда у нас есть уравнения движения для x и y как функции времени, мы можем оценить их как t = 10,0 с:
x (10,0 с) = 75,0 м + (4,1 м / с2) (10,0 с) +12 (2,0 м / с2) (10,0 с) 2 = 216,0 м x (10,0 с) = 75,0 м + (4,1 м / с2) (10,0 с ) +12 (2,0 м / с2) (10,0 с) 2 = 216,0 м vx (10,0 с) = 4,1 м / с + (2,0 м / с2) (10,0 с) = 24,1 м / svx (10,0 с) = 4,1 м / с + (2,0 м / с2) (10,0 с) = 24,1 м / с y (10,0 с) = – 50,0 м + (- 1,1 м / с) (10,0 с) +12 (−0.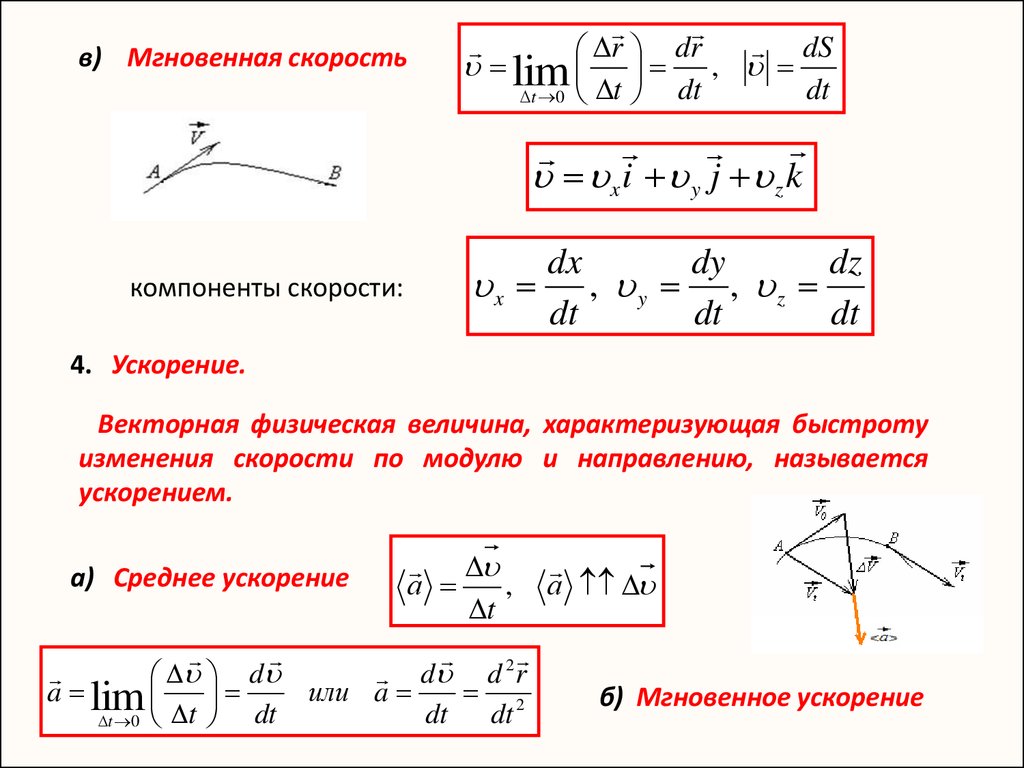 )РС.
)РС.Величина скорости лыжника на 10,0 с составляет 25 м / с, что составляет 60 миль / ч.
Значение
Полезно знать, что, учитывая начальные условия положения, скорости и ускорения объекта, мы можем найти положение, скорость и ускорение в любое более позднее время.Векторная скорость и векторное ускорение
Векторная скорость и векторное ускорениеследующий: Движение с постоянной скоростью Up: Движение в 3-х измерениях Предыдущая: Диагонали параллелограмма Представьте себе тело, движущееся в трех измерениях.Предположим, что мы знаем декартово координаты“ и этого тела с течением времени“. Давайте рассмотрим, как мы можем использовать эту информацию для определения мгновенного скорость и ускорение как функции времени.
Векторное смещение тела определяется выражением
| (43) |
По аналогии с одномерным уравнением (13) тело векторная скорость является просто производной от по .
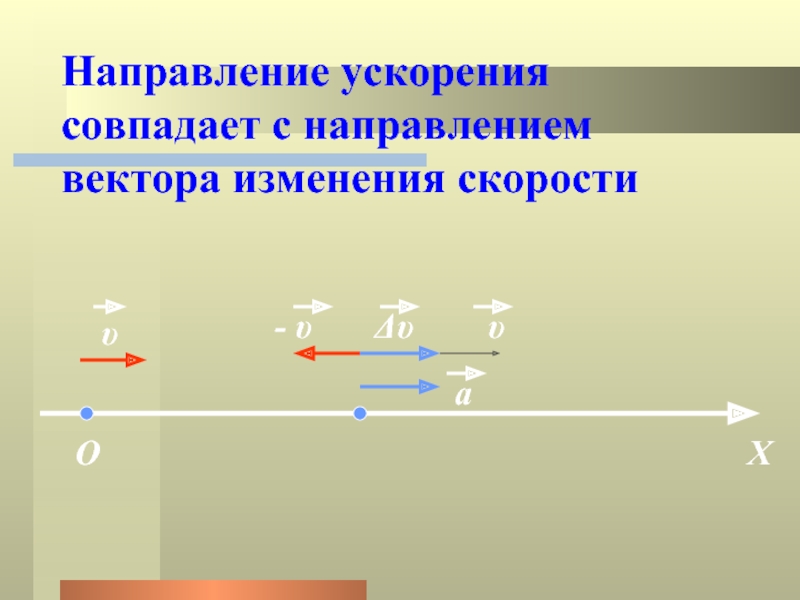 Другими словами,
Другими словами, | (44) |
При написании в форме компонентов приведенное выше определение дает
Таким образом, -компонента скорости – это просто производная по времени от -координаты, и так далее.
По аналогии с одномерным уравнением (16)
векторное ускорение
является просто производной от по
. Другими словами,
| (48) |
При написании в форме компонентов приведенное выше определение дает
Таким образом, -компонент ускорения – это просто производная по времени -компоненты скорости и т. д.
В качестве примера предположим, что координаты тела задаются следующим образом:
Соответствующие компоненты скорости тела тогда просто
в то время как компоненты ускорения тела даются
следующий: Движение с постоянной скоростью Up: Движение в 3-х измерениях Предыдущая: Диагонали параллелограмма Ричард Фицпатрик 2006-02-02
Разгон
Разгон Разгон : Ускорение – это скорость изменения скорости. Поскольку скорость имеет как величину, так и направление, она называется
векторная величина; ускорение также является векторной величиной и должно
учитывать изменения как в величине, так и в направлении
скорость. Скорость точки или объекта, движущегося по прямой.
путь может изменяться только по величине; на изогнутом пути, это может или может
не меняется по величине, но всегда будет меняться по направлению. Этот
условие означает, что ускорение точки, движущейся по криволинейной
путь никогда не может быть нулевым.
Поскольку скорость имеет как величину, так и направление, она называется
векторная величина; ускорение также является векторной величиной и должно
учитывать изменения как в величине, так и в направлении
скорость. Скорость точки или объекта, движущегося по прямой.
путь может изменяться только по величине; на изогнутом пути, это может или может
не меняется по величине, но всегда будет меняться по направлению. Этот
условие означает, что ускорение точки, движущейся по криволинейной
путь никогда не может быть нулевым.
Если скорость точки, движущейся по прямому пути, увеличивается
(я.е., если скорость, которая является величиной скорости, равна
увеличивается), вектор ускорения будет иметь то же направление, что и
вектор скорости. Если скорость уменьшается (т. Е.
точка или объект замедляется), вектор ускорения будет указывать
в обратном направлении. Среднее ускорение за время
интервал равен полному изменению скорости за время
интервал, деленный на временной интервал. Ускорение при любом
момент равен пределу отношения изменения скорости к
длина временного интервала, по мере приближения временного интервала
нуль.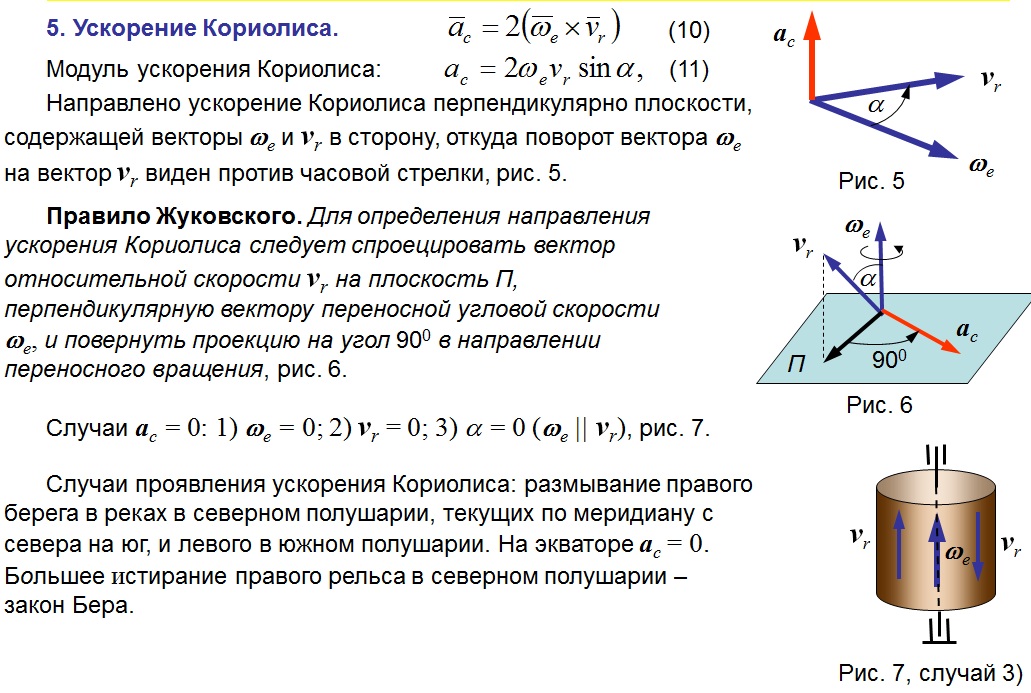
Когда точка движется по изогнутой траектории, компонент ускорение, возникающее в результате изменения направления движения Вектор скорости перпендикулярен вектору скорости и равен направлен внутрь, на вогнутую сторону дорожки; его величина дается квадратом скорости, деленной на радиус кривизна r пути: v 2 / r. Изменение величины of v может быть представлен другим вектором (то есть вторым компонент ускорения) коллинеарны v и в том же направление, если v увеличивается, и противоположное направление, если v равно уменьшается.Если скорость указана в метрах в секунду, ускорение будут указаны в метрах в секунду в секунду.
Выдержка из Британской энциклопедии без разрешения.
Выдержка из Британской энциклопедии без разрешения.
векторов: скорости, ускорения и силы
векторов: скорости, ускорения и силывекторов: скорости,
ускорения и силы
Чтобы понять открытия Ньютона, мы должны иметь
понимание трех основных величин: (1) скорость, (2) ускорение,
и (3) сила. В этом разделе мы определяем первые два, а в следующем мы
введем силы. У этих трех величин есть общая черта: они
математики называют векторами .
В этом разделе мы определяем первые два, а в следующем мы
введем силы. У этих трех величин есть общая черта: они
математики называют векторами .
Примеры скалярных величин
Векторы – это величины, которые требуют не только величины, но и направления на укажите их полностью. Проиллюстрируем это, приведя сначала несколько примеров количества, не являющиеся векторами. Количество галлонов бензина в топливе бак вашего автомобиля является примером количества, которое может быть указано единственное число — нет смысла говорить о “направлении”, связанном с количество бензина в баке.Такие количества, которые могут быть указаны дающие единственное число (в соответствующих единицах), называются скалярами . Другие примеры скалярных величин включают температуру, ваш вес, или население страны; это скаляры, потому что они полностью определяется одним числом (с соответствующими единицами измерения).Примеры векторных величин
Однако рассмотрим скорость. Если мы говорим, что машина едет со скоростью 70 км / час, мы не уточнили полностью его движение, потому что мы не указали направление , которое идет.Таким образом, скорость – это пример вектора количество. Для определения вектора обычно требуется более одного числа; в в этом примере мы могли бы указать величину скорости (70 км / час), направление по компасу, чтобы указать направление (скажем, 30 градусов от севера), и число, обозначающее вертикальный угол по отношению к поверхности Земли (ноль градусов, кроме сцен погони из боевиков!). Соседняя фигура показывает типичную систему координат для задания вектора в терминах длина r и два углы, theta и phi .Графическое представление векторов
Векторы часто отличаются от скалярных величин, поместив маленькую стрелку над величиной или написание количества жирным шрифтом. Также принято указывать вектор нарисовав стрелку, длина которой пропорциональна величине вектор, и направление которого определяет ориентацию вектора. На соседнем изображении мы показываем графические представления для
три вектора. Векторы A и C имеют одинаковые
величина, но разные направления.Вектор B имеет ту же ориентацию, что и
вектор A, но имеет вдвое большую величину. Каждый из них представляет
другой вектор, потому что для того, чтобы два вектора были эквивалентными, они должны иметь и одинаковые величины и ориентации.
Скорость и ускорение
Дадим теперь точное определение скорости и ускорения. Они есть векторы, поэтому мы должны указать для них величину и направление. В скорость v и ускорение a определены в следующих иллюстрация Эта иллюстрация также графически демонстрирует, что скорость (и, следовательно, ускорение) – вектор: направление скорости породы, безусловно, представляет критический интерес для человек, стоящий под камнем на двух иллюстрациях!Равномерное круговое движение – это ускоренное движение
Обратите внимание, что скорость, которая является вектором, изменяется, если ее величина или его направление изменилось.Таким образом, ускорение возникает, когда величина или направление скорости (или оба) изменены. В частности, обратите внимание на соседнее изображение.
это круговое движение (даже при равномерном
угловая скорость) следует
постоянное ускорение, потому что направление скорости
(указывается направлением стрелки)
постоянно меняется, даже если его величина (обозначенная длиной
стрелка) постоянна. Этот момент, что
движение по криволинейной траектории – это ускоренное движение, будет
имеют решающее значение для нашего последующего понимания движения в гравитационном
поля.
Сколько ускорителей у вашей машины?
Имейте в виду, что в популярной речи ускорение речи считается увеличение величины скорости. Как мы только что видели, ускорение также происходит при изменении направления скорости, даже если величина постоянная; кроме того, в физике уменьшение скорость – это как ускорение, так и уменьшение. Таким образом, в вашей машине действительно не менее 3 ускорителя : (1) ножная педаль, называемая «акселератором», которая изменяет величину скорость, (2) тормоз, который также изменяет величину скорости, и (3) рулевое колесо, которое меняет направление скорости!Векторы положения, скорости и ускорения
Кинематика – это раздел механики, который описывает движение частиц, объектов или групп объектов.На этих страницах мы проанализируем движение точечной частицы по любой траектории, например, показанной черным на рисунке ниже. Для простоты на рисунке изображена плоская траектория, но она может быть трехмерной.
Опорный кадр , в состоянии покоя и наблюдатель O , расположенный в начале декартовой системы координат, также показаны на предыдущем рисунке. Этот опорный кадр называется инерциальным .Ориентация трех декартовых осей обозначена единичными векторами i , j и k соответственно. Опишем движение частицы относительно этой системы отсчета.
Обнаружен блокировщик рекламы
Знания бесплатны, а серверы – нет. Пожалуйста, поддержите нас, отключив блокировку рекламы на YouPhysics. Спасибо!
Движение частицы описывается тремя векторами: положение , скорость и ускорение .
Вектор положения (обозначен зеленым на рисунке) идет от начала координат системы отсчета к положению частицы. Декартовы компоненты этого вектора даются по формуле:
Компоненты вектора положения зависят от времени , поскольку частица находится в движении. Для упрощения обозначений мы часто опускаем эту зависимость в выражениях векторов.
Вектор скорости – это производная по времени вектора положения:
Что также может быть выражено как:
Вектор скорости всегда касается траектории частицы в каждой точке .
Вектор ускорения является производной по времени вектора скорости:
Что также может быть выражено как:
Вектор ускорения – это изменение вектора скорости во времени. Следовательно, он всегда должен быть направлен внутрь траектории частицы, как показано на рисунке.
На этих страницах вы найдете множество задач, в которых вы научитесь вычислять эти три вектора в различных ситуациях.
Обнаружен блокировщик рекламы
Знания бесплатны, а серверы – нет. Пожалуйста, поддержите нас, отключив блокировку рекламы на YouPhysics. Спасибо!
Вектор ускорения может быть выражен как функция его проекций на систему отсчета, движущуюся вместе с частицей, и с осями, которые являются соответственно касательными и перпендикулярными (или нормальными) для каждой точки ее траектории. Эти проекции называются тангенциальным ускорением и нормальным ускорением (или центростремительным).
На предыдущем рисунке представлен вектор ускорения, выраженный как сумма этих компонентов.
Тангенциальное ускорение определяется по формуле:
Где u t – единичный вектор, касательный к пути в каждой точке, который определяется делением вектора скорости на его величину:
Тангенциальное ускорение дает информацию об изменении величины вектора скорости.
С другой стороны, нормальное ускорение (или центростремительное) определяется по формуле:
Где u n – единичный вектор, перпендикулярный траектории в каждой точке, а ρ – радиус кривизны траектории.
Нормальное ускорение дает информацию об изменении направления вектора скорости. Если частица описывает прямую линию, радиус кривизны бесконечен и, следовательно, ее нормальное ускорение равно нулю.
В частном случае круговой траектории нормальная величина ускорения составляет:
Различные задачи, которые вы найдете на этих страницах, помогут вам научиться вычислять компоненты вектора ускорения.
Пост-векторы положения, скорости и ускорения впервые появились на YouPhysicsDisplacement, Velocity, Acceleration
.Мы живем в мире, который определяется тремя пространственными измерениями и одним измерение времени.Объекты перемещаются в этом домене двумя способами. Объект переводит , или меняет расположение , с одного указать на другое. И объект вращается, или меняет ориентацию на . В общем, движение объекта включает оба перевода во всех три направления, и вращение вокруг три основных оси.
На этой странице мы будем рассматривать только перевод объекта. Мы можем указать местоположение объекта по адресу в любой момент t , указав три координаты x, y, и z в ортогональной системе координат.An ортогональная система координат имеет каждый его координатных направлений перпендикулярно всем остальным координатным направлениям. Изначально наш объект находится в точке «0» с координатами x0, y0, и z0 в момент времени t0 . Как правило, объект перемещается по домену до тех пор, пока через некоторое время t1 объект находится в точке “1” с координатами x1, y1, и z1 . Мы можем указать смещение – d в каждом координатном направлении по разнице координат от точки «0» до точки «1».Х-смещение равно (x1 – x0), смещение по оси y равно (y1 – y0), а смещение по оси z равно (z1 – z0). На этой веб-странице для простоты мы будем рассматривать только координату x. Смещение тогда определяется по формуле:
d = x1 – x0
Смещение – это векторная величина, означающая, что смещение имеет размер и направление, связанные с ним. Направление – от точки “0” до точка «1».Отдельные смещения x-, y-, и z- являются составные части вектора смещения в координатных направлениях. Все величины, полученные из смещения, также являются векторными величинами.скорость -V объекта через область это изменение местоположения относительно времени. В направлении X средняя скорость – это смещение, разделенное по временному интервалу:
V = (x1 – x0) / (t1 – t0)
Это просто средняя скорость, и объект может ускоряться и замедляться между точками «0» и «1».В любой момент объект может иметь скорость, отличную от средней. Если мы сократим разница во времени вплоть до очень маленького (дифференциального) размера, мы можем определить мгновенная скорость – разница в изменении положения, деленная на дифференциальное изменение во времени;
V = dx / dt
где символ d / dt – это дифференциал от исчисления. (Для младших школьников: у вас только что был первый урок математического анализа !.. это было не так уж плохо, правда? Если это не имеет смысла, не волнуйтесь и просто продолжайте чтение .. будет иметь смысл через несколько лет.)
Когда мы изначально укажите местоположение нашего объекта с x0, y0, z0, и t0 координаты, мы также должны указать начальную мгновенную скорость V0 . Точно так же в конечная позиция x1, y1, z1, и t1 , скорость изменится на скорость V1 .Опять же, для простоты, мы рассматриваем только x-компоненту скорости. На самом деле скорость меняется во всех трех направлениях. Скорость это векторная величина и имеет как величину, так и направление. Направление совпадает с направлением смещения, от которого мы определили скорость.
Ускорение (a) объекта через область – это изменение скорости по времени. В направлении X среднее ускорение – это изменение скорости деленное на временной интервал:
а = (V1 – V0) / (t1 – t0)
Как и в случае со скоростью, это только среднее ускорение.В любой момент объект может иметь ускорение, отличное от среднего. Если мы сократим разница во времени вплоть до очень маленького (дифференциального) размера, мы можем определить мгновенное ускорение – изменение разности скорости, деленное на в дифференциальное изменение во времени:
а = dv / dt
Из Ньютона второй закон движения, мы знаем, что силы, действующие на объект, вызывают ускорение.Если мы можем определить силы, действующие на объект, и то, как силы меняются со временем, мы можем использовать уравнения, представленные на этом слайде, для определения ускорения, скорости, смещения и, следовательно, местоположение объекта как функция времени. Авиационные инженеры используют эту информацию для прогнозирования движение самолета или полет ракеты.
Действия:
Экскурсии с гидом
Навигация..
- Руководство для начинающих Домашняя страница
