Time warp/ru – Kerbal Space Program Wiki
3 зеленые стрелки указывают на 10× ускорение времени без учета законов физики.
Ускорение времени (англ. “Time warp”) в игре Космическая Программа Кербала позволяет игроку ускорять время, например, во время долгих включений двигателей на низкой тяге или межпланетных перелетов. Стрелочки в левом верхнем углу экрана, около “Текущей Продолжительностью Миссии” (англ. “MET”) указывают активный коэффициент ускорения времени. По-умолчанию, ускорение времени увеличивается и уменьшается при помощи клавиш , и ., соответственно. При изменении фактора новый фактор ускорения времени показывается близко к центру экрана.
Contents
- 1 Ускорение времени с учетом законов физики
- 2 Ускорение времени без учета законов физики
- 3 Ускорение и Высота
- 4 Сравнение уровней сжатия времени
Ускорение времени с учетом законов физики
Контур из четырех уровней ускорения времени с учетом законов физики.
Ускорение времени с учетом законов физики (англ. “Physical time warp”) старается применять законы физики к существующим космическим кораблям, то есть вычисляются силы, такие как аэродинамическое сопротивление и тяга. При выполнении в нормальном (1x) игровом времени, к этому можно получить доступ в любое время, нажав клавиши Mod+. Так как эти вычисления очень сложны и следовательно создают тяжелую нагрузку на ЦП, то возможны только четыре различных коэффициента ускорения: 1× (по-умолчанию), 2×, 3× и 4×. Не рекомендуется использовать ускорение времени с учетом законов физики для самолетов, это создает дергание или разрушительные вибрации при полете.
Предупреждение: Ускорение времени с учетом законов физики может привести к погрешностям в вычислении физических величин, и может повредить космический корабль. Наиболее вероятно это в случае больших коэффициентов ускорения времени и в случае аппарата, содержащего в себе множество деталей. Во время взлёта также не рекомендуется ускорять время.
Ускорение времени при законах физики старается применять законы физики к космическим кораблям. Это занимает много процессоров, и по этому можно ускорять время только в 4 раза.
Ускорение времени без учета законов физики
Ускорение времени без учета законов физики (англ. “Non-physical time warp”)
- Космический аппарат находится в атмосфере (до тех пор, пока он не посажен и полностью не остановлен)
- Космический аппарат, у которого дроссель находится в отрытом (верхнем) положении, даже если у него нет двигателя или он не включен;
- Деталь создает момент вращения, подобно Системе Автоматической Стабилизации;
- Космический аппарат движется по поверхности, например, вращение планетохода.
Доступны следующие коэффициенты (факторы) ускорения времени: 1x (по-умолчанию), 5×, 10×, 50×, 100×,1 000×, 10 000× и 100 000×. Однако, чтобы получить доступ к большим факторам, аппарату требуется определенное расстояние от тела, на орбите которого он находится. У каждого небесного тела есть свой собственный ссылочная структура, которая определяет высоту, на которой различные коэффициенты ускорения времени становятся доступными. Как, например, показанная в таблице ниже ссылочная структура Кербина.
Один побочный эффект ускорения времени без учета законов физики состоит в том, что после его активации космический корабль немедленно прекращает вращение, поскольку все детали заморожены относительно ссылочной структуры аппарата. В результате этого, любые соединения, которые были изогнуты при включении ускорения времени без учета законов физики, останутся изогнутыми во время ускорения, и будут резко распрямляться обратно при выключении режима ускорения (что иногда приводит к незапланированной быстрой разборке).
Существуют небесные тела, подобные Муну, которые позволяют ускорение времени при столкновении с поверхностью. Обычно, ускорение времени сбрасывается до 1×, когда аппарат находится близко к поверхности.
Другая опасность, особенно высоких коэффициентов ускорения времени – то, что аппарат перемещается настолько близко и быстро к небесному телу, что игра не распознает его и не уменьшает коэффициент ускорения времени. Поскольку орбитальная скорость при высшем коэффициенте при нахождении в перицентре, то аппарат также отдельно порождает быстрое перемещение, чтобы переместиться еще быстрее с ускорением времени. Это может привести к пропуску атмосферы без входа в атмосферу или получения неумышленной помощи гравитации.
Ускорение и Высота
Надо приобрести определённую высоту прежде чем ускорять время очень быстро:
| Ускорение Скорости | Минимальная Высота |
| 1x | Любая |
| 5x | 69 078 м. (Над атмосферой) |
| 10x | 69 078 м. (Над атмосферой) |
| 50x | 69 078 м. (Над атмосферой) |
| 100x | 120 000 м. |
| 1000x | 240 000 м. |
| 10000x | 480 000 м. |
| 100000x | 600 000 м. |
Сравнение уровней сжатия времени
В следующей таблице дано настоящее время для каждого пункта.
| Фактор сжатия времени | год Кербина | От Альфы Центавра (4.3 световых лет) до Земли со скоростью света | Земной день | |
|---|---|---|---|---|
| 1× | 6 ч. | 106 д. 12 ч. 32 м. 25 с. | 1603 д. | 24 ч. |
| 2× | 3 ч. | 53 д. 6 ч. 16 м. 12.5 с. | 801 д. 16 ч. 33 м. | 12 ч. |
| 3× | 2 ч. | 35 д. 12 ч. 10 м. 48.33 с. | 534 д. 11 ч. 2 м. | 8 ч. |
| 4× | 1 ч. 30 м. | 26 д. 15 ч. 8 м. 6.25 с. | 6 ч. | |
| 5× | 1 ч. 12 м. | 21 д. 7 ч. 18 м. 29 с. | 320 д. 16 ч. 13 м. | 4 ч. 48 м. |
| 10× | 36 м. | 10 д. 15 ч. 39 м. 14.5 с. | 160 д. 8 ч. 6 м. | 2 ч. 24 м. |
| 50× | 7 м. 12 с. | 2 д. 3 ч. 7 м. 50.9 с. | 32 д. 1 ч. 37 м. 17.75 с. | 28 м. 48 с. |
| 100× | 3 м. 36 с. | 1 д. 1 ч. 33 м. 55.45 с. | 16 д. 48 м. 38.87 с. | 14 м. 28 с. |
| 1 000× | 21.6 с. | 2 ч. 33 м. 23.55 с. | 1 д. 14 ч. 28 м. 51.89 с. | 1 м. 26.4 с. |
| 10 000× | 2.16 с. | 15 м. 20.35 с. | 3 ч. 50 м. 53.19 с. | 8.64 с. |
| 100 000× | 0.216 с. | 1 м. 32.04 с. | 23 м. 5.319 с. | 0.864 с. |
2.
4 Ускорение – Физика BCIT 0312 УчебникГлава 2 Одномерная кинематика
Сводка
- Определяет и различает мгновенное ускорение, среднее ускорение и замедление.
- Вычислить ускорение, зная начальное время, начальную скорость и конечную скорость.
СРЕДНЕЕ УСКОРЕНИЕ
Среднее ускорение равно скорости изменения скорости v}}{\Delta{t}}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{v_f-v_0}{t_f-t_0}}[/latex] , 92},[/latex]метры в секунду в квадрате или метры в секунду в секунду, что буквально означает, на сколько метров в секунду скорость изменяется каждую секунду.
Вспомним, что скорость — это вектор: она имеет как величину, так и направление. Это означает, что изменение скорости может быть изменением величины (или скорости), но оно также может быть изменением направления . Например, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение происходит, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по тому и другому.
УСКОРЕНИЕ КАК ВЕКТОР
Ускорение является вектором в том же направлении, что и изменение скорости, [латекс]\boldsymbol{\Delta{v}}[/латекс]. Поскольку скорость является вектором, она может изменяться как по величине, так и по направлению. Таким образом, ускорение — это изменение либо скорости, либо направления, либо того и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда идет в направлении движения .
Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление .
ПРЕДУПРЕЖДЕНИЕ О НЕПРАВИЛЬНОМ КОНЦЕПЦИИ: ЗАМЕДЛЕНИЕ ПРОТИВ. ОТРИЦАТЕЛЬНОЕ УСКОРЕНИЕ
Под замедлением всегда подразумевается ускорение в направлении, противоположном направлению скорости. Замедление всегда снижает скорость. Однако отрицательное ускорение равно ускорению в отрицательном направлении в выбранной системе координат . Отрицательное ускорение может быть, а может и не быть замедлением, а замедление может считаться или не считаться отрицательным ускорением. Например, рассмотрим рисунок 3.
Рисунок 3. (a) Этот автомобиль ускоряется, двигаясь вправо.
Поэтому он имеет положительное ускорение в нашей системе координат. (b) Этот автомобиль замедляется, когда он движется вправо. Следовательно, в нашей системе координат он имеет отрицательное ускорение, потому что его ускорение направлено влево. Автомобиль тоже тормозит: направление его ускорения противоположно направлению его движения. (c) Этот автомобиль движется влево, но со временем замедляется. Следовательно, его ускорение положительно в нашей системе координат, потому что оно направлено вправо. Однако автомобиль замедляется, потому что его ускорение противоположно его движению. (d) Этот автомобиль ускоряется, когда он движется влево. Он имеет отрицательное ускорение, потому что он ускоряется влево. Однако, поскольку его ускорение направлено в том же направлении, что и его движение, оно ускоряется (а не замедляется).Пример 1: Расчет ускорения: скаковая лошадь покидает ворота
Скаковая лошадь, выходящая из ворот, разгоняется из состояния покоя до скорости 15,0 м/с строго на запад за 1,80 с.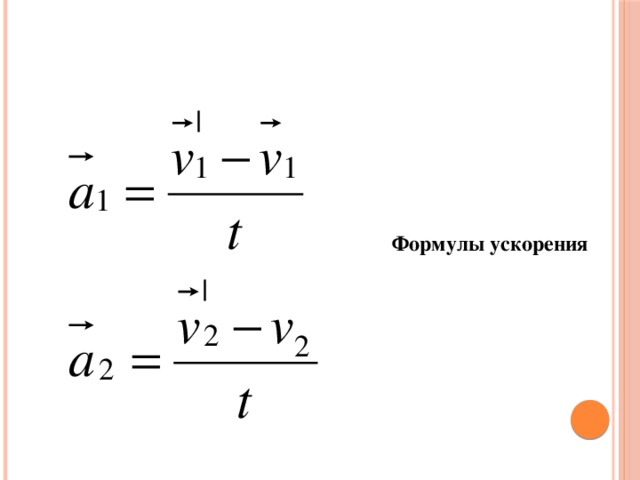
Каково его среднее ускорение?
Стратегия
Сначала мы рисуем эскиз и присваиваем задаче систему координат. Это простая задача, но ее всегда полезно визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Рисунок 5.
Мы можем решить эту проблему, идентифицируя [латекс]\жирныйсимвол{\Delta{v}}[/латекс]и[латекс]\жирныйсимвол{\Delta{t}}[/латекс ] исходя из предоставленной информации, а затем рассчитывая среднее ускорение непосредственно из уравнения {t}}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{v_f-v_0}{t_f-t_0}}[/latex].
Решение
1. Определите известные значения.[latex]\boldsymbol{v_0=0}[/latex],[latex]\boldsymbol{v_f=-15.0\textbf{ м/с}}[/latex] (знак минус указывает направление на запад),[latex]\boldsymbol{\Delta{t}=1,80\textbf{s}}[/latex].
2}[/латекс]. 92}[/латекс]. Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы, чтобы всадник удерживался с силой, почти равной его весу.
Мгновенное ускорение а или ускорение в конкретный момент времени получается с помощью того же процесса, который обсуждался для мгновенной скорости в главе 2.3 «Время, скорость и скорость», то есть путем рассмотрения бесконечно малого интервала время. Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рис. 6 показаны графики зависимости мгновенного ускорения от времени для двух очень разных движений. На рис. 6(а) ускорение немного меняется, и среднее значение по всему интервалу почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около[латекс]\boldsymbol{1.
2}[/латекс] соответственно.
В следующих нескольких примерах рассматривается движение поезда метро, показанного на рисунке 7. В (а) шаттл движется вправо, а в (б) он движется влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые рассуждения, которые используются при решении задач.
Рис. 7. Одномерное движение поезда метро, рассмотренное в Примере 2, Примере 3, Примере 4, Примере 5, Примере 6 и Примере 7.
Здесь мы выбрали ось x так, что + означает вправо и − означает влево для перемещений, скоростей и ускорений. а) Поезд метро движется вправо с x 0 до x f . Его водоизмещение Δ х составляет +2,0 км. (b) Поезд движется влево от x’ o до x’ f . Его водоизмещение Δ x’ составляет -1,5 км . (Обратите внимание, что штриховой символ (′) используется просто для того, чтобы различать перемещение в двух разных ситуациях. Расстояние пути и размер автомобилей указаны в разных масштабах, чтобы все уместить на диаграмме.).Пример 2: Расчет перемещения: поезд метро
Каковы величина и знак перемещений поезда метро, показанного в частях (a) и (b) рисунка 7?
Стратегия
Чертеж с системой координат уже предоставлен, поэтому нам не нужно делать эскиз, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает.
Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение [латекс]\жирныйсимвол{\Delta{x}=x_f-x_0}[/латекс]. Это просто, поскольку заданы начальная и конечная позиции.
Решение
1. Определите известные. На рисунке мы видим, что [латекс]\boldsymbol{x_f=6,70\textbf{ км}}[/латекс] и [латекс]\boldsymbol{x_0=4,70\textbf{ км}}[/латекс] для части (а) , и[латекс]\boldsymbol{x\prime_f=3,75\textbf{км}}[/латекс]и[латекс]\boldsymbol{x\prime_0=5,25\textbf{км}}[/латекс]для части (b) .
2. Найдите смещение в части (a).
[латекс]\boldsymbol{\Delta{x}=x_f-x_0=6,70\textbf{км}-4,70\textbf{км}=+2,00\textbf{км}}[/латекс]
3. Найдите смещение в части (b).
[латекс]\boldsymbol{\Delta{x}\prime=x\prime_f-x\prime_0=3,75\textbf{км}-5,25\textbf{км}=-1,50\textbf{км}}[/латекс]
Обсуждение
Направление движения в (а) вправо и, следовательно, его перемещение имеет положительный знак, тогда как движение в (б) происходит влево и, следовательно, имеет отрицательный знак.
Пример 3: Расчет расстояния, пройденного с перемещением: поезд метро
Какие расстояния пройдены для движений, показанных в частях (a) и (b) поезда метро на рисунке 7?
Стратегия
Чтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны с перемещением. Расстояние между двумя положениями определяется как величина смещения, которое было найдено в примере 2. Пройденное расстояние — это общая длина пути, пройденного между двумя положениями. (См. Главу 2.1 Перемещение.) В случае поезда метро, показанного на рисунке 7, пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.
Решение
1. Перемещение по части (а) составило +2,00 км. Следовательно, расстояние между начальным и конечным положениями составило 2,00 км, а пройденное расстояние составило 2,00 км.
2. Смещение для детали (b) было [латекс]\boldsymbol{-1,5\textbf{км}}[/латекс].
Следовательно, расстояние между начальным и конечным положениями составило 1,50 км, а пройденное расстояние — 1,50 км.
Обсуждение
Расстояние является скаляром. У него есть величина, но нет знака, указывающего направление.
Пример 4: расчет ускорения: поезд метро набирает скорость
Предположим, поезд на рис. 7(а) разгоняется из состояния покоя до 30,0 км/ч за первые 20,0 с движения. Каково его среднее ускорение за этот промежуток времени?
Стратегия
Сейчас стоит сделать простой набросок:
Рисунок 8.Эта задача состоит из трех шагов. Сначала мы должны определить изменение скорости, затем мы должны определить изменение времени и, наконец, мы используем эти значения для расчета ускорения.
Решение
1. Найдите известные.[latex]\boldsymbol{v_0=0}[/latex](поезда отправляются с места),[latex]\boldsymbol{v_f=30.0\textbf{ км/ч }}[/латекс] и [латекс]\boldsymbol{\Delta{t}=20,0\textbf{s}}[/латекс].
2}[/латекс]
Обсуждение
Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд стартует из состояния покоя и заканчивается со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и изменение скорости , как это всегда и бывает.
Пример 5: расчет ускорения: поезд метро замедляется
Теперь предположим, что в конце пути поезд на рис. 7(а) замедляется до полной остановки со скорости 30,0 км/ч за 8,00 с. Каково его среднее ускорение при остановке?
Стратегия
Рис. 9.В этом случае поезд замедляется, и его ускорение отрицательно, потому что он движется влево. Как и в предыдущем примере, мы должны найти изменение скорости и изменение времени, а затем найти ускорение.
Решение
1. Определите известные. [latex]\boldsymbol{v_0=30.0\textbf{ км/ч}}[/latex],[latex]\boldsymbol{v_f=0\textbf{ км/ч}}[/latex](поезд остановлен, поэтому его скорость равна 0) и[латекс]\жирныйсимвол{\Delta{t}=8,00\textbf{с}}[/латекс].
2. Найдите изменение скорости, [латекс]\жирныйсимвол{\Delta{v}}[/латекс].
[латекс]\boldsymbol{\Delta{v}=v_f-v_0=0-30,0\textbf{ км/ч}=-30,0\textbf{ км/ч}}[/латекс]
3. Подключите известные, [латекс]\boldsymbol{\Delta{v}}[/latex] и [латекс]\boldsymbol{\Delta{t}}[/latex], и найдите [латекс]\boldsymbol{\bar{a} }[/латекс].
[латекс]\boldsymbol{\bar{a}=}[/latex][латекс]\boldsymbol{\frac{\Delta{v}}{\Delta{t}}}[/latex][латекс]\ boldsymbol{=}[/latex][латекс]\boldsymbol{\frac{-30,0\textbf{км/ч}}{8,00\textbf{с}}}[/latex] 92}[/латекс].
Знак минус указывает, что ускорение направлено влево. Этот знак разумен, поскольку в этой задаче поезд изначально имеет положительную скорость, а отрицательное ускорение будет препятствовать движению. Опять же, ускорение происходит в том же направлении, что и изменение скорости, которая здесь отрицательная. Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости.
Графики зависимости положения, скорости и ускорения от времени для поездов в Примере 4 и Примере 5 показаны на Рисунке 10 .
(Мы приняли, что скорость остается постоянной от 20 до 40 с, после чего поезд замедляется.)
Пример 6: Вычисление средней скорости: поезд метро
Какова средняя скорость поезда в части b примера 2, показанном еще раз ниже, если путь до места занимает 5,00 мин?
Рисунок 11.
{\prime}_0=5,25\textbf{км}}[/latex ],[латекс]\жирныйсимвол{\Delta{t}=5,00\textbf{мин}}[/латекс]. 9{\prime}}{\Delta{t}}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{(\frac{-1,50\textbf{км}}{5,00\ textbf{ мин}})(\frac{60\textbf{ мин}}{1\textbf{ ч}})}[/latex][латекс]\boldsymbol{=-18,0\textbf{ км/ч}}[/ латекс]Обсуждение
Отрицательная скорость указывает на движение влево.
Пример 7: Расчет замедления: поезд метро
Наконец, предположим, что поезд на рис. 11 замедляется до полной остановки со скорости 20,0 км/ч за 10,0 с. Каково его среднее ускорение?
Стратегия
Еще раз нарисуем набросок:
Рис. 12.
Как и прежде, мы должны найти изменение скорости и изменение времени для расчета среднего ускорения.
Решение
1. Определите известные значения.[latex]\boldsymbol{v_0=-20\textbf{ км/ч}}[/latex],[latex]\boldsymbol{v_f=0\textbf{ km/ h}}[/latex],[latex]\boldsymbol{\Delta{t}=10,0\textbf{s}}[/latex].
2}[/латекс]
Обсуждение
Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд изначально имеет отрицательную скорость (влево) в этой задаче, а положительное ускорение противодействует движению (и, следовательно, вправо). Опять же, ускорение происходит в том же направлении, что и изменение скорости, которая здесь положительна. Как и в примере 5, это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости.
Пожалуй, самое важное, что следует отметить в этих примерах, — это знаки ответов. В выбранной нами системе координат плюс означает, что величина находится справа, а минус означает, что она находится слева. Это легко представить для смещения и скорости. Но это немного менее очевидно для ускорения. Большинство людей интерпретируют отрицательное ускорение как замедление объекта. Этого не было в примере 7, где положительное ускорение замедляло отрицательную скорость.
Решающим отличием было то, что ускорение было в направлении, противоположном скорости. В самом деле, отрицательное ускорение будет увеличить отрицательную скорость. Например, поезд, движущийся влево на рисунке 11, ускоряется за счет ускорения влево. В этом случае как [латекс]\boldsymbol{v}[/latex], так и [латекс]\boldsymbol{a}[/latex]отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и скорость, то тело ускоряется. Если ускорение имеет противоположный знак скорости, то объект замедляется.
ИССЛЕДОВАНИЯ PHET: МОДЕЛИРОВАНИЕ ДВИЖУЩЕГОСЯ ЧЕЛОВЕКА
Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка вперед-назад с помощью мыши и зарисовывайте его движение. Установите положение, скорость или ускорение, и пусть симуляция переместит человека за вас.
Рис. 13. Движущийся человек.- Ускорение — скорость изменения скорости. В символах среднее ускорение [латекс]\boldsymbol{\bar{a}}[/латекс] равно
[латекс]\boldsymbol{\bar{a}=}[/латекс][латекс]\boldsymbol{\frac{\Delta{v}}{\Delta{t}}}[/latex][латекс]\boldsymbol {=}[/латекс][латекс]\boldsymbol{\frac{v_f-v_0}{t_f-t_0}}[/латекс].
92[/латекс]. - Ускорение является вектором и поэтому имеет как величину, так и направление.
- Ускорение может быть вызвано изменением величины или направления скорости.
- Мгновенное ускорение[latex]\textbf{a}[/latex] — это ускорение в определенный момент времени.
- Замедление — это ускорение с направлением, противоположным направлению скорости.
92[/латекс].- ускорение
- скорость изменения скорости; изменение скорости во времени
- среднее ускорение
- изменение скорости, деленное на время, за которое она изменяется
- мгновенное ускорение
- ускорение в определенный момент времени
- замедление
- ускорение в направлении, противоположном скорости; ускорение, приводящее к уменьшению скорости
Помощь по физике для старших классов
Учащиеся, нуждающиеся в помощи по физике для старших классов, получат большую пользу от нашей интерактивной программы.
Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по физике в средней школе.
Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы быстро получите много помощи от старшеклассников по физике.
Получите помощь сегодня с нашей обширной коллекцией необходимой информации по физике для старших классов.
Физика средней школы
Электричество и магнетизм
Электрические цепи
Конденсаторы
Расчет общей емкости
Понимание емкости
Использование уравнений конденсатора
Схема расчетов и концепции
Расчет мощности цепи
Законы Кирхгофа
Понимание тока в цепи
Понимание электричества
Понимание последовательного и параллельного
Понимание напряжения в цепи
Используйте закон Ома
Резисторы
Расчет полного сопротивления
Удельное сопротивление
Понимание сопротивления
Электричество
Электрический заряд
Электрическая сила
Понимание электрических полей
Магнетизм и электромагнетизм
Понимание магнитных полей
Понимание отношений с текущим
Понимание правил правой руки
Энергия и работа
Энергия
Расчет кинетической энергии
Расчет потенциальной энергии
Виды механической энергии
Понимание сохранения энергии
Понимание кинетической и потенциальной энергии
Мощность
Понять силу
Работа
Расчетная работа
Понимание работы
Теорема о работе и кинетической энергии
Сил
Введение в Силы
Идентификация сил и систем
Понимание Силы
Понимание взаимосвязи между силой и ускорением
Чистая сила
Расчет силы
Интерпретация силовых диаграмм
Удельные силы
Контактные силы
Гравитационное поле
Понимание силы трения
Понимание гравитации и веса
Понимание нормальной силы
Понимание всемирного тяготения
Вводные принципы
Понимание точности и прецизионности
Понимание независимых и зависимых переменных
Понимание скалярных и векторных величин
Понимание единиц СИ
Понимание значимых цифр
Движение и механика
Круговое движение
Круговое движение
Вращательный угловой момент
Понимание крутящего момента
Понимание кругового движения
Понимание крутящего момента
Использование уравнений кругового движения
Газовые законы
Понимание изоволюметрических процессов
Гармоничное движение
Энергия ШМ
Период СГМ
Понимание маятников
Понимание пружин
Использование уравнений маятника
Использование уравнений Spring
Линейное движение
Свободное падение
Кинематические уравнения
Понимание расстояния, скорости и ускорения
Понимание движения в одном измерении
Понимание движения в двух измерениях
Понимание движения с постоянным ускорением
Использование уравнений движения
Импульс
Расчет импульса
Сохранение импульса
Упругие и неупругие столкновения
Импульс и Импульс
Понимание закона сохранения импульса
Понимание упругих и неупругих столкновений
Понимание импульса
Законы Ньютона
Закон всемирного тяготения Ньютона
Понимание первого закона Ньютона
Понимание второго закона Ньютона
Понимание третьего закона Ньютона
Представления движения
Представления движения
Термодинамика
Энтальпия и энтропия
Понимание энтальпии
Понимание энтропии
Тепло
Понимание влияния тепла на объем
Понимание тепла и температуры
Понимание тепла и работы
Понимание тепловых двигателей
Понимание концепции передачи энергии
Законы термодинамики
Понимание первого закона термодинамики
Понимание второго закона термодинамики
Понимание третьего закона термодинамики
Понимание нулевого закона термодинамики
Волны, звук и свет
Свет и электромагнитные волны
Понимание фотонов
Понимание преломления
Понимание электромагнитного спектра
Звук
Понимание Доплера
Волны
Интерференция и суперпозиция
Свойства волн
Типы волн
Понимание амплитуды и периода
Понимание расчетов со скоростью
Понимание концепции волн
Понимание типов волн
Понимание длины волны и частоты
Курсы физики в старших классах обычно проходят ближе к концу вашей школьной карьеры.
Вы, вероятно, изучали химию, биологию и науку о Земле и, возможно, обнаружили, что различия между всеми этими предметами заставляют науку чувствовать себя бессвязной и трудной для понимания. Физика дает вам возможность связать все воедино в рамках единой науки, которая объясняет все, от поведения электрона до движения планет. Из-за того, что физика является фундаментальной для всех других наук, некоторые школы продвигают учебную программу, в которой учащиеся сначала изучают физику, а затем все другие науки, которые обычно встречаются в старшей школе. Если это вариант в вашей средней школе, возможно, стоит подумать. Однако если вы продвинулись дальше в своей школьной карьере, физика по-прежнему предлагает фантастическую возможность оценить единство естественных наук.
Возможно, в значительной степени из-за своей междисциплинарной способности физика может пугать даже самых лучших учеников. Скорее всего, вы обнаружите, что уроки физики в старших классах не менее сложны, чем ваши предыдущие курсы по естествознанию, и что они будут вознаграждать практикой и часами, проведенными за лабораторными отчетами или подготовкой к тестовым вопросам с длинными ответами.
Один из ключей к успеху на уроках физики в старшей школе — развить способность сводить сложные ситуации к ряду знакомых простых уравнений.
Этот подход может показаться простым, если не учитывать огромное количество новых уравнений и математических выражений, которые вводятся на обычном школьном уроке физики. Должен быть способ сохранить правильное уравнение для центростремительного ускорения, когда вы также пытаетесь сохранить правильность второго закона Ньютона в своем уме! Одна из самых приятных частей физики приходит, когда вы понимаете, что каждое отдельное уравнение связано с другим. Учтите, что второй закон Ньютона выглядит так. . .
. . . а уравнение для центростремительной силы выглядит так:
Оказывается, эти два уравнения на самом деле просто разные выражения одного и того же понятия силы! Вместо того, чтобы запоминать третье уравнение для центростремительного ускорения, вы можете просто признать, что если вы приравняете оба уравнения друг к другу и уменьшите массу, центростремительное ускорение должно быть равно следующему уравнению:
Это всего лишь один пример из многих.
, многие другие, похожие на те, с которыми вы столкнетесь на уроке физики в старшей школе. В этом коротком примере мы только что сократили на одну треть количество уравнений, которые вам нужно будет запомнить для этого раздела на уроке физики. Учиться умнее, а не усерднее, может окупиться много времени на таком уроке, как физика. Рассмотрите возможность работы в учебных группах или один на один с успешными учениками, чтобы понять, где можно заменить логические выводы и логическое заучивание. Если вы застряли, изучая определенную концепцию, наша страница справки по физике для старших классов может помочь вам разобраться с любыми недоразумениями, стоящими между вами и пониманием данной концепции. Наша справка по физике для старших классов организована по темам как общих тем по физике для старших классов, так и конкретных концепций и типов задач, обычно встречающихся в школьных программах. Каждая концепция связана с решенными примерами вопросов, которые могут помочь вам увидеть закономерности в способах успешного решения проблемы определенного типа.