Ускоренное движение формула – Равноускоренное движение — Википедия - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Равнопеременное движение. Ускорение. | Объединение учителей Санкт-Петербурга

Равнопеременное движение. Ускорение.
Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением.
Обозначим: – вектор начальной скорости, – изменение скорости, а Δt – промежуток времени. Пусть Δt₁= Δt₂=Δt₃=…, тогда по определению
Следовательно, Т.о., это характеристика движения.
Если t₀=0, то
УСКОРЕНИЕ – физическая величина, характеризующая быстроту изменения скорости и (при равнопеременном движении) численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло.
Ускорение при равнопеременном движении показывает , насколько меняется мгновенная скорость движения тела за единицу времени. Единица ускорения в СИ – м/с².	Например, ускорение равно 5 м/с² – это значит, что, двигаясь равноускоренно, тело изменяет скорость на 5 м/с за каждую секунду своего движения.
В случае не равнопеременного движения: тогда мгновенное ускорение
Равнопеременное движение называется равноускоренным, если модуль скорости возрастает.	Условие р.у.д. –.
Равнопеременное движение называется равнозамедленным, если модуль скорости уменьшается.	Условие р.з.д. – .
Графики равнопеременного движения.

или – в проекциях; или – через модули.
Линейная функция. График – прямая.
Движения, совпадающие с направлением координатной оси: равноускоренноес начальной скоростью равноускоренное без начальной скорости равнозамедленное Движения против координатной оси. равнозамедленное равноускоренное без начальной скорости равноускоренное с начальной скоростью
Перемещение при равнопеременном движении.
Площадь под графиком скорости численно равна перемещению. Следовательно, площадь трапеции численно равна перемещению.
	Решение основной задачи механики для р.у.д. :
Графики перемещения и координаты.
Функции и – квадратичные. График – парабола!

www.eduspb.com

Что такое ускорение? Формулы ускорения при равноускоренном движении по прямой траектории

Содержание статьи:

Ускорение в физике – это одна из важных кинематических характеристик, без знания которой невозможно описать ни один вид движения. В данной статье рассмотрим, что это за величина, а также приведем формулы ускорения при движении равноускоренном прямолинейном.

Ускорение и причина его появления

В физике величину, которая характеризует изменение во времени скорости, называют ускорением. Математическая формула для ускорения выглядит так:

a¯ = dv¯/dt.

Чем быстрее изменяется скорость, тем больше будет ускорение тела. Например, значение a = 1 м/с2 говорит о том, что за 1 секунду скорость увеличилась на 1 м/с.

Вам будет интересно:Упразднить – что это значит? Когда используется?

Ускорение у тел возникает за счет действия на них внешних сил любой природы. Этот факт был установлен Ньютоном в XVII веке. В настоящее время он носит название 2-го закона Ньютона:

F¯ = m*a¯.

Обе формулы говорят о том, что вектор ускорения направлен в сторону изменения вектора скорости или в сторону вектора силы (F¯ и dv¯ направлены одинаково). Если направления векторов a¯ и v¯ совпадают, тогда тело будет ускоряться, если они противоположны, то тело будет замедлять свое движение, если же они направлены под некоторым углом, тогда траектория перемещения будет кривой линией.

Равноускоренное прямолинейное движение. Скорость и ускорение

Указанный вид движения предполагает, что траектория тела является прямой линией, а величина ускорения в процессе перемещения тела не изменяется ни по модулю, ни по направлению. Поскольку тело движется по прямой линии, то векторы a¯ и v¯ направлены либо в одну сторону, либо в противоположные.

Предположим, что тело находилось в покое. Затем на него начала действовать постоянная сила, которая придала ему ускорение. В таком случае скорость v в любой момент времени t может быть вычислена так:

v = a*t.

Где a = const. Графиком этого уравнения является возрастающая прямая, которая начинается с точки (v=0; t=0).

Если же тело до начала действия силы уже имело некоторую скорость v0, тогда будут справедливы такие формулы:

v = v0 + a*t;

v = v0 – a*t.

В первом случае речь идет об ускоренном движении, во втором – о замедленном (торможение).

Из последних двух выражений можно получить формулы ускорения при равноускоренном движении тела по прямой линии:

a = (v-v0)/t;

a = (v0-v )/t.

Время t отсчитывается от момента действия силы на тело.

Ускорение и путь

При решении задач на равноускоренное перемещение часто требуется найти ускорение, зная пройденный путь. Покажем, какие формулы для этого следует применять.

Путь рассчитать несложно при равноускоренном движении по прямой. Для этого следует взять интеграл по времени от уравнения v(t). Выполнив это математическое действие, получим три рабочие формулы:

S = a*t2;

S = v0*t + a*t2;

S = v0*t – a*t2.

Первое выражение описывает ускоренное перемещение тела из состояния покоя, второе – ускоренное перемещение с наличием начальной скорости, третье – торможение. Графики всех трех функций S(t) являются параболами.

Как выразить ускорение из формул равноускоренного движения для пути? Для этого необходимо изолировать множитель a*t2 в одной части равенства, а затем все равенство поделить на квадрат времени. Из формул выше получаем:

a = S/t2;

a = (S – v0*t)/t2;

a = (v0*t – S)/t2.

Первое уравнение используется для экспериментального определения ускорения свободного падения g, когда тяжелые тела сбрасывают вниз с некоторой высоты. Подобные эксперименты проводил еще Галилей в конце XVI века. В настоящее время для определения ускорения g в исследуемой местности используют абсолютные гравиметры, принцип работы которых также основан на свободном падении.

Два последних уравнения отличаются друг от друга лишь знаком ускорения. При торможении ускорение считают отрицательным.

Все три выражения приводят к одной и той же единице измерения величины a – м/с2.

Задача на вычисление ускорения

Разобравшись с основными формулами ускорения при равноускоренном движении, решим следующую проблему практического характера: водитель автомобиля, который двигался со скоростью 63 км/ч, увидел, что впереди загорелся красный сигнал светофора. После нажатия на педаль тормоза автомобиль полностью остановился через 100 метров. Зная, что время торможения заняло 14 секунд, необходимо рассчитать соответствующее ускорение.

Для решения задачи можно сразу же воспользоваться одной из записанных выше формул:

a = (v0*t – S)/t2.

Переведем начальную скорость автомобиля из км/ч в м/с, получаем:

v0 = 63*1000/3600 = 17,5 м/с2.

Теперь можно подставить значения из условия задачи и получить ответ: a = 0,74 м/с2. Поскольку речь идет о торможении, то данное ускорение следует взять со знаком минус: a = – 0,74 м/с2.

Источник

1ku.ru

Прямолинейное равноускоренное движение. Формулы и решение задач

Одним из самых распространенных видов перемещения объектов в пространстве, с которым человек встречается повседневно, является равноускоренное прямолинейное движение. В 9 классе общеобразовательных школ в курсе физики изучают подробно этот вид движения. Рассмотрим его в статье.

Кинематические характеристики движения

Прежде чем приводить формулы, описывающие равноускоренное прямолинейное движение в физике, рассмотрим величины, которые его характеризуют.

В первую очередь это пройденный путь. Будем его обозначать буквой S. Согласно определению, путь – это расстояние, которое тело прошло вдоль траектории перемещения. В случае прямолинейного движения траектория представляет собой прямую линию. Соответственно, путь S – это длина прямого отрезка на этой линии. Он в системе физических единиц СИ измеряется в метрах (м).

Скорость или как часто ее называют линейная скорость – это быстрота изменения положения тела в пространстве вдоль его траектории перемещения. Обозначим скорость буквой v. Измеряется она в метрах в секунду (м/с).

Ускорение – третья важная величина для описания прямолинейного равноускоренного движения. Она показывает, как быстро во времени изменяется скорость тела. Обозначают ускорение символом a и определяют его в метрах в квадратную секунду (м/с²).

Путь S и скорость v являются переменными характеристиками при прямолинейном равноускоренном движении. Ускорение же является величиной постоянной.

Связь скорости и ускорения

Представим себе, что некоторый автомобиль движется по прямой дороге, не меняя свою скорость v₀. Это движение называется равномерным. В какой-то момент времени водитель стал давить на педаль газа, и автомобиль начал увеличивать свою скорость, приобретя ускорение a. Если начинать отсчет времени с момента, когда автомобиль приобрел ненулевое ускорение, тогда уравнение зависимости скорости от времени примет вид:

v = v₀ + a * t.

Здесь второе слагаемое описывает прирост скорости за каждый промежуток времени. Поскольку v₀и a являются постоянными величинами, а v и t – это переменные параметры, то графиком функции v будет прямая, пересекающая ось ординат в точке (0; v₀), и имеющая некоторый угол наклона к оси абсцисс (тангенс этого угла равен величине ускорения a).

На рисунке показаны два графика. Отличие между ними заключается только в том, что верхний график соответствует скорости при наличии некоторого начального значения v₀, а нижний описывает скорость равноускоренного прямолинейного движения, когда тело начало из состояния покоя ускоряться (например, стартующий автомобиль).

Отметим, если в примере выше водитель вместо педали газа нажал бы педаль тормоза, то движение торможения описывалось бы следующей формулой:

v = v₀ – a * t.

Этот вид движения называется прямолинейным равнозамедленным.

Формулы пройденного пути

На практике часто важно знать не только ускорение, но и значение пути, который за данный период времени проходит тело. В случае прямолинейного равноускоренного движения эта формула имеет следующий общий вид:

S = v₀* t + a * t²/ 2.

Первый член соответствует равномерному движению без ускорения. Второй член – это вклад в пройденный путь чистого ускоренного движения.

В случае торможения движущегося объекта выражение для пути примет вид:

S = v₀* t – a * t²/ 2.

В отличие от предыдущего случая здесь ускорение направлено против скорости движения, что приводит к обращению в ноль последней через некоторое время после начала торможения.

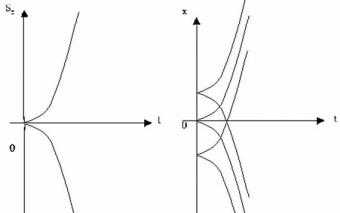
Не сложно догадаться, что графиками функций S(t) будут ветви параболы. На рисунке ниже представлены эти графики в схематическом виде.

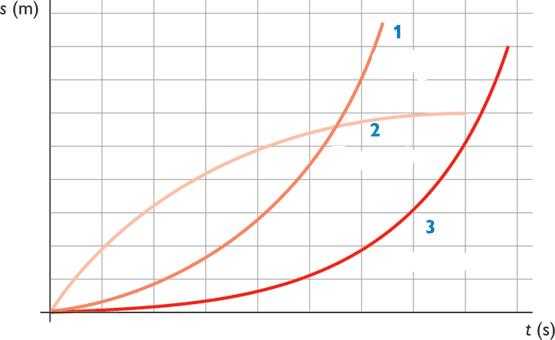
Параболы 1 и 3 соответствуют ускоренному перемещению тела, парабола 2 описывает процесс торможения. Видно, что пройденный путь для 1 и 3 постоянно увеличивается, в то время как для 2 он выходит на некоторую постоянную величину. Последнее означает, что тело прекратило свое движение.

Далее в статье решим три разные задачи на использование приведенных формул.

Задача на определение времени движения

Автомобиль должен отвести пассажира из пункта A в пункт B. Расстояние между ними 30 км. Известно, что авто в течение 20 секунд движется с ускорением 1 м/с². Затем его скорость не меняется. За какое время авто доставит пассажира в пункт B?

Расстояние, которое авто за 20 секунд пройдет, будет равно:

S₁ = a * t₁²/ 2.

При этом скорость, которую он наберет за 20 секунд, равна:

v = a * t₁.

Тогда искомое время движения t можно вычислить по следующей формуле:

t = (S – S₁) / v + t₁ = (S – a * t₁²/ 2) / (a * t₁) + t₁.

Здесь S – расстояние между A и B.

Переведем все известные данные в систему СИ и подставим в записанное выражение. Получим ответ: t = 1510 секунд или приблизительно 25 минут.

Задача на расчет пути торможения

Теперь решим задачу на равнозамедленное движение. Предположим, что грузовой автомобиль двигался со скоростью 70 км/ч. Впереди водитель увидел красный сигнал светофора и начал останавливаться. Чему равен тормозной путь авто, если он остановился за 15 секунд.

Тормозной путь S можно рассчитать по следующей формуле:

S = v₀* t – a * t²/ 2.

Время торможения t и начальную скорость v₀ мы знаем. Ускорение a можно найти из выражения для скорости, учитывая, что ее конечное значение равно нулю. Имеем:

v₀ – a * t = 0;
a = v₀/ t.

Подставляя полученное выражение в уравнение, приходим к конечной формуле для пути S:

S = v₀* t – v₀* t / 2 = v₀* t / 2.

Подставляем значения из условия и записываем ответ: S = 145,8 метра.

Задача на определение скорости при свободном падении

Пожалуй, самым распространенным в природе прямолинейным равноускоренным движением является свободное падение тел в поле гравитации планет. Решим следующую задачу: тело с высоты 30 метров отпустили. Какую скорость будет оно иметь в момент падения на поверхность земли?

Искомую скорость можно рассчитать по формуле:

v = g * t.

Где g = 9,81 м/с².

Время падения тела определим из соответствующего выражения для пути S:

S = g * t²/ 2;
t = √(2 * S / g).

Подставляем время t в формулу для v, получаем:

v = g * √(2 * S / g) = √(2 * S * g).

Значение пройденного телом пути S известно из условия, подставляем его в равенство, получаем: v = 24,26 м/с или около 87 км/ч.

fb.ru

Равноускоренное движение

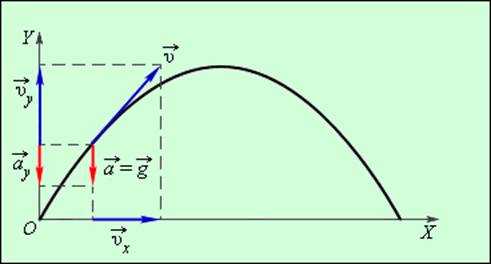
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения . Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.4.1).

Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости и ускорения направлены вдоль прямой движения. Поэтому скорость υ и ускорение a в проекциях на направление движения можно рассматривать как алгебраические величины.

Рисунок 1.4.1.

Проекции векторов скорости и ускорения на координатные оси. ax = 0, ay = –g

При равноускоренном прямолинейном движении скорость тела определяется формулой

(*)

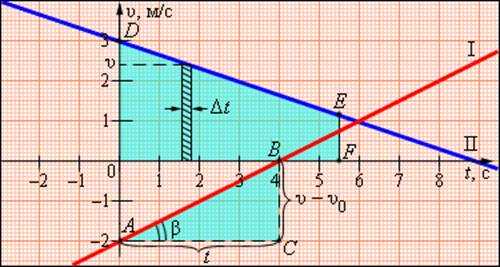
В этой формуле υ₀ – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.4.2).

Рисунок 1.4.2.

Графики скорости равноускоренного движения

По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC:

Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика I: υ₀ = –2 м/с, a = 1/2 м/с².

Для графика II: υ₀ = 3 м/с, a = –1/3 м/с²

График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.

Так как υ – υ₀ = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

(**)

Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y₀ прибавить перемещение за время t:

(***)

Это выражение называют законом равноускоренного движения.

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ₀ и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде

Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ₀, ускорение a и перемещение s:

Если начальная скорость υ₀ равна нулю, эти формулы принимают вид

Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ₀, υ, s, a, y₀ являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.

questions-physics.ru

Уравнения равноускоренного движения • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Галилео Галилей относится к числу людей, прославившихся совсем не тем, за что им следовало бы пользоваться заслуженной славой. Все помнят, как этого итальянского естествоиспытателя в конце жизни подвергли суду инквизиции по подозрению в ереси и заставили отречься от убеждения, что Земля вращается вокруг Солнца. На самом же деле, этот судебный процесс на развитие науки практически не повлиял — в отличие от ранее проделанных Галилеем опытов и сделанных им на основании этих опытов выводов, которые фактически предопределили дальнейшее развитие механики как раздела физической науки.

Движение физических тел изучалось с незапамятных времен, и основы кинематики были заложены задолго до рождения Галилея. Элементарные задачи описания движения сегодня изучают уже в начальной школе. Например, все знают, что если автомобиль равномерно движется со скоростью 20 км/ч, то за 1 час он проедет 20 км, за 2 часа — 40 км, за 3 часа — 60 км и т. д. И до тех пор, пока машина движется с постоянной скоростью (стрелка спидометра не отклоняется от заданного деления на его шкале), рассчитать пройденное расстояние труда не составляет — достаточно умножить скорость машины на время, которое она находится в пути. Этот факт известен настолько давно, что имя его первооткрывателя наглухо затерялось в тумане античных времен.

Сложности возникают, как только объект начинает двигаться с переменной скоростью. Трогаетесь вы, к примеру, от светофора — и стрелка спидометра ползет от нуля вверх, пока вы не отпустите педаль газа и не нажмете педаль тормоза. На самом деле стрелка спидометра на месте практически не стоит — она всё время движется вверх или вниз. В начале каждой отдельно взятой секунды реальная скорость машины одна, а в конце секунды — уже другая, и пройденный ею за секунду путь точно рассчитать не так-то просто. Эта проблема — описание движения с ускорением — волновала естествоиспытателей задолго до Галилея.

Сам же Галилео Галилей подошел к ней новаторски и, фактически, задал направление всего дальнейшего развития современной методологии естествознания. Вместо того чтобы сидеть и умозрительно решать вопрос о движении ускоряющихся тел, он придумал гениальные по своей простоте опыты, позволяющие экспериментально проследить, что в действительности происходит с ускоряющимися телами. Нам может показаться, что ничего особенно новаторского в таком подходе нет, однако до Галилея основным методом решения проблем «натурфилософии» — о чем говорит само название тогдашней естественной науки — было умозрительное осмысление происходящего, а не его экспериментальная проверка. Сама идея проведения физических экспериментов была в то время по-настоящему радикальной. Чтобы понять идею опытов Галилея, представьте себе тело, падающее под воздействием силы земного притяжения. Выпустите какой-нибудь предмет из рук — и он упадет на пол; при этом в первое мгновение скорость его движения будет равна нулю, но он тут же начнет ускоряться — и будет продолжать ускоряться, пока не упадет на землю. Если мы сможем описать падение предмета на землю, мы затем сможем распространить это описание и на общий случай равноускоренного движения.

Сегодня измерить динамику падения предмета не сложно — можно с большой точностью зафиксировать время от начала падения до любой промежуточной точки. Однако во времена Галилея точных секундомеров не было, да и любые механические часы по современным стандартам были весьма примитивны и неточны. Поэтому ученый первым делом разработал экспериментальный аппарат, позволяющий обойти эту проблему. Во-первых, он «разбавил» силу тяжести, замедлив время падения до разумных, с точки зрения имеющихся инструментов измерения, пределов, а именно — заставил тела скатываться по наклонной плоскости, а не просто падать отвесно. Затем он придумал, как обойти неточность современных ему механических часов, натянув на пути скатывающегося по наклонной поверхности шара ряд струн, чтобы он задевал их по дороге и можно было хронометрировать его движение по извлекаемым звукам. Раз за разом спуская шар по наклонной под рядом струн, Галилей перемещал струны, пока не добился, чтобы шар на всем своем пути, задевая натянутые струны, извлекал звуки через равные промежутки времени.

В конце концов Галилею удалось накопить достаточный объем экспериментальной информации о равноускоренном движении. Тело, стартующее из состояния покоя, далее движется так, как это описано в самом начале данной статьи. В переводе на язык математических символов равноускоренное движение описывается следующими уравнениями:

где a — ускорение, v — скорость, d — расстояние, пройденное телом за время t. Чтобы прочувствовать смысл этих уравнений, достаточно пристально пронаблюдать за падением предметов. Скорость падения зримо возрастает со временем, прошедшим с начала падения. Это следует из первого уравнения. Очевидно и то, что в процессе падения на прохождение первой части пути у тела уходит больше времени, чем на оставшуюся часть пути. Именно это и описывает вторая формула, поскольку из неё следует, что чем дольше тело ускоряется, тем больший отрезок пути оно преодолевает за одно и то же время.

Галилей сделал и еще одно важное наблюдение о теле, находящемся в состоянии свободного падения под воздействием силы гравитационного притяжения, хотя и не смог подтвердить его непосредственными измерениями. Экстраполировав результаты, полученные им при наблюдении скатывающихся по наклонной плоскости предметов, он сумел определить ускорение свободного падения тела на поверхность Земли. Ускорение свободного падения принято обозначать g, и оно равняется (приблизительно):

g = 9,8 м/с²(метра в секунду за секунду)

То есть, если уронить предмет из состояния покоя, за каждую секунду падения его скорость будет возрастать на 9,8 метра в секунду. На исходе первой секунды падения тело будет двигаться со скоростью 9,8 м/с, на исходе второй — со скоростью 2 × 9,8 = 18,6 м/с и так далее. Величина g определяет коэффициент ускорения падения тела, находящегося в непосредственной близости от земной поверхности, в связи с чем g принято называть ускорением свободного падения, или гравитационным ускорением.

Здесь следует сделать два важных замечания относительно полученных Галилеем результатов. Во-первых, ученый получил чисто экспериментальное значение величины g, ни на каких теоретических прогнозах не основывающееся. Значительно позже Исаак Ньютон в своих знаменитых работах показал, что величину g можно рассчитать теоретически, исходя из сочетания сформулированных им законов механики Ньютона и закона всемирного тяготения Ньютона. Именно первопроходческий труд Галилея и проложил дорогу последующим триумфальным открытиям Ньютона и формированию классической механики в её общеизвестном виде.

Второй важнейший момент состоит в том, что ускорение свободного падения не зависит от массы падающего тела. По сути, сила притяжения пропорциональна массе тела, но это полностью компенсируется большей инерцией, присущей более массивному телу (его нежеланию двигаться, если хотите), а посему (если не учитывать сопротивление воздуха) все тела падают с одинаковым ускорением. Это практическое заключение вступало в полное противоречие с умозрительными предсказаниями древних и средневековых натурфилософов, которые были уверены, что всякой вещи свойственно стремиться к центру мироздания (коим им, естественно, представлялся центр Земли) и что чем массивнее предмет, тем с большей скоростью он к этому центру устремляется.

Свое видение Галилей, конечно же, подкрепил экспериментальными данными, но вот опыта, который ему традиционно приписывают, он, скорее всего, вовсе не проводил. Согласно околонаучному фольклору, он сбрасывал предметы различной массы с «падающей» Пизанской башни, чтобы продемонстрировать, что они достигают поверхности земли одновременно. В этом случае, однако, Галилея ждало бы разочарование, поскольку более тяжелые предметы неизбежно падали бы на землю раньше легких из-за разницы в удельном сопротивлении воздуха. Если бы сбрасываемые с башни предметы были одного размера, сила сопротивления воздуха, тормозящая их падение, была бы одинаковой для всех предметов. При этом из законов Ньютона следует, что более легкие предметы затормаживались бы воздухом интенсивнее тяжелых и падали на землю позднее тяжелых предметов. А это, естественно, противоречило бы предсказанию Галилея.

См. также:

Суд над Галилеем

Суд римско-католической инквизиции над Галилеем — такой же стойкий околонаучный миф, как и яблоко, якобы упавшее на голову Ньютону. И, как обычно и бывает в мифологии, к действительности эта история имеет мало отношения. Если верить этому мифу, Галилей привел суду неопровержимые доказательства правильности взглядов Николая Коперника на устройство Солнечной системы, согласно которым Земля вращается вокруг Солнца, а не наоборот, а затем был сломлен Церковью, желавшей подавить эту теорию, и принужден публично отречься от своих взглядов. На самом же деле Коперник, будучи весьма изощренным церковным политиком, представил свою гелиоцентрическую теорию в таком виде, что она вполне удовлетворяла богословские авторитеты того времени (в частности, называя её не иначе, чем «гипотезой»). Теория Коперника широко обсуждалась до Галилея и учеными, и даже самими ватиканскими богословами.

В 1616 году Галилей опубликовал книгу «Звездный вестник», в которой обобщил телескопические наблюдения и привел сильные доводы в пользу системы Коперника. Причем написана книга была на итальянском, а не на латыни, что сделало ее доступной не только ученым, но и широкому кругу образованных читателей. В ответ на упреки, что книга якобы противоречит церковным канонам, Коллегия кардиналов вызвала Галилея на свое заседание. Далее начинаются неясности, вызванные противоречивостью дошедших до нас свидетельств участников этого заседания. Согласно официальной версии, Галилею было указано на недопустимость дальнейших публичных обсуждений идей Коперника в иной форме, кроме как с указанием на то, что это всего лишь гипотеза, пока не будут представлены неопровержимые доказательства ее правильности. Галилей же стоит на том, что подобного предупреждения не получал.

Как бы то ни было, в 1632 году Галилей опубликовал работу «Диалог о двух главнейших системах мира», где привел развернутые аргументы в пользу гелиоцентрической системы Коперника, вложив при этом официальные возражения Папы в уста персонажа по имени Симпличо (по-итальянски «простак». — Прим. переводчика). Вот тогда-то против Галилея и было впервые выдвинуто обвинение в «подозрении на ересь»; при этом нужно понимать, что в устах инквизиции это обвинение соотносится с обвинением в собственно «ереси», примерно так же, как в современном гражданском судопроизводстве обвинение в непреднамеренном убийстве соотносится с обвинением в предумышленном убийстве при отягчающих обстоятельствах. От подозрения в ереси Галилей себя очистил, публично заявив, что сам не верит в то, что написал, после чего остаток жизни провел всего лишь под домашним арестом у себя во Флоренции. (В 1992 году Римско-католическая церковь официально пересмотрела приговор суда на том основании, что судьи не сумели отделить вопросов веры от научных фактов.)

Так что мы выносим из всей этой истории? По моему личному разумению, она описывает не более чем умышленное раскручивание маховика неповоротливой бюрократической машины человеком, намеренно стремящимся к конфронтации с ней. (Мне, например, представляется, что у Совета кардиналов имелись в то время дела и поважней, чем разбирательство с ученым по поводу абстрактной космологической теории.) Правда тут еще и в том, что доводы Галилея в пользу системы Коперника на поверку вовсе не являются такими уж убедительными. Более того, с точки зрения современной науки можно сказать, что Галилей пришел к верному заключению путем ошибочных рассуждений. Суда над ученым это, естественно, не оправдывает, однако всё действо, в этой связи, предстает в ином — куда менее мифологическом — свете.

elementy.ru