Узел крепления натяжной УК-Н-М Рабочая нагрузка до 8 кН (☑)
Главная → Системы подвеса кабеля → Консоль-кронштейн → RC19 УК-Н-М
Бренд:
RC19
В наличии:
Пост. 1-3 дня
Центр. склад:
Ожидается
Оцени!
Код товара:
02484
Артикул:
УК-Н-М
- Описание
- Сопутствующие товары
- Отзывы
Монтаж узла крепления натяжного УК-Н-М на столбовых опорах с помощью стальной ленты.
Характеристики
Рабочая нагрузка до 8 кН.
Материал оцинкованная сталь.
Вес 0,410 кг.
| Монтажная лента | ||||||||
|---|---|---|---|---|---|---|---|---|
| 02438 | Лента стальная F 207 (50 M) (рулон 50м) | 3’914,28 | 3’802,22 |
| ||||
Отзывы УК-Н-М RC19
Отзывы о компании Анбик на Яндекс картах
Анбик РК на карте Москвы — Яндекс. Карты
Карты
Похожие товары
Узел крепления ХП-450
3 749,76 ₽/шт
В корзину
Узел натяжной ХН-570
2 178,00 ₽/шт
В корзину
Натяжной узел крепления. Рабочая нагрузка не менее 70 кН
2 166,91 ₽/шт
В корзину
Узел натяжной ХН-550
2 162,16 ₽/шт
В корзину
Узел натяжного крепления УН(3)-2200
2 002,00 ₽/шт
В корзину
Узел натяжной ХН-390
1 964,16 ₽
В корзину
Узел крепления ХП-580
1 671,12 ₽/шт
В корзину
Узел крепления ХП-500
1 595,09 ₽/шт
В корзину
Узел поддерживающего крепления УП(2)-1200
1 573,00 ₽/шт
В корзину
Узел крепления ХП-400
1 498,46 ₽/шт
В корзину
Узел крепления ХП-350
1 450,94 ₽/шт
В корзину
Узел натяжного крепления УН(3)-1200
1 430,00 ₽/шт
В корзину
Замена
| 02483 | УК-Н-01 | Узел крепления натяжной УК-Н-01. Рабочая нагрузка до 10 кН. Рабочая нагрузка до 10 кН. | 168.54 | 163.43 |
Преимущества
Комплексные поставки сетевого оборудования с честными сроками поставки.
|
Срочная доставка заказа от 3 часов в г.Москва и Московской области. Собственный грузовой транспорт это оптимальное решение для доставки крупногабаритных и комплексных заказов сетевого оборудования по Москве и Московской области. Доставка в Санкт-Петербург, Ростов-на-Дону, Екатеринбург, Новосибирск, Нижний Новгород, Казань, Красноярск, Омск, Томск, Самара, Уфа, Воронеж, Пермь, Волгоград, Краснодар и другие города России и стран СНГ осуществляем через 7 транспортных компаний для доставок грузов. |
|
|
Под собственной маркой RC19 производим в России и Беларуси телекоммуникационное и кабеленесущее оборудование и поставляем под маркой RC19 товары импортированные нами из Китая |
|
|
Два склада в Москве рядом с метро Каширская с большой номенклатурой телекоммуникационных напольных и настенных шкафов , кабельных лотков и электротехнических комплектующих. |
|
|
Надежная компания с более чем 10 летним опытом работы на рынке сетевого и кабеленесущего оборудования. Весь товар сертифицирован и является подлинным. |
|
|
Ценовая политика компании с особыми скидками для торговых, монтажных и инжиниринговых организация. Исключительно интересные цены в 3 колонке для постоянных клиентов. |
Оставить заявку
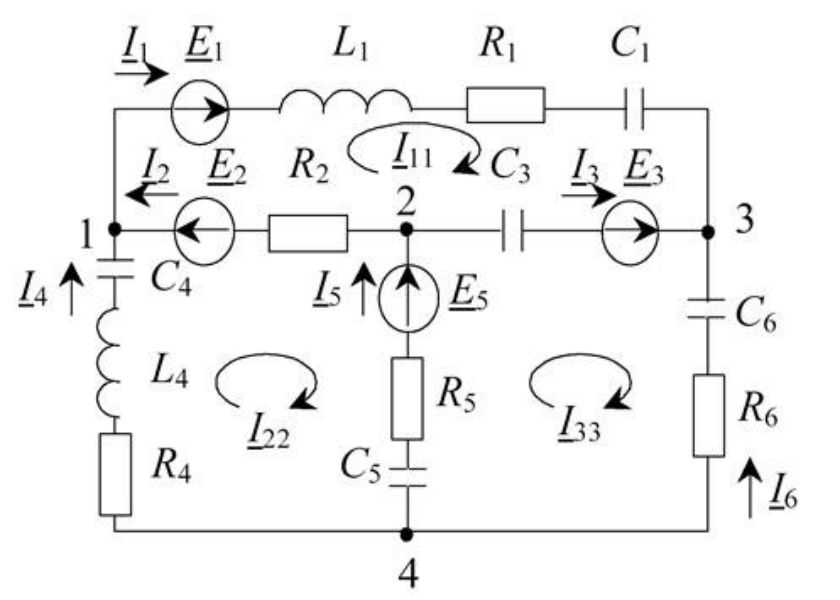
8.Электрическая схема, её ветви, узлы, контуры.
Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов рассматриваемой электрической цепи
Ветвь
образуется одним или несколькими
последовательно соединенными элементами
цепи.
Узел – место соединения трех или большего числа ветвей.
Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром
9.Последовательное и параллельное соединение элементов. Устранимый узел.
Под последовательным сопротивлением понимают такое соединение, при котором через все элементы проходит один и тот же ток.
Ветви, присоединенные к 1-ой паре узлов – параллельные ветви. Напряжение на всех параллельных ветвях одинаково.
Узел – место соединения 3-ех и большего числа ветвей.
Устранимый узел – место соединения 2-ух ветвей.
10.Закон Ома для пассивного и активного участка электрической цепи. Применение закона Ома
Закон Ома для пассивного участка электрической цепи.
При
протекании электрического тока через
сопротивление R, напряжение U и ток I на
этом участке связаны между собою согласно
закону Ома:
Сопротивление
R
– это коэффициент пропорциональности
между током и напряжением.
Закон Ома можно записать через разность потенциалов:
Закон Ома для активного участка цепи между точками а и в имеет вид:
Напряжение на участке электрической цепи Uab и ЭДС берутся со знаком «плюс», если их направление совпадает с направление протекания тока. Напряжение (разность потенциалов) и источник электродвижущей силы берутся со знаком «минус», если их направление не совпадает с направлением протекания тока.
Пример составления уравнения по закону Ома
Рассмотрим пример решения задачи на составления уравнения по закону Ома для участка линейной электрической цепи с двумя источниками ЭДС.
Пусть в данной электрической цепи направление тока будет из точки “a” в точку “b”. Напряжение Uab Направляется всегда из первой буквы (“a”) к последней (“b”).
Согласно
правилу составления уравнения по закону
Ома источник ЭДС E1 берем со знаком
“плюс”, т.
Источник ЭДС E2 берем со знаком “минус”, т.к. его направление (направление стрелочки) не совпадает с направлением протекающего тока.
Напряжение Uab или разность потенциалов φa – φb берем со знаком “плюс”, т.к. его направление совпадает с направление протекающего тока.
Сопротивление R1 и R1 соединены последовательно. При последовательном соединении сопротивлений их эквивалентное значение равно сумме.
В результате составленное уравнение по закону Ома будет иметь вид:
Пусть потенциал в данной задаче потенциал точки “а” равен 10 вольт, потенциал точки “b” = 7 вольт, E1=25 В, E2=17 В, R1=5 Ом, R2=10 Ом. Рассчитаем величину тока:
Полученный ток равен 1 Ампер.
11. Потенциальная диаграмма и ее построение
Под потенциальной
диаграммой понимают
график распределения потенциала вдоль
какого-либо участка цепи или замкнутого
контура. По оси абсцисс на нем откладывают
сопротивления вдоль контура, начиная
с какой-либо произвольной точки, по оси
ординат — потенциалы. Каждой точке
участка цепи или замкнутого контура
соответствует своя точка на потенциальной
диаграмме.
По оси абсцисс на нем откладывают
сопротивления вдоль контура, начиная
с какой-либо произвольной точки, по оси
ординат — потенциалы. Каждой точке
участка цепи или замкнутого контура
соответствует своя точка на потенциальной
диаграмме.
Потенциальная диаграмма построена, начиная с точки a, которая условно принята за начало отсчета. Потенциал aпринят равным нулю.
Точка цепи, потенциал которой условно принимается равным нулю, называется базисной.
Если в условии задачи не оговорено, какая точка является базисной, то можно потенциал любой точки условно приравнивать к нулю. Тогда потенциалы всех остальных точек будут определяться относительно выбранного базиса.
1.5: Уравнения цикла и узла
- Сохранить как PDF
- Идентификатор страницы
- 55511
- Джеймс Киртли
- Массачусетский технологический институт через MIT OpenCourseWare
Существует два хорошо разработанных формальных способа решения для потенциалов и токов в сетях, часто называемых методами уравнения контура и узла. Они тесно связаны, используя KCL и KVL вместе с ограничениями элементов для построения наборов уравнений, которые затем можно решить для потенциалов и токов.
Они тесно связаны, используя KCL и KVL вместе с ограничениями элементов для построения наборов уравнений, которые затем можно решить для потенциалов и токов.
- В методе уравнения узла KCL записывается в каждом узле сети с токами, выраженными через потенциалы узла. KVL выполняется, потому что потенциалы узлов уникальны.
- В методе петлевого уравнения KVL пишется о наборе замкнутых путей в сети. Определены «контурные токи» и сделаны так, чтобы удовлетворять KCL, а напряжения ветвей выражаются через них.
Эти два метода эквивалентны, и выбор между ними обычно зависит от личных предпочтений. Метод узлового уравнения, вероятно, более широко используется и хорошо поддается компьютерному анализу.
Чтобы проиллюстрировать, как работают эти методы, рассмотрим сеть на рис. 12.
В этой сети три узла. Мы собираемся написать KCL для каждого из узлов, но учтите, что требуются только два явных уравнения. Если KCL удовлетворяется на двух узлах, он автоматически удовлетворяется и на третьем. Обычно базовым узлом является тот, для которого мы не пишем выражение.
Обычно базовым узлом является тот, для которого мы не пишем выражение.
KCL, записанный для двух верхних узлов сети:
\[\ -i_{1}+\frac{V}{R_{1}}+\frac{V-v_{2}}{R_{2}}=0\label{9} \]
\[\ -I+\frac{v_{2}-V}{R_{2}}+\frac{v_{2}}{R_{3}}=0\label{10} \]
Эти два выражения легко решаются для двух неизвестных, \(\ i_{1}\) и \(\ v_{2}\):
\(\ \begin{array}{c}
v_{2}=\frac{R_{3}}{R_{2}+R_{3}} V+\frac{R_{2} R_{3}} {R_{2}+R_{3}} I \\
i_{1}=\frac{R_{1}+R_{2}+R_{3}}{R_{1}\left(R_{2} +R_{3}\right)} V-\frac{R_{3}}{R_{2}+R_{3}} I
\end{массив}\)
Метод уравнения контура аналогичен. Нам нужно столько же независимых выражений (два), поэтому нужно взять два независимых цикла. Для этого набрать так, как показано на рисунке 13: 9 петель.0032
- Контур, включающий источник напряжения и \(\ R_{1}\).
- Цикл, включающий \(\ R_{1}, R_{2}\) и \(\ R_{3}\).
Также необходимо определить контурные токи, которые мы будем обозначать как \(\ i_{a}\) и \(\ i_{b}\). Это токи, циркулирующие по двум петлям. Обратите внимание, что там, где контуры пересекаются, фактический ток ответвления будет суммой или разницей между токами контура. Для этого примера предположим, что контурные токи заданы циркулирующими против часовой стрелки в двух контурах. Два уравнения контура:
Это токи, циркулирующие по двум петлям. Обратите внимание, что там, где контуры пересекаются, фактический ток ответвления будет суммой или разницей между токами контура. Для этого примера предположим, что контурные токи заданы циркулирующими против часовой стрелки в двух контурах. Два уравнения контура:
\[\ V+R_{1}\left(i_{a}-i_{b}\right)=0\метка{11} \]
\[\ R_{1}\left(i_{b}-i_{a}\right)+R_{2} i_{b}+R_{3}\left(i_{b}-I\right)= 0\метка{12} \]
Они одинаково легко решаются для двух неизвестных, в данном случае двух контурных токов \(\ i_{a}\) и \(\ i_{b}\).
Эта страница под названием 1.5: Loop and Node Equations распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом Киртли (MIT OpenCourseWare) посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джеймс Киртли
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- MIT OpenCourseWare
- Показать оглавление
- нет
- Теги
- source@https://ocw.
 mit.edu/courses/6-061-introduction-to-electric-power-systems-spring-2011
mit.edu/courses/6-061-introduction-to-electric-power-systems-spring-2011
- source@https://ocw.
3.4 Анализ узловых напряжений – Основы прикладной электротехники
Анализ напряжения в узле — это систематический метод анализа цепей, основанный на определении напряжений во всех узлах цепи относительно опорного или наземного узла в цепи. Чтобы мотивировать этот метод анализа, рассмотрим схему, показанную на рис. 3.26. Схема имеет 6 элементов, в том числе известный источник напряжения, , и пять резисторов номиналами . (Представьте, что вместо переменных у нас есть реальные числа.) Рассмотрим усилия, затраченные на определение всех напряжений (пять неизвестных) и всех токов (шесть неизвестных) в этой цепи. Или рассмотрим усилия, затраченные на получение тока через резистор . В этой схеме нет последовательно или параллельно соединенных резисторов, поэтому упрощение схемы на основе эквивалентного сопротивления не способствует упрощению работы. Мы могли бы решить эту схему повторным применением KCL, KVL и закона Ома к решить все неизвестные схемы . В схеме 11 неизвестных, поэтому нам нужно разработать систему из 90 149 11 одновременных 90 150 линейных уравнений, применяя KVL, KCL и закон Ома к различным контурам, узлам и резисторам в цепи. Решение этой системы уравнений, в принципе, завершило бы задачу анализа цепи. Мы разрабатываем эти уравнения ниже, чтобы проиллюстрировать на примере этой схемы усилия, затраченные на такое «грубое» применение законов анализа цепей. Затем мы вводим анализ напряжения узла, который часто приводит к результатам со значительно меньшими усилиями.
Мы могли бы решить эту схему повторным применением KCL, KVL и закона Ома к решить все неизвестные схемы . В схеме 11 неизвестных, поэтому нам нужно разработать систему из 90 149 11 одновременных 90 150 линейных уравнений, применяя KVL, KCL и закон Ома к различным контурам, узлам и резисторам в цепи. Решение этой системы уравнений, в принципе, завершило бы задачу анализа цепи. Мы разрабатываем эти уравнения ниже, чтобы проиллюстрировать на примере этой схемы усилия, затраченные на такое «грубое» применение законов анализа цепей. Затем мы вводим анализ напряжения узла, который часто приводит к результатам со значительно меньшими усилиями.
Эта схема повторно нарисована на рисунке 2.27 с аннотациями для: напряжения на каждом элементе схемы и тока через него, которые являются искомыми переменными; четыре узла схемы, обозначенные A, B, C, D; несколько петель, а именно ABDA, BCDB, ACBDA и DACD (это далеко не все возможные петли). Записав закон Ома для пяти резисторов, применив KCL к четырем узлам и применив KVL к нескольким контурам цепи, мы получим набор одновременных уравнений.
Рисунок 3.27
Этот набор уравнений включает пять уравнений закона Ома:
(1)
(2)
(3)
(4)
(5)
в дополнение к четырем уравнениям KCL, включая KCL в узле A,
(6)
KCL в узле B,
(7)
KCL в узле C,
(8)
и KCL в узле D,
(9)
и пять уравнений КВЛ, включая КВЛ вокруг контура ABDA,
(10)
КВЛ вокруг петли BCDB,
(11)
КВЛ вокруг петли ACBA,
(12)
KCL круговая петля ACDA,
(13)
и (наконец) KCL вокруг петли ACBD,
(14)
Уравнения (1) – (14) представляют собой набор из 14 одновременных линейных уравнений для этой системы. В системе всего 11 неизвестных, и мы могли бы написать дополнительные уравнения, включив дополнительные контуры (например, ABCDA). Однако алгебраические манипуляции с уравнениями (1) – (14) (которых мы здесь делать не будем!) показали бы, что не все эти уравнения линейно независимы. Среди четырех уравнений KCL только три являются независимыми, а четвертое может быть получено из линейной комбинации любых трех. Количество независимых уравнений KCL фактически равно количеству узлов в схеме минус один. Эта схема имеет четыре узла, поэтому существует три независимых уравнения KCL. Среди пяти уравнений КВЛ только три являются независимыми. (Всего мы могли бы перечислить 7 уравнений КВЛ, используя петли ABDA, BCDB, ACBA, ACDA, ACBDA, ABCDA и DBACD). Количество независимых уравнений КВЛ фактически равно количеству открытых участков в цепи.
Среди четырех уравнений KCL только три являются независимыми, а четвертое может быть получено из линейной комбинации любых трех. Количество независимых уравнений KCL фактически равно количеству узлов в схеме минус один. Эта схема имеет четыре узла, поэтому существует три независимых уравнения KCL. Среди пяти уравнений КВЛ только три являются независимыми. (Всего мы могли бы перечислить 7 уравнений КВЛ, используя петли ABDA, BCDB, ACBA, ACDA, ACBDA, ABCDA и DBACD). Количество независимых уравнений КВЛ фактически равно количеству открытых участков в цепи.
Эта цепь имеет три открытых участка, следовательно, существует три независимых уравнения КВЛ, управляющих этой цепью. Сгруппировав вместе пять независимых уравнений закона Ома, а также три независимых уравнения KCL и три независимых уравнения KVL, мы получим 11 независимых уравнений. Подставив фактические числа для , , , , а затем решив эту систему из 11 уравнений, мы получим 11 неизвестных в схеме. (Так весело!)
(Так весело!)
Анализ напряжения узла обеспечивает более простой и компактный способ решения схемы. Снова рассмотрим ту же схему, но предположим, что мы уже знали напряжения узла , , и относительно эталонного (или заземленного) узла. Предположим, что мы хотим получить , , и . Учитывая знание узловых напряжений и относительно наземного узла, рассмотрите перерисованную схему ниже:
Рисунок 3.29. Мы можем легко записать искомые значения в терминах известных узловых напряжений:
(15)
(16)
(17)
(18)
(19)
Должно быть ясно, что знание узловых напряжений позволяет легко определить другие переменные схемы.
Определение узловых напряжений . Наша схема воспроизведена на рис. 3.30. Мы будем использовать этот рисунок для определения узловых напряжений.
Рисунок 3.30. Напряжение узламожно легко получить, заметив, что этот узел подключен непосредственно к клемме + источника напряжения, таким образом:
(20)
Чтобы определить напряжения оставшихся неизвестных узлов, мы используем KCL:
KCL, выполненный на узле, дает:
(21)
, который можно переписать как
.
(22)
и, наконец, KCL, выполненный на узле, дает:
(23)
, который можно переписать как
.(24)
Уравнения (20), (22) и (24) образуют набор одновременных линейных уравнений, решение которых дает нам узловые напряжения , и . Для этой конкретной схемы, поскольку напряжение узла всегда равно напряжению источника , не является неизвестной переменной, и система уравнений быстро сводится к системе, имеющей два уравнения и два неизвестных.
Любое из узловых напряжений может быть выбрано в качестве заземления или эталонного узла. Возможность немедленной записи иллюстрирует, почему мы выбрали конкретный наземный узел, указанный на рисунке 3.30, в качестве опорного узла. Такой выбор наземного узла сводил задачу к решению для двух неизвестных узлов, а не к решению для трех неизвестных узлов. Если бы мы выбрали в качестве опорного узла, мы все равно смогли бы анализировать схему, но нам нужно было бы решать для трех, а не двух неизвестных через систему трех, а не двух одновременных уравнений.
Пример: Решите для узловых напряжений и в схеме ниже, а затем определите токи и .
Рисунок 3.31Решение: Мы можем использовать ур. (20), (22) и (24) решить эту задачу, подставляя числовые значения, заданные в схеме. Обратите внимание, что эта система из трех одновременных уравнений легко сводится к системе из двух одновременных уравнений, поскольку = 5 В. Подстановка численных значений показанных элементов схемы в уравнения (22) и (24) и одновременное решение этих двух уравнений дает = 2,5 В и = 2,5 В. Эти напряжения отмечены красным цветом на схеме. Зная эти напряжения, легко получить токи и:
= 0,025 В или 25 мВ
и
= 0 В
Пример: В схеме, показанной на рис. делители, с и .
Рисунок 3.32Теперь рассмотрим рисунок 3.33, на котором сопротивление подключено между и . Используйте анализ напряжения узла, чтобы показать, что независимо от значения .
Рисунок 3.33
Решение. Начнем с применения KCL к узлу, соответствующему которому получается
(25)
или
(26)
.
Применение KCL к узлу, соответствующему, дает
(28)
или
(29)
, а алгебраические манипуляции для изоляции одной стороны уравнения приводят к
(30)
Подстановка уравнения (27) в уравнение (30) дает
(31)
Когда это уравнение упрощается, мы получаем результат
(32)
, и когда этот результат подставляется обратно в уравнение (30), мы находим
(33)
Таким образом, мы видим, что результаты не зависят от значения сопротивления . Этот результат также можно было интуитивно понять с самого начала, заметив, что и равны в исходной схеме на рис. 3.32а. Поскольку разница напряжений между этими двумя узлами равна нулю, любой резистор, помещенный между двумя узлами, будет иметь нулевой ток и, следовательно, не повлияет на цепь. Выводы, подобные этому, необходимо обдумывать и использовать с осторожностью, а возможность проведения анализа напряжения в узле, такого как сделанный здесь, явно предоставляет средства для аналитической проверки результата.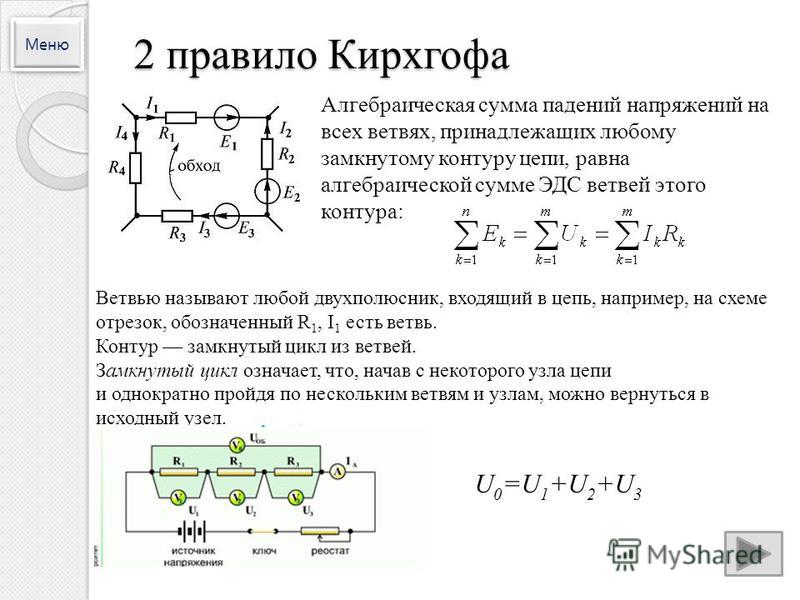
Пример. Вариант предыдущей задачи показан на рис. 3.34, где мы хотим рассмотреть влияние различных значений на схему. Если мы сначала рассмотрим случай, когда (имеется в виду, что резистор представляет собой разомкнутую цепь), то с помощью анализа деления напряжения мы обнаружим, что в то время как . Изменение до конечного значения приведет к протеканию тока из-за разницы напряжений между и , и это изменит значения и . Если (имеется в виду, что резистор представляет собой короткое замыкание), то у нас будут параллельные резисторы и верхний резистор, что даст эквивалентное сопротивление . Точно так же нижние резисторы будут включены параллельно с эквивалентным сопротивлением . В данном случае через деление напряжения. Если бы сопротивление было некоторым конечным значением, отличным от , мы использовали бы анализ напряжения узла, чтобы определить и для этой схемы.
Рисунок 3.34
Примечание: иногда мы используем имена переменных в нижнем регистре, например и , и в других случаях мы используем имена переменных в верхнем или верхнем регистре, например и .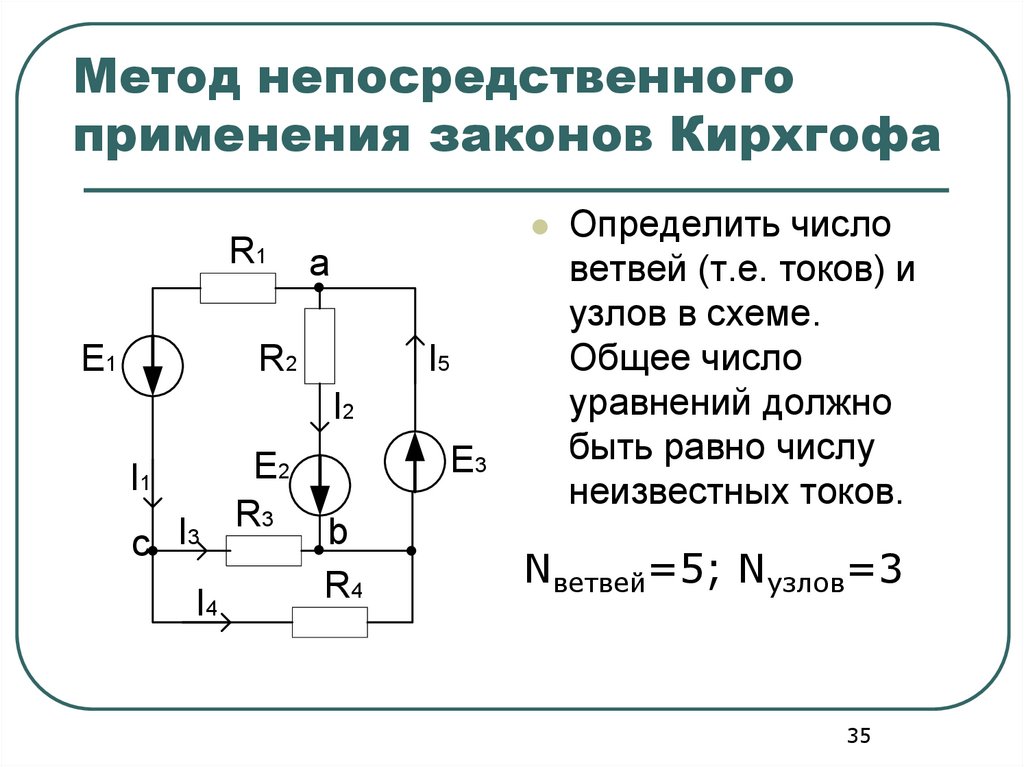

 Прямые поставки из Китая модулей вентиляторных, осевых вентиляторов, стоек 19 дюймов и медных 19 дюймовых шин .
Прямые поставки из Китая модулей вентиляторных, осевых вентиляторов, стоек 19 дюймов и медных 19 дюймовых шин . mit.edu/courses/6-061-introduction-to-electric-power-systems-spring-2011
mit.edu/courses/6-061-introduction-to-electric-power-systems-spring-2011