Узел в электротехнике это: Узел электрической цепи

Электротехника Ч1 – Стр 2

11

	Rвн	1		I т	1
E		Rн	IT	Rвн	Rн
		1′			1′
	а				б

Рис. 1.6. Схемы замещения источника электрической энергии: (а) – источником Э.Д.С., (б) – источником тока

Для схемы рис.

1.6, а это очевидно и следует из того, что Rвн и Rн включены последовательно. Для схемы цепи по рис. 1.6, б известно, что ток IT = Е/Rвн распределяется обратно пропорционально параллельно включенным Rвн и Rн, т.е.:

I = IT	Rвн	=	E		Rвн			E
							=		.
	R + R		R		(R + R	)		R + R
	вн н		вн		вн н			вн н

Каким из двух источников воспользоваться, выбирает инженер. Пример.

В схеме рис.1.6, а источник Э.Д.С. имеет параметры Е = 100В, Rвн =

2 Ом. Определить параметры эквивалентного источника тока в схеме рис. 1.6, б. Решение:

IT = E / Rвн = 50А.

Следовательно, параметры эквивалентной схемы рис. 1.6, б имеют значение:

IT = 50А; Rвн = 2 Ом.

Источники питания могут иметь постоянную Э.Д.С. – Е или переменную е(t), изменяющуюся во времени по заданному закону. В первом случае в цепи протекает постоянный ток, и она называется цепью постоянного то- ка. Во втором случае ток i(t) и напряжение u(t) переменные, поэтому цепь называется цепью переменного тока. В электротехнике чаще других применяются синусоидальные ток и напряжение.

12

3. ПРИЕМНИКИ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ

Приемники электрической энергии делятся на пассивные и активные.

Пассивными называют приемники, в которых под действием приложенного

напряжения не возникает Э.Д.С. ВАХ пассивных приемников проходят через начало координат. При отсутствии напряжения ток этих элементов равен нулю.

Основной характеристикой пассивных элементов является сопротив-

ление. Пассивные элементы, сопротивление которых не зависит от при-

ложенного напряжения, называются линейными. Реально таких элементов не существует. Но весьма близки к ним резисторы, реостаты, лампы накаливания и др. Зависимость напряжения от тока в таких элементах определяется законом Ома, т.е. U = IR, где R – сопротивление элемента. Эта зависимость не меняется, если напряжение и ток – переменные.

К приемникам электрической энергии относятся емкостные и индуктивные элементы. При постоянном напряжении, приложенном к емкости, на ее обкладках накапливается заряд

Q = C U .

(1.5)

Ток через емкость не протекает. Это означает, что сопротивление емкости в цепи постоянного тока равно бесконечности. Если к емкости приложено переменное напряжение u(t), то и заряд на ее обкладках становится переменным

Q(t) = C u(t) .

(1.6)

В этом случае в цепи возникает ток

ic (t) =	dQ(t)	= C	du(t)	.	(1.7)
	dt
			dt

Выражение (1.7) позволяет определить падение напряжения на емкости, если в цепи протекает переменный ток

13

		1	t
	uc (t) =		∫ic (t)dt .	(1.8)
		C
			0

Очевидно, что сопротивление емкостного элемента переменному току определяется законом Ома, но зависит не только от величины, но и от формы тока и напряжения.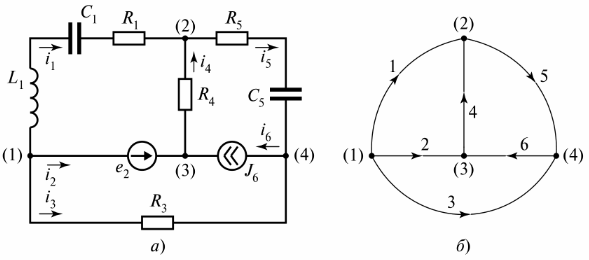

Основным параметром индуктивного элемента является индуктивность – L. Если через индуктивность L протекает постоянный ток I, то в ней возникает постоянное во времени потокосцепление самоиндукции

ψ = L I .

(1.9)

Будем полагать, что элемент L идеальный, т.е. сопротивление провода витков обмотки катушки индуктивности r отсутствует. Очевидно, что при этом падение напряжения на элементе равно нулю.

Предположим, что индуктивный элемент подключен к источнику пе-

ременного тока i(t). Потокосцепление также будет переменным – ψ(t) = L i(t). Изменяющееся потокосцепление наводит в катушке Э.Д.С. самоиндукции

eL (t) = −	dψ (t)	= −L	di(t)	.	(1.10)
	dt
			dt

Так как r=0, то Э. Д.С. еL(t) уравновешивает напряжение, приложенное к индуктивности

u(t) = −eL (t) = L	di(t)	.	(1.11)
	dt

Выражение (1.11) позволяет определить ток индуктивности, если известно приложенное к ней напряжение u(t).

		1	t
	iL (t) =		∫u(t)dt .	(1.12)
		L
			0

Кроме пассивных приемников в электротехнике применяются активные приемники. К ним относятся электродвигатели, аккумуляторы в процессе их

14

заряда и др. В цепи переменного тока при определенных условиях роль активных элементов выполняют индуктивность и емкость. В активных элементах возникает противо-Э.Д.С. Е. Приложенное к приемнику напряжение уравновешивается противо-Э.Д.С. и падением напряжения на сопротивлении элемента, т.е.

U = E + I Rвн .

(1.13)

4. ОСНОВНЫЕ ТОПОЛОГИЧЕСКИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Основными топологическими понятиями теории электрических цепей являются ветвь, узел, контур, двухполюсник, четырехполюсник, граф схемы

электрических цепей, дерево графа схемы. Рассмотрим некоторые из них.

Ветвью называют участок электрической цепи с одним и тем же

током. Она может состоять из одного или нескольких последовательно включенных элементов. Так, схема цепи на рис. 1.7 состоит из пяти ветвей.

I1	R1 а 1 I3	R3	2
	I2		I4	I5
E1	R 2		R 4	R 5
	б
	1′		2′
Рис. 1.7. Схема замещения разветвленной

электрической цепи с одним источником Э.Д.С.

Узлом называют место соединения двух элементов. Место соедине-

ния трех и более ветвей называют сложным узлом. Сложный узел обозна-

чается на схеме точкой. Сложные узлы, имеющие равные потенциалы, объ-

единяются в один потенциальный узел. На схеме рис.1.7 узлы 1′ и 2′ могут

15

быть объединены в один потенциальный узел. Поэтому схема имеет три сложных потенциальных узла.

Контуром называют замкнутый путь, проходящий через несколько ветвей и узлов электрической цепи. Для схемы рис. 1.7 один из контуров включает позиции 2; R5; 2′; R4. Независимым называется контур, в состав которого входит хотя бы одна ветвь, не принадлежащая соседним конту-

рам. Так, схема рис.1.7 содержит три независимых контура.

Двухполюсником называют часть электрической цепи с двумя выде-

ленными зажимами – полюсами. Двухполюсник обозначают прямоугольником с индексами «А» или «П». Индекс «А» применяют для обозначения активного двухполюсника, в составе которого есть источники Э.Д.С. Индекс «П» применяют для обозначения пассивного двухполюсника. Например, часть схемы рис.1.7 с зажимами а и б может быть представлена пассивным двухполюсником (рис.1.8).

R1	а
	П
E1
	б

Рис.1.8. Пассивный двухполюсник

6. ЗАКОНЫ ОМА И КИРХГОФА

Все электрические цепи подчиняются законам Ома и Кирхгофа. Краткая информация об этих законах заключается в следующем.

Закон Ома для участка цепи без Э.Д.С. устанавливает связь между током и напряжением на этом участке

16

	I =	U	или U = I R .	(1.14)
		R

Закон Ома для участка цепи, содержащего Э. Д.С., позволяет найти ток этого участка

I =	U	аб	± E	.	(1.15)
		R

здесь а, б – крайние точки участка; Е – значение Э.Д.С.

В (1.15) знак «плюс» ставится при совпадении направления тока, протекающего по участку, с направлением Э.Д.С.

Первый закон Кирхгофа имеет две формулировки.

1.Сумма токов, протекающих через любой узел, равна нулю.

2.Сумма токов, втекающих в узел, равна сумме токов, вытекающих из него.

Второй закон Кирхгофа можно сформулировать так:

Алгебраическая сумма падений напряжения в любом замкнутом кон-

туре равна алгебраической сумме Э.Д.С. вдоль этого контура, т.е.

n	m
∑Ri Ii = ∑Ei .
i =1	i =1

В каждую из сумм слагаемые входят со знаком «плюс», если они совпадают

снаправлением обхода контура.

7.ПОНЯТИЯ ОБ УСТАНОВИВШЕМСЯ И ПЕРЕХОДНОМ

ПРОЦЕССАХ

Режим работы электрической цепи, при котором токи и напряжения всех ее ветвей остаются неизменными или изменяются по периодическому закону, называется установившимся. В электрических цепях такой режим может иметь место при длительном воздействии источника электрической

17

энергии, при неизменных параметрах приемников или при отключенном источнике.

В реальных условиях необходимо управлять работой электрических цепей, т. е. включать или отключать источники энергии, изменять параметры R, L и C элементов. Перечисленные действия принято называть коммутацией, а процессы, возникающие в результате коммутации, – переходными. Физически переходные процессы представляют собой изменение энергетического состояния элементов и цепи в целом при переходе цепи от одного режима (отключенного источника) к другому режиму (включенного источника). Это быстро протекающие процессы, но именно на интервалах их существования в цепи возможны опасные броски токов и напряжений. Поэтому переходные процессы подлежат изучению.

Рассмотрим схему цепи, приведенную на рис. 1.9, а. Будем полагать, что параметры элементов цепи постоянны. При замкнутом ключе К сумма падений напряжения на индуктивности L и сопротивлении R равна Э.Д.С. Е:

	L	di	+ R i = E .	(1.16)
		dt

В выражении (1.16) ток i и Э.Д.С. Е могут принимать конечные значения. Допустим, что ток i может измениться скачком за бесконечно малый промежуток времени 2t. Тогда отношение 2i / 2t = ∞. Применение этого значения к (1.16) означает нарушение равенства, представляющего второй закон Кирхгофа. Следовательно, допущение о возможности скачкообразного изменения тока через индуктивность неприемлемо. Однако напряжение

на индуктивности, равное L dtdi , может измениться скачком. Полученный вывод является обоснованием закона коммутации:

В ветви с индуктивностью ток в момент коммутации сохраняет

значение, которое он имел до коммутации, а после коммутации плавно из-

18

меняется от этого значения:

iL (0− ) = iL (0+ ).

Ток в цепи с емкостью (рис. 1.9, б) определяется выражением (1.7). Поэтому уравнение, составленное для цепи по второму закону Кирхгофа, принимает вид:

R C	duC	+ u = E,	(1.17)
	dt	C

где uc – напряжение на емкости, Е – Э. Д.С. источника.

Напряжение uc и Э.Д.С. E могут принимать конечные значения. Допустим, что uc может измениться скачком за бесконечно малый промежуток времени 2t. Тогда 2uc/2t = ∞ и левая часть уравнения (1.17) не будет равна правой. Следовательно, допущение о возможности скачкообразного изменения напряжения на емкости неприемлемо. Однако ток через емкость, рав-

ный C dudtC , может изменяться скачком. Полученный вывод является обос-

нованием следующего закона коммутации:

В ветви с емкостью напряжение в момент коммутации сохраняет

значение, которое было до коммутации, а после коммутации плавно изме-

няется от этого значения:

uC (0− ) = uC (0+ ).

19

В зависимости от состояния энергии в индуктивных или емкостных элементах цепей вида рис. 1.9 решаются две задачи:

–расчет цепи с нулевыми начальными условиями iL (0) = 0,

–расчет цепи с ненулевыми начальными условиями iL (0) ≠ 0.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ

1.1.Назовите элементы электрических цепей и приведите их условные графические обозначения.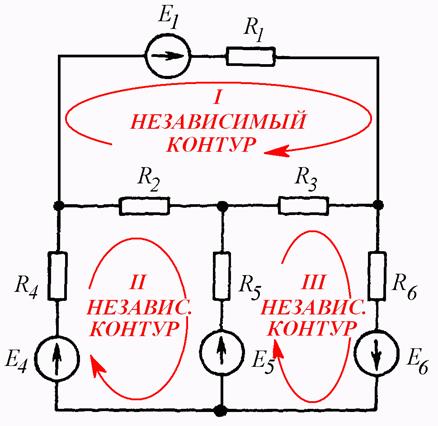 Как влияют характеристики элементов на название электрических цепей?

1.2.Что служит расчетным эквивалентом источника электрической энергии? В чем отличие идеального источника Э.Д.С. от идеального источника тока?

1.3.Как делятся все приемники электрической энергии? Приведите основные соотношения между током и напряжением для R, L и С элементов.

1.4.В каких целях введены топологические понятия электрических цепей?

1.5.Сформулируйте законы коммутации электрических цепей. Приведите математические соотношения, иллюстрирующие эти законы.

1.6.Определите внутреннее сопротивление источника Э.Д.С., если его ВАХ имеет наклон к оси токов под углом α = 30º.

1.7.В схеме рис. 1.6, б источник тока имеет параметры IТ = 10 А, Rвн = 0,5 Ом. Определите параметры эквивалентного источника Э.Д.С.

1.8.В схеме рис. 1.9, б источник Э.Д.С. Е = 10 В, сопротивление R = 10 Ом, а емкость С = 0,1 мкФ. Определите напряжение на емкости и ток цепи в момент включения ключа К.

ЛЕКЦИЯ 2. МЕТОДЫ АНАЛИЗА ЛИНЕЙНЫХ ЭЛЕКТРИЧЕ-

СКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

20

Реальные электротехнические устройства и системы имеют сложные схемы. Перед специалистами стоят задачи расчета их параметров. Процесс расчета параметров в теории электротехники принято называть «анализом схем». Электрические схемы любой сложности подчиняются законам Ома и Кирхгофа. Однако применение только этих законов часто приводит к неоп- равданно сложным решениям. Поэтому был разработан ряд методов анали- за, адаптированных к топологии электрических цепей и упрощающих про- цесс расчета их параметров. В лекции рассматриваются некоторые из таких методов.

1. АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИМЕНЕНИЕМ ЗАКОНОВ КИРХГОФА

При анализе электрических цепей определяют значение токов в их ветвях, падение напряжения на элементах или потребляемую мощность по заданному значению Э.Д.С., а также значение сопротивлений, проводимо- стей или других параметров по заданным значениям тока или напряжения. Для определенности будем полагать, что расчету подлежит значение токов ветвей схемы, приведенной на рис. 2.1.

Суть анализа электрических цепей применением законов Кирхгофа заключается в составлении системы из N независимых линейных уравнений, причем

N = (n − 1) + к,

где: n – число сложных потенциальных узлов, к – число независимых конту- ров.

По первому закону Кирхгофа составляется (n − 1) уравнение, по вто-

рому закону – к уравнений.

Основы электротехники 3 – Расчет режима цепи

Этим постом мы продолжаем серию публикаций, посвященных основам электротехники. В нем мы поговорим о расчёте режима электрической цепи. Начнем с того, что вообще значит расчёт цепи. Это определение тока на каждом её участке и потенциала в каждой её точке. Но участков и точек бесконечно много, поэтому вводят понятие узла и ветвей. Узел – это точка, где соединяются элементы. Ветвь – это участок между двумя узлами. Зачем это нужно? 

Начнем с узлов. Поскольку проводники у нас идеальные, сопротивление в них нет, это значит, что при перемещении заряда по проводнику он не совершает работы. Иначе говоря, потенциал всех точек проводника одинаковый. Если же несколько проводников соединяются вместе, как это и происходит в узле, то их потенциалы также выравниваются, то есть на схеме у нас столько разных потенциалов сколько узлов. 

Теперь ветви. На всей длине ветви ток одинаковый. Электронам просто некуда деваться из неё, поэтому и производная dq по dt остается постоянным. Значит в нашей цепи будет столько разных токов, сколько ветвей.

Из того, что электронам некуда деваться из ветви следует первое практическое правило расчета цепи, первое правило Кирхгофа. Согласно этому правилу, сумма токов узла равна нулю, то есть сколько тока в него втекает, столько же из него и вытекает. В самом деле если помнить, что ток – это движение электронов, правило становится очевидно – сколько электронов пришло, столько и ушло.

Всего правил Кирхгофа два, ко второму мы еще вернемся, но пока посмотрим, что нам дает первое. Весьма полезное и постоянно встречающиеся на практике действие с цепями это упрощение. Возьмём, к примеру, два резистора и соединим их выводы. Такое соединение называется параллельным. Для каждого из них справедлив закон Ома. Подключены они к одним и тем же узлам, а значит напряжение на них одинаковое. По правилу Кирхгофа, общий ток равен сумме отдельных токов.

Тогда можно записать, что суммарный ток равен напряжению, деленному на некоторое эквивалентное сопротивление Rx. Отсюда после несложных преобразований можно получить выражение  для параллельных резисторов. Что любопытно, в этом случае эквивалентное сопротивление всегда будет меньше меньшего. Впрочем, как мы с вами теперь понимаем это логично, для тока появляется обходной путь, а значит пройти ему проще.

Попробуем теперь смоделировать то, о чём мы сейчас говорили. Для этого воспользуемся библиотекой Simscape пакета MATLAB/Simulink, но сначала, конечно, скажем несколько слов о том, что это такое. Начинается всё с MATLAB. MATLAB – это с одной стороны математическое ядро всех остальных продуктов, а с другой – полноценный язык программирования. Работа в MATLABе – это привычный программистом исходный код. Simulink – это надстройка над MATLABом, визуальный язык программирования. В роли исходного кода выступают диаграммы, показывающие движение и преобразование потоков данных. Simscape – это надстройка над Simulink. Здесь уже составитель модели оперирует не данными, а объектами и их взаимодействиями. Simscape основан на тех уравнениях, которые мы с вами изучали в этой публикации и в предыдущих тоже, поэтому можно считать его виртуальным лабораторным стендом.

 

Соберём в нём ту схему, на примере которой мы рассуждали до этого, и измерим в ней токи какого-нибудь узла, например верхнего.

Как видим, первое правило Кирхгофа полностью выполняется, физику обмануть не удалось. С первым правилом Кирхгофа разобрались, теперь второе.

Второе правило Кирхгофа. Звучит оно так: алгебраическая сумма напряжений всех элементов, входящих в любой контур цепи равна нулю. Контур – это любой замкнутый путь на схеме, например вот такой:

Для понимания этого правила вспомним, что напряжение – это разность потенциалов и раскроем сумму. Нетрудно видеть, что из-за того, что контур замкнут, сумма всех этих разностей равна нулю. Иначе говоря заряд, прошедший по замкнутому контуру, не изменяет своего потенциала. Значит разность потенциалов, то есть напряжение, между концами контура равна нулю. Это и есть второе правило Кирхгофа. Из него почти напрямую следует упрощение цепи с последовательным элементами. 

Возьмем опять 2 резистора, но расположим их друг за другом. Это и называется последовательным соединением. Можно заметить, что это не что иное, как простая ветвь схемы, значит ток через оба резистора течет одинаковый. Теперь приложим к ней напряжение, для этого добавим источник ЭДС и замкнем цепь. По второму правилу Кирхгофа сумма напряжений на резисторах равна ЭДС источника. Выразим напряжение по закону Ома и вынесем за скобки ток. Теперь видно, что два наших резистора можно заменить на один эквивалентный, сопротивление которого равно сумме исходных.

Посмотрим теперь на модели. Как выполняется второе правило Кирхгофа? Для этого нам понадобится вольтметры.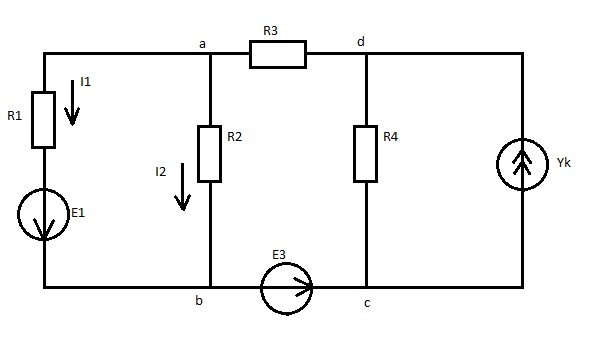 Итак, собираем схему.

Видим, что сумма напряжений вдоль произвольного контура равна нулю. Физику обмануть снова не удалось.

На правилах Кирхгофа основаны многие методы расчёта электрических цепей. Мы не будем говорить обо всех, их очень много. Разберём только один, пригодный для большинства практических задач – это метод контурных токов. Суть его довольно проста. Рассмотрим на примере нашей схемы.

Начнём с обозначения того, что мы будем искать. Зададим произвольным образом направление токов, а затем напряжение. Теперь выберем на схеме контуры, у нас их будет 3, выбирать можно произвольно, главное, чтобы были охвачены все элементы. Кстати, сразу же принимаем направление обхода каждого контура, и это тоже произвольно. 

А вот теперь основной элемент метода – собственно контурные токи. Это токи ветвей, входящих только в один контур. Суть метода в том, что вот эти самые контурные токи найти гораздо проще, чем реальные. Потом перейти от контурных уже к реальным. Соотношение между этими токами простое: если для ветвей, входящих только в один контур, реальный ток равен контурному; если же элемент входит в несколько контуров, тогда ток через него равен сумме контурных. Здесь важно не ошибиться в знаке. Если направление контурного тока совпадает с принятым направлением напряжения, то плюс, иначе – минус. Кстати, совершенно нормально, если какой-то ток получится отрицательным. Это всего лишь означает, что он течёт в противоположную сторону. Дальше для каждого контура запишем второе правило Кирхгофа. Получим систему уравнений.

Решив её, найдём контурные токи, а затем и реальные. Их можно умножить на сопротивление элементов и получить напряжение. Всё, цепь рассчитана. 

Метод контурных токов хорош ещё и тем, что легко формализуется, что позволяет автоматизировать расчёт. Вот пример в MATLAB, который его реализует. Здесь мы только выбираем контура, это единственный элемент творчества. Дальше расчет идет по заранее написанной программе. Обращаю ваше внимание на решение системы уравнений. Поскольку она записана в матричной форме, её решение занимает в MATLAB всего лишь одну строчку.

Вообще говоря, если бы мы расчёты вели не на модели, а на бумажке, то категорически необходимо сделать ещё один расчёт, поверочный. Но ведь мы никак не можем быть уверены, что нигде не сделали ошибку, например вычислительную. 

Для проверки есть простой, но абсолютно надежный метод баланса мощностей. Он основан на законе сохранения энергии. Всё очень просто. Сумма мощностей всех приёмников должна быть в точности равна сумме мощностей всех источников. Иначе у нас получится просто вечный двигатель. Для вычисления мощностей, перемножаем для каждого элемента ток на напряжение, получаем его мощность. При этом кстати важно следить за знаками. Дело в том, что мы выбирали контура и направление обхода совершенно произвольно, тогда ведь мы ещё ничего не знали о цепи, вот и выбирали в общем-то наугад. Фактические токи могут быть направлены противоположно тому, что мы выбрали. Это приводит к тому, что ток и напряжение на элементе могут быть направлены в разные стороны. Тогда при расчете баланса мощностей говорят, что у элемента отрицательная мощность.

Подведём итог. В этой публикации мы с вами посмотрели все основные методы расчёта электрической цепи:

• упрощения правильных последних элементов,
• правило Кирхгофа,
• метод контурных токов,
• поверочный расчет (метод баланса мощностей).

Вместе с теми законами, которые мы рассмотрели раньше, эти методы позволяют решать подавляющее большинство возникающих на практике задач по расчёту цепей. Причем любой сложности. Но возникает закономерный вопрос: зачем все эти методы нужны, если можно просто взять и смоделировать?

Ответ простой: для прикидки и оценки. Иначе говоря, чтобы понять похожи результаты моделирования на правду или нет. Смоделировать ведь можно неправильно, например вот такая модель.

Запускаем и убеждаемся, что источники дают меньше, чем берут потребители. Как говорится, заграница заинтересуется вашей разработкой. Получили вечный двигатель. Но, к сожалению, физику не обманешь. Ищем ошибку и выясняем, что при составлении модели неправильно подключили амперметр, просто перевернули. Нобелевской премии не сложилось.

Ценность моделирования в удобстве, скорости, точности расчетов, наглядности, возможности работать с моделью дальше, отсутствие рутинной работы, но, к сожалению, думать за нас модель не может. Поэтому нужно хотя бы в общим чертах уметь рассчитывать все самому.  На этом мы завершаем рассказ о методах расчёта цепей постоянного тока. На самом деле их конечно больше. У перечисленных способов есть более сложные варианты: закон Ома для полной цепи, правило Кирхгофа в матричной форме, но все они основываются на том, что мы сейчас с вами рассмотрели.

В следующей публикации мы расскажем о переменном токе и о новых элементах цепи: ёмкости и индуктивности.

Терминология

– В чем разница между узлами и терминалами?

спросил 5 лет, 7 месяцев назад

Изменено 5 лет, 7 месяцев назад

Просмотрено 5к раз

\$\начало группы\$

Итак, мой учебник использует оба этих термина, но не дает четкого определения каждого из них, что начинает приводить к некоторой путанице. Я читал запись в Вики о портах, в которой указано

Порт состоит из двух узлов (терминалов), подключенных к внешней цепи…

Но это меня смущает, потому что для меня это означает, что каждый терминал является отдельным узлом.

^{имитация этой цепи – Схема создана с помощью CircuitLab}

В этом случайном примере (я столкнулся с этим при замыкании цепи между клеммами a и b в задачах) не будут ли эти две клеммы совместно использовать один и тот же узел? Как они могут быть отдельными узлами? Любые разъяснения будут очень признательны!

• терминология
• терминал

\$\конечная группа\$

\$\начало группы\$

Узел — это точка, в которой встречаются два или более элемента схемы (например, резистор и источник напряжения). Статья в Википедии об узле цепи включает рисунок, на котором каждый узел в примере схемы выделен разным цветом:

Терминал — это точка подключения к внешней цепи. Терминал обычно представляет собой тип узла, хотя при замыкании двух терминалов они становятся единым узлом. Если вы подключите резистор между двумя узлами вместо того, чтобы закоротить их идеальным проводом, то каждый терминал также будет отдельным узлом.

\$\конечная группа\$

\$\начало группы\$

Терминал является частью компонента. Узел является частью цепи.

Клеммы — это провода, которые позволяют подключаться к компоненту. Например, резистор имеет два вывода. BJT имеет три клеммы и т. д.

Узел — это все провода в цепи, соединенные вместе достаточно низким сопротивлением, чтобы мы могли его игнорировать.

Таким образом, вы можете подключить клемму части к узлу в цепи (который также подключен к другим клеммам других частей). Вы даже можете подключить несколько выводов одной и той же детали к одному и тому же узлу схемы (как в транзисторе с диодным включением).

\$\конечная группа\$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. Методы формальных цепей

: метод узлов — электрические…

В некоторых (сложных) случаях мы не можем использовать методы упрощения, такие как правила параллельного или последовательного комбинирования, для определения соотношения вход-выход схемы. В других модулях мы писали v-i соотношений и законы Кирхгофа бессистемно, решая их больше на интуиции, чем на процедуре. Нам нужен формальный метод, который выводит небольшой, простой набор уравнений, который ведет непосредственно к искомому соотношению вход-выход. Одним из таких методов является метод узлов .

Node Voltage

Рисунок 1.

Метод узлов начинается с поиска всех узлов — мест, где элементы цепи соединяются друг с другом — в цепи. Мы называем один из узлов эталонным узлом ; выбор опорного узла произволен, но обычно он выбирается как точка симметрии или «нижний» узел. Для остальных узлов мы определяем узловых напряжений

, которые представляют собой напряжение между узлом и эталоном.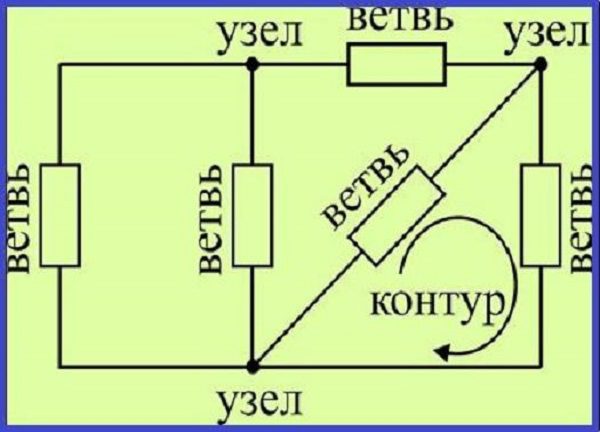 Эти узловые напряжения составляют единственные неизвестные; все, что нам нужно, это достаточное количество уравнений, чтобы решить их. В нашем примере у нас есть два напряжения узла. Сам процесс определения узловых напряжений эквивалентен использованию всех имеющихся в вашем распоряжении уравнений КВЛ . Причина этого простого, но поразительного факта заключается в том, что напряжение узла однозначно определяется независимо от того, какой путь прослеживается между узлом и эталоном. Поскольку два пути между узлом и эталоном имеют одинаковое напряжение, сумма напряжений вокруг контура равна нулю.

В некоторых случаях напряжение узла точно соответствует напряжению на источнике напряжения. В таких случаях узловое напряжение указывается источником и составляет не неизвестно. Например, в нашей схеме

; таким образом, нам нужно только найти напряжение в одном узле.

Уравнения, управляющие узловыми напряжениями, получаются путем записи уравнений KCL в каждом узле с неизвестным узловым напряжением с использованием соотношений v-i для каждого элемента.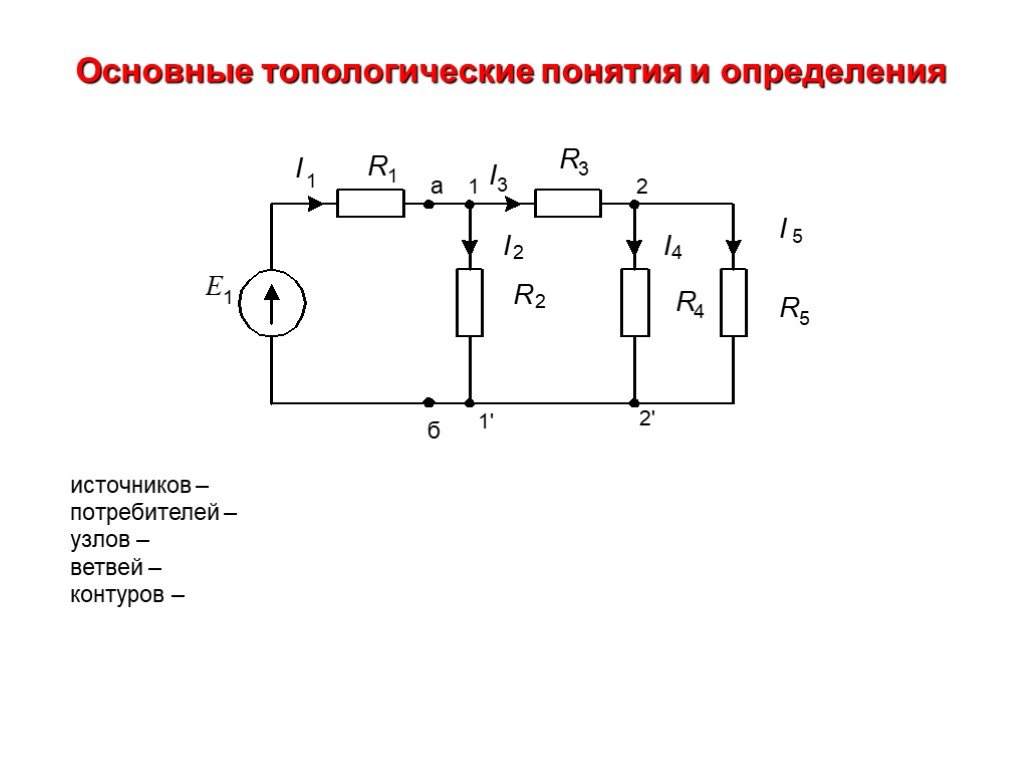 В нашем примере единственным уравнением цепи является

. Небольшое размышление показывает, что при записи уравнений KCL для суммы токов, выходящих из узла, напряжение в этом узле будет

.0085 всегда отображаются со знаком плюс, а напряжения всех остальных узлов со знаком минус. Систематическое применение этой процедуры позволяет легко писать уравнения узлов и проверять их перед решением. Также не забудьте проверить единицы измерения на этом этапе: у каждого термина должны быть единицы измерения тока. В нашем примере найти неизвестное напряжение в узле очень просто:

Действительно ли мы решили схему с помощью узлового метода? Попутно мы использовали KVL, KCL и отношения v-i . Ранее мы указывали, что система уравнений, получающаяся в результате применения этих законов, необходима и достаточна. Этот результат гарантирует, что метод узла может быть использован для «решения» любая цепь . Одним из последствий этого результата является то, что мы должны быть в состоянии найти любую переменную схемы с учетом узловых напряжений и источников. Все переменные схемы можно найти с помощью соотношений v-i и делителя напряжения. Например, ток через

равен

.

Рис. 2.

Наличие в цепи источника тока не оказывает существенного влияния на метод узла; просто включите его в запись уравнений KCL как текущий , оставив узел. Схема имеет три узла, что требует от нас определения двух узловых напряжений. Уравнения узла

Обратите внимание, что напряжение узла, соответствующее узлу, для которого мы пишем KCL, имеет положительный знак, остальные — отрицательный, и что единицы измерения каждого термина даны в амперах. Перепишите эти уравнения в стандартной форме набора линейных уравнений.

Решение этих уравнений дает

Чтобы найти указанный ток, мы просто используем

.

Рисунок 3.

В этой схеме выше (Рисунок 3) мы не можем использовать правила последовательного/параллельного комбинирования: вертикальный резистор в узле 1 предотвращает последовательное соединение двух горизонтальных резисторов 1 Ом, а резистор 2 Ом предотвращает Резисторы сопротивлением 1 Ом в узле 2 из-за того, что они включены последовательно.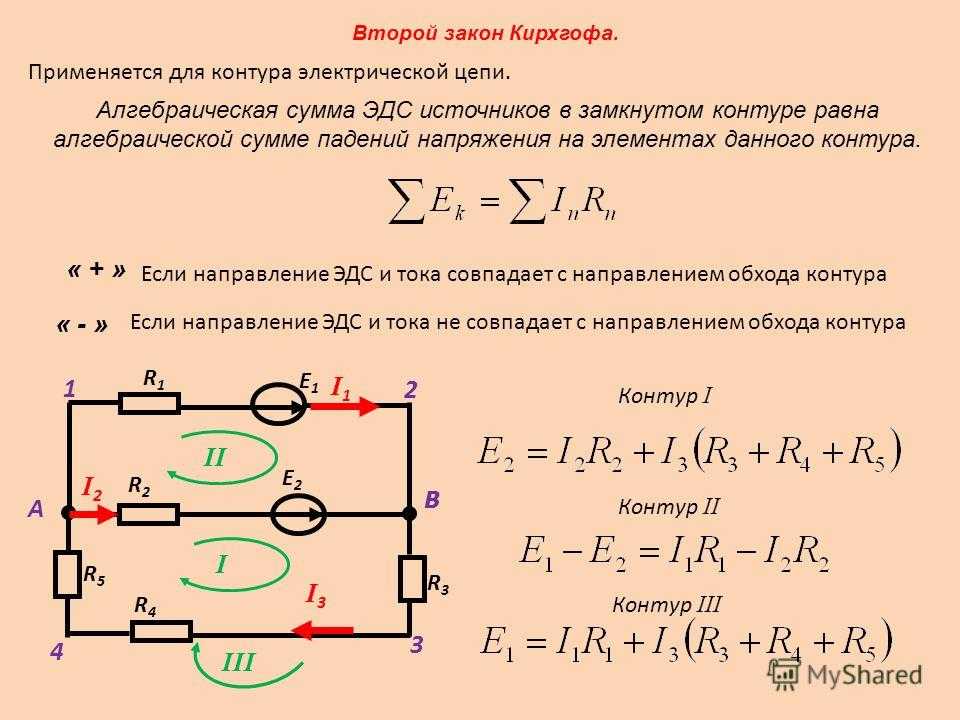 Нам действительно нужен метод узла, чтобы решить эту схему! Несмотря на наличие шести элементов, нам нужно определить только два напряжения узла. Уравнения узла

Решение этих уравнений дает

и

. Выходной ток равен

. Одним из нежелательных последствий использования числовых значений элемента с самого начала является то, что становится невозможно проверять единицы измерения при настройке и решении уравнений.

Упражнение

Каково эквивалентное сопротивление источника напряжения?

Чтобы найти эквивалентное сопротивление, нам нужно найти ток, протекающий через источник напряжения. Этот ток равен только что найденному току плюс ток, протекающий через другой вертикальный резистор 1 Ом. Этот ток равен

, прохождение полного тока через источник напряжения (вытекающего из него)

. Таким образом, эквивалентное сопротивление равно

Ом.

Узловой метод и импедансы

Рис. 4. Модификация схемы, показанной слева, для иллюстрации узлового метода и эффекта добавления резистора

.

Узловой метод применяется к цепям RLC без существенной модификации методов, используемых для простых резистивных цепей, если мы используем сложные амплитуды. Мы полагаемся на тот факт, что комплексные амплитуды удовлетворяют KVL, KCL и основанным на импедансе в-и отношения. В схеме примера мы определяем комплексные амплитуды для входных и выходных переменных и для узловых напряжений. Здесь нам нужно только одно узловое напряжение, и его уравнение KCL имеет вид

с результатом

. Чтобы найти передаточную функцию между входным и выходным напряжениями, мы вычисляем отношение

. Величина и угол передаточной функции равны

Эта схема отличается от показанной ранее тем, что резистор

был добавлен к выходным данным. Как это повлияло на передаточную функцию, которая в исходной схеме была фильтром нижних частот с частотой среза

? Как показано на рис. 5 ниже, добавление второго резистора имеет два эффекта: он снижает коэффициент усиления в полосе пропускания (диапазон частот, для которого фильтр мало влияет на вход) и увеличивает частоту среза.