Цепи постоянного тока – Физика
ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ (СИЛЫ) ТОКА .
ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ: величина (сила) тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике , где R – сопротивление проводника.
РЕЗИСТОРОМ называется устройство, обладающее заданным постоянным сопротивлением.
НАПРЯЖЕНИЕ НА РЕЗИСТОРЕ .
ЗАКОН ОМА ДЛЯ НЕОДНОРОДНОГО УЧАСТКА ЦЕПИ
, где j1 и j2 – потенциалы концов участка Е12 – э.д.с., действующая на данном участке цепи.
ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ , где Е – суммарная э.д.с., действующая в цепи, R – суммарное сопротивление всей цепи.
РАЗВЕТВЛЕННОЙ ЦЕПЬЮ называется электрическая цепь, имеющая узлы.
УЗЛОМ называется точка, в которой сходится более чем два проводника. Ток, текущий к узлу, принято считать положительным, а ток, текущий от узла, считается отрицательным.
ПЕРВОЕ ПРАВИЛО КИРХГОФА: алгебраическая сумма токов, сходящихся в узле, равна нулю = 0.
ВТОРОЕ ПРАВИЛО КИРХГОФА: в каждом из замкнутых контуров, которые можно мысленно выделить в данной разветвленной цепи, алгебраическая сумма падений напряжения равна алгебраической сумме э.д.с.
.
При анализе разветвленной цепи следует обозначать с одним индексом ток, протекающий по всем последовательно соединенным элементам от одного узла до другого. Направление каждого тока выбирается произвольно.
При составлении уравнений второго правила Кирхгофа токам и э.д.с. нужно приписывать знаки в соответствии с выбранным (как вам удобно) НАПРАВЛЕНИЕМ ОБХОДА:
- ток принято считать положительным, если он совпадает с направлением обхода, и отрицательным, если он направлен против этого направления;
- э.д.с. считается положительной, если ее действие (создаваемый ею ток) совпадает с направлением обхода.
КОЛИЧЕСТВО УРАВНЕНИЙ первого правила Кирхгофа должно быть на одно меньше количества узлов в данной цепи. Количество независимых уравнений второго правила Кирхгофа должно быть таким, чтобы общее количество уравнений оказалось равным количеству различных токов. Каждый новый контур при этом должен содержать хотя бы один участок цепи, не вошедший в уже рассмотренные контуры.
Количество независимых уравнений второго правила Кирхгофа должно быть таким, чтобы общее количество уравнений оказалось равным количеству различных токов. Каждый новый контур при этом должен содержать хотя бы один участок цепи, не вошедший в уже рассмотренные контуры.
МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ
В данной лабораторной работе исследуется модель простейшей разветвленной электрической цепи, состоящей из трех источников э.д.с., подключенных параллельно к одному резистору (нагрузке).
Закройте окно теории. Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы и зарисуйте их в конспект.
Нарисуйте в конспекте эквивалентную схему цепи, расположив источники один под другим и учитывая наличие внутреннего сопротивления у каждого источника. Укажите знаки э.д.с., направления токов в каждом участке и направления обхода каждого замкнутого контура. Составьте систему уравнений для нахождения токов в каждом участке.
ИЗМЕРЕНИЯ
Соберите на экране заданную эквивалентную цепь. Для этого сначала щелкните левой кнопкой мыши над кнопкой э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Ориентируйтесь на рисунок схемы в описании к данной ЛР. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен первый источник э.д.с. Переместите маркер мыши вниз на одну клетку и снова щелкните левой кнопкой под тем местом, где расположился первый источник. Там появится второй источник э.д.с. Аналогично разместите и третий источник.
Для этого сначала щелкните левой кнопкой мыши над кнопкой э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Ориентируйтесь на рисунок схемы в описании к данной ЛР. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен первый источник э.д.с. Переместите маркер мыши вниз на одну клетку и снова щелкните левой кнопкой под тем местом, где расположился первый источник. Там появится второй источник э.д.с. Аналогично разместите и третий источник.
Разместите далее последовательно с каждым источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку R в нижней части экрана) и амперметр (кнопка А там же). Затем расположите резистор нагрузки и последовательно соединенный с ним амперметр. Под нагрузкой расположите вольтметр, измеряющий напряжение на нагрузке.
Подключите соединительные провода. Для этого нажмите кнопку провода внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкните левой кнопкой мыши в точке, где проходит провод.
Щелкните левой кнопкой мыши в точке, где проходит провод.
Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, равное взятому из таблицы 1 для вашего варианта.
Установите сопротивления резистора нагрузки R = 1 Ом. Измерьте значения всех токов и напряжения на нагрузке (щелкнув мышью по кнопке «Счет») и запишите их в таблицу 2. Меняя сопротивление R, повторите измерения параметров и заполните таблицу 2.
Таблица 1. Значения э.д.с. и внутреннего сопротивления источников (не перерисовывать)
|
Вариат |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Е1,Е2,Е3 [В] |
3,7,-2 |
4,-3,-8 |
3,6,-4 |
6,-2,-8 |
-6,5,8 |
5,8,-4 |
-4,6,-7 |
8,-4,6 |
|
R1,R2,R3 [Ом] |
2,1,1 |
1,3,1 |
2,1,2 |
1,1,2 |
2,1,1 |
1,2,1 |
1,1,2 |
1,3,1 |
|
Таблица 2. |
Таблица 3. Результаты расчета |
||||||||||
|
R[Ом] |
I1 [A] |
I2 [A] |
I3 [A] |
I [A] |
U [В] |
I1 [A] |
I2 [A] |
I3 [A] |
I [A] |
||
|
1 |
|||||||||||
|
2 |
|||||||||||
|
3 |
|||||||||||
|
4 |
|||||||||||
|
5 |
|||||||||||
|
6 |
|||||||||||
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА
Запишите для вашей цепи решение системы уравнений для всех токов в общем виде.
Рассчитайте значения всех токов для каждого сопротивления нагрузки и запишите в таблицу 3.
Постройте график экспериментальной зависимости падения напряжения на нагрузке U от тока I через нее.
Сформулируйте выводы по графику.
Вопросы и задания для самоконтроля
- Что такое электрический ток?
- Дайте определение величины (силы) тока.
- Дайте определение разности потенциалов (напряжения).
- Напишите формулу, связывающую приращение потенциалов и напряжение.
- Что такое резистор?
- Напишите формулу для сопротивления последовательно соединенных резисторов.
- Напишите формулу для сопротивления параллельно соединенных резисторов.
- Напишите закон Ома для участка цепи. Сравните его с законом Ома в дифференциальной (локальной) форме.
- Какой участок цепи называется неоднородным?
- Запишите закон Ома для неоднородного участка цепи.
- Какими характеристиками описывается источник ЭДС?
- Сформулируйте первый закон Кирхгофа.
 Какое свойство заряда он отражает?
Какое свойство заряда он отражает? - Запишите формулу для первого закона Кирхгофа.
- Сформулируйте второй закон Кирхгофа.
- Запишите формулу для второго закона Кирхгофа.
- Что такое узел электрической цепи?
- Что такое полная электрическая цепь?
Электрическая цепь и ее элементы
Содержание
Элементы цепи
Независимо оттого, из каких частей состоят электрические цепи, их объединяет одно – их составляющие должны производить, передавать или потреблять электричество.
Элементы подразделяются на пассивные и активные. К первым из них относят всё, что потребляет или передает электроэнергию: лампы, нагревательные элементы, электродвигатели и т.д. Ко вторым – источники, вырабатывающие электроэнергию: генераторы, аккумуляторы, солнечные батареи и т.д. Также элементы делятся на двухполюсные (те, которые имеют 2 вывода) и многополюсные (те, которые имеют 4 и более вывода). В качестве примера двухполюсника можно привести резистор. В качестве четырехполюсника – повышающий или понижающий трансформатор.
В качестве четырехполюсника – повышающий или понижающий трансформатор.
Обязательными составляющими цепи являются:
- Источник (Source) – в большинстве случаев аккумулятор, гальванический элемент или генератор. Изредка – ветрогенераторы и солнечные батареи.
- Проводник (Conductor) – необходим для передачи электроэнергии от источника к электропотребителю.
- Потребитель электроэнергии (Load, consumer) (чаще всего в быту это осветительные приборы, двигатели, нагревательные приборы, электроника, бытовая техника, такая как компьютеры, пылесосы, стиральные машины).
- Замыкающее/размыкающее устройство (Switch) или выключатель.
Основными электроприемниками являются:
- Резисторы – потребитель, который имеет переменное или постоянное сопротивление.
- Конденсатор – потребитель, который имеет емкость. Он запасает энергию и имеет возможность ее возвратить.
- Катушка индуктивности – потребитель, создающий индуктивное поле.

- Электродвигатель – потребитель, превращающий энергию электронов, двигающихся вдоль проводника, в механическую.
При чтении схем и расчетах пользуются следующими понятиями: контур, узел и ветвь.
- Ветвью называют участок с одним или несколькими компонентами, соединенными последовательно.
- Узлом называют место соединения двух и более ветвей.
- Контуром называется совокупность ветвей, которые образуют для тока замкнутый путь. При этом один из узлов в контуре должен являться и началом, и концом пути, а остальные узлы должны встречаться не более одного раза.
Облегчить чтение схем можно с помощью вот такой таблички:
Режимы работы цепи
Опираясь на показатели нагрузки, различают такие режимы функционирования цепи: номинальный, холостой ход, замыкание и согласование.
При номинальной работе система выполняет характеристики, заявленные в техпаспорте оборудования. Холостой ход образуется в случае обрыва цепи. Этот режим работы относится к аварийным. Электрическая цепь в режиме короткого замыкания имеет сопротивление, которое равно нулю. Это также аварийный режим.
Электрическая цепь в режиме короткого замыкания имеет сопротивление, которое равно нулю. Это также аварийный режим.
Согласование характеризуется перемещением наибольшей мощности от источника энергии к проводнику. В таком режиме нагрузка равняется сопротивлению источника питания.
Ознакомившись с основными характеристиками и видами такой системы, как электрическая цепь, становится возможным понять принцип функционирования любого электрооборудования. Данное устройство работы системы применяется к любому электрическому бытовому прибору. Применяя полученные знания, можно понять причину поломки оборудования или оценить правильность его работы в соответствии с техническими характеристиками, заявленными производителем.
Законы электрических цепей
Закон Ома
Пусть имеется однородный участок цепи — им может служить кусок металла постоянного сечения, все точки которого имеют одинаковую температуру, и пусть на концах этого проводника поддерживается неизменная разность потенциалов U. Тогда, согласно закону Ома, в однородном участке цепи сила тока пропорциональна разности потенциалов на концах участка:
Тогда, согласно закону Ома, в однородном участке цепи сила тока пропорциональна разности потенциалов на концах участка:
U = IR, I = U/R, R = U/I
Существуют участки цепи, в которых зависимость силы тока от разности потенциалов на их концах нелинейна. В этом случае рассматривают среднее значение сопротивления:
Переходя к пределу при условии, что Di-> 0, получаем динамическое сопротивление:
Первый закон Кирхгофа — закон баланса токов в узле
Реальные электрические цепи включают в себя комбинации последовательно и параллельно соединенных нагрузок и генераторов. В рассчитывать разности потенциалов на всех участках цепи и силы токов в них, а также электродвижущие силы источников тока, входящих в данную цепь, можно с помощью закона Ома и закона сохранения заряда. Однако для упрощения расчетов Г. Кирхгофом были предложены два простых правила, нашедших широкое применение в электротехнике.
Первое из них относится к узлам разветвления цепи, в которых сходятся и из которых расходятся токи. Токи, подходящие к узлу, условились считать положительными, а токи, исходящие из узла — отрицательными. В этом случае в каждой точке разветвления проводов алгебраическая сумма всех сил токов равна нулю (первое правило Кирхгофа):
Токи, подходящие к узлу, условились считать положительными, а токи, исходящие из узла — отрицательными. В этом случае в каждой точке разветвления проводов алгебраическая сумма всех сил токов равна нулю (первое правило Кирхгофа):
Электрический заряд в узле не накапливается.
Второй закон Кирхгофа
Алгебраическая сумма ЭДС источников питания в любом контуре равна алгебраической сумме падений напряжения на элементах этого контура:
Второе закон, по существу, является следствием закона Ома для неоднородного участка цепи.
Закон Джоуля — Ленца
Количество теплоты, выделяемое проводником с током I на сопротивлении R, прямопропорционально произведению квадрата силы тока, на сопротивление и на время прохождения тока:
Электрическая цепь и ее элементы
Теория > Физика 8 класс > Электрические явления
Электрическая цепь — совокупность устройств, предназначенных для прохождения электрического тока. Цепь образуется источниками энергии (генераторами), потребителями энергии (нагрузками), системами передачи энергии (проводами).
Электрическая цепь — совокупность устройств и объектов, образующих путь для электрического тока. Её задача – передавать энергию устройству и обеспечивать требуемый режим работы.
Простейшая электрическая установка состоит из источника (гальванического элемента, аккумулятора, генератора и т. п.), потребителей или приемников электрической энергии (ламп накаливания, электронагревательных приборов, электродвигателей и т. п.) и соединительных проводов, соединяющих зажимы источника напряжения с зажимами потребителя.
Электрическая цепь делится на внутреннюю и внешнюю части.
К внутренней части электрической цепи относится сам источник электрической энергии. Источники питания цепи — это гальванические элементы, электрические аккумуляторы, электромеханические генераторы, термоэлектрические генераторы, фотоэлементы и др. В современной технике в качестве источников энергии применяют главным образом электрические генераторы.
Во внешнюю часть цепи входят потребители энергии и вспомогательные элементы.
Потребители энергии преобразовывают электрическую энергию в другие виды энергии (механическую, тепловую, световую, и т. д.) К ним относятся: электродвигатели, нагревательные и осветительные приборы и др.
В качестве вспомогательного оборудования в электрическую цепь входят аппараты для включения и отключения (например, рубильники), приборы для измерения электрических величин (например, амперметры и вольтметры), аппараты защиты (например, плавкие предохранители).
Электрический ток может протекать только по замкнутой электрической цепи. Разрыв цепи в любом месте вызывает прекращение электрического тока.
Чтобы удобнее было анализировать и рассчитывать электрическую цепь, её изображают в виде схемы. В ней содержатся условные обозначения элементов, а также способы из соединения.
Ниже приведены некоторые элементы электрической цепи:
А теперь помотрим как применяются эти обозначения при составлении схемы:
Задание 1. Начертите в тетради схему последовательного соединения потребителей электроэнергии из 2-х лампочек.
Задание 2. Начертите в тетради схему параллельного соединения потребителей электроэнергии из 2-х лампочек.
Теория | Калькуляторы | ГДЗ | Таблицы и знаки | Переменка | Главная Карта Сайта
Виды электрических цепей
Неразветвлённые и разветвлённые электрические цепи
Рисунок 1 — Разветвлённая цепь
Электрические цепи подразделяют на неразветвлённые и разветвлённые. Во всех элементах неразветвлённой цепи течёт один и тот же ток. Простейшая разветвлённая цепь изображена на рисунке 1. В ней имеются три ветви и два узла. В каждой ветви течёт свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течёт одинаковый ток) и заключённый между двумя узлами. В свою очередь, узел есть точка цепи, в которой сходятся не менее трёх ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 1), то в этом месте есть электрическое соединение двух линий, в противном случае его нет.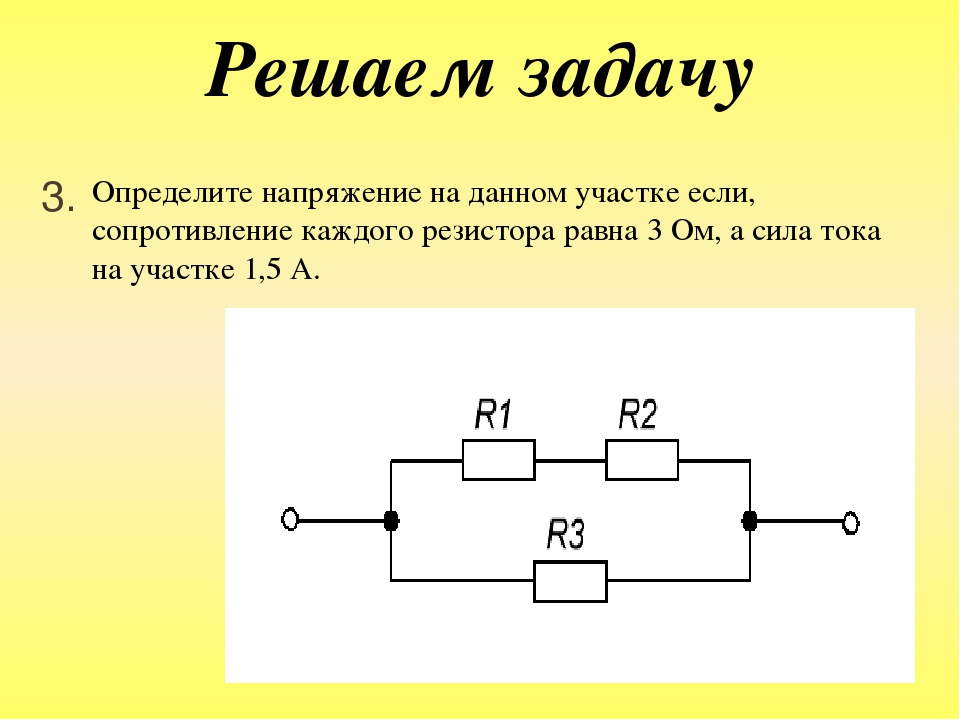 Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом.
Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом.
Линейные и нелинейные электрические цепи
Линейной электрической цепью называют такую цепь, все компоненты которой линейные. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы (подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и катушки индуктивности.
Если цепь содержит отличные от перечисленных компоненты, то она называется нелинейной.
Изображение электрической цепи с помощью условных обозначений называют электрической схемой. Функция зависимости тока, протекающего по двухполюсному компоненту, от напряжения на этом компоненте называется вольт-амперной характеристикой (ВАХ). Часто ВАХ изображают графически в декартовых координатах. При этом по оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.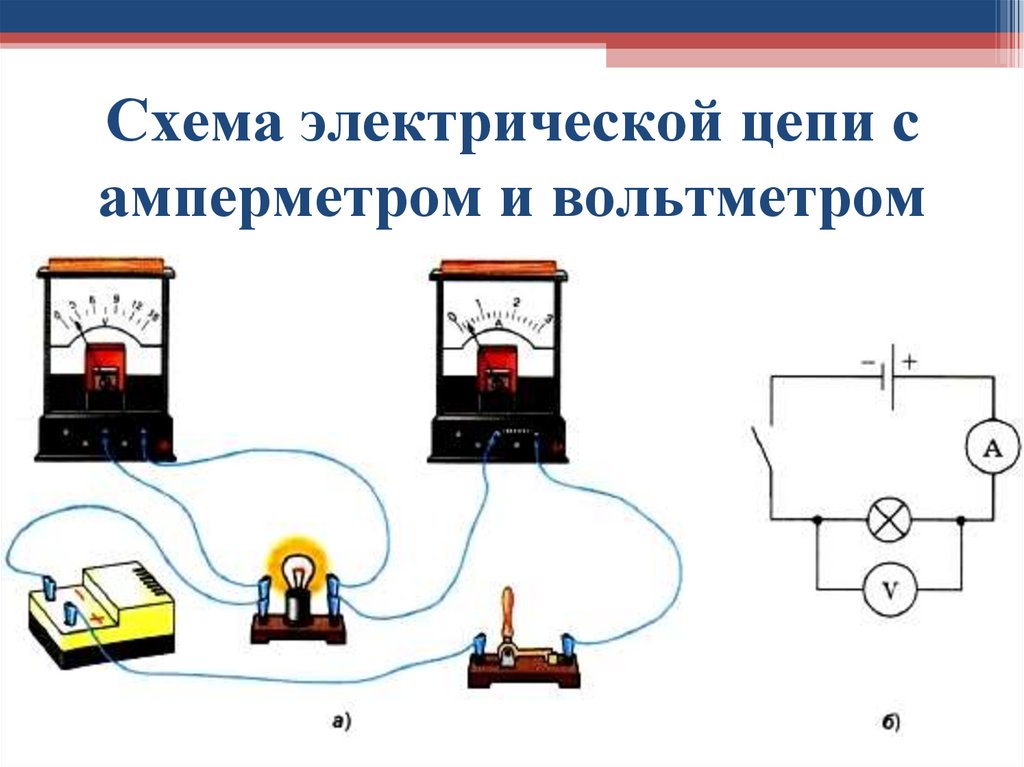
В частности, омические резисторы, ВАХ которых описывается линейной функцией и на графике ВАХ являются прямыми линиями, называют линейными.
Примерами линейных (как правило, в очень хорошем приближении) цепей являются цепи, содержащие только резисторы, конденсаторы и катушки индуктивности без ферромагнитных сердечников.
Некоторые нелинейные цепи можно приближенно описывать как линейные, если изменение приращений токов или напряжений на компоненте мало, при этом нелинейная ВАХ такого компонента заменяется линейной (касательной к ВАХ в рабочей точке). Этот подход называют «линеаризацией». При этом к цепи может быть применён мощный математический аппарат анализа линейных цепей. Примерами таких нелинейных цепей, анализируемых как линейные, являются практически любые электронные устройства, работающие в линейном режиме и содержащие нелинейные активные и пассивные компоненты (усилители, генераторы и др.).
Виды цепей
Чтобы успешно пользоваться электросхемами, необходимо иметь представление, какую электрическую цепь называют замкнутой и разомкнутой.
Замкнутой называют непрерывную цепь, состоящую из электроприборов и проводников. Как только она прерывается – становится разомкнутой. В таком состоянии она неспособна проводить ток, хотя в ней может быть напряжение, так как в ней появляется диэлектрик. В подавляющем большинстве случаев в качестве такого диэлектрика выступает обычный атмосферный воздух. На этом принципе работают приборы, предназначенные для размыкания – выключатели, рубильники, предохранители, кнопки.
Неразветвленной называют электрическую цепь, состоящую из источника и последовательно соединенных компонентов. Важнейшим признаком здесь является то, что во всех участках ток имеет одинаковую величину. Разветвленной – имеющую в своем составе одно или несколько параллельно соединенных компонентов.
Каждая может иметь одновременно несколько классификаций и названий:
- силовой – называют соединение приборов, необходимых для производства, передачи электроэнергии, ее преобразования или потребления;
- вспомогательной – ту, которая имеет разные функциональные назначения, но которая не является силовой;
- измерительной – называют необходимую для регистрации параметров сети и включенных в нее приборов;
- управляющей – называют приводящую в действие приборы или изменяющую их параметры в зависимости от общего предназначения;
- сигнализирующей называют приводящую в действия сигнальные устройства, показывающие на наличие тех или иных изменений.

Простейшей электрической цепью является источник, соединенный проводниками с электропотребителем, а простой называют любую одноконтурную. Сложными называются цепи, имеющие два и более контура. Они в свою очередь делятся на многоузловые, многоконтурные, объемные и плоскостные.
Основные компоненты
Инвентор электрического тока
Все составные части в цепи участвуют в одном электромагнитном процессе. Условно их разделяют на три группы.
- Первичные источники электрической энергии и сигналов могут преобразовывать энергию неэлектромагнитной природы в электрическую. Например, гальванический элемент, аккумулятор, электромеханический генератор.
- Вторичный тип, как на входе, так и на выходе имеет электрическую энергию. Изменяются только ее параметры – напряжение и ток, их форма, величина и частота. Примером могут быть выпрямители, инверторы, трансформаторы.
- Потребители активной энергии преобразовывают электрический ток в освещение или тепло.
 Это электротермические устройства, лампы, резисторы, электродвигатели.
Это электротермические устройства, лампы, резисторы, электродвигатели. - К вспомогательным компонентам относят коммутационные устройства, измерительные приборы, соединительные элементы и провод.
Основой электрической сети является схема. Это графический рисунок, который содержит условные изображения и обозначения элементов и их соединение. Они выполняются согласно ГОСТу 2.721-74 – 2.758-81
Схема простейшей линии включает в себя гальванический элемент. С помощью проводов к нему через выключатель подсоединена лампа накаливания. Для измерения силы тока и напряжения в нее включен вольтметр и амперметр.
Трехфазные электрические цепи
Трехфазная цепь в рабочем режиме
Среди электрических цепей распространены как однофазные, так и многофазные системы. Каждая часть многофазной цепи характеризуется одинаковым значением тока и называется фазой. Электротехника различает два понятия этого термина. Первое – непосредственная составляющая трехфазной системы. Второе – величина, изменяющаяся синусоидально.
Второе – величина, изменяющаяся синусоидально.
Трехфазная цепь – это одна из многофазных систем переменного тока, где действуют синусоидальные ЭДС (электродвижущая сила) одинаковой частоты, которые сдвинуты во времени относительно друг друга на определенный фазовый угол. Она образована обмотками трехфазного генератора, тремя приемниками электроэнергии и соединительными проводами.
Такие цепи служат для обеспечения генерации электрической энергии, для ее передачи, распределения, и имеет следующие преимущества:
- экономичность выработки и транспортировки электроэнергии в сравнении с однофазной системой;
- простое генерирование магнитного поля, которое необходимо для работы трехфазного асинхронного электродвигателя;
- одна и та же генераторная установка выдает два эксплуатационных напряжения – линейное и фазное.
Что называется электрической цепью
ЭЦ – это комплекс элементов, при помощи которых создаётся, передаётся и потребляется электрическая энергия. Данные элементы, или участки, содержат источники электрической энергии, а также промежуточные устройства и проводники между ними, обеспечивающие неразрывность соединений.
Данные элементы, или участки, содержат источники электрической энергии, а также промежуточные устройства и проводники между ними, обеспечивающие неразрывность соединений.
Как по другому называется электрическая цепь
Источниками электрической энергии являются устройства, вырабатывающие ток путём физических, химических или световых преобразований.
Важно! Приемниками электроэнергии являются устройства, работа которых напрямую зависит от активности источника. Промежуточные элементы с функциональными устройствами служат для передачи электрической энергии от источников к приемникам
В зависимости от назначения, они непосредственно передают энергию с конкретными параметрами источника
Промежуточные элементы с функциональными устройствами служат для передачи электрической энергии от источников к приемникам. В зависимости от назначения, они непосредственно передают энергию с конкретными параметрами источника.
Обозначения элементов на схеме
Прежде чем приступить к монтажу оборудования необходимо изучить нормативные сопровождающие документы. Схема позволяет донести до пользователя полную характеристику изделия с помощью буквенных и графических обозначений, занесенных в единый реестр конструкторской документации.
Схема позволяет донести до пользователя полную характеристику изделия с помощью буквенных и графических обозначений, занесенных в единый реестр конструкторской документации.
К чертежу прилагаются дополнительные документы. Их перечень может быть указан в алфавитном порядке с цифровой сортировкой на самом чертеже, либо отдельным листом. Классифицируют десять видов схем, в электротехнике обычно используют три основные схемы.
- Функциональная имеет минимальную детализацию. Основные функции узлов изображают прямоугольником с буквенными обозначениями.
- Принципиальная схема подробно отображает конструкцию использованных элементов, а также их связи и контакты. Необходимые параметры могут быть отображены непосредственно на схеме или в отдельном документе. Если указана только часть установки, это однолинейная схема, когда указаны все элементы – полная.
- В монтажной электрической схеме используют позиционные обозначения элементов, их месторасположение, способ монтажа и очередность.

Выключатель на схеме выглядит как кружок с наклоненной вправо чертой. По виду и количеству черточек определяют параметры устройства.
Кроме основных чертежей есть схемы замещения.
Энергия электрического поля
Рассмотрим систему из двух проводников, на которых распределены равные по модулю, но противоположные по знаку заряды. Опыт показывает, что разность потенциалов между этими проводниками пропорциональна модулю заряда: U=q/C, где С — постоянный коэффициент, определяемый в общем случае размерами проводников, их формой и расположением в пространстве, а также диэлектрической проницаемостью среды, в которую помещены проводники. Величину С, равную отношению заряда системы проводников к разности потенциалов между ними, называют электрической емкостью (короче — электроемкостью) данной системы проводников:
C = q/U
Единицей электроемкости является кулон на вольт (Кл/В). В честь М. Фарадея эта единица получила название фарад (Ф): 1 Ф = 1 Кл/В.
Систему из двух изолированных друг от друга металлических проводников, между которыми находится диэлектрик, называют конденсатором.
Накопление энергии в электрическом поле конденсатора
где
— заряд, Кл;
— напряжение, В;
— электрическая емкость конденсатора, Ф.
Если напряжение источника в цепи конденсатора изменяется, то происходит перераспределение зарядов на его пластинах, что приводит к возникновению тока в цепи:
Мощность конденсатора положительна при его заряде и отрицательна при разряде конденсатора.
Если напряжение возрастает, то i>0. Это значит, что ток и напряжение совпадают по направлению, энергия электрического поля в конденсаторе возрастает.
При убывании напряжения ток также уменьшается, энергия возвращается обратно к источнику.
Величины R(OM), L(Гн), С(Ф) зависят от свойств самого устройства, его конструкции и являются параметрами этого устройства.
Энергия электромагнитного поля
Опыт показывает, что в контуре из двух электроламп, соленоида и реостата при отключении источника тока еще некоторое время течет электрический ток, причем сила тока со временем уменьшается от некоторого начального значения до нуля.
Одновременно с током, как известно, исчезает и магнитное поле тока. Так как никаких других источников энергии, которые поддерживали бы электрический ток в контуре, нет, то остается предположить, что энергией обладает само магнитное поле. Найдем начальную энергию W магнитного поля, считая, что она расходуется на индуцирование э. д. с. и тока самоиндукции в контуре, когда магнитный поток убывает от некоторого начального значения до нуля.
Бесконечно малое изменение энергии поля равно элементарной работе тока в контуре:
Но э. д. с. самоиндукции , а сила тока i=dQ/dt. Отсюда
dW = — Lidi
Знак минус указывает, что энергия поля уменьшается. Интегрируя это выражение, находим
где
-потокосцепление;
— индуктивность или коэффициент пропорциональности между током и потокосцеплением;
— ток через катушку.
Потокосцеплением самоиндукции y цепи называется сумма произведений магнитных потоков, обусловленных только током в этой цепи, на число витков, с которыми они сцеплены.
Если все витки пронизываются одним и тем же магнитным потоком Ф, то потокосцепление равно произведению магнитного потока на число витков y=Фw, а w = nI, где I-длина соленоида, n — густота обмотки.
В СИ потокосцепление измеряется в веберах, индуктивность — в генри.
Генри — это индуктивность соленоида, в котором при силе тока 1 А создается магнитный поток 1 Вб.
Зависимость потокосцепления от тока может быть постоянной (линейная зависимость) или нелинейной.
При изменении тока изменяется потокосцепление и в катушке наводится ЭДС самоиндукции:
Знак минус показывает, что ЭДС противодействует изменению тока в цепи.
Напряжение и мощность индуктивности равны:
Мощность может быть как положительной (при намагничивании), так и отрицательной (при размагничивании).
При нарастании тока , направления тока и напряжения совпадают, в индуктивности запасается энергия магнитного поля.
При убывании тока , направления тока и напряжения не совпадают, энергия магнитного поля в индуктивности убывает, возвращается обратно к источнику.
Явление самоиндукции можно наблюдать на опыте, собрав цепь с источником постоянного тока и двумя параллельными ветвями (смотри рисунок выше). Одна ветвь состоит из электролампы Л1 и реостата R, другая — из такой же электролампы Л2 и соленоида. С помощью реостата в обеих ветвях устанавливают одинаковую силу постоянного тока. После включения рубильника видно, что лампа Л2 начинает светиться позже, чем лампа Л1. Это объясняется тем, что в соленоиде индуцируется э. д. с. самоиндукции, препятствующая некоторое время нарастанию силы тока. У разных соленоидов время нарастания силы тока оказывается различным, так как вокруг каждого из них создаются разной величины магнитные потоки, которые индуцируют различные э. д. с. самоиндукции.
Физические величины, характеризующие цепь
Величин, которыми можно описать любую электрическую цепь несколько. Основными из них являются:
- Напряжение – U (измеряется в вольтах (В)).
- Сила тока – I (измеряется в амперах (А)).
- Сопротивление – R (измеряется в омах (Ом)).

- Мощность – P (измеряется в Ваттах (Вт)).
- Ёмкость – С (измеряется в Фарадах (Ф).
Знание формул позволяет проводить практические расчеты. К примеру, сопротивление резистора зависит не только от тока, но и от напряжения. Формула, которая это отражает, называется Законом Ома для участка цепи и выглядит так:
I=U/R, где
- I – сила тока;
- U – напряжение;
- R – сопротивление.
Если резистор имеет постоянное сопротивление независимо от того, какой ток по нему протекает, он имеет название «линейный элемент».
Когда по резистору протекает ток, его сопротивление увеличивается из-за увеличения колебания на молекулярном уровне кристаллической решетки в проводнике. Колебания мешают движению электронов, и в результате энергия теряется понапрасну. Для того чтобы предотвратить перегорание резистора в цепь последовательно ему часто устанавливают предохранитель. Он содержит внутри легкоплавкий проводник, рассчитанный на перегорание при превышении параметров. Перегорая, предохранитель уберегает от повреждения всю схему и экономит, порой, часы при ремонте, так как поменять предохранитель легче, чем искать поврежденный компонент среди десятков таких же.
Перегорая, предохранитель уберегает от повреждения всю схему и экономит, порой, часы при ремонте, так как поменять предохранитель легче, чем искать поврежденный компонент среди десятков таких же.
Узнать больше об электрических цепях можно с помощью видео:
- Кто изобрел электрическое уличное освещение
- Статическое электричество и защита от него
- 6 простейших способов определения полярности светодиодов
Помогла ли вам статья?
Задать вопрос
Пишите ваши рекомендации и задавайте вопросы в комментариях
Схемы и узлы с сосредоточенными параметрами
Компания NI
- Внутренние инструменты
Содержание
- Схемы и узлы с сосредоточенными параметрами
- Введение
- узлов цепи
- Определения:
- Важные моменты
- Проверьте свои знания
- Ответы
Введение
Будем считать, что наши электрические цепи состоят из двух или более элементов цепи, соединенных между собой идеальными проводниками. Элементами схемы могут быть резисторы, транзисторы, конденсаторы, катушки индуктивности, интегральные схемы или любые другие устройства, влияющие на напряжение или ток. Наши «идеальные» проводники могут быть проводами, которые позволяют току течь от одного элемента к другому. Это представление электрических цепей содержит базовое предположение: только элементы цепи влияют на накопление или передачу энергии в цепи 9.0042 1) . Поскольку энергия сосредоточена в дискретных точках схемы (в компонентах), схема, представленная таким образом, называется схемой с сосредоточенными параметрами 2) .
Элементами схемы могут быть резисторы, транзисторы, конденсаторы, катушки индуктивности, интегральные схемы или любые другие устройства, влияющие на напряжение или ток. Наши «идеальные» проводники могут быть проводами, которые позволяют току течь от одного элемента к другому. Это представление электрических цепей содержит базовое предположение: только элементы цепи влияют на накопление или передачу энергии в цепи 9.0042 1) . Поскольку энергия сосредоточена в дискретных точках схемы (в компонентах), схема, представленная таким образом, называется схемой с сосредоточенными параметрами 2) .
На рис. 1 показан пример схемы с сосредоточенными параметрами. Элементы цепи A, B, C и D влияют на энергию в цепи; соединительные линии между ними являются идеальными проводниками — они могут передавать любое количество тока, не сохраняя и не рассеивая энергию.
Узлы цепи
Элементы схемы в схемах с сосредоточенными параметрами соединяются в узлах. Идентификация узлов схемы будет чрезвычайно важна для нас, когда мы создаем и анализируем схемы. Каждый узел имеет единственное уникальное напряжение, поэтому внутри узла не может быть падений напряжения (и, следовательно, элементов схемы). Идеальные проводники не вызывают падения напряжения, поэтому узел может содержать идеальные проводники. Пример схемы показан на рис. 2(а). Распространенной ошибкой было бы определение семи узлов в цепи, как указано точками a, b, c, d, e, f и g. Однако узлы b и c соединены только идеальным проводником, поэтому между этими двумя точками нет разницы в напряжении; они являются частью одного и того же узла. Точно так же идеальный проводник соединяет точки f и g. Следовательно, в схеме всего пять узлов, как показано на рис. 2(б).
Идентификация узлов схемы будет чрезвычайно важна для нас, когда мы создаем и анализируем схемы. Каждый узел имеет единственное уникальное напряжение, поэтому внутри узла не может быть падений напряжения (и, следовательно, элементов схемы). Идеальные проводники не вызывают падения напряжения, поэтому узел может содержать идеальные проводники. Пример схемы показан на рис. 2(а). Распространенной ошибкой было бы определение семи узлов в цепи, как указано точками a, b, c, d, e, f и g. Однако узлы b и c соединены только идеальным проводником, поэтому между этими двумя точками нет разницы в напряжении; они являются частью одного и того же узла. Точно так же идеальный проводник соединяет точки f и g. Следовательно, в схеме всего пять узлов, как показано на рис. 2(б).
Определения:
Узел представляет собой электрическую «точку», в которой соединены два или более элементов цепи. Поскольку идеальные проводники не обязательно считаются элементами схемы, узлы могут содержать идеальные проводники.

Узлы цепи также могут быть идентифицированы по тому факту, что они являются частями цепи, которые все находятся под одним и тем же напряжением. Поскольку на идеальном проводнике нет падения напряжения, любые точки цепи, соединенные идеальными проводниками, будут иметь одинаковое напряжение и, таким образом, будут частью одного и того же узла.
Физические узлы схемы
Макеты без пайки
Физически элементы схемы могут быть соединены между собой различными способами. Однако мы будем создавать наши схемы на макетных платах без пайки, поэтому у нас есть только несколько вариантов:
На макетной плате без пайки все отверстия в одном ряду соединены проводником. Таким образом, все пять этих отверстий автоматически образуют единый узел, как показано на рис. 3. Это позволяет нам соединять компоненты между собой, вставляя их выводы в отверстия в одном ряду.
Мы также можем выполнить соединения с помощью перемычек.
 Проволочные перемычки являются хорошими проводниками, поэтому будем считать, что точки, соединенные проволочными перемычками, становятся единым узлом. На рис. 4 показано, как этот подход можно использовать для создания узлов с более чем пятью отверстиями на макетной плате.
Проволочные перемычки являются хорошими проводниками, поэтому будем считать, что точки, соединенные проволочными перемычками, становятся единым узлом. На рис. 4 показано, как этот подход можно использовать для создания узлов с более чем пятью отверстиями на макетной плате.
Очевидно, что определение любого физического соединителя (например, провода) как «идеального» проводника будет неправильным; любой провод будет иметь некоторое ненулевое сопротивление и вызовет некоторую разницу в напряжении между его концами. Хитрость заключается в том, что сопротивление проводника должно быть незначительным по сравнению с сопротивлением других компонентов в цепи, чтобы его можно было считать «достаточно близким» к нулю, чтобы оно не имело значения. Например, проводом с сопротивлением 0,1 Ом, вероятно, можно пренебречь, если он соединяет два резистора по 10 кОм.
Важные моменты
Цепи с сосредоточенными параметрами состоят из дискретных компонентов схемы, соединенных, как предполагается, идеальными проводниками.
 Основное предположение схем с сосредоточенными параметрами состоит в том, что идеальные проводники мгновенно передают ток без падения напряжения.
Основное предположение схем с сосредоточенными параметрами состоит в том, что идеальные проводники мгновенно передают ток без падения напряжения.Модель цепи с сосредоточенными параметрами не подходит, если задействованные расстояния велики или напряжения и токи изменяются очень быстро. В этих случаях необходимо использовать модели с распределенными параметрами. Эти модели значительно сложнее математически, чем модели с сосредоточенными параметрами.
Узел представляет собой электрическую «точку», в которой соединены два или более элемента цепи. Узлы могут быть разбросаны из одной геометрической точки с идеальными проводниками.
Узлы цепи также могут быть идентифицированы по тому факту, что они являются частями цепи, которые все находятся под одним и тем же напряжением. Поскольку на идеальном проводнике нет падения напряжения, любые точки цепи, соединенные идеальными проводниками, будут иметь одинаковое напряжение и, таким образом, будут частью одного и того же узла.

Проверьте свои знания
1. Сколько узлов в приведенной ниже схеме?
2. Сколько узлов в приведенной ниже схеме?
3. Определите узлы в схеме ниже.
4. Определите узлы в схеме ниже.
Ответы
1. Три, как показано.
2. Пять, как показано.
3. Пять узлов, как показано на рисунке ниже.
4. Четыре узла, как показано на рисунке ниже. (Обратите внимание, что обе клеммы заземления соединены внутри Analog Discovery™. Это делает их одним узлом.)
учиться, основы, схемы, сосредоточенный параметр, узлы
1)
Помните, что наша цель при создании любой электрической цепи — передача энергии для выполнения какой-то полезной задачи. Поскольку только элементы цепи влияют на энергию, они являются единственными вещами, которые действительно имеют для нас значение. Проводники (или провода), соединяющие цепи, существуют только для передачи энергии между элементами.
Поскольку только элементы цепи влияют на энергию, они являются единственными вещами, которые действительно имеют для нас значение. Проводники (или провода), соединяющие цепи, существуют только для передачи энергии между элементами.
2)
Существуют случаи, когда необходимо учитывать влияние проводников между элементами цепи. Это происходит, когда время, необходимое для передачи электричества от одной точки цепи к другой, становится значительным, например, когда мы передаем электричество на большие расстояния (как в линиях электропередач по пересеченной местности) или когда напряжения и токи меняются очень быстро ( например, изменения напряжения, связанные с переключением битов в современных компьютерах). Схемы этого типа называются схемами с распределенными параметрами. Математика, необходимая для анализа этих типов схем, как и следовало ожидать, значительно сложнее, чем для схем с сосредоточенными параметрами.
Маркировка напряжений, токов и узлов
Ultimate Electronics: практическое проектирование и анализ схем
≡ Оглавление
«
2. 13
13
»
2.15
Решающие схемыПравила определения конкретных токов и напряжений для обеспечения правильного применения уравнений KCL и KVL. 16 мин чтение
Как обсуждалось в предыдущем разделе, закон Кирхгофа для напряжения и закон Кирхгофа для тока — это правила, которые описывают, как формировать уравнения тока и напряжения из связного графа цепи. По сути, они представляют собой бухгалтерских или бухгалтерских правил, устанавливающих баланс между зарядом и потенциальной энергией.
Сами по себе правила не очень сложны, но, как и бухгалтерия, новички в электронике быстро сбиваются с толку из-за двух моментов:
- Маркировка напряжений и токов последовательно и
- Постоянное отслеживание знака или направления.
Мы можем пометить каждый двухконтактный компонент напряжением и током. Обычное соглашение состоит в том, чтобы определить ток как положительный при входе в положительный вывод элемента схемы:
Линейные элементы с маркировкой тока и напряжения на клеммах
Circuitlab. com/cv5q6274rxjyv
com/cv5q6274rxjyv
Править – Имитация
Для источника напряжения положительная клемма четко обозначена знаком + знак на условном обозначении. Ток определяется как положительный переход в + Терминал.
Для источника тока символ показывает заостренную головку и тонкий конец стрелки, указывающей направление тока. На рисунке, показанном здесь, мы решили определить положительную клемму как хвост источника тока. Это удобно, потому что, если мы снова определим ток как положительный, идущий в этого терминала, то ток будет таким же, как и заданное значение источника.
Для резистора нет направленности компонента. Тем не менее, мы указываем положительную и отрицательную клемму для напряжения v9
как показано, и мы указываем направление для текущего i9
. Наш выбор в какой терминал звонить +
был произвольным, но до тех пор, пока нынешний i9
определяется как положительный вход в этого терминала, тогда закон Ома v9=i9R9
будет применяться без изменения знака. (Если мы изменим направление текущего i9без переназначения +
терминал, нам нужно было бы написать v9=−i9R9
.)
(Если мы изменим направление текущего i9без переназначения +
терминал, нам нужно было бы написать v9=−i9R9
.)
Условное обозначение тока как положительного при протекании в + Терминал произволен, но некоторые вещи с ним выполняются просто и последовательно:
- Во-первых, отношения V-I, такие как определение закона Ома, не нуждаются в знаке минус.
- Во-вторых, потребляемая мощность определяется правильно с P=vi , где Р>0 для обычных компонентов, которые потребляют энергию, например резистор, и P<0 для компонентов, которые обеспечивают питание, например аккумулятор.
Решая схему на бумаге, мы можем обозначить токи и напряжения вокруг схемы любыми именами, которые нам нравятся, при условии, что мы позаботимся о том, чтобы отслеживать их направление и знак.
Но при решении с использованием программного обеспечения для моделирования цепей, такого как CircuitLab, каждый вывод каждого компонента имеет встроенное имя, которое можно использовать для ссылки на его ток. В этом простом примере мы явно обозначили эти токи:
В этом простом примере мы явно обозначили эти токи:
Маркированные терминальные токи
Circuitlab.com/cbcmg28t4burj
Править – Моделирование
Компонент, такой как источник напряжения «V1», имеет две клеммы с именами «V1.nA» и «V1.nB». Мы можем попросить симулятор показать текущий в для конкретного терминала, запросив, например, «I(V1.nA)». Мы также можем показать напряжение на клемме относительно земли , запросив, например, «V(V1.nA)».
Для таких компонентов, как резисторы, может быть неочевидно, какая клемма «nA», а какая «nB». Однако, если вы запустите симуляцию постоянного тока, а затем наведете курсор мыши на схему, вы сможете навести курсор мыши на каждый отдельный терминал, и он покажет имя терминала, напряжение и ток.
Вы также можете добавить собственные выражения для расчета, такие как «V(R1.nA)-V(R1.nB)», которые будут вычислять падение напряжения на резисторе R1.
Вам предлагается щелкнуть схему выше, запустить эту простую симуляцию и поэкспериментировать с различными выражениями для определения токов и напряжений в цепи.
В примере схемы, показанном выше, присутствует ряд равенств, потому что у нас есть несколько имен для одних и тех же величин.
Например, для всех компонентов с двумя клеммами ток на одну клемму должен выходить из другой клеммы, поэтому:
I(V1.nA)=-I(V1.nB)I(R1.nA)=-I(R1.nB)I(R2.nA)=-I(R2.nB)
(Обратите внимание, что численно бывает, что в этой цепи имеется только одно значение тока, потому что это простая одиночная петля, но так будет не всегда.)
Напряжения в каждом узле цепи могут быть обозначены как один или несколько компонентов терминалы, которые подключаются к этому узлу, или как узел с явным именем (см. метки «A», «B» и «C») выше. Ссылка на них любым из этих способов идентична симулятору, но для вашего удобства вам рекомендуется помечать полезные узлы там, где это уместно. А для земли эти напряжения автоматически устанавливаются равными нулю:
А для земли эти напряжения автоматически устанавливаются равными нулю:
V(A)=V(V1.nA)=V(R1.nA)V(B)=V(R1.nB)=V(R2.nA)V(C)=V(V1.nB)= V(R2.nB)=0
В предыдущем разделе, посвященном закону напряжения Кирхгофа, мы обсуждали определение различных путей и то, как обозначение vAB указывает напряжение в узле A по отношению к узлу B. В среде моделирования все отдельные именованные узлы привязаны к земле. Таким образом, если мы хотим найти в CircuitLab относительное напряжение узла, мы должны написать выражение:
vAB=V(A) – V(B)
Вот пошаговая инструкция решения для vAB :
- Щелкните схематическое изображение «Маркированные клеммные токи» несколькими абзацами выше. Программное обеспечение CircuitLab откроется в новой вкладке браузера.
- В нижней части экрана нажмите Simulate , чтобы переключиться в режим имитации.
- На вкладке DC нажмите кнопку + Добавить выражение . Введите «V(A) – V(B)» (без кавычек, но с заглавными буквами!) и нажмите ввод.
 Это выражение будет добавлено в список.
Это выражение будет добавлено в список. - Нажмите кнопку Запустить DC Solver .
Следуйте инструкциям, чтобы убедиться, что вы умеете пользоваться средой моделирования для определения определенных токов и напряжений.
Рассмотрим немного более сложный пример:
Маркированные клеммные токи — с BJT и светодиодом
Circuitlab.com/cj55dff4nv229
Править – Имитация
Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему.
Эта цепь имеет 5 узлов (обозначенных A, B, C, D и заземление) и 6 элементов.
Клеммы светодиода с именем D1 называются «D1.nA» и «D1.nK», где «nA» — анод, а «nK» — катод.
Выводы биполярного транзистора с именем Q1 называются «Q1.nB» для базы, «Q1.nC» для коллектора и «Q1.nE» для эмиттера.
В то время как приведенные выше правила для компонентов с двумя выводами просто предусматривали, что ток, проходящий через один вывод, равен отрицательному току, проходящему через другой вывод, для устройств с тремя (или более) выводами правило немного отличается.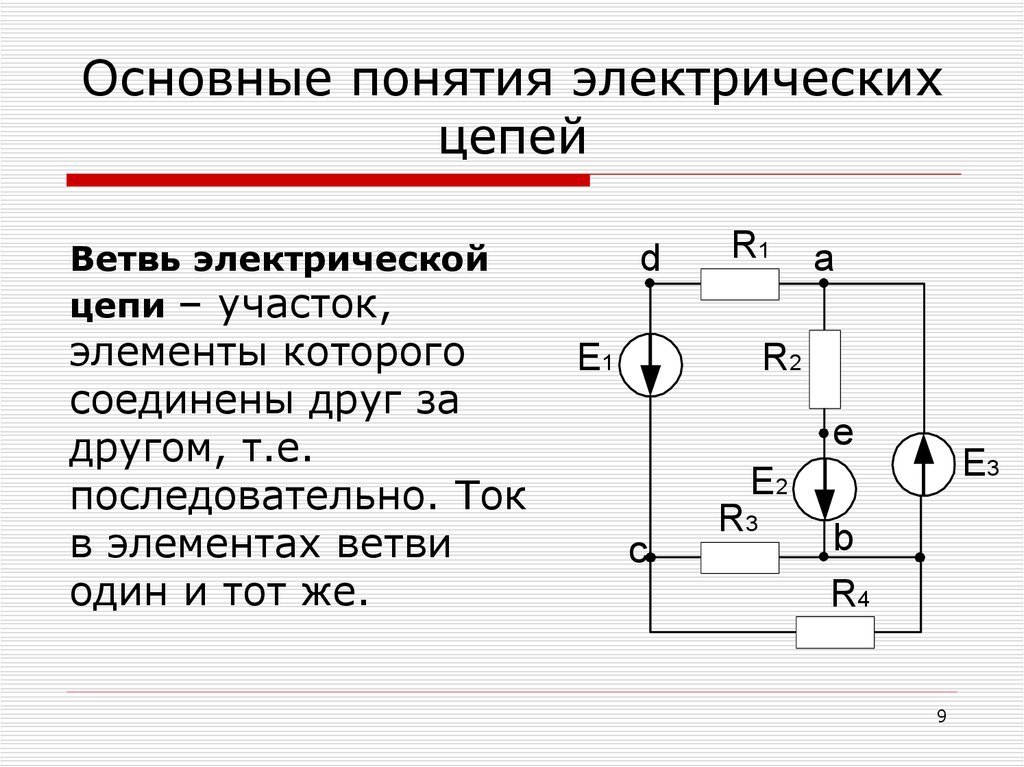 В случае транзистора Q1 имеется три терминальных тока: ток в базу, ток в коллектор и ток в эмиттер. Нас может заинтересовать любой из них, и в следующих главах мы будем им интересны. Тем не менее, по-прежнему применяется правило сохранения, поскольку модель с сосредоточенными элементами запрещает хранение чистого заряда в любом элементе схемы или в любом узле. Как следствие, общий ток в любом компоненте равен нулю, поэтому для транзистора Q1:
В случае транзистора Q1 имеется три терминальных тока: ток в базу, ток в коллектор и ток в эмиттер. Нас может заинтересовать любой из них, и в следующих главах мы будем им интересны. Тем не менее, по-прежнему применяется правило сохранения, поскольку модель с сосредоточенными элементами запрещает хранение чистого заряда в любом элементе схемы или в любом узле. Как следствие, общий ток в любом компоненте равен нулю, поэтому для транзистора Q1:
I(Q1.nB)+I(Q1.nC)+I(Q1.nE)=0
Для любого двухполюсника, даже такого нелинейного, как светодиод D1, есть только одно значение величины тока через устройство, поэтому мы обычно просто называем это, например, током через диод, не уточняя, что это «анодный ток» или «катодный ток», поскольку они тривиально связаны. Поскольку 2 терминальных тока имеют 1 уравнение, связывающее их, существует только 2−1=1 степень свободы (т. е. одно значение тока для устройства), а остальное — просто вопрос указания знака и направления.
Однако для любого N-терминального компонента существует N различных клеммных токов, которые могут нас заинтересовать. В общем, они делают очень разные вещи! Увеличение тока базы Q1 на 1 мА оказывает гораздо большее влияние на схему, чем увеличение тока коллектора Q1 на 1 мА. Тем не менее, существует 1 уравнение, связывающее сумму всех токов со всеми клеммами компонента, в результате чего остается N−1
степени свободы.
В общем, они делают очень разные вещи! Увеличение тока базы Q1 на 1 мА оказывает гораздо большее влияние на схему, чем увеличение тока коллектора Q1 на 1 мА. Тем не менее, существует 1 уравнение, связывающее сумму всех токов со всеми клеммами компонента, в результате чего остается N−1
степени свободы.
При анализе или проектировании схемы принято «задавать вопросы» о различных токах и напряжениях в цепи. (Какое напряжение VB ? Каков ток в базе Q1, I(Q1.nB) ?) Мы можем сформулировать «решение схемы» с точки зрения нахождения любых ответов (неизвестных), которые мы ищем.
В цепи с N узлов (включая 1, определенный как земля), T терминалы компонентов и C компонентов, мы можем задать много вопросов:
- [Для каждого N2 пара узлов:] Какова разность напряжений Vij ?
- [Для каждого T Терминал компонента:] Каков ток на этом терминале?
- [Для каждого T клемма компонента:] Какой ток выходит из этой клеммы?
Из этих трех случаев имеем N2+2T
«вопросы», которые мы могли бы задать. Даже для схемы среднего размера возникает много возможных вопросов, но все они являются правильными вопросами , на которые мы сможем ответить после решения схемы.
Даже для схемы среднего размера возникает много возможных вопросов, но все они являются правильными вопросами , на которые мы сможем ответить после решения схемы.
Однако, чтобы уменьшить размерность нашей проблемы, мы пытаемся упростить это большее количество вопросов (неизвестных) до меньшего числа, чтобы его было легче решать. (См. также: Системы уравнений.)
Например, для разности напряжений мы знаем, что существует нулевая разность напряжений. Vii для любой пары одного и того же узла дважды (i,i) . Кроме того, из закона Кирхгофа о напряжении мы знаем, что циклы напряжений в сумме равны нулю, поэтому мы можем использовать определенную опорную землю для преобразования парных разностей напряжений в разности точечных напряжений между узлом и землей.
- [Для каждого из N−1 незаземленные узлы:] Какое напряжение в данном узле Vi (относительно земли)?
Вместо N2
вопросы о попарных разностях напряжений, теперь у нас есть N−1
вопросов – резко меньшее количество. Важно отметить, что как только мы ответим на эти N−1
вопросы (т.е. решить для этих неизвестных), мы можем легко найти ответы на исходный N2
вопросов.
Важно отметить, что как только мы ответим на эти N−1
вопросы (т.е. решить для этих неизвестных), мы можем легко найти ответы на исходный N2
вопросов.
Для токов 2T вопросы, касающиеся «входа» и «выхода» из конкретного терминала, также легко сводятся к Т вопросы, учитывая только версию «в». Важно отметить, что как только мы ответим на эти T вопросы, мы можем легко ответить на вопросы «из» простым отрицательным знаком.
Теперь мы уменьшили исходное значение N2+2T. вопросы к (N−1)+T вопросов – гораздо меньше.
Теперь мы можем применить текущие отношения терминала компонента.
Как обсуждалось выше, каждый компонент с двумя выводами имеет тривиальное соотношение между токами двух выводов: одно уравнение. И каждый компонент с несколькими клеммами также имеет единственное уравнение, связывающее токи его клемм. В общем, хотя по-прежнему справедливо «задавать вопрос» отдельно о токах базы, коллектора и эмиттера в транзисторе Q1, дело в том, что если мы знаем значение любых двух из трех, мы также знаем и третье.
Это означает, что T вопросы о терминальных токах на C компоненты на самом деле имеют только T−C возможных степеней свободы. Как только мы узнаем значения (правильного подмножества) T−C терминальные токи, остальное мы знаем.
Даже не взглянув на структуру конкретной схемы, мы теперь знаем, что можем отобразить схему из N узлов (включая 1, определенный как земля), T терминалы компонентов и C компонентов из исходного большего пространства:
N2+2T
возможные вопросы по току и напряжению в гораздо меньшее пространство всего:
(N-1)+T-C
вопроса. Основная идея заключается в том, что гораздо проще решить систему уравнений с меньшим числом неизвестных. И что особенно важно, поиск ответов на это меньшее подмножество позволяет нам (очень легко) отбрасывать ответы на оставшиеся вопросы по мере необходимости.
Например, если у нас есть даже очень простая схема с N=8
узлов, Т=20
клеммы и C=10
компонентов (предположим, что все 10 компонентов являются двухконтактными устройствами), у нас будет 82+2∗20=104
вопросы, которые мы можем задать о различных попарных разностях напряжений и терминальных токах. Однако мы можем сопоставить эту схему с гораздо меньшим набором (8−1)+20−10=17.
вопросы, из которых мы можем легко восстановить ответы на любой из первоначальных 104 вопросов! И мы добились этого значительного сокращения, даже не взглянув на компоненты или их расположение.
Однако мы можем сопоставить эту схему с гораздо меньшим набором (8−1)+20−10=17.
вопросы, из которых мы можем легко восстановить ответы на любой из первоначальных 104 вопросов! И мы добились этого значительного сокращения, даже не взглянув на компоненты или их расположение.
Этот процесс сокращения широко используется как программным обеспечением для моделирования цепей, таким как CircuitLab, так и при решении схем вручную. (На самом деле, это часто полностью замалчивается, оставляя новичков в замешательстве относительно того, как было выполнено такое упрощение и как вернуться к ответам на вопросы, которые нас в конечном итоге интересуют, поэтому мы решили сделать это здесь более подробно.)
Как показывают два примера цепей с помеченными клеммами и токами выше, мы можем пометить T различных токов клемм в цепи с общим количеством клемм T, но они не уникальны.
В нашем предыдущем обсуждении закона тока Кирхгофа мы смогли обсудить текущие потоки, не ссылаясь на какие-либо конкретные компоненты или терминалы. Мы достигли этого, вручную пометив токи, а также поместив стрелку, чтобы указать определенное направление обычного потока тока (в отличие от потока электронов). Например:
Мы достигли этого, вручную пометив токи, а также поместив стрелку, чтобы указать определенное направление обычного потока тока (в отличие от потока электронов). Например:
Пример KCL с тремя узлами
Circuitlab.com/c4e7f729tv5s3
Править – Simulate
Мы вручную пометили стрелку тока через каждый из четырех показанных компонентов, и это само по себе позволило нам написать три уравнения KCL (по одному в каждом узле A, B, C), описывающих структуру схемы. (Обратите внимание, что, хотя было сгенерировано 3 уравнения, только 2 из них являются линейно независимыми. Просмотрите раздел KCL, чтобы просмотреть эти уравнения.) На самом деле, в простом последовательно соединенном наборе элементов мы могли бы сразу понять, что i1 = i2 и использовать только одну переменную, если направление везде одинаково.
Процесс ручной маркировки текущих переменных (и произвольного назначения направления) включает в себя большую часть только что описанных процессов редукции. Мы по-прежнему можем задавать все возможные вопросы о токе (т. е. о входных и выходных токах каждого компонента), но теперь мы можем обращаться к этим клеммным токам в терминах этих вручную выбранных токовых переменных, иногда называемых ответвленными токами .
Мы по-прежнему можем задавать все возможные вопросы о токе (т. е. о входных и выходных токах каждого компонента), но теперь мы можем обращаться к этим клеммным токам в терминах этих вручную выбранных токовых переменных, иногда называемых ответвленными токами .
Симулятор цепей обычно не представляет мир с точки зрения токов ветвей, а вместо этого вычисляет токи клемм для различных компонентов. Тем не менее, они явно тесно связаны и могут быть отображены туда и обратно, просто определяя правильный ток ветви, который отображается на клемму, и применяя знак минус, если стрелка тока ветви выходит «из» этой клеммы, а не в обычном определении. клеммных токов, являющихся положительными для потока «в» клемму.
Мы можем обозначать токи ветвей и в более сложных цепях, как это часто делается при решении вручную. Например, мы можем обозначить наш пример с несколькими терминалами выше: (щелкните, чтобы открыть в новой вкладке)
.Маркированные токи клемм и ответвлений – с BJT и светодиодом
Circuitlab. com/c95w3f4e3n69c
com/c95w3f4e3n69c
Править – Моделирование
Мы пометили 6 ветвей тока, с i1 по i6. . В общем, на схеме мы не будем так явно обозначать как токи ветвей, так и клеммные токи, но мы делаем это здесь, чтобы быть очень явными и показать сопоставление между ними.
Просто наблюдая за направлением стрелок вдоль каждой ветви цепи, мы можем написать множество уравнений, связывающих токи ветвей с токами клемм. Например, для i1 , мы можем видеть, что это описывает ток, протекающий через источник напряжения V1, и направление стрелки i1 противопоставляется I(V1.nA) но находится в том же направлении, что и I(V1.nB) . Это позволяет нам записать:
i1=-I(V1.nA)i1=I(V1.nB)
или проще:
i1=-I(V1.nA)=I(V1.nB)
Мы можем повторить этот процесс для каждого из 6 токов ветвей, пока не сопоставим все 13 токов клемм с 6 токами ветвей:
i1=−I(V1.nA)=I(V1.nB)i2 =I(R2.nA)=-I(R2.nB)i3=I(D1.nA)=-I(D1.nK)=I(Q1.nC)i4=I(Q1.nB)i5=I( R3.nA)=-I(R3. nB)i6=-I(Q1.nE)=I(R1.nA)=-I(R1.nB)
nB)i6=-I(Q1.nE)=I(R1.nA)=-I(R1.nB)
Каждый ток ответвления просто сопоставляется со всеми терминальными токами на этом ветвь, возможно, со знаком минус, указывающим на несоответствие направления стрелки. Ветвь продолжается до тех пор, пока не произойдет «расщепления», когда ток может идти двумя путями.
Для схемы с 13 терминалами это позволяет нам ответить на 26 возможных текущих вопросов (т. е. ток в любой терминал или из него) только с 6 базовыми переменными.
Процесс сопоставления тока ветви имеет тенденцию автоматически обрабатывать узлы, где встречаются только два терминала (например, узлы C и D), поскольку мы помечаем их как одну непрерывную ветвь, поэтому мы назначаем только одну текущую переменную. Для узлов, где встречаются 3 или более клемм (таких как A и B), мы можем применить закон тока Кирхгофа к токам ветвей:
i1-i2-i3=0i2-i4-i5=0
Кроме того, процесс сопоставления тока ответвления имеет тенденцию заботиться о сохранении потока заряда в устройствах с двумя выводами, поскольку они помечены одним и тем же током ответвления. Однако для компонентов с тремя или более клеммами мы можем явно сгенерировать правило суммирования дополнительных токов, заметив, что суммарные входные токи ветвей должны равняться суммарным выходным токам ветвей. Например, для транзистора Q1:
Однако для компонентов с тремя или более клеммами мы можем явно сгенерировать правило суммирования дополнительных токов, заметив, что суммарные входные токи ветвей должны равняться суммарным выходным токам ветвей. Например, для транзистора Q1:
i3+i4−i6=0
Это дополнительное и, возможно, ценное ограничение при ручном решении схемных задач. Однако в программном обеспечении для моделирования цепей, таком как CircuitLab, все многополюсные устройства эффективно моделируются внутренне как набор различных (возможно, нелинейных и взаимодействующих) двухвыводных устройств, поэтому дополнительное ограничение не требуется.
Еще один способ осмыслить процесс маркировки и сокращения — рассмотреть, как мы будем эффективно проводить измерения цепи. Для этого мы снова обратимся к гидравлической аналогии воды под давлением, протекающей через сеть труб и других компонентов. (Пока мы игнорируем практические вопросы точности и т. д. и рассматриваем только теоретическую модель. )
)
Мы можем задать вопрос о разнице напряжений (т. е. разности давлений) между любыми двумя точками в сети и в гидравлической системе. системы, мы могли бы купить дифференциальные манометры и установить их между каждой парой точек, которые нас интересуют. Однако, если у нас есть N очков, у нас есть N2 пар точек (или, возможно, N(N−1)2 пар, если игнорировать Vii=0 и разрешено измерять Vab=-Vba ). Дифференциальный манометр подобен вольтметру с двумя выводами и показывает только относительную разницу давлений. Однако для этого необходимо провести множество дифференциальных измерений, а покупка и установка этих датчиков стоит дорого! Вместо этого мы можем просто установить N−1 манометры перепада давления (взяв 1 узел за точку отсчета), а затем вычитать, когда это необходимо, чтобы ответить на любые вопросы об относительных различиях. Для небольшой гидравлической схемы, состоящей всего из 10 узлов, это разница между 45 и 9 узлами.датчики установить и читать!
Точно так же мы могли бы установить амперметр (т.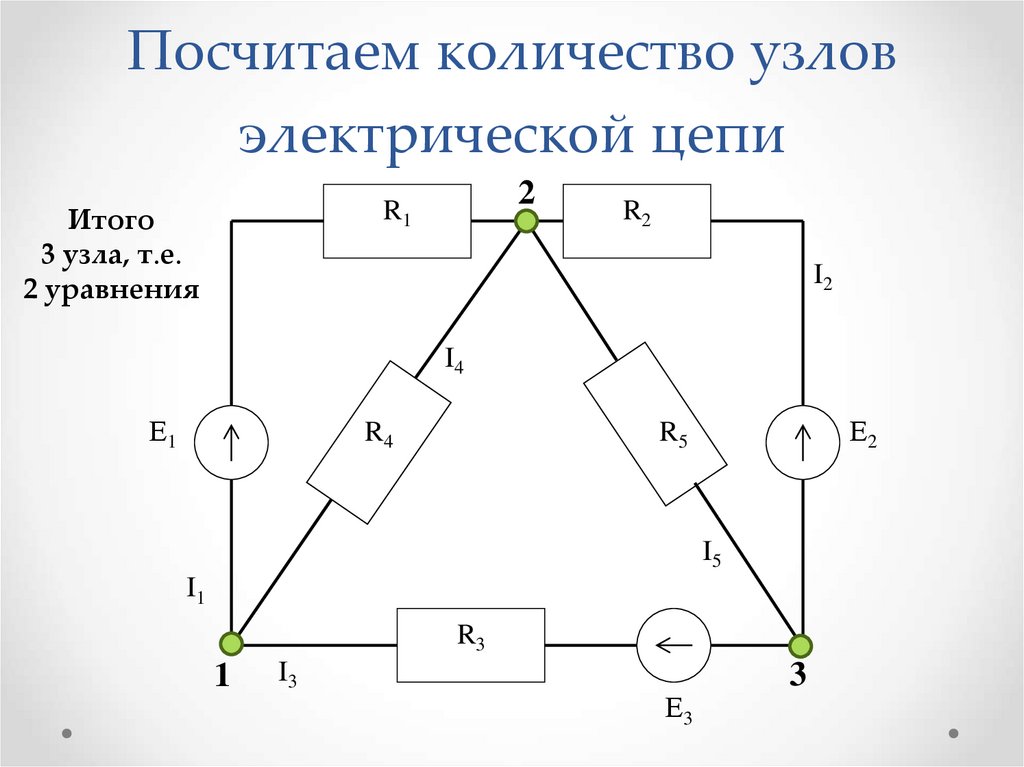 е. устройство для измерения расхода) на каждом выводе каждого компонента, но явно не имеет смысла устанавливать расходомер с обеих сторон одного двухвыводного компонента, поскольку скорость потока будет такой же при условии отсутствия утечек. Вместо этого мы должны установить только одно измерение скорости потока на ответвление. (И, если есть 3+ терминальных компонента, мы можем быть даже более умными и установить меньше, чем один расходомер на ответвление, используя сохранение расхода, как показано выше.) Это гораздо меньшее количество расходомеров для покупки, установки, и монитор.
е. устройство для измерения расхода) на каждом выводе каждого компонента, но явно не имеет смысла устанавливать расходомер с обеих сторон одного двухвыводного компонента, поскольку скорость потока будет такой же при условии отсутствия утечек. Вместо этого мы должны установить только одно измерение скорости потока на ответвление. (И, если есть 3+ терминальных компонента, мы можем быть даже более умными и установить меньше, чем один расходомер на ответвление, используя сохранение расхода, как показано выше.) Это гораздо меньшее количество расходомеров для покупки, установки, и монитор.
Точно так же, как мы естественным образом применяем эти упрощения при измерении электрической (или гидравлической) цепи, мы применяем их и при постановке задачи для алгебраического решения, потому что они значительно упрощают этот процесс.
В следующем разделе «Решение систем цепей» мы поговорим об объединении нашего маркированного структурного представления схемы с уравнениями на уровне отдельных компонентов для полной настройки и решения схем любой сложности.

 Результаты измерений
Результаты измерений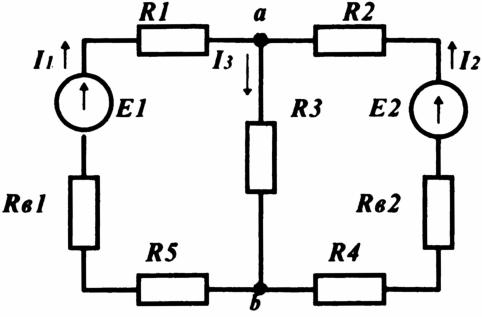 Какое свойство заряда он отражает?
Какое свойство заряда он отражает?

 Это электротермические устройства, лампы, резисторы, электродвигатели.
Это электротермические устройства, лампы, резисторы, электродвигатели.


 Проволочные перемычки являются хорошими проводниками, поэтому будем считать, что точки, соединенные проволочными перемычками, становятся единым узлом. На рис. 4 показано, как этот подход можно использовать для создания узлов с более чем пятью отверстиями на макетной плате.
Проволочные перемычки являются хорошими проводниками, поэтому будем считать, что точки, соединенные проволочными перемычками, становятся единым узлом. На рис. 4 показано, как этот подход можно использовать для создания узлов с более чем пятью отверстиями на макетной плате. Основное предположение схем с сосредоточенными параметрами состоит в том, что идеальные проводники мгновенно передают ток без падения напряжения.
Основное предположение схем с сосредоточенными параметрами состоит в том, что идеальные проводники мгновенно передают ток без падения напряжения.
 Это выражение будет добавлено в список.
Это выражение будет добавлено в список.