Главная
В чем давление в физике: Давление — урок. Физика, 7 класс.

В чем давление в физике: Давление — урок. Физика, 7 класс.

Определение давления

До сих пор мы изучали случаи, когда сила, действующая на тело, была приложена к нему в одной точке. Мы так и говорили про неё: «точка приложения силы» . Настало время ситуаций, когда сила приложена к телу во множестве точек, то есть действует на некоторую площадь поверхности. В каждом из таких случаев говорят не только о самой силе, но и о создаваемом ею давлении.

Как приятна зимняя прогулка на лыжах! Однако стоит выйти на снег без них, как ноги будут глубоко проваливаться при каждом шаге, идти будет трудно, и удовольствие будет испорчено.

На этом рисунке вес лыжника примерно равен весу «пешехода». Поэтому силы, с которыми мальчики давят на снег, будем считать равными. Но заметьте: они действуют не на одну точку, а «распределяются» по некоторым поверхностям. У лыжника – по площади касания снега и лыж, а у пешехода – снега и подошв.

Понятно, что Sлыж > Sподошв. – перпендикулярно приложенная сила, Н.
S – площадь поверхности, м2

Единица давления – 1 паскаль (обозначается: 1 Па). Из формулы-определения видно, что 1 Па = 1 Н/м2

Числовое значение давления показывает силу, приходящуюся на единицу площади её приложения. Например, при давлении 5 паскалей на каждый 1 м2 будет действовать сила 5 ньютонов.

Вернёмся к примеру с мальчиками. На рисунке не указаны числовые значения F и S. Значит, мы не можем количественно сравнить давления, которое оказывают мальчики (с лыжами и без лыж) на снег. Однако мы можем сравнить их качественно, используя слова «больше» и «меньше». Сделаем это.

Сначала запишем исходные данные: силы, с которыми мальчики давят на снег, равны, и площадь лыж больше площади подошв (см. столбик слева):

После знака «Ю», который значит «следовательно», мы составили две дроби. Обратите внимание: знак «больше», присутствовавший в исходных данных, изменился на знак «меньше». Почему? Поскольку знаменатель левой дроби больше знаменателя правой, значит, согласно свойству дроби, сама левая дробь меньше правой. Вспомнив, что каждая дробь в этом неравенстве является давлением, получим: давление лыжника меньше давления пешехода. Этим и объясняется то, что лыжник меньше проваливается в снег, чем пешеход.

Формула-определение давления подсказывает нам, как его можно изменять: чтобы увеличить давление, нужно увеличить силу или уменьшать площадь её приложения. И наоборот: чтобы уменьшить давление, нужно уменьшить силу или увеличить площадь, на которую эта сила действует.

Опубликовано в разделах: 7 класс, Давление тел

Давление атмосферное, гидростатическое. Закон Паскаля, сила. Сообщающиеся сосуды, применение

Физика->Молекулярная физика->давление->

Тестирование онлайн

  • Давление. Основные понятия

  • Механика жидкостей

Давление

Это физическая скалярная величина, которая определяется по формуле

Атмосферное давление

Атмосфера – это воздушная оболочка Земли, которая удерживается гравитационными силами. Атмосфера имеет вес и давит на все тела на Земле. Давление атмосферы составляет около 760 мм.рт.ст. или 1 атм., или 101325Па. Миллиметр ртутного столба, атмосфера – это различные внесистемные единицы измерения давления. Атмосферное давление уменьшается на 1 мм.рт.ст. при поднятии над Землей на каждые 11м.

Что такое давление в 1 атм? Рукопожатие крепкого мужчины составляет 0,1 атм, удар боксера составляет несколько атмосферных единиц. Давление каблука-шпильки составляет 100 атмосфер. Если на ладонь положить гирю в 100 кг, то получим неравномерное давление в одну атмосферу, при погружении на 10 м под воду получим равномерное давление в 1 атмосферу. Равномерное давление легко переносится человеческим организмом. Нормальное атмосферное давление, которое действует на каждого человека, компенсируется внутренним давлением, поэтому его мы совершенно не замечаем, несмотря на то, что оно является достаточно существенным.

Закон Паскаля

Давление на жидкость или газ передается во всех направлениях одинаково.

Давление внутри жидкости (газа) на одной и той же глубине одинаково во всех направлениях (влево вправо, вниз и вверх!)

Гидростатическое давление

Это давления столбика жидкости на дно сосуда. Какая сила создает давление? Жидкость обладает весом, который давит на дно.


Давление жидкости на дно


Давление на дно сосуда не зависит от формы сосуда, но зависит от площади его дна. При этом сила давления на дно может быть и больше и меньше силы тяжести жидкости в сосуде. В этом заключается “гидростатический парадокс”.

На стенку сосуда гидростатическое давление распределено неравномерно: у поверхности жидкости оно равно нулю (без учета атмосферного давления), внутри жидкости изменяется прямо пропорционально глубине и на уровне дна достигает значения . Это переменное давление можно заменить средним давлением

Сообщающиеся сосуды

Это сосуды, которые имеют общий канал внизу.

Однородная жидкость устанавливается в сообщающихся сосудах на одном уровне независимо от формы сосудов, как видно на фотографии.

Разнородные жидкости устанавливаются в сообщающихся сосудах согласно формуле


Гидравлический пресс

Гидравлический пресс состоит из двух сообщающихся сосудов цилиндрической формы. В сосудах двигаются поршни с площадями S1 и S2. Цилиндры заполнены техническим маслом.

Объем жидкости, вытесненный малым поршнем поступает в большой цилиндр.

Гидравлический пресс дает выигрыш в силе во столько раз, во сколько площадь большего поршня больше площади меньшего. Выигрыша в работе гидравлический пресс не дает.

На практике вследствие наличия трения:

11.3: Давление – Физика LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    1563
    • OpenStax
    • OpenStax

    Цели обучения

    К концу этого раздела вы сможете:

    • Определить давление.
    • Объясните взаимосвязь между давлением и силой.
    • Рассчитать силу, учитывая давление и площадь.

    Вы, несомненно, слышали, что слово давление используется по отношению к крови (высокое или низкое кровяное давление) и по отношению к погоде (погодные системы высокого и низкого давления). Это только два из многих примеров давлений в жидкостях.

    Определение: Давление

    Давление определяется как сила, деленная на площадь, перпендикулярную силе, к которой приложена сила, или

    \[P = \dfrac{F}{A}. \label{давление}\]

    где \(F\) – сила, приложенная к площади \(A\), перпендикулярной силе.

    Действие данной силы может существенно различаться в зависимости от площади, на которую она воздействует, как показано на рисунке Рисунок \(\PageIndex{1}\). Единицей давления в СИ является паскаля , где 92 \, или \, psi)\) до сих пор иногда используется в качестве меры давления в шинах, а миллиметры ртутного столба (мм рт.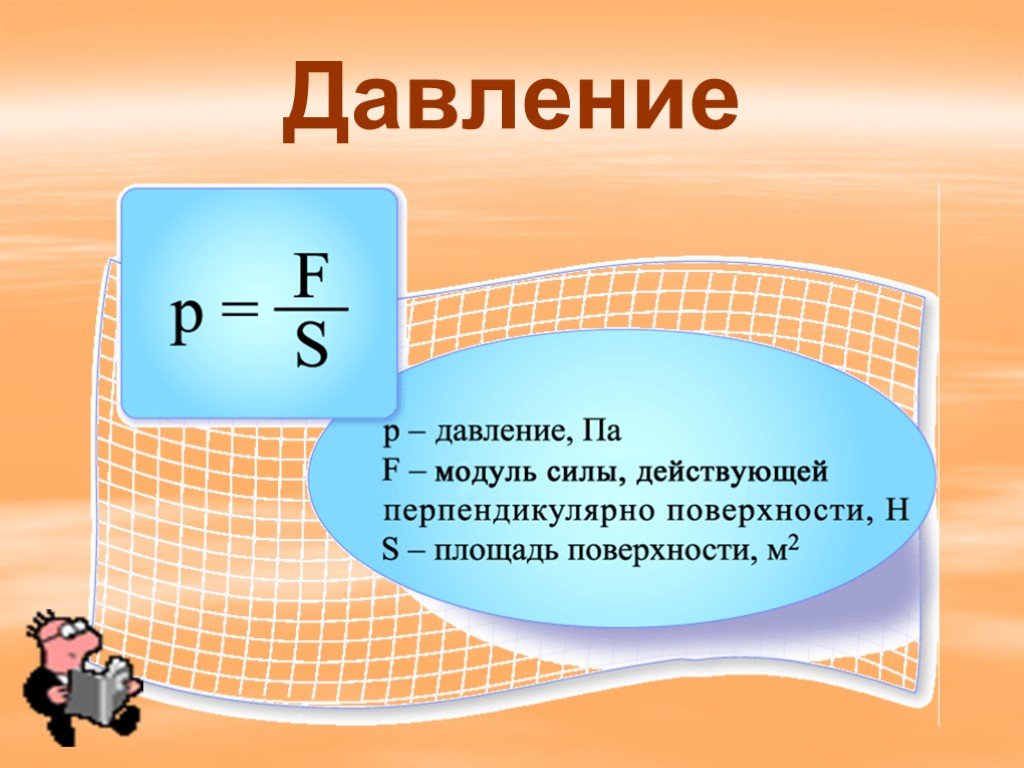

    ст.) по-прежнему часто используются для измерения кровяного давления. Давление определяется для всех состояний вещества, но особенно важно при обсуждении жидкостей.

    Рисунок \(\PageIndex{1}\): (a) Хотя человек, которого тыкают пальцем, может испытывать раздражение, сила не имеет длительного эффекта. (b) Напротив, та же самая сила, приложенная к участку размером с острый конец иглы, достаточно велика, чтобы повредить кожу. 96 \, Па\). С какой силой воздух внутри бака действует на плоский конец цилиндрического бака — диска диаметром 0,150 м?

    Стратегия

    Мы можем найти силу, действующую из определения давления (Уравнение \red{давление}), если мы можем найти площадь \(A\), на которую действует.

    Решение

    Изменяя определение давления (уравнение \red{давление}) для решения силы, мы видим, что

    \[F = PA.\nonumber\]

    95 \, N. \end{align*}\]

    Обсуждение

    Ого! Недаром танк должен быть крепким. Поскольку мы нашли \(F = PA\), мы видим, что сила давления прямо пропорциональна площади, на которую действует давление, а также самому давлению.

    Сила, действующая на конец резервуара, перпендикулярна его внутренней поверхности. Это направление связано с тем, что сила создается статической или стационарной жидкостью. Мы уже видели, что жидкости не могут выдержать

    сдвигающих (боковых) сил; они не могут также оказывают сдвигающих усилий. Давление жидкости не имеет направления, являясь скалярной величиной. Силы давления имеют четко определенные направления: они всегда действуют перпендикулярно любой поверхности. (См., например, шину на рисунке \(\PageIndex{2}\).)

    Рисунок \(\PageIndex{2}\): Давление внутри этой шины действует перпендикулярно ко всем поверхностям, с которыми она контактирует. Стрелки показывают репрезентативные направления и величины сил, действующих в различных точках. Обратите внимание, что статические жидкости не создают силы сдвига.

    Наконец, обратите внимание, что давление оказывается на все поверхности. Пловцы, как и шина, ощущают давление со всех сторон (Рисунок \(\PageIndex{3}\)).

    Рисунок \(\PageIndex{3}\): Давление на этого пловца оказывается со всех сторон, так как вода потекла бы в пространство, которое он занимает, если бы его там не было. Стрелки представляют направления и величины сил, действующих на пловца в различных точках. Обратите внимание, что силы внизу больше из-за большей глубины, что дает сеть вверх или выталкивающую силу, которая уравновешивается весом пловца.

    ИССЛЕДОВАНИЯ PHET: СВОЙСТВА ГАЗА

    В этой симуляции закачивайте молекулы газа в коробку и смотрите, что происходит при изменении объема, добавлении или удалении тепла, изменении гравитации и т. д. Измерьте температуру и давление и узнайте, как свойства газа меняются по отношению друг к другу.

    Резюме

    • Давление — это сила, приходящаяся на единицу перпендикулярной площади, к которой приложена сила. В форме уравнения давление определяется как \[F = PA. \номер\]
      • 92. \)

    Глоссарий

    давление
    сила на единицу площади, перпендикулярная силе, на которую действует сила

    Эта страница под названием 11.3: Давление распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

    1. Вернуться к началу
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        ОпенСтакс
        Лицензия
        СС BY
        Версия лицензии
        4,0
        Программа OER или Publisher
        ОпенСтакс
        Показать оглавление
        нет
      2. Теги
        1. давление
        2. источник@https://openstax. org/details/books/college-physics

      Давление

      Давление

      Давление определяется как сила на единицу площади. Обычно удобнее использовать давление, а не силу, для описания влияния на поведение жидкости. Стандартной единицей давления является паскаль, то есть ньютон на квадратный метр.

      Для объекта, находящегося на поверхности, сила, давящая на поверхность, равна весу объекта, но в разных ориентациях он может иметь разную площадь контакта с поверхностью и, следовательно, оказывать разное давление.

      Расчет давления.

      Во многих физических ситуациях давление является наиболее важной переменной. Если вы чистите яблоко, ключевой переменной является давление: если нож острый, то площадь контакта мала, и вы можете чистить с меньшим усилием, прилагаемым к лезвию. Если вам необходимо сделать инъекцию, то давление является наиболее важной переменной для введения иглы через кожу: лучше иметь острую иглу, чем тупую, поскольку меньшая площадь контакта означает, что для проталкивания иглы требуется меньшее усилие.

      через кожу.

      Когда вы имеете дело с давлением покоящейся жидкости, среда рассматривается как непрерывное распределение материи. Но когда вы имеете дело с давлением газа, к нему нужно подходить как к среднему давлению от молекулярных столкновений со стенками.

      Давление в жидкости можно рассматривать как меру энергии на единицу объема посредством определения работы. Эта энергия связана с другими формами энергии жидкости уравнением Бернулли.

      		 Индекс

      Концепции давления

       
      5

      5

      5
      Гиперфизика***** Механика ***** Жидкости R Ступица
      Назад

      Давление в жидкости может рассматриваться как мера энергии на единицу объема или плотности энергии. Для силы, действующей на жидкость, это видно из определения давления:

      Наиболее очевидным применением является гидростатическое давление жидкости, где давление может использоваться как плотность энергии наряду с плотностью кинетической энергии и плотностью потенциальной энергии в уравнении Бернулли.

      Другая сторона медали заключается в том, что плотность энергии от других причин может быть удобно выражена как эффективное «давление». Например, плотность энергии молекул растворителя, приводящая к осмосу, выражается осмотическим давлением. Плотность энергии, которая удерживает звезду от коллапса, выражается как радиационное давление.

      		 Алфавитный указатель

      Концепции Бернулли

       

      5
      Гиперфизика***** Механика ***** Жидкости R Ступица
      Назад

      Кинетическая энергия движущейся жидкости более полезна в таких приложениях, как уравнение Бернулли, когда она выражается как кинетическая энергия на единицу объема

      Когда кинетическая энергия соответствует кинетической энергии жидкости в условиях ламинарного течения через трубу, для оценки кинетической энергии необходимо учитывать профиль скорости.

      Оставить комментарий