В чем измеряется момент инерции в си: Единицы измерения момента инерции

№03определение момента инерции тел

4

Лабораторная работа № 3

определение момента инерции тел и

проверка основного зАкона динамики

вращательного движения

Цель работы: определить момент инерции маятника Обербека, изучить зависимости углового ускорения от момента инерции при неизменном моменте силы.

Приборы и принадлежности: маятник Обербека, двухметровая линейка, секундомер, штангенциркуль, шнур длиной 2,5 м, грузы массой 100 г и 200 г.

Теория работы

Момент инерции I_i материальной точки с массой Δm_i , находящейся на расстоянии r_i от оси вращения, численно равен произведению массы математической точки на квадрат расстояния её от оси, т.е. I_i = Δm_ir_i² (рис.1).

Тело можно представить состоящим из n таких элементарных масс. Тогда момент инерции тела:

I = .

Единица измерения момента инерции в СИ: [I] = кг·м². Вращение тела вокруг оси вызывается вращающим моментом или просто моментом силы. Моментом М силы относительно оси вращения называют векторную величину, численно равную произведению силы F на длину d перпендикуляра, опущенного из центра вращения на направление действия силы, называемого плечом силы:

М = F·d.

Под действием момента силы закрепленное на оси твердое тело приобретает угловое ускорение β:

β = ,

где ω – угловая скорость.

Зависимость углового ускорения β вращающегося тела от момента М действующей на тело силы и момента инерции I тела относительно оси, вокруг которой происходит вращение, определяется основным уравнением (законом) динамики вращательного движения:

М = I β = I.

Формула закона для вращательного движения аналогична формуле закона Ньютона для поступательного движения:

F = ma.

Силе F соответствует момент силы М; ускорению а – угловое ускорение β; массе m – момент инерции I. Подобно тому, как масса m характеризует инерционные свойства тела при поступательном движении, момент инерции I характеризует инерционные свойства тел при вращательном движении.

Знание момента инерции тел, а также основного закона динамики вращательного движения необходимо во многих областях науки и технике. В некоторых разделах космической и спортивной медицины, ортопедии, бионики возникает необходимость измерения момента инерции тела человека и отдельных его частей. Момент инерции при вращательном движении туловища человека или его конечностей вычисляют приблизительно по формулам момента инерции цилиндра и круглого стержня или определяют из опыта. В молекулярной биологии определяют моменты инерции сложных молекул. По их значениям классифицируют молекулы многих исследуемых веществ. Знание моментов инерции молекул необходимо также при определении вращательной энергии молекул в квантовой механике.

Описание установки

Момент инерции тела может быть определен из закона динамики вращательного движения: I = . (1)

Для измерения действующего на тело момента силы и сообщенного этому телу углового ускорения применяют крестообразный маятник Обербека (рис.2).

Прибор состоит из шкива L радиусом r, закреплённого на оси O; четырёх стержней, расположенных под углом 90º друг к другу и четырёх одинаковых цилиндрических грузов m

0, которые можно перемещать вдоль стержней и закреплять на определённых расстояниях.

Грузы закрепляются симметрично, т.е. так, чтобы центр тяжести маятника находился на оси вращения.

Прибор приводится во вращательное движение грузом, масса которого m. Груз прикрепляется к концу шнура, намотанного на шкив.

Если груз, подвешенный на нити, падает с высоты h за время t, то h = , где а – линейное ускорение на ободе шкива.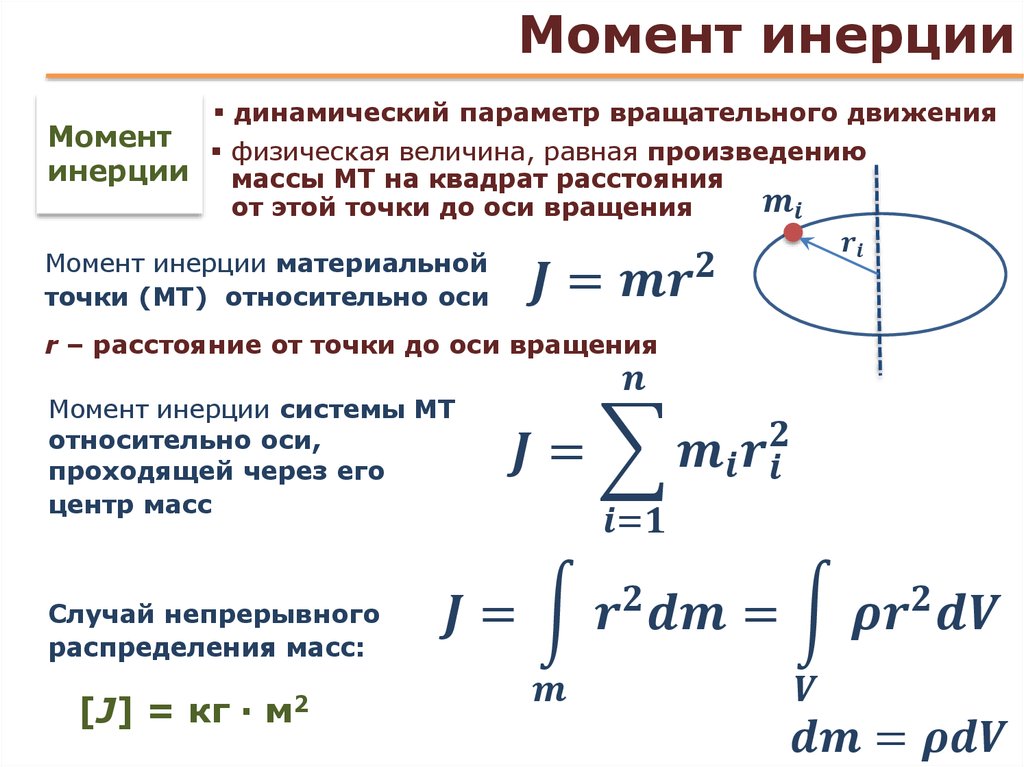 Тогда:

а = . (2)

При этом шкив со стержнями и расположенными на нём грузами будет вращаться с угловым ускорением β:

β = . (3)

Из (2) и (3) следует, что:

β = . (4)

Вращающий момент найдем по формуле: М = Т·r, где Т – сила натяжения нити, r – плечо этой силы.

Силу натяжения нити найдем из II закона Ньютона для груза массой m:

ma = , но ma = mg – T, откуда Т = mg – ma.

Тогда: М = (mg – ma) · r = m (g – ) · r. (5)

Подставив в формулу (1), формулы (4) и (5) получим:

I = . (6)

Для определения момента инерции I необходимо определить опытным путём все величины, стоящие в правой части формулы (6).

Порядок выполнения работы

1. Определение момента инерции маятника.

1. Переместить грузы к концам стержней и закрепить их винтами на последних делениях, нанесенных на стержнях. При этом маятник не должен поворачиваться, если систем правильно сбалансирована.

2. К концу нити прикрепить груз. Намотать равномерно нить на шкив.

3. На линейке нанести две метки на расстоянии, соответствующем высоте падения h.

4. С помощью штангенциркуля определить радиус шкива.

5. Предоставив возможность грузу m падать, по секундомеру определить время падения. Секундомер включить в момент начала падения груза от верхней метки на линейке и остановить в момент прохождения нижней метки.

6. Опыт повторить для двух разных грузов (например, 100 и 200 г).

   Данные опытов занести в таблицу 1.

Таблица 1

№ п/п	m, кг	r, м	h, м	t, c	I, кг·м2	<I>, кг·м2
1
2

7. Определить дважды моменты инерции маятника по формуле (6) и найти его среднее значение.

2. Исследование законов вращательного движения.

1. Последовательно закрепить грузы симметрично на размеченных на стержнях делениях и описанным в первом опыте способом найти время t для различных положений грузов.

2. Маятник приводить в движение с помощью одного и того же груза, т.е. m = const.

3. Полученные данные занести в таблицу 2.

Таблица 2

№ п/п	h, м	t, c	M, Н·м	β , c-2	I, кг·м2	Приложение
1 2						m = r =

3.

По формулам (5), (4) и (1) определить: момент силы, угловое ускорение и момент инерции маятника для каждого случая.

Контрольные вопросы

1. Что называется моментом инерции материальной точки тела? Какие свойства тел он характеризует?

2. В каких единицах в системе СИ изменяется момент инерции?

3. Что называется моментом силы? В каких единицах он измеряется?

4. В каких областях медицины необходимо знание моментов инерции тел?

5. Сформулировать и записать уравнение динамики вращательного движения. Сравнить его со II законом Ньютона для поступательного движения.

6. Вывести расчетную формулу для определения момента инерции маятника Обербека.

7. Какая зависимость между угловым ускорением и моментом инерции маятника при постоянном значении момента силы?

Что это – момент инерции? В чем измеряется момент инерции? Пример задачи

Механика представляет собой один из основных разделов физики, в котором рассматриваются законы движения и равновесия тел. При количественном описании движения вращения важной величиной является момент инерции. В данной статье изучим эту величину. Кроме того, ответим на вопрос о том, в чем измеряется момент инерции твердого тела.

Понятие о моменте инерции для точки материальной

Как физическую величину, его определяют в виде произведения массы на квадрат радиуса вращения. Предположим, что существует некоторая материальная точка, которая имеет массу m. Она вращается вокруг оси, при этом радиус окружности равен r. При заданных условиях инерции, момент вычисляется в соответствии со следующей формулой:

I = m*r².

Этой формулой можно пользоваться даже в случаях изучения тел со сложной формой. Главным условием справедливости равенства является наличие огромной разницы между расстоянием до оси вращения r и геометрическими размерами самого тела. Например, при расчете величины I для нашей планеты, которая вращается вокруг Солнца по круговой траектории, можно считать Землю материальной точкой, поскольку расстояние до звезды на несколько порядков превышает радиус планеты.

Величина I для тела произвольной формы

В случае, если геометрические размеры вращающегося тела незначительно отличаются от радиуса r, тогда следует принимать во внимание форму тела. С учетом названного фактора рассчитывают момент инерции с использованием следующей формулы:

I = ∫_m(r²*dm).

По сути, это равенство является суммой моментов инерций всех материальных точек, которые образуют тело. При проведении практических вычислений, записанной формулой пользуются в несколько ином виде, который представлен ниже:

I = ∫_V(ρ*r²*dV).

Как видно, интегрирование по массе m заменяется на интегрирование по объему V. Здесь греческой буквой ρ обозначена плотность. Если тело является однородным, то ρ будет постоянной величиной, которую можно вынести за знак интеграла. Если же масса неоднородно распределена по телу, то плотность будет функцией параметра r. Записанную формулу удобно использовать при определении I разных тел, потому что расчет выполняется с помощью мысленного деления тела на элементарные объемы dV.

Результаты применения записанного выше равенства для геометрических тел идеальной формы, например, для сферы, цилиндра или стержня, собраны в соответствующие таблицы. В чем измеряется момент инерции? Ниже на рисунке приводятся величины I для некоторых тел. Как видим, все формулы линейно зависят от массы тел и от квадрата геометрического параметра.

В чем измеряется момент инерции тела?

Получив необходимые теоретические сведения для величины I, каждый легко сможет ответить на поставленный вопрос. Действительно, если взглянуть на формулу для I материальной точки, то, отвечая на вопрос о том, в чем измеряется момент осевой инерции, следует ответить, что в килограммах на квадратный метр. Сокращенно эта единица записывается кг*м². Очевидно, что ту же самую единицу мы получим, если воспользуемся интегральным выражением через объем и плотность.

Отметим, что кг*м² также можно записать, как м²*кг. Такая форма записи тоже допускается, однако, в практической физике ее не используют.

Поскольку и килограмм, и метр являются системными единицами измерения массы и длины, соответственно, то кг*м² является также единицей СИ для момента инерции.

Не следует изучаемую единицу путать с другой, которая обозначается, как кг/м². Хотя ее используют редко, и она не является единицей СИ, тем не менее она позволяет рассчитать соответствующее давление, если ее умножить на ускорение свободного падения.

Пример задачи

Разобравшись, в чем измеряется момент инерции, и как его вычислять, решим следующую задачу: необходимо определить момент инерции Земли, полагая ее материальной точкой.

Для успешного решения этой задачи следует знать всего два параметра: массу планеты и средний радиус ее солнечной орбиты. Оба значения можно посмотреть в соответствующих справочниках. Масса M и радиус орбиты R Земли равны:

M = 5,972*10²⁴ кг;

R = 149,6*10⁹ м.

Воспользовавшись выражением для вычисления инерции момента точки материальной, приходим к следующему результату:

I = M*R² = 5,972*10²⁴*(149,6*10⁹)² = 1,3 10⁴⁷ кг*м².

Мы получили гигантское значение. Если сравнить его с моментом инерции Земли относительно ее собственной оси, то окажется, что он будет в миллиард раз меньше рассчитанной величины. Таким образом, приближение материальной точки вполне уместно для рассмотренной задачи.

[Решено] Единица СИ “Инерция”

Этот вопрос ранее задавался в

BSNL JE (TTA) 25 сентября 2016 Смена 1 Бумага

Просмотреть все Бумаги BSNL TTA >

1. кгм
9 на0 2 0 метр
2. кг
3. кгм ³

Вариант 1 : кгм ²

Бесплатно

BSNL JE (TTA) 25 сентября 03 0 0 Бумага 25 03 00 0,8 тыс. пользователей

200 вопросов

200 марок

180 минут

Когда физический объект испытывает изменения в своей скорости, направлении или состоянии покоя, свойство, которое сопротивляется этому изменению, называется инерцией. Единицей инерции в СИ является кгм ² .

 

Количество	Блок	Размер
Сопротивление (R)	Ом	[МЛ2Т-3А-2]
Емкость (Кл)	кулон/вольт или фарад	[М-1L2T4A2] ​​
Удельное сопротивление или удельное сопротивление (ρ)	Омметр	[МЛ3Т-3А-2]
Электрический ток (I)	Ампер	[А]
Электрический заряд (q)	Кулон	[АТ]
Индуктивность (Гн)	Генри	[МЛ2Т-2А-2]
Динамическая вязкость (η)	Паскаль-секунда (Па-с)	[М1Л-1Т-1]
Энергия	Джоуль	[МЛ2Т-2]
Сила	Ньютон	[МЛ1Т-2]
Угловой момент (L)	кгм2с-1	[МЛ2Т-1]
Момент инерции (I)	кгм2	[МЛ2]

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления BSNL TTA

Последнее обновление: 2 декабря 2022 г.

BSNL проводит экзамен BSNL TTA для набора кандидатов на должность технического помощника по телекоммуникациям (TTA). Для последнего цикла найма BSNL TTA было выпущено в общей сложности 2700 вакансий. Ожидается, что BSNL (Bharat Sanchar Nigam Limited) выпустит столько же или больше вакансий, чем в прошлом году. Отбор кандидатов на TTA будет зависеть от онлайн-экзамена и проверки документов. Кандидаты могут обратиться к документам BSNL TTA за предыдущие годы, чтобы увеличить свои шансы на выбор. 9{2}}$

Ответ

Подтверждено

Более 258,9 тыс. просмотров

Совет: изучите системы единиц измерения, используемые для измерений. Изучите величины, используемые в системе единиц СИ. Поймите определение момента инерции и попытайтесь получить его математическое выражение. Затем из единиц СИ его составляющих найти единицу момента инерции.

Полное пошаговое решение:
Единицы СИ или Международная система единиц — это система физических единиц, основанная на метре, килограмме, секунде, ампере, кельвине, канделе и моле.