1.6 Ускорение. Единица ускорения – Физика по учебнику 10 класса
При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо же одновременно как по модулю, так и по направлению.
Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению.
Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении). Чтобы уметь находить скорость в любой момент времени, необходимо ввести величину, характеризующую быстроту изменения скорости. Эту величину называют ускорением.
Ускорение- это величина, которая характеризует быстроту изменения скорости.
Среднее ускорение
Среднее ускорение – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
где – вектор ускорения.
Направление вектора ускорения совпадает с направлением изменения скорости Δ = – 0 (здесь 0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).
В момент времени t1 (см. рис 1.8) тело имеет скорость 0. В момент времени t2 тело имеет скорость. Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = – 0. Тогда определить ускорение можно так:
Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
В чем измеряется ускорение в физике? Центростремительное и угловое ускорение.
 Измерение ускорения свободного падения
Измерение ускорения свободного паденияПри решении задач по физике часто приходится выводить рабочие формулы с учетом предоставленного условия. Одной из самых надежных проверок правильности полученной формулы является совпадение единиц измерения в правой и левой частях равенства. В данной статье рассмотрим вопрос, в чем измеряется ускорение.
Дадим сразу определение этой величины, а затем поясним ее особенности. Под ускорением понимают быстроту, с которой изменяется скорость в каждый момент времени при движении тела. Поскольку скорость – это величина векторная, то изменяться может ее модуль и направление. Оба типа изменения описываются понятием ускорения.
Для определения мгновенного ускорения используют следующее выражение:
a¯ = dv¯/dt.
Взяв первую производную по времени от скорости, мы получим зависимость ускорения от t.
Помимо мгновенного ускорения (значение a¯ в конкретный момент времени), на практике часто применяют среднее ускорение. Оно определяется так:
Оно определяется так:
acp¯ = Δv¯/Δt.
Здесь Δv¯ – это разность скоростей в конце и в начале промежутка времени Δt. В отличие от мгновенной величины, среднее ускорение характеризует весь процесс движения, поэтому на практике оно оказывается более полезным. Очевидно, если Δt->dt, то acp¯->a¯.
В чем измеряется ускорение?
Несложно ответить на этот вопрос, если рассмотреть записанные в предыдущем пункте формулы для мгновенной и средней величины. Как известно, скорость определяется в метрах в секунду (м/с). Конечно, можно применять и другие единицы измерения для v¯, например, километры или мили в час, однако мы ведем разговор о единицах международной системы СИ. Время в СИ измеряется в секундах (c). Взяв отношение этих величин, приходим к ответу на вопрос, в чем измеряется ускорение. Его единицами являются метр в квадратную секунду или сокращенно м/с².
Что означает запись: a = 1 м/с²? Это означает, что за каждую секунду перемещения тело увеличивает свою скорость на 1 м/с.
Далее будут приведены другие возможные единицы измерения ускорения, однако м/с² является базовой, и все другие единицы сводятся к ней.
Сила и ускорение
Записанное выше математическое определение ускорения не содержит никакой информации о том, откуда оно появляется, и что заставляет тела ускоряться. Ответы на эти вопросы можно понять, если вспомнить, в чем состоит второй закон Ньютона. Он гласит, что как только появляется ненулевая внешняя сила F¯, действующая на тело массой m, то она неминуемо ведет к появлению ускорения a¯. Соответствующее выражение записывается в виде:
F¯ = m*a¯.
Мы можем, используя эту формулу, определить, в чем измеряется ускорение в данном случае. Сила выражается в ньютонах, а масса в килограммах, тогда получаем:
a¯ = F¯/m [Н/кг].
Ньютон не является базовой единицей в системе СИ, поэтому Н/кг редко применяется в задачах для выражения ускорения. Тем не менее, эту единицу можно встретить в некоторых задачах по динамике движения.
Движение по окружности
Мы специально выделили в отдельный пункт статьи вопрос перемещения тела по окружности. Дело в том, что во время вращения вокруг некоторой оси изменяться может не только абсолютное значение скорости тела, но и ее направление. Такой характер движения приводит к появлению у тела двух компонентов ускорения: нормального или центростремительного и тангенциального или касательного.
Касательная компонента описывает изменение модуля v¯, поэтому для нее используют единицу м/с². Тем не менее, вращение часто описывают в угловых величинах. Угловое же ускорение выражается в радианах в секунду в квадрате (рад/с²). Напомним, что радиан – это мера угла, который опирается на дугу длиною в один радиус окружности.
Что касается центростремительной компоненты ускорения, то для ее вычисления используют следующую формулу:
ac = v²/r.
Где r – радиус вращения. В чем измеряется центростремительное ускорение? Подставим в это выражение соответствующие единицы для v и r, получим:
ac = [м²/с²/м] = [м/с²].
Таким образом, нормальное ускорение измеряется в тех же единицах, что и полное ускорение (м/с²).
Измерение ускорения свободного падения
Это ускорение (его будем обозначать буквой g) возникает за счет действия на все тела, которые нас окружают, силы тяжести Земли. Среднее значение g на нашей планете равно 9,81 м/с², тем не менее эта величина колеблется на несколько процентов в зависимости от местности.
Наука, которая занимается измерением величины g, называется гравиметрией. Отвечая на вопрос, каким прибором измеряется ускорение, следует сказать, что это или абсолютный, или относительный гравиметр. Абсолютный гравиметр измеряет g в лоб, рассчитывая время падения тела в безвоздушном пространстве с некоторой высоты. Относительный гравиметр представляет собой пружину с грузом, удлинение которой калибруется согласно некоторому известному ускорению g в данной местности.
С помощью гравиметра ускорение свободного падения измеряется в галах. Эта единица названа в честь Галилея, который впервые в истории использовал математический маятник для вычисления ускорения g. Один гал равен сотой части м/с².
Один гал равен сотой части м/с².
Измерение g в данной местности проводят с целью анализа состава горных пород, во время поиска полезных ископаемых или подземных вод. Применяют гравиметры также в археологии и сейсмологии.
Итоговая контрольная работа по физике в виде тестирования в 9 классе
СПЕЦИФИКАЦИЯ
итоговой работы в форме тестирования
для проведения промежуточной аттестации
по физике в 9 классах
1. Назначение контрольно-измерительных материалов
Определение уровня образовательных достижений учащихся 9 классов в усвоении предметного содержания курса физики 9 класса
2. Документы, определяющие содержание работы
Содержание работы определяется на основе следующих документов.
1. Федеральный компонент государственного стандарта основного среднего образования по математике (приказ Минобразования России № 1089 от 05. 03.2004 г.).
03.2004 г.).
2. Авторская программа А.В. Перышкина по физике для 7-9 классов. Программы основной школы (авторы программы Е.М. Гутник, А.В. Перышкин) – Программа для общеобразовательных учреждений: физика, астрономия 7-11 кл. (Ю.И. Дик, В.А. Коровин) Дрофа, 2008 г.
3. Подходы к отбору содержания, разработке структуры работы
Итоговая работа для проведения промежуточной аттестации учащихся представлена 4 вариантами.
Каждый вариант включает 13 заданий.
Часть А содержит 10 заданий с выбором 1 правильного ответа. Необходимо выбрать один правильный ответ.
Часть В содержит 3 задания. Необходимо выполнить подробное решение: оформить задачи, записать формулу, провести вычисления по формуле и записать ответ.
Распределение заданий по темам
п./п
Тема
Количество
Заданий
Уровень сложности
А
(базовый)
В
(повышенный)
1
Законы взаимодействия и движения тел
6
4
2
2
Механические колебания и волны.
2
2
–
3
Электромагнитное поле
3
2
1
4
Строение атома и атомного ядра
2
2
–
Итого
13
10
3
Таблица распределения заданий по уровням сложности
задания
в тесте
1
2
3
4
5
6
7
8
9
10
11
12
13
№ темы
1
1
1
2
2
3
4
3
4
1
1
3
уровень сложности
А
А
А
А
А
А
А
А
А
А
В
В
В
4. Система оценивания результатов выполнения работы.
Система оценивания результатов выполнения работы.
Всего 19 баллов.
Каждый правильный ответ части А оценивается 1 баллом (всего 10 баллов).
Каждый правильный ответ части В оценивается 3 баллами (всего 9 баллов).
Часть В:
-приведено полное правильное решение, запись физических формул, отражающих физические законы, применение которых необходимо для решения задачи выбранным способом, проведены математические преобразования и расчеты, представлен ответ – 3 балла,
– при правильном ходе решения задачи допущены ошибки в математических расчетах – 2 балла,
– при правильной идее решения допущена ошибка (не более одной) в записи физических законов или использованы не все исходные формулы, необходимые для решения – 1 балл;
 п. – 0 баллов.
п. – 0 баллов.Таблица перевода баллов работы в пятибалльную шкалу оценивания
Оценка«2»
«3»
«4»
«5»
Число набранных баллов
Менее 7 баллов
8-12 баллов
13-15 баллов
16-19 баллов
5. Время выполнения работы
Ответы
задания
1
2
3
4
5
6
7
8
9
10
11
12
13
№
ответа
(1 вариант)
5
2
5
1
2
2
4
2
3
2
39 м
90 Н
0,5 м
№
Ответа
(2 вариант)
3
4
4
2
1
3
4
2
4
4
90 м
20 м/с2
5·1014 Гц
№
Ответа
(3 вариант)
4
5
1
1
4
4
1
1
2
2
130 м
1 Н
2,950 м
№
Ответа
(4 вариант)
4
1
3
1
3
4
3
1
1
4
420 м
30 м/с2
25·107 м/с
Промежуточная аттестация
Физика 9 класс
Вариант 1
Часть А. Выберите один правильный ответ
Выберите один правильный ответ
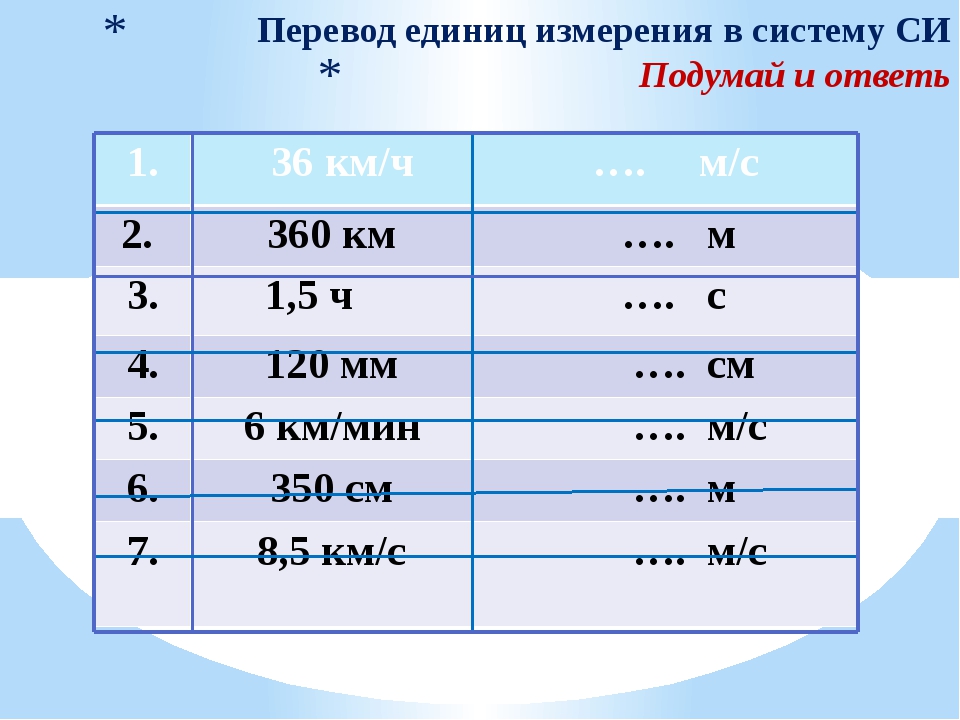
В каких единицах СИ измеряется ускорение?
1) мин 2) км/ч 3) м/с 4) с 5) м/с
2. По какой формуле можно определить скорость при равномерном прямолинейном движении?
1) 2) 3)t 4) 5)
3. Импульс тела определяется формулой:
1) 2) F=kx 3) 4) 5)
4. При измерении пульса человека было зафиксировано 75 пульсаций крови за 1 минуту. Определите период сокращений сердечной мышцы.
1) 0,8 с 2) 1,25 с 3) 60 с 4) 75 с
5. Амплитуда свободных колебаний тела равна 3 см. Какой путь прошло это тело за 1/2 периода колебаний?
1) 3 см 2) 6 см 3) 9 см 4) 12 см
6. При увеличении ёмкости конденсатора, включённого в колебательный контур, период электромагнитных колебаний:
1) не изменится 2) увеличится 3) уменьшится 4) может как увеличиться, так и уменьшиться
7. излучение – это
излучение – это
вторичное радиоактивное излучение при начале цепной реакции
поток нейтронов, образующихся в цепной реакции
электромагнитные волны
поток электронов
8. Какова индукция магнитного поля, в котором на проводник с током 25 А действует сила 0,05 Н? Длина проводника 5 см. Направления линий индукции и тока взаимно перпендикулярны.
1) 0,004 Тл 2) 0,04 Тл 3) 0,4 Тл 4) 4 Тл
9. В ядре элемента содержится
92 протона, 238 нейтронов
2) 146 протонов, 92 нейтрона
3) 92 протона, 146 нейтронов
4) 238 протонов, 92 нейтрона
10. На рисунке представлен график зависимости ускорения от времени для тела, движущегося прямолинейно. Равноускоренное движение соответствует участку
1) OA 2) AB 3) BC 4) CD
Часть В. Представьте развернутое решение задачи.
11. Лыжник съехал с горки за 6 с, двигаясь с постоянным ускорением 0,5 м/с2. Определите длину горки, если известно, что в начале спуска скорость лыжника была равна 18 км/ч.
Определите длину горки, если известно, что в начале спуска скорость лыжника была равна 18 км/ч.
12. Спустившись с горки, санки с мальчиком тормозят с ускорением 2 м/с2. Определите величину тормозящей силы, если общая масса мальчика и санок равна 45 кг.
13. Радиостанция работает на частоте 60 МГц. Найдите длину электромагнитных волн, излучаемых антенной радиостанции. Скорость распространения электромагнитных волн с = 3·108 м/с.
Промежуточная аттестация
Физика 9 класс
Вариант 2
Часть А. Выберите один правильный ответ
В каких единицах СИ измеряется скорость?
1) мин 2) км/ч 3) м/с 4) с 5) м/с2
2. По какой формуле можно определить проекцию ускорения?
1) 2) 3)t 4) 5)
3. Закон всемирного тяготения определяется формулой:
1) 2)F=kx 3) 4) 5)
4. При измерении пульса человека было зафиксировано 75 пульсаций крови за 1 минуту. Определите частоту сокращений сердечной мышцы.
При измерении пульса человека было зафиксировано 75 пульсаций крови за 1 минуту. Определите частоту сокращений сердечной мышцы.
1) 0,8 Гц 2) 1,25 Гц 3) 60 Гц 4) 75 Гц
5. Амплитуда свободных колебаний тела равна 50 см. Какой путь прошло это тело за 1/4 периода колебаний?
1) 0,5 м 2) 1 м 3) 1,5 м 4) 2 м
6. В колебательном контуре, состоящем из конденсатора и катушки, происходят электромагнитные колебания. Это подразумевает, что происходит колебание
1) пластин конденсатора
2) витков катушки
3) силы тока в катушке
4) суммарной энергии, запасенной в катушке и конденсаторе
7. – излучение – это
1) поток ядер гелия
2) поток протонов
3) поток электронов
4) электромагнитные волны большой частоты
8. При увеличении частоты колебаний в 2 раза, длина волны:
1) не изменяется 3) увеличивается в 2 раза
2) уменьшается в 2 раза 4) уменьшается в 4 раза
9. В ядре олова содержится
В ядре олова содержится
1)110 протонов, 50 нейтронов
2) 60 протонов, 50 нейтронов
3) 50 протонов, 110 нейтронов
4) 50 протонов, 60 нейтронов
10. На рисунке представлен график зависимости модуля скорости v от времени t для тела, движущегося прямолинейно. Равномерному движению соответствует участок
1) АВ 2) ВС 3) CD 4) DE
Часть В. Представьте развернутое решение задачи
11. Вагонетка, имеющая скорость 7,2 км/ч, начинает двигаться с ускорением 0,25 м/с2. На каком расстоянии окажется вагонетка через 20 с?
12. С каким ускорением будет двигаться тело массой 400 г под действием единственной силы 8 Н?
13. Длина электромагнитной волны в воздухе равна 0,6 мкм. Чему равна частота колебаний вектора напряженности электрического поля в этой волне? Скорость распространения электромагнитных волн с = 3·108 м/с.
Промежуточная аттестация
Физика 9 класс
Вариант 3
Часть А. Выберите один правильный ответ
Выберите один правильный ответ
В каких единицах СИ измеряется время?
1) мин 2) км/ч 3) м/с 4) с 5) м/с2
2. По какой формуле можно определить проекцию перемещения при равномерном прямолинейном движении?
1) 2) 3)t 4) 5)
3. Второй закон Ньютона определяется формулой:
1) 2)F = kx 3) 4) 5)
4. Частота колебаний напряжения в электрической цепи России равна 50 Гц. Определите период колебаний.
1) 0,02 с 2)1,25 с 3)50 с 4) 25 с
5. Амплитуда свободных колебаний тела равна 8 см. Какой путь прошло тело за полный период колебаний?
1) 8 см 2) 16 см 3)24 см 4) 32 см
6. Магнитное поле в пространстве может создать
1) только постоянный магнит
2) только кольцо с током
3) только Земля
4) все ответы верны
7. – излучение – это
1) поток ядер гелия
2) поток протонов
3) поток электронов
4) электромагнитные волны большой частоты
8. Выберите устройство, в котором происходит преобразование механической энергии в электрическую:
Выберите устройство, в котором происходит преобразование механической энергии в электрическую:
1) электрогенератор
2) паровая турбина
3) динамик радиоприемника
4) двигатель внутреннего сгорания
9. Сколько протонов и нейтронов содержится в ядре элемента
1) 82 протона, 214 нейтронов
2) 82 протона, 132 нейтрона
3) 132 протона, 82 нейтрона
4) 214 протонов, 82 нейтрона
10. Чему равен КПД двигателя, если от нагревателя он получил 150 МДж, передал холодильнику 75 МДж?
1) 30 % 2) 50 % 3) 20 % 4) 75 %
Часть В. Представьте развернутое решение задачи
11. Велосипедист съехал с горки за 10 с, двигаясь с постоянным ускорением 0,6 м/с2. Определите длину горки, если известно, что в начале спуска скорость велосипедиста была равна 36 км/ч.
12. Определите силу, под действием которой тело массой 500 г движется с ускорением 2 м/с2.
13. На какую длину волны нужно настроить радиоприемник, чтобы слушать радиостанцию «Наше радио», которая вещает на частоте 101,7 МГц?. Скорость распространения электромагнитных волн
с = 3·108 м/с.
Промежуточная аттестация
Физика 9 класс
Вариант 4
Часть А Выберите один правильный ответ
1. В каких единицах СИ измеряется путь?
1) км 2) км/ч 3) м/с 4) м 5) м/с2
2. По какой формуле можно определить проекцию скорости при равноускоренном прямолинейном движении?
1) 2) 3)t 4) 5)
3. Третий закон Ньютона определяется формулой:
1) 2)F=kx 3) 4) 5)
4. Цикл вдоха-выдоха у ребенка составляет 36 раз в минуту. Определите частоту цикла.
1) 0,6 Гц 2) 1,67 Гц 3) 60 Гц 4) 36 Гц
5. Амплитуда свободных колебаний тела равна 4 см. Какой путь прошло тело за ¾ периода колебаний?
1) 4 см 2) 8 см 3) 12 см 4) 16 см
6. Линии магнитного поля – это
Линии магнитного поля – это
1) линии, совпадающие с формой магнита
2) линии, по которым летит положительный заряд, попадая в магнитное поле
3) линии, по которым летит отрицательный заряд, попадая в магнитное поле
4) воображаемые линии, в каждой точке которых индукция магнитного поля направлена по касательной
7. излучение – это
1) вторичное радиоактивное излучение при начале цепной реакции
2) поток нейтронов, образующихся в цепной реакции
3) поток электронов
4) электромагнитные волны
8. Запасание энергии в конденсаторе после его контакта с клеммами источника тока демонстрирует
1) вспышка фотоаппарата, соединяемая с конденсатором
2) конденсация воды в бутылке, вынутой из холодильника
3) искры при соединении вилки адаптера в бытовую электросеть
4) хранение информации на жестком диске компьютера
9. Сколько протонов и нейтронов содержится в ядре элемента
1) 13 протонов, 14 нейтронов
2) 13 протонов, 27 нейтронов
3) 27 протонов, 13 нейтронов
4) 27 протонов, 40 нейтронов
10. Двигатель мощностью 3кВт работает в течение 5 минут. При этом от совершает работу, равную
Двигатель мощностью 3кВт работает в течение 5 минут. При этом от совершает работу, равную
1) 10 Дж 2) 600 Дж 3) 15 кДж 4) 900 кДж
Часть В. Представьте подробное решение задачи
11. Вагонетка, имеющая скорость 3,6 км/ч, начинает двигаться с ускорением 2 м/с2. На каком расстоянии окажется вагонетка через 20 с?
12. С каким ускорением будет двигаться тело массой 200 г под действием силы 6 Н?
13. В первых экспериментах по изучению распространения электромагнитных волн в воздухе были измерены длина волны 50 см и частота излучения = 500 МГц. На основе этих неточных значений скорость света примерно равна
Сила тяжести – в чем измеряется? Чему равна?
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Сила тяготения
В 1682 году Исаак Ньютон открыл Закон Всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон Всемирного тяготения F = GMm/R2 F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6. |
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Приливы и отливы существуют благодаря Закону Всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей
Несколько лет назад ученые открыли такое явление, как гравитационные волны — но это не тоже самое, что гравитация:
youtube.com/embed/0z066qp9Aaw” frameborder=”0″ allow=”accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””/>Источник: YouTube-канал «Это работает»
Сила тяжести
Сила тяжести — сила, с которой Земля притягивает все тела.
Сила тяжести F = mg F — сила тяжести [Н] m — масса тела [кг] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2 |
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Но разница все-таки есть, давайте разбираться.
Но разница все-таки есть, давайте разбираться.
Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также, важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. Вес зависит также от ускорения, с которым движутся тело или опора.
Например, в лифте вес тела зависит от того, куда и с каким ускорением движется тело. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит можем сказать, что это одно и то же. Практически.
Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения.
F = mg
F = GMm/R2
Приравниваем правые части:
mg = GMm/R2
Делим на массу левую и правую части:
g = GM/R2
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально, эта формула нужна.
Формула для ускорения свободного падения g = GM/R2 F — сила тяготения [Н] M — масса планеты [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6. |
А теперь задачка
Определить силу тяжести, действующую на тело массой 80 кг.
Решение:
Не смотря на кажущуюся простоту, тут есть над чем подумать.Вроде бы просто нужно взять формулу F = mg, подставить числа и дело в шляпе.
Да, но есть один нюанс: в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают то же значения, что мы указывали выше: g = 9,8 м/с2.
В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Итак, F = mg.
F = 80*10 = 800 Н
Ответ: 800 Н.
Учимся летать
В серии книг Дугласа Адамса «Автостопом по Галактике» говорится, что летать — это просто промахиваться мимо Земли. Если ты промахнулся мимо Земли и достиг первой космической скорости 7,9 км/с, то ты стал искусственным спутником Земли.
Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него так получалось, аппарат должен иметь начальную скорость, равную или большую первой космической скорости.
Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.
Подробнее о возможностях полетов и невесомости читайте в нашей статье про вес тела.
Научить летать по-настоящему физика, конечно, не может, но обмануть систему и найти лазейки — это всегда пожалуйста. Запишите ребенка на бесплатный вводный урок в современную школу Skysmart: покажем, как у нас все устроено, определим план развития и влюбим в науку!
Запишите ребенка на бесплатный вводный урок в современную школу Skysmart: покажем, как у нас все устроено, определим план развития и влюбим в науку!
что это такое, единица измерения, формула и определение
Мгновенная скорость в физике
ОпределениеМгновенной скоростью называется скорость объекта в данный момент времени в конкретной точке. Это векторная физическая величина, которая обозначается символом \vec v и определяется по формуле:
\(\vec v=\frac{\Delta\vec S}{\Delta t}\)
Где \(\Delta\vec S\) — перемещение, а \(\Delta t \) — промежуток времени.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Величина измеряется в м/с.
Мгновенное ускорение в физике
ОпределениеМгновенное ускорение — это векторная физическая величина, численно равная изменению скорости в единицу времени.
Обозначается \(\vec a\).
Единицами измерения мгновенного ускорения являются м/с2.
Как направлены мгновенная скорость и ускорение
Вектор мгновенной скорости всегда направлен по касательной к траектории движения объекта в любой момент времени. Графически это выглядит так:
У вектора \vec a две составляющие: \(\vec a_tg\) (касательное или тангенциальное \(\vec a\)) и \(\vec a_n\) (нормальное \(\vec a\)). Каждая из них имеет свое направление вектора.
Как найти мгновенное ускорение, формула
Ускорение определяется по формуле:
\(\vec a=\lim_{t\rightarrow0}\frac{\Delta\vec V}{\Delta t}\)
Где \(\Delta\vec V\) — изменение скорости, \(\Delta t\) — промежуток времени, когда происходило изменение скорости.
Составляющими данной векторной величины являются:
- касательное или тангенциальное ускорение;
- нормальное ускорение.
 2}r \)
2}r \)Задача на определение мгновенного ускорения
Для усвоения теоретического материала важно закрепить знания на практике. Решим задачу на определение мгновенного ускорения.
Задача
С каким ускорением движется гоночный болид, если его скорость изменилась со 144 км/ч до 216 км/ч за 6 секунд?
Решение:
Записываем все известные вводные:
\(V_0\)=144 км/ч, \(V\)=216 км/ч, t=6 с, a=?
Переводим км/ч в м/с, получаем:
\(V_0\)=40 м/с, \(V\)=60 м/с.
Формула:
\(\vec a=\frac{\Delta\vec V}{\Delta t}\)
Где \(\Delta\vec V=V-V_0\)
Получаем значение ускорения, равное 3,33 м/с2.
Как решать 2 задание ЕГЭ по физике, примеры решения (Ростов-на-Дону)
Из последних КИМов ЕГЭ по физике следует, что задание 2 относится к разделу «Динамика» и может содержать расчетные задачи по следующим темам: «Законы Ньютона, закон всемирного тяготения, закон Гука, сила трения».

Основные формулы, которые необходимо знать для успешного решения задания 2.
Сила тяжести
m – масса тела
g=10 м/с2 – ускорение свободного падения
Сила упругости
Δx – удлинение пружины
k – коэффициент жесткости пружины
Сила трения
µ – коэффициент трения
N – сила реакции опоры
Сила Архимеда (выталкивающая сила)
V – объём погруженной части тела
g=10 м/с2 – ускорение свободного падения
Сила притяжения между телами (закон Всемирного тяготения)
G = 6,67*10-11 Н*м2/кг2 – гравитационная постоянная
m1 и m2 - массы взаимодействующих тел
r – расстояние между телами
Второй закон Ньютона
m – масса тела
R – равнодействующая всех сил, действующих на тело
a – ускорение, с которым движется тело под действием этих сил
При решении задач из раздела «Динамика» желательно придерживаться следующего алгоритма решения:
1.
 Сделать рисунок, на котором указать вектора всех сил, действующих на
тело.
Сделать рисунок, на котором указать вектора всех сил, действующих на
тело.2. Если тело двигается с ускорением, указать направление этого ускорения. Если тело покоится или двигается равномерно, его ускорение a=0.
3. Составить уравнение движения (второй закон Ньютона) для рассматриваемого тела в его векторном виде.
3. Выбрать систему координат и спроецировать полученное уравнение на выбранные оси координат.
4. Расшифровать неизвестные величины, вошедшие в уравнение движения.
5. Решить полученную систему уравнений.
Задание 2 – это расчётные задачи базового уровня сложности, и для решения некоторых из них этот алгоритм будет чересчур подробным и перегруженным, так как их можно решить и без вспомогательного рисунка или даже без записи второго закона Ньютона. Это касается, например, заданий, в которых на тело действует только одна сила. Но привычка решать задания по приведенному выше алгоритму поможет ученикам успешно справиться с расчетными задачами по разделу «Динамика» повышенного и высокого уровней сложности – такие задания могут стоять в ЕГЭ под номерами 25 и 29.

Ответом на задание 2 является число, именно его нужно вписать в бланк ответов 1, не указывая единицы измерения.
Примеры решения
1. (ЕГЭ-2019)
Пружина жёсткостью 2*104 Н/м одним концом закреплена в штативе. На какую величину она растянется под действием силы 400 Н?
Ответ: ___________________________ см.
Решение:
Сделаем чертёж
Пружина под действием силы F привели в растянутое состояние. Кроме растягивающей силы F и силы упругости , стремящейся вернуть пружину в нерастянутое состояние, больше никакие силы на нее не действуют.
Запишем проекции сил на вертикальную ось Oy
F=Fупр
По закону Гука, сила упругости Fупр = k *Δx, следовательно,
k – коэффициент жёсткости пружины, Δx – её удлинение.

Выразим величину растяжения пружины
Ответ: 2
(ЕГЭ – 2020. Вариант 1 досрочного ЕГЭ)
Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.
Ответ: _______ .
Решение:
Силу трения можно найти по формуле
Fтр= µN,
где N – сила реакции опоры, или по-другому нормальная составляющая силы воздействия тела на плоскость.
Ответ: 0,25.
(ЕГЭ – 2020. Демонстрационный вариант)
Два одинаковых маленьких шарика массой m каждый, расстояние между центрами которых равно r, притягиваются друг к другу с силами, равными по модулю 0,2 пН.
 Каков
модуль сил гравитационного притяжения двух других шариков, если масса
каждого из них равна 2m,
а расстояние между их центрами равно 2r?
Каков
модуль сил гравитационного притяжения двух других шариков, если масса
каждого из них равна 2m,
а расстояние между их центрами равно 2r?Ответ: _______ пН.
Решение:
По закону Всемирного тяготения шары массами m1и m2, находящиеся друг от друга на расстоянии r, притягиваются друг к другу с силой
.
В первом случае
Во втором случае
Ответ: 0,2
(ЕГЭ – 2019. Демонстрационный вариант)
По горизонтальному полу по прямой равномерно тянут ящик, приложив к нему горизонтальную силу 35 Н. Коэффициент трения скольжения между полом и ящиком равен 0,25. Чему равна масса ящика?
Ответ _______ кг.
Решение:
Сделаем чертёж, на котором обозначим все силы, действующие на тело.

По второму закону Ньютона, равнодействующая всех сил, действующих на тело, будет равна нулю, так как по условию задачи тело движется равномерно, то есть ускорение тела a=0.
Запишем это в проекциях на оси Ox и Oy
Ox: Fтр – F = 0,
Oy: N – m g=0.
Откуда N = mg, следовательно,
Fтр = µ N = µ mg.
Масса тела
Ответ: 14
(ЕГЭ – 2018)
К пружине подвесили груз массой 150 г, вследствие чего пружина удлинилась на 1 см. Чему будет равно удлинение этой пружины, если к ней подвесить груз 450 г?
Ответ: __________ см.
Решение:
Переведём единицы измерения физических величин в систему СИ
m1 = 150 г = 0,15 кг, m2 = 450 г = 0,45 кг, Δx=1 см = 0,01 м.

Сделаем чертёж, на котором обозначим все силы, действующие на тело.
На тело действует сила тяжести (Fт = mg), направленная вертикально вниз, и сила упругости со стороны пружины (Fупр = k Δx), направленная вертикально вверх.
В проекции на вертикальную ось Oy.
Fт =Fупр
mg = kΔx (1)
k – коэффициент жёсткости пружины, Δx – её удлинение.
Найдём, чему равен коэффициент жёсткости пружины
Выразим из выражения (1) удлинение пружины во втором случае
Ответ: 3
РЕКОМЕНДУЕМЫЕ ТОВАРЫ
Измерение ускорения свободного падения на различных высотах при помощи математического маятника
- Участник: Мингалеев Артур Эдуардович
- Руководитель: Баскова Мария Аркадьевна

1. Введение
Первым человеком, изучавшим природу падения тел, был греческий ученый Аристотель. Затем Галилео Галилей обобщил и не проанализировал опыт и эксперименты нескольких поколений исследователей. Он предположил, что в среде, свободной от воздуха, все тела будут падать с одинаковой скоростью. Также Галилей предположил, что во время падения скорость тел постоянно увеличивается. Экспериментировать со свободным падением тел продолжил Исаак Ньютон. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
Цель настоящего исследования состояла в получении значения ускорения свободного падения при помощи математического маятника в условиях разного уровня высоты на уровнем моря.
 Для достижения поставленной цели были сформулированы следующие задачи исследования:
Для достижения поставленной цели были сформулированы следующие задачи исследования:
- Ознакомиться с историей открытия свободного падения тел;
- Изучить методы измерения ускорения свободного падения на поверхности Земли;
- Провести самостоятельные измерения ускорения свободного падения при помощи математического маятника;
- Провести измерения на различных высотах.
Гипотеза исследования: логично предположить, что ускорение свободного падения, полученные в разных экспериментах, должны быть близки к значению 9,8 м/с2 и отличаться на сотые или тысячные доли на глубине станции метро Кремлевская (–34 м) и на высоте небоскреба «Лазурные небеса» (+120 м). Также результаты измерений и вычислений могут отличаться погрешностью измерений.
Методы изучения: самостоятельная, индивидуальная работа в сочетании с теоретическими исследовательскими, проектными формами работы.
Читая много различной в том числе и технической литературы, я узнал о практическом применении различия ускорения свободного падения в разных точках на поверхности Земли.
 Я измерял g различными способами, рассчитывал погрешности измерений, опираясь на общепринятое значение g, учился грамотно проводить эксперимент. Выяснил, что свободное падение – движение равноускоренное. Ускорение свободного падения не зависит от массы тела. Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.
Я измерял g различными способами, рассчитывал погрешности измерений, опираясь на общепринятое значение g, учился грамотно проводить эксперимент. Выяснил, что свободное падение – движение равноускоренное. Ускорение свободного падения не зависит от массы тела. Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.
В дальнейшем я хотел бы самостоятельно исследовать зависимость значения ускорения свободного падения от географического положения.
2. Основная часть
2.1. Исторические сведения об открытии свободного падения и методах его измерения
Еще тысячелетия назад люди замечали, что большая часть предметов падает все быстрее и быстрее, а некоторые падают равномерно.
 Но как именно падают эти предметы – этот вопрос первобытных людей не занимал. Тем не менее нашлись люди, которые по мере возможностей начали исследовать это явление. Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв.
Но как именно падают эти предметы – этот вопрос первобытных людей не занимал. Тем не менее нашлись люди, которые по мере возможностей начали исследовать это явление. Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным.
Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
Предположив, что произошло бы в случае свободного падения тел в вакууме, Галилей вывел следующие законы падения тел для идеального случая: все тела при падении движутся одинаково; начав падать одновременно, они движутся с одинаковой скоростью; движение происходит с “постоянным ускорением”; темп увеличения скорости тела не меняется, т.е. за каждую последующую секунду скорость тела возрастает на одну и ту же величину. Существует легенда, будто Галилей проделал большой демонстрационный опыт, бросая легкие и тяжелые предметы с вершины Пизанской падающей башни (одни говорят, что он бросал стальные и деревянные шары, а другие утверждают, будто это были железные шары весом 0,5 и 50 кг). Описаний такого публичного опыта нет, и Галилей, несомненно, не стал таким способом демонстрировать свое правило.
 Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня. Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня. Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
Вскоре после Галилея были созданы воздушные насосы, которые позволили произвести эксперименты со свободным падением в вакууме.
 С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью. Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:
С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью. Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:
S1 : S2 : S3 : … = 1 : 2 : 3 : … (при V0 = 0)
Таким образом, можно предположить, что свободное падение есть равноускоренное движение.
 Так как для равноускоренного движения перемещение рассчитывается по формуле, то если взять три некоторые точки 1,2,3 через которые проходит тело при падении и записать: (ускорение при свободном падении для всех тел одинаково), получится, что отношение перемещений при равноускоренном движении равно:
Так как для равноускоренного движения перемещение рассчитывается по формуле, то если взять три некоторые точки 1,2,3 через которые проходит тело при падении и записать: (ускорение при свободном падении для всех тел одинаково), получится, что отношение перемещений при равноускоренном движении равно:
S1 : S2 : S3 = t12 : t22 : t32 (2)
Остается еще добавить небольшой комментарий относительно экспериментов со свободным падением тел Исаака Ньютона. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
2.
 2. Практическая значимость нахождения значения ускорения свободного падения
2. Практическая значимость нахождения значения ускорения свободного паденияЯ много читаю и, как следствие склонен фантазировать. Для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь от значения g на другой планете зависит не только сила тяжести. Люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.
2.3. Методы измерения ускорения свободного падения
На самом деле методов по измерению ускорения свободного падения достаточно много. Приведу только те, которые сам испробовал.
1) Измерение ускорения свободного падения с помощью наклонной плоскости
Понадобится следующее оборудование:деревянный брусок, трибометр, штатив с муфтой и лапкой, электронный секундомер, динамометр, измерительная лента, линейка.
 Рассматривая движение бруска вниз по наклонной плоскости, можно записать второй закон Ньютона в векторном виде:
Рассматривая движение бруска вниз по наклонной плоскости, можно записать второй закон Ньютона в векторном виде:
Записывая второй закон Ньютона в проекциях на оси координат:
Ох: – Fтр+ mgsinα = ma
Oy: N – mgcosα = 0
и учитывая, что N = mgcosα; Fтр = μN; можно решить данную систему уравнений и получить ускорение свободного падения:
g = a sinα – μcosα При этом ускорение a можно вычислить из формулы
так как начальная скорость бруска при скольжении по наклонной плоскости равна 0:
Видим, что для этого нужно измерить длину наклонной плоскости и время скольжения по ней бруска.

Для вычисления sinα и cosα нужно знать длину S и высоту h наклонной плоскости:
Для определения коэффициента трения скольжения положим трибометр на горизонтальную поверхность и с помощью динамометра равномерно протащим по нему брусок. В этом случае на брусок будут действовать 4 силы: сила тяжести, сила упругости пружины динамометра, сила трения, сила реакции опоры.
При равномерном движении бруска эти силы будут попарно равны: Fтр = Fупр, Fтяж = N, т. е. Fупр = μFтяж, тогда коэффициент трения равен
Для меня в этом методе оказалось слишком много математических действий, с которыми в курсе математики я еще не знаком. Поэтому даже не буду приводить результаты проделанных измерений и вычислений.

2) Определение
g благодаря давлению жидкостиКак известно давление столба жидкости обусловлено следующими факторами: плотность жидкости, непосредственно высота столба жидкости и само значение ускорения свободного падения на данной планете.
Если преобразовать формулу P = ρgh, получится формула нахождения g. Эта формула выглядит так g = P / ρh, где Р – давление в жидкости на глубине h, которое можно узнать с помощью манометра, ρ – плотность воды равное 1000 кг/м3.
При подобных измерениях нужно учитывать погрешность измерительного прибора, манометра. Достаточно точного мне найти не удалось, поэтому для своих исследований я выбрал другой метод.
3) Измерение ускорения свободного падения с помощью математического маятника
Необходимое оборудование: секундомер, штатив с муфтой и лапкой, шарик на нерастяжимой нити, измерительная лента.
 При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период
и ускорения свободного падения может быть вычислено по формуле
Подготовка к проведению работы
В работе используется простейший маятник – шарик на нити. При малых размерах по сравнению с длиной нити и небольших отклонениях от положения равновесия период колебаний равен периоду колебаний математического маятника
Тогда период
и ускорения свободного падения может быть вычислено по формуле
Результаты измерений и вычислений представлены в разделе 2.5
2.4. Теоретические расчеты по определению ускорения свободного падения различных высотах
Теоретически значение ускорения свободного падения на поверхности планеты Земля можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:
где G — гравитационная постоянная (G = 6,6743 · 10–11 (H ·м2)/кг2).

При вычислениях я применял такие значения:
R = 6370 · 103 м – радиус Земли на широте Казани;
M = 5,9722 · 1024 кг – масса Земли.
Таким образом теоретическое значение gт = 9,823386 м/с2.
Согласно формуле
естественно предположить, что ускорение свободного падения на разных высотах будет немного отличаться: на глубине будет больше, а на высоте меньше вычисленного выше.
Возможно эту небольшую разницу можно объяснить погрешностью измерений. Проверим.
Результаты вычислений значения ускорения свободного падения на различных высотах представлены в таблице:
В классе
На станции метро Кремлевская
На 36-м этаже небоскреба
R = 6370 км,
h = 0
R = 6370 км,
h = –16 м
R = 6370 км,
h = +120 м
9,8234
9,8231
9,8227
2.
 5. Экспериментальное определение ускорения свободного падения с помощью математического маятника
5. Экспериментальное определение ускорения свободного падения с помощью математического маятникаКак уже говорилось ранее, оборудование для проведения измерений требовалось весьма не замысловатое: секундомер, штатив с муфтой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период
и ускорения свободного падения может быть вычислено по формуле
Ход работы
Для начала я проделал все необходимые измерения в классе, в кабинете физики Лицея № 110. Кабинет находится на втором этаже. Учитывая высоту потолков (около 3 м), логично предположить, что вычисленные значения g должны быть близки к gт.

- Я установил на краю стола штатив. У его верхнего конца укрепил с помощью муфты кольцо и подвесил к нему шарик на нити. Шарик должен висеть и свободно совершать колебания.
- Нить я взял метровой длины для удобства вычислений.
- Отклонив шарик на небольшое расстояние (5-8 см), я возбудил колебания маятника.
- Измерил в пяти экспериментах время t 20 колебаний маятника и вычислил tср:
tср = t1 + t2 + t3 + t4 + t5 5 - Затем вычислил среднюю абсолютную погрешность измерения времени:
∆tср = │t1 – tср│ + │t2 – tср│+ │t3– tср│ + │t4– tср│ + │t5– tср│ 5 - Вычислил ускорение свободного падения по формуле:
Таблица результатов измерений в классе
n N
t, c
tср, с
Δtср, с
g, м/с2
1
20
40,26
39,94
0,36
9,88924
2
20
39,20
3
20
40,30
4
20
40,18
5
20
39,78
- Я определил относительную погрешность измерения времени εt.

ε = ∆t = ∆tи + ∆tотсчета = 1 с + 1 с = 2 c = 2 с = 0,05 = 5% t t t tсредн 39,94 с - Определил относительную погрешность измерения длины маятника:
εl = ∆l = ∆lи + ∆lотсчета = половина цены деления + цена деления = l l длина маятника = 0,0005 м + 0,001 м = 0,0015 м = 0,0015 м = 0,0015 = 0,15% l l 1 м - Вычислил относительную погрешность измерения g:
εg = εl+ 2εt = 0,05 + 2 · 0,0015 = 0,053 = 5,3%
- Определил абсолютную погрешность вычисления ускорения свободного падения:
∆g = εggсредняя = 0,053 · 9,73971 м/с2 = 0,5162 м/с2 ≈ 0,520
Итог моих измерений и вычислений:
9,37 ≤ g ≤ 10,41
Такие действия я проделал в казанском метрополитене, на станции метро Кремлевская и на 36-м этаже единственного в Казани небоскреба «Лазурные небеса».

Таблица результатов измерений на станции метро Кремлевская
n
N
t, c
tср, с
Δtср, с
g, м/с2
1
20
31,80
31,71
0,042
9,96232
2
20
31,72
3
20
31,62
4
20
31,69
5
20
31,71
При измерениях в метро пришлось использовать длину нити 63,5 см.

Относительная погрешность измерения времени εt = 0,063 = 6,3%.
Относительная погрешность измерения длины маятника: εl = 0,24%
Относительная погрешность измерения g: εg = 6,78%
Абсолютную погрешность вычисления ускорения свободного падения составила: 0,63 м/с2.
Итог моих измерений и вычислений:
9,33 ≤ g ≤ 10,59
Таблица результатов измерений на 36-м этаже небоскреба «Лазурные небеса»
n N
t, c
tср, с
Δtср, с
g, м/с2
1
20
28,59
28,57
0,10
9,85664
2
20
28,56
3
20
28,81
4
20
28,52
5
20
28,39
Здесь при измерениях пришлось длину нити еще сократить до 51 см.

Относительная погрешность измерения времени εt = 7%.
Относительная погрешность измерения длины маятника: εl = 0,29%
Относительная погрешность измерения g: εg = 7,58%
Абсолютную погрешность вычисления ускорения свободного падения составила: 0,75 м/с2.
Итог моих измерений и вычислений:
9,11 ≤ g ≤ 10,61
Таблица сравнения теоретически полученных значений g (м/с2) и полученных экспериментально
В классе
На станции метро Кремлевская
На 36-м этаже небоскреба
R = 6370 км,
h = 0
R = 6370 км,
h = –16 м
R = 6370 км,
h = +120 м
Теория
9,8234
9,8231
9,8227
Эксперимент
9,8892
9,9623
9,8566
3.
 Заключение
ЗаключениеПри подготовке к защите данной работы и в результате теоретического исследования, чтения разных книг и статей я узнал многое об ускорении свободного падения. Как уже упоминал, для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.
Также я узнал, что расчеты различия ускорения свободного падения в разных точках на поверхности Земли могут указывать на гравитационные аномалии.
Самое главное, я научился измерять g, различными способами, рассчитывать погрешности измерений, грамотно проводить эксперимент.
Считаю цель исследования достигнута. Средние значение ускорения свободного падения на различных высотах отличаются в зависимости от высоты над уровнем моря: при увеличении высоты значение g уменьшается, при углублении в недра Земли – увеличивается.
 Экспериментально полученные значения хорошо это показывают.
Экспериментально полученные значения хорошо это показывают.
Погрешность измерений достаточно велика, но не превышает 10%. Уменьшить погрешность возможно путем проведения большего числа измерений: ни 5, а 20; большего числа колебаний: не 20, а 100. Также при расчетах можно учесть, что Казань находится примерно на уровне 250-300 м над уровнем моря.
В дальнейшем хотелось бы усовершенствовать экспериментальные установки, чтобы измерять ускорение свободного падения с большей точностью.
Планирую самостоятельно исследовать значения ускорения свободного падения в различных уголках земного шара.
Acceleration – The Physics Hypertextbook
Обсуждение
определение
Когда скорость объекта изменяется, говорят, что он ускоряется. Ускорение – это скорость изменения скорости во времени.
В повседневном английском языке слово «ускорение» часто используется для описания состояния увеличения скорости.
 Для многих американцев единственный опыт разгона – это реклама автомобилей. Когда рекламный ролик кричит «от нуля до шестидесяти за шесть целых семь десятых секунды», они говорят, что этот автомобиль занимает шесть десятых секунды.7 с для достижения скорости 60 миль в час после полной остановки. Этот пример иллюстрирует ускорение в общепринятом понимании, но ускорение в физике – это гораздо больше, чем просто увеличение скорости.
Для многих американцев единственный опыт разгона – это реклама автомобилей. Когда рекламный ролик кричит «от нуля до шестидесяти за шесть целых семь десятых секунды», они говорят, что этот автомобиль занимает шесть десятых секунды.7 с для достижения скорости 60 миль в час после полной остановки. Этот пример иллюстрирует ускорение в общепринятом понимании, но ускорение в физике – это гораздо больше, чем просто увеличение скорости.Любое изменение скорости объекта приводит к ускорению: увеличение скорости (что люди обычно имеют в виду, когда говорят об ускорении), уменьшение скорости (также называемое замедлением или замедление ) или изменение направления (называемое центростремительным ускорением ). ).Да, верно, изменение направления движения приводит к ускорению, даже если движущийся объект не ускоряется и не замедляется. Это потому, что ускорение зависит от изменения скорости, а скорость является векторной величиной, имеющей как величину, так и направление.
 Таким образом, падающее яблоко ускоряется, машина, остановившаяся на светофоре, ускоряется, а Луна на орбите вокруг Земли ускоряется. Ускорение происходит каждый раз, когда скорость объекта увеличивается или уменьшается, или он меняет направление.
Таким образом, падающее яблоко ускоряется, машина, остановившаяся на светофоре, ускоряется, а Луна на орбите вокруг Земли ускоряется. Ускорение происходит каждый раз, когда скорость объекта увеличивается или уменьшается, или он меняет направление.Как и скорость, есть два вида ускорения: среднее и мгновенное. Среднее ускорение определяется на «большом» временном интервале. Слово «длинный» в этом контексте означает конечное – нечто, имеющее начало и конец. Скорость в начале этого интервала называется начальной скоростью , представленной символом v 0 (vee ноль), а скорость в конце называется конечной скоростью , представленной символом . v (vee).Среднее ускорение – это величина, рассчитанная на основе двух измерений скорости.
а = ∆ v = в – в 0 ∆ т ∆ т Напротив, мгновенное ускорение измеряется в течение «короткого» временного интервала.
 Слово «короткий» в этом контексте означает бесконечно малое или бесконечно малое – не имеющее вообще никакой продолжительности или протяженности.Это математический идеал, который может быть реализован только как предел. Предел ставки, когда знаменатель приближается к нулю, называется производной . Таким образом, мгновенное ускорение является пределом среднего ускорения, когда временной интервал приближается к нулю, или, альтернативно, ускорение является производной скорости.
Слово «короткий» в этом контексте означает бесконечно малое или бесконечно малое – не имеющее вообще никакой продолжительности или протяженности.Это математический идеал, который может быть реализован только как предел. Предел ставки, когда знаменатель приближается к нулю, называется производной . Таким образом, мгновенное ускорение является пределом среднего ускорения, когда временной интервал приближается к нулю, или, альтернативно, ускорение является производной скорости.а = ∆ v = d v ∆ т дт Ускорение – это производная скорости от времени, но скорость сама по себе является производной положения от времени.Производная – это математическая операция, которую можно многократно применять к паре изменяющихся величин. Выполнив это один раз, вы получите первую производную .
 Выполнение этого дважды (производная от производной) дает вам , вторую производную . Это делает ускорение первой производной скорости по времени и второй производной позиции по времени.
Выполнение этого дважды (производная от производной) дает вам , вторую производную . Это делает ускорение первой производной скорости по времени и второй производной позиции по времени.а = d v = г г с = г 2 с дт дт дт дт 2 Несколько слов об обозначениях.В формальном математическом письме векторы выделяются жирным шрифтом и . Скаляры и величины векторов написаны курсивом . Цифры, размеры и единицы измерения пишутся римским шрифтом (не курсивом, не жирным шрифтом, не наклонным шрифтом – обычный текст). Например…
a = 9,8 м / с 2 , θ = −90 ° или a = 9,8 м / с 2 при −90 ° (Примечание по дизайну: я считаю, что греческие буквы плохо смотрятся на экране, когда они выделены курсивом, поэтому я решил игнорировать это правило для греческих букв, пока красивые греческие шрифты не станут нормой в Интернете.
 )
)шт.
международных единиц
Вычисление ускорения включает деление скорости на время – или в единицах СИ, деление метра в секунду [м / с] на секунду [с]. Разделить расстояние на время дважды – это то же самое, что разделить расстояние на квадрат времени. Таким образом, единица ускорения в системе СИ – это метров в секунду в квадрате .
⎡
⎢
⎣м = м / с = м 1 ⎤
⎥
⎦с 2 с с с натуральные единицы
Еще одна часто используемая единица – стандартное ускорение свободного падения – g.Поскольку все мы знакомы с влиянием силы тяжести на себя и окружающие нас объекты, это удобный стандарт для сравнения ускорений.
 Все ощущается нормально при 1 г, вдвое тяжелее при 2 г и невесомым при 0 г. Эта единица имеет точно определенное значение 9,80665 м / с 2 , но для повседневного использования достаточно 9,8 м / с 2 , а 10 м / с 2 удобно для быстрой оценки.
Все ощущается нормально при 1 г, вдвое тяжелее при 2 г и невесомым при 0 г. Эта единица имеет точно определенное значение 9,80665 м / с 2 , но для повседневного использования достаточно 9,8 м / с 2 , а 10 м / с 2 удобно для быстрой оценки.Единица, называемая стандартным ускорением свободного падения (обозначается латинскими буквами g), отличается от естественного явления, называемого ускорением свободного падения (обозначается курсивом g ).Первое имеет определенное значение, тогда как второе необходимо измерить. (Подробнее об этом позже.)
Хотя термин «перегрузочная сила» часто используется, g является мерой ускорения, а не силы. (Подробнее о силах позже.) Особую озабоченность у людей вызывают физиологические эффекты ускорения. Для сравнения, все значения указаны в g.
- В дизайне американских горок скорость имеет решающее значение. Либо это? Если бы скорость была всем, что нужно для создания захватывающей поездки, то автострада была бы довольно захватывающей.
 Большинство американских горок редко превышают 30 м / с (60 миль в час). Вопреки распространенному мнению, именно ускорение делает поездку интересной. Хорошо спроектированные американские горки подвергают гонщика кратковременным максимальным ускорениям от 3 до 4 g. Это то, что придает поездке ощущение опасности.
Большинство американских горок редко превышают 30 м / с (60 миль в час). Вопреки распространенному мнению, именно ускорение делает поездку интересной. Хорошо спроектированные американские горки подвергают гонщика кратковременным максимальным ускорениям от 3 до 4 g. Это то, что придает поездке ощущение опасности. - Несмотря на огромную мощность двигателей, ускорение космического челнока было ниже 3 g. Что-то большее создаст ненужную нагрузку на космонавтов, полезную нагрузку и сам корабль.Оказавшись на орбите, вся система входит в длительный период свободного падения, что дает ощущение невесомости. Такую среду с нулевым ускорением можно также смоделировать внутри специально пилотируемого самолета или башни для свободного падения. (Подробнее об этом позже.)
- Пилоты-истребители могут на короткое время испытывать ускорение до 8 g во время тактических маневров. Если выдерживать более нескольких секунд, достаточно от 4 до 6 г, чтобы вызвать затемнение. Чтобы предотвратить «потерю сознания из-за перегрузки» (G-LOC), летчики-истребители носят специальные скафандры, которые сжимают ноги и живот, заставляя кровь оставаться в голове.

- Пилоты и космонавты могут также тренироваться на человеческих центрифугах, способных работать до 15 g. Воздействие таких интенсивных ускорений кратковременно из соображений безопасности. Люди редко подвергаются воздействию чего-либо выше 8 g дольше нескольких секунд.
- Ускорение связано с травмой. Вот почему наиболее распространенным датчиком манекена для краш-тестов является акселерометр. Сильное ускорение может привести к смерти. Ускорение во время аварии, в результате которой погибла Диана, принцесса Уэльская, в 1997 году, по оценкам, составило порядка 70-100 г, что было достаточно интенсивным, чтобы оторвать легочную артерию от ее сердца – травму, пережить которую практически невозможно. .Если бы она была пристегнута ремнем безопасности, ускорение было бы примерно 30 или 35 g – достаточно, чтобы сломать одно или два ребра, но не настолько, чтобы убить большинство людей.
гауссовых единиц
Точное измерение силы тяжести над поверхностью Земли или других небесных объектов называется гравиметрией .
 По историческим причинам предпочтительной единицей в этой области является сантиметр на секунду в квадрате, также известный как галлонов . В символической форме…
По историческим причинам предпочтительной единицей в этой области является сантиметр на секунду в квадрате, также известный как галлонов . В символической форме…[ галлонов = см / с 2 ]
Да, верно.Название единицы пишется строчными буквами (gal), а символ – заглавной (Gal). Галла была названа в честь итальянского ученого Галилео Галилея (1564–1642), который был первым ученым, изучавшим ускорение силы тяжести, и, возможно, первым из ученых любого рода. Поскольку ускорение силы тяжести на поверхности большинства небесных объектов изменяется лишь на небольшую величину, отклонения силы от идеализированных моделей (называемые гравитационными аномалиями ) измеряются в тысячных долях галлона или миллигал (мГал).
[1000 мГал = 1 галлон]
Гал и миллигал являются частью предшественника Международной системы единиц, называемой системой единиц сантиметр-грамм-секунда или гауссовой системой единиц. Возможно, однажды я действительно напишу что-нибудь важное в этом разделе этой книги.

Вот несколько примеров ускорений в конце этого раздела.
Ускорение выбранных событий (от наименьшего к наибольшему) a (м / с 2 ) событие 0 неподвижен или движется с постоянной скоростью 5 × 10 −14 наименьшее ускорение в научном эксперименте 2.32 × 10 −10 галактическое ускорение на Солнце 9 × 10 −10 аномальное ускорение космического корабля “Пионер” 0,5 лифт гидравлический 0,63 Ускорение свободного падения на Плутоне 1 Лифт, трос 1,6 Ускорение свободного падения на Луне 8.8 Международная космическая станция на орбите 3,7 Ускорение свободного падения на Марсе 9,8 Ускорение свободного падения на Земле 10–40 пилотируемая ракета при старте 20 космический челнок, пик 24,8 Ускорение свободного падения на Юпитере 20–50 американские горки 80 предел устойчивой толерантности человека 0–150 центрифуга для обучения человека 100–200 катапультное сиденье 270 Ускорение свободного падения на Солнце 600 подушки безопасности автоматически срабатывают 10 4 –10 6 медицинская центрифуга 10 6 Пуляв стволе пистолета 10 6 Ускорение свободного падения на звезде белого карлика 10 12 Ускорение свободного падения нейтронной звезды Автомобильные ускорения (g) событие типичный автомобиль спортивный автомобиль Гоночный автомобиль Ф-1 большой грузовик начиная с 0.  3–0,5
3–0,50,5–0,9 1,7 <0,2 торможение 0,8–1,0 1,0–1,3 2 ~ 0,6 поворот 0,7–0,9 0,9–1,0 3 Ускорение и человеческое тело Первоисточник: Ускорение нарушений повседневной жизни, 1994 год a (г) событие 02.9 чихать 03,5 кашель 03,6 толпа толпа 04,1 шлепок по спине 08,1 подножка 10,1 плюхнуться на стул 60 Ускорение грудной клетки при ДТП со скоростью 48 км / ч с подушкой безопасности 70–100 Авария, в результате которой погибла Диана, принцесса Уэльская, 1997 г. 
150–200 Предел ускорения головы при велосипедной аварии со шлемом Практика – гипертекст по физике
Ну, во-первых, мы не должны иметь дело с английскими единицами.С ними сложно работать, поэтому давайте сразу сконвертируем их, а затем сделаем старый «подключи и пей».
v = 60 миль 1609 м 1 час 1 час 1 миля 3600 с a = ∆ v = в – в 0 ∆ т ∆ т а = 26.  8 м / с – 0 м / с
8 м / с – 0 м / с6,6 с Поскольку вопрос, задаваемый для ускорения и ускорения, является векторной величиной, этот ответ не является полным. Правильный ответ также должен включать направление. Сделать это довольно просто. Поскольку машина трогается с места и движется вперед, ее ускорение также должно быть вперед. Окончательный и исчерпывающий ответ на эту проблему – автомобиль разгоняется до…
.a = 4.06 м / с 2 вперед
Мы должны преобразовать конечную скорость в единицы СИ.
v = 80 миль 1609 м 1 час 1 час 1 миля 3600 с Используйте тот факт, что изменение равно скорости, умноженной на время, а затем добавьте это изменение к нашей скорости в конце предыдущей задачи.
 Все остальное алгебра сделает за нас.
Все остальное алгебра сделает за нас.a = ∆ v = в – в 0 ∆ т ∆ т ∆ т = 35.8 м / с – 26,8 м / с 4,06 м / с 2 Альтернативное решение. С этим методом нам не нужны никакие вонючие преобразования. Отношение восемьдесят к шестидесяти простое, а именно: 4 3 . Из нашего определения ускорения должно быть очевидно, что время прямо пропорционально изменению скорости, когда ускорение постоянно. Таким образом…
∆ v 2 = ∆ т 2 ∆ v 1 ∆ т 1 80 миль / ч = ∆ т 2 60 миль / ч 6.  6 с
6 сЭто не ответ. Это время, прошедшее с момента, когда машина начала движение. Вопрос касался необходимого дополнительного времени, поэтому мы должны вычесть время, необходимое для перехода с нуля до шестидесяти. Таким образом…
∆ t = 8,8 с – 6,6 с = 2,2 с
Оба метода дают по существу одинаковый ответ.
Довольно просто. Давай сделаем это.
a = ∆ v = в – в 0 ∆ т ∆ т а = 0 м / с – 35.8 м / с 5,0 с a = −7,16 м / с 2 Ничего удивительного кроме знака минус нет.
. Когда векторная величина отрицательна, что это значит? Есть несколько интерпретаций этого, но я думаю, что моя лучшая. Когда вектор имеет отрицательное значение, это означает, что он указывает в направлении, противоположном направлению положительных векторов.В этой задаче, поскольку предполагается, что положительные векторы направлены вперед (в каком другом направлении будет двигаться нормальный автомобиль?), Ускорение должно быть обратным. Таким образом, полный ответ на эту проблему состоит в том, что ускорение автомобиля составляет…
Когда векторная величина отрицательна, что это значит? Есть несколько интерпретаций этого, но я думаю, что моя лучшая. Когда вектор имеет отрицательное значение, это означает, что он указывает в направлении, противоположном направлению положительных векторов.В этой задаче, поскольку предполагается, что положительные векторы направлены вперед (в каком другом направлении будет двигаться нормальный автомобиль?), Ускорение должно быть обратным. Таким образом, полный ответ на эту проблему состоит в том, что ускорение автомобиля составляет…a = 7,16 м / с 2 назад
Хотя обычно замедлению присваивается отрицательное значение, отрицательное ускорение не подразумевает автоматически замедление. При работе с векторными величинами любое направление можно считать положительным…
вверх, вниз, вправо, влево,
вперед, назад, север, юг, восток, запад и соответствующее противоположное направление считается отрицательным…
вниз, вверх, влево, вправо,
назад, вперед, юг, север, запад, восток. Неважно, что вы выберете, если вы последовательны в решении проблемы. Не изучайте никаких правил назначения знаков для определенных направлений и не позволяйте никому говорить вам, что определенное направление должно быть положительным или должно быть отрицательным.
Калькулятор ускорения | Определение | Формула
Калькулятор ускорения – это инструмент, который поможет вам определить, насколько быстро изменяется скорость объекта . Он работает тремя разными способами, в зависимости от:
- разница между скоростями в два различных момента времени,
- расстояние, пройденное при разгоне,
- масса ускоряющегося объекта и сила, действующая на него.
Если вы спрашиваете себя, что такое ускорение, какова формула ускорения или каковы единицы ускорения, продолжайте читать, и вы узнаете, как найти ускорение. Ускорение строго связано с движением объекта, и каждый движущийся объект обладает определенной энергией. Если вам нужно это оценить, посетите другие наши калькуляторы, где вы можете найти формулу кинетической энергии и ее угловую версию – формулу кинетической энергии вращения.
Чтобы все было понятно, мы также подготовили несколько примеров ускорения, которые распространены в физике.Вы можете найти там:
- центростремительное ускорение и тангенциальное ускорение,
- угловое ускорение,
- ускорение свободного падения,
- ускоритель частиц.
Ускорение всегда происходит, когда на объект действует ненулевая чистая сила. Вы можете почувствовать это в лифте, когда вы станете немного тяжелее (ускорение) или легче (замедление), или когда вы едете по крутому склону на санях по снегу. Более того, из общей теории относительности мы знаем, что вся Вселенная не только расширяется, но даже ускоряется! Это означает, что расстояние между двумя точками постоянно становится все больше и больше, но мы не можем чувствовать это каждый день, потому что каждый масштаб в мире тоже расширяется.
Что такое ускорение? – определение ускорения
Ускорение – скорость изменения скорости объекта; другими словами, насколько быстро меняется скорость. Согласно второму закону Ньютона, ускорение прямо пропорционально сумме всех сил, действующих на объект, и обратно пропорционально его массе. Это все здравый смысл – если несколько разных сил толкают объект, вам нужно выяснить, к чему они складываются (они могут действовать в разных направлениях), а затем разделить результирующую чистую силу на массу вашего объекта.
Это определение ускорения говорит, что ускорение и сила, по сути, одно и то же. При изменении силы изменяется и ускорение, но величина его изменения зависит от массы объекта. Это неверно в ситуации, когда масса также изменяется, например, при ракетной тяге, когда сгоревшее топливо выходит из сопла ракеты. Если вы когда-нибудь задумывались, какова физика космических путешествий, взгляните на это уравнение ракеты Циолковского.
Мы можем измерить ускорение объекта напрямую с помощью акселерометра .Если повесить объект на акселерометр, он покажет ненулевое значение. Это почему? Ну, это из-за гравитационных сил, которые действуют на каждую частицу, имеющую массу. А где чистая сила, там и ускорение. Таким образом, акселерометр в состоянии покоя измеряет ускорение свободного падения, которое на поверхности Земли составляет примерно 31,17405 фут / с² (9,80665 м / с²) . Другими словами, это ускорение свободного падения, которое любой объект получает при свободном падении в вакууме.
Кстати о пылесосах, вы когда-нибудь смотрели «Звездные войны» или другой фильм, действие которого происходит в космосе? Эпические сражения космических кораблей, звуки бластеров, двигателей и взрывов.Что ж, это ложь. Космос – это вакуум, и в нем нельзя услышать звук (для распространения звуковых волн требуется материя). Эти битвы должны быть беззвучными! В космосе никто не услышит твой крик. Чтобы проверить скорость звука в воздухе или воде, воспользуйтесь нашим калькулятором скорости звука. Учитывается даже температура!
Как найти ускорение? – счетчик ускорения
Калькулятор ускорения на этом сайте учитывает только ситуацию, в которой объект имеет равномерное (постоянное) ускорение.В этом случае уравнение ускорения по определению представляет собой отношение изменения скорости за конкретное время. Однако здесь вы можете узнать, как найти ускорение еще двумя способами. Давайте посмотрим, как пользоваться нашим калькулятором (уравнения ускорения вы можете найти в разделе после):
- В зависимости от имеющихся данных вы можете рассчитать ускорение тремя разными способами. Сначала выберите соответствующее окно (# 1, # 2 или # 3),
- [при выборе # 1] – Введите начальную
v_iи конечнуюv_fскорости объекта и сколько времениΔtпотребовалось для изменения скорости. - [при выборе # 2] – Введите начальную скорость
v_i, пройденное расстояниеΔdи времяΔt, пройденное во время ускорения. Здесь вам не нужно знать конечную скорость. - [при выборе # 3] – Введите массу
мобъекта и чистую силуF, действующую на этот объект. Это совершенно другой набор переменных, который возникает из второго закона движения Ньютона (другое определение ускорения). - Считайте результирующее ускорение из последнего поля. Вы также можете выполнить вычисления другим способом, если знаете, что такое ускорение, например, чтобы оценить расстояние
Δd. Просто укажите остальные параметры в этом окне.
Знание того, что такое ускорение, необходимо для анализа движения объектов. Например, вы можете определить изменение импульса за определенный период времени с помощью этой формулы для импульса. Это одна из физических величин, которые мы используем в нашем калькуляторе автокатастроф, где мы объясняем и визуализируем важность ремней безопасности с помощью чисел и определяем, с какой скоростью вы можете погибнуть в автокатастрофе.Повышение скорости и содержание алкоголя в крови – главные причины автомобильных аварий. Пожалуйста, водите осторожно!
Формула ускорения – три уравнения ускорения
В 17 веке сэр Исаак Ньютон , один из самых влиятельных ученых всех времен, опубликовал свою знаменитую книгу « Начала ». В нем он сформулировал закон всемирного тяготения, который гласит, что любые два объекта с массой будут притягивать друг друга с силой, экспоненциально зависящей от расстояния между этими объектами (в частности, она обратно пропорциональна квадрату расстояния).Чем тяжелее объекты, тем больше сила тяжести. Это объясняет, например, почему планеты вращаются вокруг очень плотного Солнца.
В Principia Ньютон также включает три закона движения, которые являются центральными для понимания физики нашего мира. Калькулятор ускорения основан на трех различных уравнениях ускорения, третье из которых получено из работы Ньютона:
-
а = (v_f - v_i) / Δt, -
a = 2 * (Δd - v_i * Δt) / Δt², -
a = Ф / м,
где:
-
a– ускорение, -
v_iиv_f– соответственно начальная и конечная скорости, -
Δt– время разгона, -
Δd– расстояние, пройденное при ускорении, -
F– чистая сила, действующая на объект, который ускоряется, -
м– масса этого объекта.
Теперь вы знаете, как рассчитать ускорение! В следующем абзаце мы обсудим единицы ускорения (СИ и британские). Вы уже видели наши калькуляторы конвертации? Они могут сэкономить вам много времени при работе с различными юнитами. В случае расстояния вас может заинтересовать конвертер длины, который включает в себя таблицу преобразования длины. Если вы хотите переключаться между разными единицами массы, вот наш конвертер веса. Оба калькулятора позволяют быстро выполнять вычисления с любым набором единиц измерения.Попробуйте!
Блоки ускорения
Если вы уже умеете рассчитывать ускорение, давайте сосредоточимся на единицах ускорения. Вы можете вывести их из приведенных выше уравнений. Все, что вам нужно знать, это то, что скорость выражается в футах в секунду (британская / американская система) или в метрах в секунду (система СИ), а время – в секундах. Следовательно, если вы разделите скорость на время (как мы делаем в первой формуле ускорения), вы получите единицу ускорения
фут / с²илим / с²в зависимости от того, какую систему вы используете.В качестве альтернативы можно использовать третье уравнение. В этом случае вам нужно разделить силу (фунты в США и ньютоны в СИ) на массу (фунты в США и килограммы в СИ), получив
пдл / фунтилиН / кг. Они оба представляют одно и то же, так как фунт составляетфунтов на квадратный дюйм = фунт * фут / с², а ньютон составляетН = кг * м / с². Когда вы замените его и уменьшите единицы, вы получите(фунт * фут / с²) / фунт = фут / с²или(кг * м / с²) / кг = м / с².Существует также третий вариант, который фактически широко используется.Вы можете выразить ускорение как стандартное ускорение , вызванное силой тяжести у поверхности Земли, которое определяется как
g = 31,17405 фут / с² = 9,80665 м / с². Например, если вы говорите, что лифт движется вверх с ускорением0,2g, это означает, что он ускоряется примерно со скоростью6,2 фут / с²или2 м / с²(т. Е.0,2 * g) . Мы округлили приведенные выше выражения до двух значащих цифр с помощью правил значащих цифр, которые вы можете найти в нашей математической категории.Примеры ускорения
Центростремительное ускорение и тангенциальное ускорение
Ускорение – это обычно вектор, поэтому его всегда можно разложить на компоненты. Обычно у нас есть две части, которые перпендикулярны друг другу: центростремительная и тангенциальная . Центростремительное ускорение изменяет направление скорости и, следовательно, форму дорожки, но не влияет на значение скорости. С другой стороны, тангенциальное ускорение всегда перпендикулярно траектории движения.Он изменяет только значение скорости , но не ее направление.
В круговом движении (крайний левый рисунок ниже), когда объект движется по окружности круга, присутствует только центростремительный компонент. Объект будет поддерживать постоянную скорость; подумайте о Земле, которая имеет центростремительное ускорение из-за силы тяжести Солнца (на самом деле ее скорость немного меняется в течение года – см. калькулятор орбитальной скорости и калькулятор орбитального периода для получения дополнительной информации).
Когда присутствуют оба компонента, траектория объекта выглядит как на правом изображении. Что будет, если есть только тангенциальное ускорение? Затем происходит линейное движение. Это похоже на нажатие педали газа в автомобиле на прямом участке автострады. А если вы водитель, наш счетчик бензина может вас заинтересовать; оценивает стоимость проезда на автомобиле. Вы указываете экономию топлива, расстояние и цену на бензин, и вы быстро получаете стоимость поездки. Есть даже возможность разделить его на несколько человек, ведь вместе путешествовать весело и полезно! Группа разговорчивых друзей в вашей машине будет: e.g., не дать вам заснуть.
Угловое ускорение
Угловое ускорение играет важную роль в описании вращательного движения. Однако не путайте это с ранее упомянутыми центростремительными или тангенциальными ускорениями. Эта физическая величина соответствует скорости изменения угловой скорости. Другими словами, он сообщает вам, насколько быстро ускоряется вращение объекта – объект вращается все быстрее и быстрее (или все медленнее и медленнее, если угловое ускорение меньше нуля).
Знаете ли вы, что мы можем найти аналогию между этим и законом динамики Ньютона во вращательном движении? Согласно его второму закону, если вы можете переключить ускорение на угловое ускорение, силу на крутящий момент и массу на момент инерции, вы получите уравнение углового ускорения. Вы могли заметить, что некоторые физические законы, подобные этому, универсальны, что делает их действительно важными для физики.
Ускорение свободного падения
Мы уже несколько раз упоминали ускорение свободного падения.Он возникает из-за гравитационной силы, которая существует между каждыми двумя объектами, имеющими массу (обратите внимание, что уравнение гравитации не зависит от объема объекта – здесь важна только масса). Сначала это может показаться странным, но согласно третьему закону движения Ньютона, вы действуете на Землю с той же силой, что и Земля на вас . Однако масса Земли намного больше, чем масса человека (в ~ 10 ² раз больше), поэтому наше воздействие на Землю практически равно нулю. Это аналогично всем бактериям (в ~ 10¹⁸ раз легче человека), живущим на вашей руке; вы их даже не заметите! С другой стороны, мы чувствуем влияние нашей планеты, и это ускорение силы тяжести.
Стандартная сила тяжести по определению составляет 31,17405 фут / с² (9,80665 м / с²), поэтому, если человек весит 220 фунтов (около 100 кг), на него действует сила тяжести около 7000 фунтов на квадратный дюйм (1000 Н). Давайте введем это значение в окно №3 нашего калькулятора вместе с массой Земли (1,317 × 10²⁵ фунта или 5,972 × 10²⁴ кг в экспоненциальном представлении). Что такое расчетное ускорение? Это настолько мало , что наш калькулятор считает, что это ноль . Мы ничего не значим по сравнению с планетой!
Ускоритель частиц
После разговора об огромных объектах в космосе, давайте перейдем к микроскопическому миру частиц.Хотя мы не можем видеть их глазами, мы использовали частицы высоких энергий, такие как электроны и протоны, и регулярно используем их в ускорителях частиц; распространены в физике, химии и медицине. Мы используем их для уничтожения раковых клеток, сохраняя при этом окружающую здоровую ткань, или исследуем структуру материала в атомном масштабе. В последнее время рак – одна из болезней достатка, которая, вероятно, является следствием роста благосостояния в обществе. Даже неправильное питание может увеличить риск рака! С помощью этого ежедневного калькулятора протеина вы можете проверить, сколько протеина вам нужно в день, и, если вы также хотите улучшить свою физическую форму, наш макро-калькулятор здесь, чтобы помочь вам.
Вы, наверное, знаете о Большом адронном коллайдере (ЦЕРН), самом мощном ускорителе элементарных частиц в мире. Это позволяет нам сделать шаг вперед, чтобы понять, как устроена Вселенная, и разработать технологии, которые могут найти множество важных приложений в будущем. Однако, чтобы достичь таких высоких энергий, мы должны разогнать частицы до скоростей, близких к скорости света. Вкратце, мы можем сделать это с помощью магнитных или электрических полей. Чтобы увидеть, насколько быстро частицы ускоряются по сравнению со стандартной силой тяжести, посмотрите наше ускорение в калькуляторе электрического поля, где мы объяснили, как рассчитать ускорение заряженных частиц.
Мир микроскопических частиц управляется статистической физикой, которая уделяет особое внимание концепции вероятности. У нас есть много калькуляторов, связанных с этой темой. Взгляните на калькулятор вероятностей, чтобы узнать, как найти вероятность, или попробуйте калькулятор перестановок, чтобы определить количество способов, которыми вы можете упорядочить определенное количество элементов. Физики используют перестановку для предсказания теоретических свойств материала, которые затем можно наблюдать в повседневной жизни. Например, вы можете узнать, какова средняя скорость частиц газа.
FAQ
Является ли ускорение вектором?
Да, , ускорение – это вектор, так как имеет как величину, так и направление . Величина – это скорость ускорения объекта, а направление – это ускорение в том направлении, в котором движется объект, или против него. Это соответственно ускорение и замедление.
Как масса влияет на ускорение?
Если сила, с которой объект толкает, остается прежней, ускорение будет уменьшаться по мере увеличения массы .Это потому, что F / m = a, поэтому по мере увеличения массы фракция становится все меньше и меньше.
Может ли ускорение быть отрицательным?
Да , ускорение может быть отрицательным, , которое известно как замедление . Два объекта с равным, но противоположным ускорением будут ускоряться на одинаковую величину, только в двух противоположных направлениях.
Как найти среднее ускорение?
- Определите изменение скорости на для заданного вами времени.
- Рассчитайте изменение во времени за рассматриваемый период.
- Разделите изменение скорости на изменение во времени.
- Результат – среднее ускорение за этот период.
Как узнать величину ускорения?
- Преобразуйте величину силы в Ньютоны.
- Измените массу объекта на килограммы.
- Умножьте оба значения на вместе, чтобы найти ускорение в м / с 2 .
В чем разница между ускорением и скоростью?
Скорость – это скорость, с которой объект движется в определенном направлении, а ускорение – это то, как скорость этого объекта на изменяется со временем. Оба имеют величину и направление, но их единицы измерения – м / с и м / с 2 соответственно.
Как найти угловое ускорение?
- Используйте уравнения углового ускорения:
a = Δv / Δt. - Найдите начальную и конечную угловую скорость в радианах / с.
- Вычтите начальную угловую скорость из конечной угловой скорости, чтобы получить изменение угловой скорости на .
- Найдите начальное и конечное время для рассматриваемого периода.
- Вычтите начальное время из последнего, чтобы получить изменение времени на .
- Разделите изменение угловой скорости на изменение во времени, чтобы получить угловое ускорение в радианах / с. 2 .
Разгон
Последняя математическая величина, обсуждаемая в Уроке 1, – это ускорение. Часто путают, что ускорение имеет значение, сильно отличающееся от значения, которое ассоциируется с ним спортивными комментаторами и другими людьми. Определение ускорения:
- Ускорение – это векторная величина, которая определяется как скорость, с которой объект изменяет свою скорость. Объект ускоряется, если он меняет свою скорость.
Спортивные комментаторы иногда говорят, что человек ускоряется, если он / она быстро движется. И все же ускорение не имеет ничего общего с быстрым движением. Человек может двигаться очень быстро, но при этом не ускоряться. Ускорение связано с изменением скорости движения объекта. Если объект не меняет свою скорость, значит, объект не ускоряется. Данные справа представляют движущийся на север ускоряющийся объект. Скорость меняется с течением времени.Фактически, скорость изменяется на постоянную величину – 10 м / с – каждую секунду. Каждый раз, когда скорость объекта изменяется, объект считается ускоряющимся; у него есть ускорение.
Значение постоянного ускорения
Иногда ускоряющийся объект меняет свою скорость на одну и ту же величину каждую секунду. Как упоминалось в предыдущем абзаце, приведенная выше таблица данных показывает, что объект меняет свою скорость на 10 м / с каждую последующую секунду.Это называется постоянным ускорением, поскольку скорость изменяется на постоянную величину каждую секунду. Не следует путать объект с постоянным ускорением с объектом с постоянной скоростью. Не дайте себя обмануть! Если объект меняет свою скорость – на постоянную или переменную величину – то это ускоряющийся объект. И объект с постоянной скоростью не ускоряется. Приведенные ниже таблицы данных отображают движения объектов с постоянным ускорением и изменяющимся ускорением.Обратите внимание, что каждый объект имеет изменяющуюся скорость.
Поскольку ускоряющиеся объекты постоянно изменяют свою скорость, можно сказать, что пройденное расстояние / время не является постоянной величиной. Например, падающий объект обычно ускоряется при падении. Если бы мы наблюдали движение свободно падающего объекта (движение свободного падения будет подробно обсуждено позже), мы бы заметили, что объект имеет среднюю скорость примерно 5 м / с в первую секунду, примерно 15 м / с. во второй секунде примерно 25 м / с в третью секунду, примерно 35 м / с в четвертую секунду и т. д.Наш свободно падающий объект будет постоянно ускоряться. Учитывая эти средние значения скорости в течение каждого последовательного временного интервала в 1 секунду, мы могли бы сказать, что объект упадет на 5 метров в первую секунду, 15 метров во вторую секунду (для общего расстояния 20 метров), 25 метров в третью. второй (для общей дистанции 45 метров), 35 метров в четвертой секунде (для общей дистанции 80 метров через четыре секунды). Эти числа приведены в таблице ниже.
Время
ИнтервалИзменение скорости
В течение интервалапр.Скорость
В течение интервалаПройденное расстояние
В течение интервалаОбщее пройденное расстояние с
От 0 с до конца интервала0 – 1,0 с от 0 до ~ 10 м / с ~ 5 м / с ~ 5 м ~ 5 м 1,0 – 2,0 с ~ 10-20 м / с ~ 15 м / с ~ 15 м ~ 20 м 2.0 – 3,0 с ~ от 20 до 30 м / с ~ 25 м / с ~ 25 м ~ 45 м 3,0 – 4,0 с ~ 30-40 м / с ~ 35 м / с ~ 35 м ~ 80 м Примечание. Используемый здесь символ ~ означает приблизительно.
Это обсуждение показывает, что свободно падающий объект, который ускоряется с постоянной скоростью, будет преодолевать разные расстояния за каждую последующую секунду.2) расстояние; расстояние, пройденное за четыре секунды, в 16 раз превышает расстояние, пройденное за одну секунду. Для объектов с постоянным ускорением расстояние перемещения прямо пропорционально квадрату времени перемещения.
Расчет среднего ускорения
Среднее ускорение (a) любого объекта за заданный интервал времени (t) может быть вычислено с помощью уравнения
Это уравнение можно использовать для расчета ускорения объекта, движение которого представлено приведенной выше таблицей данных скорость-время.Данные скорости-времени в таблице показывают, что объект имеет ускорение 10 м / с / с. Расчет показан ниже.
Значения ускорения выражаются в единицах скорости / времени. Типичные единицы ускорения включают в себя следующие:
м / с / с
миль / час / с
км / ч / с
м / с 2Эти устройства могут показаться немного неудобными для начинающего студента-физика. Тем не менее, это очень разумные единицы, когда вы начинаете рассматривать определение и уравнение ускорения.Причина появления единиц становится очевидной после изучения уравнения ускорения.
Поскольку ускорение – это изменение скорости во времени, единицы измерения ускорения – это единицы скорости, деленные на единицы времени, т.е. (м / с) / с или (миль / час) / с. Единицу измерения (м / с) / с можно математически упростить до м / с 2 .
Направление вектора ускорения
Поскольку ускорение является векторной величиной, с ним связано направление.Направление вектора ускорения зависит от двух вещей:
- , ускоряется или замедляется объект
- , движется ли объект в + или – направлении
Общий принцип определения ускорения:
Если объект замедляется, то его ускорение происходит в направлении, противоположном его движению.
Этот общий принцип может применяться для определения того, является ли знак ускорения объекта положительным или отрицательным, вправо или влево, вверх или вниз и т. Д.Рассмотрим две таблицы данных ниже. В каждом случае ускорение объекта находится в положительном направлении . В Примере A объект движется в положительном направлении на (т.е. имеет положительную скорость на ) и ускоряется. Когда объект ускоряется, ускорение совпадает с направлением скорости. Таким образом, этот объект имеет положительное ускорение. В примере B объект движется в отрицательном направлении (т. Е. Имеет отрицательную скорость) и замедляется.Согласно нашему общему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект также имеет положительное ускорение.
Тот же самый общий принцип может быть применен к движению объектов, представленных в двух таблицах данных ниже. В каждом случае ускорение объекта происходит в отрицательном направлении . В примере C объект движется в положительном направлении (т.е.е., имеет положительную скорость ) и замедляется. Согласно нашему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект имеет отрицательное ускорение. В Примере D объект движется в отрицательном направлении (т.е. имеет отрицательную скорость ) и ускоряется. Когда объект ускоряется, ускорение совпадает с направлением скорости. Таким образом, этот объект также имеет отрицательное ускорение.
Обратите внимание на использование положительных и отрицательных слов в приведенном выше обсуждении (Примеры A – D). В физике использование положительного и отрицательного всегда имеет физический смысл. Это больше, чем просто математический символ. Положительное и отрицательное, используемые здесь для описания скорости и ускорения движущегося объекта, описывают направление. И скорость, и ускорение являются векторными величинами, и полное описание величины требует использования прилагательного направленного действия.Север, юг, восток, запад, вправо, влево, вверх и вниз – все прилагательные направленного действия. Физика часто заимствует из математики и использует символы + и – как направленные прилагательные. В соответствии с математическим соглашением, используемым в числовых линиях и графиках, положительное значение часто означает вправо или вверх, а отрицательное – влево или вниз. Таким образом, сказать, что объект имеет отрицательное ускорение, как в примерах C и D, означает просто сказать, что его ускорение идет влево или вниз (или в любом направлении, определенном как отрицательное).Отрицательные ускорения не относятся к значениям ускорения меньше 0. Ускорение -2 м / с / с – это ускорение с величиной 2 м / с / с, которое направлено в отрицательном направлении.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Name That Motion Interactive.Он находится в разделе «Интерактивная физика» и позволяет учащемуся применять концепции скорости, скорости и ускорения. Проверьте свое пониманиеЧтобы проверить свое понимание концепции ускорения, рассмотрите следующие проблемы и соответствующие решения. Используйте уравнение ускорения, чтобы определить ускорение для следующих двух движений.
3 формулы, которые вам нужны
“Ого, ты действительно прошел с нуля до шестидесяти!”
Вы когда-нибудь слышали, чтобы кто-то использовал идиому «от нуля до шестидесяти», как я в приведенном выше примере? Когда кто-то говорит, что что-то пошло с нуля до шестидесяти, на самом деле они говорят, что все ускорилось очень быстро. Ускорение – это величина, на которую скорость чего-либо изменяется за заданный период времени.
В этой статье мы поговорим об ускорении: что это такое и как его рассчитать. Пристегнитесь!
Что такое ускорение?
Ускорение – это скорость изменения скорости за заданный период времени. Для расчета ускорения необходимо иметь как скорость, так и время.
Многие путают ускорение со скоростью (или скоростью).Прежде всего, скорость – это просто скорость с направлением, поэтому они часто используются как синонимы, даже если они имеют небольшие различия. Ускорение – это скорость изменения скорости, означающая, что что-то становится быстрее или медленнее.
Что такое формула ускорения?
Для расчета ускорения можно использовать уравнение ускорения. Вот наиболее распространенная формула ускорения:
$$ a = {Δv} / {Δt} $$
где $ Δv $ – изменение скорости, а $ Δt $ – изменение во времени.
Вы также можете записать уравнение ускорения следующим образом:
$$ a = {v (f) – v (i)} / {t (f) – t (i)} $$
В этом уравнении ускорения $ v (f) $ – это конечная скорость, а – начальная скорость $ v (i) $. $ T (f) $ – это последнее время, а $ t (i) $ – начальное время.
Еще о некоторых вещах, о которых следует помнить при использовании уравнения ускорения:
- Вам нужно вычесть начальную скорость из конечной скорости. Если вы перевернете их, вы получите неверное направление вашего ускорения.
- Если у вас нет времени начала, вы можете использовать «0».
- Если конечная скорость меньше начальной, ускорение будет отрицательным, что означает, что объект замедлился.
Теперь давайте разберем уравнение ускорения пошагово на реальном примере.
Как рассчитать ускорение: пошаговая разбивка
Теперь давайте разберем формулу ускорения шаг за шагом на реальном примере.
Гоночный автомобиль разгоняется с 15 до 35 м / с за 3 секунды. Какое у него среднее ускорение?
Сначала напишите уравнение ускорения.
$$ a = {v (f) – v (i)} / {t (f) – t (i)} $$
Затем определите свои переменные. 2 $$
$$ A = 6.2 $$
Давайте попробуем другой пример.
Велосипедист, движущийся со скоростью 23,2 м / с, полностью останавливается за 1,5 $ с $. Что было ее замедлением?
Сначала напишите уравнение ускорения.
$$ a = (v (f) – v (i)) ÷ (t (f) – t (i)) $$
Затем определите свои переменные.
a = то, что мы решаем для
$$ V (f) = 0 м / с $$
$$ V (i) = 23,2 м / с $$
$$ T (f) = 1,4 с $$
$$ T (i) = 0 с $$
Теперь подставьте переменные в уравнение и решите:
$$ A = {{(0 – 23.2} $$
2 Другие общие формулы ускорения
Не знаете, как рассчитать ускорение по другой формуле? Есть несколько других распространенных формул ускорения.
Формула углового ускорения
Угловое ускорение – это скорость, с которой угловое ускорение вращающегося объекта изменяется во времени.
Вот уравнение углового ускорения:
$$ a = {\ change \ in \ angular \ velocity} / {\ change \ in \ time} $$
Формула центростремительного ускорения
Центростремительное ускорение – это скорость движения объекта внутрь к центру круга.2} / r $$
$ a (c) $ = ускорение, центростремительное
$ v $ = скорость
$ r $ = радиус
Ключевые выводы
Ускорение – это скорость изменения скорости за заданный период времени.
Вы вычисляете ускорение, разделив изменение скорости на изменение во времени.
Что дальше?
Ищете другие научные объяснения? Мы разбиваем электрическую энергию и как определить различных типов облаков с помощью наших экспертных руководств.
Работаете над исследовательской работой, но не знаете, с чего начать? Тогда ознакомьтесь с нашим руководством, где мы собрали множество высококачественных тем для исследований, которые вы можете использовать бесплатно.
Нужна помощь с уроком английского языка – особенно с определением литературных приемов в текстах, которые вы читаете? Тогда вы обязательно захотите взглянуть на наше исчерпывающее объяснение самых важных литературных устройств и того, как они используются.
3.1 Ускорение – Физика | OpenStax
Teacher Support
[BL] Просмотрите определения терминов: время , смещение , скорость и ускорение . Обратите внимание на то, что переменные, обычно используемые для представления этих величин, являются первыми буквами соответствующего термина.
[OL] Убедитесь, что учащиеся знают единицы СИ, в которых выражаются время, смещение, скорость и ускорение. Обратите внимание, что это некоторые из семи базовых единиц метрической системы.Объясните, что преобразование в базовые единицы – хороший первый шаг при вычислении этих величин. Объясните значение секунд в квадрате в знаменателе единиц ускорения.
[AL] Проверьте все основные единицы метрической системы. Объясните, как эти единицы взаимосвязаны. Например, покажите, как длина определяется временем.
[BL] [OL] Используйте уравнение a¯ = ΔvΔt = vf − v0tf − t0a¯ = ΔvΔt = vf − v0tf − t0, чтобы подчеркнуть взаимосвязь между Δ и нижними индексами f и 0.Различают постоянное и переменное ускорение. Здесь может быть путаница, особенно в случае увеличения ускорения. Убедитесь, что учащиеся понимают, что слово замедление не используется в физике и что ускорение может быть положительным или отрицательным.
[AL] Посмотрите, могут ли учащиеся использовать понятие ускорения, чтобы понять запутанные утверждения, такие как «уменьшение скорости увеличения». Например, используйте концепцию ускорения для анализа утверждения «темпы роста затрат на здравоохранение снижаются.Если увеличение стоимости определяется как положительное, то ускорение затрат на здравоохранение будет отрицательным.
[OL] Стрелка ускорения, указывающая напротив стрелки скорости, может сбивать с толку. Объясните, что стрелка ускорения указывает в направлении, противоположном скорости, потому что скорость становится меньше, то есть стрелка скорости становится короче.
Acceleration
Оптимизация лазерного ускорения электронов
Декабрь4 февраля 2020 г. – Исследователи рассмотрели характеристики ускорения электронов в вакууме, вызванного лазерными импульсами максимальной мощности, достижимыми сегодня, в поисках ключа к максимальной полезной энергии …
Не так быстро! Контроль скорости легких пуль
14 декабря 2020 г. – Исследователи точно и произвольно контролируют скорость полета легких пуль, открывая новые возможности для оптических и физических …
Обеспечение более длительных космических миссий
Авг.20, 2019 – Подруливающее устройство Холла – это двигательная установка, которая часто используется космическими кораблями, выполняющими более длительные миссии. Недавнее исследование показало, как можно увеличить срок службы этих систем …
Методы пропуска камней могут улучшить возвращение космических аппаратов
20 апреля 2021 г. – Ученые выявили несколько ключевых факторов, влияющих на количество отскоков, которым прыгает камень при ударе о воду. Исследование включало теоретическое моделирование и экспериментальную установку…
Мировой рекорд: плазменный ускоритель работает круглосуточно
19 августа 2020 г. – Исследователи достигли важной вехи на пути к ускорителю элементарных частиц будущего. Впервые лазерно-плазменный ускоритель проработал более суток в непрерывном режиме …
Веха для экспериментов по ускорению нового поколения
30 апреля 2021 г. – Будущее ускорения частиц наступило. Пробуждение – многообещающая концепция совершенно нового метода, с помощью которого частицы можно ускорять даже на короткие расстояния.Основанием для этого служит …
Новый математический инструмент может выбрать лучшие датчики для работы
17 сентября 2020 г. – В результате авиакатастрофы Boeing 737 Max в 2019 году восстановленный черный ящик после аварии намекал, что отказавший датчик давления, возможно, привел к тому, что злополучный самолет нырнул в нос. Этот и другие инциденты имеют …
Методы количественной оценки острых ощущений и судороги игрока в гольф
19 июля 2018 г. – Почти каждому гольфисту знакомо это чувство.Через несколько минут после идеальной езды по фарватеру каскад необъяснимых пропущенных паттов приводит к разочаровывающему тройному результату …
Переносной датчик вибрации для точного распознавания голоса
24 июня 2019 г. – Ученые разработали гибкий и носимый чувствительный к вибрации датчик. Когда этот датчик прикреплен к шее, он может точно распознавать голос по вибрации кожи шеи и не …
«Оптическая ракета», созданная с использованием интенсивного лазерного излучения
Сен.14, 2018 – Эксперимент продемонстрировал, как применение интенсивного света увеличивает количество электронов до максимально достижимого уровня .


 67 × 10-11 м3 кг-1 с-2
67 × 10-11 м3 кг-1 с-2 67 × 10-11 м3 кг-1 с-2
67 × 10-11 м3 кг-1 с-2 2}r \)
2}r \)
 Сделать рисунок, на котором указать вектора всех сил, действующих на
тело.
Сделать рисунок, на котором указать вектора всех сил, действующих на
тело.
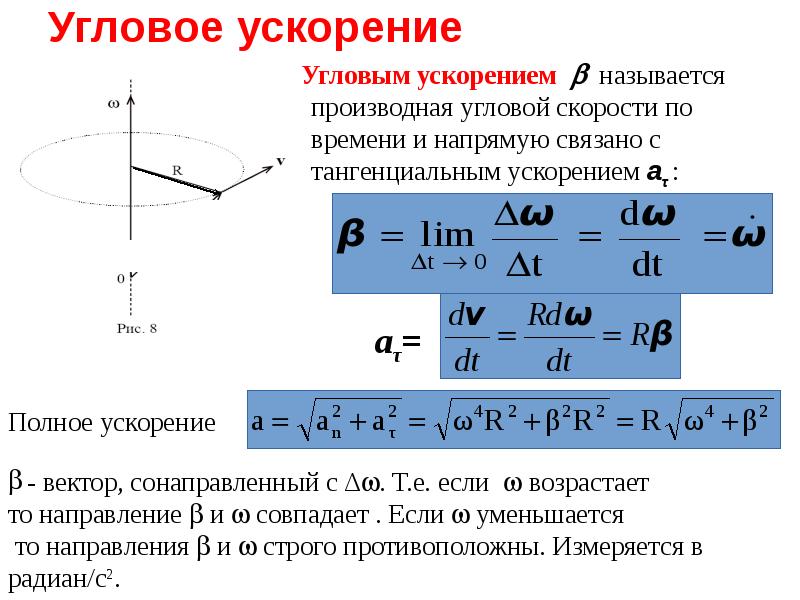
 Каков
модуль сил гравитационного притяжения двух других шариков, если масса
каждого из них равна 2m,
а расстояние между их центрами равно 2r?
Каков
модуль сил гравитационного притяжения двух других шариков, если масса
каждого из них равна 2m,
а расстояние между их центрами равно 2r?


 Для достижения поставленной цели были сформулированы следующие задачи исследования:
Для достижения поставленной цели были сформулированы следующие задачи исследования:
 Я измерял g различными способами, рассчитывал погрешности измерений, опираясь на общепринятое значение g, учился грамотно проводить эксперимент. Выяснил, что свободное падение – движение равноускоренное. Ускорение свободного падения не зависит от массы тела. Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.
Я измерял g различными способами, рассчитывал погрешности измерений, опираясь на общепринятое значение g, учился грамотно проводить эксперимент. Выяснил, что свободное падение – движение равноускоренное. Ускорение свободного падения не зависит от массы тела. Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.
 Но как именно падают эти предметы – этот вопрос первобытных людей не занимал. Тем не менее нашлись люди, которые по мере возможностей начали исследовать это явление. Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв.
Но как именно падают эти предметы – этот вопрос первобытных людей не занимал. Тем не менее нашлись люди, которые по мере возможностей начали исследовать это явление. Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным.
Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
 Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня. Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня. Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
 С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью. Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:
С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью. Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:
 Так как для равноускоренного движения перемещение рассчитывается по формуле, то если взять три некоторые точки 1,2,3 через которые проходит тело при падении и записать: (ускорение при свободном падении для всех тел одинаково), получится, что отношение перемещений при равноускоренном движении равно:
Так как для равноускоренного движения перемещение рассчитывается по формуле, то если взять три некоторые точки 1,2,3 через которые проходит тело при падении и записать: (ускорение при свободном падении для всех тел одинаково), получится, что отношение перемещений при равноускоренном движении равно:
 2. Практическая значимость нахождения значения ускорения свободного падения
2. Практическая значимость нахождения значения ускорения свободного падения Рассматривая движение бруска вниз по наклонной плоскости, можно записать второй закон Ньютона в векторном виде:
Рассматривая движение бруска вниз по наклонной плоскости, можно записать второй закон Ньютона в векторном виде:


 При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника

 5. Экспериментальное определение ускорения свободного падения с помощью математического маятника
5. Экспериментальное определение ускорения свободного падения с помощью математического маятника




 Заключение
Заключение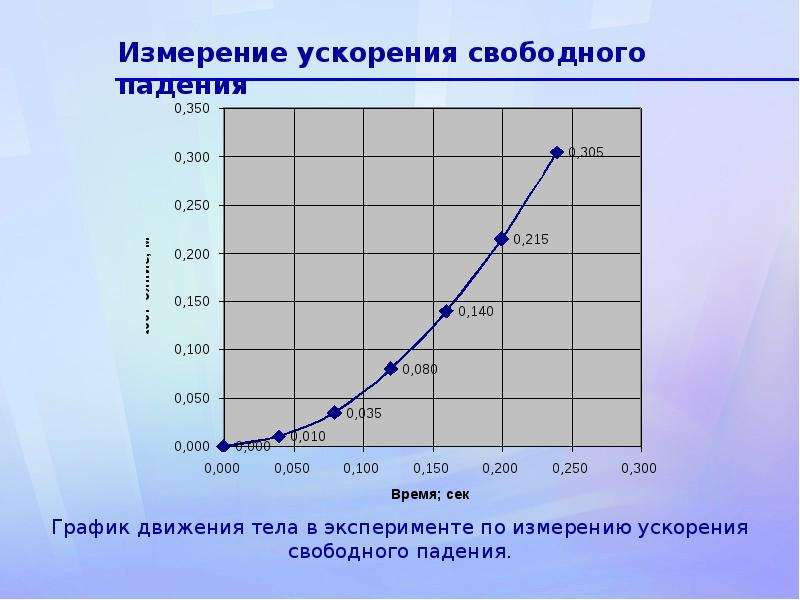 Экспериментально полученные значения хорошо это показывают.
Экспериментально полученные значения хорошо это показывают.
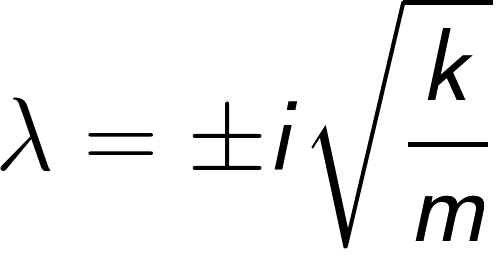 Для многих американцев единственный опыт разгона – это реклама автомобилей. Когда рекламный ролик кричит «от нуля до шестидесяти за шесть целых семь десятых секунды», они говорят, что этот автомобиль занимает шесть десятых секунды.7 с для достижения скорости 60 миль в час после полной остановки. Этот пример иллюстрирует ускорение в общепринятом понимании, но ускорение в физике – это гораздо больше, чем просто увеличение скорости.
Для многих американцев единственный опыт разгона – это реклама автомобилей. Когда рекламный ролик кричит «от нуля до шестидесяти за шесть целых семь десятых секунды», они говорят, что этот автомобиль занимает шесть десятых секунды.7 с для достижения скорости 60 миль в час после полной остановки. Этот пример иллюстрирует ускорение в общепринятом понимании, но ускорение в физике – это гораздо больше, чем просто увеличение скорости. Таким образом, падающее яблоко ускоряется, машина, остановившаяся на светофоре, ускоряется, а Луна на орбите вокруг Земли ускоряется. Ускорение происходит каждый раз, когда скорость объекта увеличивается или уменьшается, или он меняет направление.
Таким образом, падающее яблоко ускоряется, машина, остановившаяся на светофоре, ускоряется, а Луна на орбите вокруг Земли ускоряется. Ускорение происходит каждый раз, когда скорость объекта увеличивается или уменьшается, или он меняет направление. Слово «короткий» в этом контексте означает бесконечно малое или бесконечно малое – не имеющее вообще никакой продолжительности или протяженности.Это математический идеал, который может быть реализован только как предел. Предел ставки, когда знаменатель приближается к нулю, называется производной . Таким образом, мгновенное ускорение является пределом среднего ускорения, когда временной интервал приближается к нулю, или, альтернативно, ускорение является производной скорости.
Слово «короткий» в этом контексте означает бесконечно малое или бесконечно малое – не имеющее вообще никакой продолжительности или протяженности.Это математический идеал, который может быть реализован только как предел. Предел ставки, когда знаменатель приближается к нулю, называется производной . Таким образом, мгновенное ускорение является пределом среднего ускорения, когда временной интервал приближается к нулю, или, альтернативно, ускорение является производной скорости. Выполнение этого дважды (производная от производной) дает вам , вторую производную . Это делает ускорение первой производной скорости по времени и второй производной позиции по времени.
Выполнение этого дважды (производная от производной) дает вам , вторую производную . Это делает ускорение первой производной скорости по времени и второй производной позиции по времени. )
) Все ощущается нормально при 1 г, вдвое тяжелее при 2 г и невесомым при 0 г. Эта единица имеет точно определенное значение 9,80665 м / с 2 , но для повседневного использования достаточно 9,8 м / с 2 , а 10 м / с 2 удобно для быстрой оценки.
Все ощущается нормально при 1 г, вдвое тяжелее при 2 г и невесомым при 0 г. Эта единица имеет точно определенное значение 9,80665 м / с 2 , но для повседневного использования достаточно 9,8 м / с 2 , а 10 м / с 2 удобно для быстрой оценки. Большинство американских горок редко превышают 30 м / с (60 миль в час). Вопреки распространенному мнению, именно ускорение делает поездку интересной. Хорошо спроектированные американские горки подвергают гонщика кратковременным максимальным ускорениям от 3 до 4 g. Это то, что придает поездке ощущение опасности.
Большинство американских горок редко превышают 30 м / с (60 миль в час). Вопреки распространенному мнению, именно ускорение делает поездку интересной. Хорошо спроектированные американские горки подвергают гонщика кратковременным максимальным ускорениям от 3 до 4 g. Это то, что придает поездке ощущение опасности.
 По историческим причинам предпочтительной единицей в этой области является сантиметр на секунду в квадрате, также известный как галлонов . В символической форме…
По историческим причинам предпочтительной единицей в этой области является сантиметр на секунду в квадрате, также известный как галлонов . В символической форме…
 3–0,5
3–0,5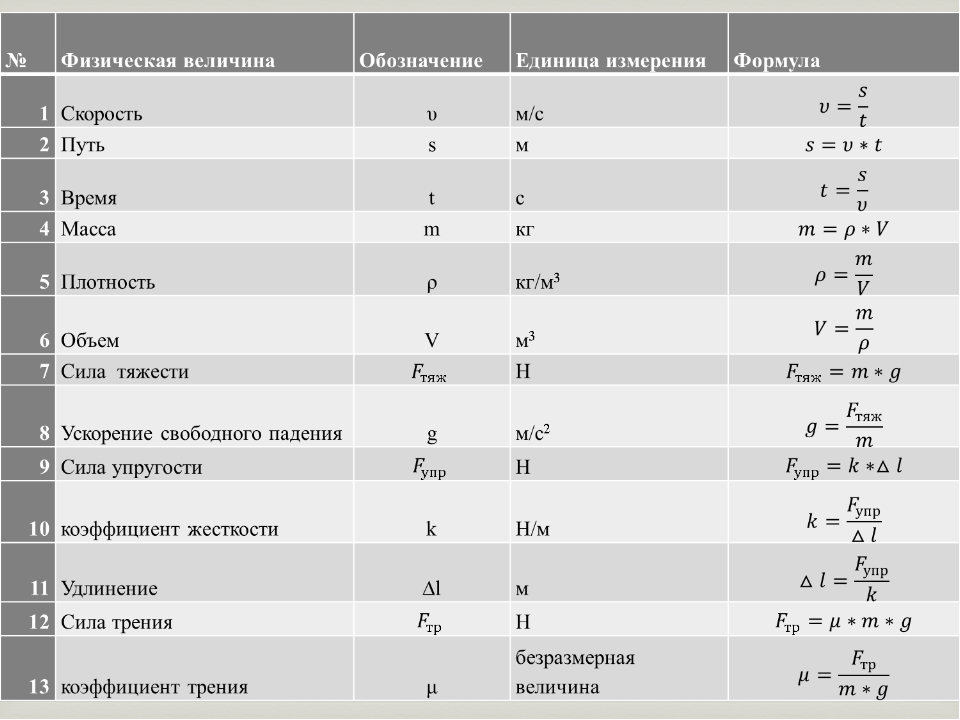
 8 м / с – 0 м / с
8 м / с – 0 м / с Все остальное алгебра сделает за нас.
Все остальное алгебра сделает за нас. 6 с
6 с Когда векторная величина отрицательна, что это значит? Есть несколько интерпретаций этого, но я думаю, что моя лучшая. Когда вектор имеет отрицательное значение, это означает, что он указывает в направлении, противоположном направлению положительных векторов.В этой задаче, поскольку предполагается, что положительные векторы направлены вперед (в каком другом направлении будет двигаться нормальный автомобиль?), Ускорение должно быть обратным. Таким образом, полный ответ на эту проблему состоит в том, что ускорение автомобиля составляет…
Когда векторная величина отрицательна, что это значит? Есть несколько интерпретаций этого, но я думаю, что моя лучшая. Когда вектор имеет отрицательное значение, это означает, что он указывает в направлении, противоположном направлению положительных векторов.В этой задаче, поскольку предполагается, что положительные векторы направлены вперед (в каком другом направлении будет двигаться нормальный автомобиль?), Ускорение должно быть обратным. Таким образом, полный ответ на эту проблему состоит в том, что ускорение автомобиля составляет…