| 1. |
Меры длины. Задача
Сложность: лёгкое |
2 |
| 2. |
Единицы времени
Сложность: лёгкое |
4 |
3.
|
Интервал времени
Сложность: лёгкое |
2 |
| 4. |
Преобразование единиц длины
Сложность: среднее |
4 |
5.
|
Меры длины
Сложность: среднее |
4 |
| 6. |
Преобразование миллиметров в другие меры длины
Сложность: среднее |
4 |
7.
|
Меры площади
Сложность: среднее |
3 |
| 8. |
Из аров в другие меры площади
Сложность: среднее |
5 |
9.
|
Округление десятичных долей
Сложность: среднее |
1 |
| 10. |
Округление мер
Сложность: среднее |
3 |
11.
|
Интервал времени
Сложность: среднее |
2 |
| 12. |
Високосный год
Сложность: среднее |
1 |
13.
|
Меры времени
Сложность: среднее |
1 |
| 14. |
Измерение времени
Сложность: среднее |
2 |
| Fluke
Talk to a Fluke sales expert
Связаться с Fluke по вопросам обслуживания, технической поддержки и другим вопросам»What is your favorite color?
Имя *
Фамилия *
Электронная почта *
FörКомпанияetag *
Номер телефона *
Страна * – Пожалуйста, выберите значение -United States (Estados Unidos)CanadaAfghanistanAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarticaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAzerbaijanBahamasBahrainBangladeshBarbadosБеларусь (Belarus)Belgien/Belgique (Belgium)BelizeBeninBermudaBhutanBoliviaBonaireBosnia and HerzegovinaBouvet IslandBotswanaBrasil (Brazil)British Indian Ocean TerritoryBrunei DarussalamBulgariaBurkina FasoBurundiCambodiaCameroonCape VerdeCayman IslandsCentral African RepublicČeská republika (Czech Republic)ChadChile中国 (China)Christmas IslandCittà Di VaticanCocos (Keeling) IslandsCook IslandsColombiaComorosCongoThe Democratic Republic of CongoCosta RicaCroatiaCyprusCôte D’IvoireDanmark (Denmark)Deutschland (Germany)DjiboutiDominicaEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEspaña (Spain)EstoniaEthiopiaFaroese FøroyarFijiFranceFrench Southern TerritoriesFrench GuianaGabonGambiaGeorgiaGhanaGilbralterGreeceGreenlandGrenadaGuatemalaGuadeloupeGuam (USA)GuineaGuinea-BissauGuyanaHaitiHeard Island and McDonald IslandsHondurasHong KongHungaryIcelandIndiaIndonesiaIraqIrelandIsraelIslas MalvinasItalia (Italy)Jamaica日本 (Japan)JordanKazakhstanKenyaKiribati대한민국 (Korea Republic of)KuwaitKyrgyzstanLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMéxico (Mexico)MicronesiaMoldovaMonacoMongoliaMontenegroMonserratMoroccoMozambiqueMyanmarNamibiaNauruNederland (Netherlands)Netherlands AntillesNepalNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorge (Norway)Norfolk IslandNorthern Mariana IslandsOmanÖsterreich (Austria)PakistanPalauPalestinePanamaPapua New GuineaParaguayPerú (Peru)PhilippinesPitcairn IslandPuerto RicoРоссия (Russia)Polska (Poland)Polynesia (French)PortugalQatarRepública Dominicana (Dominican Republic)RéunionRomânia (Romania)RwandaSaint HelenaSaint Pierre and MiquelonSaint Kitts and NevisSaint LuciaSaint Vincent and The GrenadinesSan MarinoSao Tome and PrincipeSaudi ArabiaSchweiz (Switzerland)SenegalSerbiaSeychellesSierra LeoneSingaporeSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia and The South Sandwich IslandsSouth SudanSri LankaSudanSuomi (Finland)SurinameSvalbard and Jan MayenSverige (Sweden)SwazilandTaiwanTajikistanTanzaniaThailandTimor-LesteTokelauTogoTongaTrinidad and TobagoTunisiaTürkiye (Turkey)TurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUnited KingdomUnited States Minor Outlying IslandsUruguayUzbekistanVanuatuVirgin Islands (British)Virgin Islands (USA)VenezuelaVietnamWallis and FutunaWestern SaharaWestern SamoaYemenZambiaZimbabwe
Почтовый индекс *
Интересующие приборы
iGLastMSCRMCampaignID
?Отмечая галочкой этот пункт, я даю свое согласие на получение маркетинговых материалов и специальных предложений по электронной почте от Fluke Electronics Corporation, действующей от лица компании Fluke Industrial или ее партнеров в соответствии с политикой конфиденциальности.
consentLanguage
Политика конфиденциальностиЭлектрическая емкость: определение, формулы, единицы измерения
В электротехнике часто встречается понятие ёмкости. При этом речь идёт не о ведре или другом сосуде, а об электрической ёмкости проводника, аккумулятора и конденсатора. Путать эти понятия нельзя. В этой статье мы разберемся, что такое электрическая ёмкость, от чего она зависит и в каких единицах измеряется.
Определение
Для проводников электрической ёмкостью называется величина, которая характеризует способность тела накапливать электрический заряд. Это и есть её физический смысл. Обозначается латинской буквой C. Она равна отношению заряда к потенциалу, если это записать в виде формулы, то получается следующее:
C=q/Ф
Электроемкость любого предмета зависит от его формы и геометрических размеров. Если рассмотреть проводник в форме шара, в качестве примера, то формула для расчета её величины будет иметь вид:
Эта формула справедлива для уединенного проводника.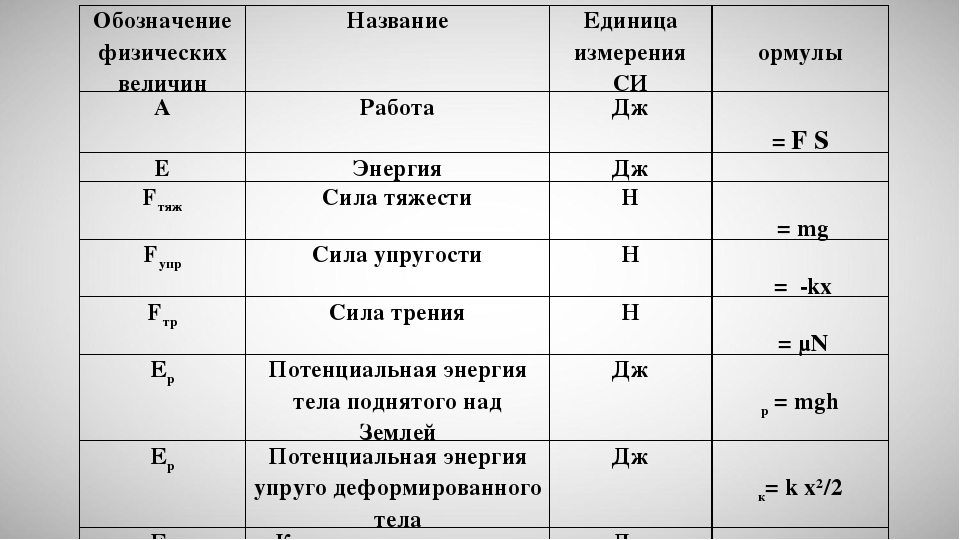 (-12) Ф
(-12) Ф
Конденсаторы
Конденсатор — это две пластины из проводящего материала, расположенные друг напротив друга, между которым находится слой диэлектрика. В заряженном состоянии обкладки имеют разные потенциалы: одна из них будет положительной, а вторая отрицательной. Электроемкость конденсатора зависит от величины заряда на его обкладках и разности потенциалов, напряжения между ними. Между пластинами возникает электростатическое поле, которое удерживает заряды на обкладках. Формула электрической емкости конденсатора в общем случае:
C=q/U
Если сказать простыми словами, то емкость конденсатора зависит от площади пластин и расстояния между ними, а также относительной диэлектрической проницаемости материала, расположенного между ними. Их различают по используемому диэлектрику:
- керамические;
- плёночные;
- слюдяные;
- металлобумажные;
- электролитические;
- танталовые и пр.
По форме обкладок:
- плоские;
- цилиндрические;
- сферические и пр.

Так как формула площади фигуры зависит от её формы, то и формула ёмкости будет разной для каждого случая.
Для плоского конденсатора:
Для двух концентрических сфер с общим центром:
Для цилиндрического конденсатора:
Как и у других элементов электрической цепи и в этом случае есть два основных способа соединения конденсаторов: параллельное и последовательное.
От этого зависит итоговая электрическая емкость полученной цепи. Расчёты ёмкости нескольких конденсаторов напоминают расчёты сопротивления резисторов в разном включении, только формулы для способов соединения расположены наоборот, то есть:
- При параллельном соединении общая электроемкость цепи является суммой емкостей каждого из элементов. Каждый следующий подключенный увеличивает итоговую емкость
Cобщ=C1+C2+C3
- При последовательном подключении электроемкость цепи снижается, подобно снижение сопротивления в цепи параллельно включённых резисторов.
 То есть:
То есть:
Cобщ=(1/С1)+ (1/С2)+ (1/С3)
Важно! В параллельной схеме соединения напряжения на обкладках каждого элемента одинаковы. Это используют для получения больших значений электроемкости. В последовательном включении двух элементов напряжения на обкладках каждого из конденсаторов составляют по половине общего напряжения. Для трёх – трети и так далее.
Аккумуляторы и электроемкость
Основными характеристиками аккумуляторных батарей является:
- Номинальное напряжение.
- Емкость.
- Максимальный ток разряда.
В данном случае для определения количественной характеристики времени работы или, говоря простым языком, чтобы рассчитать, на какое время работы прибора хватит аккумулятора, используют величину ёмкости.
В аккумуляторных батареях для описания электрической ёмкости используют следующие размерности:
- А*ч — ампер-часы для больших аккумуляторов, например автомобильных.

- мА*ч — милиампер-часы, для аккумуляторов для носимых устройств, например смартфонов, квадрокопетров и электронных сигарет.
- Вт*часы — ватт-часы.
Эти характеристики позволяют определить, сколько времени работы выдержит аккумулятор при конкретной нагрузке. Для определения электрическую емкость аккумулятора измеряют в кулонах (Кл). В свою очередь кулон равен количеству электричества, переданному аккумулятору при силе тока 1А за 1с. Тогда если перевести в часы, то при токе в 1А за 1 час передается 3600 Кл.
Одним из способов измерения емкости аккумулятора является его разряд заведомо известным током, при этом вы должны замерить время разряда. Допустим, если аккумулятор разрядился до минимального уровня напряжения за 10 часов током в 5А – значит его емкость 50 А*ч
Электроемкость – это важная величина в электронике и электротехнике. На практике конденсаторы применяются практически в каждой схеме электронного устройства. Например, в блоках питания – для сглаживания пульсаций, уменьшения влияния высоковольтных всплесков на силовые ключи. Во времязадающих цепях различных схем, а также в ШИМ-контроллерах для того, чтобы задать рабочую частоту. Аккумуляторы также применяются повсеместно. Вообще задачи накапливания энергии и сдвига фаз встречаются очень часто.
Во времязадающих цепях различных схем, а также в ШИМ-контроллерах для того, чтобы задать рабочую частоту. Аккумуляторы также применяются повсеместно. Вообще задачи накапливания энергии и сдвига фаз встречаются очень часто.
Более подробно изучить вопрос поможет предоставленное видео:
Кратко объяснение изложено в этом видео уроке:
Теперь вы знаете, что такое электрическая емкость, в каких единицах происходит ее измерение и от чего зависит данная величина. Надеемся, предоставленная информация была для вас полезной и понятной!
Материалы по теме:
Единицы измерения нужно знать в лицо
СИ (Система Интернациональная) – международная система измерений различных величин. СИ самая широко используемая система единиц в мире. Данная система принята XI Генеральной конференцией по мерам и весам в 1960 году и до сих пор является основной системой единиц в большинстве стран мира.
Данная система принята XI Генеральной конференцией по мерам и весам в 1960 году и до сих пор является основной системой единиц в большинстве стран мира.
СИ определяет семь основных единиц, которые нельзя получить алгебраическими действиями из других единиц, их можно только измерить. Это метр, секунда, килограмм, ампер, моль, кандела и кельвин. Остальные единицы – производные.
Многие единицы названы именами известных учёных. Например, единица измерения электрического тока Ампер названа в честь французского физика Андре Ампера, исследовавшего магнитное поле, электрический ток. Основные работы учёного выполнены в области электродинамики. Хорошо известен закон Ампера и правило Ампера.
Единица и измерения температуры Кельвин была предложена в 1848 году. Названа она именем британского физика Уильяма Томсона (барона Кельвина), который проводил исследования в таких областях, как термодинамика и термоэлектричество. Учёный изобрёл и улучшил многие приборы: гальванометр, ондулятор, электрометры (квадратный и абсолютный), нормальный элемент компаса, ампер – весы.
Учёный изобрёл и улучшил многие приборы: гальванометр, ондулятор, электрометры (квадратный и абсолютный), нормальный элемент компаса, ампер – весы.
Английский физик Исаак Ньютон открыл законы движения. Несмотря на то, что в своих работах учёный не вводил единиц измерения силы и рассматривал её, как абстрактное явление, с момента принятия системы СИ единица измерения силы стала называться Ньютон.
В 1960 году было принято решение заменить единицу измерения частоты периодических процессов с числа циклов в секунду на Герц. Единица названа в честь немецкого физика Генриха Герца, который внёс неоценимый вклад в развитие электродинамики.
Работу и энергию электрического тока измеряют Джоулями. Джоуль был введён на Втором международном конгрессе электриков, который проходил в 1889 году, в этом году умер Джеймс Джоуль.
Ватт является единицей измерения мощности. Единица названа в честь шотландско-ирландского изобретателя-механика Джеймса Уатта (Ватта), который изобрёл и создал универсальную паровую машину. До 1889 года для расчётов использовались лошадиные силы, которые ввёл сам Джеймс Уатт.
Единица названа в честь шотландско-ирландского изобретателя-механика Джеймса Уатта (Ватта), который изобрёл и создал универсальную паровую машину. До 1889 года для расчётов использовались лошадиные силы, которые ввёл сам Джеймс Уатт.
Единица измерения давления – Паскаль. Французский физик и математик Блез Паскаль – создатель первых образцов счётной техники, автор основного закона гидростатики.
Единица измерения электрического заряда – Куло́н названа в честь французского физика и инженера Шарля Кулона, который занимался исследованием электромагнитных и механических явлений. Его именем назван также закон взаимодействия электрических зарядов.
Вольт – единица измерения электрического потенциала, электрического напряжения и электродвижущей силы. Единица названа в честь итальянского физика и физиолога Алессандро Вольта, который изобрёл первую электрическую батарею и вольтов столб.
Единица измерения электрического сопротивления – Ом названа в честь немецкого учёного Георга Симона Ома, который длительное время исследовал вопрос о прохождении электрического тока. Открытия Ома дали возможность количественно рассмотреть электрический ток. Огромное значение для науки имеет и знаменитый закон Ома.
Фарад – единица измерения электрической ёмкости названа в честь английского физика и химика Майкла Фарадея, который является основоположником учения о ядерном поле. С именем ученого связано и открытие нержавеющей стали.
Единица измерения магнитного потока – Ве́бер носит имя немецкого учёного Вильгельма Эдуарда Вебера, впервые определившего скорость распространения электромагнитной индукции в воздухе.
Именем инженера и изобретателя в области электротехники и радиотехники Николы Те́сла названа единица измерения индукции магнитного поля – Тесла. НиколаТе́славнёс огромный вклад в изучение свойств магнетизма и электричества.
НиколаТе́славнёс огромный вклад в изучение свойств магнетизма и электричества.
Ге́нри – единица измерения индуктивности названа в честь американского учёного Джозефа Генри, который открыл самоиндукцию – новое явление в электромагнетизме.
Си́менс – единица измерения электрической проводимости названа в честь немецкого учёного Вернера фон Сименса (основатель фирмы Siemens). Серьёзно занимался электротелеграфией, точной механикой и оптикой, а также созданием электромедицинских аппаратов. Ввёл в обиход термин «электротехника».
Единица измерения активности радиоактивного источника – Беккерель названа в честь французского учёного, лауреата Нобелевской премии по физике Антуана Анри Беккереля, который стал одним из первооткрывателей радиоактивности.
Британский учёный Льюис Грей, изучавший воздействие радиации на биологические организмы, в 1975 году определил поглощённую дозу радиации, единица измерения которой была названа в его честь – Грэй.
В честь шведского учёного Рольфа Зиверта, который изучал воздействие радиационного излучения на биологические организмы, названа единица измерения эффективной и эквивалентной доз ионизирующего излучения – Зиверт.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Измерение физических величин. Точность и погрешность измерений. 7 класс
Измерение физических величин. Точность и погрешность измерений. 7 класс
- Подробности
- Просмотров: 356
При изучений физических явлений проводят различные измерения.
Физики измеряют физические величины.
Например:
При изучении падение тела, надо измерить высоту, с которой падает тело, массу тела, его скорость и время падения.
Чтобы узнать, например, зависит ли объем воды или другой жидкости от ее температуры и как зависит, нужно, нагревая воду, измерять и объем, и температуру.
Объем и температура, время и длина, площадь, скорость, масса, сила — это физические величины.
1. Что значит измерить?
Измерить какую-либо физическую величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины.
Например:
Измерить длину стола — значит сравнить ее с другой длиной, которая принята за единицу длины, например с метром.
В результате измерения величины получаем ее числовое значение, выраженное в принятых единицах.
2. Какие бывают единицы имерения?
Для каждой физической величины приняты свои единицы измерения.
Очень удобно пользоваться одинаковыми единицами физических величин во всех странах мира.
Поэтому с 1963 г. применяется Международная система единиц — СИ (система интернациональная).
единица длины — 1 метр (1м),
единица времени — 1 секунда (1с),
единица массы — 1 килограмм (1 кг).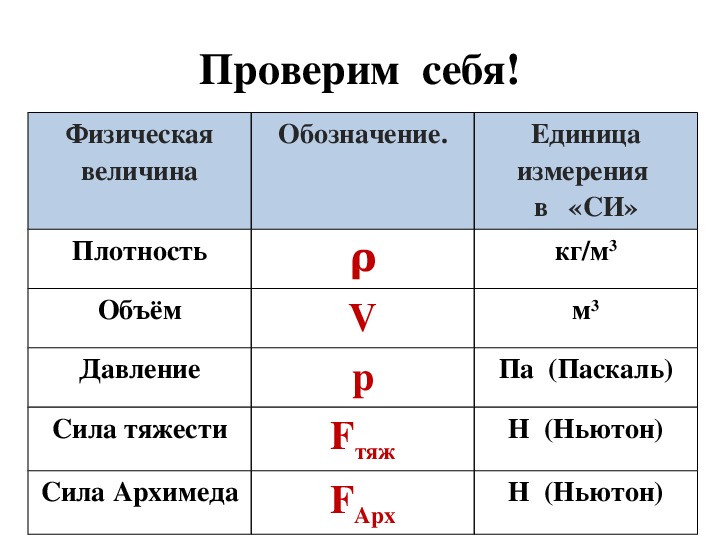
Кроме того, используются кратные единицы (кратные основной единице), которые в 10, 100, 1000 и т. д. раз больше.
Эти единицы получили наименования с приставками, взятыми из греческого языка.
«Дека» — 10, «гекто» — 100, «кило» — 1000 и др.
Используются и дольные единицы, которые в 10, 100, 1000 и т. д. раз меньше принятых единиц величин.
В них применяют приставки, также взятые из латинского языка. «Деци» — 0,1, «санти» — 0,01, «милли» — 0,001 и др.
Некоторые приставки к названиям единиц:
г — гекто (100 или 102)
к — кило (1000 или 103)
М — мега (1 000 000 или 106)
д — деци (0,1 или 10-1)
с — санти (0,01 или 10-2)
м — милли (0,001 или 10-3)
Например:
Длина столовой ложки 20 см.
Ее длина в метрах (м):
20 см = 0,20 м или 2 • 10-1 м.
3. Что такое измерителный прибор?
Что такое измерителный прибор?
Для измерения физических величин нужны измерителные приборы.
Есть измерителные приборы для простых измерений. Например, измерительная линейка, рулетка, мензурка, применяемая для измерения объема жидкости.
Есть сложные измерительные приборы: секундомеры, термометры и другие.
По мере развития физики и техники приборы усложнялись и появились, например, приборы, при помощи которых изучают строение вещества.
У измерительных приборов есть измерительная шкала, на которой штрихами нанесены деления и написаны значения величин.
Между двумя большими штрихами могут быть дополнительно нанесены несколько делений, не обозначенных числами.
Значение измеряемой величины между ближайшими штрихами называется ценой деления прибора.
Например, у обычной школьной линейки расстояние между двумя ближайшими штрихами составляет 1 мм, это цена деления линейки.
4. Как определить цену деления измерительной шкалы прибора?
Прежде чем использовать измерительный прибор, надо определить цену деления этого прибора.
Надо установить, какому значению величины соответствует каждое самое малое деление.
Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.
5. Примеры определения цены деления
а) Определение цены деления секундомера.
Используем любые два штриха, около которых нанесены значения измеряемой величины (времени), например штрихи с обозначениями 5 и 10 с.
Расстояние между этими штрихами разделено на 10 делений. Значит, цена каждого деления равна:
Секундомер показывает 22 с.
б) Определение цены деления термометра.
Возьмем, например, ближайшие друг к другу штрихи с обозначениями 10 °С и 20 °С. Расстояния между ними разделены на 10 делений. Следовательно,
цена каждого деления будет равна: 20 °С – 10 °С = 10 °С, далее 10 °С : 10 = 1 °С.
Термометр показывает 24 °С.
6.
Что такое точность и погрешность измерений?
Любое измерение может быть выполнено с большей или меньшей точностью.
В физике допускаемую при измерении неточность называют погрешностью измерения.
Погрешность измерения не может быть больше цены деления измерительного прибора.
Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.
Чем меньше цена деления, тем больше точность измерения.
При измерении принято считать, что: погрешность измерений равна половине цены деления шкалы измерительного прибора.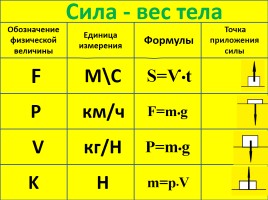
При записи величин, с учетом погрешности, пользуются формулой:
где А — измеряемая величина,
а — результат измерений,
дельта а — погрешность измерений (треуголник — греч. буква «дельта»).
Например:
Если длина книги 20 см, а цена деления линейки 1 мм, то погрешность измерения будет равна 0,5 мм, или 0,05 см.
Следовательно, длину книги можно записать так:
L = (20 ±0,05) см,
где L — длина книги.
Истинное значение длины книги находится в интервале от 19,95 см до 20,05 см.
Главное:
Измерить какую-либо величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины.
Основные единицы системы СИ: метр, килограмм, секунда.
Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.
Следующая страница – смотреть
Назад в “Оглавление” – смотреть
| Длина |
| 1 см = 10 мм = 0,01 м |
| 1 дм = 10 см = 0,1 м |
| 1 м = 100 см = 10 дм |
| 1 км = 1000 м |
| 1 дюйм (inch) = 2.54 см |
| 1 фут (foot) = 12 дюймов = 30,48 см = 0,3048 м |
| 1 ярд (yard)= 3 фута = 91,44 см = 0,9144 м |
| 1 миля (mile) = 5280 футов = 1609,34 м = 1,609 км |
| 1 морская миля (nautical mile) =1,852 км |
| 1 м = 3,28 фута = 1,094 ярда = 0,00062 мили |
| 1 см = 0,393 дюйма |
| Площадь |
| 1 см2 = 100 мм2 |
| 1 дм2 = 100 см2 = 0,01 м2 |
| 1 м2 = 100 дм2 |
| 1 км2 = 1 000 000 м2 |
| 1 ар (1 а) = 100 м2 = 1 сотка |
| 1 гектар (1 га) = 10 000 м2 |
1 кв. дюйм (square inch) = 6,4516 см2 дюйм (square inch) = 6,4516 см2 |
| 1 кв. фут (square foot) = 144 кв. дюймам = 929,03 см2 |
| 1 кв. ярд (square yard) = 9 кв. футам = 0,83613 м2 |
| 1 акр (acre) = 4046,86 м2 |
| 1 кв. миля (square mile) = 640 акрам = 2,59 км2 |
| 1 м2 = 10,76 кв. футов = 1,196 кв. ярдов |
| 1 см2 = 0,155 кв. дюймов |
| Объем |
| 1 см3 = 0,001 дм3 = 0,001 л |
| 1 литр = 1 дм3 = 61,03 куб. дюйм = 0,22 галлона |
| 1 куб. дюйм = 16,387 см3 = 0,016 л |
1 куб. фут = 28316,8 см3 =28,316 л фут = 28316,8 см3 =28,316 л |
| 1 куб. ярд = 764555 см3 = 764,555 л |
| 1 пинта англ. = 0,568 л |
| 1 пинта амер. = 0,473 л |
| 1 галлон англ. = 4,54 л |
| 1 галлон амер. = 3,78 л |
| 1 баррель нефти =42 галлона = 158,988 л = 0,136 тонн |
| Вес |
| 1 кг = 1000 г |
| 1 ц = 100 кг = 0,1 т |
| 1 т = 1000 кг = 10 ц |
| 1 фунт = 453,6 г = 0,4536 кг |
| 1 унция = 1/16 фунта = 28,35 г |
| 1 г = 0,035 унций = 0,002205 фунтов |
| 1 кг = 2,2 фунта |
| Тройская система мер для благородных металлов и драгоценных камней |
| 1 гран = 64,8 мг |
| 1 карат = 3,086 грана = 0,2 г |
1 тройская унция = 31,10 г = 1/12 тр. фунта = 480 гран фунта = 480 гран |
| 1 тройский фунт = 373,24 г |
| Температура |
| 40°С = 104 F; 0°С= 32 F |
| F = (°C *1.8)+32 |
| °C = (F — 32)/1,8 |
| Разница температур в 1 °C эквивалентна разнице температур в 1,8 F |
Что такое сила и как ее измерить?
Определения силы:
1) Сила — это толчок или тяга
2) Сила – это способность выполнять работу или вызывать физические изменения
3) Сила = Масса, умноженная на ускорение (F = ma)
4) Сила – это то, что изменяет или стремится изменить состояние покоя или движения тела.
Примеры:
Для простоты все силы (взаимодействия) между объектами можно разделить на две широкие категории: контактные силы и силы, возникающие в результате действия на расстоянии.
Контактные силы включают: силы трения, выталкивающие силы, нормальные силы и силы сопротивления воздуха
Силы действия на расстоянии включают гравитационные, электростатические и магнитные силы.
Измерительное усилие:
Сила измеряется с использованием либо Английской системы измерений, либо Международной системы единиц (СИ).
Общие единицы силы
—>> СИ : Ньютон (Н) 1 Н = 0.225 фунтов;
Сила в один ньютон (Н) определяется как сила, необходимая для ускорения 1 килограмма (кг) массы со скоростью 1 метр в секунду в квадрате (м/с2).
1 Ньютон = 1 кг м/с2 (Килограмм — это вес, при котором сила 1 Н ускоряет скорость 1 м/с2.)
—>> Английская система : фунт (фунт) 1 фунт = 4,448 Н
В английской системе измерений слаг — это количество массы, которое 1 фунт силы ускоряет со скоростью 1 фут/с2, а фунт массы — это количество массы, которое 1 фунт силы ускоряет со скоростью 32 фута/с2.
Описание силы:
Сила является векторной величиной. Векторная величина – это величина, которая имеет как величину, так и направление. Чтобы полностью описать силу, действующую на объект, вы должны описать как ее величину, так и направление. Таким образом, сила в 10 ньютонов не является полным описанием силы, действующей на объект. 10 ньютонов вниз — это полное описание силы, действующей на объект.
(Примечание. В чем разница между векторными и скалярными величинами? Вектор имеет как силу, так и направление, скалярную величину можно описать, используя только одну величину — величину.Примерами скалярных величин являются: время, энергия и объем, поскольку они представляют только величину, а не направление.
В чем разница между массой и весом?
Ниже показаны два типа весов, обычно используемых в классе: пружинные весы (слева) и простые весы с бревном справа.
На Земле пружинные весы показывают 100 г, а внизу прикреплена неизвестная масса. Чтобы уравновесить весы справа, также понадобилась 100-граммовая масса.
Чтобы уравновесить весы справа, также понадобилась 100-граммовая масса.
Если бы мы взяли обе шкалы на Луну, что бы показывали весенние шкалы? Какая масса потребуется, чтобы уравновесить груз массой 100 г на бревне? Можете ли вы объяснить свой ответ? Дополнительные сведения см. на странице “Масса и вес”.
Что делает приложение Силы? Сила вызывает ускорение. Второй закон Ньютона гласит: ускорение (a) объекта прямо пропорционально приложенной силе (F) и обратно пропорционально массе объекта (m). Что такое трение? Трение – это сила, противодействующая относительному движению или стремлению к такому движению двух соприкасающихся тел. Если мы пытаемся толкнуть деревянный брусок по столу, действуют две противодействующие силы: сила, связанная с толчком, и сила, связанная с трением, которое действует в противоположном направлении. По мере того как силы трения уменьшаются (например, при размещении масла на столе), объект движется все дальше и дальше, прежде чем остановиться.Это демонстрирует закон инерции Галилея, который гласит: объект в состоянии движения обладает «инерцией», которая заставляет его оставаться в этом состоянии движения, если на него не действует внешняя сила. Попробуйте это упражнение! Пожалуйста введите свой ответ в отведенное место:1) Какая полезная сила требуется для ускорения автомобиля массой 1500 кг со скоростью 6,00 м/с2? Пожалуйста, введите свой ответ в отведенное место: | |||||||
F. Процентная неопределенность :: Физика
Неопределенность измеренного значения также может быть представлена в процентах или в виде простого отношения.(относительная неопределенность). Процентная неопределенность знакома. Вычисляется как:
Неопределенность в процентах можно интерпретировать как описание неопределенности, которая возникла бы, если бы измеренное значение было равно 100 единицам. Аналогичной величиной является относительная неопределенность (или дробная неопределенность). Это проще вычислить и определяется как:
Относительная неопределенность может быть интерпретирована как описание неопределенности, которая возникла бы, если бы измеренное значение составляло всего одну единицу.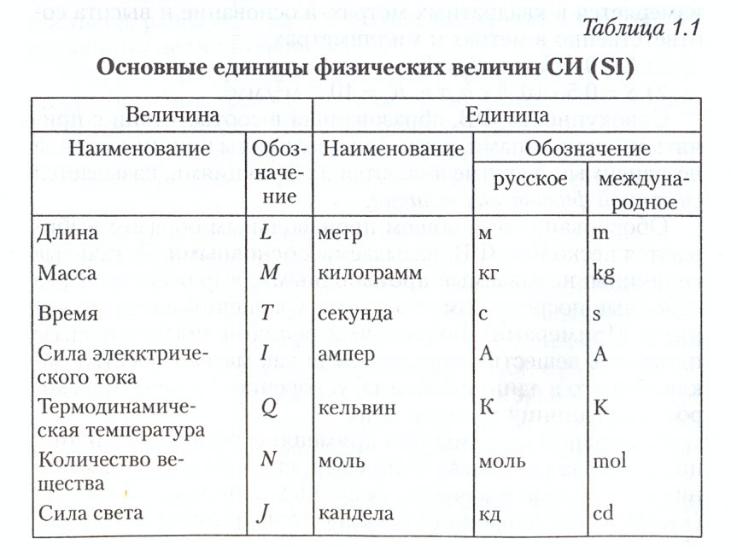 С этими двумя новыми репрезентациями неопределенности мы должны быть осторожны в устной и письменной речи, чтобы наша аудитория четко понимала, какое из них используется. Следующий список описывает допустимое использование.
С этими двумя новыми репрезентациями неопределенности мы должны быть осторожны в устной и письменной речи, чтобы наша аудитория четко понимала, какое из них используется. Следующий список описывает допустимое использование.
- Абсолютная неопределенность: это простая неопределенность самого значения, как мы обсуждали до сих пор. Этот термин используется, когда нам нужно отличить эту неопределенность от относительной или процентной неопределенности. Если нет возможности путаницы, мы все равно можем просто сказать «неопределенность», когда речь идет об абсолютной неопределенности.Абсолютная неопределенность имеет те же единицы измерения, что и значение. Таким образом, это: 3,8 см ± 0,1 см.
- Относительная неопределенность: это простое отношение неопределенности к сообщаемому значению. Как отношение подобных величин, относительная неопределенность не имеет единиц. На самом деле для относительной погрешности не существует специального символа или обозначения, поэтому вы должны четко указывать его, когда сообщаете об относительной погрешности.
 2,95 кг ± 0,043 (относительная погрешность)
2,95 кг ± 0,043 (относительная погрешность) - Процентная неопределенность: это просто относительная неопределенность, умноженная на 100.Поскольку процентная неопределенность также является отношением подобных величин, она также не имеет единиц измерения. К счастью, существует специальное обозначение для процентной неопределенности (%), так что ее будет легко распознать в письменной форме. 2,95 кг ± 4,3%
Обратите внимание, что допустимо указывать относительную и процентную неопределенности в двух цифрах. Это сделано для предотвращения ошибок округления, когда мы возвращаемся к абсолютной неопределенности.
Процентная неопределенность имеет большое значение при сравнении относительной точности различных измерений.Например, если мы ограничимся точностью 0,1 процента, мы будем знать длину метровой палки с точностью до 1 мм, моста длиной в 1000 метров с точностью до 1 метра, а расстояние до солнца (93 миллиона миль) с точностью до 93 000 миль. . Таким образом, при представлении результата измерения следует привести достаточное количество цифр, чтобы показать точность измерения, не больше и не меньше, и вдобавок следует указать AD или процентную неопределенность.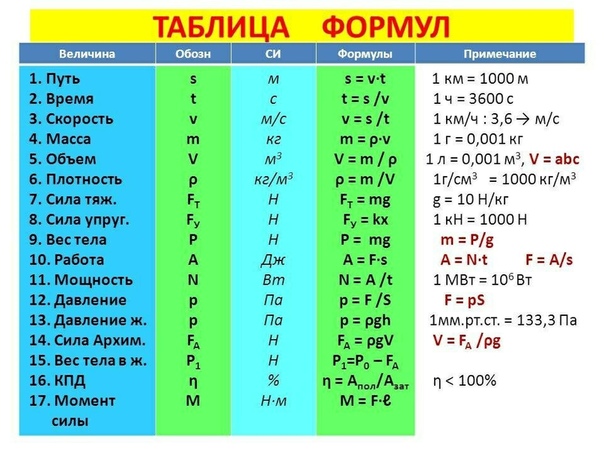 Для трех приведенных выше примеров следует написать:
Для трех приведенных выше примеров следует написать:
1.000 ± 0,001 метра (или 1,000 метра ± 0,1%)
1000 ± 1 метр (или 1000 метров ± 0,1%)
(93,00 ± 0,09) x 10 6 мили (или 93,00 x 10 6 мили ± 0,0, %)
Последнее обновление 19 ноября 2014 г.
Эксперимент Месяца | Университет Миллерсвилля
Текущий баланс XIX века с образцом промежуточного лабораторного отчета
В нашей промежуточной лаборатории в этом году мы заменили измерение текущими балансами на измерение с использованием лазеров с четырьмя различными длинами волн для определения постоянной Планка. С точки зрения истории физики мы перешли от эксперимента 19-го века к эксперименту 20-го века.
С точки зрения истории физики мы перешли от эксперимента 19-го века к эксперименту 20-го века.
Текущие весы — сентиментальный фаворит, демонстрирующий прямую связь между механическими силами Ньютона и электромагнитными силами Ампера и Максвелла. В этом выпуске мы отдаем дань уважения великому старому эксперименту на великом старом оборудовании.
На фотографии показаны балансы, а на приведенной ниже диаграмме показаны важные компоненты этого замечательно усовершенствованного инструмента.
Мы использовали текущий баланс, чтобы установить единицу силы тока, Ампер, сравнив магнитную силу (связанную с парой токов) с гравитационной силой (на измеренные массы). Два тока установлены в проводах, помеченных G (образный провод) и H (прямой провод) на чертеже. Важной частью провода G является та, которая проходит параллельно проводу H.
Чтобы не усложнять анализ, мы делаем оба тока одинаковыми, используя клеммы A, B, C и D на чертеже.Ток поступает на клемму A, огибает петлю G и вытекает на клемму B. Оттуда он течет по соединительному проводу к клемме C. От C течет по проводу H и возвращается к источнику питания через клемму D.
Оттуда он течет по соединительному проводу к клемме C. От C течет по проводу H и возвращается к источнику питания через клемму D.
В эксперименте между двумя проводами действует сила, и эта сила пропорциональна произведению двух токов (квадрат тока в нашем эксперименте). Говоря современным языком, сила создается магнитным полем одного провода (скажем, H) и током в другом проводе (скажем, G) и имеет величину F, определяемую уравнением
.{F}{2 p R} = m 0 i 2 L
, где R — межосевое расстояние между проводами, L — длина провода H, а
м 0 = 4p x 10 -7 {Ньютон}/{ампер 2 }
— произвольная константа, задающая шкалу измерения магнитных сил.
В уравнении силы после определения m 0 все можно измерить механически, кроме силы тока. Таким образом, это уравнение можно использовать для определения величины ампера, используя только механические измерения. Знание значения ампера, в свою очередь, приводит к знанию величины кулона на основе механических измерений.
В этом смысле текущий баланс является фундаментальным связующим звеном между механикой и электроникой. Когда через весы пропускают неизвестный ток, механические измерения определяют величину тока в амперах.Поскольку этот эксперимент выходит за рамки нашего вращения, он будет описан более подробно, чем обычно.
Текущие балансы построены по принципу старомодных балансировочных весов. Проволока G поддерживается двумя кромками ножа. (Нарисована только одна кромка лезвия, обозначенная J; другая находится рядом с клеммой B. При внимательном рассмотрении фотографии видны обе кромки лезвий.) Изолирующая перемычка соединяет кромки лезвий и поддерживает (в дополнение к проводу G) два одинаковых лезвия. гири (масса каждой здесь обозначена M), обозначенные буквами E и F.Сначала рассмотрим вес E.
E представляет собой пару гаек с накаткой большого диаметра, вращающихся на резьбовом стержне, прикрепленном к поперечной балке. Когда они находятся в желаемом положении вдоль резьбового стержня, они затягиваются друг относительно друга, чтобы зафиксировать их на месте. Целью E является уравновешивание проволоки G, а также стержня, который изгибается, чтобы поддерживать плоскую лопасть, обозначенную N.
Целью E является уравновешивание проволоки G, а также стержня, который изгибается, чтобы поддерживать плоскую лопасть, обозначенную N.
Во время работы провод G уравновешен в пределах нескольких миллиметров от провода H без подачи тока. Затем подается ток.Когда ток течет, как описано выше, направление силы между проводами толкает G вверх. Грузы (в виде отрезков медной проволоки) добавляют в лоток Т до тех пор, пока проволока Г не вернется в исходное положение. Измеряя массу балансировочных грузов, мы определяем магнитную силу для этого конкретного разделения проводов, R. По силе мы вычисляем ток в проводах.
Остальные компоненты работают, чтобы сделать измерения эффективными и точными.
Установочные винты в стойках C и D позволяют отрегулировать проволоку H так, чтобы она была параллельна соответствующему отрезку проволоки G.
Винты K и L соединяются со столом, на котором установлены весы, и служат для выравнивания весов.
Зеркало на балке (только фотография) используется для определения углового положения весов. Горизонтальный лазер падает на зеркало и отражается вверх из-за небольшого наклона зеркала, управляемого винтом за зеркалом.Расположение лазерного пятна на удаленном экране является хорошим индикатором для оценки возврата баланса в исходное положение после добавления гирь. Заметим, что если баланс изменяет угол на и величину @, то угол отражения светового луча изменяется на угол 2@
Горизонтальный лазер падает на зеркало и отражается вверх из-за небольшого наклона зеркала, управляемого винтом за зеркалом.Расположение лазерного пятна на удаленном экране является хорошим индикатором для оценки возврата баланса в исходное положение после добавления гирь. Заметим, что если баланс изменяет угол на и величину @, то угол отражения светового луча изменяется на угол 2@
На практике удобно поместить небольшой груз на лоток, который приводит баланс почти в состояние нулевого тока, и, наконец, отрегулировать ток как точную настройку нулевого баланса.
Гири F имеют ту же конструкцию, что и гири Е, но с другим назначением. В отсутствие грузов F при правильной установке грузов E балка находится в равновесии с центром масс несколько выше оси вращения. Если центр масс находится на той же высоте, что и лезвия ножа, или выше, баланс будет неустойчивым; небольшая угловая скорость будет продолжаться до тех пор, пока противовесы не сойдут с краев.
Гири F, расположенные на расстоянии D ниже оси вращения, перемещают центр масс ниже оси вращения с двумя целями:
- Они обеспечивают восстанавливающий крутящий момент, который приводит баланс в четко определенную точку равновесия.
 (Легче всего это представить, но не обязательно, если представить себе, что груз F находится прямо под центром масс в состоянии равновесия.) Уменьшение D уменьшает восстанавливающий крутящий момент и позволяет небольшому току вызывать большие изменения в равновесии. разделение проводов G и H. Удлинение D увеличивает восстанавливающий момент и делает баланс менее чувствительным к трению о кромки ножей.
(Легче всего это представить, но не обязательно, если представить себе, что груз F находится прямо под центром масс в состоянии равновесия.) Уменьшение D уменьшает восстанавливающий крутящий момент и позволяет небольшому току вызывать большие изменения в равновесии. разделение проводов G и H. Удлинение D увеличивает восстанавливающий момент и делает баланс менее чувствительным к трению о кромки ножей. - Расстояние D от F до оси вращения определяет собственную частоту колебаний баланса следующим образом: Обычные аргументы простого гармонического движения говорят нам, что квадрат угловой частоты равен моменту инерции I, деленному на по максимальному восстанавливающему моменту:
w 2 = (DMg)/{ I}
Момент инерции включает момент MD 2 из-за F, но преобладает момент I 0 из-за балки, E, G и лопасти в N.Эффект этого доминирования заключается в том, что сокращение D * снижает * частоту колебаний (в отличие от сокращения длины простого маятника).
Лопасть возле области N изготовлена из алюминия и свободно проходит между двумя магнитами, обращенными друг к другу так, что они создают максимальное магнитное поле в алюминии. Вихревые токи индуцируются движением алюминия через магнитное поле. Электрическое сопротивление алюминия потоку отнимает энергию от движения алюминия.То есть колебания маятника гасятся эффектом вихревых токов.
Ток через весы, определяемый по весу отрезков проволоки, такой же ток проходит через некалиброванный амперметр. Показание амперметра маркируется известным током. Ток изменяется, и процесс балансировки повторяется, что приводит к таблице калибровки амперметра. В конце амперметр калибруется с помощью силы тяжести.
Лабораторный отчет на основе текущего баланса
В качестве помощи нашим младшим физикам ниже приводится образец лабораторного отчета для промежуточной лаборатории, использующий текущие весы в качестве оборудования. Следующее не должно быть примером совершенства, но примером одного из форматов отчета, который работает.
Следующее не должно быть примером совершенства, но примером одного из форматов отчета, который работает.
Калибровка амперметра
Джон В. Дули
15 января 2003 г.
Аннотация
Калибровка амперметра проверена с помощью текущих весов. Текущий баланс измеряет ток, измеряя силу между двумя параллельными проводами, по которым течет этот ток. Он обеспечивает связь законов Ньютона и силы тяготения с Ампером, а значит, и с Кулоном.Наклон показаний амперметра в зависимости от измеренного тока должен быть равен 1. В нашем эксперименте он был равен 1,052 со стандартным отклонением наклона 0,009. Неопределенности в двух расстояниях, в 9 массах и в настройках балансировочного провода допускают возможность правильной калибровки амперметра.
Введение
Проект заключался в использовании токовых балансов для калибровки амперметра, оба поставляются вместе с низковольтным сильноточным источником питания. 20 поколений физиков, работавших до меня над этим проектом, помогли мне понять, как это сделать. Использовалась шкала 10 ампер на амперметре. Наименьшее деление составляет 0,1 ампер, и устройство имеет зеркальную шкалу для облегчения интерполяции.
Использовалась шкала 10 ампер на амперметре. Наименьшее деление составляет 0,1 ампер, и устройство имеет зеркальную шкалу для облегчения интерполяции.
Текущий баланс показан на рисунке справа. Этикетки будут использоваться в качестве ссылок при описании работы весов.
Источник питания подключен к контактам A и D. Ток протекает через острие J в U-образный провод, обозначенный G, и выходит через немаркированный острие рядом с контактом B. Внешний провод соединяет контакт B с контактом C, поэтому что тот же самый ток течет по нижнему проводу (обозначенному H), прежде чем вернуться к источнику питания на контакте D.
Крайний правый отрезок провода G подвешен над проводом H. При расположении токов, как указано выше, магнитное взаимодействие между G и H вызывает силу, которая наклоняет G (и его опорную балку) вверх, вращаясь на лезвиях ножей.
На этом рисунке не показано зеркало, установленное на стержне, который поддерживает элементы E и F. Лазер отражается от этого зеркала, а положение лазерного пятна на удаленной стене является индикатором угла баланса. К желобу добавляются небольшие массы T, чтобы вернуть лазерное пятно в положение нулевого тока (без грузов). Когда это сделано, расстояние между проводами остается таким же, как и без тока, а вес масс имеет ту же величину, что и сила между двумя проводами.
К желобу добавляются небольшие массы T, чтобы вернуть лазерное пятно в положение нулевого тока (без грузов). Когда это сделано, расстояние между проводами остается таким же, как и без тока, а вес масс имеет ту же величину, что и сила между двумя проводами.
Сила между двумя проводами обычно описывается в терминах магнитного взаимодействия. Однако для этой лаборатории все, что нам нужно знать, это выражение для силы F:
.{F}{2 p R} = m 0 i 2 L
, где R — межосевое расстояние между проводами, L — длина провода H, а
м 0 = 4p x 10 -7 {Ньютон}/{ампер 2 }
— произвольная константа, задающая шкалу измерения магнитных сил.
Все величины, кроме тока, могут быть измерены текущими весами, так что текущая величина может быть определена путем измерения весов.
Эксперимент
Баланс был выровнен с помощью пузырькового уровня на платформе путем регулировки винтовых ножек K и L. Поскольку баланс установлен на 4 ножках, для двух задних ножек требуются прокладки (коврик для мыши в одном случае и медная прокладка в другом). другое), чтобы выровнять платформу.
Поскольку баланс установлен на 4 ножках, для двух задних ножек требуются прокладки (коврик для мыши в одном случае и медная прокладка в другом). другое), чтобы выровнять платформу.
Два магнита (N) были установлены на расстоянии 2 мм друг от друга, так что алюминиевая лопасть двигалась между ними, не касаясь, когда весы изменяли угол.Вихревые токи, индуцируемые в движущейся лопасти магнитами, извлекали энергию из движущихся весов; лопасть действует как демпфер для простого гармонического движения баланса вокруг равновесия. При таком зазоре балансу потребовалось около 10 секунд, чтобы прийти в состояние покоя.
Пара гаек E перемещается по резьбовому стержню для регулировки баланса. E был установлен таким образом, чтобы (без тока) между G и H появился зазор в 1 мм (с погрешностью 0,2 мм). Оба провода были слегка согнуты, а H был отрегулирован по вертикали на стойке D так, чтобы два провода были параллельны внутри. .2мм. Когда гайки Е находятся в неправильном положении, их затягивают друг против друга, чтобы они не сдвинулись во время эксперимента. Диаметр каждой проволоки, G и H, составлял 3 мм (с погрешностью 0,2 мм), так что межцентровое расстояние между проволоками составляло
Диаметр каждой проволоки, G и H, составлял 3 мм (с погрешностью 0,2 мм), так что межцентровое расстояние между проволоками составляло
R = 4 мм с погрешностью 0,4 мм.
Длина части G, по которой протекает ток выше H, составляла от 26,5 до 26,0 см. В расчетах использовалось значение 26,3 см с погрешностью 0,2 см. Все эти расстояния измерялись линейкой с наименьшим делением 1 мм.
В этом состоянии лазерный луч отражался от зеркала на стену на расстоянии 5 метров. Луч был отрегулирован так, чтобы он был практически горизонтальным, путем регулировки угла зеркала. (Зеркало не показано, но находится поверх луча, поддерживаемого лезвием ножа J и его противоположным номером.) На стене на стене на пути лазерного луча был наклеен кусок малярной ленты. На ленте был нарисован круг по окружности пятна луча. Когда добавляются веса, чтобы вернуть токоведущие провода в направление нулевого тока, пятно возвращается в этот круг.
Текущая юстировка была довольно грубой, так что пятно иногда не попадало в окружность на 1 мм; слишком высоко на 1 мм для одной настройки тока и слишком низко на 1 мм для соседней настройки тока. При высоких токах (6 или 8 ампер) это приводило к погрешности около (+/-) 0,15 ампер в правильном токе для баланса.
При высоких токах (6 или 8 ампер) это приводило к погрешности около (+/-) 0,15 ампер в правильном токе для баланса.
F были отрегулированы примерно на половину их резьбового стержня. При их поднятии центр масс перемещается ближе к оси вращения. Таким образом, увеличение F снижает энергию, необходимую для небольшого вращения вокруг оси.Повышение F приводит к тому, что весы на заданную силу смещаются дальше от токов. То есть повышение F увеличивает чувствительность баланса.
При положении F наполовину весы реагировали не только на ток и малые массы, но и на потоки воздуха и на людей, опирающихся на стол или проходящих мимо. В положении наполовину удержать точку на стене было трудно, но возможно. Это был выбранный баланс между чувствительностью к току и чувствительностью к внешнему шуму.
Изменение F также изменяет собственную частоту колебаний весов при возмущении. Установлено, что собственные колебания имели период около 2 секунд.
Небольшие грузы для добавления в желоб были подготовлены следующим образом: 3,5 см многожильного провода №20 отрезали от катушки и удалили изоляцию. Масса этого отрезка проволоки составила 0,17 грамма с погрешностью 0,005 грамма (частичная погрешность 0,03). В образце было 10 нитей, поэтому масса каждой нити равнялась 0.017 грамм. Одну из нитей разрезали пополам (0,0085 г), а одну из половин разрезали еще раз, чтобы получить пару нитей на 1/4 первоначальной длины (0,0043 г).
Масса этого отрезка проволоки составила 0,17 грамма с погрешностью 0,005 грамма (частичная погрешность 0,03). В образце было 10 нитей, поэтому масса каждой нити равнялась 0.017 грамм. Одну из нитей разрезали пополам (0,0085 г), а одну из половин разрезали еще раз, чтобы получить пару нитей на 1/4 первоначальной длины (0,0043 г).
Для проведения измерения к желобу добавлялась масса, а ток увеличивался до тех пор, пока лазерное пятно не возвращалось в исходное положение. Массу записывают, а также записывают показания амперметра. Результаты собраны в двух столбцах выделенных полужирным шрифтом в таблице ниже.
Просмотр таблицы
Первые три столбца таблицы показывают массу (м) на желобе, вес (мг) на желобе и ток (I).Ток рассчитывается от
Ошибка в I, вызванная ошибками в измеренных величинах, вычисляется путем сначала вычисления дифференциала I:
С нашим выражением для I это становится
Размер ошибки в каждой величине был оценен выше, но знак ошибки неизвестен.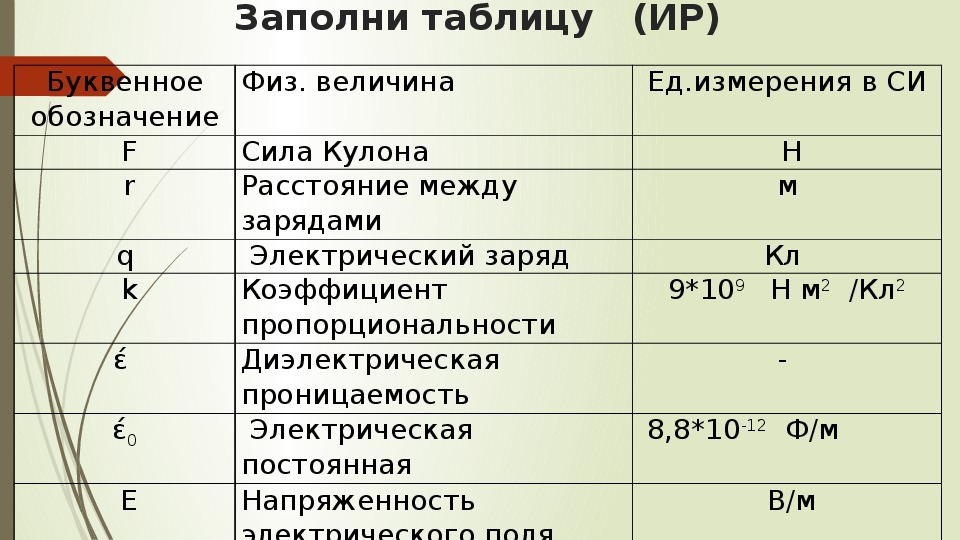 В худшем случае каждая ошибка вызывает отклонение I с тем же знаком. Отклонение в наихудшем случае можно рассчитать, взяв абсолютное значение каждого члена в дифференциале:
В худшем случае каждая ошибка вызывает отклонение I с тем же знаком. Отклонение в наихудшем случае можно рассчитать, взяв абсолютное значение каждого члена в дифференциале:
Записано с точки зрения отдельных ошибок, это дает дробную ошибку в токе
Со значениями в этом эксперименте относительная погрешность тока равна 0.07.
Калибровочная кривая
Калибровочный график представляет собой график зависимости измеренного тока от показаний амперметра. Если калибровка амперметра правильная, наклон этого графика будет равен 1, а точка пересечения будет равна нулю. График для этого набора измерений показан справа.
Используя функцию Linest в Excel, наклон оказался равным 1,052 с погрешностью 0,009. Перехват составляет 0,12 с неопределенностью 0,05.
При максимальном токе расчетная погрешность измерения около 0.6 ампер. Если данные увеличить до наименьшего измеренного тока, допускаемого оценкой погрешности, наклон линии уменьшится на 7%. Таким образом, измерение допускает возможность того, что калибровка амперметра является правильной по наклону.
Таким образом, измерение допускает возможность того, что калибровка амперметра является правильной по наклону.
Значение точки пересечения значительно отличается от нуля. Вероятно, имеет значение то, что разница становится незначительной, если из расчета исключить три самых низких измерения тока. В этом случае наклон равен 1,06 с погрешностью .01, а точка пересечения равна 0,01 с неопределенностью 0,06.
Как указано в таблице, первые три тока были измерены, когда лазерное пятно находилось в немного другом положении баланса. Ожидается, что если измерения слабого тока будут повторены, амперметр окажется хорошо откалиброванным.
Измерение мк
с Простой способ измерения коэффициента статического трения состоит в том, чтобы поместить два объекта вместе, а затем наклонить их, пока верхний не начнет скользить.Угол, под которым один объект начинает скользить по другому, напрямую связан с коэффициентом.
Когда два объекта расположены горизонтально, сила трения отсутствует. Поскольку объекты медленно наклоняются, сила трения покоя должна увеличиваться от нуля, чтобы противодействовать составляющей силы тяжести, действующей вдоль поверхности раздела.
В конце концов, по мере увеличения угла эта составляющая силы тяжести превышает максимальное значение силы трения покоя, и верхний объект соскальзывает.
Как угол, под которым это происходит, связан с коэффициентом статического трения?
Возьмите предельный случай, угол, достигнутый непосредственно перед тем, как блок начнет скользить, и нарисуйте диаграмму свободного тела.
Здесь мы можем использовать:
f с = f с max = μ с Н
, потому что это угол, при котором сила трения покоя достигает своего максимального значения.
Используйте систему координат с +x вниз по склону и +y перпендикулярно склону.
Разделить силу тяжести на составляющие x и y.
Дважды примените второй закон Ньютона.
| ΣF x = m a x = 0 | | | ΣF y = m a y = 0 |
| mg sin(θ) – f с = 0 | | | N – мг cos(θ) = 0 |
| мг sin(θ) = μ с N | | | N = мг cos(θ) |
Подставляем второе выражение в первое:
мг sin(θ) = μ с мг cos(θ)
Коэффициенты мг отменяются.Перестановка дает:
| = | тан(θ) | = | мк с |
Итак, коэффициент трения покоя равен тангенсу угла, под которым объекты скользят.
Аналогичный метод можно использовать для измерения μ k .Для этого вы толкаете верхний объект, увеличивая угол. Когда верхний объект продолжает скользить с постоянной скоростью, тангенс этого угла равен μ k .
Микроскопический вид трения
Простая модель того, что происходит на микроскопическом уровне, помогает нам понять трение. Под микроскопом поверхность обычно выглядит довольно шероховатой, с холмами и впадинами. Когда вы соединяете две поверхности вместе, они на самом деле соприкасаются в очень немногих местах.При попытке сдвинуть поверхности друг за другом высокие части каждой поверхности застревают друг в друге.
Что-то во взаимодействии между поверхностями должно измениться, когда площадь поверхности уменьшится. Сила конечно одинаковая. Какие изменения?
С той же силой уменьшение площади увеличивает давление, в основном сжимая поверхности ближе друг к другу. Вещи уравновешиваются, поэтому сила трения в первом приближении одинакова.
Измерение силы: Урок для детей – Видео и стенограмма урока
Использование стрелок для иллюстрации силы
Когда мы рисуем силы, мы обычно рисуем стрелку в направлении, в котором сила перемещает объект. Можете ли вы представить себе все силы, действующие на самолет?
На самолет в полете действует сила тяжести, направленная вниз, и подъемная сила, направленная вверх от крыльев. Он также испытывает силу тяги вперед (потому что двигатели толкают самолет вперед) и сопротивление воздуха.Нарисуем все эти силы в нужных направлениях с помощью стрелок.
Измерение силы
Вы можете использовать устройство, называемое измерителем силы , для измерения величины силы. У большинства измерителей силы есть крючок, который можно использовать, чтобы повесить или потянуть за что-либо. Это заставит пружину двигаться и покажет вам, какое усилие приложено.
Мы измеряем силы в единицах измерения, называемых ньютонами. Они получили это имя от одного из самых известных ученых всех времен: Исаака Ньютона. Он был первым, кто описал силу, известную нам как гравитация.
Он был первым, кто описал силу, известную нам как гравитация.
Ньютон можно описать и по-другому, измеряя его в кг * (м/сек2).
Сила = Масса x Ускорение
Это потому что:
- Сила = Масса * Ускорение
Ньютон описал это в своих законах физики, которые говорят нам, что движение создается неуравновешенными силами. Он понял, что объекты, которые не движутся, останутся неподвижными, а движущиеся объекты останутся в движении, если не вмешается сила.
Сила, масса и ускорение взаимосвязаны. Если мы знаем любые два из трех, мы можем найти третий.
- Ускорение = Сила / Масса
- Масса = Сила / Ускорение
Ньютона интересовала сила гравитации, из-за которой яблоки падают с деревьев. Попробуем измерить силу гравитации, действующую на одно яблоко. Среднее яблоко весит около 1/3 фунта. Это примерно 0,13 кг. Ускорение свободного падения вблизи поверхности Земли довольно близко к 9.8 м/с2. Следовательно, сила, действующая на одно яблоко, равна:
Сила = 0,1 кг * 9,8 м/с2 = 0,98
0,98 — это почти ровно один ньютон! Разве не приятный факт, что при падении яблока действует сила в один ньютон?
Оценка больших сил
Представьте, что вы толкаете автомобиль весом 1500 кг. Каждую секунду, когда вы толкаете автомобиль, его скорость увеличивается на 0,05 м/с. В конце концов, машина наберет обороты и поедет, но какую силу вы прикладываете к машине, толкая ее?
Каждую секунду, когда вы толкаете автомобиль, его скорость увеличивается на 0,05 м/с. В конце концов, машина наберет обороты и поедет, но какую силу вы прикладываете к машине, толкая ее?
Мы можем ответить на этот вопрос, используя определение силы, данное ранее.Чтобы найти силу, мы хотим умножить массу автомобиля на ускорение, которое испытывает автомобиль, когда мы его толкаем.
Сила = 1500 кг * 0,05 м/с2 = 75 Ньютонов
Резюме урока
Силы заставляют вещи вокруг вас двигаться. Сила измеряется в ньютонах , что является единицей, равной 1 кг * м/сек2. Вы можете рассчитать величину силы, которую испытывает объект, с помощью уравнения сила = масса * ускорение. Если вам известны любые два из этих значений, вы можете использовать их для нахождения третьего.Измеритель силы используется для измерения силы, и на схемах силы показаны стрелками.
Измерение времени жизни нейтрона с рекордной точностью
• Физика 14, 142
Усовершенствованная версия эксперимента с «бутылкой» позволяет исследователям снизить неопределенность этого важного параметра, но мучительное несоответствие остается.
Рисунок 1: Карикатурное изображение эксперимента UCN𝜏 Collaboration.Известное количество ультрахолодных нейтронов (голубое облако) удерживается в магнитогравитационной ловушке (асимметричная розовая чаша) в течение заданного времени. В этот период некоторые нейтроны подвергаются бета-распаду (вставка). В конце периода в ловушку опускают детектор (серый лист), чтобы подсчитать, сколько нейтронов осталось. Карикатурное изображение эксперимента коллаборации UCN𝜏. Известное количество ультрахолодных нейтронов (голубое облако) удерживается в магнитогравитационной ловушке (асимметричная розовая чаша) в течение заданного времени.В этот период часть нейтронов подвергается бета-распаду (в… Подробнее Рис. 1: Карикатурное изображение эксперимента UCN𝜏 Collaboration. Известное количество ультрахолодных нейтронов (голубое облако) удерживается в магнитогравитационной ловушке (асимметричная розовая чаша) в течение заданного времени. В этот период некоторые нейтроны подвергаются бета-распаду (вставка). В конце периода в ловушку опускают детектор (серый лист), чтобы подсчитать, сколько нейтронов осталось.
Известное количество ультрахолодных нейтронов (голубое облако) удерживается в магнитогравитационной ловушке (асимметричная розовая чаша) в течение заданного времени. В этот период некоторые нейтроны подвергаются бета-распаду (вставка). В конце периода в ловушку опускают детектор (серый лист), чтобы подсчитать, сколько нейтронов осталось. Вне атомных ядер нейтроны быстро распадаются на другие частицы со средним временем жизни 𝜏n примерно 15 минут.Получение точного значения для 𝜏n может иметь далеко идущие последствия для нашего понимания Вселенной, поскольку предлагает способ проверить важные детали законов физики, которые имеют отношение к физике элементарных частиц, астрономии и космологии. Теперь, благодаря эксперименту в Лос-Аламосском центре нейтронных наук (LANSCE) в Нью-Мексико, коллаборация UCN добилась наиболее точного измерения 𝜏n на сегодняшний день [1]. При 877,75 с с общей неопределенностью 0,039% это измерение имеет менее чем половину неопределенности предыдущих лучших экспериментов — одного, проведенного той же группой [2] и одного из европейского сотрудничества [3].
Новое измерение было выполнено с использованием так называемого эксперимента с бутылкой, в котором ловушка («бутылка») заполняется известным количеством ультрахолодных нейтронов (УХН). Подсчитав, сколько нейтронов остается после определенного интервала, можно рассчитать скорость распада нейтрона и, следовательно, среднее время жизни нейтрона. Одна из проблем при выполнении этого измерения заключается в том, что время жизни нейтрона велико. Хотя 15 минут могут показаться управляемым интервалом, достижение достаточного количества распадов для достижения требуемой статистической точности за практический промежуток времени требует удержания большого количества частиц.Дальнейшие задачи включают замедление или замедление нейтронов (реакторы или источники расщепления генерируют нейтроны с энергиями в несколько сотен МэВ, тогда как для захвата требуются нейтроны с энергиями в несколько сотен нэВ), контроль потерь нейтронов и выравнивание флуктуаций в накопленной энергии. Энергетический спектр УХН.
Эти проблемы были до некоторой степени решены в ходе более ранних измерений, проведенных в LANSCE, но новый эксперимент снижает неопределенность, вытекающую из этих эффектов, до беспрецедентно низкого уровня.Исследователи используют установку, аналогичную их предыдущим экспериментам, в которой УХН с энергией примерно 180 нэВ поляризуются так, чтобы они искали минимумы магнитного поля, прежде чем попасть в магнитогравитационную ловушку — чашу с открытым верхом, сделанную из постоянных магнитов, расположенных в так называемая решетка Хальбаха (рис. 1). Затем образец УХН «очищается», то есть частицы с наибольшей энергией либо захватываются поверхностями ZnS, покрытыми бором-10, либо рассеиваются из ловушки. Этот процесс очистки важен для обеспечения того, чтобы ловушка содержала только самые низкоэнергетические УХН, у которых мало шансов ускользнуть в течение периода хранения.Любые вылетающие нейтроны могут привести к ошибке в определении 𝜏n. После очистки УХН выдерживают в ловушке от 20 до 1550 с, а затем подсчитывают.
Новое исследование отличается от предыдущих экспериментов добавлением буферного объема между источником нейтронов и ловушкой, в которой удерживаются УХН до начала периода хранения. Этот буфер выравнивает энергетическое распределение УХН, сводя к минимуму влияние флуктуаций источника, и служит дополнительной ступенью очистки.
Еще одна разница появляется в конце периода хранения. В то время как в других экспериментах с бутылками УХН УХН выгружались из ловушки, чтобы их можно было подсчитать на отдельном детекторе, в коллаборации UCN𝜏 используется детектор in situ , который можно поэтапно опускать в ловушку. Этот метод не только устраняет возможность потерь при транспортировке УХН к детектору, но также позволяет команде наносить на карту энергии и траектории УХН, проводя измерения на разных высотах.Эта дополнительная информация обеспечивает способ проверки систематических потерь частиц.
Исследователи UCN𝜏 также улучшили способ анализа своих данных. В своем последнем исследовании они используют три независимых слепых анализа, чтобы уменьшить вклад всех систематических эффектов, ненормальных условий бега и нефизических точек данных, а также статистических погрешностей. Каждый анализ определяет 𝜏n двумя разными методами: «парным» анализом, который усредняет прогоны с коротким и длинным временем хранения, и «глобальным» анализом, который использует максимальное правдоподобие для всех полученных данных.Результаты слепого анализа сравниваются, и данные не ослепляются только тогда, когда три значения 𝜏n согласуются в пределах 0,1 с. Окончательный результат для 𝜏n получается из невзвешенного среднего центральных значений трех анализов.
Каждый анализ определяет 𝜏n двумя разными методами: «парным» анализом, который усредняет прогоны с коротким и длинным временем хранения, и «глобальным» анализом, который использует максимальное правдоподобие для всех полученных данных.Результаты слепого анализа сравниваются, и данные не ослепляются только тогда, когда три значения 𝜏n согласуются в пределах 0,1 с. Окончательный результат для 𝜏n получается из невзвешенного среднего центральных значений трех анализов.
В результате этих экспериментальных и аналитических улучшений исследователи смогли уменьшить эффект всей известной систематики до уровня, при котором несколько поправок, которые необходимо применить, меньше общей неопределенности эксперимента.Полученная точность может помочь сформировать наши самые фундаментальные теории. Например, время жизни нейтрона является одним из входных данных, используемых для расчета распространенности гелия-4 в ранней Вселенной из-за нуклеосинтеза Большого взрыва (BBN) [4]. Таким образом, объединение расчетов BBN с астрономическими наблюдениями предлагает мощный зонд новой физики.
Анализ 𝜏n в сочетании с другими свойствами бета-распада нейтрона также можно использовать для проверки стандартной модели. Например, такой анализ может помочь уменьшить неопределенность значения константы связи слабого аксиального вектора, которая управляет процессами, включающими заряженные слабые взаимодействия, включая BBN, образование нейтронных звезд, солнечный синтез и обнаружение (анти)нейтрино.Стандартная модель предсказывает, что этот параметр вместе с векторной константой связи полностью описывает такие взаимодействия, в то время как некоторые теории, выходящие за рамки стандартной модели, требуют дополнительных скалярных и тензорных членов, которые, в свою очередь, могут повлиять на значение 𝜏n. Комбинированный анализ может также определить важный параметр, описывающий слабое взаимодействие, называемый матричным элементом смешивания кварков Vud. Текущее лучшее значение для Vud получено при наблюдении за набором ядерных бета-распадов с участием сложных ядер, но такие выводы требуют поправок к ядерной структуре. Эти поправки не нужны для распада свободных нейтронов, поэтому извлечение этого параметра из 𝜏n может быть более надежным. Новый результат коллаборации UCN означает, что определение Вуда на свободных нейтронах почти конкурентоспособно с определением сверхразрешенного ядерного распада, что дает физикам еще одну возможность в их поисках новой физики.
Эти поправки не нужны для распада свободных нейтронов, поэтому извлечение этого параметра из 𝜏n может быть более надежным. Новый результат коллаборации UCN означает, что определение Вуда на свободных нейтронах почти конкурентоспособно с определением сверхразрешенного ядерного распада, что дает физикам еще одну возможность в их поисках новой физики.
Каким бы впечатляющим и важным ни был этот результат, следует отметить, что улучшенная точность недостаточна для устранения сохраняющегося несоответствия, влияющего на измерения времени жизни нейтрона.Эксперименты с бутылкой, подобные тем, что проводятся коллаборацией UCN, в которых подсчитываются оставшиеся нейтроны, представляют собой лишь один из способов измерения 𝜏n. Это значение также можно измерить, наблюдая продукты бета-распада нейтрона в пучке холодных нейтронов. В среднем эти эксперименты с пучком дают значение 𝜏n примерно на 8 с больше, чем указанное в экспериментах с бутылкой [5]. Сам по себе новый результат коллаборации UCN𝜏 не закрывает этот пробел (неопределенность в обоих типах экспериментов уже была намного меньше 8 с). Устранение несоответствия потребует новых дополнительных измерений, например, с использованием лучевого метода, измерений, сочетающих как лучевой, так и бутылочный методы, или даже новых космических методов [6]. К счастью, многие эксперименты проводятся или разрабатываются, чтобы сделать именно это [7].
Устранение несоответствия потребует новых дополнительных измерений, например, с использованием лучевого метода, измерений, сочетающих как лучевой, так и бутылочный методы, или даже новых космических методов [6]. К счастью, многие эксперименты проводятся или разрабатываются, чтобы сделать именно это [7].
Ссылки
- Ф. М. Гонсалес и др. (UCNτ Collaboration), «Улучшенное измерение времени жизни нейтрона с помощью UCN𝜏», Phys. Преподобный Летт. 127 , 162501 (2021).
- р.В. Патти и др. , «Измерение времени жизни нейтрона с использованием магнито-гравитационной ловушки и обнаружения на месте», Science 360 , 627 (2018).
- Серебров А. и др. , «Измерение времени жизни нейтрона с использованием гравитационной ловушки и низкотемпературного покрытия Фомблина», Phys. лат. В 605 , 72 (2005).
- Р. Х. Сайбурт и др. , «Нуклеосинтез Большого взрыва: Текущее состояние», Rev. Mod. физ. 88 , 015004 (2016).

- Г. Л. Грин и П. Гельтенборт, «Загадка лежит в основе атома», Sci. Являюсь. 314 , 36 (2016).
- Д. Дж. Лоуренс и др. , «Космические измерения времени жизни нейтрона: подходы к устранению аномалии времени жизни нейтрона», Nucl. Инструм. Методы физ. Рез. А 988 , 164919 (2021).
- D. Dubbers и B. Märkisch, “Точные измерения распада свободных нейтронов”, Annu. Преподобный Нукл. Часть. науч. 71 , 139 (2021).
Об авторе
Шеннон Хугерхайд — штатный физик группы нейтронной физики Национального института стандартов и технологий (NIST).Ее исследования сосредоточены на точных измерениях фундаментальной физики с использованием нейтронов, включая эксперименты по измерению времени жизни нейтрона и вращения спина поляризованных нейтронов. Она также занимается нейтронной интерферометрией, разработкой детекторов, нейтронным облучением и калибровкой. Она получила B.S. по физике из Колледжа Кальвина и A.M. и доктор философии. по физике Гарвардского университета, где она работала над измерениями магнитных моментов электронов и позитронов. До прихода в Группу нейтронной физики она была научным сотрудником Национального исследовательского совета в группе атомной спектроскопии в NIST, где она работала с высокозаряженными ионами.
по физике Гарвардского университета, где она работала над измерениями магнитных моментов электронов и позитронов. До прихода в Группу нейтронной физики она была научным сотрудником Национального исследовательского совета в группе атомной спектроскопии в NIST, где она работала с высокозаряженными ионами.
Тематические области
Статьи по теме
Частицы и поляОхотник за темной материей
XinRan Liu разрабатывает технологию для детекторов темной материи, которые, как он надеется, скоро обнаружат эти таинственные частицы. Подробнее »
Другие статьиПонимание измерения в свете его происхождения
Front Psychol. 2013; 4: 113.
Stephen Humphry
1 Факультет образования, Университет Западной Австралии, Перт, штат Вашингтон, Австралия
1 Факультет образования, Университет Западной Австралии, Перт, штат Вашингтон, Австралия
Под редакцией: Джошуа А. McGrane, Университет Западной Австралии, Австралия
McGrane, Университет Западной Австралии, Австралия
Рецензент: Бен Коладжиури, Университет Нового Южного Уэльса, Австралия; Эндрю Стюарт Кингдон, Офис Исследовательского совета Нового Южного Уэльса, Австралия; Пол Т. Барретт, Advanced Projects R&D Ltd., Новая Зеландия
*Переписка: Стивен Хамфри, Высшая школа образования, Университет Западной Австралии, M428, 35 Stirling Highway, Crawley, WA 6009, Австралия. e-mail: [email protected]Эта статья была отправлена в Frontiers in Quantitative Psychology and Measurement, специальность Frontiers in Psychology.
Поступила в редакцию 29 ноября 2012 г .; Принято 21 февраля 2013 г.
Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает использование, распространение и воспроизведение на других форумах при условии указания авторов и источника и любых уведомлений об авторских правах. относительно любой сторонней графики и т. д.
Abstract
В ходе истории естествознания стали свидетелями развития все более удобных сокращенных символических устройств для обозначения физических величин. Эти устройства в конечном итоге приняли форму физической алгебры. Однако за удобство алгебры, возможно, пришлось заплатить — потеря ясности прямого понимания Евклидом, Галилеем и Ньютоном естественных количественных отношений. Физическая алгебра часто интерпретируется как обычная алгебра; т. е. интерпретируется так, как если бы символы обозначали (а) числа и операции над числами, в отличие от (б) физических величин и количественных отношений. В статье вновь рассматривается то, как Ньютон понимал и выражал физические определения и законы.Соответственно, в нем рассматривается компактная форма записи, которая использовалась для обозначения как: (а) отношений физических величин; и (b) составные отношения, включающие два или более видов количества. Цель состоит в том, чтобы показать, что с историческим развитием согласуется рассмотрение физической алгебры как средства обозначения отношений между отношениями. Понятая в историческом контексте, цель измерения состоит в том, чтобы установить, что физическая величина находится в определенном отношении к другой величине того же рода.
Эти устройства в конечном итоге приняли форму физической алгебры. Однако за удобство алгебры, возможно, пришлось заплатить — потеря ясности прямого понимания Евклидом, Галилеем и Ньютоном естественных количественных отношений. Физическая алгебра часто интерпретируется как обычная алгебра; т. е. интерпретируется так, как если бы символы обозначали (а) числа и операции над числами, в отличие от (б) физических величин и количественных отношений. В статье вновь рассматривается то, как Ньютон понимал и выражал физические определения и законы.Соответственно, в нем рассматривается компактная форма записи, которая использовалась для обозначения как: (а) отношений физических величин; и (b) составные отношения, включающие два или более видов количества. Цель состоит в том, чтобы показать, что с историческим развитием согласуется рассмотрение физической алгебры как средства обозначения отношений между отношениями. Понятая в историческом контексте, цель измерения состоит в том, чтобы установить, что физическая величина находится в определенном отношении к другой величине того же рода. Прояснение значения измерения с точки зрения исторических истоков физики влечет за собой основные последствия для способа понимания и подхода к измерению. Рассмотрены возможные последствия для социальных наук.
Прояснение значения измерения с точки зрения исторических истоков физики влечет за собой основные последствия для способа понимания и подхода к измерению. Рассмотрены возможные последствия для социальных наук.
Ключевые слова: измерение, отношение, пропорция, классическая теория, репрезентативная теория, психометрия, метрология
Согласно определениям измерения, принятым в социальных науках, измерение включает в себя ассоциацию или присвоение чисел объектам.Определения такого рода носят репрезентативный характер. Возможно, наиболее влиятельным является определение, сформулированное Стивенсом (1946, стр. 677): «измерение в самом широком смысле определяется как присвоение числовых значений объектам или событиям в соответствии с правилами». Мичелл (1999, стр. 15–19) представил убедительный аргумент в пользу того, что, несмотря на несовместимость с традиционной концепцией измерения в естественных науках, определение Стивенса стало образцом для многих психологов. Соответственно, репрезентативные определения также были сформулированы в теории ответов на вопросы, возможно, в первую очередь Лордом и Новиком (1968).
Соответственно, репрезентативные определения также были сформулированы в теории ответов на вопросы, возможно, в первую очередь Лордом и Новиком (1968).
Самая сложная попытка связать измерения в социальных науках с измерениями в физике содержится в Foundations of Measurement (Krantz et al., 1971) и предшествующих работах. Авторы попытались изложить аксиоматическое основание измерения, включающее так называемые теоремы о представлении. В Томе 1 Основ Измерения Кранц и др. (1971, стр. 1) характеризуют измерение следующим образом: «При измерении некоторого атрибута класса объектов или событий мы связываем числа… с объектами таким образом, что свойства атрибута точно представляются как числовые свойства.Основы по существу доводят использование удобных сокращенных символических устройств до крайности, посредством чего символы физической алгебры интерпретируются так, как будто они относятся только к числам и их операциям. Аксиомы репрезентативной теории относятся либо к качественным отношениям, либо к числовым свойствам, но не непосредственно к количественным атрибутам. Таким образом, формальный аспект теории отделяется от ссылки на качественное эмпирическое содержание.В соответствии с этим Мичелл (1999, стр. 208) сказал о репрезентативной школе: «По большей части Суппес, Люс и их коллеги избегали (этой концепции количества) при трактовке измерения». Кибург (1996) и Берка (1983) выдвинули соответствующие наблюдения и критику репрезентативной теории.
Таким образом, формальный аспект теории отделяется от ссылки на качественное эмпирическое содержание.В соответствии с этим Мичелл (1999, стр. 208) сказал о репрезентативной школе: «По большей части Суппес, Люс и их коллеги избегали (этой концепции количества) при трактовке измерения». Кибург (1996) и Берка (1983) выдвинули соответствующие наблюдения и критику репрезентативной теории.
В отличие от репрезентативной теории Мичелл обратил внимание на то, что он называет классической теорией измерения: «Научное измерение правильно определяется как оценка или открытие отношения некоторой величины количественного атрибута к единице измерения. один и тот же атрибут» (Мишелл, 1997, с.358). В этом определении количественным признакам придается онтологический статус, а отношение между величинами количеств принимается за действительное число.
Эта классическая теория часто используется в физике и метрологии. В метрологии Бюро мер и весов (BIPM) претендует на то, чтобы поддерживать всемирное единообразие измерений и их прослеживаемость до Международной системы единиц (СИ).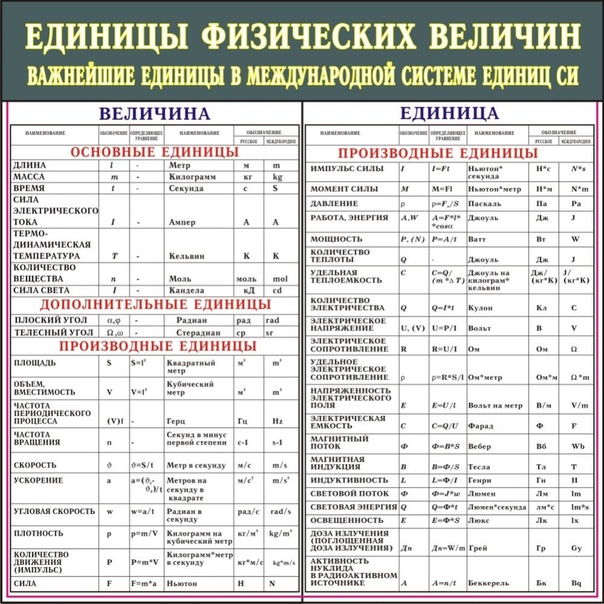 BIPM неявно принимает классическое определение в своем определении единицы: «Таким образом, единица измерения — это скалярная величина, определенная и принятая по соглашению, с которой можно сравнить любую другую величину того же вида, чтобы выразить отношение две величины как число» [Bureau International des Poids et Mesures (BIPM), 2006, p.24].
BIPM неявно принимает классическое определение в своем определении единицы: «Таким образом, единица измерения — это скалярная величина, определенная и принятая по соглашению, с которой можно сравнить любую другую величину того же вида, чтобы выразить отношение две величины как число» [Bureau International des Poids et Mesures (BIPM), 2006, p.24].
Галилей, Ньютон и другие пионеры выражали физические отношения как пропорциональности между отношениями физических величин. Как мы увидим, классическая теория измерения более тесно связана с истоками физики, чем репрезентативная теория, в силу своей ссылки на понятие отношения.
Этот документ имеет следующую структуру. Он начинается с акцента на генезисе физики и, в частности, вдохновленной греками традиции понимания физических отношений с точки зрения пропорций и отношений.Затем в нем приводится обзор все более удобных сокращений, которые использовались для заявлений о пропорциональности, что привело к последующему расхождению взглядов в форме классического и репрезентативного взглядов на измерение.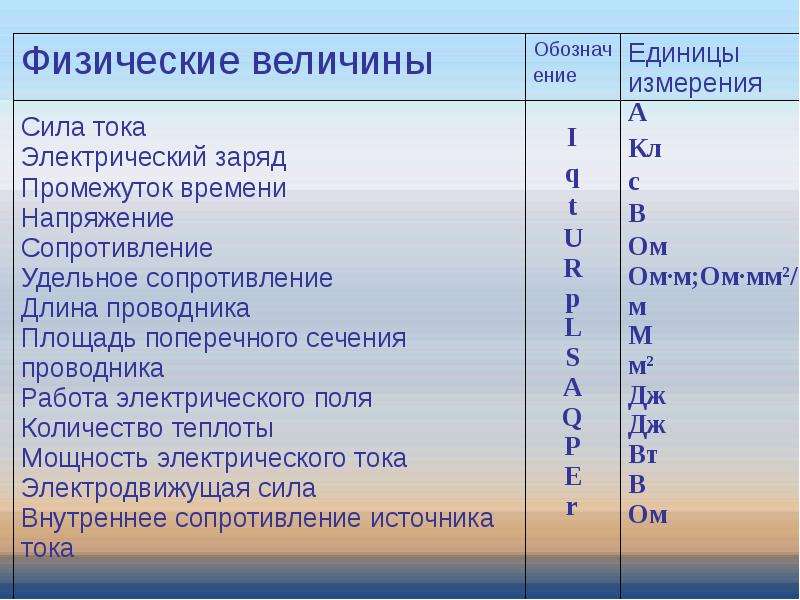 Утверждается, что использование все более абстрактных и сокращенных утверждений дорого обходится прямоте понимания естественных отношений. Затем используется компактная форма записи для обозначения отношений, сложных отношений и пропорциональности между отношениями; и это обозначение используется, чтобы показать параллель между утверждениями алгебры и пропорциональности.Затем объясняется понятие сложного отношения и показывается, что, хотя сложные отношения имеют формальное сходство с умножением, они имеют различную концептуальную основу. Наконец, объясняются самые основные следствия измерения в физике и кратко рассматриваются последствия для социальных наук.
Утверждается, что использование все более абстрактных и сокращенных утверждений дорого обходится прямоте понимания естественных отношений. Затем используется компактная форма записи для обозначения отношений, сложных отношений и пропорциональности между отношениями; и это обозначение используется, чтобы показать параллель между утверждениями алгебры и пропорциональности.Затем объясняется понятие сложного отношения и показывается, что, хотя сложные отношения имеют формальное сходство с умножением, они имеют различную концептуальную основу. Наконец, объясняются самые основные следствия измерения в физике и кратко рассматриваются последствия для социальных наук.
Пропорции и отношения в геометрии и классической физике
Исторически сложилось так, что пионеры классической физики, от Галилея до Ньютона и Фарадея, выражали физические отношения как пропорциональность отношений двух или более видов величин.Ньютон широко использовал геометрические линии для обозначения таких величин, как силы (Newton, 1846; Roche, 1998). В Principia он неоднократно упоминал величины как пропорциональные или обратно пропорциональные друг другу в динамических физических ситуациях. Так, Ньютон сказал:
В Principia он неоднократно упоминал величины как пропорциональные или обратно пропорциональные друг другу в динамических физических ситуациях. Так, Ньютон сказал:
Если при сравнении неопределенных количеств разного рода одно с другим говорят, что какое-либо из них прямо или обратно равно любому другому, то это означает, что первое увеличивается или уменьшается в том же отношении, что и последнее, или с его взаимное (1846, с.100).
Например, если сила f увеличивается до f′, а результирующее ускорение тела a увеличивается до a′, то отношение f:f′ может быть таким же, как отношение a:a′. Здесь Ньютон использует евклидово выражение «в том же отношении» для описания пропорциональности. Кулон и Фарадей также называли величины пропорциональными или обратно пропорциональными друг другу (Silsbee, 1962).
Символы для чисел в физико-математике
Пропорция и отношение были центральными элементами Евклида .В вдохновленной греками традиции пропорций и соотношений отношения не воспринимались как буквально равные числам. Скорее «[r]atio принадлежало… к категории отношений и не было простой величиной или единичным числом» (Roche, 1998, p. 46). Таким образом, отношения даже не считались буквально равными 90 257 90 260 друг другу. В своем историческом анализе Евклида Граттан-Гиннесс (1996) отмечает: «Хотя он говорит о равенстве чисел и величин, Евклид никогда не говорит, что отношения «равны» друг другу, а только говорит, что они «находятся в одном и том же отношении». », или что одно отношение «подобно» другому в предложении о пропорции.
Скорее «[r]atio принадлежало… к категории отношений и не было простой величиной или единичным числом» (Roche, 1998, p. 46). Таким образом, отношения даже не считались буквально равными 90 257 90 260 друг другу. В своем историческом анализе Евклида Граттан-Гиннесс (1996) отмечает: «Хотя он говорит о равенстве чисел и величин, Евклид никогда не говорит, что отношения «равны» друг другу, а только говорит, что они «находятся в одном и том же отношении». », или что одно отношение «подобно» другому в предложении о пропорции.
Поэтому неудивительно, что идея о том, что отношение может быть обозначено одним числом, называемым либо его показателем степени, либо номиналом, встретила значительное сопротивление в определенный исторический период. В конечном счете, однако, «медленно растущее требование представлять все отношения числами постепенно привело к слиянию концепции отношения как единого числа» (Roche, 1998, стр. 76). Эта объединенная концепция очевидна в классической теории (или определении) измерения.
Поскольку репрезентативные определения преобладают в социальных науках, полезно понять развитие физико-математических наук, которые позволили появиться этим определениям.Путь от истоков физики к современной репрезентативной концепции выглядит примерно следующим образом. Во-первых, физические отношения выражались словами и геометрическими аналогиями в виде отношений и сложных отношений. Ньютон последовал этой традиции и использовал обозначение, отождествляющее линии с физическими величинами, так что длины и направления линий обозначали величины и направления величин. Рош (1998, стр. 89) резюмирует это и последующее историческое развитие следующим образом.
Это не было сведением физического к линии… Но это было нотное отождествление двух понятий. Конечно, это было чрезвычайно удобно, так как теперь к этим понятиям можно было применять все операции геометрической алгебры без ограничений, налагаемых символикой пропорциональности, которая относилась непосредственно к натуральной величине.
Эта идентификация со временем перешла от линий к числам и даже к самому формальному символу, обозначавшему физическую величину.
Позже Лаплас интерпретировал символы в физических уравнениях как представление «чисел, абстрагированных от четко определенных процедур измерения» (Roche, 1998, стр. 138). Это был критический отход, потому что, как только числа стали рассматриваться как абстрактные и независимые от эмпирического мира, стало возможным истолковать цель измерения как представление эмпирических объектов с помощью чисел; то есть стало возможным появление репрезентативного взгляда. Мичелл (1993) подробно описывает более поздние разработки и утверждает, что теория Рассела (1903) была первой явно репрезентативной теорией измерения.Сами репрезентативные теоретики предлагают совершенно иную версию с акцентом на событиях, которые произошли в конце восемнадцатого и начале девятнадцатого веков (Diez, 1997; Luce and Suppes, 2002).
Расхождение во взглядах на измерение
Рош (1998, стр. 138) утверждает, что мнение о том, что только «абстрактные числа могут появляться в алгебре физики, возможно, отражает реакцию на классическую традицию обращения с самими физическими величинами, а не чем его мера, и необходимость дистанцировать алгебру физики от манипуляций с такими величинами.Возможно, тогда неудивительно, что впоследствии возникло расхождение в способах интерпретации абстрактных чисел, которое сохраняется и сегодня. С классической точки зрения, как определено Мичеллом (1993), отношения — это числа. Эта точка зрения сохраняет ключевой аспект греческой традиции, но включает в себя использование аббревиатуры, как объясняется ниже. В репрезентативном представлении нет никакой связи с отношениями, как обобщается в следующем отрывке.
138) утверждает, что мнение о том, что только «абстрактные числа могут появляться в алгебре физики, возможно, отражает реакцию на классическую традицию обращения с самими физическими величинами, а не чем его мера, и необходимость дистанцировать алгебру физики от манипуляций с такими величинами.Возможно, тогда неудивительно, что впоследствии возникло расхождение в способах интерпретации абстрактных чисел, которое сохраняется и сегодня. С классической точки зрения, как определено Мичеллом (1993), отношения — это числа. Эта точка зрения сохраняет ключевой аспект греческой традиции, но включает в себя использование аббревиатуры, как объясняется ниже. В репрезентативном представлении нет никакой связи с отношениями, как обобщается в следующем отрывке.
Таким образом, по существу, есть две черты, разделяющие классическую и репрезентативную теории измерения: роль отношений величин и место чисел.Согласно классической теории, эти два явления логически связаны: отношения величин являются числами, и этот факт лежит в основе измерения.
Согласно репрезентативной теории, числа не выводятся из отношений количеств. Они совершенно от них не зависят, и место чисел в измерении определяется структурным сходством качественной и количественной систем. Следовательно, согласно репрезентативной теории, числа присваиваются эмпирическим сущностям измерения.Согласно классической теории, числа обнаруживаются как отношения между эмпирическими сущностями в измерении (Мишелл, 1993, с. 190).
Несмотря на появление репрезентативного взгляда, классический взгляд продолжает существовать в физике. Почему абстрактно-алгебраический взгляд не вытеснил полностью классический? Было бы несколько удивительно, если бы утверждения о пропорциональности, используемые в концепции физики, были менее подходящими для описания естественных отношений, чем алгебра, которая применялась позже.Кажется более вероятным, что удобство сокращенных устройств было основной причиной их более широкого использования. Однако утверждалось, что удобство физической алгебры было достигнуто за счет явного внимания к ключевым особенностям физических отношений, как показано в следующем отрывке.
Несколько ключевых особенностей этой греческой традиции… заслуживают пристального внимания. Пары одинаковых величин сравниваются с другими парами, которые часто физически различны, например, пары весов с парами расстояний в теории равновесия.Это очень отличается от современного алгебраического языка физики, который сравнивает отдельные значения различных величин. Кроме того, утверждение о пропорциональности, кажется, немного ближе к описанию естественного отношения, чем язык алгебры (Roche, 1998, p. 47).
Два направления мысли продолжают оставаться очевидными и сегодня, так что алгебра и арифметика физики кажутся «интерпретируемыми формально в одних контекстах и физически в других» (Roche, 1998, p. 222).
Согласование современных физических обозначений с их происхождением
Как же тогда мы можем согласовать современную ссылку на равенство отношений и чисел в физике с ее происхождением? Кранц и др. (1971, стр. 459) заметил: «Большинство текстов по анализу размерностей, кажется, принимают (физическую) алгебру как должное, и они не пытаются явно сформулировать, о чем идет речь». Хотя это достаточно верно, используя соответствующие обозначения, можно явно сформулировать утверждения о пропорциональности таким образом, чтобы показать четкую и прямую параллель с современными алгебраическими обозначениями.
Хотя это достаточно верно, используя соответствующие обозначения, можно явно сформулировать утверждения о пропорциональности таким образом, чтобы показать четкую и прямую параллель с современными алгебраическими обозначениями.
Формулировка Ньютона о втором законе движения используется для иллюстрации этой параллели. Ньютон (1846, стр. 83) сформулировал второй закон следующим образом: «Изменение движения всегда пропорционально приложенной движущей силе; и производится в направлении правой линии, по которой действует сила». Здесь движение относится к тому, что сейчас обычно называют импульсом. Мы можем выразить второй закон Ньютона в виде формального утверждения о пропорциональности следующим образом:
где f и p относятся к силе, действующей на тело в данный момент времени, и результирующему импульсу тела, а f’ и p’ относятся к силе, действующей в другой момент на то же тело, и его результирующему импульсу соответственно. .В утверждении (1) «::» означает «как» или «пропорционально». Таким образом, изменение количества движения выражается отношением p’: p и пропорционально изменению движущей силы f’: f. Обозначение «::» использовал Уоллис (1685 г.). Учитывая цели статьи, следует отметить, что утверждение (1) уже представляет собой сокращенную форму утверждения о пропорциональности, которая опускает словесные ссылки на ключевые элементы полного изложения закона Ньютоном, такие как природа причинности через ссылку на силу, действующую на тело.
Таким образом, изменение количества движения выражается отношением p’: p и пропорционально изменению движущей силы f’: f. Обозначение «::» использовал Уоллис (1685 г.). Учитывая цели статьи, следует отметить, что утверждение (1) уже представляет собой сокращенную форму утверждения о пропорциональности, которая опускает словесные ссылки на ключевые элементы полного изложения закона Ньютоном, такие как природа причинности через ссылку на силу, действующую на тело.
Как было сказано ранее, Евклид не считал отношения равными друг другу. Точно так же Ньютон не ссылался ни на какое равенство в своем изложении закона. Соответственно, уместно обращаться к (уравнению 1) как к утверждению физического закона, а не как к уравнению , потому что оно не утверждает, что члены равны , численно или в каком-либо другом смысле.
Очевидно, однако, что физическая алгебра в настоящее время успешно применяется как в прикладных, так и в теоретических целях; и современные уравнения должны быть совместимы с их происхождением.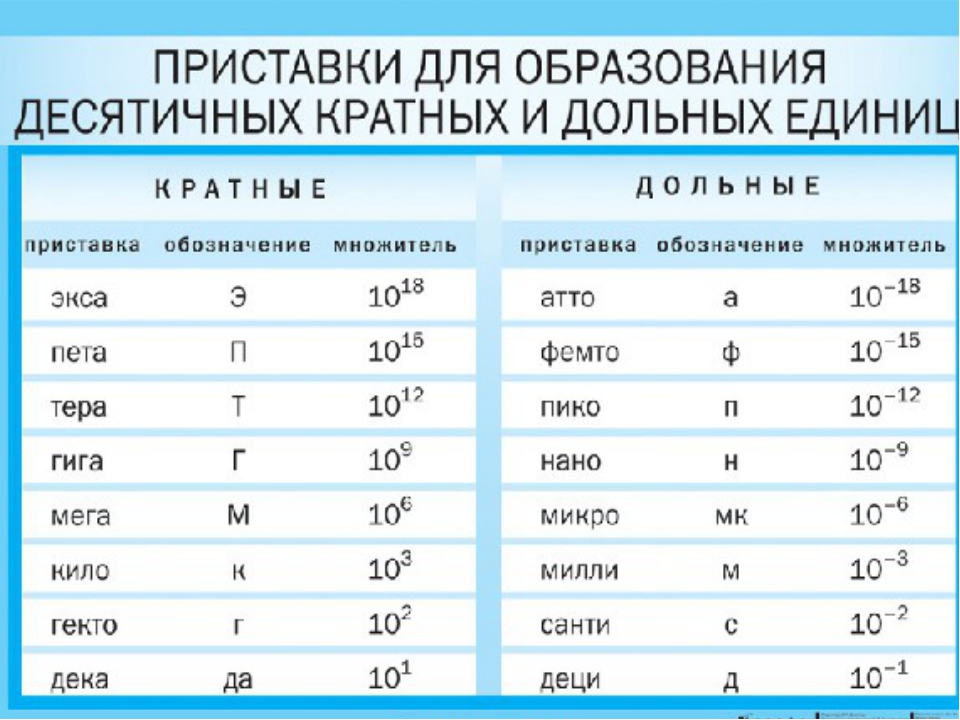 Выбранный пример можно использовать, чтобы показать эту совместимость.
Выбранный пример можно использовать, чтобы показать эту совместимость.
Второй закон Ньютона обычно формулируется алгебраически так:
где p = m a или, как выразился Ньютон (1846, стр. 72): «Количество движения [импульса] есть мера того же самого, возникающая из скорости и количества материи совместно ».
Чтобы увидеть параллель между утверждением (1) и уравнением. 2, мы можем выразить члены как отношения между величинами и единицей следующим образом:
f ′ :[f]::m ′ :[m] ⋅ a ′ :[a],
где
F = f′:[f], m = m′:[m] и a = a′:[a].Здесь [f], [m] и [a] приняты за единицы силы, массы и ускорения соответственно. Срок “.” означает, что эти два отношения составлены в том смысле, в каком термин использовался Евклидом в геометрии, а затем Галилеем (1638 г.) для выражения сложных физических отношений. Далее будет объяснена концепция начисления соотношений для выражения сложных соотношений.
Очевидно, уравнение 3 и утверждение (1) имеют аналогичную форму с «=» в уравнении. 3 вместо «::» в утверждении (1) и алгебраическое умножение, используемое в уравнении.3 вместо сложения в утверждении (1). Дополнительный шаг (который не был бы предпринят Евклидом), заключающийся в том, что F = f′:[f] и так далее, приравнивает отношения к числам. Этот шаг обычно используется в метрологии. Уоллис (1670) сделал именно этот шаг, от «::» до «=», хотя Рош (1998, стр. 99) утверждает, что «отрывки в других местах у Уоллиса убедительно свидетельствуют о том, что он интерпретировал это выражение не как истинное алгебраическое уравнение, но как сокращенное уравнение отношения, которое связывает сложное отношение с простым отношением.
Составные коэффициенты в заявлениях о пропорциональности
Представляется, что термин составной коэффициент не имеет явного исторического определения в большинстве источников, за исключением ссылок на конкретные примеры. Когда два соотношения составляются, второе количество первого отношения является первым количеством второго отношения, а составное отношение является отношением первого к последнему количеству. Исторические корни компаундирования, вероятно, лежат в физике музыки, где можно составить два музыкальных интервала, чтобы получить заданное соотношение (Grattan-Guinness, 1996).
Когда два соотношения составляются, второе количество первого отношения является первым количеством второго отношения, а составное отношение является отношением первого к последнему количеству. Исторические корни компаундирования, вероятно, лежат в физике музыки, где можно составить два музыкальных интервала, чтобы получить заданное соотношение (Grattan-Guinness, 1996).
Галилей смог использовать составные отношения, сделав одно отношение длин пропорциональным двум скоростям, а другое отношение длин пропорционально двум временным интервалам. Сложив два отношения длин (первое ко второму и второе к третьему), он показал, что расстояния тел с разными скоростями, пройденные в разные промежутки времени, «несут друг к другу сложное отношение скоростей и временных интервалов» (Галилей , 1638, стр. 194). Аналогичные рассуждения можно использовать для демонстрации пропорциональности в уравнении.3 следует из закона Ньютона. Следующее подражает рассуждениям Галилея.
Рассмотрим тело A, на которое действует сила f A , ускоряющая тело в точке a A . Рассмотрим также тело B, на которое действует сила f B , ускоряющая тело в точке a B . Предложение, которое необходимо продемонстрировать, состоит в том, что отношение f A к f B является составным отношением масс и ускорений.Утверждение можно продемонстрировать в два этапа со ссылкой на закон Ньютона.
Рассмотрим также тело B, на которое действует сила f B , ускоряющая тело в точке a B . Предложение, которое необходимо продемонстрировать, состоит в том, что отношение f A к f B является составным отношением масс и ускорений.Утверждение можно продемонстрировать в два этапа со ссылкой на закон Ньютона.
Сначала рассмотрим пропорциональность
Поскольку отношение сил, необходимых для ускорения двух тел с одинаковым ускорением, пропорционально отношению масс этих тел, и поскольку f A движет тело A с ускорением a A , отсюда следует, что F сила, необходимая для перемещения тела B, имеющего массу m B с ускорением a A .
Во-вторых, учитывайте также пропорциональность
Поскольку отношение сил, необходимых для ускорения одного тела при двух разных ускорениях, пропорционально отношению этих ускорений, и поскольку F — это сила, необходимая для перемещения тела B с ускорением a A , отсюда следует, что f B — сила, необходимая для перемещения тела B с ускорением a B .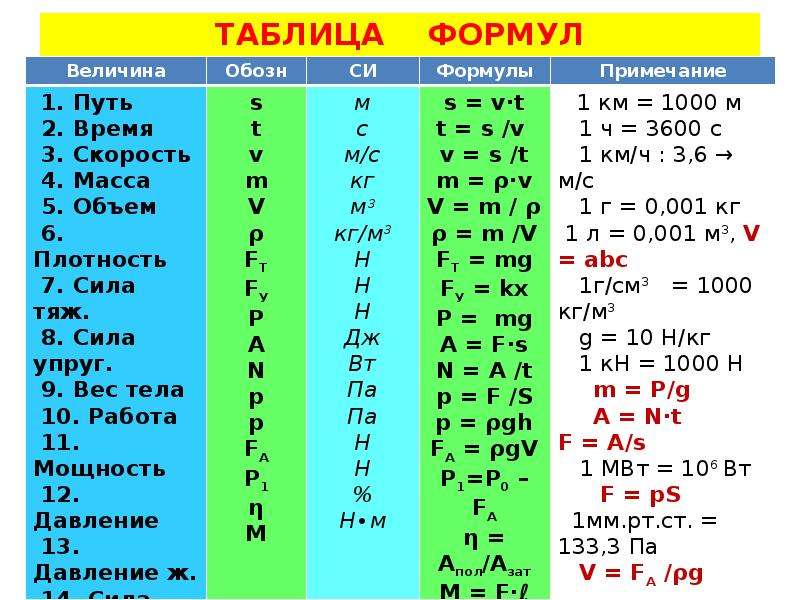
Таким образом, показано, что утверждение о сложном соотношении выполняется.Логика следующая. Предположим, нам нужно подумать об изменении силы от силы, необходимой для ускорения тела А в точке 90 257, 90 199, А, 90 200, 90 260, до силы, необходимой для ускорения тела В в точке 90 199, 90 257, В, 90 260, 90 200 через промежуточную стадию. На первом этапе, используя терминологию Ньютона, f A равно , увеличенному (или уменьшенному ) на определенную величину, чтобы стать F, и изменение силы таково, что f A :F пропорционально к м А :м В .На втором этапе F увеличивается (или уменьшается), чтобы стать f B , а изменение силы таково, что F:f B пропорционально a A :a B . То есть первая и последняя силы находятся в соотношении f A :f B , а комбинация ступеней обозначается составным отношением f A :F·F:f Б . Таким образом, под компаундированием понимается отношение между начальным и конечным количеством через их отношение к общему или промежуточному количеству.
Таким образом, под компаундированием понимается отношение между начальным и конечным количеством через их отношение к общему или промежуточному количеству.
Пропорциональность отношения сил составному соотношению может быть выражена непосредственно следующим образом:
f A :f B ::f A :F ⋅ F:f B
(6)
Пропорциональность отношения сил также может быть выражена «косвенно» в терминах составного отношения масс и ускорений следующим образом:
F
F A : F : F B :: M :: M A : M B ⋅ A A : A B .
(7)
В утверждении (7) силу снова можно представить так, как если бы она изменялась через промежуточную стадию. На первом этапе изменение силы (от f A к f) пропорционально m A :m B , а на втором этапе изменение силы (от F к f B ) пропорционально a A :a B . Комбинированная переделка с ф А на ф В .Конечно, не обязательно, чтобы имел место реальный процесс изменения сил на последовательных стадиях. Вместо этого утверждение (7) предназначено для обобщения сложного набора отношений между отношениями сил, масс и ускорений. По сути, утверждение (7) является не более и не менее аббревиатурой полной цепочки рассуждений, используемых для демонстрации того, что предложение верно.
Комбинированная переделка с ф А на ф В .Конечно, не обязательно, чтобы имел место реальный процесс изменения сил на последовательных стадиях. Вместо этого утверждение (7) предназначено для обобщения сложного набора отношений между отношениями сил, масс и ускорений. По сути, утверждение (7) является не более и не менее аббревиатурой полной цепочки рассуждений, используемых для демонстрации того, что предложение верно.
Таким образом, «метод составления соотношений Евклида совсем не то же самое, что умножение, хотя обе теории демонстрируют структурное сходство» (Grattan-Guinness, 1996, с.362). Структурное сходство становится очевидным при сравнении утверждения (7) с уравнением F = m × a , учитывая современную тенденцию думать об отношениях как об отдельных числах. Таким образом, физическая алгебра является еще одним сокращением для полной линии рассуждений. При условии использования согласованной системы единиц существует прямая параллель между утверждениями о пропорциональности и физической алгеброй, как обсуждается далее.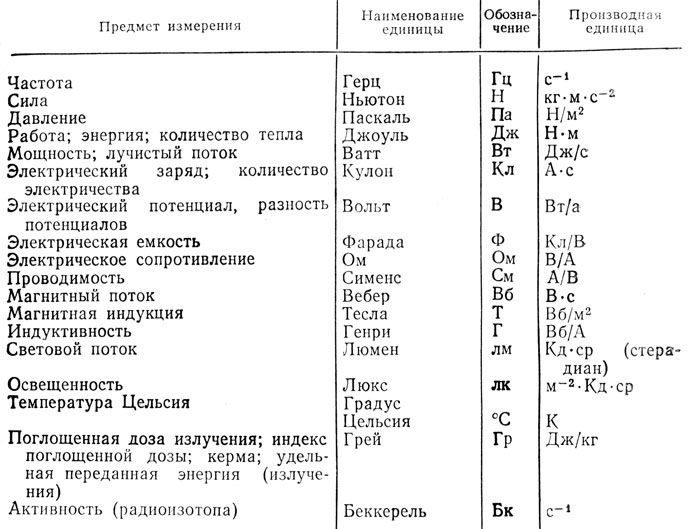
Метрологические правила умножения величин
В метрологии принято рассматривать отношения как чистые числа.Если отношения в утверждении (7) трактовать как числа, умножение измерений дает результат, согласующийся с законом, но только при использовании когерентных единиц. Согласованная система единиц — это система, в которой единицы определены таким образом, чтобы избежать введения мультипликативных констант, которые считаются «лишними» (например, константы типа, необходимого для преобразования имперских единиц в метрические). При условии, что используются единицы из согласованной системы единиц, многие уравнения физики могут быть поняты как сокращенные символические устройства для заявлений о пропорциональности, включающих составные соотношения.В частности, таким образом можно понять уравнения физики, которые используются в определениях единиц СИ. Однако, в первую очередь, связная система возможна только благодаря когерентной совокупности физических отношений (de Boer, 1994/95).
Исходя из этого пункта, когерентные единицы определяются с помощью этих уравнений в сочетании с метрологическим «правилом», согласно которому «значение произведения значений двух конкретных величин в данной системе измеряемых величин и единиц есть произведение их численных значений и единицы новой величины, если такая реализуемая величина может существовать» (Эмерсон, 2008, с.136). В прошлом была признана связь между этим правилом и его историческим происхождением. Как заявил Рош (1998, стр. 108): «На протяжении семнадцатого и восемнадцатого веков произведение или деление физических величин часто понималось как сокращенное выражение составного отношения». Таким образом, пример второго закона движения Ньютона иллюстрирует общую связь между современными алгебраическими выражениями и историческими истоками физической науки.
Было бы интересно рассмотреть онтологическую и эмпирическую основу концепции пропорциональности отношений.Однако сделать это выходит далеко за рамки данной статьи. Здесь достаточно подчеркнуть, что физические отношения сначала мыслились как пропорциональность между отношениями и что поэтому эта концепция, по-видимому, заслуживает тщательного рассмотрения.
Здесь достаточно подчеркнуть, что физические отношения сначала мыслились как пропорциональность между отношениями и что поэтому эта концепция, по-видимому, заслуживает тщательного рассмотрения.
Современные измерения в физике
Теперь мы можем рассмотреть влияние исторического и концептуального анализа на то, как измерения понимаются сегодня. В первую очередь рассматривается прямое измерение, потому что без него не было бы косвенного измерения.Затем рассматривается косвенное измерение.
Прямое измерение устанавливает пропорциональность между отношением непрерывных величин и отношением дискретных величин. Например, мы можем установить, что отношение длины L к единице длины [L] пропорционально отношению 90 257 r 90 260 длин волн к одной длине волны, что выражается в следующем утверждении о пропорциональности:
L:[L]:: r < wl > : < wl > ,
(8)
где  На практике, например, можно установить отношение расстояния к одной длине волны с помощью инструмента, такого как интерферометр, который позволяет подсчитать количество длин волн света, охватывающих измеряемое расстояние.
На практике, например, можно установить отношение расстояния к одной длине волны с помощью инструмента, такого как интерферометр, который позволяет подсчитать количество длин волн света, охватывающих измеряемое расстояние.
Приведенный выше пример прямого измерения особенно важен для SI, поскольку основные единицы расстояния и времени в настоящее время определяются в терминах волновых явлений, и есть предложение определить килограмм в терминах соотношения Планка в будущем ( Миллс, 2010).Прототипы прямого измерения, используемые Krantz et al. (1971) предусматривают формирование «стандартного ряда», получаемого, например, при соединении стержней равной длины. Стандартный ряд может использоваться для установления пропорциональности, такой как L:[L]:: r  определенным образом для получения промежуточной температуры (Kyburg, 1984; Sherry, 2011).
определенным образом для получения промежуточной температуры (Kyburg, 1984; Sherry, 2011).
Как мы видели, давно произошло слияние понятия соотношения и числа. Отношение r
В метрологии большинство единиц Международной системы (СИ) определяются таким образом, который включает в себя законы и/или определения и не затрагивает непосредственно отношения между непрерывными величинами и дискретными величинами. Кибург (1984) назвал измерения, применяемые таким образом, косвенными и/или систематическими измерениями, а Кэмпбелл (1928) назвал производными измерениями.
Примером косвенного измерения является определение единицы силы.Максвелл (1876 г., ст. SLVII) говорил, что «единицей силы является та сила, которая, действуя на единицу массы в единицу времени, порождает единицу скорости». Точно так же определяется единица силы в системе СИ — ньютон. Определение основано на втором законе движения Ньютона, который может быть выражен в единицах СИ с использованием следующего утверждения о пропорциональности:
f ′ :N::m ′ :kg ⋅ a ′ :a,
(9)
где N — ньютон, кг — килограмм, а — единица ускорения, 1 м в секунду в секунду.Используя косвенные измерения, можно установить соотношение между величиной, такой как F’, и единицей, такой как ньютон, с помощью инструмента и процедуры, предназначенных для этой цели. Любой такой инструмент должен быть разработан на основе физических соотношений, которые включают, но не ограничиваются этим отношением, используемым для косвенного определения единицы измерения. В выбранном примере прибор, как правило, будет спроектирован таким образом, чтобы сила воздействовала на массу, ускоряя ее в контролируемых условиях.
В выбранном примере прибор, как правило, будет спроектирован таким образом, чтобы сила воздействовала на массу, ускоряя ее в контролируемых условиях.
Последствия для социальных наук
Подробный анализ возможных последствий для социальных наук выходит за рамки данной статьи.Тем не менее можно коснуться некоторых относящихся к делу соображений и сделать некоторые предварительные замечания.
Один очевидный вопрос, который можно было бы задать, состоит в том, возможно ли понимать психологические явления в терминах пропорциональности и отношения, аналогично тому, как понимаются физические отношения. Существуют ли психологические признаки, пропорциональные друг другу в определенных условиях? Существуют ли психологические атрибуты, пропорциональные физическим атрибутам в определенных условиях? Если бы ответ на любой вопрос был утвердительным, это могло бы послужить основой для измерения психологических характеристик посредством косвенного измерения.
Однако может быть более плодотворно начать с другого вопроса: существуют ли психологические способности для распознавания соотношений и пропорциональности? Кажется, что такие способности должны существовать, ибо физические отношения схватываются восприятием через знакомство с физическими явлениями. Маловероятно, чтобы люди могли воспринимать отношения как основной вид отношений и успешно развивать на этой основе физику, не имея для этого какого-либо сенсорного и умственного аппарата.
Маловероятно, чтобы люди могли воспринимать отношения как основной вид отношений и успешно развивать на этой основе физику, не имея для этого какого-либо сенсорного и умственного аппарата.
Простым примером, показывающим, что люди, вероятно, обладают такой способностью, является соотношение горизонт-отношение, которое применяется к вертикально вытянутым объектам, таким как деревья и столбы. Отношение горизонта — это отношение доли высоты объекта, видимой над горизонтом, к доле высоты объекта, видимой ниже горизонта. Независимо от расстояния до наблюдателя это отношение одинаково для любого объекта одинаковой высоты (Sedgwick, 1973; Gibson, 1986; Rokes, Willson, 2000). Так, например, если ряд фонарных столбов одинаковой высоты простирается к горизонту, наблюдатель увидит одинаковое соотношение высоты над горизонтом и под горизонтом для каждого столба.Имеются свидетельства того, что люди опираются на это отношение, независимо от того, используется ли в качестве ориентира реальный горизонт или неявный горизонт (Bermanini et al. , 1998). Более общий прогноз, который можно сделать, заключается в том, что люди непосредственно воспринимают и реагируют на соотношения и пропорциональности соотношений способами, которые соответствуют функциональным и целенаправленным действиям и реакциям. Это было бы важно для психофизики, потому что это означает сосредоточение внимания на том, как люди воспринимают физические отношения, связанные с функциональным поведением, а также на сенсорных реакциях на стимулы, которые были основным направлением дисциплины на протяжении всей ее истории.
, 1998). Более общий прогноз, который можно сделать, заключается в том, что люди непосредственно воспринимают и реагируют на соотношения и пропорциональности соотношений способами, которые соответствуют функциональным и целенаправленным действиям и реакциям. Это было бы важно для психофизики, потому что это означает сосредоточение внимания на том, как люди воспринимают физические отношения, связанные с функциональным поведением, а также на сенсорных реакциях на стимулы, которые были основным направлением дисциплины на протяжении всей ее истории.
Несмотря на сложное расхождение во взглядах, исторически психофизика сосредоточивалась, в частности, на предполагаемых отношениях между физическими стимулами и ощущениями , где последние принимались за количественные признаки. Однако некоторое время назад было замечено, что человеческая способность непосредственно воспринимать и оценивать соотношения является скупым объяснением эмпирических результатов в психофизике, а именно:
Почему мы должны предполагать, что [человек] основывает свои оценки физических соотношений на оценках психологических соотношений? Почему следующего объяснения недостаточно? Глаза [человека] нормальные, и он узнал, как выглядят палочки, когда они стоят в соотношении 1:2; следовательно, когда он смотрит на стержни, он может с некоторой точностью сказать, находятся ли они в таком соотношении или нет (Savage, 1970, p.
383).
Если люди обладают способностями воспринимать физические отношения и функционально реагировать на них, открывается другой возможный путь. Изучение сенсорного и перцептивного аппаратов может быть плодотворным так же, как мы могли бы изучать сложный набор измерительных инструментов. Такой подход, по существу, имел место в ходе ранних попыток измерить интенсивность света. В этом контексте «центральная проблема касалась установления стандартов яркости на сильно различающихся людях-наблюдателях и на сложном механизме зрительного восприятия.(Джонстон, 2001, стр. 7). Действительно, многое из существующей психофизики может быть понято с этой точки зрения, без необходимости обращаться ни к сенсорным величинам, ни к представлению психологических атрибутов числами. Однако было бы предпочтительнее рассмотреть способы, которыми оценки вытекают из функциональных реакций, поскольку нет никаких причин, по которым люди должны были развить в себе способность устно сообщать об отношениях любого данного вида количества при заданном наборе условий.
Прямые и косвенные измерения в социальных науках
Ранее рассмотренный вопрос заключается в том, можно ли понимать психологические явления с точки зрения пропорциональности и соотношения.Чтобы соответствовать истокам количественной науки, задача состоит в том, чтобы прямо или косвенно измерить предполагаемый количественный психологический атрибут, установив такие пропорции.
Возможность или невозможность прямого измерения в психологии обсуждалась в течение некоторого времени, возможно, наиболее заметно в рамках обсуждений Комитета Фергюсона (Ferguson et al., 1940). Стивенс попытался обойти эти последствия. Кранц и др. (1971) стремились предоставить аксиоматическую основу для измерения, которая позволяет избежать необходимости в эмпирических операциях конкатенации.Аксиоматический репрезентативный подход основан на идее, что для успешного измерения атрибута в психологии требуется теория измерения. Однако история показывает, что физика не развивалась на основе применения репрезентативной теории измерения. Исторический анализ в этой статье показывает, что физическая теория, первоначально выраженная в терминах пропорциональности и отношения, формирует основу для измерения. В соответствии с этим, из прикладной метрологии ясно видно, что для разработки приборов и процедур используется содержательная теория (Hebra, 2010, стр.7). Эта зависимость измерения в физике от субстантивной теории также явно отражена в определениях единиц в SI (de Boer, 1994/95; Massey, 1971; Emerson, 2004; Humphry, 2011a). Таким образом, Кранц и соавт. (1971) отстаивали подход к измерению в социальных науках, который отличается от подхода, используемого в физике, тем, что они обращаются к «теориям, отличным от тех, которые работали в физике» (стр. 17).
Исторический анализ в этой статье показывает, что физическая теория, первоначально выраженная в терминах пропорциональности и отношения, формирует основу для измерения. В соответствии с этим, из прикладной метрологии ясно видно, что для разработки приборов и процедур используется содержательная теория (Hebra, 2010, стр.7). Эта зависимость измерения в физике от субстантивной теории также явно отражена в определениях единиц в SI (de Boer, 1994/95; Massey, 1971; Emerson, 2004; Humphry, 2011a). Таким образом, Кранц и соавт. (1971) отстаивали подход к измерению в социальных науках, который отличается от подхода, используемого в физике, тем, что они обращаются к «теориям, отличным от тех, которые работали в физике» (стр. 17).
Хотя репрезентативные теоретики допускают, что измерение некоторых величин может быть основано на физических законах, Кранц (1972) утверждал, что «измерение физических величин, таких как длина, масса и продолжительность, логически предшествует формулировке количественных законов». физики.Однако было замечено, что единицы СИ длины и длительности определяются с точки зрения физической теории и закона, и что есть предложение определить единицу массы с точки зрения физического отношения. Определения единиц СИ основаны на физических количественных отношениях, включающих соответствующие виды величин, в соответствии с историческим способом выражения отношений в физической науке. Эти определения имеют родственный mise en pratique (набор прикладных инструкций) для измерения в единицах, основанных на определениях.Это означает, что можно подойти к измерению этих величин, используя теорию, определение и закон для разработки измерительных инструментов и процедур. Даже если оставить в стороне вопрос о том, можно ли таким образом подойти к измерению таких величин, как масса, измерение длины может быть достигнуто на основе волновых явлений без обращения к операциям конкатенации. Измерение длины использовалось в качестве прототипа при установке фундамента. Поэтому никоим образом не ясно, является ли измерение физических величин, таких как длина, основанное на операциях конкатенации, логически предшествующим формулировке количественных законов.
физики.Однако было замечено, что единицы СИ длины и длительности определяются с точки зрения физической теории и закона, и что есть предложение определить единицу массы с точки зрения физического отношения. Определения единиц СИ основаны на физических количественных отношениях, включающих соответствующие виды величин, в соответствии с историческим способом выражения отношений в физической науке. Эти определения имеют родственный mise en pratique (набор прикладных инструкций) для измерения в единицах, основанных на определениях.Это означает, что можно подойти к измерению этих величин, используя теорию, определение и закон для разработки измерительных инструментов и процедур. Даже если оставить в стороне вопрос о том, можно ли таким образом подойти к измерению таких величин, как масса, измерение длины может быть достигнуто на основе волновых явлений без обращения к операциям конкатенации. Измерение длины использовалось в качестве прототипа при установке фундамента. Поэтому никоим образом не ясно, является ли измерение физических величин, таких как длина, основанное на операциях конкатенации, логически предшествующим формулировке количественных законов. Вместо этого остается возможным, что к измерению большинства, если не всех, физических величин можно подойти на основе понимания физических отношений.
Вместо этого остается возможным, что к измерению большинства, если не всех, физических величин можно подойти на основе понимания физических отношений.
Таким образом, в попытках связать психологию с фундаментальными измерениями, как они определены Кэмпбеллом (1928, стр. 14), наибольшее внимание привлекли прямые измерения, основанные на конкатенации или аналогичной операции (безуспешно, по крайней мере, назначить свидание). Гораздо меньше внимания уделялось, по крайней мере явно, тому, что Кибург (1984, с.143), именуемый «систематическим измерением» в качестве основного способа приближающегося измерения. Систематические измерения включают в себя величины, которые систематически соотносятся в теоретической структуре. Было бы несколько удивительно, если бы в психологии существовал количественный признак, не имеющий отношения ни к какому физическому признаку. Наоборот, кажется более вероятным, что количественные психологические атрибуты будут связаны с физическими величинами (или их расширением), что делает разумным сослаться, как Берка (1983, с. 13), к «внефизическим измерениям». В той мере, в какой это предположение верно, систематические и косвенные измерения, по-видимому, будут иметь больше шансов на успех.
13), к «внефизическим измерениям». В той мере, в какой это предположение верно, систематические и косвенные измерения, по-видимому, будут иметь больше шансов на успех.
Достаточно просто постулировать количественные отношения в социальных науках, которые чисто формально аналогичны тем, которые составляют основу измерений в физике (см. Humphry, 2011b). Однако, как правило, существует одна из немногих проблем. В некоторых случаях постулируемые отношения включают только непрерывные величины и не имеют основы для прямого измерения.В других случаях речь идет о дискретных величинах, но ясного и прозрачного объяснения пропорциональности отношений непрерывных величин и отношений дискретных величин нет (хотя в психофизике и экономике существуют возможные исключения). В других случаях все же экспоненциальные и логарифмические отношения вызываются таким образом, что это влечет за собой разрыв с истоками физики. Задача состоит в том, чтобы выяснить, существует ли продуктивный подход к систематическим измерениям, позволяющий избежать таких проблем.
Резюме и заключение
Было замечено, что, следуя вдохновленной греками традиции, пионеры физики, такие как Галилей, Ньютон, Кулон и Фарадей, явно формулировали физические отношения как пропорциональности между отношениями. В этой традиции отношения рассматривались как принадлежащие к категории отношения. Поскольку оно основано на этой концепции отношения, классическое определение измерения больше соответствует истокам количественных наук, чем репрезентативная теория.Однако в течение определенного периода истории числа использовались для представления соотношений и линий, и в конце концов стало обычным делом интерпретировать символы в физических уравнениях как числа. Алгебра возникла как сокращение от пропорциональности между отношениями. Эти и другие разработки проложили путь к появлению репрезентативного взгляда на измерение.
Компактная форма обозначений использовалась, чтобы показать параллель между греческой традицией и современной алгеброй. Эта параллель, по-видимому, является причиной того, что классический взгляд на измерение продолжает существовать наряду с репрезентативным взглядом в физических науках. Однако в социальных науках преобладают репрезентативные определения. Вероятной причиной этого является неспособность установить основу для измерения, которая напрямую связана с его происхождением в физической науке.
Однако в социальных науках преобладают репрезентативные определения. Вероятной причиной этого является неспособность установить основу для измерения, которая напрямую связана с его происхождением в физической науке.
В свете зарождения физико-математики цель измерения состоит в том, чтобы установить, что величины находятся в определенном отношении друг к другу. Эта цель может быть достигнута путем сочетания прямого и косвенного измерения. Если речь идет о чем-то похожем на косвенное измерение, основная задача социальных наук состоит в том, чтобы установить четкую основу для прямого измерения.Более непосредственным путем к измерению в социальных науках является углубление нашего понимания того, как люди воспринимают и функционально реагируют на отношения и пропорциональности между отношениями.
Заявление о конфликте интересов
Автор заявляет, что исследование проводилось в отсутствие каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Ссылки
- Берка К. (1983).Измерение: его концепции, теории и проблемы. Бостонская серия по философии науки. Голландия: Reidel Publishing Company, 72 [Google Scholar]
- Bermanini M., Yang T.L., Proffitt D.R. (1998). Восприятие относительного размера на расстоянии лучше всего на уровне глаз. Восприятие. Психофиз. 60, 673–68210.3758/BF03206054 [PubMed] [CrossRef] [Google Scholar]
- Bureau International des Poids et Mesures (BIPM) (2006). Международная система единиц (СИ), 8-е изд. Париж: Organization Intergouvernementale de la Convention du Mètre [Google Scholar]
- Campbell N.Р. (1928). Отчет о принципах измерения и расчета. Лондон: Longmans, Green [Google Scholar]
- Купер Г., Хамфри С. М. (2012). Онтологическое различие между единицами и сущностями. Синтез 187, 393–40110.1007/s11229-010-9832-1 [CrossRef] [Google Scholar]
- de Boer J. (1994/95). К истории количественного исчисления и международной системы. Метрология
31, 405–42910.
 1088/0026-1394/31/6/001 [CrossRef] [Google Scholar]
1088/0026-1394/31/6/001 [CrossRef] [Google Scholar] - Diez J. A. (1997). Сто лет цифр.Историческое введение в теорию измерений 1887–1990 гг. Стад. История Филос. науч. 28, 167–18510.1016/S0039-3681(96)00014-3 [CrossRef] [Google Scholar]
- Emerson WH (2004). Об алгебре величин и их единицах. Метрология 45, 134–13810.1088/0026-1394/45/2/002 [CrossRef] [Google Scholar]
- Emerson WH (2008). О количественном исчислении и единицах измерения. Метрология 45, 134–13810.1088/0026-1394/45/2/002 [CrossRef] [Google Scholar]
- Фергюсон А., Майерс К.С., Бартлетт Р.Дж., Банистер Х., Бартлетт Ф.К., Браун В. и др. (1940). Количественные оценки сенсорных событий: окончательный отчет комитета, назначенного для рассмотрения и отчета о возможности количественных оценок сенсорных событий. Доп. науч. 1, 331–349 [Google Scholar]
- Галилео Г. (1638). «Диалоги о двух новых науках Галилео Галилея», Перевод с итальянского и латинского на английский Х. Крю и А. де Сальвио.
 С введением Антонио Фаваро (Нью-Йорк: Macmillan; ), 1914 [Google Scholar]
С введением Антонио Фаваро (Нью-Йорк: Macmillan; ), 1914 [Google Scholar] - Гибсон Дж.Дж. (1986). Экологический подход к зрительному восприятию. Хиллсдейл, Нью-Джерси: Эрлбаум; (Оригинальная работа опубликована в 1979 г.). [Google Scholar]
- Grattan-Guinness I. (1996). Числа, величины, отношения и пропорции в элементах Евклида: как он с ними обращался? История Мат. 23, 355–37510.1006/hmat.1996.0038 [CrossRef] [Google Scholar]
- Hebra A.J. (2010). Все об инструментах: от вращающихся колес до атомных часов. Нью-Йорк: Springer Wien New York [Google Scholar]
- Хамфри С.М. (2011а). Роль единицы в физике и психометрии. Измерение (Mahwah NJ) 9, 1–24 [Google Scholar]
- Хамфри С. М. (2011b). Роль единицы в физике и психометрии: Ответ. Измерение (Mahwah NJ) 9, 1–24 [Google Scholar]
- Johnston SF (2001). История измерения света и цвета: наука в тени. Бристоль: Издательство Института физики [Google Scholar]
- Кранц Д. Х. (1972). Измерительные структуры и психологические законы.
 Наука
175, 1427–143510.1126/science.175.4029.1427 [PubMed] [CrossRef] [Google Scholar]
Наука
175, 1427–143510.1126/science.175.4029.1427 [PubMed] [CrossRef] [Google Scholar] - Кранц Д. Х., Люс Р. Д., Суппес П., Тверски А. (1971). Основы измерения, Vol. I: Аддитивные и полиномиальные представления. Нью-Йорк: Academic Press [Google Scholar]
- Kyburg HE (1984). Теория и измерение. Кембридж: Издательство Кембриджского университета [Google Scholar]
- Kyburg HE (1996). Величины, величины и числа. Филос. науч. 64, 377–41010.1086/392558 [CrossRef] [Google Scholar]
- Lord F.М., Новик М. Р. (1968). Статистические теории результатов умственных тестов. Рединг, Массачусетс: Addison-Wesley [Google Scholar]
- Luce RD, Suppes P. (2002). «Теория репрезентативных измерений», в Справочнике Стивенса по экспериментальной психологии, том. 4 Methodology in Experimental Psychology, 3rd Edn, eds Pashler H., Wixted J. (New York: Wiley; ), 1–41 [Google Scholar]
- Massey BS (1971). Единицы измерения, анализ размеров и физическое подобие. Лондон: Компания Van Nostrand Reinhold [Google Scholar]
- Maxwell J.
 К. (1876 г.). Материя и движение. Нью-Йорк: Довер, 1952 [Google Scholar]
К. (1876 г.). Материя и движение. Нью-Йорк: Довер, 1952 [Google Scholar] - Мишелл Дж. (1993). Истоки репрезентативной теории измерения: Гельмгольц, Гёльдер и Рассел. Стад. История Филос. науч. 24, 185–20610.1016/0039-3681(93)-L [CrossRef] [Google Scholar]
- Michell J. (1997). Количественная наука и определение измерения в психологии. бр. Дж. Психол. 88, 355–38310.1111/j.2044-8295.1997.tb02641.x [CrossRef] [Google Scholar]
- Michell J.(1999). Измерение в психологии. Кембридж: Издательство Кембриджского университета [Google Scholar]
- Миллс I. (2010). Проект главы 2 для брошюры СИ, после переопределения основных единиц. центральный блок управления; Доступно по адресу: http://www.bipm.org/utils/en/pdf/si_brochure_draft_ch3.pdf [по состоянию на 21 ноября 2012 г.]. [Google Scholar]
- Ньютон И. (1846 г.). Принципы Ньютона: математические принципы естественной философии / сэр Исаак Ньютон; Переведено на английский Эндрю Моттом. Нью-Йорк: Daniel Adee [Google Scholar]
- Roche J.
 (1998). Математика измерения: критическая история. Лондон: The Athlone Press [Google Scholar]
(1998). Математика измерения: критическая история. Лондон: The Athlone Press [Google Scholar] - Рукс П., Уилсон Дж. (2000). Восприятие: теория, развитие и организация. Лондон: Routledge [Google Scholar]
- Рассел Б. (1903). Принципы математики. Кембридж: Издательство Кембриджского университета [Google Scholar]
- Savage CW (1970). Измерение ощущений: критика перцептивной психофизики. Лондон: University of California Press [Google Scholar]
- Sedgwick H.(1973). Видимый горизонт: потенциальный источник визуальной информации для восприятия размера и расстояния. Дисс. Абстр. Междунар. 34, 1301–1302B [Университетские микрофильмы № 73-22530]. [Google Scholar]
- Шерри Д. (2011). Термоскопы, термометры и основы измерения. Стад. История Филос. науч. 42, 509–52410.1016/j.shpsa.2011.07.001 [CrossRef] [Google Scholar]
- Silsbee F. B. (1962). Системы электрических агрегатов. Рез. Натл. Бур. Стоять. сек. С 2, 137–17710.6028/jres.066C.014 [CrossRef] [Google Scholar]
- Stevens S.



 То есть:
То есть:
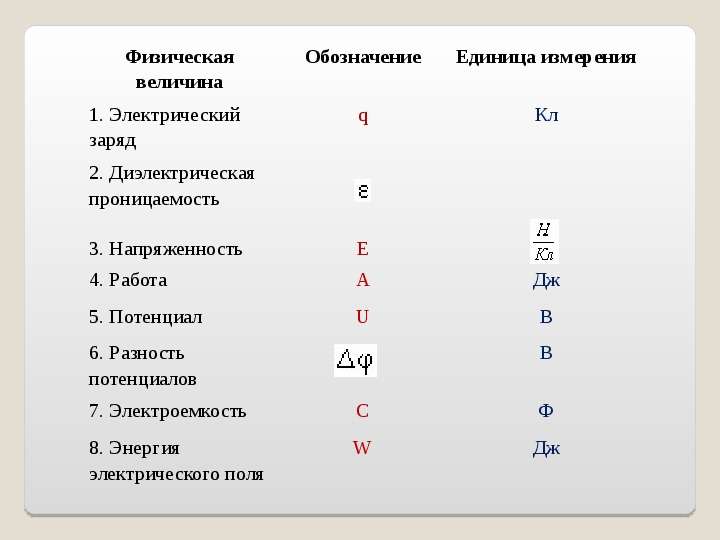 2
2 8 м/с2).
8 м/с2). 2,95 кг ± 0,043 (относительная погрешность)
2,95 кг ± 0,043 (относительная погрешность) (Легче всего это представить, но не обязательно, если представить себе, что груз F находится прямо под центром масс в состоянии равновесия.) Уменьшение D уменьшает восстанавливающий крутящий момент и позволяет небольшому току вызывать большие изменения в равновесии. разделение проводов G и H. Удлинение D увеличивает восстанавливающий момент и делает баланс менее чувствительным к трению о кромки ножей.
(Легче всего это представить, но не обязательно, если представить себе, что груз F находится прямо под центром масс в состоянии равновесия.) Уменьшение D уменьшает восстанавливающий крутящий момент и позволяет небольшому току вызывать большие изменения в равновесии. разделение проводов G и H. Удлинение D увеличивает восстанавливающий момент и делает баланс менее чувствительным к трению о кромки ножей.
 Эта идентификация со временем перешла от линий к числам и даже к самому формальному символу, обозначавшему физическую величину.
Эта идентификация со временем перешла от линий к числам и даже к самому формальному символу, обозначавшему физическую величину. 383).
383). 1088/0026-1394/31/6/001 [CrossRef] [Google Scholar]
1088/0026-1394/31/6/001 [CrossRef] [Google Scholar] С введением Антонио Фаваро (Нью-Йорк: Macmillan; ), 1914 [Google Scholar]
С введением Антонио Фаваро (Нью-Йорк: Macmillan; ), 1914 [Google Scholar] Наука
175, 1427–143510.1126/science.175.4029.1427 [PubMed] [CrossRef] [Google Scholar]
Наука
175, 1427–143510.1126/science.175.4029.1427 [PubMed] [CrossRef] [Google Scholar] К. (1876 г.). Материя и движение. Нью-Йорк: Довер, 1952 [Google Scholar]
К. (1876 г.). Материя и движение. Нью-Йорк: Довер, 1952 [Google Scholar] (1998). Математика измерения: критическая история. Лондон: The Athlone Press [Google Scholar]
(1998). Математика измерения: критическая история. Лондон: The Athlone Press [Google Scholar]