Дифракция света: явление, наблюдение, примеры
Шесть важных явлений описывают поведение световой волны, если она встречает на своем пути какое-либо препятствие. К этим явлениям относятся отражение, преломление, поляризация, дисперсия, интерференция и дифракция света. В данной статье речь пойдет о последнем из них.
Споры о природе света и опыты Томаса Юнга
В середине XVII века на равных правах существовали две теории, касающиеся природы световых лучей. Основоположником одной из них был Исаак Ньютон, который полагал, что свет – это совокупность быстро движущихся частичек материи. Вторую теорию выдвинул голландский ученый Кристиан Гюйгенс. Он считал, что свет – это особый тип волн, распространяющийся в среде подобно тому, как звук движется в воздухе. Средой для света, согласно Гюйгенсу, был эфир.
Поскольку эфира никто не обнаружил, а авторитет Ньютона был огромным на то время, теорию Гюйгенса отклонили. Однако в 1801 году англичанин Томас Юнг провел следующий эксперимент: он пропускал монохроматический свет через две узкие щели, расположенные близко друг от друга. Проходящий свет он проецировал на стену.
Проходящий свет он проецировал на стену.
Каков был результат этого опыта? Если бы свет представлял собой частицы (корпускулы), как полагал Ньютон, то изображение на стене соответствовало бы четким двум ярким полосам, происходящим от каждой из щелей. Однако Юнг наблюдал совершенно иную картину. На стене появлялась череда темных и светлых полос, причем светлые линии появлялись даже за пределами обеих щелей. Схематическое изображение описанной световой картины представлено на рисунке ниже.
Эта картина говорила об одном: свет является волной.
Явление дифракции
Световая картина в опытах Юнга связана с явлениями интерференции и дифракции света. Оба явления трудно отделить друг от друга, поскольку в ряде экспериментов можно наблюдать их совокупный результат.
Дифракция света заключается в изменении волнового фронта, когда он встречает на своем пути препятствие, размеры которого сравнимы или меньше длины волны. Из этого определения понятно, что дифракция характерна не только для света, но и для любых других волн, например звуковых или волн на поверхности моря.
Также понятно, почему в природе не удается наблюдать это явление (длина световой волны составляет несколько сотен нанометров, поэтому любые макроскопические объекты отбрасывают четкие тени).
Принцип Гюйгенса – Френеля
Явление дифракции света объясняется благодаря названному принципу. Его суть заключается в следующем: распространяющийся прямолинейный плоский волновой фронт приводит к возбуждению вторичных волн. Эти волны являются сферическими, однако если среда однородная, то, налагаясь друг на друга, они приведут к первоначальному плоскому фронту.
Как только возникает какое-либо препятствие (например, две щели в опыте Юнга), то оно становится источником вторичных волн. Поскольку количество этих источников ограничено и определяется геометрическими особенностями препятствия (в случае двух тонких щелей вторичных источников всего два), то результирующая волна уже не даст первоначальный плоский фронт. Последний изменит свою геометрию (например, приобретет сферическую форму), более того, появятся максимумы и минимумы интенсивности света в разных его частях.
Принцип Гюйгенса – Френеля демонстрирует, что явления интерференции и дифракции света являются неразделимыми.
Какие условия необходимы, чтобы можно было наблюдать дифракцию?
Одно из них уже было озвучено выше: это наличие небольших (порядка длины волны) препятствий. Если же препятствие будет относительно больших геометрических размеров, то дифракционная картина будет наблюдаться только вблизи его краев.
Вторым важным условием дифракции света является когерентность волн от разных источников. Это означает, что они должны иметь постоянную разность фаз. Только в этом случае благодаря интерференции можно будет наблюдать устойчивую картину.
Когерентность источников достигается простым способом, достаточно любой световой фронт от одного источника пропустить через одно или несколько препятствий. Вторичные источники от этих препятствий уже будут действовать, как когерентные.
Заметим, что для наблюдения интерференции и дифракции света совершенно не обязательно, чтобы первичный источник был монохроматическим. Об этом будет сказано ниже при рассмотрении дифракционной решетки.
Об этом будет сказано ниже при рассмотрении дифракционной решетки.
Дифракция Френеля и Фраунгофера
Говоря простым языком, дифракция Френеля заключается в рассмотрении картины на экране, расположенном близко к щели. Дифракция же Фраунгофера рассматривает картину, которая получается на расстоянии гораздо большем ширины щели, кроме того, она предполагает, что падающий на щель волновой фронт является плоским.
Выделяют эти два вида дифракции потому, что картины в них получаются разными. Связано это со сложностью рассматриваемого явления. Дело в том, что для получения точного решения дифракционной задачи необходимо использовать теорию электромагнитных волн Максвелла. Принцип же Гюйгенса – Френеля, упомянутый ранее, является хорошим приближением для получения практически пригодных результатов.
Ниже на рисунке показано, как изменяется изображение на дифракционной картине, когда экран удаляют от щели.
На рисунке красная стрелка показывает направление приближения экрана к щели, то есть верхний рисунок соответствует дифракции Фраунгофера и нижний – Френеля. Как видно, при приближении экрана к щели картина становится более сложной.
Как видно, при приближении экрана к щели картина становится более сложной.
Далее в статье будем рассматривать только дифракцию Фраунгофера.
Дифракция на тонкой щели (формулы)
Как выше отмечалось, дифракционная картина зависит от геометрии препятствия. В случае тонкой щели, имеющей ширину a, которую освещают монохроматическим светом с длиной волны λ, положение минимумов (тени) можно наблюдать для углов, соответствующих равенству
sin(θ) = m × λ/a, где m = ±1, 2, 3…
Угол тета здесь отсчитывается от перпендикуляра, соединяющего центр щели и экран. Благодаря этой формуле можно рассчитать, при каких углах будет происходить полное гашение волн на экране. Более того, можно рассчитать порядок дифракции, то есть число m.
Поскольку речь идет о дифракции Фраунгофера, то L>>a, где L – расстояние до экрана от щели. Последнее неравенство позволяет заменить синус угла простым отношением координаты y к расстоянию L, что приводит к следующей формуле:
ym = m×λ×L/a.
Здесь ym – это координата положения минимума порядка m на экране.
Дифракция на тонкой щели (анализ)
Приведенные в предыдущем пункте формулы позволяют проанализировать изменения дифракционной картины при изменении длины волны λ или ширины щели a. Так, увеличение величины a приведет к уменьшению координаты минимума первого порядка y1, то есть свет будет концентрироваться в узком центральном максимуме. Уменьшение же ширины щели приведет к растяжению центрального максимума, то есть он становится расплывчатым. Эта ситуация продемонстрирована на рисунке ниже.
Изменение длины волны действует наоборот. Большие значения λ приводят к размыванию картины. Это означает, что длинные волны лучше дифрагируют, чем короткие. Последнее имеет принципиальное значение при определении разрешающей способности оптических приборов.
Дифракция и разрешающая способность оптических приборов
Наблюдение дифракции света является ограничителем разрешающей способности любых оптических приборов, например телескопа, микроскопа и даже человеческого глаза. Когда речь идет об этих приборах, то рассматривают дифракцию не на щели, а на круглом отверстии. Тем не менее все выводы, сделанные ранее, остаются верными.
Когда речь идет об этих приборах, то рассматривают дифракцию не на щели, а на круглом отверстии. Тем не менее все выводы, сделанные ранее, остаются верными.
Для примера будем рассматривать две светящиеся звезды, которые находятся на огромном расстоянии от нашей планеты. Отверстие, через которое свет попадает в наш глаз, называется зрачком. От двух звезд на сетчатке глаза формируются две дифракционные картины, каждая из которых имеет центральный максимум. Если в зрачок свет от звезд падает под некоторым критическим углом, то оба максимума будут сливаться в один. В этом случае человек будет видеть одну-единственную звезду.
Критерий разрешающей способности был установлен лордом Дж. У. Рэлеем, поэтому в настоящее время он носит его фамилию. Соответствующая математическая формула выглядит так:
sin(θc) = 1,22×λ/D.
Здесь D – диаметр круглого отверстия (объектив, зрачок и так далее).
Таким образом, разрешающую способность можно увеличить (уменьшить θc), если увеличить диаметр объектива или уменьшить длину волны. Первый вариант реализуется в телескопах, позволяющих в несколько раз уменьшать θc по сравнению с глазом человека. Второй вариант, то есть уменьшение λ, находит применение в электронных микроскопах, которые обладают в 100 тысяч раз лучшей разрешающей способностью, чем аналогичные световые приборы.
Первый вариант реализуется в телескопах, позволяющих в несколько раз уменьшать θc по сравнению с глазом человека. Второй вариант, то есть уменьшение λ, находит применение в электронных микроскопах, которые обладают в 100 тысяч раз лучшей разрешающей способностью, чем аналогичные световые приборы.
Дифракционная решетка
Она представляет собой совокупность тонких щелей, находящихся на расстоянии d друг от друга. Если фронт волны является плоским и падает параллельно на эту решетку, тогда положение максимумов на экране описывается выражением
sin(θ) = m×λ/d, где m = 0, ±1, 2, 3…
Формула показывает, что максимум нулевого порядка возникает по центру, остальные расположены под некоторыми углами θ.
Поскольку в формуле стоит зависимость θ от длины волны λ, то это означает, что дифракционная решетка может разлагать свет на цвета подобно призме. Этот факт применяют в спектроскопии для анализа спектров различных светящихся объектов.
Пожалуй, самым известным примером дифракции света является наблюдение цветных оттенков на DVD-диске. Бороздки на нем представляют собой дифракционную решетку, которая, отражая свет, разлагает его на ряд цветов.
Бороздки на нем представляют собой дифракционную решетку, которая, отражая свет, разлагает его на ряд цветов.
Дифракция света. Дифракционная решетка. | Объединение учителей Санкт-Петербурга
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Дифракция света. Дифракционная решетка.
Дифракция света | |
Характерным проявлением волновых свойств света является дифракция света — отклонение света от прямолинейного распространения на резких неоднородностях среды. Дифракция была открыта Ф.Гримальди в конце XVII в. Объяснение явления дифракции света дано Т. Юнгом и О. Френелем, которые не только дали описание экспериментов по наблюдению явлений интерференции и дифракции света, но и объяснили свойство прямолинейности распространения света с позиций волновой теории. |
|
Зоны Френеля Принцип Гюйгенса — Френеля Для того чтобы найти амплитуду световой волны от точечного монохроматического источника света А в произвольной точке О изотропной среды, надо источник света окружить сферой радиусом r=ct. Интерференция волны от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке О, т. е. необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности. Так как расстояния от них до точки О различны, то колебания будут приходить в различных фазах. Наименьшее расстояние от точки О до волновой поверхности В равно Аналогично определяются границы других зон. Если разность хода от двух соседних зон равна половине длины волны, то колебания от них приходят в точку О в противоположных фазах и наблюдается интерференционный минимум, если разность хода равна длине волны, то наблюдается интерференционный максимум. Таким образом, если на препятствии укладывается целое число длин волн, то они гасят друг друга и в данной точке наблюдается минимум (темное пятно). Если нечетное число полуволн, то наблюдается максимум (светлое пятно). Расчеты позволили понять, каким образом свет от точечного источника, испускающего сферические волны, достигает произвольной точки О пространства. | |
Дифракция от различных препятствий:
| |
Дифракция происходит на предметах любых размеров, а не только соизмеримых с длиной волны | |
Дифракция наблюдается хорошо на расстоянии . Если , то дифракция невидна и получается резкая тень (d – диаметр экрана). Эти соотношения определяют границы применимости геометрической оптики. Если наблюдение ведется на расстоянии , где d—размер предмета, то начинают проявляться волновые свойства света. На рис. показана примерная зависимость результатов опыта по распространению волн в зависимости от соотношения размеров препятствия и длины волны. | |
Интерференционные картины от разных точек предмета перекрываются, и изображение смазывается, поэтому прибор не выделяет отдельные детали предмета. Дифракция устанавливает предел разрешающей способности любого оптического прибора. где D — диаметр зрачка; телескопа α=0,02” микроскопа: увеличение не более 2-10 | |
Дифракционная решетка | |
Дифракционная решетка – система препятствий (параллельных штрихов), сравнимых по размерам с длиной волны. Величина d = a + b называется постоянной (периодом) дифракционной решетки, где а — ширина щели; b — ширина непрозрачной части. Угол φ – угол отклонения световых волн вследствие дифракции. Наша задача – определить, что будет наблюдаться в произвольном направлении φ – максимум или минимум. Оптическая разность хода Из условия максимума интерференции получим: . ( равен 0, ± 1, ± 2 и т.д.). | |
Определение λ с помощью дифракционной решетки | |
Теги:
конспект
| Дифракция света Классически считается, что свет всегда движется по прямой линии, но на самом деле световые волны имеют тенденцию огибать близлежащие барьеры, распространяясь в процессе. Очень простую демонстрацию дифракции можно провести, держа руку перед источником света и медленно сжимая два пальца, наблюдая за светом, проходящим между ними. Когда пальцы приближаются друг к другу и очень близко друг к другу, начинает появляться серия темных линий, параллельных пальцам. Параллельные линии являются примером  Величина возникающей дифракции зависит от длины волны света, и более короткие волны преломляются под большим углом, чем более длинные. Величина возникающей дифракции зависит от длины волны света, и более короткие волны преломляются под большим углом, чем более длинные.Изображение ниже также иллюстрирует, что происходит, когда световая волна, проходящая через атмосферу, сталкивается с каплей воды. Как показано, свет сначала преломляется на границе раздела воздуха и воды, а затем отражается, когда снова встречается с границей раздела. Луч, все еще путешествующий внутри капли воды, затем еще раз преломляется, когда он в третий раз попадает на поверхность раздела. Это последнее взаимодействие с границей раздела преломляет свет обратно в атмосферу, но также преломляет часть света, как показано ниже. Этот элемент дифракции приводит к явлению, известному как Гало Челлини , или Эффект Хайлигеншайна , при котором тень головы наблюдателя окружает яркое кольцо света. Термины дифракция и рассеяние часто используются взаимозаменяемо и считаются почти синонимами. Однако дифракция описывает особый случай светорассеяния, при котором объект с регулярно повторяющимися элементами, например дифракционная решетка, создает упорядоченную дифракцию света на дифракционной картине. Одна из самых классических и фундаментальных концепций дифракции может быть продемонстрирована экспериментом по оптической дифракции с одной щелью, впервые проведенным в начале девятнадцатого века. То есть, когда световая волна распространяется через щель, физический размер апертуры по отношению к длине волны падающего луча определяет реакцию света. Эта же концепция проиллюстрирована ниже на рисунке 2. Как показано в левой части рисунка, когда длина волны ( l ) намного меньше ширины апертуры ( d ), волна просто движется вперед по прямой линии, как если бы это была частица или апертура отсутствовала. Однако правая часть рис. 2 иллюстрирует другую ситуацию. В этом случае длина волны света, прошедшего точечным источником, превышает размер апертуры, и свет дифрагирует, при этом первичный падающий световой пучок попадает в точку P и первые вторичные максимумы в точке Q . , где q — угол между центральным направлением распространения падающего излучения и первым минимумом дифракционной картины. Ниже на Рисунке 3 эта точка дополнительно иллюстрируется графиком зависимости интенсивности луча от дифракционного радиуса. Обратите внимание, что минимумы, расположенные между вторичными максимумами, расположены кратно p . Эксперимент по дифракции с одной щелью впервые объяснил Огюстен Френель, который вместе с Томасом Янгом представил важные доказательства, подтверждающие, что свет распространяется волнами. где A – амплитуда падающей волны, r – расстояние между d и Q , а f ( c ) – функция угла наклона 7 c 9003 введен Френелем. Важно отметить, что и это уравнение Френеля, и уравнение, связанное ранее, предназначены только для описания поведения дифракции через отверстие в форме щели.
Тем не менее, чрезвычайно важно учитывать круглые апертуры, поскольку все оптические инструменты имеют круглые апертуры. Зрачок глаза и круглая диафрагма и линзы микроскопа являются свидетельством этого факта. Круглые апертуры создают дифракционные картины, подобные тем, которые были описаны ранее, но эти картины естественным образом демонстрируют круговую симметрию. где q(1) — угловое положение дифракционных минимумов первого порядка (первое темное кольцо), l — длина волны падающего света, d — диаметр апертуры, 1,22 — a постоянный. В большинстве случаев угол q(1) очень мал, поэтому приближение, согласно которому sin и тангенс угла почти равны, дает: Из этих уравнений становится очевидным, что центральный максимум прямо пропорционален l/d , что делает этот максимум более размытым для более длинных волн и для меньших апертур. Дифракция играет первостепенную роль в ограничении разрешающей способности любого оптического прибора. Разрешающая способность — это способность оптического прибора создавать отдельные изображения двух соседних точек. Какой бы совершенной ни была линза, изображение точечного источника света, создаваемое линзой, сопровождается максимумами вторичного и более высокого порядка. Поэтому важно понимать, что хотя предыдущие уравнения были выведены для изображения точечного источника света на бесконечном расстоянии от апертуры, разумное приближение разрешающей способности микроскопа может быть получено при замене d для диаметра объектива. Следовательно, если два объекта находятся на расстоянии 90 037 D 90 039 друг от друга и находятся на расстоянии L от наблюдателя, угол (выраженный в радианах) между ними: Затем два предыдущих уравнения можно сжать, чтобы получить: , где D(0) — минимальное расстояние между объектами, которое позволит их разрешить. Согласно этому уравнению, человеческий глаз должен иметь возможность различать объекты, находящиеся на расстоянии 0,056 миллиметра. Разрешающая способность оптических микроскопов определяется рядом факторов, таких как оптическая юстировка микроскопа, качество линз и преобладающие длины волн света, используемые для изображения образца. В самых идеальных условиях разрешающая способность составляет около 0,2 мкм. Однако часто нет необходимости рассчитывать точную разрешающую способность каждого используемого объектива, но важно понимать возможности объективов микроскопа применительно к реальному миру. Соавторы Мортимер Абрамовиц – Olympus America, Inc., Two Corporate Center Drive., Мелвилл, Нью-Йорк, 11747. Shannon H. Neaves и Michael W. Davidson – Национальная лаборатория сильного магнитного поля, 1800 г. Восточный Пол Дирак Доктор, Государственный университет Флориды, Таллахасси, Флорида, 32310. НАЗАД К СВЕТУ И ЦВЕТУ Вопросы или комментарии? Отправить нам письмо.© 1998-2022 автор Майкл В. Дэвидсон и Государственный университет Флориды. Все права защищены. Никакие изображения, графика, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения владельцев авторских прав. Использование этого веб-сайта означает, что вы соглашаетесь со всеми правовыми положениями и условиями, изложенными владельцами.Этот веб-сайт поддерживается нашимиГруппа графического и веб-программирования в сотрудничестве с Optical Microscopy в Национальной лаборатории сильного магнитного поля. Последнее изменение: пятница, 13 ноября 2015 г., 14:18Количество обращений с 10 марта 2003 г.: 77931Посетите сайты наших партнеров в сфере образования: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Учебное пособие по физике: волновое поведение света
Вековые споры, которые продолжаются среди ученых, связаны с вопросом: “Свет – это волна или поток частиц?” Очень примечательные и выдающиеся физики приняли каждую сторону аргумента, предоставив множество доказательств для каждой стороны. Дело в том, что свет проявляет поведение, характерное как для волн, так и для частиц. В этом разделе учебника по физике основное внимание будет уделено волнообразной природе света.
Дело в том, что свет проявляет поведение, характерное как для волн, так и для частиц. В этом разделе учебника по физике основное внимание будет уделено волнообразной природе света.
Свет демонстрирует определенное поведение, характерное для любой волны, которое трудно объяснить с точки зрения чисто частиц. Свет отражается так же, как отражается любая волна. Свет преломляется так же, как преломляется любая волна. Свет дифрагирует так же, как дифрагирует любая волна. Свет претерпевает интерференцию точно так же, как интерферирует любая волна. И свет проявляет эффект Доплера точно так же, как любая волна проявляет эффект Доплера. Свет ведет себя так, как это согласуется с нашим концептуальным и математическим пониманием волн. Поскольку свет ведет себя как волна, у кого-то были бы веские основания полагать, что это может быть волна. В Уроке 1 мы исследуем разнообразие поведения, свойств и характеристик света, которые, кажется, поддерживают волновую модель света. На этой странице мы сосредоточимся на трех конкретных характеристиках — отражении, преломлении и дифракции.
Волна не просто останавливается когда достигает конца среды. Скорее волна будет вести себя определенным образом, когда встретит конец среды. В частности, будет некоторое отражение от границы и некоторая передача в новую среду. Прошедшая волна преломляется (или изгибается), если подходит к границе под углом. Если граница представляет собой просто препятствие, внедренное в среду, и если размеры препятствия меньше длины волны, то будет очень заметна дифракция волны вокруг объекта. Каждое из этих явлений — отражение, преломление и дифракция — характеризуется определенными концептуальными принципами и математическими уравнениями. Отражение, преломление и дифракция волн были впервые представлены в Разделе 10 Учебного пособия по физике. В разделе 11 учебника по физике обсуждались отражение, преломление и дифракция звуковых волн. Теперь мы увидим, как световые волны демонстрируют свою волновую природу путем отражения, преломления и дифракции.
Отражение световых волн
Известно, что все волны претерпевают отражение или отражаются от препятствия. Большинство людей очень привыкли к тому, что световые волны тоже претерпевают отражение. Отражение световых волн от зеркальной поверхности приводит к формированию изображения. Одной из характеристик отражения волн является то, что угол, под которым волна приближается к плоской отражающей поверхности, равен углу, под которым волна покидает поверхность. Эта характеристика наблюдается для волн на воде и звуковых волн. Это наблюдается и для световых волн. Свет, как и любая волна, следует закону отражения при отражении от поверхностей. Отражение световых волн будет обсуждаться более подробно в Разделе 13 Класса физики. А пока достаточно сказать, что отражательное поведение света свидетельствует о волнообразной природе света.
Большинство людей очень привыкли к тому, что световые волны тоже претерпевают отражение. Отражение световых волн от зеркальной поверхности приводит к формированию изображения. Одной из характеристик отражения волн является то, что угол, под которым волна приближается к плоской отражающей поверхности, равен углу, под которым волна покидает поверхность. Эта характеристика наблюдается для волн на воде и звуковых волн. Это наблюдается и для световых волн. Свет, как и любая волна, следует закону отражения при отражении от поверхностей. Отражение световых волн будет обсуждаться более подробно в Разделе 13 Класса физики. А пока достаточно сказать, что отражательное поведение света свидетельствует о волнообразной природе света.
Преломление световых волн
Известно, что все волны претерпевают преломление при переходе из одной среды в другую. То есть, когда фронт волны пересекает границу между двумя средами, направление движения фронта волны резко меняется; путь «изогнут». Такое поведение рефракции волн можно описать как концептуальными, так и математическими принципами. Во-первых, направление «изгиба» зависит от относительной скорости двух сред. Волна изгибается в одну сторону, когда она проходит из среды, в которой она распространяется медленно, в среду, в которой она распространяется быстро; а при переходе с быстрая среда до медленная среда , фронт волны будет изгибаться в противоположном направлении. Во-вторых, величина изгиба зависит от фактической скорости двух сред по обе стороны от границы. Величина изгиба представляет собой измеримое поведение, которое подчиняется определенным математическим уравнениям. Эти уравнения основаны на скорости волны в двух средах и углах, под которыми волна приближается к границе и отходит от нее. Известно, что свет, как и любая волна, преломляется при переходе из одной среды в другую. Фактически, изучение преломления света показывает, что его преломляющее поведение подчиняется тем же концептуальным и математическим правилам, которые управляют преломлением других волн, таких как водные волны и звуковые волны.
Такое поведение рефракции волн можно описать как концептуальными, так и математическими принципами. Во-первых, направление «изгиба» зависит от относительной скорости двух сред. Волна изгибается в одну сторону, когда она проходит из среды, в которой она распространяется медленно, в среду, в которой она распространяется быстро; а при переходе с быстрая среда до медленная среда , фронт волны будет изгибаться в противоположном направлении. Во-вторых, величина изгиба зависит от фактической скорости двух сред по обе стороны от границы. Величина изгиба представляет собой измеримое поведение, которое подчиняется определенным математическим уравнениям. Эти уравнения основаны на скорости волны в двух средах и углах, под которыми волна приближается к границе и отходит от нее. Известно, что свет, как и любая волна, преломляется при переходе из одной среды в другую. Фактически, изучение преломления света показывает, что его преломляющее поведение подчиняется тем же концептуальным и математическим правилам, которые управляют преломлением других волн, таких как водные волны и звуковые волны. Преломление световых волн будет обсуждаться более подробно в Разделе 14 Учебного пособия по физике. А пока достаточно сказать, что преломление света свидетельствует о волнообразной природе света.
Преломление световых волн будет обсуждаться более подробно в Разделе 14 Учебного пособия по физике. А пока достаточно сказать, что преломление света свидетельствует о волнообразной природе света.
Дифракция световых волн
Отражение включает изменение направления волн, когда они отражаются от преграды. Преломление волн связано с изменением направления волн при переходе из одной среды в другую. А дифракция предполагает изменение направления волн, когда они проходят через отверстие или вокруг препятствия на своем пути. Водяные волны могут огибать углы, препятствия и отверстия. Звуковые волны делают то же самое. Но как насчет света? Огибают ли световые волны препятствия и отверстия? Если они это сделают, то это даст еще больше доказательств в поддержку веры в то, что свет ведет себя как волна.
Когда свет встречает препятствие на своем пути, это препятствие блокирует свет и может вызвать образование тени в области позади препятствия. Свет не проявляет очень заметной способности огибать препятствие и заполнять светом область за ним. Тем не менее, свет дифрагирует вокруг препятствий. На самом деле, если вы внимательно понаблюдаете за тенью, вы заметите, что ее края чрезвычайно размыты. Эффекты интерференции возникают из-за дифракции света вокруг разных сторон объекта, в результате чего тень объекта становится нечеткой. Это часто демонстрируется в классе физики с помощью лазерного света и демонстрации копейки. Свет, преломляющийся вокруг правого края монеты, может конструктивно и деструктивно мешать свету, преломляющемуся вокруг левого края монеты. В результате создается интерференционная картина; узор состоит из чередующихся колец света и тьмы. Такой рисунок заметен только в том случае, если узкий пучок монохроматического света (т. Е. Света с одной длиной волны) проходит, направленный на пенни. На фотографии справа показана интерференционная картина, созданная таким образом. Поскольку световые волны дифрагируют вокруг краев монеты, волны разбиваются на разные волновые фронты, которые сходятся в точке на экране, создавая интерференционную картину, показанную на фотографии.
Свет не проявляет очень заметной способности огибать препятствие и заполнять светом область за ним. Тем не менее, свет дифрагирует вокруг препятствий. На самом деле, если вы внимательно понаблюдаете за тенью, вы заметите, что ее края чрезвычайно размыты. Эффекты интерференции возникают из-за дифракции света вокруг разных сторон объекта, в результате чего тень объекта становится нечеткой. Это часто демонстрируется в классе физики с помощью лазерного света и демонстрации копейки. Свет, преломляющийся вокруг правого края монеты, может конструктивно и деструктивно мешать свету, преломляющемуся вокруг левого края монеты. В результате создается интерференционная картина; узор состоит из чередующихся колец света и тьмы. Такой рисунок заметен только в том случае, если узкий пучок монохроматического света (т. Е. Света с одной длиной волны) проходит, направленный на пенни. На фотографии справа показана интерференционная картина, созданная таким образом. Поскольку световые волны дифрагируют вокруг краев монеты, волны разбиваются на разные волновые фронты, которые сходятся в точке на экране, создавая интерференционную картину, показанную на фотографии.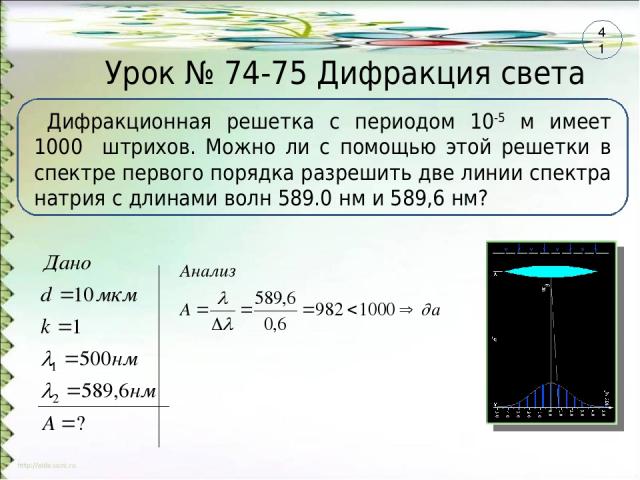


 Вторая зона .
Вторая зона .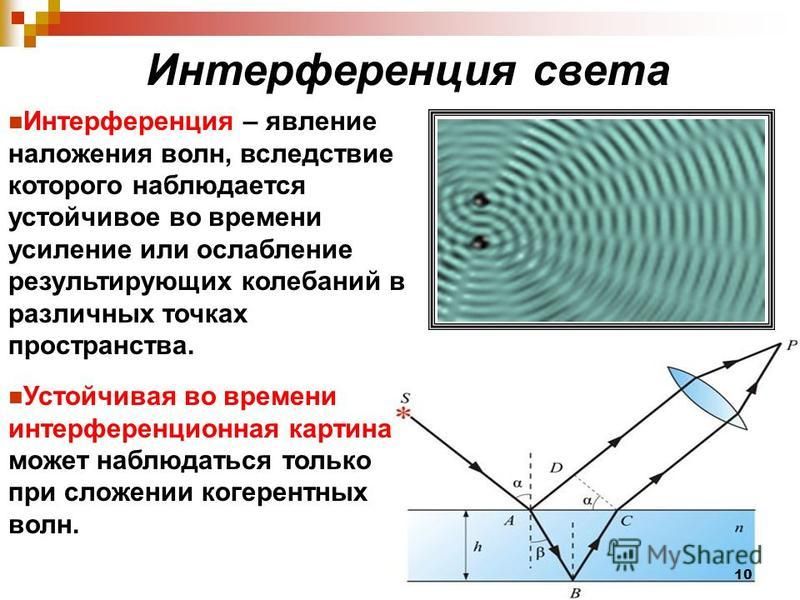 Трудности наблюдения заключаются в том, что вследствие малости длины световой волны интерференционные максимумы располагаются очень близко друг к другу, а их интенсивность быстро убывает.
Трудности наблюдения заключаются в том, что вследствие малости длины световой волны интерференционные максимумы располагаются очень близко друг к другу, а их интенсивность быстро убывает. Разрешающая способность человеческого глаза приблизительно равна одной угловой минуте: ,
Разрешающая способность человеческого глаза приблизительно равна одной угловой минуте: ,

 В реальном мире большинство объектов имеют очень сложную форму, и их следует рассматривать как состоящие из множества отдельных дифракционных элементов, которые в совокупности могут создавать случайное рассеяние света.
В реальном мире большинство объектов имеют очень сложную форму, и их следует рассматривать как состоящие из множества отдельных дифракционных элементов, которые в совокупности могут создавать случайное рассеяние света. Такая ситуация приводит к дифракционной картине, которая состоит из яркой центральной части, называемой первичным максимумом , окруженной с обеих сторон вторичными максимумами , которые разделены темными участками, известными как минимумов . Интенсивность вторичных максимумов уменьшается по мере их удаления от центра, области наибольшей интенсивности. Связь между размером апертуры и возникающей дифракцией можно продемонстрировать с помощью уравнения:
Такая ситуация приводит к дифракционной картине, которая состоит из яркой центральной части, называемой первичным максимумом , окруженной с обеих сторон вторичными максимумами , которые разделены темными участками, известными как минимумов . Интенсивность вторичных максимумов уменьшается по мере их удаления от центра, области наибольшей интенсивности. Связь между размером апертуры и возникающей дифракцией можно продемонстрировать с помощью уравнения: Основываясь на своих выводах, Френель предположил, что амплитуда максимумов первого порядка в точке Q (определяется как e Q ) будет задано уравнением:
Основываясь на своих выводах, Френель предположил, что амплитуда максимумов первого порядка в точке Q (определяется как e Q ) будет задано уравнением: Математический анализ дифракционных картин, создаваемых круглой апертурой, дает уравнение:
Математический анализ дифракционных картин, создаваемых круглой апертурой, дает уравнение: Устранить это явление можно было бы только в том случае, если бы линза имела бесконечный диаметр. Два объекта, разделенные расстоянием менее q(1) не может быть решен, независимо от того, насколько велико увеличение.
Устранить это явление можно было бы только в том случае, если бы линза имела бесконечный диаметр. Два объекта, разделенные расстоянием менее q(1) не может быть решен, независимо от того, насколько велико увеличение. Однако фоторецепторы в сетчатке расположены недостаточно близко друг к другу, чтобы обеспечить такую степень разрешения, и 0,1 миллиметра является более реалистичным числом при нормальных обстоятельствах.
Однако фоторецепторы в сетчатке расположены недостаточно близко друг к другу, чтобы обеспечить такую степень разрешения, и 0,1 миллиметра является более реалистичным числом при нормальных обстоятельствах.