Статья: «Графики в курсе физики по теме “Основы кинематики”» – Другое – Физика и астрономия
Главным при обучении физике является создание единого представления о физике как науке, которая изучает окружающий нас мир. Физика без математики не была бы наукой. Учащимся надо дать понять, что любая физическая закономерность становится законом только в том случае, если она обличена в математическую формулу. Очень важно формулировку законов сопровождать видом графической зависимости. В этом плане само умение строить графики является очень важным. Построение графиков по результатам измерений – важнейшее из метапредметных умений. В диагностических работах апробационного исследования ученики показали низкую грамотность при построении графиков. В большинстве случаев ученики испытывают трудности: как при построении, так и при интерпретации результатов. Основные проблемы – это выбор масштабов (эти масштабы не обязательно должны быть одинаковы, как обычно бывает в заданиях по математике) , построение графика, учет нуля, конкретное использование графиков для обоснования выводов и др.
Но я в данной работе хотела показать как на графических задачах по кинематике можно, применяя математические знания учащихся, не только решать качественные задачи, но и количественные задачи по определению кинематических величин( ускорения, скорости, перемещения и координаты тела). При решении таких графических задач закрепляются понятие системы отсчета, расчетные формулы кинематических величин, геометрическая интерпретация понятий пути, перемещения и координаты тела. В связи с этим высвобождается время для решений задач повышенной сложности, повышается графическая грамотность и идет подготовка для дальнейшего применения графиков при изучении более сложных процессов( в разделах МКТ и термодинамики, электростатики, электродинамики, квантовой физики и т.
В связи с тем, что к 9 классу в курсе математики получены навыки построения графиков линейной зависимости, обратной пропорциональности и параболы квадратного уравнения, нужно научить строить графики зависимости ускорения, скорости, пройденного пути, перемещения и координаты . Начнем с примеров задач построения графиков кинематических величин.
Задача 1. Тело из состояния покоя увеличил свою скорость до 5 м/с за 10 секунд. Затем двигаясь в том же направлении увеличил скорость до 7 м/с за 2 секунду. Постройте график зависимости проекции скорости и проекции ускорения ось Х от времени.
Задача 2. Тело, движущееся со скоростью 2 м/с, останавливается через 10 с, а затем движется к началу координат с таким же ускорением и увеличивает свою скорость до 3 м/с в течение 6 с. Постройте график зависимости проекции скорости и проекции ускорения ось Х от времени.
При построении первого графика обращаем внимание на разные уклоны графиков зависимости скорости на разных участках пути, при решении второй задачи на направления скорости и ускорения.
Построение графиков зависимости координаты и пройденного пути от времени носит качественный характер из- за нехватки достаточных умений по математике.
Задача 3. Тело на первом участке пути двигался равномерно прямолинейно , а потом оставшийся отрезок пути прошло равноускоренно. Постройте график зависимости пройденного пути от времени в течение всего движения. Начальная координата равна 0.
Задача 4. Дан график зависимости скорости тела от времени. Движение прямолинейное. Построить графики зависимости ускорения, координаты и пройденного пути от времени. Начальная координата равна 0.
Решая задачу 4 обращаем внимание учащихся на то, что движение является прямолинейным, и пока тело удаляется от начала координат, х(t), s(t) совпадают. При t Є[t3;t4] координата уменьшается, но пройденный путь продолжает возрастать( пройденный путь – неубывающая функция от времени). Так как a1= tgα1<|tgα2| = |a2|, то парабола на участке t Є[t2;t4] проходит более круто, чем на участке [0 ; t1].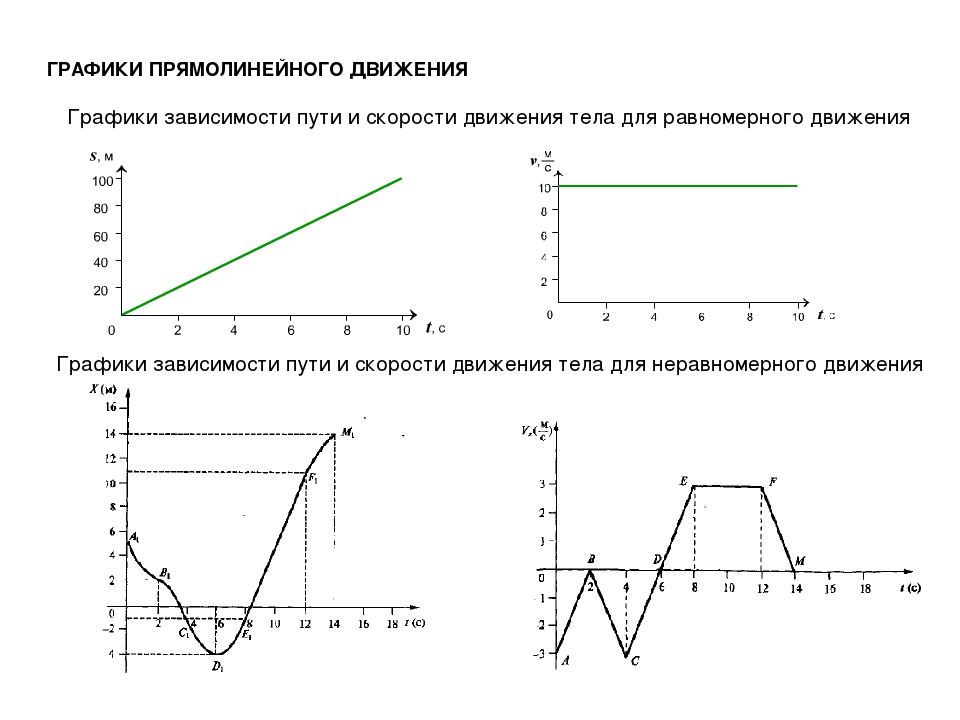
Задача 5. На рисунке представлен график зависимости координаты от времени для материальной точки, движущейся прямолинейно. Построить графики зависимостей проекции ускорения на ось х, а также пройденного пути от времени. Все указанные интервалы времени равны.
[иллюстрации см. в скачиваемом файле]
При разборе данной задачи можно смело оперировать понятиями угловых коэффициентов и для парабол- старшими коэффициентами. Нужно показать, что СD, КL, NG – отрезки прямых с равными по модулю угловыми коэффициентами; ВС, DE, FK, LMN, GT – участки парабол с равными по модулю старшими коэффициентами; АВ и EF – отрезки прямых.
Задача 6. На рисунке представлен график зависимости проекции ускорения от времени для материальной точки, движущейся прямолинейно. А) Как тело двигалось на каждом участке пути? В) Написать уравнение скорости тела на каждом участке пути, если начальная скорость тела равна 2 м/с.
[иллюстрации см. в скачиваемом файле]
График Задача 7.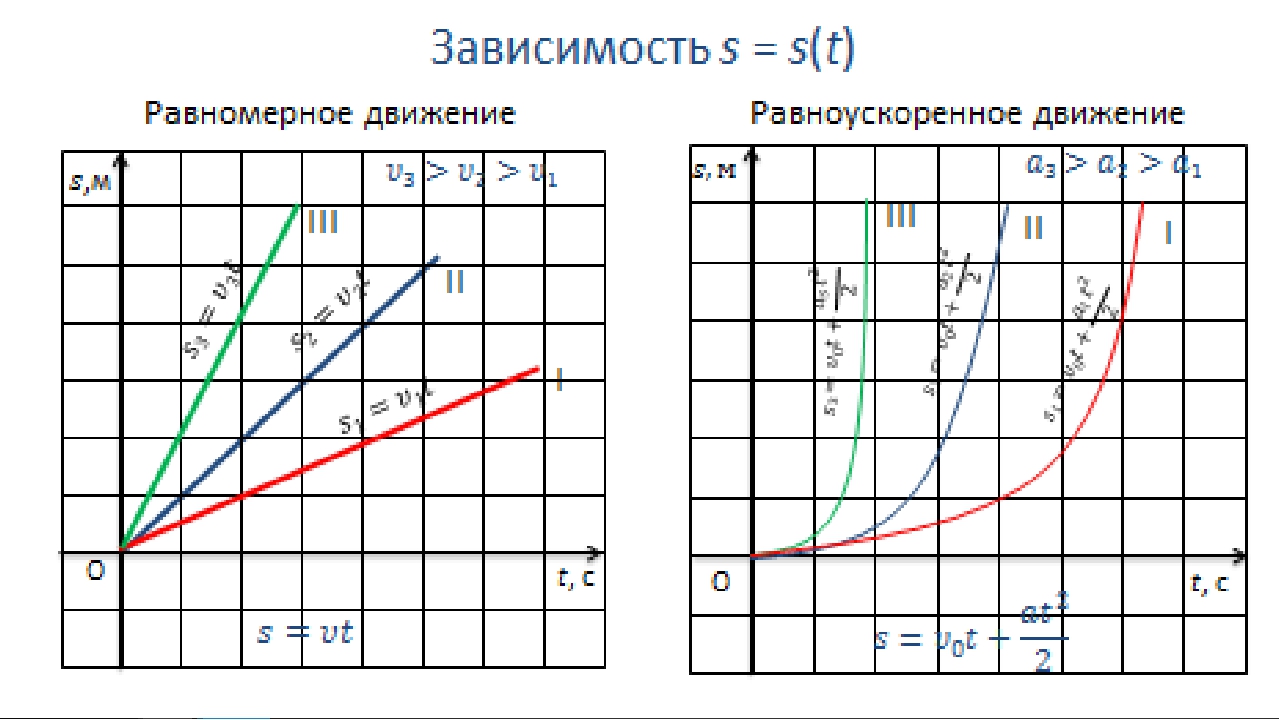 На рисунке представлен график зависимости проекции скорости от времени для материальной точки, движущейся прямолинейно. А) Как тело двигалось на каждом участке пути? В) Написать уравнение движения тела на каждом участке пути, если начальная координата равна 500 м.
На рисунке представлен график зависимости проекции скорости от времени для материальной точки, движущейся прямолинейно. А) Как тело двигалось на каждом участке пути? В) Написать уравнение движения тела на каждом участке пути, если начальная координата равна 500 м.
[иллюстрации см. в скачиваемом файле]
Задача 8. На рисунке представлен график зависимости проекции координаты от времени для материальной точки, движущейся прямолинейно. А) Как тело двигалось на каждом участке пути? В) Написать уравнение движения тела на каждом участке пути, если ускорение движения на всех участках пути одинаково и равно 3 м/с.
[иллюстрации см. в скачиваемом файле]
Решая данные графические задачи удается повторить и закрепить формулы расчета кинематических величин; ученики начинают понимать важность нахождения проекции векторов в разных осях ; одновременно оттачиваются вычислительные и графические навыки, что высвобождает время на изучение сути явлений, на экспериментальную деятельность.
При решении правильно подобранных графических задач обучающиеся овладевают следующими метапредметными умениями:
- Выделение главного, существенных признаков понятий, обобщение понятий;
- Построение логических рассуждений и выводов на основе текстовой информации, рисунков, графиков и схем;
- Сравнение объектов на основе известных характерных свойств;
- Сопоставление полученной информации из различных источников с жизненным опытом в соответствии с поставленными задачами.
Полный текст материала Статья: «Графики в курсе физики по теме “Основы кинематики”» смотрите в скачиваемом файле
На странице приведен фрагмент.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение?
Оставьте комментарий
3.
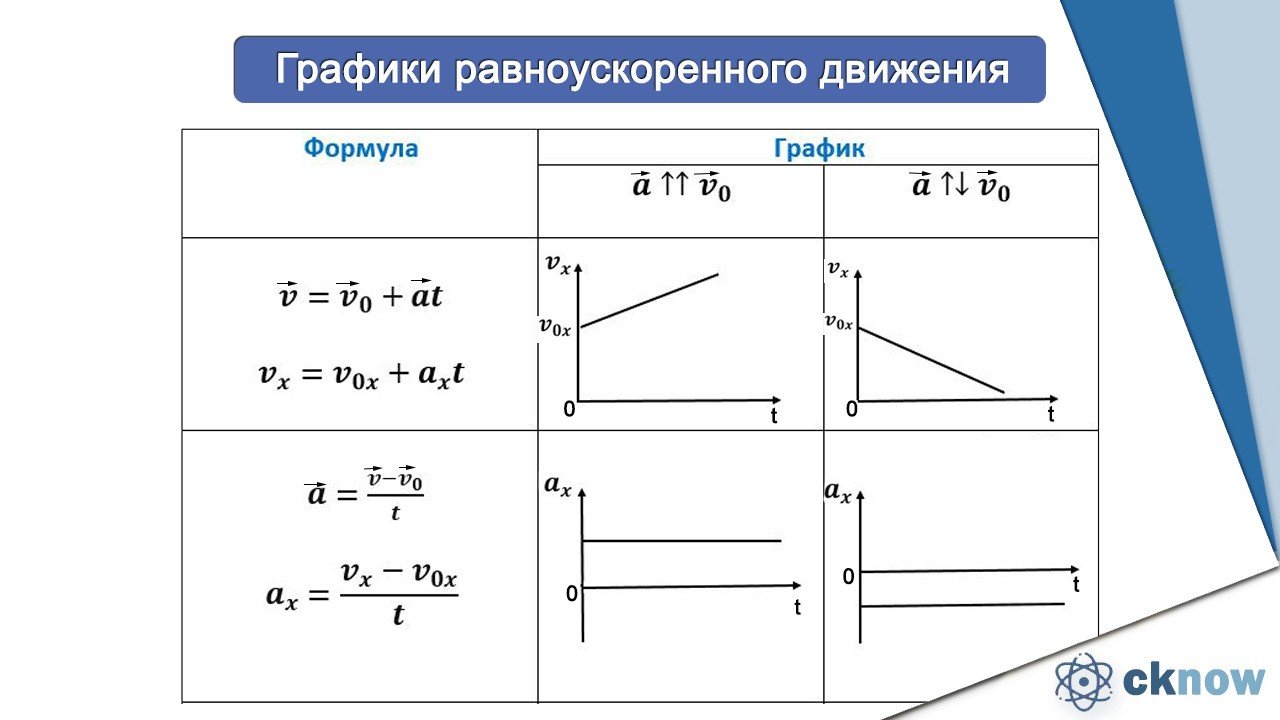
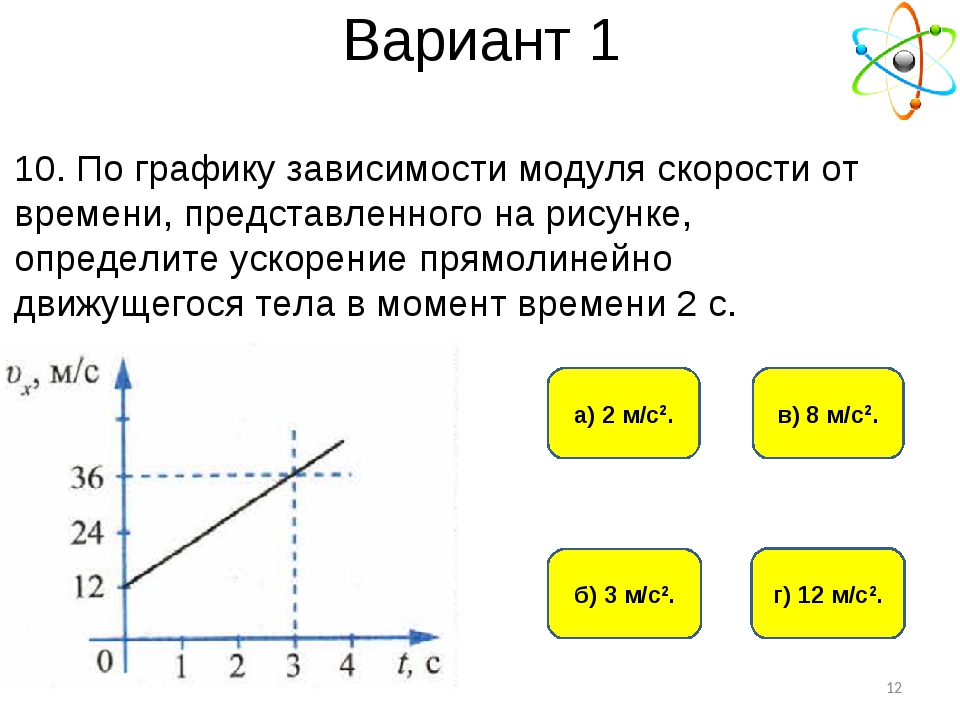 Графики зависимости кинематических величин равноускоренного движения
Графики зависимости кинематических величин равноускоренного движенияКогда на тело действует постоянная сила \(\vec{F}\), скорость тела \(\vec{v}\) изменяется с течением времени \(t\).
Если скорость тела возрастает на одну и ту же величину Δυ за промежуток времени \(\Delta t\), то движение называют равноускоренным:
a→=υ2→−υ1→t2−t1.
Обозначение ускорения \(a\) — первая буква латинского слова \(acceleratio\).
Если скорость тела возрастает \(v_2>v_1\), то ускорение является положительным: a>0.
Если скорость тела убывает \(v_2<v_1\), то ускорение является отрицательным: a<0.
Обрати внимание!
При равномерном движении скорость тела не изменяется с течением времени \(v(t)=const\), ускорение тела равно нулю: a=0.
Рис. \(1\). Графики зависимости ускорения от времени при различных видах движения тела
Скорость при равноускоренном движении вычисляется по формуле:
\(\vec{\upsilon}(t)=\vec{\upsilon}_0+\vec{a}\cdot\Delta t\),
где \(\Delta\)\(t=t-t_0\) — время изменения скорости.
Графики зависимости скорости от времени при равноускоренном движении изображаются прямыми или отрезками прямых. Чем больше ускорение, тем больше угол наклона графика скорости относительно оси времени.
При положительном значении ускорения графики скорости направлены вверх.
Рис. \(2\). Графики зависимости скорости от времени при равноускоренном движении тела
При равнозамедленном движении графики скорости направлены вниз.
Рис. \(3\). Графики зависимости скорости от времени при равноускоренном движении тела с отрицательным ускорением
Уравнение координаты тела при равноускоренном движении:
x(t)=x0+υ0x⋅t+ax⋅t22,
где \(\vec{v}_0\)\(_x\) — проекция вектора начальной скорости \(\vec{v}_0\) на ось \(x\),
\(a_x\) — проекция вектора ускорения \(\vec{a}\) на ось \(x\).
Графиком зависимости координаты от времени при равноускоренном движении будет часть параболы.
При равноускоренном движении ветвь параболы направлена вверх.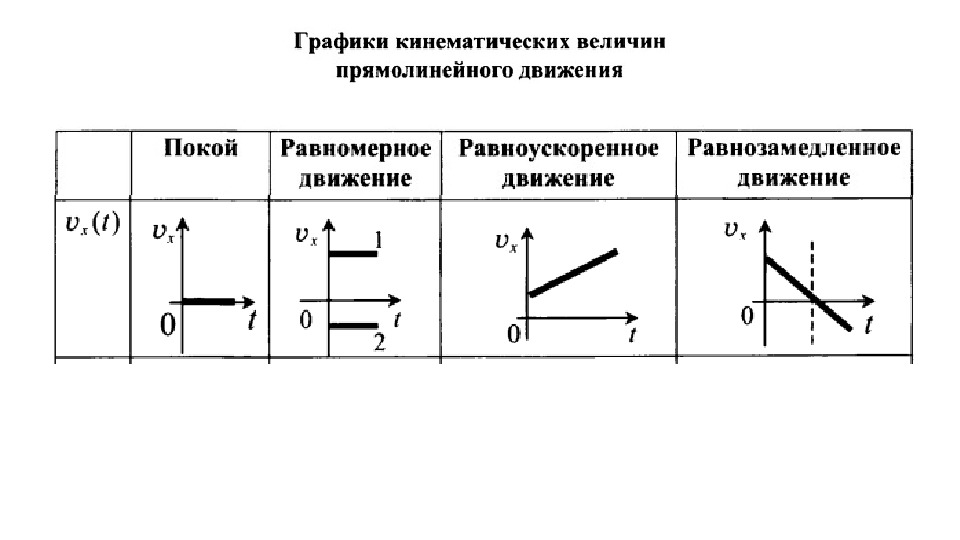
a>0
Рис. \(4\). Графики зависимости координаты от времени при равноускоренном движении тела
При равнозамедленном движении ветвь параболы направлена вниз.
a<0
Рис. \(5\). Графики зависимости координаты от времени при равноускоренном движении тела с отрицательным ускорением
Графический метод решения задач на уроках физики и астрономии. / HEDClub
Методика компьютеризации преподавания фундаментальных дисциплин, в том числе физики и астрономии, сегодня является одной из ключевых проблем организации учебного процесса в колледже.
Интегрирование обычного урока с компьютером позволяет преподавателю значительно разнообразить процесс обучения, делая его более интересным и интенсивным. При этом компьютер не заменяет преподавателя, а только дополняет его.
Для исследования функций и построения графиков требуется много времени, приходится выполнять много громоздких вычислений, это не удобно, на помощь приходят компьютерные технологии.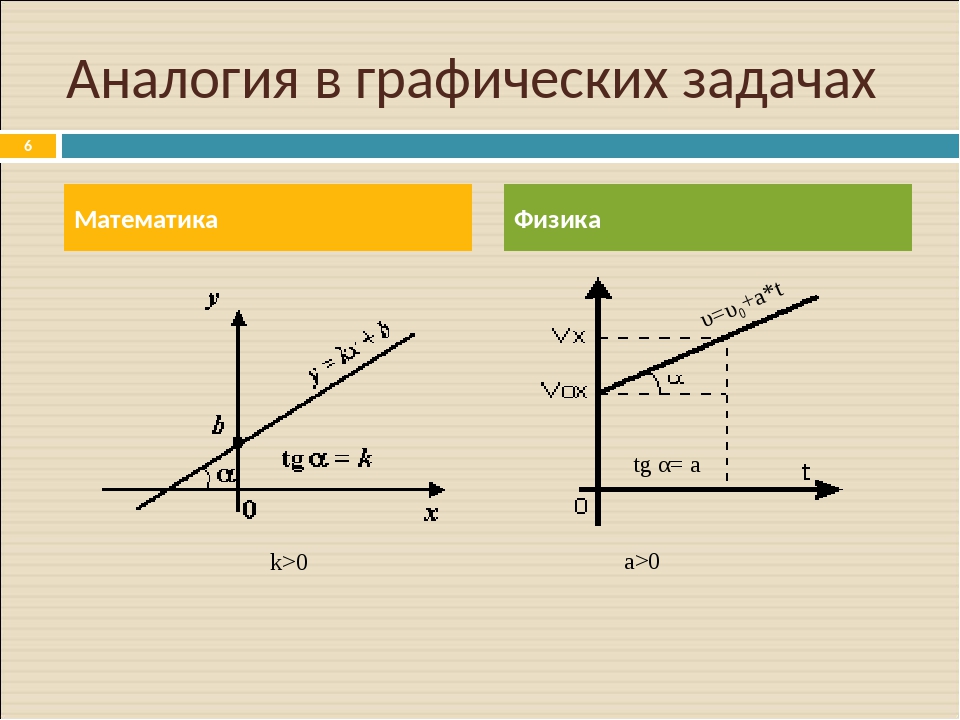 Использование компьютерной техники в решении задач значительно облегчает интеллектуальный труд студента.
Использование компьютерной техники в решении задач значительно облегчает интеллектуальный труд студента.
В своей педагогической практике я использую программу Microsoft Excel в решении графических задач на различных уроках. Такие задачи развивают интерес обучающихся к дисциплине “Физика” и “Астрономия”. Данная программа может сделать урок более эффективным, попутно способствуя расширению знаний и в информатике.
По роли графиков в решении задач различают такие, ответ на которые может быть получен на основе анализа уже имеющегося графика и в которых требуется графически выразить функциональную зависимость между величинами. Решение графических задач способствует уяснению функциональной зависимости между величинами, привитию навыков работы с графиками. В этом их познавательное значение. Графическая грамотность обучающихся, связанная с умением пользоваться графиками, занимает особое и важное место в политехническом обучении, в подготовке обучающихся к работе на производстве, в их профессиональной подготовке.
Приведу примеры следующих задач, для решение которых нужна программа Microsoft Excel.
По дисциплине “Астрономия” при изучение темы: “Планеты Солнечной системы” можно предложить решить следующую задачу:
Рассчитайте плотность планет “Солнечной системы”, если предположить о шарообразной форме планет (данное предположение позволяет находить объём планеты, как объём шара по известному значению среднего радиуса). Построить график зависимости объема планет от их радиуса.
Средний радиус планет (км):
Меркурий | Венера | Земля | Марс | Юпитер | Сатурн | Уран | Нептун |
2440 | 6052 | 6371 | 3396 | 69 911 | 58232 | 25560 | 25000 |
В результате получается вот такой график:
Далее студенты анализируют и определяют, у каких планет получился объем практически одинаковый.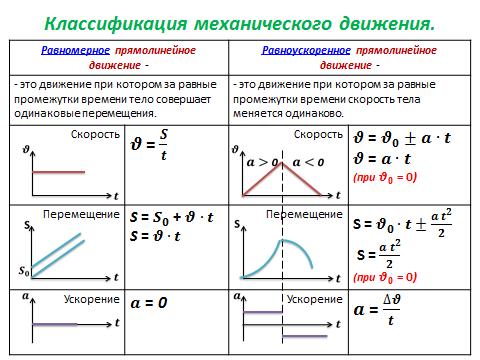
Затем нужно рассчитать плотность планет, если массы планет в (кг):
Меркурий | Венера | Земля | Марс | Юпитер | Сатурн | Уран | Нептун |
0.3 · 1024 | 4.8 · 1024 | 5.9 · 1024 | 0.6 · 1024 | 1876 · 1024 | 561 · 1024 | 86 · 1024 | 101 · 1024 |
Построить график зависимости плотности от массы и объема.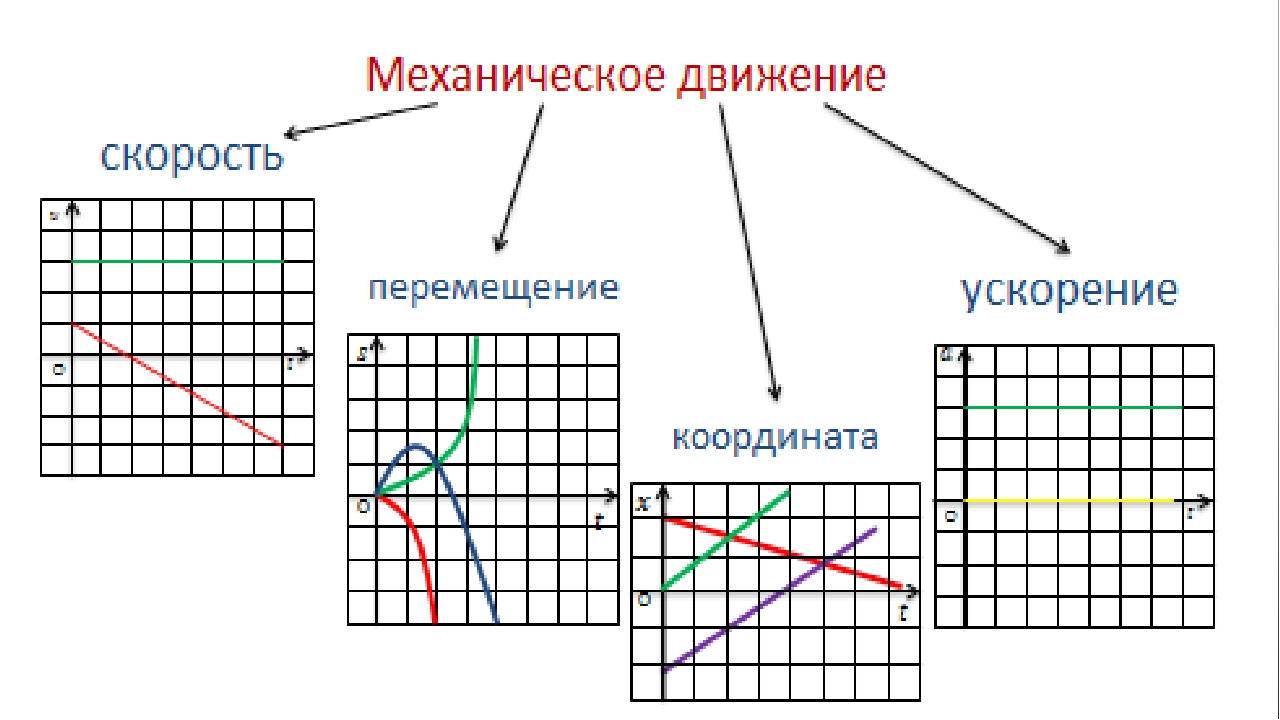 Проанализировать полученные графики.
Проанализировать полученные графики.
По теме: “Переменный ток и его параметры” можно разобрать следующие задачи:
1. Построить график синусоидального тока по данным таблицы.
t,с | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 |
I,А | 0 | 50 | 0 | -50 | 0 | 50 | -50 |
В итоге должен получится вот такой график:
По графику студенты определяют период , амплитудное значение силы тока и составляют уравнение гармонических колебаний.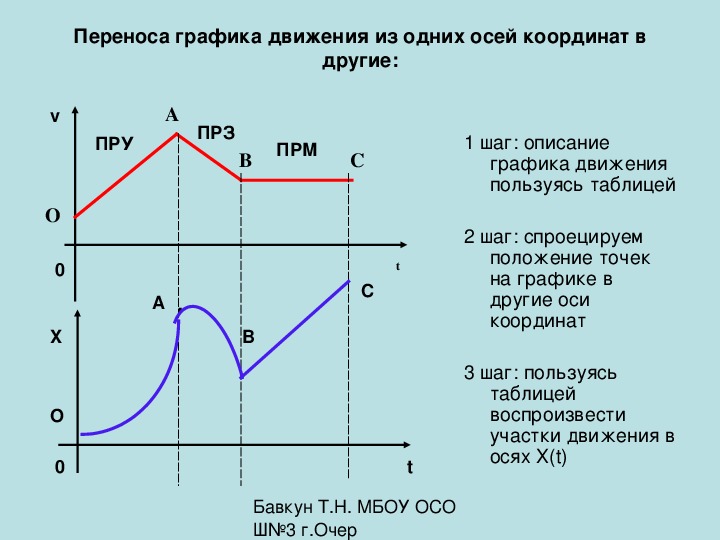
2. Уравнение гармонических колебаний силы переменного тока имеет вид: I=sinπt.Построить график гармонических колебаний силы тока от времени, t от 0 до 2 с, с шагом 0,1.
В итоге должен получится вот такой график
После того как график построен, студенты определяют параметры переменного тока.
3. Построить графики функций в одной системе координат:
U=50 cos (100πt) и U=100cos (100πt ), t от 0 с до 0,15 с, с шагом 0,01. Сравнить параметры переменного тока, и выяснить, что у них общее и в чем отличие.
В заключение хочется сказать, что программа Microsoft Excel предоставляет большие возможности для построения и исследования графиков функций. Используя прикладные программы на уроках физики, конечно же экономят время на достижение результата. Студенты младших курсов, как правило, достаточно хорошо владеют компьютерными программами семейства Microsoft Office, поскольку они изучаются в школьном курсе информатики и поэтому уроки физики несомненно можно проводить с использованием электронной таблицы.
Библиография:
- Дмитриева В.Ф. Физика для профессий и специальностей технического профиля – М.: Образовательно-издательский центр “Академия”, 2010. – 448
- Информатика: Учебник для среднего профессионального образования. И.И. Сергеева, А.А. Музавлевская, Н.В. Тарасова., М.ИД “ФОРУМ” – ИНФА –М 2009. – 336 с:ил.
- Мякишев Г.Я. Физика 11 класс [Текст]: Базовый уровень / Г.Я. Мякишев.- М.: Просвещение,2015.-399 с.
Изопроцессы. Примеры решения графических задач по физике. 10-11 класс
Изопроцессы. Примеры решения графических задач по физике. 10-11 класс
- Подробности
- Просмотров: 1076
Задачи по физике – это просто!
Вспомним
Изопроцессы – это термодинамические процессы при неизменной массе и постоянном значении одного из параметров.

Выше представлены изотермы (графики изменения параметров газа при изотермическом процессе) в разных координатных осях.
(х)1 – начальное состояние газа
(х)2 – последующее состояние газа
Стрелочкой на графике показывают направление перехода из состояния 1 в состояние 2.
2. Изобарный процесс описывается законом Гей-Люсака.
Ниже представлены изобары в разных координатных осях.
3. Изохорный процесс описывается законом Шарля.
Не забываем
Решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики по теродинамике на процессы в газах.
Задача 1
Задан процесс изменения состояния газа в координатах VОТ.
На каждом участке
1). Назвать процессы и указать законы, их описывающие, показать изенения макропарамметров газа.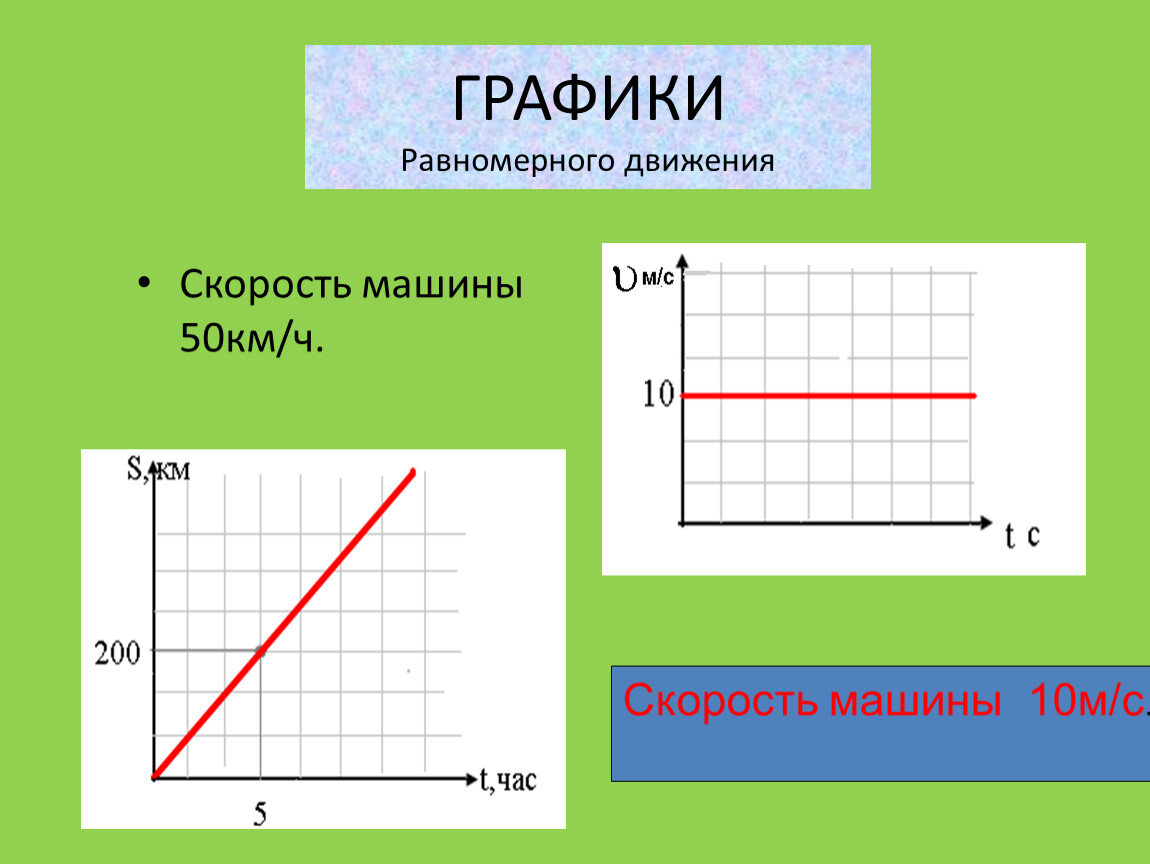
2). Начертить графики изменения состояния газа в координатах pOT и pOV.
Задача 2
Задан процесс изменения состояния газа в координатах рОТ.
На каждом участке
1). Назвать процессы и указать законы, их описывающие, показать изменения макропараметров газа.
2). Начертить графики изменения состояния газа в координатах pOV и VOT.
Задача 3
Задан процесс изменения состояния газа в координатах VОТ.
На каждом участке
1). Назвать процессы и указать законы, их описывающие, показать изменения макропараметров газа.
2). Начертить графики изменения состояния газа в координатах pOT и pOV.
Задача 4
Задан процесс изменения состояния газа в координатах VОТ.
На каждом участке
1). Назвать процессы и указать законы, их описывающие, показать изменения макропараметров газа.
2). Начертить графики изменения состояния газа в координатах pOV и pOT.
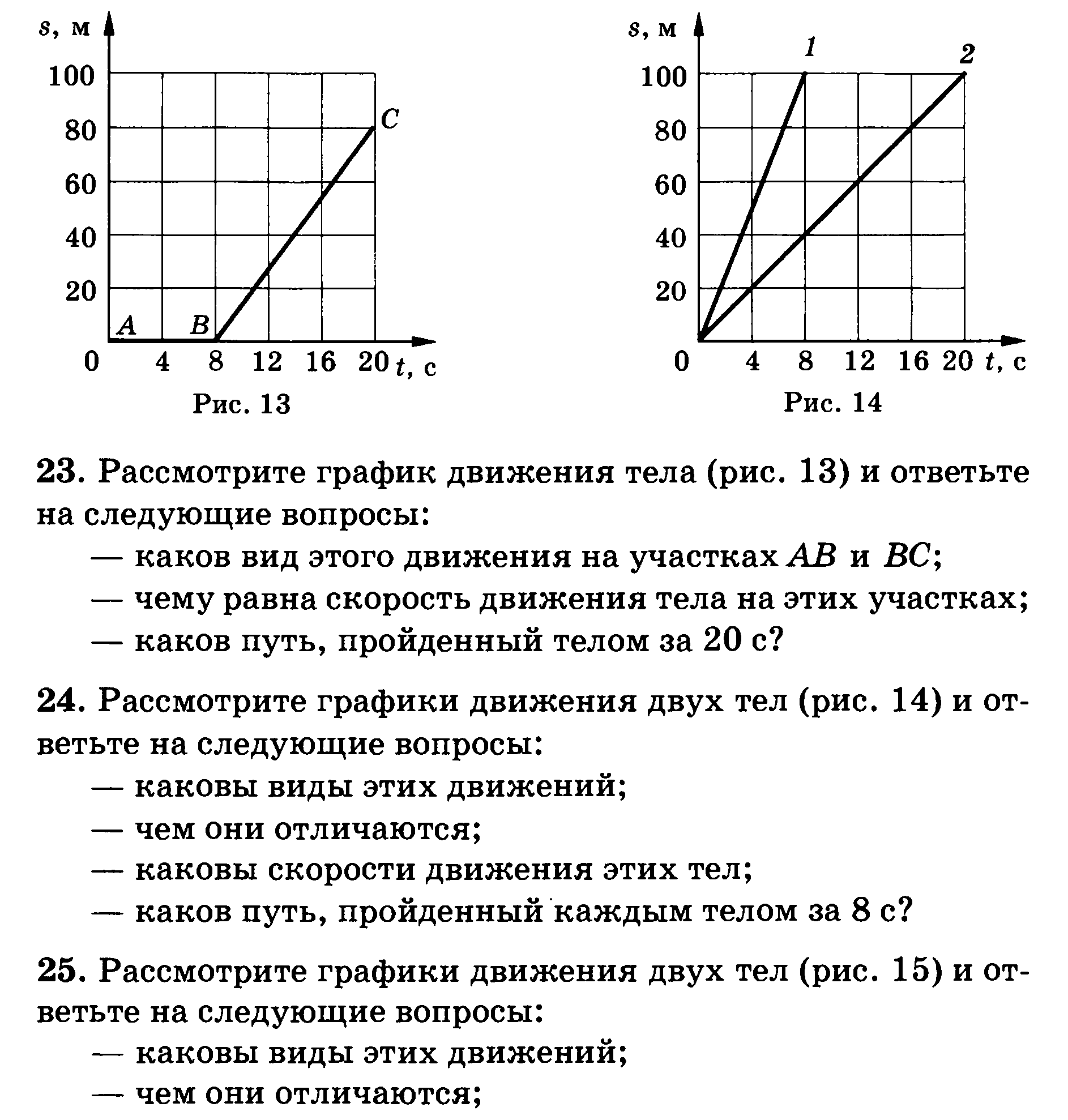
Разбираем графики движения в заданиях по физике
Решим сегодня тест из раздела механика, кинематика
Часто у ребят возникают вопросы при решении задач с графиками движения. В школе данным задачам не уделяется достаточно внимания. Формулы по физике можно просто выучить, а подставив в них нужные величины, получится даже решить несложную задачу. Однако когда условие задачи задано графиком, тут нужно подумать и поразмышлять.
Для начала я всегда учу своих учеников внимательно посмотреть, что за график перед ними. График координаты, перемещения, скорости или, может быть, ускорения? Дальше нужно определить, какой тип движения изображен. Как известно, движение может быть равномерным и неравномерным. Неравномерное, в свою очередь, может быть равнопеременным.
Рассмотрим график зависимости y(x). Как следует из самого названия, это график зависимости координаты y от координаты x, то есть график траектории движения тела.
Нужно определить по графику:
- Координату начального положения тела.

- Координату конечного положения тела.
- Проекцию перемещения точки на ось OX и ось OY, а также модуль перемещения тела.
Отмечу, что по графику траектории никогда нельзя определить вид движения, ведь на нем нет самого главного – времени. Но в данной задаче вопрос определения вида движения, скорости и ускорения не стоит.
Что ж, начнем с определения начальной координаты. Из графика очевидно, что начальное положение обозначено цифрой “1”. Вспоминаем, как определяются координаты точки в декартовой системе координат. Координата по оси х равна 10 км, по оси y – 20 км. Конечное положение находится под номером 2, его координаты x = 40 км, y = -30 км.
Для того чтобы определить проекцию перемещения на ось OX и ось OY, нужно опустить перпендикуляры из начальной и конечной точек на указанные оси. На рисунке показано, как это сделать.
Далее определяем длину получившихся проекций. Отмечу, что проекция может быть как положительной, так и отрицательной. Проекция берется со знаком плюс (если ее направление совпадает с направлением оси) и со знаком минус, если нет. Проекция на ось Sx=30 км, проекция на ось y Sy=-50 км.
Проекция на ось Sx=30 км, проекция на ось y Sy=-50 км.
Осталось определить модуль перемещения тела. Сделать это нужно так же как в геометрии определяется длина вектора. Подробно вычисления выполнены на моем рисунке.
Если данная задача вам показалась сложной, то не откладывайте и обращайтесь к проверенному репетитору.
Ярлыки: график движения, егэ, кинематика, механика, ОГЭ, физика
Графическое представление информации бывает весьма полезным именно в силу своей наглядности. По графикам можно определять характер функциональной зависимости, определять значения величин. Графики позволяют сравнить результаты, полученные экспериментально, с теорией. На графиках легко находить максимумы и минимумы, легко выявлять промахи и т. д. 1. График строят на бумаге,
размеченной сеткой. Для ученических практических работ лучше всего брать
миллиметровую бумагу. 2. 3. Если планируете некую количественную обработку данных по графику, то экспериментальные точки надо наносить настолько «просторно», чтобы абсолютные погрешности величин можно было изобразить отрезками достаточно заметной длины. Погрешности в этом случае отображают на графиках отрезками, пересекающимися в экспериментальной точке, либо прямоугольниками с центром в экспериментальной точке. Их размеры по каждой из осей должны соответствовать выбранным масштабам. Если погрешность по одной из осей (или по обеим осям) оказывается слишком малой, то предполагается, что она отображается на графике размером самой точки. 4. По горизонтальной оси откладывают значения аргумента,
по вертикальной – значения функции. Чтобы различать линии, можно одну проводить сплошной, другую –
пунктирной, третью – штрихпунктирной и т. 5. Когда приходится откладывать по оси «длинные», многозначные числа, лучше множитель, указывающий порядок числа, учитывать при записи обозначения. 6. На тех участках графика, где имеются некие особенности, такие как резкое изменение кривизны, максимум , минимум, перегиб и др., следует брать большую густоту экспериментальных точек. Чтобы не пропустить такие особенности, есть смысл строить график сразу во время эксперимента. 7. В ряде случаев удобно пользоваться функциональными масштабами. В этих случаях на осях откладывают не сами измеряемые величины, а функции этих величин. 8. Проводить линию «на глаз» по экспериментальным точкам всегда довольно сложно, наиболее простым случаем, в этом смысле, является проведение прямой. 9. Графики обязательно нужно подписывать. Подпись должна отражать содержание графика. Следует объяснить в подписи либо основном тексте изображенные на графике линии. 10. Экспериментальные точки, как правило, не соединяются между собой ни отрезками прямой, ни произвольной кривой. Вместо этого строится теоретический график той функции (линейной, квадратичной, экспоненциальной, тригонометрической и т.д.), которая отражает проявляющуюся в данном опыте известную или предполагаемую физическую закономерность, выраженную в виде соответствующей формулы. 11. В лабораторном практикуме встречаются два случая: проведение теоретического графика преследует цель извлечения из эксперимента неизвестных параметров функции (тангенса угла наклона прямой, показателя экспоненты и т.д.), либо делается сравнение предсказаний теории с результатами эксперимента. 12. В первом случае график соответствующей функции проводится “на глаз” так, чтобы он проходил по всем областям погрешности возможно ближе к экспериментальным точкам. Существуют математические методы, позволяющие провести теоретическую кривую через экспериментальные точки в определенном смысле наилучшим образом. При проведении графика “на глаз” рекомендуется пользоваться зрительным ощущением равенства нулю суммы положительных и отрицательных отклонений точек от проводимой кривой. 13. Во втором случае график строится по результатам расчетов, причем расчетные значения находятся не только для тех точек, которые были получены в опыте, а с некоторым шагом по всей области измерений для получения плавной кривой. Нанесение на миллиметровку результатов расчетов в виде точек является рабочим моментом – после проведения теоретической кривой эти точки с графика убираются. Если в расчетную формулу входит уже определенный (или заранее известный) экспериментальный параметр, то расчеты проводятся как со средним значением параметра, так и с его максимальным и минимальным (в пределах погрешности) значениями. 1. http://iatephysics.narod.ru/knowhow/knowhow7.htm 2. Мацукович Н.А., Слободянюк А.И. Физика: рекомендации к лабораторному практикуму. Минск, БГУ, 2006 г. |
На стыке графики и физики — Look At Me
Графических дизайнеров, о которых я хотела бы рассказать, я условно для себя определяю как последователей Питера Сэвилла.Того самого, что делал обложки для пластинок Joy Division, New Order, Suede, Pulp, а еще плакаты для Фабрики Тони Уилсона и клуба Hacienda.
Тут, конечно, нужно сказать, что во время своей учебы в Манчестерском Политехникуме с 1974 по 1978, он находился под большим влиянием графических дизайнеров, работавших в 20-30 годах, таких как Херберт Байер (Herbert Bayer) и Ян Чихольд (Jan Tschichold). Оба они были модернистами, что напрямую связано с абстракционизмом и супрематизмом, для которого характерна комбинация разноцветных плоскостей простейших геометрических очертаний. Возможно, поэтому даже обращаясь к класическим образам (как в обложке альбома Power Corruption & Lies группы New Order), он часто сопоставлял их с комплексом систем цветового кодирования.
Оба они были модернистами, что напрямую связано с абстракционизмом и супрематизмом, для которого характерна комбинация разноцветных плоскостей простейших геометрических очертаний. Возможно, поэтому даже обращаясь к класическим образам (как в обложке альбома Power Corruption & Lies группы New Order), он часто сопоставлял их с комплексом систем цветового кодирования.
Энди Гилмор живет и работает в Рочестере, штат Нью-Йорк. Сотрудничает с такими изданиями как New York Times, Dazed & Confused и рядом других. К сожалению, о нем не очень много информации. Все, что мне удалось выяснить, это то, что он также является музыкантом. Кажется, во многом это формирует его стилистику. Его работы – словно воплощенный в графику звук, в физическом и эмциональном проявлении.
http://kunstformen.blogspot.com/
http://birdbrid.blogspot.com/
http://www.birdbrid.com/
http://www.flickr.com/photos/birdbrid/
Дизайнер с псевдонимом Network Osaka на своем сайте признается, что был одержим графическим дизайном еще до того, как узнал что это такое. К увлечению графикой его (или ее) подтолкнул первый компьютер Macintosh LC и наличие в нем таких программ как KidPix и MacPaint в частности.
К увлечению графикой его (или ее) подтолкнул первый компьютер Macintosh LC и наличие в нем таких программ как KidPix и MacPaint в частности.
“Как дизайнер я стремлюсь к соединению формы и функции в полной гармонии. Упразднение ненужных элементов с кратким и прямым подходом к проблемам дизайна, в конечном счете создадут успешный продукт, ценный своим содержанием и формой.”
http://www.networkosaka.com/
http://www.flickr.com/photos/networkosaka/
Преподавание физики с графикой. Мне нравится, чтобы мое обучение было очень наглядным… | Эндрю Робинсон | Precarious Physicist
Кинематика объектов, движущихся с постоянным ускорением Мне нравится, когда я обучаюсь очень наглядно, поэтому я стараюсь создавать графику, которая может передавать понятия и то, как они связаны. Вы также помните, что в предыдущем рассказе («Тайна недостающих математических навыков») я упомянул, что учащиеся должны построить структуру знаний как часть процесса обучения. Это попытка создать основу для важной части любого вводного курса физики. Эти уравнения (выделены зеленым цветом) показывают, как работает движение, и являются уравнениями, используемыми в «физических движках» популярных игр. Они просто описывают, что происходит, когда объект движется в гравитационном поле Земли, где гравитационное ускорение можно считать постоянным, при условии, что вы находитесь в пределах 100 километров или около того от поверхности Земли. Мы также используем бессмертную физическую фразу «игнорирование сопротивления воздуха», потому что это все путает и проблема становится намного сложнее!
Эти уравнения (выделены зеленым цветом) показывают, как работает движение, и являются уравнениями, используемыми в «физических движках» популярных игр. Они просто описывают, что происходит, когда объект движется в гравитационном поле Земли, где гравитационное ускорение можно считать постоянным, при условии, что вы находитесь в пределах 100 километров или около того от поверхности Земли. Мы также используем бессмертную физическую фразу «игнорирование сопротивления воздуха», потому что это все путает и проблема становится намного сложнее!
Это было создано с помощью бесплатного веб-приложения Drawio.Это довольно аккуратный пакет, который создает XML-файл, который можно прочитать в веб-приложении с вашего собственного компьютера в облачных вычислениях. Это очень аккуратное и полезное приложение. У него очень низкая кривая обучения, что я искренне одобряю. Если я не могу заставить программу производить что-то пригодное для использования в течение десяти минут после того, как я ее открою, то она больше никогда не будет использоваться.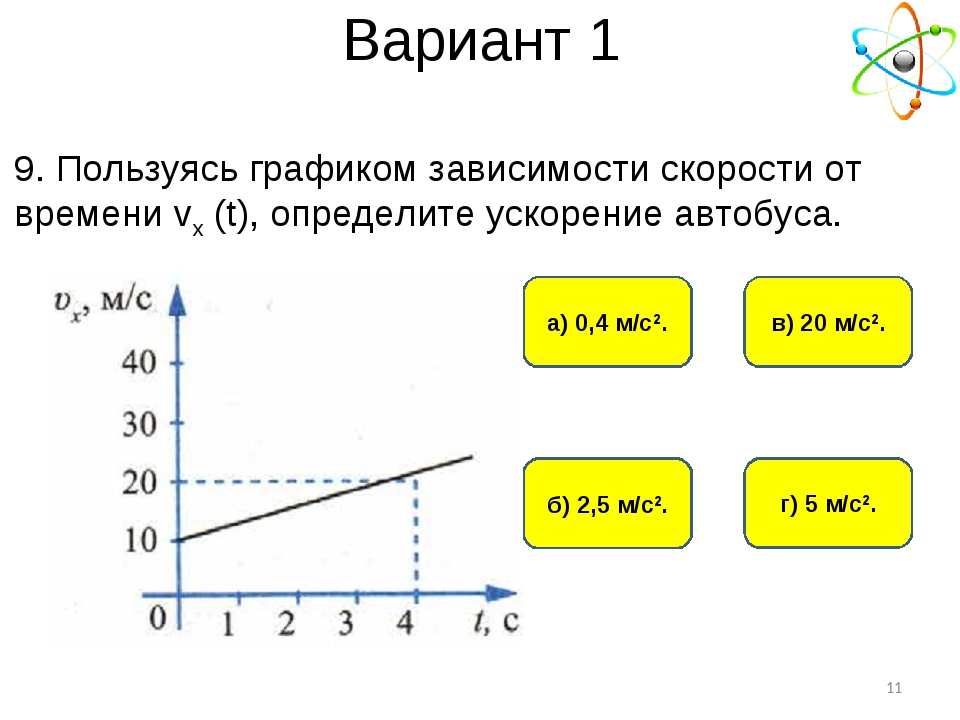 Я мог бы назвать это законом юзабилити Робинсона, , если бы был претенциозным, но это потому, что после многих лет разработки программ сбора и визуализации данных и пользовательских интерфейсов у меня теперь очень низкий порог скуки!
Я мог бы назвать это законом юзабилити Робинсона, , если бы был претенциозным, но это потому, что после многих лет разработки программ сбора и визуализации данных и пользовательских интерфейсов у меня теперь очень низкий порог скуки!
Это изображение находится под лицензией Creative Commons, поэтому вы можете бесплатно загрузить его для собственного некоммерческого использования, если оно вам нравится.Если вы можете внести улучшения, сделайте это, и просто укажите меня как автора.
Я был бы рад, если бы вы сообщили мне, как вы используете визуальную информацию в преподавании любого предмета, а не только науки. Мы все можем учиться друг у друга. Пожалуйста, добавьте комментарий.
Стажирование: графический дизайн – Американский институт физики
Стажировка: Графический дизайн
Сводка
Сводка
80 Название:
Оплачиваемая стажировка по графическому дизайну с полной занятостью, возможность получить ценный опыт в оказании дизайнерской поддержки графическому и веб-дизайнеру. Американская ассоциация физиков в медицине (AAPM) ищет увлеченного и надежного студента колледжа или недавнего выпускника, специализирующегося в области графического дизайна/искусства под руководством отдела информационных услуг.
Американская ассоциация физиков в медицине (AAPM) ищет увлеченного и надежного студента колледжа или недавнего выпускника, специализирующегося в области графического дизайна/искусства под руководством отдела информационных услуг.
В этой роли вы должны рассчитывать на дальнейшее развитие вашего опыта за счет:
- Разработка и подготовка графики для нашего веб-сайта и аккаунтов в социальных сетях
- Помощь в разработке и верстке печатных и веб-материалов
- Работа в профессиональной и веселой среде
- Прочие родственные обязанности по назначению
Вакансия доступна с гибкой датой начала работы с середины апреля до 8 июля 2022 года.Наш офис удобно расположен в Старом городе Александрии, рядом со станцией метро King Street.
Должен находиться в MD, VA, DC, NC или FL.
Пакет предложений должен включать: Сопроводительное письмо, резюме и заполненную заявку.
КВАЛИФИКАЦИЯ:
Студент колледжа, обучающийся или недавний выпускник, имеющий степень в области графического дизайна/искусства, который хорошо разбирается в дизайне страниц, верстке, типографике, пространственной ориентации, обработке изображений и манипулировании ими, а также графике от руки. Предпочтение отдается концептуальному мыслителю с исключительным вниманием к деталям и творческим взглядом. Идеальный кандидат должен быть командным игроком с сильными организационными навыками для участия в разработке проекта и отличными навыками межличностного общения для эффективного общения с персоналом и членами. Предыдущий опыт стажировки/ассоциации приветствуется. Требуется знание среды Mac с опытом работы в Adobe Creative Suite (в частности, InDesign, Illustrator и Photoshop) и Microsoft Office.
Предпочтение отдается концептуальному мыслителю с исключительным вниманием к деталям и творческим взглядом. Идеальный кандидат должен быть командным игроком с сильными организационными навыками для участия в разработке проекта и отличными навыками межличностного общения для эффективного общения с персоналом и членами. Предыдущий опыт стажировки/ассоциации приветствуется. Требуется знание среды Mac с опытом работы в Adobe Creative Suite (в частности, InDesign, Illustrator и Photoshop) и Microsoft Office.
* Кандидаты, пожалуйста, предоставьте ссылку на примеры последних дизайн-проектов, чтобы увеличить шансы быть рассмотренными.
Американская ассоциация физиков в медицине является
Работодатель равных возможностей
Работодатель равных возможностей
AIP является работодателем, поддерживающим позитивные действия и равные возможности
EOE, включая инвалидность/ветеринары
Кроме того, вы можете подать заявку на эту вакансию, используя свой профиль на одном из следующих сайтов:
Расчеты электронной структуры на графических процессорах: от квантовой химии до физики конденсированного состояния
Список участников xiii
Предисловие xvii
Благодарности xix
Глоссарий xxi
Сокращения xxv
1. Почему графические процессоры 1”
Почему графические процессоры 1”
Perri Needham, Andreas W. Götz and Ross C. Walker
1.1 Исторический взгляд на параллельные вычисления 1
1.2 Возникновение GPU 5
1.3 Параллельные вычисления на 7
1.4 Параллельные вычисления на графических процессорах 12
1.5 Приложения с ускорением на графическом процессоре 15
Ссылки 19
2. Графические процессоры: от аппаратного к программному обеспечению 23
Андреас Перри.Гётц и Росс C. Walker
2.1 Базовая терминология GPU 24
2.2 Архитектура GPU 24
2.3 CUDA Программирование Модель 26
2.4 Концепции программирования и оптимизации 30
2.5 Программные библиотеки для GPUS 34
2.6 Особенности Графические процессоры с поддержкой CUDA 35
Ссылки 36
3. Обзор методов электронной структуры 39
Андреас В. Гётц
3.1 Введение 39
3.2 Теория Hartree-Fock 42
3. 3 Функциональная теория плотности 46
3 Функциональная теория плотности 46
3.4 Основы наборы 49
3.5 Полуэмпирические методы 53
3.6 Функциональная плотность плотно привязки 56
3.7 Волна на основе функциональной связи Методы корреляции 57
Благодарности 60
Ссылки 61
4. Базисный набор Гаусса Хартри-Фок, теория функционала плотности и другие на графических процессорах 67
Nathan Luehr, Aaron Sisto and Todd J.Martínez
4.1 4,1 квантовой химический обзор 68
4.2 Обзор оборудования и CUDA 92
4.3 ERI ERI Оценка 73
4.4 Конструкция интеграл-прямой формы на GPUS 78
4.5 Точные соображения 88
4.6 Методы Post-SCF 91
4.7 Пример расчетов 93
4.8 Выводы и прогноз 97
Ссылки 98
5. Ускорение графического процессора для плотности Функциональная теория с орбиталими сверху 101
Hans Van Schoot и Lucas Visscher
5.1 фон 101
5.2 Реализация теории и процессора 102
5. 3 Реализация ГПУ 105
3 Реализация ГПУ 105
5.4 Заключение 112
5.4. 113
Ссылки 113
6.
6. Функциональная теория плотности на основе вейвлет на основе массивно параллельных гибридных архитектур 115
Luigi Genovese Видо, Дэмиен Калист, Жан-Франсуа Мео, Стефан Гедекер и Тьерри Дойч
6.1 Вводные замечания о базисных наборах вейвлетов для реализаций теории функционала плотности 115
6.2 Операторы в вейвлет-базисных наборах 117
6.3 Параллелизация 123
6.4 ГПУ Архитектура 124
6.5 Выводы и прогноз 132
Ссылки 133
7. Функциональная теория плоской волны 135
Maxwell Huchinson, Paul Fleurat- Lessard, Ani Anciaux-Sedrakian, Dusan Stosic, Jeroen Bédorf и Sarah Tariq
7.1 Введение 135
7.2 Теоретическая основа 136
7.3 Реализация 143
7.4 Оптимизации 148
7.5 Примеры производительности 151
7.6 Точная обмен с самолетными волнами 159
7. 7 Сводка и Outlook 165
7 Сводка и Outlook 165
Благодарности 165
Рекомендации 165
Приложение A: Определения и конвенции 168
Приложение B: Пример ядер 168
8. Умножение разреженной матрицы на умножение матриц с ускорением на GPU для теории линейного масштабирования плотности 173
Оле Шютт, Питер Мессмер, Юрг Хаттер и Йост ВандеВонделе
8.1 ВВЕДЕНИЕ 173
8.2 Архитектура программного обеспечения для GPU-ускорения 177
8.3 Максимизация асинхронного прогресса 180
8.4 Libcusmm: GPU Ускоренные матрицы Matrix 183
8.5 ориентиры и выводы 18000
Благодарности 189
Ссылки 189
9 Волновой метод, дополненный проектором на основе сетки 191
Samuli Hakala, Jussi Enkovaara, Ville Havu, Jun Yan, Lin Li, Chris O’Grady
и Risto M.Nieminen
9.1 ВВЕДЕНИЕ 191
9.2 Общий обзор 193
9.3 Использование графических процессоров в основных расчетах наземных состояний 196
9. 4. Функциональная функциональная плотность 202
4. Функциональная функциональная плотность 202
9.5. Случайное фазовое приближение для корреляционной энергии 203
9.6 Резюме и Outlook 207
Благодарности 208
Ссылки 208
Ссылки 208
10. Применение графических устройств для ускорения плотности реального пространства Функциональная теория и зависимость от времени. Функциональная теория теории 211
Xavier Adrade и Alán Aspuru-Guzik
10.1 ВВЕДЕНИЕ 212
10.2 Реальный пространственный представитель 213
10.3 Числовые аспекты реального пространства 214
10.4 Общая стратегия оптимизации ГПУ 216
10,5 Kohn-Sham Hamiltonian 217
10.6 Ортогонализация и подпространственная диагонализация 221
10.7 Возведение в степень 222
10.8 Потенциал Хартри 223
10.9 Другие операции 224
10.10 Числовые характеристики 225
10.11 выводов 228
10.12 Вычислительные методы 228
Acconnowdgments 229
Ссылки 229
Ссылки 229
11. Полуэмпирическая квантовая химия 239
Полуэмпирическая квантовая химия 239
Xin Wu, Axel Koslowski и Walter Thiel
11.1 Введение 239
11.2 Обзор полуэмпирических методов 240
11.3 Узкие места в вычислениях 241
11.4 Оптимизация на основе профиля для гибридной платформы 244
11.5 Производительность 249
11.6 Приложений 251
11.7 Заключение 252
Подтверждение 252
Ссылки 253
Ссылки 253
12. Ускорение процессора в процессе второго порядка теории возмущений Møller-Plesset с разрешением идентификатора 259
Roberto Olivares-Amaya, Адриан Цзинич Уотсон и Алан Аспуру-Гузик
12.1 Теория возмущений Мёллера–Плессета с разрешением аппроксимации тождества (RI-MP2) 259
12.2 Библиотека умножения матриц смешанной точности 263
12.3 Выполнение ускоренного RI-MP2 266
12.4. Пример приложения 270
12.4. 12.5 Выводы 270003
12.5. Выводы 273
Ссылки 273
Список литературы 273
13. Методы итеративные соединительные кластеры на графических установках 279
Методы итеративные соединительные кластеры на графических установках 279
A. Eugene Enanse III, Джефф Р. Hammond и C. David Sherrill
13.1 Введение 279
13.2.6 Результаты 290
13.7 Выводы 295
13.7 Выводы 295
Благодарности 296
Ссылки 296
Ссылки 296
14. Ответственные сочетания методы кластера на графических установках: одно- и многоссоложные составы 301
Wenjing MA, Kiran Bhaskaran-Nair, Oreste Villa, Edoardo Aprà, Antonino Tumeo, Sriram Krishnamoorthy and Karol Kowalski
14.1 Введение 302
14.2 Обзор методов электронной структуры 303
14.3 NWCHEM Software Architecture 308
14.4 процессор реализации 309
14.4 9000 9000
14.5 14.6 Outlook 319
Благодарности 320
ссылки 320
индекс 327
(PDF) Вычислительная физика на графических установках
22
обработка (PDP), 2012 20-я Международная конференция Euromicro. (февраль 2012 г.)
(февраль 2012 г.)
368 –375
59. Ван, Л., Ву, Ю., Цзя, В., Гао, В., Чи, С., Ван, Л.W.: Крупномасштабная плоскость
вычисления теории функционала плотности псевдопотенциала волны на кластерах GPU. В:
Труды Международной конференции по высокопроизводительным вычислениям 2011 г.,
Сети, хранение и анализ. SC ’11, New York, NY, USA, ACM (2011)
71:1–71:10
60. Jia, W., Cao, Z., Wang, L., Fu, J., Chi, X., Gao, W., Wang, LW: Анализ
кода функциональной теории плотности псевдопотенциала плоской волны на машине с графическим процессором.
Computer Physics Communications 184(1) (2013) 9 – 18
61. Enkovaara, J., Rostgaard, C., Mortensen, JJ, Chen, J., Dulak, M., Ferrighi,
L. , Гавнхольт, Дж., Глинсвад, К., Хайкола, В., Хансен, Х.А., Кристофферсен, Х.Х.,
Куисма, М., Ларсен, А.Х., Лехтоваара, Л., Юнгберг, М., Лопес-Асеведо, О. .,
Мозес П.Г., Оянен Дж., Ольсен Т., Петцольд В., Ромеро Н.А., Штаусхольм-Мёллер,
Дж.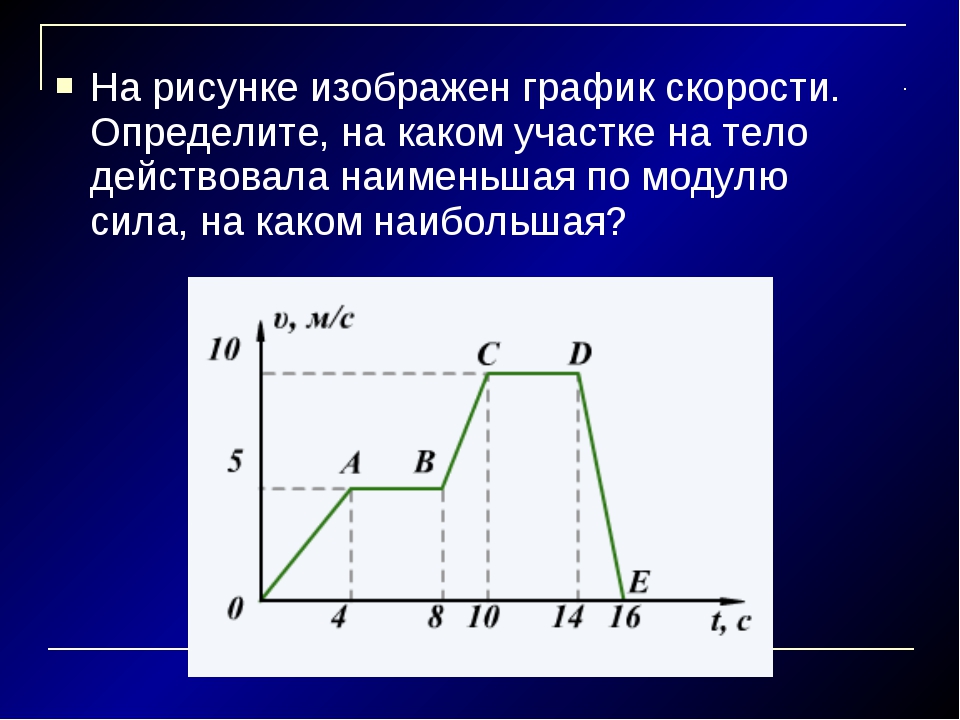 , Стрейндж М., Трицарис Г.А., Ванин М., Уолтер, М., Hammer, B., H¨akkinen,
, Стрейндж М., Трицарис Г.А., Ванин М., Уолтер, М., Hammer, B., H¨akkinen,
H., Madsen, GKH, Nieminen, RM, Nørskov, JK, Puska, M., Rantala, TT,
Schiøtz, J., Thygesen, KS, Jacobsen, KW : Расчеты электронной структуры
с помощью GPAW: реализация метода дополненной волны проектора
в реальном пространстве. Journal of Physics: Condensed Matter 22(25) (2010) 253202
62. Хакала С., Хаву В., Энковаара Дж., Ниеминен Р.М.: Параллельная электронная структура
расчеты с использованием нескольких графических процессоров (GPU). ).В: Конспект лекций
по информатике. PARA 2012, Springer-Verlag (2013)
63. Castro, A., Appel, H., Oliveira, M., Rozzi, CA, Andrade, X., Lorenzen, F., Mar-
ques, MAL, Гросс, ЭКУ, Рубио, А.: Осьминог: инструмент для приложения
теории функционала плотности, зависящей от времени. Physica Status Solidi (B) 243(11)
(2006) 2465–2488
64. Andrade, X., Alberdi-Rodriguez, J., Strubbe, D. A., Oliveira, M.J.T., Nogueira,
A., Oliveira, M.J.T., Nogueira,
F., Castro, A., Muguerza, J., Arruabarrena, A., Louie, SG, Aspuru-Guzik, A.,
Rubio, A., Marques, MAL: Зависимая от времени теория функционала плотности в мас-
Сильно параллельные компьютерные архитектуры: проект Octopus. Journal of Physics:
Condensed Matter 24(23) (2012) 233202
65. Isborn, CM, Luehr, N., Ufimtsev, IS, Martinez, TJ: Электронная структура в возбужденном состоянии
с конфигурацией взаимодействия синглов и и Tamm-Dancoff time-
зависимая теория функционала плотности на графических процессорах.Journal of
Chemical Theory and Computation 7(6) (2011) 1814–1823
66. Пескин М.Е., Шредер Д.В.: Введение в квантовую теорию поля. West-
view Press (1995)
67. Крютер, Р.Дж.: Введение в квантовую теорию поля. ArXiv High Energy Physics
– Theory e-prints (1995)
68. Fodor, Z., Hoelbling, C.: Массы легких адронов из решеточной КХД. Reviews of
Modern Physics 84 (2012) 449–495
69. G¨ockeler, M., H¨agler, P., Horsley, R., Pleiter, D., Rakow, PEL, Schäfer, A.,
G¨ockeler, M., H¨agler, P., Horsley, R., Pleiter, D., Rakow, PEL, Schäfer, A.,
Schierholz, G., Zanotti, JM: Обобщенные партонные распределения и структура
функций из полных решеточная КХД. Nuclear Physics B Proceedings Supplements
140 (2005) 399–404
70. Alexandrou, C., Brinet, M., Carbonell, J., Constantinou, M., Guichon, P., et al.:
Nucleon формфакторы и моменты партонных распределений в закрученной решетке масс
КХД. В кн.: Материалы XXI Международной Еврофизической конференции
Физика высоких энергий.21-27 июля 2011. Гренобль, Рон-Альпы, Франция. Том
EPS-HEP2011. (2011) 308
Геометрические инструменты
Геометрические инструменты Добро пожаловать на официальный сайт Geometric Tools, сборник исходных
код для вычислений в области математики, геометрии, графики, изображения
анализа и физики. Движок написан на C++ 14 и поэтому имеет
переносимый доступ к стандартным конструкциям для многопоточного программирования на
ядра. Движок также поддерживает высокопроизводительные вычисления с использованием общих
целевое программирование GPU (GPGPU).Части кода описаны в
различные книги, а также в
документы, имеющиеся в этом
сайт. Исходный код свободно
загружаемый, подпадающий под действие
Повышение лицензии.
Расписание выпусков и соответствующая информация приведены ниже.
Движок также поддерживает высокопроизводительные вычисления с использованием общих
целевое программирование GPU (GPGPU).Части кода описаны в
различные книги, а также в
документы, имеющиеся в этом
сайт. Исходный код свободно
загружаемый, подпадающий под действие
Повышение лицензии.
Расписание выпусков и соответствующая информация приведены ниже.
Если вы используете Linux и OpenGL, вам потребуется OpenGL 4.5 или более поздней версии. я использую Проприетарные драйверы NVIDIA, а не драйверы Nouveau с открытым исходным кодом, чтобы для удовлетворения этого ограничения. Любая попытка запуска примеров приложений без указанная версия корректно завершится ошибкой с выводом окна консоли: OpenGL 4.5 требуется .
Механизм геометрических инструментов 6.1 . Математический код находится только в заголовке
библиотека (GTMathematics). Математическая библиотека с реализациями на базе графического процессора
при условии (GTMathematicsGPU). Код общего графического движка на базе процессора находится в его
собственная библиотека (GTGraphics). Для графики предусмотрены оболочки DirectX 11.
(GTGraphicsDX11) и приложений (GTApplicationsDX11). Обертки OpenGL 4.5
предусмотрен для графики (GTGraphicsGL45) и приложений (GTApplicationsGL45).
Код общего графического движка на базе процессора находится в его
собственная библиотека (GTGraphics). Для графики предусмотрены оболочки DirectX 11.
(GTGraphicsDX11) и приложений (GTApplicationsDX11). Обертки OpenGL 4.5
предусмотрен для графики (GTGraphicsGL45) и приложений (GTApplicationsGL45).
| • | Выпущено 7 февраля 2022 г. |
| • | Microsoft Windows 10 или 11; DirectX 11.1 или OpenGL 4.5; Microsoft Visual Studio 2019 и 2022; Компилятор Intel C++ 2022; Инструменты C++ Clang для Windows 12.0.0 |
| • | Убунту 20.04.1 ЛТС; OpenGL 4.5, графические драйверы NVIDIA; Код Visual Studio 1.49,2; CMake 3.15.2; gcc 9.3.0 |
| • | Федора 35;
OpenGL 4.5, графические драйверы NVIDIA;
Код Visual Studio 1. 49.2;
CMake 3.18.3;
gcc 11.2.1 49.2;
CMake 3.18.3;
gcc 11.2.1 |
Дистрибутив исходного кода доступен для загрузки с этого сайта. но также доступен в Геометрические инструменты на GitHub. Онлайн-код — это моментальный снимок, который публикуется после значительной партии. вносятся изменения.Однако дистрибутив GitHub всегда содержит последние исправления и обновления, сделанные в GTE.
Библиотека геометрических инструментов . Мотивация для создания геометрических инструментов была моей
аспирантура в области обработки медицинских изображений; тогда он назывался MAGIC
Программное обеспечение ( M y A чередование G графика и I магия С ода). Когда я пришел в индустрию 3D-видеоигр, я тратил меньше
время на код изображения и еще раз на графику, физику и математику
код.Большая часть кода была результатом помощи людям, которые сообщали о проблемах.
на форум Usenet comp.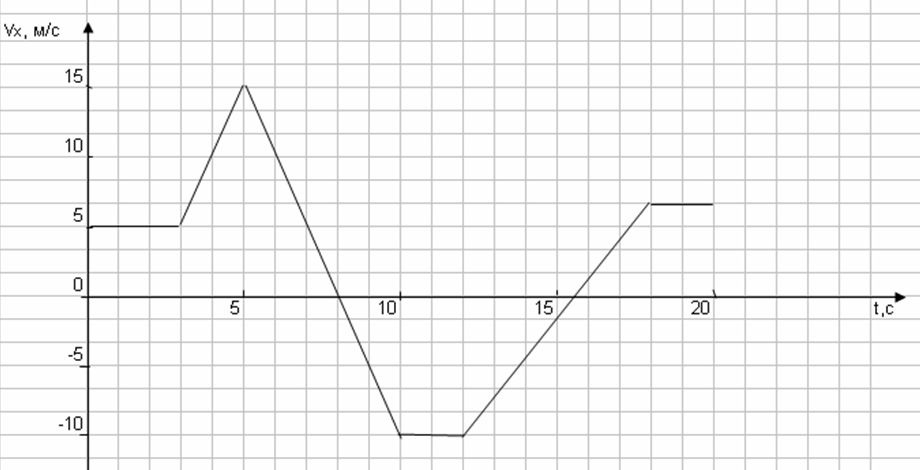 graphics.algorithms . Техническая поддержка
вопросы последних лет дали мне понять, что математика
и код геометрии — это то, что люди используют больше всего, поэтому я сосредоточусь на тех,
темы сейчас.
graphics.algorithms . Техническая поддержка
вопросы последних лет дали мне понять, что математика
и код геометрии — это то, что люди используют больше всего, поэтому я сосредоточусь на тех,
темы сейчас.
Библиотека геометрических инструментов (GTL) будет переработкой математических
и код геометрии в GTE с последующим добавлением нового кода, если позволяет время. я
пытаясь упростить код, чтобы обеспечить согласованное именование и
интерфейсы и расширить возможности.Некоторый код геометрии GTE
уже содержит многопоточность, особенно полезно, когда числовой тип
включает в себя рациональную арифметику и арифметику произвольной точности, и я
планируют включить многопоточность в большее количество алгоритмов. Отдельный код будет
доступны для реализации на основе GPGPU с использованием HLSL, GLSL и CUDA и
для реализаций на основе SIMD с использованием Intel SSE или AVX. я буду добавлять
основа для сочетания рациональных и символьных вычислений, которая
описан в моей книге «Надежные и безошибочные геометрические вычисления ».
Кодовая база по математике и геометрии имеет соответствующую документацию и набор модульных тестов. Код для графики и приложений существует только для образцы, иллюстрирующие алгоритмы GTL. Они будут содержаться в отдельные библиотеки, которые предоставляются как есть без поддержки модульного тестирования. Исходный код GTL будет доступен для бесплатной загрузки и подлежит ускорению. Лицензия.
У меня нет надежной предполагаемой даты публикации GTL. Когда я это сделаю, я объявить об этом здесь.Код GTL будет доступен на GitHub.
| Особая благодарность Джастину «Сатриани» Ханту за дизайн и поддержку сайта. |
Физика твердого тела в долларах США Предложение — Универсальная сцена Описание 21.11 документация
Это первое предложение касается только моделирования твердого тела. Жесткое тело
симуляции являются наиболее широко применимой категорией, которую мы можем выделить.
общее и давнее использование во всех дисциплинах, описанных выше.
Жесткое тело
симуляции являются наиболее широко применимой категорией, которую мы можем выделить.
общее и давнее использование во всех дисциплинах, описанных выше.
Грунтовка для моделирования жесткого тела
По сути, симуляторы твердого тела принимают в качестве входных данных список твердых тел и список ограничений. Учитывая состояние тел на текущий момент, они вычислить обновленное состояние тел моментом позже, с общим Желание состоит в том, чтобы движение тел, ограниченное ограничениями подчиняется законам физики. Можно вызвать последовательность таких обновлений моделирования для создания анимации.
Твердое тело можно описать его позицией (положением и ориентацией в скважине). определенной системе отсчета), а также его массовое распределение (заданное положение центра масс, полную массу и тензор инерции).Тело также будет имеют скорость (линейный и угловой векторы). Поза и скорость являются входными данными и выходные данные обновления моделирования.
Ограничения могут принимать разные формы, но в основном делятся на две категории:
Явные зависимости, часто называемые соединениями, которые создают фиксированную отношения между двумя твердыми телами.
Одним из примеров является требование, одно тело никогда не вращается относительно другого тела, даже если относительно возможен перевод.
Неявные ограничения, чаще всего контакты, которые обычно создаются «за кулисами» с помощью симулятора, чтобы гарантировать, что e.г. твердые объекты делают не проходить друг через друга. Чтобы симулятор вывел эти ограничений, каждое тело должно быть снабжено представлением столкновения (так называемая «форма столкновения» или «коллайдер») и физические свойства материала.
Симуляции часто имеют общий набор глобальных параметров, влияющих на симуляцию. всех тел. Как правило, можно одновременно создавать несколько симуляции, каждая со своим набором настроек параметров.
долл. США Реализация
Значение
Во-первых, ясно, что некоторая терминология, обычно используемая при моделировании физики
сообщества, такие как «сцена», «совместное» и «материал» имеют разные значения, чем
в VFX и уже используется USD, поэтому мы решили добавить префикс ко всей нашей схеме
классы с «физикой», а также использовать пространство имен, чтобы избежать двусмысленности.
Основные возможности редактирования
Основное предположение при разработке этой схемы заключалось в том, что один из наиболее распространенных варианты использования будут заключаться в добавлении физического поведения к существующему контенту в долларах США. Более того, общепринятое мнение заключалось в том, что для максимизации производительности доллара США реализации, лучше избегать завышения количества объектов USD в место действия. Таким образом, мы считаем, что лучший подход — это присоединение новых схем API, которые содержать физические атрибуты существующих объектов USD всякий раз, когда это имеет смысл.В редких случаях нет уже доступного объекта, для которого можно было бы выполнить симуляцию. атрибуты могут быть присоединены рациональным образом, и в этих случаях мы решили для создания новых схем USD IsA.
Крайне важно, чтобы любая операция по добавлению физики также могла быть отменена; мы будем
используя недавно добавленную возможность RemoveAPI().
Аналогичным образом, в случаях использования редактора это обычная возможность временно иметь возможность чтобы заглушить/отключить свойства, не удаляя их напрямую. Удаление имеет Недостатком является полная потеря сохраненных настроек.доллар США позволяет полностью объекты для деактивации с помощью активного флага, но это невозможно для каждого API. В В некоторых случаях приглушение поведения является действительно распространенным вариантом использования. Для этих случаев имеем определил логический атрибут включения. (Обратите внимание, что изначально мы хотели включить флаг в базовом классе для классов, которым он нужен, но это создает проблемы, когда к объекту применяется несколько доступных API. В таком случае USD создает только один общий флаг включения, а это не то, что нам нужно.)
Физические сцены
Как обсуждалось выше, мы хотим включить несколько независимых физических симуляций.
в рамках одного этапа USD.Мы обнаружили, что лучший способ сделать это — создать
Класс PhysicsScene. Было предложено использовать концепцию уровней долларов США для
разделить физику на отдельные сцены, но мы были обеспокоены тем, что сцена
концепция уже настолько чрезмерно используется для многих различных вещей (например, сотрудничество,
контроль версий), что мы предпочли бы не растягивать его для еще одного использования
кейс. Если на сцене несколько сцен, тела назначаются
определенные сцены с использованием ссылки от тела к сцене. Если есть только один уникальный
сцена, явное отношение не требуется, и предполагается, что тела связаны
с одиночной сценой.Невозможно поместить одно тело в несколько
сцены, так как все они пытались бы повлиять и написать противоречивые
информации в такой орган.
Было предложено использовать концепцию уровней долларов США для
разделить физику на отдельные сцены, но мы были обеспокоены тем, что сцена
концепция уже настолько чрезмерно используется для многих различных вещей (например, сотрудничество,
контроль версий), что мы предпочли бы не растягивать его для еще одного использования
кейс. Если на сцене несколько сцен, тела назначаются
определенные сцены с использованием ссылки от тела к сцене. Если есть только один уникальный
сцена, явное отношение не требуется, и предполагается, что тела связаны
с одиночной сценой.Невозможно поместить одно тело в несколько
сцены, так как все они пытались бы повлиять и написать противоречивые
информации в такой орган.
Сцены могут определять атрибут вектора гравитации, который ускоряет все содержащиеся в нем объекты.
тела надлежащим образом. Гравитация предоставляется как отдельный вектор направления и
величина. Это сделано для того, чтобы направление по умолчанию (отрицательная ось вверх) и
величина по умолчанию (гравитация Земли) может быть запрошена независимо.
Типы
USD различает типы базовых и ролевых значений.Мы попытались использовать доступные типы ролей, когда это применимо. Например, скорость – это vector3f, а не float3.
Мы решили использовать поплавки одинарной, а не двойной точности, поскольку они широко доступны. Программное обеспечение для моделирования физики в реальном времени повсеместно использует типы с одинарной точностью для лучшая производительность, а использование двойной или расширенной точности гарантируется только для позиций в очень больших пространствах, которые уже покрыты с использованием встроенного в USD типа xform.
Единиц
В единицах измерения физика использует установленные в долларах США концепции расстояния.
и время, а также добавляет понятие массы.Все физические величины, которые мы
использование может быть разложено на продукт этих трех основных типов. доллар США не
установить единицы измерения расстояния и времени. Однако в нем есть концепция
метаданные metresPerUnit и timeCodesPerSecond, что делает его
можно правильно масштабировать контент, созданный в разных масштабах, относительно
друг друга при переносе их в общую сцену. Это расширение физики
уважает эту возможность расстояния и времени с физикой и добавляет
метаданные килограммов на единицу, которые остаются совместимыми с системой СИ.
Это расширение физики
уважает эту возможность расстояния и времени с физикой и добавляет
метаданные килограммов на единицу, которые остаются совместимыми с системой СИ.
Все одномерные угловые значения указаны в градусах по причинам интуиция создателя контента и согласованность с существующими значениями степени в долларах США как камера FOV или вращения Эйлера.
В схеме указываем единицы для каждой заданной величины в виде выражения
используя термины «расстояние», «градусы», «масса» и «время», как они определены выше. доллар США
Этап может быть составлен путем ссылки на несколько файлов USD, каждый из которых использует свой собственный
отдельные метаданные преобразования единиц измерения. Это означает, что перед моделированием все значения
могут быть преобразованы с использованием соответствующих метаданных преобразования единиц измерения в
общая система единиц, зависящая от реализации, прежде чем их можно будет смоделировать.Точно так же любые выходные данные моделирования могут быть преобразованы обратно в их исходные данные. единиц перед их обратной записью в доллары США.
единиц перед их обратной записью в доллары США.
Значения по умолчанию
Возникли некоторые проблемы при указании этой схемы в связи со значением по умолчанию
ценности. Во-первых, недавний переход на доллары США исключает возможность
отказа от создания атрибутов для API схемы, что раньше было удобным способом
обозначают запрос на использование значения по умолчанию для атрибута. Теперь мы вместо
явно указать значения по умолчанию, как правило, контрольные значения, которые лежат за пределами
диапазон допустимых значений для конкретного атрибута.Например, если
атрибут обычно должен быть неотрицательным, мы используем \(-1.0\) для
запросить определенное поведение по умолчанию. Иногда атрибут может использовать весь
диапазон с плавающей запятой, и в этом случае мы резервируем фактически +/- бесконечность
на краях этого диапазона в качестве часовых. Мы будем использовать плавающую точку
\(inf\) литерал, который USD поддерживает в файлах и схемах для обозначения этого. Мы
задокументируйте такое поведение дозорного по умолчанию в каждом конкретном случае в схеме.
Жесткие корпуса
Мы представляем физические твердые тела с помощью PhysicsRigidBodyAPI, который может применяться к любому UsdGeomXformable.UsdGeomXformable — это подходящий базовый класс, так как он обеспечивает размещение в пространстве через xform, который также фундаментальное свойство физических тел.
Твердые тела имеют атрибуты линейной и угловой скорости, указанные в локальное пространство, чтобы соответствовать скоростям в точечных экземплярах и узлам xform.
Тела могут указывать ссылку на сцену SimulationOwner для вышеупомянутого сценарий многосценового моделирования.
Взаимодействие с иерархией USD
Если узел в иерархии графа сцены USD помечен
PhysicsRigidBodyAPI поведение таково, что все дочерние элементы отмеченного
узел считается частью этого твердого тела и жестко перемещается вместе с
тело.Это согласуется с обычным поведением, которого можно ожидать во время
ручная анимация поддерева. Если совокупные свойства всего твердого тела
должны быть вычислены, например, общая масса или весь объем столкновения,
затем рассматривается содержимое всего поддерева.
Обратите внимание, что, конечно, разрешено изменять/анимировать преобразования в таком поддерево, и в этом случае любые производные величины в физическом движке, такие как центр масс или относительное положение формы будут обновлены.Такая анимация будет однако не генерировать импульс. Например, быстрая анимация жестких частей Luxo Jr. не заставит лампу прыгать, так как для вычисления такого поведения мы потребуется зафиксировать относительные массы нескольких независимых частей лампа, что невозможно, если все рассматривать как единое жесткое сборка. Правильным подходом будет моделирование каждой жесткой части лампу как самостоятельные твердые тела и соединить их шарнирами, которые мы обсудим позже.
Невозможно иметь вложенные тела. PhysicsRigidBodyAPI применяется к
что-либо в поддереве под узлом, который уже имеет
PhysicsRigidBodyAPI игнорируются. Исключением является, если у прайма есть
resetXformStack op. В этом случае он игнорирует унаследованный API твердого тела. Затем можно использовать собственный API твердого тела, чтобы снова сделать его динамическим.
Затем можно использовать собственный API твердого тела, чтобы снова сделать его динамическим.
Сон
Чтобы сделать возможным крупномасштабное моделирование земной поверхности, где, как правило, все тела
в конце концов падают на землю и останавливаются, самая жесткая симуляция тела
программное обеспечение имеет концепцию «спящего режима» этих тел для повышения производительности.Это означает, что взаимодействия перестают обновляться, когда достигается состояние равновесия.
достигнуто, и снова начать обновляться, как только равновесное состояние каким-то образом
был нарушен. Также можно запускать симуляции в спящем режиме.
государство. Мы предоставляем PhysicsRigidBodyAPI:startsAsleep для поддержки этого. Мы
рассматривали возможность раскрытия состояния сна во время выполнения каждого тела в моделировании
чтобы он был виден доллару США, когда симуляция деактивировала тело, и
чтобы позволить USD заставить тело спать во время симуляции.Мы решили против этого
поскольку точные правила деактивации являются деталями реализации, которые могут варьироваться
значительно между симуляциями, поэтому мы предпочитаем держать это как скрытый
детали реализации на данный момент.
Кинематические тела
В играх и визуальных эффектах часто желательно, чтобы аниматор взял на себя полный контроль. над телом, даже когда оно взаимодействует с другими телами, управляемыми физикой. Мы называем такие тела «кинематичны». Кинематические тела по-прежнему «притягивают» суставы и «толкают» касается твердых тел, но их xform только читается, но не записывается симулятор физики, позволяя системе анимации писать свои xforms.Мы поддерживаем такие тела с использованием атрибута PhysicsRigidBodyAPI:kinematicEnabled. Кинематические тела — это не совсем то же самое, что анимированное статическое тело с коллайдер: моделирование предполагает непрерывную скорость кинематического тела от ключевого кадра, и эта скорость будет сообщаться динамическим телам во время столкновения.
Анимация атрибутов
Мы исходили из предположения, что каждый атрибут каждого класса, который не
явно помеченные как «униформа», могут быть анимированы.Явно беспорядочная смена
некоторые параметры могут привести к тому, что некоторые симуляции взорвутся на практике, но мы считаем,
это сильно зависит от реализации и не является причиной вообще запрещать
анимация атрибутов.
Массовые характеристики тела
Мы решили отделить массовые свойства от PhysicsRigidBodyAPI и поместить их в отдельном PhysicsMassAPI. PhysicsMassAPI не требуется в большинстве распространенных случаев, когда массовые свойства объекта могут быть получены из геометрия столкновения (обсуждается далее в этом документе) и API физики материалов.Чаще всего PhysicsMassAPI применяется в дополнение к PhysicsRigidBodyAPI.
В отличие от PhysicsRigidBodyAPI также можно применять PhysicsMassAPI несколько раз в поддереве графа сцены USD, чтобы позволяют аккумулировать массу жестких компонентов.
Масса объекта может быть указана несколькими способами, и несколько конфликтующих настройки разрешаются с использованием системы приоритетов, которая поначалу может показаться довольно сложный, но на самом деле интуитивно понятный и практичный:
Явные общие массы родителей переопределяют любые заданные свойства массы ниже в поддереве.
Плотность имеет более низкий приоритет, чем масса, поэтому явная масса всегда имеет приоритет неявная масса, которую можно вычислить по объему и плотности.
Плотность в дочернем элементе имеет приоритет над плотностью, заданной в родительском для всех поддерево под дочерним элементом.
Плотность, указанная через PhysicsMassAPI, даже если она унаследована из узла выше в дереве, переопределяет любую плотность, указанную с помощью материала (см. PhysicsMaterialAPI далее в этом документе).3\) (приблизительно плотность воды) для расчета объема, когда не указана другая плотность локально или в соответствующих материалах либо локально, либо выше в дереве, и это значение преобразуется в собственные единицы измерения коллайдера перед используется для массовых вычислений.
Предполагается, что масса равна \(1,0\) в используемых единицах массы, если ни одна предоставляется явно, и нет никаких объемов коллизий, из которых можно было бы вывести.
Поскольку реализация этого набора правил может быть нетривиальной, мы планируем сделать
доступный псевдокод системы массовых вычислений, основанный на базовом
Физическая система для вычисления объема геометрии столкновения.
Формы столкновения
Наш дизайн для форм столкновения определяет API PhysicsCollision, который может быть прикрепляется к объектам типа USDGeomGprim, представляющим графическую геометрию. В частности, мы предлагаем поддержку USDGeomCapsule, USDGeomCone, USDGeomCube, USDGeomCylinder, USDGeomSphere и USDGeomMesh, хотя точный набор поддерживаемых geoms может зависеть от реализации. Отметим также, что некоторые реализации может поддерживать некоторые из этих форм, используя потенциально граненые выпуклые приближения.
Как мы, возможно, уже упоминали, поддерево под
Узел PhysicsRigidBodyAPI может содержать несколько узлов формы столкновения (или
«коллайдеры»), которые необходимы для разрешения движения тела при соприкосновении с
другие тела. Например, чайник представляет собой единое твердое тело (узел верхнего уровня
помечен PhysicsRigidBodyAPI), но может состоять из нескольких
Сетка и другие геометрии в этом узле и под ним. Каждая из этих частей может получить
PhysicsCollisionAPI, который инструктирует систему сделать геометрию этой формы. в коллайдер для моделирования физики.
в коллайдер для моделирования физики.
Также возможно иметь PhysicsCollisionAPI на узлах, которые не под PhysicsRigidBodyAPI. Они рассматриваются как статические коллайдеры — формы, которые не двигаются физикой, но все же могут сталкиваться с телами при в этой точке они интерпретируются как имеющие нулевую скорость и бесконечную массу.
Обратите внимание, что для этого случая статического коллайдера, когда у нас нет соответствующего PhysicsRigidBodyAPI, PhysicsCollisionAPI может укажите сцену SimulationOwner. Если есть PhysicsRigidBodyAPI, который к которому принадлежит этот коллайдер, атрибут владельца симуляции коллайдера игнорируется.
Обратите внимание, что, поскольку в соответствии с правилами USD, USDGeomGprims обычно должен быть конечным
узлы, и поскольку PhysicsCollisionAPI может применяться только к
USDGeomGprim, значит нет возможности наследовать
Атрибуты PhysicsCollisionAPI вниз по графу сцены. Если сетка
состоит из подсетей, все подсетки считаются частью
коллайдер.
Стоит отметить, что данная конструкция имеет тот недостаток, что она невозможно напрямую добавить несколько коллайдеров к одному объекту geom.К добавить несколько коллайдеров, необходимо создать родительскую Xform (которая получает PhysicsRigidBodyAPI), а затем добавьте исходную геометрию в качестве дочерней и добавьте любые дополнительные коллайдеры как дополнительные дети. Это немного более инвазивно чем мы бы предпочли, но единственной альтернативой было бы создание коллайдеров Is-A схемы, а не API, которых хотелось избежать, чтобы предотвратить количество долларовых объектов значительно увеличилось.
Превращение сеток в фигуры
Простые призмы в долларах США, такие как сфера, цилиндр, куб, конус и капсула, обычно
можно использовать для моделирования физики напрямую, просто добавив
PhysicsCollisionAPI.USDMesh немного сложен, потому что современный
при моделировании произвольных сеток в реальном времени приходится идти на некоторые компромиссы, на которые пользователи
вообще хотят контролировать. Чтобы поддержать это, мы разрешаем
PhysicsMeshCollisionAPI будет применяться только к USDGeomMeshes, наряду с
API PhysicsCollision. Этот API имеет атрибут приближения, который
позволяет пользователю выбирать между отсутствием приближения (как правило, самая низкая производительность) и
упрощенная сетка, набор выпуклых оболочек, одна выпуклая оболочка, ограничительная рамка или
ограничивающая сфера.Если реализация не поддерживает определенный тип
приближение, рекомендуется вернуться к наиболее похожему
поддерживаемый вариант.
Чтобы поддержать это, мы разрешаем
PhysicsMeshCollisionAPI будет применяться только к USDGeomMeshes, наряду с
API PhysicsCollision. Этот API имеет атрибут приближения, который
позволяет пользователю выбирать между отсутствием приближения (как правило, самая низкая производительность) и
упрощенная сетка, набор выпуклых оболочек, одна выпуклая оболочка, ограничительная рамка или
ограничивающая сфера.Если реализация не поддерживает определенный тип
приближение, рекомендуется вернуться к наиболее похожему
поддерживаемый вариант.
Можно явно указать меш коллизий (например, тот, который был обработан конкретным дециматором), добавив пользовательскую сетку коллайдера в качестве брата исходную графическую сетку, установите для нее значение «направляющая», чтобы она не отображалась, и примените PhysicsCollisionAPI и PhysicsMeshCollisionAPI с указанием нет приближения.
Физические материалы
Как и в графике, в физике используются свойства материалов.Эти в основном используются
информировать поведение восстановления трения и столкновения, в дополнение к тому, что
из нескольких способов указать плотность объекта, как обсуждалось ранее. Все эти
свойства хранятся в PhysicsMaterialAPI, который можно применять к
узел материала USD, так как мы считаем целесообразным добавить физические свойства
в установленную библиотеку материалов USD.
Все эти
свойства хранятся в PhysicsMaterialAPI, который можно применять к
узел материала USD, так как мы считаем целесообразным добавить физические свойства
в установленную библиотеку материалов USD.
PhysicsMaterials связываются так же, как и графические материалы, используя UsdShadeMaterialBindingAPI либо без квалификатора цели, либо с конкретная «физика» цель.Обратите внимание, что этот подход также позволяет использовать привязку различные материалы для GeomSubsets. Не все физические симуляции поддерживают разные материалы для каждого GeomSubset, и возможно, что все, кроме одного подмножества на коллайдер будет игнорироваться реализацией.
Безразмерные коэффициенты dynamicFriction и staticFriction определяются
Кулоновская модель трения. Коэффициент реституции – это отношение
конечная к начальной относительной скорости между двумя объектами после их столкновения.
Эти три свойства фактически должны быть определены для каждой комбинации двух
материалов, но это обычно считается нецелесообразным. Обычная практика в
физика реального времени состоит в том, чтобы определить их для каждого материала, а затем использовать простой
формула для их объединения, например, взяв произведение или минимум.
В настоящее время поведение по умолчанию, которое мы предлагаем, заключается в усреднении значений, что является
поведение по умолчанию в популярных игровых движках в реальном времени. В будущем другие комбайны
режимы должны быть выставлены.
Обычная практика в
физика реального времени состоит в том, чтобы определить их для каждого материала, а затем использовать простой
формула для их объединения, например, взяв произведение или минимум.
В настоящее время поведение по умолчанию, которое мы предлагаем, заключается в усреднении значений, что является
поведение по умолчанию в популярных игровых движках в реальном времени. В будущем другие комбайны
режимы должны быть выставлены.
Плоские фигуры
Неявные плоские формы — очень распространенный физический примитив, используемый в основном для тестирование простых симуляций.Планируется добавить в USD класс Plane в качестве USDGeomGPrim. Мы надеемся на поддержку таких плоских форм, как статические коллайдеры, когда они станут доступны.
Фильтрация столкновений
Даже в простейших практических приложениях необходимо игнорировать некоторые коллизии.
происходит часто. Возможно, понадобится меч игрового персонажа, чтобы пройти сквозь
врага, а не отскакивать, желая, чтобы он отскакивал от стен, ибо
пример.
Мы определяем CollisionGroup как схему IsA с Применен UsdCollectionAPI, определяющий принадлежность коллайдеров (объекты с PhysicsCollisionAPI) в группе.В каждой группе также есть список соотношений к другим группам (потенциально включая себя), с которыми ему нужно чтобы не столкнуться. Коллайдеры, не входящие ни в одну CollisionGroup, сталкиваются со всеми другие коллайдеры в сцене.
Попарная фильтрация
Иногда групповая фильтрация недостаточно мощна, чтобы позаботиться о некоторых
фильтрация особых случаев. Например, можно было бы настроить групповую фильтрацию, такую как
что тела человеческих персонажей сталкиваются с конечностями, такими как руки и ноги,
обычно предполагая, что эти руки и ноги принадлежат другим людям, чем
тела.Однако часто не хочется, чтобы конечности конкретного человека
столкнуться с собственным телом, чего трудно избежать во время множества постоянных сближений.
приближение движения. Чтобы покрыть этот случай, у нас есть FilteringPairsAPI,
который содержит список отношений с другими объектами, с которыми конфликты
явно отключен.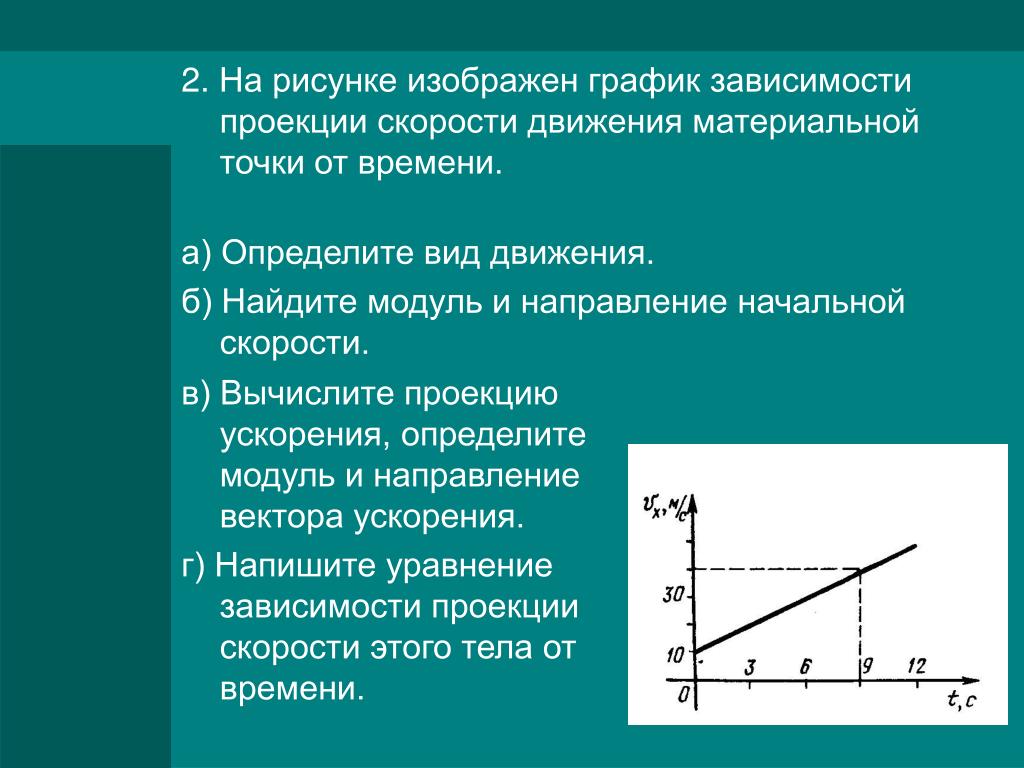 Эта попарная фильтрация имеет приоритет над групповой фильтрацией.
фильтрация.
Эта попарная фильтрация имеет приоритет над групповой фильтрацией.
фильтрация.
API FilteringPairsAPI можно применять к объектам с PhysicsRigidBodyAPI, PhysicsCollisionAPI или API физикиАртикуляции.
Достаточно иметь связь от объекта A к объекту B, чтобы получить фильтрующее поведение. В этом случае обратная связь от B к A является неявной и не обязательно.
Соединения
Соединения — это, как правило, фиксированные крепления, которые могут отображать форму ящика. прикрепленные к шкафу, колесо к автомобилю или звенья робота друг к другу. Здесь мы пытаемся сосредоточиться на наборе возможностей, которые являются общими для большинства симуляторов. пакеты и достаточно выразительны для большого количества приложений.
Математически сочлененные узлы можно моделировать как в максимальном (мировом
пространстве) или приведенные (относительно других тел) координаты. Оба представления
есть плюсы и минусы. Мы предлагаем представление в долларах США, которое будет работать с
оба подхода.
Совместные опорные кадры
Наш базовый тип сустава — это PhysicsJoint класса IsA. Суставы не обязательно имеют единственную уникальную X-форму в пространстве, скорее, они определяются двумя различными рамки, по одной относительно каждого из двух тел, которые они соединяют.
Эти два кадра могут не совпадать по положению и ориентации в мировое пространство из-за разрешенного относительного движения сустава (представьте себе автомобильную подвеску, движущуюся вверх и вниз: шарнирная рама подвески постоянна как относительно кузова автомобиля, так и оси автомобиля, однако ось и ходовой части относительно друг друга) или погрешность приблизительного симуляции, которые могут позволить суставу слегка разойтись при воздействии значительные силы или скорости.
Из-за этих двойных преобразований для нас не имело смысла выводить
PhysicsJoint от Xformable, который имеет только одну Xform. Мы могли бы
создали асимметричное решение, в которое добавлена вторичная xform, или
разделить объект соединения на два отдельных кадра соединения, которые являются родительскими в
граф сцены, а затем каким-то образом попарно связаны перекрестными ссылками, но мы решили пойти
с совершенно новым классом, который содержит всю необходимую нам информацию в симметричном
мода.
Сочлененные тела
Соединение определяет отношения между двумя объектами Xformable.Возможна имитация сустава если хотя бы на одном из них есть PhysicsRigidBodyAPI, или на предок. Если какой-либо из rel не определен, он считается эквивалентным присоединению в статическую мировую рамку, хотя рекомендуется всегда работать с двумя хорошо определенные Xformables.
Совместное пространство относительно каждого тела представляет собой только перемещение и ориентацию,
масштабирование не поддерживается. (Это общее противоречие между графикой и
физика. В реальном мире, как правило, невозможно масштабировать реальные объекты.
и симуляции, как правило, не поддерживают масштабирование во время симуляции твердого тела).По этой причине мы не используем общую долларовую форму xform, которая слишком гибка для наших целей.
потребности, а скорее отдельное положение и кватернион ориентации. (Обратите внимание, однако
что это локальное совместное пространство фиксируется в локальном пространстве узла, что, конечно,
МОЖЕТ масштабироваться с использованием собственного масштабирования Xform узла.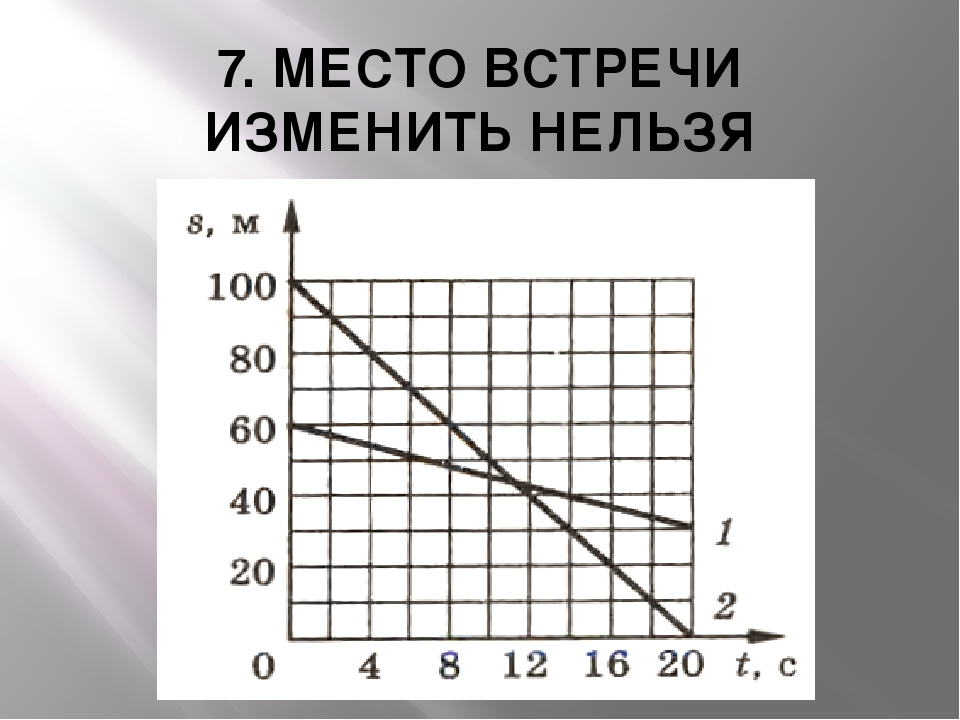 Это означает, что если дверная ручка
прикреплен к двери в определенном месте, он будет продолжать появляться в
одно и то же правильное положение на двери независимо от масштаба двери,
без необходимости корректировать положение сустава.)
Это означает, что если дверная ручка
прикреплен к двери в определенном месте, он будет продолжать появляться в
одно и то же правильное положение на двери независимо от масштаба двери,
без необходимости корректировать положение сустава.)
Обратите внимание, что обычно мы хотим, чтобы два шарнирных фрейма выровнялись в мире. пространстве, по крайней мере, вдоль их ограниченных степеней свободы. Это условие может нарушаться, если какое-либо тело перемещается в мировом пространстве либо путем изменения собственного или одно из его родительских преобразований, или если любое тело rels изменено. Как результате желательно пересчитать шарнирные кадры, когда связанные тела или их преобразования мирового пространства изменились.
Совместная фильтрация столкновений
Обычной практикой является отключение коллизий между соединенными объектами, чтобы
их формы столкновения не мешают, и поэтому это значение по умолчанию
поведение, которое можно изменить с помощью атрибута соединения CollisionEnabled .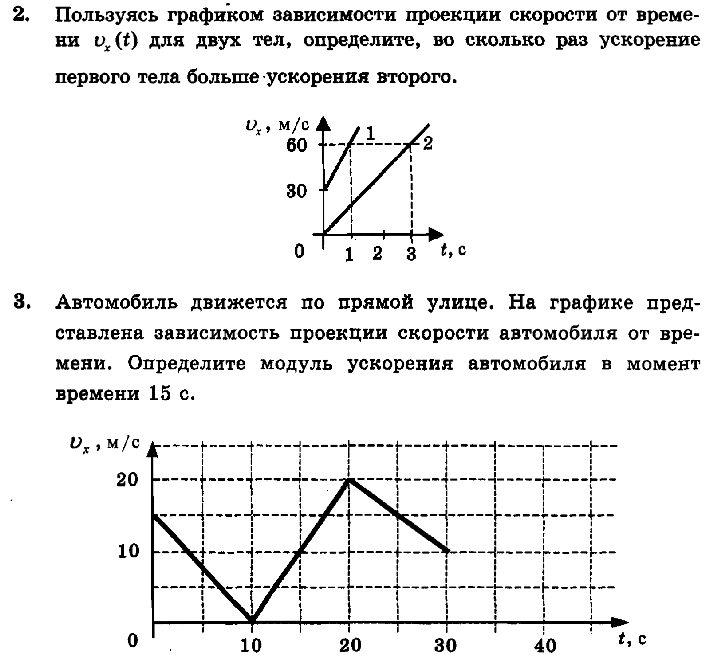 Это относится только к соединениям с двумя явными телами: соединение с миром не
НЕ отключайте столкновения между телом и миром.
Это относится только к соединениям с двумя явными телами: соединение с миром не
НЕ отключайте столкновения между телом и миром.
Разрушение и выведение из строя суставов
Одно из свойств, которое, по нашему мнению, может быть полезным для всех суставов, заключается в том, что они могут сломаться. при приложении достаточной силы. Например, дверь можно оторвать. петли. Это можно смоделировать с помощью атрибутов breakForce и breakTorque.
Соединения могут быть полностью временно отключены, как твердые тела или коллайдеры.В отличие от взлома, который представляет собой (в ходе симуляции необратимое) симулированное поведение, отключение — просьба не симулировать вообще сустав.
Совместные подтипы
Соединения имеют ряд возможных производных типов, которые позволяют использовать определенные типы соединений.
соединения, однако его также можно использовать для представления общего конфигурируемого соединения,
так что в этом смысле это не абстрактный тип.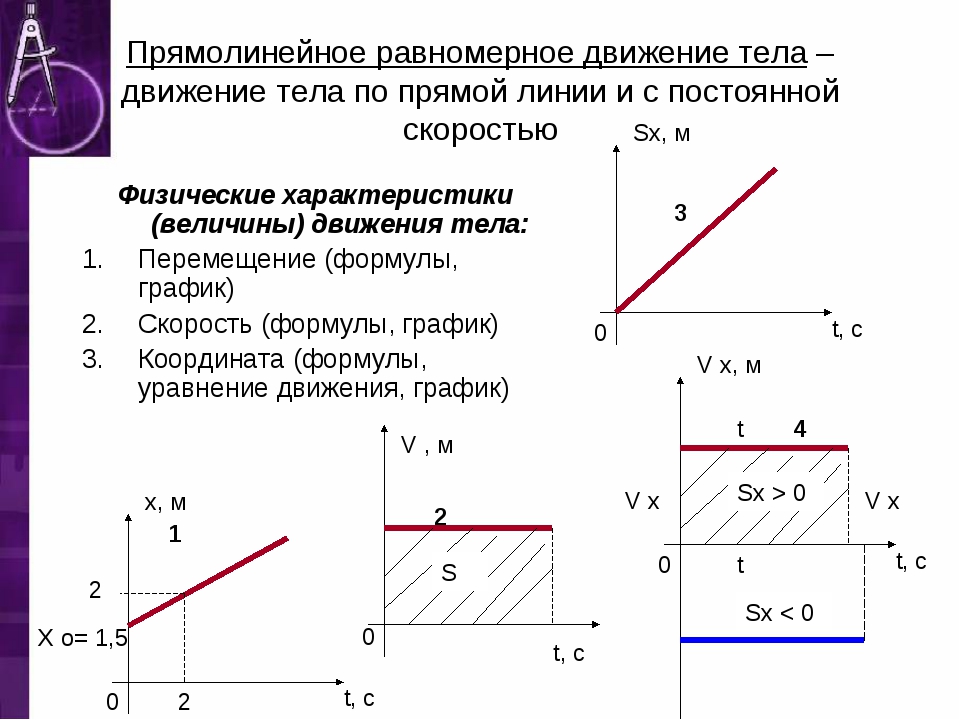
Подтипы PhysicsSphericalJoint, PhysicsRevoluteJoint и Оба PhysicsPrismaticJoint определяют основную ось (после оси USD шаблон определения, установленный в e.г. GeomCapsule и GeomCylinder) и топ и предел движения дна по ней. PhysicsDistanceJoint определяет мин. максимальное расстояние между точками крепления. PhysicsFixedJoint не имеет дополнительные свойства и просто блокирует все относительные степени свободы.
Совместные ограничения и приводы
Вместо использования одного из предопределенных подтипов соединения также можно составить пользовательское соединение из набора ограничений и приводов. Ограничения и драйвы схемы множественного применения, поэтому можно применять несколько экземпляров, по одному для каждой степени Свобода.Степень свободы указывается через TfToken (фактически строка, одна из «transX», «transY», «transZ», «rotX», «rotY», «rotZ», «distance», который добавляется после имени класса.)
Кроме того, API ограничений содержит необязательные атрибуты нижнего и верхнего пределов.
API привода позволяет моторизовать соединения по степеням свободы. Это может указать либо силовой, либо ускоренный привод (сила силовых приводов под действием массы тел, прикрепленных к суставу, привод ускорения не является).У него также есть целевое значение, которого нужно достичь, и можно указать, является ли целевое значение является целевым положением или скоростью. Можно ограничить максимальное усилие, которое привод может применяются, и можно указать пружину и коэффициент демпфирования. Результирующий движущая сила или ускорение пропорциональны:
\(жесткость * (targetPosition – p) + демпфирование * (targetVelocity – v)\)
, где p — относительное позиционное движение сустава в пространстве (осевое вращение вращательное соединение или осевое перемещение для призматического соединения), а v – скорость изменение этого движения.
Для всех пределов, указывающих диапазоны, «нижний» предел больше, чем «верхний» предел
означает, что совместное движение вдоль этой оси заблокировано.
Артикуляции
Выше мы сказали, что мы также поддерживаем уменьшенные координатные соединения, которые требуют
некоторая дополнительная спецификация. Мы решили сделать это с минимальным расширением
вышеуказанные максимальные суставы. Любой узел иерархии графа сцены USD может быть
помечены ArticulationRootAPI. Это информирует моделирование о том, что любой
суставы, найденные в поддереве, должны предпочтительно моделироваться с использованием уменьшенного
Координационный подход.Для плавающих сочленений (жаргон робототехники для чего-то
не прикручен, т.е. колесный робот или квадрокоптер), следует использовать этот API
на корневом корпусе (обычно к центральной массе крепятся колеса или роторы
to) или прямой или косвенный родительский узел. Для фиксированных сочленений (робототехника)
жаргон для напр. манипулятор для сварки, привинченный к полу), этот API
может быть на прямом или косвенном родительском корневом суставе, который связан с
мире или на самом суставе. Если имеется несколько квалификационных органов или
суставы под узлом ArticulationRootAPI, каждый из которых выделен в отдельный
артикуляционный корень.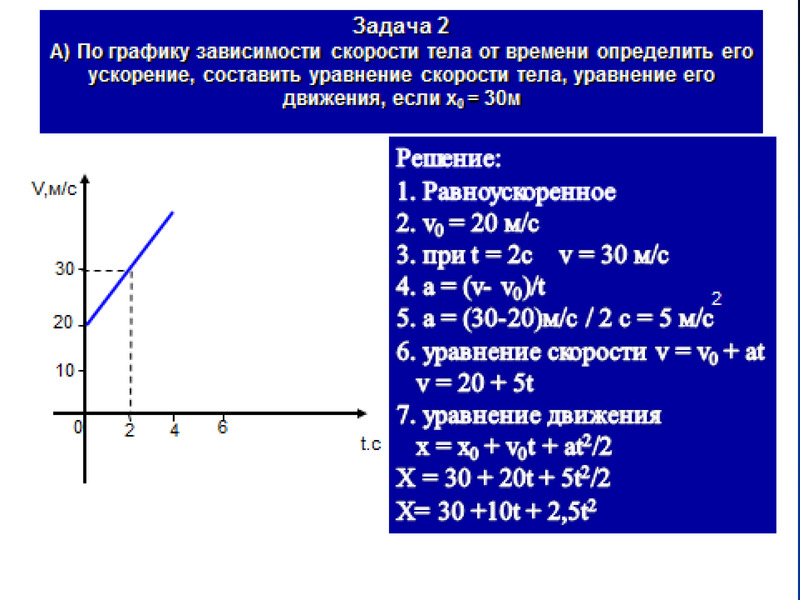
В целом это должно позволять однозначно идентифицировать выделенный корневое тело или корневой сустав для сочленения. Из этого корня дерево тел и определены соединения, которые не должны содержать петель (которые могут быть закрыты совместные коллекции). Если петли обнаружены, они могут быть разорваны в произвольном место расположения. В качестве альтернативы соединение в цикле может использовать его excludeFromArticulation. флаг атрибута, чтобы обозначить, что он хочет оставаться максимальным соединением, и в этом точка, петля затем разорвана.
студентов, изучающих физику и графический дизайн, вместе работают над COVID-19
- Дом
- Физика
- Детали новостей
17.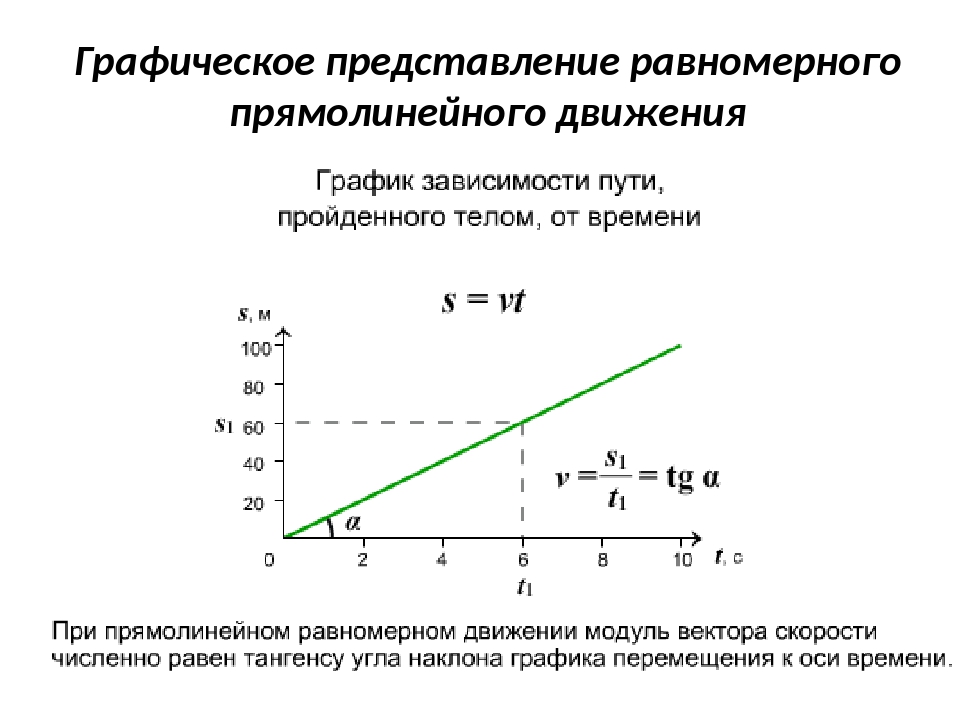 05.2020
05.2020
Рассказывать историю пандемии COVID-19 сложно.
Как лучше всего объединить исследования по медицинским, экономическим и политическим вопросам, связанным с вирусом, и скомпилировать их в простой для восприятия визуальный пакет?
Что ж, группа студентов SUNY Cortland, изучающих физику и графический дизайн, решила сделать именно это в этом семестре.
Доцент Эрик Эдлунд с кафедры физики и доцент Сильвия Кадас с кафедры искусства и истории искусств работали со студентами над этой темой.
В начале семестра студентам было поручено составить список вопросов социальной или экологической важности.Коронавирус занял в этом первоначальном списке 9-е место среди 26 тем, первоначально отставая от таких тем, как изменение климата, личные и студенческие долги, биоразнообразие и психическое здоровье. Когда в марте проект приблизился к дате начала, очевидной целью стал COVID-19.
Студенты, изучающие графический дизайн и физику, начали проект вместе, разделившись на междисциплинарные группы для изучения трех тем:
- Как социальное дистанцирование и карантин влияют на распространение COVID-19
- Как доступность медицинских ресурсов, таких как персонал, больничные койки, вентиляторы и маски, влияет на распространение COVID-19
- Как социальное дистанцирование и карантин меняют экономику
Студенты обменивались новостными статьями и обсуждали возможные исследовательские вопросы.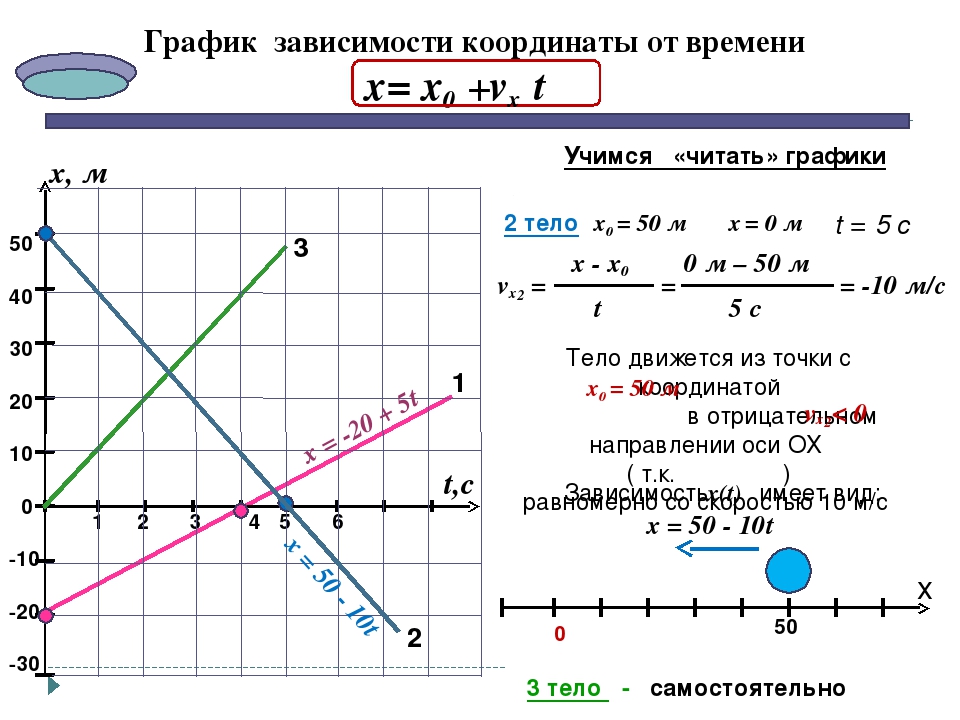 Затем студенты-физики более подробно изучили эти исследовательские вопросы и создали численные модели.
Затем студенты-физики более подробно изучили эти исследовательские вопросы и создали численные модели.
«Мы пытались понять, сможем ли мы построить набор уравнений, подобный хрустальному шару, который позволит нам хоть как-то заглянуть в будущее», — сказал Эдлунд. «В этом процессе мы много думали о том, какие факторы имеют значение».
Когда модель была готова, студенты-физики взяли графические модели и написали технические отчеты, чтобы объяснить эту сложную математику словами.
Студенты, изучающие графический дизайн, взяли эти отчеты и попросили создать плакат размером 17×23 дюйма, который наглядно представлял результаты. У Кадаса было три основных результата обучения: как визуально рассказывать и рассказывать историю, как использовать инфографику и как читать научные данные и осмысливать их.
«Я хотел, чтобы они визуализировали это и создали визуальные формы из данных, а также придумали историю, которая была бы актуальна для широкой публики», — сказал Кадас.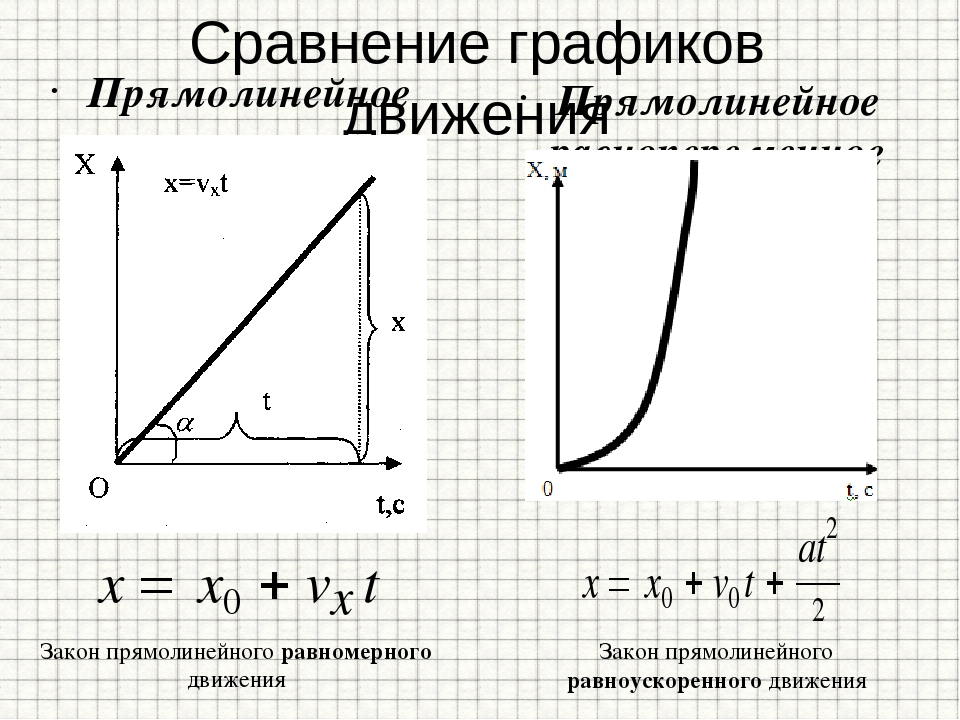 «Это отличное упражнение и задание для них.Это неотъемлемая часть графического дизайна».
«Это отличное упражнение и задание для них.Это неотъемлемая часть графического дизайна».
Полная галерея работ учащихся доступна онлайн.
Уже второй год подряд факультеты физики и искусства и истории искусств работают вместе в рамках участия SUNY Cortland в проекте Common Problem Pedagogy Project, совместном проекте четырех кампусов SUNY, направленном на использование научных кругов для решения реальных проблем.
После весенних каникул студенты двух факультетов собрались вместе, чтобы поделиться идеями и помочь друг другу понять свою сторону проекта.
«Мне было довольно трудно читать отчет и его научные аспекты, но я просто попытался выделить ключевые моменты для иллюстрации», — сказала Жаклин Алоя, уроженка Плезантвилля, штат Нью-Йорк, старший специалист по коммуникациям, специализирующаяся на графическом дизайне.
«Это было интересно, — сказал Алекс Гентнер, старший специалист по новым медиакоммуникациям и графическому дизайну из Уэст-Вэлли, штат Нью-Йорк.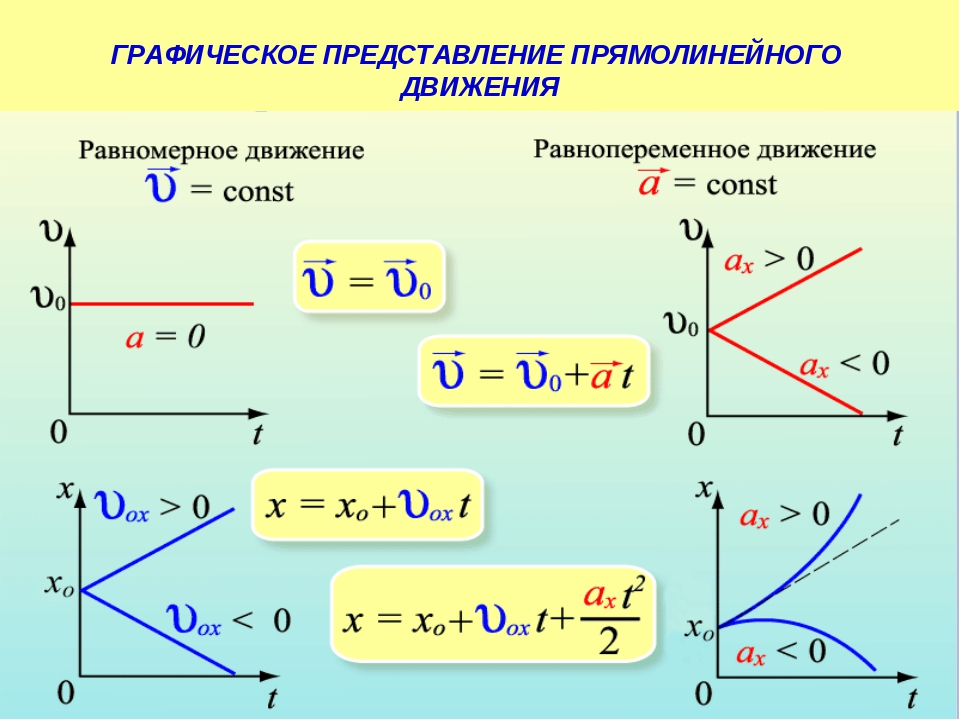 работал с людьми из другого отдела, так что это был хороший опыт.
работал с людьми из другого отдела, так что это был хороший опыт.
Выбор COVID-19 в качестве темы для этого совместного проекта нашел отклик у студентов, которым не терпелось узнать больше о том, как вирус меняет нашу жизнь.
Плакат Алекса Гентнера«Вообще, каждый раз, когда мы можем преподнести учащемуся актуальный урок, это делает его значимым», — сказал Эдлунд. «Им очень легко увлечься этим, что и было именно так. В этом смысле это очень упростило процесс обучения, потому что нам не нужно было работать над мотивацией.
Один из этих студентов, Хосе Диас Дюран, младший специалист по физике из Бронкса, штат Нью-Йорк, изучал потенциальные экономические последствия COVID-19. Он рассматривал Великую депрессию 1930-х годов и Великую рецессию 2008–2009 годов как сравнительные показатели текущих экономических проблем, с которыми сталкиваются американцы.
«Меня заинтересовала эта тема, потому что это было что-то новое», — сказал Диас Дюран. «Мы никогда не делали этого раньше. Было интересно провести исследование и попросить профессора Эдлунда помочь нам с математикой.Мы придумали модель, которая была очень близка к тому, что мы живем в данный момент. Мне это очень понравилось».
Было интересно провести исследование и попросить профессора Эдлунда помочь нам с математикой.Мы придумали модель, которая была очень близка к тому, что мы живем в данный момент. Мне это очень понравилось».
Для Эйвери Томпкинс, ученицы младшего подросткового возраста по специальности физика и математика из Овего, штат Нью-Йорк, проект помог ей понять меняющийся мир и сделал ее более связанной с новостями о пандемии.
«Вначале я не думала, что смогу понять такую модель», — сказала она. «Он (Эдлунд) помог нам понять, как это работает. Мы живем в нем, так что это сделало его более интересным, чем некоторые другие идеи, которые мы изначально придумали.
Многие из студентов, изучающих графический дизайн, которые учатся удаленно из дома, нашли аудиторию в лице родителей, братьев, сестер и других членов семьи, которые помогли сформировать их работу. Поскольку COVID-19 настолько актуален, сторонние мнения информировали их о том, адекватно ли их работа передает их сообщение.

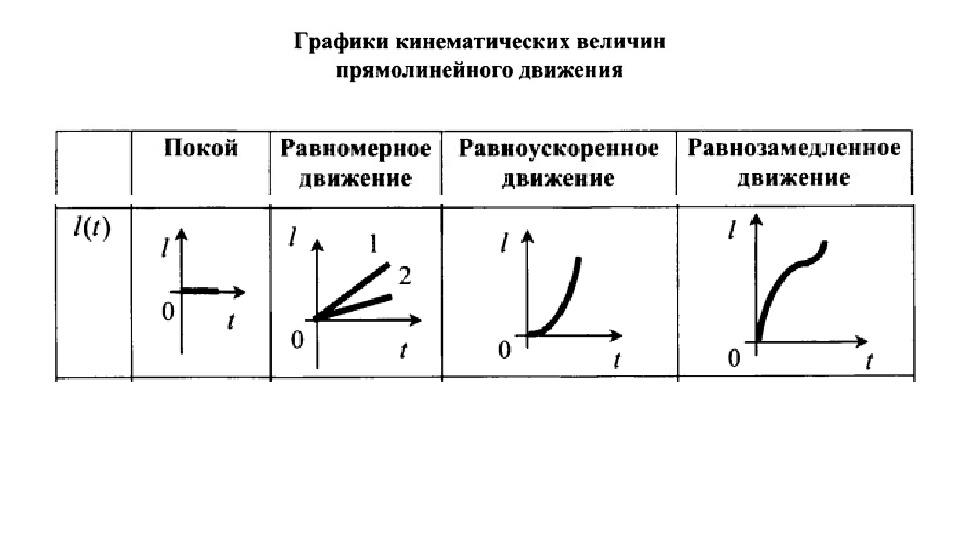 Особо следует сказать о размере графика: он определяется
не размером имеющегося у вас кусочка «миллиметровки», а масштабом. Масштаб
выбирают прежде всего с учетом интервалов измерения (по каждой оси он
выбирается отдельно).
Особо следует сказать о размере графика: он определяется
не размером имеющегося у вас кусочка «миллиметровки», а масштабом. Масштаб
выбирают прежде всего с учетом интервалов измерения (по каждой оси он
выбирается отдельно).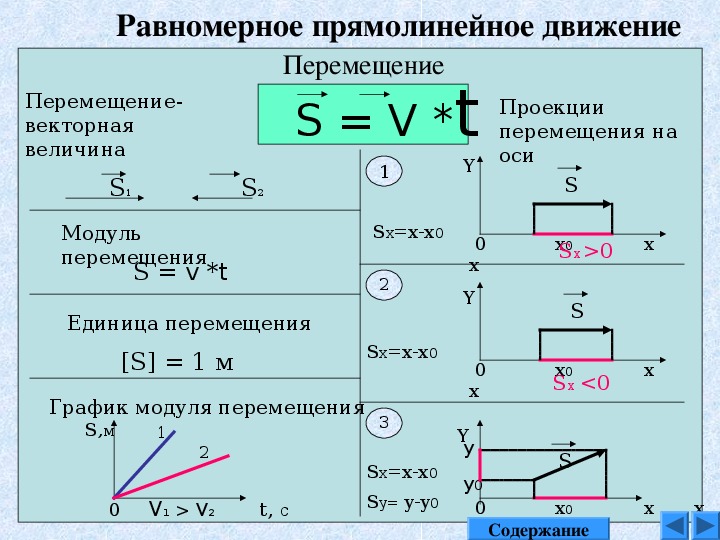 п. Допустимо выделять линии различным цветом. Вовсе не обязательно, чтобы в точке пересечения осей было начало координат 0:0). По каждой из осей можно отображать только интервалы измерения исследуемых величин.
п. Допустимо выделять линии различным цветом. Вовсе не обязательно, чтобы в точке пересечения осей было начало координат 0:0). По каждой из осей можно отображать только интервалы измерения исследуемых величин. Поэтому посредством
удачного выбора функционального масштаба можно привести зависимость к линейной.
Поэтому посредством
удачного выбора функционального масштаба можно привести зависимость к линейной.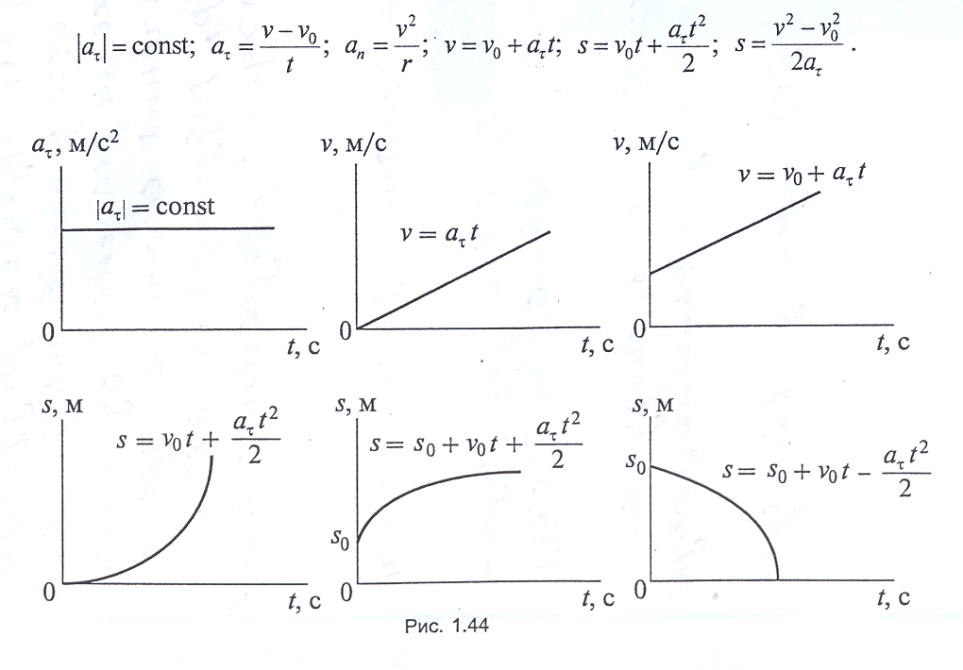
 На графике в этом случае изображается кривая, полученная со средним значением параметра, и полоса, ограниченная двумя расчетными кривыми для максимального и минимального значений параметра.
На графике в этом случае изображается кривая, полученная со средним значением параметра, и полоса, ограниченная двумя расчетными кривыми для максимального и минимального значений параметра.