Что означает формула E=mc2 и как с ее помощью раздобыть много энергии — T&P
Все знают формулу E=mc
2, и все слышали, что ее Эйнштейн придумал. Многие даже знают, что Е обозначает энергию, m — массу, а c — скорость света. Но что все это означает?Если взять обычную пальчиковую батарейку из пульта от телевизора, и превратить ее в энергию, то точно такую же энергию можно получить от 250 миллиардов таких же батареек, если использовать их по-старинке. Не очень хороший получается КПД.
А то и означает, что масса и энергия — это одно и то же. То есть масса — это частный случай энергии. Энергию, заключенную в массе чего угодно, можно посчитать по этой простой формуле.
Скорость света — это очень много. Это 299 792 458 метров в секунду или, если вам так удобнее, 1 079 252 848,8 километров в час. Из-за этой большой величины получается, что если превратить чайный пакетик целиком в энергию, то этого хватит, чтобы вскипятить 350 миллиардов чайников.
У меня есть пара грамм вещества, где мне получить мою энергию?
Перевести всю массу предмета в энергию можно, только если вы где-нибудь найдете столько же антиматерии. А ее получить в домашних условиях проблематично, этот вариант отпадает.
Термоядерный синтез
Существует очень много природных термоядерных реакторов, вы можете их наблюдать, просто взглянув на небо. Солнце и другие звезды — это и есть гигантские термоядерные реакторы.
Другой способ откусить от материи хоть сколько-то массы и превратить ее в энергию — это произвести термоядерный синтез. Берем два ядра водорода, сталкиваем их, получаем одно ядро гелия. Весь фокус в том, что масса двух ядер водорода немного больше, чем масса одного ядра гелия. Вот эта масса и превращается в энергию.
Но тут тоже не так все просто: ученые еще не научились поддерживать реакцию управляемого ядерного синтеза, промышленный термоядерный реактор фигурирует только в самых оптимистичных планах на середину этого столетия.
Ядерный распад
Ближе к реальности — реакция ядерного распада. Она вовсю используется в ядерных электростанциях. Это когда два больших ядра атома распадаются на два маленьких. При такой реакции масса осколков получается меньше массы ядра, пропавшая масса и уходит в энергию.
Ядерный взрыв — это тоже ядерный распад, но неуправляемый, прекрасная иллюстрация этой формулы.
Горение
Превращение массы в энергию вы можете наблюдать прямо у вас в руках. Зажгите спичку — и вот она. При некоторых химических реакциях, например, горения, выделяется энергия от потери массы. Но она очень мала по сравнению с реакцией распада ядра, и вместо ядерного взрыва у вас в руках происходит просто горение спички.
Более того, когда вы поели, еда через сложные химические реакции благодаря мизерной потере массы отдает энергию, которую вы потом используете, чтобы сыграть в настольный теннис, ну или на диване перед телеком, чтобы поднять пульт и переключить канал.
Так что, когда вы едите бутерброд, часть его массы превратится в энергию по формуле E=mc2.
Игорь Гладкобородов
764 605
«Формулы скорости, времени, расстояния?» — Яндекс Кью
ПопулярноеСообщества
Как выразить эти понятия друг одно через другие?
ФизикаМатематикаМеханика
Анонимный вопрос
·
232,9 K
Ответить3УточнитьЕкатерина Лебедева
21
Учусь в гимназии №17. Увлекаюсь математикой, русским языком, родным языком, литературой и… · 20 мая 2021
(Обратите внимание, что для записи формулы пути используются строчные буквы s, v и t. Это сделано, чтобы не путать их с обозначением площади — S и объёма — V.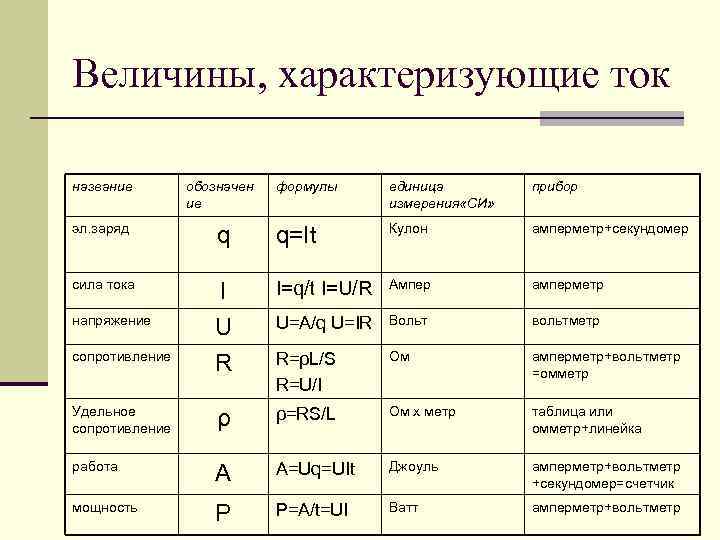 )
)
17,5 K
Комментировать ответ…Комментировать…
Сауле Абдулина
9
Ученик 7 класса , кинокритик · 27 мар 2021
V = S : t t = S : V S = V * t S = расстояние V = скорость t = время : = деление * = умножение Пример : Решил найти расстояние ( S) Для этого скорость ( V) которая равна 4км/ч *время ( t) 4 часа Ответ : 16 км Читать далее
18,6 K
АЛЕКСАНДР ЕРМОЛАЕВ
14 октября
Подскажите а как посчитать, за если я прохожу допустим растояние 9 метров за 7 минут, то за сколько я пройду 300 метров?
Комментировать ответ…Комментировать…
Тоха Манзулин
13 дек 2021
Чтобы найти скорость, нужно расстояние разделить на время движения: v = S: t. Время – это продолжительность каких-то действий, событий. Время движения обозначается маленькой латинской буквой t. Чтобы найти время, нужно расстояние разделить на скорость движения: t = S: v. Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Время движения обозначается маленькой латинской буквой t. Чтобы найти время, нужно расстояние разделить на скорость движения: t = S: v. Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Комментировать ответ…Комментировать…
Первый
79
15 мая 2020
Короче! Если у вас расстояние нужно найти то: S=t*v, S=50*20(пример) Если нужно найти время то: t=S:V Если нужно найти скорость то : V=S:T. Это все формулы. Читать далее
58,7 K
Маргарет
16 октября 2020
спасибо, Warrior! Было не понятно, но
ты помог мне выровнять математику!
Комментировать ответ…Комментировать…
Достоверно
Таня К.
1,4 K
Любопытство – не порок) · 3 нояб 2018
Если вам известна скорость v и время t, то вы сможете найти расстояние S по формуле S=vt. Обратите внимание на единицы измерения! Если вам дана скорость в километрах в час, то и время должно быть выражено в часах (или в метрах в секунду и секундах соответственно). Выразить скорость из этой формулы можно следующим образом: v=S/t А если вы хотите посчитать время, то восп… Читать далее
2 эксперта согласны
199,5 K
Александр Андросов
спосибо
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
4 ответа скрыто(Почему?)
Секретное оружие в физике – особой важности
Не все понимают, как часто физики могут угадать ответ на задачу, даже не начав вычислять.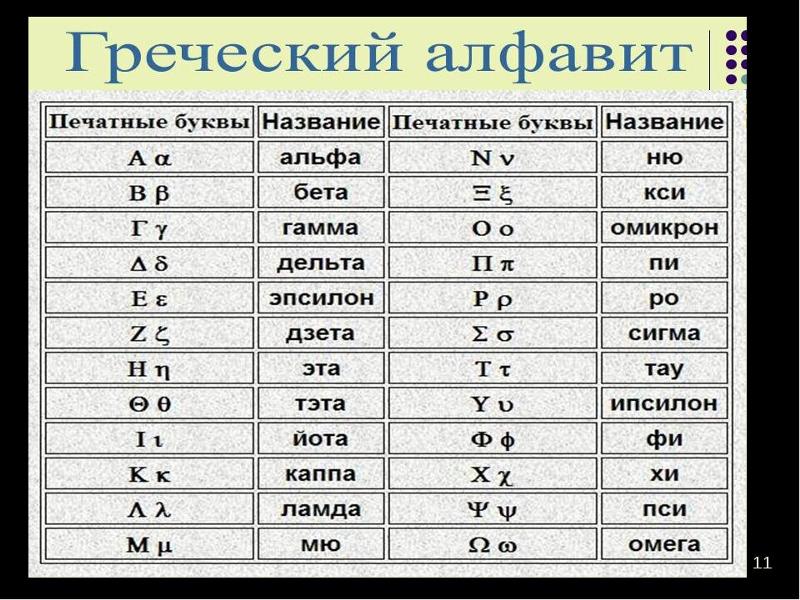 Сочетая основное требование согласованности с научными рассуждениями, они часто могут использовать эвристический подход к решению проблем, который позволяет им вывести большую часть формулы, вообще не выполняя никакой работы. На этой неделе я хочу представить вам это и показать вам некоторые его возможности.
Сочетая основное требование согласованности с научными рассуждениями, они часто могут использовать эвристический подход к решению проблем, который позволяет им вывести большую часть формулы, вообще не выполняя никакой работы. На этой неделе я хочу представить вам это и показать вам некоторые его возможности.
Хитрость, называемая «анализ размерностей», или «анализ единиц», или «рассуждения измерений», включает в себя требование согласованности между единицами, иногда называемыми «размерностями». Например, расстояние от Земли до Солнца, очевидно, равно длина . Мы можем указать длину в километрах, или в милях, или в дюймах; каждая единица длины. Но для сегодняшних целей не имеет значения, какой из них мы используем. Важно вот что: расстояние Земля-Солнце должно быть выражено в или единицах длины, потому что, ну, это длина! Или, говоря языком физики, он имеет «размеры и длину ».
Для любого уравнения в физике вида X = Y, две части уравнения должны быть согласованы друг с другом.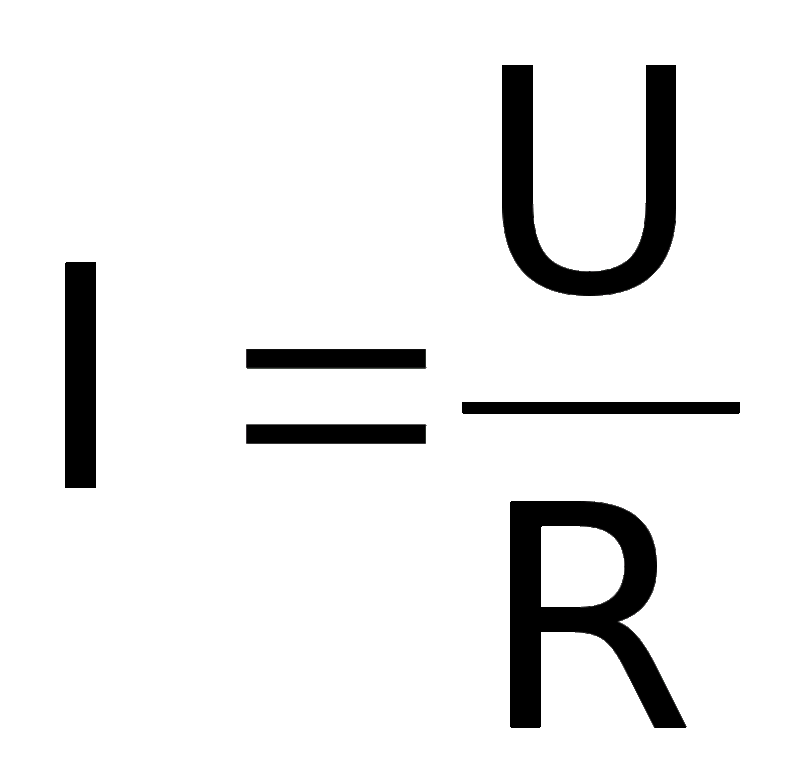 Если X имеет размеры длины, то Y также должен иметь размеры длины. Если X имеет размеры массы, то Y также должен. Точно так же, как вы не можете осмысленно сказать «Я вешу двенадцать метров» или «Мне семьдесят килограммов», физические уравнения должны иметь смысл , связывая веса с весами, или длины с длинами, или энергии с энергиями. Если вы видите уравнение X=Y, где X в метрах, а Y в джоулях (мера энергии), то вы знаете, что в уравнении есть опечатка или концептуальная ошибка.
Если X имеет размеры длины, то Y также должен иметь размеры длины. Если X имеет размеры массы, то Y также должен. Точно так же, как вы не можете осмысленно сказать «Я вешу двенадцать метров» или «Мне семьдесят килограммов», физические уравнения должны иметь смысл , связывая веса с весами, или длины с длинами, или энергии с энергиями. Если вы видите уравнение X=Y, где X в метрах, а Y в джоулях (мера энергии), то вы знаете, что в уравнении есть опечатка или концептуальная ошибка.
На самом деле поиск этого типа несоответствия является мощным инструментом, используемым как студентами, так и профессионалами при проверке расчетов на наличие ошибок. Я использую его как в своих исследованиях, так и при выставлении оценок, пытаясь выяснить, где ученик ошибся.
Это хорошо, но почему это полезно, кроме проверки на ошибки?
Иногда, когда вам нужно решить задачу, включающую несколько физических величин, может быть только одно непротиворечивое уравнение, связывающее их — только один способ приравнять X к Y. И вы можете угадать это уравнение, ничего не делая.
И вы можете угадать это уравнение, ничего не делая.
Ну, это довольно абстрактно; давайте посмотрим, как это работает на паре примеров.
Простой пример: скорость, радиус и период
Во-первых, очень простой пример, чтобы проиллюстрировать суть. Предположим, мы хотим найти скорость v Земли, когда она движется вокруг Солнца. Если мы назовем средний радиус примерно круговой орбиты Земли R, а T назовем временем, которое требуется для обращения вокруг Солнца, то какую формулу мы должны записать? Ну, есть только одна возможность, которая непротиворечива. Скорость v — длина, пройденная за время; он имеет размеры длины во времени. R — длина. Т – это время. И поэтому уравнение, которое их связывает, должно иметь форму
- v = # R / T
, где «#» — неизвестное число, не указанное в этом аргументе.
Поскольку мы не знаем этого числа, действительно ли мы что-то узнали? Да у нас есть! Формула не может установить v равным R 2 /T, или T 2 /R, или R T, или R 1,4 /T 2,6 . Любая формула, отличная от v = # R/T, связала бы длину за время с чем-то, что не является длиной за время … и поэтому было бы бессмысленным. Просто требуя смысла, мы в основном решили проблему, вообще не выполняя никакой работы , за исключением одного неизвестного #.
Любая формула, отличная от v = # R/T, связала бы длину за время с чем-то, что не является длиной за время … и поэтому было бы бессмысленным. Просто требуя смысла, мы в основном решили проблему, вообще не выполняя никакой работы , за исключением одного неизвестного #.
Если мы хотим быть точными, нам все равно придется вычислить неизвестное #. Если бы орбита была круговой, это было бы легко; # = 2π. Чтобы получить реалистичную эллиптическую орбиту, вам нужно ее вычислить. Тем не менее, для почти круговой орбиты, такой как у Земли, это # не будет ни миллиардом для почти круговой орбиты, ни миллиардной. Это будет число недалеко от 2π, что, в свою очередь, не слишком далеко от 1. (2π примерно равно 6.) Таким образом, мы можем сделать оценку без особых вычислений, если вообще вообще.
Интересный пример: закон Кеплера в деталях
Теперь давайте возьмем менее тривиальный пример, хотя его все же легко реализовать другими методами. Недавно, используя методы «сделай сам», я показал вам, как вы сами можете вывести третий закон Кеплера, который связывает радиус орбиты планеты R с периодом ее обращения T, в частности, что R 3 пропорционально T 2 . Мы обнаружили, что это справедливо для объектов, вращающихся вокруг Солнца. Мы также обнаружили, что это верно для объектов, вращающихся вокруг Земли, но с другими деталями. Можем ли мы найти формулу, которая верна и для Солнца и для Земли — кто объясняет разницу?
Недавно, используя методы «сделай сам», я показал вам, как вы сами можете вывести третий закон Кеплера, который связывает радиус орбиты планеты R с периодом ее обращения T, в частности, что R 3 пропорционально T 2 . Мы обнаружили, что это справедливо для объектов, вращающихся вокруг Солнца. Мы также обнаружили, что это верно для объектов, вращающихся вокруг Земли, но с другими деталями. Можем ли мы найти формулу, которая верна и для Солнца и для Земли — кто объясняет разницу?
Что ж, при допущении — что гравитация Ньютона каким-то образом задействована — можем. Вот тут-то и пригодятся физические рассуждения и некоторый опыт.
Во-первых, если действует гравитация, то опытный физик знает, что постоянная Ньютона G всегда имеет значение , потому что эта константа характеризует общую силу гравитации. Размеры G должны соответствовать уравнению гравитационной силы Ньютона 9.0003
- F = G M m / r 2
дает силу притяжения между двумя объектами массой M и m, которые находятся на расстоянии r друг от друга. Переставив для удобства, мы можем записать это как
Переставив для удобства, мы можем записать это как
- G = F r 2 /(M m)
На первом курсе физики мы узнаем, что сила имеет размерность масса, умноженная на длину, деленная на время в квадрате . M и m имеют размеры , массу , а r имеет размеры , длину . Из приведенного выше уравнения G = F r 2 /(М м), находим размеры самого G:
- размеры G = размеры F r 2 /(М м) [для согласованности!]
- = (размеры F) * (размеры r 2 )/(размеры M m)
- = (масса * длина / время 2 ) * (длина 2 )/(масса 2 = длина 4 () /время 2 /масса)
каким-то образом появляется масса этого центрального тела. Обозначим эту массу как «М».
Итак, теперь к закону Кеплера: может ли быть уравнение, которое связывает вездесущую гравитационную постоянную G, массу центрального тела M, период T объекта, вращающегося вокруг этого центрального тела, и радиус R этого тела? орбита? Well, how about
- G / M = # R 4 /T 2
or
- G M 5 = # R 9 T 2
or
or
- Г М 3/2 = # Т 5 /R 7/3 ?
Ни за что! Каждое из этих возможных уравнений — чепуха! потому что размеры левой стороны не равны размерам правой стороны!
Но на самом деле существует (в чем я вас сейчас убедю) один и только один возможный ответ, который может иметь смысл! Вот этот:
- G M = # R 3 /T 2
И это подтверждает, что для конкретного центрального объекта с массой M все объекты, вращающиеся вокруг него, имеют одинаковое отношение для R 3 до Т 2 . Другими словами, вы можете догадаться о третьем законе орбит Кеплера, просто используя анализ размерностей. Никаких сложных уравнений не требуется.
Другими словами, вы можете догадаться о третьем законе орбит Кеплера, просто используя анализ размерностей. Никаких сложных уравнений не требуется.
Опять же, # — это неизвестное число, которое нам нужно вычислить. Но даже если мы этого еще не знаем, мы уже на пути к формуле, которую хотим найти, и мы не сделали никакой работы, кроме проверки размеров!
Почему это единственная возможная формула? Можно быть систематическим в этом, но вот быстрый способ увидеть это. R и T не имеют единиц массы, но G и M имеют. Таким образом, чтобы связать G и M с R и T, должна существовать некоторая комбинация G и M, в которой размеры массы сокращаются. Поскольку, как мы только что видели выше, G имеет размеры чего-то, деленного на массу, G M — единственная комбинация, в которой измерения массы отменяют , оставляя только измерения длины и времени! На самом деле GM имеет размеры длины 3 , разделенные на время 2 , и это означает, что GM может быть связано только с R 3 /T 2 .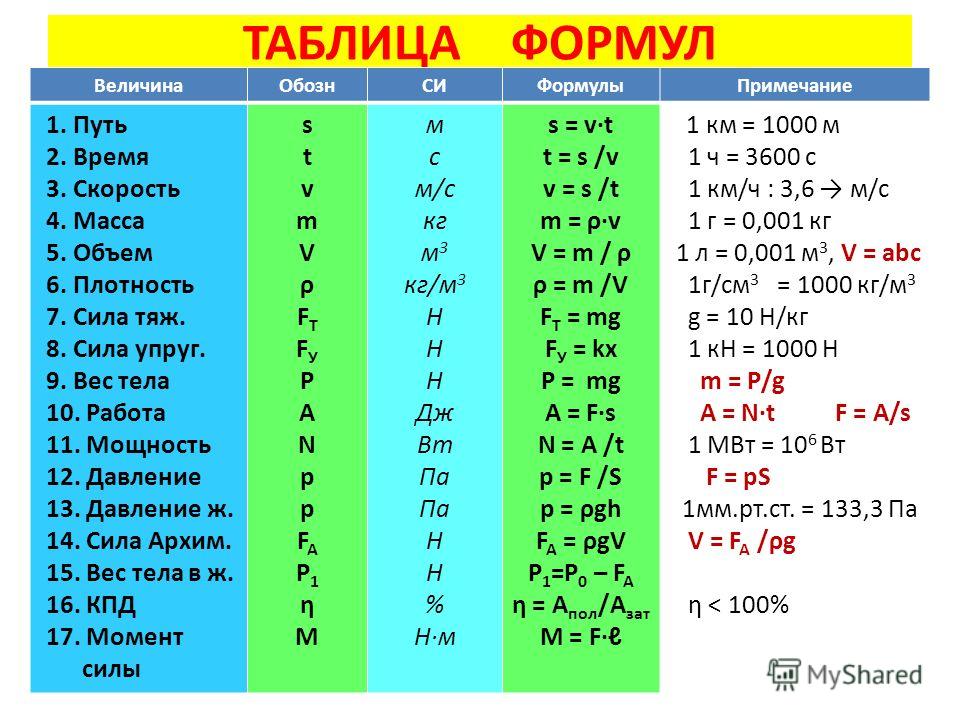 Вот и все !
Вот и все !
Небольшой подсчет показывает, что неизвестное # равно (2π) 2 , приблизительно 39,5, что не слишком далеко от 1. (Правда, это не так близко. Но помните, что это неизвестное # могло быть 483 248 342,198 или 0,000000000000932 — и поэтому, по сравнению с тем, что могло бы быть, это все еще довольно близко к 1.) Нам нужно следить за этой тенденцией к тому, чтобы эти неизвестные # не были так далеки от 1.
Но нам даже не нужно знать неизвестное #, чтобы узнать что-то чрезвычайно важное! Предположим, мы изучили R 3 /T 2 для Луны и спутников, движущихся вокруг Земли, и R 3 /T 2 для планет, вращающихся вокруг Солнца. У нас есть
- G M солнце = # R 3 /T 2 для объектов, вращающихся вокруг Солнца. R ES и T равно одному земному году T E . Между тем,
- G M земля = # R 3 /T 2 для объектов, вращающихся вокруг Земли
ME и T будет одним лунным месяцем T M .
 Теперь мы можем взять отношение этих двух выражений! G отменяется, как и неизвестный # ! That leaves us with
Теперь мы можем взять отношение этих двух выражений! G отменяется, как и неизвестный # ! That leaves us with- M sun /M earth = ( R 3 /T 2 ) earth_around_sun /( R 3 /T 2 ) moon_around_earth = (R ES 3 /R ME 3 )(T M 2 /T E 2 )
Поскольку расстояние Земля-Солнце R ES примерно в 388 раз больше расстояния Луна-Земля, а Земной год примерно в 13,4 раза больше Луны-месяца, мы Найти
- M Sun /M Земля = (388) 3 /(13.4) 2 = 325 000
, что является правильным, до нескольких процентов. Посмотри на это! Мы рассчитали отношение массы Солнца к массе Земли только с помощью анализа измерений ! Все, что нам нужно было знать, — это расстояния и время, относящиеся к орбитам Земли и Луны.

Нам никогда не приходилось решать уравнение гравитации, чтобы понять это! Нам просто нужно было предположить, что каким-то образом была задействована гравитация .
Я надеюсь, что это убедит вас в том, что если вы правильно используете это рассуждение, оно может быть чрезвычайно мощным и потенциально значительно упростить сложные проблемы. В следующий раз мы рассмотрим, как многомерный анализ может использоваться (и использовался) для изучения теории относительности и черных дыр, а затем мы рассмотрим атомную физику и не только.
Нравится:
Нравится Загрузка…
Как построить законы физики » Нераздельный взгляд
Предположим, вы хотите записать законы физики. Как бы вы это сделали?
Что? Хочешь сначала провести несколько экспериментов? Забудь об этом. Это теоретическая физика. Давайте не будем беспокоиться о таких педантичных вещах, как то, что на самом деле являются правильными законами физики.
 Вместо этого давайте попробуем спросить, как они должны выглядеть в более общем плане. Каковы основные правила для попыток построить законы физики?
Вместо этого давайте попробуем спросить, как они должны выглядеть в более общем плане. Каковы основные правила для попыток построить законы физики?(Конечно, на самом деле мы получаем эти основные правила из эксперимента. Это работает так: мы составляем правила для описания множества конкретных систем, которые мы фактически измеряем, и затем, в конце концов, мы получаем некоторое представление о том, что мета- правила есть, т.е. правила построения правил. Но давайте просто попробуем что-нибудь здесь придумать, и посмотрим, насколько мы приблизимся к реальности.)
Попробуем сделать это шаг за шагом. Примем как должное существование пространства-времени. На первом шаге нам нужно решить какие существа перемещаются в этом пространстве-времени. Поскольку мы стремимся дать точное описание, лучше начать с чего-то математически простого. Например, мы могли бы постулировать, что вокруг летает кучка точечных частиц. Если частицы есть, а пространство трехмерное, то мы можем описать все их положения параметрами.

Или, может быть, вокруг болтается куча струн. Или, возможно, есть поля, значения которых определены в каждой точке пространства. (В этих случаях нам понадобится бесконечное количество параметров для описания того, что происходит в каждый момент времени! Но не беспокойтесь — поскольку мы не будем выполнять никаких реальных расчетов, это не обязательно приведет к каким-либо изменениям. сложнее.)
Хорошо. Теперь, когда мы решили, какие вещи у нас есть, нам нужно знать, как они меняются со временем. Для этого нужно написать уравнения движения.
Мы могли бы написать уравнение, включающее одну производную положения по времени. Это определило бы скорость каждой части частицы/струны/поля/чего бы то ни было с точки зрения его положения. Но это не будет похоже на реальную физику, поскольку реальные физические объекты обладают инерцией.

Вместо этого нам нужно написать уравнение, включающее две производные позиции по времени. Это определит ускорение каждого объекта в зависимости от его положения и/или скорости. Это немного больше похоже на реальную жизнь. (Другими словами, чтобы выяснить, что происходит, нам нужно знать как о положениях, так и о скоростях. Если у нас есть частицы, это многомерное пространство, называемое
Итак, вы можете просто сесть и записать некоторые
дифференциальное уравнение второго порядкауравнение, включающее ускорение, и назовем это законами физики. Но большинство из них все же качественно отличались бы от фундаментальных законов реальной физики. Например, ничто не помешает вам включить условий трения , которые заставят движение объектов замедляться с течением времени.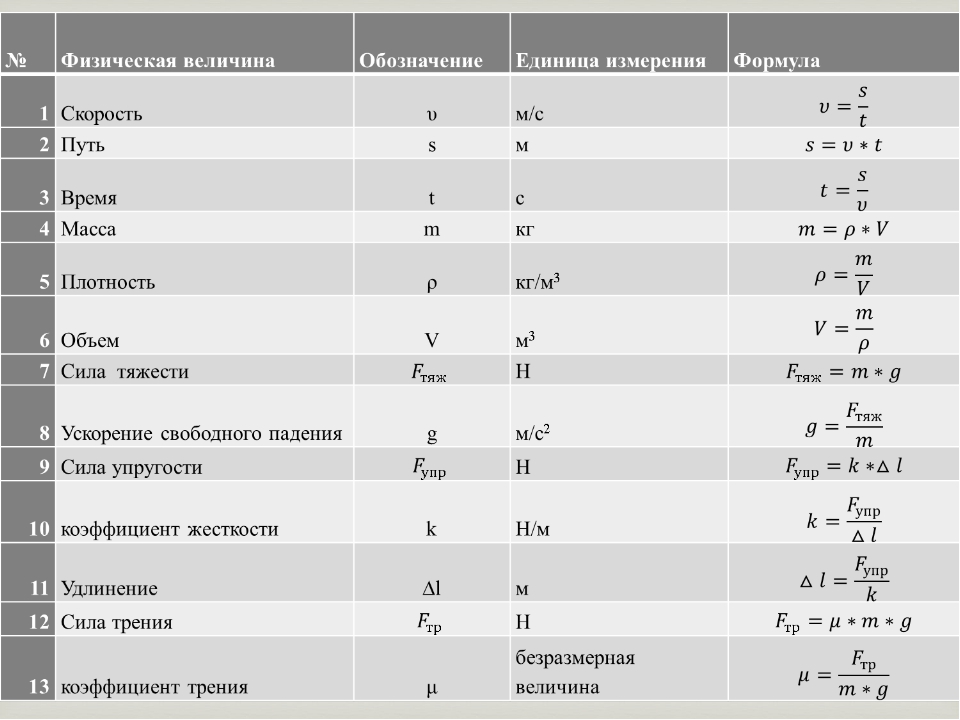 Например, если у нас есть частица, движущаяся вдоль оси X, мы могли бы записать такое уравнение:
Например, если у нас есть частица, движущаяся вдоль оси X, мы могли бы записать такое уравнение:Это заставило бы частицу замедляться с течением времени. Но в действительности трение происходит только тогда, когда какой-либо объект трется о другой объект . Движение не исчезает, оно просто входит в другой объект. Это связано с третьим законом Ньютона, также известным как сохранение импульса.
Таким образом, в физике больше правил, чем можно было бы подумать. Вы не можете просто записать любые старые уравнения движения. Это должны быть специальные магические уравнения, удовлетворяющие определенным свойствам.
Мы могли бы просто составить гигантский список желаемых законов. Но это было бы скорее ad hoc . Вместо этого физики пытаются извлечь все волшебство из какой-то простой схемы. Мы только что видели, что простое написание уравнений движения — это
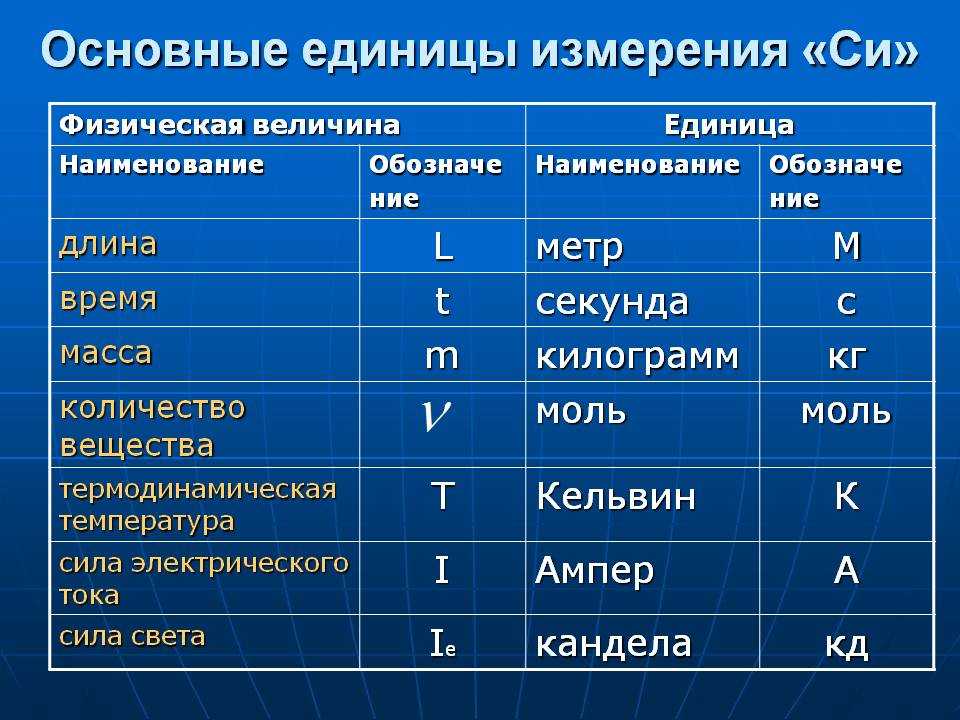
Можно использовать две очень простые схемы. Для большинства систем они эквивалентны, и вы можете вывести одну структуру из другой. Я просто суммирую их здесь со скоростью света:
- Лагранжева механика: здесь фундаментальным понятием является действие , число, полученное путем интегрирования некоторой функции положений и скоростей во все моменты времени. (называется «лагранжианом» и обычно равен кинетической энергии
.
В качестве простого примера рассмотрим точечную частицу, движущуюся по одномерной координате , потенциал которой зависит от вашего положения. Это может описать поезд, скользящий без трения по дорожке американских горок, где длина измеряется вдоль дорожки и пропорциональна его высоте, измеренной от земли. Лагранжиан – это кинетическая энергия минус потенциальная энергия: Правило здесь состоит в том, что при данных начальном и конечном положениях поезда в течение некоторого короткого промежутка времени поезд движется таким образом, что минимизирует полное действие его траектории, что подразумевает, согласно основным принципам исчисления, что малые вариации путь должен оставить действие без изменений.
Это может описать поезд, скользящий без трения по дорожке американских горок, где длина измеряется вдоль дорожки и пропорциональна его высоте, измеренной от земли. Лагранжиан – это кинетическая энергия минус потенциальная энергия: Правило здесь состоит в том, что при данных начальном и конечном положениях поезда в течение некоторого короткого промежутка времени поезд движется таким образом, что минимизирует полное действие его траектории, что подразумевает, согласно основным принципам исчисления, что малые вариации путь должен оставить действие без изменений.
.
Представьте, что вы идете из дома в магазин. Вы выходите из дома в 9 утра, и вам нужно быть в магазине ровно в 10 утра. Вам не нравится ходить слишком быстро, потому что на это уходит слишком много энергии. С другой стороны, если немного прохладно, вы также можете предпочесть проводить больше времени в солнечных местах и меньше в тени. Чтобы ты делал? Если вы хотите максимизировать свое счастье (или свести к минимуму ваше несчастье), вы пойдете на компромисс, идя быстрее в тени, чем на солнце.
