j — Викисловарь
| См. также J, j, Ĵ, ĵ, ϳ, j’, ⒥, Ⓙ, ⓙ, J, j, 𝐉, 𝐣, 𝐽, 𝑗, 𝚥, 𝑱, 𝒋, 𝒥, 𝒿, 𝓙, 𝓳, 𝔍, 𝔧, 𝕵, 𝖏, 𝕁, 𝕛, 𝖩, 𝗃, 𝗝, 𝗷, 𝘑, 𝘫, 𝙅, 𝙟, ȷ, -j. |
| Этот подраздел описывает символ в латинице. См. тж. ј (кириллица). |
Буква (латиница)[править]
| заглавная | строчная |
|---|---|
| J | j |
10-я буква базового современного латинского алфавита, аналогичная кирилл. «й».
Произношение[править]
Транскрипции[править]
|
Смотри также:[править]
Другие внешности P:[править]
Общие значения[править]
- j.

- j=−1{\displaystyle j={\sqrt {-1}}}
Технические данные[править]
Этимология[править]
От написания латинской I.
Морфологические и синтаксические свойства[править]
j
13-я буква эсперантского алфавита.
Морфологические и синтаксические свойства[править]
j
Существительное.
Произношение[править]
Семантические свойства[править]
Значение[править]
- Это слово или выражение пока не переведено. Вы можете предложить свой вариант перевода. ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
Этимология[править]
3) волны, классический вид / Хабр
1.
Шар на пружине, ньютоновская версия 2.
3.
Волны, классический вид4.
Волны, классическое уравнение движения5.
Квантовые волны6.
Поля7.
Частицы – это кванты8.
Как частицы взаимодействуют с полямиРазобравшись с уравнениями для колебаний – описывающими практически всё, что скачет, вибрирует, катается вперёд-назад, как шар на пружине – можно переходить к настолько же распространённому явлению природы, волнам. Волны есть везде: звук и свет, землетрясения, рябь на поверхности пруда, и т.п.
Рис. 1
Но перед этим предупреждаю, что термин «волна» может вводить в заблуждение, поскольку в физике он означает не то же самое, что в английском языке. В физике он не означает того, что мы обычно могли бы назвать волной на краю океана – один гребень и одна впадина. В физике волны – это последовательность волн, несколько гребней и впадин, совместно движущихся в одном направлении. У волны простейшего вида все гребни одинаковой высоты и отстоят друг от друга на одно расстояние.
Волны – выдающееся явление, если задуматься. Представьте, что вы с другом взяли длинную верёвку и туго натянули её в комнате (рис. 2). Затем представьте, что ваш друг поболтал несколько раз вверх и вниз одним концом верёвки (зелёным). На его конце верёвки появится волна, и она пройдёт по комнате к вашему концу верёвки (красному).
Рис. 2
Это удивительно. Я имею в виду – на самом деле поразительно, сильно и критически важно для всего в нашей Вселенной, включая и вас лично. Посмотрите, что произошло. Ни один физический объект слева направо не перемещался – до того, как ваш друг начал двигать конец верёвки, она была протянута через комнату, а в конце, после того, как ваш конец верёвки закончит колебаться и волна пропадёт, верёвка так и останется натянутой через всю комнату, как и было. И всё-таки! Энергия и информация переместились по комнате. Волна в пути переносит энергию, потраченную вашим другом на колебания верёвки – и несёт в своей форме информацию о том, сколько раз и как быстро он её дёргал – к вам, где она заставляет трястись уже вашу руку.
Или, подождите. А не должны ли мы рассматривать волну, как физический объект? Такой же физический, как сама верёвка?
Помня этот глубочайший вопрос, обратимся к небольшому количеству математических формул, необходимых для описания внешнего вида и поведения волны, а затем используем чуть больше математики, чтобы записать уравнения, решениями которых будут волны. Это похоже на то, что мы делали для классического шара на пружине.
Формула для бесконечной волны в определённый момент времени
Эта серия статей сразу после шара на пружине переходит к волнам потому, что волна – это разновидность двойного осциллятора. Она колеблется как во времени, так и в пространстве. Время мы обозначим буквой «t», а пространство – «x».
Обратите внимание на рис. 3. На нём изображена волна, простирающаяся в обоих направлениях на большое расстояние, на которой уместилось множество гребней и впадин.
Рис. 3
Сначала нам нужно определиться с обозначениями и записать формулу, описывающую движение и форму волны на рис. 3, как мы делали для шара на пружине.
На графике показана величина волны Z как функция от пространства в определённый период времени t = t0 — мы записываем это, как Z(x, t0). Отслеживая волну в пространстве мы видим, что она колеблется вперёд и назад, и Z периодически увеличивается и уменьшается. В любой момент времени волна колеблется в пространстве.
Заметьте, что Z не обязательно должна быть связана с физическим расстоянием. Это может быть высота верёвки, как на рис. 2, или это может быть нечто совсем другое, к примеру, температура воздуха в определённой точке пространства и времени или ориентация магнитного атома в определённом месте магнита. Но x всё же представляет физическое расстояние, а t – время.
У снимка этой волны, Z(x, t0), есть три интересных свойства, два из которых также относятся и к шару на пружине.
1. Существует значение равновесия Z0, лежащее посередине между самым большим значением Z на гребне и самым малым значением Z во впадине. Большую часть времени мы изучаем волны, у которых Z0 = 0, поскольку часто величина Z0 не имеет значения – но не всегда.
2. У волны есть амплитуда А, величина, на которую меняется Z от равновесного значения до вершины каждого гребня или на ту же величину до дна каждой впадины.
3. У волны есть длина – расстояние λ между соседними гребнями, или, что то же самое, между соседними впадинами, или, что то же самое, удвоенное расстояние между соседними гребнем и впадиной.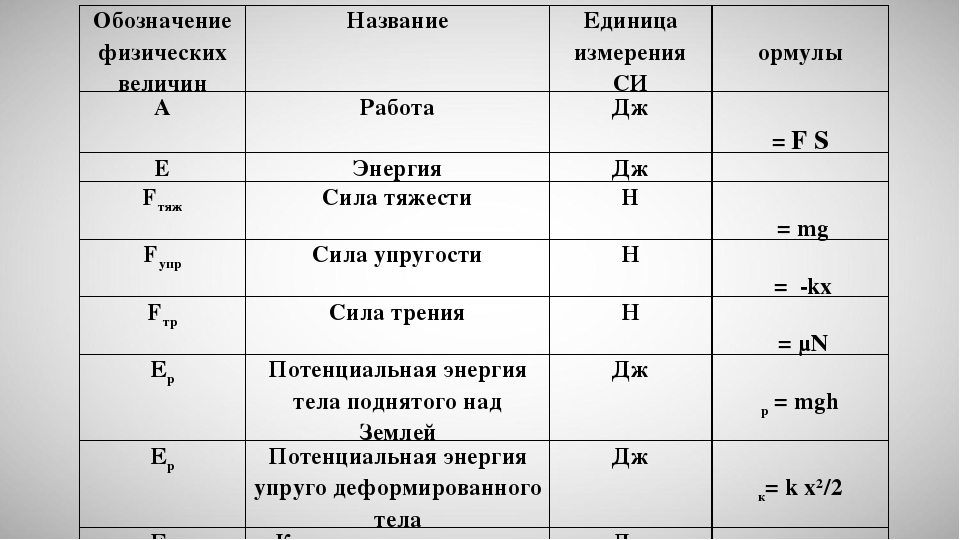
Рис. 4
Что же напоминает нам форма на рис. 3? Она выглядит, как график функции синуса или косинуса – см. рис. 4, где cos(w) построен на графике по w. Cos(w) – функция осциллирующая, у которой есть очевидная позиция равновесия в нуле, её амплитуда 1, а длина волны — 2π. Как перейти от рис. 4 к формуле для волны на рис. 3? Сначала мы умножим cos(w) на А, чтобы амплитуда сравнялась с А. Затем мы добавим Z
Это практически та же формула, что описывала движение шара на пружине во времени:
Где ν – частота колебаний, а T = 1/ν – период колебаний. Видите аналогию: период относится ко времени, как длина волны к пространству.
Видите аналогию: период относится ко времени, как длина волны к пространству.
Ещё одно замечание до того, как мы продолжим. Я мог записать также:
Поскольку cos[w] = cos[-w]. То, что мы спокойно можем подставить минус в формулу формы волны, будет важно позднее.
Формула для бесконечной волны в определённом месте
Рис. 5
Теперь зададим другой вопрос: посмотрим, как волна меняется во времени, отслеживая определённую точку на верёвке, и увидим, как она себя ведёт и двигается. Это показано на рис. 5: там я обозначил определённую точку x0, которая в момент времени t0 находится на гребне. Волна двигается вправо и следует размеру волны Z в точке x0, меняясь во времени: Z(x0, t). И вы немедленно увидите, что высота волны в определённой точке ведёт себя точно так же, как шар на пружине! Поэтому у неё будет точно такая же формула, как у шара на пружине, как функция частоты ν, или периода T = 1/ν, где T – это время между моментом, когда волна в x0 находится н а гребне, и моментом, когда она снова приближается к гребню в следующий раз.
Полная формула бесконечной волны
Теперь нам нужна формула для Z(x, t), описывающая волну, изображённую на рис. 3 и 5 (или любую похожую) в точках x в любой момент времени t. Правильный ответ:
Он включает обе формулы, для фиксированной точки во времени и для фиксированной точки в пространстве.
Отметим знак минуса перед x. Я упоминал, что в формулу для Z(x, t0) можно подставить минус по желанию. С минусом перед x и плюсом перед t формула описывает волну, движущуюся вправо, как на анимациях. Чтобы проверить это, заметьте, что когда t/T – x/λ = 0, волна будет гребнем, потому что cos[0]=1. Когда t = 0, в точке x = 0 гребень. Но если немного сдвинуть t вперёд, допустим, на T/10, то гребень будет в точке x = λ/10, правее от того места, где он был в t = 0 – поэтому гребень (и вся волна) движется вправо.
Что изменится, если разместить плюс вместо минуса в формуле для Z(x, t)? Тогда гребень будет в точке t/T + x/λ = 0, и в этом случае во время t = T/10 гребень будет в точке x = -λ/10, левее того места, где он был в t = 0 – значит, теперь волна движется влево (рис. 6).
6).
Рис. 6
Волны, являющиеся функциями x и t, могут двигаться в любом направлении, так что нам просто нужно выбрать правильную формулу для заданной волны. Вообще говоря, когда мы работаем с волнами, которые могут двигаться не только вдоль одного пространственного измерения x, но вдоль всех трёх координат x, y и z, то эти волны могут двигаться в любом направлении, и нам нужно будет выбрать правильную формулу на основании направления движения волны.
Мелкий шрифт: мы можем поставить знак минуса перед t, а не перед x. Но +t, +x – это то же самое, что и –t, -x, поскольку это будет равнозначно умножению всей формулы внутри косинуса на -1, а cos[w]=cos[-w]. Поэтому +t, +x и -t, -x дают волну, двигающуюся влево, а +t, -x и -t, +x дают волну, двигающуюся вправо.
Уравнение движения волн
Теперь, как и в случае для шара на пружине, когда мы сначала нашли формулу для колебательного движения шара, а затем посмотрели на уравнение движения, для которого эта формула была решением, сделаем то же самое и тут. Мы нашли формулу для формы и движения волны. У какого уравнения движения среди решений встречается такая формула? Узнаем в следующей статье.
Мы нашли формулу для формы и движения волны. У какого уравнения движения среди решений встречается такая формула? Узнаем в следующей статье.
Y – символ современного университета
Основой логотипа предлагается знак «Y» (буква Y – обозначает гласный звук в якутском алфавите, произносится примерно как французский [у], например, в слове salut). В восточных языках есть такой иероглиф, в немецком – звук «U».
Этот сквозной символ в культурах разных народов. Буква «Y» есть во многих алфавитах (в языках романской, тюркской групп и большинстве языков индоевропейской семьи).
Это известная всем буква саха (якутского) алфавита. В языке саха (якутском) есть много слов, которые начинаются с этой буквы и обозначают доброе, созидательное начало. Например, үрдүк үөрэх – высшее образование, үлэ – работа, труд, занятие, үгэс – традиция, обычай, үөрэх – учёба, учение, занятия, үрдэл – высота,үп – капитал, финансы, үргэл – плеяда, созвездие, үөрэтээччи – учитель, наставник, үөрэнээччи – ученик, учащийся, үөлээннээх – ровесник, сверстник, современник, үөрүү – радость, үтүө – добрый, очень хороший, прекрасный, превосходный, замечательный, отличный, үчүгэй – хорошо, үүнүү– рост, урожай, үгүс – много, многочисленный.
В верованиях народа саха (якутов) знак Y обозначает развитие и процветание, преемственность и благоденствие. В древних сказаниях Y является знаком благословения человеческого рода духом Матери-Земли с пожеланиями благополучия, благосостояния, плодородия.
В английском языке Y– это youth, young – юность, молодость, молодежь. Известно, что во всем мире Y признают как знак, символ обозначающий поколение Y. Известно, что представители этого поколения «молоды и умны. … Они любят свою работу и готовы взять на себя большую ответственность … Они ставят перед собой более высокие цели и стремятся достигнуть их быстрее… Они стремятся решать задачи, требующие творческого подхода…». То есть это знак, который ассоциируется, прежде всего, с молодежью и ее стремлениями и надеждами на свою личностную реализацию. You, your переводится с английского, как «ты», «твой». Часто такой символ используется в молодежном сленге (Yo). Примечательно, что по своему образу символ походит на логотипы популярных социальных сетей (facebook, twitter, в контакте).
Научный символ
«Y» – это сквозной символ в науке. Для химии – обозначение элемента иттрий (Y ttrium), буква в кириллице. В математике «Y» – игрек, система координат, в физике – это гамма, в медицине Y – хромосома и др. То есть, он символично объединяет все научные сферы.
В начертании Y – контур голубя мира или стерха. Классический логотип с восточным акцентом, который обозначает волю к победе, готовность ко всему новому и прогрессивному. Голубь в мировой культуре ассоциируется с миром, умиротворением и возрождением. Стерх (журавль) – северная птица, которая символизирует счастье, чистоту и верность. Этот символ стремится вверх, как бы тянется к знаниям, совершенству, новому.
Символ своим начертанием напоминает галочку, которая может символизировать утверждение, согласие, выбор.
Значение
Символ несет в себе доброе, жизнеутверждающее начало. Он, можно сказать, всеобъемлющ: каждый язык, культура, научное направление, социум может найти в нем свое значение, свой смысл, единый в своей основе – это развитие, истина, современность.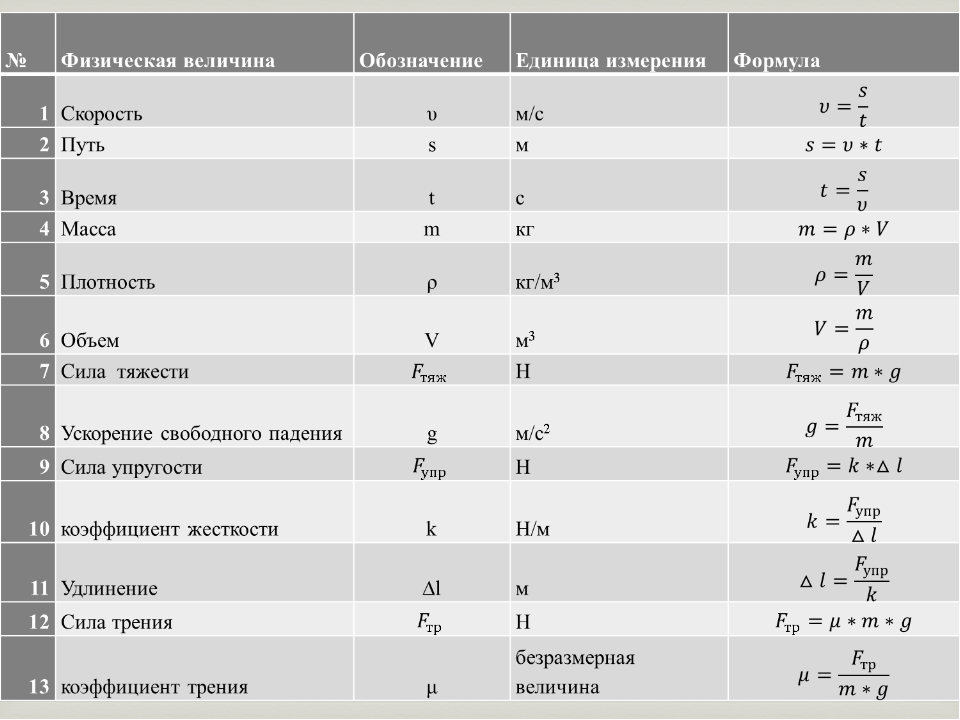
Мощность какая буква в физике. Основные физические величины, их буквенные обозначения в физике
Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Физика и основные физические величины
Благодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.
Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике.
Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:
- длина,
- масса,
- время,
- сила тока,
- температура,
- количество вещества,
- сила света.
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль.
Производные физические величины
Производных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным.
Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф.
СИ: общие сведения
Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.
Заключение
Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.
Построение чертежей – дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.
Величины
Площадь, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.
Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения – это ширина и длина, если их три – добавляется еще и высота.
Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как “width”.
Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как “width”.
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Длина
Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина – в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова – «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.
Высота
Наличие этой величины указывает на то, что приходится иметь дело с более сложным – трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском она пишется как “height”. Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Радиус и диаметр
Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.
Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как “radius”. Отсюда и строчная или заглавная «R»/«r».
Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.
Численно диаметр равен двум радиусам. По-английски это слово пишется так: “diameter”. Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».
Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».
Толщина
Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как “thickness”, а в латинском варианте – “crassities”. Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Периметр и площадь
В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от “περιμετρέο” («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык (“perimeter”) и закрепилось в системе СИ в виде сокращения буквой «Р».
Оно образовано от “περιμετρέο” («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык (“perimeter”) и закрепилось в системе СИ в виде сокращения буквой «Р».
Площадь – это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
Некоторые по незнанию думают, что это связано с английским написанием слова “square”. Однако в нем математическая площадь – это “area”, а “square” – это площадь в архитектурном понимании. Кстати, стоит вспомнить, что “square” – название геометрической фигуры “квадрат”. Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода “area” в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» (“fortis”).
Из-за перевода “area” в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» (“fortis”).
Другие распространенные сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера – это шаг (винтовых пружин, и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые – «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Наиболее применяемые – «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?
Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?
Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.
Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.
Что обозначает прописная буква N в физике?
Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.
Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).
Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).
Что такое N в физике, помимо уже указанных величин? Это может быть:
постоянная Авогадро;
увеличение оптического прибора;
концентрация вещества;
число Дебая;
полная мощность излучения.
Что может обозначать строчная буква n в физике?
Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:
показатель преломления, причем он может быть абсолютным или относительным;
нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;
частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).
Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.
Какая физическая величина может быть обозначена n и N?
Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.
Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.
Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.
Формулы, в которых фигурирует прописная N
Первая из них определяет мощность, которая равна отношению работы ко времени:
В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :
Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.
Чтобы определить электрический заряд, потребуется формула:
Еще одна формула с N в физике – частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:
Чтобы ее сосчитать, нужно их число разделить на время:
Появляется буква «эн» в формуле для периода обращения:
Формулы, в которых встречается строчная n
В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.
Так, для абсолютного показателя преломления формула записывается следующим образом:
Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.
Формула для относительного показателя преломления несколько сложнее:
n 21 = v 1: v 2 = n 2: n 1 ,
где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.
Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.
Чему равно n в физике, если это показатель преломления?
Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.
Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.
Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.
Задача на мощность
№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.
Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.
Выбор формул. Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.
Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.
Второе действие дает 12 000 000: 600 = 20 000 Вт.
Ответ. Мощность трактора равна 20 000 Вт.
Задачи на показатель преломления
№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.
В СИ переводить данные не требуется.
При выборе формул остановиться нужно на этой: n = с: v.
Решение. Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.
Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.
№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.
Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.
Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.
Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.
Решение. В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).
Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.
Ответ. Значение угла преломления — 26º.
Задачи на период обращения
№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.
Вычислите число оборотов этих лопастей за 1 час.
Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.
Подбор формул . Период вращения и число оборотов связаны формулой Т = t: N.
Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.
Ответ. Число оборотов лопастей мельницы равно 720.
№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?
Все данные приведены с СИ, поэтому переводить ничего не нужно.
Необходимая формула : частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.
Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.
Ответ. Винт самолета совершает 3000 оборотов за 120 с.
Подведем итоги
Когда ученику в задаче по физике встречается формула, содержащая n
или
N, ему нужно
разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение.
Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.
Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение.
Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.
Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.
Во-первых, меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами:
(читается ¾икс с точкой¿).
Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:
производная функции x(t) обозначается | ||
(читается ¾дэ икс по дэ тэ¿).
Остановимся подробнее на смысле обозначения (1.16 ). Математик понимает его двояко либо как предел:
либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.
Физик, не скованный требованиями математической строгости, понимает обозначение (1.16 ) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (1.17 ) с устраивающей нас точностью.
И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло.
Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.
Производная x(t) физической величины x(t) снова является функцией времени, и эту функцию снова можно продифференцировать найти производную производной, или вторую производную функции x(t). Вот одно обозначение второй производной:
вторая производная функции x(t) обозначаетсяx (t)
(читается ¾икс с двумя точками¿), а вот другое:
вторая производная функции x(t) обозначаетсяdt 2
(читается ¾дэ два икс по дэ тэ квадрат¿ или ¾дэ два икс по дэ тэ дважды¿).
Давайте вернёмся к исходному примеру (1.13 ) и посчитаем производную координаты, а заодно посмотрим на совместное использование обозначений (1.15 ) и (1.16 ):
x(t) = 1 + 12t 3t2 )
x(t) = dt d (1 + 12t 3t2 ) = 12 6t:
(Символ дифференцирования dt d перед скобкой это всё равно что штрих сверху за скобкой в прежних обозначениях.)
Обратите внимание, что производная координаты оказалась равна скорости (1.14
). Это не случайное совпадение. Связь производной координаты со скоростью тела будет выяснена в следующем разделе ¾Механическое движение¿.
1.1.7 Предел векторной величины
Физические величины бывают не только скалярными, но и векторными. Соответственно, часто нас интересует скорость изменения векторной величины то есть, производная вектора. Однако прежде чем говорить о производной, нужно разобраться с понятием предела векторной величины.
Рассмотрим последовательность векторов ~u1 ; ~u2 ; ~u3 ; : : : Сделав, если необходимо, параллельный перенос, сведём их начала в одну точку O (рис.1.5 ):
Рис. | |||||||||
Концы векторов обозначим A1 ; A2 ; A3 ; : : : Таким образом, имеем: | |||||||||
Предположим, что последовательность точек A1 ; A2 ; A3 ; : : : ¾втекает¿2 в точку B:
lim An = B:
Обозначим ~v = OB. Мы скажем тогда, что последовательность синих векторов ~un стремится к красному вектору ~v, или что вектор ~v является пределом последовательности векторов ~un :
~v = lim ~un :
2 Вполне достаточно интуитивного понимания этого ¾втекания¿, но вас, быть может, интересует более строгое объяснение? Тогда вот оно.
Пусть дело происходит на плоскости. ¾Втекание¿ последовательности A1
; A2
; A3
; : : : в точку B означает следующее: сколь бы малый круг с центром в точке B мы ни взяли, все точки последовательности, начиная с некоторой, попадут внутрь этого круга. Иными словами, вне любого круга с центром B имеется лишь конечное число точек нашей последовательности.
¾Втекание¿ последовательности A1
; A2
; A3
; : : : в точку B означает следующее: сколь бы малый круг с центром в точке B мы ни взяли, все точки последовательности, начиная с некоторой, попадут внутрь этого круга. Иными словами, вне любого круга с центром B имеется лишь конечное число точек нашей последовательности.
А если дело происходит в пространстве? Определение ¾втекания¿ модифицируется незначительно: нужно лишь заменить слово ¾круг¿ на слово ¾шар¿.
Предположим теперь, что концы синих векторов на рис. 1.5 пробегают не дискретный набор значений, а непрерывную кривую (например, указанную пунктирной линией). Таким образом, мы имеем дело не с последовательностью векторов ~un , а с вектором ~u(t), который меняется со временем. Это как раз то, что нам и нужно в физике!
Дальнейшее объяснение почти такое же. Пусть t стремится к некоторому значению t0 . Если
при этом концы векторов ~u(t) ¾втекают¿ в некоторую точку B, то мы говорим, что вектор
~v = OB является пределом векторной величины ~u(t):
t!t0
1.
 1.8
Дифференцирование векторов
1.8
Дифференцирование векторовВыяснив, что такое предел векторной величины, мы готовы сделать следующий шаг ввести понятие производной вектора.
Предположим, что имеется некоторый вектор ~u(t), зависящий от времени. Это означает, что длина данного вектора и его направление могут меняться с течением времени.
По аналогии с обычной (скалярной) функцией вводится понятие изменения (или приращения) вектора. Изменение вектора ~u за время t есть векторная величина:
~u = ~u(t + t) ~u(t):
Обратите внимание, что в правой части данного соотношения стоит разность векторов. Изменение вектора ~u показано на рис. 1.6 (напомним, что при вычитании векторов мы сводим их начала в одну точку, соединяем концы и ¾укалываем¿ стрелкой тот вектор, из которого производится вычитание).
~u(t) ~u
Рис. 1.6. Изменение вектора
Если промежуток времени t достаточно мал, то и вектор ~u за это время меняется мало (в физике, по крайней мере, так считается всегда). Соответственно, если при t ! 0 отношение~u= t стремится к некоторому пределу, то этот предел называется производной вектора ~u:
При обозначении производной вектора мы не будем использовать точку сверху (так как символ ~u_
не слишком хорошо смотрится) и ограничиваемся обозначением (1. 18
). Но для производной скаляра мы, разумеется, свободно используем оба обозначения.
18
). Но для производной скаляра мы, разумеется, свободно используем оба обозначения.
Напомним, что d~u=dt это символ производной. Его можно понимать и как дробь, в числителе которой стоит дифференциал вектора ~u, соответствующий промежутку времени dt. Выше мы не стали обсуждать понятие дифференциала, так как в школе его не проходят; не будем обсуждать дифференциал и здесь.
Однако на физическом уровне строгости производную d~u=dt можно считать дробью, в знаменателе которой стоит очень малый интервал времени dt, а в числителе соответствующее малое изменение d~u вектора ~u. При достаточно малом dt величина данной дроби отличается от
предела в правой части (1.18 ) столь мало, что с учётом имеющейся точности измерений этим отличием можно пренебречь.
Этого (не вполне строгого) физического понимания производной нам окажется вполне достаточно.
Правила дифференцирования векторных выражений во многом аналогичны правилам дифференцирования скаляров. Нам понадобятся лишь самые простые правила.
1. Постоянный скалярный множитель выносится за знак производной: если c = const, то
d(c~u) = c d~u: dt dt
Мы используем это правило в разделе ¾Импульс¿, когда второй закон Ньютона
будет переписан в виде: | ||||
2. Постоянный векторный множитель выносится за знак производной: если ~c = const, то dt d (x(t)~c) = x(t)~c:
3. Производная суммы векторов равна сумме их производных:
dt d (~u + ~v) =d~u dt +d~v dt :
Последними двумя правилами мы будем пользоваться неоднократно. Посмотрим, как они работают в важнейшей ситуации дифференцирования вектора при наличии в пространстве прямоугольной системы координат OXY Z (рис. 1.7
).
1.7
).
Рис. 1.7. Разложение вектора по базису
Как известно, любой вектор ~u единственным образом раскладывается по базису единичных
векторов ~ ,~ ,~ : i j k
~u = ux i + uy j + uz k:
Здесь ux , uy , uz проекции вектора ~u на координатные оси. Они же являются координатами вектора ~u в данном базисе.
Вектор ~u в нашем случае зависит от времени, а это значит, что его координаты ux , uy , uz являются функциями времени:
~u(t) = ux (t) i | Uy (t) j | Uz (t)k: |
Дифференцируем это равенство. Сначала пользуемся правилом дифференцирования суммы:
ux (t)~ i + | uy (t)~ j | uz (t)~ k: | ||||||||||||
Затем выносим постоянные векторы за знак производной: | ||||||||||||||
Ux (t)i + uy (t)j + uz (t)k: | ||||||||||||||
Таким образом, если вектор ~u имеет координаты (ux
; uy
; uz
), то координаты производной d~u=dt являются производными координат вектора ~u, а именно (ux
; uy
; uz
).
Ввиду особой важности формулы (1.20 ) дадим более непосредственный её вывод. В момент времени t + t согласно (1.19 ) имеем:
~u(t + t) = ux (t + t) i + uy (t + t) j + uz (t + t)k:
Напишем изменение вектора ~u:
~u = ~u(t + t) ~u(t) =
Ux (t + t) i + uy (t + t) j + uz (t + t)k ux (t) i + uy (t) j + uz (t)k =
= (ux (t + t) ux (t)) i + (uy (t + t) uy (t)) j + (uz (t + t) uz (t)) k = | ||||||||||
Ux i + uy j + uz k: | ||||||||||
Делим обе части полученного равенства на t: | ||||||||||
T i + | t j + | |||||||||
В пределе при t ! 0 дроби ux
= t, uy
= t, uz
= t переходят соответственно в производные ux
, uy
, uz
, и мы снова получаем соотношение (1. 20
):
20
):
Ux i + uy j + uz k.
Назад в прошлое Физики объяснили направление движения времени: Наука и техника: Lenta.ru
Во вторник на Ленте.Ру появилась заметка, в которой излагалась суть открытия, сделанного итальянским физиком Лоренцо Макконе. Макконе удалось с позиций квантовой механики объяснить, почему для нас время движется в некотором выбранном направлении. Формат новостной заметки не позволил изложить многие детали открытия, поэтому Лента.Ру решилась написать более подробный комментарий на данную тему.
Начнем с того, что работа физика хоть и вышла в солидном журнале Physical Review Letters (ее препринт доступен здесь), однако одобрения научного сообщества еще не получила. Заслуживающим внимания эту работу (в которой, к слову, всего четыре страницы) делает то, что специалисты, успевшие с ней ознакомиться, называют подход Макконе “новаторским”. Но при этом соглашаться со всеми выводами итальянского физика они не спешат.
Т-симметрия и энтропия
Есть такие слова, так называемые палиндромы, которые можно читать в любом направлении – справа налево или слева направо. Например, слово “топот”. Так вот, T-симметрия – это что-то похожее: между событиями, описываемыми симметричными законами, которые работают в прямом порядке и обратном, нет никакой разницы. Формально последнее означает, что формулы, описывающие те или иные явления, остаются верными, если в них t (переменную, отвечающую за время) заменить на -t.
Например, слово “топот”. Так вот, T-симметрия – это что-то похожее: между событиями, описываемыми симметричными законами, которые работают в прямом порядке и обратном, нет никакой разницы. Формально последнее означает, что формулы, описывающие те или иные явления, остаются верными, если в них t (переменную, отвечающую за время) заменить на -t.
С другой стороны, всем известно, что если чашку горячего чая поставить в холодильник (делать этого, правда, не рекомендуют производители бытового оборудования), то она со временем остынет. Можно представить, что в какой-то момент процесс повернет вспять: чай снова разогреется, а воздух в холодильнике охладится (как будто мы “промотали” время в реальном опыте с чаем назад), – однако в действительности такого еще никто не наблюдал.
Здесь в действие вступает так называемая энтропия – мера необратимого рассеяния энергии (сейчас этот термин перекочевал во всевозможные области знаний от статистической физики до теории информации, о чем будет сказано чуть ниже). Согласно второму закону термодинамики, все происходящие в замкнутой системе процессы приводят к росту этой самой энтропии. Поэтому в опыте с чаем и холодильником обратный по времени процесс с разогревом невозможен.
Согласно второму закону термодинамики, все происходящие в замкнутой системе процессы приводят к росту этой самой энтропии. Поэтому в опыте с чаем и холодильником обратный по времени процесс с разогревом невозможен.
Направление времени
Впервые понятие энтропии было введено в работах физика Рудольфа Клаузиуса в 1865 году как мера необратимого рассеяния энергии. Клаузиус использовал этот термин для объяснения того факта, что тепло всегда передается от горячего тела к холодному.
За замечательную идею роста энтропии физики ухватились и попытались применить ее в более общем случае для объяснения глобального направления движения времени во Вселенной. Однако эти попытки почти сразу наткнулись на серьезные трудности. Согласно одним теориям, Вселенная постоянно увеличивает энтропию потому, что изначально находилась в состоянии с очень малым значением этой величины. Согласно другим, второе начало термодинамики работает не только в частных случаях (горячее/холодное), но и в космических масштабах (против последнего, например, возражал знаменитый физик Лев Ландау: он полагал, что подобный подход не учитывает общую теорию относительности). Самые “резкие” исследователи вообще предлагают отменить саму теоретическую возможность обратимости времени и поправить физические законы так, чтобы T-симметрия стала в принципе, даже в рассуждениях, невозможна.
Самые “резкие” исследователи вообще предлагают отменить саму теоретическую возможность обратимости времени и поправить физические законы так, чтобы T-симметрия стала в принципе, даже в рассуждениях, невозможна.
Изучив список возможных вариантов решения проблемы (он приводится в конце работы итальянского физика), Макконе предложил новое и элегантное решение. Согласно его теории, события, в которых время движется в обратном направлении, вполне могут происходить. Может быть, даже происходят. Однако информационное устройство Вселенной таково, что никаких данных об этих событиях не сохраняется (и не может сохраниться). Таким образом, они абсолютно неотличимы от тех событий, которые никогда не происходили.
Теория Макконе
В качестве основного аппарата для формализации этого несколько философского объяснения Макконе выбрал квантовую механику. Полезным свойством этой теории является то, что в ней имеется прекрасный аналог термодинамической энтропии – энтропия фон Неймана, которая, в некотором смысле, является мерой хаотичности информации в квантовой системе.
Для пояснения своей идеи Макконе предлагает следующий умозрительный эксперимент. Представим, что у нас имеется получатель информации Алиса и передатчик информации Боб (двух этих персонажей физики мучают своими экспериментами еще со времен Эйнштейна). Представим, что Алиса сидит в удобной, но совершенно отгороженной от всего остального мира лаборатории. В этом случае она является подсистемой системы “лаборатория”. Ее друг Боб, который обитает вне лаборатории, посылает Алисе атом, спин которого находится в состоянии квантовой неопределенности (суперпозиции двух базовых состояний). В результате появляется система “атом-лаборатория”.
Когда Алиса измеряет спин атома, то она получает некоторое конкретное значение. При этом с точки зрения системы “лаборатория” (которая стала подсистемой системы “атом-лаборатория”) энтропия возрастает. В свою очередь Боб, который находится вне лаборатории, ничего не знает о результатах измерения. Таким образом, для него энтропия системы “атом-лаборатория” не изменилась. Более того, с точки зрения Боба взаимодействие Алисы и атома привело к их “квантовому запутыванию”, то есть две подсистемы системы “атом-лаборатория” оказались взаимосвязаны.
Более того, с точки зрения Боба взаимодействие Алисы и атома привело к их “квантовому запутыванию”, то есть две подсистемы системы “атом-лаборатория” оказались взаимосвязаны.
Представим теперь, что в нашем эксперименте Боб наделен сверхспособностями – квантовая система “атом-лаборатория” находится в его полной власти. Предположим, он решает распутать атом и Алису. С точки зрения системы “лаборатория” это приводит к уменьшению энтропии фон Неймана. При этом спин атома снова переходит в неопределенное состояние. Последнее означает, что вся прежняя информация об измерениях должна исчезнуть (иначе никакой неопределенности не получится). В результате, все данные в лаборатории Алисы исчезают, включая память о проведенном эксперименте. Таким образом, энтропия уменьшилась, однако никто этого не запомнил. В рамках своей работы Макконе формализует данный мысленный эксперимент математически.
Отсюда итальянский физик делает замечательные выводы. Действительно, пусть процессы, в которых время идет в обратном направлении, происходят.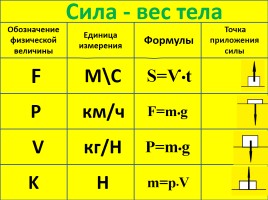 Но тогда эти процессы приводят к уменьшению энтропии. Однако, как было доказано в мысленном эксперименте (а в работе Макконе – математически), эти события не оставляют информационных следов, а значит, их невозможно изучать.
Но тогда эти процессы приводят к уменьшению энтропии. Однако, как было доказано в мысленном эксперименте (а в работе Макконе – математически), эти события не оставляют информационных следов, а значит, их невозможно изучать.
И в заключение
Еще раз хочется отметить, что новая теория пока не является общепринятой, но элегантность рассуждений подкупает. Хочется верить, что идеи Макконе получат дальнейшее естественное развитие. А мы пока продолжим двигаться вперед во времени.
что такое n в физике
Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Физика и основные физические величины
Благодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.
Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.
Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике.
Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:
- длина,
- масса,
- время,
- сила тока,
- температура,
- количество вещества,
- сила света.
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль.
Производные физические величины
Производных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным.
Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф.
Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф.
СИ: общие сведения
Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.
Заключение
Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.
Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.
Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.
Во-первых, меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами:
(читается ¾икс с точкой¿).
Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:
производная функции x(t) обозначается | ||
(читается ¾дэ икс по дэ тэ¿).
Остановимся подробнее на смысле обозначения (1.16 ). Математик понимает его двояко либо как предел:
либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.
Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.
Физик, не скованный требованиями математической строгости, понимает обозначение (1.16 ) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (1.17 ) с устраивающей нас точностью.
И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло.
Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.
Производная x(t) физической величины x(t) снова является функцией времени, и эту функцию снова можно продифференцировать найти производную производной, или вторую производную функции x(t). Вот одно обозначение второй производной:
вторая производная функции x(t) обозначаетсяx (t)
(читается ¾икс с двумя точками¿), а вот другое:
вторая производная функции x(t) обозначаетсяdt 2
(читается ¾дэ два икс по дэ тэ квадрат¿ или ¾дэ два икс по дэ тэ дважды¿).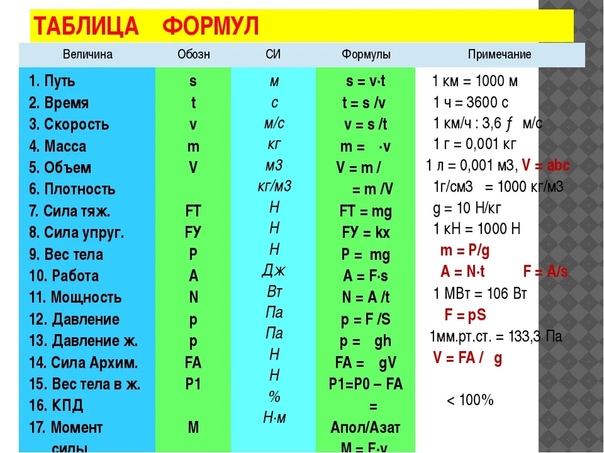
Давайте вернёмся к исходному примеру (1.13 ) и посчитаем производную координаты, а заодно посмотрим на совместное использование обозначений (1.15 ) и (1.16 ):
x(t) = 1 + 12t 3t2 )
x(t) = dt d (1 + 12t 3t2 ) = 12 6t:
(Символ дифференцирования dt d перед скобкой это всё равно что штрих сверху за скобкой в прежних обозначениях.)
Обратите внимание, что производная координаты оказалась равна скорости (1.14 ). Это не случайное совпадение. Связь производной координаты со скоростью тела будет выяснена в следующем разделе ¾Механическое движение¿.
1.1.7 Предел векторной величины
Физические величины бывают не только скалярными, но и векторными. Соответственно, часто нас интересует скорость изменения векторной величины то есть, производная вектора. Однако прежде чем говорить о производной, нужно разобраться с понятием предела векторной величины.
Рассмотрим последовательность векторов ~u1
; ~u2
; ~u3
; : : : Сделав, если необходимо, параллельный перенос, сведём их начала в одну точку O (рис. 1.5
):
1.5
):
Рис. 1.5. lim ~un = ~v | |||||||||
Концы векторов обозначим A1 ; A2 ; A3 ; : : : Таким образом, имеем: | |||||||||
Предположим, что последовательность точек A1 ; A2 ; A3 ; : : : ¾втекает¿2 в точку B:
lim An = B:
Обозначим ~v = OB. Мы скажем тогда, что последовательность синих векторов ~un
стремится к красному вектору ~v, или что вектор ~v является пределом последовательности векторов ~un
:
Мы скажем тогда, что последовательность синих векторов ~un
стремится к красному вектору ~v, или что вектор ~v является пределом последовательности векторов ~un
:
~v = lim ~un :
2 Вполне достаточно интуитивного понимания этого ¾втекания¿, но вас, быть может, интересует более строгое объяснение? Тогда вот оно.
Пусть дело происходит на плоскости. ¾Втекание¿ последовательности A1 ; A2 ; A3 ; : : : в точку B означает следующее: сколь бы малый круг с центром в точке B мы ни взяли, все точки последовательности, начиная с некоторой, попадут внутрь этого круга. Иными словами, вне любого круга с центром B имеется лишь конечное число точек нашей последовательности.
А если дело происходит в пространстве? Определение ¾втекания¿ модифицируется незначительно: нужно лишь заменить слово ¾круг¿ на слово ¾шар¿.
Предположим теперь, что концы синих векторов на рис. 1.5
пробегают не дискретный набор значений, а непрерывную кривую (например, указанную пунктирной линией). Таким образом, мы имеем дело не с последовательностью векторов ~un
, а с вектором ~u(t), который меняется со временем. Это как раз то, что нам и нужно в физике!
Это как раз то, что нам и нужно в физике!
Дальнейшее объяснение почти такое же. Пусть t стремится к некоторому значению t0 . Если
при этом концы векторов ~u(t) ¾втекают¿ в некоторую точку B, то мы говорим, что вектор
~v = OB является пределом векторной величины ~u(t):
t!t0
1.1.8 Дифференцирование векторов
Выяснив, что такое предел векторной величины, мы готовы сделать следующий шаг ввести понятие производной вектора.
Предположим, что имеется некоторый вектор ~u(t), зависящий от времени. Это означает, что длина данного вектора и его направление могут меняться с течением времени.
По аналогии с обычной (скалярной) функцией вводится понятие изменения (или приращения) вектора. Изменение вектора ~u за время t есть векторная величина:
~u = ~u(t + t) ~u(t):
Обратите внимание, что в правой части данного соотношения стоит разность векторов. Изменение вектора ~u показано на рис. 1.6
(напомним, что при вычитании векторов мы сводим их начала в одну точку, соединяем концы и ¾укалываем¿ стрелкой тот вектор, из которого производится вычитание).
~u(t) ~u
Рис. 1.6. Изменение вектора
Если промежуток времени t достаточно мал, то и вектор ~u за это время меняется мало (в физике, по крайней мере, так считается всегда). Соответственно, если при t ! 0 отношение~u= t стремится к некоторому пределу, то этот предел называется производной вектора ~u:
При обозначении производной вектора мы не будем использовать точку сверху (так как символ ~u_ не слишком хорошо смотрится) и ограничиваемся обозначением (1.18 ). Но для производной скаляра мы, разумеется, свободно используем оба обозначения.
Напомним, что d~u=dt это символ производной. Его можно понимать и как дробь, в числителе которой стоит дифференциал вектора ~u, соответствующий промежутку времени dt. Выше мы не стали обсуждать понятие дифференциала, так как в школе его не проходят; не будем обсуждать дифференциал и здесь.
Однако на физическом уровне строгости производную d~u=dt можно считать дробью, в знаменателе которой стоит очень малый интервал времени dt, а в числителе соответствующее малое изменение d~u вектора ~u. При достаточно малом dt величина данной дроби отличается от
предела в правой части (1.18 ) столь мало, что с учётом имеющейся точности измерений этим отличием можно пренебречь.
Этого (не вполне строгого) физического понимания производной нам окажется вполне достаточно.
Правила дифференцирования векторных выражений во многом аналогичны правилам дифференцирования скаляров. Нам понадобятся лишь самые простые правила.
1. Постоянный скалярный множитель выносится за знак производной: если c = const, то
d(c~u) = c d~u: dt dt
Мы используем это правило в разделе ¾Импульс¿, когда второй закон Ньютона
будет переписан в виде: | ||||
2. Постоянный векторный множитель выносится за знак производной: если ~c = const, то dt
d
(x(t)~c) = x(t)~c:
Постоянный векторный множитель выносится за знак производной: если ~c = const, то dt
d
(x(t)~c) = x(t)~c:
3. Производная суммы векторов равна сумме их производных:
dt d (~u + ~v) =d~u dt +d~v dt :
Последними двумя правилами мы будем пользоваться неоднократно. Посмотрим, как они работают в важнейшей ситуации дифференцирования вектора при наличии в пространстве прямоугольной системы координат OXY Z (рис. 1.7 ).
Рис. 1.7. Разложение вектора по базису
Как известно, любой вектор ~u единственным образом раскладывается по базису единичных
векторов ~ ,~ ,~ : i j k
~u = ux i + uy j + uz k:
Здесь ux , uy , uz проекции вектора ~u на координатные оси. Они же являются координатами вектора ~u в данном базисе.
Вектор ~u в нашем случае зависит от времени, а это значит, что его координаты ux , uy , uz являются функциями времени:
~u(t) = ux (t) i | Uy (t) j | Uz (t)k: |
Дифференцируем это равенство. Сначала пользуемся правилом дифференцирования суммы:
Сначала пользуемся правилом дифференцирования суммы:
ux (t)~ i + | uy (t)~ j | uz (t)~ k: | ||||||||||||
Затем выносим постоянные векторы за знак производной: | ||||||||||||||
Ux (t)i + uy (t)j + uz (t)k: | ||||||||||||||
Таким образом, если вектор ~u имеет координаты (ux
; uy
; uz
), то координаты производной d~u=dt являются производными координат вектора ~u, а именно (ux
; uy
; uz
).
Ввиду особой важности формулы (1.20 ) дадим более непосредственный её вывод. В момент времени t + t согласно (1.19 ) имеем:
~u(t + t) = ux (t + t) i + uy (t + t) j + uz (t + t)k:
Напишем изменение вектора ~u:
~u = ~u(t + t) ~u(t) =
Ux (t + t) i + uy (t + t) j + uz (t + t)k ux (t) i + uy (t) j + uz (t)k =
= (ux (t + t) ux (t)) i + (uy (t + t) uy (t)) j + (uz (t + t) uz (t)) k = | ||||||||||
Ux i + uy j + uz k: | ||||||||||
Делим обе части полученного равенства на t: | ||||||||||
T i + | t j + | |||||||||
В пределе при t ! 0 дроби ux
= t, uy
= t, uz
= t переходят соответственно в производные ux
, uy
, uz
, и мы снова получаем соотношение (1. 20
):
20
):
Ux i + uy j + uz k.
Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?
Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.
Что обозначает прописная буква N в физике?
Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.
Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).
Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).
Что такое N в физике, помимо уже указанных величин? Это может быть:
постоянная Авогадро;
увеличение оптического прибора;
концентрация вещества;
число Дебая;
полная мощность излучения.
Что может обозначать строчная буква n в физике?
Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:
показатель преломления, причем он может быть абсолютным или относительным;
нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;
частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).
Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.
Какая физическая величина может быть обозначена n и N?
Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.
Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.
Формулы, в которых фигурирует прописная N
Первая из них определяет мощность, которая равна отношению работы ко времени:
В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :
Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :
Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.
Чтобы определить электрический заряд, потребуется формула:
Еще одна формула с N в физике – частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:
Появляется буква «эн» в формуле для периода обращения:
Формулы, в которых встречается строчная n
В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.
Так, для абсолютного показателя преломления формула записывается следующим образом:
Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.
Формула для относительного показателя преломления несколько сложнее:
n 21 = v 1: v 2 = n 2: n 1 ,
где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.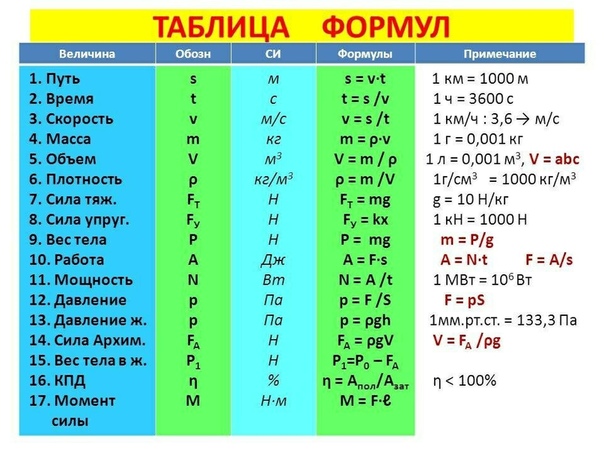
Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.
Чему равно n в физике, если это показатель преломления?
Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.
Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.
Задача на мощность
№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.
Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.
Выбор формул.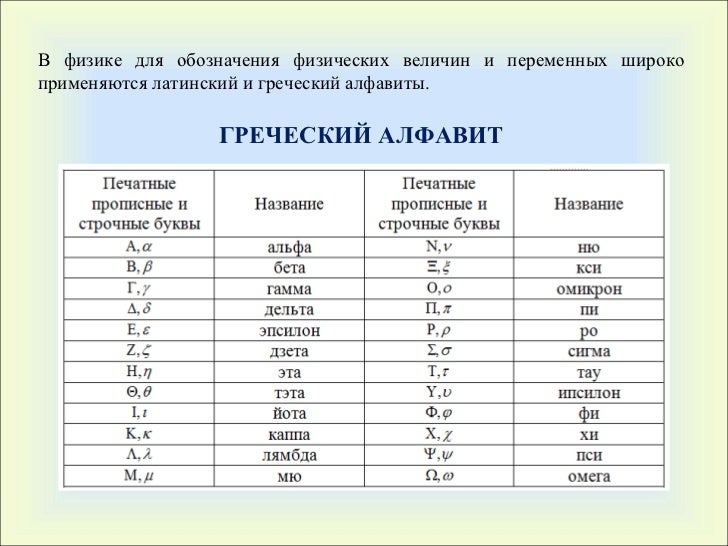 Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.
Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.
Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.
Ответ. Мощность трактора равна 20 000 Вт.
Задачи на показатель преломления
№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.
В СИ переводить данные не требуется.
При выборе формул остановиться нужно на этой: n = с: v.
Решение. Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.
Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.
№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.
Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.
Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.
Решение. В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).
Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.
Ответ. Значение угла преломления — 26º.
Задачи на период обращения
№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.
Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.
Подбор формул . Период вращения и число оборотов связаны формулой Т = t: N.
Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.
Ответ. Число оборотов лопастей мельницы равно 720.
№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?
Все данные приведены с СИ, поэтому переводить ничего не нужно.
Необходимая формула : частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.
Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.
Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.
Ответ. Винт самолета совершает 3000 оборотов за 120 с.
Подведем итоги
Когда ученику в задаче по физике встречается формула, содержащая n или N, ему нужно разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение. Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.
Буквенные обозначения в физике и их единицы. Основные физические величины, их буквенные обозначения в физике
В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования. Кроме указанных… … Википедия
Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования. Кроме указанных… … Википедия
Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия
Список знаковых систем (систем обозначений и т.п.), используемых человеческой цивилизацией, за исключением письменностей, для которых имеется отдельный список. Содержание 1 Критерии включения в список 2 Математика … Википедия
Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8& … Википедия
Дирак, Поль Адриен Морис Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8 августа 1902(… Википедия
Готфрид Вильгельм Лейбниц Gottfried Wilhelm Leibniz … Википедия
У этого термина существуют и другие значения, см. Мезон (значения). Мезон (от др. греч. μέσος средний) бозон сильного взаимодействия. В Стандартной модели, мезоны это составные (не элементарные) частицы, состоящие из чётного… … Википедия
Мезон (значения). Мезон (от др. греч. μέσος средний) бозон сильного взаимодействия. В Стандартной модели, мезоны это составные (не элементарные) частицы, состоящие из чётного… … Википедия
Ядерная физика … Википедия
Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности (ОТО) или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации… … Википедия
Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации часто… … Википедия
Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Физика и основные физические величины
Благодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.
Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике.
Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:
- длина,
- масса,
- время,
- сила тока,
- температура,
- количество вещества,
- сила света.

Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль.
Производные физические величины
Производных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным.
Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф.
СИ: общие сведения
Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.
Заключение
Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.
Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?
Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.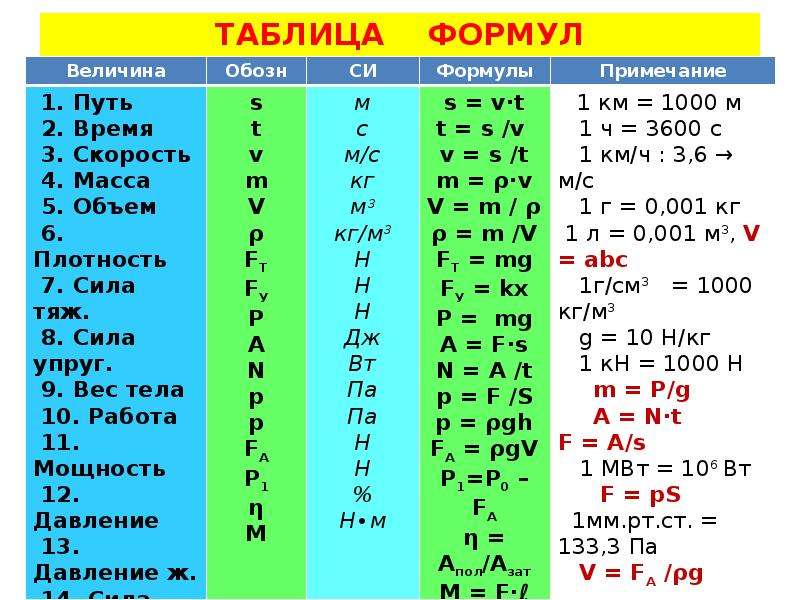
Что обозначает прописная буква N в физике?
Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.
Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).
Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).
Что такое N в физике, помимо уже указанных величин? Это может быть:
постоянная Авогадро;
увеличение оптического прибора;
концентрация вещества;
число Дебая;
полная мощность излучения.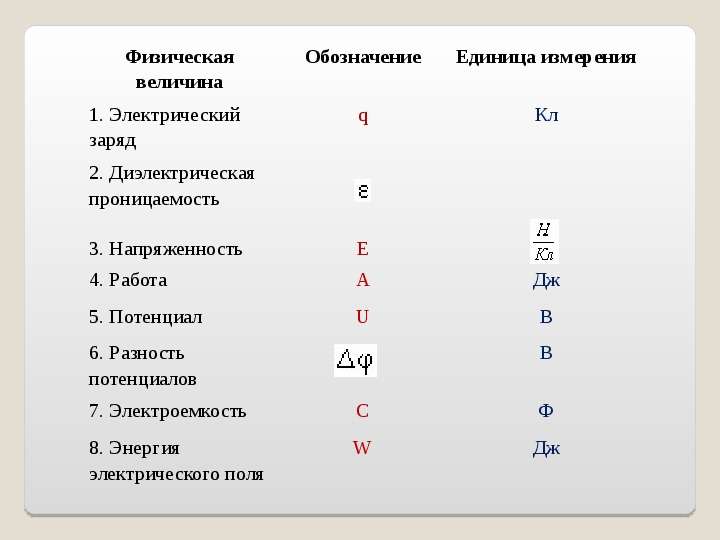
Что может обозначать строчная буква n в физике?
Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:
показатель преломления, причем он может быть абсолютным или относительным;
нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;
частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).
Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.
Какая физическая величина может быть обозначена n и N?
Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.
Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.
Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.
Формулы, в которых фигурирует прописная N
Первая из них определяет мощность, которая равна отношению работы ко времени:
В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :
Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.
Чтобы определить электрический заряд, потребуется формула:
Еще одна формула с N в физике – частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:
Чтобы ее сосчитать, нужно их число разделить на время:
Появляется буква «эн» в формуле для периода обращения:
Формулы, в которых встречается строчная n
В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.
Так, для абсолютного показателя преломления формула записывается следующим образом:
Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.
Формула для относительного показателя преломления несколько сложнее:
n 21 = v 1: v 2 = n 2: n 1 ,
где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.
Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.
Чему равно n в физике, если это показатель преломления?
Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.
Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.
Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.
Задача на мощность
№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.
Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.
Выбор формул. Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.
Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.
Второе действие дает 12 000 000: 600 = 20 000 Вт.
Ответ. Мощность трактора равна 20 000 Вт.
Задачи на показатель преломления
№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.
В СИ переводить данные не требуется.
При выборе формул остановиться нужно на этой: n = с: v.
Решение. Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.
Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.
№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.
Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.
Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.
Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.
Решение. В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).
Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.
Ответ. Значение угла преломления — 26º.
Задачи на период обращения
№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.
Вычислите число оборотов этих лопастей за 1 час.
Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.
Подбор формул . Период вращения и число оборотов связаны формулой Т = t: N.
Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.
Ответ. Число оборотов лопастей мельницы равно 720.
№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?
Все данные приведены с СИ, поэтому переводить ничего не нужно.
Необходимая формула : частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.
Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.
Ответ. Винт самолета совершает 3000 оборотов за 120 с.
Подведем итоги
Когда ученику в задаче по физике встречается формула, содержащая n
или
N, ему нужно
разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение.
Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.
Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение.
Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.
Шпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 –υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ –υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 – Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 – Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
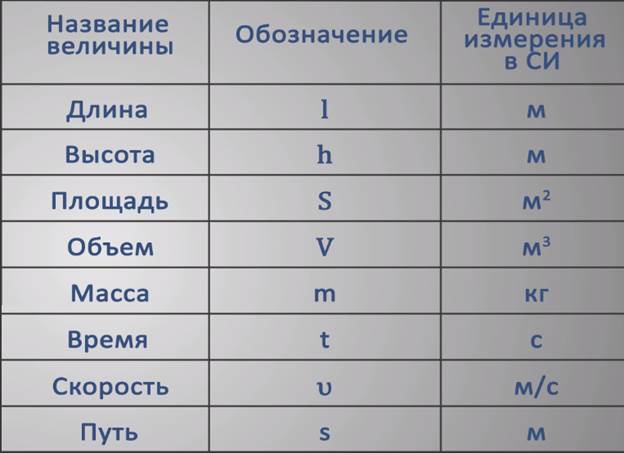 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
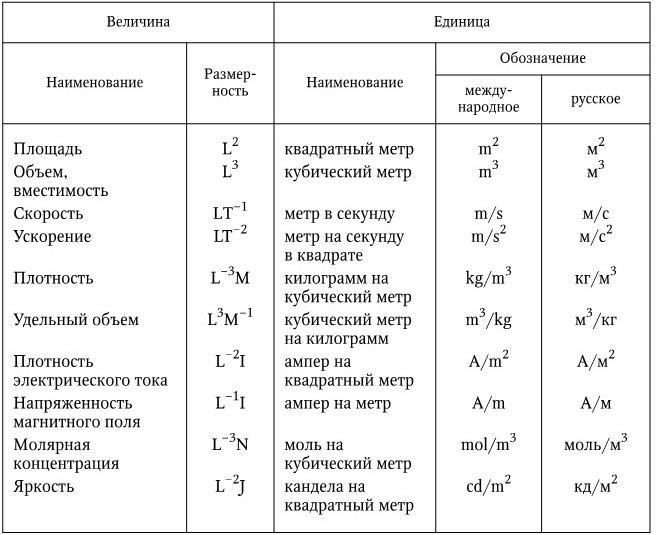 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N 0 ∙2 – t / T
- Энергия связи атомных ядер
| #1 Общий | Только единицы СИ и единицы, признанные для использования с
СИ используются для выражения значений величин. Эквивалентные значения
в других единицах приведены в скобках следующие значения в допустимых
единицы только тогда, когда это необходимо для целевой аудитории. Эквивалентные значения
в других единицах приведены в скобках следующие значения в допустимых
единицы только тогда, когда это необходимо для целевой аудитории. | ||||||||||||||||||||||||||||
| #2 Сокращения | Сокращения, такие как sec, cc или mps, избегаются и используются только стандартные символы единиц, символы префиксов, имена единиц и имена префиксов использовал. | ||||||||||||||||||||||||||||
| собственно: | с или секунды; см 3 или кубический сантиметр; м/с или метр в секунду | ||||||||||||||||||||||||||||
| неправильный: | сек; копия; мпс | ||||||||||||||||||||||||||||
| #3 Множественное число | Символы единиц во множественном числе не изменяются. | ||||||||||||||||||||||||||||
собственно: | л = 75 см | ||||||||||||||||||||||||||||
неправильно: | л = 75 см | ||||||||||||||||||||||||||||
| #4 Пунктуация | Символы единиц измерения не сопровождаются точкой, если в конце предложение. | ||||||||||||||||||||||||||||
собственно: | Длина штанги 75 см. Длина штанги 75 см. | ||||||||||||||||||||||||||||
неправильно: | Штанга 75см. длинная. | ||||||||||||||||||||||||||||
| #5 Умножение & подразделение | Пробел или полувысокая точка используются для обозначения умножения единиц.
Солид ( i. т. е., косая черта ), горизонтальная линия или минус
показатель степени используется для обозначения деления единиц. Солидус не должен повторяться на
той же строке, если не используются круглые скобки. т. е., косая черта ), горизонтальная линия или минус
показатель степени используется для обозначения деления единиц. Солидус не должен повторяться на
той же строке, если не используются круглые скобки. | ||||||||||||||||||||||||||||
собственно: | Скорость звука около 344 м·с -1 (метров в секунду) Скорость затухания 113 Cs составляет примерно 21 мс -1 (обратные миллисекунды) м/с, м·с -2 , м·кг/(с 3 ·A), м·кг·с -3 ·A -1 м/с, м с -2 , м кг/(с 3 А), м кг с -3 А -1 | ||||||||||||||||||||||||||||
неправильный: | Скорость звука около 344 мс -1 (обратные миллисекунды) Скорость затухания 113 Cs составляет около 21 м·с -1 (метров в секунду) м ÷ с, м/с/с, м·кг/с 3 /A | ||||||||||||||||||||||||||||
| #6 Шрифт | Переменные и символы количества выделены курсивом. Символы единиц измерения
написаны римским шрифтом. Цифры, как правило, должны быть написаны латинскими буквами.
тип. Эти правила применяются независимо от шрифта, используемого в
окружающий текст. Для получения дополнительной информации см. Шрифты для символов в научных рукописях Символы единиц измерения
написаны римским шрифтом. Цифры, как правило, должны быть написаны латинскими буквами.
тип. Эти правила применяются независимо от шрифта, используемого в
окружающий текст. Для получения дополнительной информации см. Шрифты для символов в научных рукописях | .||||||||||||||||||||||||||||
собственно: | воскликнула она восклицала, « , что собака весит 10 кг ! » T = 3 S, где T – это время и S – это второй T = 22 K, где T – термодинамическая температура, а K – | Кельвинов.||||||||||||||||||||||||||||
неправильно: | Он воскликнул: ” Эта собака весит 10 кг! t = 3 с, где t — время, а s — секунда T = 22 K, где T — термодинамическая температура, а K — | Кельвинов.||||||||||||||||||||||||||||
| #7 Шрифт | Верхние и нижние индексы выделены курсивом, если они обозначают
переменные, количества или порядковые числа. они написаны римским шрифтом
если они описательные. они написаны римским шрифтом
если они описательные. | ||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
| #8 Сокращения | Комбинации букв “ppm”, “ppb” и “ppt” и термины
часть на миллион, часть на миллиард и часть на триллион, и
подобные, не используются для выражения значений величин. | ||||||||||||||||||||||||||||
| собственно: | 2,0 мкл/л; 2,0 x 10 -6 В; 4,3 нм/м; 4,3 x 10 -9 л; 7 пс/с; 7 x 10 -12 т , где V , l и t — количественные символы объема, длины и времени. | ||||||||||||||||||||||||||||
| неправильный: | “ppm”, “ppb” и “ppt”, а также части на миллион, часть на миллиард, и часть на триллион, и тому подобное | ||||||||||||||||||||||||||||
| #9 Блок модификации | Символы единиц (или имена) не изменяются путем добавления индексов или другую информацию.Например, используются следующие формы вместо. | ||||||||||||||||||||||||||||
| собственный: | В макс. = 1000 В массовая доля 10 % | ||||||||||||||||||||||||||||
| неправильный: | В = 1000 В макс. 10 % ( м / м ) или 10 % (по весу) | ||||||||||||||||||||||||||||
| #10 Процент | Символ % используется для представлять просто число 0.01. | ||||||||||||||||||||||||||||
| собственный: | л 1 = л 2 (1 + 0,2 %), или D = 0,2 %, где D определяется соотношением D = ( l 1 – l 2 )/ l 2 . | ||||||||||||||||||||||||||||
| неправильный: | длина l 1 превышает длину l 2 на 0.2 % | ||||||||||||||||||||||||||||
| #11 Информация и единиц | Информация не смешивается с символами или названиями единиц. | ||||||||||||||||||||||||||||
| собственный: | содержание воды 20 мл/кг | ||||||||||||||||||||||||||||
| неправильный: | 20 мл H 2 O/ кг 20 мл воды/кг | ||||||||||||||||||||||||||||
| #12 Математика обозначение | Ясно, какому символу единицы принадлежит числовое значение и какая математическая операция применяется к значению количества. | ||||||||||||||||||||||||||||
| собственный: | 35 см x 48 см от 1 МГц до 10 МГц или (от 1 до 10) МГц от 20 °C до 30 °C или (от 20 до 30) °C 123 г ± 2 г или (123 ± 2) г 70 % ± 5 % или (70 ± 5) % 240 х (1 ± 10 %) В | ||||||||||||||||||||||||||||
| неправильный: | 35 х 48 см 1–10 МГц или от 1 до 10 МГц 20 °C-30 °C или от 20 до 30 °C 123 ± 2 г 70 ± 5 % 240 В ± 10 % (нельзя добавить 240 В и 10 %) | ||||||||||||||||||||||||||||
| #13 Единица измерения символов и имена | Символы единиц и названия единиц не смешиваются и математические операции
не применяются к именам юнитов. | ||||||||||||||||||||||||||||
| собственно: | кг/м 3 , кг · м -3 , или килограмм на кубический метр | ||||||||||||||||||||||||||||
| неправильный: | кг/м 3 , кг/куб.м, кг/куб.м, кг на м 3 , или килограмм на метр 3 . | ||||||||||||||||||||||||||||
| #14 Цифры и единица измерения символов | Значения величин выражены в допустимых единицах с использованием арабского языка. цифры и символы единиц измерения. | ||||||||||||||||||||||||||||
| собственный: | м = 5 кг ток был 15 А | ||||||||||||||||||||||||||||
| неправильный: | м = пять килограммов м = пять кг ток был 15 ампер | ||||||||||||||||||||||||||||
| #15 Блок интервал | Между числовым значением и символом единицы есть пробел,
даже когда значение используется в смысле прилагательного, за исключением
случай надстрочных единиц для плоского угла. | ||||||||||||||||||||||||||||
| собственный: | Шар весом 25 кг угол 2° 3 ‘ 4 ” Если используется прописанное название единицы, обычные правила Английский применяется: «рулон 35-миллиметровой пленки». | ||||||||||||||||||||||||||||
| неправильный: | Шар весом 25 кг угол 2° 3 ‘ 4 ” | ||||||||||||||||||||||||||||
| #16 Цифра интервал | Цифры числовых значений, имеющие более четырех цифр на по обе стороны от десятичного маркера разделены на группы три с использованием тонкого фиксированного пространства, считая как слева, так и справа от десятичного знака.Запятые не используются для разделения цифр на группы по три. | ||||||||||||||||||||||||||||
собственно: | 15 739.012 53 | ||||||||||||||||||||||||||||
неправильно: | 15739. 01253 01253 15 739.012 53 | ||||||||||||||||||||||||||||
| #17 Количество уравнения | Уравнения между величинами используются вместо уравнений между числовыми значениями и символами, представляющими числовые значения отличаются от символов, обозначающих соответствующие величины.Когда используется уравнение с числовым значением, оно правильно записывается и соответствующее количественное уравнение дается там, где это возможно. | ||||||||||||||||||||||||||||
| собственно: | ( л /м) = 3,6 -1 [ v /(км/ч)]( t /с) | ||||||||||||||||||||||||||||
| неправильный: | л = 3,6 -1 вт ,
в сопровождении текста, говорящего, “где l – в метрах, v – в километрах в час, а t в секундах” | ||||||||||||||||||||||||||||
| #18 Стандарт символов | Используются стандартные символы количества. Точно так же стандартизированы
используются математические знаки и символы. В частности,
основание «логарифма» в уравнениях указывается при необходимости записью
log x (Значение log к базе A из x ), LB x (Значение log 2 x ), ln x (Значение log E x ) или lg x (что означает log 10 x ). Точно так же стандартизированы
используются математические знаки и символы. В частности,
основание «логарифма» в уравнениях указывается при необходимости записью
log x (Значение log к базе A из x ), LB x (Значение log 2 x ), ln x (Значение log E x ) или lg x (что означает log 10 x ). | ||||||||||||||||||||||||||||
| собственный: | желтовато-коричневый x R для сопротивления A r для относительной атомной массы | ||||||||||||||||||||||||||||
| неправильный: | тг х по касательной х слова, аббревиатуры или специальные группы букв | ||||||||||||||||||||||||||||
| #19 Вес по сравнению с масса | Когда используется слово “вес”, предполагаемое значение ясно. (В науке и технике вес – это сила, для которой СИ
единица – ньютон; в торговле и повседневном использовании вес обычно
синоним массы, для которой единицей СИ является килограмм.) (В науке и технике вес – это сила, для которой СИ
единица – ньютон; в торговле и повседневном использовании вес обычно
синоним массы, для которой единицей СИ является килограмм.) | ||||||||||||||||||||||||||||
| #20 Частное количество | Частное количество записывается явно. | ||||||||||||||||||||||||||||
| собственный: | масса разделить на объем | ||||||||||||||||||||||||||||
| неправильный: | масса на единицу объема | ||||||||||||||||||||||||||||
| #21 Объект и количество | Объект и любая величина, описывающая объект, различаются.(Обратите внимание на разницу между «поверхностью» и «площадью», «телом» и
«масса», «резистор» и «сопротивление», «катушка» и «индуктивность»).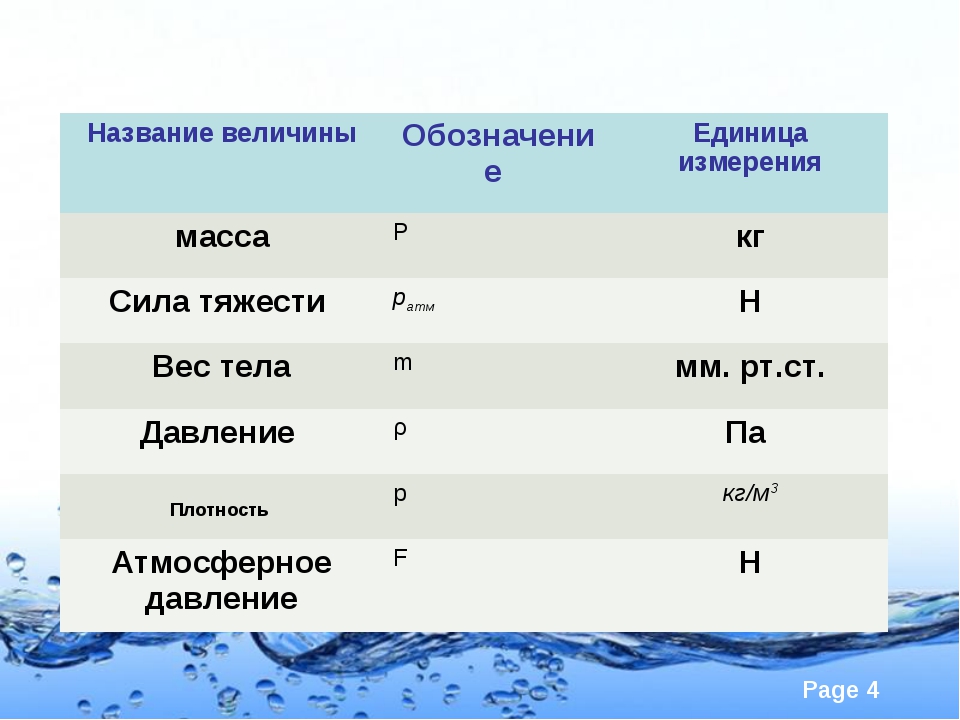 | ||||||||||||||||||||||||||||
| собственно: | Тело массой 5 г | ||||||||||||||||||||||||||||
| неправильный: | Масса 5 г | ||||||||||||||||||||||||||||
| #22 Устарело Условия | Устаревшие термины нормальность, молярность и моляль и их символы N, M и m не используются. | ||||||||||||||||||||||||||||
| собственный: | количество-концентрация вещества B (чаще
называется концентрацией B), и его символ c B и единица СИ моль/м 3 (или соответствующая допустимая единица) | ||||||||||||||||||||||||||||
| неправильный: | нормальность и символ N , молярность и символ М моляль и символ м | ||||||||||||||||||||||||||||
ДАВАЙТЕ ОЧИСТИМ НАШ ФИЗИЧЕСКИЙ ЯЗЫК
Дональд Э.
 Симанек
Симанек«Чтобы вы не подумали, что я придираюсь к второстепенным вопросам языка, я отмечу, что, по моему опыту, многие заблуждения, питаемые людьми, берут свое начало в неточном языке … Точный язык нужен в науке не для того, чтобы угодить педантам, а чтобы избежать поглощения ерунда, на то, чтобы очистить наши умы, потребуются годы, если вообще когда-либо». – Доктор Крейг Ф. Борен, из его «Облаков в стакане пива»: Простые эксперименты по физике атмосферы”“…(язык) становится уродливым и неточным, потому что наши мысли глупы, но неряшливость нашего языка облегчает нам глупые мысли.” – Джордж Оруэлл
«Поиск mot juste — это не педантичная прихоть, а жизненная необходимость. Слова — наши точные инструменты. Неточность порождает двусмысленность, и часы тратятся на устранение словесных недоразумений, прежде чем можно будет начать спор по существу». – Анонимный государственный служащий (с веб-страницы Roget’s Thesaurus)
«Многие заблуждения, по правде говоря, состоят просто в применении неправильных названий вещей.
“-Спиноза
ВВЕДЕНИЕ
Иногда кажется проигрышной битвой бороться с упадком Английский язык. По мере того, как язык становится неточным дряблость, как и наша способность выражать мысли. Это плохо достаточно в быту, но гибельно в науках, ибо наука требует точности мысли и выражения. Физику, например, достаточно сложно выучить без необходимости
преодолевать семантические препятствия. Хотя мы утверждаем, что физика является «точной
наука» в том смысле, что она стремится к максимально возможному
точность измерения, физики, как класс, общеизвестно
менее точны, когда говорят и пишут о предмете.Когда они
разговаривают друг с другом, они часто принимают разговорный режим, поэтому
сокращенно, с таким количеством опущенных деталей, что любой, кто не работает
в этой конкретной области находит это непонятным. Они должны делать
это, конечно, иначе они часами объясняли бы вещи, которые
для них тривиальны. Они эффективно общаются друг с другом
через общую базу знаний и согласованные словесные
соглашения, которые редко когда-либо записываются. Они играют очень
хорошая игра “чтение мыслей”, в которой каждый слышит, что имеет в виду другой,
не то, что он говорит.И это работает! Но посторонние сбиты с толку.
Они играют очень
хорошая игра “чтение мыслей”, в которой каждый слышит, что имеет в виду другой,
не то, что он говорит.И это работает! Но посторонние сбиты с толку.
| Дилемма учителя физики. |
|---|
Некоторые из этих трудностей неизбежны. Но нет оправдания
за некоторые неточные и вводящие в заблуждение выражения, которые мы иногда
найти в учебниках, и часто найти на уроках физики. Там
это небольшое оправдание для увеличения количества слов, которые все означают
то же самое. Нет оправдания использованию расплывчатого или неточного слова
когда доступен совершенно хороший точный.
Нет оправдания использованию расплывчатого или неточного слова
когда доступен совершенно хороший точный.
Ниже я перечисляю несколько скромных предложений в этом направлении.
СООТНОШЕНИЕ
Словарь напоминает нам, что следует использовать только слово «отношение» при сравнении двух «подобных» вещей.«Пи» (р), отношение длина окружности к диаметру круга, в порядке, так как оба окружность и диаметр – длины. Но мы не должны говорить о отношение площади круга к его радиусу, и мы не должны говорить об отношении массы к объему, потому что мы будем сравнивать различные физические величины. Это просто частные.ЗА ЕД.
Даже учебники совершают этот языковой грех. “Плотность – это масса на единицу объема». «Напряженность электрического поля равна силе на единицу объема. заряд.” Я с удовлетворением отмечаю, что многие ученые сейчас быть более осторожным в этом, говоря вместо этого: “Плотность – это масса деленная на объем», или «Плотность есть отношение массы к объему. ”
Дело в том, что определение не обязательно требует одна единица количества в знаменателе. В случае
определение электрического поля как силы/заряда в системе МКС,
мы, конечно, не хотели бы использовать заряд одного
единица, кулон, для такого большого заряда, скорее всего, потревожит
ситуацию, которую мы пытаемся измерить. [На самом деле правильное определение
электрического поля является «пределом силы/заряда, поскольку размер заряда
стремится к нулю”.]
”
Дело в том, что определение не обязательно требует одна единица количества в знаменателе. В случае
определение электрического поля как силы/заряда в системе МКС,
мы, конечно, не хотели бы использовать заряд одного
единица, кулон, для такого большого заряда, скорее всего, потревожит
ситуацию, которую мы пытаемся измерить. [На самом деле правильное определение
электрического поля является «пределом силы/заряда, поскольку размер заряда
стремится к нулю”.]СИЛА, НАПРЯЖЕНИЕ, МОЩНОСТЬ
Эти слова закрепились в разговорном языке науки, но они совершенно не нужны.у нас отлично хорошие технические слова для этих измеряемых величин: ток, потенциал, мощность. Учебники по физике подают хороший пример при описании ток и мощность; хорошие почти никогда не используют «силу тока» или «мощность». Тогда почему они продолжают использовать «напряжение»? Это кажется непоследовательным, не так ли?СТАВКА
Худшими грешниками здесь являются люди в средствах массовой информации. Как часто вы слышали: «Он путешествовал с большой скоростью».
скорость”? Скорость – это уже скорость изменения положения.«скорость
скорость” либо избыточна, либо неправильно подразумевает ускорение,
что не то, что имеется в виду. Просто скажите “высокая скорость”.
Как часто вы слышали: «Он путешествовал с большой скоростью».
скорость”? Скорость – это уже скорость изменения положения.«скорость
скорость” либо избыточна, либо неправильно подразумевает ускорение,
что не то, что имеется в виду. Просто скажите “высокая скорость”.РАВНОЕ И ПРОТИВОПОЛОЖНОЕ
Эта вездесущая фраза часто появляется в учебниках, например, утверждение третьего закона Ньютона: «Взаимодействующие тела действуют равные и противоположные силы друг на друга». Что на самом деле имеется в виду заключается в том, что на них действуют силы, равные по величине и противоположные по знаку друг на друга. Как любые два ненулевых вектора могут быть «равны» и тоже “наоборот”?[Спасибо Полу Ли за то, что обратил на это мое внимание после Я сам совершил ошибку.]
В ПОКОЕ
| Момент инерции. |
|---|
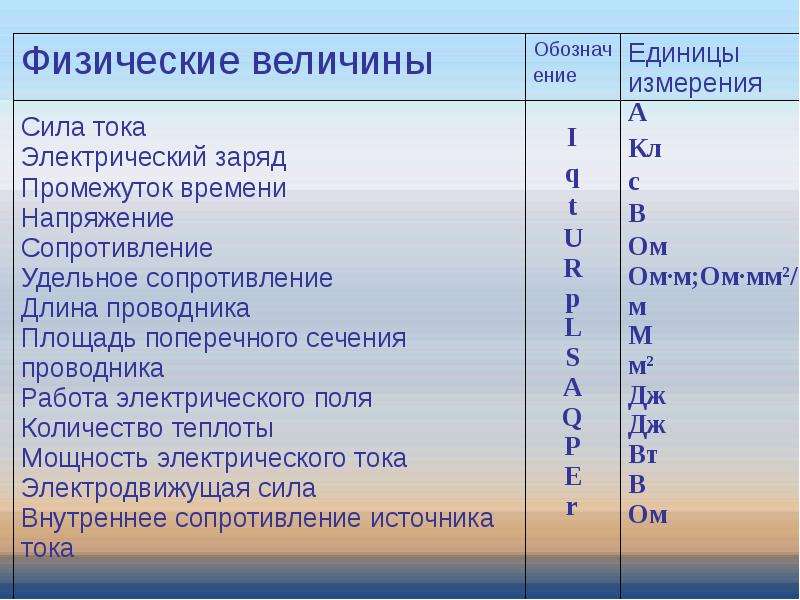 Затем в главах, посвященных динамике, мы можем увидеть: «Тело, брошенное прямо вверх,
на мгновение в состоянии покоя в высшей точке своего движения». Студент
затем логически заключают, что в этот момент результирующая сила, действующая на тело
равно нулю и, следовательно, его ускорение в этой точке равно нулю.Это заблуждение «в состоянии покоя = нулевая результирующая сила = равновесие = нулевое ускорение».
Мы не можем обвинять студентов в том, что они верят учебникам на слово.
Затем в главах, посвященных динамике, мы можем увидеть: «Тело, брошенное прямо вверх,
на мгновение в состоянии покоя в высшей точке своего движения». Студент
затем логически заключают, что в этот момент результирующая сила, действующая на тело
равно нулю и, следовательно, его ускорение в этой точке равно нулю.Это заблуждение «в состоянии покоя = нулевая результирующая сила = равновесие = нулевое ускорение».
Мы не можем обвинять студентов в том, что они верят учебникам на слово.Что означают «в покое» и «на мгновение в покое» и чем они отличаются? Большинство людей понимает, что тело в состоянии покоя находится в неподвижном состоянии в течение некоторого периода времени. Может ли тело даже быть «на мгновение» покоящимся? Один читатель предложил «в покое в определенный момент времени». Боюсь, это усугубляет проблему, поскольку определение скорость включает в себя предельный процесс исчисления, начинающийся с конечного времени интервал.
Вместо того, чтобы решить эту липкую проблему семантики, лекарство простое. Когда
описывая ситуацию, когда скорость тела меняет знак и
поэтому должно пройти значение v = 0 ,
просто скажите «скорость на мгновение равна нулю» в этой точке. Этот
происходит в верхней части траектории, в крайних точках движения маятника, и
может произойти в какой-то момент при столкновении двух тел. Отказ от использования
фразы «на мгновение в покое» разрушает эту логическую ошибку, прежде чем она
начинается, кладя его в покой навсегда.
Когда
описывая ситуацию, когда скорость тела меняет знак и
поэтому должно пройти значение v = 0 ,
просто скажите «скорость на мгновение равна нулю» в этой точке. Этот
происходит в верхней части траектории, в крайних точках движения маятника, и
может произойти в какой-то момент при столкновении двух тел. Отказ от использования
фразы «на мгновение в покое» разрушает эту логическую ошибку, прежде чем она
начинается, кладя его в покой навсегда.
Один читатель предлагает «мгновенный ноль» как предпочтительнее «мгновенного нуля».
ЗАМЕДЛЕНИЕ
Рик Глейзер напомнил мне об этом распространенном заблуждении. Большинство учебников избегают этой ловушки, но студенты все равно попадают в нее, не зная, означает ли «замедление» то же самое, что и «отрицательное ускорение». Рик предполагает: “Замедление” на самом деле не термин в физике. Это всего лишь английское слово, используемое в просторечии и означающее «уменьшение скорости».Проблема с этим словом заключается в том, что некоторые студенты ошибочно принимают его за то же самое, что и отрицательное ускорение. Но поскольку отрицательный знак просто определяет направление в конкретной задаче относительно выбранной оси, скорость объекта на самом деле УВЕЛИЧИВАЕТСЯ, если он имеет ускорение. отрицательная скорость, а также отрицательное ускорение
Но поскольку отрицательный знак просто определяет направление в конкретной задаче относительно выбранной оси, скорость объекта на самом деле УВЕЛИЧИВАЕТСЯ, если он имеет ускорение. отрицательная скорость, а также отрицательное ускорение Так как же нам избежать этой дилеммы? Я нахожу это интересным как пример того, как мы думаем о движении. Сравните, как мы говорим о скорости, и как мы говорим об ускорении:
- Мы почти никогда не говорим об отрицательной скорости, даже в разговорной речи.Большинство студентов признают, что скорость является положительной величиной, величиной скорости. У нас нет разговорного слова для скорости в отрицательном направлении.
- В просторечии мы часто говорим о замедлении, имея в виду уменьшение размера ускорения, независимо от направления ускорения. У нас нет разговорного слова для ускорения в отрицательном направлении.
- Величина скорости – это скорость.
- Нет единого слова для величины ускорения, ни разговорного, ни технического.

При решении физических задач в системе координат мы должны воздерживаться от использования слова «замедление», поскольку, фактически, разговорное понятие, которое оно называет, не является тем, которое мы часто используем при математическом обсуждении движения.Когда нам нужна концепция, мы должны сказать: «ускорение в отрицательном направлении». «Скорость» следует использовать только для «величины скорости». Редко когда возникает необходимость называть «величину ускорения»
Я мог бы добавить, что эти путаницы возникают в случаях двумерного движения вдоль прямой линии. Когда тело движется по криволинейной или запутанной траектории, мы имеем дело с силами, смещениями, скоростями и ускорениями с помощью векторной математики, а «положительные» или «отрицательные» в любом случае недостаточные дескрипторы.
Когда тело движется по криволинейной или запутанной траектории, мы имеем дело с силами, смещениями, скоростями и ускорениями с помощью векторной математики, а «положительные» или «отрицательные» в любом случае недостаточные дескрипторы.
Я не хочу преуменьшать крайнюю скорбь, которую это доставляет многим ученикам, и я бы приветствовал мнение учителей о том, как они справляются с этим.
СИЛА ТРЕНИЯ
Многие концептуальные трудности возникают, когда не учитываются ключевые слова. Фраза «сила трения» подсказывает учащемуся, что трение вид силы, или что трение — это физическая «вещь», которая способен оказывать воздействие на другие вещи. Это путает процесс с следствием этого процесса.Трение – это процесс, происходящий на контактных границах раздела материальных тел. Трение порождает две силы, пару действие/противодействие в соответствии с третьим законом Ньютона: тело А действует на тело с силой В и В действуют на А силы одинаковой величины и противоположного направления, из-за процесса трения на их границе раздела или в точках контакта. Из-за упругости
сжатие тел, они также оказывают силу перпендикулярно (перпендикулярно)
поверхность контакта. Небольшая путаница возникает из-за ярлыка «нормальная сила».
поскольку ни один студент вряд ли подумает, что это «сила, обусловленная нормальным».(Однако некоторые могут задаться вопросом, что может быть за «аномальная» сила.)
Нормальная сила и сила трения составляют составляющие
сила, которую мы просто называем «силой реакции» на тело из-за ее
контакта с другим телом. Во избежание заблуждений лучше говорить о «силе трения».
Некоторые читатели предлагают «силу трения» на том основании, что суффикс «-al»
предлагает «из-за» и предупреждает студентов, что это нечто иное, чем
«сила трения». Сомневаюсь, что студенты это поймут.
Из-за упругости
сжатие тел, они также оказывают силу перпендикулярно (перпендикулярно)
поверхность контакта. Небольшая путаница возникает из-за ярлыка «нормальная сила».
поскольку ни один студент вряд ли подумает, что это «сила, обусловленная нормальным».(Однако некоторые могут задаться вопросом, что может быть за «аномальная» сила.)
Нормальная сила и сила трения составляют составляющие
сила, которую мы просто называем «силой реакции» на тело из-за ее
контакта с другим телом. Во избежание заблуждений лучше говорить о «силе трения».
Некоторые читатели предлагают «силу трения» на том основании, что суффикс «-al»
предлагает «из-за» и предупреждает студентов, что это нечто иное, чем
«сила трения». Сомневаюсь, что студенты это поймут.ПРЕДЛОЖИТЕЛЬНОЕ ЗАНИМАНИЕ
Если говорить об «ускорении автомобиля». мы, конечно, имеем в виду, что автомобиль — это то, что ускоряется. Теперь рассмотрим «ускорение силы тяжести». Это высказывание что гравитация ускоряется? Маленький предлог “из” должен означать разные вещи в этих похожих предложениях.
Учителя английского говорят мне, что учащиеся начальной школы находят предлоги единственная часть речи, которую труднее всего усвоить. Ясно, что физики, которые изобретают эти названия для физических понятий так и не преодолел эту трудность.Если бы они проверили словарь, то обнаружили бы, что «из» может означать:
|
из
благодаря
далеко от
отделено от
составлено или изготовлено из
связан с
придерживаясь
принадлежат или связаны с
обладающий, имеющий (как в «почетном лице»)
содержащие или перевозящие
указывается как
Теперь я спрашиваю вас, имеет ли смысл фраза “ускорение силы тяжести”
точно соответствует какому-либо из этих критериев?
Список значений слова «из»
включают «из-за», «вызвано»
или “результат”?
Ближайшие совпадения «связаны с»,
«от» и «благодаря». “Связано с” слабо,
и может охватывать целый ряд ассоциативных отношений.
“Связано с” слабо,
и может охватывать целый ряд ассоциативных отношений.
Мы не должны говорить о «силе гравитации». но скажем “сила гравитации” или, еще лучше, «сила, обусловленная (вытекающая из)» силы тяжести. Мы не хотим предполагать, что гравитация — это «вещь». наравне с планетами и кирпичами.
Но важно то, что ученики интерпретируют «из». иметь в виду в таких контекстах. Я задавал студентам этот вопрос на протяжении многих лет, и результаты:
содержится в, состоит из (как в «Соединенных Штатах Америки»)
принадлежит (как в «активах банка»)
вызвано, порождено (например, «последствия образования», «заработная плата
грех”)
сделано из (как в «магнезиальном молоке»)
о (как в “О мышах и людях”)
Вы можете легко себе представить концептуальные трудности, которые могут возникнуть из-за эти интерпретации применительно к понятиям физики.
Предлоги в английском языке обозначают отношения между вещами. Физика
очень озабочен точными отношениями между вещами.
А вот предлоги в наличии:
«at», «by», «to», «from» и «with» в лучшем случае являются тупыми инструментами.
Проблема с предлогами в том, что они
имеют такой широкий спектр несовместимых значений, что очень легко
интерпретировать их не так, как задумано автором или говорящим.
Лекарство: замените другими словами, передающими большую точность и ясность,
даже если это требует более длинных заявлений.
Физика
очень озабочен точными отношениями между вещами.
А вот предлоги в наличии:
«at», «by», «to», «from» и «with» в лучшем случае являются тупыми инструментами.
Проблема с предлогами в том, что они
имеют такой широкий спектр несовместимых значений, что очень легко
интерпретировать их не так, как задумано автором или говорящим.
Лекарство: замените другими словами, передающими большую точность и ясность,
даже если это требует более длинных заявлений.
Маленькое слово “из” также мутит концептуальные воды в других случаях. Я иллюстрирую:
Сила трения . Лучше: сила из-за трения.
Сила гравитации . Лучше: гравитационная сила. Сила из-за силы тяжести.
Механический эквивалент из тепла. Лучше: постоянная Джоуля.
Можем ли мы просто выбросить некоторые из этих надоедливых предлогов? Посмотрите, как это работает, в моем документе P-prime.
Плыви по течению
Очень распространенная ошибка в учебниках — говорить о «потоке ток». Ток сам по себе является потоком заряда; что тогда могло бы «течь
текущего»? Это избыточно, вводит в заблуждение или неправильно.
Это выражение следует вычеркнуть из нашего лексикона.
Сравните аналогичную ошибку: «Скорость движется на запад».
Ток сам по себе является потоком заряда; что тогда могло бы «течь
текущего»? Это избыточно, вводит в заблуждение или неправильно.
Это выражение следует вычеркнуть из нашего лексикона.
Сравните аналогичную ошибку: «Скорость движется на запад».ПОЧУВСТВУЙТЕ ЭЛЕКТРИЧЕСТВО
Иногда слово электричество в просторечии используется неправильно, как если бы он называл физическую величину, например «Конденсатор накапливает электричество» или «Электричество в резистор выделяет тепло.” Такого использования следует избегать ! Во всех таких случаях имеется более конкретный или точный слова, такие как «Конденсатор хранит электрической энергии», «Конденсатор резистор нагревается электрическим током ,» и «Утилита Компания взимает с меня плату за электроэнергии, которую я использую за “. я не заряжаюсь на основе мощности , поэтому эти компании не должны называть себя Власть компаний. У некоторых уже есть изменили свои названия на что-то вроде «Acme Energy»)ЭВОЛЮЦИЯ ЭМП
Термин «электродвижущая сила» определяется при потенциале через клеммы химического элемента или другого источника электроэнергии в условиях холостого хода (нулевой ток). Раньше его сокращали
«ЭДС», но затем такие аббревиатуры упростили до «ЭДС» (обычно
сопровождается пояснением, что это означает «электродвижущая сила»,
и наконец,
сегодня вы видите, что это написано в учебниках как «ЭДС» (без каких-либо объяснений).
Оно превратилось из аббревиатуры в слово. Его историческое происхождение
были заметены под ковер, и, может быть, это хорошо, потому что
старое название вызвало много путаницы у современных студентов.
Раньше его сокращали
«ЭДС», но затем такие аббревиатуры упростили до «ЭДС» (обычно
сопровождается пояснением, что это означает «электродвижущая сила»,
и наконец,
сегодня вы видите, что это написано в учебниках как «ЭДС» (без каких-либо объяснений).
Оно превратилось из аббревиатуры в слово. Его историческое происхождение
были заметены под ковер, и, может быть, это хорошо, потому что
старое название вызвало много путаницы у современных студентов. Слово возникло, когда слово «сила» имело более широкое техническое значение.
для описания «того, что может вызвать что-то».Итак, «электродвижущая сила» означала,
«То, что может заставить электрические заряды двигаться». В настоящее время у нас есть
сузили и ограничили понятие силы, поэтому в современном
смысл, ЭДС не сила , это электрический потенциал .
Это совершенно разные понятия, с разными единицами измерения и измерениями.
Кроме того, сила — это вектор, а потенциал — это скаляр. Много диссонанса
здесь понятия расходятся.
ПРОЦЕНТ
В более старых словарях предлагалось, чтобы процента были используется, когда делается неколичественное утверждение: «Процент рост экономики был обнадеживающим.” Но используйте процента , когда с указанием числового значения: «Валовой национальный продукт увеличился на 2 процентов прошлого года.” Однако уместно еще одно использование «процента».
При сравнении процентной меры, которая меняет , обычно это изменение выражается в «процентных пунктах».
Например, если уровень безработицы составляет 5% в один месяц и 6% в следующий, мы
скажем, «Безработица увеличилась на один процентный пункт». Абсолют
изменение в безработице было, однако, увеличением на 20 процентов.То
средний человек, слыша такие цифры, редко останавливается, чтобы подумать, что
слова означают, и многие думают, что «процент» и «процентный пункт»
являются синонимами. Они не. Это еще одна причина избегать использования
слово «процент» при выражении процентных мер. Термин «процент
точка” почти никогда не используется в науках. (Если только вы
считать экономику наукой.)
Термин «процент
точка” почти никогда не используется в науках. (Если только вы
считать экономику наукой.)
Студенты, изучающие естественные науки, не зная об этом различии, иногда говорят: «Экспериментальный процент неопределенность в нашем результате составила 9%.«Возможно, они пытаются «звучать глубокомысленно». В свете приведенного выше обсуждения, это не то, что студент имел в виду. Студент должен был просто сказать: «Экспериментальная неопределенность нашего результата составила 9%».
КВАНТОВЫЙ Прыжок
Это еще одна ошибочная попытка углубиться: «Государственные расходы в этом году совершили квантовый скачок». Словарь Значение «квант» – это «количество или количество». Таким образом, цитируемое использование слова пусто или избыточно, ибо любое изменение было бы квантовая сумма.В физике это слово имеет более конкретное значение: Квантовый «скачок» — это переход из одного разрешенного состояния системы в Другая; и это используется только для описания систем, в которых разрешенные состояния имеют дискретные, измеримо разные значения.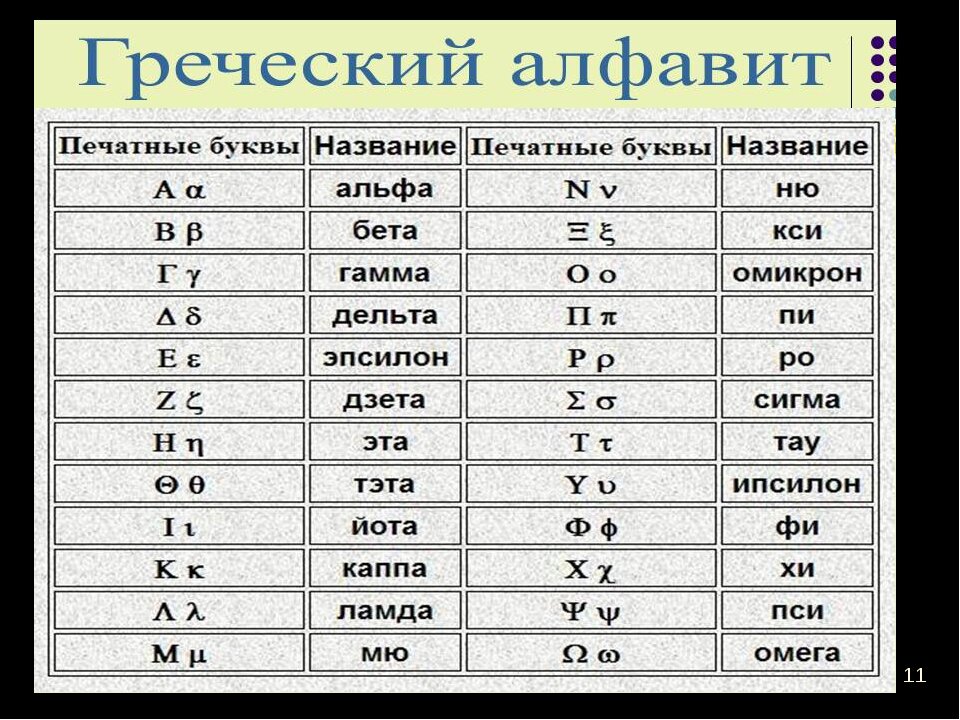 Государственные расходы вряд ли поддаются количественной оценке в этом смысле, если только вы не
считать квантовой единицей пенни, единицу, слишком маленькую, чтобы
признаны государственными тратами. В физике квантовые скачки энергии
обычно довольно мало по сравнению с полным диапазоном энергий системы.
могу иметь.Неправильное употребление этого слова в разговорной речи трактует его как
это всегда означало «очень большой».
Государственные расходы вряд ли поддаются количественной оценке в этом смысле, если только вы не
считать квантовой единицей пенни, единицу, слишком маленькую, чтобы
признаны государственными тратами. В физике квантовые скачки энергии
обычно довольно мало по сравнению с полным диапазоном энергий системы.
могу иметь.Неправильное употребление этого слова в разговорной речи трактует его как
это всегда означало «очень большой».МЫ ПРЕОДОЛИМ
В учебниках часто говорится о «преодолении трения». Что это может означать? Скорее всего имелось в виду сказать, что составляющая чистой приложенной силы в плоскости контакт между двумя телами был равен или больше максимального сила, которая могла бы возникнуть в этом случае из-за трения покоя. Слово «преодолеть» не имеет конкретного технического значения. Это
скользкое слово, способное на множество неправильных толкований.Рассмотрим другой
злоупотребление словом: «Когда сила преодолевает инерцию тела
в покое тело начинает двигаться”. Да, я действительно видел такие
абсурдные высказывания в учебниках и слышал их на уроках. Сила
и инерция две совершенно разные вещи и не могут быть
математически приравнивается. Инерция — это просто масса, ни больше, ни меньше.
Как «преодолеть» массу? Уничтожьте это?
Да, я действительно видел такие
абсурдные высказывания в учебниках и слышал их на уроках. Сила
и инерция две совершенно разные вещи и не могут быть
математически приравнивается. Инерция — это просто масса, ни больше, ни меньше.
Как «преодолеть» массу? Уничтожьте это?
ТЯНИ МЕНЯ, ТЯНИ МЕНЯ
Учителя и учебники пытаются «разговорить» физику различными способами, надеясь связать понятия с повседневной жизнью и повседневный язык.Обычно это имеет неприятные последствия, создавая заблуждения. Например, в учебнике сказано: «Сила — это толчок или тянуть.» Это кажется достаточно невинным, но разговорная концепция толкать и тянуть – это то, что вы делаете обязательно вызывает движение, понятие аристотелевской физики. Студент думает «толкать автомобиль» или «тянуть повозку», производя движение. Поэтому, когда в учебниках обсуждают приливы, мы иногда видим: «Приливы вызваны тем, что луна притягивает больше сильно на ближней стороне земли, меньше на теле земле, и еще меньше на дальней стороне. Поэтому вода на
ближняя сторона тянется на большее расстояние к луне, земле
тянет меньше, и вода на дальней стороне движется меньше всего,
поэтому профиль океана сплющивается, а приливы
как на ближней, так и на противоположной стороне земли”. Это совершенно
ложное представление о том, что происходит. См. мой документ Заблуждения о приливах.
Поэтому вода на
ближняя сторона тянется на большее расстояние к луне, земле
тянет меньше, и вода на дальней стороне движется меньше всего,
поэтому профиль океана сплющивается, а приливы
как на ближней, так и на противоположной стороне земли”. Это совершенно
ложное представление о том, что происходит. См. мой документ Заблуждения о приливах.ДЕЙСТВИЕ И РЕАКЦИЯ
Технический термин действие является историческим пережитком 17-го века. века, прежде чем были поняты энергия и импульс.В современном терминологии, действие имеет размерность энергия × время. Планка константа имеет эти размерности, и поэтому иногда называется Планковский квант действия . Пары измеримых величин произведение которых имеет размерность энергия × время, называются сопряженных величин в квантовой механике, и имеют особое отношение друг к другу, выраженное в принцип неопределенности. К сожалению слово действие сохраняется в элементарном
учебники бессмысленными формулировками третьего закона Ньютона: «Действие
равняется реакции. «Этот заученный лозунг бесполезен для современного студента,
кто не имеет ни малейшего представления о том, что такое действие. Спросите у ученика, кто
запомнил этот лозунг для определения «действия» и «реакции». Если
вы не можете определить что-то, вы не можете использовать это разумно. То
Самая полезная формулировка третьего закона Ньютона такова:
«Если тело А действует на тело В с силой, то тело В действует и равно
размер, но противоположно направленная сила на A.”
«Этот заученный лозунг бесполезен для современного студента,
кто не имеет ни малейшего представления о том, что такое действие. Спросите у ученика, кто
запомнил этот лозунг для определения «действия» и «реакции». Если
вы не можете определить что-то, вы не можете использовать это разумно. То
Самая полезная формулировка третьего закона Ньютона такова:
«Если тело А действует на тело В с силой, то тело В действует и равно
размер, но противоположно направленная сила на A.”
Использование терминов «действие» и «реакция» также дает ложное
создается впечатление, что «действие» имеет какой-то первичный статус и
«реакция» — это вторичный «эффект», возникающий в результате действия силы.Это заблуждение является следствием
«причинно-следственное» мышление (см. в другом месте этого документа). Два
силы пары действия и противодействия имеют совершенно равноправный статус, и
ни одно из них не следует рассматривать как причину или следствие другого.
Оба они являются следствием физических явлений. которые вызывают силы, такие как упругие свойства материалов,
гравитационное притяжение, электрические или магнитные взаимодействия и т. д.
которые вызывают силы, такие как упругие свойства материалов,
гравитационное притяжение, электрические или магнитные взаимодействия и т. д.
| Взвешивание моля. |
|---|
НОМЕР AVOGADRO
Постоянная Авогадро имеет единицу измерения моль -1 . Это , а не просто число, и следует ли , а не называть номером Авогадро. — это . Можно сказать, что число частиц равно . в грамм-моле 6,02252 х 10 23 . В некоторых старых книгах это значение называется числом Авогадро . и когда это сделано, к нему не прикрепляются никакие подразделения. Это может быть сбивает с толку и вводит в заблуждение учащихся, которые добросовестно пытаются чтобы узнать, как сбалансировать единицы в уравнениях. Один должен указать, будет ли значение постоянной Авогадро
выражается для
грамм-моль или килограмм-моль. Несколько книг предпочитают килограмм-моль. Название единицы измерения грамм-моль просто моль .
Название единицы килограмм-моль кмоль .
Когда используется килограмм-моль, постоянная Авогадро должна
можно записать: 6,02252 x 10 26 кмоль -1 . Факт
что постоянная Авогадро
единиц, убеждает нас в том, что это , а не , «просто
номер.”
Название единицы измерения грамм-моль просто моль .
Название единицы килограмм-моль кмоль .
Когда используется килограмм-моль, постоянная Авогадро должна
можно записать: 6,02252 x 10 26 кмоль -1 . Факт
что постоянная Авогадро
единиц, убеждает нас в том, что это , а не , «просто
номер.”
Хотя это кажется непоследовательным, базовой единицей СИ является грамм-моль. Как напомнил мне Марио Иона, СИ — это , а не , это система МКС. Некоторые учебники по-прежнему предпочитают использовать килограмм-моль или, что еще хуже, используйте его и грамм-моль. Это влияет на их указанные значения универсальной газовой постоянной. и постоянная Фарадея.Является ли постоянная Авогадро просто числом? А как же эти учебники которые говорят: «У вас может быть моль из звезд, песчинок или людей»? В науке мы делаем используем сущности, которые просто чисел, например p и e (основание натуральных логарифмов).
 Хотя эти используются в науке, их определения независимы от науки . Ни один научный эксперимент не может никогда
определить их стоимость, кроме приблизительно. постоянная Авогадроса,
однако должно быть определено экспериментально, например считая количество атомов в кристалле. Значение
Число Авогадро, найденное в справочниках, – это экспериментально .
определенное число. Вы не обнаружите его ценность экспериментально,
считать звезды, песчинки или людей.Вы найдете его только по
подсчет атомов или молекул в чем-либо с известной относительной молекулярной массой.
И вы не обнаружите, что это играет какую-либо роль в каком-либо уравнении или теории о
звезды, песок или люди.
Хотя эти используются в науке, их определения независимы от науки . Ни один научный эксперимент не может никогда
определить их стоимость, кроме приблизительно. постоянная Авогадроса,
однако должно быть определено экспериментально, например считая количество атомов в кристалле. Значение
Число Авогадро, найденное в справочниках, – это экспериментально .
определенное число. Вы не обнаружите его ценность экспериментально,
считать звезды, песчинки или людей.Вы найдете его только по
подсчет атомов или молекул в чем-либо с известной относительной молекулярной массой.
И вы не обнаружите, что это играет какую-либо роль в каком-либо уравнении или теории о
звезды, песок или люди.ПОТОМУ ЧТО
Потому что — это слово, которого лучше избегать в физике. Всякий раз, когда он появляется можно быть почти уверенным, что это слово-заполнитель в предложении которое не говорит ничего стоящего, или слово, используемое, когда не можешь придумать уважительная или конкретная причина. В то время как использование слова , потому что как
звено в цепочке логических шагов доброкачественное, его все равно следует заменить
со словами, более конкретно указывающими на тип ссылки, которая имеется в виду.
В то время как использование слова , потому что как
звено в цепочке логических шагов доброкачественное, его все равно следует заменить
со словами, более конкретно указывающими на тип ссылки, которая имеется в виду.Иллюстративная басня: Искатель истины искал мудрости у Гуру, который жил отшельником на вершине гималайской горы. После долгого и трудный подъем на вершину горы искателю была дарована аудиенция. Сидя у ног великого Гуру, искатель смиренно сказал: «Пожалуйста, ответь мне на вечный вопрос: “Почему?” Гуру поднял глаза на небо, немного помедитировал, затем посмотрел ищущему прямо в глаза и ответил, с видом проницательной глубины, “Потому что!”
ПРИЧИНА И СЛЕДСТВИЕ
Многие считают, что некий «закон причины и следствия» является очень важным принципом. в науке.Философы науки основательно разрушили это наивное представление. Но учителя по-прежнему задают двусмысленные вопросы, такие как «Какая сила вызывает ускорение автомобиля вперед?» Один действительный ответом будет: «Сила, с которой нога действует на педаль акселератора».
Студенты до сих пор думают, что «Каждое следствие имеет причину» и «Причина предшествует эффекту» являются глубокими утверждениями. Правда, некоторые события физически связаны так, что одно всегда предшествует другому.Нам нравится называть более ранний набор событий причиной более поздних событий. Но на самом деле заявления о причине и эффект производится только “постфактум”, после уточнения конкретных деталей связности событий найдены и поняты. Навешивание ярлыков на «причину» и «следствие» совершенно не имеет значения для учить что-либо о природе и бесполезно строить логические рассуждения о природе. Мы ничего не теряем, вычищая эти слова из научные дискуссии.Избегание этих слов заставляет нас выражать себя более ясным и точным языком, и это хорошо.
Такой язык мало вредит, когда мы говорим о событиях в пределах наблюдаемой вселенной.
Но когда кто-то пытается ссылаться на это как на философский/физический принцип, получается бессмыслица.
Один из примеров запутанного мышления, возникающего из-за языка причин и следствий. этот глупый аргумент все еще крутится вокруг:
этот глупый аргумент все еще крутится вокруг:
Все, что происходит во Вселенной, имеет определенную причину.Мы знаем без исключений. Следовательно, сама Вселенная должна была иметь причину, и что причиной был Бог.Примечательно то, что люди, которые говорят это или принимают это как «аргумент», кажется, думаю, что это действительно и глубоко. Это ни то, ни другое. Даже если для ради аргумента, мы принимаем предпосылку, это необоснованная экстраполяция от наблюдений за вещами во вселенной к чему-то «вне» Вселенная, независимая от Вселенной и предположительно не связаны теми же законами, которые действуют в Вселенная.Тем не менее, я слышал людей с докторской степенью (которые должны знать лучше) представить этот аргумент, как если бы он имел большой вес. Последняя фраза логический скачок, ведь даже если бы мы могли установить, что у Вселенной есть причина, мы даем этой причине имя только в том случае, если утверждаем, что это был «Бог». (или любое другое придуманное имя).
 Насколько нам известно, причина может быть в чем-то другом, но у нас нет возможности узнать.
Насколько нам известно, причина может быть в чем-то другом, но у нас нет возможности узнать.В этой мошеннической псевдологике есть еще один недостаток. Это экстраполяция нашей несовершенной и, возможно, ошибочной науки к заключению что человек, приводящий аргумент, рассматривает как абсолютную и непогрешимую истину.Это возражение также опровергает все аргументы, которые, как я видел, сторонники так называемых «научных креационистов» и «разумного замысла».
Становится хуже. Во Вселенной причины всегда предшествуют следствиям во времени.
Когда это применяется к тео-алогичному аргументу, и если у вселенной была «причина», тогда все во вселенной и все, что происходит во вселенной, являются «следствиями».
Пространство, время, материя, суперструны, черные дыры и все остальное — «следствия» этой гипотетической «причины».Само время есть следствие этой причины.
Поскольку причинно-следственная связь требует, чтобы два события происходили в разное время, как может
причина (или следствие) имеют какое-либо значение вне времени?
Эта ненужная путаница проникла в дискуссии о «происхождении» и
породил невероятное количество слов впустую по бессмысленным вопросам.
РЕФИКАЦИЯ
Овеществление означает «сделать реальным». Слово используется в философии. описать процесс, с помощью которого мы относимся к определенным наши умственные конструкции, как если бы они были так же реальны, как камни, вода и деревья.Мы говорим о «любви» и «патриотизме», «добре», «зле» и “душа”, как если бы они были чем-то, что можно определить с помощью медицинских экспертиза. Какое определение для слова “настоящий”? Это скользко, слишком. По этому вопросу написаны целые книги. Не вдаваясь в глубокую философию, просто укажем на некоторые
опасности овеществления в преподавании физики. Некоторые вещи
в каком-то смысле реален почти каждый (кроме извращенно спорящего
человек) согласились бы действительно являются “настоящими”.Это понятия непосредственно
доступным для нашего сенсорного аппарата и частью нашего общего
опыт. Камни, вода и деревья подходят. Они также
доступным для прямого и точного измерения с помощью измерительных
инструменты или аппарат. Возможно, несколько менее «реальными» являются силы
и температура. Наше чувственное восприятие их в лучшем случае грубо,
и косвенные – в значительной степени зависят от условий и окружающей среды
переменные. Измерительные приборы и методы измерения дают
последовательные результаты, поэтому мы рассматриваем их как реальные в физике, но мы
не доверяйте нашим невооруженным чувствам точную информацию о них.
Возможно, несколько менее «реальными» являются силы
и температура. Наше чувственное восприятие их в лучшем случае грубо,
и косвенные – в значительной степени зависят от условий и окружающей среды
переменные. Измерительные приборы и методы измерения дают
последовательные результаты, поэтому мы рассматриваем их как реальные в физике, но мы
не доверяйте нашим невооруженным чувствам точную информацию о них.
Можно также провести различие между материальными понятиями и свойств материалов. Масса, расстояние и время обычно считается настолько основным, что его можно квалифицировать как «вещи» природы (но я мог бы легко оспорить это). Однако цвет, температура и твердость являются свойствами материалы, а не «вещи» сами по себе.
Энергия и импульс не являются свойствами, присущими конкретному материалу.
но полезные концепции, которые мы изобрели, которые помогают нам описать, как вещи
взаимодействовать.Сама по себе энергия не имеет материального существования. Вы не можете поместить чистую энергию
в бутылке; вы можете ставить только материальные вещества, которые имеют энергию в эту бутылку.
Вы не можете поместить чистую энергию
в бутылке; вы можете ставить только материальные вещества, которые имеют энергию в эту бутылку.
Затем есть такие понятия, как линии поля и световые лучи. Они также не имеют материального существования, но помогают нам описывать то, что мы наблюдаем. В следующих нескольких разделах обсуждаются опасности их лечения. как настоящий.
| Обрезка линий поля. |
|---|
ЛИНИИ ПОЛЯ РЕЗКИ
В некоторых книгах говорится о разрезании линий поля.Это вызывает образы резки строк с ножницами. Фактически в начале 20-х гг. В учебниках века часто говорилось о «количестве» линий поля, исходящих от единицы заряда, как будто их можно было сосчитать. [В системе cgs это было 4п силовых линий от единичного заряда, на случай, если ты уход.] Это явный случай вводящего в заблуждение овеществления.ИЗГИБАЮЩИЕ СВЕТОВЫЕ ЛУЧИ
В учебнике сказано: «Световые лучи изгибаются на границе раздела сред. с разным показателем преломления». Здесь изгиб представляет собой разрыв
направления статического рисунка световых лучей.Мы должны помнить
что эти линии являются лишь геометрической конструкцией, помогающей нам
визуализировать направление распространения световой энергии, а не
что-то столь же реальное, как движущийся автомобиль. Вейвлеты Гюйгенса
другой случай овеществления, так как они только геометрические
конструкции для осуществления вычислительного процесса.
с разным показателем преломления». Здесь изгиб представляет собой разрыв
направления статического рисунка световых лучей.Мы должны помнить
что эти линии являются лишь геометрической конструкцией, помогающей нам
визуализировать направление распространения световой энергии, а не
что-то столь же реальное, как движущийся автомобиль. Вейвлеты Гюйгенса
другой случай овеществления, так как они только геометрические
конструкции для осуществления вычислительного процесса.ЭНЕРГИЯ
Энергия не является материальной субстанцией. При взаимодействии тел энергия одного может возрастать за счет другое, и это иногда называют передачей энергии .Этот означает ли , а не , что мы могли бы перехватить эту энергию в пути и разлить по бутылкам. После передачи одно из тел может иметь более высокую энергии, чем раньше, и мы говорим об этом как о «накопленной энергии». Но затем не означает, что энергия «содержится в нем» в том же смысле, что и вода в ведре. Пример неправильного использования: “Полярное сияние Земли” северное и южное
огни иллюстрируют, как энергия солнца распространяется на нашу планету». [ Science News, 149 , 1 июня 1996 г.].Эта фраза размывает понимание
процесса взаимодействия энергичных заряженных частиц Солнца
с магнитным полем Земли и нашей атмосферой, чтобы
полярные сияния.
[ Science News, 149 , 1 июня 1996 г.].Эта фраза размывает понимание
процесса взаимодействия энергичных заряженных частиц Солнца
с магнитным полем Земли и нашей атмосферой, чтобы
полярные сияния.
Всякий раз, когда вы слышите, как люди говорят об «энергетических полях», «психической энергии», и другие выражения, рассматривающие энергию как «вещь» или «вещество», вы знаете, что они не говорят о физике; они говорят о самогоне.
Утверждение «Энергия есть свойство, связанное с телом».
нуждается в уточнении.В виде
со многими вещами в физике размер энергии зависит от выбранного
система координат. Тело, движущееся со скоростью V в одной системе координат, имеет
кинетическая энергия ½ мВ 2 . Это же тело имеет нулевую кинетическую
энергии в системе координат, движущейся вместе с ней со скоростью V. Поскольку никакая
инерциальную систему координат можно считать «специальной» или «абсолютной», мы
не следует говорить: «Кинетическая энергия тела равна. ..», а следует
сказать: «В
кинетическая энергия тела, движущегося в этой системе отсчета, равна …”
..», а следует
сказать: «В
кинетическая энергия тела, движущегося в этой системе отсчета, равна …”
Мы даже не должны называть энергию или импульс «свойствами тела». Такие физические понятия полезны для занятий физикой, но суть заключается в том, что они всего лишь абстракции от геометрии, массы и движения тело или частицы, из которых состоит тело.
Крутящий момент представляет ту же трудность. Крутящий момент не является уникальным свойство силы, но также зависит от местоположения произвольно выбранный центр моментов.
ЗЛОУПОТРЕБЛЕНИЕ НАРКОТИКОВ
Теплота, как и работа, является мерой количества энергии. перенес из одного тела в другое из-за температуры разница между этими телами. Тепло — это , а не энергия. обладал телом. Мы должны , а не говорить о «тепловом в тело.” Энергия, которой тело обладает из-за его температуры, является другая вещь, называемая внутренней тепловой энергией . Тепловая энергия является внутренней по отношению к телу и не зависит от координаты. система.Это кинетическая энергия движения микроскопических частиц из которых состоит тело.Неправильное употребление слова «тепло» восходит, вероятно, к 18 веку, когда еще считалось, что тела, подвергающиеся тепловым процессам, обмениваются веществом, называемым калорийность или флогистон , вещество, позже названное тепло . Теперь мы знаем что тепло не является веществом. Ссылка: Zemansky, Mark W. Использование и неправильное использование слова «тепло» в преподавании физики» The Physics Учитель, 8 , 6 (сентябрь 1970) с.295-300.
РАДИОАКТИВНЫЙ (Вы сцинтилляционный?)
Радиоактивность – это процесс , а не вещь , а не вещество . Так же неправильно скажем, «U-235 излучает радиоактивность», то есть «течет ток». А неисправный ядерный реактор не выделяет радиоактивность , хотя он может выбрасывать радиоактивные материалы в окружающую среду окружающая обстановка. Пациент, получающий лучевую терапию, не поглощает радиоактивность , но поглощает часть излучение (альфа, бета, гамма), испускаемое радиоактивным используемые материалы.Это неправильное использование слова радиоактивность заставляет многих людей неправильно думать о радиоактивности как о чем-то, что можно получить путем нахождение рядом с радиоактивными материалами. Есть только один процесс который ведет себя как угодно, и это называется искусственно наведенным радиоактивность , процесс, в основном проводимый в исследовательских лабораториях. Когда некоторые материалы бомбардируются протонами, нейтронами или другими ядерными частицы соответствующей энергии, их ядра могут трансмутироваться, создавая нестабильные изотопы, которые являются радиоактивными.
УМЕНЬШИТЬ
Отрезание и удаление части предмета уменьшает его масса (уменьшает оставшуюся массу). Добавление резистора в серию цепочка резисторов уменьшает ток. В чем здесь опасность? Многие студенты думают, что «уменьшение тока» означает, что текущий «Выход» из резистора меньше, чем «входящий» ток. Но действующие законы Кирхгофа уверяют нас что токи, входящие и исходящие из компонента в цепи постоянного тока, равны в любой момент. Проблема здесь отчасти одна «овеществления» абстрактного понятия тока.«Уменьшение» — это изменение, наблюдаемое между двумя различными цепями , одна с дополнительный резистор, один без него. Это не сокращение, наблюдаемое между две точки той же цепи . У нас похожие проблемы, когда говоря о «падении напряжения» на резисторе. Назвать это «разность потенциалов» на резисторе с меньшей вероятностью вызовет спутанность сознания.ВЗВЕШИВАНИЕ
Когда мы используем чашечные весы для определения массы, мы называем этот процесс “взвешивание”, хотя весы дают ответы в единицах массы.Некоторые весы дают ответы в единицах веса, так как они соотношение в данной лаборатории. Термин «взвешивание» оправдан потому что процесс зависит от гравитационного притяжения земля на телах. Мы сравниваем их вес. Студентам нужно знать об этом. Я не призываю избегать термина «взвешивание». Некоторые предложили название «массирование», которое я считаю довольно уродливый.| Провод под напряжением становится соком. |
|---|
ЗАРЯДКА A
КОНДЕНСАТОР, ЕМКОСТЬ Емкость конденсатора равна измеряется следующей процедурой: поместите заряды одинаковой величины и противоположные знак на конденсаторе пластин, а затем измерить потенциал между пластинами.потом С = |Q/V| , где Q — заряд на одной пластины.
Конденсаторы для использования в цепях состоят из двух проводников (пластин). Мы говорим о конденсаторе как о «заряженном», когда он имеет заряд Q на одном заряде. пластине и -Q на другой. Конечно, чистый заряд всего объект нулевой; то есть заряженный конденсатор не имел сети заряд добавлен к нему, но подвергся внутреннему разделению обвинение. К сожалению, этот процесс обычно называют зарядка конденсатора, что вводит в заблуждение потому что он предлагает «добавить заряд в конденсатор».На самом деле это процесс состоит только в перемещении заряда от одного конденсатора пластина к другой.
Вероятно, нам следует избегать фразы «заряженный конденсатор» или «зарядка конденсатора». Некоторые предложили альтернативу выражение «подключение конденсатора», потому что процесс приводит к увеличению электрического заряда конденсатора. потенциальной энергии путем перестановки зарядов на ней.
Емкость отдельного объекта, скажем изолированной сферы, равна определяется, рассматривая его как одну пластину конденсатора и другая пластина должна быть бесконечной сферой, окружающей ее.Объект получает заряд, движущийся заряд из бесконечной сферы, который действует как бесконечный резервуар заряда («земля»). То потенциал объекта есть потенциал между объект и бесконечная сфера. На практике «другая тарелка» — это окружающую лабораторную среду.
Емкость зависит только от геометрии конденсатора. физическая структура и диэлектрическая проницаемость материала среда, в которой существует электрическое поле конденсатора.Размер емкость конденсатора одинакова независимо от его заряда и потенциал (при условии, что диэлектрическая проницаемость не меняется). Этот верно, даже если заряд на обеих пластинах уменьшен до нуля, и поэтому потенциал конденсатора равен нулю. Если конденсатор с заряд на его обкладках имеет емкость, скажем, 2 мкФ, то его емкость также 2 мкФ, когда пластины не имеют заряда. Это должно напомнить нам, что С = |Q/V| ; является не само по себе определение емкости, а просто формула, которая позволяет нам связать емкость с заряд и потенциал , когда обкладки конденсатора имеют заряды одинакового размера и противоположного знака.
ЕМКОСТЬ
Вместимость контейнера – это количество того, что он вмещает. Это разговорное значение слова. Но как это часто бывает, разговорные слова перенимаются как технические слова, с более конкретными, или измененное значение.Слово емкость используется в названиях физических величин. которые выражают относительную сумму одного количества по отношению к другой величине, от которой она зависит. Например, теплоемкость dU/dT , где U — внутренняя энергия и T температура.Электрическая емкость (обычно называемая емкостью) С = |dQ/dV| где Q – величина заряда на каждой пластине, В – разность потенциалов между пластинами. Это правильное техническое использование слова. Ни один из них не имеет ничего общего с максимальной суммой, которую что-то удержит.
Обычно мы избегаем путаницы, называя C «емкостью».Распространенным заблуждением относительно электрической емкости является предположение, что эта емкость представляет собой максимальное количество заряда конденсатор может хранить. Это вводит в заблуждение, потому что конденсаторы не хранят заряд (их общий заряд равен нулю), но их пластины имеют заряды одинаковой величины и противоположного знака. Это неправильно, потому что максимальный заряд можно положить на пластину конденсатора, определяется потенциалом на при котором происходит пробой диэлектрика.
Но те же заблуждения могут возникнуть и с электрической емкостью. как и в других случаях использования слова «емкость» в физике, и мы у них нет других имен, которые могли бы помочь избежать этого.Теплоемкость не является максимальным количеством тепла что-то может иметь. Это было бы также неправильно предполагают, что тепло – это «вещество», а это не так.
РОКОВОЕ ВЛЕЧЕНИЕ
Слушаем ли мы то, что говорим? Думаем ли мы о том, что говорим? Действительно ли мы верим в то, что говорим? Студенты верят? Может быть, они не должны. Вот пример, чтобы проверить это.| Левитация? |
|---|
Рассмотрим пустую кофейную чашку на иллюстрации. если ты действительно поверил утверждению предыдущего абзаца вы бы проанализировали это таким образом. Центр чашки масса находится где-то внутри пустой части, в точке C. Теперь бросьте маленький предмет В, скажем, камешек или монету, чтобы он упал в эту точку. По мере приближения к точке расхождение центров масс чашки и галька становится очень маленькой и сила притяжения между становится очень большим, пока не станет преобладать над силой гравитация земли.Камень будет колебаться вокруг точки С, или еще хуже, остановитесь в точке C (потому что сила 1/r 2 становится бесконечным при r = 0). Тогда камешек просто висит там приостановлено, и для его удаления потребовалась бы бесконечная сила. Абсурд? Конечно; поскольку заявление, сделанное в предыдущем абзаце было абсурдно.
Ключевая фраза была исключена из нашей версии утверждения о гравитационная сила и центр масс, как это часто встречается во многих учебниках.Принцип, выведенный Ньютоном, относился к сферическим телам со строго симметричное распределение масс относительно их центров масс, и это применяется только к отдельным массам, а не к смежным.
Иногда слова, которые мы пропускаем, так же важны, как и те, которые мы вставляем. Следующий пункт иллюстрирует ту же ошибку.
ВСЕГДА ТРЕНИЕ ПРОТИВ ДВИЖЕНИЯ?
Утверждение «Трение всегда препятствует движению» не указывает , что движение.В более полной форме это: «Сила трения действует в направлении, препятствующем скольжению в соприкасающихся поверхностей, и действует вдоль касательной плоскости соприкосновения поверхностей». Или: «Трение противодействует относительному движению двух соприкасающихся поверхностей». Слишком часто студенты думают, что сила трения, действующая на тело выступает против любого движения это тело. Повседневные примеры показывают, что это неправильно. Сила трения о дорогу действует на автомобильные шины вперед, по направлению движения автомобиля вперед движение, когда автомобиль движется с постоянной скоростью или ускоряется вперед.Предотвращает проскальзывание шин на дороге, которое вы обнаружите при езде по лед. Это сила, которая поддерживает движение вперед. Другой пример: сила трения пол на ваших ногах находится в направлении, в котором вы идете.РАБОТА ТРЕНИЕМ
Одной из опасностей отношения к силе как к объекту является распространенное хрестоматийная ошибка, говорящая о «работе, совершаемой трением». Работа, совершаемая над объектом, есть произведение расстояния, на которое он перемещается, и сила, действующая на него со стороны какого-либо другого объекта.Если два тела соприкасаются, силы реакции между ними имеют составляющие, касательные контактная поверхность. Не трение совершает работу над каждым тела, а сила, с которой одно тело действует на другое тело, что может случиться из-за процессов трения в их интерфейс.Рассмотрим блок, скользящий по плоскости. Во многих учебниках написано, что скользящий блок теряет энергию из-за «работы, совершаемой над ним за счет трения». Но «трение» здесь — движущаяся мишень, постоянно меняющееся граница между телом и плоскостью.Арнольд Аронс давно раздел в его книге «Руководство по вводному преподаванию естественных наук». детализируя Опасности такого обращения с учебниками. Одна очевидная проблема как “изолировать систему” в таких случаях. Часть плоскость, в которой соприкасаются тела, не может быть “прижата” и рассматривается как единая физическая «вещь» во время движения. Обычное лечение учебников имеет очень серьезный недостаток: довольно легко применить и случается, чтобы дать правильные ответы на тщательно отдельные проблемы, поставленные в учебнике.То есть до тех пор, пока студент не думает об этом слишком глубоко.
СИЛА ОТКЛОНЕНИЯ
| Физика отклоняющих сил. Мультфильм Джона Холдена. |
|---|
На языке инженерных и боевых искусств можно услышать термин «отклоненный сила”. У этого термина есть много возможных неправильных толкований, и его лучше избегать если не нужно говорить с людьми, которые используют его в своей специализированной области.Клинкер “дефлект”. Отклонение имеет четкое значение применительно к материальному объекту. Но сила не является материальным объектом. Означает ли «отклонение силы», что сама сила отклоняется? Если да, то изменилась ли сила в направление? Сила отскакивает от чего-то, как стрела отскакивает от костюма? доспехов?
Правильно используемое в технике отклонение силы относится к ситуации, когда массовая нагрузка на объект или систему объектов вызывает реакцию сил, поддерживающих равновесие этого объекта.Распределенные нисходящие силы сжатия по всему изгибу классической арки противостоят более локальные силы в опорные концы арки. Обратите внимание, что при приложении силы к объект, а другая сила регулирует его размер, чтобы поддерживать объект равновесия, другая сила называется «уравновешивающей» (та, которая сохраняет равновесие). Сила и ее равновесие — это , а не реакция. силы друг друга.
В боевых искусствах этот термин, кажется, относится к отражению удара, такого как как удар.Отклоняется не сила, а движение объекта нанесение удара. Смещение цели или приложение силы к часть тела, наносящая удар, может изменить направление удара так что удар теряет меньшую долю своего импульса и энергии для вас. Представь кого-нибудь наносит вам удар, но до того, как удар достигает цели, вы попадаете в руку противника сбоку, отклонив его руку . Или ты меняешь свое тело так вместо этого ударил тебя прямо в нос, его удар просто задел твое плечо, передавая вам лишь небольшую часть своего импульса и энергии.По крайней мере, это как кажется, что эти люди используют этот термин. Они используют «отклоненную силу». означать «отклонить все, что наносит удар, чтобы вы получили меньше его воздействие (импульс и энергия)”.
«Отклоненная сила» также может описывать квазистатическую ситуацию. в котором используются ограничения человеческой мускулатуры. Когда кто-то толкает или поднимает руку, действие может быть становится менее эффективным, если кто-то толкает эту руку в сторону.
СВЯЗАННЫЕ ССЫЛКИ
Аронс, Арнольд Б. Руководство по вводному обучению физике . Уайли, 1990.Аронс, Арнольд Б. Преподавание вводной физики . Уайли, 1997.
Иона, Марио. Учитель физики . Регулярная колонка под названием «Не могли бы вы верить?», которые в течение 24 лет документировали и обсуждали ошибки и вводящие в заблуждение высказывания в учебниках по физике.
Шварц, Клиффорд и Томас Майнер. Введение в физику, Справочник . Американский институт физики, 1997.
Символы, единицы и номенклатура в физике. Из документа U.I.P 11 (SUN 65-3) Международный союз теоретической и прикладной физики. Содержалась в Справочник по химии и физике , Химическая резина Компания.
Уоррен, Дж. В. Преподавание физики . Баттерворта, 1965, 1969.
Текст © 1979, 2002, 2008, Дональд Э.Симанек.
Мультяшные рисунки © 1979, Джон К. Холден.
Еще одна аббревиатура уравнения. Использование математики на уроках физики… | Мэтью Бениохаи
Использование математики на уроках физики уже давно вызывает ужас как у учителей, так и у учеников. Воспринимаемая сложность решения математических задач привела к тому, что учащиеся разработали некоторые очень хорошо продуманные стратегии, которые помогут устранить некоторую двусмысленность и дать учащимся последовательный метод, к которому можно вернуться.
К ним относятся;
Так зачем нам еще один? Четыре вышеуказанных метода имеют одну общую черту; замена перед перестановкой. Есть две основные причины, по которым это так популярно. Во-первых, потому что его предпочитают экзаменационные комиссии. Это раздражало меня в течение некоторого времени, и я не вижу, чтобы это изменилось в ближайшее время. Во-вторых, многие учителя думают, что ученикам это легче. Я не могу комментировать то, что происходит в других классах, но я хотел бы представить аргументы и предварительное предположение о том, что может быть лучший способ.
Для пояснения: в настоящее время я работаю в независимой школе для девочек, где мы ожидаем, что все девочки наберут >6 баллов по физике или комбинированным наукам на экзамене GCSE. Это соответствует требованиям для поступления на курс физики уровня A в большинстве школ, поэтому наша философия заключается в том, что мы готовим всех девочек к дальнейшему изучению физики, если они захотят это сделать. (Однако мы реалисты и знаем, что это не относится к большинству девушек! Однако мы очень гордимся тем, что в настоящее время удваиваем среднее количество учащихся, изучающих A-Level).Используя расширенный анализ результатов AQA, мы можем сравнить наши результаты по конкретным вопросам с результатами других школ. По простым расчетным вопросам наши девочки стабильно выигрывают у аналогичных школ. Здесь есть три оговорки; подобные центры по e-AQA — это просто другие независимые школы, так что это очень широко, использование этого сравнения очень и очень грубо, но это лучшие данные, которые у нас есть, и, наконец, это не предназначено для хвастовства! Есть и другие области, в которых мы недостаточно эффективны по сравнению с другими центрами.Это то, что дает мне немного больше уверенности в том, что наш подход к математике может принести некоторую пользу, и это может быть тем, о чем другие захотят подумать. Контекст — король. Я понимаю, что это может не сработать для всех.
Мы начинаем курс GCSE в 9 классе с Energy. Первые 3 урока включают в себя восстановление запасов энергии и передачи из KS3, а также введение математического подхода к сохранению энергии.
Это разбито на три урока, потому что именно в этот момент мы вводим наши ожидания для вычислений.
- Единицы — запишите все значения в единицах СИ
- Формула — запишите формулу, которая будет использоваться ответ
Некоторые учителя используют мнемонику «вы обыщите вопрос»; другие нет. Некоторые учителя пишут буквы сбоку страницы; другие нет. Все учителя учат перестановке перед заменой.Мы видим преимущества этого подхода;
- Буквы легче переставлять, чем цифры
- Некоторые термины могут отменяться и не нужны (маловероятно на GCSE, но мы показываем им примеры этого)
- Копирование чисел может привести к ошибкам транскрипции используется один раз, что снижает распространение ошибок.
Ожидается, что после этих первых трех уроков все девочки успешно изменят уравнения кинетической и гравитационной потенциальной энергии, которые будут охватывать все элементы, ожидаемые от уравнений GCSE.Хотя они могут совершать ошибки, особенно при попытке сделать это с новыми уравнениями, у них будет два с половиной года, чтобы обрести уверенность и последовательность.
Я надеюсь, что это дает альтернативный взгляд, и я повторяю; контекст это король. Это может не работать для всех, но, возможно, стоит попробовать.
Что означает «r» в уравнениях для силы тяжести и центростремительной силы?
С одной стороны, мне легко ответить:
В уравнении гравитационной силы F = GMm/r , 2 r представляет собой расстояние между центрами двух объектов.Я часто использую переменную d , чтобы подчеркнуть это значение.
В уравнении центростремительной силы F = mv 2 /r r представляет радиус кругового движения.
Эти факты также легко читать и запоминать учащимся. Студентам не так просто применить на практике. Они видят букву r , слышат « радиус, » и вставляют любое случайное расстояние, которое они могут вытащить из проблемного ствола.
И этот
Так какое же это имеет значение, если учащиеся действительно понимают разницу между этими двумя значениями и ? В какой возможной физической ситуации во вводной физике это различие вообще имеет значение? Вот один.
Две звезды, каждая из которых имеет одинаковую массу M , находятся на постоянном расстоянии x друг от друга и вращаются вокруг точки посередине между ними со скоростью один оборот за каждый момент времени t 1 .
(а) Почему две звезды не сталкиваются друг с другом из-за гравитационной силы между ними?
(b) Выведите выражение для массы одной звезды. Используйте только заданные переменные и фундаментальные константы. Вы должны аннотировать свой расчет — если в вашем ответе нет слов, вы переделаете его с нуля на консультации.
Это сложный вопрос для осмысления учащимися, особенно потому, что, хотя мы решали множество простых задач на орбиту, учащиеся очень часто вспоминали успокаивающие алгоритмы и не обязательно усваивали физический смысл. И я не буду отвечать на вопросы учеников, пока они не сдадут его. (Они могут обсуждать и спорить друг с другом столько, сколько захотят!) как это решить. И в этой модели я не буду просто вдаваться в мое решение здесь.Вместо этого я покажу вам тест, с которого я начинаю урок:
Для #1 , r в этом уравнении представляет собой расстояние между центрами двух планет. В задаче сказано явно – звезды всегда находятся на расстоянии 8,0 x 10 10 м друг от друга. (Самое распространенное заблуждение: потому что в каждой задаче, которую они ранее решали, спутник вращается вокруг центральной планеты, они думают, что «точка на полпути» между звездами — это местонахождение какой-то планеты — или что эта «средняя точка» что действует на звезду.)
Для #2 , r в этом уравнении представляет собой радиус орбиты. В задаче прямо сказано, что звезды «вращаются примерно на полпути между собой». Поскольку расстояние между звездами составляет 8,0 x 10 10 м, точка на полпути между ними находится на половине расстояния от одной из звезд, или 4,0 x 10 10 м. (Неправильно, что одна звезда неподвижна, а другая вращается вокруг неподвижной звезды. Проблема не в этом и не в том, как ведут себя двойные звезды.И половина 8,0 x 10 10 м не означает деление показателя степени на два: половина 80 миллиардов метров точно не 4 сотни тысяч метров!) знать период кругового движения тела. Это происходит из-за того, что орбитальная скорость постоянна – для постоянной скорости скорость – это расстояние/время. Релевантным временем здесь является период, время одного оборота. Соответствующее расстояние, таким образом, является окружностью круговой орбиты.Из класса геометрии эта длина окружности равна 2 πr , где r — радиус окружности. Нам нужно то же расстояние, что и в номере 2, радиус орбиты 4,0 x 10 10 м .
Для #4 отвлекающие факторы практически дословно взяты из прошлых ответов учащихся. Обсуждая викторину, я выбираю неверный ответ, чтобы объяснить, почему он неверен:
Для (A) сначала мы обсудим и согласимся с тем, что гравитационные силы на каждой звезде действительно представляют собой пару сил по третьему закону Ньютона.Затем я подхожу к парте студента, даю студенту веревку и дергаю*. Равна ли моя сила на мистера Чемберлена силе мистера Чемберлена на меня? Так это силовая пара N3L? да. Мы вращаемся вокруг друг друга по кругу? Нет. Значит, логика выбора (А) вовсе не логика.
*В прежние времена я брал студента за руку и слегка тянул.
Затем я прошу учащихся закрыть глаза. Все, кто выбрал этот неверный ответ, поднимите руки вверх.Теперь опустите руки и откройте глаза. Суть в том, чтобы учащиеся признали свои заблуждения. Ничего страшного, что они допустили ошибку — в конце концов, в моем классе все получают пятерки до экзамена AP, тесты даются и оцениваются, но не «засчитываются». Я не хочу, чтобы студенты чувствовали стыд за свою ошибку. Но что более важно, я не хочу, чтобы они в стиле кислого винограда убеждали себя, что они знали это и что на самом деле они не ошибались. Нет. Признайте заблуждения и не делайте их больше!
Для (B) сначала мы обсудим и согласимся с тем, что гравитационные силы на каждой звезде действительно представляют собой пару сил третьего закона Ньютона.Я снова подхожу к парте ученика, даю ученику веревку и дергаю. Силы на каждого из нас равны. Мы вращаемся вокруг друг друга? Нет? Тогда (В) неверно.
Для (D) я прошу ученика указать на среднюю точку между нами. Только объекты могут оказывать воздействие… так какой же объект в «средней точке» может оказывать воздействие? Нет объекта. Так что (Д) ошибается.
И, наконец, для правильного выбора (С) я рисую две звезды, вращающиеся по орбите. Я рисую направление мгновенной скорости одной звезды, касательной к орбите.Я спрашиваю о направлении чистой силы на этой звезде, которая направлена к центру. Все видят, что скорость действительно перпендикулярна результирующей силе. И мы обсуждаем, как это переформулирует один из наших фактов о круговом движении: когда объект движется с постоянной скоростью по кругу, его ускорение направлено к центру круга. Скорость всегда будет касательной к окружности, которая по геометрии перпендикулярна направлению к центру.
— Викисловарь
Определение из Викисловаря, бесплатного словаря
Перейти к навигации Перейти к поискуТранслингвальный[править]
Альтернативные формы
- (МФА глухая альвеолярная аффриката): ʦ, ts
Символ[править]
тс
- Используется не в переносном или идиоматическом смысле: см. t, s.
- Английское слово «ca ts » произносится как /kæ ts /.
- (IPA) глухая альвеолярная аффриката
- используется в латинизации:
- иврита ץ \ צ («цади», «цади», «цади», «ṣāḏē») в схеме транслитерации Еврейской академии 2006 года
- на иврите צּ («цади», «цади», «ẕadi», «ṣāḏē ḥāzāq») в схеме транслитерации Еврейской академии 2006 года
Синонимы[править]
- (латинизация ץ \ צ, «цади», «цади», «ẕadi», «ṣāḏē»): tz (общеизраильская схема транслитерации), ẕ (схема транслитерации Еврейской академии 1953 г.), ṣ (схема транслитерации ISO 259)
- (латинизация צּ, «цади», «цади», «цади», «ṣāḏē ḥāzāq»): tz (общая израильская схема транслитерации), ẕẕ (схема транслитерации Еврейской академии 1953 г.), ṣṣ (схема транслитерации ISO 259)
См. также[править]
английский[править]
Существительное[править]
тс
- множественное число от t
Замечания по использованию[править]
- Существуют некоторые расхождения во мнениях относительно использования апострофов во множественном числе ссылок на буквы как символы. New Fowler’s Modern English Usage , отметив, что использование изменилось, на странице 602 говорится, что «после букв обязателен апостроф». В 15-м издании Чикагского руководства по стилю в параграфе 7.16 говорится: «Во избежание путаницы строчные буквы … образуют множественное число с апострофом и буквой s». Оксфордское руководство по стилю на стр. 116 рекомендует руководствоваться здравым смыслом.
Анаграммы[править]
Норвежский букмол[править]
Существительное[править]
тс
- Сокращение от teskje или teskei
Норвежский нюнорск[править]
Существительное[править]
тс
- Сокращение от teskei .
Почему нам пришлось изменить смысл ничего – Наутилус
«Ничто» в физике — это нечто. Фото www.cafecredit.com / Flickr
Ничего» уже не то, что раньше. Раньше это было чем-то самоочевидным: противоположностью или отсутствием чего-то. Конечно, мы до сих пор используем это слово в разговорной речи. Когда на тротуаре меня спрашивают, могу ли я оставить мелочь или доллар, я говорю, если у меня нет ни того, ни другого: «Извините, у меня ничего нет.
Но этот термин не имеет особого смысла в науке — по крайней мере, сейчас. «Ничто» раньше принималось за пустую пустоту, пространство, в котором не существует частиц. Этот образ мышления работает на деньги. Они либо есть в вашем кошельке или банке, либо их нет. Но это не работает с материей, энергией, пространством и временем. «Ничто» в физике — это действительно что-то.
Космолог и физик-теоретик Лоуренс Краусс получил некоторую негативную реакцию на это новое определение.Его книга 2012 года « Вселенная из ничего: почему существует нечто, а не ничто» казалось, судя по названию, готовой ответить на извечный и сбивающий с толку вопрос: почему существует что-то, а не ничто? Но то, что он предложил, выглядело для некоторых концептуальной ловкостью рук: вместо ответа на вопрос он определял «ничто» вне существования!
«Некоторых людей расстраивает, что мы меняем значение слова «ничего», — сказал он нам в интервью Ingenious, когда мы спросили, не избегает ли он вопроса, — но мы изменили значение света, когда поняли, что фотонов.Я имею в виду, что это действительно то, чему учится». Старое определение «ничто» — Краусс называл его «то, из чего только Бог может что-то создать» — в любом случае не годилось для продолжения. Когда-то считалось общепринятым мнение, что ничего подобного не окружало нашу галактику, прежде чем мы узнали, что там есть другие, сказал он. Тем не менее, «такое ничто создает что-то все время , потому что элементарные частицы появляются и исчезают из этого ничего все время — они называются виртуальными частицами.
Так почему бы не изменить определение? «Теперь мы понимаем, — сказал он, — что «ничто» — очень тонкое понятие». Посмотрите, почему, в этом клипе нашего разговора с Крауссом ниже:
Вы можете посмотреть весь наш разговор с ним здесь.
Брайан Галлахер — редактор Facts So Romantic, блога Nautilus . Подпишитесь на него в Твиттере @brianga11agher.
Получить информационный бюллетень Nautilus
Самые свежие и популярные статьи доставляются прямо на ваш почтовый ящик!
Новости о собаках: Колли замечают, когда компьютерная анимация нарушает законы физики Ньютона
Собаки, кажется, понимают, как должны вести себя объекты, и смотрят дольше, если анимированные мячи нарушают ожидания, откатываясь без видимой причины
Жизнь 22 декабря 2021 г.Криста Лесте-Лассер
Собака, участвующая в исследовании
Руберт Байер
Когда трехмерные анимированные мячи на экране компьютера бросают вызов определенным законам физики, собаки ведут себя так, будто им кажется, что их глаза обманывают их.
Домашние собаки смотрят дольше, а их зрачки расширяются, если виртуальные мячи начинают катиться сами по себе, а не приводятся в движение при столкновении с другим мячом. Это говорит о том, что животные удивлены тем, что шарики не двигаются так, как они ожидали, — говорит Кристоф Фёльтер из Университета ветеринарной медицины в Вене.
«Это отправная точка для обучения», — говорит Фёльтер. «У вас есть ожидания относительно окружающей среды — закономерности в вашей среде, которые связаны с физикой, — а затем происходит что-то несоответствующее.А теперь обратите внимание. А теперь попробуй понять, что происходит».
Человеческие младенцы, начиная примерно с 6-месячного возраста, и шимпанзе дольше смотрят во время таких тестов на «нарушение ожиданий», касающихся их физического окружения, говорит он.
Исследования на людях также показали, что зрачки расширяются больше в ответ на повышенные умственные усилия, такие как вычисления, или более сильные эмоции, такие как волнение или удивление, известные как психосенсорная реакция зрачков. И предыдущие исследования на собаках намекнули, что их зрачки расширяются больше, когда они смотрят на злые человеческие лица, чем на счастливые.
Фёльтер и его коллега Людвиг Хубер из Университета ветеринарной медицины решили посмотреть, как собаки воспринимают анимированные катящиеся мячи, которые не всегда подчиняются основным законам контактной физики. Они обучили 14 взрослых домашних собак — в основном бордер-колли, лабрадоров-ретриверов и смешанных пород — класть голову на подставку для подбородка перед экраном компьютера и оборудованием для отслеживания глаз. Затем они показывали животным короткие видеоролики в случайном порядке с движущимися цветными 3D-мячиками.
В одном видео мяч катится ко второму, неподвижному мячу, а затем врезается в него.Первый шар останавливается, а второй начинает двигаться — как описывают законы движения Ньютона. В другом видео, однако, первый мяч катится ко второму мячу, но внезапно останавливается, не долетев до него. И тут второй шар вдруг начинает катиться сам по себе — вопреки основным физическим принципам.
Подобно человеческим младенцам и шимпанзе, собаки дольше фиксировали взгляд на шарах, которые не двигались логическим образом, говорит Фёльтер. Однако еще более убедительной была реакция их зрачков: они постоянно рассматривали «неправильные» сценарии с более расширенными зрачками, предполагая, что это противоречило их ожиданиям.
Это не означает, что собаки обязательно понимают физику с ее сложными вычислениями, говорит Фёльтер. Но это предполагает, что у собак есть неявное понимание своего физического окружения.

 1.5. lim ~un
= ~v
1.5. lim ~un
= ~v