Урок в 10-м классе по теме “Правила дифференцирования” (алгебра и начало анализа)
- Лагойда Светлана Ивановна
Разделы: Математика
Учебник: А.Г. Мордкович “Алгебра и начала анализа, 10-11 кл.”
Технологическая особенность:учащиеся с опережением изучают новый материал по учебнику (§33, п.2). На предшествующем уроке учитель сообщает вопросы к данному параграфу, среди них обязательно один-два вопроса «с изюминкой», это настраивает учащихся на более внимательное изучение теории. (Например, к данному пункту один из вопросов: в чем состоит «уловка» автора при выводе формул?)
Цель урока: создание условий для введения и усвоения правил дифференцирования и их первичного закрепления; для развития информационной компетенции; для воспитания интереса к предмету и стремления выхода на новый уровень в обучении алгебре.
I этап.
Актуализация знаний + обсуждение нового материала1) Вывод правил (3 человека работают у доски – сильные учащиеся)
- производная суммы
- вынесение постоянного множителя за знак производной
- производная произведения
2) Таблица производных (1 человек работает у доски)
3) Тест «Верю – не верю» (остальные учащиеся выполняют на местах)
- Производной функции в точке х0 называется отношение приращения функции к приращению аргумента при Δх → 0.
- С’ = С
- ()’ = 2х
- (sin х )’ = cos х
- (cos х)’ = sin х
- =
- Производная произведения равна произведению производных.
- Постоянный множитель нужно вынести за знак производной.
4) Проверка теста
- до черты (подвести итог по ранее изученному материалу)
- после черты – самопроверка (подвести итог по новому материалу)
5) Знакомство с выводом правил (в сильном классе)
6) Проверка формул (Формулы и правила дифференцирования остаются на боковых досках как опорный материал)
7) Алгоритм нахождения производной: сначала примени одно из правил дифференцирования, затем нужные формулы.
II этап.
Закрепление изученного материала.№737(а), 740(а), 741(а), 743(а), 745(а), 747(а), 749(а).
III этап.
Первичный контроль усвоения изученного материала + рефлексия.Игра «Поле чудес». Учащиеся получают карточки с двумя однотипными заданиями. Выполняют только первое задание (второе задание будет использовано на следующем уроке для организации работы в парах сменного состава («научился сам – научи другого»)). На доске заготовлена таблица и шифр. Учащиеся, выполнив задание, вписывают букву, соответствующую полученному ответу, в клеточку с номером, указанным на карточке. Последнее слово ученики отгадывают, когда заполнены все остальные клетки (это слово – ЕГЭ).
| 1 | 10 | 3 | 2 | 18 | 5 | 19 | 9 | 6 | 13 | 11 | 7 | 20 | 14 | 12 | 8 | 15 | 17 | ||||||
Шифр:
| а | в | г | е | ж | л | н | о | т | у | ч | ь | я | |
| 0 | -2 | -3 | 1 | 2 | 136 | 5 | 4 |
Задания на карточках:
- Найдите значение производной в точке:
- у = + 2х – 1, = 0
- у = – 4 – 3, = -1
- Найдите значение производной в точке х0:
- у = х3 – 3х + 2, х0 = -1
- у = х5 + 9х20 + 1, х0 = 0
- Найдите значение производной в точке х0:
- , х0 = 4
- у =, х0 = 1
- Найдите значение производной в точке х0:
- у = , х0 = 9
- у = , х0 = 4
- Найдите значение производной в точке х
- у = cos x + tg x, x0 = π
- y = ctg x – cos x, x0 =
- Найдите значение производной в точке х0:
- y = (x2 + 3)(x4 – 1), x0 = 0
- y = (x2 – 1)(x4 + 2), x0 = 2
- Найдите значение производной в точке х0:
- y = (x2 – 2)(x7 + 4), x0 = 0
- y = (x2 + 3)(x6 – 1), x0 = -1
- Найдите значение производной в точке х0:
- y = x sin x, x0 =
- y = x tg x, x0 =
- Найдите значение производной в точке х0:
- у = , х0 = 4
- у = , х0 = 9
- Найдите значение производной в точке х0:
- у = , х0 = 1
- у = , х0 = 1
- Найдите значение производной в точке х0:
- у =sin x – cos x, х0 =
- у =2cos x + sin x, х0 =
- Найдите значение производной в точке х0:
- у = , х0 = 1
- у = , х0 = 2
- Найдите значение производной в точке х0:
- у = , х0 = 1
- у = , х0 = 1
- Найдите значение производной в точке х0:
- у = , х0 = 1
- у = , х0 = 1
- Найдите значение производной в точке х0:
- у = , х0 = -1
- у = , х0 = 1
- Найдите значение производной в точке х0:
- у = x6 + 13x10 + 12, х0 = 1
- у = x4 – 12x5 + 2, х0 = -1
- Найдите значение производной в точке х0:
- у = , х0 = 1
- у = , х0 = 2
- Найдите значение производной в точке х0:
- у = , х0 = 2
- у = , х0 = 1
- Найдите значение производной в точке х0:
- у = , х0 =
- у = , х0 = π
- Найдите значение производной в точке х0:
- у = , х0 = 0
- у = , х0 = 1
IV этап.
Подведение итогов. Домашнее задание.Индивидуальные задания (для сильных учащихся). 1)Самостоятельно доказать правило нахождения производной частного. 2) Подготовить доказательство формул tg’ x, ctg’ x. 3) Метод математической индукции для производной степенной функции.
Дифференцированное задание.
I уровень №№ 737-750(б)
II уровень + №№ 787-789(а)
Урок по русскому языку в 5 классе. «Правописание корней с чередованием гласных е-и»
Государственное бюджетное образовательное учреждение
«средняя общеобразовательная школа №648 Колпинского района г. Санкт-Петербурга»
Конспект
урока по русскому языку в 5 классе.
«Правописание корней с чередованием гласных е-и»
подготовила
учитель русского языка и литературы
Марченко Анжелика Александровна
Санкт-Петербург
2013
Тема урока: «Правописание корней с чередованием гласных е-и».
Тип урока по цели: сообщение новых знаний.
Тип урока по содержанию: по морфемики и орфографии.
Цель урока: научить грамотному написанию корней –бер-бир-; –мер-мир-; –дер-дир-: –тер-тир-; –пер-пир-; –стел-стил-; –блест-блист-; –жег-жиг-; –чет-чит-.
Задачи:
Обучающие:
научить правильно писать корни с чередующимися гласными: –бер-бир-; –мер-мир-; –дер-дир-: –тер-тир-; –пер-пир-; –стел-стил-; –блест-блист-; –жег-жиг-; –чет-чит-;
научить правильно устно и письменно комментировать данную орфограмму;
научить самостоятельно формулировать правило на основе изученного материала.
Развивающие:
развивать словарный запас.
Воспитывающие
1) воспитывать культуру речи;
2) воспитать навыки самоконтроля и самооценки.
Оборудование: компьютер, карточки с заданиями, презентация.
План проведения урока:
Организационный момент.
Актуализация изученного ранее (систематизация знаний и умений, закрепление изученного).
Постановка цели обучения перед учащимися.
Усвоение новых знаний, формирование новых умений и навыков.
Закрепление знаний, умений и навыков.
Информация о домашнем задании.
Подведение итогов урока. Выставление оценок.
Ход урока.
Организационный момент.
Предварительная организация класса.
Готовность учителя к уроку.
Мобилизующее начало урока.
Приветствие.
Актуализация ранее изученного (систематизация знаний и умений, закрепление изученного).
Повторение правила чередования корней а-о (-кас-кос-; -лаг-лож-).
– Ребята, вы изучили правило чередования гласных а-о в корнях -кас-кос-; -лаг-лож-.
– Вспомните, когда в корне пишется гласная о , а когда а?
а) – кас – кос – пишется а, если после корня есть суффикс – а -, а в остальных случаях пишется о.
б) – лаг – лож- пишется а перед г, а о перед ж. Искл.: полог.
– А теперь проверим, как вы усвоили это правило.
2) Словарный диктант на чередование корней -кас-кос-; -лаг-лож-.
Предл_гать, выл_жить, к_салась, прол_гать, прик_снуться, прил_жение, возл_гать.
Постановка цели обучения перед учащимися.
– Ребята, вы изучили чередование гласных а-о в корнях -кас-кос-; -лаг-лож-.
Но на этом правило чередования корней не заканчивается. С чередованием гласных существует множество правил. Цель сегодняшнего урока – чередование гласных е-и в корнях –бер-бир-; -мер-мир-; -дер-дир-: -тер-тир-; -пер-пир-; -стел-стил-; -блест-блист-; -жег-жиг-; -чет-чит-.
4. Усвоение новых знаний, формирование новых умений и навыков.
1) Объяснение нового материала.
– Тема сегодняшнего урока «Правописание корней с чередованием гласных е-и».
– Посмотрите на слайд. А теперь попробуйте сформулировать это правило (пишется и, если дальше следует суффикс – а -; в остальных случаях пишется е).
– Откройте учебники на стр… . Прочтите правило. Устно прокомментируйте примеры из учебника.
– А теперь мы научимся графически комментировать нашу орфограмму.
2) Первичное закрепление.
Задание: дети выходят к доске по цепочке и выполняют задание (выходят по 2 человека).
Проби͡рались, разбе͡ру, заст͡елю, выж͡игаю, дочи͡таю, выс͡т͡и͡лаю, сте͡реть, запе͡реть, сде͡ру, сти͡раю, распи͡раю, бл͡е͡с͡теть, перечи͡таю, расст͡и͡лается.
3) Физминутка.
– Мы с вами немножко отдохнем и проведем физминутку.
Задание: вы хлопаете в ладоши, если → и, а если е → нет.
Блестел на солнце, взбирался медленно, опереться на друга, набирали высоту, замерли от восторга, звёзды зажигаются, костёр разжигается, умереть со смеху, отпираю дверь, постели скатерть.
5. Закрепление знаний, умений и навыков.
1) Тест (раздаточный материал).
а) 1вар. В каком ряду во всех словах пропущена буква и?
1. Уб_ру, зам_р, расст_лается.
2. Зам_реть, подст_лил, выт_рла.
3. Зап_реть, изб_ратели, бл_стеть.
4. Разж_гают, выд_рать, отп_рать.
б) 2вар. В каком ряду во всех словах пропущена буква е?
1. Изб_рать, бл_стеть, выб_ру.
2. Пост_лить, оп_реться, ум_реть.
3. Выд_раю, соб_рались, отп_реть.
4. Сж_гаю, соч_тать, зам_реть.
2) Вставить пропущенные буквы (Вспомнить, из каких сказок А. Пушкина взяты эти цитаты.).
*На девичник взять соб_раясь,
Вот царица, наряжаясь,
Перед зеркальцем своим,
Перемолвилась с ним.
*Как наешься ты своей полбы,
Соб_ри-ка ты с чертей оброк полный.
*Кто-то терем приб_рал
Да хозяев поджидал.
3) Творческий диктант.
Задание: заменить словосочетания глаголами, обозначить гласную в корне с чередованием.
Например: сверкать на солнце (блестеть).
Подниматься на гору (взбираться), выдергивать сорную траву (выдирать), закрыть дверь (запирать), оцепенеть от страха (замереть), разгораться ярко (зажигаться), убегать от погони (удирать).
6. Информация о домашнем задании.
Повторить §52
7. Подведение итогов урока. Выставление оценок.
Литература:
Капинос В.И., Пучкова Л.И. Сборник заданий учебных тематических тестов для 5-го класса по русскому языку. – М., 1999 г.
Правила и упражнения по русскому языку 5-8 класс: /Пособие для средней школы. – К., 1998 г.
Романова С.А. Тематическая разработка уроков русского языка для 5 класса. – М., «Школа – Пресс» – 1999 г.
Химия. Уроки в 9 классе. (Гара Н.Н.)
%PDF-1.6 % 486 0 obj > endobj 483 0 obj > endobj 485 0 obj >stream Adobe Illustrator CS32015-06-11T15:34:46+03:002015-06-11T17:12:01+03:002015-06-11T17:12:01+03:00
999996212.000001Millimeters
~~t7ʂqt>.bv$[ZgxAeƠ#5|PmS5K
m~9″`r.ŭeLL3 OmoLzp|{5c &m[ߺzИстории о великих математиках • Arzamas
У вас отключено выполнение сценариев Javascript. Измените, пожалуйста, настройки браузера.
- История
- Искусство
- Литература
- Антропология
Мне повезёт!
История, Антропология
Как получилось, что в 1950–60-е годы механико-математический факультет МГУ стал удивительным свободным местом, где, несмотря на противодействие советской власти, работали величайшие ученые мирового уровня? Ученики Колмогорова, Успенского, Арнольда, Манина и других математиков рассказывают о золотом веке мехмата. Аудиоверсию слушайте в «Радио Arzamas»
«Было два мехмата: мехмат парткома и мехмат Петровского»
Петровский был уникальным человеком. Прекрасных математиков в это время было немало, и можно спорить, кто из них первый.
Обычно называют Колмогорова. Но не было ни одного человека, который совершил столько добрых дел, сколько Петровский. И именно это восхищает меня в нем, и именно поэтому я о нем решил рассказывать. Кроме того, Петровский — мой математический предок: он учитель одного из двух моих учителей, Евгения Ландиса (второй мой учитель — Владимир Арнольд, ученик Колмогорова).
Иван Георгиевич прославился тремя сторонами своей жизни. Во-первых, он был великий математик, во-вторых, великий ректор Московского университета, строитель и созидатель, а третья его сторона — гуманитарная: необыкновенно сильная, чрезвычайно редкая и, может быть, не так ярко освещенная, как первые две. Во многих опубликованных текстах встречается фраза, что за свою жизнь Петровский сделал десять тысяч добрых дел. Существует такое выражение «переломить судьбу», и, как правило, судьба человека переламывается к худшему. Петровский имел власть, страсть и умение переламывать судьбы людей к лучшему. И об этом написано и сказано не так много.
Поскольку времени с его смерти прошло уже немало, большая часть того, что он сделал, погружается в забвение, но кое-что записано, и, может быть, я немножко добавлю сегодня.
О Петровском-математике
Что сделал Петровский в математике? Есть несколько областей математики, которые вполне понятны широкой публике. Все знают, что такое окружность. А если нарисовать окружность на эластичном листе и растянуть его, из окружности получится эллипс. Если посмотреть на Шуховскую башню, то она состоит из нескольких секций. Контуры этих секций — это гиперболы. Есть еще параболы — параболу прославил Алексей Николаевич Толстой в фантастической повести «Гиперболоид инженера Гарина». Но он, гуманитарий, перепутал гиперболу и параболу: свойствами отражателя, которые использовал инженер Гарин, обладает параболоид, а не гиперболоид.
Параболы, гиперболы и эллипсы к нашей практической жизни имеют прямое отношение. Вот еще одна иллюстрация того, что такое эллипс. На столе стоит стакан. Он круглый.
Если вы на него смотрите сверху и сбоку, вы видите, что его верхний край — эллипс, а не окружность. Оказывается, что у этих понятий есть невероятно глубокое развитие в математике, причем в двух направлениях — в так называемой теории алгебраических кривых и в теории уравнений с частными производными.
Уравнения с частными производными тоже описывают процессы, с которыми мы постоянно сталкиваемся в повседневной жизни. Вот я сейчас говорю, а вы меня слышите. Это работает волновое уравнение. Оно относится к числу гиперболических. Если вы возьмете в руку холодный стакан, постепенно ваша ладонь начнет остывать, а стакан — нагреваться. Так работает уравнение теплопроводности, и оно параболическое. Если вы натянете мыльную пленку на проволочный контур, то она примет равновесную форму, которой заведует эллиптическое уравнение.
Эти уравнения — частные случаи огромной физической реальности, которую описывает огромная же математическая теория.
В полном систематическом виде эту теорию создал Петровский в конце 30-х и начале 40-х годов. Он разделил уравнения с частными производными на эллиптические, гиперболические и параболические. Одна из самых знаменитых его работ — это работа о лакунах. «Лакуна» по-гречески «пробел», «отверстие», «промежуток». Суть дела в следующем. Если вы закричите и ваш крик будет длиться долго, то удаленный свидетель не услышит звука, когда вы начали кричать, но потом звук докатится до него — он будет слышать его некоторое время, и затем звук прекратится. Это так называемая лакуна в распространении звуковой волны. Она прошла, и ее больше нет — пустота, лакуна. Если бы наше пространство было двумерным, что, конечно, очень трудно вообразить, и мы жили бы на плоскости, то те же самые уравнения дали бы другой эффект. Крик никогда не закончился бы: дойдя до удаленного слушателя, он продолжал бы длиться бесконечно, все более и более затихая, но продолжая звучать.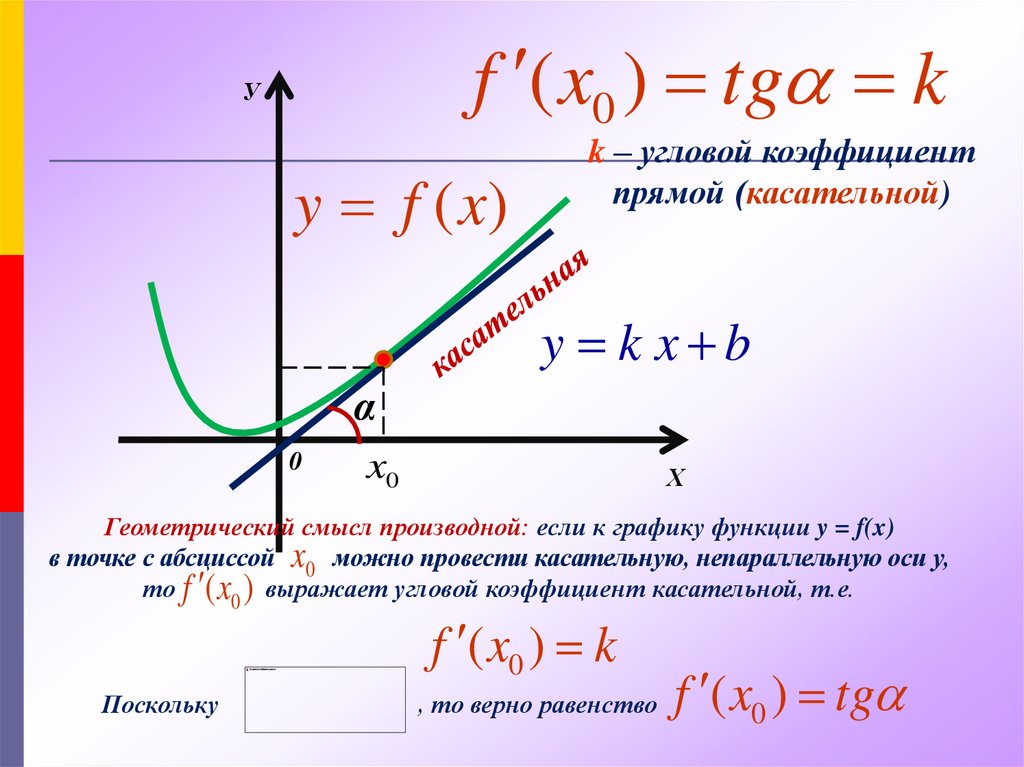
Тем самым уравнение распространения звука — волновое уравнение — в двумерном и трехмерном пространстве ведет себя по-разному. И в самом общем виде этот эффект исследован Петровским.
Он изучил большой класс гиперболических уравнений с частными производными и выделил среди них те, которые обладают лакунами, и те, которые ими не обладают. Мой учитель Ландис рассказывал, что эта работа стоила Петровскому такого напряжения, что некоторое время его близкие видели у него физические признаки утомления.
Можно сказать несколько слов про алгебраические кривые. И эллипс, и парабола, и гипербола задаются уравнениями. И эти уравнения студенты изучают на первом курсе далеко не только математических факультетов. Но уравнения можно усложнять. Можно усложнять постановку задачи об эллипсах, параболах и гиперболах, и так мы придем к одной из знаменитых проблем ХХ века, поставленных математиком Давидом Гильбертом Проблемы Гильберта — двадцать три задачи в математике, сформулированные Давидом Гильбертом на парижском Международном математическом конгрессе 1900 года.
Они оказали определяющее влияние на развитие математики XX столетия.. Петровский очень сильно продвинул решение этой проблемы и, в частности, доказал утверждение, которое не мог доказать сам Гильберт. А Гильберт был одним из величайших математиков на границе XIX и ХХ веков.
Могу рассказать один курьезный случай. Слушая какой-то доклад, Петровский особенно оживился, когда рассказывали некоторую теорему. Он сказал: «Очень симпатичная теорема — чья она?» — «Да она ваша, Иван Георгиевич», — ответил докладчик.
О деканстве Петровского
Петровский был замечательным администратором. Ему принадлежит фраза «Административную работу можно поручать только тем, кто ее ненавидит». И он как администратор сделал невероятно много. Еще не достигнув сорока лет, он был избран деканом недавно образованного тогда мехмата — механико-математический факультет Московского университета выделился из физико-математического факультета. Время деканства Петровского пришлось на Великую Отечественную войну.
Петровский руководил эвакуацией мехмата в Ташкент, а затем — в Ашхабад и в Свердловск. Петровский заботился о жизни сотрудников факультета и студентов в эвакуации. Петровский же организовал возвращение в Москву. И когда стало ясно, что победа не за горами и существование факультета снова будет устойчивым, летом 1944 года Петровский попросил освободить его от должности декана.
О том, как Сталин назначил Петровского ректором
Ректор МГУ Иван Петровский и президент Датской королевской академии наук, Нобелевский лауреат, физик Нильс Бор во время визита в МГУ. 1961 год © Летопись Московского университетаВ 1951 году Иван Георгиевич был назначен ректором Московского университета и пробыл им 21 с лишним год, до самой своей смерти. В 1951 году полным ходом шло строительство нового здания на Воробьевых — тогда Ленинских — горах. Забота о строительстве, о том, как будут размещаться факультеты нового университета, во многом легла на плечи Петровского.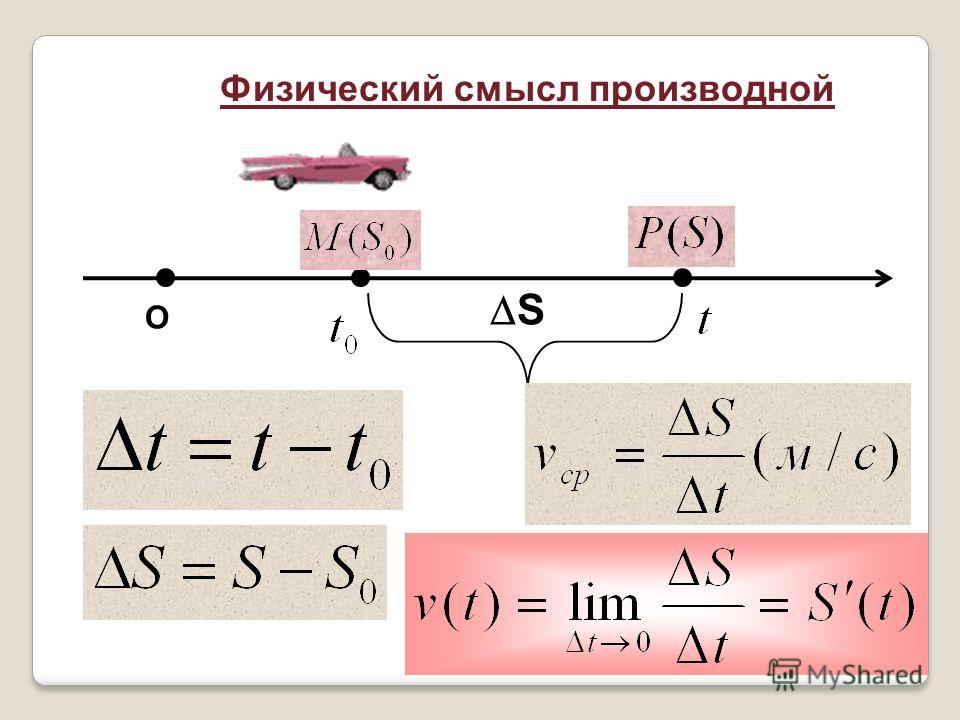
И одновременно он заботился о том, чтобы учебный процесс гладко шел в старых зданиях.
Рассказывают, что ему неоднократно предлагали должность ректора и он отказывался. Наконец на каком-то совещании у Сталина зашел разговор о том, кто мог бы быть хорошим ректором МГУ, и Сталину сообщили, что есть Петровский, но он отказывается. Тогда Сталин начертал своей рукой: «Назначить Петровского ректором Московского университета», и сомнения были сняты. И все же это назначение совершенно удивительно и непонятно. В те времена на ведущие посты выдвигались люди партийные и созвучные государственной идеологии. Петровский был человеком беспартийным и так им и оставался.
О кабинете на 9-м этаже
Петровский был невероятно доступен — к нему со своей проблемой мог прийти любой человек. Было примерно известно, в какое время нужно приходить. Человек поднимался или спускался на 9-й этаж, в предбанник кабинета Петровского, где сидели две пожилые и очень добрые секретарши старого интеллигентного образца.
И они говорили, что через несколько минут Иван Георгиевич выйдет. Петровский стремительно выходил из своего кабинета и обращался к человеку, который его ожидал.
Ученики говорили ему: «Иван Георгиевич, ректорство лишает вас возможности творить. Вы не хотите вернуться к научному творчеству?» Он отвечал: «Если я перестану быть ректором, я сделаю еще несколько хороших работ; если я буду ректором, то таких работ в университете будет сделано тысячи».
Об организации новых кафедр и поддержке опальных ученых
Иван Петровский ведет заседание совета МГУ. 1972 год © Летопись Московского университетаПетровский организовывал массу новых лабораторий и кафедр, да и факультетов тоже, и в период его ректорства появилось 70 новых кафедр и более 200 лабораторий. Например, совершенно невозможно было создать на биофаке в 50-е годы кафедру генетики В эпоху Большого террора 1930–40-х годов генетика стала опальной наукой, и многие генетики были арестованы, расстреляны или погибли в тюрьмах.
Период гонений продолжался вплоть до 1964 года.. Невозможно было привлечь на биофак таких гигантов, как Тимофеев-Ресовский Николай Владимирович Тимофеев-Ресовский (1900–1981) — опальный биолог, генетик, был выдвинут на Нобелевскую премию, но не получил ее из-за противодействия властей.. Петровский организовал кафедру физических методов в биологии на физфаке (я говорю приблизительное название), и там все опальные генетики совершенно легально читали лекции, в том числе Тимофеев-Ресовский. Господствующая система преследовала людей неарийского происхождения и вообще непартийных. Петровский все свои силы употреблял на то, чтобы талантливые люди оставались в университете. Например, чрезвычайно талантливых выпускников университета Пятецкого-Шапиро и Березина направили преподавать в среднюю школу и в школу рабочей молодежи. Но Петровский употребил свою власть на то, чтобы их сначала взяли на часть ставки, а потом перевели в университет на полную ставку.
Еще один случай противостояния антисемитизму
Мой учитель Ландис не был принят в аспирантуру, несмотря на то что прошел всю войну, имел ранения, военные награды и репутацию одного из талантливейших студентов на курсе.
Но как еврея его не взяли в аспирантуру и направили преподавать в школу рабочей молодежи в системе железнодорожного транспорта. В какой-то момент Петровский пригласил его работать в университет. Начальство сказало Ландису, что если он найдет себе замену, то его отпустят. Ландис нашел себе замену — его не отпустили. После этого история повторилась. Ему опять сказали, что если он найдет себе замену, то его отпустят. Он нашел себе вторую замену — его не отпустили. Тогда Петровский сказал ему, чтобы он просто прекратил ходить на эту работу и начинал работать в университете. Ландиса вызвали в так называемый линейный суд — суд железнодорожного ведомства. Петровский сказал ему ни в коем случае на суд не являться. И в конце концов справедливость восторжествовала: Ландис стал сотрудником университета, а железнодорожное ведомство прекратило свои претензии.
О способе брать на работу способных выпускников
Пожалуй, еще более выразительным является тот способ, которым Петровский брал на работу наиболее способных выпускников аспирантуры.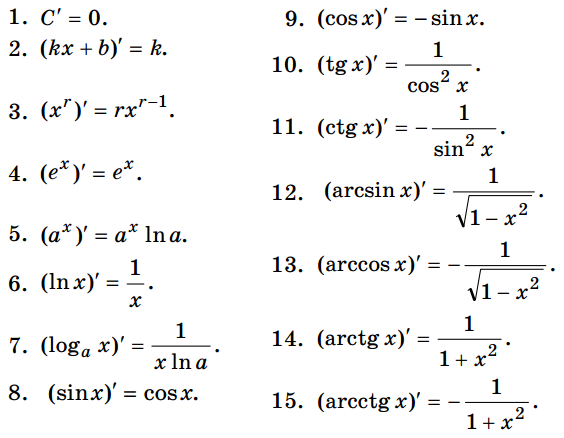
Это касалось и Владимира Арнольда, и Якова Синая, и Дмитрия Фукса, и многих других. Меня тоже коснулся этот способ. После окончания очной аспирантуры нужно было проходить процедуру распределения. Согласие на то, чтобы человека взяли в университет, должны были дать три организации: профком, партком и администрация. Для людей, которые не отличались общественными заслугами и грешили, так сказать, непокровительствуемой национальностью, пройти эту процедуру было практически невозможно. Петровский эту процедуру обошел. Примерно за полгода до окончания аспирантуры он переводил аспиранта в заочную аспирантуру и своей властью ректора брал его сотрудником в университет. Удивительным образом эта схема не была заблокирована. Таким способом Петровский набрал ядро сотрудников мехмата золотых годов.
О мехмате парткома и мехмате Петровского
Иван Георгиевич Петровский, ректор Московского государственного университета им. М. В. Ломоносова, математик. 1962 год © Леонид Великжанин / ТАССЯ работал на мехмате с 1968 года и продолжаю работать сейчас, то есть 50 с лишним лет, и мой доперестроечный опыт сводится к тому, что было два мехмата: мехмат парткома и мехмат Петровского — огромная сила, тот самый золотой состав факультета, общность людей талантливых и единодушных, которые благодаря власти Петровского могли реализовать заложенные в них дарования.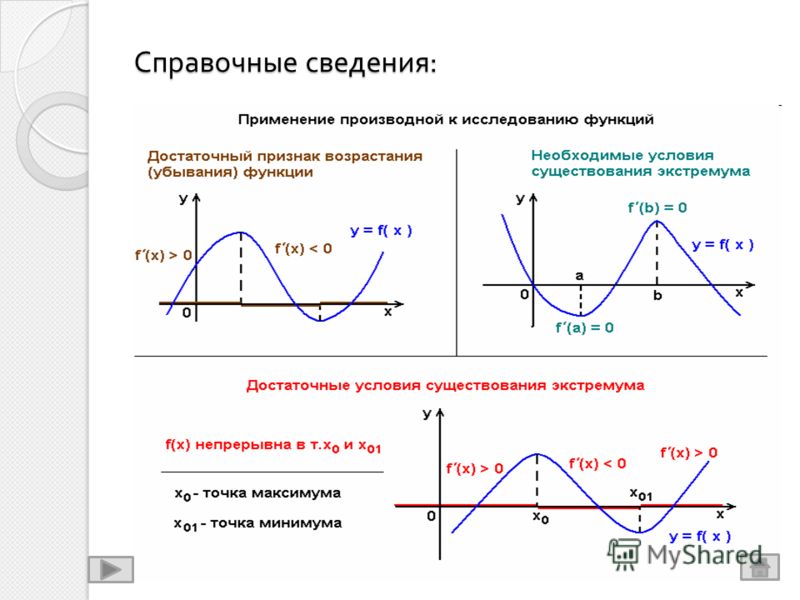
Вопреки мехмату парткома, мехмат Петровского приобрел огромную силу и прославился на весь мир.
О письме 99-ти и конце золотого века
В 1968 году многие сотрудники мехмата подписали письмо в защиту математика и диссидента Александра Есенина-Вольпина: так противостояние властей и интеллигенции наконец докатилось до мехмата. Началось с того, что писателей Юлия Даниэля и Андрея Синявского, которые публиковали свои произведения за границей под псевдонимами и чьи псевдонимы были наконец раскрыты, судили и приговорили к тюремным срокам. Диссидент Александр Гинзбург написал, точнее скомпоновал, «Белую книгу», собрав в ней все отзывы о процессе Даниэля и Синявского — от самых коммунистических до самых буржуазных, — и сделал эту книгу достоянием гласности. Хотя он не скрывался и хотя в книге были только документы, его тоже привлекли к суду. Суд был открытый, но открытый по-советски — все места были предоставлены своим. Есенин-Вольпин отправился на Петровку, 38, с требованием, чтобы ему выдали пропуск на этот суд.
С Петровки,38, его отправили в сумасшедший дом. И тут математики всколыхнулись и написали очень резкое письмо в защиту Есенина-Вольпина. Подписи под ним поставили 99 человек.
Чем опасен самиздат
Как игнорировали советскую действительность с помощью поэзии и почему за это сажали
Колесо истории, вращаясь, наконец накатилось на мехмат. Разразилась гроза: партком университета написал жалобу в ЦК о том, что Петровский развалил идеологическую работу в университете. После этого началось разрушение мехмата Петровского. Порядки на факультете резко переменились. Ефимова, который был деканом золотого времени на мехмате, сменил механик Огибалов — человек преклонных лет, который в 1937 году был парторгом на мехмате. Начался антисемитский прием на мехмате — об этом я написал очерк «„Черное 20-летие“ мехмата МГУ». Этот период длился 20 лет. Арнольд передавал слова Петровского: «Я не хотел бы видеть своими глазами, как разрушается дело моей жизни».
Но дело жизни Петровского не было разрушено. Лучшие традиции мехмата в меру сил воплотил Независимый университет. А сейчас эти традиции воплощает матфак Вышки. Кроме того, огонь, зажженный Петровским на мехмате, никогда полностью не угасал. Хочется надеяться, что сейчас он разгорается с новой силой.
О давлении системы и борьбе с ним
Иван Петровский и Юрий Гагарин. 1961 год © Летопись Московского университетаУвы, Петровскому как ректору приходилось делать вещи, которые он никогда бы не сделал, если бы на него не оказывалось давление. Например, власти решили очень жестоко расправиться с теми, кто подписал письмо в защиту Есенина-Вольпина, — профессоров лишали профессорских званий. Петровский уговаривал тех, кто подписал, забрать свою подпись. Если человек забирал подпись, никаких репрессий к нему не применялось. Но по отношению к тем, кто проявлял твердость и отказывался забрать подпись, Петровский вынужден был осуществить указание сверху, этих людей наказать — несомненно, против собственного желания.
Ученики ему говорили: «Иван Георгиевич, что вы делаете?» Он отвечал: «Я легко могу сделать так, как вы мне советуете, но тогда я через три дня перестану быть ректором».
Петровский постоянно жил в борьбе со своим окружением и со всей системой в целом, несмотря на то что это была одна сторона его жизни. Другая сторона состояла в том, что он укреплял и создавал силу и славу нашей страны и науки, и система это вполне принимала и этого же хотела. Так что жизнь Петровского была в определенном смысле двойственной — и в согласии с системой, и в постоянном противоборстве с ней. Недаром Петровский был не только ректором МГУ, но и членом Президиума Верховного Совета СССР.
О работе дворником в детском саду
Люди не рождаются великими математиками — они ими становятся. И мне хочется сказать несколько слов о ранних годах жизни Петровского. Он родился в 1901 году. Ему было 16 лет, когда грянула революция. В 1918 году он вернулся в свой родной город Севск, за пределами которого уже начинал учиться.
Он происходил из купеческой семьи и понимал, что его семья принадлежала к тому социальному слою, который во время революции подвергался репрессиям. Он сказал, что им надо уезжать из Севска как можно дальше и туда, где их никто не знает. Семья уехала в Елисаветград и спаслась.
Несколько лет спустя Петровский пошел работать дворником в детский сад. Меня это долгое время удивляло, пока наконец я не узнал причину. Годовая работа дворником изменила социальный статус Петровского: из купеческих детей он стал пролетарием и как таковой мог поступить в высшее учебное заведение. Это ограничение было совершенно не формальным — например, мой отец, родившийся в дворянской семье, так и не получил высшего образования и защитил кандидатскую диссертацию, а потом и докторскую, не имея университетского диплома. В детском саду Петровский познакомился со своей будущей женой Ольгой Афанасьевной, которая была заведующей этим садом, и это определило его судьбу на все дальнейшие годы.
О математике, поразившей своей красотой
В юности, еще до работы дворником, он читал книгу Дирихле Иоганн Петер Густав Лежён Дирихле (1805–1859) — немецкий математик, внесший существенный вклад в математический анализ, теорию функций и теорию чисел.
Имеется в виду его книга «О сходимости тригонометрических рядов, служащих для представления в данных пределах произвольной функции»., которая его поразила своей красотой и навсегда приковала к математике. После этого он решил поступать на математический факультет, и в 1922 году он поступил на мехмат, тогда физмат. В 1927 году он приветствовал Первый Всесоюзный съезд российских математиков от имени студенчества, тогда же поступил в аспирантуру к профессору Егорову Дмитрий Федорович Егоров (1869–1931) — математик, член-корреспондент Академии наук СССР. Ректор Московского университета с 1917 года, а с 1921 по 1924 год — директор Научно-исследовательского института математики и механики МГУ. В 1929 году Егоров был подвергнут гонениям по религиозным убеждениям, в октябре 1930 года арестован. Умер 10 сентября 1931 года в больнице, после голодовки, объявленной в тюрьме., которую и окончил в 1930 году. 1930 год для Егорова был трагическим. Егоров был убежденный монархист, не скрывал своих убеждений и был арестован.
Через год он скончался в тюремном госпитале в Казани. Петровский никогда не боялся говорить о том, что он ученик Егорова, несмотря на то что в те времена это было опасно. Это несколько слов о том, как вырастал в свой реальный масштаб Петровский.
О том, как Петровский помогал людям
Иван Петровский © Летопись Московского университетаЯ расскажу несколько историй, которые не вошли в публикации и которые я слышал от разных людей. Некий студент в 40-е годы участвовал в философском кружке, члены которого собирались и изучали немарксистских философов. Их всех посадили. Счастливым образом герой нашего рассказа вышел из лагеря всего лишь через пять лет. Он пробовал восстановиться в университете — его посылали от одного проректора к другому, и так он ходил по кругу, которому не было видно конца. Наконец он пришел на прием к Петровскому и рассказал свою историю. Петровский спросил: «Вы можете доказать, что вы были реабилитированы, а не амнистированы?» Тот сказал: «Могу».
И Петровский написал приказ о его восстановлении. «Реабилитирован» означает «признан невиновным», а «амнистирован» означает «прощен», то есть вина не снята, а человека просто больше не наказывают.
Другую историю мой коллега рассказал мне много лет спустя после того, как она произошла с ним и его матерью. На четвертом курсе мехмата рассказчик пытался решить какую-то проблему, сделать что-то выдающееся. У него ничего не получилось, он плюнул на все и ушел в геологическую экспедицию. И его как задолжника, не сдавшего сессию, должны были отчислить. Его мама пошла к Петровскому, взяв зачетку, и рассказала Ивану Георгиевичу всю историю, объяснив, что сын ее отлично учился, и в доказательство показав зачетку. Но по ошибке она взяла не его зачетку, а зачетку своей дочери. Петровский не рассердился и, несмотря на этот ляпсус, тут же отдал приказ о восстановлении.
Еще один эпизод записан Владимиром Михайловичем Тихомировым. Профессорам университета выдавали квартиры в новом университетском доме.
Николаю Владимировичу Ефимову, тогда еще не декану мехмата, а просто профессору, выдали квартиру на девятом этаже. Петровский знал, что у его дочери больное сердце: он сделал поправки в списке, квартира перешла на третий этаж.
О десяти тысячах добрых дел
Иосиф Самуилович Шкловский Иосиф Самуилович Шкловский (1916–1985) — советский астроном, астрофизик., ознакомившись с деятельностью Петровского, посчитал, что за свою жизнь тот сделал десять тысяч добрых дел. Когда я обдумывал деятельность Петровского, его отношение к себе и к людям, мне стало казаться, что такую жизнь мог прожить только человек, живущий в мире христианства. Я знал, что ленинградский академик Ольга Александровна Ладыженская, ученица Петровского, была христианкой и этого не скрывала. Я спросил ее, был ли верующим Петровский. Она отвечала, что, конечно, да, и рассказала, в какую церковь он ходил, о том, как он вел свою христианскую жизнь. Удивительно, на какую высоту советская власть подняла беспартийного верующего и, очевидно, не в лад с ней действующего человека.
Но слава богу, что это произошло, и хотя я советскую власть не люблю, но то, что она так поступила, говорит, несомненно, в ее пользу.
В 1969 году с Петровским случился тяжелый инфаркт, и было непонятно, вернется ли он к обязанностям ректора. Долго длилось тревожное ожидание, но, когда он поправился, он снова стал ректором, хотя, конечно, здоровье его было подорвано. Он скончался в здании ЦК, куда поехал представить проект некоего доклада. С ним поговорили очень резко, и в вестибюле у Ивана Георгиевича случился приступ стенокардии. Он упал на пол. Вместо того чтобы вызвать медицинскую помощь, охранник стал поднимать его со словами, что здесь не велено, и старался посадить на стул. Петровский умер там же, в вестибюле здания ЦК.
Для меня Петровский — недостижимый образец.
Его жизнь я воспринимаю как победу. Не только победу великого ученого над трудными проблемами, но и победу добра над злом, особенно трудную в те годы.
«Истории о велких математиках» также в «Радио Arzamas»
Ученики Колмогорова, Арнольда, Манина и других — о своих учителях
«Все, что он сажал, — все приживалось, все росло»
О сеятеле и деревьях
Академик Андрей Колмогоров дома в рабочем кабинете. 1980 год © Валерий Христофоров / Фотохроника ТАССУ Андрея Николаевича была дача в Комаровке, под Москвой, и она была вся усажена самыми разнообразными деревьями, цветами, растениями. Все, что он сажал, — все приживалось, все росло. Он передавал своим ученикам саженцы, и они все приживались. Таким сеятелем он был в гораздо более глубоком смысле слова: он сеял мысли, разбрасывал идеи, как зерна. Он никого не учил так, как учат школьников или студентов, — он просто высказывал на семинарах мысли о том, как что-то, по идее, должно выглядеть, и после этого человек начинал работать и достигал больших успехов.
Был один математик, у которого что-то не выходило. И он приехал к Андрею Николаевичу в эту самую Комаровку, они беседовали. И Андрей Николаевич спросил, как у него дела. Он ответил: «Вы знаете, все хорошо, я составил все уравнения, но одного уравнения не хватает для того, чтобы замкнуть систему». Андрей Николаевич сказал: «У вас же случайный процесс, а случайный процесс не терпит изломов. Значит, слева и справа все должно соединиться — это будет дополнительным условием, которое приведет к цели». Из этого замечания родилось целое научное направление.
О первом открытии, сделанном в четыре года
Андрей Колмогоров с тетей Верой Яковлевной. 1909 год vivovoco.astronet.ruАндрей Николаевич имел не совсем обычную судьбу. Мать умерла при его рождении, и мальчика воспитывали две тетушки по матери — собственно, одна из них его усыновила. Это все происходило в имении его деда под Ярославлем: оно называлось Туношна, там прошло его раннее детство. Очень интересно то, что его старались воспитать, как он сам говорил, «по лучшим традициям педагогики того времени».
В частности, он вместе со своим другом Петром Саввичем Кузнецовым, впоследствии известным лингвистом, «издавал» журнал «Весенние ласточки». Андрей Николаевич, которому еще не было пяти лет, отвечал за математическую часть. Тогда же, готовясь к публикации в этом журнале, он испытал первую творческую радость. Он обнаружил следующее свойство чисел: один в квадрате — это один, а если к одному прибавить три, то есть два нечетных числа подряд, будет четыре. То есть два в квадрате. А если 1 + 3 + 5, то это будет 9: три нечетных числа — это три в квадрате. И так далее. Это свойство не исчезает, и чем далее, тем оно все более и более подтверждает себя: сумма первых n нечетных чисел равна n квадрат. Вот это открытие Андрей Николаевич сделал между четырьмя и пятью годами. Он всегда говорил, что оно дало ему первое творческое наслаждение.
О событии, перевернувшем жизнь Колмогорова
Андрей Колмогоров в молодости © ЯркипедияВ 1910 году они с тетушкой переехали в Москву, и с тех пор Москва стала основным городом его жизни.
Он был болезненным мальчиком, иногда падал в обморок. Его жизнь перевернуло следующее событие. С 1920 по 1925 год он преподавал в Потылихинской школе, школе Наркомпроса, и старался понравиться своим ученикам. У Андрея Николаевича был любимый класс, который его очень уважал: детям страшно нравилось, что совсем молодой человек преподает и физику, и математику, ведет кружок юных биологов. Тогда была такая система, что классного руководителя выбирали сами школьники. Андрей Николаевич был уверен, что этот самый класс его и выберет. И вдруг они выбрали физкультурника. Но физкультурники не могли быть классными руководителями, и при перевыборах все-таки выбрали Андрея Николаевича. И тогда он понял, что надо менять стиль жизни, понял, что ему чего-то не хватает, а именно физической культуры. На следующий год он поехал в поход в Крым вместе со своими школьниками, и с тех пор походы стали фундаментальнейшей частью его жизни.
О лыжах
Он научился очень хорошо ходить на лыжах и ходил на лыжах лучше всех своих аспирантов.
Это было испытанием для каждого из нас. Андрей Николаевич приглашал в Комаровку, и потом устраивалось лыжное путешествие, вообще говоря очень далекое, на 40–60 км. Там были лыжники, имевшие разряды и даже первый разряд по лыжам, но и они не выдерживали такого длительного путешествия. Иногда он выходил с этими перворазрядниками, а потом ему приходилось брать их лыжи и нести их, в то время как человек шел пешком. Для меня это было неожиданно: я тоже рос очень болезненным ребенком без всякой физкультуры — меня воспитывали бабушка и дедушка. Но когда мы пошли с Андреем Николаевичем, я неожиданно для себя прошел с ним эти 40 километров. Андрей Николаевич очень любил путешествовать на лыжах раздетым по пояс в самый лютый мороз. Мы брали с собой бутерброды, но надо было чем-то запить. Мы заходили в деревню и просили молочка, и все недоумевали, видя раздетых странных чудаков.
Умение кататься на лыжах считалось обязательным. Обычно мы приезжали на дачу, потом были разговоры, вечерняя музыка всегда — такой вечерний музыкальный час.
А после этого утром, в девять часов или, может быть, даже немножко раньше, выходили на лыжах. Возвращались домой часов в пять, обедали, потом прощались.
О фантастическом даре
Андрей Колмогоров на симпозиуме по теории вероятности. 1964 год © РИА «Новости»Андрей Николаевич брал в аспирантуру тех, кто каким-то образом себя проявлял независимо, и или лично ставил задачу, или на семинаре. Аспирант размышлял, и время от времени были разговоры о том, что получилось. Бывали случаи, когда одновременно приходило два человека. Например, механик Григорий Исаакович Баренблатт, который позже занимался гидродинамикой и аэродинамикой, и Владимир Андреевич Успенский, который был математический логик. И вот они за чаем вели математические разговоры. Сначала Андрей Николаевич разговаривал с Баренблаттом, и Успенский не понимал ни слова, а потом с Успенским, и Баренблатт не понимал ни слова. Владимир Арнольд был очень разнообразный математик, но две основные свои темы он получил от Колмогорова.
Израиль Гельфанд был мало с кем сравнимый математик, но первые свои исследования он сделал под руководством Колмогорова. Учение не есть движение, когда собачку ведут на привязи: это прикосновение, это импульс, который раскрывает тебе глаза. И вот Андрей Николаевич обладал фантастическим умением дать такой импульс.
О широте научного мировоззрения
У него была совершенно необычайная широта научного мировоззрения. Он был естествоиспытателем, физиком, механиком. Он имел крупные открытия в области биологии, в области геологии. Он был большим мыслителем. Выдающийся ученый во всех отношениях, которые только можно придать этому слову. Но в первую очередь Андрей Николаевич был, конечно, математиком. Вообще говоря, обычный ученый работает в двух-трех, редко четырех областях математики. У Андрея Николаевича их было порядка двадцати, и в каждой из них он имел совершенно замечательные достижения.
О теории вероятности как части математики
Пожалуй, самой главной его специальностью была теория вероятностей.
То, что мир во многом предопределен, впервые установил Ньютон. Если задать начальные условия, то дальше все будет двигаться совершенно предопределенным образом. А с другой стороны, есть масса вещей, которые никак не предопределены: результат бросания монеты, бросания кости. Погода, океан, атмосфера и другие явления влияют на события, которые считаются случайными. Крупнейшее достижение Андрея Николаевича заключается в том, что он привел это в математический порядок — он создал аксиоматику теории вероятностей, которая превратила теорию вероятностей в часть математики. Случайные явления, скажем погоду, надо как-то прогнозировать. Или осциллограф рисует какую-то кривую, но на нее действуют разные случайные обстоятельства, которые меняют естественное движение. И вот Андрей Николаевич создал теорию прогнозов случайных процессов. А потом выяснилось, что такую же теорию создал человек, имя которого известно каждому, — это Винер, придумавший слово «кибернетика».
Об открытии турбулентности
Перед самой войной Андрей Николаевич занялся наукой, которая называется турбулентность, написал три маленькие заметочки на десяти страницах и опубликовал в «Докладах Академии наук».
Англичанин Чарли Тейлор, выдающийся механик, увидел резюме публикации Колмогорова и попросил своего ученика Джорджа Бэтчелора прочитать статьи. Тот выучил русский язык и опубликовал статью о достижениях Колмогорова, и они стали всемирно известными. А что это практически означает? Вот течет Волга. Скорость течения — ну, я не знаю, 5 километров в час или что-то в этом духе. А если бы не было турбулентности, то она двигалась бы со скоростью гоночного автомобиля — 300–400 километров в час. Турбулентность — это завихрения, из-за которых происходит колоссальнейшее уменьшение скорости. Это закон природы, который открыл Колмогоров и который можно использовать для объяснения полетов самолетов, движения рек, водопадов, снежных лавин. Это еще одно величайшее достижение Андрея Николаевича, и оно считается одним из крупнейших завоеваний ХХ века.
О КАМ-теории
Андрей Колмогоров. 1980 год © Валерий Христофоров / Фотохроника ТАССВеликое открытие о том, что планеты устойчивы, было сделано методом, источником которого была работа Колмогорова.
Потом ее развил Арнольд, а после него — Мозер, и сейчас это называется КАМ-теория: Колмогоров, Арнольд, Мозер.
Имеется большое тело и меньшее тело — Солнце и Земля. Если ничто на них больше не воздействует, никаких других планет нет, то Земля будет двигаться вокруг Солнца по эллипсу. Но если пустить небольшой спутник, то он исказит движение, и Земля будет двигаться не по эллипсу. Возникает вопрос: что произойдет? Либо спутник упадет, либо Земля. Это был великий нерешенный мировой вопрос о том, устойчива или неустойчива система типа Солнечной. Вот она существует, планеты крутятся, крутятся… Может ли она сама по себе, без всякого влияния каких-то посторонних, иных сил, вдруг развалиться? Предсказать это очень трудно, и первый шаг к решению этой проблемы сделал Андрей Николаевич. Он доказал, что если тел три, то возможна вечная устойчивость на массивном множестве начальных условий.
О лекциях Колмогорова
Андрей Колмогоров читает лекцию учащимся в школе-интернате № 18 физико-математического профиля при Московском государственном университете им.
М. В. Ломоносова. 1964 год © Лев Шерстенников / РИА «Новости»Для студентов лекции Андрея Николаевича были очень сложными, понимать их было нелегко. Мы устроили команду человек в шесть, по очереди все записывали и размножили перед экзаменом. И вот когда я стал разбираться в них, я понял, что это лучший лекционный курс в моей жизни.
У Андрея Николаевича была своя, особая манера речи, которую, вообще говоря, было трудно воспринимать. Порой он сбивался, иногда говорил громким голосом, а иногда — тихим. Иногда пропускал детали, которые можно было бы разъяснить подробнее. Тем не менее его публичные выступления всегда собирали огромную аудиторию. Он около ста раз выступал на заседаниях Московского математического общества, некоторые из его публичных лекций стали легендарными — например, лекция о том, может ли машина мыслить. Он доказывал, что может.
«Успенский не боялся объяснять простые вещи»
Об импровизациях
Его лекции были совершенно не похожи на другие лекции.
Он никогда не читал по бумажке — об этом даже речи быть не могло. Я думаю, что он и сам не знал, чем закончится лекция. То есть это всегда была некоторая импровизация с участием слушателей. Он смотрел на их реакцию, задавал вопросы, а иногда они выходили к доске и что-то рассказывали. То есть шел некоторый диалог. В одной из своих книжек он вспоминал, что, читая свой первый спецкурс, он приходил, что-то рассказывал, а потом, придя домой, записывал конспект сказанного. То есть человек думал на месте, а не пытался излагать что-то заранее подготовленное. Это было такое творчество в момент лекции. И аудитория это понимала.
О феодальной структуре
Как-то Успенский мне объяснял устройство советской научной жизни — что это такая феодальная структура. Каждый начальник, с одной стороны, пользуется услугами своих вассалов, а с другой стороны, защищает их в борьбе с другими феодалами, которые могут их съесть. И вот Успенский умело находил для кафедры логики разных защитников.
О том, почему Успенский не подписал письмо 99-ти
Любое хорошее математическое рассуждение состоит в том, что мы смотрим на предмет с другой стороны — стороны, с которой он становится очевидным.
И вот это умение он использовал в жизни, как будто смотря заново на окружающую действительность. Кстати, благодаря этому отчасти он понимал, как устроена советская жизнь. Он не был диссидентом — скажем, письмо в защиту Есенина-Вольпина он осторожно не подписал, объясняя это тем, что у него не хватит сил потом не каяться за это, а подписывать и каяться — это еще хуже, чем не подписывать. Он понимал, как все устроено, и это ему помогло в его административной деятельности при создании отделения и кафедры.
О картошке
Владимир Успенский на прогулке во время семинара Евгения Дынкина. 1954 год © Cornell University LibraryЕсть история, как, когда он был комсоргом, ему поручили послать аспирантов на картошку. Посылать кого бы то ни было на картошку ему очень не хотелось, и он нашел выход, издав распоряжение, что каждый аспирант должен поехать на картошку, представив письмо от своего научного руководителя о том, что это не повредит подготовке диссертации.
Администрация была в безумной злобе, но придраться было не к чему, ведь действительно главное занятие аспиранта — это подготовка диссертации. С другой стороны, нельзя обвинять научного руководителя в том, что он не дает такого письма.
О принципе Дон Кихота
Он как-то мне сказал, что есть такой принцип Дон Кихота: если последствия действий неясны, то нужно действовать смело и благородно. И потом рассказал историю про Есенина-Вольпина, который работал в ВИНИТИ Всероссийский институт научной и технической информации РАН — один из крупнейших центров развития информатики в СССР и России. — в лаборатории, начальником которой был Успенский. А над ним начальником был человек по фамилии Васильев, прообраз Яконова из «Круга первого» Имеется в виду роман Александра Солженицына «В круге первом» (1958).. А директором ВИНИТИ был Михайлов. И как-то вызывает Васильев Успенского и говорит, что ему от Михайлова пришло указание приготовить проект приказа об увольнении Есенина-Вольпина.
После чего он показал Успенскому проект приказа в папке, а затем, оставив папку открытой, ушел из комнаты. И тут Успенский взял этот приказ, положил себе в карман и папку закрыл. Васильев пошел к Михайлову — выяснилось, что приказа нету. Но никто из них — ни Васильев, ни Михайлов — не потребовал издать приказ заново, и после этого дело было временно заморожено. Наверное, теперешним слушателям это непонятно, но в советское время такое действие выглядело совершенно вызывающе.
О том, как Успенский стал учеником Колмогорова
Владимир Успенский с портретом Андрея Колмогорова. Фрагмент обложки первой книги Владимира Успенского из серии «Труды по нематематике» © Объединенное гуманитарное издательство; фонд «Математические этюды»Успенский был победителем олимпиад для школьников. После этого он стал ходить в кружок такого замечательного математика Евгения Борисовича Дынкина. Поступив на мехмат, Успенский продолжал заниматься с Дынкиным, а потом вместе с ним преподавал школьникам.
Дынкин рассказал о нем Колмогорову, и Успенский стал учеником Колмогорова — как он сам говорил, это было одно из самых важных событий в его жизни. В начале 50-х годов у Колмогорова было много учеников — это был период расцвета его математической педагогической деятельности. И вот Успенский попал в их число и с тех пор работал на мехмате — сначала в разных лабораториях, а потом, когда при некотором его участии была основана кафедра математической логики, на ней — и до самой смерти.
О том, что такое падеж
Объявив о первом семинаре для гуманитариев на филологическом факультете, он пришел к Колмогорову и спросил, что бы такое с ними разбирать. Колмогоров сразу предложил две темы: обсудить с участниками семинара, что такое падеж и что такое ямб. Что здесь поучительно: оба слова были хорошо известны и никакому гуманитарию не пришло бы в голову спрашивать, что такое падеж. Но Колмогоров и Успенский обратили внимание на то, что это не совсем ясно. В школьном курсе говорится, что в русском языке шесть падежей.
А что это значит? Допустим, кто-то возражает, что их не шесть. Как убедить в своей правоте? Или наоборот, как доказать, что их шесть? На самом деле это не чисто словесное упражнение. Когда говорят «в лесу», то какой это падеж? В одной песне есть строчка «Мы увидимся все в позаброшенном аэропорте…» — она рифмуется с предыдущей строкой. Но на самом деле стандартное словоизменение — «в аэропорту». И вот спрашивается, какой это падеж. То же самое с ямбом: что значит ямб? Считается, что каждый второй слог должен быть ударный, а это ведь не так. Слово «велосипедист» вполне может быть в стихотворении, хотя из всех слогов там только один ударный. То есть нужно четко определить, что это значит. И четко сформулированного определения до Успенского и Колмогорова просто не было.
О том, зачем Успенский преподавал математику гуманитариям
Владимир Успенский во время лекции © Механико-математический факультет МГУ им. М. В. ЛомоносоваВ «Игре в бисер» герой Гессе Йозеф Кнехт, становясь взрослее и мудрее, начинает работать со все более младшими слушателями и в конце концов преподает детям.
Так же и Успенский сначала преподавал математическую логику математикам, а потом стал преподавать математику гуманитариям. Я прошу прощения за такое сравнение, но гуманитарии действительно с трудом понимают разные простые математические вещи. И он относился к ним как к неразумным детям, которые не виноваты в том, что они неразумны, но которых надо постепенно вразумлять.
У него была идея занятий математикой при создании ОСИПЛа и ОТИПЛа, и многие студенты вспоминали об этом с ненавистью, потому что не понимали, зачем им это нужно. Но Успенский говорил, что это очень важно, что это тренировка и приучение людей к структурному мышлению. Что гуманитарии должны четко понимать три вещи: имеет ли смысл высказывание, истинно ли оно и поняли ли они его. Он объяснял это так: если в гуманитарных науках делают какое-нибудь высказывание — например, что это произведение относится к романтизму, — то заранее считается очевидным, что это высказывание имеет смысл, а вопрос о том, что, собственно, имеется в виду, задавать неприлично.
В то время как в естественных науках и математике — особенно если вводится новое слово — автор обязан определить, что он имеет в виду, а если он делает утверждение, то он обязан доказать это утверждение, а не просто публиковать его в ожидании, что другие начнут с ним спорить. Успенский понимал на самом деле, что есть два разных взгляда на вещи и разные подходы. Но считал, что гуманитариям важно понимать существование другого взгляда, и подчеркивал это.
О просветительстве и популяризаторстве
Успенский постоянно занимался просветительством. Не то что он ходил и думал, кого бы просветить, но он старался писать популярно и выступать на популярные темы: что такое математическое доказательство, что такое аксиоматический метод, что такое парадокс. И в конце он собрал эти свои выступления в книжке, которая называется «Апология математики». Она имела удивительный для меня успех. Я, честно говоря, скептически относился к интересу гуманитариев к математическим наукам и был удивлен тем, что эту книгу прочли и заметили.
Успенский был большим любителем разных историй и не боялся объяснять простые вещи. Когда пишешь какую-нибудь популярную статью, всегда ощущаешь неловкость, что надо объяснять подробно, разжевывать то, что все знают. Например, невозможно объяснять популярно и подробно то, что Луна движется вокруг Земли. А между тем если спросить у обычных людей, почему Луна видна не полностью, а в виде серпа, то очень многие ответят: это потому, что на нее падает тень от Земли. Так вот, Успенский не боялся объяснять простое подробно, настойчиво, повторять это разными словами.
О комплексе неполноценности и умении прояснять систему понятий
Владимир Успенский во время лекции © Механико-математический факультет МГУ им. М. В. ЛомоносоваЕсли оценивать математиков в терминах математической силы — сильный математик, сильный олимпиадник, впервые решил конкретные трудные задачи, — то Успенский таковым не был. Его лучшие результаты были получены в кандидатской диссертации и немного опередили то, что делалось в этом отношении за границей.
Но, к сожалению, текст диссертации был недоступен, и это мало повлияло на мировую науку. Он испытывал по этому поводу некоторый комплекс неполноценности и часто говорил, что бывают великие математики, которые занимаются чем-то сложным, а он ненастоящий математик. Я думаю, что на самом деле он видел свою заслугу в прояснении системы понятий, в правильном взгляде на вещи. Он любил цитировать старинную китайскую мудрость о том, что очень важно вещи правильно именовать. В некоторых случаях мне даже казалось, что эти попытки внедрить правильную терминологию безнадежны и только запутывают больше. Но он настаивал и считал это очень важным.
О парадоксах и любопытстве
Владимир Успенский и Михаил Поливанов. 1950-е годы © Из личного архива Владимира УспенскогоОн любил парадоксальные истории и был исключительным наблюдателем, смотрел на окружающую действительность с большим любопытством, интересом и удивлением и замечал то, что другие не замечают. В свое время меня поразил один случай.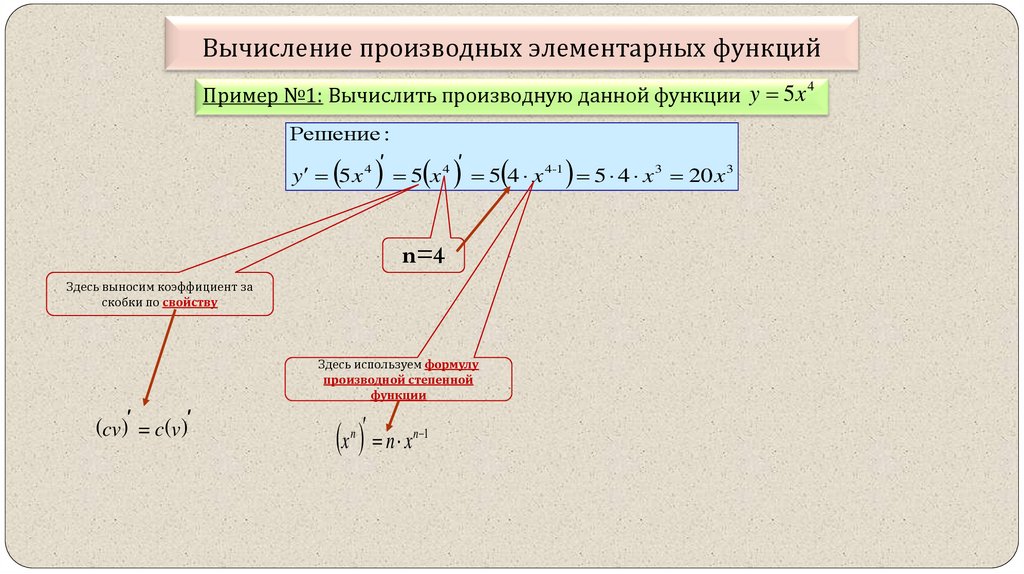
В начале 80-х годов я участвовал в подготовке радиопередач для школьников. И там была песенка, начинающаяся со слов:
Однажды Лобачевский
Думал, кутаясь в пальто,
Как мир прямолинеен —
Видно, что-то здесь не то.
Но он вгляделся пристальней
В загадочную высь,
И там все параллельные
Его пересеклись.
В подготовке этой передачи участвовало несколько человек, и, естественно, все мы слушали эту песню, но ни один из нас не заметил, что это совершенный абсурд. По определению параллельные прямые — это прямые, которые не пересекаются, а у Лобачевского на самом деле неверно другое: в его геометрии несколько прямых, параллельных данной, проходящих через одну точку. Успенский это заметил, хотя я не понимаю, как он мог это заметить.
Он объяснял, что в современной математике короткие слова используются для общих понятий, а если понятие более частное, то это короткое слово снабжается уточнениями в виде прилагательных.
И дальше он объяснял, что вот раньше был просто мед, а если вы теперь купите баночку, то на ней будет написано: «Мед пчелиный натуральный». Тем самым понятие меда резервируется для чего-то более общего, не обязательно пчелиного или натурального.
О формулировках
Лекция лауреата премии «Просветитель» Владимира Успенского в Государственном центре современного искусства в Нижнем Новгороде. 2010 год © Премия «Просветитель»Он любил интересные формулировки. Например, что такое доказательство? Доказательство, говорил он, — это рассуждение, убеждающее нас настолько, что мы готовы с его помощью убеждать других. И вот действительно, это четкая и точная формулировка. Еще он сказал однажды, что источник конфликтов не в том, что одни считают, что что-то хорошо, а другие считают, что что-то плохо: чаще люди соглашаются с тем, что и то, и это хорошо. Но из двух хороших вещей одни считают важнее одну, а другие — другую.
Когда его спрашивали, как он стал математиком, он говорил, что если бы не время и не место, то он стал бы не математиком, а, например, юристом по конституционному или каноническому праву.
Это некоторое преувеличение, но тем не менее склонность к четким формулировкам и формальным загогулинам у него, безусловно, имелась.
«Говоря о научных работах, Людмила Всеволодовна употребляла выражение „мухобойная возня“»
О мухобойной возне и низкопробном шике
Говоря о научных работах, Людмила Всеволодовна часто употребляла выражение «мухобойная возня» — это касалось тех работ, где были длинные и сложные технические вычисления, а также выражение «низкопробный шик» — для случая, когда автор пытался словесной красотой прикрыть отсутствие реальной математической мысли.
Математик, доктор физмат наук, профессор мехмата МГУ и вообще удивительная женщина, Людмила Всеволодовна приобрела свою математическую известность ранними работами по теории множеств, а именно по теории так называемых А- и B-множеств, где она успешно соревновалась с Лузиным Николай Николаевич Лузин (1883–1950) — математик, член-корреспондент, академик АН СССР , профессор Московского университета, создатель Московской математической школы.
Учитель Андрея Колмогорова и других великих математиков., Александровым Павел Сергеевич Александров (1896–1982) — математик, академик АН СССР, профессор МГУ, президент Московского математического общества и вице-президент Международного математического союза. и Колмогоровым. Наверное, ее самым известным результатом было построение открытого монотонного отображения трехмерного куба на четырехмерный. Андрей Николаевич Колмогоров однажды мне прокомментировал этот результат следующими словами. Он сказал, что, когда Людмила Всеволодовна сумела построить это уникальное отображение, он, Андрей Николаевич, решил, что ему лучше заниматься другой тематикой.
О скромности
Людмила Всеволодовна как ученый получила высокое международное признание, но не удостоилась на родине ни тех званий, ни тех почестей, ни той известности, которых она заслуживала. Почему? По одной причине: всю жизнь она была абсолютно честным человеком и никогда не позволяла себе лицемерно поддакивать тоталитарному советскому строю.
Математика для нее была не средством карьерного успеха, а целью жизни и объектом бескорыстной любви. Характерно, что на могиле на Новодевичьем кладбище, где ее прах покоится вместе с прахом ее мужа, академика Петра Сергеевича Новикова, написаны лишь их имена. Там нет никаких указаний на звания, лишь одно слово — «математики».
О порядочности
Людмила Келдыш © Проект «Личности»Эпизод, о котором я сейчас расскажу, иллюстрирует взаимоотношения Людмилы Всеволодовны с советской властью. В 1937-м , когда Людмиле Всеволодовне было 33 года и она была сотрудником Математического института имени Стеклова при Академии наук, происходила политическая травля Николая Николаевича Лузина — замечательного математика и великого педагога. Кто-то из партийных начальников подошел к Людмиле Всеволодовне, ученице Лузина, с требованием осудить своего учителя. Но она отказалась, ссылаясь на беременность. Беременность была реальной и заметной. И ее результатом стал мальчик Сережа — будущий академик, лауреат медали Филдса Сергей Петрович Новиков.
Партийный деятель от Людмилы Всеволодовны отстал.
Другой эпизод такого же рода произошел в конце 60-х , когда брат Людмилы Всеволодовны, Мстислав Всеволодович Келдыш, президент Академии наук, в центральной печати осудил некоторых математиков за игнорирование «партийности науки». На это Людмила Всеволодовна ответила публичным выступлением на ученом совете в Стекловке, где в резких выражениях нападала на своего брата за его лицемерные слова, недостойные ученого. Еще один политический эпизод. В 1968 году Людмила Всеволодовна подписала знаменитое письмо 99-ти в защиту математического логика и правозащитника Есенина-Вольпина Подробнее об этой истории вы можете прочитать в главе про Ивана Петровского..
О семье
Людмила Всеволодовна была главой большого семейства и любила всех своих пятерых детей — Лёню Келдыша, будущего академика, Андрея Келдыша, который рано и трагически умер, Сережу Новикова, будущего академика, Елену, биолога, и Нину. Она уделяла всем много времени: как она при этом умудрялась успешно заниматься наукой, для меня остается загадкой.
О знакомстве
Я познакомился с Людмилой Всеволодовной на кафедральном семинаре по топологии, руководимом Павлом Сергеевичем Александровым. Там происходило распределение курсовых работ, а я был студентом третьего курса. Но не самым обычным студентом: за год до этого я перевелся на мехмат из Нью-Йоркского университета. Людмила Всеволодовна сформулировала тему курсовой работы, и я задал по этому поводу вопрос. Людмила Всеволодовна на него ответила. А потом тихо спросила у Павла Сергеевича на французском языке, что он может сказать про студента, задавшего этот вопрос. Дело в том, что было известно, что я перевелся из Нью-Йоркского университета, но ни Павел Сергеевич, ни Людмила Всеволодовна не знали, что я вообще-то француз и что французский язык у меня родной наряду с русским. Значит, они переговаривались по-французски , а я все слышал, но не подал виду. Павел Сергеевич очень лестно меня охарактеризовал. Он сам хотел меня взять в ученики, но я не клюнул на его темы курсовых работ, понимая, что это темы вчерашнего дня.
О взаимопонимании
Людмила Келдыш в молодостиWikimedia CommonsЗа время нашей совместной работы с Людмилой Всеволодовной у нас установились не только тесные научные связи, но и глубокие человеческие взаимоотношения. Где-то начиная с конца 60-х годов я постепенно стал другом дома большого и дружного семейства Новиковых — Келдыш. Людмила Всеволодовна меня часто приглашала на семейные праздники. Они проходили в трехкомнатной квартире недалеко от Стекловки. Туда приходили все дети и внуки и два-три человека вроде меня на правах друзей дома. Эти вечера были всегда оживленными, с интересными разговорами не только на математические темы.
О смерти
В 1973 году произошел важный и очень грустный эпизод в жизни Людмилы Всеволодовны. Она решила устроить своего наиболее известного ученика Лешу Чернавского на свою ставку ведущего научного сотрудника Института Стеклова. И для этого была готова уйти на пенсию, освободив ставку для Чернавского.
Но тут руководство МИАН ее обмануло — приняло ее заявление об уходе на пенсию, но на освободившуюся ставку не взяло Чернавского. Вскоре после этого Людмила Всеволодовна заболела и в феврале 1976 года умерла от рака.
«От членства в Папской академии наук он отказался, потому что Католическая церковь не отменила решения о признании еретиком Джордано Бруно»
О том, как Арнольд переплыл пролив Золотые Ворота и высадился на острове Алькатрас
Однажды Арнольд был в Сан-Франциско, и ему хотелось проплыть под мостом Золотые Ворота. Я пробовал купаться под Сан-Франциско — там довольно холодная вода. Владимир Игоревич плавал очень хорошо и решил проплыть от одного конца моста до другого — это, насколько я понимаю, больше двух километров. Хороший пловец и при этом человек, очень тщательно относящийся к всевозможному планированию и подготовке, он несколько раз проплыл в той же бухте это расстояние вдоль берега и только потом взялся плыть вдоль моста. В какой-то момент он обнаружил, что не справляется с течением: начался сильный прилив — его отнесло довольно далеко внутрь пролива.
Он понял, что дальше плыть не может, и вылез на остров. Остров оказался Алькатрасом — это тюрьма для особо опасных преступников в центре пролива, которая знаменита тем, что из нее не было ни одного успешного побега. То есть попытки были, но ни про одну из них не известно, чтобы беглецам удалось добраться до берега. И вот Арнольд переждал там прилив и потом доплыл до берега. Свидетелей у этой истории не было, а он любил истории, у которых не было свидетелей, потому что чувствовал себя совершенно свободно. К счастью, к тому моменту тюрьма уже не работала.
О соревнованиях
Профессор МГУ им. М. В. Ломоносова Владимир Арнольд на заседании кафедры. 1985 год © Алексей Курбатов / РИА «Новости»Эта история очень характерна для Владимира Игоревича. С одной стороны, он был чрезвычайно спортивен, бегал и катался с гор на лыжах, плавал, ездил на велосипеде до последних дней своей жизни, но при этом он никогда не участвовал ни в каких соревнованиях. Он стремился быть лучшим, но не за счет того чтобы обогнать кого-то или сделать что-то быстрее, а в том, что никто другой не делал.
И никаких других соревнований он не признавал. И в математике он старался не заниматься задачами, которыми занимались другие люди и которых нужно было опередить, получить решение раньше, чем соперники.
О семинаре на лыжах
Зимой по выходным семинар часто выходил на лыжные прогулки. Обычно собирались на вокзале, чаще всего Белорусском, или на какой-нибудь промежуточной станции — например, Кунцево. Дальше садились на электричку и вместе ехали до станции, от которой начинался путь. Владимир Игоревич очень любил ходить на лыжах, и многие участники семинара с удовольствием к нему присоединялись. Правда, темп удавалось выдержать не всем, многие сходили с дистанции раньше, чем было запланировано. Сам он в одиночку ходил в очень длинные переходы — могло быть и 100, и 120 километров. Ближе к концу марта он любил бегать на лыжах в одних плавках, чтобы приобрести первый весенний загар, добежать до Москвы-реки и тут же в нее окунуться. И там тоже были разные истории — например, как он не мог вылезти на лед, потому что скользили руки.
Но всякий раз все заканчивалось успешно.
О математических достижениях
Доктор математических наук Владимир Арнольд. Институт прикладной математики Академии наук СССР. 1964 год © Всеволод Тарасевич / РИА «Новости»Многие математики мыслят в терминах задач: математическое достижение — это решение некоторой задачи. Есть такой список задач, который называется проблемами Гильберта. Эти проблемы были поставлены на рубеже XIX и ХХ веков, и потом десятки и сотни математиков занимались их решением. Владимир Игоревич решил одну из них, и это сделало его заметной фигурой на математическом небосклоне уже в самые первые годы его научной деятельности. Сам Арнольд создал уникальное собрание задач, которые во многом определили развитие нескольких направлений математики во второй половине ХХ века. Среди этих задач изредка попадались те, которые Владимир Игоревич узнал от кого-то , но я думаю, что больше 90 % этих задач принадлежат ему самому. Толстый том задач Арнольда с комментариями его учеников был издан издательством Springer.
О теории катастроф, или теории особенностей
Владимир Арнольд. 1957 год © Е. А. Ермакова / Газета «Троицкий вариант»Рассказать про вклад Владимира Игоревича Арнольда в науку — трудная задача. Он воспринимал математику как единое целое — для него в ней не было различных частей, не было ощущения, что в какой-то момент своей исследовательской деятельности он занимается узкой областью. И его результаты направлены в первую очередь на объединение разных частей математики, на сведение их во что-то единое. Одно из центральных достижений Арнольда и школы Арнольда (а школа — это тоже крайне существенная характеристика его научной деятельности, одно из центральных достижений) — это разработка теории особенностей.
Другое название теории особенностей — это теория катастроф. Под этим именем она развивалась в западных странах — во Франции, в Соединенных Штатах. Но Владимир Игоревич всегда считал, что теория катастроф скорее рекламное название математической теории, а математическую суть ее составляют особенности.
Но и катастрофы имеют непосредственное отношение к особенностям, потому что катастрофа — это термин для описания резкого изменения состояния динамических систем при совсем малых изменениях значений определяющих их параметров. Так, например, корабль может раскачиваться с одного борта на другой, возвращаясь всякий раз в свое изначальное устойчивое состояние. Но если качка становится слишком сильной, может наступить момент, когда очень небольшое изменение положения корабля так меняет положение его центра тяжести, что он не возвращается в состояние равновесия, а оказывается кверху дном — происходит катастрофа. Ровно такими структурными изменениями и занимается теория особенностей, и ровно такими вопросами и занимался Арнольд.
О членстве в Лондонском королевском обществе и отказе от приглашения в Папскую академию наук
Слева направо: Андрей Сахаров, Андре Гинье, глава делегации Французской академии наук, и Владимир Арнольд после вручения медалей и почетных дипломов иностранных членов Французской академии наук в посольстве Французской Республики в СССР.
1987 год © Борис Кауфман / РИА «Новости»Он стал лауреатом Ленинской премии вместе со своим учителем Андреем Николаевичем Колмогоровым за создание теории Колмогорова — Арнольда — Мозера. Ему тогда еще не было и 30 лет. Больше всего он ценил членство в Лондонском королевском обществе и считал, что круг лауреатов этого звания практически безупречен с точки зрения научных достижений. А вот, скажем, от членства в Папской академии наук он отказался, хотя его туда приглашали. Он сказал папе Иоанну Павлу II, что не может принять этой чести, потому что Католическая церковь до сих пор не отменила своего решения о признании еретиком Джордано Бруно.
«Плачу 10 копеек за идею»
На 50-летие Юрия Ивановича Манина, пришедшееся на 1987 год, его учитель Игорь Ростиславович Шафаревич произнес следующие слова: «1937 год — значимый год в российской истории. В этот год родился Юрий Иванович Манин. 1953 год — тоже очень значимый год в российской истории: в этот год Юрий Иванович Манин поступил на математический факультет Московского университета».
О заборах как метафоре свободы
Лауреат Международной премии короля Фейсала в номинации «Наука» Юрий Манин. 2002 год © King Faisal PrizeРасскажу с его слов один очень характерный эпизод из его жизни. Летом 1953 года он приехал из Симферополя поступать на мехмат. После этого он снова уехал к себе на родину и вернулся в сентябре. За это время город полностью преобразился: исчезли заборы. В то лето и, соответственно, до этого Москва была огорожена глухими деревянными заборами, за которыми скрывались какие-то секретные и псевдосекретные учреждения. Эти рухнувшие заборы стали для него метафорой свободы.
Об идеях за 10 копеек
Когда в стране наступила перестройка, Юрий Иванович взял складной столик и складной стульчик, поехал на Арбат, поставил там эти столик и стульчик, повесил объявление: «Плачу 10 копеек за высказанную идею» — записывал мысли случайных прохожих и платил за это. Идеи в основном были глупые, но сам по себе замысел приводит в совершенный восторг.
Вообще надо сказать, что он воспринял перестройку с гигантским восторгом, а когда оказалось, что далеко не все его мечты и чаяния воплотились, очень огорчился. Может быть, его отъезд в Германию и Америку во многом был мотивирован этими несбывшимися мечтами. Потому что дух свободы 60-х годов, который совпал с его молодостью, был для него необыкновенно важен. Когда рухнул Советский Союз, он с восторгом ждал возвращения этого духа свободы. А этот дух свободы вернулся, может быть, даже в большей степени, чем он ожидал, но далеко не всегда в приятных формах. Мечта была гораздо чище и сильнее, чем грубая реальность.
Об особом поколении математиков
Юрий Манин, доктор физико-математических наук, старший научный сотрудник Математического института имени В. А. Стеклова АН СССР, лауреат Ленинской премии за труды по алгебраической геометрии и теории чисел. 1967 год © Александр Невежин / РИА «Новости»Существует удивительный феномен. В московской математике был особый период, или особое поколение, — люди, которые родились между 1936 и 1938 годом.
В эти три года появились на свет совершенно замечательные математики мирового уровня. Всех я, наверное, не перечислю, но достаточно вспомнить Владимира Игоревича Арнольда, Сергея Петровича Новикова, Якова Григорьевича Синая, Дмитрия Викторовича Аносова, Александра Александровича Кириллова и моего учителя Юрия Ивановича Манина. В другие годы были математики этого уровня, но никогда так много сразу. Я часто задавался вопросом: почему так получилось? И ответ несколько парадоксален: с одной стороны, советская власть в ее худшем, сталинском варианте выталкивала способных людей из всех остальных сфер деятельности в математику, а с другой стороны, глоток свободы, начавшийся в середине 50-х и продолжавшийся до середины 60-х , дал некий дополнительный импульс. Вот это сочетание тоталитаризма и свободы и дало необыкновенно мощный рывок.
О широте интересов
Юрий Манин (лектор) и Владимир Арнольд. 1970-е годы © Факультет математики и компьютерных наук ИвГУМанин являлся и является для меня образцом ученого.
Это было связано не только с тем, как он подходил к собственно научной работе, к математике, но и с тем, насколько широки были его интересы — как внутри математики, так и вне ее. Он много и плодотворно интересовался физикой и написал не одну физическую работу. Он занимался такими вещами, как глоттогенез — возникновение речи, в связи с чем изучал нейрофизиологию. Он рассказывал нам о структуре генома и читал курс на филфаке по средневековой французской литературе.
О журфиксах по пятницам
Один раз на своем семинаре Юрий Иванович сказал, что у дореволюционных профессоров была традиция общаться со своими учениками далеко не только на работе и далеко не только на темы, связанные с их научной работой. Что обычно у такого профессора был журфикс — день, когда без приглашения к нему в гости мог прийти любой студент и поговорить с ним о чем угодно, чаще всего совершенно не о своей собственной работе и даже не о той науке, которой он занимается. И ему пришла в голову мысль сделать это же для своих учеников и их друзей.
И вот по пятницам в их маленькой двухкомнатной квартире у метро «Юго-Западная» стали собираться его ученики и разговаривать на самые разные темы. Темы эти обычно задавал сам Юрий Иванович. Это могла быть художественная литература или уже упомянутый глоттогенез — в общем, любой элемент как естественно-научного, так и гуманитарного знания. После этого все говорили, кто что об этом думает.
О математиках, которым приятно заниматься математикой и трудно общаться с людьми
Юрий Манин. Фотография из серии «Who’s That Mathematician?». Беркли, 1989 год © Paul R. Halmos Photograph Collection / Mathematical Association of AmericaОсобенно ярко вспоминаю два заседания. На одно из них я пришел с женой, а у нас были маленькие дети, и поэтому вырваться ей было очень трудно. Поэтому мы немножко опоздали. Нас встретила жена Юрия Ивановича, Ксения Глебовна, которая, посмотрев на Алену, сказала: «Как всегда, самые красивые» — и провела в комнату, где уже шел разговор.
Юрий Иванович говорит: мы тут без вас уже начали обсуждать такую тему — почему нам так легко и приятно заниматься математикой и достаточно трудно общаться с людьми. Что вы по этому поводу думаете? Я ответил, что лично мне очень трудно заниматься математикой и очень легко общаться с людьми.
О поэме и частушке
Второй эпизод — это день рождения Юрия Ивановича, который для учеников праздновался на журфиксе, в пятницу. По всей видимости, это было 50-летие. Естественно, его все поздравляли, в том числе стихотворно. Мне запомнилась поэма Миши Розенблюма, в которой были строки:
Скажи, затем ли Мартин Лютер
Швырял чернильницей во тьму,
Чтоб мы изобрели компьютер
И душу продали ему?
Юрий Иванович в это время написал цикл статей о компьютерной метафоре и вообще о роли компьютера в изменении мира. А еще были частушки, по-моему принадлежащие Саше Бейлинсону (сейчас он профессор в Чикаго) и Олегу Огивецкому (он профессор в Марселе). Из них помню такую:
Раз по улице иду,
Вижу — девка гарная.
Присмотрелся, поглядел –
Левополушарная.
Эти частушка и поэма были написаны и прочитаны не просто так. Юрий Иванович интересовался и ролью компьютера в обществе, тем, как он изменит жизнь, и нейрофизиологией. Он читал работы, связанные с ролью правого и левого полушария головного мозга: они его интересовали в том числе в применении к развитию речи и к разным другим вещам.
Об интересе к математике как к целому
Юрий Манин на конференции по дифференциальной геометрии и глобальному анализу. Гарвиц, 1981 год © Archives of the Mathematisches Forschungscinstitut OberwolfachПримерно тогда же в Москве в аспирантуре у Юрия Ивановича учился польский математик Мариуш Водзицкий, позже эмигрировавший в Соединенные Штаты и писавший Юрию Ивановичу письма о том, как он устроился в Америке. Письма эти были бумажные, шли очень долго, проходили цензуру, часть из них терялись, и Юрий Иванович их нам зачитывал. Там были замечательные истории, и одну я расскажу.
До Беркли Мариуш устроился в какой-то провинциальный американский университет. Ему там было скучно, и он писал, что о математике здесь говорить не с кем, нет никого, кто был бы ему интересен. А потом от него пришло совершенно восторженное письмо со словами, что по части математики он по-прежнему никого не нашел, но нашел одного профессора древней истории. И вот они вместе пишут статью о Древнем Риме и что в этом университете он, видимо, больше будет заниматься древнеримской историей, чем математикой. А следующее письмо было скорее удивленное. Как-то он сказал этому коллеге и соавтору: «То, что вы мне рассказываете про такой-то эпизод римской истории, страшно напоминает то, что случилось с Карлом Великим». А тот ответил: «А Карл Великий — это кто?» — «Ну как же. Карл Великий, человек, создавший королевство франков». Тогда профессор облегченно вздохнул и сказал: «А, это не важно — это было уже после Древнего Рима». Эта история до некоторой степени иллюстративна, потому что Московской математической школе свойственен интерес к математике и к науке как к целому, а не к каким-то узким, отдельным ее задачам и проблемам.
О теории кодирования и удивительных приложениях математики
О научных достижениях Манина широкой аудитории рассказывать трудно. Потому что если задать вопрос, где применяется то, что он сделал в науке, то ответ будет выглядеть так: он сделал нечто, на основе которого другие математики сделали что-то другое, а дальше появились еще какие-то люди, которые сделали что-то третье, это третье перехватили инженеры, и вот благодаря всему этому в телефоне, который мы носим в кармане, например, меньше помех. Кажется, в 1981 году он позвал на свой семинар Валерия Денисовича Гоппу, который рассказал, как, с его точки зрения, алгебраическая геометрия может использоваться в теории помехоустойчивого кодирования. Это то, как автоматически исправлять ошибки на телефонной линии, или на диске компьютера, или в телефоне (по-русски это назвалось коды, исправляющие ошибки). Это такая наука, часть математики, которая возникла из инженерных приложений. И вот возникла совершенно гениальная, как мы сегодня понимаем, идея — применить к этому делу трудную область математики, называемую алгебраической геометрией.
Гоппа рассказывал об этом разным людям в разных местах (в том числе и мне), и ни один математик его не понял. А Юрий Иванович понял и сумел это пересказать на другом своем семинаре нам. И после того буквально за несколько недель или месяц появилась такая область, которую мы сегодня называем алгеброгеометрические коды и которая в тот момент была совершенно сенсационным продвижением вперед для тех, кто специализировался в теории кодирования.
Об алгебраической геометрии и теории квантового компьютера
Юрий Манин. 2011 год © Denis Mironov / CC BY-NC-ND 2.0Юрий Иванович всю свою жизнь занимался алгебраической геометрией. Это некоторая область, которая геометрическими методами изучает алгебраические уравнения. В школе нас учили, что окружность на плоскости можно задать уравнением 𝑥2+𝑦2=𝑅2. Оказывается, что с такого рода кривыми поверхностями и куда более сложными объектами можно работать методами как алгебры, так и геометрии, а в каких-то ситуациях и методами математического анализа.
Одним боком эта наука прилегает к древнегреческой классике — работам Диофанта, а другим боком — к самой современной математической физике. Наши представления о том, как устроена Вселенная, были бы куда менее полными без алгебраической геометрии. С другой стороны, Юрий Иванович интересовался и другими вещами. В какой-то момент он написал две книжки по математической логике. Кроме того, он писал статьи по теоретической физике и по другим наукам: например, ему принадлежит идея квантового компьютера.
Об учениках
У Юрия Ивановича совершенно замечательная плеяда учеников. Самый известный из них — филдсовский лауреат Филдсовская премия — высшая математическая награда, аналог Нобелевской премии, — международная премия и медаль, которые вручаются раз в четыре года на Международном математическом конгрессе нескольким молодым математикам не старше 40 лет. Володя Дринфельд. Но и остальные его ученики совершенно замечательные. Можно упомянуть Сашу Бейлинсона, Витю Колывагина и многих-многих других.
В какой-то момент он сам составил список своих учеников, защитивших у него диссертации. На тот момент их было 40–50 человек. Очень немногие из них потом бросили науку, а из большинства выросли очень хорошие математики.
«Та харизма, с которой он выступал у доски, тот внутренний огонь, который им двигал, очаровывали и притягивали»
О взрыве гранаты и потерянном зрении
Толя Витушкин учился в Суворовском училище и собирался становиться вовсе даже не математиком, а офицером. В качестве учащегося Суворовского училища он участвовал в Параде Победы 1945 года. А через год в результате несчастного случая он лишился зрения и доучивался уже почти ничего не видя. Этот несчастный случай произошел в районе Ходынского поля. В послевоенной Москве валялось много остатков боеприпасов. Толя был мальчиком любопытным и взял в руки запал от гранаты. Раздался взрыв, в результате которого он лишился фрагментов пальцев и зрения: оно угасало постепенно и в какой-то момент пропало окончательно.
О том, как математика связана с эпохой Великих географических открытий
Студенты мехмата Анатолий Витушкин и Роберт Минлос. 1953 год © Механико-математический факультет Московского государственного университета им. М. В. ЛомоносоваКогда человек лишается какого-то важного канала связи с миром, компенсаторно ему открывается что-то новое. Греки объясняли, что математику нужно учить, потому что она отрывает от вещей чувственного мира и обращает человека к умозрению. Наверное, что-то похожее произошло с Витушкиным. Он обладал каким-то внутренним зрением математических вещей, математического мира. Математики занимаются чем-то, похожим на географические открытия. Эпоха Великих географических открытий вроде бы закончилась, но мы по-прежнему словно являемся жителями неимоверно огромной и при этом малонаселенной страны. И количество неизведанного там чудовищно велико. В этот загадочный мир меня ввел Анатолий Георгиевич Витушкин.
О харизме и внутреннем огне
Анатолий Витушкин.
1980-е годы© Механико-математический факультет Московского государственного университета им. М. В. Ломоносова Я познакомился с Анатолием Георгиевичем в 1970 году, будучи первокурсником, когда пришел на семинар по теории функций. Была полная аудитория, и он вдохновенно расхаживал вдоль доски. Почему я остался? Студенту-первокурснику разобраться в областях математики не представляется возможным, но та харизма, с которой он выступал у доски, то горение, тот внутренний огонь, который им двигал, очаровывали и притягивали.
О математике как вирусе и семинарах как концертах
Жизнь математиков оформляется в виде жизни семинаров. Это что-то типа концертов, где математики собираются и что-то друг другу рассказывают. Математика, видимо, распространяется воздушно-капельным путем. У многих иммунитет со школьной скамьи, а некоторые болеют — какая-то ограниченная эпидемия происходит. Семинар, на который я пришел, работал в университете с 60-х годов. Исходно там было три руководителя — кроме Анатолия Георгиевича его вели Андрей Александрович Гончар и Борис Владимирович Шабат.
Потом Шабат скончался, а Гончар стал вице-президентом Академии наук, и семинар продолжал функционировать благодаря Витушкину.
О рояле и изобретательстве
Студент 2-го курса Анатолий Витушкин играет на пианино в доме отдыха «Красновидово». 1951 год © Механико-математический факультет Московского государственного университета им. М. В. ЛомоносоваВитушкин, когда поступил на мехмат, стал пианистом и выступал на конкурсах, несмотря на то что у него была травма пальцев. У него в доме стоял рояль, который он сам настраивал вслепую. Была фонотека. Он тонко воспринимал все связанное с музыкой и разные акустические вещи. У него была мысль создать устройство, которое заменит зрение. Он очень плотно вошел в радиотехнику, в звукозапись. Под его руководством Валентина Петровна, его супруга, паяла, и вместе они создавали совершенно невообразимые радиотехнические конструкции. Он ездил в Америку и привез оттуда какую-то невозможную акустическую систему, которую многократно усовершенствовал.
А когда его дочка завела машину, он устроил ей антиугонную систему.
О заботе
Как-то мы с Анатолием Георгиевичем возвращались из Германии. В аэропорту Дюссельдорфа я забыл свою сумку с документами и деньгами и вспомнил об этом только на подлете к Москве. Анатолий Георгиевич, чтобы моя жена не расстраивалась, тут же мне отдал половину гонорара. При этом с сумкой и с моим багажом все сложилось очень благополучно — я все потихонечку получил. А Анатолий Георгиевич продемонстрировал заботу. Вообще его отношения со студентами были домашние и отеческие. Все постоянно собирались у него: он жил неподалеку от университета. Мы регулярно приходили — до семинара, после семинара. Ходили на совместные прогулки и по ходу дела постоянно обсуждали математику и все на свете.
О загадочном древе и ветви на нем
Анатолий Витушкин с учениками: слева — Александр Лобода, справа — Валерий Белошапка. 1970-е годы © Механико-математический факультет Московского государственного университета им.
М. В. ЛомоносоваЕсли посмотреть на всемирную историю, то в мире все меняется — образ жизни, земледелия, экономическое устройство. А математика продолжает расти как некое загадочное невидимое древо. Теорему Пифагора мы никуда не денем — с ней ничего не происходит. В нашем мире нет ничего более прочного и фундаментального, чем математика. Это дерево растет, потому что кто-то испытывает восхищение перед красотой этого мира или осознает свою душевную склонность и посвящает жизнь участию в этом загадочном, надчеловеческом процессе. Анатолий Георгиевич Витушкин дал жизнь определенной ветви на этом древе.
«Израиль Моисеевич был в какой-то степени визионер в математике»
Израиль Моисеевич Гельфанд — выдающийся, если не великий ученый, на мехмате руководил самым крупным семинаром всех времен и народов, сложный, порой противоречивый человек, который вызывал целый спектр эмоций — от восхищения до ненависти. Я не был учеником Израиля Моисеевича — лишь скромным посетителем его семинара.
Поэтому не берусь характеризовать его как ученого и как человека. Я могу только привести несколько эпизодов из его жизни, свидетелем или участником которых был сам.
О поступлении в аспирантуру и знакомстве с Колмогоровым
Израиль Моисеевич Гельфанд поступил в аспирантуру Стекловского института, не имея даже школьного образования. Он окончил свою учебу в предпоследнем школьном классе, а потом самостоятельно изучал математику. Существует легенда, что Андрей Николаевич Колмогоров застал его в библиотеке и разговорился с ним, а результатом этого разговора стало то, что через некоторое время не окончившего среднюю школу Гельфанда приняли в аспирантуру Института Стеклова. Таким образом, изначально Израиль Моисеевич был учеником Андрея Николаевича, хотя разность в возрасте у них очень небольшая. Я считаю, что очень часто легенда лучше передает суть дела, чем перечисление реальных фактов.
Об аудитории 1408 и опозданиях
Семинар проходил на мехмате в аудитории 1408.
Я начал его посещать в начале 70-х годов и продолжал быть его участником до 1989-го, когда Израиль Моисеевич уехал в Америку. Аудитория почти полностью заполнялась: на семинаре бывало около 120 участников. Они размещались определенным образом — каждый как бы знал свое место. Я, например, садился в самом конце аудитории, недалеко от выхода, чтобы не опоздать на последнюю электричку. Семинар официально начинался в семь часов, но Израиль Моисеевич вполне мог прийти с опозданием на полчаса или даже на 45 минут. При этом, если он приходил вовремя, а кто-нибудь опаздывал, он негодовал.
О школьнике Максиме
Израиль Гельфанд перед школьниками на математической олимпиаде. 1959 год cyclowiki.orgХарактерный эпизод произошел в 1979 году с участием школьника Максима, ученика 10-го класса московской математической спецшколы (на семинаре было несколько таких умных школьников). В начале семинара доклад делал известный ученый, фамилию которого я не хочу называть.
Он успел проговорить всего пять-шесть минут, но Гельфанд его резко прервал и сказал: то, что он делает, — полная ерунда, все нужно делать совсем не так, а по-другому. И объяснил, как это нужно делать, явным образом обращаясь к школьнику Максиму. Закончив это объяснение, он спросил школьника, понял ли тот, что он, Израиль Моисеевич, ему рассказал, и Максим скромно ответил, что понял. Тогда Гельфанд заявил, что на этом сегодняшний доклад кончается, а в следующий раз Максим Концевич расскажет всем, как на самом деле надо заниматься этим вопросом. И действительно, на следующем заседании Максим Концевич, ученик 10-го класса, сделал прекрасный доклад на эту тему. Конечно, в промежутке Максим успел побывать у Гельфанда дома и тот его вышколил, но тем не менее Максим понимал все то, что он тогда рассказывал.
Об обращении к докладчикам
Невежливое, а порой даже хамское отношение к докладчикам было, к сожалению, характерно для семинара Гельфанда. Израиль Моисеевич прежде всего не разрешал докладчикам как-либо комментировать то, что они рассказывают.
То есть доклад должен был начинаться со строгих определений и формулировок теорем. Единственным человеком, который имел право комментировать происходящее, был сам Израиль Моисеевич, и он очень часто пользовался этим правом. Особенно мне было неприятно то, как Израиль Моисеевич систематически третировал Георгия Шилова — замечательного математика, глубоко интеллигентного и мягкого человека, соавтора самого Израиля Моисеевича во время его докладов.
Еще мне запомнилось выступление на семинаре Гельфанда известного американского математика российского происхождения Липмана Берса. Гельфанд вполне вежливо себя вел по отношению к Липману Берсу, разрешал тому комментировать собственные работы, выслушал его до конца, не вмешиваясь в рассказ, а после этого объяснил, что, конечно, это все очень интересно, но ясно, что профессор Берс все делает не так, как нужно, а нужно делать совсем по-другому, — и объяснил, как это следует делать. Но, разумеется, Израиль Моисеевич не все доклады комментировал отрицательно — бывали случаи и когда он просто воздерживался от комментариев, и когда хвалил докладчика.
О том, почему на семинаре Гельфанда собирались лучшие математики
Израиль Гельфанд в мантии доктора Оксфордского университета. 1973 год © Василий Малышев / РИА «Новости»Кажется противоречивым то обстоятельство, что человек, который так возмутительно вел себя по отношению к докладчикам, собирал огромную толпу лучших математиков, ходивших на его семинар. На самом деле причина совершенно объяснима. На этих семинарах было чрезвычайно интересно, и особенно интересны были комментарии самого Гельфанда. Очень часто прямо во время семинара он выдвигал новые математические идеи, которые позволяли дальше развивать тематику доклада. Очень часто он позволял себе отступления, выходящие за тему доклада.
Особенно мне запомнилось его длинное выступление, где он стал объяснять, что такое математика. Он объяснил, что математика состоит из алгебры, анализа, геометрии и топологии, но самая главная часть математики — это комбинаторика, наука, которая еще не существует.
И действительно, следующие десятилетия показали, что комбинаторика, которая в тот момент была маргинальной наукой, связанной с арифметикой, стала центром математических наук. Если посмотреть на крупнейших математиков современности, то почти все их работы включают существенную комбинаторную часть.
О статьях и соавторстве с учениками
Важный инцидент в моей жизни, связанный с Гельфандом, произошел в начале 70-х. Был какой-то доклад, где обсуждались разные вопросы, связанные с алгеброй и алгебраической топологией. Когда доклад закончился, я вместе с моим другом и коллегой Дмитрием Фуксом подошел к освободившейся доске, и мы стали обсуждать возможную спектральную последовательность, которая решала бы одну из задач, поставленных докладчиком. Я стал писать на доске какие-то формулы, ко мне присоединился Митя, мы начали рассуждать о том, как построить и как вычислить эту спектральную последовательность, и не заметили, что к нам подошел Израиль Моисеевич и внимательно слушал, что мы говорили.
Тут наступило время второго доклада. Израиль Моисеевич нас прервал и сказал: «Очень интересно. На следующей неделе принесите текст нашей совместной статьи на эту тему». Уже после окончания семинара мы с Митей обсудили этот вопрос и решили, что не нужно писать эту статью, потому что получающийся результат был на уровне студенческой курсовой работы — задача оказалась легкой и недостойной отдельной публикации. Характерно, что на следующей неделе Израиль Моисеевич не спросил, написали ли мы работу. Раз мы ничего ему не сказали, он понял, что мы решили ее не писать, и с этим согласился.
Тут стоит отметить, что многие говорят о том, что Израиль Моисеевич очень злоупотреблял написанием совместных работ. Я могу расставить точки над i. В начале своей математической карьеры Израиль Моисеевич, как правило, сначала предлагал тему совместной работы, потом вместе с другими участниками ее проделывал и окончательный текст полностью писал сам. Со временем он стал ограничиваться только начальной идеей и постепенно перестал писать окончательный текст.
А в конце своей жизни он ставил себя соавтором работ, которые писали его ученики, иногда даже не читая саму работу. Это обобщение я привожу со слов одного из самых известных учеников Израиля Моисеевича, фамилию которого также не хочу называть.
О чуткости
Академик Израиль Гельфанд. 1970 год © Олег Кузьмин /Фотохроника ТАСССледующий эпизод, который касается меня в наибольшей степени, произошел в начале 70-х, когда Израиль Моисеевич пригласил меня и Дмитрия Борисовича Фукса на работу в его математико-биологическую лабораторию на биофаке. Я тогда отказался, а Митя принял это приглашение. Почему я отказался? Честно должен признать, что я испугался. И не Гельфанда, а себя самого. Я боялся, что, если Гельфанд начнет меня третировать так, как он третировал многих своих коллег и учеников, я не выдержу, и это приведет к конфликту, который закончится тем, что я хлопну дверью и уйду. Видимо, я зря это думал. Как я потом выяснил, Гельфанд был очень чутким человеком — он прекрасно чувствовал реакции окружающих его людей.
К примеру, он никогда не хамил Саше Кириллову — своему самому известному ученику, понимая, что Саша тоже не выдержал бы такое отношение. Думаю, что если бы я пришел к нему на работу, он и ко мне относился бы с осторожностью. Так или иначе, на биофак я не перешел, о чем, кстати сказать, нисколько не жалею.
О помощи
В 1975 году я оказался без работы. На самом деле я работал и зарабатывал деньги переводами, но при этом не состоял ни на какой ставке, поэтому известный закон о тунеядстве можно было применить и ко мне. Разные люди пытались устроить меня на работу, и среди них оказался, к моему удивлению, Израиль Моисеевич. Он обратился к одному из своих учеников, директору известного академического института, и тот позвал меня на освободившуюся ставку. Я с радостью туда явился, но, когда дело дошло до отдела кадров, выяснилось, что ставка исчезла в неизвестность. Несколько позже, когда подобные инциденты повторились, я понял, что состою в каком-то черном списке КГБ, и поэтому устроить меня на работу в научном институте или в университете невозможно.
Но я очень благодарен Израилю Моисеевичу, что он про меня вспомнил и не обиделся на то, что когда-то я не захотел прийти к нему на работу.
О попытке восстановить семинар в США
Израиль Гельфанд. 1982 год © Department of Mathematics Rutgers UniversityВ 1989 году Израиль Моисеевич уехал в США и стал профессором в Ратгерсе, где пытался восстановить свой семинар. Он прекрасно понимал, что его манера обращения с докладчиками совершенно невозможна в Соединенных Штатах. Тем не менее его попытки устроить в Америке такой же грандиозный семинар, как в Москве, полностью провалились — уж не знаю почему. Где-то в начале или середине 2000-х годов, когда я был в Америке, я выступил с докладом на этом семинаре, и это выступление произвело на меня очень грустное впечатление. Было очень мало народу, и сам Гельфанд был какой-то вялый — видимо, я не сумел его заинтересовать. Потом я вспоминал с грустью те героические времена, когда он так блистал на мехмате.
О визионерстве
Израиль Гельфанд.
1982 год © Department of Mathematics Rutgers University Израиль Моисеевич был в какой-то степени визионер в математике. Его собственные работы очень часто опережали время и были чрезвычайно разнообразны, относились к самым разным частям математики и не только математики. Несколько лет подряд его семинар был посвящен теоретической физике, которая благодаря его усилиям превратилась в то, что сегодня называют математической физикой. Наконец, Израиль Моисеевич занимался биологическими вопросами — и не только биологическими, но и медицинскими. Именно поэтому он создал математико-биологическую лабораторию на биофаке. То, что Израиль Моисеевич сделал в науке, пригодилось в самой математике, в физике, в биологии, но не имело, как ни странно, никаких прямых применений к непосредственным приложениям математики, в частности к приложениям к компьютерной науке. Особенно стоит выделить его замечательные работы по теории представлений, которые фактически составили чуть ли не основную главу теоретической физики в наши времена.
О школе
После себя Израиль Моисеевич оставил целую школу выдающихся математиков и физиков, каждый из которых эксплуатировал одну из сторон его математической деятельности. Учеников столь же универсального характера, как он сам, у него не было. Здесь он вполне сравним с Андреем Николаевичем Колмогоровым, у которого тоже была огромная научная школа, но каждый из его участников занимался лишь одной из многочисленных тем, которыми занимался сам Колмогоров.
«Александр Михайлович был самый неконформистский неконформист»
О нонконформизме
Вы, наверное, заметили с каким пиететом все математики говорят о своих учителях, своих научных руководителях. Это очень типично: мы все очень любим тех, кто нас научил математике. Меня математике научил Александр Михайлович Виноградов, который был на десять лет старше и совсем недавно умер. Из всех известных мне людей Александр Михайлович был самый неконформистский неконформист. Для него не существовало никаких устоявшихся правил.
Например, если было жарко, он приходил в университет во вьетнамках. Мы, студенты, к этому относились с некоторым восхищением, а у профессуры это вызывало, конечно, отторжение. Он со всеми был на равных — и со студентами, и со всякими высокопоставленными людьми. Если у него возникала какая-то идея, которую он считал важной (а это происходило регулярно), он ни перед чем не останавливался, чтобы попытаться ее реализовать. Он мог пойти на прием к Гавриилу Попову, который тогда был мэром Москвы, и проповедовать ему свои идеи о создании международного университета. Или к министру образования, чтобы тоже убедить его в необходимости каких-то других проектов.
Он не был профессором и никогда им не стал в России, но был прирожденным и замечательным математиком. Но этим его достоинства не ограничивались. Он плавал как рыба. Будучи студентом и аспирантом, он играл в водное поло за сборную мехмата. Он играл в футбол. И играл на скрипке. Он писал стихи. Он очень любил и хорошо знал поэзию Пушкина.
И этот его неконформизм проявлялся не только в жизни, но и в математике.
О необычном математике и воровстве идей
Он был необычным математиком. Студентом он учился у знаменитого Бориса Николаевича Делоне (деда диссидента Вадима Делоне) и написал с ним статью по теории чисел. Потом он ушел из теории чисел и уже аспирантом специализировался в алгебраической топологии, совершенно новой и поразительной науке, которая тогда только-только возникала. Долгое время он занимался алгебраической топологией и получил в этой области совершенно нетривиальные результаты мирового уровня, а потом бросил ее и стал заниматься совершенно другой наукой.
Очень трудно объяснить профану, что он сделал в математике. Если на пальцах, то, наверное, так: мы все знаем со школы, что бывает арифметика, бывает алгебра, а бывает анализ, или высшая математика, где проходят производные и пределы. Грубо говоря, Виноградов показал, что все это — одна и та же наука.
Очень многим его идеи были непонятны, и из-за этого возникали такие коллизии: люди читали его статьи, не понимали, потом как-то так по-своему перепонимали это, думали, что это они сами придумали, и публиковали результаты, которые на самом деле были результатами Виноградова.
Это его дико злило — он считал, что у него воруют, хотя это не было воровством и они искренне думали, что сами эти результаты получили. Но его невозможно было уговорить, что этот человек чист, что он не вор. Правда, и воровали тоже.
О семинаре, начинавшемся с футбола
Александр Виноградов — лидер московской школы геометрии нелинейных дифференциальных уравнений. 1970-е годы © Факультет математики и компьютерных наук ИвГУОкончив аспирантуру и став ассистентом на кафедре высшей геометрии и топологии, Виноградов организовал семинар по алгебраической топологии. Собственно, на этот семинар я к нему в 1968 году и пришел, будучи студентом второго курса. Когда Виноградов сменил область интересов и перешел к исследованию дифференциальных уравнений, этот семинар превратился в семинар по геометрии дифференциальных уравнений и стал заметным явлением в тогдашней мехматской, да и вообще математической жизни. Так возникло то, что потом стало называться московской школой по геометрии уравнений.
Семинар заседал по средам (и сейчас продолжается, но уже под моим руководством, тоже по средам, но в Московском независимом университете). Начинался он часов в пять, а приходили мы на него в два, потому что семинар начинался с футбола. Виноградов оформил себя руководителем группы по общей физической подготовке, поэтому нам были доступны раздевалки и душевые трехзального спортивного корпуса МГУ. Мы приходили и часа два играли в футбол. Команды либо назывались свои-чужие — например, когда мы играли с физиками, — либо старики на молодежь. «Старики» — это были Сосинский, Виноградов, его старший ученик Валя Лычагин, который всего на год меня старше, Митя Алексеевский. А молодежь — это мы и те, кто помладше. После этого мы принимали душ и шли обедать в профессорскую столовую. При этом разговоры велись о математике, о том, что интересного появилось в самиздате, и еще о чем-то в таком роде.
О бескомпромиссной битве
Потом начинался семинар, который состоял из двух частей. На первую образовательную часть приходили все и рассказывали вещи, которые не входили в тогдашнюю обязательную программу студентов мехмата.
Потом был перерыв: мы шли пить кофе или сок — это называлось «сачковать». После чего начиналась научная часть семинара, где мы рассказывали о том, какие новые результаты получили мы сами, включая самого Виноградова. И тут уже начиналась бескомпромиссная битва. Несмотря на то что все к нему относились с большим уважением, если что-то не нравилось, можно было сказать: «Саша, что за херню вы несете?» И он воспринимал это как должное.
Об учениках
Александр Виноградов с Иосифом Красильщиком. 2001 год © Из личного архива Иосифа КрасильщикаОн всегда был очень внимателен к своим ученикам — это вообще свойство многих хороших математиков. Не жалел времени и мог часами возиться с кем-нибудь, объясняя, рассказывая на примерах, спрашивая, пытаясь выяснять, поняли его или нет. А уж если вспомнить разговоры о науке, то он мог действительно бесконечно ее обсуждать. Он звонил мне поздно вечером и говорил: «Давайте поболтаем». И эта «болтовня» длилась час-полтора.
Но час-полтора разговора про математику по телефону — это ужасно трудно, это как игра в шахматы вслепую, потому что формулы ты не видишь. Но это его не останавливало, и он говорил, и говорил, и спрашивал, и предлагал. В общей сложности, я думаю, он воспитал где-то 50 учеников. К сожалению, правда, очень многие его бросили из-за сложности его характера.
О моделировании Древней Греции и мечте открыть институт в здании тюрьмы
Он всегда был полон идей, и математических, и организационных. У него была мечта создать свой институт, который под его руководством занимался бы только геометрией уравнений. Виноградов называл эту науку диффеотопия. Он вообще любил игру в слова и был такой математический полиглот и математический лингвист — в смысле любви выдумывать термины, иногда ужасные, а иногда очень удачные.
Начиная с 1990 года он жил на юге Италии, в районе Салерно. Я к нему очень часто приезжал по математическим делам, и мы с ним гуляли по окрестностям. Это было его любимое занятие — такое моделирование Древней Греции.
Он идет с учениками, и все обсуждают высокие материи. И вот он останавливался у каждой руины — и чем сильнее она была разрушена, тем более она ему нравилась, — и говорил: «Иосиф, смотрите, какое здание — здесь мы с вами устроим институт диффеотопии». Последней его идеей было перестроить в институт диффеотопии заброшенную тюрьму в городе Авеллино. Это, к сожалению, не осуществилось.
О зоопарке геометрических структур
Александр Виноградов. 2014 год © Katya Hayes / личная страница Александра ВиноградоваСейчас я как раз редактирую его трехтомник. Там есть статьи под названием «Зоопарк геометрических структур» и «Атомарная структура алгебр Ли» — это как раз примеры его любимой игры в слова. Он был геометром, как говорится, по жизни и по рождению, и обладал замечательным геометрическим воображением. Он себе все это представлял и рисовал картинки. Действительно, эти совершенно абстрактные конструкции, которые к геометрии имеют только косвенное отношение, можно сопоставить с некоторыми образами, похожими на чудовищных зверей, которых он изобретал в своей статье и которым придумывал имена.
Я думаю, он придумал с дюжину слов, новую терминологию — сороконожки, пауки, ежи и прочее. Страшно сложно это переводить, потому что по-английски это звучит еще ничего, а по-русски иногда совсем дико.
Виноградов замечательно знал итальянский — он приехал в Италию в 1990 году и сразу стал говорить по-итальянски, не уча его, и стал настоящим итальянцем. Итальянцы его обожали совершенно — он был человек их культуры. А с английским у него всегда были проблемы — он такой романский человек, не англосаксонский. И при этом человек без комплексов, поэтому все, что он хотел сказать по-русски, он ничтоже сумняшеся пытался говорить по-английски. Выходило подчас очень странно и смешно. И тексты он так же писал.
О создании Института Шрёдингера
Александр Виноградов в Израильском технологическом институте (Технионе). 2017 год © Vladimir Lin / личная страница Александра ВиноградоваЕго мечты о создании института диффеотопии не реализовались так, как он хотел, но многое ему удалось.
Например, в 90-е годы, когда началась свобода и научный Запад слился с научным Востоком, ему пришла идея, что нужно создавать институт, в котором могли бы общаться ученые Западной и Восточной Европы, включая Россию. И он посчитал, что самое лучшее место для этого — Вена. Он говорил, что Вена — это такая европейская Одесса, где смешаны самые разные народы. Кроме того, помимо многих великих композиторов, там работало довольно много великих математиков и физиков. В частности, Шрёдингер Эрвин Рудольф Йозеф Александр Шрёдингер (1887–1961) — австрийский физик-теоретик, один из создателей квантовой механики. Лауреат Нобелевской премии по физике, член Австрийской академии наук и многих других академий наук мира..
Виноградов стал носиться с этой идеей, охмурил — а он любил и умел охмурять — некоторых физиков и математиков из Венского университета. Они этой идеей загорелись, и в итоге организовался Институт математической физики имени Эрвина Шрёдингера в Вене. Сначала этот институт занимал две комнаты в большой и старой венской квартире, и я был одним из немногих первых его визитеров (уже позже он получил помещение внутри Венского университета).
У входа в институт лежала тетрадка, на которой было написано: «История Института Шрёдингера». Она начиналась словами, что в таком-то году русский математик Александр Виноградов решил создать институт математической физики в Вене. И вот прошло несколько лет, и вместо этого текста на первой странице написали: «В таком-то году группа математиков, в число которых входил русский математик Александр Виноградов, решила создать…» Потом прошло еще несколько лет, и текст оставался похожим, но имени Виноградова там уже не было. А еще через несколько лет Виноградов исчез из числа членов совета этого института. Он был занозой в глазу у чопорных венских физиков и математиков. Они не хотели делать так, как он хотел, не хотели приглашать тех людей, которых он хотел приглашать, не хотели заниматься той наукой, какой он хотел. И в итоге он с ними расплевался.
К сожалению, так очень часто случалось с его идеями и начинаниями. Ему трудно было ладить с людьми, а людям трудно было ладить с ним.
И при этом он был милейшим человеком — общаться с ним было наслаждением. Причем разным людям — не только математикам: он очаровывал всех.
Математиком он был до самой своей смерти. Его дочка Катя мне рассказывала, что буквально за день-два до смерти, в редкий момент, когда он еще был в сознании, она сказала ему: «Папа, может, тебе попить дать?» Он ответил: «Кать, какой попить, *****. Я наконец понял, что такое квантование». И это, возможно, были его последние слова.
«Он с нуля создал целую школу»
О чтении западных математических журналов в троллейбусе и поступлении в университет в 14 лет
Мой отец Игорь Ростиславович Шафаревич был не просто выдающимся, великим математиком, но совершенно уникальным явлением в культурной жизни нашей страны. Начнем с того, что он был вундеркиндом. В 14 лет он поступил в Московский университет и одновременно учился в школе и в университете. И вот он ходил к тогдашним знаменитым ученым, слушал их лекции, потом экстерном сдавал экзамены.
Будучи совсем молодым человеком, был знаком со всеми выдающимися математиками. Тогда, после войны, в 50–60-е годы, было время потрясающего расцвета советской математики — на факультете работала целая плеяда математиков величайшего уровня. Он был среди них.
В 23 года он уже стал доктором наук и защитил докторскую диссертацию, при этом решив ряд мировых проблем. Была такая знаменитая книжка немецкого математика Хельмута Хассе, специалиста в области алгебраической теории чисел, со списком проблем, стоявших в этой области. Почти все эти проблемы Шафаревич решил, как будто идя по списку. Когда ему было чуть-чуть за тридцать, он создал свою школу алгебраической геометрии. Сейчас эта область одна из самых популярных в математике, а тогда в Советском Союзе никто ей не занимался. Он рассказывал мне, что во время езды в троллейбусе листал западные журналы. Было почти ничего не понятно, потому что область была абсолютно незнакомой. Вдруг раз — что-то мелькнет. И снова непонятно. Вот так один и учил эти разделы.
О любви к музыке и горам
Он очень любил музыку. Кстати говоря, у него есть статья о Шостаковиче: я тут не специалист, но, на мой взгляд, это профессиональная музыковедческая статья. Он был блестящим лектором — студенты его обожали. Он каждый год читал новый спецкурс — это были уникальные курсы, некоторые из которых записаны, а некоторые, к сожалению, остались в рукописях. Летом он ходил в походы в горы и продумывал, какой новый спецкурс прочесть, и потом, возвращаясь осенью в Москву, начинал читать эти лекции. Вспомню один анекдот, который он мне рассказывал. Честно говоря, я не был уверен, что это на сто процентов правда, но уже после его смерти нашел у него в столе документ, подтверждавший эту историю. Он поехал в поход в горы и был там в альпинистском лагере. Случилось какое-то ЧП, и его забрали на спасательные работы. А у него начинались занятия на мехмате, и он отправил своему отцу телеграмму: «Задержан на спасательных работах. Сообщите в деканат». На почте перепутали, и телеграмма пришла такая: «Задержан на постельных работах.
Сообщите в деканат».
Насчет альпинизма — это тогда было довольно модно среди ученых. Игорь Ростиславович не был альпинистом высочайшего класса — у него был второй разряд. Тем не менее он ходил на вершины самой высокой категории: тогда категории были до пяти — он ходил на «пятерки». Но чаще он не совершал восхождения, а ходил в походы и позже к этому привлек своих учеников — среди них было много и горных туристов, и альпинистов, и они ходили в самые разные горы — от Кавказа до Памира.
О диссидентстве и подписании писем
Игорь Шафаревич © Archives of P. Roquette, Heidelberg / Oberwolfach Photo CollectionПомимо математической и общекультурной деятельности, он был известен своей общественно-политической деятельностью. Он был диссидентом: писал массу писем в защиту разных людей — Сахарова, Солженицына, людей, которых отправляли в психиатрические больницы, судили и сажали в тюрьму за политическую деятельность. Кроме того, он писал статьи политического характера, в которых обсуждал вопросы, связанные с социалистическим строем и развитием нашей страны.
Мягко говоря, взгляды его кардинальным образом отличались от взглядов тогдашней коммунистической верхушки.
Есть один смешной эпизод, связанный с общественно-политической деятельностью отца. Мне, наверное, было лет одиннадцать — его диссидентская деятельность тогда была в разгаре. И вот звонок в нашу квартиру. Он открывает дверь — там стоит стандартная пара, которая приходила перед арестом или обыском: милиционер в форме и человек в штатском. «Гражданин Шафаревич здесь живет?» Он понимает, что, наверное, дело плохо: «Да-да, это я». — «Ваш сын разбил стекло в сберкассе — с вас штраф 3 рубля». А мы играли с друзьями в хоккей, и я действительно залепил шайбой в окно сберкассы.
О дружбе с Солженицыным
Игорь Шафаревич и Александр Солженицын © Из личного архива Андрея ШафаревичаНачалось с того, что Солженицын зашел к нам домой — просто с ним познакомиться. Он тогда был начинающим писателем, хотя уже в возрасте, старше моего отца. Первое знакомство оказалось неудачным.
Дело в том, что изредка Игоря Ростиславовича отпускали в заграничные командировки. Он как-то катался на лыжах в Альпах, в Шамони, на знаменитом французском курорте. Оттуда у него были открытки с видами разных гор, и он их показал Солженицыну. Тот сразу подумал, что это прикормленный властью человек, советский функционер и разговаривать с ним не о чем. Они поговорили, чаю выпили, и он ушел. А после этого Солженицын увидел его подпись под каким-то очередным письмом протеста, и опять к отцу обратился. Они были очень дружны до того момента, когда Солженицына выслали.
У Солженицына есть книжка «Бодался теленок с дубом», и несколько эпизодов касаются Игоря Ростиславовича. В одном он как раз описывает свой арест, после которого его выслали из Советского Союза. Мой отец при этом присутствовал — он пришел к нему обсуждать финальный вариант «Из-под глыб», и тут Солженицына пришли арестовывать. Я помню, что он пришел домой очень поздно взволнованный и рассказывал, в какой драматической ситуации оказался.
В той же книге, «Бодался теленок с дубом», описан такой эпизод. Они как-то гуляли за городом. Кажется, была весна, шли через речку по каким-то бревнышкам. Вокруг прекрасная подмосковная природа. И Солженицын говорит: как будет тяжело все это вспомнить, если жить не в России. На что отец ему ответил: да невозможно жить не в России.
У него всегда было такое отношение — он себя не представлял в других странах. После высылки Солженицына он заготовил несколько писем на случай своего ареста, которые лежали у разных людей, в частности у моей сестры. В них он призывал никакое иностранное государство его не принимать, потому что он отказывается жить где бы то ни было, кроме как в России.
Он несколько раз мне говорил, что ощущает себя человеком русской культуры. Хотя мировую культуру очень любил и знал в совершенстве три языка: английский, немецкий и французский, кроме того, немного древнегреческий, который специально выучил для того, чтобы читать в подлиннике Эсхила и Гомера.
Но русская культура была ему как-то особенно, нутряным образом близка.
Об академиках Иване Петровском и Иване Виноградове
Игорь Шафаревич после вечера встречи с ним © Из личного архива Андрея ШафаревичаЛюди, у которых он работал, подвергались определенному давлению. Среди них был Иван Георгиевич Петровский, знаменитый академик, тоже математик, ректор Московского университета. Отец рассказывал, что тот несколько раз к нему подходил и говорил: «Игорь Ростиславович, от меня требуют вашей крови, — то есть требовали, чтобы он уволил его из университета. — Но я не сдаюсь». И действительно, пока Петровский был жив, Игорь Ростиславович Шафаревич продолжал преподавать в Московском университете и прямо на первом курсе читал обязательный курс алгебры.
В 1973 году Петровский умер, а буквально через год или два Игоря Ростиславовича уволили. Тогда не только умер Петровский, но и велась кампания, связанная с высылкой Солженицына, а Солженицын и мой отец вместе организовали сборник «Из-под глыб», в котором были статьи с философскими рассуждениями о судьбах России.
Солженицына арестовали, выслали, и этот сборник тут же вышел на Западе. По этому поводу отец дал интервью иностранным корреспондентам в нашей квартире — он специально подгадал так, чтобы ни меня, ни мамы не было дома, чтобы нам не могли ничего пришить. После этого его из университета уволили.
Был и еще один человек — Иван Матвеевич Виноградов, тоже знаменитый математик, академик, директор Института Стеклова, в котором Игорь Ростиславович работал всю свою жизнь. В Советском Союзе для всех сотрудников была обязательна общественная работа. Не такая общественная работа, которой занимался мой отец, а, скажем, в комсомоле, или в профсоюзе, или куратор над школой, или еще что-нибудь. И вот встречает как-то Иван Матвеевич Виноградов Игоря Ростиславовича в коридоре и говорит: «Игорь Ростиславович, мне все время говорят, что вы не занимаетесь общественной работой». Тот ответил: «Помилуйте, Иван Матвеевич, я ли ей не занимаюсь!» Виноградов тоже его защищал всячески до самой своей смерти.
Об учениках
Игорь Шафаревич © Konrad Jacobs, Erlangen / Oberwolfach Photo CollectionУ него была масса учеников — они к нему просто рвались.
На лекциях или научно-учебных семинарах он формулировал сразу несколько вопросов, которыми был готов заниматься со студентами, — от довольно простых до мировых проблем. Один раз он сказал, что готов дать разным людям три задачи на выбор. Одну настоящую научную задачу, чье решение он знает. Вторую — с вопросами, которые совсем плохо изучены. А третью — с кругом вопросов, которые совершенно не исследованы. И вот — прямо как в сказке про трех сыновей — к нему подошли три студента. Один попросил задачу попроще, другой — посложнее, а третий сказал, что хочет заниматься этой великой задачей — так называемой проблемой Бёрнсайда. Игорь Ростиславович испугался: как у этого студента такое получится — нужно же писать курсовые, диплом. Тем не менее он начал с ним заниматься, и в итоге этот студент, Алексей Иванович Кострикин, эту проблему решил и стал знаменитым математиком (кстати, он стал впоследствии деканом мехмата).
О свободе
Игорь Шафаревич. 1994 год © Владимир Первенцев / РИА «Новости»Я сам был еще слишком молод для того, чтобы наблюдать его общение со студентами, но с очень многими его учениками я знаком, и они говорили, что он давал большую свободу.
Не заставлял их жестко делать вот это, это и это, а открывал перед ними область и давал выбирать путь по склонностям, всячески им при этом помогая. У него было огромное количество учеников, которые его очень любили. Я помню, что у нас дома его ученики все время занимались, писали работы. Когда у него были дни рождения или юбилеи, у нас был полный дом учеников. Как-то раз я вышел на балкон и увидел, как к нему идут гости — по-моему, это ему 60 лет исполнялось. Весь двор нашего дома заполнен огромной толпой, которая к нему шла. Последнюю свою работу по математике он написал, когда ему было 90 лет. Так что он всю жизнь отдал математической науке.
О научных достижениях и школе
Борис Делоне и Игорь Шафаревич. Конец 1940-х годов kolmogorov.livejournal.comЕсть такой математический термин — «группа». И есть группа Шафаревича — Тейта. Джон Тейт — это знаменитый американский математик. Они параллельно ее придумывали, но во всех языках она обозначается русской буквой Ш. Но я не думаю, что это его самое главное научное достижение. Как я уже говорил, будучи совсем молодым, он решил ряд задач, которые тогда считались очень сложными и представляли собой мировые проблемы. Общий закон взаимности из области алгебраической теории чисел — это развитие вопроса, который еще Гаусс обсуждал в конце XVIII века. Знаменитейшая его работа посвящена обратной задаче теории Галуа для разрешимых групп. За эти работы он получил Ленинскую премию. А потом, начиная со второй половины 50-х годов, то есть когда ему было где-то 34 года, он начал заниматься новой для себя областью — алгебраической геометрией. В Советском Союзе этой области никто не знал. Он говорил, что ему не с кем было обсудить эти вопросы, не с кем поговорить, и только когда у него стали появляться ученики, он смог обсуждать эту область с ними. В этой науке у него есть достижения самого высочайшего уровня — и он с нуля создал целую школу. И сейчас эта область, алгебраическая геометрия, — одна из самых популярных и модных в математике. В ней присуждают престижные международные математические премии, а школа Игоря Ростиславовича до сих пор в мировом топе — возможно, сильнейшая в мире.
«Он своим ученикам верил»
О секрете успеха
Меня очень интересовал вопрос: почему не каждый из хороших и даже великолепных математиков, имеющих достаточно много учеников, создает научную школу? В чем в данном случае секрет успеха? Для себя я ответил на этот вопрос так: в очень многих случаях научный руководитель, даже будучи очень крупным ученым, дает своим ученикам темы, которые лежат в области его интересов. К чему это приводит? К тому, что каждый занимается более узкой тематикой и за два-три научных поколения происходит вырождение: люди изучают настолько мелкие проблемы, что это не рассматривается математическим сообществом как нечто значимое. Подход Петра Лаврентьевича был совершенно иной: он своим ученикам верил. Он мог оценить значимость задач не только в своей области, но и в смежных, и охват тем был очень широк. Поэтому среди учеников Петра Лаврентьевича, если я правильно помню, 14 докторов наук, многие из которых создали свои собственные школы. Например, школы теории функций в Грузии и Армении в значительной мере состоят из учеников Петра Лаврентьевича. Это очень важный момент: даже спустя много лет после кончины их основателя научные школы развиваются вполне успешно.
О лыжах, разгрузке вагонов и подсолнечном жмыхе
Биография Петра Лаврентьевича была достаточно тяжелая. Родился он в 1928 году в крестьянской семье в селе Слепцовка. Он был вынужден ходить в школу через лес — пять километров на лыжах, а может, даже больше. Кстати, Петр Лаврентьевич потом сумел это обернуть себе на пользу и стал хорошим лыжником и спортсменом вообще, что ему помогало всю жизнь.
В 1945 году он поступил в Саратовский университет. Время было очень сложное, и родные не могли ему помогать. Он учился отлично, а по ночам ходил на станцию и разгружал вагоны. Платили ему подсолнечным жмыхом, часть которого употреблялась в пищу, а часть менялась на что-то еще.
При поступлении ему пришлось выдержать большую конкуренцию: это был год окончания войны и пришло поступать много фронтовиков. У них Петр Лаврентьевич много чему научился в жизненном плане — например, хорошо понимать людей.
Об умении видеть людей
Петр Ульянов и Борис Кашин (теперь академик РАН). Около 1995 года © Из личного архива Михаила ДьяченкоВ 2000 году мы вместе поехали на один локальный математический конгресс в Польшу. На обратном пути мы приехали на вокзал в Познань. Было уже совсем темно, и мы увидели, что на перроне собралась компания молодых людей накачанного вида и в спортивных штанах. Я сказал Петру Лаврентьевичу: «Давайте поосторожнее — явно они будут ехать с нами в одном вагоне». Он на меня посмотрел и говорит: «Михаил Иванович, вы не правы — это спортсмены, я сразу вижу». И действительно потом оказалось, что это команда борцов, возвращающихся с соревнований. Вообще Петр Лаврентьевич очень хорошо умел раскрывать натуру человека, давая людям высказаться. При этом он задавал какие-то вопросы, на первый взгляд совершенно невинные, и было любопытно смотреть, как человек проявляется и что он из себя представляет.
О семинаре и обзоре курсовых
Каждую осень одно из первых занятий семинара было посвящено обзору возможных тем курсовых работ. Курсовые работы — название очень обобщенное: это могли быть и темы докторских диссертаций. На эти обзоры сбегалось очень много народу. В аудиторию притаскивали стулья, было не протолкнуться. Пожалуй, недовольны этим были только уборщицы, а все остальные с удовольствием слушали то, что Петр Лаврентьевич рассказывал.
Широта его кругозора была уникальна. Он тратил на эти встречи очень много времени: прочитывал огромное количество научной литературы и потом черпал оттуда темы. После того как человек брал тему курсовой работы, он должен был периодически приходить к Петру Лаврентьевичу и отчитываться о том, что сделал. Первые работы все писали по многу раз, писали, переписывали, он это все читал, подчеркивал все непонятные места, то есть прочитывал абсолютно все работы и говорил, что нужно переделать. Это переписывание могло происходить раз пять-шесть.
У Петра Лаврентьевича было два семинара. Один — в пятницу вечером, с 18:30 до восьми, и там выступали достаточно известные люди. А другой — в среду, и на него ходили студенты и аспиранты. После семинара Петр Лаврентьевич всегда устраивал встречу с учениками. Это затягивалось до полпервого ночи, и нужно было тренировать волю — сидеть дожидаться.
Об отношении к ученикам
Петр Ульянов с группой участников школы по теории функций. Байкал, бухта Песчаная, 1987 год© Из личного архива Михаила ДьяченкоПетр Лаврентьевич очень заботился и о своих учениках, и о студентах вообще. Например, один из его студентов, достаточно талантливый парень, в какой-то момент перестал появляться на семинарах. А жил он километрах в трехстах от Москвы. Петр Лаврентьевич собрался, поехал, нашел его родственников и выяснил, что с этим человеком произошло. Хотя в тот момент он уже был немолодым человеком и заслуженным профессором. Мне доводилось видеть, как у других научных руководителей пропадали достаточно талантливые студенты, и никто не интересовался, почему это произошло, почему он бросил заниматься.
О сходстве с Петром I
Петр Ульянов. Калязин, 1990-е годы © Из личного архива Михаила ДьяченкоПетр Лаврентьевич очень гордился, что его зовут Петром. И надо сказать, что в его высказываниях было большое сходство с Петром I. Например, указ Петра об отмечании Нового года в России начинался словами «с сего числа перестать дурить головы людям», а заканчивался так: «А взрослым людям пьянства и мордобоя не учинять — на то других дней хватает». Однажды мы были на конференции под Казанью на берегу Волги. Расслабленная атмосфера не на всех действовала положительно, и один человек чересчур увлекался употреблением горячительных напитков, но на лекции ходил и даже там выступал. Петру Лаврентьевичу это сильно не нравилось, потому что он считал это совершенно недопустимым. И вот однажды он поймал этого человека на улице и сказал: «Я вам хочу сказать две вещи: первая — на лекции пьяным не ходить, второе — глупых вопросов не задавать, потому что пьяный человек ничего, кроме глупостей, сказать не может». Мне показалось, что это очень созвучно тому, что в свое время писал Петр I.
«В 26 лет Сергей Львович был избран членкором Академии наук, а в 30 лет — академиком»
О гусях
Отрочество и молодость Сергея Соболева были бурными. Эвакуация в Харьков во время Гражданской войны, возвращение в Петроград, окончание экстерном школы, занятия в музыкальной студии (где познакомился с будущей женой Ариадной Дмитриевной), увлечение математикой. Школу Сергей окончил в 15 лет и поступить в университет не смог по двум причинам. Первая — «неправильное» социальное происхождение (разночинное дворянство), вторая — малолетство. Соболев решил, что окончит музыкальное училище и продолжит карьеру музыканта. Учительница из школы, где он учился последние выпускные полгода, встретив Сергея на улице и узнав, что он собирается стать музыкантом, сказала: «Если ты не будешь заниматься математикой, я при следующей встрече тебе руки не подам». Сергей понял, что судьба его определилась и надо решать проблему поступления. В анкете пришлось написать, что, находясь в эвакуации, он пас гусей, а второе препятствие исчезло само собой, когда мать, которая была медиком, то есть специалистом, нужным советской власти, получила «путевку в вуз» для сына. В те годы не было вступительных экзаменов — требовалась путевка с места работы родителей.
О первой научной работе
Сергей Соболев в молодости. Ленинград, 1930-е годы © Институт математики им. С. Л. СоболеваБудучи на втором курсе, Сергей слушал лекции профессора Николая Максимовича Гюнтера. Речь шла о математической теории потенциала. Соболев не понял одну из теорем, засомневавшись в ее точности. После лекции он подошел к профессору и сказал, что не понял теорему. Гюнтер ответил: «Молодой человек, от кого угодно ждал такого вопроса, но не от вас! Сядьте и разберитесь». Соболев вернулся домой, разобрался в теореме, понял, что она действительно неверна, и построил контрпример. Перед следующей лекцией он показал этот пример Гюнтеру. Николай Максимович отменил лекцию и сел разбираться. Он был шокирован: пример оказался точным и правильным, а теорема — неверной. Гюнтер попросил Соболева написать заметку и представил ее в журнал «Доклады Академии наук». Так вышла первая печатная работа молодого Сергея, был он в самом начале своей выдающейся научной карьеры…
О выбитой двери
Академик Сергей Соболев выступает на кафедре новосибирского Академгородка. 1972 год © РИА «Новости»Однажды Сергей Львович сидел у себя в кабинете в Курчатовском институте. В этот кабинет вели огромные, тяжеленные дубовые двери с массивными замками — такие типичные входные двери, как в главное здание МГУ. Сергей Львович занимался оборонными задачами, применяя новые подходы, связанные с обобщенными решениями. И вдруг раздался стук в дверь: оказалось, что это человек из первого отдела с каким-то вопросом. А первый отдел — это отдел НКВД в учреждении, следивший за работой ученых. И вот замок заклинило. Сергей Львович понял, что, если он сейчас не откроет дверь, последствия будут ужасные — вплоть до того, что могут и отстранить от работы, и посадить. Поэтому он разбежался — а он был большого роста, крупный, мощный, с мышцами — и высадил эту дубовую дверь вместе с петлями. При этом он сломал ключицу, его отправили лечиться. Так у него появилась возможность спокойно сесть и написать книгу «Некоторые применения функционального анализа в математической физике», обобщив свои новые подходы.
О лекции на открытии МГУ
1 сентября 1953 года первую лекцию на открытии главного здания на Ленинских горах читал Соболев. Он вошел в аудиторию и сразу начал лекцию — даже никаких вводных слов. Студенты удивились: обычно сначала хоть какие-то вводные слова говорятся — какой курс, о чем, что будет. А он сразу написал уравнение.
О работе в атомном проекте
Академик Академии наук СССР, математик Сергей Соболев (справа на втором плане) с аспирантами. 1958 год © Лев Портер / ТАСССергей Львович был выдающимся математиком, очень честным человеком, потрясающим отцом и дедом, интересным преподавателем. Можно перечислять еще много свойств, качеств и заслуг, но я хочу заострить внимание на одном. В 26 лет Сергей Львович был избран членом-корреспондентом Академии наук, а в 30 лет — академиком. Потому что в этот момент он создал совершенно революционную новую теорию — теорию обобщенных решений дифференциальных уравнений. Окончив вуз, он попал по распределению в Сейсмологический институт. Ему была поставлена задача выяснить, каким образом можно предсказывать землетрясения. Эту задачу он сначала сформулировал математически, а потом придумал метод и решил — сейсмологи до сих пор пользуются формулами, которые он тогда вывел. Аналогичные подходы он использовал, занимаясь в ядерном проекте — разработкой атомной бомбы, расчетом структуры атомного реактора, упрощением и удешевлением обогащения урана. Он был первым заместителем Курчатова Игорь Васильевич Курчатов (1903–1960) — физик, основатель и первый директор Института атомной энергии, главный научный руководитель атомной проблемы в СССР, один из инициаторов использования ядерной энергии в мирных целях. по науке и курировал в атомном проекте всю математику. На основе его обобщенной теории строятся мосты, космические корабли и вообще рассчитывается все, что движется, включая тайфуны и вихри в атмосфере.
О трех этапах
Сергей Соболев. 1970-е годы © Изображение предоставлено Григорием ЧечкинымЕго жизнь делится на три этапа. Первые 25 лет он жил в Петербурге, а потом Ленинграде, учился на матмехе Ленинградского университета и работал в Сейсмологическом институте. Потом он перешел в Институт Стеклова. Вторые 25 лет он провел в Москве и там работал тоже в Институте Стеклова, МГУ и Институте Курчатова, который тогда назывался Лабораторией № 2. С Московским университетом судьба Соболева связана необычным образом. Он работал на кафедре дифференциальных уравнений под руководством Петровского. Вместе с Петровским и Андреем Николаевичем Тихоновым, одним из величайших наших математиков, он вел семинар мирового уровня. А потом в какой-то момент Петровский предложил Сергею Львовичу возглавить кафедру вычислительной математики. Параллельно он как раз разрабатывал атомный проект, занимаясь численными расчетами. Тогда только создавались компьютеры, и, по сути, Соболев стоял у истоков, готовя для них программное обеспечение. И нужна была кафедра, которая готовила бы специалистов. Соболев согласился на предложение Петровского и вывел эту кафедру на мировой уровень: потом из нее вырос факультет вычислительной математики и кибернетики. И наконец, последние 25 лет жизни он провел в Новосибирске, став одним из организаторов Сибирского отделения Академии наук.
Партнерский материал
\n’ + ‘‘ + first_and_last_name + ‘
\n’ + ‘Алгебра и геометрия, 10 класс ЕМН, СОР и СОЧ
Решение заданий СОР и СОЧ за 10 класс ЕМН
(если непонятно, то запишитесь на наши дистанционные занятия)
1 четверть
СОР 1 по алгебре, объясняет Дария:
СОР 2 по алгебре, объясняет Дария:
СОР 3 по алгебре, объясняет Дария:
СОР по геометрии, объясняет Айгерим:
СОЧ по алгебре:
СОЧ по геометрии, объясняет Айгерим:
2 четверть
СОР 1 по алгебре, объясняет Айгерим:
СОР 2 по алгебре, объясняет Айгерим:
СОР 3 по алгебре, объясняет Айгерим:
СОЧ по алгебре, объясняет Айгерим:
СОР по геометрии, объясняет Айгерим:
СОЧ по геометрии, объясняет Айгерим:
3 четверть
СОЧ по алгебре, объясняет Айгерим:
СОЧ по геометрии:
СОР 1 по алгебре:
СОР 2 по алгебре:
СОР 3 по алгебре:
СОР 1 по геометрии, объясняет Айгерим:
СОР 2 по геометрии:
4 четверть
СОЧ по алгебре, объясняет Айгерим:
СОЧ по геометрии, объясняет Айгерим:
СОР по геометрии, объясняет Айгерим:
Псст, есть ещё физика.
Школьников будут тщательнее проверять на пристрастие к наркотикам
С 1 сентября в России начнут действовать новые правила профилактических осмотров школьников, которые ежегодно проводят для борьбы с наркоманией среди подростков. Пробы, взятые у детей, проверят на девять видов запрещённых веществ. А если предварительный результат будет отрицательным, но врач-нарколог заподозрит у ребёнка пагубное пристрастие, то анализы проведут повторно в специальной лаборатории. Родители в этом году получат доступ к результатам исследований — 31 июля президент подписал закон, который разрешает законным представителям получать информацию о здоровье подростков вплоть до совершеннолетия, а не до 15-летнего возраста, как было раньше.
Как проводят «антинаркотические» осмотры школьников
В 2018 году 2,9 тысячи юношей и девушек в возрасте от 15 до 17 лет состояли на учёте из-за вредных последствий употребления наркотиков. Чтобы не доводить до этого и как можно раньше выявлять употребление детьми запрещённых веществ, в школах, колледжах и вузах проводят профилактические осмотры. При этом у детей, которых привлекают к таким мероприятиям, и их родителей, есть права, которые перечислены в приказе Минздрава от 2014 года.
Осматривать могут только детей, которым уже исполнилось 13 лет. На это требуется письменное согласие. За детей до 15 лет документы подписывает родитель, а более старшие ученики принимают решение сами. От осмотра можно отказаться.
Для прохождения процедур дети приходят в медицинскую организацию. Во время осмотра:
Медицинские работники беседуют с учениками или студентами о вреде наркотиков;
Собирают сведения о наркотических и психотропных препаратах, которые дети принимают по назначению врача;
Психиатр-нарколог проводит поверхностный осмотр каждого ребёнка: осматривает кожные покровы, лимфатические узлы, слизистые оболочки, ощупывает кости, суставы и кровеносные сосуды, слушает органы дыхания и сердце, измеряет артериальное давление, частоту дыхания и пульса, исследует вестибулярные функции. Результаты врач вносит также в историю развития или медицинскую карту обучающегося.
Собирают пробы мочи.
После этого проводятся исследования проб, а результаты разъясняют самому ребёнку, если ему есть 15, или одному из его родителей, если он младше. Если в моче обнаруживают следы наркотиков или психотропных веществ, врач выдаёт направление в наркологический диспансер. Но для этого опять-таки требуется информированное согласие в письменной форме законного представителя ребёнка или самого ученика, если ему исполнилось 15 лет.
Осмотры проводят не в каждой школе, а в образовательных учреждениях из списка, который каждый год составляют власти регионов в сфере здравоохранения и образования.
Что изменится в этом году
Приказом Минздрава, который вступает в силу 1 сентября, эти правила уточняются. В том числе в документе расписано, на какие вещества проводят анализ в обязательном порядке. Это опиаты, каннабиноиды, фенилалкиламины (амфетамин, метамфетамин), синтетические катиноны, кокаин, метадон, бензодиазепины, барбитураты и фенциклидин, их производные и аналоги. Исследования должны будут успеть провести в течение двух часов после того, как взяли пробы. Кроме этого, в приказе чётче прописаны методы, которые должны применяться при проведении анализов.
Эти изменения понадобились, так как постоянно создаются и распространяются новые психоактивные вещества, и пора обновить методологию и ресурсы, пояснил «Парламентской газете» зампред Комитета Госдумы по охране здоровья Николай Говорин. «Подобные исследования будут проводиться на уровне центральных районных больниц, что естественно требует определённых материальных затрат, чтобы каждая центральная районная больница была обеспечена техническими возможностями, аппаратурой», — сказал он.
Отбирать школы и вузы для участия в ежегодном осмотре региональные власти теперь будут не по своему усмотрению, а исходя из численности обучающихся, имеющих риск потребления наркотических средств и психотропных веществ.
Кроме этого, документ расширяет количество случаев, когда результаты будут перепроверять. Раньше, если предварительный анализ показывал, что в моче нет следов наркотиков, на этом исследование завершали. На дополнительную диагностику в химико-токсикологическую лабораторию направляли только те пробы, где обнаружили запрещённые вещества. Теперь же отрицательные результаты станут тоже отправлять на дополнительное исследование, если психиатр-нарколог обнаружит при осмотре ребёнка хотя бы три из признаков, в числе которых, в частности, неадекватность поведения, заторможенность, сонливость или возбуждение, эмоциональная неустойчивость, ускорение или замедление темпа мышления, необычный цвет кожных покровов и слизистых, сухость кожи или слизистых, повышенное потоотделение, вялая реакция зрачков на свет, тремор век, языка или рук, нарушение речи в виде дизартрии.
Говорин пояснил, зачем могут понадобиться дополнительные исследования. Дело в том, что даже если анализ на препараты из десяти основных групп отрицательный, есть вероятность, что ребёнок употребляет что-то ещё. И чтобы дать объективную оценку его состоянию и начать лечение, если заболевание подтвердится, может понадобится сделать анализы в специализированной лаборатории. Для этого на исследование отправят анализ мочи. Комиссия врачей также может направить школьника или студента на дополнительное обследование и забор крови, рассказал Говорин.
По его словам, изначально против практики профилактических осмотров были многие родители. Они опасались огласки — вдруг их ребёнок что-то употребил, и все об этом узнают. Но бояться, по его мнению, не нужно. Результаты сообщают только родителям и детям, а если окажется, что ребёнок болен наркоманией, можно будет начать лечить его как можно раньше.
Родители будут в курсе результатов анализов
В конце июля Президент России Владимир Путин подписал разработанный парламентариями закон, который позволяет родителям получать информацию о состоянии здоровья своего ребёнка вплоть до совершеннолетия. Раньше, как только человеку исполнялось 15 лет (или 16 лет, если он признан больным наркоманом), он получал доступ к своим медицинским данным, а родители лишались такого права. Теперь информация о здоровье доступна как самому подростку, так и его законным представителям.
Когда документ ещё только разрабатывался, один из его авторов, председатель Комитета Совета Федерации по экономполитике Андрей Кутепов рассказал «Парламентской газете», зачем это понадобилось. Дело в том, что подросток может скрывать проблему, которая требует срочного решения, в то время как медицинские работники могут выявить её во время приёма или профилактического осмотра. В том числе если речь идёт о наркотической или алкогольной зависимости, ранней беременности, венерических заболеваниях, травмах, полученных в результате конфликтов со сверстниками, психологических трудностях.
Теперь же родители будут в курсе, так как смогут получить информацию напрямую у медиков. При этом несовершеннолетние пациенты старше 15 по-прежнему имеют право, например, узнать результаты своих анализов без присутствия взрослых.
“Класс” и его производные
Марк Никол
Латинское существительное classis , означающее «категория» или «флот» или относящееся к группе граждан, призванных на военную службу, является источником слова class и других производных от него слов, которые перечислены и определены в этом посте. .
В контексте образования класс относится к группе учащихся (независимо от того, зачислены ли они на определенный курс или в один и тот же класс), учебному курсу или собранию такого курса. В социально-экономическом смысле он относится к слою социального положения, в науке он обозначает уровень организации живых существ и вообще относится к категории. Глагол class , означающее «категоризировать», используется в научном и общем смысле, и это слово служит прилагательным, в том числе в идиоме «классовый акт», которая предлагает дополнительное значение, эквивалентное прилагательному classy, означающему «элегантный, «утонченный», «искусный» или «хорошо воспитанный».
Прилагательные первого класса и второго класса буквально относятся к высокому и среднему качеству размещения во время путешествия, соответственно, и образно обозначают соответственно превосходство и неполноценность. ( Высокий класс и низкий класс эквивалентны последним значениям. ) Существительные «высший класс» (относящиеся к богатым), «средний класс» (те, кто ведет умеренный образ жизни) и «низший класс» ( лица с низкими доходами или вообще без доходов) также выступают в качестве прилагательных.
«Развлекательный класс» относится к людям, достаточно состоятельным, чтобы не зарабатывать на жизнь трудом. «Рабочий класс» описывает людей, занятых на работах, которые не обязательно требуют высшего образования в качестве квалификации для трудоустройства. ( Underclass имеет сходное значение.) Уничижительное, снисходительное выражение «болтующие классы» намекает на политических оппонентов, которые высказывают то, что считается бессмысленными мнениями.
Термины, относящиеся к образованию с корневым классом, включают одноклассник , относящийся к тому, кто зачислен на тот же курс или класс, и классную комнату, обозначающую комнату, используемую для обучения. Старшеклассник — это учащийся одного из двух более высоких уровней среднего или послесреднего образования (часто определяемый как младший или старший), а младшеклассник имеет положение на одном из двух более низких уровней (первокурсник или второкурсник). Женские эквиваленты старшеклассница и младшеклассница встречаются редко.)
Несколько терминов, основанных на классе, указывают на высокое качество художественных достижений. Классический , как существительное или прилагательное, намекает на что-то авторитетное или типичное, или долгое время считавшееся образцом великих достижений или высокого качества, хотя в более широком смысле теперь оно описывает что-либо запоминающееся, даже если просто потому, что это очень забавно или иронично. («Вы видели, как она споткнулась и упала в ее свадебный торт? Это классика!») «Классика» описывает либо дошедшие до нас произведения знаменитых греческих и римских писателей, либо смутную массу более поздней литературы, которую те, кто претендует на эрудицию, должен быть ознакомлен.
Стиль архитектуры или искусства, включая литературу, напоминающий о характерных чертах греческих или римских достижений, называется классицизмом. Неоклассицизм – это эстетическая форма, на которую повлиял классицизм, а постклассицизм обозначает тот, который следует за периодом, который считается периодом классицизма. (Формы прилагательных: классический , неоклассический и постклассический .) Классическая музыка – это форма сложного музыкального выражения, отличная от более простой музыки, такой как фолк или джаз.
С точки зрения качества или социальных слоев, другие слова, производные от класса, включают классизм , означающий «дискриминацию на основе класса», а также бесклассовый , который может относиться либо к отсутствию утонченности, которое считается результатом воспитанный в низшем классе ( déclassé – синоним этого значения, заимствованный непосредственно из французского) или тому, кто живет вне классовых ограничений или свободе от классовых различий.
Слова, относящиеся к категоризации, включают глагол классифицировать и прилагательное классифицировать , которое просто означает «распределить по классам», но также является частью постоянной фразы «классифицированные объявления» (иногда сокращенной до «объявления»), которая относится к рекламным объявлениям, разделенным на категории; прилагательное также описывает что-то, относящееся к категории ограниченного для определенной аудитории, например, правительственный документ. То, что можно классифицировать, поддается классификации, и классификатор описывает что-то, относящееся к классификации.
Превзойти означает превзойти кого-то, кто считается принадлежащим к тому же классу, а подкласс — это дальнейшее подразделение категории.
Хотите улучшить свой английский за пять минут в день? Оформите подписку и начните ежедневно получать наши советы по письму и упражнения!
Продолжай учиться! Просмотрите категорию «Словарь», просмотрите наши популярные посты или выберите похожий пост ниже:
- Творческое письмо 101
- 11 лучших приложений для письма для iOS (iPhone и iPad)
- «Наименее», «Меньше», «Больше» и «Больше всего»
Перестаньте делать эти досадные ошибки! Подпишитесь на ежедневные советы по письму сегодня!
- Вы гарантированно улучшите свой английский всего за 5 минут в день!
- подписчиков получают доступ к нашему архиву с более чем 800 интерактивными упражнениями!
- Вы также получите три бонусные электронные книги совершенно бесплатно! 9{n-1}$ или даже цепное правило: $\frac{df(g(x)}{dx} = \frac{df(g)}{dg}\frac{dg(x)}{dx}$ . Но для использования производных в науке (а также любой математики в науке) вам необходимо иметь более концептуальное представление о том, что производная означает и почему нам нужно ее использовать. На этой странице мы обсудим общие , что такое и , почему выдает. Подробные способы анализа и расчета производных будут даны на следующей странице (что вообще такое производная?)
Зачем нам нужны производные в науке
То, как вещи меняются, является важной частью того, над чем работает наука.
Когда у нас есть что-то ($f$), которое зависит от чего-то еще ($x$), мы описываем это, написав, что $f$ является функцией от $x$, $f(x)$. Затем мы часто хотим знать: когда что-то другое ($x$) изменяется, как что-то ($f$) изменяется?
Это очень важно для применения математики в науке, поскольку мы всегда хотим заниматься в науке тремя вещами:
- предсказать будущее,
- посмотрите, как поворот некоторых циферблатов меняет какой-то результат,
- выяснить, насколько важен тот или иной эффект.
Предсказание будущего требует знания того, как что-то меняется со временем.
Циферблаты, которые мы собираемся изменить, не обязательно должны быть настоящими циферблатами — они могут быть параметрами, определяющими выживание организма, которые могут быть установлены в популяции путем вариации и естественного отбора.
Вычисление скорости изменения также говорит нам, насколько важен тот или иной параметр. При моделировании физической или биологической системы мы могли бы сказать: «О! Это изменение приведет к такому результату». Но если мы не знаем насколько велик результат, мы не знаем, является ли он действительно причиной эффекта, который мы пытаемся объяснить.
Многие из ключевых физических понятий, рассматриваемых в этом классе, такие как сила, давление или движение, связаны друг с другом посредством изменений. Давайте рассмотрим два примера:
- Разница в давлении между двумя разными точками в жидкости может быть причиной движения этой жидкости — за то, как кровь течет в ваших венах, как движется сок в дереве и как дует ветер. созданный.
- Когда к объекту приложены силы, это может привести к изменению скорости объекта со временем.
Для обоих этих примеров основной концепцией является производная — как изменение одной величины вызывает изменение величины, которая от нее зависит. Таким образом, если давление является функцией положения, $p(x)$, объем потока вязкой жидкости через трубу пропорционален скорости изменения давления в трубе с расстоянием. Если давление упадет на величину $\Delta p$ на расстоянии $\Delta x$, то поток в трубе $J$ будет удовлетворять
$$\frac{\Delta p}{\Delta x} = ZJ$$
где $Z$ — константа, зависящая от свойств жидкости и трубы.
Мы можем определить производную как наклон $p$ как функцию $x$ или как она меняется на очень малых расстояниях:
$\frac{dp}{dx} = \frac{\Delta p} {\Delta x} $ для $\Delta x$ меньше, чем нам нужно беспокоиться.
Мы обсудим это ниже.
Хотя вы уже изучали производные на уроках математического анализа, их использование в науке может потребовать некоторого изменения точки зрения.
На занятиях по математическому анализу вы, возможно, сосредоточились на механике получения производных, а не на размышлениях о том, как их понять. Когда мы применяем эту математику в качестве модели реальной физической системы, не все математические детали всегда актуальны или даже правильны.Математика производной
Проблемы с обозначениями
Суть идеи производной с использованием стандартных математических обозначений заключается в том, что функция (зависимая переменная) $f$ зависит от независимой переменной $x$. Мы будем ссылаться на значение, которое $f$ принимает как $y$. Таким образом, мы напишем
$$y = f(x)$$
Будьте осторожны и не слишком привязывайтесь к этому конкретному выбору букв! У нас будет лота разных символов и функций. В некоторых ситуациях в этом классе $x$ будет обозначать независимую переменную — что-то, указывающее местоположение в пространстве. В других ситуациях $x$ будет обозначать зависимую переменную — положение чего-то конкретного, которое может меняться со временем, и поэтому мы могли бы иметь $x=f(t)$.
В других ситуациях $x$ снова станет независимой переменной, указывающей, на какой именно объект мы ссылаемся. Это может сбивать с толку, если вы думаете только о символе, а не о том, что он должен представлять! [Этот аргумент очень похож на заявление о том, что вместо графика $y$ против $x$ мы также изучаем графики $x$ против $t$ или $y$ против $t$!]Мы определяем среднюю скорость изменения в значении, которое принимает $f$ при изменении $x$ по выражению $\frac{\Delta f}{\Delta x}$. Если $\Delta x$ меньше, чем любое изменение переменной $x$, о котором мы беспокоимся, мы записываем изменения как $dx$ и $df$ и определяем производную как отношение небольших изменений:
$$ g(x) = f ‘(x) = \frac{df}{dx}$$.
Обозначение штрихом (или точкой, если независимой переменной является время) принадлежит Исааку Ньютону, одному из изобретателей исчисления. Обозначение отношения связано с Готфридом Лейбницем, который изобрел исчисление независимо от Ньютона примерно в то же время*.
Обозначение Ньютона скрывает тот факт, что производная является отношением, и затрудняет определение единиц производной. Мы будем придерживаться обозначений Лейбница.Как насчет лимитов?
При создании полной и непротиворечивой математической структуры для выполнения вычислений математики часто говорят о “установлении пределов” по мере того, как изменение стремится к нулю (ссылаясь, например, на то, что математики имеют в виду, когда они переходят от $\Delta x$ к $дх$). Они сочли бы наш язык «меньше, чем любое изменение, о котором мы заботимся», как небрежную математику. Что ж, это так. Но мы не занимаемся математикой. Мы используем математику как модель системы в физическом мире, а гладкие («дифференцируемые») функции, о которых любят говорить математики, не часто существуют в физическом мире.
В учебнике по математике вам могут показать график кривой, представляющей функцию. Затем они могут «увеличить» небольшой участок кривой, показывая, что она становится все прямее и прямее по мере того, как вы приближаетесь все ближе и ближе.
кривая считается гладкой. Но в реальном примере увеличение масштаба может сделать кривую немного гладкой и прямой, но дальнейшее увеличение часто начинает показывать что-то забавное: как на картинке ниже.(Источник: Алмквист и Мелош, Слияние биомиметических зондов-невидимок в ядра липидного бислоя, PNAS 2010, 107:13, 5815-5820.)
В этой статье исследователи изучили свойства липидной мембраны, прикрепив щеточку из гидрофобных молекул к гидрофильному наконечнику атомно-силового микроскопа. Затем они измерили силу, которая потребовалась, чтобы протолкнуть наконечник через мембрану, и сделали выводы о свойствах мембраны.
Дело в том, что кривая, которую они нашли справа, не гладкая. У него есть шипы и тряски, и чем ближе вы смотрите, тем хуже они становятся. Взять производную этой кривой в таком масштабе было бы не очень осмысленно. Мы все еще можем каким-то образом сгладить кривую и взять производную от сглаженной кривой и получить информацию о скорости изменения силы в важном интервале времени, выделенном красным.
Вот почему мы говорим, что наша производная есть отношение двух изменений, когда «изменение меньше, чем все, о чем мы заботимся». На приведенном выше графике нас может волновать только то, какова средняя сила, когда мы начинаем проталкивать зонд через мембрану, и сколько времени требуется для прохождения. Для этого мы можем захотеть сгладить кривую. Если нас интересует действительный механизм того, как отдельные молекулы на щетке взаимодействуют с мембраной, нас могут заинтересовать детали отдельных колебаний на графике, а не в средней производной.
В общем, в физических системах мы не можем ограничиться 0, так как по мере того, как мы становимся слишком маленькими, физика системы меняется. Когда мы переходим к микронному уровню, нам приходится беспокоиться о тепловых флуктуациях, а когда мы переходим к молекулярным размерам, нам приходится беспокоиться о дискретности материи, вызванной тем, что она состоит из атомов. В еще меньших масштабах нам нужна квантовая механика, и само понятие положения становится нечетким.
Так что, если ваш курс математики суетился из-за пределов, можно узнать об этом ради самой математики — пределы позволяют очень хорошо доказать и представить математику производных. Однако, когда вы думаете об использовании производных для моделирования чего-либо в физической системе, гораздо лучше думать о них как о соотношениях небольших изменений.
Этот взгляд также проясняет то, что смущает многих студентов. Хотя мы говорим о производной «в точке» — поэтому мы пишем «$g(x) = f'(x)$» — производная от $f$ в точке $x$ — думая в терминах отношения изменения показывают нам, что производная на самом деле соответствует значениям $f$ в двух различных точках. Смотрите обсуждение скорости для примера.
* Интересной книгой о битве за доверие между Ньютоном и Лейбницем является книга Джейсона Барди, Войны вычислений: Ньютон, Лейбниц и величайшее математическое столкновение всех времен.
Julia Gouvea, Kerstin Nordstrom и Joe Redish 9 сентября 2013 г.
заключает контракты через клиринг центрального контрагента (CCP). Для внебиржевых производных контрактов без централизованного клиринга EMIR устанавливает методы снижения риска.Регламент (ЕС) 2019/834, вносящий поправки в EMIR, EMIR Refit, вносит изменения в нормативную базу безрецептурных препаратов. Некоторые из наиболее важных аспектов включают изменение способа определения того, на каких контрагентов распространяется обязательство по клирингу, и включение механизма приостановки обязательства по клирингу.
- Клиринг
- Уведомления
- Внебиржевые производные инструменты
- Страны, не входящие в ЕС
- Снижение рисков
Обязательство по клирингу
Контрагенты, на которых распространяется обязательство по клирингу
Обязательство по клирингу распространяется на фирмы ЕС, которые являются контрагентами по внебиржевому производному контракту, включая процентные, валютные, фондовые, кредитные и товарные производные.
EMIR определяет две категории контрагентов, на которых распространяется обязательство по клирингу , в зависимости от того, выше или ниже их позиции порога клиринга:
- Финансовые контрагенты (FC), такие как банки, страховщики, управляющие активами и т. д.
- Нефинансовые контрагенты (NFC), фирмы, занимающие позиции по внебиржевым производным контрактам, кроме финансовых контрагентов.
Внутригрупповые операции освобождаются от централизованного клиринга при определенных условиях.
Аналогичным образом пенсионные фонды также временно освобождены.
Уведомления
Финансовые контрагенты и нефинансовые контрагенты должны информировать ESMA и соответствующий национальный компетентный орган, когда они превышают порог клиринга и когда они больше не превышают его.
Для получения дополнительной информации о расчете позиций и процедуре уведомления ESMA см. раздел «Клиринг пороговых значений».
Классы внебиржевых деривативов, на которые распространяется обязательство центрального клиринга
EMIR вводит обязательство проводить клиринг определенных классов внебиржевых деривативов в ЦКА, которые были авторизованы (для европейских ЦКА) или признаны (для ЦКА, не входящих в ЕС) в рамках EMIR.
EMIR предусматривает два возможных процесса идентификации соответствующих классов внебиржевых деривативов:
- Подход «снизу вверх», описанный в статье 5(2) EMIR, согласно которому определение классов, на которые распространяется обязательство по клирингу, будет осуществляться на основе классов, которые уже прошли клиринг уполномоченными или признанными центральными контрагентами. .
- Подход «сверху вниз», описанный в статье 5(3) EMIR, согласно которому ESMA по собственной инициативе будет определять классы, на которые должно распространяться обязательство по клирингу, но для которых ни один ЦКА еще не получил разрешения.
В соответствии с процедурой обязательства по клирингу и мандатом ЕС, ESMA должно разработать и представить в ЕС на одобрение проекты регулятивных технических стандартов (RTS), определяющих:
- класс внебиржевых деривативов, на которые должно распространяться обязательство по клирингу;
- дата или даты, с которых вступает в силу обязательство по клирингу, включая любой этап и категории контрагентов, к которым применяется обязательство.
Процедура выполнения обязательств по клирингу началась в первом квартале 2014 года после получения первых разрешений ЦКА ЕС. С тех пор ESMA проанализировала несколько классов процентных, кредитных, долевых и валютных внебиржевых деривативов и предложила некоторые из них для клиринговых обязательств.
В таблице ниже представлен обзор текущего состояния процесса клиринговых обязательств для этих классов.
Класс активов Классы Документ для консультаций Заключительный отчет Прочие документы Статус РТС Последнее обновление Процентная ставка Базис, Fixed-to-float, FRA и IOS в EUR, GBP, JPY и USD 11 июля 2014 г.
Документ для консультаций (№ 1)
1 октября 2014 г.
Заключительный отчет (№ 1)
06 марта 2015 г.
Заключение РТС по IRS
РТС 2015/2205
RTS 2017/751 вносит изменения в RTS 2015/2205
20 фев 2018 Процентная ставка FRA и свопы с фиксированным плавающим курсом в норвежских кронах, злотых и шведских кронах 11 мая 2015 г.
Документ для консультаций (№
°4)10 ноября 2015 г.
Заключительный отчет (№ 3)РТС 2016/1178
РТС 2017/751 вносит изменения в РТС 2016/1178
20 фев 2018 Капитал Двойные/гибкие производные ценные бумаги и CFD 11 июля 2014 г.
Документ для консультаций (№ 1)
1 октября 2014 г.
Заключительный отчет (№ 1)
На данном этапе RTS не предлагается 1 октября 2014 г. Кредит Индексные дефолтные свопы 11 июля 2014 г.
Документ для консультаций (№ 2)
1 октября 2015 г.
Заключительный отчет (№ 2)20 ноября 2014 г.
Письмо в Комиссию РТС по СО
РТС 2016/592
РТС 2017/751 вносит изменения в РТС 2016/592
20 фев 2018 Обмен иностранной валюты Недоставленная переадресация (NDF) 1 октября 2014 г. Консультационный документ (№ 3) 4 февраля 2015 г.
Обратная связь по NDF
На данном этапе RTS не предлагается 4 февраля 2015 г. Публичный реестр обязательств по клирингу включает классы внебиржевых деривативов, которые уполномочены клиринговать ЦКА, и внебиржевых деривативов, на которые распространяется обязательство клиринга.
Контрагенты из стран, не входящих в ЕС
При определенных условиях обязательство по клирингу может также применяться к контрагентам из третьих стран (не из ЕС), в том числе когда:
- Контрагенты из ЕС торгуют с организациями, зарегистрированными за пределами ЕС;
- Две организации, созданные за пределами ЕС, торгуют вместе, и;
- Влияние на рынки ЕС существует (прямое, существенное и предсказуемое влияние в ЕС)
Окончательный отчет ESMA о проектах нормативных технических стандартов прямого, существенного и предсказуемого воздействия в ЕС был одобрен Европейской комиссией 13 февраля 2014 г.
(Регламент делегированной Комиссии (ЕС) № 285/2014.)Методы снижения рисков
Требования EMIR по снижению рисков применяются ко всем операциям с внебиржевыми производными финансовыми инструментами без централизованного клиринга. Эти методы включают своевременное подтверждение, согласование и сжатие портфеля, процедуры разрешения споров и обмен залогом. РТС будет применяться пропорционально, чтобы позволить контрагентам поэтапно вводить требования
Дата подачи заявки ФК NFC+ NFC- Ежедневная рыночная переоценка 15.03.2013 Да Да № Своевременное подтверждение 15.03.2013 Фаза ввода для каждого класса активов. Окончательный срок = T+1
Фаза ввода для каждого класса активов. Окончательный срок = T+2Сверка портфеля 09.15.2013 Каждый день, неделю или квартал в зависимости от размера портфеля. Каждый квартал или год в зависимости от размера портфеля. Сжатие портфолио 09.15.2013 Когда контрагенты имеют более 500 незавершенных контрактов друг с другом, обязательно наличие процедур для анализа возможности проведения исполнения. Разрешение споров 09.15.2013 Действующие процедуры + отчетность компетентному органу Действующие процедуры Обмен залога* Фаза в расчете на количество производных инструментов, не прошедших централизованный клиринг. Окончательный срок, сентябрь 2020 г. Да № * Внутригрупповые операции не подпадают под действие налогового кодекса необходимо обменивать как начальную, так и вариационную маржу.
Эти резервы снижают кредитный риск контрагента, смягчают любой потенциальный системный риск и обеспечивают соответствие международным стандартам. - Перечень приемлемого залога для обмена маржей, критерии обеспечения достаточной диверсификации залога и отсутствия риска ошибочных действий, а также методы определения соответствующих дисконтов залога.
- Операционные процедуры, связанные с документацией, правовой оценкой возможности принудительного исполнения соглашений и сроков обмена залога.
- Процедуры для контрагентов и компетентных органов в отношении внутригрупповых производных контрактов.
- Производная функции, f ‘(x) = Наклон касательной = lim h→0 [f(x + h) – f(x) / h.
- Производная функции в точке представляет собой наклон касательной, проведенной к этой кривой в таком случае.
- Также представляет мгновенную скорость изменения в точке функции.
- Скорость частицы находится путем нахождения производной функции смещения.
- Производные используются для оптимизации (максимизации/минимизации) функции.
- Они также используются для нахождения интервалов возрастания/убывания функции, а также интервалов вогнутости функции вверх/вниз.
Правило произведения — производные | Класс 11 Математика
Производная — это скорость изменения функции по отношению к переменной. Производные имеют очень много правил, таких как правило мощности, правило частного, правило произведения и многое другое. Они также помогают в решении очень сложных проблем. Производные и дифференциация действительно входят в высшие исследования, а также в продвинутые концепции.
Здесь мы рассмотрим, что такое правило произведения и как его использовать с помощью формулы.
Что такое правило продукта?
Когда необходимо получить производную от двух или более функций, применяется правило произведения. Это помогает различать две или более функций в заявленной функции.
Обозначение производной Лейбница
Производная f обозначается как d/dx*f(x). Поэтому, когда уравнение имеет вид y = f(x), производная называется dy/dx. Итак, здесь d/dx выражает дифференцирование по x. Это также указывает, что производная любой заданной функции без использования зависимой переменной, такой как y², может быть обозначена как d/dx*y². Это наиболее часто используемая производная запись по сравнению с записью Ньютона и Лагранжа.
Вывод формулы
Возьмем две функции a(x) и b(x). Таким образом, правило произведения возникает, когда вы умножаете первую функцию a(x) на производную второй функции b(x) плюс производную первой функции a(x), умноженную на вторую функцию b(x). Итак,
(ab)’ = a’b + ab’
Мы можем доказать правило производного произведения, используя основное определение производной. Мы можем найти увеличение функции ab, приняв это изменение аргумента за ∆x :
∆(ab) = a(x + ∆x)b (x + ∆x) – a(x)b(x)
Принимая во внимание
a(x + ∆x) = a(x) + ∆a, b(x + Δx) = b(x) + Δb,
Δa и Δb — приращения функции a и b. Пренебрегая краткостью аргумента x функции b и a, приращение Δ(ab) можно записать в виде:
Δ(ab) = (a + Δa)( b + Δb) – ab =
ab+ aΔb + bΔa + ΔaΔb –ab= aΔb + bΔa + ΔaΔb.
Используя свойства предела, мы можем найти производную произведения
(ab)` = limΔx→0 ∆(ab)/∆x
= lim∆x→0 (a∆b + b∆a + ∆b∆a)/∆x
= lim∆x→0 a∆b /∆x + lim∆x+→0 ∆x∆a/∆x 0 Δa/Δx . limΔx→0 Δb.
Функция a не зависит от увеличения Δx. Таким образом, она вынесена за предельный знак. То же самое относится и к б. мы можем вычислить предел limΔx→0 Δb отдельно
limΔx→0 Δb = limΔx→0 {(Δb/Δx) . Δx }
= lim Δx→0 ( Δb )/Δx. limΔx→0 Δx
= b`.0 = 0,
Следовательно, производная произведения определяется выражением:
(ab)′ = limΔx→0 aΔb /Δx + limΔx→0 ( bΔa )/Δx + limΔx→0 Δa/Δx ⋅ limΔx→0 Δb
= a limΔx→0 Δb /Δx + b limΔx→0 Δa/Δx + limΔx→0 Δa/Δx⋅ limΔx→0 Δb ‘.
Из приведенной выше формулы легко сделать вывод, что вывод z f(x), где z — константа:
(z f(x))’= z’ f(x) + z f'(x ) = 0.f(x) + z f'(x) = z f'(x)
Получение произведения двух функций
Здесь мы рассмотрим пример, чтобы понять, как применяется правило произведения для получения произведения двух функций.
Производная от (х 2 + х)(3х + 5) = ?
Решение:
Теперь, используя формулу правила произведения, f′(x) = X(x)* Y′(x) + Y(x)* X′(x), мы положим требуемое ценности.
Итак, здесь наша первая функция X будет (x 2 + x), а вторая функция Y будет (3x + 5)
Итак, умножьте производную первой функции на вторую производную и прибавьте ее к производной первой секции, умноженной на вторую функцию.
Это будет выглядеть так:
(х 2 + х)'(3х + 5) + (х 2 + х)(3х + 5)’,
= (2х + 1)(3х + 5) + (x 2 + x)(3),
Теперь умножьте все
= 6x 2 + 10x + 3x + 5 + 3x 2 + 3x
Итак, теперь окончательный результат равен
=9x 2 + 16x + 5
Иногда учащиеся путаются при вычислении правила произведения. Они неправильно понимают это, вычисляя произведение производных. Но в таком случае ответ будет неверным. Позвольте вам понять это на том же примере.
Предположим, вы вычисляете произведение производных заданной функции
d/dx(x 2 + x) * (3x + 5),
= d/dx (x 2 + x) d/ dx(3x + 5)
= (2x + 1) * (3)
= 6x + 3
Таким образом, здесь ответ 6x + 3, что не совпадает с 9x 2 + 16x + 5
Примеры задач на правило произведения
Икс. Выделите эту функцию, используя правило произведения .
Решение:
Мы можем представить функцию как
y(x) = cosxcosx .
Используя правило произведения,
y′(x)= (cosx cosx)′ = (cosx)′cosx + cosx(cosx)′.
Так как (cosx)′ = -sinx, получаем
y′(x) = -sinxcosx + cosx(-sinx) = -2sinxcosx = -sin2x
Задача 2. Найти производную функции y = E x SINX
Решение:
, применяя правило продукта
y ′ (x) = (E x SINX) ′ = (E x ) ′ SINX) ′ x ) ′ SINX + E r ′ SINX + E r ′ SINX + E r ′ SINX + E ′ SINX + x r ′ x . (sinx)′
= e x sinx + e x (cosx)
= e x (синх + cosx).
Задача 3. Найдите производную функции y = xsinx.
Решение:
По правилу произведения получаем:
y′(x) = (x sinx)′ = (x)′sinx + x (sinx)′
= sinx + x cosx
Задача 4. Найдите производную функции y = x(1 + x).
Решение:
Применяя правило произведения:
y'(x) = {x(1 + x)}’ = x'(1 + x) + x(1 + x)’
= (1 + x) + x(0 + 1)
= 1 + 2x
Применение в реальном мире
Производные и дифференцирование действительно помогают в решении многих реальных задач, предоставляя простые решения. Чтобы достичь максимального и минимального значений прибыли, убытков, численности населения, стоимости материала и т. д., можно определить формулу правила продукта.
Производные – исчисление, значение, интерпретация
Производная в исчислении – это скорость изменения величины y по отношению к другой величине x. Его также называют дифференциальным коэффициентом y по отношению к x. Дифференцирование – это процесс нахождения производной функции.
Давайте узнаем, что именно означает производная в исчислении и как ее найти вместе с правилами и примерами.
| 1. | Значение производных в исчислении |
| 2. | Интерпретация производных финансовых инструментов |
| 3. | Производная функции, использующая первый принцип |
| 4. | Производные формулы в исчислении |
| 5. | Основные правила деривативов |
| 6. | Производные сложных функций (цепное правило) |
| 7. | Производные неявных функций |
| 8. | Параметрические производные |
| 9. | Производные высшего порядка |
| 10. | Частные производные |
| 11. | Нахождение производной с помощью логарифмического дифференцирования |
| 12. | Максимум/минимум с использованием производных |
| 13. | Часто задаваемые вопросы о деривативах |
Значение производных в исчислении
Производная функции f(x) обычно представляется как d/dx (f(x)) (или) df/dx (или) Df(x) (или) f'(x). Давайте посмотрим, что технически означает производная. Рассмотрим кривую функции f(x) и пусть две точки на ней будут (x, f(x)) и ((x + h), f(x + h)). Тогда наклон секущей, проходящей через эти точки, равен [f(x + h) – f(x)]/(x + h – x) = [f(x + h) – f(x)/h. Посмотрите на рисунок ниже и обратите внимание, что когда расстояние между двумя точками почти равно 0 (т. е. когда h приближается к 0), вторая точка перекрывает исходную точку, а секущая становится касательной. В исчислении наклон касательной называется производной функции. то есть
Эта формула широко известна как «предельное определение производной» (или) «производной по первому принципу».
Интерпретация производных финансовых инструментов
Производная функции f(x) в математике обозначается как f'(x) и может быть контекстуально интерпретирована следующим образом:
Таким образом, всякий раз, когда мы видим такие фразы, как «наклон/градиент», «скорость изменения», «скорость (учитывая смещение)», «максимизировать/минимизировать» и т. д., это означает, что используется понятие производных.
Производная функции, использующая первый принцип
Производная функции может быть получена с помощью предельного определения производной: f'(x) = lim h→0 [f(x + h) – f(x) / h. Этот процесс известен как дифференцирование по первому принципу. Пусть f(x) = x 2 , и мы найдем его производную, используя приведенную выше формулу производной. Здесь f(x + h) = (x + h) 2 , так как f(x) = x 2 . Тогда производная от f(x) равна
f ‘(x) = lim h→0 [(x + h) 2 – x 2 ] / h
= lim h→0 [ x 2 + 2xh + h 2 – x 2 ] / h
= lim ч → 0 [ 2xh + ч 2 ] / ч
= lim ч → 0 [ ч (2x + ч) ] / ч
= lim ч→0 (2x + ч)
= 2х + 0
= 2x
Таким образом, производная x 2 равна 2x. Но может быть трудно использовать это предельное определение для нахождения производных сложных функций. Таким образом, есть некоторые производные формулы (конечно, выведенные из приведенного выше определения предела), которые мы можем легко использовать в процессе дифференцирования.
Производные формулы в исчислении
Три основные производные алгебраической, логарифмической/экспоненциальной и тригонометрической функций выводятся из первого принципа дифференцирования и используются как стандартные формулы производных. Они следующие.
Степенное правило производных
Используя приведенный выше пример, производная x 2 равна 2x. Точно так же мы можем доказать, что производная x 3 равна 3x 2 9x is, d/dx (a x ) = a x ln a
Производные тригонометрических функций
Здесь представлены производные тригонометрических функций.
- Если y = sin x, y’ = cos x
- Если y = cos x, y’ = -sin x
- Если y = tan x, y’ = sec 2 x
- Если y = cot x, y’ = -cosec 2 x
- Если y = сек x, y’ = сек x тангенс x
- Если y = cosec x, y’ = -cosec x cot x
Производные обратных тригонометрических функций
Здесь представлены производные обратных тригонометрических функций.
- Производная обратного синуса, d/dx (sin -1 x) = 1/√(1-x 2 )
- Производная арккосинуса: d/dx (cos -1 x) = -1/√(1-x 2 )
- Производная обратного тангенса, d/dx (тангенс -1 х) = 1/(1 + х 2 )
- Производная обратной кроватки равна d/dx (кроватка -1 х) = -1/(1 + х 2 )
- Производная обратного коэффицента, d/dx (csc -1 x) = -1/ [|x| √(х 2 – 1) ], х ≠ 1, -1, 0
- Производная обратной сек, d/dx (сек -1 x) = 1/ [|x| √(х 2 – 1) ], х ≠ 1, -1, 0
Основные правила деривативов
Ниже приведены основные правила производных. Давайте обсудим их подробно.
Степенное правило: По этому правилу, если y = x n , то dy/dx = n x n-1 . Пример: d/dx (x 5 ) = 5x 4 .
Правило суммы/разности: Процесс производной можно распределить на сложение/вычитание. т. е. dy/dx [u ± v] = du/dx ± dv/dx.
Правило произведения: Правило произведения производных гласит, что если функция является произведением двух функций, то ее производная есть производная второй функции, умноженная на первую функцию, прибавленная к производной первой функции, умноженной на вторая функция. dy/dx [u × v] = u · dv/dx + v · du/dx. Если у = х 5 e x , мы имеем y’ = x 5 . e x + e x . 5x 4 = e x (x 5 + 5x 4 )
Правило частных: Правило частных производных утверждает, что d/dx (u/v) = (v · du/dx – u · dv/dx)/ v 2
Постоянное кратное Правило: Постоянное кратное правило производных утверждает, что d/dx [c(f(x)] = c · d/dx f(x), т. е. , константа, которая при умножении на функцию получается в результате дифференцирования, например, d/dx (5x 2 ) = 5 д/дх (х 2 ) = 5(2х) = 10х.
Правило констант: Правило констант производных утверждает, что производная любой константы равна 0. Если y = k, где k — константа, то dy/dx = 0. Предположим, y = 4, y’ = 0. Это правило непосредственно следует из правила мощности.
Производные составных функций (цепное правило)
Если f и g — дифференцируемые функции в своей области определения, то f(g(x)) также дифференцируема. Это известно как цепное правило дифференцирования, используемое для составных функций. (туман)'(x) = f'[(g(x)] g'(x). Это также можно записать как “если y = f(u) и u = g(x) , то dy/dx = dy/du · du/dx.
Например, рассмотрим y = tan 2 x. Это составная функция. Мы можем записать эту функцию как y = u 2 , где u = tan x. Тогда
dy/dx = 2u
du/dx = d/dx (tan x) = sec 2 x
По цепному правилу
dy/dx = dy/du · du/dx
= 2u · сек 2 x
= 2 тан x сек 2 x
Производные неявных функций
В уравнениях, где y как функция x не может быть явно определена переменными x и y, используется неявное дифференцирование. Если f(x, y) = 0, то продифференцируйте обе стороны по x и сгруппируйте члены, содержащие dy/dx, с одной стороны, а затем найдите dy/dx.
Например, 2x + y = 12
d/dx(2x + y) = d/dx(0)
2 + dy/dx = 0
dy/dx = -2
Параметрические производные
В функции у нас могут быть зависимые переменные x и y, которые зависят от третьей независимой переменной. Если x = f(t) и y = g(t), то производная вычисляется как dy/dx = f'(x)/g'(x). Предположим, что если x = 4 + t 2 и y = 4t 2 -5t 4 , то мы находим dy/dx следующим образом.
dx/dt = 2t и dy/dt = 8t -20t 3
dy/dx = (dy/dt)/(dx/dt)
dy/dx = (8t -20t 3 )/ 2т
= 2т (4 – 10т 2 ) / 2т
dy/dx = 4 – 10т 2
Производные высшего порядка
Мы можем найти последовательные производные функции и получить производные более высокого порядка. Если y — функция, то ее первая производная равна dy/dx. Вторая производная d/dx (dy/dx), которую также можно записать как d 2 у/дх 2 . Третья производная d/dx (d 2 y/dx 2 ) и обозначается как d 3 y/dx 3 и так далее.
В качестве альтернативы первая, вторая и третья производные f(x) могут быть записаны как f'(x), f”(x) и f”'(x). Для производных более высокого порядка мы пишем число в скобках как показатель степени. Предположим y = 4x 3 , мы получаем последовательные производные следующим образом. y’ = 12x 2 , y” = 24 x и y”’ = 24, y (4) = 0,
Частные производные
Если u = f(x,y), мы можем найти частную производную по y, оставив x константой, или мы можем найти частную производную по x, оставив y константой. Предположим, что f(x, y) = x 3 y 2 , частные производные функции:
Кроме того, мы можем найти частные производные второго порядка также как и ∂ 2 f/∂y ∂x.
Нахождение производной с помощью логарифмического дифференцирования
Иногда функции слишком сложны, чтобы найти производные (или) одна функция может быть возведена в другую функцию, например y = f(x) g(x) . В таких случаях мы можем взять log (или) ln с обеих сторон, применить логарифмические правила, а затем дифференцировать обе стороны, чтобы получить dy/dx. Этот процесс известен как логарифмическое дифференцирование в исчислении.
Пример: Найдите производную от y = x x .
Решение:
Применив ln с обеих сторон,
ln y = ln x x
ln y = x ln x
Взяв производную с обеих сторон,
3 1
(1/x) + ln x (1) (цепное правило слева и правило произведения справа)
1/y dy/dx = 1 + ln x
dy/dx = y (1 + ln x ) = х х (1 + ln х)
Максимум/минимум с использованием производных
Понятие наклона и, следовательно, производных используется для нахождения максимального или минимального значения функции. Есть два теста, которые используют производные и используются для нахождения максимумов/минимумов функции. Они
- тест первой производной
- тест второй производной
Проверка первой производной
Мы можем просто использовать первую производную для определения максимума или минимума, соблюдая следующие пункты:
- f'(x) представляет наклон касательной.
- Следовательно, если f'(x) > 0, функция возрастает, а если f'(x) < 0, функция убывает.
- Если f'(x) > 0 меняется на f'(x) < 0 в какой-либо точке, то функция имеет локальный максимум в этой точке.
- Если f'(x) < 0 меняется на f'(x) > 0 в какой-то точке, то функция имеет минимум в этой точке.
- Обратите внимание, что f'(x) = 0 в локальном максимуме и локальном минимуме.
Тест второй производной
Тест второй производной использует критические точки и вторую производную для нахождения максимума/минимума. Чтобы выполнить этот тест:
- Найдите критические точки, установив f'(x) = 0.
- Подставьте каждое из них в f”(x). Если f”(x) < 0, то функция максимальна в этой точке, а если f''(x)>0, то функция в этой точке минимальна.
- Если f”(x) = 0, функция не имеет ни максимума, ни минимума в этой точке, и в этом случае она называется точкой перегиба.
Важные замечания по расчету производных:
- Производная функции — это скорость изменения одной величины по сравнению с другой.
- Производная любой непрерывной функции, дифференцируемой на отрезке [a, b], выводится с использованием первого принципа дифференцирования с использованием пределов.
- Если f(x) задано, то его производная равна f'(x) = lim h→0 [f(x + h) – f(x) / h.
- Каждая дифференцируемая функция непрерывна, но обратное может быть неверным.
☛ Статьи по теме:
- Расчетный калькулятор
- Калькулятор производных
- Калькулятор второй производной
Часто задаваемые вопросы о деривативах
Что такое производные в исчислении?
Производная в исчислении — это мгновенная скорость изменения функции по отношению к другой переменной. Дифференцирование – это процесс нахождения производной функции. Производная функции совпадает с наклоном касательной, скоростью изменения и т. д.
Определить производную.
Производная f(x) при x = a определяется выражением f'(x) = lim h→0 [f(x + h) – f(x)] / h. Это наклон касательной к функции f(x). В этой формуле [f(x + h) – f(x)]/h называется разностным коэффициентом.
Как найти производные?
Производные функций в математике находятся с использованием определения производной из первого фундаментального принципа дифференцирования. Если f(x) — заданная функция, ее производная получается с использованием f'(x) = lim ч → 0 [f(x + h) – f(x)] / ч. Многие правила выводятся с использованием этого определения предела, которое можно напрямую использовать для поиска производных без использования пределов.
Что такое основные производные формулы?
Формулы основных производных: d/dx (x n ) = nx n-1 , d/dx (ln x) = 1/x, d/dx (e x ) = e x , d/dx (a x ) = a x ln a, d/dx (sin x) = cos x, d/dx (cos x) = – sin x, d/dx (tan x) = сек 2 х.
Сложно ли вычислять производные?
Процесс нахождения производных с использованием определения предела немного сложен. Чтобы сделать это проще, мы используем правила, полученные с помощью формулы. Пока мы можем помнить правила, процесс нахождения производных в исчислении очень прост, если немного попрактиковаться.
Каково применение деривативов в реальной жизни?
В реальной жизни существуют различные применения деривативов. Скорость изменения функции по отношению к другой величине называется производной. Чтобы проверить, является ли функция возрастающей или убывающей, чтобы найти уравнение касательной / нормали, чтобы найти максимальное и минимальное значения на графике, чтобы найти задачи смещения-движения, найти скорость при заданном смещении, найти заданное ускорение смещение и так далее.
Что такое производный пример?
Скорость — это мгновенная скорость изменения расстояния, пройденного объектом в определенное время. Первая производная от смещения объекта есть его скорость. Вторая производная смещения — это ускорение объекта. Третья производная смещения — это рывок объекта и так далее.
В чем разница между производными и дифференцированием в исчислении?
Производная функции f(x) в точке есть не что иное, как наклон тангенса функции в этой точке и находится по пределу f'(x) = lim ч → 0 [f(x + h) – f(x)] / ч. Дифференцирование – это процесс нахождения производных.
Что такое производные? Определение производных, значение производных
Что такое производные? Определение деривативов.5 лет Возврат
12,62 %
Invest Now
Поиск
+
Business News ›Определения› Собственность ›Деривативы
Предоставьте новое определение
Предлагаемые определения будут рассмотрены для включения в Economictimes.com
. Определение: Производный инструмент – это договор между двумя сторонами, стоимость/цена которого определяется базовым активом. Наиболее распространенными типами деривативов являются фьючерсы, опционы, форварды и свопы.
Описание: Это финансовый инструмент, стоимость/цена которого определяется базовыми активами. Первоначально сначала создается базовый корпус, который может состоять из одной ценной бумаги или комбинации различных ценных бумаг. Стоимость базового актива неизбежно будет меняться, поскольку стоимость базовых активов постоянно меняется.
Как правило, базовым активом являются акции, облигации, валюта, товары и процентные ставки.
Что такое производные? Смотрите видео, чтобы узнать больше …
macromedia.com/go/getflashplayer” quality=”high” src=”http://timesofindia.indiatimes.com/configspace/ads/timesChannelWrapper.swf” type=”application/x-shockwave-flash” wmode=”transparent”/>
Прочитайте больше новостей на
- DerivativeContractbondscommodities
- Стокол. «Индекс Nifty Midcap значительно вырос с недавнего минимума колебаний и с небольшим отрывом превзошел максимум колебания апреля 2022 года. Но, учитывая неопределенность на мировых рынках, мы можем увидеть рост волатильности в ближайшей перспективе в корзине средней капитализации. , Таким образом, лучше быть очень специфичным для акций и сосредоточиться на компаниях, которые сосредоточились на возможностях внутреннего роста и наблюдают стабильный рост прибыли».
- Высокие затраты могут отвратить FPI от товарных деривативов. В настоящее время компоненты затрат на выполнение товарных сделок в Индии включают налог на товарные сделки (CTT), сборы за биржевые операции, комиссионные сборы Sebi за оборот, налог на товары и услуги (GST), гербовый сбор и брокерские услуги. , среди прочего, они указали.
- Учитесь с ETMarkets: руководство для начинающих по торговле F&OИзначально выделите только 10% своего инвестируемого капитала, чтобы начать торговать на F&O. Почему? Потому что F&O — это игра с использованием заемных средств. Вы можете столкнуться с искушением более высокой доходности и более высокого риска, что может не соответствовать вашему аппетиту к риску.
- HNI сталкиваются с новыми правилами и запретами на иностранные ставкиДо сих пор человек (помимо инвестиций в котирующиеся акции) мог инвестировать до 10% в иностранный «холдинг» или незарегистрированную инвестиционную компанию, часто создаваемую группой инвесторов HNI. собираются вместе. Этот инвестиционный инструмент, в свою очередь, торговал производными финансовыми инструментами и криптовалютами, которые запрещены LRS.
- HNI сталкиваются с новыми правилами и запретами на иностранные ставкиДо сих пор человек (помимо инвестиций в зарегистрированные на бирже акции) мог инвестировать до 10% в иностранный «холдинг» или незарегистрированную инвестиционную компанию, часто созданную группой инвесторов HNI. собираются вместе. Этот инвестиционный инструмент, в свою очередь, торговал производными финансовыми инструментами и криптовалютами, которые запрещены LRS.
- Nifty, вероятно, возобновит восходящий тренд, может пересечь 16 350. Nifty формирует более высокие минимумы в течение последних четырех недель и сумел удержаться в зонах 15 850-15 888. Падение волатильности с ростом коэффициента пут-колл дает некоторое утешение быкам. Теперь Nifty должен удержаться выше 16 061, чтобы стать свидетелем движения вверх к 16 350 зонам; в то время как с другой стороны, поддержка существует на уровнях 15 950 и 15 888.
- Возможно, пришло время покупать акции, растущие из-за падения цен на нефть, но «ожидать прибыли с задержкой» На фоне опасений по поводу рецессии аналитики рекомендуют инвесторам начать покупать такие акции на среднесрочной и долгосрочной основе, поскольку коррекция цен на нефть ослабнет стоимость производства, улучшить объем спроса и впоследствии увеличить свою валовую прибыль.
- Nifty необходимо удержаться выше 15 800, чтобы двигаться к 16 300: АналитикиИнвесторы могут использовать это снижение, чтобы добавить качественные акции из автомобильного, частного банковского, финансового и потребительского секторов, в то время как трейдерам предлагается играть с отскоком движения с правильным размером позиции, чтобы справиться с этот изменчивый рынок.
- Товарные фьючерсы могут скоро открыться для FPIСовет по ценным бумагам и биржам Индии (Sebi) на этой неделе обратился к нескольким крупным участникам рынка, многонациональным банкам и клиринговым палатам, чтобы совместно изучить меры, позволяющие иностранным портфельным инвесторам (FPI) торговать товарными деривативами. котируются на местных биржах, сообщили ET два человека, осведомленные о сообщении регулятора.
- Плательщики высоких налогов могут вложиться в безналоговые облигации и заработать больше, чем банковские FDs. государственный сектор. Какими бы непривлекательными они ни казались на первый взгляд, эти инструменты приносят богатым вкладчикам более высокую прибыль, чем когда-либо могут быть фиксированные депозиты или схемы с небольшими сбережениями.