V в физике как найти: A = (V-V0)/t как найти V?

Что означает V в физике? – Обзоры Вики

вольт (V) объем. кубические метры (м³) сдвигающая сила. скорость.

Итак, что означает XF в физике? Скорость — это всего лишь скорость изменения положения объекта относительно выбранной точки отсчета, то есть изменение положения, деленное на время. «Xf» — это конечное положение объекта в то время как «X0» является начальным положением. Точно так же «Tf» — это конечный период времени, а «T0» — начальный период времени. «Мне нравится физика.

Что обозначает буква B в физике? Б= плотность магнитного потока.

Дополнительно Что означает V в науке? вольт, Всуществительное. единица потенциала, равная разности потенциалов между двумя точками на проводник с током в 1 ампер, когда мощность, рассеиваемая между двумя точками, составляет 1 ватт; эквивалентна разности потенциалов на сопротивлении 1 Ом при протекании через него тока силой 1 ампер.

Что такое r в кинематике физики? смех радиус кривизны кругового пути. 2 + 2AD (см. раздел объявлений для соглашений о линейном написании уравнений). Это уравнение связывает конечная скорость V_f объекта начиная со скорости V_i и двигаясь с постоянным ускорением А на расстояние D.

Что такое V в магнитном поле?

Сила, с которой магнитное поле действует на заряд q, движущийся со скоростью v, называется магнитной силой Лоренца. Его дают. F = qv × B. (Единица СИ для B равна Ns / (Cm) = T (Tesla)) Сила F перпендикулярна направлению магнитного поля B.

Также Что означает B в физике магнетизма? Определение H таково: H = B/µ − M, где B есть плотность магнитного потокамера фактического магнитного поля в материале, рассматриваемая как концентрация линий магнитного поля или потока на единицу площади поперечного сечения; μ — магнитная проницаемость; М — намагниченность.

Что такое N в физике?

Компания ньютон является Международной стандартной (СИ) единицей силы. В физике и инженерной документации термин «ньютон(ы)» обычно обозначается аббревиатурой Н. Один ньютон — это сила, необходимая для ускорения массы в один килограмм со скоростью один метр в секунду в квадрате при отсутствии других силовых воздействий. .

Что такое V в 9 классе физики? Скорость: Скорость скорость объекта, движущегося в определенном направлении. Единицей СИ является м/с. • Ускорение: изменение скорости объекта в единицу времени.

Каково значение V в физике?

v это конечная скорость. а – ускорение.

Что такое V и U в физическом зеркале?

Расстояние между объектом и полюсом зеркала называется расстоянием до объекта (u). Чай расстояние между изображением и полюсом зеркала называется расстоянием изображения (v).

Что обозначают символы VI и VF? vf = конечная скорость vi = начальная скорость a = ускорение ∆x = перемещение Используйте эту формулу, если у вас нет ∆t.

Как вы находите ускорение от VF?

Что означает v0 в математике? Глоссарий V: скорость V_0: Начальная скорость (когда t = 0) a: ускорение t: время S: положение (иногда вместо этого используется «d») S_0: исходное положение.

Как переставить VF VI в vi?

Что означает ∆?

дельта (/ˈdɛltə/; прописная Δ, строчная δ или ; греческий: δέλτα, дельта, [ˈðelta]) — четвертая буква греческого алфавита. В системе греческих цифр имеет значение 4. Оно произошло от финикийской буквы далет. Буквы, происходящие от дельты, включают латинскую D и кириллицу Д.

Что такое V и U в физике? Уравнения движения относятся к следующим пяти величинам: u – начальная скорость. v – конечная скорость. а – ускорение.

Официальный сайт НИЯУ МИФИ

• Главные новости
• Новости регионов
• Спорт и культура

28.02.2023

113

Образовательные проекты НИЯУ МИФИ получили высокую оценку Минобрнауки России

27.02.2023

154

Ученый НИЯУ МИФИ предложил новую модель передачи информации в нелинейной среде

27.02.2023

142

“СтудАк-2023” на базе отдыха “Волга”

28.02.2023

1

Студенты СФТИ НИЯУ МИФИ стали наставниками на онлайн-интенсивах «АТОМ–ЛАБ»

28.02.2023

2

В Центре цифровых технологий СарФТИ заработал Клуб Cyber Alliance

22.02.2023

13

Сотрудники НТИ НИЯУ МИФИ провели выездные встречи со школьниками региона

28.02.2023

4

Cтудентка СарФТИ НИЯУ МИФИ завоевала серебро Первенства России по легкой атлетике

27. 02.2023

13

Команда ИФТЭБ выиграла турнир по тэг-регби «Первый шаг в будущее»

21.02.2023

39

В НИЯУ МИФИ прошел фестиваль “Ледовые хитрушки”

• Анонсы
• Рабочие будни

Объявляется конкурс по отбору кандидатов на получение именных стипендий Международной межправительственной организации ОИЯИ для студентов и аспирантов в 2022-2023 учебном году

28.02.2023

35

4 марта в НИЯУ МИФИ пройдут мастер-классы от компании Positive technologies

27.02.2023

37

28 февраля – открытое собрание Совета общежитий

27.02.2023

29

Концерт Мужского хора МИФИ 12 марта

27.02.2023

32

День Донора в НИЯУ МИФИ пройдет 6 и 7 марта

27.02.2023

13

IX Международная конференция «Лазерные, плазменные исследования и технологии – ЛаПлаз-2023»

21.02.2023

136

Кадетам прочтут лекцию о геополитике

21.02.2023

72

Заключительные туры физико-математической олимпиады школьников «Росатом» состоятся 4-5 марта

20. 02.2023

80

На конкурсе блогеров появится номинация “Лучший блог об инженерии”

20.02.2023

45

Открыта регистрация на конкурс «МИФИ ищет таланты»

20.02.2023

85

Образовательный форум «Атомная школа» состоится в апреле

17.02.2023

105

День Сбера в НИЯУ МИФИ

17.02.2023

239

Объявлен конкурс молодёжных проектов «Книга будущего»

16.02.2023

73

До 28 февраля проводится ежегодный опрос учащихся и НПР НИЯУ МИФИ

15.02.2023

398

Специальная акция для выпускников в честь 80-летия НИЯУ МИФИ

13.02.2023

223

Стартовал Всероссийский конкурс «Моя страна – моя Россия» 2023

13.02.2023

104

Акция «Ученые – в школы» проходит до 30 марта

09.02.2023

103

13 февраля стартует ежегодное исследование вовлеченности и удовлетворенности учащихся и НПР НИЯУ МИФИ

09.02.2023

427

Открыт набор в Школу Вожатых-2023

09.02.2023

248

1 марта стартует II Всероссийская олимпиада по матмоделированию

08. 02.2023

201

12 февраля состоится День открытых дверей ИИКС НИЯУ МИФИ

07.02.2023

277

РНФ и NSFC открыли прием заявок на совместный конкурс международных научных проектов

01.02.2023

94

5 февраля пройдет День открытых дверей ИНТЭЛ НИЯУ МИФИ

01.02.2023

80

Программа поддержки студентов «Лети! Мы поможем»

26.01.2023

256

В СарФТИ НИЯУ МИФИ пройдет молодежная научная школа «Математика и математическое моделирование»

26.01.2023

95

Открыт прием заявок на Международный конкурс фотожурналистики имени Андрея Стенина

17.01.2023

87

10 января стартует V Международная инженерно-физическая олимпиада НИЯУ МИФИ

10.01.2023

710

Выпускники и студенты НИЯУ МИФИ приглашаются к участию в конкурсе «Стажер Минобрнауки»

13.12.2022

316

Студенты НИЯУ МИФИ могут стать авторами медиапроекта

07.12.2022

197

В НИЯУ МИФИ прошел заключительный этап олимпиады «Я – профессионал» по направлению «Технологии медицины будущего»

28. 02.2023

2

В НИЯУ МИФИ прошел День открытых дверей ФБИУКС

27.02.2023

9

Роспотребнадзор предупредил о продолжении роста заболеваемости COVID-19

16.02.2023

34

Заболеваемость коронавирусной инфекцией может вырасти

18.01.2023

36

Студенты и аспиранты НИЯУ МИФИ получат именные стипендии ОИЯИ

11.01.2023

93

В НИЯУ МИФИ завершилась акселерационная программа по поддержке студенческих инициатив

20.12.2022

62

Урок Видео: Кинематические уравнения | Нагва

Расшифровка видео

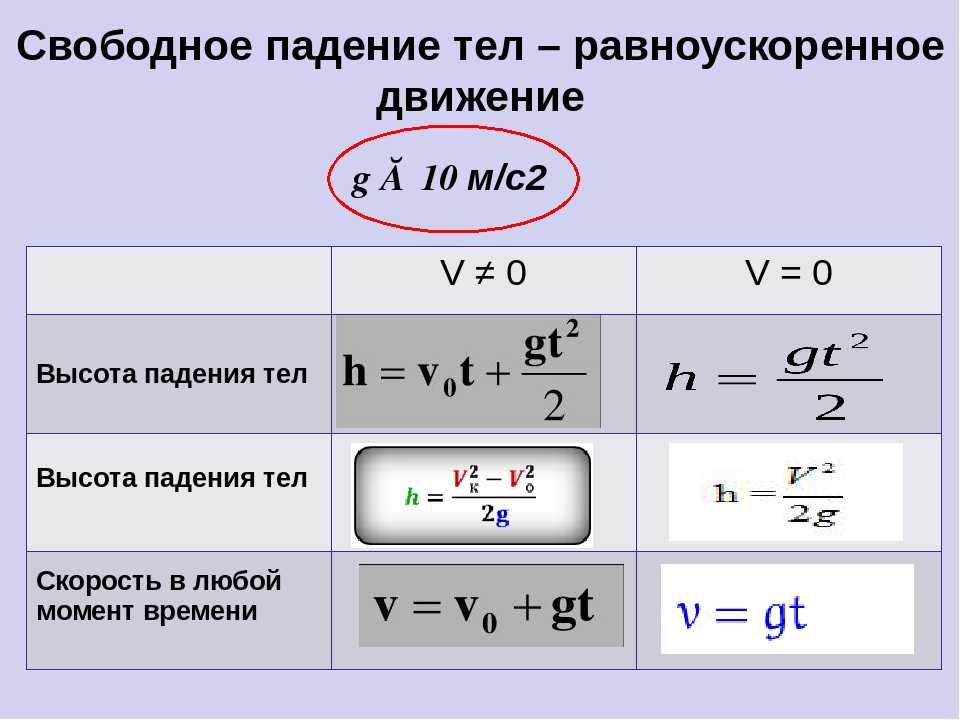
В этом видео мы узнаем, как применять законы равномерного ускоренного движения частицы по прямой линия. До сих пор мы использовали Формула скорость-расстояние-время. Скорость это расстояние деленное на время. Эта формула применима, когда ускорение тела равно нулю. Мы могли бы также рассмотреть ускорение по градиенту или наклону линии по скорости-времени график.

Теперь мы хотим представить некоторые новые уравнения. Эти уравнения иногда называются уравнениями постоянного или равномерного ускорения, названными так потому, что они применяется при работе с равномерным ускорением, то есть ускорением, не изменять. Итак, давайте посмотрим, где эти уравнения родом из.

Начнем с рассмотрения график скорость-время. 𝑣 ноль или 𝑣 ниже нуля начальная скорость или исходная скорость нашего объекта. 𝑣, то это скорость после время 𝑡. Положим 𝑎 равным ускорение. А Δ𝑥 или изменение 𝑥 — это смещение объекта, которое иногда обозначается как 𝑠. Теперь мы знаем, что ускорение определяется наклоном линии на графике скорость-время. Поскольку ускорение постоянно, у нас прямая. И найти наклон или градиент прямой линии, мы используем формулу подъема над пробегом или изменения 𝑦 над изменением 𝑥.

На нашей диаграмме изменение 𝑦 равно вот эта длина. Это разница между начальная скорость и скорость через 𝑡 единиц времени. Это 𝑣 минус 𝑣 ноль. Изменение в 𝑥 – это длина этого линия. Это 𝑡 минус ноль или просто 𝑡. Итак, наклон нашей линии, которая представляет собой ускорение 𝑎, в этих условиях определяется как 𝑣 минус 𝑣 ничего более 𝑡. Если мы умножим обе части уравнение на 𝑡, мы получаем 𝑎𝑡 равно 𝑣 минус 𝑣 ноль. И тогда, если мы добавим 𝑣 ноль к обе стороны, мы получаем 𝑣 равно 𝑣 ноль плюс 𝑎𝑡. Итак, 𝑣 равно 𝑣 ноль плюс 𝑎𝑡. Это наша первая кинематика уравнение.

Теперь рассмотрим нашего второго. На этот раз мы вернемся к нашему графику и напомним, что смещение находится путем вычисления площади между линией и 𝑥-ось. Мы можем разделить эту область на прямоугольник и треугольник. Площадь прямоугольника равна произведение его размеров. Так что это 𝑣 ноль раз 𝑡. А площадь треугольника равна половина произведения основания на высоту. Так вот, это в полтора раза 𝑣 минус 𝑣 ноль раз 𝑡. Итак, это означает, что смещение Δ𝑥, которое, конечно, является площадью между линией и осью 𝑥, равно 𝑣 ноль 𝑡 плюс в два раза 𝑣 минус 𝑣 ноль 𝑡. Но ранее мы определили 𝑣 минус 𝑣 ничто как равное 𝑎𝑡. Итак, мы заменяем это на 𝑎𝑡 в наше уравнение, и мы получаем Δ𝑥 равно 𝑣 нулю 𝑡 плюс половина, умноженная на 𝑎𝑡, умноженная на 𝑡, или половина 𝑎𝑡 в квадрате. А это наша вторая кинематика уравнение.

Теперь это выходит за рамки этого видео, чтобы вывести все наши уравнения. Но либо переставляя два у нас есть или мы рассматриваем другой графический подход, мы можем получить еще два формулы. Это Δ𝑥 равно половине раза 𝑣 ноль плюс 𝑣 умноженный на 𝑡 и 𝑣 в квадрате равно 𝑣 ноль в квадрате плюс два раза 𝑎 раз Δ𝑥.

Итак, как мы применяем эти формулы? Начнем с перечисления всех известные нам измерения. Затем мы определяем тот, который мы не знаю и не пытаюсь найти. Это устранит все уравнения, которые нас не интересуют, оставив только одно. Давайте посмотрим, как это выглядит.

Если частица начала движение в прямой с начальной скоростью 25,1 сантиметра в секунду и равномерным ускорение 2,4 сантиметра в секунду в квадрате, определите его скорость через девять секунды.

В вопросе указано, что частица имеет равномерное ускорение. Это хороший показатель для нас что нам нужно будет использовать уравнения равномерного или постоянного ускорение. Это четыре кинематических уравнения. Итак, начнем с перечисления уравнения. Наша задача — уничтожить все, кроме одного. этих уравнений. И мы делаем это, перечисляя измерения, которые мы дали в вопросе. Нам дана начальная скорость 𝑣 ничего. Это 25,1 сантиметра на второй. У нас ускорение 2.4 сантиметры в секунду в квадрате и время девять секунд.

Нам нужно рассчитать скорость через девять секунд. Обратите внимание, что это означает, что мы действительно не интересует Δ𝑥, смещение нашего объекта. И так, проходим и устраняем все уравнения, содержащие Δ𝑥. Это два, уравнение три, и четыре. Итак, у нас остался один уравнение; это 𝑣 равно 𝑣 ноль плюс 𝑎𝑡. Далее подставляем все что нужно знать о нашей частице в эту формулу. Мы хотим вычислить 𝑣, поэтому мы говорим, что 𝑣 равно 𝑣 нулю, что равно 25,1, плюс 𝑎 умножить на 𝑡, это 2,4 раз девять. 2,4 умножить на девять будет 21,6. Таким образом, скорость равна 25,1 плюс 21,6, что составляет 46,7.

Обратите внимание, что мы работаем в сантиметры в секунду, сантиметры в секунду в квадрате и секунды. Итак, единицы измерения нашей скорости через девять секунд это сантиметры в секунду. Скорость частицы следовательно, 46,7 сантиметра в секунду.

В нашем следующем примере мы рассмотрим как рассчитать расстояние, пройденное объектом.

Маленький мячик начал движение по горизонтали со скоростью 16,3 метра в секунду. Он двигался прямолинейно с равномерное замедление три метра в квадратную секунду. Определить расстояние до мяча покрывается в первые две секунды.

Мяч имеет форму замедление. Другими словами, он имеет униформу. отрицательное ускорение. Это указание нам на то, что мы собираемся использовать кинематические уравнения, уравнения равномерного ускорение. И так, первое, что мы делаем список этих четырех уравнений. Для начальной скорости 𝑣 равна нулю, ускорение 𝑎, скорость 𝑣 в единицах времени 𝑡 времени и перемещение Δ𝑥, они такие, как показано.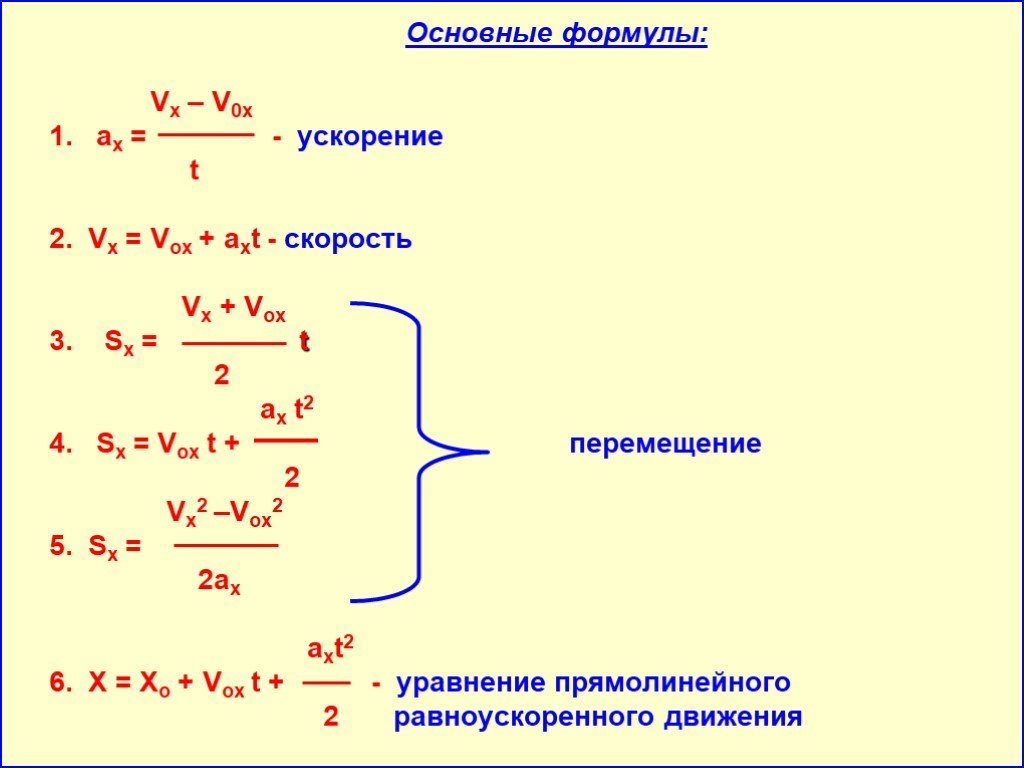

Наш следующий шаг — устранить все но одно из этих уравнений, и мы делаем это, перечисляя все, что мы знаем о движение нашего объекта. Нам говорят, что маленький мяч начинает двигаться со скоростью 16,3 метра в секунду, так что это его начальная скорость. Имеет равномерное замедление три метра в секунду в квадрате. Другими словами, замедляется вниз. Поэтому мы говорим, что его ускорение равно минус три. Время 𝑡 составляет две секунды, и мы пытаясь найти расстояние, которое проходит мяч.

Напомним, что расстояние просто величина смещения. Итак, расстояние здесь равно Δ𝑥. Это изменение в 𝑥. А это значит, что мы не заинтересованы в 𝑣 конечная скорость объекта. Итак, мы проходим через наши уравнения и мы исключаем каждое уравнение, содержащее 𝑣. Это раз, три и четыре, оставляя нас, конечно, только с уравнением два.

Наша следующая задача — заменить то, что мы знаем о нашем шаре в это уравнение. Δ𝑥 — это то, что мы пытаемся рассчитать. Тогда 𝑣 ноль 𝑡 в 16,3 раза два. Половина 𝑎𝑡 в квадрате становится половиной умножить на минус трижды на два в квадрате. Тогда 16,3 умножить на два будет 32,6. Полтора раза минус три умножить на два в квадрате будет минус шесть. Итак, Δ𝑥 равно 32,6 минус шесть, что равно 26,6, и мы измеряем это в метрах. Итак, мяч преодолел расстояние 26,6 метра за первые две секунды движения.

Теперь может показаться, что информация о прямолинейном движении мяча несколько избыточна. Однако на самом деле это действительно важный. Это позволяет нам просто рассмотреть один направление движения. Если бы нам пришлось рассматривать два направления, которые усложнили бы ситуацию немного больше.

Давайте перейдем к другому пример.

Частица, движущаяся по прямой линия ускорялась со скоростью 22 сантиметра в секунду в квадрате в том же направление в качестве начальной скорости. Если величина его водоизмещение через 10 секунд после начала движения составило 29метров, рассчитать величина его начальной скорости 𝑣 равна нулю, а его скорость 𝑣 в конце этого период.

Нам дано, что частица ускорение с постоянной скоростью 22 сантиметра в секунду в квадрате. То есть ответить на этот вопрос, нам нужно будет использовать кинематические уравнения. Это, конечно, уравнения постоянное ускорение. Для начальной скорости 𝑣 ноль, скорость 𝑣 через 𝑡 единиц времени, ускорение 𝑎 и перемещение Δ𝑥, они как показано.

Начнем с перечисления все, что мы знаем о нашем движении. Мы уже говорили, что знаем, что ускорение постоянно и составляет 22 сантиметра в секунду в квадрате. Он находится в том же направлении, что и его Начальная скорость. Теперь мы не знаем его начального скорости, но предполагая, что они движутся в одном и том же направлении, мы можем ускорение и 𝑣 не должны быть положительными. Нам также говорят, что величина водоизмещения через 10 секунд после начала движения было 29метров. Помните, что смещение может иметь направление. Таким образом, рассматривая только величина, мы думаем о расстоянии; это 29 метров. Время 𝑡 составляет 10 секунд.

Теперь вопрос на самом деле задает нам вычислить величину начальной скорости и ее скорость в конце Период. Начнем с расчета его начальная скорость 𝑣 нулевая. В данном случае нас не интересует в 𝑣, поэтому мы проходим наши уравнения и исключаем те, которые содержат 𝑣. Это один, три и четыре. Нашим следующим шагом обычно было бы подставить все, что мы знаем о движении нашей частицы, в эту секунду уравнение. У нас есть немного проблема однако. Мы замечаем, что единицы для нашего ускорение и наше перемещение различны. Нам нужно, чтобы они были одинаковыми. Итак, умножаем водоизмещение на 100. и мы находим, что это на самом деле равно 2900 сантиметров.

Затем, подставив все, что мы в эту формулу, и мы получаем 2900 равно 10 𝑣 ноль плюс половина, умноженная на 22. раз 10 в квадрате. Половина умножить на 22 умножить на 10 в квадрате 1100. Итак, отнимаем 1100 от обоих сторон, и мы находим, что 1800 равно 10 умножить на 𝑣 ноль. Наш последний шаг состоит в том, чтобы разделить на 10. 1800 разделить на 10 будет 180. Теперь мы работаем в сантиметры. Итак, наша скорость, наша начальная скорость 𝑣 равна нулю, равна 180 сантиметрам в секунду. Мы могли бы дать наш ответ в метрах в секунду, разделив на 100. И когда мы это сделаем, мы найдем, что 𝑣 ноль составляет 1,8 метра в секунду.

Мы еще не закончили. Мы все еще пытаемся рассчитать его скорость 𝑣 в конце периода. Теперь, когда мы ничего не знаем, мы можем на самом деле использовать любое из наших уравнений. Итак, воспользуемся первым. Мы заменяем все, что знаем о движении нашей частицы в эту формулу, продолжая работать в сантиметры и сантиметры в секунду. Когда мы это делаем, мы получаем 𝑣 180 плюс 22 умножить на 10. 22 умножить на 10 — это 220. А 180 плюс 220 — это 400. Мы по-прежнему, конечно, работаем в сантиметров в секунду. Чтобы дать наш ответ в метрах на во-вторых, мы разделим на 100. И когда мы это сделаем, мы обнаружим, что скорость 𝑣 в конце движения составляет четыре метра в секунду.

В нашем последнем примере мы рассмотрим найти конечную скорость тела.

Частица двигалась по прямой линия с постоянным ускорением два сантиметра в секунду в квадрате. Учитывая, что его начальная скорость была 60 см в секунду, найдите скорость тела, когда оно было на расстоянии 15 м от отправная точка.

У нас постоянное ускорение, поэтому мы собираемся использовать наши кинематические уравнения. Для начальной скорости 𝑣 ноль, ускорение 𝑎 и скорость 𝑣 через 𝑡 единиц времени, первое уравнение 𝑣 равно 𝑣 ноль плюс 𝑎𝑡. Введем ∆𝑥 для представления смещение объектов. И мы получаем Δ𝑥 равно 𝑣 нулю 𝑡 плюс половина 𝑎𝑡 в квадрате. Наше третье уравнение Δ𝑥 равно половина 𝑣 ноль плюс 𝑣 раз 𝑡. И тогда у нас есть еще один уравнение. То есть 𝑣 в квадрате равно 𝑣 нулю в квадрате плюс два раза 𝑎 раз Δ𝑥.

Давайте перечислим, что мы знаем о движение нашей частицы. У нас есть ускорение как два сантиметров в секунду в квадрате, начальная скорость 60 сантиметров в секунду, и водоизмещение Δ𝑥 15 метров. Теперь, собственно, наше ускорение и скорость выражается в сантиметрах в секунду и сантиметрах в секунду в квадрате. Итак, мы хотим, чтобы единицы были то же самое для Δ𝑥. Умножаем 15 на 100 и видим что это 1500 сантиметров. Мы пытаемся найти скорость тела, когда оно находится на этом расстоянии от начальной точки. Обратите внимание, что это означает, что мы не интересует время, которое это занимает.

Итак, проходим к нашей четверке кинематические уравнения и избавляемся от тех, которые содержат 𝑡. Ну, это уравнение один, два, и три. Это оставляет нам только один уравнение, 𝑣 в квадрате равно 𝑣 ноль в квадрате плюс два раза 𝑎 умножить на Δ𝑥. Мы собираемся заменить все, что мы знаем о движении нашей частицы, в это уравнение. Когда мы это делаем, мы получаем 𝑣 в квадрате равно 60 в квадрате плюс дважды два раза 1500. 60 в квадрате равно 3600. И два раза два раза 1500 равно 6000. Итак, 𝑣 в квадрате равно 9600.

Отсюда следует, что мы можем найти 𝑣 найдя квадратный корень из обеих частей нашего уравнения. 𝑣, следовательно, равно квадрату корень из 9600. Это 97,97 и так далее. Исправить до ближайшего целого число, это 98. И поэтому мы можем сказать, что скорость тела на расстоянии 15 м от начальной точки равна 98 см. в секунду.

Из этого видео мы узнали, что мы можем использовать кинематические уравнения для моделирования движения, включающего постоянное ускорение в прямая линия. Четыре уравнения, которые мы используем, показано. В этих уравнениях 𝑣 ничто не начальная скорость, 𝑣 — скорость через 𝑡 единиц времени, 𝑎 — постоянная ускорение, а Δ𝑥 — перемещение объекта. Мы также увидели, что это действительно Важно при работе с этими уравнениями убедиться, что все единицы такой же.

Расчет движения в двух измерениях

Все ресурсы AP Physics B

65 Практические тесты Вопрос дня Карточки Learn by Concept

AP Physics B Справка » Ньютоновская механика » Движение ” Линейное движение » Расчет движения в двух измерениях

Объект падает с земли со скоростью 75 м/с под углом 45⁰ над горизонтом. На какую высоту поднимется объект перед началом спуска?

Возможные ответы:

70M

420M

280M

140M

Правильный ответ:

140M

Объяснение:

Скорость должна быть разбита на компоненты x (горизонтальная) и y (вертикальная). Мы можем использовать компонент y, чтобы узнать, насколько высоко поднимается объект. Чтобы найти вертикальную скорость, v _y , используйте .

Затем мы находим, сколько времени потребуется, чтобы достичь вершины траектории, используя .

t = 5,3 с

Наконец, найдите, на какую высоту поднимается объект .

 

Сообщить об ошибке

Объект выстреливается с земли со скоростью 125 м/с под углом 30 ^o над горизонтом. На каком расстоянии приземляется объект?

Возможные ответы:

675M

1350M

62,5M

250M

Правильный ответ:

1350M

Объяснение:

Сначала найдите горизонтальную (x) и вертикальную (y) составляющие скорости. верхней части своего пути и удвоить это число.

t = 6,25 с

Таким образом, общее время в воздухе составляет 12,5 с (удвоенное значение).

Наконец, найдите пройденное расстояние, умножив горизонтальную скорость и время.

Сообщить об ошибке

Коробка массой 2 кг находится на вершине наклонной поверхности без трения под углом 60 ^o . Верх рампы находится на высоте 30 м над землей. Ящик неподвижно стоит наверху рампы, а затем его отпускают.

Какова скорость ящика непосредственно перед тем, как он упадет на землю?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем начать эту задачу с определения того, сколько времени потребуется ящику, чтобы достичь земли. Так как расстояние по вертикали 30м и мы знаем угол рампы.

Теперь, когда мы знаем пройденное расстояние, мы можем определить ускорение коробки под действием силы тяжести, используя уравнение .

Мы можем подставить эти значения в следующее уравнение расстояния и найти время.

Теперь, когда мы знаем ускорение коробки и время движения, мы можем использовать уравнение для определения скорости.

Сообщить об ошибке

Мяч отталкивается от высокого стола с горизонтальной скоростью . Какое расстояние пролетит мяч по горизонтали, прежде чем упадет на землю?

Возможные ответы:

Правильный ответ:

Объяснение:

Это двухшаговая задача. Первый шаг — рассчитать время, за которое мяч достигнет земли. Чтобы найти это время, мы используем следующее кинематическое уравнение, относящееся к вертикальному движению.

Выбрав землю в качестве нулевой высоты, мы имеем и .

Также, зная, что начальная вертикальная скорость равна нулю, мы знаем, что .

Кинематическое уравнение упрощает использование этих значений.

Измените уравнение, чтобы изолировать время.

Мы знаем, что это ускорение свободного падения: . Подставьте значения для определения времени.

Теперь у нас есть время, за которое мяч движется до того, как он упадет на землю. Используйте это значение, чтобы найти горизонтальное расстояние до того, как он упадет на землю с помощью кинематического уравнения.

Мы знаем это и это . Используя эти значения и время, мы можем определить пройденное расстояние по горизонтали.

Сообщить об ошибке

Автомобиль едет на север со скоростью , затем поворачивает на восток и едет со скоростью . Каковы модуль и направление средней скорости за поездку?

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала определите, как далеко машина проедет в каждом направлении:

Теперь, когда у нас есть направленные перемещения, мы можем найти полное перемещение, используя теорему Пифагора.

Найдите среднюю скорость, разделив общее перемещение на общее время.

Скорость является вектором, то есть имеет как величину, так и направление. Теперь, когда у нас есть величина, мы можем найти направление с помощью тригонометрии.

Используйте смещения на север и восток, чтобы найти угол.

Наш окончательный ответ будет:

Сообщить об ошибке

Мяч брошен под углом  над горизонталью с начальной скоростью . В какое время его вертикальная скорость ?

Возможные ответы:

Правильный ответ:

Пояснение:

Любой снаряд имеет нулевую вертикальную скорость на пике своего полета. Чтобы решить этот вопрос, нам нужно найти время, за которое мяч достигнет этой высоты. Самый простой способ — определить начальную вертикальную скорость с помощью тригонометрии, а затем использовать соответствующее уравнение кинематики для определения времени.

Мы знаем, что конечная вертикальная скорость будет равна нулю. Мы можем определить начальную вертикальную скорость, используя заданный угол и общую скорость.

Используя это в нашей формуле кинематики, мы находим время.

Имейте в виду, что это только вертикальная скорость. Суммарная скорость в пике не равна нулю, так как мяч по-прежнему будет иметь горизонтальную скорость.

Сообщить об ошибке

Коробка массой 2 кг находится на вершине пандуса без трения под углом . Верх рампы находится на высоте 30 м над землей. Ящик неподвижно стоит наверху рампы, а затем его отпускают.

Когда коробку отпустят, через какое время она упадет на землю?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем начать эту задачу с определения того, как далеко ящик пройдет по рампе, прежде чем упадет на землю.