Вектор мгновенного ускорения: Мгновенное ускорение

Мгновенное ускорение | это… Что такое Мгновенное ускорение?

Если движение точки прямолинейно, можно построить график зависимости скорости от времени. При этом величина ускорения будет равна тангенсу угла наклона касательной к графику в указанной точке.

Ускоре́ние (обычно обозначается , в теоретической механике ), производная скорости по времени — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).

Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².

Раздел механики, изучающий движение в трёхмерном евклидовом пространстве, его запись, а также запись скоростей и ускорений в различных системах отсчёта, называется кинематикой.

Единицей ускорения служит метр в секунду за секунду (m/s²

, м/с²), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с².

Производная ускорения по времени т.е. величина, характеризующая быстроту изменения ускорения по времени называется рывок.

Содержание 1 Кинематика точки 1.1 Ускорение точки при прямолинейном движении 1.2 Ускорение точки при движении по окружности 1.3 Ускорение точки при движении по кривой 2 Ускорения в твёрдом теле 3 Ускорение при сложном движении 4 Динамика точки 5 Единицы измерения ускорения 6 См. также 7 Ссылки

Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости частицы по времени:

.

Ускорение точки при прямолинейном движении

Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:

.

Частным случаем равноускоренного движения является случай, когда ускорение равно нулю во всё время движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), так что говорят, что движение прямолинейно и равномерно.

Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное не верно.)

Ускорение точки при движении по окружности

Если точка движется по окружности с постоянной по модулю скоростью, ее ускорение все равно не равно 0, поскольку направление вектора скорости постоянно изменяется. Ускорение в этом случае называется центростремительным, посколку его вектор всегда направлен к центру окружности, а его модуль равен:

Если при движении по окружности модуль скорости изменяется, удобно ввести такое понятие, как угловое ускорение, аналогичное угловой скорости. Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:

Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растет, и наоборот.

Ускорение точки при движении по кривой

Разложение ускорения по сопутствующему базису для движения в плоскости

Вектор ускорения можно разложить по сопутствующему базису :

,

где

• v — величина скорости,
•  — единичный касательный к траектории вектор, направленный вдоль скорости (касательный орт),
•  — орт нормали к траектории,
•  — орт бинормали к траектории,
• R — радиус кривизны траектории.

Известно, что всегда равно нулю.

Векторы и называются касательным (тангенциальным), нормальным и бинормальным ускорениями соответственно.

Ускорения в твёрдом теле

Основная статья: Кинематика твёрдого тела

Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:

,

где  — вектор угловой скорости тела, а  — вектор углового ускорения тела.

Второе слагаемое называется центростремительным ускорением.

Ускорение при сложном движении

Основная статья: Сложное движение

Абсолютное ускорение равно сумме относительно, переносного и кориолисова:

.

Первый закон Ньютона постулирует существование инерциальных систем отсчета. В этих системах отсчета равномерное прямолинейное движение имеет место всякий раз, когда материальная точка (но не тело!) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом постулируется, что причиной возникновения ненулевого ускорения

в инерциальной системе отсчета всегда является некоторое внешнее силовое воздействие.

Второй закон Ньютона утверждает, что приложенная (к точке) сила и порождаемое ей ускорение точки всегда пропорциональны, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):

.

Единицы измерения ускорения

• метр в секунду в квадрате, м/с², производная единица системы СИ
• сантиметр в секунду в квадрате, см/с², производная единица системы СГС

См. также

• Ускорение свободного падения
• Замедление

Ссылки

Мгновенное линейное ускорение равно первой производной от вектора мгновенной скорости по времени или второй производной от радиус – вектора по времени.

Так же как и для вектора мгновенной скорости проекции вектора ускорения на оси координат являются первыми производными от соответствующих скоростей и вторами производными от соответствующих координат по времени: , , . И модуль вектора ускорения:

В СИ единицей измерения ускорения является метр на секунду в квадрате (м/с²).

При криволинейном движении материальной точки ее скорость изменяется как по величине, так и по направлению.

Вектор мгновенного ускорения всегда направлен внутрь кривизны траектории и составляет некоторый угол с вектором мгновенной скорости .

Плоское движение – это такое движение, при котором все участки траектории движения точки лежат в одной плоскости.

Для случая плоского криволинейного движения часто находят проекции вектора линейного ускорения не на оси x, y, z, а на два других взаимно перпендикулярных направления: касательное к траектории движения тела в данной точке и нормаль. Проекция ускорения на направление касательной – тангенциальная составляющая , на нормаль – нормальная составляющая . В этом случае модуль вектора мгновенного ускорения может быть найден как .

Тангенциальное ускорение определяется как первая производная от модуля мгновенной скорости по времени: . Оно «отвечает» за изменение скорости по величине. Нормальное ускорение «отвечает» за изменение направления скорости. Его величина определяется по формуле: , где R – радиус кривизны траектории.

Плоское движение – это движение, при котором все точки твердого тела движутся в параллельных плоскостях.

Основными видами движения твердого тела являются: поступательное и вращательное. Остальные виды движения твердого тела можно свести к одному из основных движений либо к их совокупности.

Поступательное движение – это движение, при котором все точки твердого тела совершают за один и тот же промежуток времени одинаковые перемещения. При таком движении любая прямая, связанная с телом, все время остается параллельной самой себе.

Поскольку при поступательном движении все точки тела движутся одинаково, то задача описания движения твердого тела сводится к задаче кинематики материальной точки.

Простое вращательное движение (вращение вокруг неподвижной оси) – это движение, при котором все точки твердого тела движутся по концентрическим окружностям, центры которых лежат на оси вращения.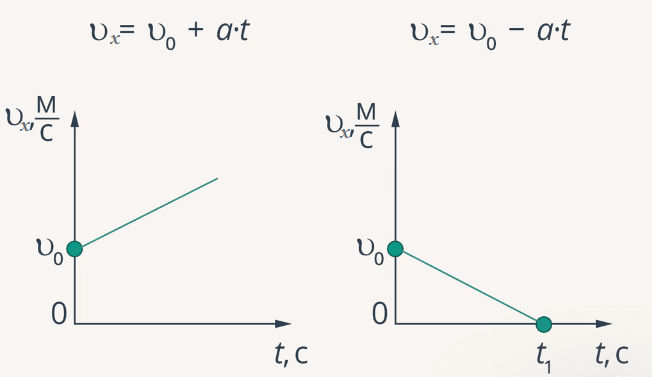

При простом вращательном движении угловые величины (перемещения, скорости, ускорения) всех точек тела одинаковы, а линейные – различны и зависят от расстояния точки до оси вращения.

Рассмотрим вращение твердого тела вокруг неподвижной оси.

Поскольку твердое тело – это совокупность материальных точек и при его вращении вокруг неподвижной оси каждая из них движется по окружности, рассмотрим движение одной материальной точки по окружности.

Вектор называется вектором углового п еремещения, он численно равен углу поворота, направление его определяется по правилу правого винта. Единицей измерения углового перемещения в СИ является радиан (рад).

Кинематической характеристикой направления и быстроты вращения материальной точки служит угловая скорость, которая определяется как первая производная от углового перемещения по времени: Она всегда направлена так же, как и вектор углового перемещения. Единицей измерения угловой скорости в СИ является радиан в секунду (рад/с).

В том случае, если вектор меняется с течением времени, вводят понятие углового ускорения , вектора характеризующего быстроту изменения угловой скорости:

Вектор углового ускорения совпадает по направлению с вектором угловой скорости , если движение материальной точки равноускоренное ( >0).

В случае равнозамедленного движения ( <0) вектор углового ускорения направлен в сторону, противоположную вектору .

В СИ угловое ускорение измеряется в радианах на секунду в квадрате (рад/с²).

Если материальная точка движется по окружности радиуса , и за время перемещается из положения 1 в положение 2, то путь S, пройденный по дуге окружности, связан с углом поворота известным из курса математики соотношением . Тогда или .

Продифференцировав это выражение по времени: получим выражение, связывающее угловое и тангенциальное ускорения: .

Рассмотрим полученную связь линейных и угловых величин в векторной форме. Остановимся для удобства на рассмотрении равноускоренного движения ( ).Применим правило правого винта. При вращении от к поступательное движение правого винта осуществляется вдоль , поэтому . Аналогично .

Нормальное ускорение противоположно по направлению радиус-вектору , следовательно:

При описании равномерного движения материальной точки по окружности и равномерного вращения тела часто используются такие величины как период (Т) и частота вращения (n или ).

Период вращения – это время, за которое тело совершает один полный оборот. Период измеряется в СИ в секундах (с).

Частота вращения – это число оборотов, совершенное телом за единицу времени. В СИ частота вращения измеряется в с^-1 (1/с).

Если за некоторое время t тело совершило N полных оборотов, то и . Следовательно, и .

Поскольку период – это время одного полного оборота ( ), то . А, следовательно, .

Модули углового перемещения и угловой скорости связаны с числом полных оборотов N и частотой вращения n:

9

3.3 Среднее и мгновенное ускорение — Университетская физика, том 1

Цели обучения

К концу этого раздела вы сможете:

• Вычислите среднее ускорение между двумя моментами времени.
• Рассчитайте мгновенное ускорение, учитывая функциональную форму скорости.
• Объясните векторную природу мгновенного ускорения и скорости.
• Объясните разницу между средним ускорением и мгновенным ускорением.
• Найдите мгновенное ускорение в указанное время на графике зависимости скорости от времени.

Важность понимания ускорения охватывает наш повседневный опыт, а также обширные просторы космоса и крошечный мир субатомной физики.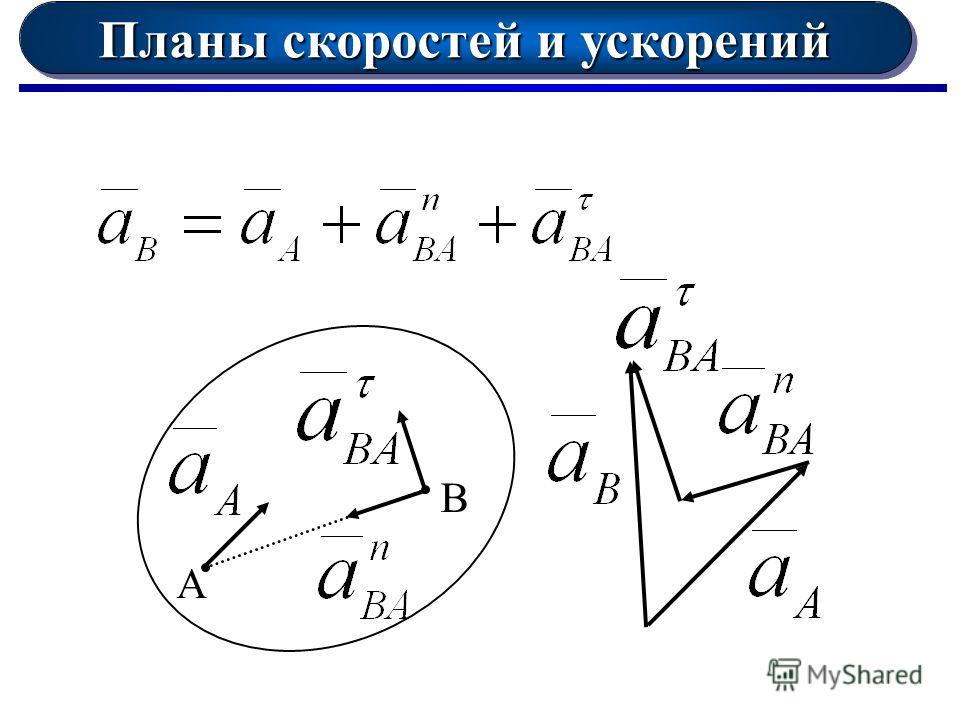 В повседневном разговоре ускорить означает ускорить; при нажатии на педаль тормоза автомобиль замедляется. Например, мы знакомы с ускорением нашего автомобиля. Чем больше ускорение, тем больше изменение скорости за данное время. Ускорение широко используется в экспериментальной физике. В экспериментах с линейным ускорителем частиц, например, субатомные частицы разгоняются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной. В космосе космические лучи — это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывах массивных звезд) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат сильно проникающее излучение, которое может повредить электронику, например, на космическом корабле.

Среднее ускорение

Формальное определение ускорения согласуется с только что описанными понятиями, но является более всеобъемлющим.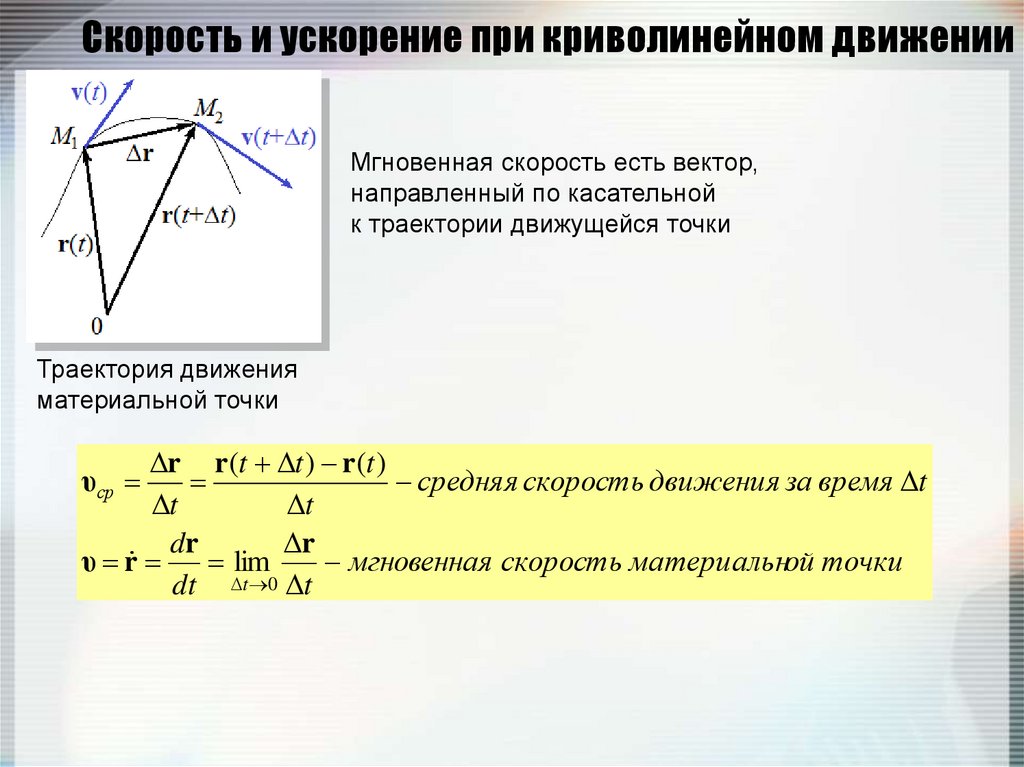

Среднее ускорение

Среднее ускорение – скорость изменения скорости:

a–=ΔvΔt=vf−v0tf−t0,a–=ΔvΔt=vf−v0tf−t0,

3,8

где a−a− среднее ускорение, v — это скорость, а t — это время. (Полоса над и означает в среднем ускорение.)

Поскольку ускорение представляет собой скорость в метрах в секунду, деленную на время в секундах, единицы измерения ускорения в системе СИ часто обозначаются аббревиатурой м/с ² , то есть метры в секунду в квадрате или метры в секунду в секунду. Это буквально означает, на сколько метров в секунду скорость изменяется каждую секунду. Напомним, что скорость — это вектор — она имеет как величину, так и направление — это означает, что изменение скорости может быть изменением величины (или скорости), но также может быть и изменением направления. Например, если бегун, движущийся со скоростью 10 км/ч строго на восток, замедляется до остановки, меняет направление и продолжает свой бег со скоростью 10 км/ч строго на запад, его скорость изменилась в результате изменения направления, хотя величина скорости одинакова в обоих направлениях. Таким образом, ускорение возникает, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по тому и другому.

Ускорение как вектор

Ускорение — это вектор в том же направлении, что и изменение скорости, ΔvΔv. Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Таким образом, ускорение — это изменение скорости или направления, или и того, и другого.

Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда совпадает с направлением движения. Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называют замедление На рисунке 3.10 мы говорим, что поезд ускоряется в направлении, противоположном направлению его движения.

Рисунок 3.10 Поезд метро в Сан-Паулу, Бразилия, ускоряется против движения, когда он подходит к станции. Он ускоряется в направлении, противоположном направлению его движения. (кредит: модификация работы Юсуке Кавасаки)

Термин замедление может вызвать путаницу в нашем анализе, поскольку он не является вектором и не указывает на конкретное направление относительно системы координат, поэтому мы не используем Это. Ускорение — это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат. В случае поезда на рис. 3.10 ускорение равно в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.

Если объект в движении имеет скорость в положительном направлении по отношению к выбранному началу координат и приобретает постоянное отрицательное ускорение, объект в конце концов приходит в состояние покоя и меняет направление. Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это показано на рис. 3.11.

Рисунок 3.11 Объект, движущийся с вектором скорости на восток с отрицательным ускорением, останавливается и меняет направление на противоположное. Он проходит начало координат, двигаясь в противоположном направлении через достаточно долгое время.

Пример 3,5

Расчет среднего ускорения: скаковая лошадь покидает ворота

Скаковая лошадь, выходящая из ворот, разгоняется из состояния покоя до скорости 15,0 м/с строго на запад за 1,80 с. Каково его среднее ускорение?

Рисунок 3.12 Скаковые лошади ускоряются из ворот. (кредит: модификация работы Джона Салливана)

Стратегия

Сначала мы рисуем эскиз и назначаем системе координат задачу Рисунок 3.13. Это простая задача, но ее всегда полезно визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.

Рисунок 3.13 Определите систему координат, предоставленную информацию и то, что вы хотите определить.

Мы можем решить эту проблему, определив ΔvandΔtΔvandΔt из данной информации, а затем рассчитав среднее ускорение непосредственно из уравнения a–=ΔvΔt=vf−v0tf−t0a–=ΔvΔt=vf−v0tf−t0.

Раствор

Сначала выделим известные: v0=0,vf=-15,0м/sv0=0,vf=-15,0м/с (знак минус указывает направление на запад), Δ t = 1,80 с.

Во-вторых, найдите изменение скорости. Поскольку лошадь движется от нуля до –15,0 м/с, изменение ее скорости равно ее конечной скорости:

Δv=vf−v0=vf=−15,0 м/с. /с.

Наконец, подставьте известные значения (ΔvandΔtΔvandΔt) и найдите неизвестное a–a–: /с1,80с=-8,33 м/с2.

Значение

Отрицательный знак ускорения указывает на то, что ускорение направлено на запад. Ускорение 8,33 м/с ² строго на запад означает, что лошадь увеличивает свою скорость на 8,33 м/с строго на запад каждую секунду; то есть 8,33 метра в секунду за секунду, что мы запишем как 8,33 м/с ² . Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы от всадника удержания силы, почти равной его весу.

Проверьте свое понимание 3.3

Протоны в линейном ускорителе ускоряются из состояния покоя до 2,0×107 м/с2,0×107 м/с за 10 ^–4 с. Каково среднее ускорение протонов?

Мгновенное ускорение

Мгновенное ускорение a или ускорение в конкретный момент времени получается с использованием того же процесса, который обсуждался для мгновенной скорости. То есть мы вычисляем среднее ускорение между двумя моментами времени, разделенными ΔtΔt, и позволяем ΔtΔt приближаться к нулю. Результатом является производная функции скорости v ( t ), что представляет собой мгновенное ускорение и математически выражается как

a(t)=ddtv(t).a(t)=ddtv(t).

3,9

Таким образом, аналогично тому, как скорость является производной функции положения, мгновенное ускорение является производной функции скорости. Мы можем показать это графически так же, как мгновенную скорость. На рис. 3.14 мгновенное ускорение в момент времени t ₀ представляет собой наклон касательной к графику зависимости скорости от времени в момент времени 9.0019 т ₀ . Мы видим, что среднее ускорение a–=ΔvΔta–=ΔvΔt приближается к мгновенному ускорению, когда ΔtΔt приближается к нулю. Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, так как наклон кривой и там равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.

Рисунок 3.14 На графике зависимости скорости от времени мгновенное ускорение представляет собой наклон касательной. (a) Показано среднее ускорение a–=ΔvΔt=vf–vitf–tia–=ΔvΔt=vf–vitf–ti между моментами времени Δt=t6–t1, Δt=t5–t2 Δt=t6–t1, Δt=t5–t2, и Δt=t4−t3 Δt=t4−t3. Когда Δt→0Δt→0, среднее ускорение приближается к мгновенному ускорению в момент времени t ₀ . На виде (а) показано мгновенное ускорение для точки на кривой скорости при максимальной скорости. В этой точке мгновенное ускорение представляет собой наклон касательной, который равен нулю. В любой другой момент времени наклон касательной и, следовательно, мгновенное ускорение не были бы равны нулю. (b) То же, что и (a), но показано для мгновенного ускорения при минимальной скорости.

Чтобы проиллюстрировать эту концепцию, рассмотрим два примера. Во-первых, показан простой пример с использованием рисунка 3.9(b), графика зависимости скорости от времени из примера 3.4, для графического определения ускорения. Этот график изображен на рис. 3.15(а) в виде прямой линии. Соответствующий график зависимости ускорения от времени находится по наклону скорости и показан на рис. 3.15(b). В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным. В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.

Рисунок 3.15 (а, б) График зависимости скорости от времени является линейным и имеет отрицательный постоянный наклон (а), равный ускорению, показанному на (б).

Если мы знаем функциональную форму скорости, v ( t ), мы можем рассчитать мгновенное ускорение a ( t ) в любой момент времени в движении, используя уравнение 3.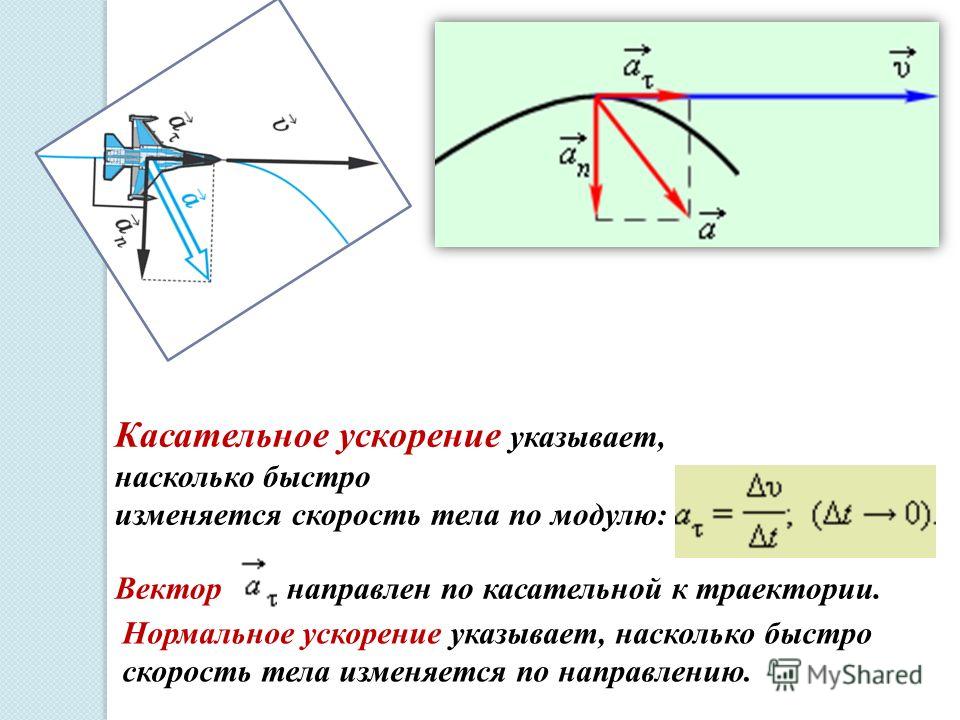 9.

Пример 3,6

Расчет мгновенного ускорения

Частица движется и ускоряется. Функциональная форма скорости имеет вид v(t)=(20м/с)t–(5м/с2)t2v(t)=(20м/с)t–(5м/с2)t2.

1. Найдите функциональную форму ускорения.
2. Найти мгновенную скорость в точке t = 1, 2, 3 и 5 с.
3. Найти мгновенное ускорение в точке т = 1, 2, 3 и 5 с.
4. Интерпретируйте результаты (c) с точки зрения направлений векторов ускорения и скорости.

Стратегия

Найдем функциональную форму ускорения, взяв производную функции скорости. Затем вычисляем значения мгновенной скорости и ускорения по заданным функциям для каждого. Для части (d) нам нужно каждый раз сравнивать направления скорости и ускорения.

Решение

1. a(t)=dv(t)dt=(20м/с2)–(10м/с3)ta(t)=dv(t)dt=(20м/с2)–(10м/с3) т
2. v(1s)=15м/сv(1s)=15м/с, v(2s)=20м/сv(2s)=20м/с, v(3s)=15м/сv(3s)=15м/с, v (5с)=-25м/с(5с)=-25м/с
3. а(1 с)=10 м/с2а(1 с)=10 м/с2, а(2 с)=0 м/с2а(2 с)=0 м/с2, а(3 с)=-10 м/с2а( 3 с)=-10 м/с2, a(5 с)=-30 м/с2a(5 с)=-30 м/с2
4. При t = 1 с скорость v(1s)=15 м/сv(1s)=15 м/с положительна, а ускорение положительно, поэтому и скорость, и ускорение имеют одинаковое направление. Частица движется быстрее.

В t = 2 с скорость увеличилась tov(2s)=20м/sv(2s)=20м/с, где она максимальна, что соответствует времени, когда ускорение равно нулю. Мы видим, что максимальная скорость возникает, когда наклон функции скорости равен нулю, что равно нулю функции ускорения.

При t = 3 с скорость v(3s)=15м/сv(3s)=15м/с и ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицателен. Частица замедляется.

В t = 5 с скорость v(5s)=-25м/сv(5s)=-25м/с и ускорение становится все более отрицательным. Между моментами времени t = 3 с и t = 5 с скорость частицы уменьшилась до нуля, а затем стала отрицательной, тем самым изменив свое направление. Теперь частица снова ускоряется, но в противоположном направлении.

Мы можем увидеть эти результаты графически на рис. 3.16.

Рисунок 3.16 (а) Скорость в зависимости от времени. Касательные линии указаны в моменты времени 1, 2 и 3 с. Наклоны касательных линий являются ускорениями. В t = 3 с, скорость положительна. При t = 5 с скорость отрицательна, что указывает на то, что частица изменила направление. (b) Ускорение в зависимости от времени. Сравнивая значения ускорений, заданные черными точками, с соответствующими наклонами касательных (наклоны линий, проведенных через черные точки) на (а), мы видим, что они идентичны.

Значение

Выполняя как численный, так и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении. Численный анализ дополняет графический анализ, давая общее представление о движении. Ноль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительно и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю, со временем становясь отрицательным, скорость достигает максимума, после чего начинает уменьшаться. Если мы подождем достаточно долго, скорость также станет отрицательной, указывая на изменение направления. Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление.

Проверьте свое понимание 3.4

Самолет приземляется на взлетно-посадочной полосе, направляясь на восток. Опишите его ускорение.

Почувствуйте ускорение

Вероятно, вы привыкли ощущать ускорение, когда входите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит и со многими другими объектами в нашей Вселенной, с которыми у нас нет прямого контакта. В таблице 3.2 представлены ускорения различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.

Ускорение	Значение (м/с 2 )
Скоростной поезд	0,25
Лифт	2
Гепард	5
Объект в свободном падении без сопротивления воздуха у поверхности Земли	9,8
Максимум космического корабля во время запуска	29
Пик парашютиста при нормальном раскрытии парашюта	59
Выход самолета F16 из пикирования	79
Катапультирование кресла взрывом из самолета	147
Спринт ракета	982
Самое быстрое пиковое ускорение ракетных саней	1540
Прыгающая блоха	3200
Бейсбольный мяч после удара битой	30 000
Закрывающие челюсти муравья-ловушки	1 000 000
Протон в большом адронном коллайдере	1,9×1091,9×109

Стол 3. 2 Типичные значения ускорения (кредит: Википедия: Orders of Magnitude (ускорение))

В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют ничего общего с размером объекта или его массой. Ускорение также может сильно меняться со временем во время движения объекта. Дрэг-рейсер имеет большое ускорение сразу после старта, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения. На рис. 3.17 графически среднее ускорение сравнивается с мгновенным ускорением для двух очень разных движений.

Рисунок 3.17 Графики зависимости мгновенного ускорения от времени для двух различных одномерных движений. а) Ускорение меняется незначительно и всегда в одном и том же направлении, так как оно положительно. Среднее значение по интервалу почти такое же, как ускорение в любой момент времени. (b) Ускорение сильно различается, возможно, это представляет собой пакет на ленточном конвейере почтового отделения, который ускоряется вперед и назад, когда он толкается. В такой ситуации необходимо рассматривать небольшие промежутки времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.

Интерактивный

Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка вперед-назад с помощью мыши и зарисовывайте его движение. Установите положение, скорость или ускорение, и пусть симуляция переместит человека за вас. Посетите эту ссылку, чтобы использовать симуляцию движущегося человека.

кинематика – Мгновенный вектор ускорения к вогнутой стороне криволинейного пути

Чтобы двигаться по вогнутому пути, агент должен передать силу линейно движущемуся объекту. Объект в силу своего движения в отсутствие какой-либо внешней силы всегда движется или стремится двигаться в направлении вектора скорости в рассматриваемый момент.

Итак, когда объект должен пересечь кривую траекторию, основным требованием является введение силы, которая манипулирует направлением скорости таким образом, чтобы результирующее геометрическое место было требуемой криволинейной траекторией, иначе объект двигался бы прямо.

---

Теперь вопрос на миллион долларов: каким должно быть направление силы?

Направление силы, очевидно, является направлением ускорения или пределом изменения скорости во времени. Итак, чтобы найти направление, давайте представим бесконечно малую ситуацию.

Пусть за короткое время $\Delta t$ пройдено расстояние $v(t)\Delta t$ по дуге окружности радиуса $r$. Тогда пройденный угол равен $$\Delta\theta = \dfrac{v(t) \Delta t}{r}$$.

Представьте себе биссектрису угла. Теперь рассмотрим изменения скорости параллельно и перпендикулярно этой биссектрисе. Первоначально скорость имеет составляющую $v\sin(\frac{\Delta\theta}{2})$ вдали от центра и $v\cos(\frac{\Delta\theta}{2})$ в поперечном направлении. , у него есть компонента $v\sin(\frac{\Delta\theta}{2})$ 92 \dfrac{\Delta\theta}{r}$$. И направление к центру. Таким образом, сила вращает вектор положения по криволинейной траектории, и изменение происходит радиально внутрь, независимо от того, отслеживается ли он по часовой стрелке или против часовой стрелки.

---

Картинка становится более яркой, если считать по полярной координате.

Сначала мы запишем вектор положения как $\mathbf{r} = r\cdot e_r$ . Теперь рассмотрим изменение $\mathbf{r}$ со временем. Его изменение в течение $\Delta t$ равно $r\Delta\theta \cdot e_{\theta}$. $e_r \quad \& \quad e_{\theta}$ взаимно перпендикулярны, первая равна наружу радиально от центра. Следовательно, скорость равна $$v = \dfrac{d\mathbf{r}}{dt} = r\dfrac{d\theta}{dt}\cdot e_{\theta} = \omega r \cdot e_{\theta} $$.

Полагая $r = 1$, получаем $$\dfrac{d}{dt} (e_r) = \omega e_{\theta}$$.

Аналогично, изменение $\theta$ влечет за собой изменение $e_{\theta}$.