Вектор перемещения в физике это: Система отсчёта, радиус-вектор, траектория, путь, перемещение — урок. Физика, 10 класс.

Модуль вектора — это модуль перемещения, в Международной системе единиц (СИ) измеряется в метрах; в системе СГС — в сантиметрах.

Можно определить перемещение, как изменение радиус-вектора точки .

Модуль перемещения совпадает с пройденным путем в том и только в том случае, если при движении направление скорости не изменяется . Об этом говорит сайт https://intellect.icu . При этом траекторией будет отрезок прямой. В любом другом случае, например, при криволинейном движении, из неравенства треугольника следует, что путь строго больше.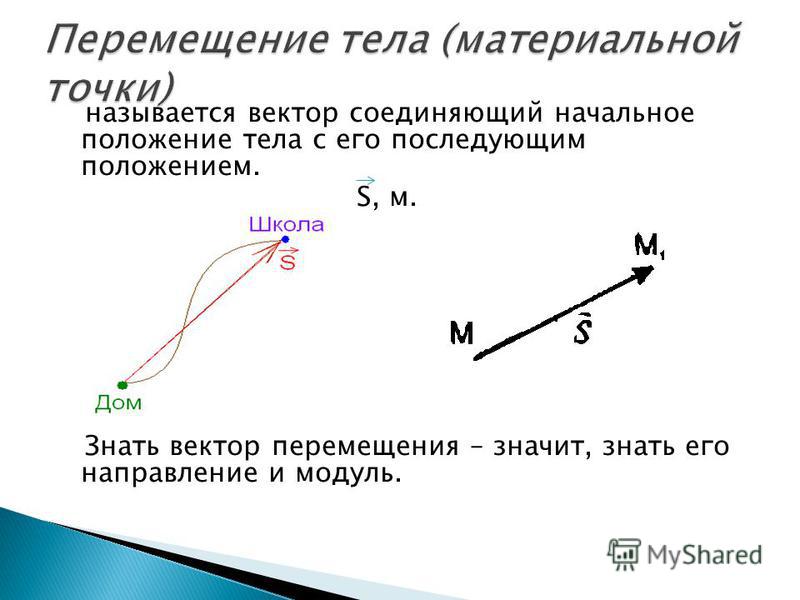

Мгновенная скорость точки определяется как предел отношения перемещения к малому промежутку времени, за которое оно совершено. Более строго:

.

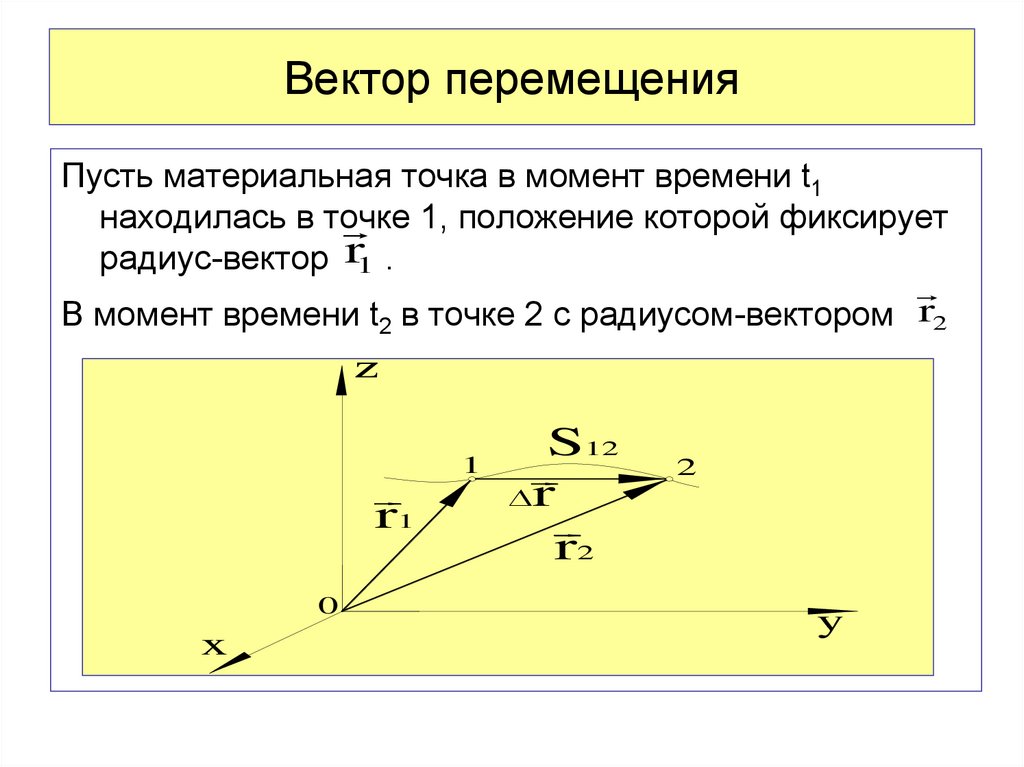
Вектором перемещения материальной

точки за время от , т.е. приращение радиуса-вектора точки за рассматриваемый промежуток времени

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории. Из того, что перемещение является вектором, следует подтверждающийся на опыте закон независимости движений: если материальная точка участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме ее перемещений, совершаемых ею за тоже время в каждом из движений порознь.

Производные функции перемещения

Для вектора положения {\ displaystyle \ mathbf {s}} это функция времени {\ displaystyle t}, производные могут быть вычислены по {\ displaystyle t}. {3}}}}

Эти общие названия соответствуют терминологии, используемой в базовой кинематике.

См. также

• Поступательное движение
• Плоскопараллельное движение
• Вращательное движение
• Сложное движение
• Сферическое движение
• Прецессия
• Нутация
• Ламинарное течение
• Турбулентное течение
• скорость , скорость материальной точки ,

• ускорение , обобщённое ускорение ,

• производная
• угловое ускорение ,
• криволинейное движение тангенциальное , нормальное ускорения ,
• рывок ,

• скорость , скорость материальной точки ,
• Вектор движения
• Вектор положения
• Аффинное пространство
• Поле смещения (механика)
• Эквиполентность (геометрия)

Статью про перемещение я написал специально для тебя.

Перемещение и описание движения | Частная школа. 8 класс

Конспекты по физике    Учебник физики    Тесты по физике

Система отсчёта используется для того, чтобы определить положение тела в пространстве в некоторый момент времени. В случае когда тело движется, возникает задача вычисления его координат в некоторые моменты времени.

ПРОЕКЦИИ ПЕРЕМЕЩЕНИЯ НА КООРДИНАТНЫЕ ОСИ

Если известен вектор перемещения тела, то при расчетах, как правило, используют не координаты вектора, как такового, а его проекции на оси координат. Если опустить перпендикуляры из начала и конца вектора перемещения s на координатную ось X, то получится отрезок s_x, который называют проекцией перемещения. При этом проекция вектора на ось считается положительной, если координата конца вектора перемещения оказывается больше координаты его начала. В противном случае проекция считается отрицательной.

Если вектор и ось параллельны, то длина вектора равна его проекции на эту ось.

При решении многих задач необходимо уметь находить проекции вектора перемещения на координатные оси. Если (х₀; у₀) и (х; у) — координаты начала и конца вектора, то его проекции на оси абсцисс и ординат будут равны соответственно

s_x = x – x₀,     (1)
s_y = y – y₀

Зная проекции вектора перемещения, можно найти его длину (модуль) по теореме Пифагора:

ОПРЕДЕЛЕНИЕ КООРДИНАТ ДВИЖУЩЕГОСЯ ТЕЛА И ЕГО ПЕРЕМЕЩЕНИЯ

Если тело движется прямолинейно, то траектория его движения совпадает с перемещением. При этом пройденный телом путь равен значению модуля вектора перемещения.

А как описать движение тела в более сложном случае? На рисунке представлен график движения самолёта. Сначала он набирал высоту, двигаясь из точки А в точку В, затем двигался на одной и той же высоте (до точки С) и, наконец, приземлился в точке D. На какой высоте проходил полёт? Высоте полёта соответствуют координаты по оси OY, значит, в точке В самолёт набрал высоту 3 км.

Теперь ответим на вопрос: какой путь проделал самолёт на этой высоте? Проекция перемещения s_2x = 80 — 20 = 60 км.

Так как всё это время самолёт двигался параллельно оси ОХ, длина вектора перемещения равна его проекции на эту ось. Следовательно, модуль перемещения самолёта из точки В в точку С равен 60 км. Этому же значению равен и путь самолёта из точки В в точку С.

И наконец, определим дальность полёта самолёта. Для этого нам надо найти модуль перемещения самолёта из точки А в точку D: |s| = s_x = 100 — 0 = 100 км.

Таким образом, при помощи перемещения и его проекций мы описали сложное движение самолёта.

ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ РАВНОМЕРНОМ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ

Так как при прямолинейном движении пройденный телом путь равен значению модуля вектора перемещения, мы можем сказать, что скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела ко времени, за которое это перемещение произошло. При равномерном прямолинейном движении векторы скорости и перемещения направлены в одну сторону. Зная скорость равномерного движения, можно найти перемещение тела за любой промежуток времени:

Поскольку скорость υ является векторной величиной, её тоже можно изобразить графически. Обозначим её проекцию на координатную ось υ_x. Если направление координатной оси совпадает с направлением движения тела, то для расчёта перемещения тела можно использовать формулу

УРАВНЕНИЕ ДВИЖЕНИЯ

Уравнение зависимости координаты тела от времени называют уравнением движения.

Пусть тело совершило перемещение s. Направим координатную ось X по направлению перемещения тела. Обозначим начальную координату тела

Но по формуле (3) s_x = υ_xt. Следовательно,

Таким образом, координату тела при равномерном прямолинейном движении в любой момент времени можно определить, если известны его начальная координата и проекция скорости движения на ось X.

Ранее при решении задач мы использовали формулу s = υt без стрелочек. Почему? Символом s здесь обозначался путь, пройденный телом, а символом и — модуль скорости.

Вы смотрели Конспект по физике для 8 класса «Перемещение и описание движения».

Вернуться к Списку конспектов по физике

Просмотров: 11 097

Что такое вектор смещения? | AP Физика 1 (Кинематика)

Например, вы проехали из точки A в точку B . И если вы посмотрите на путь своего путешествия, то увидите, что ваше полное перемещение равно AB . Что зависит от двух моментов.

И если вы выражаете это смещение в векторной форме, оно называется вектором смещения. Например,

Это изогнутый путь, который вы переместили из точки 9.0003 А в точку В . И этот вектор смещения не зависит от этого пути. Это просто зависит от вашего начального и конечного положения.

В чем разница между смещением и вектором смещения?

Вы можете подумать, что смещение и вектор смещения — это два разных понятия, но нет, это одно и то же.

Когда частица движется из точки A в точку B , вы не можете выразить ее перемещение скалярами. Всегда выражается в векторной форме.

Точно так же представлен вектор смещения.

И это правда, что если даны векторы положения двух точек, то их перемещение всегда называется вектором смещения.

Графическое представление вектора положения

При движении частицы из точки A в точку B для определения смещения частицы необходимо знать положение обеих точек.

Таким образом, вы не можете определить смещение между двумя точками, пока не знаете положение обеих точек.

В этом случае для представления перемещения точка должна быть выражена в виде вектора без записи в системе координат, поскольку перемещение является векторной величиной.

Когда положение точки представлено в векторной форме, оно называется вектором положения.

Вы можете понять, взглянув на изображение выше. Здесь положение соответствует системе координат точек (x,y,z) . То есть смещение частицы по x , y и z оси равны x , y и z . Тогда вектор из точки будет

Графическое представление вектора смещения

Частица движется из точки A в точку B в свободном пространстве, как показано на рисунке ниже. Здесь r ₁ — вектор положения начального состояния частицы, а r ₂ — вектор положения конечной точки.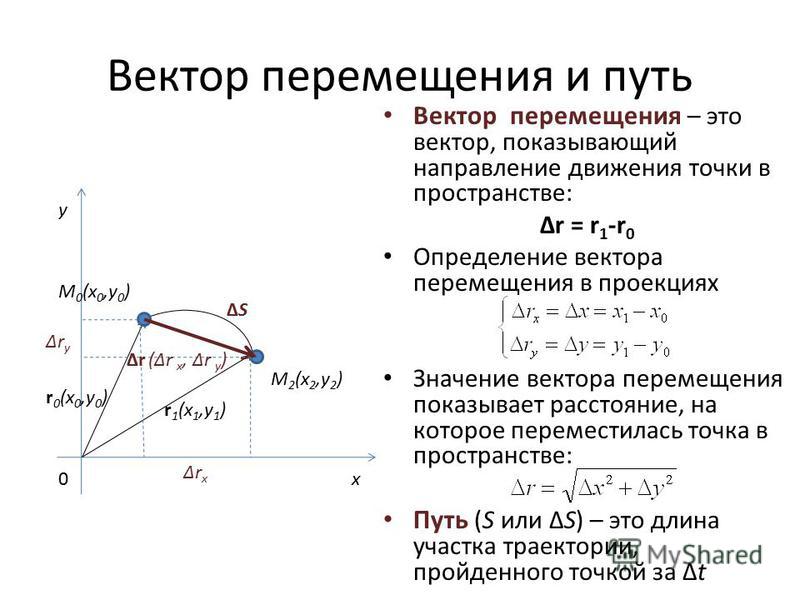 ∇r — вектор смещения частицы.

Мы можем записать в соответствии с векторным законом треугольника

Таким образом, вектор смещения означает, что положение движущейся частицы отличается между двумя векторами положения.

А так как вектор смещения здесь в компонентной форме, то он будет иметь абсолютное значение

Единица измерения и размерность

Длина прямой показывает величину смещения. Таким образом, единицей длины является единица перемещения. Единицы перемещения в различных стандартных методах приведены ниже

• Метод СГС: Сантиметр ( см )
• Метод PFS: фута ( футов)
• Метод СИ: Метр ( м )

А размерность смещения – это размерность длины, т.е. L.

Нулевое смещение

Если начальное и конечное положение объекта совпадают, его смещение будет равно нулю. То есть, если человек начинает путешествие из одного места, проходит какое-то расстояние и снова возвращается в это место, его движение будет равно нулю.

В этом случае расстояние до объекта будет не равно нулю. И нет направления нулевых перемещений.

Вопросы и ответы

Q1. Частица объекта движется по круговой траектории. Радиус которого равен двум единицам. Так каким же будет вектор смещения частицы в каждом из следующих случаев?

• A(3,6)→B(5,8) : Когда объект перемещается из точки A в точку B, его положение увеличивается на две единицы по обеим осям. Тогда произойдет смещение объекта.

• A(3,6)→C(7,6) : В этом случае положение объекта не изменится по оси y. Скорее, будет смещение по оси x.

• A(3,6)→D(5,4) : В этом случае значение смещения частицы будет равно значению смещения в первом случае. Но в обоих случаях направление смещения всегда будет разным.

Q2. Частица движется с постоянной скоростью. А график скорости и времени нарисован ниже по его траектории. И по этому графику вы рисуете график между перемещением и временем.

Здесь частица движется с постоянной скоростью. Таким образом, наклон графика смещения и времени будет определять постоянную скорость. Здесь график будет представлять собой прямую линию, которая будет наклонена под определенным углом по оси времени.

Заключение

С помощью этого урока вы поймете, что такое вектор смещения! Конечно, это важная концепция векторов. Эта концепция используется при определении смещения между двумя положениями.

Векторы положения и смещения – определение, объяснение и часто задаваемые вопросы

Мы все имеем дело с графиком, отмечаем линию от начала координат и доходим до другого конца до требуемого. Все эти требования выполняются в системе координат. Итак, координата, где заканчивается наша линия, указанная стрелкой, является координатой этого луча.

Предположим, вы начали свое путешествие из дома, чтобы добраться до любимого пункта назначения, а затем направились к другому пункту назначения, поэтому ваша стрелка меняет как длину, так и направление, что означает, что вектор вашего положения меняется, и в случае, если вы выбираете кратчайший путь, т. е. смещение, вы представляете его вектором смещения.

Определение вектора положения

Мы определяем вектор положения как прямую линию, один конец которой прикреплен к объекту, а другой конец прикреплен к движущейся точке (отмеченной стрелкой) и используется для представления положения точки относительно данный объект. По мере движения точки вектор положения изменяется по длине или по направлению, а иногда изменяются и длина, и направление.

Знакомство с вектором положения и вектором смещения

В изучении нашего физического мира концепции положения и смещения являются основополагающими темами главы, посвященной движению. Понятие «вектор положения» было заимствовано из евклидовых пространств или геометрии и также известно как вектор положения или радиус-вектор. Положение любой точки в пространстве выражается в терминах трех координат, а именно расстояний «x», «y» и «z» от любой произвольной точки, обозначенной как «O» или начала координат. Прямая линия от начала до точки обозначается буквой «r» или «s». В физике этот вектор используется при описании объекта в состоянии покоя или движения в пространстве относительно другого объекта. в зависимости от различных мест в разные моменты времени вектор соответственно меняет длину и направление.

Три координаты, описанные в векторах каждого направления, также называются тремя измерениями. Смещение — это любое изменение любого из этих векторов. На обычном языке мы знаем перемещение как любое перемещение объекта из одного места в другое по прямому пути. Если какой-либо объект не следует прямолинейному пути, то общий пройденный путь измеряется как расстояние. И смещение в этом случае будет прямым расстоянием между начальной и конечной точками. При описании смещения, которое сообщает кратчайшее расстояние между двумя точками, также важно указать направление смещения, чтобы знать точное местоположение конечной точки. Таким образом, когда мы обозначаем направление точки, оно называется вектором положения, а когда упоминается направление смещения, оно называется вектором смещения.

Что такое вектор положения?

В приведенном выше заявлении мы взяли систему координат, чтобы представить ваше путешествие от исходной точки, то есть от вашего дома до ваших любимых мест назначения, сначала в Дарджилинг, затем в Карнатаку.

Каждый пункт назначения отмечен стрелкой на графике, которая изменяется или меняется по мере изменения пункта назначения. Ниже приведен график, представляющий то же самое:

(Изображение будет загружено в ближайшее время) т. е. вдвое или в два раза больше длины, и направление вектора положения меняется по этому сценарию. 9{\rightarrow }\] = i (cap) + j (cap)……(1)

Определение вектора смещения           

Вектор смещения — одно из важных понятий математики. Это вектор. Он представляет направление и расстояние, пройденное объектом по прямой линии. Мы часто используем термин «вектор смещения» в физике, чтобы продемонстрировать скорость, ускорение и расстояние объекта, движущегося в направлении относительно контрольной точки или исходного положения объекта.

Что такое вектор смещения?

Определение вектора смещения очень просто для понимания. Давайте обсудим сценарий, вы решаете отправиться в две локации для работы в офисе за минимально возможное время, и обе эти локации примыкают друг к другу посреди двух дорог, проходящих друг напротив друга. Теперь вам нужно решить, по какому пути вы должны пойти, чтобы добраться за требуемое время, так как на дороге много трафика и мысли о том, чтобы вас отругал ваш босс. Итак, ниже наглядное схематическое изображение вашей ситуации:

(Изображение будет загружено в ближайшее время)

Итак, здесь зеленая линия — это кратчайший путь, который поможет вам добраться до середины двух дорог и добраться до двух мест вовремя. Таким образом, вектор смещения представляет собой минимальное расстояние, которое нужно пройти вовремя, а не длинный путь с потерей большого количества времени.

Теперь, после того, как ваша работа сделана, вы принимаете противоположную клятву, так что здесь ваше перемещение не меняется, меняется только направление. Таким образом, с направлением вектор смещения изменяется по направлению, а не по величине. 9{\rightarrow }\] P (крышка) =- 6i (крышка) – 3j (крышка) -2k (крышка)…. (c)

Уравнение (c) представляет собой формулу вектора смещения и схематическое представление этой уравнение выглядит следующим образом:

(изображение будет загружено в ближайшее время)

Мы также можем определить смещение объекта как векторное расстояние между начальной точкой и конечной/конечной точкой назначения. Предположим, что объект движется из точки P в точку Q по пути, показанному черной кривой:

(изображение скоро будет загружено)

Мы можем представить, что смещение частицы было бы векторной линией PQ, направленной в направлении P к Q, и направление вектора смещения всегда начинается с начальной точки и заканчивается в конечной точке.