Полное ускорение при криволинейном движении
При движении по криволинейной траектории скорость точки может изменяться и по направлению, и по величине. Изменение скорости в единицу времени определяется ускорением.
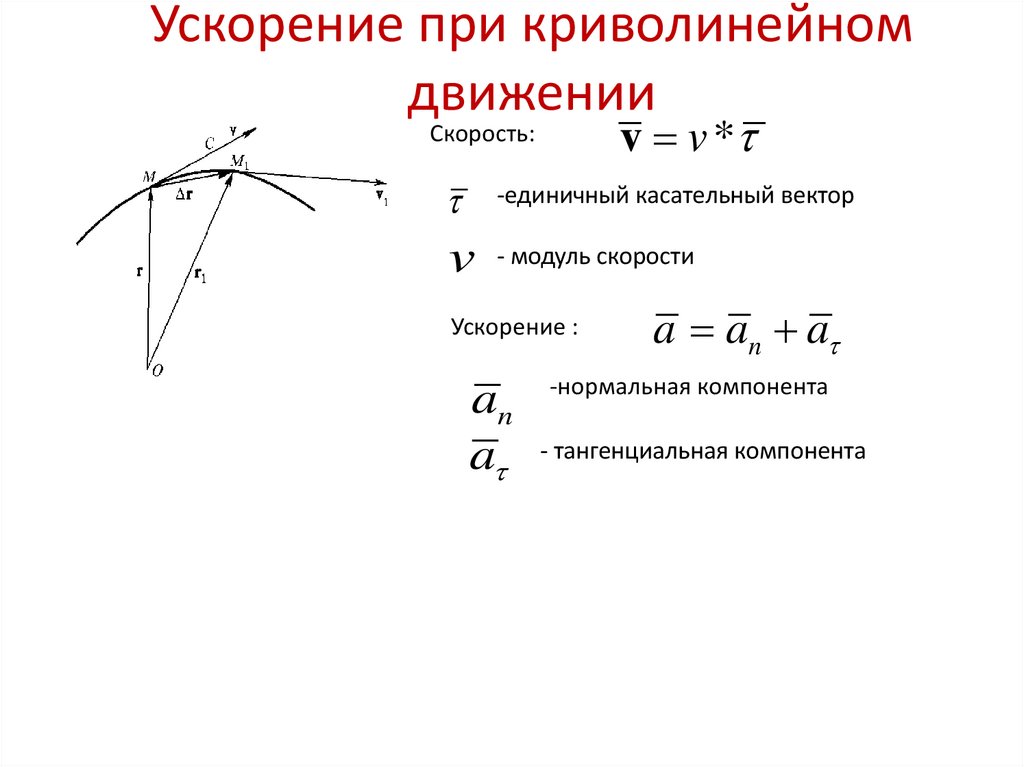
Пусть точка М (рис.а) движется по какой-то криволинейной траектории и за время t переходит из положения М в положение M1. Расстояние, пройденное точкой, представляет собой дугу ММ1; ее длину обозначим s. В положении М точка имела скорость v, в положении M1 — скорость v1. Геометрическую разность скоростей найдем, построив из точки М вектор v1.
Скорость точки при перемещении ее из положения М в положение M1 изменилась и по величине, и по направлению. Среднее значение ускорения, характеризующего отмеченное изменение скорости можно найти, разделив вектор приращения скорости v на соответствующее время движения:
Переходя
к пределу при
Найденное
ускорение характеризует изменение
численного значения скорости и ее
направления. Для удобства ускорение
раскладывают на взаимно перпендикулярные
составляющие по касательной и нормали
к траектории движения (рис.б)
Для удобства ускорение
раскладывают на взаимно перпендикулярные
составляющие по касательной и нормали
к траектории движения (рис.б)
Касательная составляющая совпадает по направлению со скоростью или противоположна ей. Она характеризует изменение модуля скорости и соответственно определяется как производная от функции скорости:
Нормальная составляющая перпендикулярна к направлению скорости точки. Она определяет изменение направления вектора скорости. Численное значение нормального ускорения определяется по формуле:
где r — радиус кривизны траектории в рассматриваемой точке.
Составляющие и взаимно перпендикулярны, и поэтому значение полного ускорения определяется по формуле:
Как известно из геометрии, положение точки в пространстве и его изменение можно описать двумя способами:
Один из них требует введения понятия “радиус-вектор”.
 Радиусом-вектором
(r) называется направленный отрезок,
соединяющий начало координат и точку
с произвольными координатами. Положение
точки в пространстве в заданной системе
отсчета будет полностью определено,
если известен r (его положение относительно
осей координат и его размеры) (рис. 1).
Радиусом-вектором
(r) называется направленный отрезок,
соединяющий начало координат и точку
с произвольными координатами. Положение
точки в пространстве в заданной системе
отсчета будет полностью определено,
если известен r (его положение относительно
осей координат и его размеры) (рис. 1).Второй способ описания местоположения точки связан с первым: точка может быть задана с помощью трех координат, которые в данном случае равны проекциям вектора на оси Ox; Oy; Oz (проекция вектора r на ось Ох обозначается rх, на ось Оу – rу, на ось Oz – rz). Следует отличать проекции вектора от составляющих вектора.
Второй
способ приводит к сложению алгебраических
величин – координат, что является более
привычной операцией.
Таким образом, оба способа описания положения точки в пространстве однозначно связаны между собой, но в школьном курсе при решении задач предпочтение отдается координатному методу (хотя есть ряд задач повышенной трудности, решить которые можно только с помощью векторного подхода).
Заметим, что Государственным стандартом введены следующие обозначения:
При этом нетрудно доказать, что модуль вектора будет равен
Рассмотрим, как меняется радиус-вектор при движении точки в пространстве.
Пусть в момент времени t0 = 0 точка А имеет координаты х0, у0, z0, (что соответственно описывается радиусом-вектором r0), а по истечении некоторого промежутка времени t1 материальная точка переместилась в точку В, ее координаты стали равными x1, у1, z1 (что соответственно описывается радиусом-вектором r1
Для
того чтобы рассчитать, как изменилась
величина, необходимо вычесть из ее
нового значения предыдущее, то есть
дельта r = r1 – r0 . Эту величину
называют перемещением. Нетрудно заметить,
что для координат это изменение можно
записать следующим образом:
Эту величину
называют перемещением. Нетрудно заметить,
что для координат это изменение можно
записать следующим образом:
Отсюда следует:
Следовательно, для того чтобы определить местоположение точки через какой-то промежуток времени t1, необходимо знать начальный радиус-вектор и перемещение за промежуток времени t1
Очень важно отметить, что перемещение чаще всего не совпадает с траекторией, поэтому модуль перемещения отличается от пройденного пути (за исключением того случая, когда траектория точки есть прямая линия) (см. рис. 2).
Перемещение
показывает, на какое расстояние и в
каком направлении точка сместилась при
своем движении. Однако эта величина не
позволяет оценить характер движения.
Для этого необходимо ввести еще одну
величину, характеризующую быстроту
движения.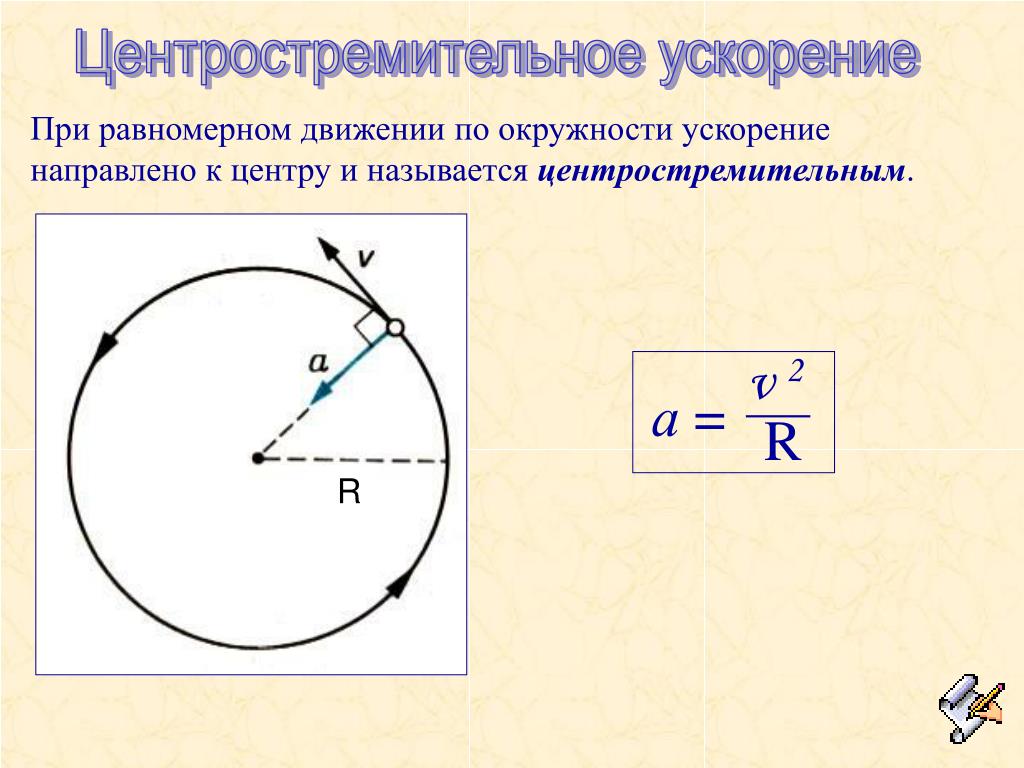 Такой величиной является
Такой величиной является
где vср – средняя скорость; дельта r– перемещение; дельта t – промежуток времени, за который перемещение произошло.
В Международной системе единиц (СИ) модуль скорости измеряется в м/с. В практике применяются и другие единицы: км/ч; см/с и т. д.
Знания средней скорости недостаточно для подробного описания движения. Средняя скорость позволяет тем точнее описывать процесс движения, чем за меньший промежуток времени рассматривается перемещение точки.
При стремлении
Это значение, т. е. предел, к которому стремится дробь дельта r/ дельта t при стремлении дельта t к нулю, называют мгновенной скоростью в данной точке или в данный момент времени и обозначают v:
Так как дельта t – скалярная величина, то направление скорости совпадает с направлением вектора перемещения. Если
Итак, вектор v скорости точки направлен по касательной к траектории точки в сторону ее перемещения. Модуль вектора скорости v характеризует быстроту перемещения точки по траектории.
Прибор, которым измеряют скорость, называется спидометром.
Любой
вектор можно разложить на его составляющие,
при этом следует выполнить требование:
векторная сумма составляющих вектора
должна быть равна вектору, который
подлежал разложению.
На рис. 4, а и б изображены векторы и их составляющие. Напомним, что проекция вектора на ось – алгебраическая величина, численно равна произведению модуля вектора на косинус угла между вектором и осью (при этом в трехмерном пространстве рассматривается угол между плоскостью, которая проходит через вектор, и интересующей нас осью). Рассмотрим пример в двухмерном пространстве: если вектор r расположен на плоскости хОу, то его проекция на ось Ох равна rx = r*cosa (рис. 5).
Вектор скорости с течением времени может изменяться: либо его модуль, либо направление, либо то и другое. Для характеристики быстроты изменения скорости движущейся точки вводится понятие
Если
выбирать все меньшие и меньшие промежутки
времени, то аср будет более
точно описывать характер изменения
скорости точки, и в пределе можно получить мгновенное ускорение точки, которое
будет направлено туда же, куда направлен
вектор изменения скорости дельта v.
Отметим, что ускорение направлено в сторону изменения скорости, но не в сторону самой скорости. Например, при движении брошенного вверх тела скорость направлена вверх, но она убывает, при этом изменение скорости направлено вниз. Следовательно, и ускорение направлено в этом случае вниз. Оно носит название ускорения свободного падения (обозначение g).
Ускорение измеряется в Международной системе единиц (СИ) в 1 м/с2. Физический смысл единицы ускорения: 1 м/с2 – это такое ускорение, при котором за 1 с скорость изменяется на 1 м/с при условии, что ускорение в этот промежуток времени остается постоянным.
Ускорение измеряется прибором, который называется акселерометром
определение вращательного и поступательного движения
1)
вращательное движение вокруг оси —
движение твёрдого тела, при котором
какие-нибудь две его точки А. и В остаются всё время неподвижными (см. рис.). Прямая AB, проходящая
через эти точки, называется осью вращения;
все точки тела при В. д. описывают
окружности в плоскостях, перпендикулярных
к оси вращения, и с центрами, лежащими
на этой оси. Тело, совершающее В. д., имеет
одну степень свободы и его положение
определяется углом φ между проведёнными
через ось вращения неподвижной
полуплоскостью и полуплоскостью, жёстко
связанной с телом и вращающейся вместе
с ним. Основные кинематические
характеристики В. д. тела — его угловая
скорость ω и угловое
ускорение ε. Для любой точки
тела, отстоящей от оси на расстоянии h,
линейная скорость v = hω, касательное
ускорение wτ = hω, нормальное
ускорение wn = hω2 и полное ускорение
д. описывают
окружности в плоскостях, перпендикулярных
к оси вращения, и с центрами, лежащими
на этой оси. Тело, совершающее В. д., имеет
одну степень свободы и его положение
определяется углом φ между проведёнными
через ось вращения неподвижной
полуплоскостью и полуплоскостью, жёстко
связанной с телом и вращающейся вместе
с ним. Основные кинематические
характеристики В. д. тела — его угловая
скорость ω и угловое
ускорение ε. Для любой точки
тела, отстоящей от оси на расстоянии h,
линейная скорость v = hω, касательное
ускорение wτ = hω, нормальное
ускорение wn = hω2 и полное ускорение
Основными
динамическими характеристиками В. д.
тела являются его кинетический момент
относительно оси вращения Kz = Izω (см. Момент
количества движения) и кинетическая
энергия Т = 1/2Izω2,
где Iz — момент
инерции тела относительно оси
вращения.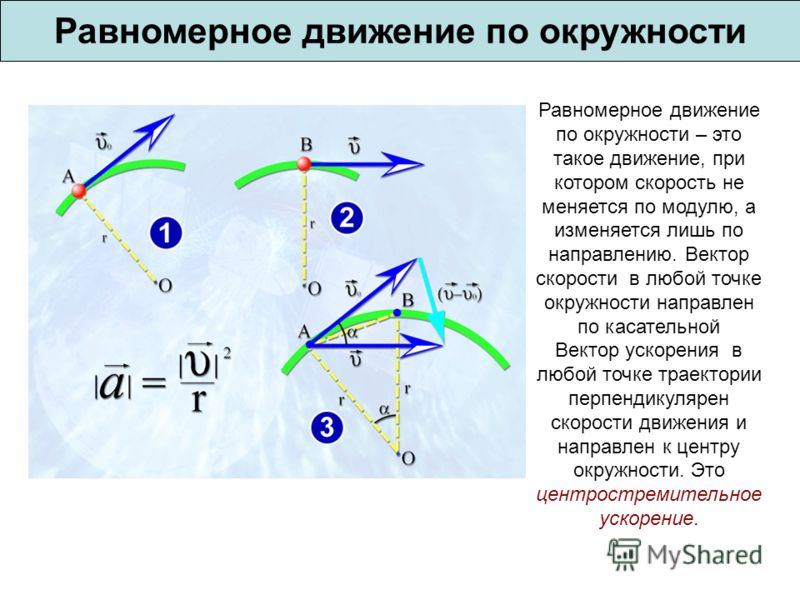 Закон вращения определяется
из основного уравнения Iz ε = Mz, где Mz — вращающий момент (см. Момент
силы).
Закон вращения определяется
из основного уравнения Iz ε = Mz, где Mz — вращающий момент (см. Момент
силы).
2) Вращательное движение вокруг точки (или сферическое движение) — движение твёрдого тела, при котором какая-то одна его точка О остаётся неподвижной, а все другие точки движутся по поверхности сфер, имеющих центр в точке О. При таком В. д. тела любое его элементарное перемещение представляет собой элементарный поворот вокруг некоторой оси, проходящей через точку О и называется мгновенной осью вращения. Со временем эта ось, в отличие от неподвижной, непрерывно изменяет своё направление. В результате В. д. тела слагается из серии элементарных поворотов вокруг непрерывно меняющих своё направление мгновенных осей. Пример такого В. д. тела даёт движение гироскопа.
Поступательное
движение — это механическое
движение системы точек (тела),
при котором любой отрезок прямой,
связанный с движущимся телом,
форма и размеры которого во время
движения не меняются, остается параллельным
своему положению в любой предыдущий
момент времени. [1]
[1]
Приведённая иллюстрация показывает, что, в отличие от распространённого утверждения [2]. поступательное движение не является противоположностью движению вращательному, а в общем случае может рассматриваться как совокупность поворотов — не закончившихся вращений. При этом подразумевается, что прямолинейное движение есть поворот вокруг бесконечно удалённого от тела центра поворота.
В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе.
Математически поступательное движение по своему конечному результату эквивалентно параллельному переносу.Однако, рассматриваемое как физический процесс оно представляет собой в трёхмерном пространстве вариант винтового движения
1.7. Криволинейное движение. Тангенциальное и нормальное ускорения…
Сразу хочу сказать, что здесь никакой воды про криволинейное движение тангенциальное, и только нужная информация. Для того чтобы лучше понимать что такое
криволинейное движение тангенциальное, нормальное ускорения , настоятельно рекомендую прочитать все из категории Физические основы механики.
Для того чтобы лучше понимать что такое
криволинейное движение тангенциальное, нормальное ускорения , настоятельно рекомендую прочитать все из категории Физические основы механики.
Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.
Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).
Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.
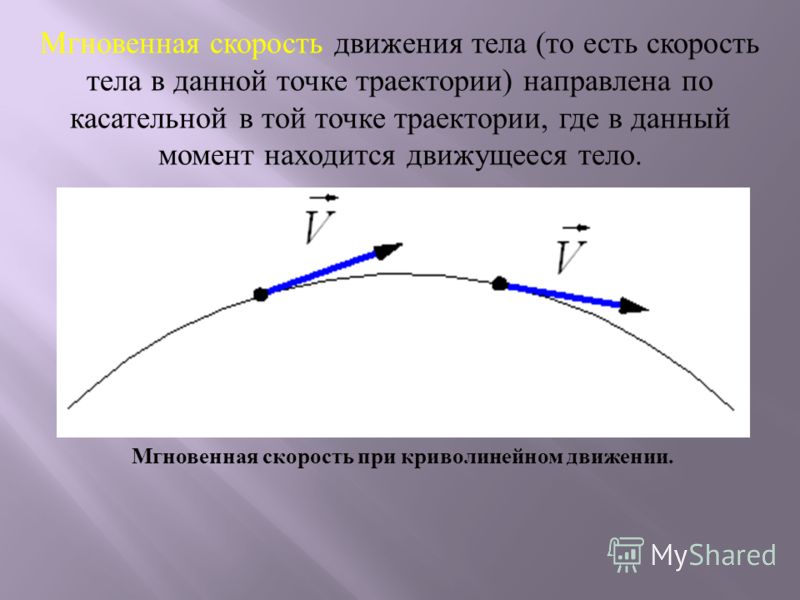
При движении по криволинейной траектории вектор перемещения направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).
1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).
Рис. 1.20. Мгновенная скорость при криволинейном движении.
Криволинейное движение – это всегда ускоренное движение. То естьускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:
или
Где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0соответственно.
Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.
Нормальное ускорение – это изменение скорости по направлению за единицу времени:
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения) .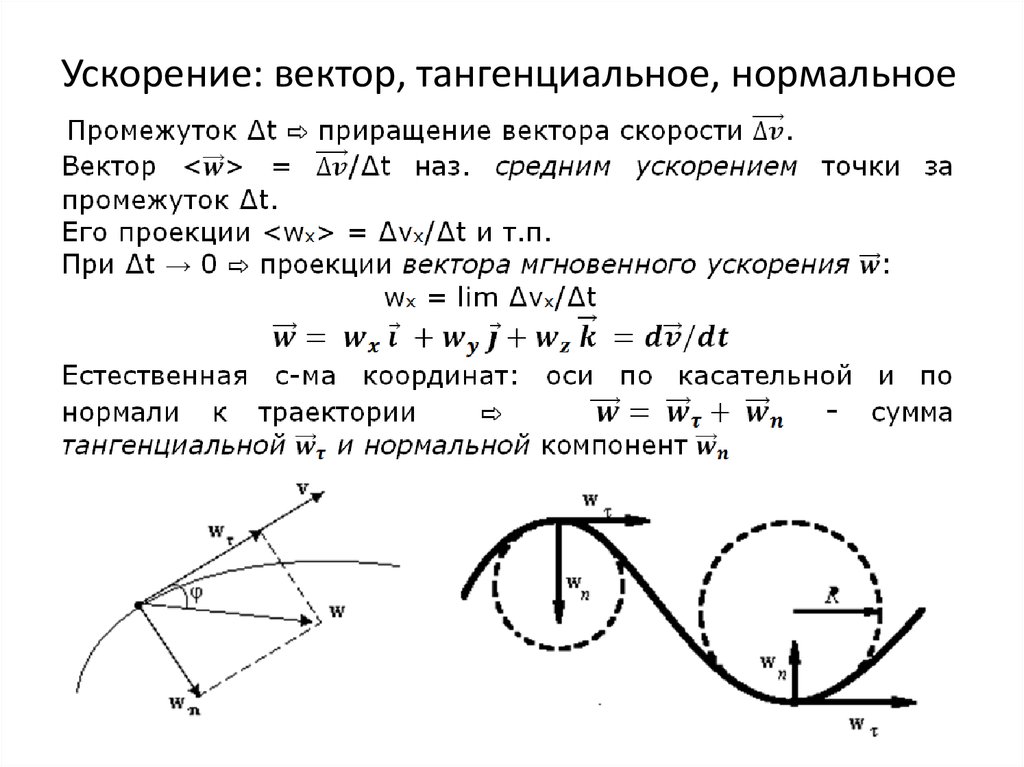 Об этом говорит сайт https://intellect.icu . Нормальное ускорение перпендикулярно направлению скорости.
Об этом говорит сайт https://intellect.icu . Нормальное ускорение перпендикулярно направлению скорости.
Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.
Полное ускорение при равнопеременном криволинейном движении тела равно:
Движение тела по криволинейной траектории можно приближенно представить как движение по дугам некоторых окружностей (рис. 1.21).
Рис. 1.21. Движение тела при криволинейном движении.
При прямолинейном движении векторы скорости и ускорения совпадают с направлением траектории. Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости в любой точке траектории направлен по касательной к ней. Допустим, что в т.М траектории скорость была , а в т.М1стала . При этом считаем, что промежуток времени при переходе точки на пути из М в М1 настолько мал, что изменением ускорения по величине и направлению можно пренебречь. Для того, чтобы найти вектор изменения скорости , необходимо определить векторную разность:
Для того, чтобы найти вектор изменения скорости , необходимо определить векторную разность:
Для этого перенесем параллельно самому себе, совмещая его начало с точкой М. Разность двух векторов равна вектору, соединяющему их концы равна стороне АС МАС, построенного на векторах скоростей, как на сторонах. Разложим вектор на две составляющих АВ и АД, и обе соответственно через и . Таким образом вектор изменения скорости равен векторной сумме двух векторов:
По определению:
| (1.15) |
Тангенциальное ускорение характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории.
Следовательно
| (1.16) |
Нормальное ускорение характеризует быстроту изменения скорости по направлению. Вычислим вектор:
Вычислим вектор:
Для этого проведем перпендикуляр через точки М и М1 к касательным к траектории (рис. 1.4) Точку пересечения обозначим через О. При достаточно малом участок криволинейной траектории можно считать частью окружности радиуса R. Треугольники МОМ1 и МВС подобны, потому, что являются равнобедренными треугольниками с одинаковыми углами при вершинах. Поэтому:
или
Но , тогда:
Переходя к пределу при и учитывая, что при этом , находим:
,
| (1.17) |
Так как при угол , направление этого ускорения совпадает с направлением нормали к скорости , т.е. вектор ускорения перпендикулярен . Поэтому это ускорение часто называют центростремительным.
Полное ускорение определяется векторной суммой тангенциального нормального ускорений (1.15). Так как векторы этих ускорений взаимноперпендикулярны, то модуль полного ускорения равен:
(1. 18) 18) |
Направление полного ускорения определяется углом между векторам и :
Статью про криволинейное движение тангенциальное я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое криволинейное движение тангенциальное, нормальное ускорения и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Из статьи мы узнали кратко, но емко про криволинейное движение тангенциальное
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 4 из 28Следующая ⇒ Если траектория движения материальной точки представляет собой кривую линию, то такое движение мы будем называть криволинейным. При таком движении изменяется как по величине, так и по направлению. Следовательно, при криволинейном движении . Рассмотрим движение материальной точки по криволинейной траектории (рис. 2.11). Вектор скорости движения в любой точке траектории направлен по касательной к ней. Пусть в точке M0 скорость , а в точке М – . При этом считаем, что промежуток времени Dt при переходе из точки М0 в точку М настолько мал, что изменением ускорения по величине и направлению можно пренебречь. Вектор изменения скорости . (В данном случае разность 2х векторов и будет равна ). Разложим вектор , который характеризует изменение скорости как по величине, так и по направлению на две составляющие и . Таким образом, вектор изменения скорости равен сумме двух векторов . Тогда можно записать, что . При бесконечном уменьшении Dt®0 угол Da при вершине DM0АС будет стремиться к нулю. Тогда вектором можно пренебречь по сравнению с вектором , а вектор будет выражать тангенциальное ускорение и характеризовать быстроту изменения скорости движения по величине. Следовательно, тангенциальное ускорение численно равно производной от модуля скорости по времени и направлено по касательной к траектории. Вычислим теперь вектор , называемый нормальным ускорением. При достаточно малом Dt участок криволинейной траектории можно считать частью окружности. В этом случае радиусы кривизны M0O и MO будут равны между собой и равны радиусу окружности R. Повторим рисунок. ÐМ0ОМ = ÐМСD, как углы со взаимно перпендикулярными сторонами (рис. 2. 12). При малом Dt можно считать |v0|=|v|, поэтому DМ0ОМ = DМDC подобны как равнобедренные треугольники с одинаковыми углами при вершине. Поэтому из рис. 2.11 следует Þ , но DS = vср.×Dt, тогда . Переходя к пределу при Dt ® 0 и учитывая, что при этом vср. = v находим , т.е. (2.5) Т.к. при Dt ® 0 угол Da ® 0, то направление этого ускорения совпадает с направлением радиуса R кривизны или с направлением нормали к скорости , т.е. вектор . Поэтому это ускорение часто называют центростремительным. Оно характеризует быстроту изменения скорости движения по направлению. Полное ускорение определяется векторной суммой тангенциального и нормального ускорений (рис. 2.13). Т.к. вектора этих ускорений взаимно перпендикулярны , то модуль полного ускорения равен ; Направление полного ускорения определяется углом j между векторами и : ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
4.4 Равномерное круговое движение | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Находить центростремительное ускорение объекта, движущегося по круговой траектории.
- Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.
- Объясните разницу между центростремительным ускорением и тангенциальным ускорением в результате неравномерного кругового движения.
- Оцените центростремительное и тангенциальное ускорения при неравномерном круговом движении и найдите вектор полного ускорения.
Равномерное круговое движение — это особый тип движения, при котором объект движется по окружности с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Центростремительное ускорение
В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости изменяется, или [латекс] d\overset{\to }{v}\text{/}dt\ne 0. [/latex] Это показано на (Рисунок). По мере того, как частица движется против часовой стрелки во времени [латекс] \текст{Δ}t [/латекс] по круговой траектории, ее вектор положения перемещается от [латекс] \overset{\to}{r}(t) [/латекс] к [латекс] \overset{\to}}{r}(t+\text{Δ}t). [/latex] Вектор скорости имеет постоянную величину и касается пути при изменении от [latex] \overset{\to }{v}(t) [/latex] до [latex] \overset{\to }{ v}(t+\text{Δ}t), [/latex] меняет только свое направление. Поскольку вектор скорости [латекс] \overset{\to }{v}(t) [/latex] перпендикулярен вектору положения [латекс] \overset{\to }{r}(t), [/latex] треугольники, образованные векторами положения и [латекс] \text{Δ}\overset{\to }{r}, [/latex] и векторами скорости и [латекс] \text{Δ}\overset{\to }{v } [/latex] похожи. Кроме того, поскольку [латекс] |\overset{\to }{r}(t)|=|\overset{\to }{r}(t+\text{Δ}t)| [/латекс] и [латекс] |\overset{\to }{v}(t)|=|\overset{\to }{v}(t+\text{Δ}t)|, [/latex] два треугольники равнобедренные. Из этих фактов мы можем сделать утверждение
[/latex] Вектор скорости имеет постоянную величину и касается пути при изменении от [latex] \overset{\to }{v}(t) [/latex] до [latex] \overset{\to }{ v}(t+\text{Δ}t), [/latex] меняет только свое направление. Поскольку вектор скорости [латекс] \overset{\to }{v}(t) [/latex] перпендикулярен вектору положения [латекс] \overset{\to }{r}(t), [/latex] треугольники, образованные векторами положения и [латекс] \text{Δ}\overset{\to }{r}, [/latex] и векторами скорости и [латекс] \text{Δ}\overset{\to }{v } [/latex] похожи. Кроме того, поскольку [латекс] |\overset{\to }{r}(t)|=|\overset{\to }{r}(t+\text{Δ}t)| [/латекс] и [латекс] |\overset{\to }{v}(t)|=|\overset{\to }{v}(t+\text{Δ}t)|, [/latex] два треугольники равнобедренные. Из этих фактов мы можем сделать утверждение
[латекс] \frac{\text{Δ}v}{v}=\frac{\text{Δ}r}{r} [/latex] или [латекс] \text{Δ}v=\frac{ v}{r}\text{Δ}r. [/latex]
Рисунок 4.18 (a) Частица движется по окружности с постоянной скоростью, с векторами положения и скорости в моменты времени [latex] t [/latex] и [latex] t+\text{Δ} т. [/latex] (b) Векторы скорости, образующие треугольник. Два треугольника на рисунке подобны. Вектор [латекс] \text{Δ}\overset{\to }{v} [/latex] указывает на центр окружности в пределе [латекс] \text{Δ}t\to 0. [/latex] 9{2}}{р}. [/latex]
[/latex] (b) Векторы скорости, образующие треугольник. Два треугольника на рисунке подобны. Вектор [латекс] \text{Δ}\overset{\to }{v} [/latex] указывает на центр окружности в пределе [латекс] \text{Δ}t\to 0. [/latex] 9{2}}{р}. [/latex]
Направление ускорения также можно найти, заметив, что по мере приближения [латекс] \текст{Δ}t [/латекс] и, следовательно, [латекс] \текст{Δ}\тета [/латекс] к нулю , вектор [латекс] \текст{Δ}\overset{\to }{v} [/latex] приближается к направлению, перпендикулярному [латексу] \overset{\to }{v}. [/latex] В пределе [latex] \text{Δ}t\to 0, [/latex][latex] \text{Δ}\overset{\to }{v} [/latex] перпендикулярно [latex ] \overset{\to}. [/latex] Поскольку [latex] \overset{\to }{v} [/latex] касается окружности, ускорение [latex] d\overset{\to }{v}\text{/}dt [/ латекс] указывает на центр круга. Подводя итог, частица, движущаяся по окружности с постоянной скоростью, имеет ускорение величиной 9{2}}{р}. [/latex]
Вектор ускорения направлен к центру окружности ((Рисунок)).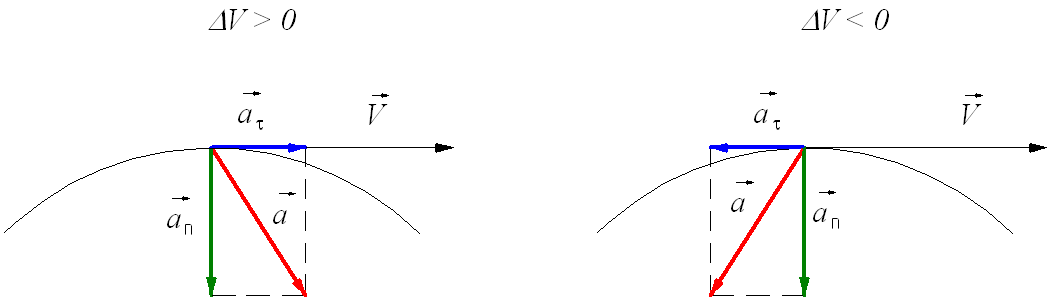 Это радиальное ускорение называется центростремительным ускорением , поэтому мы даем ему нижний индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает искать) и, таким образом, принимает значение «искание центра».
Это радиальное ускорение называется центростремительным ускорением , поэтому мы даем ему нижний индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает искать) и, таким образом, принимает значение «искание центра».
Рисунок 4.19 Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении. Вектор скорости также показан и касается окружности.
Давайте рассмотрим несколько примеров, иллюстрирующих относительные величины скорости, радиуса и центростремительного ускорения.
Пример
Создание ускорения 1
g Струя летит со скоростью 134,1 м/с по прямой линии и делает поворот по круговой траектории на уровне земли. Каким должен быть радиус окружности, чтобы пилот и реактивный самолет получили центростремительное ускорение 1 g по направлению к центру круговой траектории? 9{2}}=1835\,\text{м}=1,835\,\text{км}\text{. {2}? [/латекс]
{2}? [/латекс]
Показать решение
Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны кругового пути. Типичные центростремительные ускорения приведены в следующей таблице.
| Объект | Центростремительное ускорение (м/с 2 или коэффициенты g ) |
|---|---|
| Земля вокруг Солнца | [латекс] 5,9{22} [/латекс] |
Уравнения движения для равномерного кругового движения
Частица, совершающая круговое движение, может быть описана ее вектором положения [латекс] \overset{\to }{r}(t). [/latex] (Рисунок) показывает частицу, совершающую круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол [латекс]\тета[/латекс] с осью x-. Вектор [латекс] \overset{\to }{r}(t) [/латекс], образующий угол [латекс] \тета [/латекс] с 9Ось 0039 x показана с ее компонентами вдоль осей x и y . Величина вектора положения равна [латекс] A=|\overset{\to }{r}(t)| [/латекс], а также радиус окружности, так что с точки зрения ее компонентов,
[/latex] (Рисунок) показывает частицу, совершающую круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол [латекс]\тета[/латекс] с осью x-. Вектор [латекс] \overset{\to }{r}(t) [/латекс], образующий угол [латекс] \тета [/латекс] с 9Ось 0039 x показана с ее компонентами вдоль осей x и y . Величина вектора положения равна [латекс] A=|\overset{\to }{r}(t)| [/латекс], а также радиус окружности, так что с точки зрения ее компонентов,
[латекс] \overset{\to }{r}(t)=A\,\text{cos}\,\ омега т\шляпа{я}+А\,\текст{грех}\,\омега т\шляпа{j}. [/latex]
Здесь [latex] \omega [/latex] — константа, называемая угловой частотой частицы. Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду. Угол [латекс] \тета [/латекс], который имеет вектор положения в любой конкретный момент времени, равен [латекс] \омега t [/латекс].
Если T – это период движения или время, необходимое для совершения одного оборота ([латекс] 2\пи [/латекс] рад), то
[латекс] \омега =\фрак{2\пи }{ Т}. [/latex]
Рис. 4.20 Вектор положения частицы, совершающей круговое движение, с компонентами вдоль осей x и y. Частица движется против часовой стрелки. Угол [латекс] \тета [/латекс] — это угловая частота [латекс] \омега [/латекс] в радианах в секунду, умноженная на t.
Скорость и ускорение можно получить из функции положения дифференцированием:
[латекс] \ overset {\ to {v} (t) = \ frac {d \ overset {\ to {r} (t)} {dt} = \ text {−} A \ omega \, \ text{sin}\,\omega t\hat{i}+A\omega \,\text{cos}\,\omega t\hat{j}. [/latex]
Из (рис.) видно, что вектор скорости касается окружности в месте нахождения частицы с величиной [латекс] A\omega . [/latex] Точно так же вектор ускорения находится путем дифференцирования скорости:
[латекс] \overset{\to }{a}(t)=\frac{d\overset{\to}}{v}(t) }{dt} = \ text {−} A {\ omega} ^ {2} \, \ text {cos} \, \ omega t \ hat {i} -A {\ omega} ^ {2} \, \ text {грех}\,\омега т\шляпа{j}. [/латекс] 9{-7}\text{s}=200\,\text{ns}\text{.} [/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
[/латекс] 9{-7}\text{s}=200\,\text{ns}\text{.} [/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
Значение
Мы выбрали начальное положение частицы на оси x-. Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас была бы другая конечная позиция при t = 200 нс.
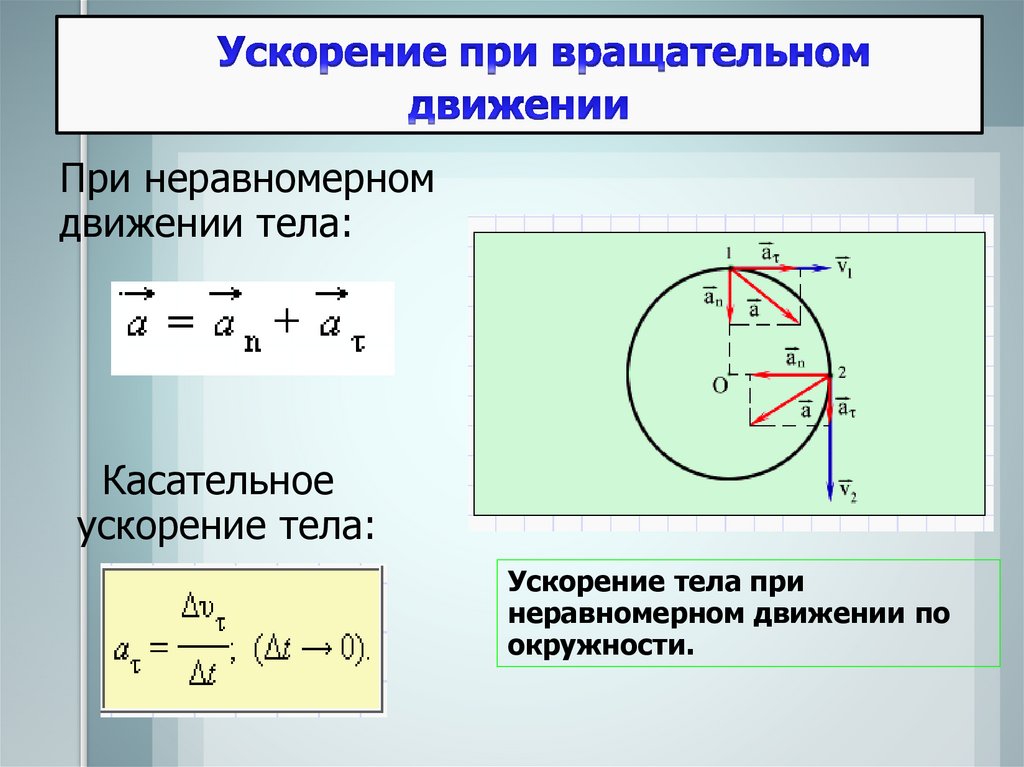
Неравномерное круговое движение
Круговое движение не обязательно должно быть с постоянной скоростью. Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а окружность имеет фиксированный радиус. Если меняется и скорость частицы, то вводим дополнительное ускорение в направлении, касательном к окружности. Такие ускорения возникают в точке на волчке, меняющем скорость вращения, или на каком-либо ускоряющемся роторе. В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
[латекс] {a}_{\text{T}}=\frac{d|\overset{\to}{v}| {дт}. [/latex]
Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения направлено радиально внутрь к центру окружности. Таким образом, частица, движущаяся по окружности с тангенциальным ускорением, имеет полное ускорение , которое представляет собой векторную сумму центростремительного и тангенциального ускорений:
[латекс] \ overset {\ to }{a} = {\ overset {\ to }{a}} _ {\ text {C}} + {\ overset {\ to }{a}} _ {\ text {Т}}. [/latex]
Векторы ускорения показаны на (Рисунок). Обратите внимание, что два вектора ускорения [латекс] {\overset{\to }{a}}_{\text{C}} [/latex] и [латекс] {\overset{\to }{a}}_{\ text{T}} [/latex] перпендикулярны друг другу, с [latex] {\overset{\to }{a}}_{\text{C}} [/latex] в радиальном направлении и [latex] {\overset{\to}{a}}_{\text{T}} [/latex] в тангенциальном направлении. Полное ускорение [латекс] \overset{\to }{a} [/latex] указывает на угол между [латекс] {\overset{\to }{a}}_{\text{C}} [/latex] и [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/латекс]
Полное ускорение [латекс] \overset{\to }{a} [/latex] указывает на угол между [латекс] {\overset{\to }{a}}_{\text{C}} [/latex] и [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/латекс]
Рисунок 4.22 Центростремительное ускорение направлено к центру окружности. Тангенциальное ускорение касается окружности в месте нахождения частицы. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений, которые перпендикулярны.
Пример
Полное ускорение при движении по окружности
Частица движется по окружности радиусом r = 2,0 м. За интервал времени от t = 1,5 с до 9{2}},\enspace{c}_{1}=4.0\,\text{m}\text{/}\text{s,}\enspace{c}_{2}=6.0\,\text{ m}·\text{s}\text{.} [/latex]
Чему равно полное ускорение частицы в точке t = 2,0 с?
Стратегия
Нам известны скорость частицы и радиус окружности, поэтому мы можем легко рассчитать центростремительное ускорение. Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекса] |v(t)| [/latex] используя (Рисунок) и оценивая его на 9{-1}\frac{3.1}{1.5}=64\text{°} [/latex] от касательной к окружности. См. (Рисунок).
Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекса] |v(t)| [/latex] используя (Рисунок) и оценивая его на 9{-1}\frac{3.1}{1.5}=64\text{°} [/latex] от касательной к окружности. См. (Рисунок).
Рисунок 4.23 Векторы тангенциального и центростремительного ускорения. Чистое ускорение [латекс] \overset{\to }{a} [/латекс] представляет собой векторную сумму двух ускорений.
Значение
Направления центростремительных и тангенциальных ускорений удобнее описывать в полярной системе координат с единичными векторами в радиальном и тангенциальном направлениях. Эта система координат, используемая для движения по криволинейным траекториям, подробно обсуждается далее в книге. 9{2}\text{/}р. [/латекс]
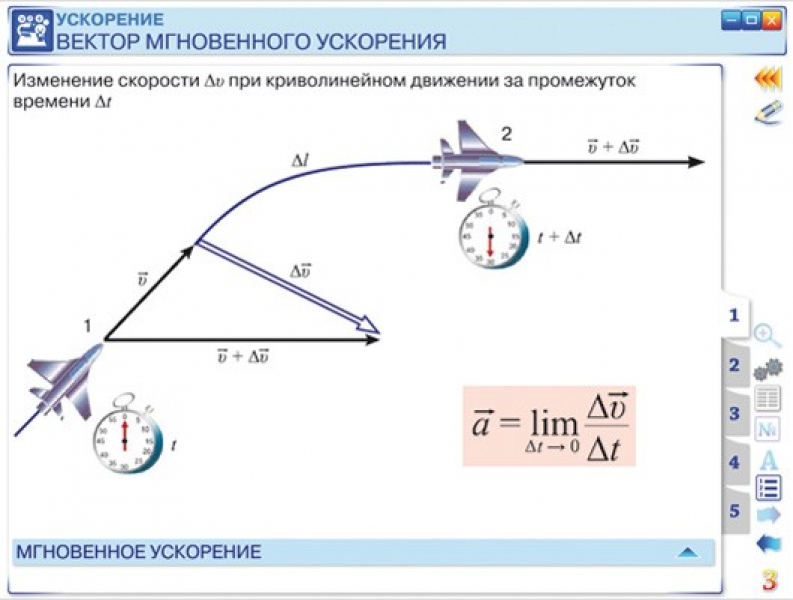 Это ускорение называется тангенциальным ускорением [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/latex] Величина тангенциального ускорения – это скорость изменения во времени величины скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.
Это ускорение называется тангенциальным ускорением [латекс] {\ overset {\ to {a}} _ {\ text {T}}. [/latex] Величина тангенциального ускорения – это скорость изменения во времени величины скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.Концептуальные вопросы
Может ли центростремительное ускорение изменить скорость частицы, совершающей круговое движение?
Может ли тангенциальное ускорение изменить скорость частицы, совершающей круговое движение?
Показать решение
Проблемы
Маховик вращается со скоростью 30 об/с. На какой угол в радианах поворачивается точка маховика за 40 с?
На какой угол в радианах поворачивается точка маховика за 40 с?
Частица движется по окружности радиусом 10 м с постоянной скоростью 20 м/с. Какова величина ускорения?
Показать решение
Кэм Ньютон из команды «Каролина Пантерз» делает идеальную футбольную спираль со скоростью 8,0 об/с. Радиус профессионального футбольного мяча составляет 8,5 см посередине короткой стороны. Чему равно центростремительное ускорение шнурков футбольного мяча?
Ярмарочный аттракцион вращает своих пассажиров внутри контейнера в форме летающей тарелки. Если горизонтальный круговой путь, по которому следуют всадники, имеет радиус 8,00 м, при каком числе оборотов в минуту всадники испытывают центростремительное ускорение, равное силе тяжести?
Показать решение
Бегун, участвующий в забеге на 200 м, должен обежать конец дорожки, имеющей дугу окружности с радиусом кривизны 30,0 м. Бегун начинает гонку с постоянной скоростью. Если она пробежит 200 м за 23,2 с и будет бежать с постоянной скоростью на протяжении всей гонки, каково будет ее центростремительное ускорение, когда она пробегает кривую часть трассы?
Если она пробежит 200 м за 23,2 с и будет бежать с постоянной скоростью на протяжении всей гонки, каково будет ее центростремительное ускорение, когда она пробегает кривую часть трассы?
Каково ускорение Венеры по отношению к Солнцу, если предположить, что она движется по круговой орбите?
Показать решение
Экспериментальная реактивная ракета летит вокруг Земли по экватору прямо над ее поверхностью. С какой скоростью должна двигаться струя, если модуль ее ускорения равен g ?
Вентилятор вращается с постоянной скоростью 360,0 об/мин. Чему равно ускорение точки одной из его лопастей на расстоянии 10,0 см от оси вращения?
Показать решение 9{2}. [/latex] Как далеко точка от оси вращения секундной стрелки?
Глоссарий
- угловая частота
- [латекс] \omega , [/латекс] скорость изменения угла, с которым объект движется по круговой траектории
- центростремительное ускорение
- составляющая ускорения объекта, движущегося по окружности, направленная радиально внутрь к центру окружности
- тангенциальное ускорение
- величина которого есть скорость изменения скорости во времени.
 Его направление касается окружности.
Его направление касается окружности.
- общее ускорение
- векторная сумма центростремительного и тангенциального ускорений
Криволинейное движение
Общее криволинейное движение
Криволинейное движение определяется как движение, которое происходит, когда частица движется по криволинейной траектории. Изогнутый путь может быть двухмерным (в плоскости) или трехмерным. Этот тип движения более сложен, чем прямолинейное (прямолинейное) движение.
Трехмерное криволинейное движение описывает наиболее общий случай движения частицы.
Чтобы найти скорость и ускорение частицы, совершающей криволинейное движение, достаточно знать положение частицы как функцию времени.
Допустим, нам дано положение частицы P в трехмерных декартовых ( x , y , z ) координатах относительно времени, где
Скорость частицы P определяется выражением
Ускорение частицы P определяется выражением
Как видите, если мы знаем положение частицы как функцию времени, найти скорость и ускорение довольно просто. Вы просто берете первую производную, чтобы найти скорость, и вторую производную, чтобы найти ускорение.
Вы просто берете первую производную, чтобы найти скорость, и вторую производную, чтобы найти ускорение.
Величина скорости частицы P дается
Величина ускорения частицы P определяется выражением
Обратите внимание, что направление скорости частицы P всегда касается кривой (т. е. пройденного пути, обозначенного синей кривой на рисунке выше). Но направление ускорения обычно , а не по касательной к кривой.
Однако составляющая ускорения, касательная к кривой, равна производной по времени от модуля скорости частицы P (по кривой). Другими словами, если v t является величиной скорости частицы (касательной к кривой), то составляющая ускорения частицы, касательная к кривой ( a t ), равна просто
Кроме того, нормальная к кривой составляющая ускорения ( a n ) определяется выражением
где R радиус кривизны кривой в данной точке кривой ( x p , y p , z p ).
The figure below illustrates the acceleration components a t and a n at a given point on the curve ( x p , y p , z p ).
Для конкретного случая, когда путь синей кривой определяется как y = f(x) (двумерное движение), радиус кривизны равен R дается
где | х | означает «абсолютное значение» x . Например, |-2,5| = 2,5 и |3,1| = 3,1.
Однако обычно нет необходимости знать радиус кривизны R вдоль кривой. Но тем не менее информативно понимать его на основе его отношения к нормальному ускорению ( a n ).
Криволинейное движение в полярных координатах
Иногда удобно выразить плоскостное (двумерное) движение частицы через полярные координаты ( R , θ ), чтобы можно было явно определить скорость и ускорение частицы в радиальной ( R -направление) и по окружности ( θ -направление).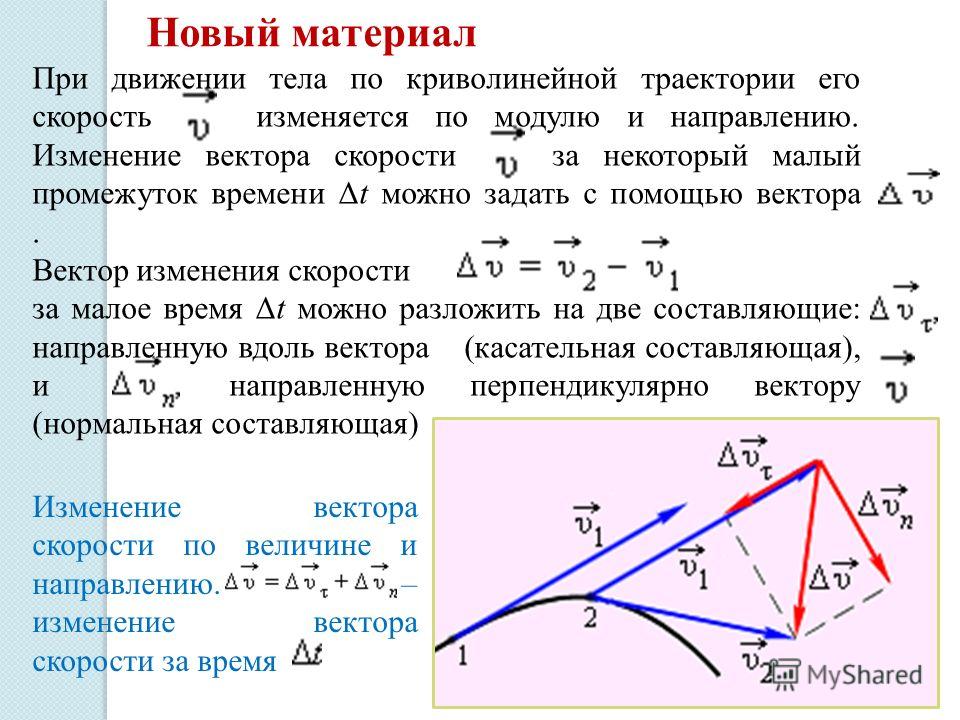 Для этого типа движения частице разрешено двигаться только в радиальном R -направлении на заданный угол θ .
Для этого типа движения частице разрешено двигаться только в радиальном R -направлении на заданный угол θ .
Для частицы P в полярных координатах (как показано ниже), мы можем вывести общее уравнение для его радиальной скорости ( v r ), радиального ускорения ( a r ), окружной скорости ( v c ) ) и окружное ускорение ( a c ).
Обратите внимание, что окружное направление перпендикулярно радиальному направлению.
Положение частицы P задано относительно времени, где
Чтобы найти скорость, возьмите первую производную от x(t) и y(t) по времени:
Чтобы найти ускорение, возьмите вторую производную от x(t) и y(t) по времени:
Без ограничения общности мы можем оценить скорости и ускорения под углом θ = 0, зная, что (при этом угле) радиальная скорость и радиальное ускорение находятся в x -направление, а окружная скорость и окружное ускорение находятся в y -направлении.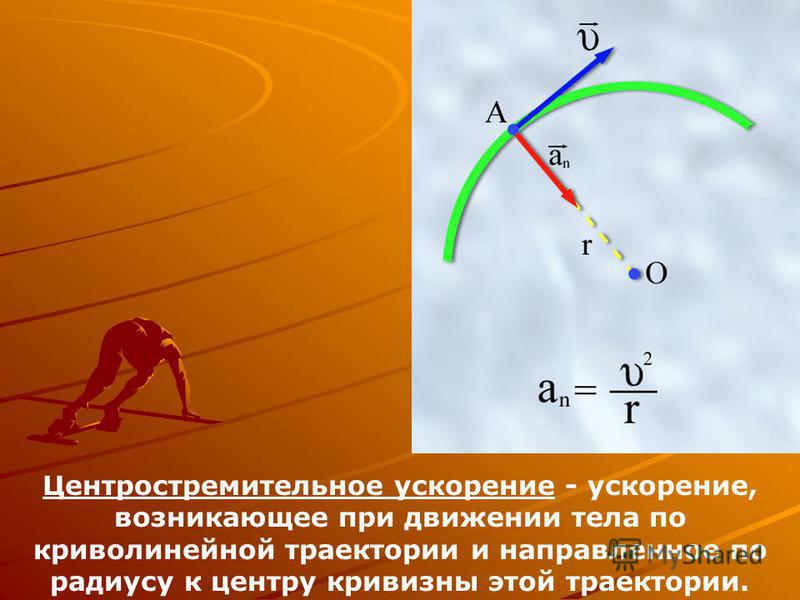
Настройка θ = 0 имеем:
Уравнения (1), (2), (3) и (4) полностью описывают криволинейное движение частицы P в полярных координатах.
Термин dθ/dt называется угловой скоростью. Она измеряется в рад/с. Один рад (радиан) = 57,296 градуса.
Срок д 2 θ/dt 2 называется угловым ускорением. Он имеет единицы рад/с 2 .
Поскольку v r и v c перпендикулярны друг другу, модуль скорости частицы P определяется выражением
Поскольку a r и a c перпендикулярны друг другу, величина ускорения частицы P определяется выражением
Пример задачи для криволинейного движения
Щелевое звено вращается вокруг неподвижного шарнира O с угловой скоростью против часовой стрелки 3 рад/с и угловым ускорением по часовой стрелке 2 рад/с 2 .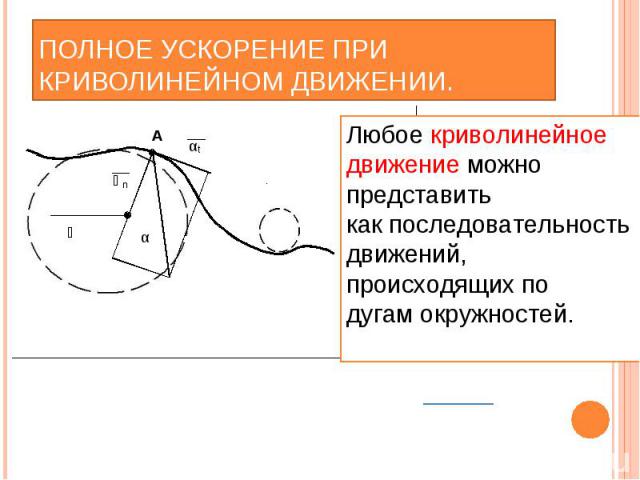 Движение звена заставляет стержень скользить по изогнутому каналу, как показано на рисунке. Радиус канала как функция θ определяется как R = 0,7 θ (с R в метрах и θ в радианах). Определить составляющие скорости и ускорения стержня при θ = 45°
Движение звена заставляет стержень скользить по изогнутому каналу, как показано на рисунке. Радиус канала как функция θ определяется как R = 0,7 θ (с R в метрах и θ в радианах). Определить составляющие скорости и ускорения стержня при θ = 45°
Решение
Угол θ = 45° равен π /4 радиан. В уравнениях угловая скорость против часовой стрелки положительна, а угловое ускорение по часовой стрелке отрицательно (поскольку оно «замедляет» скорость вращения звена).
Радиальная скорость стержня определяется уравнением (1):
(Радиальная скорость в направлении увеличения R ).
Окружная скорость стержня определяется уравнением (3):
(Окружная скорость направлена в сторону увеличения θ ).
Радиальное ускорение стержня определяется уравнением (2):
(Радиальное ускорение в сторону уменьшения R ).
Окружное ускорение стержня определяется уравнением (4):
(окружное ускорение направлено в сторону увеличения θ ).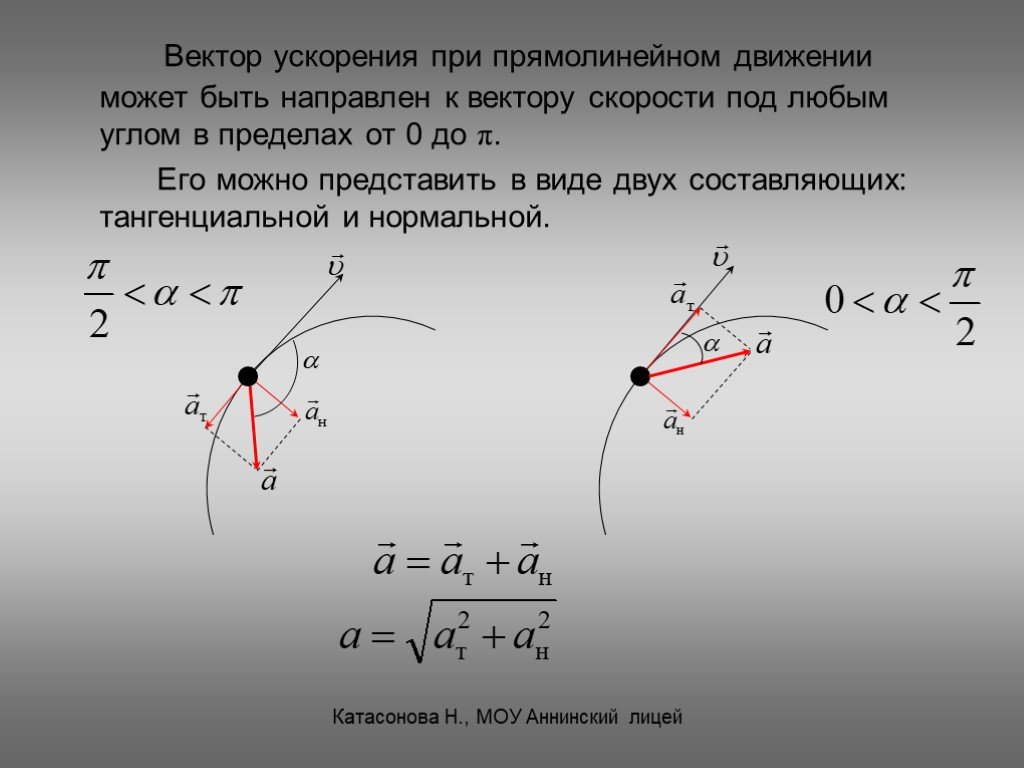
Вернуться на страницу Кинематика
Вернуться на домашнюю страницу Real World Physics Problems
сообщить об этом объявлении
4.4 Равномерное движение по окружности – University Physics Volume 1
4 Движение в двух и трех измерениях
Цели обучения
К концу этого раздела вы сможете:
- Найдите центростремительное ускорение объекта, движущегося по круговой траектории.
- Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.
- Объясните разницу между центростремительным ускорением и тангенциальным ускорением в результате неравномерного кругового движения.
- Оцените центростремительное и тангенциальное ускорения при неравномерном круговом движении и найдите вектор полного ускорения.
Равномерное круговое движение — это особый тип движения, при котором объект движется по окружности с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Центростремительное ускорение
В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости меняется, или [latex]d\mathbf{\overset{\to }{v}}\text{/}dt\ne 0.[/latex] Это показано на рисунке. Когда частица движется против часовой стрелки во времени [латекс]\Delta t[/латекс] по круговой траектории, ее вектор положения перемещается из [латекс]\mathbf{\overset{\to }{r}}(t)[/латекс] to [latex]\mathbf{\overset{\to }{r}}(t+\Delta t).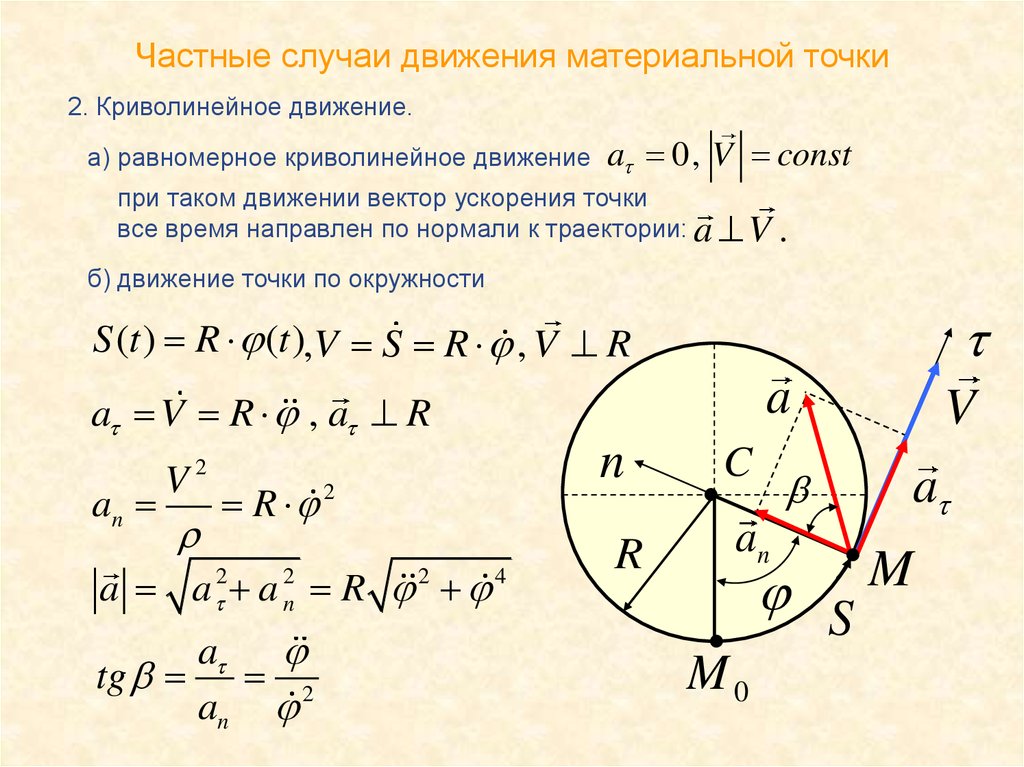 [/latex] Вектор скорости имеет постоянную величину и касается пути при изменении от [latex]\mathbf{ \overset{\to }{v}}(t)[/latex] to [latex]\mathbf{\overset{\to }{v}}(t+\Delta t),[/latex] меняет только свое направление. Поскольку вектор скорости [латекс]\mathbf{\overset{\to }{v}}(t)[/latex] перпендикулярен вектору положения [латекс]\mathbf{\overset{\to }{r}}( t), [/latex] треугольники, образованные векторами положения и [latex]\Delta \mathbf{\overset{\to }{r}},[/latex] и векторами скорости и [latex]\Delta \mathbf {\overset{\to}}{v}}[/latex] похожи. Кроме того, поскольку [латекс]|\mathbf{\overset{\to }{r}}(t)|=|\mathbf{\overset{\to }{r}}(t+\Delta t)|[/latex] и [латекс]|\mathbf{\overset{\to }{v}}(t)|=|\mathbf{\overset{\to }{v}}(t+\Delta t)|,[/latex] два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение
[/latex] Вектор скорости имеет постоянную величину и касается пути при изменении от [latex]\mathbf{ \overset{\to }{v}}(t)[/latex] to [latex]\mathbf{\overset{\to }{v}}(t+\Delta t),[/latex] меняет только свое направление. Поскольку вектор скорости [латекс]\mathbf{\overset{\to }{v}}(t)[/latex] перпендикулярен вектору положения [латекс]\mathbf{\overset{\to }{r}}( t), [/latex] треугольники, образованные векторами положения и [latex]\Delta \mathbf{\overset{\to }{r}},[/latex] и векторами скорости и [latex]\Delta \mathbf {\overset{\to}}{v}}[/latex] похожи. Кроме того, поскольку [латекс]|\mathbf{\overset{\to }{r}}(t)|=|\mathbf{\overset{\to }{r}}(t+\Delta t)|[/latex] и [латекс]|\mathbf{\overset{\to }{v}}(t)|=|\mathbf{\overset{\to }{v}}(t+\Delta t)|,[/latex] два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение
[латекс]\frac{\Delta v}{v}=\frac{\Delta r}{r}[/latex] или [латекс]\Delta v=\frac{v}{r}\Delta r. [/latex]
Рисунок 4.18 (a) Частица движется по окружности с постоянной скоростью, с векторами положения и скорости в моменты времени [latex]t[/latex] и [latex]t+\Delta t. [/ латекс] (б) Векторы скорости, образующие треугольник. Два треугольника на рисунке подобны. Вектор [латекс]\Delta \mathbf{\overset{\to }{v}}[/latex] указывает на центр окружности в пределе [latex]\Delta t\to 0.[/latex] 9{2}}{r}.[/latex]
[/ латекс] (б) Векторы скорости, образующие треугольник. Два треугольника на рисунке подобны. Вектор [латекс]\Delta \mathbf{\overset{\to }{v}}[/latex] указывает на центр окружности в пределе [latex]\Delta t\to 0.[/latex] 9{2}}{r}.[/latex]Направление ускорения также можно найти, заметив, что as [latex]\Delta t[/latex] и, следовательно, [latex]\Delta \theta[/latex] приближается к нулю, вектор [латекс]\Delta\mathbf{\overset{\to }{v}}[/latex] приближается к направлению, перпендикулярному [латексу]\mathbf{\overset{\to }{v}}.[ /latex] В пределе [латекс]\Delta t\to 0,[/latex] [латекс]\Delta \mathbf{\overset{\to }{v}}[/latex] перпендикулярно [латексу]\mathbf {\ overset {\ to {v}}. [/latex] Поскольку [latex] \ mathbf {\ overset {\ to {v}} [/latex] касается окружности, ускорение [латекс] d \ mathbf{\overset{\to}}{v}}\text{/}dt[/latex] указывает на центр круга. Подводя итог, частица, движущаяся по окружности с постоянной скоростью, имеет ускорение величиной 9{2}}{r}.[/latex]
Вектор ускорения направлен к центру окружности (рисунок).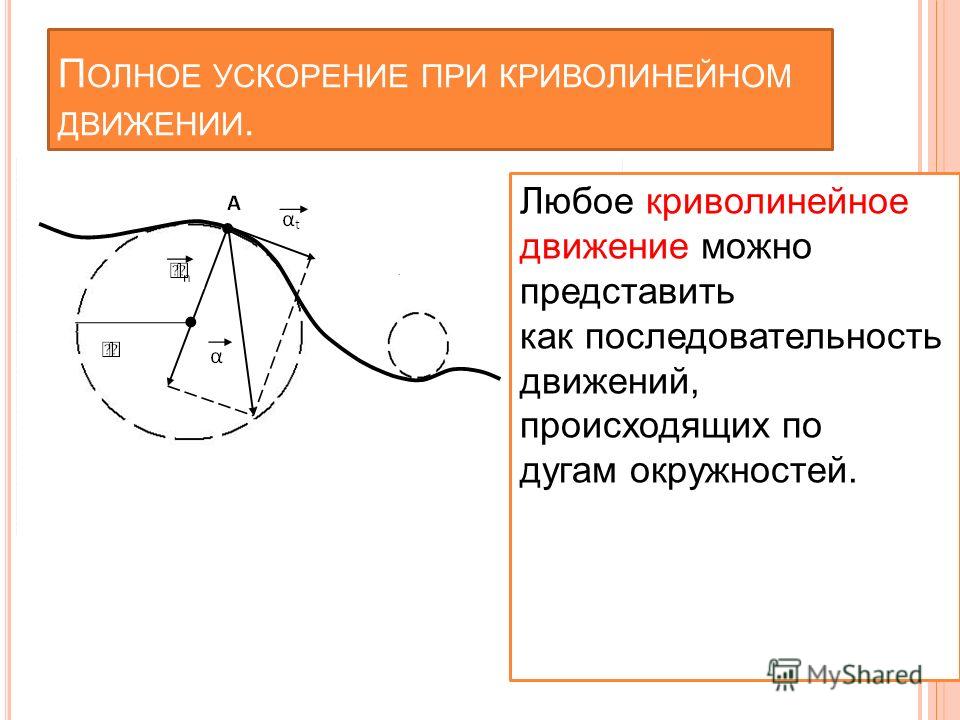 Это радиальное ускорение называется центростремительным ускорением , поэтому мы даем ему нижний индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает искать) и, таким образом, принимает значение «искание центра».
Это радиальное ускорение называется центростремительным ускорением , поэтому мы даем ему нижний индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает искать) и, таким образом, принимает значение «искание центра».
Давайте рассмотрим несколько примеров, иллюстрирующих относительные величины скорости, радиуса и центростремительного ускорения.
Пример
Создание ускорения 1
g Струя летит со скоростью 134,1 м/с по прямой линии и делает поворот по круговой траектории на уровне земли. Каким должен быть радиус окружности, чтобы пилот и реактивный самолет получили центростремительное ускорение 1 g по направлению к центру круговой траектории? 9{2}}=1835\,\text{м}=1,835\,\text{км}\text{. {2}?[/ латекс]
{2}?[/ латекс]
134,0 см/с
Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны кругового пути. Типичные центростремительные ускорения приведены в следующей таблице.
| Объект | Центростремительное ускорение (м/с 2 или коэффициенты g ) |
|---|---|
| Земля вокруг Солнца | [латекс]5. 9{22}[/латекс] 9{22}[/латекс] |
Уравнения движения для равномерного кругового движения
Частица, совершающая круговое движение, может быть описана ее вектором положения [латекс]\mathbf{\overset{\to }{r}}(t).[/latex] На рисунке показана частица совершая круговые движения против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол [латекс]\тета[/латекс] с осью x-. Вектор [латекс]\mathbf{\overset{\to }{r}}(t)[/латекс], образующий угол [латекс]\тета[/латекс] с 9Ось 0039 x показана с ее компонентами вдоль осей x и y . Величина вектора положения равна [латекс] A = |\ mathbf {\ overset {\ to }{r}} (t) | [/ латекс], а также радиусу окружности, так что с точки зрения его компонентов ,
[латекс] \ mathbf {\ overset {\ to {r}} (t) = A \, \ text {cos} \, \ omega t \ mathbf {\ hat {i}} + A \, \ text{sin}\,\omega t\mathbf{\hat{j}}.[/latex]
Здесь [latex]\omega[/latex] — константа, называемая угловой частотой частицы. Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду. Угол [латекс]\тета[/латекс], который имеет вектор положения в любой конкретный момент времени, равен [латекс]\омега t[/латекс].
Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду. Угол [латекс]\тета[/латекс], который имеет вектор положения в любой конкретный момент времени, равен [латекс]\омега t[/латекс].
Если T – это период движения или время, необходимое для совершения одного оборота ([латекс]2\пи[/латекс] рад), то
[латекс]\омега =\фрак{2\пи }{ T}.[/latex]
Рис. 4.20 Вектор положения частицы в круговом движении с компонентами вдоль осей x и y. Частица движется против часовой стрелки. Угол [латекс]\тета[/латекс] — это угловая частота [латекс]\омега[/латекс] в радианах в секунду, умноженная на t.Скорость и ускорение можно получить из функции положения дифференцированием:
[латекс] \ mathbf {\ overset {\ to {v}} (t) = \ frac {d \ mathbf {\ overset {\ to {r}} (t)} {dt} = \ text { −} A \ omega \, \ text {sin} \, \ omega t \ mathbf {\ hat {i}} + A \ omega \, \ text {cos} \, \ omega t \ mathbf {\ hat {j} }. {2} \, \ text{sin}\,\omega t\mathbf{\hat{j}}.[/latex] 9{-7}\text{s}=200\,\text{ns}\text{.}[/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
{2} \, \ text{sin}\,\omega t\mathbf{\hat{j}}.[/latex] 9{-7}\text{s}=200\,\text{ns}\text{.}[/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
Значение
Мы выбрали начальное положение частицы на оси x-. Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас была бы другая конечная позиция при t = 200 нс.
Неравномерное круговое движение
Круговое движение не обязательно должно быть с постоянной скоростью. Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а окружность имеет фиксированный радиус. Если меняется и скорость частицы, то вводим дополнительное ускорение в направлении, касательном к окружности. Такие ускорения возникают в точке на волчке, меняющем скорость вращения, или на каком-либо ускоряющемся роторе. В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
[латекс] {a} _ {\ text {T}} = \ frac {d | \ mathbf {\ overset {\ to }{ v}}|}{dt}.[/latex]
Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения направлено радиально внутрь к центру окружности. Таким образом, частица, движущаяся по окружности с тангенциальным ускорением, имеет полное ускорение , которое представляет собой векторную сумму центростремительного и тангенциального ускорений:
[латекс] \ mathbf {\ overset {\ to {a}} = {\ mathbf {\ overset {\ to {a}}} _ {\ text {C}} + {\ mathbf {\ overset { \to }{a}}}_{\text{T}}.[/latex]
Векторы ускорения показаны на рисунке. Обратите внимание, что два вектора ускорения {a}}}_{\text{T}}[/latex] перпендикулярны друг другу, при этом [latex]{\mathbf{\overset{\to}}{a}}}_{\text{C}} [/latex] в радиальном направлении и [latex]{\mathbf{\overset{\to }{a}}}_{\text{T}}[/latex] в тангенциальном направлении.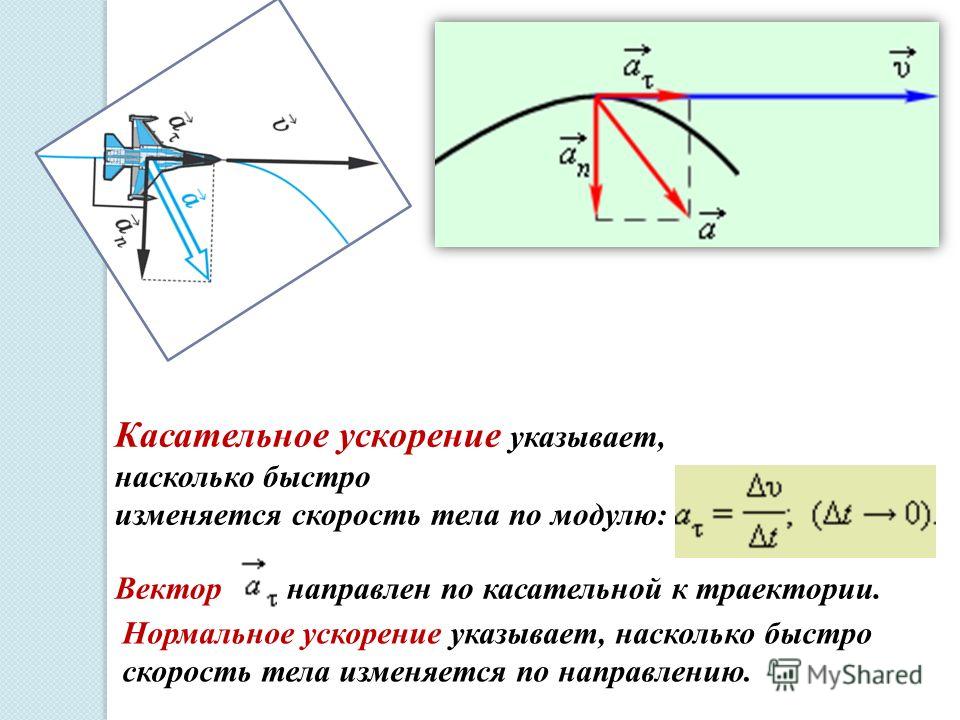 Полное ускорение [латекс]\mathbf{\overset{\to }{a}}[/latex] указывает на угол между [латекс]{\mathbf{\overset{\to }{a}}}_{\text {C}}[/latex] и [latex]{\mathbf{\overset{\to}}{a}}}_{\text{T}}.[/latex]
Полное ускорение [латекс]\mathbf{\overset{\to }{a}}[/latex] указывает на угол между [латекс]{\mathbf{\overset{\to }{a}}}_{\text {C}}[/latex] и [latex]{\mathbf{\overset{\to}}{a}}}_{\text{T}}.[/latex]
Пример
Полное ускорение при движении по окружности
Частица движется по окружности радиусом r = 2,0 м. За интервал времени от t = 1,5 с до 9{2}},\enspace{c}_{1}=4.0\,\text{m}\text{/}\text{s,}\enspace{c}_{2}=6.0\,\text{ m}\cdot \text{s}\text{.}[/latex]
Чему равно полное ускорение частицы при t = 2,0 с?
Стратегия
Нам известны скорость частицы и радиус окружности, поэтому мы можем легко рассчитать центростремительное ускорение. Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекс]|v(t)|[/латекс] с помощью рисунка и оценив ее в 9\circ[/latex] от касательной к окружности. См. рисунок.
Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекс]|v(t)|[/латекс] с помощью рисунка и оценив ее в 9\circ[/latex] от касательной к окружности. См. рисунок.
Значение
Направления центростремительных и тангенциальных ускорений удобнее описывать в полярной системе координат с единичными векторами в радиальном и тангенциальном направлениях. Эта система координат, используемая для движения по криволинейным траекториям, подробно обсуждается далее в книге. 9{2}\text{/}р.[/латекс]
 [/latex] величина скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.
[/latex] величина скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.Концептуальные вопросы
Может ли центростремительное ускорение изменить скорость частицы, совершающей круговое движение?
Может ли тангенциальное ускорение изменить скорость частицы, совершающей круговое движение?
Показать решениеда
Проблемы
Маховик вращается со скоростью 30 об/с.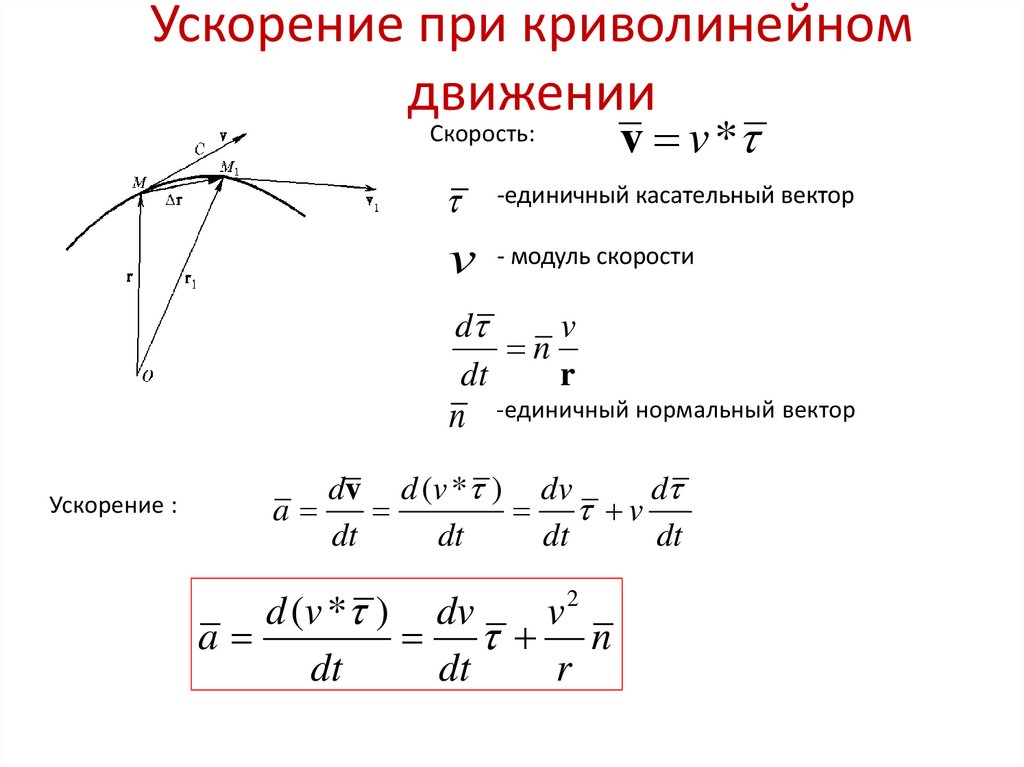 {2} [/latex]
{2} [/latex]
Кэм Ньютон из команды «Каролина Пантерз» делает идеальную футбольную спираль со скоростью 8,0 об/с. Радиус профессионального футбольного мяча составляет 8,5 см посередине короткой стороны. Чему равно центростремительное ускорение шнурков футбольного мяча?
Ярмарочный аттракцион вращает своих обитателей внутри контейнера в форме летающей тарелки. Если горизонтальный круговой путь, по которому следуют всадники, имеет радиус 8,00 м, при каком числе оборотов в минуту всадники испытывают центростремительное ускорение, равное силе тяжести? 9{2}=r\enspace{a}_{\text{C}}=78,4,\enspace v=8,85\,\text{m}\text{/}\text{s}[/latex]
[латекс]T=5,68\,\text{s,}[/latex], что составляет [латекс]0,176\,\text{rev}\text{/}\text{s}=10,6\,\text{rev }\текст{/}\текст{мин}[/латекс]
Бегун, участвующий в забеге на 200 м, должен обежать конец дорожки, имеющей дугу окружности с радиусом кривизны 30,0 м. Бегун начинает гонку с постоянной скоростью. Если она пробежит 200 м за 23,2 с и будет бежать с постоянной скоростью на протяжении всей гонки, каково будет ее центростремительное ускорение, когда она пробегает кривую часть трассы? 9{2}[/latex]
Экспериментальная реактивная ракета летит вокруг Земли вдоль ее экватора прямо над ее поверхностью.

 Радиусом-вектором
(r) называется направленный отрезок,
соединяющий начало координат и точку
с произвольными координатами. Положение
точки в пространстве в заданной системе
отсчета будет полностью определено,
если известен r (его положение относительно
осей координат и его размеры) (рис. 1).
Радиусом-вектором
(r) называется направленный отрезок,
соединяющий начало координат и точку
с произвольными координатами. Положение
точки в пространстве в заданной системе
отсчета будет полностью определено,
если известен r (его положение относительно
осей координат и его размеры) (рис. 1).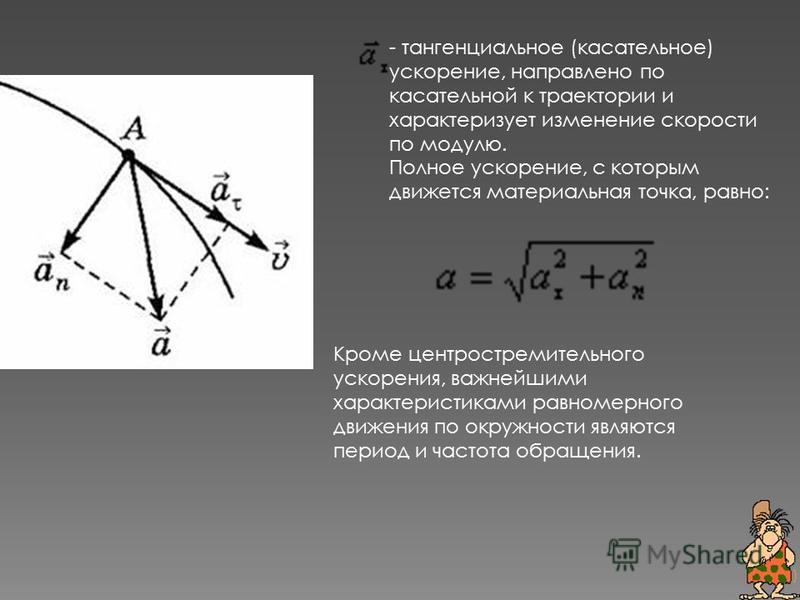
 Все правила по сольфеджио
Все правила по сольфеджио
 Составляющая , которая является касательной к траектории в точке М0,характеризует изменение скорости по величине за время Dt, в течение которого была пройдена дуга М0М и называется тангенциальной составляющей вектора изменения скорости ( ). Вектор , направленный в пределе, когда Dt ® 0, по радиусу к центру, характеризует изменение скорости по направлению и называется нормальной составляющей вектора изменения скорости ( ).
Составляющая , которая является касательной к траектории в точке М0,характеризует изменение скорости по величине за время Dt, в течение которого была пройдена дуга М0М и называется тангенциальной составляющей вектора изменения скорости ( ). Вектор , направленный в пределе, когда Dt ® 0, по радиусу к центру, характеризует изменение скорости по направлению и называется нормальной составляющей вектора изменения скорости ( ).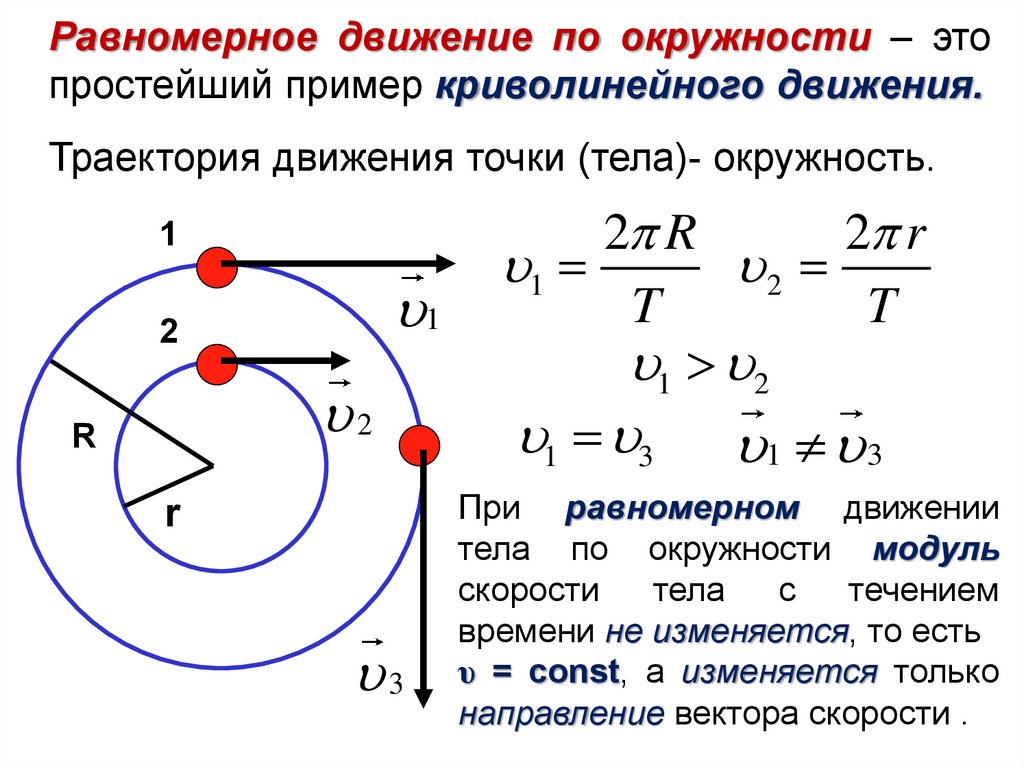

 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.005 с.) Его направление касается окружности.
Его направление касается окружности.