Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| Jkmrf |
| ||
17/11/13 |
| ||
| |||
| Izdesbyll |
| ||
22/01/12 Черновцы Украина |
| ||
| |||
| iifat |
| |||
16/02/13 |
| |||
| ||||
| nikvic |
| |||
06/04/10 |
| |||
| ||||
| DimaM |
| |||
28/12/12 |
| |||
| ||||
| Jkmrf |
| ||
17/11/13 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из | [ Сообщений: 6 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Физика для углубленного изучения 1.
 Механика Физика для углубленного изучения 1. Механика
Механика Физика для углубленного изучения 1. Механика
ОглавлениеПРЕДИСЛОВИЕI.  КИНЕМАТИКА КИНЕМАТИКА§ 1. Пространство. Время § 2. Механическое движение. Система отсчета § 3. Материальная точка. Поступательное движение § 4. Радиус-вектор. Перемещение § 5. Одновременные перемещения. Сложение перемещений § 6. Средняя скорость § 7. Скорость § 8. Ускорение § 9. Одномерное движение § 10. Неравномерное одномерное движение § 11. Движение по окружности § 12. Равнопеременное движение в пространстве § 13. Траектории § 14. Относительность механического движения II. ДИНАМИКА § 15. Инерция. Первый закон Ньютона § 16. Сила — мера взаимодействия § 17. Связь между силой и ускорением. Второй закон Ньютона § 18. Взаимодействие тел. Третий закон Ньютона § 19. Применение законов динамики § 20. Силы в природе. Трение § 21. Проявления сухого трения § 22. Силы тяготения § 23. Движение в поле тяготения § 24. Силы упругости и деформации § 25. Механическое состояние. Уравнение движения § 26. Принцип относительности Галилея § 27.  Системы единиц Системы единиц§ 28. Метод анализа размерностей III. ЗАКОНЫ СОХРАНЕНИЯ § 29. Импульс. Импульс силы § 30. Центр масс. Реактивное движение § 31. Механическая работа. Кинетическая энергия § 32. Потенциальная энергия § 33. Закон сохранения механической энергии § 34. Связь законов сохранения с симметрией пространства и времени § 35. Применение законов сохранения при решении задач § 36. Космическая динамика и законы сохранения § 37. Столкновения частиц § 38. Фазовая плоскость. Адиабатические инварианты § 39. Механическое равновесие § 40. Движение твердого тела IV. КОЛЕБАНИЯ И ВОЛНЫ § 41. Собственные колебания § 42. Затухающие колебания § 43. Собственные колебания в разных физических системах § 44. Вынужденные колебания. Резонанс § 45. Энергетические превращения при вынужденных колебаниях. Установление колебаний § 46. Волны § 47. Интерференция и дифракция волн. Эффект Доплера V. ДВИЖЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ § 49.  Движение идеальной жидкости Движение идеальной жидкости§ 50. Вязкая жидкость. Обтекание тел |
Вектор ускорения – Ключ физики
Скорость изменения вектора скорости называется вектором ускорения. При прямолинейном движении вы могли пренебречь векторной природой ускорения. Это не твоя вина, такое бывает! Это потому, что движение было прямолинейным, и отрицательное ускорение означает, что частица замедляется, а положительное ускорение означает, что частица ускоряется.
От вас даже не требовалось думать о векторном характере ускорения при прямолинейном движении. Вы можете просто вычесть скорости, чтобы найти ускорение. В двух- и трехмерном движении величины перемещения, скорости и ускорения не лежат на одной прямой, и здесь существенна их векторная природа. Но не забывайте о векторном характере этих величин даже при прямолинейном движении!
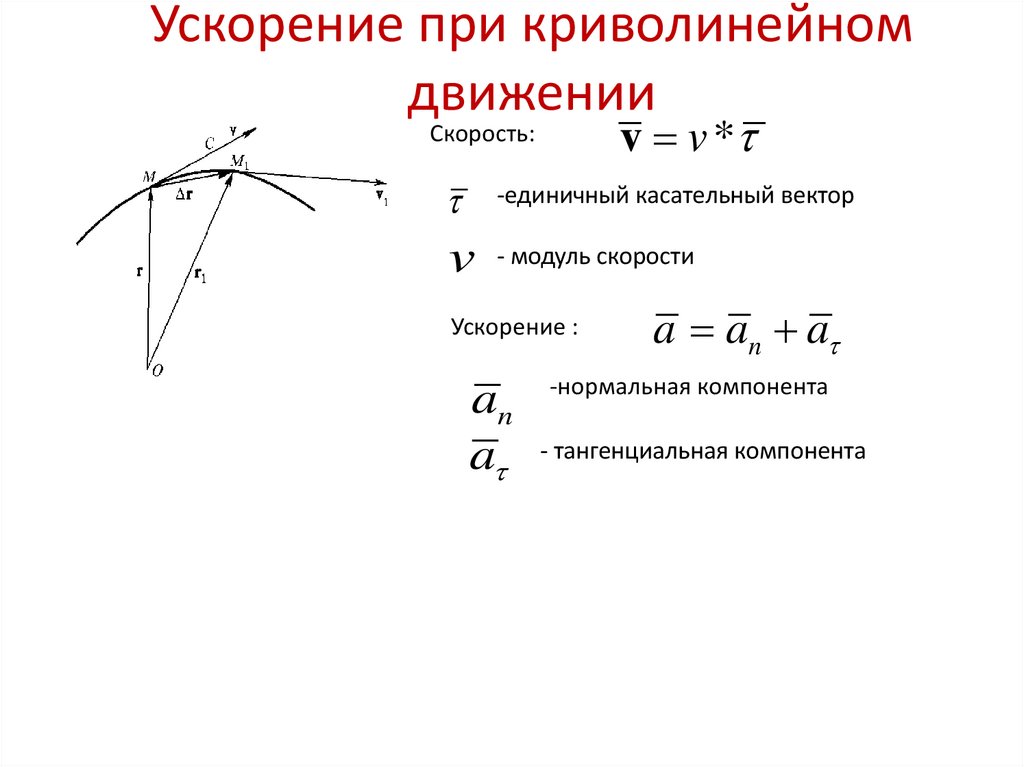
До сих пор вы должны были понимать, что ускорение является векторной величиной. Если вы мало знакомы с векторами и скалярами, вы можете сначала просмотреть эту статью о векторах и скалярах. Скорость также является векторной величиной, и если изменяется только направление скорости, а не ее величина, ускорение все равно сохраняется. Предположим, что частица движется по криволинейной траектории (см. рис. 8). Когда частица движется по криволинейной траектории, ее величина и направление могут изменяться. Величина скорости в любой точке есть скорость в этой точке.
Если вы мало знакомы с векторами и скалярами, вы можете сначала просмотреть эту статью о векторах и скалярах. Скорость также является векторной величиной, и если изменяется только направление скорости, а не ее величина, ускорение все равно сохраняется. Предположим, что частица движется по криволинейной траектории (см. рис. 8). Когда частица движется по криволинейной траектории, ее величина и направление могут изменяться. Величина скорости в любой точке есть скорость в этой точке.
Скорость на рисунке 8 в точке ${{p}_1}$ равна $\vec{v}_1$, а в точке ${{p}_2}$ равна $\vec{v}_2$. Изменение скорости равно $\vec {\Delta v} = {\vec v _2} + ( – {\vec v _1}) = {\vec v _2} – {\vec v _1}$. Если время в ${{p}_1}$ равно ${{t}_1}$, а в ${{p}_2}$ равно ${{t}_2}$, то интервал времени при движении по кривой между двумя точками $\Delta t = {t_2} – {t_1}$. Теперь средний вектор ускорения при движении между точками равен
\[{{\vec{a}}_{\text{av}}}=\frac{\Delta \vec v}{\Delta t} \tag{6} \label{6}\]
Когда временной интервал $\Delta t$ приближается к нулю, вектор среднего ускорения в уравнении \eqref{6} становится вектором мгновенного ускорения . Обратите внимание, что мы называем вектор мгновенного ускорения просто вектором ускорения.
Обратите внимание, что мы называем вектор мгновенного ускорения просто вектором ускорения.
\[{{\vec{a}}_{\text{ins}}}=\vec{a}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{ \Delta \vec v}{\Delta t}=\frac{d\vec{v}}{dt}\]
Вы знаете, что направление вектора среднего ускорения совпадает с направлением $\Delta \vec v$. На рисунке 1 обратите внимание, что направление вектора среднего ускорения направлено (как показано направлением $\Delta \vec v$) внутрь криволинейного пути.
Если частица ускоряется при прямолинейном движении, то ускорение положительно, то есть ускорение имеет то же направление, что и скорость, а если замедляется, то ускорение отрицательно и имеет направление, противоположное направлению скорости.
Обычно в повседневных жизненных ситуациях мы понимаем «ускорение» как «ускорение», но в физике это не так. Если транспортное средство замедляется, ускорение сохраняется, и «ускорение» может также означать «замедление», а не только «ускорение». Это означает, что это слово относится к любой ситуации, когда есть ускорение.
Это означает, что это слово относится к любой ситуации, когда есть ускорение.
Когда частица движется по кривой, частица всегда имеет ускорение, даже если ее скорость постоянна. Это потому, что направление скорости постоянно меняется. Изменение величины, направления или того и другого вместе со скоростью означает наличие ускорения. На рисунке 1 скорость частицы постоянна, поэтому меняется только направление частицы, а ускорение по-прежнему направлено внутрь кривой.
Рис. 4. Частица движется с постоянной скоростью по кривой. Возможно, вы испытывали ускорение как по прямой, так и по криволинейной траектории. Если автобус, на котором вы едете, ускоряется, вы двигаетесь назад, а если замедляется, вы двигаетесь вперед. Если он идет по кривой дороге, вы двигаетесь к внешней стороне кривой (однако на вас не действует никакая сила, даже если вы чувствуете, что вас толкают или тянут . Для получения более подробной информации вы можете обратиться к первому закону Ньютона. движения и инерциальной системы отсчета).
движения и инерциальной системы отсчета).
Любая частица, движущаяся по кривой или круговой траектории, всегда имеет ускорение по направлению к внутренней части кривой или окружности, даже если она движется с постоянной скоростью.
Вектор ускорения может быть выражен через его компоненты x, y и z в трехмерной системе координат, то есть
\[\vec a = a_\text{x}\hat i + a_\text{y}\hat j + a_\text{z}\hat k\]
и $a_x = {dv_x}/{dt}$, $a_y = {dv_y}/{dt}$ и $a_z = {dv_z}/{dx}$. Скорость изменения скорости — это ускорение, поэтому составляющая ускорения — это скорость изменения соответствующей составляющей скорости.
Вы уже представляли вектор ускорения в виде компонент в виде компонентов x, y и z в трехмерной системе координат, но на этот раз мы используем другой способ представления компонентов вектора ускорения, а именно параллельные и перпендикулярные компоненты. Часто оказывается, что это простой и полезный способ представления компонентов вектора ускорения.
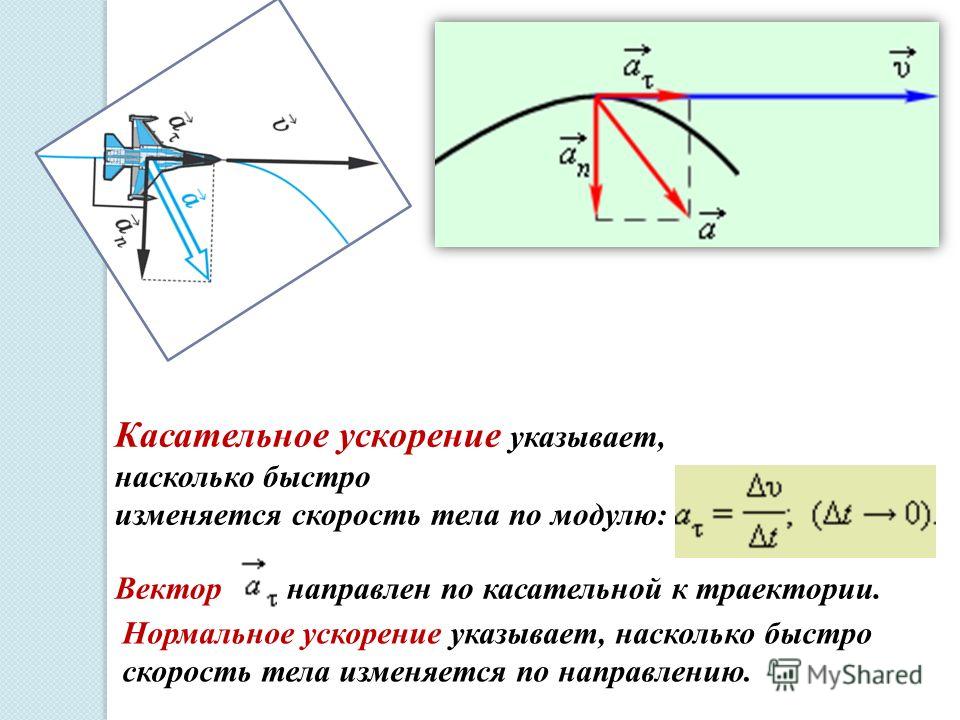
Параллельная составляющая вектора ускорения — это составляющая, параллельная вектору скорости, а перпендикулярная составляющая — составляющая, перпендикулярная вектору скорости. Если частица, движущаяся по круговой траектории, либо ускоряется, либо замедляется, частица имеет обе составляющие ускорения (см. рис. 2 и рис. 3). Если частица движется с постоянной скоростью по окружности или кривой, то она имеет только перпендикулярную составляющую вектора ускорения (направление вектора скорости непрерывно меняется) и не имеет параллельной составляющей (см. рис. 4).
Рис. 4. Частица движется с постоянной скоростью по кривой; вектор ускорения совпадает с нормальным. Из приведенных выше рисунков легко понять, что если частица ускоряется по кривой, то вектор ускорения опережает нормаль, а если замедляется, то вектор ускорения отстает от нормали. Но если частица движется с постоянной скоростью, то она имеет только перпендикулярную составляющую вектора ускорения, а вектор ускорения совпадает с нормалью. Обратите внимание, что вектор ускорения частицы, движущейся по кривой или окружности, всегда указывает внутрь кривой.
Но если частица движется с постоянной скоростью, то она имеет только перпендикулярную составляющую вектора ускорения, а вектор ускорения совпадает с нормалью. Обратите внимание, что вектор ускорения частицы, движущейся по кривой или окружности, всегда указывает внутрь кривой.
Была ли эта статья полезной?
домашнее задание и упражнения – Вектор ускорения простого маятника
спросил
Изменено 6 лет, 4 месяца назад
Просмотрено 15 тысяч раз
$\begingroup$
На этом рисунке вектор ускорения $\vec{a}$ указывает вверх, когда маятник находится на полпути
Нажмите, чтобы увидеть анимированный GIF
Но согласно этому рисунку сила действует по касательной: тоже должен быть тангенциальным и никогда не указывать вверх?
Так что правильно?
- домашние задания и упражнения
- ньютоновская механика
- силы
- ускорение
$\endgroup$
1
$\begingroup$
Диаграмма вводит в заблуждение.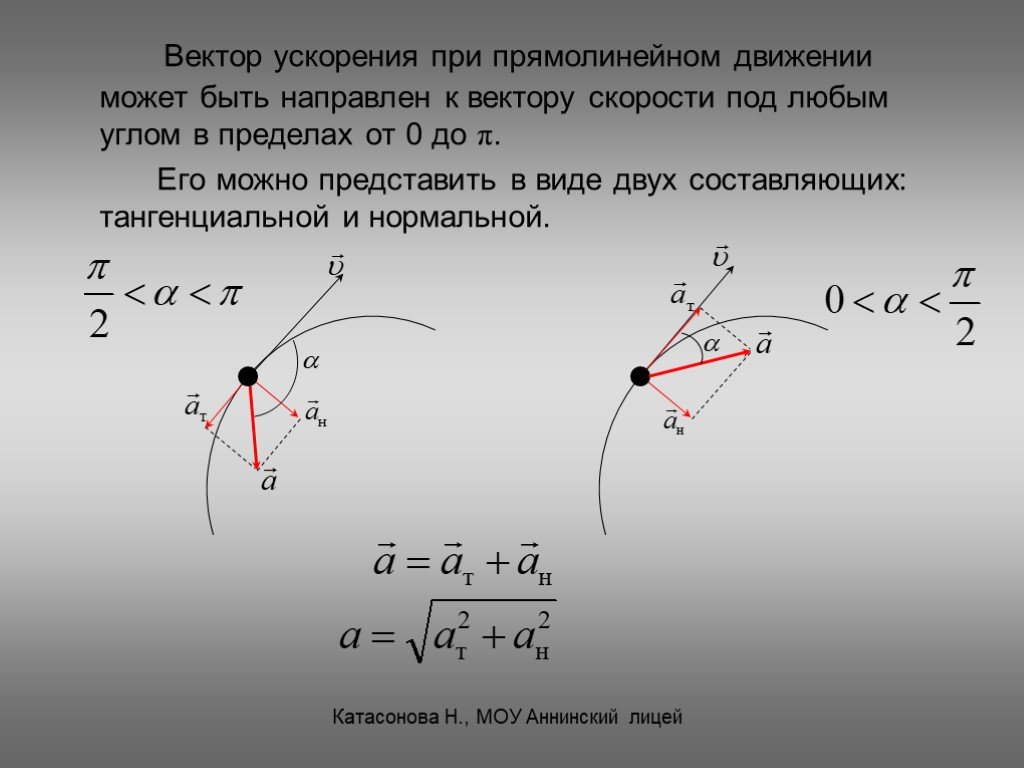 Посмотрите на это:
Посмотрите на это:
В любой момент времени на частицу действуют следующие силы:
- Гравитация
- Натяжение струны
Когда вы находитесь в нижней части пути, натяжение нити равно натяжению, необходимому для противодействия гравитации, ПЛЮС натяжение, необходимое для удержания массы на своем пути (другими словами, чтобы сохранить постоянную длину струны) . Суммарный эффект этих двух сил представляет собой силу, направленную точно вверх, а поскольку $a=F/m$, это означает, что в этот момент масса ускоряется вверх.
$\endgroup$
$\begingroup$
Обратите внимание, что на рисунке действуют две силы: 1) вес, мг, который действует вертикально вниз и не изменяется, и 2) натяжение струны, Z, которое направлено от массы к точка, в которой струна соединяется с потолком, при условии, что струна остается натянутой. Z периодически меняется со временем.
Эти две силы объединяются, чтобы дать результирующую силу, и это результирующая сила, которая действует в том же направлении, что и ускорение, как показано на рисунке.
Зеленые стрелки на картинке на самом деле просто тангенциальная и нормальная составляющие гравитации.
Редактировать: кроме того, я считаю, что источник путаницы мог заключаться в предположении, что нормальная составляющая гравитации уравновешивается с натяжением. Это не так: нельзя пользоваться уравнениями равновесия, если система не находится в равновесии, т.е. ускоряется.
$\endgroup$
5
$\begingroup$
Верно: Но полное решение этой проблемы
1) Используйте ОДУ
, что даст Theta(t)= Theta0*cos(w*t) w=Sqrt(g/L):
Из ОДУ: d2( Theta)/dt2+(g/L) *(Theat)=0: Однородный отклик, начальные условия дают Theta(t) выше
2) Примените динамические уравнения в 2-мерной полярности: эти УСКОРЕНИЯ [относительно вращающейся СИСТЕМЫ КООРДИНАТ] равны :
Помните, что “w” взято из решения ОДУ и является функцией времени: w(t)=d(Theta(t))/dt
Радиально= (dL2/d2t)-(wsquared)*L: Радиальное ускорение/Центростремительное ускорение
Тангенциально=[d2(Theta)/dt2] L+2 (Theta/dt)*L: Тангенциальное ускорение/Кориолис Ускорение.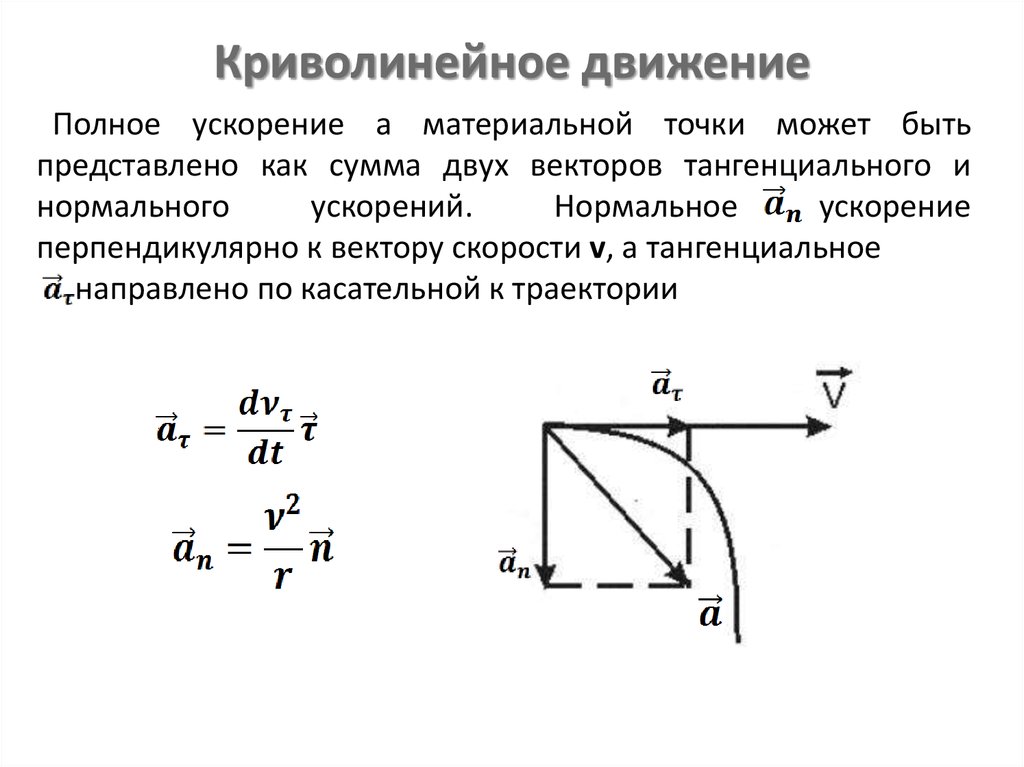


 11.2013, 15:07
11.2013, 15:07  11.2013, 15:35
11.2013, 15:35  11.2013, 16:38
11.2013, 16:38  11.2013, 19:14
11.2013, 19:14